В этой статье посмотрим, как определяются координаты центра тяжести сложной фигуры — состоящей из простых. В задачах по сопромату часто приходится находить положение центра тяжести составных сечений, для дальнейшего вычисления моментов инерции и т. д.
Также часто, при изучении теоретической механики, студентам предлагается решить подобную задачу, и найти центр тяжести какой-нибудь фигуры.
Условие задачи
Предлагаю рассмотреть следующую фигуру:

В сопромате принято заштриховывать сечения тонкими линиями, вот так:

В своих же уроках я буду использовать заливку. Так, штриховка не будет мешать наносить обозначения.
Разбивка сложной фигуры на простые
Как видишь, сечение состоит из прямоугольника, прямоугольного треугольника, четверти круга, а также имеет круглый вырез:

Отметим центры тяжести (С1, С2, С3, С4) каждой отдельной фигуры, с учётом справочной информации.
Открой эту страничку, и пока не закрывай, она нам ещё понадобится!

Покажем вспомогательные оси (x0, y0) для всего сечения, которые будем использовать для нахождения положения центра тяжести (C):

Как определить положение центра тяжести?
Чтобы определить координату центра тяжести сечения, например, вертикальное расстояние от оси x0 до центра тяжести сечения (yc):

Нужно статический момент сечения относительно этой вспомогательной оси (x0) разделить на площадь всего сечения (A):

Площадь всего сечения (A) найти просто – это алгебраическая сумма площадей всех фигур:

Статический момент сечения, относительно вспомогательной оси будет равен алгебраической сумме статических моментов каждой фигуры (с учётом знака):

где Ai – площадь отдельной фигуры;
yi – расстояние от центра тяжести отдельной фигуры до вспомогательной оси (x0).
Координата центра тяжести (xc), находится аналогично:

Определение площади сечения
Для начала предлагаю сделать самое простое, используя формулы, указанные на этой странице, найти площадь всего сечения (A):


Как видишь, круглый вырез, нужно учесть с «минусом», что очевидно.
Определение расстояний от вспомогательных осей до центров тяжести отдельных фигур
Найдём расстояния от вспомогательных осей (x0, y0) до центров тяжести отдельных фигур, опять же, используя нашу шпаргалку:

Определение статических моментов
Определяем статические моменты сечения относительно вспомогательных осей (x0, y0):


Важно! Статические моменты могут быть и отрицательными.
Определение координат центра тяжести
И, наконец, определяем положение центра тяжести всего сечения (C):

Покажем центр тяжести всего сечения (C):

Если остались какие-то вопросы по данному уроку, можешь смело задавать их в комментариях. Также, другие уроки, на сайте – ssopromat.ru, по определению геометрических характеристик, можешь найти здесь.
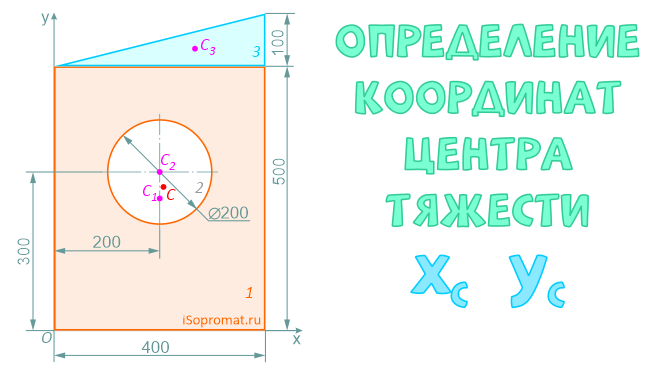

Определение координат центра тяжести xC и yC плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.
Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.
Способы определения координат центра тяжести
Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.
Существует 5 способов расчета координат положения центра тяжести:
- Аналитический (путем интегрирования).
- Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
- Экспериментальный. (метод подвешивания тела).
Этот способ подходит в основном для плоских и линейных тел. - Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.
Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A1 и A2 (A = A1+ A2).
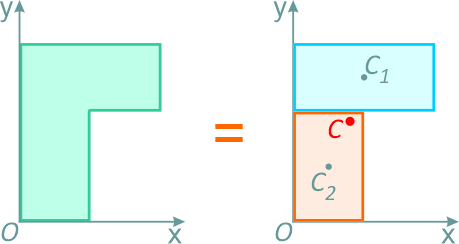
Рисунок 1.8
Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны:
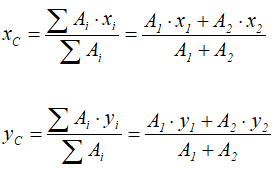
- Дополнение (Метод отрицательных площадей или объемов).
Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
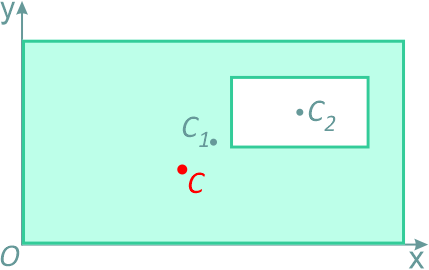
Рисунок 1.9
Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
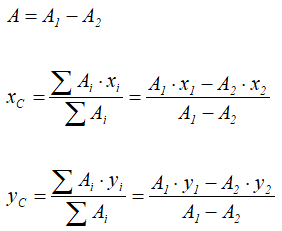
При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).
Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:
Другие видео
Пример определения координат центра тяжести плоской фигуры
Задача
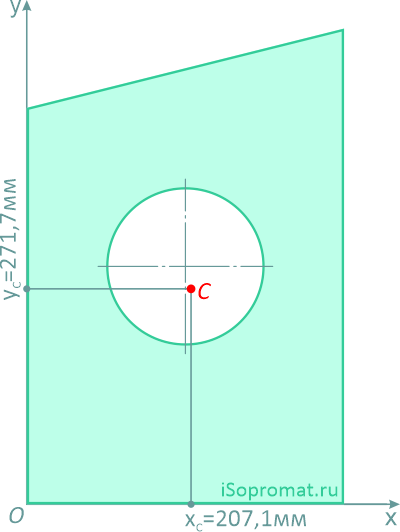
Определить координаты центра тяжести плоской фигуры с круглым отверстием
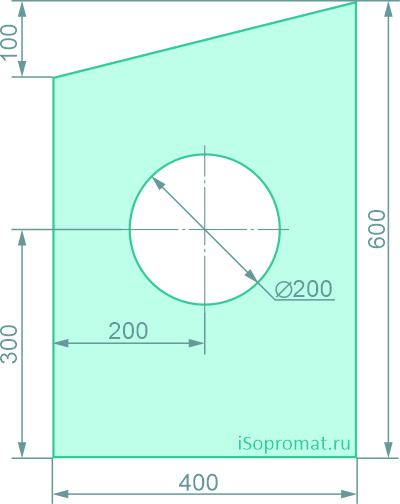
Решение
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.
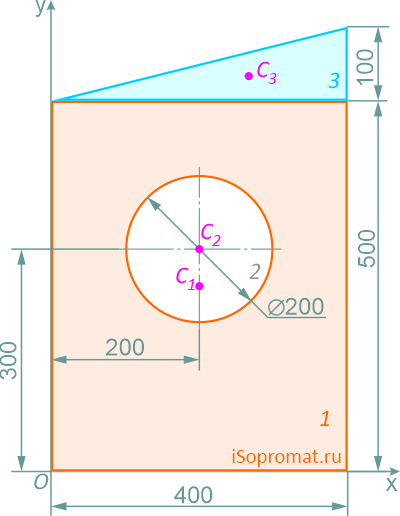
Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести Ci отдельных фигур:
Прямоугольник (фигура 1)
Площадь
A1=400×500=200000 мм2
Положение центра тяжести
x1=200мм
y1=250мм
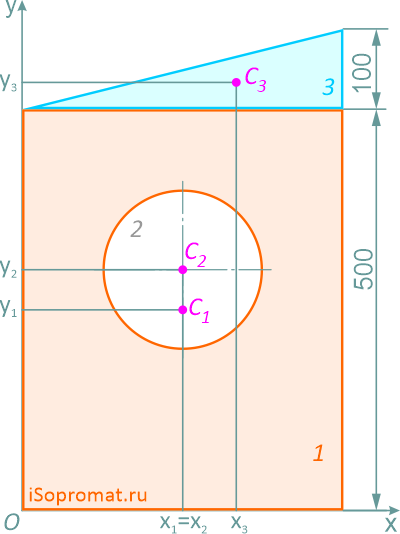
Круг (2) (вычитаемая фигура)
Площадь
A2=π×2002/4=31416 мм2
Центр тяжести
x2=200мм
y2=300мм
Прямоугольный треугольник (3)
Площадь
A3=400*100/2=20000 мм2
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x3=400×2/3=266,7мм
y3=500+100×1/3=533,3мм
Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:
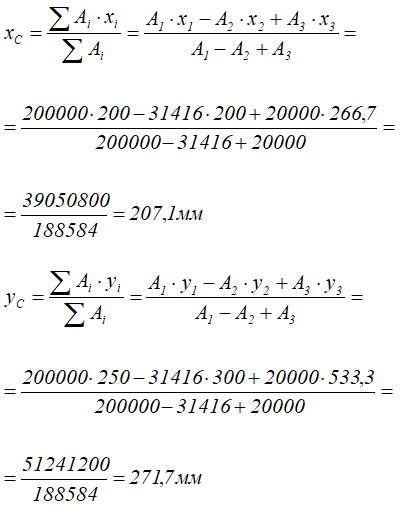
Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами xC=207,1мм, yC=271,7мм.
Другие примеры решения задач >
Центры тяжести простейших фигур >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Координаты центра тяжести поперечного сечения стержня
Из формул  следует, что статический момент инерции относительно оси, проходящей через центр тяжести (центральной оси) равен нулю.
следует, что статический момент инерции относительно оси, проходящей через центр тяжести (центральной оси) равен нулю.
Сопоставляя формулы 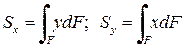 и
и  , получим формулы центра тяжести поперечного сечения стержня:
, получим формулы центра тяжести поперечного сечения стержня:

Если площадь фигуры можно разбить на n простых частей, для которых известны или легко находятся площадь 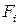 и положение центра тяжести
и положение центра тяжести 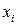 и
и 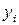 , получим формулы координат центра тяжести:
, получим формулы координат центра тяжести:

Содержание:
Центр тяжести:
При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести.
Определения и формулы для вычисления центров тяжести
Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом 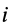
Радиус-вектор центра тяжести тела 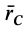 вычисляем как радиус-вектор центра параллельных сил (рис. 88) по формуле
вычисляем как радиус-вектор центра параллельных сил (рис. 88) по формуле
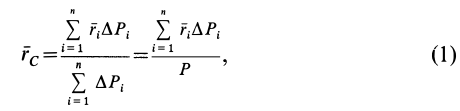
где 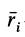 — радиус-вектор точки приложения силы тяжести элементарной части тела, принятой за точку;
— радиус-вектор точки приложения силы тяжести элементарной части тела, принятой за точку;  — сила тяжести элементарной частицы;
— сила тяжести элементарной частицы; 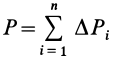 — сила тяжести всего тела;
— сила тяжести всего тела;  — число частей, на которое мысленно разбито все тело. Центр тяжести является точкой приложения равнодействующей силы тяжести, если силы тяжести отдельных его частей считать системой параллельных сил.
— число частей, на которое мысленно разбито все тело. Центр тяжести является точкой приложения равнодействующей силы тяжести, если силы тяжести отдельных его частей считать системой параллельных сил.
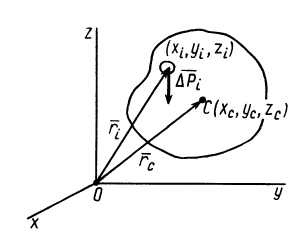
Рис. 88
Если в (1) перейти к пределу, увеличивая число элементарных частей  до бесконечности, то после замены
до бесконечности, то после замены  дифференциалом
дифференциалом 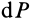 , а суммы — интегралом получим
, а суммы — интегралом получим

где 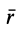 — радиус-вектор элементарной части тела, принятой за точку. В проекциях на оси координат из (1) и (1′) получаем:
— радиус-вектор элементарной части тела, принятой за точку. В проекциях на оси координат из (1) и (1′) получаем:

где 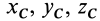 — координаты центра тяжести;
— координаты центра тяжести; 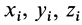 — координаты точки приложения силы тяжести
— координаты точки приложения силы тяжести 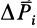 .
.
Используя понятие центра тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела и всего тела можно выразить через их массы 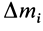 и
и 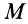 и ускорение силы тяжести
и ускорение силы тяжести  с помощью формул
с помощью формул
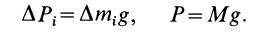
Подставляя эти значения сил тяжести в (1) и (1′) после сокращения на  , которое принимаем одинаковым для всех частей тела, имеем
, которое принимаем одинаковым для всех частей тела, имеем

и соответственно

По формулам (2) и (2′) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор, которой вычисляется по формулам (2) или (2′). В проекциях на оси координат из (2) и (2′) получаем:
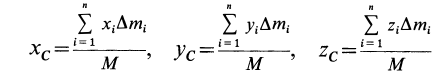
и
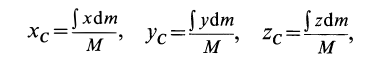
где 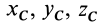 — координаты центра масс тела.
— координаты центра масс тела.
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам

где 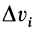 — объем элементарной частицы тела;
— объем элементарной частицы тела;  и
и  — соответственно удельный вес и плотность тела. Сила тяжести и масса всего тела
— соответственно удельный вес и плотность тела. Сила тяжести и масса всего тела

где 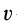 — объем тела. Подставляя эти значения в (2) и (2′), после сокращения на
— объем тела. Подставляя эти значения в (2) и (2′), после сокращения на  и
и  соответственно получим формулы
соответственно получим формулы
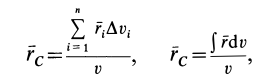
по которым определяют центр тяжести объема тела.
Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем
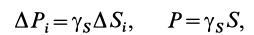
где 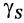 — удельный вес;
— удельный вес; 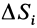 — площадь элементарной частицы поверхности;
— площадь элементарной частицы поверхности; 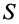 — площадь всей поверхности. После сокращения на
— площадь всей поверхности. После сокращения на 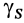 для однородной поверхности получим следующие формулы для определения центра тяжести ее площади:
для однородной поверхности получим следующие формулы для определения центра тяжести ее площади:
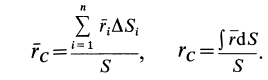
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
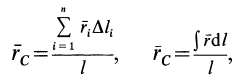
где 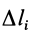 — длина элемента линии;
— длина элемента линии; 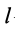 —общая длина линии, центр тяжести которой определяется.
—общая длина линии, центр тяжести которой определяется.
Методы определения центров тяжести (Центров масс)
Метод симметрии
При определении центров тяжести широко используется симметрия тел. Докажем, что для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для доказательства выберем начало координат в плоскости симметрии тела и одну из осей координат, ось 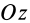 направим перпендикулярно плоскости симметрии, а две других оси расположатся в плоскости симметрии (рис. 89). Каждая частица массой
направим перпендикулярно плоскости симметрии, а две других оси расположатся в плоскости симметрии (рис. 89). Каждая частица массой 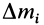 , находясь по одну сторону плоскости симметрии, имеет симметричную частицу такой же массы по другую сторону этой плоскости. Координаты
, находясь по одну сторону плоскости симметрии, имеет симметричную частицу такой же массы по другую сторону этой плоскости. Координаты 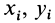 у симметричных частиц одинаковы при сделанном выборе осей координат, а координаты по оси
у симметричных частиц одинаковы при сделанном выборе осей координат, а координаты по оси 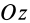 отличаются только знаком. Для координаты центра масс
отличаются только знаком. Для координаты центра масс 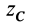 имеем следующее выражение:
имеем следующее выражение:
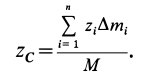
Разбивая сумму в числителе на две по симметричным частям тела, получаем, что
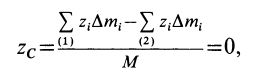
так как симметричные части тела 1 и 2 одинаковы.
Таким образом, центр масс расположен в плоскости симметрии и для его определения достаточно вычислить только две его координаты 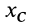 и
и 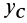 в этой плоскости.
в этой плоскости.
Аналогично доказывается, что для однородного тела, имеющего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.
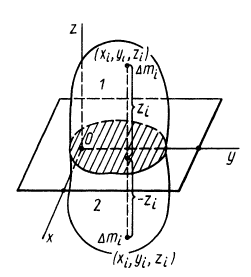
Рис. 89
Метод разбиения на части (метод группировки)
Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 90. Плоскую фигуру можно разбить на три части, центры тяжести которых 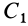 ,
, 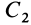 и
и 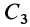 известны. Они находятся на пересечении диагоналей прямоугольников. Их радиусы-векторы обозначим
известны. Они находятся на пересечении диагоналей прямоугольников. Их радиусы-векторы обозначим 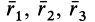 и площади
и площади 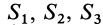 . Общая площадь сложной фигуры будет
. Общая площадь сложной фигуры будет 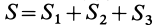 .
.
Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим
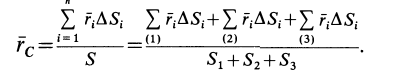
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:
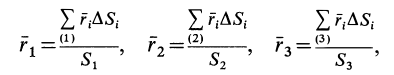
или
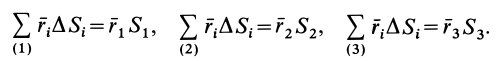
Используя эти формулы для радиуса-вектора всей фигуры, имеем
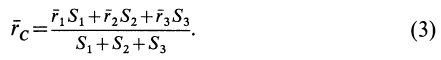
Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.
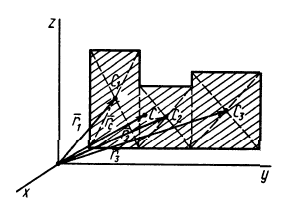
Рис. 90
Метод отрицательных масс
Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 91). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 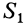 и центром масс
и центром масс 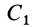 полностью заполнен массой (имеет положительную площадь). На той части фигуры, которую добавили, следует распределить отрицательную массу (отрицательную площадь) той же плотности. Площадь этой фигуры с отрицательной массой обозначим
полностью заполнен массой (имеет положительную площадь). На той части фигуры, которую добавили, следует распределить отрицательную массу (отрицательную площадь) той же плотности. Площадь этой фигуры с отрицательной массой обозначим 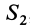 , а ее центр масс —
, а ее центр масс — 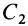 . Применяя метод разбиения на части, радиус-вектор заданной фигуры определим по формуле
. Применяя метод разбиения на части, радиус-вектор заданной фигуры определим по формуле

В отличие от обычного метода разбиения на части в формуле (4) массы и, следовательно, площади входят со знаком минус.
Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
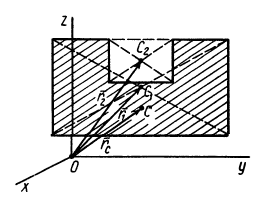
Рис. 91
Центры тяжести простейших тел
Для определения центров тяжести тел сложной формы методом разбиения на части или методом отрицательных масс необходимо уметь вычислять центры тяжести простейших тел, на которые разбивается тело сложной формы. Рассмотрим некоторые из тел, для определения центров тяжести которых известны простые способы их нахождения или вычисления по формулам.
Прямолинейный отрезок
Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного— на самом отрезке и не может находиться вне отрезка.
Площадь треугольника
Для определения центра тяжести площади треугольника разобьем его прямыми линиями, параллельными одной из его сторон 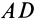 , на полоски, которые в пределе можно принять за прямолинейные отрезки (рис. 92). Центры тяжести отрезков и, следовательно, полосок находятся посередине полоски. Все они расположатся на медиане
, на полоски, которые в пределе можно принять за прямолинейные отрезки (рис. 92). Центры тяжести отрезков и, следовательно, полосок находятся посередине полоски. Все они расположатся на медиане  . В пределе центры тяжести полосок непрерывно покроют медиану, но не равномерно, так как площади полосок разные. В каждом центре масс полоски следует считать сосредоточенной массу или площадь этой полоски, пропорциональную длине полоски, если ширину полосок выбирать одинаковой.
. В пределе центры тяжести полосок непрерывно покроют медиану, но не равномерно, так как площади полосок разные. В каждом центре масс полоски следует считать сосредоточенной массу или площадь этой полоски, пропорциональную длине полоски, если ширину полосок выбирать одинаковой.
Затем разобьем треугольник на полоски прямыми линиями, параллельными другой стороне  треугольника. Центры их тяжести в пределе покроют неравномерно медиану
треугольника. Центры их тяжести в пределе покроют неравномерно медиану 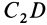 . Центры тяжести неоднородных прямолинейных отрезков
. Центры тяжести неоднородных прямолинейных отрезков  и
и 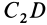 должны располагаться на этих отрезках, а следовательно, в точке их пересечения
должны располагаться на этих отрезках, а следовательно, в точке их пересечения 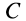 , являющейся точкой пересечения медиан треугольника. Эта точка делит медианы в отношении 1 к 2, т. е. если длина медианы
, являющейся точкой пересечения медиан треугольника. Эта точка делит медианы в отношении 1 к 2, т. е. если длина медианы  равна
равна 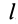 , то
, то 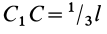 ,
, 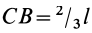 .
.
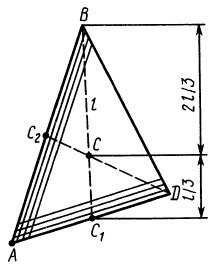
Рис. 92
Дуга окружности
Дуга окружности  определяется радиусом
определяется радиусом 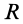 и стягиваемым ею центральным углом
и стягиваемым ею центральным углом 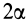 (рис. 93). Она имеет ось симметрии, делящую угол пополам. Центр тяжести находится на оси симметрии дуги, которую примем за ось координат
(рис. 93). Она имеет ось симметрии, делящую угол пополам. Центр тяжести находится на оси симметрии дуги, которую примем за ось координат 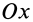 . Координату центра тяжести дуги
. Координату центра тяжести дуги  вычисляем по формуле
вычисляем по формуле
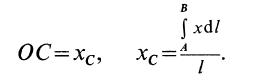
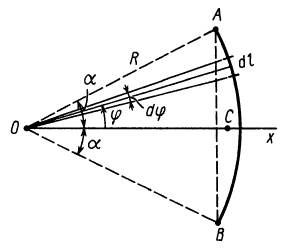
Рис. 93
В рассматриваемом случае
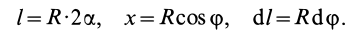
Подставляя эти значения в формулу для 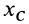 , получим
, получим
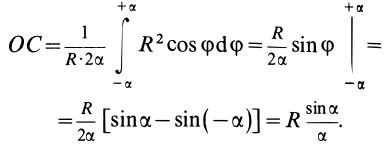
Таким образом,

Для полуокружности 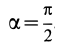 . Приняв
. Приняв 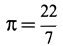 , получим:
, получим:
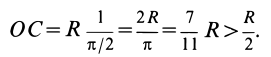
Площадь кругового сектора
Центр тяжести площади кругового сектора с радиусом 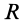 и центральным углом
и центральным углом 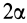 находится на оси симметрии, принимаемой за ось
находится на оси симметрии, принимаемой за ось 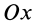 (рис. 94). Разобьем сектор на элементарные треугольники одинаковой величины. Центры тяжести треугольников в пределе при увеличении их числа до бесконечности равномерно покроют дугу окружности радиусом
(рис. 94). Разобьем сектор на элементарные треугольники одинаковой величины. Центры тяжести треугольников в пределе при увеличении их числа до бесконечности равномерно покроют дугу окружности радиусом 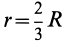 .
.
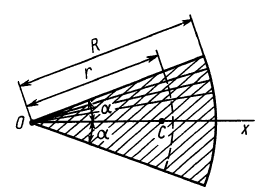
Рис. 94
Используя формулу для центра тяжести дуги окружности, получим
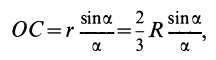
или

Для площади полукруга 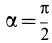 ,
, 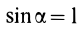 . При
. При 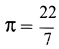 получим
получим
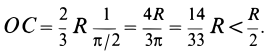
Объем пирамиды и конуса
Определим положение центра тяжести объема конуса (рис. 95). Для простоты рассмотрим прямой конус, у которого высота является осью симметрии. Высотой конуса является отрезок, соединяющий его вершину 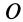 с центром тяжести площади основания
с центром тяжести площади основания 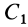 . Выберем начало координат в вершине конуса, а ось
. Выберем начало координат в вершине конуса, а ось 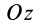 направим по оси симметрии конуса. Тогда центр тяжести объема конуса расположится на оси
направим по оси симметрии конуса. Тогда центр тяжести объема конуса расположится на оси 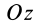 .
.
Разобьем конус плоскостями, перпендикулярными оси 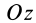 , на элементарные тонкие диски толщиной
, на элементарные тонкие диски толщиной 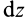 и площадью
и площадью 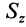 . Все полученные сечения (диски) конуса подобны его основанию. Координату
. Все полученные сечения (диски) конуса подобны его основанию. Координату 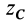 центра тяжести объема конуса вычислим по формуле
центра тяжести объема конуса вычислим по формуле
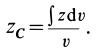
Отношения линейных размеров сечений к соответствующим размерам основания конуса пропорциональны их расстояниям до вершины конуса. Отношения площадей пропорциональны квадратам расстояний. Приняв 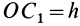 , получим
, получим
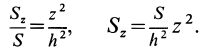
Учитывая, что
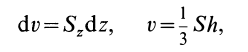
имеем
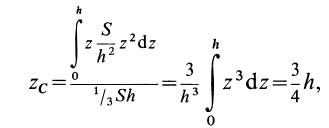
или

Таким образом, центр тяжести прямого конуса находится на расстоянии 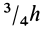 от вершины или
от вершины или 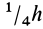 от основания.
от основания.
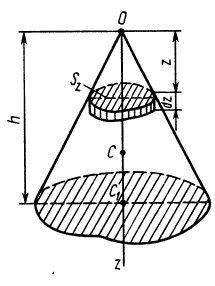
Рис. 95
Это справедливо для объема любого конуса и любой пирамиды, как прямых, так и наклонных, т. е. центр тяжести объема пирамиды или конуса находится на расстоянии 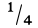 расстояния от центра тяжести площади основания до вершины.
расстояния от центра тяжести площади основания до вершины.
Объем полушара
Полушар имеет ось симметрии, которую примем за координатную ось 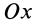 (рис. 96). Разобьем объем полушара на элементарные диски толщиной dx и радиусом у, который является координатой точки окружности, которая получилась от пересечения полушара с координатной плоскостью
(рис. 96). Разобьем объем полушара на элементарные диски толщиной dx и радиусом у, который является координатой точки окружности, которая получилась от пересечения полушара с координатной плоскостью 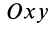 . Уравнение этой окружности
. Уравнение этой окружности
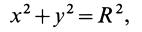
где 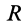 — радиус полушара. Для координаты центра тяжести объема полушара имеем
— радиус полушара. Для координаты центра тяжести объема полушара имеем
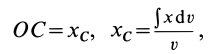
где 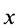 — координата центра тяжести элементарного диска. Объем полушара
— координата центра тяжести элементарного диска. Объем полушара
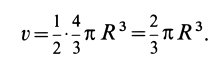
Объем элементарного диска
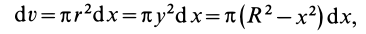
так как радиус диска 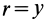 . Выполняя интегрирование в пределах от
. Выполняя интегрирование в пределах от 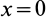 до
до 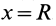 , получим
, получим
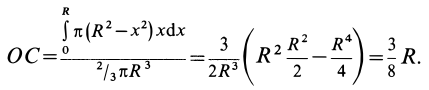
Таким образом, центр тяжести объема полушара находится от его центра на расстоянии

Это расстояние меньше половины радиуса полушара.
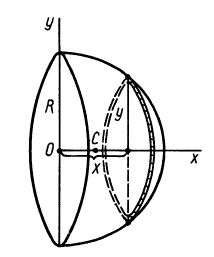
Рис. 96
Задача №1
Определить координаты центра тяжести площади плоской фигуры, имеющей размеры, указанные на рис. 97.
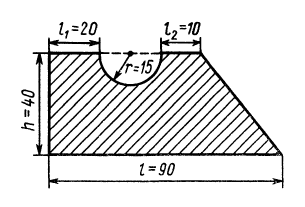
Рис.97
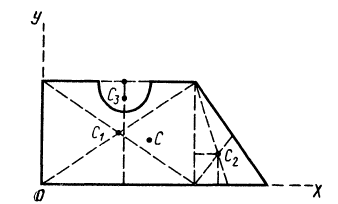
Рис. 98
Решение. Присоединим к заданной фигуре дополнительно полукруг 3 и разобьем полученную фигуру на прямоугольник 1 и треугольник 2. Получили три фигуры, две из которых имеют положительные площади (прямоугольник 1 и треугольник 2) и одна — отрицательную (полукруг 3). В выбранной системе координат для координат центра тяжести заданной фигуры имеем
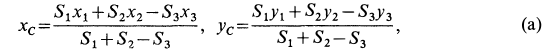
где 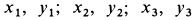 — координаты центров тяжести отдельных фигур;
— координаты центров тяжести отдельных фигур; 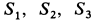 — площади этих фигур.
— площади этих фигур.
Вычислим площади и координаты центров тяжести отдельных фигур, учитывая рис. 98 Имеем:
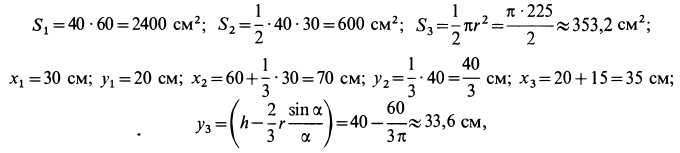
так как 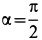 .
.
Подставляя полученные значения в (а), получим:

Центр тяжести плоской фигуры
постановка задачи. Найти площадь и координаты центра тяжести плоской фигуры.
План решения:
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
2. Выбираем систему координат. Вычисляем площади и координаты 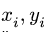 центров тяжести отдельных частей. Площади вырезанных частей берем со знаком минус.
центров тяжести отдельных частей. Площади вырезанных частей берем со знаком минус.
3. Находим общую площадь фигуры по формуле 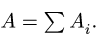
4. Определяем координаты центра тяжести фигуры:
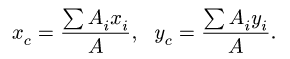
Задача №2
Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны 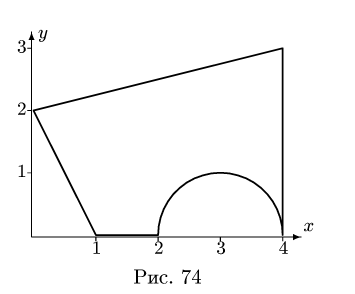
Решение
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в задачах, изображено на рис. 75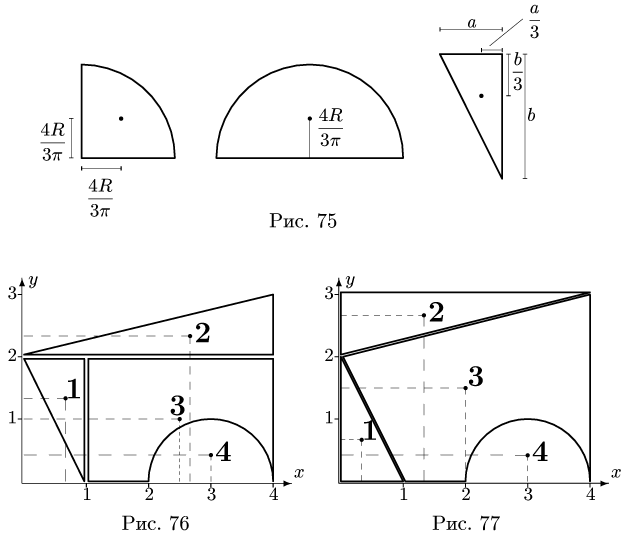
Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в 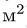 ) и координаты центра тяжести (в м) каждого элемента:
) и координаты центра тяжести (в м) каждого элемента: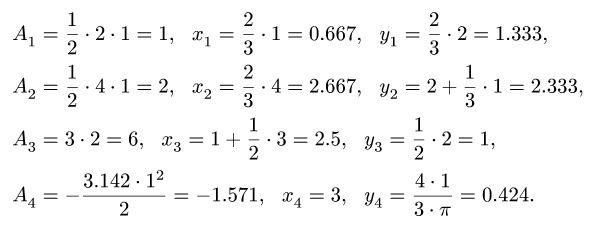
Площадь выреза берем со знаком минус.
3.Площадь фигуры 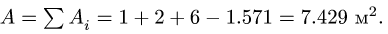
4. Находим координаты центра тяжести всей фигуры:

Вычисления удобно свести в таблицу: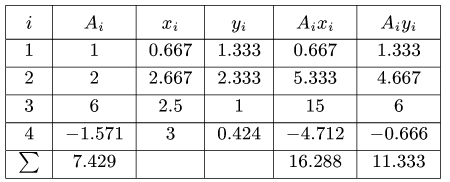
Сначала заполняем столбцы 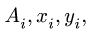 затем вычисляем статические моменты
затем вычисляем статические моменты 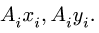 Внизу записываем суммы столбцов, необходимые для вычисления координат центра тяжести. Таким образом
Внизу записываем суммы столбцов, необходимые для вычисления координат центра тяжести. Таким образом
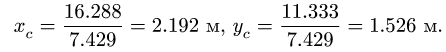
Замечание 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 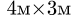 и вырезанных из него полукруга 4 и двух треугольников 1 и 2 (рис. 77).
и вырезанных из него полукруга 4 и двух треугольников 1 и 2 (рис. 77).
Замечание 2. Решение задачи в системе Maple V методом контурного интегрирования.
- Заказать решение задач по теоретической механике
Пространственная стержневая система
Постановка Задачи. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.
План решения:
1. Разбиваем фигуру на отдельные стержни.
2. Выбираем систему координат. Вычисляем длины и координаты 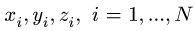 центров тяжести отдельных стержней. Координаты центра прямолинейного однородного стержня вычисляем как полусумму координат его концов.
центров тяжести отдельных стержней. Координаты центра прямолинейного однородного стержня вычисляем как полусумму координат его концов.
3. Находим суммарную длину стержней системы 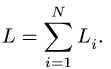
4. Определяем координаты центра тяжести тела по формулам
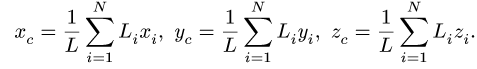
Задача №3
Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры: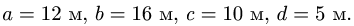
Решение
1. Разбиваем фигуру на шесть стержней.
2. Выбираем систему координат (рис. 78). Вычисляем длины и координаты 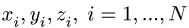 центров тяжести отдельных стержней.
центров тяжести отдельных стержней.
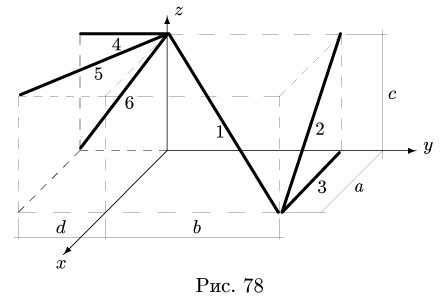
3. Находим суммарную длину стержней системы:
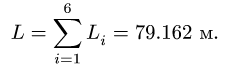
Промежуточные результаты удобно занести в таблицу:
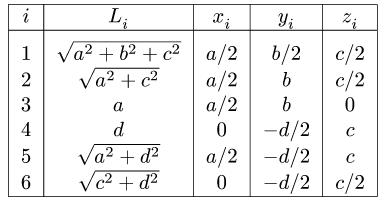
4. Определяем координаты центра тяжести тела по формулам
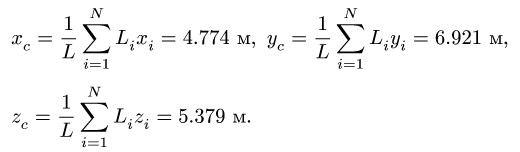
Постановка задачи. Найти координаты центра тяжести однородного объемного тела.
План решения:
1. Разбиваем тело на простые части, положение центров тяжести которых известно.
2. Выбираем систему координат. Вычисляем объемы 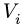 и координаты
и координаты 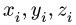 центров тяжести отдельных частей. Объемы вырезанных частей берем со знаком минус.
центров тяжести отдельных частей. Объемы вырезанных частей берем со знаком минус.
3. Находим общий объем тела по формуле 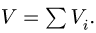
4. Определяем координаты центра тяжести тела:
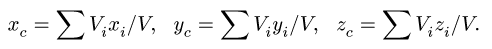
Задача №4
Найти координаты центра тяжести однородного объемного тела (рис.79);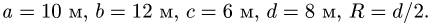
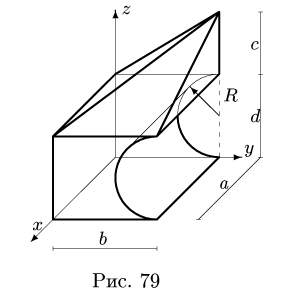
Решение
1. Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).
2. Выбираем систему координат. Вычисляем объемы 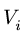 и координаты
и координаты 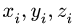 центров тяжестей отдельных частей. Центр тяжести пирамиды 1 лежит в точке
центров тяжестей отдельных частей. Центр тяжести пирамиды 1 лежит в точке 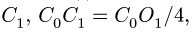
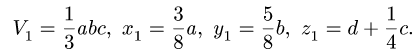
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:
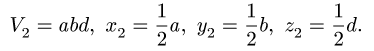
Объем половины цилиндра 3 берем со знаком минус:
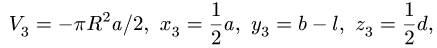
где 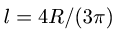 — расстояние по оси у от оси цилиндра до его центра тяжести
— расстояние по оси у от оси цилиндра до его центра тяжести 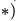 .
.
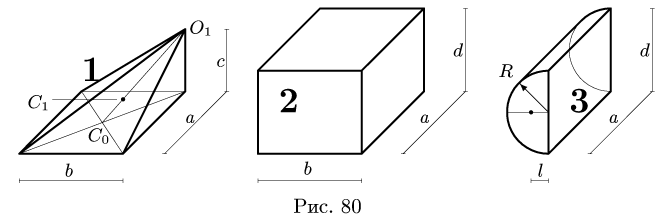
3. Находим общий объем тела:
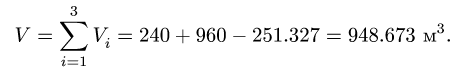
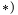 В общем случае объем тела, лежащего в области
В общем случае объем тела, лежащего в области 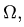 можно найти, вычисляя тройной интеграл по области
можно найти, вычисляя тройной интеграл по области 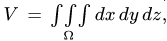 а координаты центра тяжести, например,
а координаты центра тяжести, например, 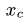 однородного тела можно определить по формуле
однородного тела можно определить по формуле 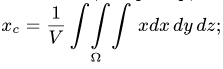 см.
см.
4. Определяем координаты центра тяжести тела:

Центр тяжести
Центр тяжести — точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
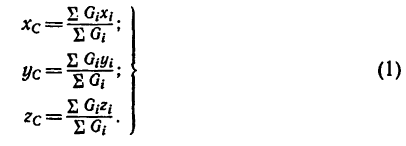
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес 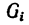 каждого отрезка
каждого отрезка 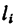 можно представить в виде произведения
можно представить в виде произведения
где d — постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо 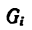 их значений
их значений 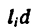 постоянный множитель d в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий, примут вид:
постоянный множитель d в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий, примут вид:
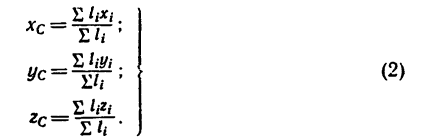
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174),
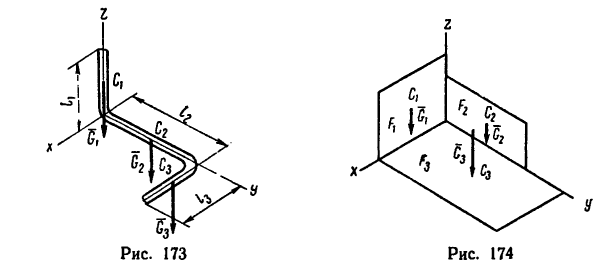
то вес каждой плоскости (поверхности) можно представить так:
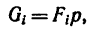
где 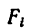 — площади каждой поверхности, ар — вес единицы площади фигуры.
— площади каждой поверхности, ар — вес единицы площади фигуры.
После подстановки этого значения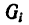 в формулы (1) получаем формулы координат центра тяжести фигуры, составленной из площадей:
в формулы (1) получаем формулы координат центра тяжести фигуры, составленной из площадей:
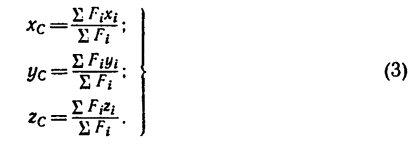
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
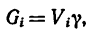
где 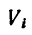 — объем каждой части, а у — вес единицы объема тела.
— объем каждой части, а у — вес единицы объема тела.
После подстановки значений 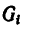 в формулы (I) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов;
в формулы (I) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов;
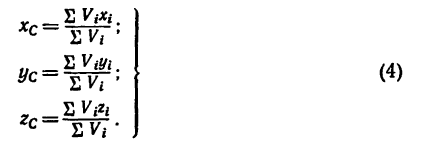
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
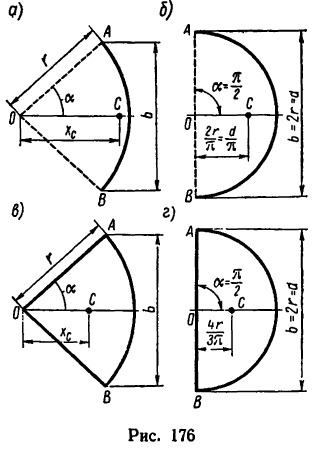
Если известен радиус дуги г и центральный угол 2а, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 176, а) относительно центра дуги О определится формулой
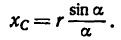
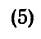
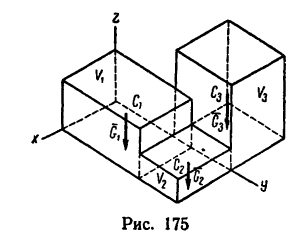
Если же задана хорда 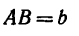 дуги, то в формуле (5) можно произвести замену
дуги, то в формуле (5) можно произвести замену
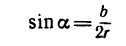
и тогда

В частном случае для полуокружности обе формулы примут вид (рис. 176, б)
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы

Если же задана хорда сектора, то

В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
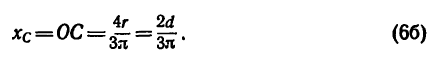
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
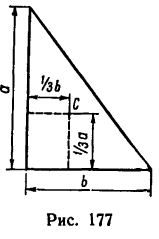
При решении задач на определение положения центра тяжести любого однородного тела, й составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
- выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
- разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
- определить или длины, или площади, или объемы составных частей;
- выбрать расположение осей координат;
- определить координаты центров тяжести составных частей;
- найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
- по найденным координатам указать на рисунке положение центра тяжести тела.
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Условия равновесия системы сил
- Плоская система сил
- Трение
- Пространственная система сил
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РФ
СЕВМАШВТУЗ
Лобанов Н.В.
Морозов А.С.
Сопротивление материалов
Учебное
пособие к выполнению РГР.
Часть
I
Северодвинск
2003
УДК
539.3/.8
Лобанов
Н.В., Морозов А.С.
Сопротивление
материалов. Учебное пособие к выполнению
РГР. Часть I.
Северодвинск.
Севмашвтуз, 2003.- с.
Учебное
пособие содержит подробно разобранные
задачи по основным разделам курса
сопротивления материалов, которые
могут быть использованы студентами
при самостоятельном выполнении
расчетно-графических работ (РГР). В
начале каждого раздела приведены
основные положения и зависимости
рассматриваемой темы.
Учебное
пособие предназначено для студентов
всех специальностей, изучающих курс
«Сопротивление материалов».
Ответственный
редактор: к. т. н., доц. кафедры
«Проектирование подъемно-транспортного
и технологического оборудования»
Севмашвтуза Лобанов Н.В.
Рецензенты:
д. т. н., профессор кафедры «Прикладная
механика» АГТУ Прокофьев Г.Ф.;
к.т.н.,
доцент кафедры «Сопротивления
материалов» АГТУ
Лицензия
на издательскую деятельность
Код
221. Серия ИД №01734 от 11 мая 2000 года
ISBN
5-7723-
СЕВМАШВТУЗ, 2003
Содержание
|
Предисловие |
||
|
1. |
Раздел |
|
|
1.1 |
Основные |
|
|
1.2 |
Задача |
|
|
2. |
Раздел |
|
|
2.1 |
Основные |
|
|
2.2 |
Задача |
|
|
2.3 |
Задача |
|
|
2.4 |
Задача |
|
|
3. |
Раздел |
|
|
3.1 |
Основные |
|
|
3.2 |
Задача |
|
|
4. |
Раздел |
|
|
4.1 |
Основные |
|
|
4.2 |
Задача |
|
|
4.3 |
Задача |
|
|
5. |
Раздел |
|
|
5.1 |
Основные |
|
|
5.2 |
Задача |
|
|
5.3 |
Задача |
|
|
5.4 |
Задача |
|
|
6. |
Литература |
ПРЕДИСЛОВИЕ
Сопротивление
материалов – основополагающая дисциплина
инженерной подготовки по механическим,
машиностроительным, строительным,
транспортным и другим специальностям
высших технических учебных заведений.
В контрольных заданиях сборника
рассматриваются схематизированные
типовые элементы машиностроительных,
строительных, транспортных и других
конструкций, которые и предлагаются к
расчету на прочность, жесткость и
устойчивость.
В
учебном пособии подробно рассмотрены
решения типовых задач по основным
разделам курса «Сопротивления материалов»
что позволяет использовать его выполнения
домашних заданий расчетно-графических
работ. Сборник предназначен для
использования при изучении курса
«Сопротивление материалов», а также
для курсов «Прикладная механика»,
«Техническая механика», имеющих раздел
«Сопротивление материалов» студентами
всех специальностей.
Раздел I
ОПРЕДЕЛЕНИЕ
ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СЛОЖНЫХ
СОСТАВНЫХ СЕЧЕНИЙ.
Основные понятия и зависимости.
Одним
из основным объектом сопротивления
материалов является
стержень. Главными
атрибутами стержня являются его ось и
поперечное
(перпендикулярного
оси) сечение.
Для нахождения
оси стержня необходимо определить
положения центров тяжести поперечных
сечений стержня. Кроме того, для расчетов
прочности и жесткости стержня необходимо
определить положение главных центральных
осей инерции стержня и геометрические
характеристики поперечного сечения
как плоской фигуры.
Статическим
моментом площади сечения (плоской
фигуры) относительно оси
(произвольной расположенной в плоскости
фигуры) называется интеграл вида:
![]() где:
где:
dF
– площадь произвольной элементарной
площадки; h
– расстояние
от этой площадки до оси,
знак
F
под интегралом означает, что интеграл
берется по всей площади рассматриваемого
сечения (фигуры). Обычно сечение
рассматривается в некоторой системе
координат ZY
(в дальнейших выкладках система координат
всегда подразумевается правой то есть
ось Z вправо ось Y вверх ),
тогда
статические моменты сечения относительно
этих осей
могут быть
выражены как:
![]() ;
;
![]() ,
,
где z и
y
– координаты произвольной элементарной
площадки. Размерность статического
момента – единица длины в кубе, например
– см3.
По определению
статический момент площади обладает
свойством аддитивности, то есть если
сечение состоит из нескольких фигур,
то статический момент всего сечения
относительно любой оси может быть
найден как
![]() где
где
Si
– статический
момент i–ой
фигуры сечения.
Центром
тяжести
сечения
(фигуры)
называется точка обладающая следующим
свойством: статический момент фигуры
относительно любой оси проведенной
через центр тяжести равен нулю.
Центральными
осями сечения
называются оси, проходящие через его
центр тяжести. Очевидно, что для любого
сечения центральных осей бесконечное
множество.
Если
положение центра тяжести, какой либо
фигуры известно, то статический момент
ее относительно любых осей Z
и Y
может быть определен просто
(без
операции интегрирования)
как
![]() ;
;![]() гдеF
гдеF
– площадь фигуры
![]() ,
,![]() –
–
координаты центра тяжести в осяхZY.
В
практических расчетах для определения
статического момента сложное сечение
разбивают (часто
приближенно)
на фигуры, положение центра тяжести
которых заранее известно и находят
статический момент всего сечения как:
![]() ;
;
![]() ,где:
,где:
Fi
– площадь i–ой
фигуры;
![]() ,
,![]() –
–
координаты центра тяжестиi–ой
фигуры в осях ZY.
Также
просто определяются координаты центра
тяжести сложного сечения осях ZY:
![]() ;
;
![]() .
.
Формулы
для определения положение центров
тяжести и площадей большого количества
фигур можно найти в справочниках по
Сопротивлению материалов, например
[1].
Моментом
инерции площади сечения относительно
оси (лежащей
в плоскости фигуры)
или осевым
моментом инерции сечения называется
интеграл вида:
![]() где:
где:
dF
– площадь произвольной элементарной
площадки; h
– расстояние
от этой площадки до оси,
знак
F
под интегралом означает, что интеграл
берется по всей площади рассматриваемого
сечения (фигуры). Моменты инерции
относительно произвольных декартовых
осей ZY:
![]() ;
;
![]() ,
,
где z и
y
– координаты произвольной элементарной
площадки.
Полярным
моментом инерции
площади
сечения
относительно произвольной точки
(полюса О) называется интеграл вида:
![]()
где
– расстояние
от произвольной элементарной площадки
dF
до полюса. Полярный момент инерции
сечения относительно начала декартовой
системы координат YZ
связан с моментами инерции относительно
координатных осей простым соотношением:
![]() .
.
Размерности
осевых и полярных моментов инерции –
единица длины в четвертой степени,
например см4.
По определению осевые и полярные моменты
инерции сечения не могут быть
отрицательными или равными нулю.
Центробежным
моментом инерции сечения фигуры
относительно произвольных декартовых
осей ZY
называется интеграл вида:
![]()
где z и
y
– координаты произвольной элементарной
площадки dF.
Размерность центробежного момента
инерции – единица длины в четвертой
степени, например см4.
Центробежный момент инерции сечения
в отличие от осевого может быть
отрицательным или равным нулю.
Главными
осями инерции сечения
называются оси относительно, которых
центробежный момент инерции равен
нулю:
![]() .
.
Положение
главных осей инерции легко найти для
фигур имеющих хотя бы одну ось симметрии,
для таких фигур одна из главных осей
совпадает с осью симметрии, а вторая
ей перпендикулярна.
Главными
центральными осями инерции сечения
называются
главные оси проходящие через центр
тяжести сечения. Главные центральные
оси сечения часто обозначают U
и V
для главных центральных осей сечения
выполняются одновременно условия:
![]() ;
;![]() ;
;
![]() .
.
Главными
моментами инерции площади сечения
называются
осевые моменты инерции, вычисленные
относительно главных осей инерции:
![]() ,
,![]() .Главные
.Главные
моменты инерции сечения обладают
свойством экстремальности, то есть
один из главных моментов является
максимальным, а другой минимальным из
всех моментов инерции относительно
центральных осей.
Определение
положения главных центральных осей и
главных моментов инерции поперечного
сечения является необходимым этапом
в расчетах стержней.
Также
как и статические моменты, моменты
инерции обладают свойством аддитивности
и моменты инерции сложного сечения
относительно декартовых осей
ZY:
![]() ;
;![]() ;
;![]() ;
;![]() где
где
![]() ,
,![]() ,
,![]() ,
,![]() – моменты
– моменты
инерции i–ой
фигуры составляющей сечение относительно
осей ZY.
В
расчетах моментов инерции широко
используется теорема
Штейнера,
которая позволяет найти моменты инерции
относительно осей
Y1Z1
параллельных
произвольным центральным
ZсYс
(при условии,
что моменты инерции относительно этих
центральных осей известны):
![]() ;
;![]() ;
;![]() где
где
![]() и
и
![]() расстояния
расстояния
соответственно между осями
Yс
и
Y1
,
Zс
и
Z1.
Теорема
Штейнера и свойство аддитивности
моментов инерции позволяет в практических
расчетах находить моменты инерции
сложных сечений, не прибегая к операции
интегрирования.
Рассмотрим
порядок определения моментов инерции
сложного (составного) сечения относительно
произвольных центральных осей. Будем
считать, что положение центра тяжести
сечения определено заранее.
а).
Сложное сечение разбивают на простые
фигуры моменты инерции, которых можно
найти по готовым формулам.
б).
Вычисляют моменты инерции отдельных
фигур относительно их собственных
центральных осей:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
В справочниках
(например [1]) приводятся формулы для
вычисления моментов инерции большого
количества фигур. Например, момент
инерции прямоугольника с высотой – h
и основанием – b
относительно его собственных главных
центральных осей (осей симметрии):
![]() – относительно оси параллельной
– относительно оси параллельной
основанию; Y:![]() – относительно оси перпендикулярной
– относительно оси перпендикулярной
основанию.
в).
Используя теорему Штейнера и свойство
аддитивности определяют моменты инерции
сложного сечения относительно осей
Zс
Yс:
![]() ;
;![]() ;
;![]() ,где
,где
![]() и
и
![]() расстояния
расстояния
между соответствующими собственными
центральными осями инерции i-ой
фигуры и центральными осями всего
сечения Zс
Yс.
Необходимо
отметить, что координаты аi
и bi,
входящие в формулы, следует подставлять
с учетом их знака (в зависимости от
взаимного расположения осей).
Положение
главных центральных осей инерции
сечения определяется углом поворота
произвольных центральных осей:
![]() ,
,
причем положительный угол![]() соответствует повороту против часовой
соответствует повороту против часовой
стрелки. Угол![]() не может быть больше45.
не может быть больше45.
Главные
моменты инерции сечения могут быть
определены по формуле:
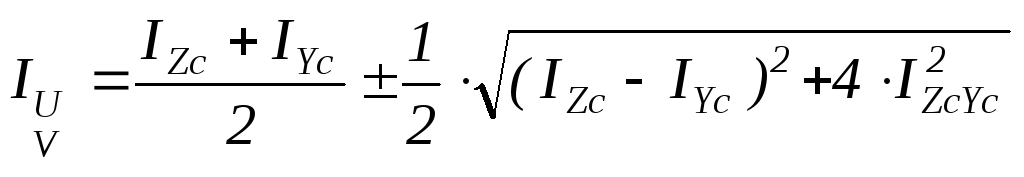 .
.
Максимальный
главный момент инерции будет относительно
той оси которая получается поворотом
на угол
![]() центральной оси момент инерции
центральной оси момент инерции
относительно которой был максимален.
Очевидно, что должно выполнятся
равенство:
![]() .
.
Важными геометрическими
характеристиками поперечных сечений
при расчете стержней на прочность при
изгибе и на устойчивость являются
радиусы инерции сечения и моменты
сопротивления.
Радиусом
инерции
сечения относительно главных центральных
осей называется отношение:
![]() ;
;![]() .
.
Осевым
моментом сопротивления (или моментом
сопротивления изгибу)
называется отношение момента инерции
относительно главной центральной оси
к расстоянию zmax
и ymax
от нее до наиболее удаленной точки
поперечного сечения:
![]() ;
;![]() .
.
Задача №1
Задание
Для заданного составного сечения
определить положение главных центральных
осей инерции сечения и рассчитать
главные моменты инерции сечения.
Исходные
данные. Справочные величины:
Каждый
элемент сечения уголок(№11/7(8))-1,
швеллер(№20)-2, прямоугольник-3 вычерчиваем
на чертеже собственные центральные
оси для каждого составного элемента
сечения ziyi
(координаты ЦТ берутся из справочника)
и относим их к параллельным осям Z0Y0.
-для уголка:
F1=1390
мм2
– площадь поперечного сечения
z1=36.1
мм; y1=16.4
мм – координаты центра тяжести
Izc1=546000
мм4;
Iyc1=1720000
мм4
– осевые моменты инерции
Iu
min=323000 мм4
– главный момент инерции
tgα=0.400 – угол
наклона главных осей
-для швеллера:
F2=2340
мм2
– площадь поперечного сечения
z2=100
мм; y2=20.7
мм – координаты центра тяжести
Izc2=1130000
мм4;
Iyc2=15200000
мм4
– осевые моменты инерции
Решение:
Сечение,
вычерченное в масштабе, относим к осям
координат Z0Y0,
параллельным сторонам контура сечения.
-
для прямоугольника:
F3=4000
мм2
– площадь поперечного сечения
z3=10
мм; y3=100
мм – координаты центра тяжести
![]()
![]()
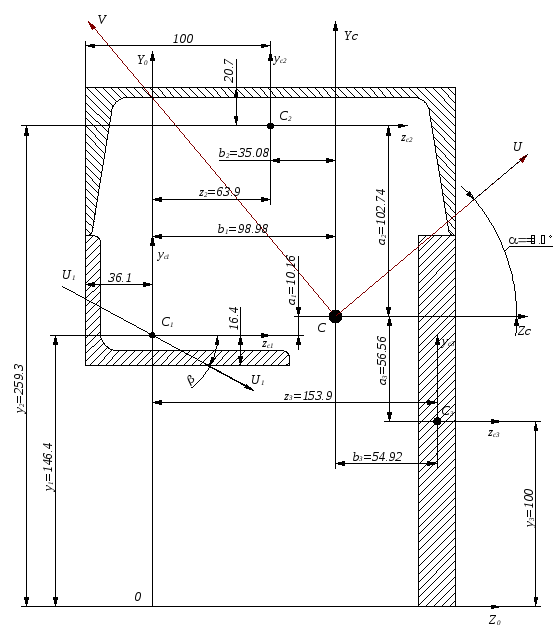
рис.1
1. Определение координат центра тяжести сечения относительно произвольных осей z0y0.
Статические
моменты отдельной фигуры относительно
оси Z0:
Sz1=y1∙F1=146.4∙1390=203496
мм3
– уголка;
Sz2=y2∙F2=259.3∙2340=606762
мм3
– швеллера;
Sz3=y3∙F3=100∙4000=400000
мм3
– прямоугольника;
Статический
момент всего сечения относительно оси
Z0:
Sz0=
Sz1+
Sz2+
Sz3=203496+606762+400000=1210258
мм3
Статические
моменты отдельной фигуры относительно
оси Y0:
Sy1=z1∙F1=0∙1390=0
мм3
– уголка;
Sy2=z2∙F2=63.9∙2340=149526
мм3
– швеллера;
Sy3=z3∙F3=153.9∙4000=615600
мм3
– прямоугольника;
Статический
момент всего сечения относительно оси
Y0:
Sy0=
Sy1+
Sy2+
Sy3=0+149526+615600=765126
мм3
(значения
yi
и zi
снимаем с чертежа сечения)
Координаты
центра тяжести сечения относительно
осей Z0Y0:
![]() мм
мм
– координата центральной оси сечения
Zc
![]() мм
мм
– координата центральной оси сечения
Yc
где
F0=
F1+F2+F3=1390+2340+4000=7730
мм2
–площадь всего сечения
2. Определение моментов инерции сечения
Для
учета параллельного переноса осевых
моментов инерции отдельных фигур
используем поправку Штейнера (ai2∙Fi)
прибавляя ее к осевому моменту инерции
относительно собственных центральных
осей отдельной фигуры Zci
и Yci.
Момент
инерции всего сечения относительно
оси Zc:
Izc=(Izc1+a12∙F1)+(Izc2+a22∙F2)+(Izc3+a32∙F3)
Izc=(546000+(-10)2∙1390)+(1130000+(102)2∙2340)+(13333333+(-56)2∙4000)
= 52648839 мм4
Момент
инерции всего сечения относительно
оси Yc:
Iyc=(Iyc1+b12∙F1)+(Iyc2+b22∙F2)+(Iyc3+b32∙F3)
Iyc=(1720000+(-99)2∙1390)+(15200000+(-35)2∙2340)+(133333+(55)2∙4000)
= 45615664 мм4
Центробежный
момент инерции всего сечения относительно
оси ZcYc:
Iyczc=(Iyc1zc1+a1∙
b1∙F1)+(Iyc2zc2+a2∙
b2∙F2)+(
Iyc3zc3+a3∙
b3∙F3)
При вычислении
центробежного момента инерции составного
сечения следует иметь в виду, что Iyc2zc2
и Iyc3zc3
будут равны нулю, так как их собственные
центральные оси являются главными и
параллельны центральным осям всего
сечения.
Вычислим центробежный
момент уголка относительно осей ZcYc:
Исходя из равенства:
Imax+Imin=Ixc+Iyc,
то Imax=Ixc+Iyc–
Imin
![]() -для
-для
неравнобокого уголка
![]() -для
-для
равнобокого уголка
где
– угол между осью ZС1
и главной осью U
уголка (рис.1). Знак угла
берем, исходя из рис.2:
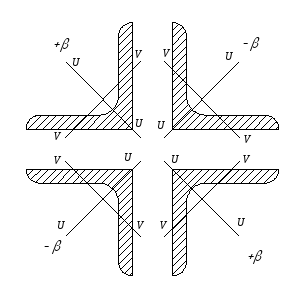
рис.2
Центробежный момент инерции уголка
![]() мм4
мм4
Центробежный
момент инерции всего сечения относительно
осей ZcYc:
Iyczc=(300669+(-10)∙(-99)∙1390)+(0+102∙(-35)∙2340)+(0+(-56)∙55∙4000)
Iyczc=
19761573
мм4
Для
проверки правильности выбора знака
угла
следует разбить уголок на два
прямоугольника (рис.3) пересчитать и
сравнить их расхождение в центробежном
моменте инерции. Если расхождение
велико это означает, что угол выбран
не с тем знаком.
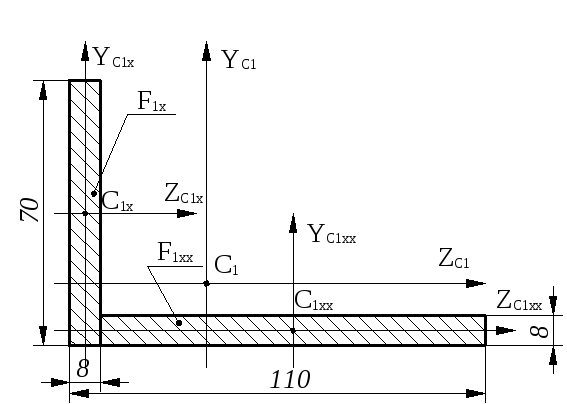
рис.3
Центробежный
момент для всего сечения с уголком,
разделенным на два простых прямоугольника
равен:
F1x=560
мм2
– площадь поперечного сечения
F1xx=880
мм2
– площадь поперечного сечения
a1x=8.4
мм – координата от оси Zc1x
до Zс
b1x=-131
мм – координата от оси Yc1x
до Yс
a1xx=-76
мм – координата от оси Zc1xx
до Zс
b1xx=-22.5
мм – координата от оси Yc1xx
до Yс
Iyczc=(Iyc1zc1+((a1x∙
b1x∙F1x)+(a1xx∙
b1xx∙F1xx)))+(Iyc2zc2+a2∙
b2∙F2)+(
Iyc3zc3+a3∙
b3∙F3)
Iyczc=(0+((8.4)∙(-131)∙560)+((-76)∙(-22.5)∙880))+(0+102∙(-35)∙2340)+(0+(-56)∙55∙4000)
Iyczc=19785224
мм4
Как
видно из расчетов центробежные моменты
инерции вычисленные разными способами
расходятся в значениях не более чем на
0.12%. Это означает, что знак угла α выбран
правильно.
3. Нахождение положения главных осей и моментов инерции:
Угол
наклона главных осей инерции, проходящих
через центр тяжести составного сечения,
к центральным осям инерции ZcYc
определим по формуле:
![]()
![]()
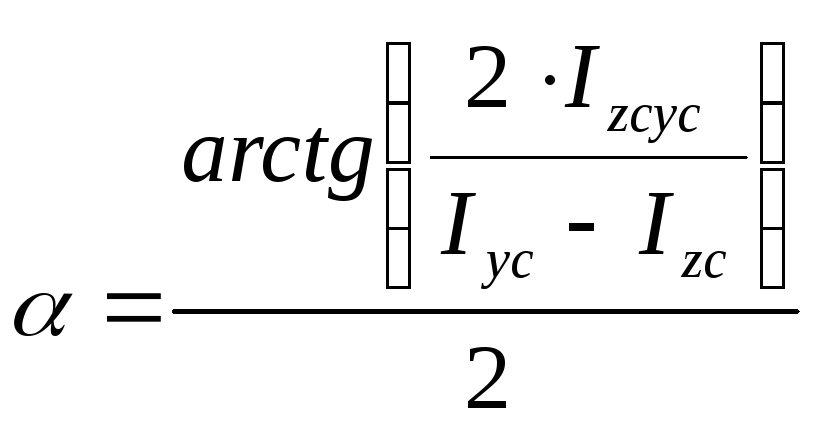
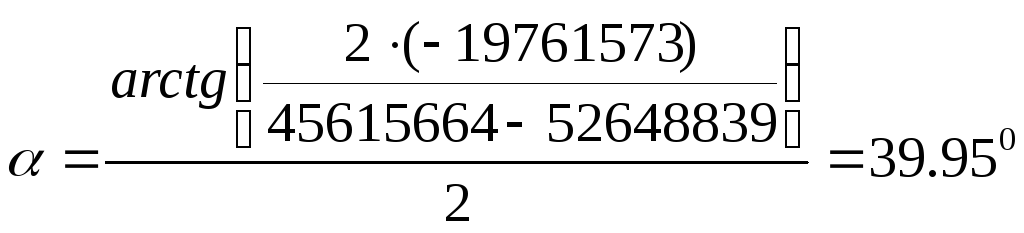
Так
как угол >0,
то откладываем его по оси Z
против движения часовой стрелки.
Определение
величин главных моментов инерции Iu
и Iv
сечения:
![]()
![]()
Верхние знаки
следует брать при Izc
> Iyc
, а нижние
Izc
< Iyc
![]() =69204276мм4
=69204276мм4
![]() =
=
29060227 мм4
Проверка
IU
+ IV
= Izc
+ Iyc
69204276+29060227
= 52648839+45615664
98264503=98264503
Главная
центральная ось U
получается на чертеже поворотом оси
Zc
против часовой стрелки, так как >0
и ось U
будет являться осью относительно
которой момент инерции будет максимальным.
Раздел II
ЦЕНТРАЛЬНОЕ
РАСТЯЖЕНИЕ (СЖАТИЕ ) СТЕРЖНЕЙ .
СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ.
Основные понятия и зависимости.
Центральным
растяжением (сжатием)
называется такой вид деформации, при
котором в поперечных сечениях стержня
возникает только нормальная (продольная)
сила N
остальные силовые факторы равны нулю.
В дальнейшем центральное растяжение
(сжатие) коротко называется просто
растяжением (сжатием). Нормальная
(продольная) сила
в поперечном сечении представляет
собой равнодействующую нормальных
внутренних сил распределенных по
площади поперечного сечения и связана
с нормальными напряжениями![]() в этом сечении зависимостью:
в этом сечении зависимостью:![]() .
.
Принято считатьположительной
нормальную силу, вызывающую растяжение,
отрицательной нормальную силу, вызывающую
сжатие.
Нормальные силы в поперечных сечениях
определяют методом сечений. Считается
что при растяжении (сжатии) справедлива
гипотеза плоских сечений (гипотеза
Бернулли) следовательно, нормальные
напряжения в поперечных сечениях
стержня распределены равномерно и
![]() ,
,
где![]() –
–
площадь поперечного сечения. Положительным
считается растягивающее нормальное
напряжение. Согласно гипотезе плоских
сечений материал стержня при растяжении
(сжатии) находится в линейном напряженном
состоянии. На основании закона Гука
относительное удлинение бесконечно
малого участка стержня:![]() ,
,
где модуль продольной упругости
материала (модуль Юнга). Полное удлинение
стержня в общем случае, когда нормальная
сила и площадь поперечного сечения
меняются по длине:![]() ,
,
где![]() –
–
длина стержня. В частном случае, когда
нормальная сила и площадь по длине
постоянны:![]() .
.
Для ступенчатого стержня полное
удлинение вычисляется как сумма
удлинений его участков:![]() ,
,
где![]() соответственно длина, площадь поперечного
соответственно длина, площадь поперечного
сечения, нормальная сила наi
– том участке.
Растяжение
(сжатие) сопровождается изменением
поперечных размеров стержня. Между
относительной поперечной –
![]() и относительной продольной –
и относительной продольной –![]() деформациями при растяжении (сжатии)
деформациями при растяжении (сжатии)
существует связь![]() ,
,
где![]() – коэффициент Пуассона (коэффициент
– коэффициент Пуассона (коэффициент
поперечной деформации) является
константой материала. Знак «-» в уравнении
отражает тот факт, что![]() и
и![]() всегда имеют противоположные знаки.
всегда имеют противоположные знаки.
Условия
прочности
для стержней работающих на растяжение
сжатие записываются для опасных сечений
стержня, в которых действуют наибольшие
по величине растягивающие и сжимающие
напряжения. В случае, когда материал
стержня имеет одинаковую прочность на
растяжение и сжатие достаточно одного
условия прочности
![]() ,
,
где допускаемое напряжение для материала
стержня. Если материал стержня имеет
разную прочность при растяжении и
сжатии необходимо выполнение одновременно
двух условий прочности:![]() ,
,![]() ,
,
где![]() ,
,![]() –
–
допускаемые напряжения для материала
стержня соответственно на растяжение
и сжатие.
Статически
неопределимыми системами
называются такие системы, в которых
количество неизвестных сил (реакций,
внутренних силовых факторов) превышает
число уравнений равновесия. Степенью
статической неопределимости n
называется разность между r
– количеством неизвестных и u
– числом уравнений статики:
![]() .
.
В статически неопределимых задачах не
удается определить силовые факторы из
условий равновесия и прежде чем решать
задачи прочности и жесткости необходимо
раскрыть статическую неопределимость.Общий принцип
раскрытия статической неопределимости
заключается в том, что в дополнении к
имеющимся уравнениям равновесия всегда
можно составить n
условий совместности деформаций
(совместности перемещений). Условия
совместности деформаций (перемещений)
связывают между собой деформации
отдельных элементов системы или
перемещения ее точек. Затем в условиях
совместности деформации (или перемещения)
выражаются через внутренние усилия,
которые в свою очередь могут быть
выражены методом сечений через внешние
силы. После решения условий совместности
вместе с уравнениями равновесия
относительно неизвестных усилий,
статическая неопределимость будет
раскрыта.
Для
реальных стержней на основании принципа
Сен-Венана гипотеза плоских сечений
справедлива лишь вдали от мест приложения
внешних сосредоточенных нагрузок и
мест изменения размеров и формы
поперечного сечения.
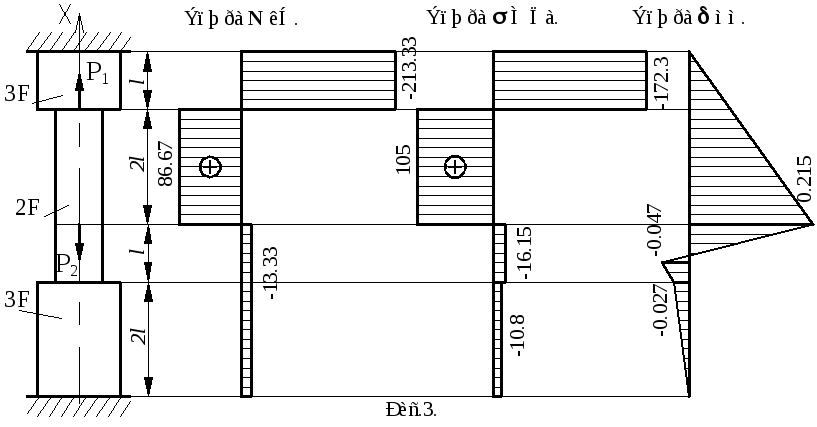
Задача №1
Задание:
Для заданного чугунного стержня (рис.1)
из условия прочности подобрать площадь
поперечного сечения. Построить эпюру
перемещений сечений стержня.
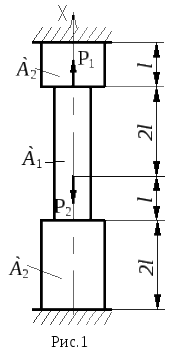
Исходные
данные:
l
= 150
мм; P1
= 3Р;
P2
= Р;
Р = 100кН;
площади поперечных сечений участков
– А1=
2F,
А2=
3F.
Материал стержня чугун СЧ21-40,
Е=120000
МПа,
вр
= 210 МПа, вс
= 1000 МПа.
Коэффициент запаса прочности для чугуна
n
= 2.
Решение:
1).
Определим
допускаемые напряжения для материала
стержней:
![]()
2).
Рассмотрим равновесие стержня, отбросив
заделки и заменив их неизвестными
реакциями R1,
R2
(см. рис.2) для их определения имеется 1
уравнения равновесия
![]() из которого следует
из которого следует![]() .
.
Таким образом, система один раз статически
неопределима.

3).
Далее, для раскрытия статической
неопределимости следует составить
уравнение совместности деформаций, в
рассматриваемом примере таким уравнением
может быть:
![]() –(1)
–(1)
– отражающее тот факт, что из-за наличия
жестких опор длина стержня не изменяется.
Удлинения участков стержня можно
выразить по закону Гука через нормальные
силы в сечениях:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
нумерация участков принята снизу вверх.
Нормальные силы выразим через неизвестные
реакции и внешнюю нагрузку методом
сечений: проводя произвольное поперечное
сечение в пределах каждого из участков,
отбрасываем любую часть и заменяем ее
реакцией взаимодействия частей, которая
и является нормальной силой (см. рис.2).
Примечание:
неизвестные нормальные силы в сечениях
следует показывать всегда в положительном
направлении, то есть так, чтобы они были
растягивающими.
Из условий равновесия рассматриваемых
частей находим нормальные силы:
![]() ;
;
![]() ;
;
![]() ;
;
![]()
(2).
Подставляя
выражения для нормальных сил в выражения
для удлинений участков, а затем в
уравнение совместности деформаций
получим следующее уравнение:
![]() –(2),
–(2),
разрешая которое относительно R1
найдем
–![]() .
.
Таким образом, статическая неопределенность
раскрыта.
Теперь
можно рассчитать нормальные силы:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
и выразить нормальные напряжения в
сечениях:
![]() ;
;![]() ;
;![]() ;
;![]() –(3).
–(3).
Теперь необходимо записать два условия
прочности:
а).
По максимальным сжимающим напряжениям![]() откуда
откуда
требуемая площадь определится как![]() ;
;
б). По максимальным растягивающим
напряжениям![]() откуда
откуда
требуемая площадь определится как![]() .
.
Так как должны выполнятся одновременно
оба условия прочности то следует принять
площадь![]() .
.
Тогда напряжения![]() ;
;![]() ;
;![]() ;
;![]() .
.
По рассчитанным значениям построим
эпюрыN
и
(см. рис3).
Вычисляем
удлинения участков стержней:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Убедимся
что, условие совместности деформаций
выполняется –![]() .
.
Строим эпюру
– смещений поперечных сечений стержня.
Примем за отсчетное сечение нижнюю
заделку стержня, а за положительное
направление смещение сечений вверх,
тогда если участок стержня растягивается,
то его сечения перемещаются в положительном
направлении. Легко доказать, что при
N
= const
эпюра
смещений в пределах участка будет
линейной, следовательно, для построения
эпюры смещений достаточно вычислить
перемещения сечений находящихся на
границах участков. Смещение верхней
границы 1-го участка –![]() ,
,
2-го –
![]() ,
,
3-го –
![]() .
.
По
рассчитанным значениям строим эпюру
(см. рис.3),
учитывая, что на границах участков
разрыва эпюры быть не может и в заделках
перемещение равно нулю.
Более
сложная постановка задачи.
(с учетом температурных и монтажных
напряжений ).
Будем
считать, что температура стержня после
сборки была повышена на Т
= 200.
В свободном (незакрепленном ) состоянии
удлинился бы на величину – Т
=
ТLп
,
где =1.110-5
град-1–
коэффициент линейного расширения
материала стержня (СЧ21-40), Lп=6l
– полная длина стержня:
![]() .
.
Закрепления стержня не позволяют ему
удлинится и при повышении температуры
стержень окажется сжатым на величину
Т
(при
понижении температуры соответственно
растянутым).
Тогда
уравнение
совместности деформаций (1)
перепишется в виде
![]()
(1).
Используя принцип суперпозиции нагрузок,
найдем отдельно напряжения возникающие
при изменении температуры и затем
сложим их с напряжениями от внешней
нагрузки, которые были найдены ранее.
При отсутствии внешних нагрузок
уравнение (2)
предстанет в виде:
![]()
![]()
где
![]()
реакция возникающая только от изменения
температуры. Решая это уравнение, найдем
![]() ,
,
при этом нормальные силы:
![]() тогда
тогда
нормальные напряжения, возникающие
только от изменения температуры
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Заметим, что эти напряжения не зависят
от величины площади поперечных сечений
и условие прочности выполняется
![]() ,
,
(если
это условие не выполняется то прочность
стержня за счет подбора площади сечений
обеспечить невозможно, необходимо
уменьшать температурные напряжения).
Складывая температурные напряжения с
напряжениями от внешней нагрузки (3)
получим следующие выражения:
![]() ;
;
![]() ;
;![]() ;
;![]() –(3).
–(3).
Теперь
снова определим площадь поперечных
сечений из условий прочности. Анализ
выражений (3)
показывает, что теоретически растянутым
может оказаться только участок №3,
записывая для него условие прочности
![]()
![]() определим площадь
определим площадь![]() .
.
Максимальное сжимающее напряжение
будет действовать в участке №2 или №4.
Записывая условия прочности участка
№2 найдем![]()
![]() площадь
площадь![]() .
.
Из условия прочности для участка №4![]()
![]() площадь
площадь![]() .
.
Для удовлетворения одновременно всем
условиям прочности мы должны принять
площадь![]() .
.
Интересно отметить, что при одновременном
действии внешних нагрузок и температуры
площадь поперечного сечения необходимая
для обеспечения прочности оказывается
существенно меньше, чем в первом
варианте. Это объясняется тем, что при
действии только внешних сил опасным
является растянутый 3-й участок, при
повышении температуры все участки
испытывают дополнительное сжатие и
опасным становится сжатый участок №4
чугун же имеет большую прочность на
сжатие чем на растяжение. Окончательно
принять площадь![]() можно
можно
только в случае если внешняя нагрузка
и температура изменяются синхронно.
Если же нагрузки могут прикладыватся
по отдельности, то опасным состоянием
в рассматриваемом примере будет действие
только внешних сил и следует принять![]() .
.
Примечание.
Точно так же решается задача в случае
монтажных напряжений, когда стержень
имеет начальную длину, отличающуюся
от номинальной (равной расстоянию между
опорами) на величину .
Во всех вышеприведенных расчетах нужно
Т
заменить на .
Величина
– считается
положительной, если начальная длина
стержня больше номинальной.
ЗАДАЧА
№2
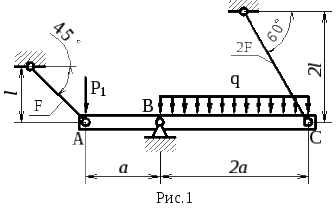 Задание:
Задание:
Для стержневой конструкции (рис.1) из
условия прочности подобрать максимально
допускаемую внешнюю нагрузку (выраженную
через q).
Исходные
данные: F
= 300 мм2;
l =
600 мм; a =
1000 мм; P1
= 3qa;
Материал стержней чугун СЧ32-52, Е=1.1105
МПа,
вр
= 320 МПа, вс
= 1200 МПа.
Определим допускаемые напряжения для
материала стержней:
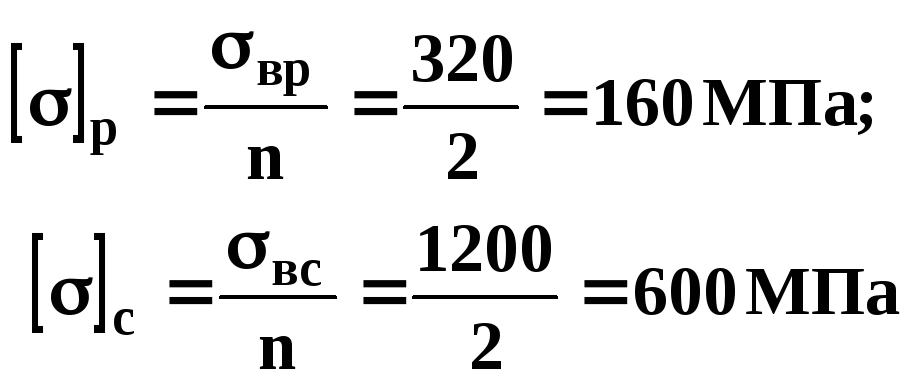
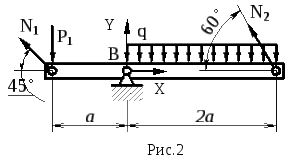 Решение:
Решение:
Рассмотрим
равновесие абсолютно жесткого бруса,
отбросив стержни (рис.2). В данном случае
рациональнее заменить отброшенные
стержни нормальными силами N1,
N2,
N3,
возникающими в них (примечание:
неизвестные нормальные силы в стержнях
следует показывать всегда в положительном
направлении, то есть так, чтобы они были
растягивающими).
Имеется 3 уравнения равновесия и 4
неизвестных: N1,
N2,
YB,
XB,
следовательно, система один раз
статически неопределима. Из трех
уравнений равновесия имеет смысл
составить только одно, содержащее
нужные неизвестные N1,
N2,
в данном
случае это:
![]()
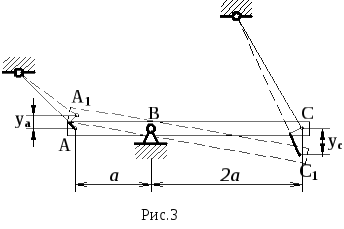
![]() .
.
Необходимо составить одно уравнение
совместности деформаций. Для этого
рассмотрим возможное деформированное
состояние конструкции В данном случае
таким состоянием будет поворот жесткого
бруса вокруг шарнира В,
показанное на рис.3 (совершенно
необязательно, чтобы выбранное
направление перемещения и поворота
совпадало с действительным).
Шарниры А, С
займут новые положения А1,
С1,
их вертикальные перемещения обозначим
соответственно yа,
yс.
(В силу малости
перемещений и деформаций можно заменить
дуги окружностей, по которым перемещаются
шарниры, вертикальными отрезками АА1
и
СС1.
Кроме того, можно считать, что углы
наклона стержней не изменились).
Очевидно, что перемещения yа,
yс
связаны между собой условием,
![]() ,
,
которое получается из подобия
треугольниковАВА1
и
ВСС1.
Очевидно, что эти перемещения связаны
с абсолютными удлиннениями стержней
следующими зависимостями:
![]() ,
,![]() (3),
(3),
знак «-» учитывает, что первый стержень
сжат. Эти зависимости получены из
рассмотрения рис.4.
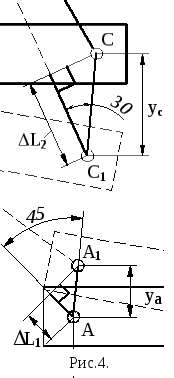 Следовательно:
Следовательно:
![]()
и выражая ΔL
по закону Гука, получим:![]() .
.
Учитывая, что F1
= F,
F2
= 2F,
l1
= l/sin45,
l2
=
2l/sin60
получим:
![]()
или
подставляя значения
![]()
(4). Подставляя
(4) в
выражение (1)
выразим нормальные силы в стержнях:
![]()
![]() .
.
Нормальные напряжения в стержнях
выразятся следующим образом:
![]() (5).
(5).
Из условий прочности определим
допускаемую внешнюю нагрузку. Для
первого стержня,
![]() следовательно:
следовательно:
![]() .
.
Для второго стержня:
![]() (здесь
(здесь
учтено, что при составлении условия
прочности по сжимающим напряжениям
расчетные напряжения всегда берутся
по модулю, так как допускаемые напряжения
всегда положительны),
следовательно:
![]() .
.
Из двух нагрузок выбираем меньшую, так
как должны выполнятся условия прочности
для обоих стержней, таким образом,
окончательно принимаем максимально
допускаемую внешнюю нагрузку![]() .
.
Для проверки
вычислим напряжения в стержнях:
![]()
![]() – условие прочности выполнено для обоих
– условие прочности выполнено для обоих
стержней.
Более
сложная постановка задачи.
(с учетом монтажных напряжений )
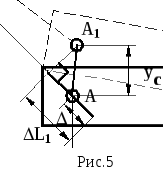 Будем
Будем
считать, что стержень №1 до сборки
конструкции имел длину отличающуюся
от номинальной на малую величину
= – 0.6 мм (знак
“-” означает, что начальная длина
меньше номинальной).
Используя принцип суперпозиции нагрузок,
найдем отдельно монтажные напряжения
и затем сложим их с напряжениями
возникающими от внешней нагрузки. При
отсутствии нагрузок уравнение равновесия
(1)
предстанет в виде:
![]() .
.
Уравнение
(3)
для 2-го
стержня не изменится, а для 1-го
запишется в виде:
![]() ,
,
см. рис.5 (на
рис.5 формально показана ситуация
соответствующая положительному
).
Уравнение совместности деформаций
тогда запишется в виде:
![]() .
.
Подставляя
(1)
в последнее выражение после элементарных
преобразований получим:
![]()
Подставляя
значения, вычислим нормальные силы и
монтажные напряжения в стержнях:
![]()
![]() .
.
Оба стержня после монтажа растянуты
(здесь важно
отметить, что условия прочности выполнены
для обоих стержней, то есть при монтаже
их прочность не нарушена).
Добавляя монтажные напряжения к
напряжениям, возникающим от внешних
нагрузок (5)
получим выражения для суммарных
напряжений в стержнях нагруженной
конструкции:
![]() .
.
Для определения допускаемой внешней
нагрузки можно записать условия
прочности для обоих стержней. Очевидно,
что первый стержень растянут и из
условия прочности для него:
![]() .
.
Со
вторым стержнем дело обстоит сложнее,
он может оказаться как сжатым, так и
растянутым в зависимости от величины
параметра внешней нагрузки – q,
и в принципе
для второго стержня можно записать
условия прочности, как на сжатие так и
на растяжение. Однако, если второй
стержень растянут (второе
слагаемое по модулю больше первого),
то наибольшее растягивающее напряжение
не превосходит 14МПа
(=14МПа
только
при отсутствии внешней нагрузки)
и меньше допускаемого напряжения на
растяжение. Следовательно, для второго
стержня имеет смысл записать только
условие прочности на сжатие:
![]()
(при
подстановке в условие прочности берется
модуль напряжения 2
следовательно меняются на противоположные,
знаки у обоих слагаемых в его выражении).
Из двух полученных нагрузок выбираем
меньшую, таким образом, окончательно
принимаем максимально допускаемую
внешнюю нагрузку
![]() .
.
Для проверки вычислим напряжения в обоих стержнях:
![]()
Условия
прочности выполняются для обоих
стержней, следовательно, самый опасный
стержень был выбран правильно. Удлиннения
стержней можно определить по формулам:
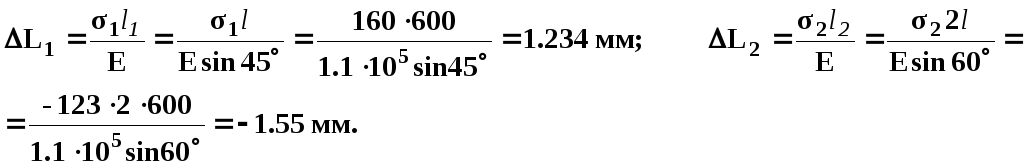
Перемещения:
![]()
![]() удовлетворяют условию совместности
удовлетворяют условию совместности
перемещений(2).
(Знак «-»
означает, что действительные перемещения
шарниров противоположны показанным
на рис.2).
Задача №3
 Задание:
Задание:
Для стержневой конструкции (рис.1) из
условия прочности подобрать максимально
допускаемую внешнюю нагрузку (выраженную
через q).
При найденной нагрузке определить
перемещение точки приложения силы P1.
Исходные
данные:
F
= 700 мм2;
l =
500 мм; a =
500 мм;P1
= qa;
P2
= 3qa;
M1
= 2qa2.
Материал всех стержней Сталь 5, с пределом
текучести т
= 270 МПа; E=2105
МПа.
Определим
допускаемое напряжение для материала
стержней (принимая
для стали коэффициент запаса прочности
n
= 1.5).
![]() .
.
Решение:
Рассмотрим
равновесие абсолютно жесткого бруса,
отбросив стержни (рис.2). В данном случае
рациональнее заменить отброшенные
стержни нормальными силами N1,
N2,
N3,
возникающими в них (неизвестные
нормальные силы в стержнях следует
показывать всегда в положительном
направлении, то есть так, чтобы они были
растягивающими).
Для 3-х неизвестных сил можно составить
2 уравнения равновесия:
![]()
![]()

Следовательно,
задача 1 раз статически неопределима,
и необходимо составить одно уравнение
совместности деформаций. Для этого
рассмотрим возможное деформированное
состояние конструкции (возможное
означает допускаемое связями и включающее
перемещение по всем возможным степеням
упругой подвижности).
В данном случае таким состоянием будет
вертикальное поступательное перемещение
жесткого бруса и его поворот, показанное
на рис.3 (совершенно
необязательно, чтобы выбранное
направление перемещения и поворота
совпадало с действительным).
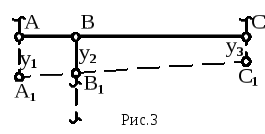
Шарниры
А, В, С
займут новые положения А1,
В1,
С1,
их вертикальные перемещения обозначим
соответственно y1,
y2,
y3.
Очевидно,
что эти перемещения связаны между собой
условием, которое получается из
рассмотрения трапеции АВСА1В1С1:
![]() .
.
Очевидно, что эти перемещения связаны
с абсолютными удлинениями стержней:![]()
![]()
![]() ,
,
откуда следует условие совместности
деформаций:![]() .
.
Выражая
удлинения стержней по закону Гука,
получим дополнительное уравнение
связывающее нормальные силы в стержнях:
![]() .
.
Решая
совместно уравнения (1),
(2), (5) выразим
нормальные силы в стержнях:
![]() (для
(для
проверки следует убедится, что полученные
нормальные силы удовлетворяют исходным
уравнениям).
Нормальные напряжения в стержнях
выразятся следующим образом, чтобы их
можно было сравнить в общем виде:
![]() .
.
Так
как материал стержней имеет одинаковую
прочность на растяжение и сжатие, то
опасным будет третий стержень (с
наибольшим по модулю напряжением).
Из условия прочности для 3-го стержня
определим допускаемую внешнюю нагрузку,
выраженную через q:
![]() .
.
Тогда внешние силы будут равны:
P1
=
132.6500
= 66300Н = 66.3кН; P2
=
3132.6500
= 199000Н = 199кН; M1
=
2132.65002
=
6.63107
Нмм
= 66.3кНм.
Напряжения:
![]() ;
;![]() ;
;![]() ,
,
действующие в стержнях удовлетворяют
условиям прочности.
Более
сложная постановка задачи.
(с учетом монтажных напряжений )
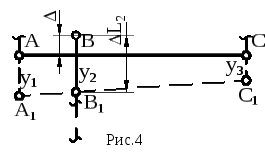
Будем
считать, что стержень №2 до сборки
конструкции имел длину, отличающуюся
от номинальной на малую величину
= 0.5 мм (знак
“+” означает, что начальная длина
стержня больше номинальной).
Уравнения (1),
(2),
(3)
останутся
без изменений, изменится только
зависимость между перемещением шарнира
B
и удлинением стержня №2:
![]() ,тогда
,тогда
уравнение совместности деформаций
(4)
перепишется в виде:
![]() ,
,
(смотри рис.4). Используя закон Гука,
получим:
![]() ,
,
откуда выразим:
![]() .
.
Решая совместно (1),
(2), (5)
выразим нормальные силы и напряжения
в стержнях:
; Embed Equation.3 ;.
![]() Вычисляя
Вычисляя
величины вторых слагаемых в выражениях
для напряжений (E/l
=200 МПа.):
![]() убеждаемся,
убеждаемся,
что монтажные напряжения не превосходят
допускаемых и следовательно условие
прочности при сборке конструкции не
нарушается.
Очевидно,
что стержень №2 сжат, из условия
прочности второго стержня допускаемую
внешнюю нагрузку, выраженную через q:
![]()
Стержни
№1 и №3 могут оказаться как сжатыми,
так и растянутыми, в зависимости от
величины параметра внешней нагрузки
– q,
однако,
проводя анализ (смотри
предыдущую задачу)
можно
установить, что в любом случае напряжения
сжатия в этих стержнях не превосходят
соответственно
31.8 МПа и 14.2 МПа.
Следовательно, для стержней №1 и №3
достаточно записать только условия
прочности на растяжение, кроме того,
очевидно, что наибольшее растягивающее
напряжение будет в стержне №3. Определим
из условия прочности третьего стержня
допускаемую внешнюю нагрузку, выраженную
через q:
![]()
Учитывая,
что должны выполнятся оба условия
прочности, принимаем наименьшее значение
qmax
= 143.1
Н/мм. Тогда
внешние силы будут равны:
P1
=
143.1500
= 71550Н = 71.55кН; P2
=
3143.1500
= 214650Н = 214.65кН; M1
=
2143.15002
=
7.16107
Нмм
= 71.6кНм.
Для
проверки найдем напряжения в стержнях
и убедимся, что условия прочности
выполняются:
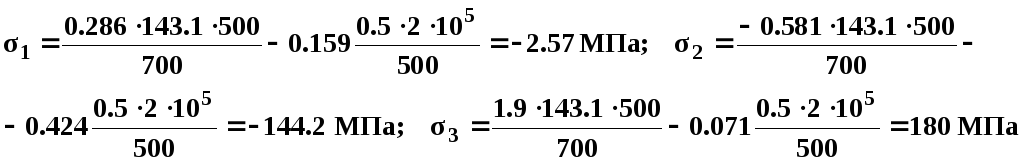 .
.
Удлиннения
стержней:
![]() ;
;
![]() ;
;
![]()
Перемещение
шарниров А,
В, С соответственно:
![]() ;
;
![]() ;
;
![]() – удовлетворяют условию совместности(3).
– удовлетворяют условию совместности(3).
Знак «-»
означает, что действительные перемещения
шарниров противоположны показанным
на рис.4.
Раздел III
СДВИГ.
РАСЧЕТЫ ПРОЧНОСТИ ПРИ СРЕЗЕ И СМЯТИИ.
Основные понятия и зависимости.
Деформация
сдвига характеризуется тем, что из всех
силовых факторов в сечении отлична от
нуля только поперечная сила Q.
Практически деформацию сдвига в чистом
виде получить трудно, так как она
сопровождается другими видами деформаций.
Однако условный (упрощенный) расчет на
чистый сдвиг часто выполняется для
деталей, в которых наибольшее влияние
на прочность оказывают касательные
напряжения, например при расчетах
болтов шпонок и других деталей. Для
таких деталей, как правило, является
характерным разрушение срезом,
по сечению (поверхности) в котором
действуют максимальные касательные
напряжения. Поверхность, по которой
может произойти срез, называют
поверхностью (сечением) среза. Связь
между касательными напряжениями и
поперечной силой
![]() ,
,
где площадь сечения (поверхности) среза.
В практических расчетах обычно
считается, что касательные напряжения
по сечению среза распределяются
равномерно, на основании чего легко
определить величину касательных
напряжений:![]() .Допущение о
.Допущение о
равномерности распределения касательных
напряжений является условным и
действительности не соответствует,
однако широко используется на практике.
Условия
прочности при срезе записываются
следующим образом:
![]() ,
,
где![]() –
–
допускаемое напряжение на срез,
определяемое экспериментально. При
отсутствии экспериментальных данных
допускаемое напряжение ориентировочно
может быть определено как![]() – для пластичных,
– для пластичных,![]() – для хрупких материалов, где
– для хрупких материалов, где![]() – допускаемое для материала напряжение
– допускаемое для материала напряжение
на растяжение.
Смятие.
При выполнение расчетов на срез следует
учитывать, что, как правило, нагрузка
к поверхности среза передается через
поверхность рассматриваемой детали.
Считается, что нагрузка всегда направлена
по нормали к поверхности контакта, то
есть на поверхности контактирующих
деталей действуют только нормальное
напряжение смятия
![]() .
.
Помимо среза может произойти смятие
контактирующих поверхностей деталей.
Под смятием понимают пластическую
деформацию поверхностей контакта.
Расчет на смятие проводят приближенно,
так как закон распределения давления
(напряжения смятия) по поверхности
контакта точно неизвестен и в практических
расчетах законом распределения задаются
априорно. Например, в случае плоских
поверхностей контакта часто принимают
равномерное распределение давлений и![]() ,
,
где![]() – сила действующая на поверхность
– сила действующая на поверхность
смятия,![]() – реальная площадь поверхности смятия.
– реальная площадь поверхности смятия.
В случае плотного контакта цилиндрических
поверхностей смятия принимается
нелинейный закон распределения
напряжений смятия, и максимальные
напряжения смятия рассчитываются по
формуле![]() ,
,
где![]() –
–
площадь проекции поверхности контакта
на диаметральную плоскость. Площадь![]() ,
,
где –диаметр контактной поверхности,
– длина
поверхности смятия.
Условие
прочности при смятии имеет вид:![]() .
.
Допускаемое по смятию напряжения
определяется опытным путем или принимают
равным![]() ,
,
где![]() допускаемое
допускаемое
напряжение на сжатие.
Задача №1
Задание:
Два вала диаметра D1
соединены
втулкой с помощью двух одинаковых
штифтов диаметра d,
от одного вала к другому передается
вращающий момент
M
и осевая сила Р
(см. рис.1). Из условий прочности определить
необходимый диаметр штифтов и наружный
диаметр втулки
D2.
Исходные
данные:
D1
= 30 мм;
Р = 8 кН;
M
= 200 Нм.
Материал валов и втулки Сталь 3, материал
штифтов Сталь 45.
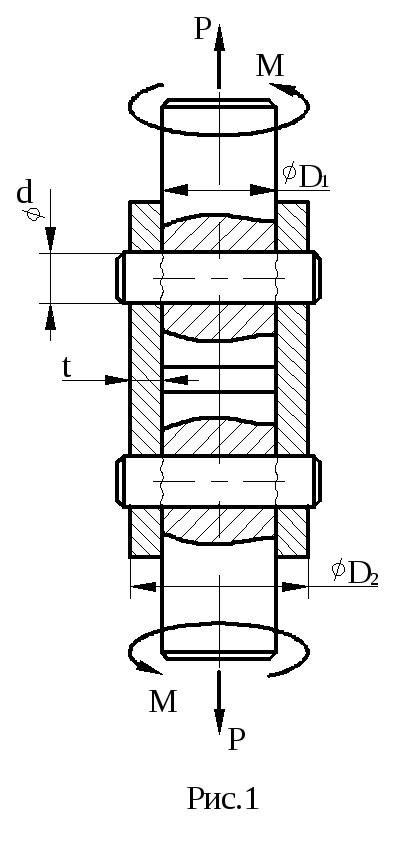 Решение:
Решение:
1).В
данной конструкции могут иметь место
следующие виды разрушения:
а).
Срез штифтов. Штифты могут разрушится
по поверхностям среза показанным на
рис.1 волнистой линией. В силу симметрии
достаточно рассмотреть условие прочности
для одной (любой) поверхности среза –
![]() ,
,
где Q
– перерезывающая
сила приходящаяся на одну поверхность
среза,
![]() –
–
площадь одной поверхности среза. С
небольшой погрешностью можно считать
равной площади поперечного сечения
штифта –![]() – (на самом деле поверхности среза будут
– (на самом деле поверхности среза будут
цилиндрическими и иметь немного большую
площадь). Тогда условие прочности
перепишется в виде![]() .
.
Прочность на срез штифта зависит только
от одного размераd,
тогда из условия прочности можно сразу
выразить
![]() –(1).
–(1).
б).
Смятие контактирующих поверхностей
между штифтами и втулкой. Условие
прочности на смятие для них
![]() ,
,
где![]() –
–
сила смятия приходящаяся на поверхность
смятия,![]() –
–
допускаемое напряжение для менее
прочного материала. Поверхности смятия
цилиндрические поэтому![]() и условие прочности перепишется в виде
и условие прочности перепишется в виде![]() .
.
При известном диаметре штифта из условия
прочности на смятие можно выразить
толщину стенки втулки![]() –(2).
–(2).
2).
Определим
допускаемые напряжения. По справочнику
[1] определяем пределы текучести
материалов: Сталь 3 – Т1
= 240 МПа; Сталь
45 – Т2
= 360 МПа. Принимая
коэффициент запаса прочности n
= 1.5, определим
допускаемые нормальные напряжения для
материала штифтов –
![]() ;
;
для материала валов и втулки –![]() .
.
Пользуясь известной зависимостью,
определим допускаемые напряжения на
срез для штифтов –![]() .
.
Допускаемые напряжения на смятие для
менее прочного материала втулки
ориентировочно примем![]() .
.
2).Очевидно,
что перерезывающая сила Q
действующая на одну поверхность среза
и сила смятия
![]() приходящаяся
приходящаяся
на одно поверхность смятия штифта
равны суммарная сила, действующая на
поверхность штифта со стороны отверстия
втулки. Определим силы действующие на
штифты со стороны втулки. Используем
принцип наложения нагрузок определим
силы возникающие от внешней силыР
и внешнего момента M
по отдельности.
Рассмотрим сначала действие силы Р.
В силу симметрии можно рассмотреть
одну половину конструкции, например
верхнюю, мысленно уберем втулку заменив
ее действие силами Рр
(см.
рис.2). Из условия равновесия очевидно
–
![]() .
.
Рассматривая действие момента снова
отбросим втулку и заменим ее действие
силами![]() .
.
Для обеспечения равновесия момент этих
сил относительно оси вала должен
уравновешивать внешний момент
M
(см. рис.3) –
![]() .
.
Следовательно![]() .
.
Величина плечаh
зависит от
реального распределения усилий
взаимодействия по поверхности штифта,
однако очевидно, что
![]() .
.
Если мы предположим, что![]() то, очевидно, получим завышенное по
то, очевидно, получим завышенное по
сравнению с реальным значение![]() ,
,
следовательно, наше предположение
(упрощение) пойдет в запас прочности.
Итак, принимаем![]() тогда
тогда![]() .
.
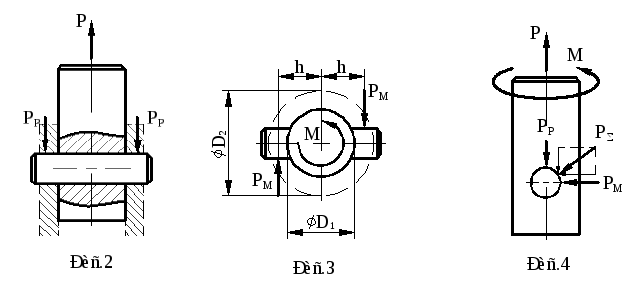
Совместное
действие сил
![]() и
и![]() заменим их равнодействующей
заменим их равнодействующей![]() (см. рис.3), величина которой определится
(см. рис.3), величина которой определится
по теореме Пифагора![]()
![]() .
.
Подставляя значения (в
размерностях:
[Н]; [мм]; [МПа]) получим:
![]() .
.
Тогда из условия(1)
учитывая, что
![]() определим диаметр штифта:
определим диаметр штифта:![]() .
.
Округляя до целого, окончательно примем![]() .
.
Из условия прочности на смятие(2)
![]() .
.
Тогда наружный диаметр втулки![]() .
.
Округляя до целого, окончательно примем![]() .
.
В
заключение отметим, что следовало бы
проверить так же условие прочности на
смятие между штифтом и валом, однако
распределение напряжений смятия по
длине цилиндрической поверхности
смятия уже не может быть принято
равномерным. Для определения максимального
напряжения смятия в таких случаях
обычно задаются некоторым априорным
законом его распределения по длине.
Раздел V
РАСЧЕТ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ
СИСТЕМ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ
ПЛОСКОМ ПРЯМОМ ИЗГИБЕ.
Основные понятия и зависимости.
Изгибом
стержня
называется такой вид деформации, при
котором в поперечных сечениях возникают
изгибающие моменты и перерезывающие
силы, деформированная ось стержня
представляет пространственную кривую.
Стержень, работающий на изгиб, обычно
называется балкой.
Плоский
изгиб такой
вид деформации стержня, при котором
деформированная ось стержня является
плоской кривой.
Плоский
изгиб
называется прямым,
если изогнутая ось лежит в грузовой
(силовой) плоскости.
Чтобы изгиб был плоским необходимо,
чтобы грузовая плоскость совпадала с
одной из главных центральных плоскостей
инерции стержня.
Грузовой
(силовой) плоскостью
называется плоскость, в которой лежит
вся внешняя нагрузка, включая реакции.
Пересечение грузовой плоскости с
поперечным сечением называется силовой
линией.
Главной
центральной плоскостью инерции стержня
называется плоскость, проходящая через
главные центральные оси всех его
поперечных сечений. При рассмотрении
плоского прямого изгиба принято главную
центральную плоскость стержня,
совпадающую с грузовой плоскостью
обозначать XY
(где X
– ось стержня). Тогда при плоском прямом
изгибе в поперечных сечениях стержня
будут возникать перерезывающая сила
![]() и
и
изгибающий момент –![]() .
.
В дальнейшем иногда индексы не ставятся,
но подразумеваются. Плоский изгиб
называетсяпоперечным,
если в поперечных сечениях стержня
возникают изгибающие моменты и
перерезывающие силы. Плоский изгиб
называется чистым,
если в поперечных сечениях действуют
только изгибающие моменты,
![]() .
.
Примечание.
В случае, когда грузовая плоскость
совпадает с главной центральной
плоскостью стержня, не являющейся
плоскостью симметрии стержня, кроме
изгиба возникает еще и закручивание
стержня. Чтобы при плоском изгибе не
происходило дополнительное закручивание
стержня необходимо, чтобы внешняя
нагрузка в каждом поперечном сечении
проходила через точку называемую
центром
сдвига (изгиба). Центр
изгиба всегда лежит на оси симметрии
(если она есть) поперечного сечения.
Поэтому при рассмотрении примеров
ограничимся случаем сечений имеющих
ось симметрии и нагруженных в плоскости
симметрии.
Правило
знаков
![]() ,
,![]()
![]() :
:
-изгибающий
момент
![]()
считается положительным, если в
рассматриваемом поперечном сечении
сжимает верхние волокна;
-перерезывающая
сила
![]() считается
считается
положительной, если стремится вращать
рассматриваемую часть стержня по
часовой стрелке;
-распределенная
нагрузка
![]() считается
считается
положительной, если направлена вверх.
Эпюрами
![]() и
и![]() называются графики иллюстрирующие
называются графики иллюстрирующие
изменение этих силовых факторов по
длине стержня. Эпюры![]() и
и![]() строятся по участкам стержня, значения
строятся по участкам стержня, значения![]() и
и![]() определяются методом сечений. Между
определяются методом сечений. Между
распределенной нагрузкойq
и силовыми факторами
![]() ,
,![]() – существуют дифференциальные
– существуют дифференциальные
зависимости:1)![]() 2)
2)![]() 3)
3)![]() ,
,
которые используются как при построении
эпюр, так и при их проверке. Например,
из третьей зависимости следует, чтовыпуклость
эпюры моментов всегда направлена
навстречу распределенной нагрузке.
Напряжения
в поперечных сечениях и условия
прочности при плоском прямом изгибе
стержней.
При
изгибе всегда часть волокон сжата,
часть растянута и в стержне имеется
слой волокон, длина которых не изменяется
называемый нейтральным
слоем.
Пересечение нейтрального слоя с
поперечным сечением называется
нейтральной
линией. При
плоском прямом изгибе нейтральный слой
перпендикулярен грузовой плоскости,
а нейтральная линия в сечении
перпендикулярна силовой линии и
совпадает с главной центральной осью
сечения Z.
При чистом изгибе в поперечных сечениях
возникают только нормальные напряжения,
величина которых изменяется пропорционально
расстоянию до нейтральной линии сечения.
На нейтральной линии нормальные
напряжения равны нулю.
При
чистом плоском изгибе
нормальные напряжения
![]() – для волокон расположенных на расстоянииy
– для волокон расположенных на расстоянииy
от нейтральной
линии, рассчитываются по формуле:
![]() ,
,
где
![]() – момент инерции сечения относительно
– момент инерции сечения относительно
главной центральной оси сечения (или,
то же самое относительно нейтральной
линии). В формулу подставляется модуль
величинy
и
![]() ,
,
а знак нормальных напряжений![]() при
при
этом определяется характером деформации
сечения, например, при отрицательном
моменте волокна верхние будут растянуты
и следовательно для них![]() >0.
>0.
Наибольшие по модулю нормальные
напряжения будут возникать в наиболее
удаленных от нейтральной линии волокнах
![]()
и рассчитываются по формуле
![]() ,
,
где величина![]() – момент сопротивления сечения изгибу
– момент сопротивления сечения изгибу
относительно осиZ.
Условия прочности при чистом изгибе
запишутся в виде: для материалов имеющих
одинаковую прочность на растяжение и
сжатие
![]() ;
;
для материалов имеющих разную прочность
на растяжение и сжатие, должны выполнятся
одновременно два условия –![]() и
и![]() ,
,
где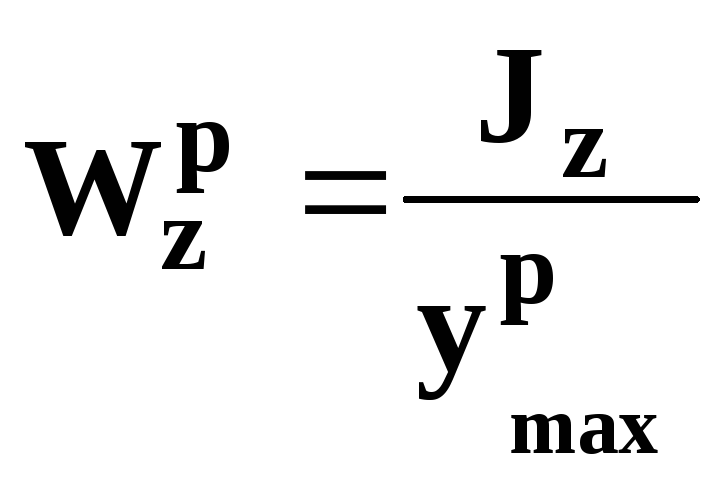 момент сопротивления растянутых
момент сопротивления растянутых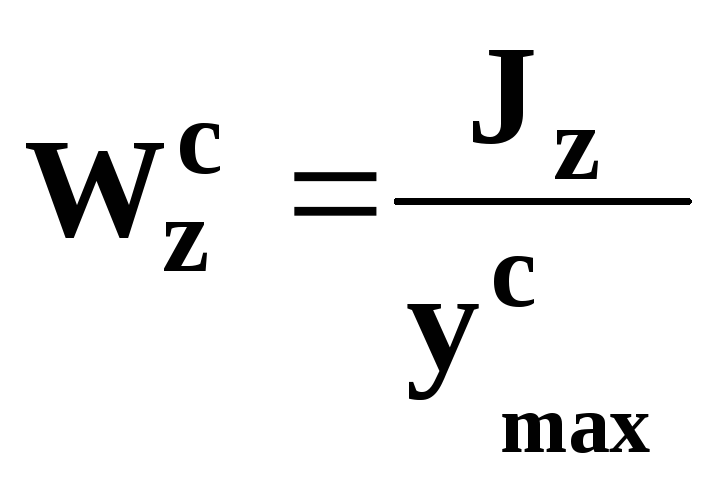 сжатых
сжатых
волокон.
При
поперечном изгибе
нормальные напряжения в сечениях
стержня рассчитываются по формулам
чистого изгиба кроме, приближенно,
возникают так же касательные напряжения.
Касательные напряжения в волокнах
отстоящих на расстоянии y
от нейтральной линии определяются по
формуле Журавского:
![]() ,
,
где![]() – статический момент отсеченной части
– статический момент отсеченной части
сечения (лежащей выше или ниже
рассматриваемых волокон),
![]()
– ширина сечения в месте, где определяются
напряжения![]() .
.
Имеются особенности в использовании
формулы Журавского для массивных
(толстостенных) сечений и для тонкостенных
сечений.
В
толстостенных сечениях предполагается,
что касательные напряжения направленными
параллельно силовой линии (оси Y)
и по направлению действующей в сечении
![]() ,
,
и распределены равномерно по ширине
сечения. Такие предположения справедливы
только для прямоугольных сечений
имеющих ширину меньшую высоты, для всех
остальных форм сечений формула Журавского
является приближенной.
В
тонкостенных сечениях предполагается,
что касательные напряжения распределены
равномерно по толщине стенки сечения
и направленными параллельно средней
линии (средняя линия делит толщину
стенки пополам). Такие предположения
не являются строгими, однако, формула
Журавского, дает достаточно точные
результаты за исключением мест резкого
изменения толщины и направления стенок
сечения.
При
поперечном изгибе в сечениях одновременно
действуют и нормальные и касательные
напряжения, следовательно, напряженное
состояние материала стержня является
двухосным (плоским). Оценка прочности
в этом случае должна учитывать вестись
на основании теорий прочности.
В
массивных (толстостенных) сечений
величина касательных напряжений обычно
незначительна по сравнению с величиной
нормальных напряжений и оценку прочности
допускается вести как при одноосном
напряженном состоянии. Таким образом,
для стержня с массивным сечением при
поперечном изгибе кроме условий
прочности по нормальным напряжениям
изгиба считается достаточным записать
условие прочности по касательным
напряжениям –
![]() .
.
Следовательно, кроме сечений с наибольшим
изгибающим моментом нужно рассматривать
сечения с максимальной перерезывающей
силой.
В
тонкостенных сечениях величина
касательных напряжений может оказаться
сравнимой с величиной нормальных
напряжений и при оценке прочности
необходимо использовать соответствующую
теорию прочности. Для средне пластичных
и пластичных материалов обычно используют
III или IV – теорию прочности. Для случая
поперечного изгиба условие прочности
по III-ей теории прочности –
![]() ,
,
условие прочности по IV-ой теории
прочности –![]() ,
,![]() –
–
нормальные эквивалентные напряжения
в соответствующей теории прочности.
Опасными точками в сечении будут точки
с![]() и
и![]() а также точки, где нормальные и касательные
а также точки, где нормальные и касательные
напряжения одновременно велики. Для
определения опасных точек сечения
следует строить эпюры![]() и
и![]() для опасных сечений. Опасными сечениями
для опасных сечений. Опасными сечениями
будут сечения, где действуют максимальные
изгибающие моменты и перерезывающие
силы, а также сечения, где одновременно
действуют моменты и силы близкие к
максимальным.
Проектировочный
расчет стержней при поперечном изгибе
ведется обычно приближенно с учетом
только нормальных напряжений. Уточненный
расчет по эквивалентным напряжениям
(или с учетом касательных напряжений)
выполняется как проверочный.
Определение перемещений при поперечном изгибе интегрированием дифференциального уравнения изогнутой оси стержня. (с постоянным по длине сечением)
Деформация
стержня при поперечном изгибе
представляется в виде прогибов y
(перемещений перпендикулярных
недеформированной оси) и
поворотов
поперечных сечений стержня. Считается,
что поперечное сечение стержня после
изгиба остается плоским и перпендикулярным
изогнутой оси стержня, откуда следует,
что
![]() .
.
Принято следующееправило
знаков:
прогиб считается положительным, если
направлен вверх; угол поворота считается
положительным, если сечение поворачивается
против часовой стрелки. Для всех
последующих выкладок принята следующая
система координат: ось стержня X
(в недеформированном состоянии)
направлена вправо, ось Y
вверх.
Для
жестких балок максимальные прогибы,
которых малы по сравнению с длиной,
следовательно,
![]() связь углов поворота с прогибами
связь углов поворота с прогибами
упрощается![]() .
.
Для определения перемещения в таких
балках используется линеаризованное
дифференциальное уравнение:![]() ,
,
где![]() – уравнение изогнутой оси стержня
– уравнение изогнутой оси стержня
(кривая изгиба). В этом дифференциальном
уравнении не учитываются перемещениями,
связанными с деформацией сдвига (то
есть с действием перерезывающей силы)
в связи с их малости по сравнению с
деформацией связанной с изгибом.
Последовательно интегрируя это уравнение
два раза, получим соответственно
уравнение углов поворота
![]() уравнение
уравнение
прогибов![]() .
.
Константы интегрирования![]() и
и![]() определяются из граничных условий.
определяются из граничных условий.
Непосредственное
интегрирование дифференциального
уравнения и особенно определение
констант интегрирования для балок
более чем 2-мя участками является
трудоемкой задачей. Так, например, для
балки с N
участками необходимо записать и
проинтегрировать N
дифференциальных уравнений при этом
появится 2N
констант интегрирования
![]() ;
;![]() и для их определения необходимо записать
и для их определения необходимо записать
и использовать2N
граничных условий. Два граничных
условия отражают условия закрепления
стержня в опорах. Для каждой шарнирной
опоры можно записать
![]() ,
,![]() –
–
координата сечения, где расположена
опора. Для жесткой заделки![]() и
и![]() ,
,
где![]() – координата жесткой заделки. Остальные2N-2
– координата жесткой заделки. Остальные2N-2
констант интегрирования находятся из
условий непрерывного (![]() )
)
и плавного (![]() )
)
сопряжения изогнутой оси стержня наN-1
границах между участками, здесь
![]() – координата границы междуi
– координата границы междуi
и i+1
участком.
Метод
начальных параметров
является более удобным для балок со
сложной нагрузкой (с большим количеством
участков). Суть метода начальных
параметров заключается в выравнивания
констант интегрирования по участкам,
в результате, которого неизвестными
остаются лишь две из них
![]() ,
,![]() .
.
Оставшиеся константы интегрирования
имеют простой физический смысл:![]() – прогиб начального (приx
– прогиб начального (приx
= 0) сечения,
![]() – угол поворота начального сечения и
– угол поворота начального сечения и
определяются из условий закрепления
балки. Для произвольной балки постоянного
по длине сечения нагруженнойk
– моментами
![]() иm
иm
-сосредоточенными силами
![]() (включая реакции опор), а такжеn
(включая реакции опор), а такжеn
– равномерно
распределенными нагрузками
![]() уравнения углов поворота и прогибов
уравнения углов поворота и прогибов
записываются одним выражением сразу
для всей балки (для всех участков):
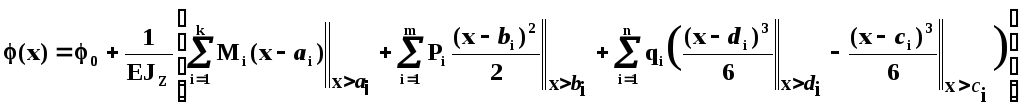
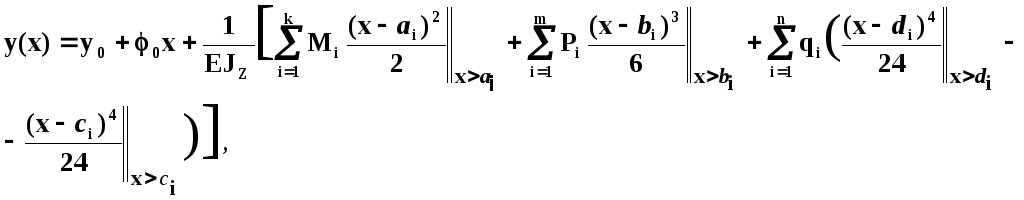
где
ai,
bi
– координаты сечений где приложена
соответственно i
– сосредоточенная сила и i
– сосредоточенный момент, ci,
di
координаты соответственно начала и
конца i
– равномерной распределенной нагрузки.
Двойные черточки у каждого из слагаемых
показывают, при каком условии данное
слагаемое включается в вычисления, а
именно при определении прогибов или
углов поворота в произвольном сечении
с координатой – x
в вышеприведенных выражениях удерживаются
только те слагаемые, которые учитывают
нагрузки, приложенные к балке левее
рассматриваемого сечения. В выражениях
метода начальных параметров принято
следующее правило знаков для внешних
нагрузок:
![]() если он направлен по часовой стрелке;
если он направлен по часовой стрелке;![]() и
и![]() если они направлены вверх.
если они направлены вверх.
Определение перемещений при поперечном изгибе энергетическими методами.
Рассмотренное
выше дифференциальное уравнение
неприменимо для стержней с криволинейной
осью и для рам. Более универсальными в
этом смысле являются энергетические
методы. Наиболее популярным является
метод Мора
(интеграл
Мора).
Согласно
методу Мора рассматриваются два
состояния системы (балки, рамы):
грузовое
и единичное.
Грузовое состояние
обусловлено действием на систему
заданной внешней нагрузки, возникающие
при этом силовые факторы и их эпюры
называются грузовыми. Единичное
состояние
обусловлено действием на систему
единичной обобщенной
нагрузки
приложенной по направлению искомого
перемещения, возникающие при этом
силовые факторы и их эпюры, называются
единичными. Под обобщенной
нагрузкой
понимается либо сосредоточенная сила,
либо сосредоточенный момент. Обобщенной
нагрузке соответствуют обобщенные
перемещения: сосредоточенной
силе соответствует линейное перемещение;
моменту соответствует угол поворота
сечения.
Пренебрегая
перемещениями, связанными с деформацией
сдвига ввиду их малости по сравнению
с деформацией изгиба интеграл Мора для
случая прямого плоского изгиба запишется
в виде:
![]() ,
,
здесь![]() –
–
обобщенное перемещение соответствующее
приложенной единичной обобщенной
нагрузке,![]() выражение грузового изгибающего момента
выражение грузового изгибающего момента
наi
– том участке![]() выражение
выражение
единичного
изгибающего момента на i
– том участке.
Во
всех энергетических методах знак
результата означает: знак «+», что
искомое перемещение совпадает по
направлению с приложенной единичной
нагрузкой; знак «-», что искомое
перемещение противоположно по направлению
приложенной единичной нагрузке.
В
инженерной практике широко используется
графический способ вычисления интеграла
Мора – способ
Верещагина.
Формула Верещагина в виде:
![]() ,
,
где![]() –
–
площадьi
– го участка грузовой эпюры,
![]() ордината эпюры единичного момента
ордината эпюры единичного момента
взятая под центром тяжести участка
грузовой эпюры. Знак «+» перед слагаемым
в формуле ставится в случае когда и
единичная и грузовая эпюры моментов
построены на одноименных волокнах,
знак «-» в противном случае. Минимальное
количество слагаемых в формуле Верещагина
равно количеству участков эпюры
единичного момента. Если границы эпюры
грузового момента не совпадают с
границами эпюры единичного момента,
то грузовую эпюру необходимо дополнительно
разбить по границе единичной эпюры.
Если
имеются трудности с определением
площадей и положений центров тяжести
участков грузовых эпюр, то для вычисления
интеграла Мора рационально использовать
формулу Симпсона-Корнаухова:
![]() ,
,
где![]() – длинаi
– длинаi
– го
участка,
![]() – значения единичных и грузовых моментов
– значения единичных и грузовых моментов
на левой и правой границе и посерединеi
–
го участка соответственно. Формула
Симпсона-Корнаухова справедлива только
для стержней с прямолинейными участками
(для балок и рам) и только если грузовая
эпюра либо линейна, либо является
параболой не выше 2-ой степени.
Отметим,
что перемещения, определенные с помощью
дифференциального уравнения изогнутой
оси и с помощью энергетического метода
получаются одинаковыми по абсолютной
величине.
Задача №1
Задание:
Для заданной стальной балки с поперечным
сечением в виде двутаврового профиля
нагруженной в плоскости XY
(рис.1) из условия прочности подобрать
величину допускаемой внешней нагрузки
[q].
При найденной нагрузке определить
перемещения некоторых произвольных
сечений балки двумя способами: а)
используя дифференциальное уравнение
упругой линии; б) энергетическим методом.
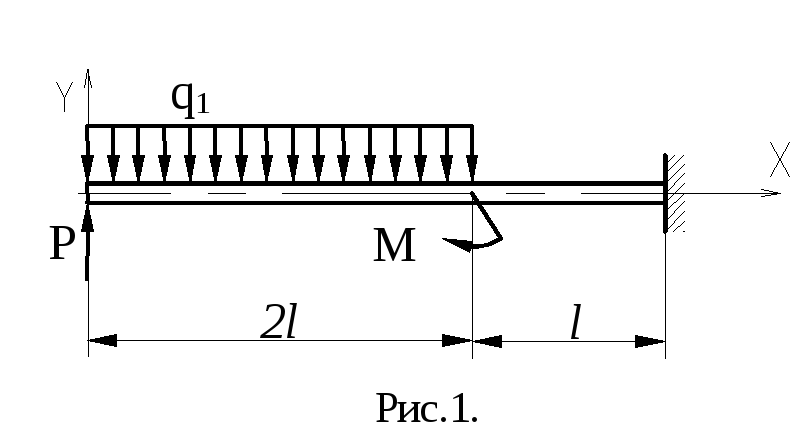 Исходные
Исходные
данные:
l =
1.5 м; P
= 1.5ql;
М
= 2ql2;
q1
= 2q.
Сечение балки двутавр №27 по ГОСТ 8239
–72. Материал балки Сталь30, с модулем
продольной упругости (модулем Юнга) –
Е=2105
МПа
и пределом текучести т
= 300 МПа.
Решение:
1).Определим
допускаемые напряжения для материала
стержней на растяжение и сжатие,
коэффициент запаса прочности, учитывая
что материал балки относительно
пластичный, примем: n=1.5:
![]() .
.
2).Заменим
жесткую заделку ее реакциями (см. рис.2.)
и определим их из условий равновесия
всей балки: из суммы моментов относительно
жесткой заделки получим –![]()
![]() откуда
откуда![]() ,
,
а
из суммы моментов относительно начального
(крайнего левого) сечения
![]()
![]()
![]() .
.
Для проверки правильности нахождения
реакций составим еще одно уравнение
равновесия:
![]() .
.
Найденные реакции удовлетворяют этому
условию, следовательно, реакции
определены верно.
3).
Построим эпюры перерезывающих сил – Q
и изгибающих моментов – M
по участкам балки, используя метод
сечений в следующей последовательности:
-
в
пределах каждого участка проводим
произвольное поперечное сечение на
расстоянии xi
от начала
координат, (которое
выбирается, как правило, в центре
тяжести крайнего левого сечения балки)
затем любая (в
нашем случае правая)
часть балки отбрасывается; -
отброшенная
часть заменяется внутренними силовыми
факторами Q
и M
(т.е.
внутренними
силами взаимодействия частей балки,
которые можно считать реакциями
отброшенной части); -
силовые
факторы Q
и M
определяются
из условий равновесия оставшейся
части, при этом искомые силовые факторы
всегда следует показывать в положительных
направлениях, так чтобы изгибающий
момент стремился сжимать верхние
волокна, а перерезывающая сила стремилась
вращать рассматриваемую часть по
часовой стрелке.
Первый
участок 0
x1
2l
. Перерезывающую силу Q1(x1)
найдем из
уравнения для равновесия рассматриваемой
части (смотри рис.2):
![]() или
или![]() .
.
Зависимость
Q1(x1)
– линейная,
следовательно, эпюру строим по двум
значениям на границах:
![]() и
и![]() .
.
Изгибающий моментM1(x1)
найдем из
уравнения для равновесия рассматриваемой
части (распределенную
нагрузку при этом заменяем равнодействующей
см. рис.2):
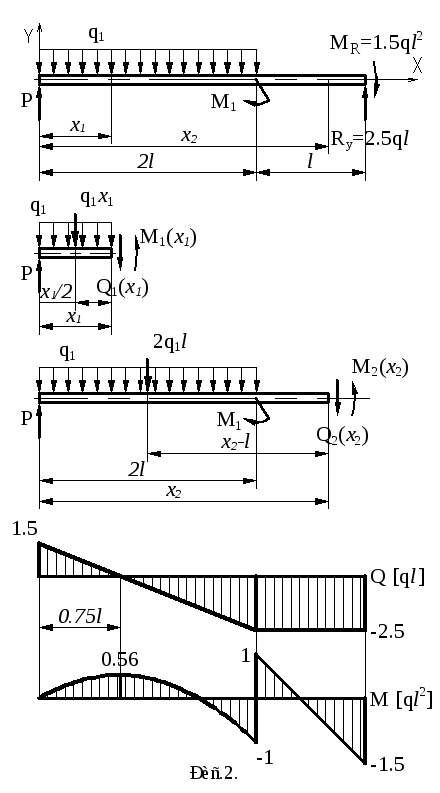
![]()
![]() ,
,
(здесь и
далее при определении изгибающих
моментов в сечении в качестве моментной
точки удобно выбирать центр тяжести
рассматриваемого сечения)
откуда следует:
![]()
![]() .
.
Зависимость M1(x1)
– квадратичная,
эпюра соответственно парабола,
следовательно, кроме значений на
границах участка:
![]() ;
;![]() ,
,
требуется определить значение момента
в вершине параболы. Координату вершины
параболы –![]() найдем как точку экстремума из условия:
найдем как точку экстремума из условия:![]() .
.
Согласно известной дифференциальной
зависимости:
![]() ,
,
тогда из условия
![]() определим:
определим:![]() .
.
Вычислим
значение
![]()
![]() .
.
Кроме того, в дальнейшем для определения
перемещений энергетическим методом
нам понадобится значение момента
посередине участка![]() .
.
По рассчитанным значениям моментов
строим эпюру изгибающего момента и
перерезывающей силы на первом участке
(см. рис.2).
Второй
участок 2l
x2
3l
. Перерезывающую силу Q2(x2)
найдем из
уравнения для равновесия рассматриваемой
части (смотри рис.2):
![]()
![]()
![]() –
–
очевидно, что эпюрой будет горизонтальная
прямая. Изгибающий момент M2(x2)
найдем из
уравнения равновесия рассматриваемой
части (см. рис.2):
![]()
![]() откуда:
откуда:
![]() или окончательно
или окончательно![]() .
.
ЗависимостьM2(x2)
– линейная,
следовательно, эпюру можно построить
по двум значениям на границах участка:
![]() ;
;![]() .
.
Снова для определения перемещений
энергетическим методом определим
значение момента посередине участка
–![]() .
.
По
рассчитанным значениям моментов строим
эпюру изгибающего момента и перерезывающей
силы на первом участке (см. рис.2).
После
построения эпюр Q
и M
нужно
выполнить их качественную проверку по
дифференциальным зависимостям: по
первой зависимости –![]() можно проверить построение эпюры
можно проверить построение эпюры
перерезывающей силы по приложенной
(или
отсутствующей)
распределенной нагрузке; по второй
зависимости –![]() можно проверить построение эпюры
можно проверить построение эпюры
изгибающего момента по эпюре
перерезывающей силы. Кроме того, следует
учитывать следующие правила: в сечениях,
где приложена сосредоточенная сила,
на эпюреQ
имеет место
разрыв (скачек) на величину приложенной
силы; в сечениях, где приложен
сосредоточенный момент, на эпюре
M
имеет место
разрыв (скачек) на величину приложенного
момента.
4).
Для заданного поперечного сечения
балки выпишем из сортамента необходимые
геометрические характеристики:
![]() –
–
момент инерции сечения относительно
нейтральной линии;![]() – момент сопротивления сечения изгибу
– момент сопротивления сечения изгибу
относительно нейтральной линии;![]() – площадь поперечного сечения;
– площадь поперечного сечения;![]() – статический момент половины сечения
– статический момент половины сечения
относительно нейтральной линии;![]() – толщина стенки;
– толщина стенки;![]() – средняя толщина полки;h
– средняя толщина полки;h
= 270 мм – высота
сечения; b
= 125 мм –
ширина полок двутавра.
Из
условия прочности по нормальным
напряжениям определим допускаемую
величину внешней нагрузки. Определим
сначала опасные с точки зрения прочности
сечения. Учитывая, что сечение симметрично
относительно нейтральной линии (кроме
того, материал имеет одинаковую прочность
на растяжение и сжатие) опасным будет
сечение с наибольшим по модулю моментом
изгибающим моментам
![]() .
.
В этом сечении опасными будут точки
наиболее удаленные от нейтральной
линии, то есть крайние верхние или
крайние нижние волокна. Записывая
условия прочности для опасного сечения
(все расчеты
прочности и жесткости в дальнейшем
удобнее вести в размерностях:
[Н]; [мм]; [МПа]): получим допускаемое
значение внешней нагрузки
![]()
![]()
![]() .
.
5).Для
сравнения определим при найденной
величине внешней нагрузки подберем
прямоугольное сечение с отношением
сторон
![]() ,
,
момент сопротивления изгибу для него![]() .
.
Записывая условие прочности для такого
сечения![]() откуда ширина –
откуда ширина –![]() ,
,
высота –![]() ,
,![]() .
.
Тогда при одинаковой прочности расход
материала на балку прямоугольного
сечения будет в![]() раза
раза
больше чем на балку двутавровую.
6).Для
балки двутаврового профиля выполним
уточненную проверку прочности. Сечение
балки является тонкостенным величина
касательных напряжений в поперечных
сечениях может оказаться сравнимой с
величиной нормальных напряжений. Таким
образом,
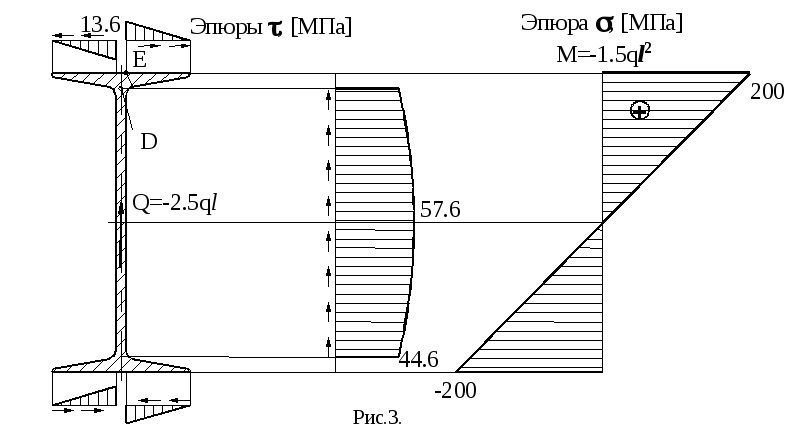 напряженное
напряженное
состояние балки при поперечном изгибе
является существенно двумерным (плоским)
и при проверке прочности следует
воспользоваться одной из теорий
прочности, например IV-ой
теорией. Опасными сечениями могут
оказаться сечения, в которых одновременно
действуют большие по величине Q
и M.
В рассматриваемом примере очевидно,
что опасным является сечение в заделке
x2=3l
где действуют одновременно максимальные
по модулю перерезывающая сила и
изгибающий момент (![]() ,
,![]() )
)
и следовательно возникают наибольшие
нормальные и касательные напряжения.
Эпюра нормальных напряжений в опасном
сечении показана на рис.3. Для расчета
касательных напряжений в тонкостенном
сечении применима формула Журавского:![]() ,
,
где![]() –
–
статический момент отсеченной части
сечения относительно оси нейтральной
линии. В тонкостенных сечениях касательные
напряжения считаются направленными
параллельно средней линии сечения
(которая делит толщину стенки (полки)
пополам), и постоянными по толщине.
Эпюра касательных напряжений в сечении
показана на рис.3. Направления касательных
напряжений в стенке и полках двутавра
зависят от направления перерезывающей
силы и показаны на том же рисунке
стрелками. Для построения эпюры
касательных напряжений достаточно
вычислить их значения в трех точках
сечения. В расчетах обычно полки
переменной толщины заменяются
прямоугольниками с размерами![]() .
.
Максимальные касательные напряжения
возникают на нейтральной линии, где
наибольший статический момент отсеченной
части сечения и минимальная толщина
сечения равная –s:
![]() .
.
Для определения касательных напряжений
в стенке в месте соединения с полкой
–![]() ,
,
необходимо вычислить статический
момент площади полки относительно
нейтральной линии сечения:![]() .
.
Тогда
![]() .
.
Максимальные
касательные напряжения в полках равны
![]() .
.
По
эпюрам нормальных и касательных
напряжений представленным на рис.3
видно, что опасными точками в сечении
являются т. D
и E.
Определим в этих точках эквивалентные
напряжения по IV-ой
теории прочности. Эквивалентное
напряжение в т.D
![]() ,
,
нормальное напряжение![]() можно определить графически по эпюре
можно определить графически по эпюре
рис.3 или используя общую формулу![]() ,
,
где![]() – расстояние от нейтральной линии до
– расстояние от нейтральной линии до
точки D. Эквивалентное напряжение в т.E
![]() .
.
Эквивалентные напряжения в опасных
точках превосходят допускаемые![]() ,
,
однако перегрузка составляет < 5% и
прочность балки можно считать
обеспеченной. В случаях, когда максимальные
напряжения превосходят допускаемые
более чем на 5% для выполнения условий
прочности следует пропорционально
уменьшить нагрузку или увеличить
размеры сечения.
7).Запишем
и решим дифференциальное уравнение
упругой линии для рассматриваемой
балки. Балка состоит из двух участков
и следовательно необходимо записать
и проинтегрировать дифференциальные
уравнения для каждого из них.
Первый
участок – 0
x1
2l
:
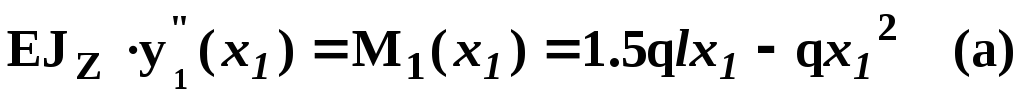 .
.
Интегрируя
два раза, получим соответственно
выражения для углов поворота и прогибов:
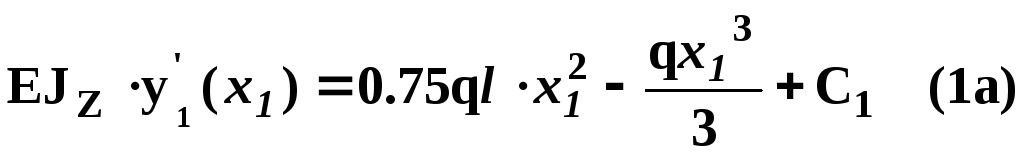
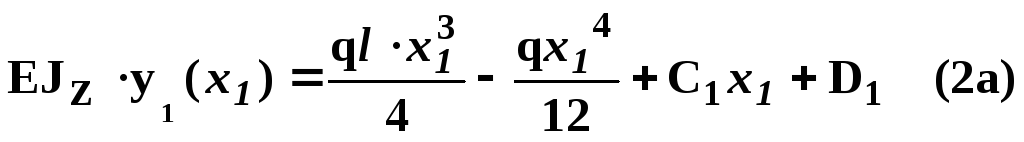 .
.
Второй
участок – 2l
x1
3l
:
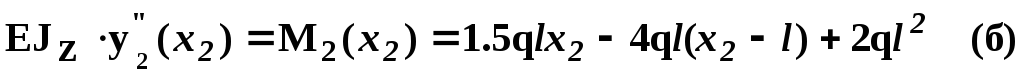 .
.
Интегрируя,
получим выражения для углов поворота
и прогибов для второго участка:
![]()
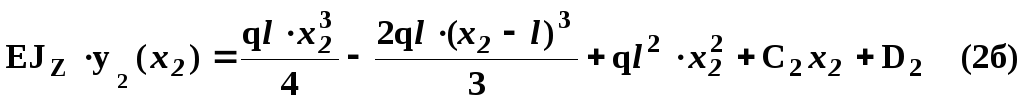 .
.
Для
определения 4-х констант интегрирования
имеются 4 граничных условия. Два граничных
условия должны учесть способ закрепления
балки, то есть тот факт, что прогиб и
угол поворота сечения в жесткой заделке
равны нулю:
![]() ;
;![]() .
.
Два других граничных условия являются
условиями неразрывности балки на
границе между участками:![]() ;
;![]() .
.
Поставляя уравнения![]() и
и![]() в граничное условие
в граничное условие![]() ,
,
уравнения![]() и
и![]() в условие
в условие![]() ,
,
уравнение![]() в условие
в условие![]() ,
,
уравнение![]() в условие
в условие![]() получим следующую систему линейных
получим следующую систему линейных
уравнений относительно констант
интегрирования:
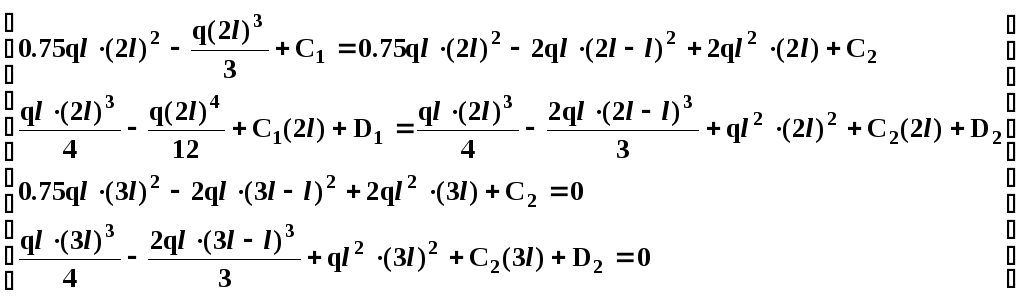
Упрощая
и преобразуя запишем систему ее в виде:
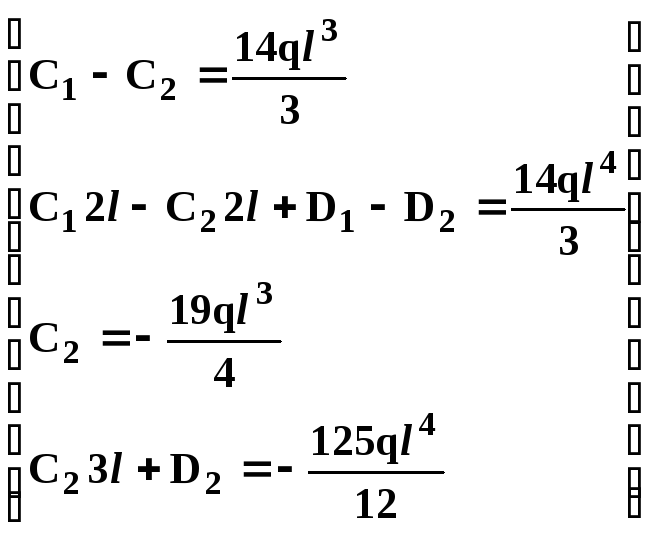
Разрешая
последнюю систему, определяем неизвестные:
![]() ;
;![]() ;
;![]() ;
;![]() .
.
Теперь выражения для прогибов и углов
поворота для обоих участков становятся
полностью определенными и записываются
в виде:
![]()
![]()
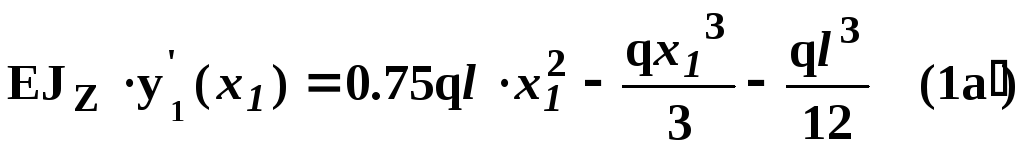
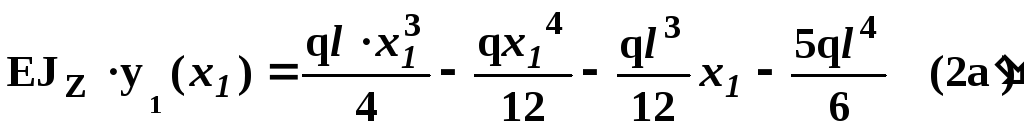 .
.
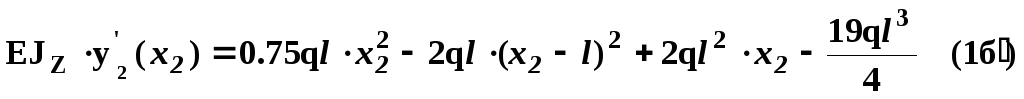
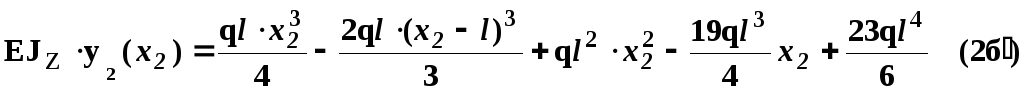 .
.
Используя эти выражения можно рассчитать
прогиб и угол поворота любого сечения
балки, например прогиб –![]() и угол поворота –
и угол поворота –
![]() крайнего
крайнего
левого сечения балки. Отрицательные
значения прогиба означают, что прогиб
направлен вниз, отрицательные значения
угла поворота означают, что поворот
сечения происходит по часовой стрелке.
Отметим, что определение 4-х констант,
несмотря на относительную простоту
рассматриваемой балки, оказалось
довольно трудоемкой процедурой, поэтому
для определения перемещений рационально
использовать метод начальных параметров.
Использование метода начальных
параметров для определения перемещений
рассмотрено в задаче №2.
8).
Снова определим прогиб и угол поворота
крайнего левого сечения, но уже
энергетическим методом используя
интеграл Мора.
Согласно
методу Мора для определения прогиба в
сечении рассмотрим 1-е единичное
состояние, приложим в сечении единичную
вертикальную силу и построим эпюру
единичного момента
![]() см. рис.4. Далее интеграл Мора для прогиба
см. рис.4. Далее интеграл Мора для прогиба
данного сечения будем вычислять способом
Верещагина, согласно которому необходимо
перемножить эпюру грузового (изгибающего
момента от внешней нагрузки) момента
на соответствующую единичную![]()
![]() .
.
На рис.4 для наглядности перенесена
эпюра грузового момента построенная
ранее (рис.2). Так как вычисление центров
тяжести и площадей участков грузовой
эпюры в данном случае достаточно
трудоемко воспользуемся формулой
Симпсона-Корноухова. На рис.4 показаны
ординаты единичной и грузовой эпюр на
левой и правой границах и в средних
сечениях каждого участка, необходимые
для формулы Симпсона-Корноухова.
Подставляя необходимые значения с эпюр
в формулу Симпсона-Корноухова, получим
искомый прогиб сечения:
![]()
![]() .
.
Для определения
угла поворота крайнего левого сечения
рассмотрим 2-е единичное состояние,
приложим в сечении единичный момент.
Построим эпюру единичного момента
![]() см. рис.4. Перемножая эпюры
см. рис.4. Перемножая эпюры![]()
![]() по Верещагину, снова используем формулу
по Верещагину, снова используем формулу
Симпсона-Корноухова. Подставляя
необходимые значения с эпюр в формулу
Симпсона-Корноухова, получим угол
поворота сечения:
![]() Найденные
Найденные
значения совпадают по модулю с полученными
при решении дифференциального уравнения
упругой линии. В энергетических методах
знак «+»
означает, что направление перемещения
совпадает с направлением соответствующей
единичной нагрузки, знак «-»
означает, что направление перемещения
противоположно направлению единичной
нагрузки. Следовательно в рассматриваемом
случае прогиб сечения направлен вниз,
а поворот сечения происходит по
направлению единичного момента
(см.рис.4) то есть по часовой стрелке.
Таким образом направления перемещений
совпадают с полученными при решении
дифференциального уравнения упругой
линии, что является подтверждением
правильности определения перемещений.
Задача №2.
Задание:
Для заданной балки нагруженной в
плоскости XY
(рис.1) из условия прочности подобрать
размеры поперечного сечения в виде
нестандартного тавра (сечение показано
там же). Определить перемещения и углы
поворота некоторых сечений балки,
используя дифференциальное уравнение
упругой линии балки. Определить
перемещения и углы поворота некоторых
сечений балки, используя энергетический
метод.
Исходные
данные:
l =
2000 мм; P
= 20 кН;
М
= 10 кНм;
q1
= 15 кН/м;
q2
= 10 кН/м.
Материал стержней чугун СЧ15-32,
с модулем продольной упругости (модулем
Юнга) – Е=1.1105
МПа
и пределами прочности на растяжение и
сжатие вр
= 150 МПа, вс
= 650 МПа.
Решение:
1).Определим
допускаемые напряжения для материала
стержней на растяжение и сжатие,
коэффициент запаса прочности, учитывая
что материал балки хрупкий, примем:
n=2:
; .
2).Определим
реакции опор из условий равновесия
всей балки (см. рис.1): из суммы моментов
относительно первой (левой) опоры
получим –
![]()
из
суммы моментов относительно второй
(правой) опоры получим –
![]()
Из
уравнения (1)
выразим и определим реакцию левой
шарнирной опоры R2
а из уравнения
(2)
реакцию левой шарнирной опоры R1
(нагрузку
подставляем в [кН] а размеры в [м]):
![]()
![]()
Для
проверки правильности нахождения
реакций составим еще одно уравнение
равновесия:
![]() .
.
Найденные реакции удовлетворяют этому
условию, следовательно, реакции
определены верно.
3).
Построим эпюры перерезывающих сил – Q
и изгибающих моментов – M
по участкам балки, используя метод
сечений в следующей последовательности:
-
в
пределах каждого участка проводим
произвольное поперечное сечение на
расстоянии xi
от начала
координат, (которое
выбирается, как правило, в центре
тяжести крайнего левого сечения балки)
затем любая (в
нашем случае правая)
часть балки отбрасывается; -
отброшенная
часть заменяется внутренними силовыми
факторами Q
и M
(т.е.
внутренними
силами взаимодействия частей балки,
которые можно считать реакциями
отброшенной части); -
силовые
факторы Q
и M
определяются
из условий равновесия оставшейся
части, при этом искомые силовые факторы
всегда следует показывать в положительных
направлениях, так чтобы изгибающий
момент стремился сжимать верхние
волокна, а перерезывающая сила стремилась
вращать рассматриваемую часть по
часовой стрелке.
Первый
участок 0
x1
l
. Перерезывающую силу Q1(x1)
найдем из
уравнения для равновесия рассматриваемой
части (смотри рис.1):
![]() –
–
очевидно, что эпюрой будет горизонтальная
прямая. Изгибающий момент M1(x1)
найдем из
уравнения для равновесия рассматриваемой
части (см. рис.1):
![]() (здесь и
(здесь и
далее при определении изгибающих
моментов в сечении в качестве моментной
точки удобно выбирать центр тяжести
рассматриваемого сечения)
откуда:
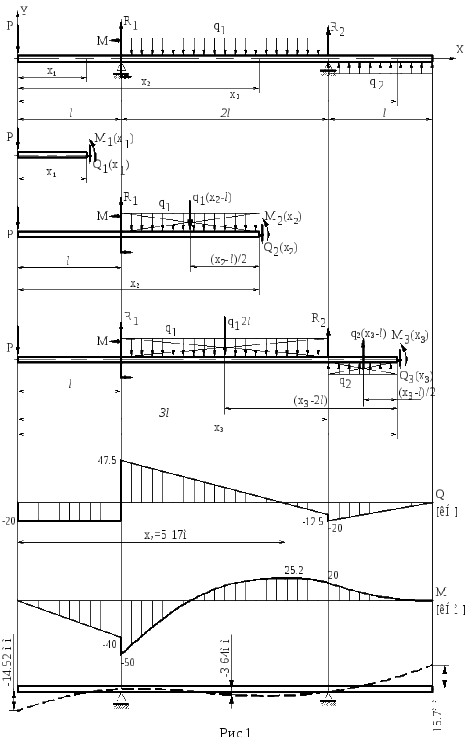
![]() .
.
Зависимость M1(x1)
– линейная,
следовательно, эпюру можно построить
по двум значениям на границах участка:
![]() и
и![]() .
.
Второй
участок l
x2
3l
. Перерезывающую силу Q2(x2)
найдем из
уравнения равновесия для рассматриваемой
части (смотри рис.1):
![]() .
.
Зависимость
Q2(x2)
– линейная,
следовательно, эпюру строим по двум
значениям на границах:
![]() и
и![]() .
.
Изгибающий моментM2(x2)
найдем из
уравнения для равновесия рассматриваемой
части (распределенную
нагрузку при этом заменяем равнодействующей
см. рис.1):
![]()
![]() ,
,
откуда следует:
![]() .
.
Зависимость M2(x2)
– квадратичная,
эпюра соответственно парабола,
следовательно, кроме значений на
границах участка:
![]() ;
;
![]() требуется
требуется
определить значение момента в вершине
параболы. Координату вершины параболы
–
![]() найдем как точку экстремума из условия:
найдем как точку экстремума из условия:![]() .
.
Согласно дифференциальной зависимости:![]() ,
,
значит,![]() откуда определим:
откуда определим:![]() .
.
Вычислим значение
![]()
По
рассчитанным трем значениям моментов
строим эпюру изгибающего момента на
втором участке (см. рис.1).
Третий
участок 3l
x3
4l
. Перерезывающую силу Q3(x3)
найдем из
уравнения для равновесия рассматриваемой
части (смотри рис.1):
![]() откуда
откуда
выразим перерезывающую силу –
![]() .
.
Зависимость
Q3(x3)
– линейная,
следовательно, эпюру строим по двум
значениям на границах:
![]()
![]() .
.
Изгибающий
момент M3(x3)
найдем из
уравнения равновесия
![]() ,
,
рассматриваемой части (распределенные
нагрузки при этом заменяем равнодействующими
см. рис.1):
![]() ,
,
откуда:
![]() .
.
ЗависимостьM3(x3)
– квадратичная,
эпюра моментов парабола, следовательно,
кроме значений на границах участка:
![]()
![]() ;
;
![]()
![]() ,
,
требуется
определить значение момента в вершине
параболы. Однако, используя дифференциальную
зависимость
![]() легко определить, что вершина эпюры
легко определить, что вершина эпюры
моментов совпадает с правой границей
участка (x3
= 4l),
так как в этом сечении Q3(x3)=0.
Значит, эпюру можно построить по
значениям на границах участка, учитывая,
что выпуклость эпюры моментов всегда
направлена навстречу направлению
распределенной нагрузки на участке
(см. рис.1).
После
построения эпюр Q
и M
нужно
выполнить их качественную проверку по
дифференциальным зависимостям: по
первой зависимости –![]() можно проверить построение эпюры
можно проверить построение эпюры
перерезывающей силы по приложенной
(или
отсутствующей)
распределенной нагрузке; по второй
зависимости –![]() можно проверить построение эпюры
можно проверить построение эпюры
изгибающего момента по эпюре
перерезывающей силы. Кроме того, следует
учитывать следующие правила: в сечениях,
где приложена сосредоточенная сила,
на эпюреQ
имеет место
разрыв (скачек) на величину приложенной
силы; в сечениях, где приложен
сосредоточенный момент, на эпюре
M
имеет место
разрыв (скачек) на величину приложенного
момента.
4).
Для заданного поперечного сечения
балки (рис.2)
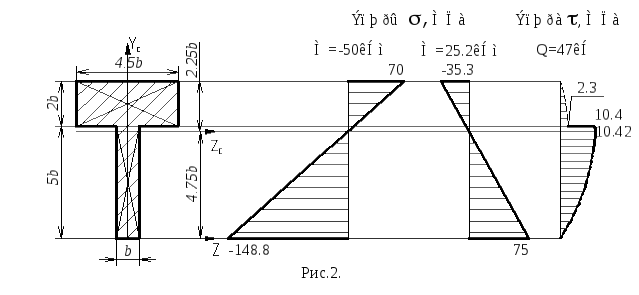
определим
положение нейтральной линии. Как
известно, нейтральная линия совпадает
главной центральной осью перпендикулярной
грузовой плоскости, в нашем случае
грузовой плоскостью является – XY,
следовательно, нейтральная линия
совпадает с осью Zc.
Выберем начальную систему координат
как показано на рис.2. Разобьем сечение
на простейшие фигуры – два прямоугольника
верхний и нижний с площадями соответственно:
![]() и
и![]() .
.
Вычислим статический момент сечения
относительно начальной осиZ
как сумму статических моментов верхнего
и нижнего прямоугольников
![]() где:
где:![]() соответственно координаты центров
соответственно координаты центров
тяжести верхнего и нижнего прямоугольника.
Положение нейтральной линии (осиZc)
определится координатой
![]() .
.
Определим момент инерции сечения
относительно нейтральной линии (осиZc):
![]() ,
,
где –![]() и
и![]() соответственно
соответственно
моменты инерции верхнего и нижнего
прямоугольников:
![]()
![]()
первые
слагаемые в приведенных выражениях
есть моменты инерции верхнего и нижнего
прямоугольников относительно собственных
центральных осей (параллельных
оси Zc),
вторые слагаемые являются поправками
Штейнера для перехода от собственных
центральных осей прямоугольников к
оси Zc.
Таким образом, момент инерции сечения
относительно нейтральной линии Zc
:
![]() .
.
Вычислим моменты
сопротивления сечения для верхних и
нижних волокон:
![]() ;
;
![]() ,
,
где
![]() ,
,![]() соответственно расстояния от нейтральной
соответственно расстояния от нейтральной
линии до крайних верхних и крайних
нижних волокон (см. рис.2).
5).Из
условия прочности по нормальным
напряжениям определим минимально
необходимый размер поперечного сечения
– b.
Определим сначала опасные с точки
зрения прочности сечения. Потенциально
опасными будут сечения с наибольшим
положительным
![]() и наибольшим отрицательным
и наибольшим отрицательным![]() изгибающими
изгибающими
моментами, так как поперечное сечение
стержня несимметрично относительно
нейтральной линии и материал стержня
имеет разные допускаемые напряжения
на растяжение и сжатие (в
других случаях, если хотя бы одно из
этих условий не выполняется, то опасным
будет сечение с наибольшим по модулю
моментом).
В каждом из этих сечений опасными могут
оказаться точки наиболее удаленные от
нейтральной линии, то есть крайние
верхние или крайние нижние волокна. В
самом общем случае для двух опасных
сечений следует рассмотреть четыре
условия прочности.(Все
расчеты прочности и жесткости в
дальнейшем удобнее вести в размерностях:
[Н]; [мм]; [МПа]).
Записывая
условия прочности для сечения с
![]() для сжатых (верхних) волокон:
для сжатых (верхних) волокон:![]()
![]()
![]() ;
;
для
растянутых (нижних) волокон:
![]()
![]()
![]() .
.
Из
условия прочности для сечения с
![]() для растянутых (верхних) волокон (в
для растянутых (верхних) волокон (в
формулах для расчета напряжений
изгибающий момент всегда берется по
модулю а знак напряжений определяется
характером деформации соответствующих
волокон):
![]()
![]()
![]() ;
;
для
сжатых (нижних) волокон:
![]()
![]()
![]() .
.
Максимальное
значение –
![]() получилось из условия прочности
получилось из условия прочности
растянутых (нижних) волокон сечения с
моментом![]() ,
,
значит самыми опасными являются эти
волокна. Окончательно принимаем –![]() .
.
Для
проверки рассчитаем действующие в
опасных напряжения и убедимся, что
условия прочности выполнены. Для
сечения с моментом
![]() :
:
в верхних волокнах напряжения сжатия
–![]() ;
;
в нижних волокнах напряжения растяжения
–![]() .
.
Для
сечения с моментом
![]() :
:
в верхних волокнах напряжения
растяжения –![]() ;
;
в нижних волокнах напряжения сжатия
–![]() .
.
По полученным значениям строим эпюры
нормальных напряжений в опасных сечениях
(см. рис.2). Определим величину момента
инерции сечения относительно осиZc:
![]()
6).Выполним
проверку прочности балки. Напряженное
состояние в сечениях балки при поперечном
изгибе является плоским и в прочностных
расчетах в общем случае следует
использовать теории прочности. Однако,
в рассматриваемом примере сечение не
является тонкостенным и следовательно
касательные напряжения малы по сравнению
с нормальными, кроме того большие по
величине нормальные и касательные
напряжения действуют в разных точках
сечения (см. эпюры рис.2). Учитывая
изложенное выше, проверку прочности
можно свести к условию прочности
отдельно по касательным напряжениям.
Допускаемые
касательные напряжения ориентировочно
можно определить как:
![]() .
.
Для расчета касательных напряжений в
поперечном сечении используем формулу
Журавского:![]() ,
,
где![]() –
–
статический момент отсеченной части
(лежащей выше
или ниже линии с координатой y,
на которой определяются напряжения
)
сечения относительно оси Zc.
Формула Журавского выведена в
предположении, что касательные напряжения
направлены по оси Y
и постоянны по ширине сечения.
Максимальные касательные напряжения
возникают в сечении с
![]() .
.
Для сечения любой формы статический
момент отсеченной части максимален на
нейтральной линии:![]() ,
,
в рассматриваемом сечении на той же
линии ширина сечения минимальна и равна![]() ,
,
следовательно![]() .
.
Удобно вычислить![]() как статический момент прямоугольника
как статический момент прямоугольника
расположенного нижеZc.
Тогда,
![]() условие прочности по касательным
условие прочности по касательным
напряжениям выполняется. Для построения
эпюры касательных напряжений в опасном
сечении (см. рис.2) учтем, что на крайних
волокнах верхних и нижних касательные
напряжения всегда равны нулю, так как
для них![]() (нет
(нет
отсеченной части).
Кроме того, по формуле Журавского
вычислим касательные напряжения на
границе верхнего и нижнего прямоугольников
при
![]() :
:![]() – для ширины
– для ширины![]() и соответственно в 4.5 раза меньше
и соответственно в 4.5 раза меньше![]() –
–
для ширины![]() .
.
Эпюра
(y)
для верхнего прямоугольника условна
и показана штрихами, так как ширина
прямоугольника больше его высоты и
формула Журавского здесь применима
только для ориентировочных расчетов.
7).Запишем
уравнение изогнутой оси балки, используя
общие выражения метода начальных
параметров, учитывая направление
нагрузок показанное на рис.1:
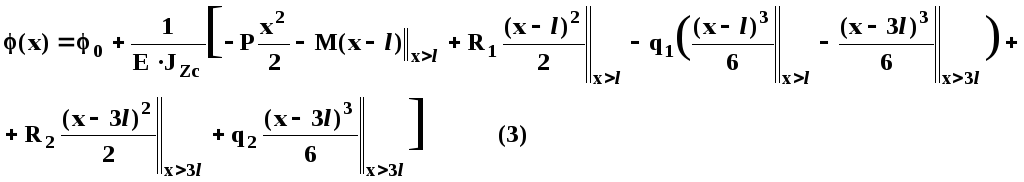 –
–
уравнение углов поворота поперечных
сечений;
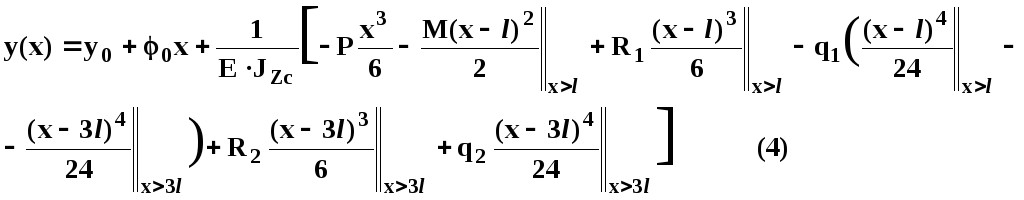
уравнение
прогибов поперечных сечений. При
определении прогибов или углов поворота
в произвольном сечении с координатой
– x
в вышеприведенных уравнениях удерживаются
только те слагаемые, которые учитывают
нагрузки, приложенные к балке левее
рассматриваемого сечения. Двойные
черточки у слагаемых показывают, при
каком условии данное слагаемое включается
в вычисления.
Начальные
параметры –
![]() имеют
имеют
смысл соответственно прогиба и угла
сечения находящегося в начале координат
(приx
= 0), и должны
быть определены из граничных условий.
В качестве граничных условий используем
тот факт что прогибы сечений где
расположены опоры равны нулю, которые
могут быть записаны:
![]() ;
;![]() .
.
Подставляя условие(а)
в выражение (4)
получим
следующее уравнение:
![]()
![]() .
.
Подставляя
условие (b)
в выражение (4)
получим
соответственно:
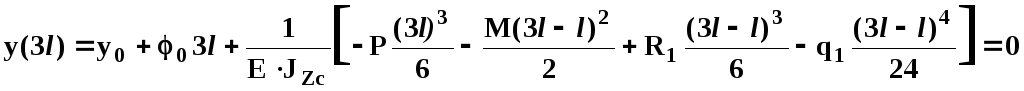
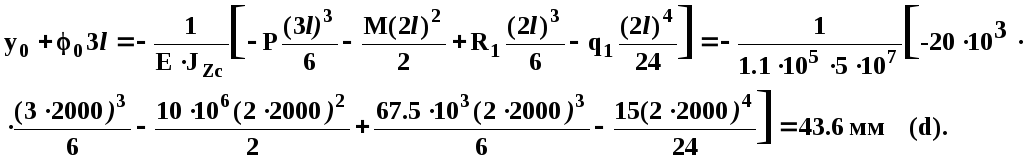
Решая
совместно уравнения (c),
(d)
определяем:
![]() и
и![]()
Теперь,
когда определены начальные параметры
![]() по формулам(3)
по формулам(3)
и (4)
можно определить угол поворота и прогиб
любого сечения балки. Определим,
например, прогиб среднего сечения
второго участка (x
= 2l):
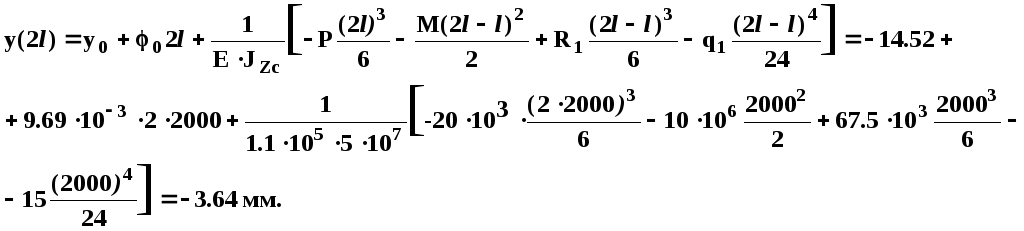 Кроме
Кроме
того, определим прогиб крайнего правого
сечения балки (x
= 4l):
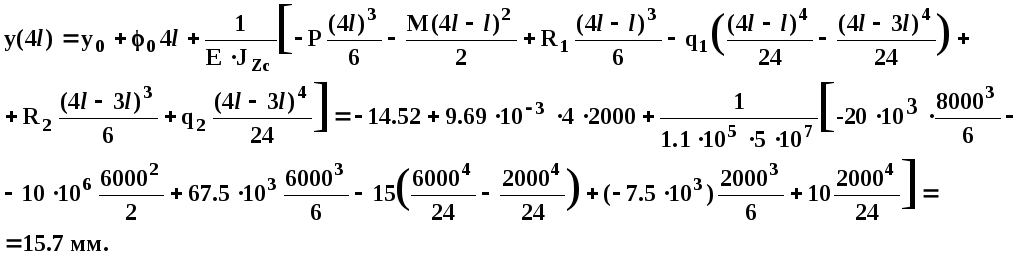 По
По
рассчитанным прогибам можно построить
приблизительную форму изогнутой оси
балки смотри рис.1. При
этом следует учитывать, что выпуклость
изогнутой оси направлена вверх, если
изгибающий момент отрицательный, а при
положительном изгибающем моменте
выпуклость изогнутой оси направлена
вниз.
8).
Определим перемещения сечения
![]() и угол поворота сечения
и угол поворота сечения![]() и энергетическим способом, а именно
и энергетическим способом, а именно
способом Верещагина.
Сначала
определим сначала
![]() ,
,
для этого приложим в искомом сечении
единичную силу см. рис.3. Определим
реакции опор, используя уравнения
равновесия всей балки: из суммы моментов
относительно опоры левой получим –![]() ,
,
откуда![]() ,
,
из![]()
![]() .
.
Строим эпюру единичного изгибающего
момента (от
действия только единичной нагрузки)
по тем же правилам что и грузовую,
описание построения эпюры опускаем в
силу элементарности. Единичная эпюра
представлена на рис.3, там же для удобства
повторена эпюра грузового момента с
обозначенными площадями участков и
положением их центров тяжести (участки
эпюры разбиты на простейшие фигуры для
удобства определения площадей и центров
тяжести).
Теперь для определения
![]() нужно перемножить эпюры
нужно перемножить эпюры![]() и
и![]() по формуле Верещагина:
по формуле Верещагина:
![]() ,
,
отрицательный знак означает, что
участок
грузовой эпюры и единичная эпюра лежат
на разноименных волокнах.
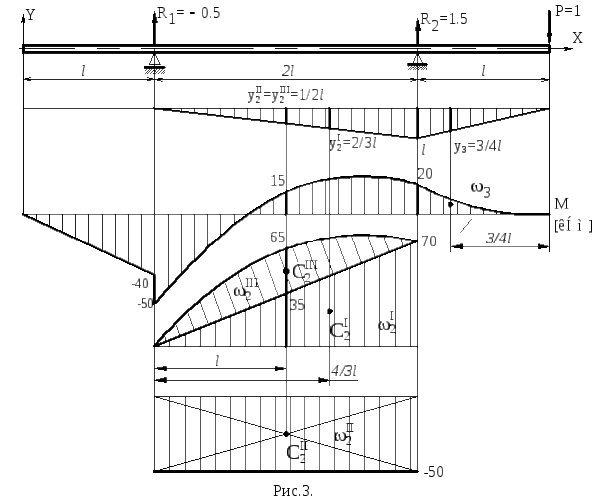
Вычисляя
площади треугольника –
![]() ,
,
прямоугольника –
![]() ,
,
симметричной (относительно
середины участка)
параболы –
![]() ,
,
криволинейного треугольника (парабола
с вершиной на правой границе)
–
![]() .
.
Кроме того, на рис.3 показаны ординаты
единичного момента в сечениях, где
находятся центры тяжестей соответствующих
участков эпюры грузового момента,
значения которых –
![]() ,
,
![]() ,
,
![]() .
.
Подставляя значения в формулу Верещагина
(в размерностях
– Н, МПа, мм)
получим:
![]() ,
,
знак «-» означает, что перемещение
направлено против направления единичной
силы, то есть вверх. Таким образом,
результат совпадает с полученным ранее.
Для
определения
![]() к балке в сеченииx=2l
к балке в сеченииx=2l
приложим единичный момент (см. рис.4).
Составляя уравнение равновесия
относительно левой опоры
![]()
![]() ,
,
а из условия![]() очевидно,
очевидно,
что![]() .
.
Эпюра единичного момента совместно с
грузовой эпюрой представлена на рис.4.
Для использования формулы Верещагина
грузовую эпюру на втором участке
необходимо разбить еще на 2 участка
(соответственно
единичной)
каждый из которых ограничен квадратичной
параболой. Вычисление площадей и центров
тяжести грузовой эпюрой в этом случае
весьма трудоемкая задача и для
перемножения эпюр по Верещагину
рационально использовать формулу
Симпсона-Корноухова, на рис. 4 проставлены
необходимые для перемножения ординаты
эпюр – значения ординат на границах
и серединах участков.
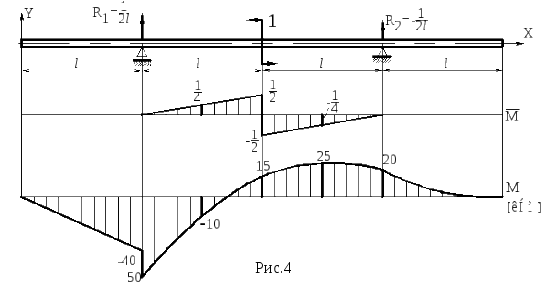
Применяя
формулу Симпсона-Корноухова для значения
в (в размерностях
– Н, МПа, мм)
получим следующий результат:
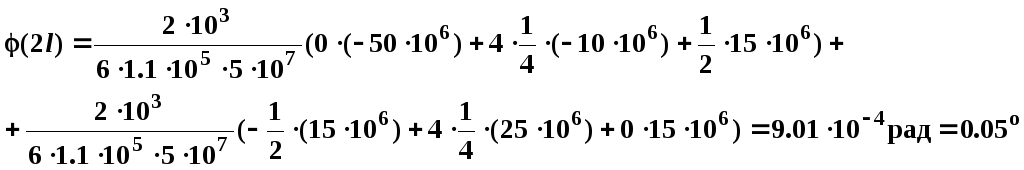
Знак
«+» означает, что сечение поворачивается
по направлению единичного момента
против часовой стрелки.
Задача №3.

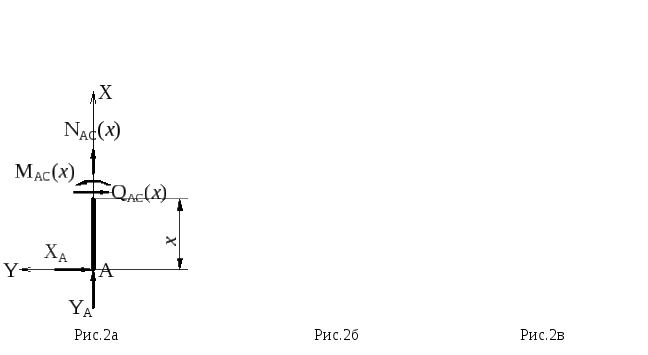
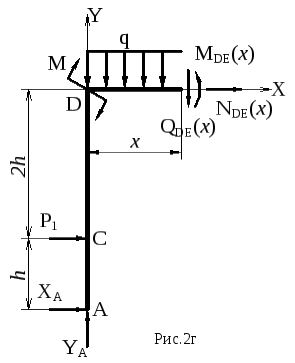
Задание:
Для заданной плоской рамы нагруженной
в плоскости XY
(рис.1) из условия прочности подобрать
размеры поперечного сечения в виде
двух швеллеров (ориентация сечения
показано там же). Рассчитать перемещение
одного и угол поворота другого произвольно
выбранных поперечных сечений рамы.
Исходные
данные:
h
= 2000 мм;
l
= 4000 мм;
P1
= 20 кН;
P2
= 30 кН;
М
= 40 кНм;
q
= 20 кН/м.
Материал
стержней Сталь 6, с модулем продольной
упругости (модулем Юнга) – Е=2105
МПа
и пределом текучести т
= 300 МПа.
Решение:
1).Определим
допускаемые напряжения для материала
стержней, принимая коэффициент запаса
прочности n
= 1.5:
![]() .
.
2).Определим
реакции опор из условий равновесия
всей рамы: из суммы моментов относительно
опоры А
(левой) получим –
![]() ,
,
откуда получим
![]() .
.
Из уравнений:
![]()
![]() ;
;
и![]()
![]()
![]() .
.
Для
проверки правильности нахождения
реакций используем уравнение равновесия:
![]() :
:![]() ,
,
подставляя значения![]() ,
,
убеждаемся, что найденные реакции
удовлетворяют этому условию,
следовательно, они определены верно.
3).
Построим эпюры нормальных – N,
перерезывающих сил – Q
и изгибающих моментов – M
на участках рамы, используя метод
сечений в следующей последовательности:
-
в
пределах каждого участка проводим
произвольное поперечное сечение на
расстоянии xi
от начала
координат, (которое
выбирается в центре тяжести одного из
граничных сечений участка рамы, ось
Х как всегда совпадает с осью
рассматриваемого участка стержня)
затем любая часть балки отбрасывается; -
отброшенная
часть заменяется внутренними силовыми
факторами N,
Q
и M
(то есть
внутренними силами взаимодействия
частей рамы, которые можно считать
реакциями отброшенной части); -
силовые
факторы N,
Q
и M
определяются
из условий равновесия оставшейся
части, при этом искомые силовые факторы
всегда следует показывать в положительных
направлениях: N
– так чтобы
стремилась растягивать рассматриваемый
участок (то есть должна быть направлена
из сечения); Q
– так чтобы стремилась вращать
рассматриваемую часть участка рамы
по часовой стрелке; M
– при построении эпюры изгибающего
момента в рамах правило знаков не
устанавливается, эпюра моментов всегда
строится на сжатых волокнах без указания
знака.
Участок
АС – 0
x
h.
(рис.2а)
Нормальную
силу NАС(x)
найдем из
условия равновесия
![]() ;
;![]() ,
,
откуда очевидно, что нормальная сила
на участке постоянна и равна![]() .
.
Перерезывающую
силу QАС(x)
найдем из
условия
![]() ;
;![]() ,
,
откуда очевидно, что перерезывающая
сила на участке постоянна и равна![]() .
.
Изгибающий
момент MАС(x)
найдем из
условия
![]() ;
;![]() (здесь и
(здесь и
далее при определении изгибающих
моментов в сечении в качестве моментной
точки удобно выбирать т. С
– центр
тяжести рассматриваемого сечения),
откуда следует, что изгибающий момент
на участке линейно изменяется –
![]() ,
,
и его эпюру строим по двум значениям
на границах участка в т.А (x=0)
и С (x=2
м.):
![]() ,
,![]() .Знак «-»
.Знак «-»
означает, что сжимаются правые
(внутренние) волокна, так как сначала
(см. рис.2а) момент выбран сжимающим
левые (внешние) волокна.
Эпюры представлены на рис. 3а,б,в.
Участок
СD
– h
x
3h.
(рис.2б)
Нормальную
силу NСD(x)
найдем из
условия равновесия
![]() ;
;![]() ,
,
откуда очевидно, что нормальная сила
на участке постоянна и равна:![]() .
.
Перерезывающую
силу QСD(x)
найдем из
условия
![]() ;
;![]() ,
,
откуда очевидно, что перерезывающая
сила на участке постоянна и равна![]() .
.
Изгибающий
момент MСD(x)
найдем из
условия
![]() ;
;![]() откуда следует, что изгибающий момент
откуда следует, что изгибающий момент
на участке линейно изменяется –![]() ,
,
и его эпюру строим по двум значениям
на границах участка в т.С (x=2
м.) и D
(x=6
м.):
![]() ,
,![]() .Знак «-»
.Знак «-»
означает, что сжимаются правые
(внутренние) волокна, так как сначала
(см. рис.2б) момент выбран сжимающим
левые (внешние) волокна.
Эпюры представлены на рис. 3а,б,в.
Участок
BE
– 0
x
h.
(рис.2в).
Нормальную
силу NBE(x)
найдем из
условия равновесия
![]() ;
;![]() .
.
Перерезывающую
силу QBE(x)
найдем из
условия
![]() ;
;![]() ,
,
откуда очевидно, что перерезывающая
сила на участке постоянна и равна![]() .
.
Изгибающий
момент MBE(x)
найдем из
условия
![]() ;
;![]() ,
,
откуда следует, что изгибающий момент
на участке линейно изменяется –![]() ,
,
и его эпюру строим по двум значениям
на границах участка в т.B
(x=0)
и E
(x=2
м.):
![]() ,
,![]() .Знак «-»
.Знак «-»
означает, что сжимаются левые (внутренние)
волокна, так как сначала (см. рис.2в)
момент выбран сжимающим правые (внешние)
волокна.
Эпюры представлены на рис. 3а,б,в.
Участок
DE
– 0
x
l.
(рис.2г).
Нормальную
силу NDE(x)
найдем из
условия равновесия
![]() ;
;![]() ,
,
откуда очевидно, что нормальная сила
на участке постоянна и равна:![]() .
.
Перерезывающую
силу QDE(x)
найдем из
условия
![]() ;
;![]() ,
,
откуда очевидно, что перерезывающая
сила на участке линейно изменяется –![]() ,
,
и для построения эпюры нужно вычислить
два значения т.D
(x=0
м.) и E
(x=4
м.):
![]() ;
;![]() .
.
Изгибающий
момент MDE(x)
найдем из
условия
![]() ;
;![]() откуда следует, что эпюра изгибающего
откуда следует, что эпюра изгибающего
момента на участке является квадратичной
параболой –![]() ,
,
и его эпюру строим по двум значениям
на границах участка в т.D
(x=0
м.) и E
(x=4
м.):
![]() ;
;![]() .
.
Для построения эпюры необходимо также
определить положение вершины параболы
и значение момента в ней, однако,
учитывая дифференциальную зависимость
–![]() ,
,
замечаем, что вершина параболы находится
в точке Е (так как![]() ).
).
Таким образом, эпюру строим по двум
значениям, учитывая кроме того, известный
факт – выпуклость эпюры моментов всегда
направлена навстречу распределенной
нагрузке. Для определения перемещений
потребуется определить значение
изгибающего момента посередине участка
–![]() .Отрицательные
.Отрицательные
значения изгибающего момента означают,
что сжимаются нижние (внутренние)
волокна так как сначала (см. рис.2г)
момент выбран сжимающим верхние
(внешние) волокна.
Эпюры представлены на рис. 3а,б,в.

4).После
построения эпюр необходимо выполнить
проверку их правильности методом
вырезания узлов.
Суть
метода вырезания узлов заключается в
следующем: каждый узел мысленно
вырезается из рамы поперечными сечениями
бесконечно близкими к узлу; в каждом
сечении прикладываются все силовые
факторы значения и направления, которых
берутся с эпюр; производится проверка
равновесия узла под действием силовых
факторов и внешних нагрузок, приложенных
непосредственно к узлу; если условия
равновесия для узлов выполняются, то
эпюры силовых факторов построены
правильно.
На рис.4 представлены вырезанные узлы d и e с силовыми факторами (взятыми с эпюр рис.3а,б,в) и внешней нагрузкой.
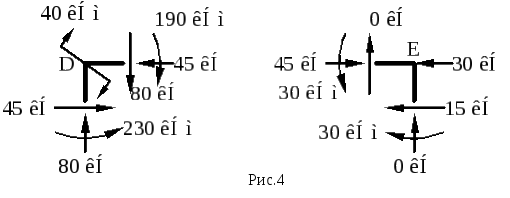
Очевидно, что для каждого из узлов выполняются все три уравнения равновесия – ,,. Таким образом, проверка правильности построения эпюр выполнена.
5).
Подберем сечение рамы в виде прямоугольной
трубы составленной из двух прокатных
швеллеров ГОСТ 8240-72 из условия прочности.
Ориентация швеллеров рациональная,
т.е. плоскость наибольшей жесткости
совпадает с грузовой. Условие прочности
запишем только для нормальных напряжений
изгиба (учет
нормальных напряжений растяжения-сжатия
существенно усложняет условия прочности,
в то же время в большинстве случаев
напряжения растяжения-сжатия малы по
сравнению напряжениями изгиба).
Для опасного сечения
![]() (узелD
(узелD
участок CD
смотри рис.3в)
![]() откуда
откуда
находим требуемый момент сопротивления
сечения:
![]() .
.
Учитывая, что в сечении два одинаковых
швеллера из сортамента выбираем наиболее
подходящий номер по половине момента
сопротивления. Наиболее подходящим
оказывается швеллер №36 со следующими
геометрическими характеристиками:
![]() ;
;![]() ;
;![]() .
.
Тогда подобранное сечение имеет
следующие характеристики (фактические):
момент сопротивления –![]() ,
,
момент инерции –![]() ,
,
площадь –![]() ,
,
максимальный статический момент
отсеченной части сечения –![]() ,
,
суммарная толщина полок –![]() .
.
Выполним
теперь проверку подобранного сечения
рамы на прочность (уточненный прочностной
расчет). В опасном сечении D
фактическое напряжения изгиба составит
–
![]() ,
,
в этом же сечении действуют максимальные
напряжения сжатия (т.к.
![]() )
)
–![]()
и тогда наибольшее нормальное напряжение
составит –
![]() .
.
Наибольшее касательное напряжение в
этом сечении будет действовать на
нейтральной линии сечения, и величина
его по формуле Журавского составит –
![]() .
.
Так
как в рассматриваемом сечении действуют
одновременно и нормальные и касательные
напряжения то проверку выполним по
четвертой теории прочности, опасными
точками в сечении будем считать
соединение полок со стенками предполагая,
что там действуют одновременно наибольшие
касательные и нормальные напряжения
(на самом
деле в этих точках будут действовать
напряжения несколько меньшие максимальных,
что пойдет в запас прочности – в
проверочном расчете это вполне
допустимо).
Тогда наибольшее эквивалентное
напряжение в сечении
![]() и условие прочности выполняется.
и условие прочности выполняется.
Кроме
рассмотренного выше сечения опасным
может оказаться сечение D участка DE где
действует большой изгибающий момент
–
![]() ,
,
максимальная перерезывающая сила –![]() и нормальная сила –
и нормальная сила –![]() .
.
Вычисляя соответствующие напряжения
для этого сечения получим:
![]() ;
;![]()
![]() ;
;
![]() .
.
Снова
принимая (в
запас прочности),
что максимальные нормальные и касательные
напряжения действуют в сечении в местах
сопряжения полок со стенками вычисли
эквивалентное напряжения в сечении:
![]() .
.
Таким образом, подобранное сечение
условиям прочности удовлетворяет.
6).
Определим угол поворота узла D – D
и вертикальное перемещения узла E –
yE,
используя энергетические методы
(перемещениями
связанными с деформациями растяжения-сжатия
и сдвига пренебрегаем, ввиду их малости
по сравнению с перемещениями от изгиба,
таким образом, в расчетах будут
учитываться только изгибающие моменты).
6.1).
Угол поворота узла D
определим, используя способ Верещагина,
для этого в узле приложим единичный
момент (смотри рис.5). Определим реакции
опор как обычно используя уравнения
равновесия всей рамы: из суммы моментов
относительно опоры А
(левой) получим –![]() ,
,
откуда![]() ,
,
из![]() ,
,
и из![]()
![]()
![]() .
.
Строим эпюру единичного изгибающего
момента (от
действия только единичной нагрузки),
описание построения эпюры опускаем в
силу элементарности, сама эпюра
представлена на рис.6.

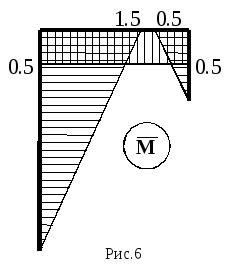
Теперь
для определения угла поворота D
нужно перемножить эпюру грузового
момента
![]() (рис.3в) и
(рис.3в) и![]() (рис.6) по формуле Верещагина. На рис.7
(рис.6) по формуле Верещагина. На рис.7
показана эпюра грузового изгибающего
момента с обозначенными площадями
участков и положением их центров тяжести
(участки
эпюры разбиты на простейшие фигуры для
удобства определения площадей и центров
тяжести),
вычисляя площади получим –
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() .
.
На
рис.8 на эпюре показаны ординаты
единичного момента в сечениях, где
находятся центры тяжестей соответствующих
участков эпюры грузового момента,
вычисляя значения ординат получим –
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Учитывая,
что эпюры единичного и грузового момента
на всех участках расположены на
одноименных волокнах в формуле Верещагина
все слагаемые будут иметь знак «+»:
![]() .
.
Подставляя
значения (в
размерностях – Н, МПа, мм)
получим:
![]()
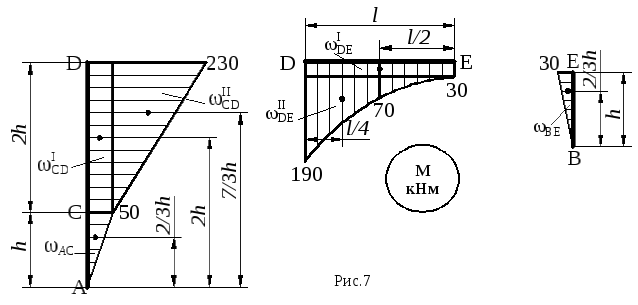
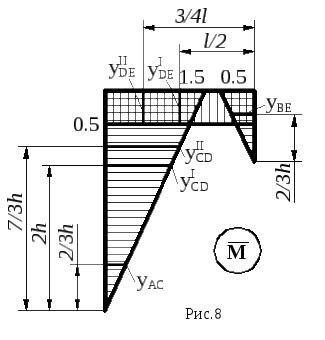
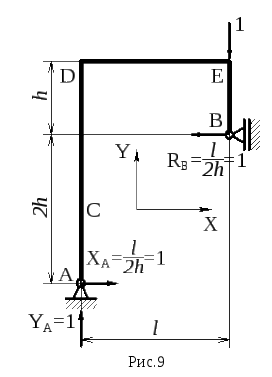
Положительное
значение найденного угла поворота
означает что направление угла поворота
совпадает с направлением единичного
момента, то есть узел D
поворачивается по часовой стрелке.
7).
Вертикальное перемещения узла E –
yE,
найдем с помощью интеграла Мора. Снова
по направлению искомого перемещения
прикладываем единичную нагрузку (см.
рис.9). Определяя реакции из условий
равновесия –
из![]() ,
,
из![]()
![]() ,
,
из![]()
![]()
![]() .
.
В
интеграле Мора перемножаются
непосредственно выражения грузового
и единичного моментов по участкам нужно
записать выражения единичного изгибающего
момента, причем для каждого из участков
начало отсчета и направление оси Х в
выражениях единичного и грузового
моментов должны совпадать, так же как
и принятое за начальное направление
изгибающего момента. Так как выражения
для грузового изгибающего момента уже
получены в пункте 3, то выражения для
единичных моментов получим рассматривая
те же схемы (рис.2а,б,в,г), прикладывая
вместо внешней нагрузки единичную
(используя только что найденные
реакции):

![]()
![]()
![]()
![]() .
.
Так как вычисление интеграла Мора для
нескольких участков трудоемко, то
выполним его в среде MathCad.
Знак
перемещения показывает, что перемещение
направлено вниз туда же куда и единичная
сила
Литература.
-
Писаренко
Г.С., Яковлев А.П., Матвеев В.В.
Справочник по сопротивлению материалов.
Киев.: Наукова думка, 1988. -
Писаренко
Г.С. и др.
Сопротивление материалов. Киев, 1986. -
Феодосьев
В.И.
Сопротивление материалов. М., 1986. -
Буланов
Э.А. Решение
задач по сопротивлению материалов.
Москва.: Высшая школа, 1994. -
Фомин
А.П. Прикладная
механика твёрдого деформируемого
тела, том I, “Наука” , М. ,1975. -
Фомин
А.П. Прикладная
механика твёрдого деформируемого
тела, том II, “Наука” , М. , 1978. -
Качурин
В.К. Сборник
задач по сопротивлению материалов,
“Наука”, М.,1970. -
Миролюбов
И.Н. и др.
Пособие к решению задач по сопротивлению
материалов, “Высшая школа”, М., 1967.
Лобанов Николай Владимирович
Морозов Алексей
Сергеевич
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ.
Учебное
пособие к выполнению РГР
Компьютерный набор
и верстка авторов
Подготовка к
изданию – В.Ф.Усынин
Корректировка
выполнена авторами
Сдано
в производство . .2002 г. Подписано в печать
2002 г.
Уч.-изд.
л. Усл.-печ. л.
Изд.№
Заказ № Тираж экз.
Редакционно-издательский
отдел Севмашвтуза
164500,
г.Северодвинск, ул. Воронина, д.6
1
60
2
59
3
58
4
57
5
56
6
55
7
54
8
53
9
52
10
51
11
50
12
49
13
48
14
47
15
46
16
45
17
44
18
43
19
42
20
41
21
40
22
39
23
38
24
37
25
36
26
35
27
34
28
33
29
32
30
31
