
ГОСТ 8509-93 устанавливает сортамент на уголки стальные горячекатаные равнополочные (равнобокие).
Сокращенная и полная версии сортамента.
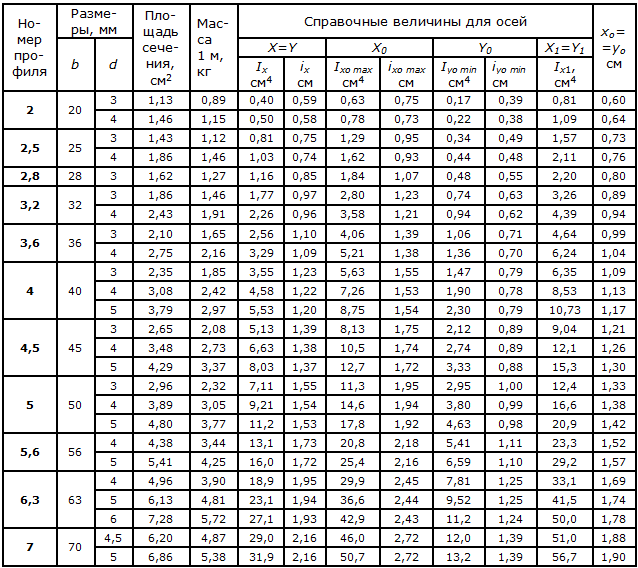
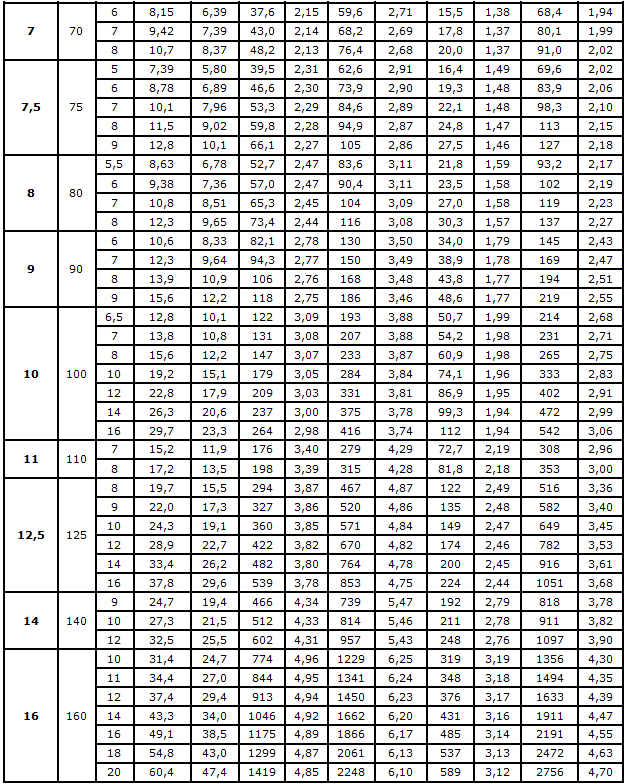
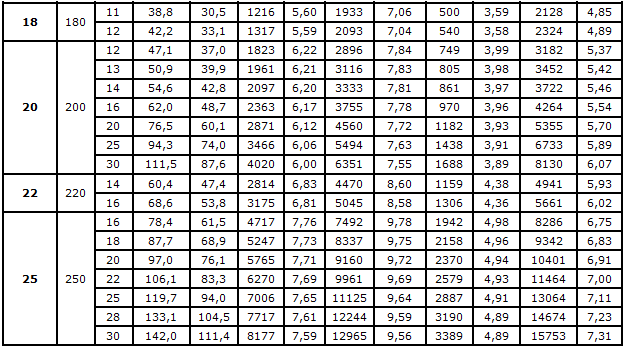
Сокращенная версия сортамента
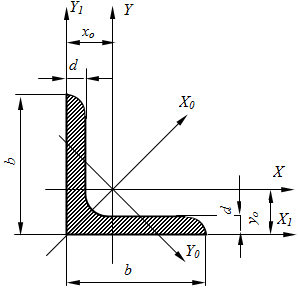
Размеры и геометрические характеристики сечения:
b — размер полки;
d — толщина стенки;
A — площадь поперечного сечения;
m — масса погонного метра;
Ix — момент инерции уголка относительно оси x (Ix=Iy);
x0, y0 — расстояния до главных осей;
i — радиусы инерции.
Примеры решения задач >
Краткая теория >
Полный вариант ГОСТа

Страница 1. Предисловие к стандарту на стальные равнополочные уголки.

Страница 2. Форма профиля и обозначения размеров поперечного сечения уголков равнополочных.
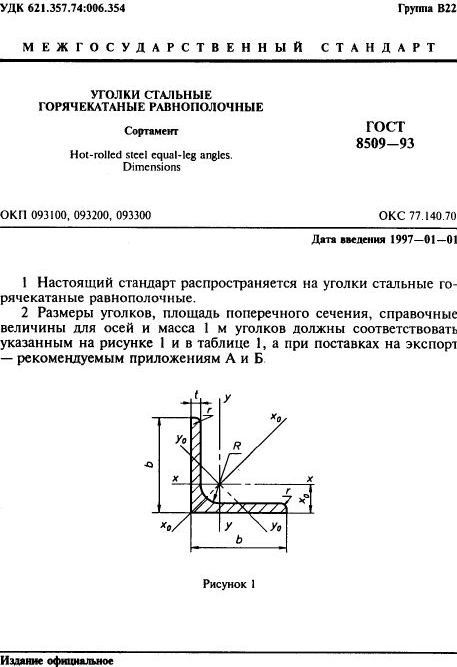
Страница 3. Размеры, площадь поперечного сечения, масса 1 метра и справочные значения величин для уголков равнополочных №№2-5.
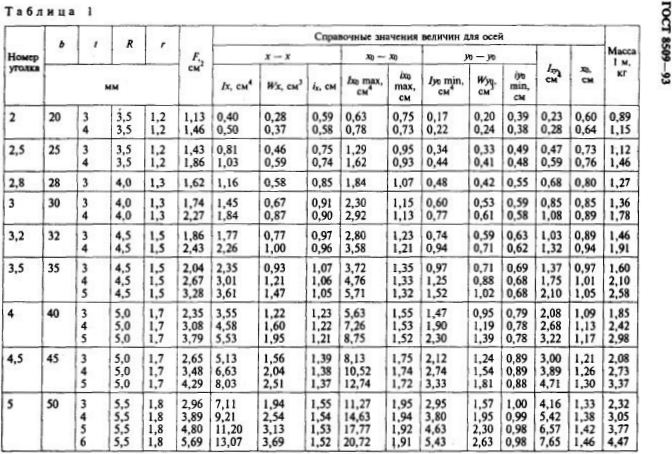
Страница 4. Размеры, площадь поперечного сечения, масса 1 метра и справочные значения величин для уголков равнополочных №№5,6-9.
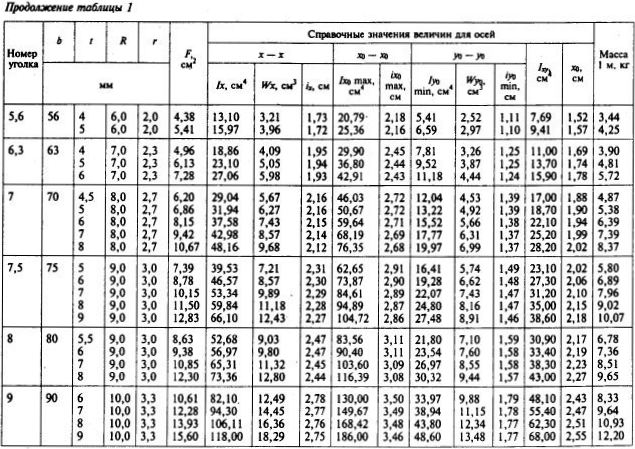
ГОСТ 8509-93 Страница 5. Размеры, площадь поперечного сечения, масса 1 метра и справочные значения величин для уголков равнополочных №№10-16.
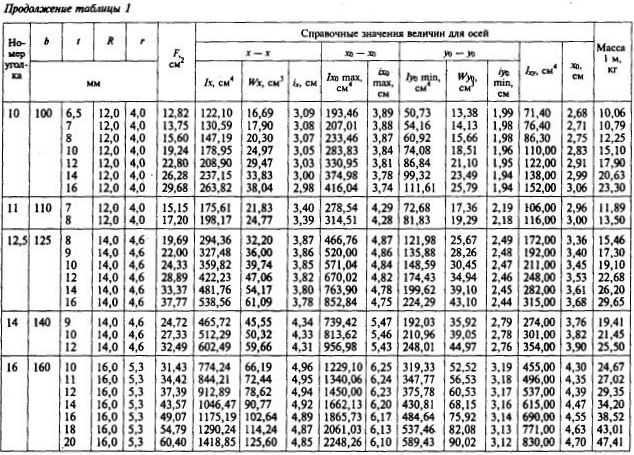
Страница 6. Размеры, площадь поперечного сечения, масса 1 метра и справочные значения величин для уголков равнополочных №№18-25.
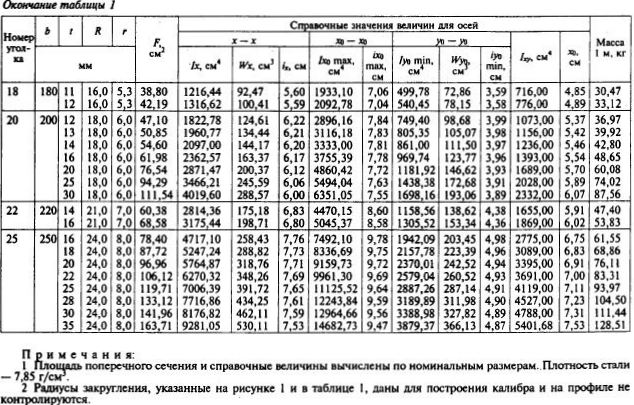
Страница 7. Условные обозначения и таблица предельных отклонений размеров равнополочных уголков.

ГОСТ 8509-93 Страница 8. Предельные отклонения по массе равнополочных уголков I и II класса.

Страница 9. Приложение А. Область распространения, размеры и свойства профиля равнополочных уголков.

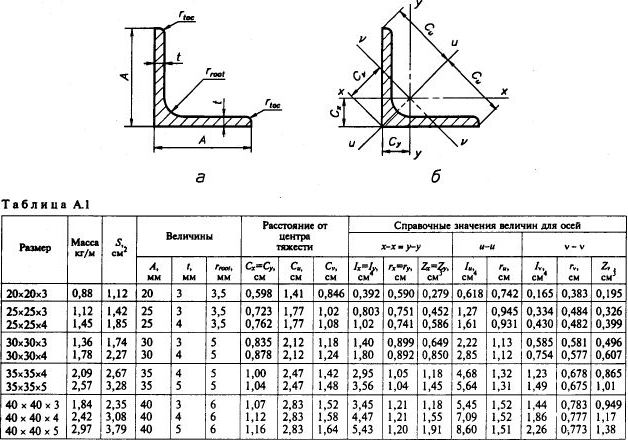
Страница 10. Таблица А.1. Расстояния от центра тяжести до осей сечения для равнополочных уголков №№20-40.
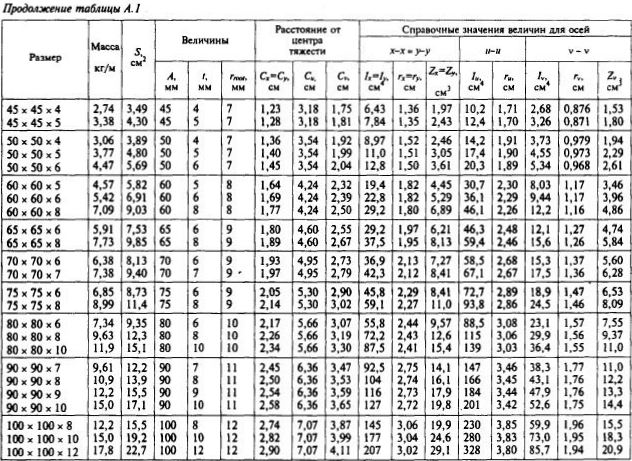
ГОСТ 8509-93 Страница 11. Таблица А.1 (продолжение). Расстояния от центра тяжести до осей сечения для равнополочных уголков №№45-100.
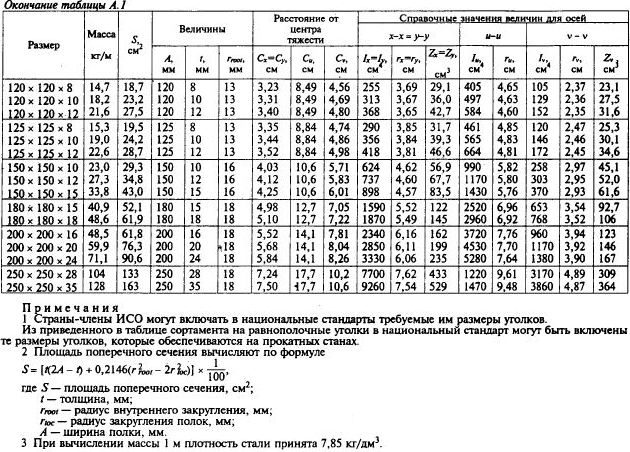
Страница 12. Таблица А.1 (окончание). Расстояния от центра тяжести до осей сечения для равнополочных уголков №№120-250.
Страница 13. Приложение Б. Предмет стандарта и область применения. Предельные отклонения по ширине и толщине полки равнополочных уголков.
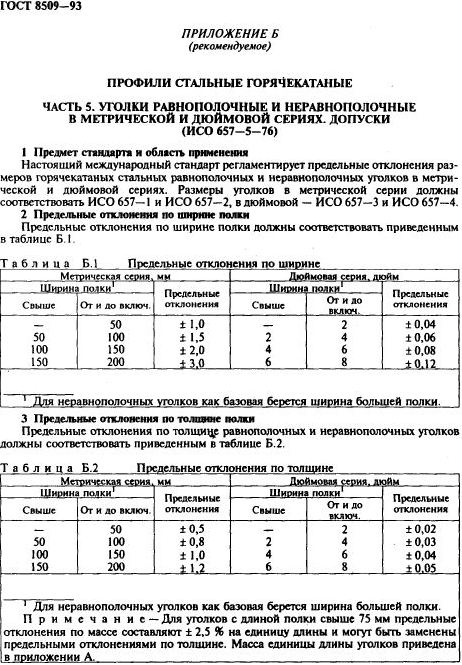
Страница 14. Предельные отклонения по порезке на длины, кривизна и неперпендикулярность равнополочных уголков.
ГОСТ 8509-93 Страница 15. Предельные отклонения по массе равнополочных уголков. Выходные данные стандарта.

Другие сортаменты >>
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Про уолок (только для умных)
Знаток
(402),
закрыт
14 лет назад
Gricha Cot
Мыслитель
(9965)
14 лет назад
Формула-то как раз есть, но с интегралами и дифференциалами – общая формула для определения центра тяжести любой плоской фигуры. К уголку её громоздить ни к чему. Все правы в одном – в практической деятельности определение центра тяжести прокатного или гнутого ГОСТовского уголка не требуется – это все дано в таблицах ГОСТа на конкретный вид проката. Но, уголок теоретически может быть и не обязательно прокатным, а, например, сварным из двух полос металла (чего только в жизни не бывает) . Так вот, центр тяжести любого плоского тела ( в данном случае это сечение уголка) может быть определен исходя из условия равновесия тела. Тело, закрепленное на оси, проходящей через центр тяжести должно находится в равновесии. Поэтому, делаем так – уголок разделяем на два взаимно перпендикулярных прямоугольника. Находим центр тяжести каждого прямоугольника- это элементарно, он находится в центре симметрии. Ставим там точки ( именно в них сосредоточена масса каждого прямоугольника) . Соединяем точки прямой линией. Именно на ней будет расположена точка равновесия, т. е. центр тяжести сечения в целом. Длина этой линии (а) находится очень просто, по теореме Пифагора, исходя из геометрических размеров сечения. Далее – условия равновесия для двух центров тяжести . F1 х а1 = F2 х а2. F1- площадь одного прямоугольника, F2 – второго, а1 – расстояние от центра тяжести первого прямоугольника до искомого центра тяжести сечения, а2 – соответственно. Естественно, а1 + а2 = а. Всё очень просто определяется.
Обратите внимание, на этом сайте есть онлайн-сервис для вычисления центра тяжести и моментов инерции составных сечений, которые состоят из прокатных профилей (двутавр, уголок и т.д.) и из простых фигур.
Часто при расчете элементов строительных конструкций приходится определять геометрические характеристики профилей, составленных из элементарных геометрических фигур (прямоугольник, круг и т.п.) и прокатных профилей. Рассмотрим подробно пример расчета.
Необходимо определить геометрические характеристики составного сечения (рис.), который состоит из уголка 20/12,5/1,2, уголка 14/1 и прямоугольника 20х2см.
Определение собственных характеристик отдельных профилей – составляющих сечения
Собственные характеристики прокатных профилей определяются из сортамента.
Для неравнополочного уголка 20/12,5/1,2:
– высота и ширина уголка h = 20 см, b = 12,5 см;
– площадь $A$= 37,9 см2;
– собственные осевые моменты инерции ${I_x}$=1570 см4, ${I_y}$= 482 см4;
– собственный центробежный момент инерции ${I_{xy}}$=505 см4;
– координаты центра тяжести ${x_c}$= 2,83 см, ${y_c}$= 6,51 см.
Для равнополочного уголка 14/1:
– высота и ширина уголка h = b = 14 см;
– площадь $A$= 27,3 см2;
– собственные осевые моменты инерции ${I_x}$= ${I_y}$= 512 см4;
– собственный центробежный момент инерции ${I_{xy}}$=301 см4;
– координаты центра тяжести ${x_c}$= ${y_c}$= 3,82 см.

Для прямоугольника 20х2см:
– высота и ширина прямоугольника h = 20 см, b = 2 см;
– площадь $A$= 20∙2 = 40 см2;
– собственные осевые моменты инерции ${I_x} = frac{{2 cdot {{20}^3}}}{{12}} = 1330$ см4, ${I_y} = frac{{20 cdot {2^3}}}{{12}} = 13,3$см4;
– собственный центробежный момент инерции ${I_{xy}}$= 0, так как профиль имеет ось симметрии.
Определение центра тяжести сечения
Общая площадь всего сечения A = 37,9+27,3+40 = 105см2.
Проводим вспомогательные оси $X$ и $Y$ и определяем относительно них центр тяжести сечения:
${X_c} = frac{{sum {{X_i} cdot {A_i}} }}{A} = frac{{{text{37}}{text{,9}} cdot {text{( – 13}}{text{,5) + 27}}{text{,3}} cdot {text{( – 3}}{text{,82) + 40}} cdot {text{1}}}}{{{text{105}}}}{text{ = – 5}}{text{,49}}$см;
${Y_c} = frac{{sum {{Y_i} cdot {A_i}} }}{A} = frac{{{text{37}}{text{,9}} cdot {text{( – 2}}{text{,83) + 27}}{text{,3}} cdot {text{10}}{text{,2 + 40}} cdot {text{10}}}}{{105}} = 5,44$.
При этом в координатах центров тяжести составных обязанности’обязательно учитываем знак. Откладываем оси, которые проходят через центр тяжести –центральные оси $Xc$ и ${Y_c}$.
Определение центральных моментов инерции
Осевые и центробежный моменты инерции сечения определяем по формулам перехода между параллельными осями. Для этого находим и показываем на чертеже расстояния между центральными осями всего сечения и собственными осями каждой из фигур.
$Ix = sum {left( {I{x_i} + A cdot {b^2}} right) = {text{482 + 8}}{text{,2}}{{text{7}}^{text{2}}} cdot {text{37}}{text{,9 + 512 + 4}}{text{,7}}{{text{6}}^{text{2}}} cdot {text{27}}{text{,3 + 1330 + 4}}{text{,5}}{{text{6}}^{text{2}}} cdot {text{40 = 6360}}} $см4;
$Iy = sum {left( {I{y_i} + A cdot {a^2}} right)} = {text{1570 + 8}}{text{,0}}{{text{1}}^{text{2}}} cdot {text{37}}{text{,9 + 512 + 1}}{text{,6}}{{text{7}}^{text{2}}} cdot {text{27}}{text{,3 + 13}}{text{,3 + 6}}{text{,4}}{{text{9}}^{text{2}}} cdot {text{40 = 6280}}$см4;
${I_{xy}} = sum {left( {{I_{xy}}_i + A cdot a cdot b} right)} = $
$ = 505 + ( – 8,01) cdot ( – 8,27) cdot 37,9 – 301 + 1,67 cdot 4,76 cdot 27,3 + 0 + 6,49 cdot 4,56 cdot 40 = 4120$см4.
При этом обязанности’обязательно учитываем размещения фигур относительно рассматриваемых осей. Так, при определении момента инерции ${I_x}$ в формулу подставляем собственный момент инерции неравнополочного уголка относительно оси, которая параллельна оси ${X_c}$, в сортаменте это ось $Y$, и наоборот.
Определение положения главных осей и главных моментов инерции
Угол поворота главных осей относительно осей, для которых известны моменты инерции, определяется по формуле
[tg,2alpha = frac{{2 cdot {I_{xy}}}}{{{I_y} – {I_x}}} = frac{{2 cdot 4120}}{{6280 – 6360}} = – 97] $alpha = frac{{arctg( – 97)}}{2} = – 44,7^circ $.
Если $alpha > 0$, главные оси откладываются против часовой стрелки, и наоборот.
Главные моменты инерции определяются так
${I_{x0}} = {I_x} cdot {cos ^2}alpha + {I_y} cdot {sin ^2}alpha – {I_{xy}} cdot sin 2alpha = $
$ = 6360 cdot {cos ^2}( – 44,7^circ ) + 6280 cdot {sin ^2}( – 44,7^circ ) – 4120 cdot sin ( – 2 cdot 44,7^circ ) = 10430$см4.
${I_{y0}} = {I_y} cdot {cos ^2}alpha + {I_x} cdot {sin ^2}alpha + {I_{xy}} cdot sin 2alpha = $
$ = 6280 cdot {cos ^2}( – 44,7^circ ) + 6360 cdot {sin ^2}( – 44,7^circ ) + 4120 cdot sin ( – 2 cdot 44,7^circ ) = 2210$см4.
Центробежный момент инерции относительно главных осей равен нулю.
Радиусы инерции. Моменты сопротивления
Радиусы инерции сечения
${i_x} = sqrt[{}]{{frac{{{I_x}}}{A}}} = sqrt[{}]{{frac{{10430}}{{105}}}} = 9,96$см, ${i_y} = sqrt[{}]{{frac{{{I_y}}}{A}}} = sqrt[{}]{{frac{{2210}}{{105}}}} = 4,58$см.
Моменты сопротивления сечения определяем относительно центральных осей. Для этого необходимо определить расстояния ${x_{max }}$ и ${y_{max }}$ до максимально удаленных точек от главных осей. Сначала необходимо по чертежам определить, какие точки являются наиболее удаленными. В нашем случае это точки $A$ и $B$ (рис.). Искомые расстояния можно определить, имея координаты этих точек в центральных (не возвращенных осям).
${x_{max }} = {x_A} cdot cos left( alpha right) + {y_A} cdot sin left( alpha right)$
${y_{max }} = {y_B} cdot cos left( alpha right) – {x_B} cdot sin left( alpha right)$
XА= –8,53см YA=8,57см
XB= –14,5см YB= –18см
xmax = –12,1см ymax = –23см
Моменты сопротивления
${W_x} = frac{{{I_x}}}{{{y_{max }}}} = frac{{10430}}{{23}} = 454$см3; ${W_y} = frac{{{I_y}}}{{{x_{max }}}} = frac{{2210}}{{12.1}} = 183$см3.
ГОСТ 8239
– 89: ДВУТАВРЫ СТАЛЬНЫЕ ГОРЯЧЕКАТАНЫЕ
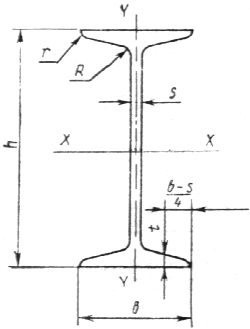
h —
высота двутавра;
b —
ширина
полки;
s —
толщина стенки;
t —
средняя толщина полки;
С –
центр тяжести (на пересечении осей y
– y и х
– х)
Номер двутавра
определяется высотой h.
Например у двутавра №10 – h
= 100мм
С
ГОСТ
8240-89 ШВЕЛЛЕРЫ СТАЛЬНЫЕ ГОРЯЧЕКАТАНЫЕ

h –
высота;
b –
ширина полки;
s –
толщина стенки;
t – толщина
полки;
z0
– расстояние
от оси y – y до наружной грани стенки.
С –
центр тяжести (на пересечении осей y
– y и х
– х)
Номер швеллера
определяется высотой h.
Например у швеллера №12 – h
= 120мм
С
ГОСТ
8510 – 72 СТАЛЬ ПРОКАТНАЯ УГЛОВАЯ
НЕРАВНОПОЛОЧНАЯ
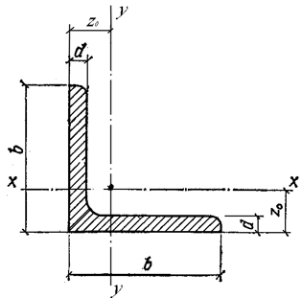
b —
ширина
полки;
d
— толщина полки;
z0
– расстояние
от центра тяжести до полки
С –
центр тяжести (на пересечении осей y
– y и х
– х)
Обозначение уголка
определяется шириной (b)
и
толщиной (d)
полки. Например, уголок №5 (или 504)
b
= 50мм, d
= 4 мм.
С
ГОСТ
8509 – 72 СТАЛЬ ПРОКАТНАЯ УГЛОВАЯ
РАВНОПОЛОЧНАЯ
В –
ширина
большой полки
b —
ширина
малой полки;
d
— толщина полки;
х0,
у0
– расстояния
от центра тяжести до наружных граней
полки
С –
центр тяжести (на пересечении осей y
– y и х
– х)
Обозначение уголка
определяется размерами В,
b,
d.
Например уголок № 7,5/5 (или 75505):
В= 75 мм, b=
50мм,d
= 5 мм.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение положения центра тяжести сечения составленного из стандартных

Определение положения центра тяжести сечения, составленного из стандартных прокатных профилей (двутавров, швеллеров, уголков, полос) Фаюстов Анатолий Афанасьевич доцент кафедры инновационного менеджмента ГУУ
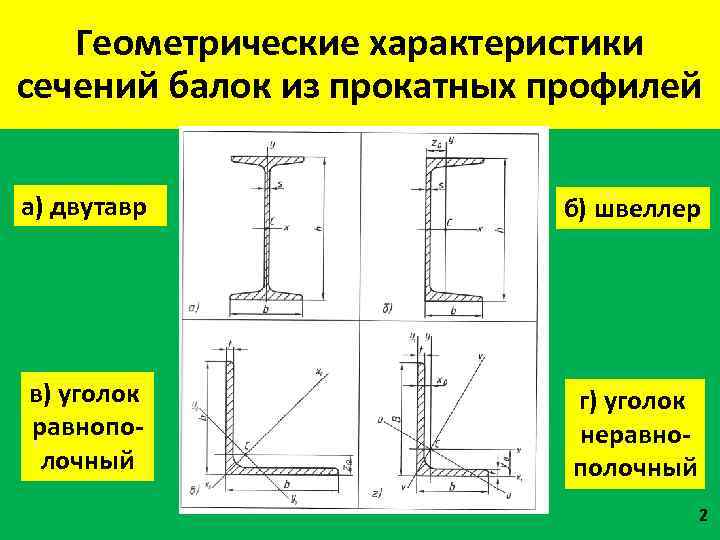
Геометрические характеристики сечений балок из прокатных профилей а) двутавр б) швеллер в) уголок равнополочный г) уголок неравнополочный 2

Обозначения h – высота балки (для двутавра и швеллера); b – ширина полки (для двутавра, швеллера и уголков); s – толщина стенки (для двутавра и швеллера); B – ширина большей полки (для неравнополочного уголка); t – толщина полки (для уголков); z 0 – расстояние от центра тяжести, находящегося на оси y-y, до наружной грани стенки (для швеллера) или до наружной грани полки (для равнополочного уголка); x 0, y 0 – расстояние от центра тяжести до наружных граней полок (для неравнополочного уголка). 3
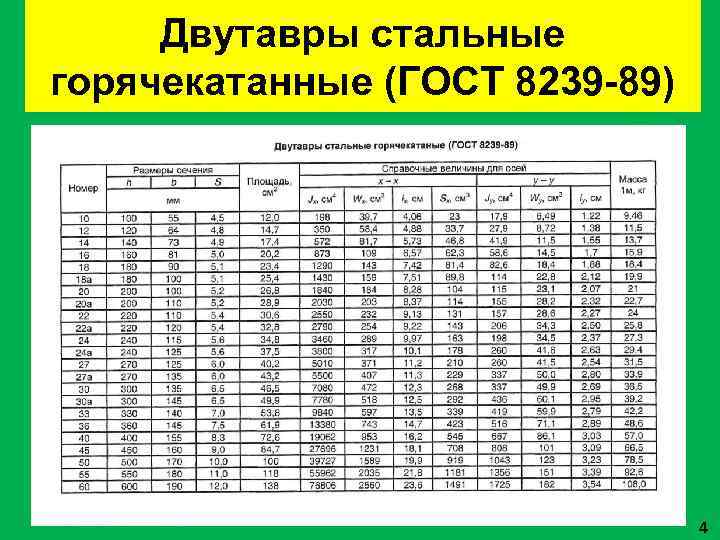
Двутавры стальные горячекатанные (ГОСТ 8239 -89) 4
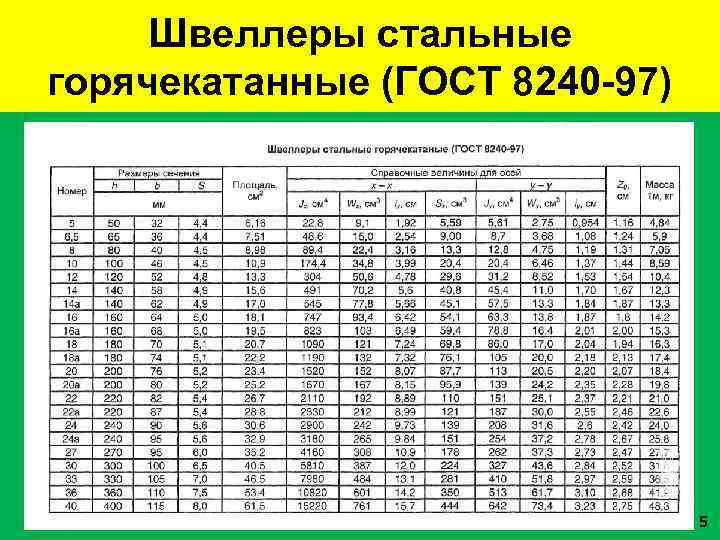
Швеллеры стальные горячекатанные (ГОСТ 8240 -97) 5
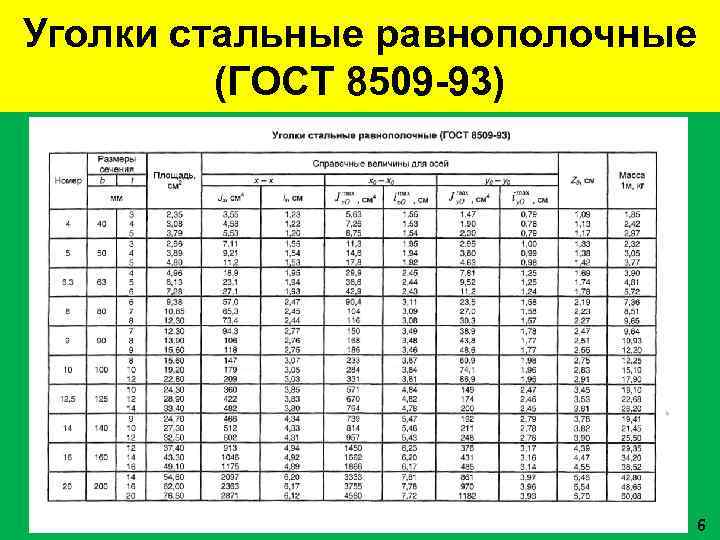
Уголки стальные равнополочные (ГОСТ 8509 -93) 6
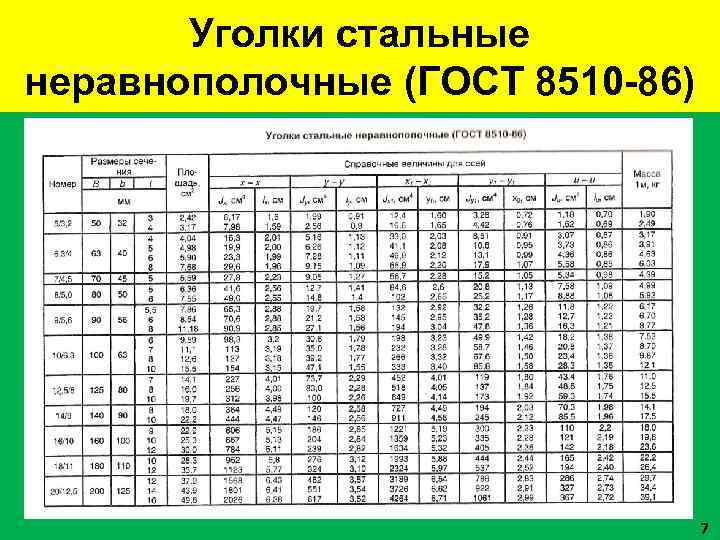
Уголки стальные неравнополочные (ГОСТ 8510 -86) 7
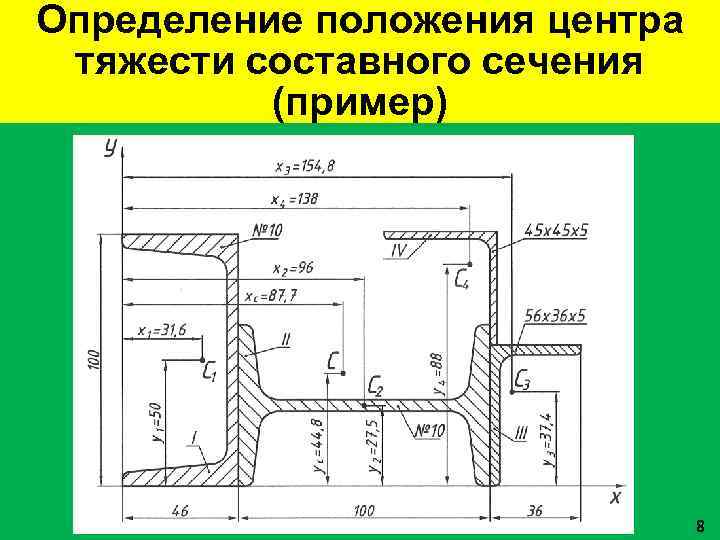
Определение положения центра тяжести составного сечения (пример) 8

Определение положения центра тяжести составного сечения (ход решения) Выбираем систему координат так, чтобы сечение было расположено в первом квадранте. Составными частями сечения являются швеллер № 10 (I), двутавр № 10 (II), неравнополочный уголок 56× 36× 5 мм (III), равнополочный уголок 45× 5 мм (IV). Значения площадей и координаты центров тяжести швеллера, двутавра и уголков берем из таблиц прокатной стали ГОСТ 8240 -97, ГОСТ 8239 -89, ГОСТ 8510 -86, ГОСТ 8509 -93. 9

Определение положения центра тяжести составного сечения (ход решения) для швеллера № 10 F 1 = 10, 9 см 2, z 0 = 1, 44 см; для двутавра № 10 F 2 = 12, 0 см 2; для неравнополочного уголка 56× 36× 5 F 3 = 4, 41 см 2, x 0 = 0, 88 см, y 0 = 1, 86 см; для равнополочного уголка 45× 5 F 4 = 4, 29 см 2, z 0 = 1, 30 см. Координаты центров тяжести швеллера, двутавра, уголков указаны на чертеже в миллиметрах. 10

Определение положения центра тяжести составного сечения (окончание) Определяем положение центра тяжести сечения (координата хс): 11

Определение положения центра тяжести составного сечения (окончание) Определяем положение центра тяжести сечения (координата ус): 12
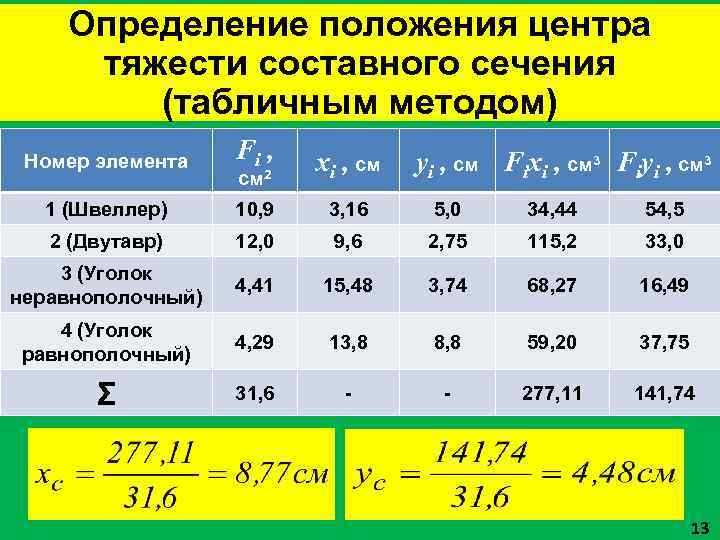
Определение положения центра тяжести составного сечения (табличным методом) Номер элемента Fi , см 2 xi , см 1 (Швеллер) 10, 9 3, 16 5, 0 34, 44 54, 5 2 (Двутавр) 12, 0 9, 6 2, 75 115, 2 33, 0 3 (Уголок неравнополочный) 4, 41 15, 48 3, 74 68, 27 16, 49 4 (Уголок равнополочный) 4, 29 13, 8 8, 8 59, 20 37, 75 Σ 31, 6 – – 277, 11 141, 74 yi , см Fixi , см 3 Fiyi , см 3 13
