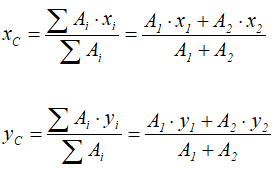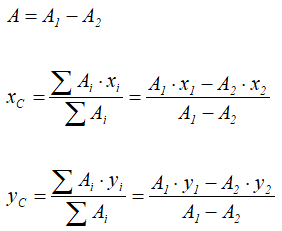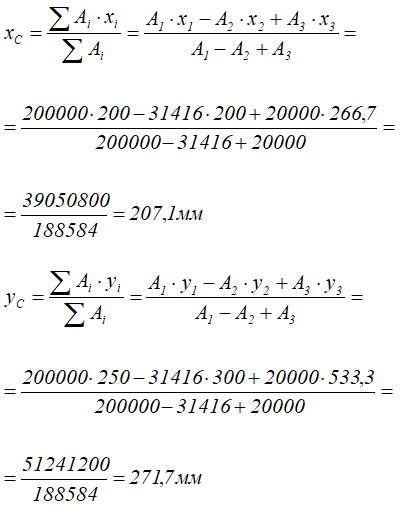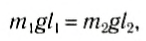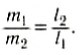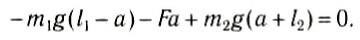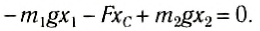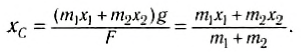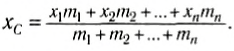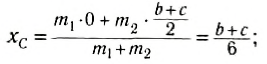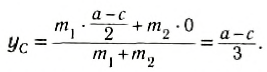Как найти центр тяжести сосуда

4-я лекция.

4. ГИДРОСТАТИКА-2

4.1. Сила давления жидкости па плоскую стенку.

4.2. Точка приложения силы давления.

4.3 Сила давления жидкости на криволинейную стенку.

4.4.Плавание тел.

4.5. Прямолинейное равноускоренное движение сосуда с жидкостью.

4.6. Равномерное вращение сосуда с жидкостью.

4.1. Сила давления жидкости па плоскую стенку

Рекомендуемые материалы

Давление жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом  α, определяется по  основному уравнению гидростатики

Р=Р₀+hρg

Определим силу давления F, действующую со стороны жидкости, на участок рассматриваемой стенки, ограниченный произвольным контуром, имеющим площадь S.

Ось Ох направим перпендикулярно плоскости стенки от точки ее пересечения со свободной поверхностью жидкости, а ось Оу — перпендикулярно оси Ох в  плоскости стенки.

Выразим элементарную силу давления, приложенную к бесконечно малой площадке δS , для остальных площадок силы будут определяться таким же образом

δFж = P*δS =(P₀ + ρhg) δS = P₀*δS + ρhg*δS,

где Р₀ — давление на свободной поверхности, h — глубина расположения площадки  δS. 

Переходя к пределу при  стремлении  площадки δS→0, получим выражение для дифференциала силы давления:

dFж = P₀*dS + ρhg*dS,

Проинтегрировав этот дифференциал по площади S,  получим выражение для определения полной силы Fж

,

где у — координата площадки dS, h = у*Sinα .

Интеграл  представляет собой статический момент площади S относительно оси Ох , который  равен произведению  площади S на координату у_с ее центра тяжести – точки С:

Усилие давления жидкости на плоскую, наклоненную стенку равно

Fж = P₀S+ρg(y_c Sinα) S = P₀S+ρgh_cS,    (4.1)

здесь h_c = (y_c Sinα)— глубина расположения центра тяжести площади S.

Fж = ρg (H₀ +h_c)S = P_cS,                     (4. 2)

Сила давления жидкости Fж  = ρgh_cS – это вес объема V = h_cS жидкости.

Полная сила давления жидкости Fж на плоскую стенку равна произведению площади стенки S  на гидростатическое давление Р_с в центре тяжести этой площади.

1.В частном случае, когда давление Р₀ является атмосферным и действует также с другой стороны стенки, сила избыточного давления жидкости F_{изб ж}  на плоскую стенку равна лишь силе Fж давления от веса столба жидкости, т. е.

F_{изб ж} = P_cS= ρgh_cS.

2. В общем случае давление Р₀ может существенно отличаться от атмосферного, поэтому полную силу F давления жидкости на стенку можно  рассматривать как сумму двух сил: F₀ от внешнего давления Р₀ и силы Fж   от веса столба жидкости, т. е.

F= F₀ + Fж = (P₀+Pс)S.        (4.3.)

4.2. Точка приложения силы давления.

Внешнее давление Р₀ передается всем точкам площади S одинаково, и его равнодействующая сил внешнего давления F₀ будет приложена в центре тяжести площади S  с координатой  –  у_с.

Для нахождения точки D приложения силы давления Fж от веса жидкости применим теорему механики, согласно которой момент равнодействующей силы относительно оси Ох равен сумме моментов составляющих сил, в данном случае элементарных сил.

где у_D — координата точки приложения силы, h=y*Sinα.

Используя выражение для:

 F_ж = ρgh_c*S = ρg(y_cSinα)*S  – силы жидкости, действующей на плоскую стенку,

и для:

dF_ж= ρgh*dS= ρg(ySinα)*dS –  силы жидкости, действующей на элементарную площадку, получим 

        (4.4)

где  – момент инерции площади S относительно оси Оx.

Подставляя в формулу (4.4) значение:

 момента инерции и площади S – Jx  относительно оси х,  через момент инерции той же площади  – Jx₁  относительно центрально оси х₁ параллельной оси Ох, находим

Jx = Jx₁+y_C²S,                    (4.5)

у_D = у_C+ J_x1/(у_сS),              (4.6.)

Точка D  приложения силы F_ж расположена ниже центра тяжести площади стенки; расстояние между ними

Δу_D= у_D -Δу_C = J_x0/( у_сS),                 (4.7) .

Если давление Р₀ равно атмосферному, то точка D  будет центром давления.

При Р₀ > Pат  центр давления находят по правилам механики, как точку приложения равнодействующей двух сил F₀ и F_ж ,  чем больше первая сила по сравнению со второй  тем, очевидно, центр давления ближе к центру тяжести площади S.

Если стенка имеет форму прямоугольника размерами а × b (рис. 4.2) и с одной стороны  – атмосферное давление, центр давления D находится па расстоянии b/3 от нижней стороны.

4.3 Сила давления жидкости на криволинейную стенку.

Нахождение силы давления жидкости на поверхности произвольной формы в общем случае приводится к определению трех составляющих суммарной силы и трех моментов.

Рассмотрим действие жидкости на цилиндрические или сферические поверхности, имеющие вертикальную плоскость симметрии. Сила давления жидкости в этом случае сводится к равнодействующей силе, лежащей в плоскости симметрии.

Возьмем криволинейную поверхность АВ,  образующая которой  перпендикулярна к плоскости чертежа (рис.4.3а), определим силу давления жидкости на эту поверхность.

Выделим объем жидкости, ограниченный поверхностью АВ, вертикальными плоскостями, проведенными через границы этого участка ВС и AD,  свободной поверхностью жидкости. Рассмотрим  условия равновесия объема АВСD  в вертикальном и горизонтальном направлениях.

Сила давления  жидкости P действует на стенку АВ, стенка АВ удерживает действие  жидкости силой реакции стенки Rс = P, направленной в противоположную сторону. На рис. 4.3 сила реакции стенки и сила давления жидкости  разложены на горизонтальные и вертикальные составляющие.

Условие равновесия объема АВСD в вертикальном направлении имеет вид

Rс_в =Pжв= Р₀F_г + G = Р₀F_г + ρgV₀,                (4.8)

где Р₀  – давление на свободной поверхности жидкости; F_г – площадь горизонтальной проекции поверхности АВ; G – вес выделенного объема жидкостиV_0. Объем V₀  называют – объем тела давления..

Условие равновесия того же объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности ЕС и АD взаимно уравновешиваются и остается лишь сила давления на площадь ВЕ т. е. на вертикальную проекцию поверхности S_в = L_EB*B. Тогда

Rсг=Pжг= F_вρgh_c+ F_в Р₀ = F_в(ρgh_c+ Р₀).            (4.9)

Определив по формулам (4.8) и (4.9) вертикальную и горизонтальную составляющие полной силы Рж, найдем

 ,              (4.10).

Сила давления жидкости на криволинейную стенку будет равна сила реакции стенки Rж =  P и направлена в противоположную сторону.

Когда жидкость расположена снаружи (рис.4.3б), сила гидростатического давления на криволинейную поверхность АВ определяется также, но направление ее будет противоположным.

При этом под величиной G следует понимать так же, как и в первом случае вес жидкости в объеме АВСD, хотя этот объем и не заполнен жидкостью.

Положение центра давления на  цилиндрической стенке можно найти, если известны силы Fв и Fг и определены центр давления на вертикальной проекции h_D стенки и центр тяжести выделенного объема АВСD.

Задача значительно облегчается в том случае, когда рассматриваемая криволинейная  поверхность является круговой. Равнодействующая сила при этом пересекает ось поверхности, так как любая элементарная сила давления нормальна к поверхности, т. е. направлена по радиусу.

Изложенный способ определения силы давления на цилиндрические поверхности применим и к сферическим поверхностям, причем равнодействующая сила в этом случае также проходит через центр поверхности и лежит в вертикальной плоскости симметрии.

4.4. Плавание тел.

Описанный выше прием нахождения вертикальной составляющей силы давления жидкости па криволинейную стенку используют для доказательства закона Архимеда.

Пусть в жидкость погружено тело произвольной формы объемом V (рис.4.4).

Спроектируем его на свободную поверхность жидкости и проведем проек-тирующую цилиндрическую поверхность W, которая касается поверхности тела по замкнутой кривой. Эта кривая отделяет верхнюю часть поверхности тела АСВ от нижней ее части ADB.  Вертикальная составляющая F_в1 силы избыточного давления жидкости на верхнюю часть поверхности тела направлена вниз и равна весу жидкости в объеме АА’BВ’CA. Вертикальная составляющая F_в2 силы давления жидкости на нижнюю часть поверхности тела направлена вверх и равна весу жидкости в объеме АА’В’BDA. Отсюда следует, что вертикальная равнодействующая сил давления жидкости на тело будет направлена вверх и равна весу жидкости в объеме, равном разности указанных двух объемов, т. е.

F_А = F_в2  – F_в1  = G_ACBD =Vρg.                     (4.11)

Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила направленная вертикально вверх, численно равная весу жидкости вытесненной телом и приложенная в центре тяжести объема погруженной части тел.

Сила F_А называется архимедовой силой,  а точка ее приложения, т. е. центр тяжести объема V — центром водоизмещения.

В зависимости от соотношения веса G тела и архимедовой силы возможны три случая:

 1) G> F_А — отрицательная  плавучесть, тело тонет;

2) G<F_А — положительная плавучесть, тело всплывает и плавает на поверхности жидкости;

3) G = F_А нулевая плавучесть, тело плавает погруженным в жидкость полностью.

Для равновесия плавающего тела, кроме равенства G = F_А  должен быть равен нулю суммарный момент. Последнее условие соблюдается тогда, когда центр тяжести тела лежит на одной вертикали с центром водоизмещения. Условие устойчивого равновесия тела, плавающего в полностью погруженном состоянии,  заключается в следующем: центр тяжести тела должен находиться ниже центра водоизмещения.

4.5. Прямолинейное равноускоренное движение

сосуда с жидкостью.

Если при движении сосуда на частицы жидкости, кроме сил тяжести действуют еще силы инерции,  под действием этих сил жидкость принимает новое положение равновесия – положение  относительного покоя.

Относительным покоем называется равновесие жидкости, находящейся под действием сил тяжести и инерции в  движущемся сосуде.

При относительном покое положение свободной поверхности и поверхностей уровня,  отличается от их положения для жидкости в неподвижном сосуде.

При определении формы и положения этих поверхности учитывается основное свойство поверхности уровня. 

Основное свойство поверхностей уровня  –  равнодействующая массовых сил всегда нормальна  к этим поверхностям.

В полном дифференциале давления

dP=ρ(X*dх+У*dy+Z*dz),          (4.12)

Х,У,Z – алгебраическая сумма проекций на оси координат ускорений силы тяжести и сил инерции переносного движения.

Вдоль поверхности уровня  dР=0 , так как поверхности уровня  – это поверхности равного давления. Дифференциальное уравнение поверхности равного давления:

X*dх+У*dy+Z*dz = 0          (4.13),

Этот трехчлен (4.13) определяет элементарную работу массовых сил X,У,Z на перемещениях dх, dy, dz. В данном случае перемещение взято по поверхности равного давления, dР=0.

Из этого выражения следует, что  работа массовых сил вдоль поверхности равного давления равна нулю. Это значит, что в состоянии относительного покоя результирующее ускорение перпендикулярно к  соответствующему элементу поверхности равного давления.

Рассмотрим два случая относительного покоя.

Первый случай:   сосуд, движущийся прямолинейно и равноускоренно.

Второй случай: сосуд, вращающийся вокруг вертикальной оси с постоянной угловой скоростью.

На рис.4.5 изображен сосуд, движущийся вниз с ускорением а по плоскости наклонённой под углом  α   к горизонту. Оси координат оси координат связаны с движущимся телом. 

1. Пусть на жидкость действует  суммарная массовая сила F, проекции которой F_x, Fy, Fz , поделенные на  массу: Fx/m  являются проекциями единичной массовой силы на оси Ох, Оу, Oz:  Х, У и Z.

F = Fx+Fy+Fz = mа,  F/m = Fx/m +Fy/m +Fz/m = X +Y + Z = а.

Все выделенные составляющие являются векторными величинами.

 Проекции массовых сил, действующие на выделенный объем в направлении координатных осей, будут равны произведениям проекций единичных сил, умноженным на массу выделенного объема.

Fx = mX,               Fy = mY,                     Fz = mZ.

Результирующую единичную массовую силу, действующую на жидкость,  найдем как сумму единичных векторов силы инерции j  и силы тяжести g. Единичная сила инерции Fи = j = – a направлена в сторону  противоположную ускорению а (рис.4.5).

Проекции сумм массовых сил на оси:

          Ox: X = j – gSinα,   

         Oz : Z = –gCosα,

Оx: Y = 0.

При подстановке этих проекций в дифференциал давления, получим

(1/ρ)dp = [(j – gSinα)dx – (gCosα)dz].

Проинтегрировав дифференциал в проекциях, получим выражение для давления на поверхностях уровня

Р = ρ [(j – gSinα) x – (gCosα)z] + С.  (4.14)

На произвольной поверхности уровня давление постоянно Р = const и,  обозначив новую постоянную  С₁ – Р = const, где Р получим уравнение  изобарических поверхностей

ρ [(j – gSina) x – ρgCosa* z] +С₁ = 0                (4.15)

Это уравнение дает семейство плоскостей, параллельных оси Оу. Одной из них является свободная поверхность.

Обозначим через z₀ координату пересечения свободной поверхности с осью z. Подставив в формулу (4.15) х₀ = 0, z = z₀, находим С₁=ρg z₀Cosα для свободной поверхности. Уравнение этой поверхности имеет вид

ρ [(j – gSina) x – ρgCosa* z] + ρg z₀Cosα = 0

 (j – gSina) x –gCosa*( z + z₀) = 0

  

 где коэффициент в линейном уравнении равен тангенсу угла β .

Для определения положения свободной поверхности жидкости в сосуде, движущемся прямолинейно   и   равноускоренно к уравнению (4.16) нужно добавить уравнение объемов, т. е. нужно знать первоначальный объем жидкости в сосуде и выразить его через размеры сосуда В и Н и первоначальный уровень h.

Если сосуд движется только под действием силы тяжести, то j= gSinα β = 0, то свободная поверхность параллельна  плоскости движения.

 При нулевых условиях: х = 0, z = z₀, P = P₀  в  формуле (4.14),   получим C = P₀+ (ρgCosa)z₀:  

Р = ρ [(j – gSinα) x – (gCosα)z + С

Р = P₀+ρ(j-gSina)x+ρgCosa(z₀ – z).   (4.19)

Эта формула используется для определения давления в любой точке жидкости, находящейся в относительном покое при прямолинейном движении

Можно также использовать суммарную массовую единичную силу q для определения давления в любой точке.

Возьмем на рис.4.5 около точки М площадку dS, параллельную свободной поверхности, и на этой площадке построим цилиндрический  объем с осью, нормальной к  свободной поверхности. Условие равновесия указанного объема жидкости в направлении нормали к свободной поверхности будет иметь вид

РdS = P₀dS + q(ρldS),

где последний член представляет собой полную массовую силу,  q – суммарная единичная массовая сила, М = ρldS –   масса выделенного объема жидкости,  l — расстояние от точки М до свободной поверхности.

После сокращения на dS получим давление в точке

Р = P₀ + qρl,                          (4.20)

4.6. Равномерное вращение сосуда с жидкостью

Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему вращение с постоянной угловой скоростью ω  вокруг его вертикальной оси. Силы трения о стенки вращающегося сосуда будут увлекать за собой жидкость. Она постепенно приобретет ту же угловую скорость, что и сосуд, находясь по отношению к  сосуду в покое. Свободная поверхность жидкости  изменится.

В центральной части уровень жидкости опустится, у стенок  она поднимется, и вся свободная поверхность жидкости станет поверхностью вращения (рис.4.6).

На жидкость будут действовать силы давления, силы тяжести и силы инерции переносного движения. Частица жидкости будет находиться под действием ускорения силы тяжести и центростремительного ускорения, а  равное ему ускорение силы инерции будет центробежным. Единичная массовая сила тяжести F_g = g и единичная массовая центробежная сила F_цб = ω²r.

Проекции этих сил на оси координат дадут следующие выражения

X = (V²/r) Cos(r^x) = ω²r Cos(r^x)= ω²X

Y = (V²/r) Cos(r^y) = ω²r Cos(r^у)= ω²Y,  

                                      Z = -g

Подставляя эти проекции в дифференциальное уравнение поверхности   равного давления и интегрируя :                 

X*dх+У*dy+Z*dz = 0,

получим                                 ρ(ω²/2) (X²  + Y²) – ρgz + С = 0.

Уравнение  свободной поверхности, например, получим, при нулевых условиях:    Р₀ = const, х = у = 0, z= z₀,  где  координата вершины параболоида свободной поверхности. Тогда   С = ρgz₀.  

ρ(ω²/2) (X²  + Y²) – ρgz + ρgz₀  = 0,

(ω²/2) (X²  + Y²) =g(z – z₀)

и после деления на g   уравнение свободной поверхности получит вид

                      (4.22)

Таким образом, поверхности равного давления, в том числе и свободная поверхность, образуют семейство параболоидов, сдвинутых вдоль вертикальной оси. Каждому значению р соответствует свой параболоид, положение которого определяет константа С.

Эти поверхности  будут конгруэнтными параболоидами вращения  с осью Oz. Один из этих параболоидов – свободная поверхность жидкости, где Р₀= Ратм.

Две геометрические фигуры называются конгруэнтными, если их можно совместить одну с другой, изменив их положение в пространстве.

Подставляя проекции массовых сил в дифференциал давления

dp  = ρ(Xdx  +  Ydy + Zdz), 

получим                                  dp  = ρω² (Xdx  + Ydy) –ρ gdz,

вынесем знак дифференциала за скобки,

dp  = ρ d[(ω²/2) (X²  + Y²)] –ρ gdz,

и проинтегрировав,  получим выражение для определения давления в любой точке

 p  = ρ(ω²/2) (X²  + Y²) –ρ gz + С₁,    (4.21)

Значение константы для свободной поверхности Р = Р₀, x=y=0, z = z₀: С₁ = Р₀ + ρgz_0.

Получим уравнение для определения давления в любой точке:

             (4.22)

Пользуясь этими уравнениями  можно определить положение свободной поверхности и давление в сосуде.

Максимальная высота Н подъема жидкости в параболоиде со свободной поверхностью может быть определена, следующим образом.

 На практике часто рассматривается вращение сосуда с жидкостью, когда угловая скорость ω столь велика, что силой тяжести можно пренебречь по сравнению с центробежными силами. При этом закон изменения давления в жидкости легко получить из формулы (4.22),  в которой следует принять g(z₀ – z) = 0.

Поверхности уровня примут вид цилиндров с общей осью  –   осью вращения сосуда. Если сосуд не был заполнен перед началом вращения,  давление Р₀ будет действовать не в центре, а при r = r₀,  вместо выражения (4.22) будем иметь

Р = Р₀ + ρ ω² (r —r₀²)/2g,                          (4.23)

Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к оси вращения (или на кольцевую часть этой стенки).

Для этого необходимо выразить сначала силу давления, приходящуюся на элементарную кольцевую площадку dS = 2πrdr радиусом r и шириной dr;

 

Уравнение, выражающее величину давления имеет вид

Ещё посмотрите лекцию “Лекция 11.1” по этой теме.

При определении давления на верхнюю крышку где Z=0,  Z₀ может быть больше нуля Z0>0, равно нулюи меньше нуля

В первом случае

а затем выполнить интегрирование в требуемых пределах.

При большой угловой скорости жидкости можно получить весьма значительную суммарную силу давления на стенку. Этот эффект используется в некоторых фрикционных муфтах, где для осуществления сцепления двух валов требуется создание больших сил нормального давления. Способ, указанный выше,  применяют для определения силы осевого давления жидкости на рабочие колеса центробежных насосов, а также на крышки центрифуг.

Определение координат центра тяжести x_C и y_C плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.

Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.

Способы определения координат центра тяжести

Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.

Существует 5 способов расчета координат положения центра тяжести:

1. Аналитический (путем интегрирования).
2. Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3. Экспериментальный. (метод подвешивания тела).
   Этот способ подходит в основном для плоских и линейных тел.
4. Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.

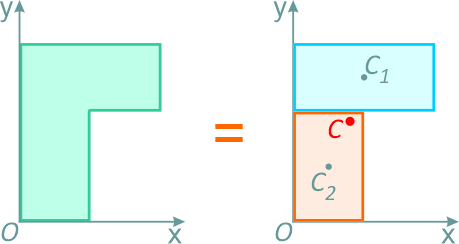
   Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A₁ и A₂ (A = A₁+ A₂).
   

   Рисунок 1.8

   Центры тяжести этих фигур находятся в точках C₁(x₁, y₁) и C₂(x₂, y₂). Тогда координаты центра тяжести тела равны:
   

5. Дополнение (Метод отрицательных площадей или объемов).
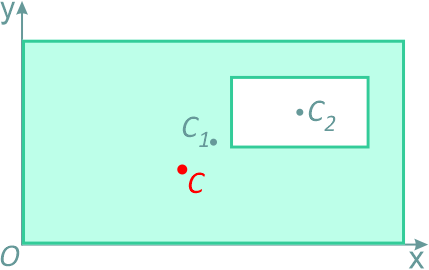
   Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.

   Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
   

   Рисунок 1.9

   Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
   

При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).

Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:

Другие видео

Пример определения координат центра тяжести плоской фигуры

Задача
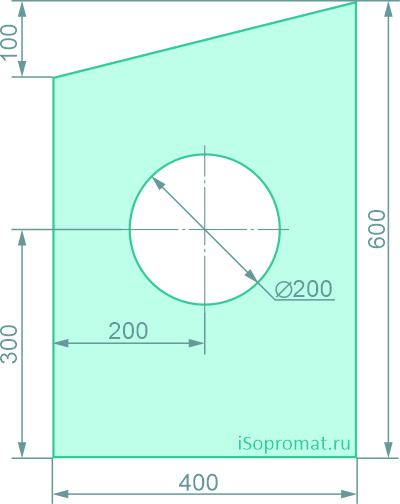
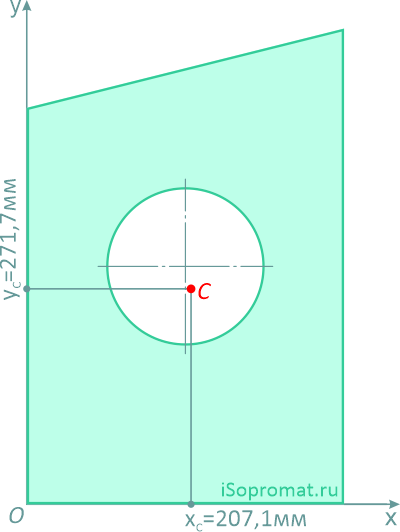
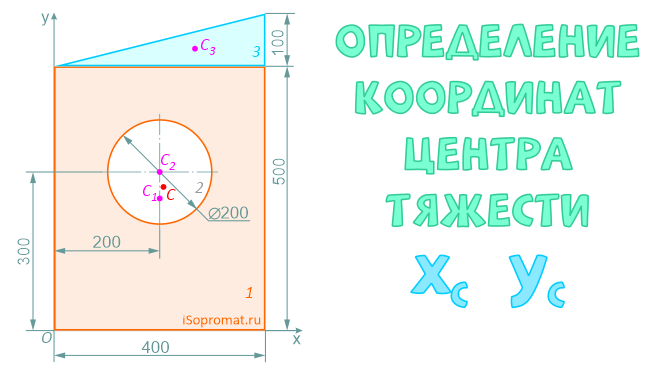
Определить координаты центра тяжести плоской фигуры с круглым отверстием

Решение
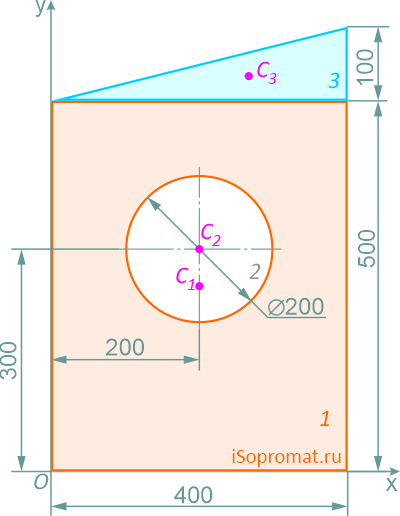
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.

Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести C_i отдельных фигур:

Прямоугольник (фигура 1)
Площадь
A₁=400×500=200000 мм²
Положение центра тяжести
x₁=200мм
y₁=250мм

Круг (2) (вычитаемая фигура)
Площадь
A₂=π×200²/4=31416 мм²
Центр тяжести
x₂=200мм
y₂=300мм

Прямоугольный треугольник (3)
Площадь
A₃=400*100/2=20000 мм²
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x₃=400×2/3=266,7мм
y₃=500+100×1/3=533,3мм

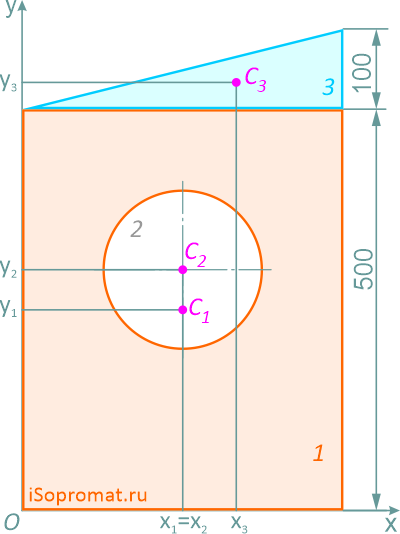
Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:

Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами x_C=207,1мм, y_C=271,7мм.

Другие примеры решения задач >
Центры тяжести простейших фигур >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Центр тяжести (центр масс):

Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.

Центр тяжести – геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.

На каждую точку тела в поле сил тяжести действует сила, а на все тело – равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.

Центр масс (центр инерции) – точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе  внешние силы.

При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.

Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.

При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, – параллельными.

Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.

 Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.

Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.

Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.

Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.

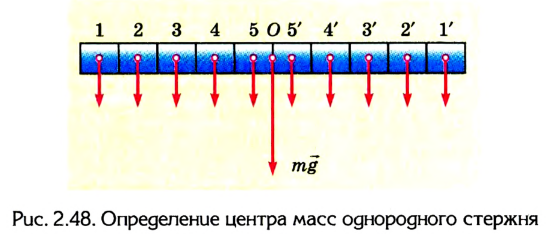
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О – середине стержня.

Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.

Центр тяжести однородного стержня расположен в середине стержня.

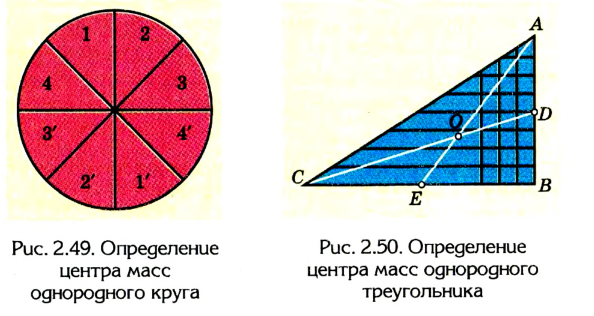
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).

Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.

Центр тяжести однородного круга совпадает с его центром.

Центр тяжести однородного треугольника находится в точке пересечения его медиан.

3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.

Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.

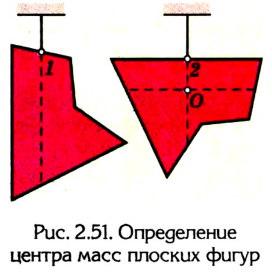
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).

Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.

Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.

Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.

• Заказать решение задач по физике

Центр тяжести тела и центр масс тела

Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.

Рис. 151

Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.

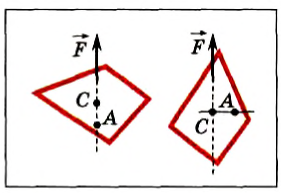
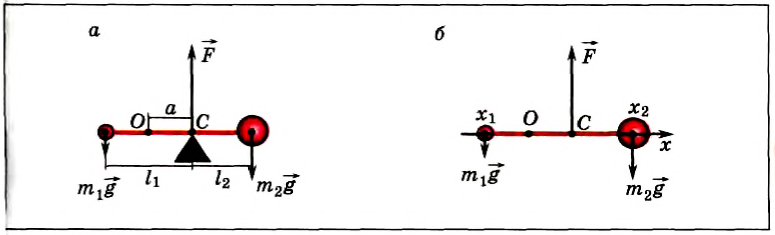
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m₁ и m₂, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:

или

Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:

Рис. 152

Поскольку F=(m₁ + m₂)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.

Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х₁, х_с и х₂. Запишем условие моментов относительно точки О:

Отсюда

При выводе этой формулы было использовано значение силы F = (m₁ + m₂) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии х_с, определенном формулой (2).

Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.

Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.

Если произвольное тело можно разбить на n элементов, массы которых m₁, m₂…,    m_n, и если известны координаты центров масс этих элементов x₁, x₂…,   x_n относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:

Естественно, что такие же соотношения можно записать и для у_с и z_c. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m₁ = 2m₂). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C₁) и линейки (C₂).

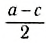
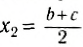
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х₁ = 0, y₁ =, а координаты центра масс линейки: , y₂ = 0 .
По формуле (3):    .

Таким образом, центр масс угольника находится вне тела.

Главные выводы:

1. Центр тяжести — точка, в которой приложена сила тяжести.
2. Центр масс симметричных однородных тел находится в их геометрическом центре.
3. Координаты центра масс тела можно вычислить по формуле (3).

Была ли эта статья полезной?