Как найти центр тяжести стены

Определить координаты центра тяжести стены.

Торцевая стена ангара (рис. 1.5.2) имеет форму полукруга 1 радиуса с прямоугольным дверным проемом 2 высотой и шириной Определить координаты центра тяжести стены.

Решение:

1. Применим методы симметрии и отрицательных площадей, рассматривая полукруг 1 и прямоугольный вырез 2.

2. Найдем координаты центра тяжести стены.

Поскольку ось Оy является осью симметрии, то координата

Координату центра тяжести пластины определим по формуле

где , , , – площади и координаты центров тяжести фигур 1 и 2.

Площади и координаты центров тяжести фигур:

Тогда

Центром
тяжести твердого тела называется центр
параллельных сил тяжести

частиц данного тела.

,

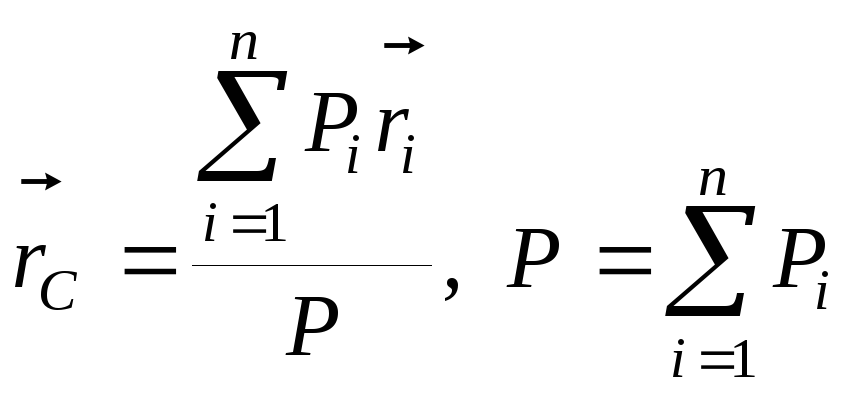или

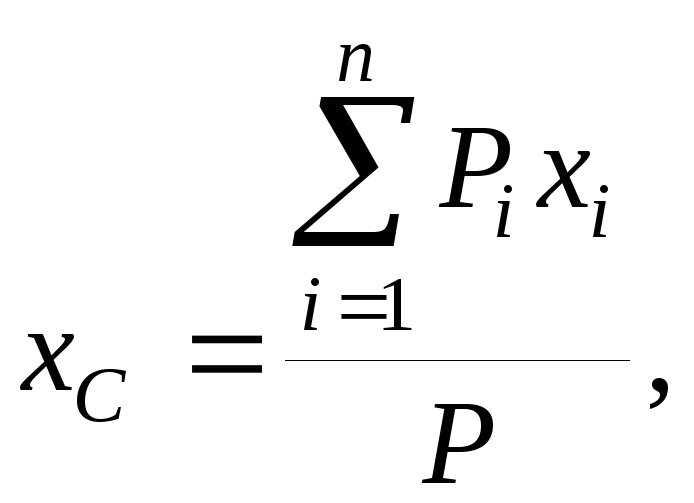
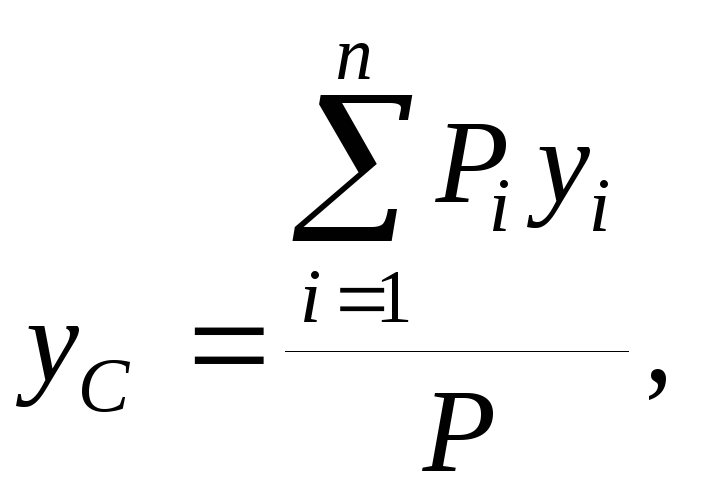
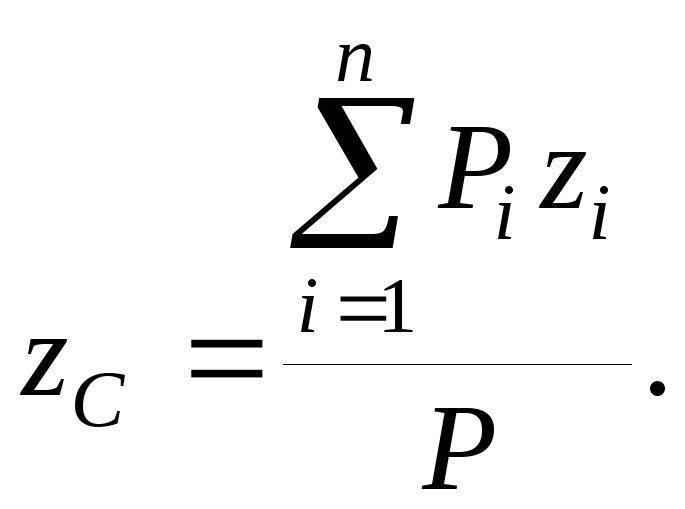
Для
определения положения центра тяжести
однородных тел используют метод
симметрии, метод разбиения на тела
простой формы с известным положением
центров тяжести, а также метод отрицательных
масс (линий, площадей, объемов).

Пример
1.5.1. Определить координаты центра
тяжести плоской фермы (рис. 1.5.1),
составленной из однородных стержней с
одинаковым погонным весом.

Решение:

1.
Применим метод разбиения, то есть
представим ферму как совокупность семи
стержней.

2.
Найдем координаты центра тяжести фермы
по формулам:

;

,

где
,
,

– длина и координаты центра тяжести
стержня с номером .

Длины
и координаты центров тяжести стержней:

Тогда

,

Пример
1.5.2. Торцевая стена ангара (рис. 1.5.2)
имеет форму полукруга 1 радиуса

с прямоугольным дверным проемом 2
высотой

и шириной

Определить координаты центра тяжести
стены.

Решение:

1.
Применим методы симметрии и отрицательных
площадей, рассматривая полукруг 1
и прямоугольный вырез 2.

2.
Найдем координаты центра тяжести стены.

Поскольку
ось Оy является
осью симметрии, то координата

Координату

центра тяжести пластины определим по
формуле

где
,
,
,

– площади и координаты центров тяжести
фигур 1 и 2.

Площади
и координаты центров тяжести фигур:

Тогда

Задачи
1.5.1 – 1.5.4. Определить координаты
центров тяжести плоских ферм (рис.
1.5.3 – 1.5.6), составленных
из однородных стержней с одинаковым
погонным весом.

Ответы
к задачам 1.5.1 – 1.5.4:

Номер задачи	1.5.1	1.5.2	1.5.3	1.5.4
, м	1,52	3,88	3,0	1,59
, м	0,69	1,96	1,73	0,17

Рис. 1.5.3	Рис. 1.5.4
Рис. 1.5.5	Рис. 1.5.6
Рис. 1.5.7	Рис. 1.5.8

Задачи
1.5.5 – 1.5.7. Определить координаты
центров тяжести однородных составных
линий (рис. 1.5.7 – 1.5.9).

Ответы
к задачам 1.5.5 – 1.5.7:

Номер задачи	1.5.5	1.5.6	1.5.7
, см	14	19	–4,76
, см	9	14,16	3,31

Рис. 1.5.9	Рис. 1.5.10
Рис. 1.5.11	Рис. 1.5.12

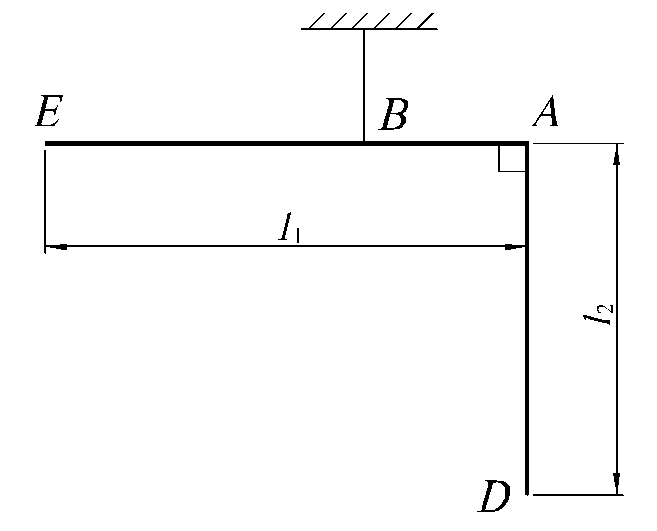
Задача 1.5.8. Изогнутая
под прямым углом однородная проволока
подвешена на нити (рис. 1.5.10). Найти
соотношение между длинами участков AD
и AE, при котором участок
AE находится в
горизонтальном положении. АВ = 0,3 l₁.

Ответ:

Задача
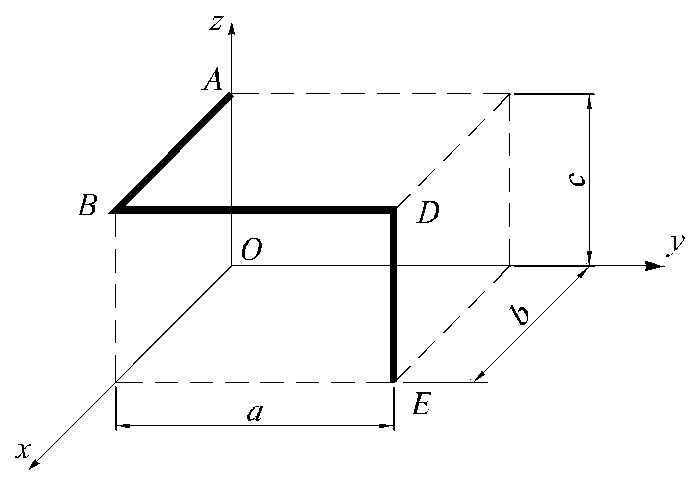
1.5.9. Определить координаты центра
тяжести однородной проволоки (рис.
1.5.11), если a = 3 м,
b = 2 м,
c = 1,5 м.

Ответ:
x_C = 1,69
м, y_C = 1,38
м, z_C = 1,33
м.

Задача
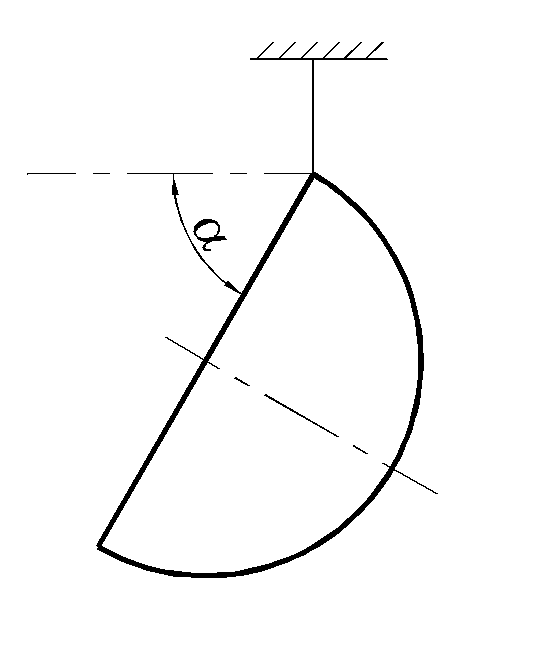
1.5.10. Однородный замкнутый контур,
ограничивающий полукруг, подвешен на
нити (рис. 1.5.12). Определить угол α
между горизонталью и диаметром
полуокружности.

Ответ:
α = 68,74º.

Задачи
1.5.11 – 1.5.14. Определить координаты
центров тяжести однородных плоских
фигур (рис. 1.5.13 – 1.5.16).

Ответы
к задачам 1.5.11 – 1.5.14:

Номер задачи	1.5.11	1.5.12	1.5.13	1.5.14
	0	37,07 см	32,38 см	2,31 м
	11,88 см	0	24,83 см	1,56 м

Рис. 1.5.13	Рис. 1.5.14
Рис. 1.5.15	Рис. 1.5.16
Рис. 1.5.17	Рис. 1.5.18

Задача 1.5.15. Подставка
для цапфы подшипника представляет собой
деталь, состоящую из опоры в виде
параллелепипеда и шпонки в форме куба
(рис. 1.5.17). Определить координаты центра
тяжести подставки. Размеры указаны в
миллиметрах.

Ответ:

Задача
1.5.16. Цапфа подшипника скольжения
представляет собой деталь, состоящую
из параллелепипеда и цилиндрической
опоры (рис. 1.5.18). Определить координаты
центра тяжести цапфы. Размеры
указаны в миллиметрах.

Ответ:
,
,

Задача
1.5.17. Однородное тело, сечение которого
изображено на рисунке 1.5.19,
состоит из полушара, цилиндрической
части и кругового конуса. Определить
координаты центра тяжести тела. Размеры
указаны в миллиметрах.

Ответ:
,
,

Задача
1.5.18. Ствол танковой пушки имеет
форму усеченного конуса длины

(рис. 1.5.20). Наружный диаметр ствола в
месте крепления к казенной части пушки

наружный диаметр в сечении, соответствующем
дульному срезу канала ствола,

Калибр пушки d =100 мм.
Определить координату

центра тяжести ствола.

Ответ:

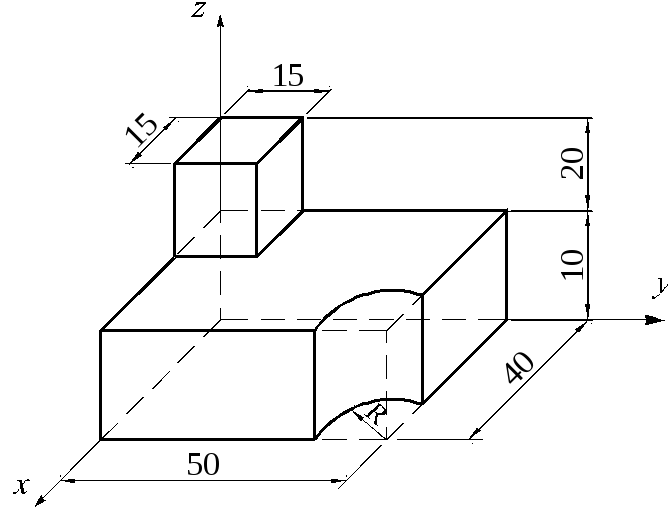
Задача
1.5.19. Определить координаты центра
тяжести однородного тела, состоящего
из двух прямоугольных параллелепипедов
(рис. 1.5.21). В нижнем параллелепипеде
сделан вырез в форме четверти цилиндра
с радиусом основания R = 10 см.
Размеры на рисунке указаны в см.

Ответ:
x_C = 17,1
см, y_C = 20,99
см, z_C = 7,84
см.

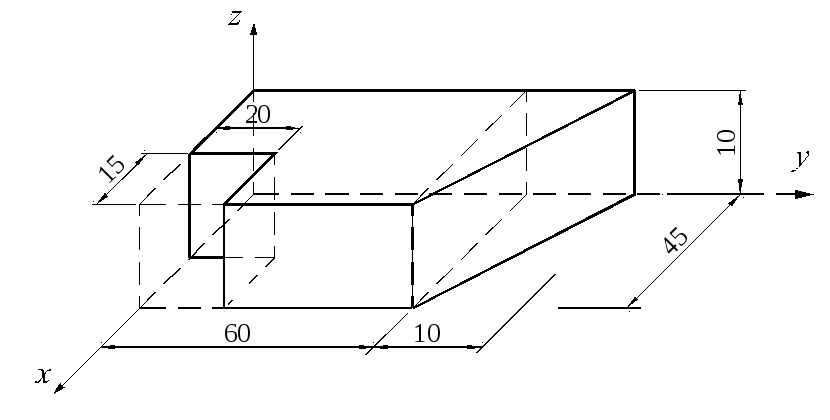
Задача
1.5.20. Определить координаты центра
тяжести однородного тела (рис. 1.5.22),
состоящего из треугольной призмы и
параллелепипеда с вырезом. Размеры на
рисунке указаны в см.

Рис. 1.5.19	Рис. 1.5.20
Рис. 1.5.21	Рис. 1.5.22

Ответ:
x_C = 20,14
см, y_C = 35,14
см, z_C = 5
см.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Часто перед началом монтажа дома мы задаемся вопросами, а какое количество стен я могу погрузить в грузовой автомобиль? Сможет ли кран поднять тяжелую наружную стену? На каких точках лучше всего выполнить сверления или установить петли для транспорта?  С помощью программы Dietrich´s эти вопросы можно решить всего в несколько шагов:

1. Определение центра тяжести

Находясь в Конструкции стены, вызовите функцию «1 Файл – 4 Дополнительные опции – 1 Центры тяжести».

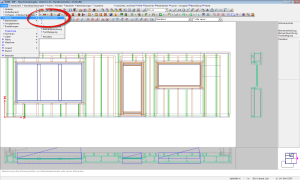
Активируйте режим «Все стены» чтобы рассчитать центры тяжести всех стен за один приход. Если при расчете разных стен сооружения должны быть учтены различные слои материалов, выберите функцию «Текущая стена» или «Выбрать стену».

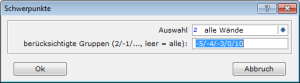
В строку «Учитываемые группы» занесите материалы, релевантные для перевозки. Как правило, номер группы соответствует номеру слоя. При необходимости вы можете проверить принадлежность конкретного материала к группе с помощью функции: «Средняя кнопка мыши: Свойства элемента – MOS». Подсказка: если во время ввода окон вместе с ними были созданы оконные рамы и стекла за счет использования шаблона, с помощью этой функции можно учитывать такие окна, предварительно собранные на заводе. Для этого активируйте группу 18.

Если в меню «1 – 7 – 1 Изображение» активировать изображение «обмерных элементов», то после вызова команды по определению центра тяжести кнопкой «ОК» рассчитанный центр тяжести стены отобразится в Конструкции стены.

2. Вывод чертежа стены

Если вы хотите, чтобы рассчитанный центр тяжести отобразился на чертеже стены, а также при необходимости размерить горизонтальное расстояние от центра тяжести до наружных кромок стены, воспользуйтесь функцией «Размеры» – «Размерить центр тяжести» в меню Вывод чертежа стены.

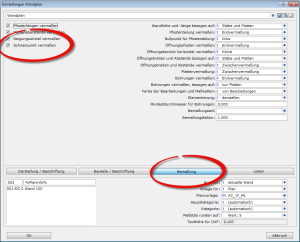
После выполнения этих действий в текстовой части чертежа стены отобразится вес учитываемых материалов:

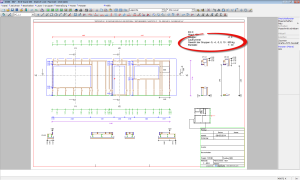
3. Позиционирование отверстий и петель для перевозки

Чтобы при подъеме краном стена оставалась висеть ровно, позиционирование креплений для транспортировки стен должно осуществляться на равном расстоянии от центра тяжести. Посредством комбинированного элемента «Траверс» можно с легкостью позиционировать вырубки (для конвейерных лент) и отверстия. На эту темы мы поговорим в следующих информационных статьях.

Определение координат центра тяжести x_C и y_C плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.

Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.

Способы определения координат центра тяжести

Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.

Существует 5 способов расчета координат положения центра тяжести:

1. Аналитический (путем интегрирования).
2. Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3. Экспериментальный. (метод подвешивания тела).
   Этот способ подходит в основном для плоских и линейных тел.
4. Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.

   Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A₁ и A₂ (A = A₁+ A₂).
   

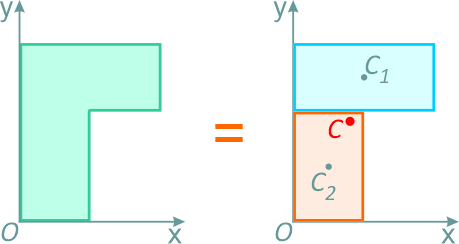
   Рисунок 1.8

   Центры тяжести этих фигур находятся в точках C₁(x₁, y₁) и C₂(x₂, y₂). Тогда координаты центра тяжести тела равны:
   
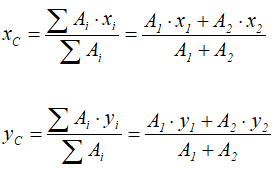
5. Дополнение (Метод отрицательных площадей или объемов).
   Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.

   Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
   

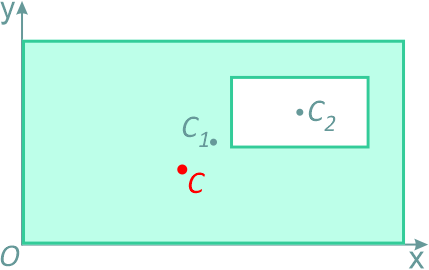
   Рисунок 1.9

   Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
   

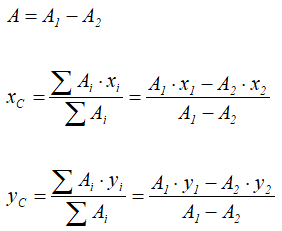
При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).

Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:

Другие видео

Пример определения координат центра тяжести плоской фигуры

Задача
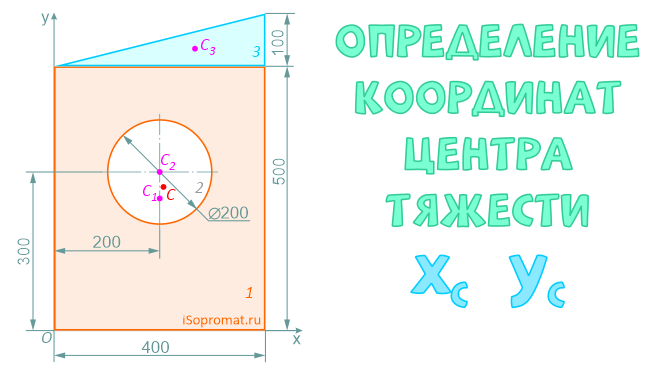
Определить координаты центра тяжести плоской фигуры с круглым отверстием

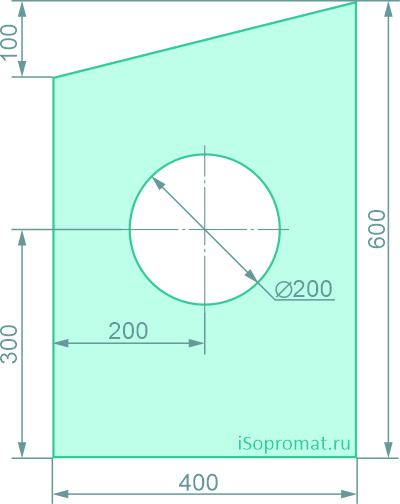
Решение
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.

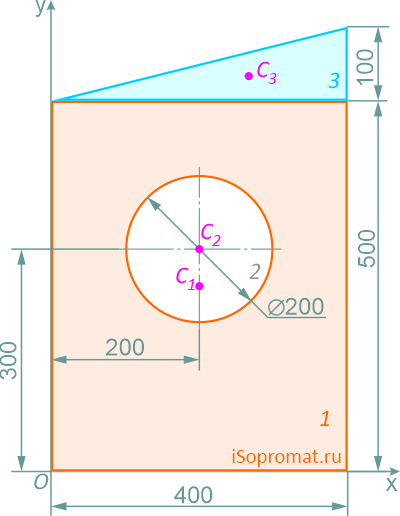
Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести C_i отдельных фигур:

Прямоугольник (фигура 1)
Площадь
A₁=400×500=200000 мм²
Положение центра тяжести
x₁=200мм
y₁=250мм

Круг (2) (вычитаемая фигура)
Площадь
A₂=π×200²/4=31416 мм²
Центр тяжести
x₂=200мм
y₂=300мм

Прямоугольный треугольник (3)
Площадь
A₃=400*100/2=20000 мм²
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x₃=400×2/3=266,7мм
y₃=500+100×1/3=533,3мм

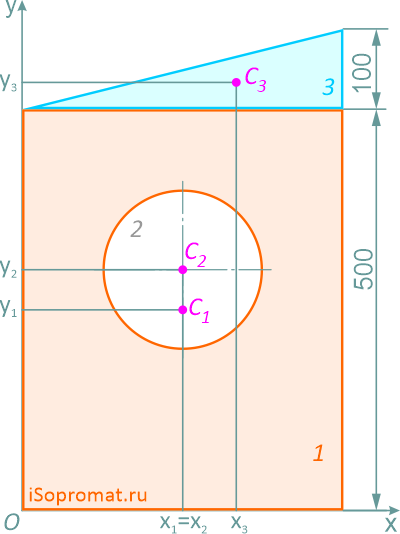
Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:

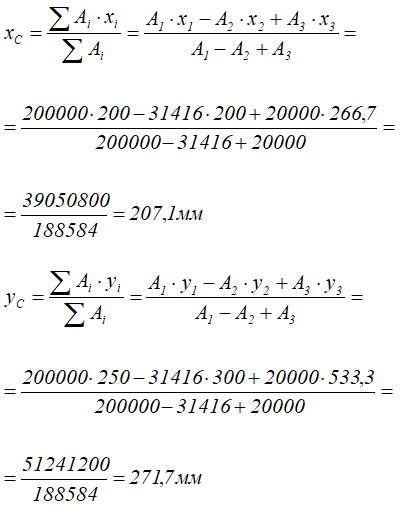
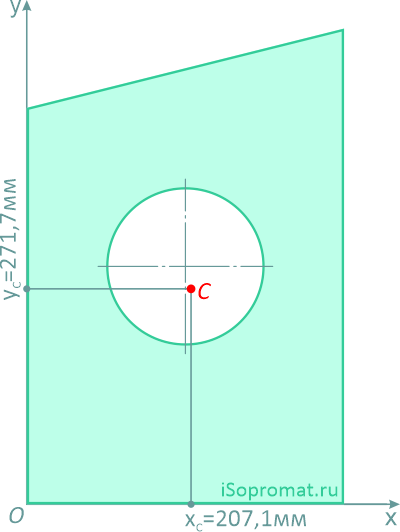
Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами x_C=207,1мм, y_C=271,7мм.

Другие примеры решения задач >
Центры тяжести простейших фигур >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

В этой статье посмотрим, как определяются координаты центра тяжести сложной фигуры — состоящей из простых. В задачах по сопромату часто приходится находить положение центра тяжести составных сечений, для дальнейшего вычисления моментов инерции и т. д.

Также часто, при изучении теоретической механики, студентам предлагается решить подобную задачу, и найти центр тяжести какой-нибудь фигуры.

Условие задачи

Предлагаю рассмотреть следующую фигуру:

В сопромате принято заштриховывать сечения тонкими линиями, вот так:

В своих же уроках я буду использовать заливку. Так, штриховка не будет мешать наносить обозначения.

Разбивка сложной фигуры на простые

Как видишь, сечение состоит из прямоугольника, прямоугольного треугольника, четверти круга, а также имеет круглый вырез:

Отметим центры тяжести (С₁, С₂, С₃, С₄) каждой отдельной фигуры, с учётом справочной информации.

Открой эту страничку, и пока не закрывай, она нам ещё понадобится!

Покажем вспомогательные оси (x₀, y₀) для всего сечения, которые будем использовать для нахождения положения центра тяжести (C):

Как определить положение центра тяжести?

Чтобы определить координату центра тяжести сечения, например, вертикальное расстояние от оси x₀ до центра тяжести сечения (y_c):

Нужно статический момент сечения относительно этой вспомогательной оси (x₀) разделить на площадь всего сечения (A):

Площадь всего сечения (A) найти просто – это алгебраическая сумма площадей всех фигур:

Статический момент сечения, относительно вспомогательной оси будет равен алгебраической сумме статических моментов каждой фигуры (с учётом знака):

где A_i – площадь отдельной фигуры;
y_i – расстояние от центра тяжести отдельной фигуры до вспомогательной оси (x₀).

Координата центра тяжести (x_c), находится аналогично:

Определение площади сечения

Для начала предлагаю сделать самое простое, используя формулы, указанные на этой странице, найти площадь всего сечения (A):

Как видишь, круглый вырез, нужно учесть с «минусом», что очевидно.

Определение расстояний от вспомогательных осей до центров тяжести отдельных фигур

Найдём расстояния от вспомогательных осей (x₀, y₀) до центров тяжести отдельных фигур, опять же, используя нашу шпаргалку:

Определение статических моментов

Определяем статические моменты сечения относительно вспомогательных осей (x₀, y₀):

Важно! Статические моменты могут быть и отрицательными.

Определение координат центра тяжести

И, наконец, определяем положение центра тяжести всего сечения (C):

Покажем центр тяжести всего сечения (C):

Если остались какие-то вопросы по данному уроку, можешь смело задавать их в комментариях. Также, другие уроки, на сайте – ssopromat.ru, по определению геометрических характеристик, можешь найти здесь.