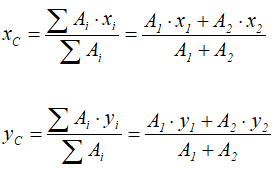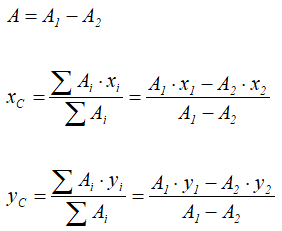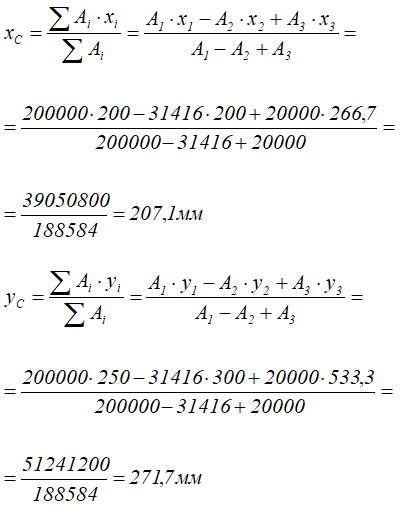как найти центр тяжести тела неправильной формы?!?!)) помогите пожалуйста)
Ученик
(102),
закрыт
6 лет назад
rafael ahmetov
Высший разум
(122431)
11 лет назад
Для плоской фигуры достаточно просто. Подвесить тело за какую-нибудь точку, и с помощью отвеса через эту точку провести вертикальную линию. Сделать то же самое, подвесив за другую точку. Пересечение полученных двух линий даст центр тяжести. Для объемных тел сложнее, так как в общем случае (за исключением, пожалуй, тела наподобие бублика) центр тяжести оказывается внутри тела, и как найти точку пересечения трех линий внутри тела, и как провести сами линии.
Leonid
Высший разум
(388685)
11 лет назад
Если экспериментально – то подвесить его на нитке за две разные точки. Сначала за одну, потом за другую. Центр тяжести находится на пересечении линий – продолжений нити.
Галямов Равиль
Знаток
(406)
7 лет назад
Если экспериментально – то подвесить его на нитке за две разные точки. Сначала за одну, потом за другую. Центр тяжести находится на пересечении линий – продолжений нити
Алиса супер
Ученик
(102)
2 недели назад
Для плоской фигуры достаточно просто. Подвесить тело за какую-нибудь точку, и с помощью отвеса через эту точку провести вертикальную линию. Сделать то же самое, подвесив за другую точку. Пересечение полученных двух линий даст центр тяжести. Для объемных тел сложнее, так как в общем случае (за исключением, пожалуй, тела наподобие бублика) центр тяжести оказывается внутри тела, и как найти точку пересечения трех линий внутри тела, и как провести сами линии.
При создании машин, механизмов и различных конструкций важно знать, при каких условиях они будут устойчивыми, т. е. находиться в равновесии. Каким же образом можно добиться равновесия тела? Возьмём линейку и, обвязав её петлей, подвесим на нити. Затем, перемещая петлю по линейке, можно найти положение, в котором линейка будет находиться в равновесии. В этом случае говорят, что линейка подвешена в центре тяжести. Центр тяжести имеется у каждого тела. Что же такое центр тяжести? Разделим мысленно тело на несколько частей. На каждую часть будет действовать сила тяжести, которая всегда направлена вертикально вниз (рис. 184). При всевозможных изменениях положения тела расположение центра тяжести не меняется (см. рис. 184).
Рис. 184. Направление действия силы тяжести

Точку приложения равнодействующей сил тяжести, действующих на отдельные части тела, называют центром тяжести тела. |
Как же найти центр тяжести в различных твёрдых телах? Проделаем следующий опыт. Возьмём фигуру неправильной формы из картона (рис. 185, а) и подвесим её на гвоздь вместе с отвесом. На фигуру действуют две силы: сила тяжести и сила упругости. Поскольку картон находится в покое, то эти две силы взаимно уравновешиваются, т. е. они равны по величине и направлены в разные стороны. Это значит, что точки приложения сил лежат на одной вертикальной прямой, отмеченной отвесом.
Рис. 185. Нахождение центра тяжести плоского тела неправильной формы
Рис. 186. Центр тяжести твёрдых тел
Проведём на фигуре вертикальную линию по отвесу. Затем подвесим её в другой точке и снова проведём по отвесу вертикальную линию (рис. 185, б). Сколько бы ни проводили таким способом линий, все они пересекутся в одной точке, которая и будет центром тяжести тела С (рис. 185, в). Проверить это можно, если на остриё карандаша поместить фигуру в найденном центре тяжести. Она окажется в равновесии (рис. 185, г).
Во время опыта мы несколько раз меняли положение картонной фигуры, но центр тяжести её оставался в одной и той же точке.
187. Центр тяжести кольца
При любом положении тела центр тяжести его находится в одной и той же точке.
Например, центр тяжести шара лежит в его геометрическом центре, у цилиндра он находится на середине линии, соединяющей центры его оснований, у параллелепипеда — в точке пересечения диагоналей (рис. 186). Иногда центр тяжести может находиться и вне тела. Например, у кольца он лежит на пересечении диаметров (рис. 187).
Положение центра тяжести может изменяться только при изменении относительного расположения частей тела.

1.Расположив карандаш на указательном пальце руки, найдите его центр тяжести.
2.Определите центр тяжести ластика, ключа, используя нить.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,926 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
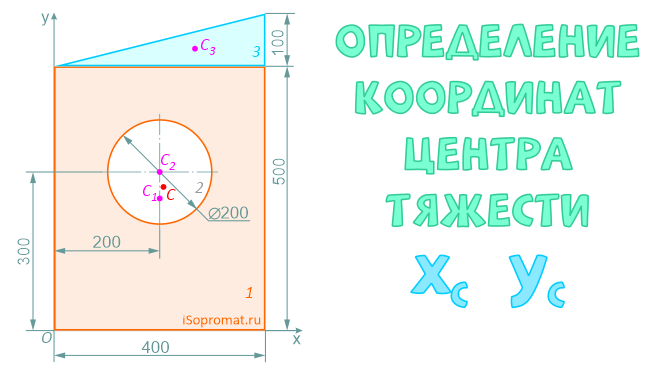
Определение координат центра тяжести xC и yC плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.
Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.
Способы определения координат центра тяжести
Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.
Существует 5 способов расчета координат положения центра тяжести:
- Аналитический (путем интегрирования).
- Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
- Экспериментальный. (метод подвешивания тела).
Этот способ подходит в основном для плоских и линейных тел. - Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.
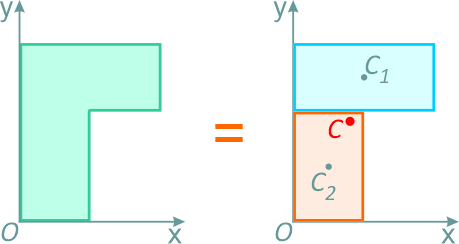
Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A1 и A2 (A = A1+ A2).
Рисунок 1.8
Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны:
- Дополнение (Метод отрицательных площадей или объемов).
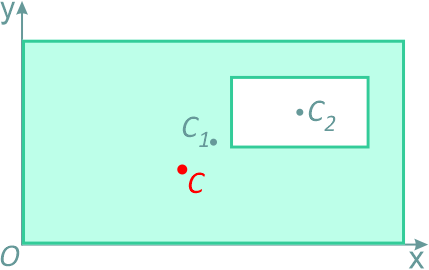
Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.9
Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).
Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:
Другие видео
Пример определения координат центра тяжести плоской фигуры
Задача
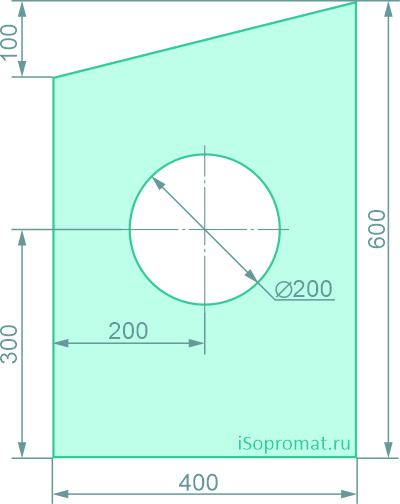
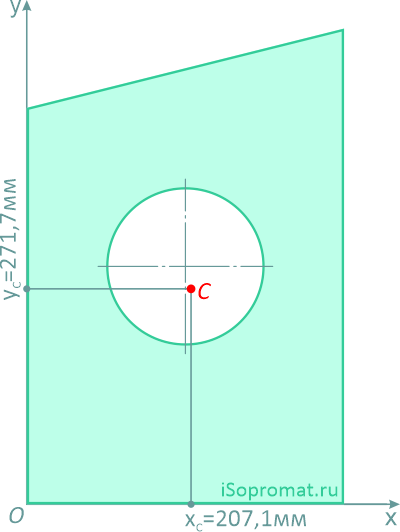
Определить координаты центра тяжести плоской фигуры с круглым отверстием
Решение
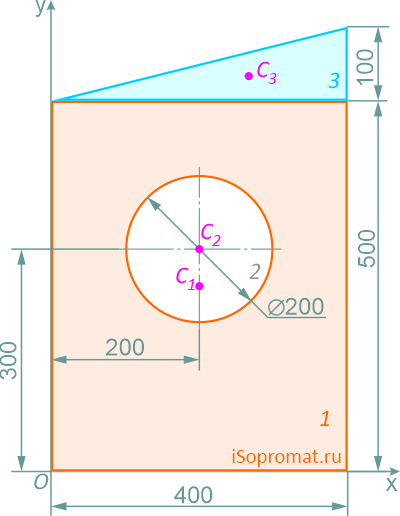
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.
Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести Ci отдельных фигур:
Прямоугольник (фигура 1)
Площадь
A1=400×500=200000 мм2
Положение центра тяжести
x1=200мм
y1=250мм
Круг (2) (вычитаемая фигура)
Площадь
A2=π×2002/4=31416 мм2
Центр тяжести
x2=200мм
y2=300мм
Прямоугольный треугольник (3)
Площадь
A3=400*100/2=20000 мм2
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x3=400×2/3=266,7мм
y3=500+100×1/3=533,3мм
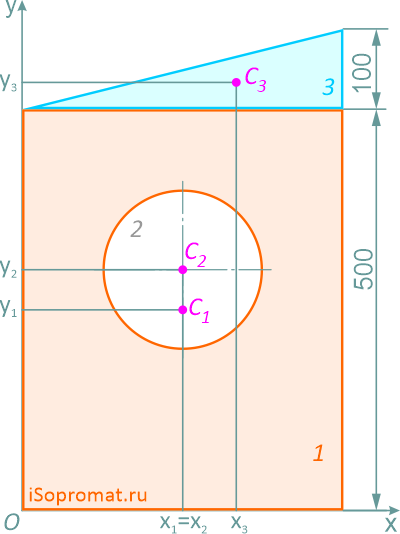
Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:
Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами xC=207,1мм, yC=271,7мм.
Другие примеры решения задач >
Центры тяжести простейших фигур >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Борис Трушин39
Учитель математики · 23 янв 2019 · youtube.com/trushinbv
Если в самом общем виде, то зная как меняется плостность тела G находим его массу М (если плотность постоянная, то можно вместо нее подставить единицу). Зная массу находим координаты центра масс (x0, y0, z0):
Если же у вас фигура G постоянной плотности на плоскости, то формулы сильно упрощаются:
2,7 K
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос