Про уолок (только для умных)
Знаток
(402),
закрыт
14 лет назад
Gricha Cot
Мыслитель
(9965)
14 лет назад
Формула-то как раз есть, но с интегралами и дифференциалами – общая формула для определения центра тяжести любой плоской фигуры. К уголку её громоздить ни к чему. Все правы в одном – в практической деятельности определение центра тяжести прокатного или гнутого ГОСТовского уголка не требуется – это все дано в таблицах ГОСТа на конкретный вид проката. Но, уголок теоретически может быть и не обязательно прокатным, а, например, сварным из двух полос металла (чего только в жизни не бывает) . Так вот, центр тяжести любого плоского тела ( в данном случае это сечение уголка) может быть определен исходя из условия равновесия тела. Тело, закрепленное на оси, проходящей через центр тяжести должно находится в равновесии. Поэтому, делаем так – уголок разделяем на два взаимно перпендикулярных прямоугольника. Находим центр тяжести каждого прямоугольника- это элементарно, он находится в центре симметрии. Ставим там точки ( именно в них сосредоточена масса каждого прямоугольника) . Соединяем точки прямой линией. Именно на ней будет расположена точка равновесия, т. е. центр тяжести сечения в целом. Длина этой линии (а) находится очень просто, по теореме Пифагора, исходя из геометрических размеров сечения. Далее – условия равновесия для двух центров тяжести . F1 х а1 = F2 х а2. F1- площадь одного прямоугольника, F2 – второго, а1 – расстояние от центра тяжести первого прямоугольника до искомого центра тяжести сечения, а2 – соответственно. Естественно, а1 + а2 = а. Всё очень просто определяется.
Содержание
- Определение положения центра тяжести сечений, составленных из профилей стандартного проката
- Условие задачи
- Решение задачи
- Определение положения центра тяжести сечений, составленных из профилей стандартного проката
- Условие задачи
- Решение задачи
- ПроСопромат.ру
- Технический портал, посвященный Сопромату и истории его создания
- Задача 1
- Теоретическая механика: Центр тяжести
- § 23. Определение положения центра тяжести тела, составленного из тонких однородных стержней
- § 24. Определение положения центра тяжести фигур, составленных из пластинок
- § 25. Определение положения центра тяжести сечений, составленных из профилей стандартного проката
- § 26. Определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму
- Определение положения центра тяжести сечений, составленных из профилей стандартного проката
- Условие задачи
- Решение задачи
Определение положения центра тяжести сечений, составленных из профилей стандартного проката
Условие задачи
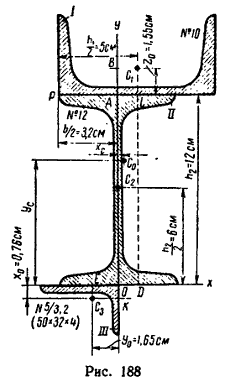
Определить положение центра тяжести сечения, составленного, как показано на рис. 188, из трех профилей стандартного проката: швеллера № 10 (ГОСТ 8240–56), двутавра № 12 (ГОСТ 8239–56) и неравнобокого уголка № 5/3,2 (размеры 50x32x4 мм ГОСТ 8510–57).
Решение задачи
1. Разбиваем сечение на три части: I – швеллер, II – двутавр и III – неравнобокий уголок.
2. Начало координат поместим в вершине прямого угла неравнобокого уголка; ось х совместим с нижней полкой двутавра, а ось у – с его вертикальной осью симметрии.
3. При помощи таблиц из ГОСТа находим:
площадь сечения швеллера № 10
F1 = 11,7 см 2 ;
площадь сечения двутавра № 12
F2 = 14,7 см 2 ;
площадь сечения уголка № 5/3,2
F3 = 3,17 см 2 .
4. В таблицах из ГОСТа положение центра тяжести С1 швеллера № 10 показано одной координатой z=1,55 см, так как швеллер имеет одну ось симметрии. Положение центра тяжести С2 двутавра в таблицах не показано, так как он имеет две оси симметрии и его центр тяжести расположен на их пересечении. Положение центра тяжести С3 неравнобокого уголка № 5/3,2 показано двумя координатами: х=0,76 и y=1,65 см.
Располагаем центры тяжести C1, C2 и C3 на рисунке (см. рис. 188), а затем при помощи таблиц находим их координаты в выбранных осях, учитывая другие необходимые размеры профилей, которые также берутся из таблиц:
координаты центра тяжести C1:
x1 = OD = PL — PA = 5 — 3,2 = 1,8 см;
y1 = OB = OA + AB = 12 + 1,55 = 13,55 см;
координаты центра тяжести C2:
x2 = 0;
y2 = OC2 = 6 см;
координаты центра тяжести C3:
x3 = -OE = -y = -1,65 см;
y3 = -OK = -x = -0,76 см.
6. Подставляем эти значения в расчетные формулы:
xc = (11,7*1,8+14,7*0-3,17*1,65)/(11,7+14,7+3,17) = 15,9/29,6 = 0,54 см;
yc = (11,7*13,55+14,7*6-3,17*0,76)/(11,7+14,7+3,17) = 244,2/29,6 = 8,23 см.
7. Центр тяжести данного составного сечения имеет координаты (в мм) С(5,4; 82,3).
Источник
Определение положения центра тяжести сечений, составленных из профилей стандартного проката
Условие задачи
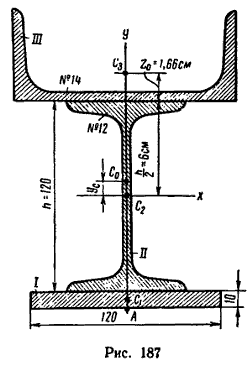
Определить положение центра тяжести симметричного сечения, составленного, как показано на рис. 187, из полосы размером 120×10 мм, двутавра № 12 (ГОСТ 8239–56) и швеллера № 14 (ГОСТ 8240–56).
Решение задачи
1. Разбиваем сечение на три части: I – полоса, II – двутавр и III – швеллер.
2. Находим площади каждой части, выражая их в см 2 . Площадь полосы определяем путем перемножения двух данных размеров, а площади двутавра и швеллера – по таблицам из ГОСТа.
Площадь сечения полосы
F1 = 12 * 1 = 12 см 2 .
Площадь сечения двутавра № 12
F2 = 14,7 см 2 .
Площадь сечения швеллера № 14
F3 = 15,7 см 2 .
3. Данное сечение имеет вертикальную ось симметрии. Совместим с этой осью ось у, а ось х проведем через середину двутавра через точку С2 – центр тяжести его сечения. Центр тяжести сечения полосы С1 расположен ниже точки С2, принятой в данном случае за начало координат, на расстоянии
y1= -(h/2 + 0,5) = -6,5 см.
Центр тяжести швеллера С3 находим при помощи тех же таблиц из ГОСТа. Положение центра тяжести швеллеров в таблицах обозначено одной координатой z; для швеллера № 14 z=1,66 см, следовательно,
y3= h/2 + z = 7,66 см.
4. Подставляем эти значения в расчетную формулу для ординаты yc:
yc = (-12*6,5+14,7*0+15,7*7,66)/(12+14,7+15,7) = 42,3/42,4 = 1,0 см.
В выбранных осях положения центра тяжести сечения выражены координатами С(0; 1).
Это значит, что центр тяжести сечения находится от его нижнего края (от точки А) на расстоянии AC=8 см.
Источник
ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Задача 1
Требуется определить положение главных центральных осей и величины главных центральных моментов инерции.
Сечение имеет сложную форму, состоит их 4 х простых фигур:
I – швеллера №30 а ,
II – прямоугольника 2×40см,
III – двутавра №20 а ,
IV – равнобокого уголка №12 (d=10мм).
Всё начинается с подготовки исходных данных. С этой целью необходимо сделать выписки из таблиц Сортамента прокатных сечений (см. рубрику «Таблицы»).

Этап 0. Подготовительный
Фигура I. Швеллер №30 а

Фигура II – прямоугольник 2×40см, В сортаменте прокатной стали этой фигуры нет, поскольку все геометрические характеристики ее свободно вычисляются
Фигура III. Двутавр №20 а .

Фигура IV. Равнобокий уголок №12 (d=10мм).

Пользуясь данными сортамента, на схеме сечения, вычерченной в достаточно крупном масштабе, показываем положение центров тяжести каждой из фигур и собственные центральные оси хi, уi.
Этап 1. Определение положения центра тяжести сечения. Сечение не имеет осей симметрии. Поэтому придётся определять две координаты центра тяжести, используя формулы:

Для реализации этих формул выбираем вспомогательные оси х‘ и у‘ (см.схему сечения).
Площади отдельных фигур: А1=43,89см 2 , А2=2×40=80см 2 ,
Координаты центров тяжести отдельных фигур:
Площадь всего сечения А=182,7см 2 .

Тогда координаты собственных центров тяжести отдельных фигур в системе случайных центральных осей хс, усбудут:
Этап 2. Определение моментов инерции относительно случайных центральных осей хс, ус.

Справочные сведения о знаке собственного центробежного момента инерции уголка (равнобокого и неравнобокого):

Справочные сведения для определения собственного центробежного момента инерции неравнобокого уголка:

Этап 3. Определение положения главных центральных осей

Положительный угол α соответствует повороту против часовой стрелки главных осей относительно случайных (см.схему).
Этап 4. Определение величин главных центральных моментов инерции

Правило: Ось с максимальным главным моментом инерции «тяготеет» к более тяжелой случайной оси. Поэтому в нашем случае:

Проверки.
- Выполнение закона суммы осевых моментов инерции.
Для этого сравним

Разница в последней цифре дает незначительную погрешность Запись опубликована 11.09.2014 автором admin в рубрике Задачи, Задачи на геометрические характеристики.
Источник
Теоретическая механика:
Центр тяжести
Смотрите также решения задач по нахождению центра тяжести в онлайн решебниках Яблонского (С.8) и Мещерского (§ 9).
Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил (Е. М. Никитин, § 42). Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
xc = (∑ Gixi) / ∑ Gi;
(1) yc = (∑ Giyi) / ∑ Gi;
zc = (∑ Gizi) / ∑ Gi.
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес Gi каждого отрезка li можно представить в виде произведения
Gi = lid,
где d – постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо Gi их значений lid постоянный множитель d в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий , примут вид:
xc = (∑ lixi) / ∑ li;
(2) yc = (∑ liyi) / ∑ li;
zc = (∑ lizi) / ∑ li.
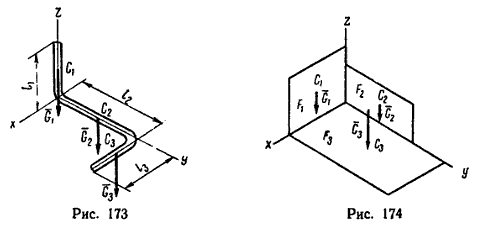
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174), то вес каждой плоскости (поверхности) можно представить так:
Gi = Fip,
где Fi – площади каждой поверхности, а p – вес единицы площади фигуры.
После подстановки этого значения Gi в формулы (1) получаем формулы координат центра тяжести фигуры, составленной из площадей :
xc = (∑ Fixi) / ∑ Fi;
(3) yc = (∑ Fiyi) / ∑ Fi;
zc = (∑ Fizi) / ∑ Fi.
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
Gi = Viγ,
где Vi – объем каждой части, а γ – вес единицы объема тела.
После подстановки значений Gi в формулы (1) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов :
xc = (∑ Vixi) / ∑ Vi;
(4) yc = (∑ Viyi) / ∑ Vi;
zc = (∑ Vizi) / ∑ Vi.
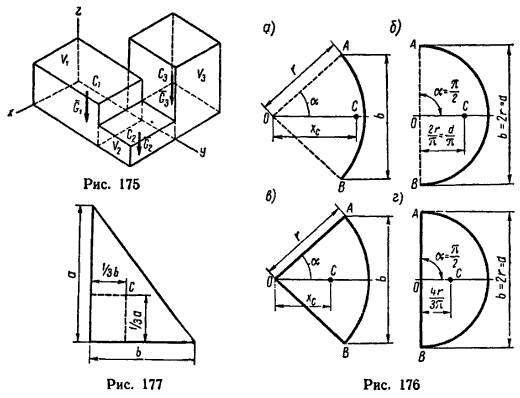
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
Если известен радиус дуги r и центральный угол 2α, стягиваемый дугой и выраженный в радианах, то положение центра тяжести C (рис. 176, а) относительно центра дуги O определится формулой:
(5) xc = (r sin α)/α.
Если же задана хорда AB=b дуги, то в формуле (5) можно произвести замену
sin α = b/(2r)
и тогда
(5а) xc = b/(2α).
В частном случае для полуокружности обе формулы примут вид (рис. 176, б):
(5б) xc = OC = 2r/π = d/π.
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы:
(6) xc = (2r sin α)/(3α).
Если же задана хорда сектора, то:
(6а) xc = b/(3α).
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
(6б) xc = OC = 4r/(3π) = 2d/(3π).
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
1) выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
2) разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
3) определить или длины, или площади, или объемы составных частей;
4) выбрать расположение осей координат;
5) определить координаты центров тяжести составных частей;
6) найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
7) по найденным координатам указать на рисунке положение центра тяжести тела.
§ 23. Определение положения центра тяжести тела, составленного из тонких однородных стержней
§ 24. Определение положения центра тяжести фигур, составленных из пластинок
В последней задаче, а также в задачах, приведенных в предыдущем параграфе, расчленение фигур на составные части не вызывает особых затруднений. Но иногда фигура имеет такой вид, который позволяет разделить ее на составные части несколькими способами, например тонкую пластинку прямоугольной формы с треугольным вырезом (рис. 183). При определении положения центра тяжести такой пластинки ее площадь можно разделить на четыре прямоугольника (1, 2, 3 и 4) и один прямоугольный треугольник 5 – несколькими способами. Два варианта показаны на рис. 183, а и б.
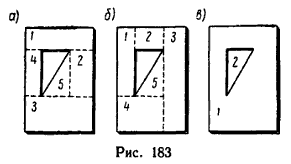
Наиболее рациональным является тот способ деления фигуры на составные части, при котором образуется наименьшее их число. Если в фигуре есть вырезы, то их можно также включать в число составных частей фигуры, но площадь вырезанной части считать отрицательной. Поэтому такое деление получило название способа отрицательных площадей.
Пластинка на рис. 183, в делится при помощи этого способа всего на две части: прямоугольник 1 с площадью всей пластинки, как будто она целая, и треугольник 2 с площадью, которую считаем отрицательной.
§ 25. Определение положения центра тяжести сечений, составленных из профилей стандартного проката
При решении задач, приведенных в этом параграфе, нужно пользоваться таблицами из ГОСТа на прокатную сталь: ГОСТ 8509–57, ГОСТ 8510–57, ГОСТ 8239–56, ГОСТ 8240–56.
Эти таблицы для каждого профиля содержат их размеры и площадь, а для уголков и швеллера, кроме того, – координаты центров тяжести.
§ 26. Определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму
Чтобы решать задачи на определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму, необходимо иметь навыки определения координат центра тяжести фигур, составленных из линий или площадей.
Источник
Определение положения центра тяжести сечений, составленных из профилей стандартного проката
Условие задачи
Определить положение центра тяжести сечения, составленного, как показано на рис. 188, из трех профилей стандартного проката: швеллера № 10 (ГОСТ 8240–56), двутавра № 12 (ГОСТ 8239–56) и неравнобокого уголка № 5/3,2 (размеры 50x32x4 мм ГОСТ 8510–57).
Решение задачи
1. Разбиваем сечение на три части: I – швеллер, II – двутавр и III – неравнобокий уголок.
2. Начало координат поместим в вершине прямого угла неравнобокого уголка; ось х совместим с нижней полкой двутавра, а ось у – с его вертикальной осью симметрии.

3. При помощи таблиц из ГОСТа находим:
площадь сечения швеллера № 10
F1 = 11,7 см 2 ;
площадь сечения двутавра № 12
F2 = 14,7 см 2 ;
площадь сечения уголка № 5/3,2
F3 = 3,17 см 2 .
4. В таблицах из ГОСТа положение центра тяжести С1 швеллера № 10 показано одной координатой z=1,55 см, так как швеллер имеет одну ось симметрии. Положение центра тяжести С2 двутавра в таблицах не показано, так как он имеет две оси симметрии и его центр тяжести расположен на их пересечении. Положение центра тяжести С3 неравнобокого уголка № 5/3,2 показано двумя координатами: х=0,76 и y=1,65 см.
Располагаем центры тяжести C1, C2 и C3 на рисунке (см. рис. 188), а затем при помощи таблиц находим их координаты в выбранных осях, учитывая другие необходимые размеры профилей, которые также берутся из таблиц:
координаты центра тяжести C1:
x1 = OD = PL — PA = 5 — 3,2 = 1,8 см;
y1 = OB = OA + AB = 12 + 1,55 = 13,55 см;
координаты центра тяжести C2:
x2 = 0;
y2 = OC2 = 6 см;
координаты центра тяжести C3:
x3 = -OE = -y = -1,65 см;
y3 = -OK = -x = -0,76 см.
6. Подставляем эти значения в расчетные формулы:
xc = (11,7*1,8+14,7*0-3,17*1,65)/(11,7+14,7+3,17) = 15,9/29,6 = 0,54 см;
yc = (11,7*13,55+14,7*6-3,17*0,76)/(11,7+14,7+3,17) = 244,2/29,6 = 8,23 см.
7. Центр тяжести данного составного сечения имеет координаты (в мм) С(5,4; 82,3).
Источник
Обратите внимание, на этом сайте есть онлайн-сервис для вычисления центра тяжести и моментов инерции составных сечений, которые состоят из прокатных профилей (двутавр, уголок и т.д.) и из простых фигур.
Часто при расчете элементов строительных конструкций приходится определять геометрические характеристики профилей, составленных из элементарных геометрических фигур (прямоугольник, круг и т.п.) и прокатных профилей. Рассмотрим подробно пример расчета.
Необходимо определить геометрические характеристики составного сечения (рис.), который состоит из уголка 20/12,5/1,2, уголка 14/1 и прямоугольника 20х2см.
Определение собственных характеристик отдельных профилей – составляющих сечения
Собственные характеристики прокатных профилей определяются из сортамента.
Для неравнополочного уголка 20/12,5/1,2:
– высота и ширина уголка h = 20 см, b = 12,5 см;
– площадь $A$= 37,9 см2;
– собственные осевые моменты инерции ${I_x}$=1570 см4, ${I_y}$= 482 см4;
– собственный центробежный момент инерции ${I_{xy}}$=505 см4;
– координаты центра тяжести ${x_c}$= 2,83 см, ${y_c}$= 6,51 см.
Для равнополочного уголка 14/1:
– высота и ширина уголка h = b = 14 см;
– площадь $A$= 27,3 см2;
– собственные осевые моменты инерции ${I_x}$= ${I_y}$= 512 см4;
– собственный центробежный момент инерции ${I_{xy}}$=301 см4;
– координаты центра тяжести ${x_c}$= ${y_c}$= 3,82 см.

Для прямоугольника 20х2см:
– высота и ширина прямоугольника h = 20 см, b = 2 см;
– площадь $A$= 20∙2 = 40 см2;
– собственные осевые моменты инерции ${I_x} = frac{{2 cdot {{20}^3}}}{{12}} = 1330$ см4, ${I_y} = frac{{20 cdot {2^3}}}{{12}} = 13,3$см4;
– собственный центробежный момент инерции ${I_{xy}}$= 0, так как профиль имеет ось симметрии.
Определение центра тяжести сечения
Общая площадь всего сечения A = 37,9+27,3+40 = 105см2.
Проводим вспомогательные оси $X$ и $Y$ и определяем относительно них центр тяжести сечения:
${X_c} = frac{{sum {{X_i} cdot {A_i}} }}{A} = frac{{{text{37}}{text{,9}} cdot {text{( – 13}}{text{,5) + 27}}{text{,3}} cdot {text{( – 3}}{text{,82) + 40}} cdot {text{1}}}}{{{text{105}}}}{text{ = – 5}}{text{,49}}$см;
${Y_c} = frac{{sum {{Y_i} cdot {A_i}} }}{A} = frac{{{text{37}}{text{,9}} cdot {text{( – 2}}{text{,83) + 27}}{text{,3}} cdot {text{10}}{text{,2 + 40}} cdot {text{10}}}}{{105}} = 5,44$.
При этом в координатах центров тяжести составных обязанности’обязательно учитываем знак. Откладываем оси, которые проходят через центр тяжести –центральные оси $Xc$ и ${Y_c}$.
Определение центральных моментов инерции
Осевые и центробежный моменты инерции сечения определяем по формулам перехода между параллельными осями. Для этого находим и показываем на чертеже расстояния между центральными осями всего сечения и собственными осями каждой из фигур.
$Ix = sum {left( {I{x_i} + A cdot {b^2}} right) = {text{482 + 8}}{text{,2}}{{text{7}}^{text{2}}} cdot {text{37}}{text{,9 + 512 + 4}}{text{,7}}{{text{6}}^{text{2}}} cdot {text{27}}{text{,3 + 1330 + 4}}{text{,5}}{{text{6}}^{text{2}}} cdot {text{40 = 6360}}} $см4;
$Iy = sum {left( {I{y_i} + A cdot {a^2}} right)} = {text{1570 + 8}}{text{,0}}{{text{1}}^{text{2}}} cdot {text{37}}{text{,9 + 512 + 1}}{text{,6}}{{text{7}}^{text{2}}} cdot {text{27}}{text{,3 + 13}}{text{,3 + 6}}{text{,4}}{{text{9}}^{text{2}}} cdot {text{40 = 6280}}$см4;
${I_{xy}} = sum {left( {{I_{xy}}_i + A cdot a cdot b} right)} = $
$ = 505 + ( – 8,01) cdot ( – 8,27) cdot 37,9 – 301 + 1,67 cdot 4,76 cdot 27,3 + 0 + 6,49 cdot 4,56 cdot 40 = 4120$см4.
При этом обязанности’обязательно учитываем размещения фигур относительно рассматриваемых осей. Так, при определении момента инерции ${I_x}$ в формулу подставляем собственный момент инерции неравнополочного уголка относительно оси, которая параллельна оси ${X_c}$, в сортаменте это ось $Y$, и наоборот.
Определение положения главных осей и главных моментов инерции
Угол поворота главных осей относительно осей, для которых известны моменты инерции, определяется по формуле
[tg,2alpha = frac{{2 cdot {I_{xy}}}}{{{I_y} – {I_x}}} = frac{{2 cdot 4120}}{{6280 – 6360}} = – 97] $alpha = frac{{arctg( – 97)}}{2} = – 44,7^circ $.
Если $alpha > 0$, главные оси откладываются против часовой стрелки, и наоборот.
Главные моменты инерции определяются так
${I_{x0}} = {I_x} cdot {cos ^2}alpha + {I_y} cdot {sin ^2}alpha – {I_{xy}} cdot sin 2alpha = $
$ = 6360 cdot {cos ^2}( – 44,7^circ ) + 6280 cdot {sin ^2}( – 44,7^circ ) – 4120 cdot sin ( – 2 cdot 44,7^circ ) = 10430$см4.
${I_{y0}} = {I_y} cdot {cos ^2}alpha + {I_x} cdot {sin ^2}alpha + {I_{xy}} cdot sin 2alpha = $
$ = 6280 cdot {cos ^2}( – 44,7^circ ) + 6360 cdot {sin ^2}( – 44,7^circ ) + 4120 cdot sin ( – 2 cdot 44,7^circ ) = 2210$см4.
Центробежный момент инерции относительно главных осей равен нулю.
Радиусы инерции. Моменты сопротивления
Радиусы инерции сечения
${i_x} = sqrt[{}]{{frac{{{I_x}}}{A}}} = sqrt[{}]{{frac{{10430}}{{105}}}} = 9,96$см, ${i_y} = sqrt[{}]{{frac{{{I_y}}}{A}}} = sqrt[{}]{{frac{{2210}}{{105}}}} = 4,58$см.
Моменты сопротивления сечения определяем относительно центральных осей. Для этого необходимо определить расстояния ${x_{max }}$ и ${y_{max }}$ до максимально удаленных точек от главных осей. Сначала необходимо по чертежам определить, какие точки являются наиболее удаленными. В нашем случае это точки $A$ и $B$ (рис.). Искомые расстояния можно определить, имея координаты этих точек в центральных (не возвращенных осям).
${x_{max }} = {x_A} cdot cos left( alpha right) + {y_A} cdot sin left( alpha right)$
${y_{max }} = {y_B} cdot cos left( alpha right) – {x_B} cdot sin left( alpha right)$
XА= –8,53см YA=8,57см
XB= –14,5см YB= –18см
xmax = –12,1см ymax = –23см
Моменты сопротивления
${W_x} = frac{{{I_x}}}{{{y_{max }}}} = frac{{10430}}{{23}} = 454$см3; ${W_y} = frac{{{I_y}}}{{{x_{max }}}} = frac{{2210}}{{12.1}} = 183$см3.

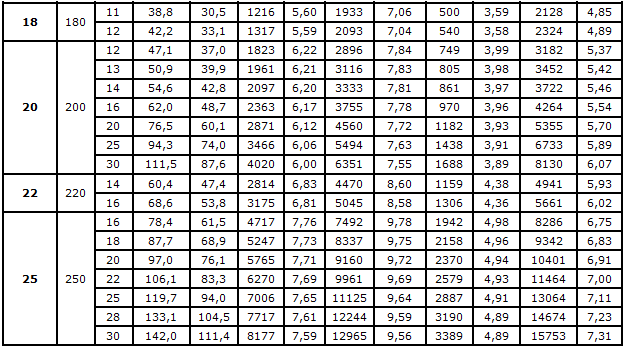
ГОСТ 8509-93 устанавливает сортамент на уголки стальные горячекатаные равнополочные (равнобокие).
Сокращенная и полная версии сортамента.
Сокращенная версия сортамента
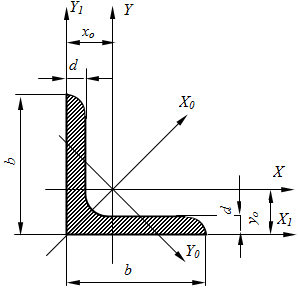
Размеры и геометрические характеристики сечения:
b — размер полки;
d — толщина стенки;
A — площадь поперечного сечения;
m — масса погонного метра;
Ix — момент инерции уголка относительно оси x (Ix=Iy);
x0, y0 — расстояния до главных осей;
i — радиусы инерции.
Примеры решения задач >
Краткая теория >
Полный вариант ГОСТа

Страница 1. Предисловие к стандарту на стальные равнополочные уголки.

Страница 2. Форма профиля и обозначения размеров поперечного сечения уголков равнополочных.
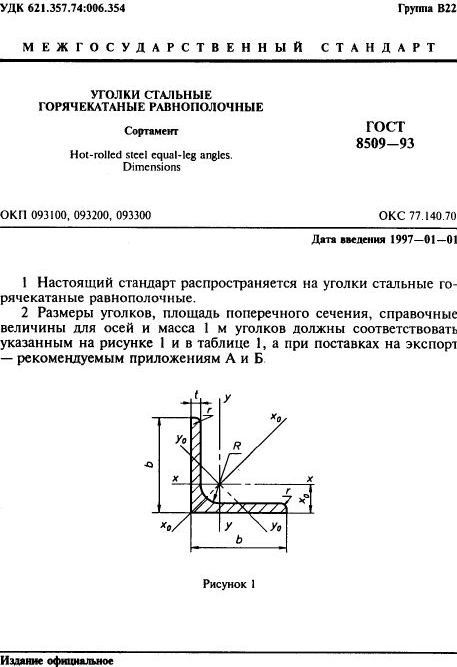
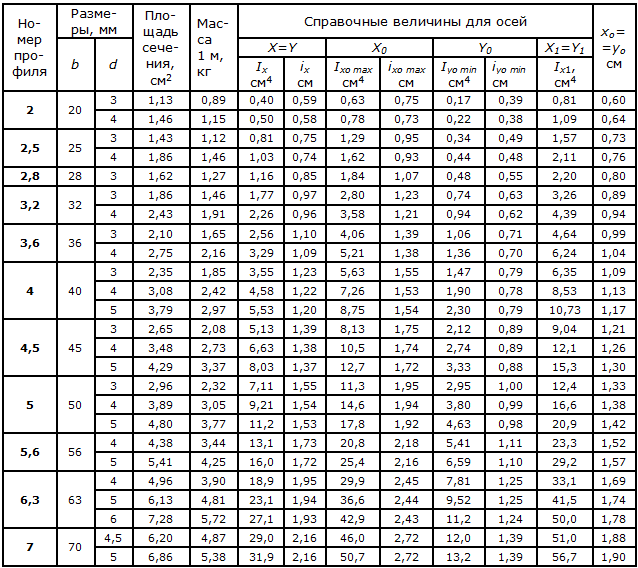
Страница 3. Размеры, площадь поперечного сечения, масса 1 метра и справочные значения величин для уголков равнополочных №№2-5.
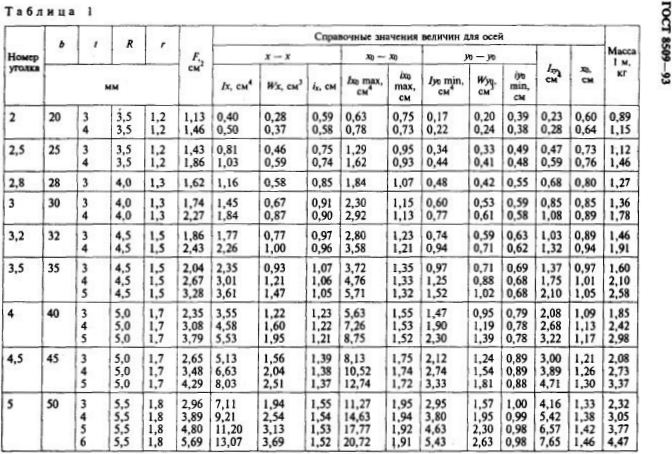
Страница 4. Размеры, площадь поперечного сечения, масса 1 метра и справочные значения величин для уголков равнополочных №№5,6-9.
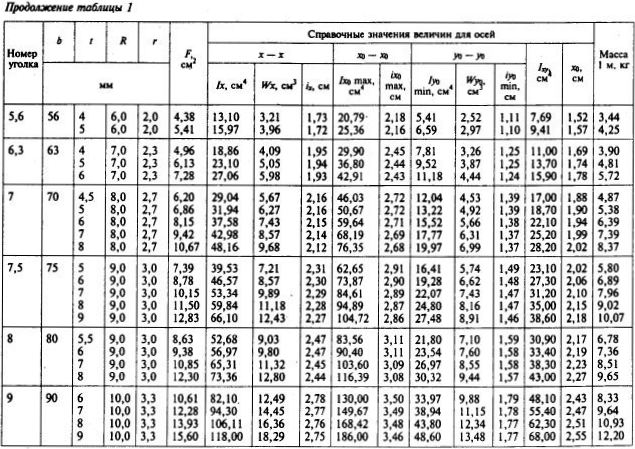
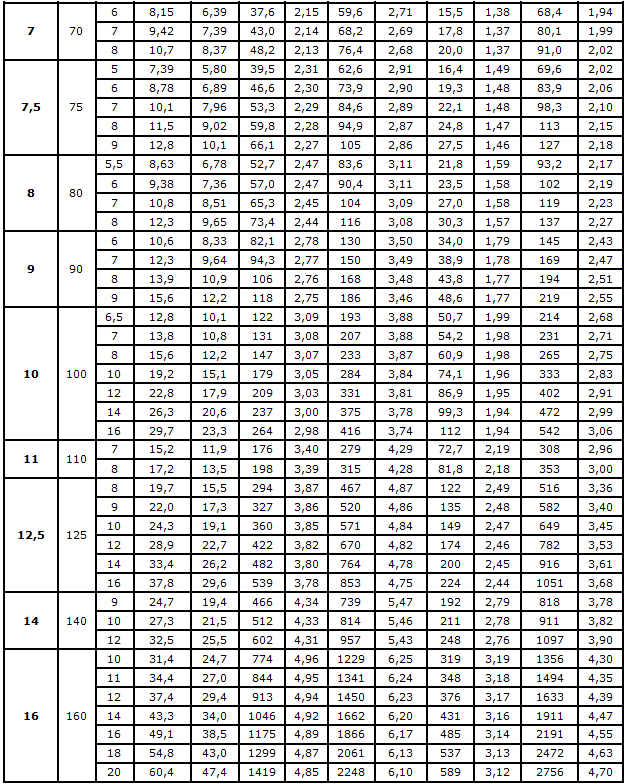
ГОСТ 8509-93 Страница 5. Размеры, площадь поперечного сечения, масса 1 метра и справочные значения величин для уголков равнополочных №№10-16.
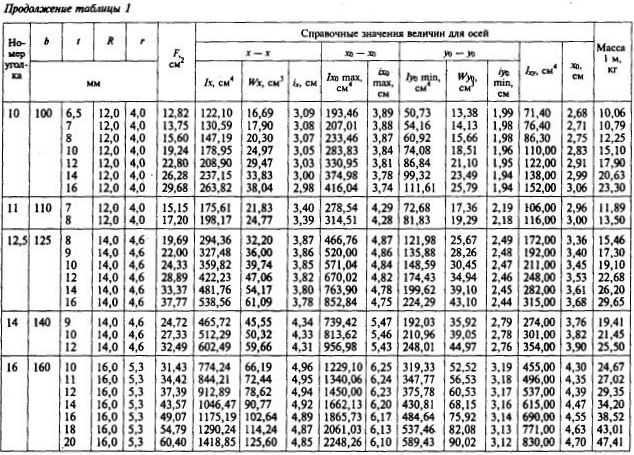
Страница 6. Размеры, площадь поперечного сечения, масса 1 метра и справочные значения величин для уголков равнополочных №№18-25.
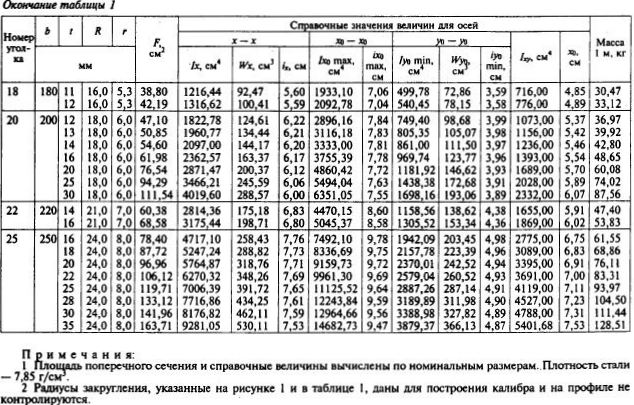
Страница 7. Условные обозначения и таблица предельных отклонений размеров равнополочных уголков.

ГОСТ 8509-93 Страница 8. Предельные отклонения по массе равнополочных уголков I и II класса.

Страница 9. Приложение А. Область распространения, размеры и свойства профиля равнополочных уголков.

Страница 10. Таблица А.1. Расстояния от центра тяжести до осей сечения для равнополочных уголков №№20-40.
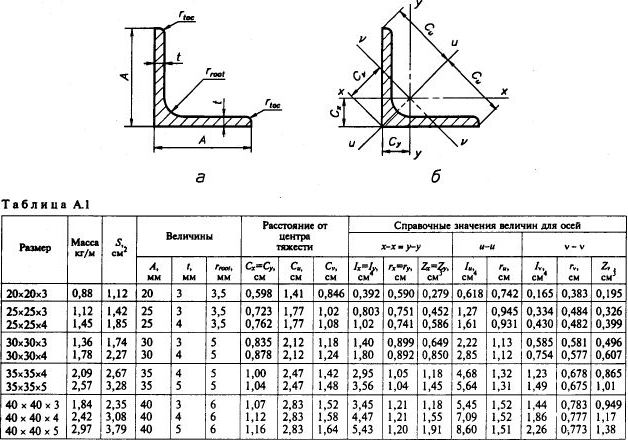
ГОСТ 8509-93 Страница 11. Таблица А.1 (продолжение). Расстояния от центра тяжести до осей сечения для равнополочных уголков №№45-100.
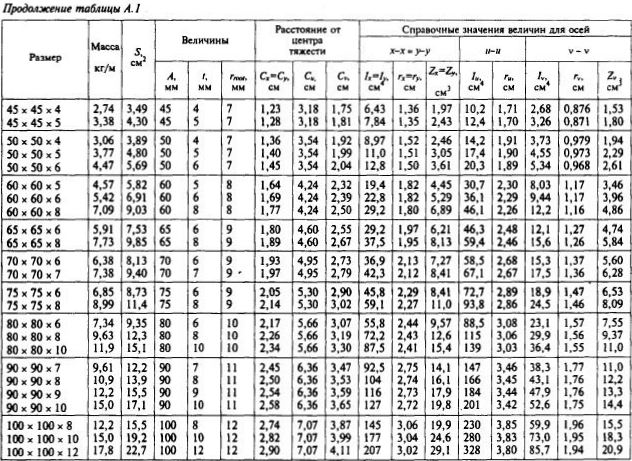
Страница 12. Таблица А.1 (окончание). Расстояния от центра тяжести до осей сечения для равнополочных уголков №№120-250.
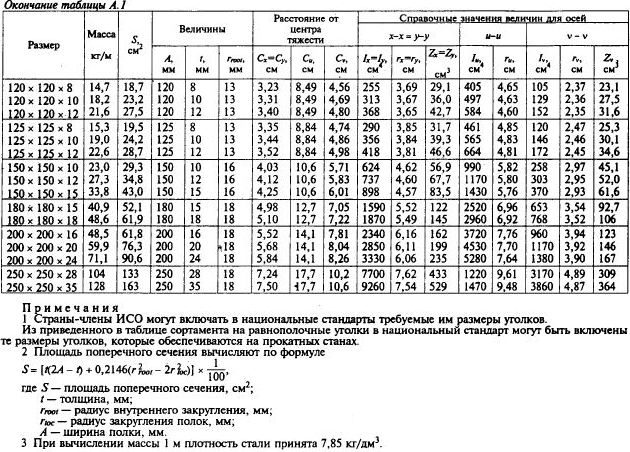
Страница 13. Приложение Б. Предмет стандарта и область применения. Предельные отклонения по ширине и толщине полки равнополочных уголков.
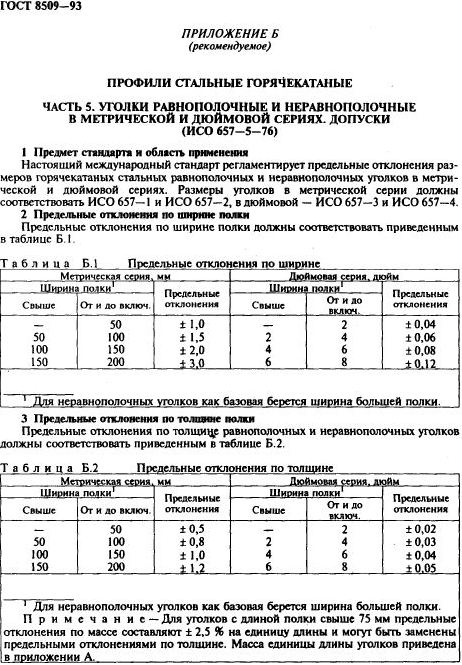
Страница 14. Предельные отклонения по порезке на длины, кривизна и неперпендикулярность равнополочных уголков.
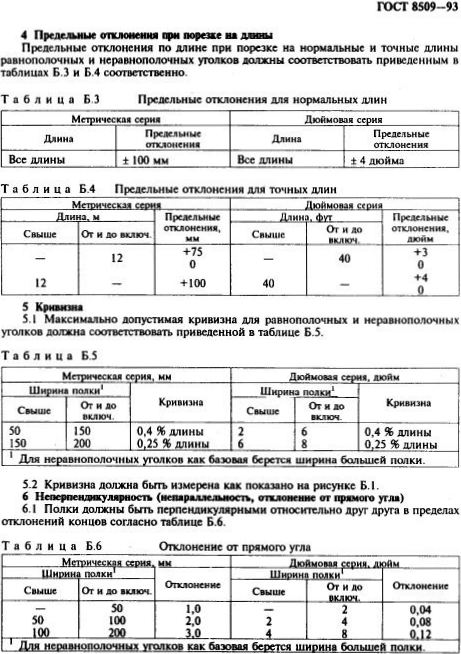
ГОСТ 8509-93 Страница 15. Предельные отклонения по массе равнополочных уголков. Выходные данные стандарта.

Другие сортаменты >>
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
И. В. Богомаз. Механика
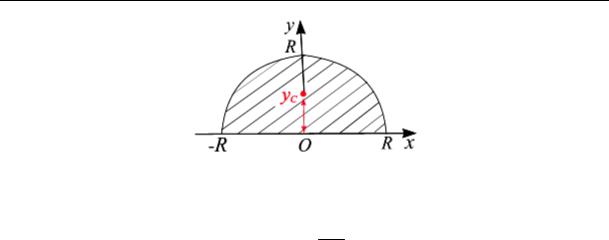
Рис. 5.7
Центр тяжести полукруга yC = 43Rπ .
Метод разбиения на части. Некоторые тела сложной формы можно разбить на части, положение центра тяжести которых известно. В таких случаях центр тяжести составного тела вычисляют по формуле
|
n |
n |
|||
|
∑Ai xi |
∑Ai yi |
|||
|
x = |
i=1 |
, y = |
i=1 |
. |
|
C |
A |
C |
A |
|
Здесь A = ∑Ai – площадь сечения; xi, yi – центр тяжести i-го сечения; Ai – площадь i-го сечения.
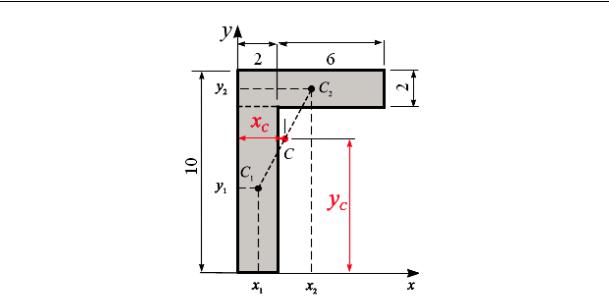
Пример 5.1. Вычислить координаты центра тяжести однородного сечения, составленного из двух прямоугольников (рис. 5.8). Размеры прямоугольников показаны на рис. 5.8 в см.
Решение. Разбиваем сечение на два прямоугольника (линии разреза показаны пунктиром) и проводим оси координат (рис. 5.8).
Вычислим координаты центров тяжести и площадь каждого из прямоугольников:
|
x =1cм, |
x = 4 см, |
|||
|
1 |
2 |
|||
|
y1 = 4 см, |
y2 = 9 см, |
|||
|
А = 2 8 =16cм2 |
; |
А =8 2 =16см2. |
||
|
1 |
2 |
112
5. Центр тяжести
Рис. 5.8
Площадь всего сечения
|
3 |
|||||||
|
А= ∑Аk = А1 + А2 =16 +16 = 32 см2. |
|||||||
|
Тогда |
k=1 |
||||||
|
x1 A1 + x2 A2 |
= 1 16 + 4 16 = 80 = 2,5см; |
||||||
|
x |
= |
||||||
|
С |
A |
32 |
32 |
||||
|
y |
= |
y1 A1 + y2 A2 |
= 4 16 +9 16 = 64 +144 = 6,5см. |
||||
|
С |
A |
32 |
32 |
||||
Положение центра тяжести совпадает с точкой С {2,5; 6,5}
(рис. 5.7).
Метод отрицательных площадей. В данном методе вырезан-
ные сечения заменяют отрицательными площадями. Проиллюстрируем этот метод на примере сечения.
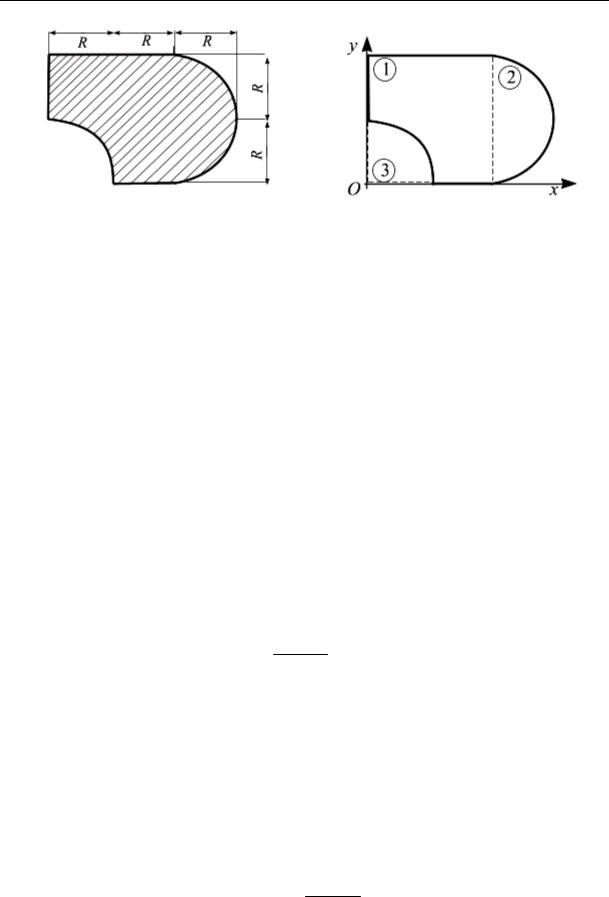
Пример 5.2. Задано сечение (рис. 5.9, а). Дано: R = 6 см. Вычислить центр тяжести сечения.
Решение. Разобьем сечение на простые фигуры: дополним квадрат – сечение 1, полукруг – сечение 2 и четверть круга – сечение 3 (рис. 5.9, б). За вспомогательную систему координат выберем стороны квадрата: Oxy. Вычислим площадь и координаты центров тяжести каждого сечения.
113
И. В. Богомаз. Механика
Рис. 5.9
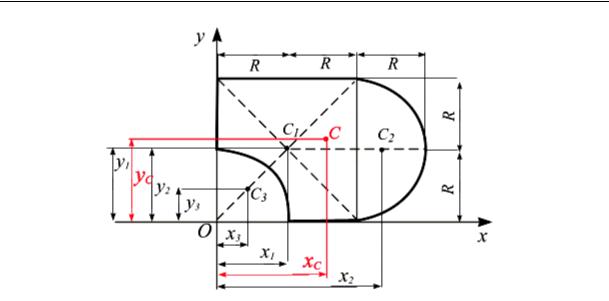
Имеем (рис. 5.10) 1. Квадрат:
A1 = 2R 2R = 4R2 = 4 62 = 4 36 =144 см2;
x1 = R = 6 см; y1 = R = 6 см.
2. Полукруг:
A2 = πR2 2 = 3,142 62 = 56,52 см2;
x2 = 2R + 43Rπ = 2 6 + 343,146 =12 + 2,55 =14,55см;
y2 = R = 6 см.
3. Четверть круга:
A3 = − πR4 2 = −3,144 62 = −28,26 см2; xC = yC = 43Rπ = 3 43.146 = 2,6 см.
114
5. Центр тяжести
Рис. 5.10
|
Итак, |
|||||
|
x |
= x1 A1 + x2 A2 + x3 A3 |
= 6 144 +14,55 56,52 −2,6 28,26 = |
|||
|
С |
A1 + A2 + A3 |
144 |
+56,52 −28,26 |
||
|
= 864 +822,37 −73,5 |
= 9, 4см; |
||||
|
172, 26 |
|||||
|
y |
= y1 A1 + y2 A2 + y3 A3 = 6 144 +6 56,52 −2,6 28,26 = |
||||
|
С |
A1 + A2 + A3 |
144 |
+56,52 −28,26 |
||
|
= 864 +339,12 −73,5 |
= 6,6см. |
||||
|
172, 26 |
Положение центра тяжести совпадает с точкой С {9,4; 6,6}
(рис. 5.11).
Статические моменты. Статические моменты сечения Sx и Sy определим, как сумму произведений элементарных площадей dAi на кратчайшее расстояния до осей Ox, Oy соответственно (рис. 5.11), т. е.
S x = ∑Ai yi → Sx = ∫y dA, Sy = ∑Ai xi → Sy = ∫x dA.
A A
115

И. В. Богомаз. Механика
Рис. 5.11
Статические моменты имеют размерность см3 или м3.
При параллельном переносе осей (Oxy → O1x1 y1 ) значения ста-
тических моментов изменяются и могут иметь как положительное, так и отрицательное значение. Следовательно, существует ось, относительно которой статический момент равен нулю.
Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей совпадает с точкой центра тяжести сечения.
Координаты центра тяжести тела через статические моменты будут вычисляться следующим образом:
|
x |
= |
Sy |
= ∑Ai xi →, |
y |
= |
Sx |
= ∑Ai yi . |
|
C |
A A |
C |
A |
A |
|||
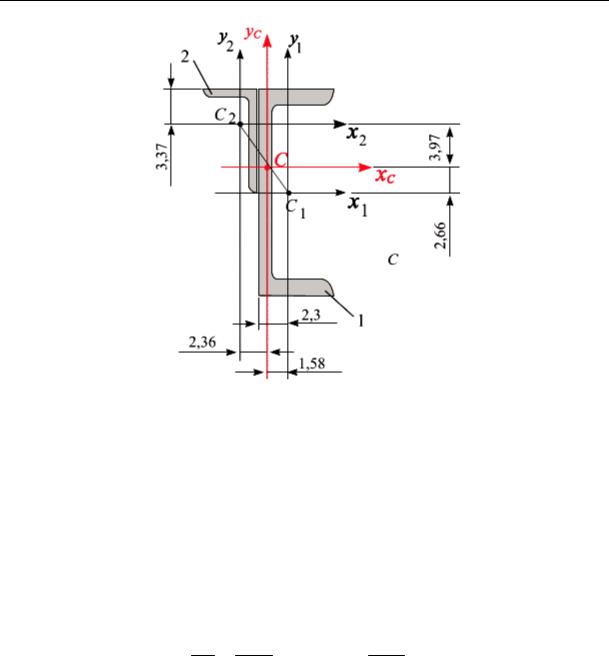
Пример 5.3. Для заданного несимметричного поперечного сечения, составленного из швеллера № 20 и неравнополочного уголка № 10/6,5 (рис. 5.12), найти положение центральных осей.
Рис. 5.12
116

I – момент инерции;
5. Центр тяжести
Решение. Из сортамента выберем геометрические характеристики швеллера № 20 и неравнополочного уголка № 10/6,5 (табл. 5.1) и построим чертеж в масштабе (рис. 5.13).
Таблица 5.1
Сталь горячекатаная. Швеллеры. Сортамент (ГОСТ 8240–89)
|
I – момент инерции; |
||||||||
|
h – высота швеллера; |
z0 – расстояние от оси y до на- |
|||||||
|
b – ширина полки |
ружной грани стенки; |
|||||||
|
А – площадь поперечного сече- |
||||||||
|
ния |
||||||||
|
Номер |
Размеры, |
|||||||
|
швел- |
мм |
А, см2 |
Ix, см4 |
Iy, см4 |
x0, см |
|||
|
лера |
h |
b |
||||||
|
20 |
200 |
76 |
23,4 |
1530 |
134 |
2,3 |
Уголки стальные горячекатаные неравнополочные. Сортамент (ГОСТ 8510–86)
В – ширина
большей полки; z0 – расстояние от оси y до наружной b – ширина грани стенки;
меньшей полки А – площадь поперечного сечения
|
Но- |
Разме- |
|||||||
|
мер |
ры, мм |
А, см2 |
Ix, см4 |
Iy, см4 |
Ixy, см4 |
x0, см |
||
|
угол- |
В |
b |
||||||
|
ка |
||||||||
|
10/6,5 |
200 |
65 |
15,67 |
155,52 |
51,68 |
51,18 |
2,3 |
Для вычисления положения центра тяжести заданного сечения за вспомогательные оси примем центральные оси швеллера C1x1y1
(рис. 5.13).
Вычислим координаты центра тяжести сечения осей C1x1y1:
|
y |
= ∑Sxi |
= |
S1x1 |
+ S2x1 |
= |
А1 уС1 + А2 уС2 |
= |
0 +15,67 6,63 |
= 2,66; |
||||||||
|
A1 |
+ A2 |
А1 + А2 |
23,4 +15,67 |
||||||||||||||
|
C |
∑Ai |
||||||||||||||||
|
х |
= |
∑Sуi = |
S1у1 + S2 у1 |
= |
А1 хС1 + А2 хС2 |
= |
0 +15,67 (−3,94) |
= −1,58. |
|||||||||
|
23,4 +15,67 |
|||||||||||||||||
|
C |
∑Ai |
A1 + A2 |
А1 + А2 |
117
И. В. Богомаз. Механика
Рис. 5.13
Откладываем на схеме координаты точки центра тяжести сечения С{xC , yC }. Координаты центра тяжести сечения «легли» на отре-
зок С1С2, соединяющий центры тяжести частей (профилей), составляющих заданное сечение. Проверим правильность расчета. Соотношение отрезков должно быть равно соотношению площадей. Измеряем отрезки С1С и С2С, уточняем правильность соотношения
A2 = C1C →15,67 = C1C = 0,67.
A1 C2C 23,4 C2C
Проводим центра центральные оси CxCyC (рис. 5.13).
118
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
