
Центр удара – это точка вращающегося тела, при действии на которую ударного импульса не возникают ударные реакции.
Если такая точка K (рисунок 3) существует, то
SAx = SAy = SAz = SBx = SBy = 0.
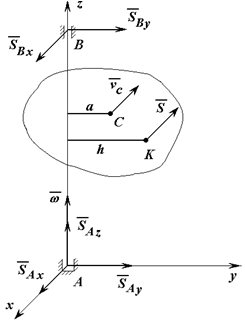
Рисунок 3
Из формул (28) следует, что приложенный к телу импульс направлен по оси Ox и равен
S = ma(ω1 — ω0).
Если расстояние от точки приложения ударного импульса K& до оси вращения обозначить через h, то получим
Jz(ω1 — ω0) = S∙h,
h = Jz/(m∙a), (29)
где a – расстояние от оси вращения до центра масс тела.
Для того, чтобы при действии ударного импульса на вращающееся тело в подшипниках не возникали ударные реакции, необходимо выполнение условий:
- центр удара лежит в плоскости, проходящей через центр масс и ось вращения на расстоянии h;
- ударный импульс направлен перпендикулярно этой плоскости;
- ось вращения является главной для точки ее пересечения с плоскостью действия ударного импульса.
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Сначала
найдем условия, которые необходимы для
того, чтобы при ударе не возникали
ударные импульсы реакции. Примем, что
ударные импульсы в точках А
и В
равны нулю, и найдем те ограничения,
которые эти условия накладывают на
остальные величины, входящие в уравнения
(6.17) и (6.18) . Из этих уравнений получим:
![]()
![]()
![]()
(6.19)
![]()
![]()
Из
второго и третьего уравнений следует,
что внешний ударный импульс должен
иметь направление, параллельное оси
ох,
т. е. он должен быть перпендикулярен к
плоскости, проведенной через ось
вращения и центр масс тела. Для удобства
дальнейших рассуждений введем новую
систему координат
![]()
с осями, параллельными исходным осям,
и с началом в точке О
(рис 73), находящейся на оси вращения тела
Оz,
причем
![]()
.
В новой системе координат
![]()
.
В новой системе координат уравнения
(6.19) сохраняют свой вид. Имея в виду
условие
![]()
и
,
получим
![]()
,
т. е. ось вращения должна быть главной
осью инерции для точки О.
Из первого и последнего уравнения
находим
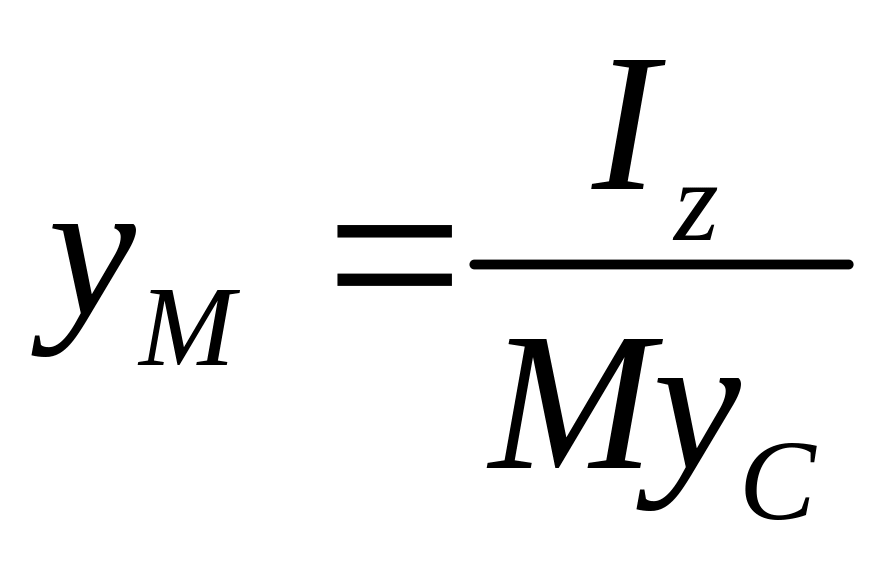
(6.20)
Здесь
мы воспользовались тем, что
![]()
.
Значит, линия действия импульса S
должна отстоять
от оси вращения на расстоянии, равном
приведенной длине физического маятника
(см. §……..).
Таким
образом, если удар не передается на
опоры, то должны выполняться следующие
условия:
1)
линия действия ударного импульса должна
быть перпендикулярна к плоскости,
содержащей центр масс тела и ось вращения;
2)
плоскость, содержащая ударный импульс
и перпендикулярная к оси вращения,
должна пересекаться с этой осью в точке,
для которой ось вращения, является
главной осью инерции;
3)
линия действия ударного импульса должна
отстоять от оси вращения на расстоянии,
определяемом равенством (6.20).
Точка
М
в плоскости yAz
(см. рис. 73), в которой приложен ударный
импульс
,
удовлетворяющий всем указанным условиям,
называется центром
удара.
Следует
отметить, что центр удара может и не
существовать. Такая ситуация возникает,
например, тогда, когда ни для одной из
точек на оси вращения сама ось вращения
не является главной осью инерции.
Р
ассмотрим
пример. Найти центр удара круглой мишени
радиуса R,
представленной
на рисунке. Ось вращения будет главной
в верхней точке мишени – точке А,
Действительно,
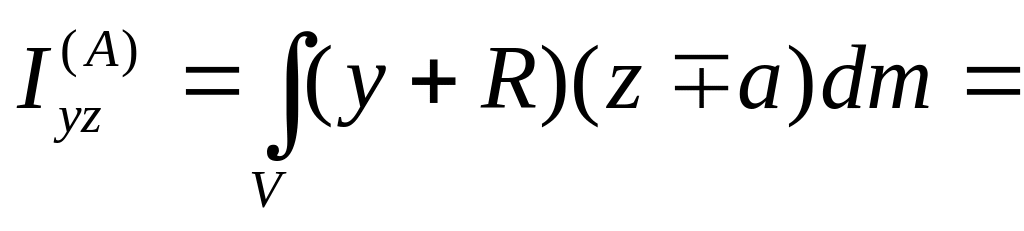

.
П
цу

ервое
слагаемое равно нулю, так как в точке С
(центре мишени) центробежный момент
![]()
,
второе слагаемое также равно нулю
![]()
.
Ось ОY
направлена вниз и проходит через точки
С и А.
третье слагаемое равно нулю, если a=0,
где a –
расстояние от точки подвеса до оси ОY
. Расстояние до центра удара определим
по формуле (3.89)
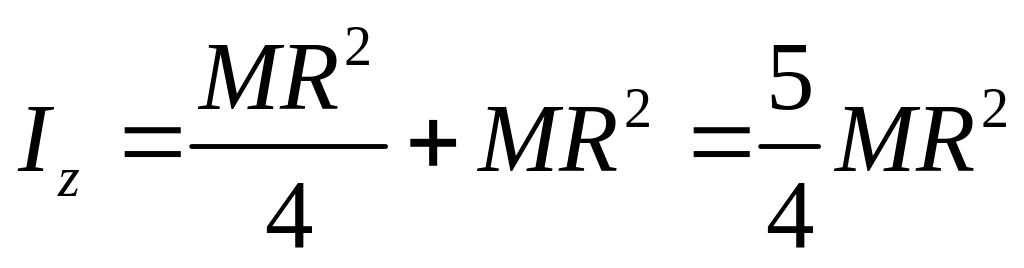
,
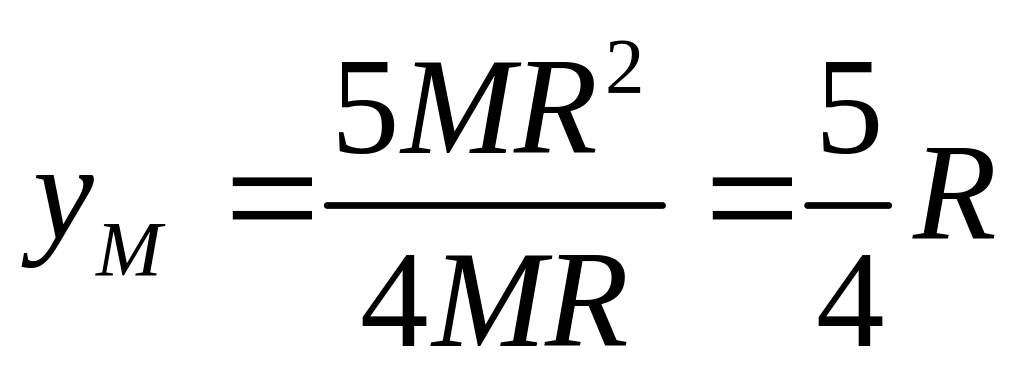
.
Программа
предлагаемого курса « Теоретической
механики»
1.Статика.
1.1.
Сила как вектор, момент силы, главный
вектор и главный момент системы сил.
Роль
и значение аксиом и абстракций в механике.
Материальная точка. Абсолютно твердое
и деформируемое твердое тело, принцип
затвердевания. Аксиомы статики. Векторное
представление силы. Моменты силы
относительно точки и оси, связь между
ними. Пара сил. Момент пары как свободный
вектор. Теорема Пуансо. Приведение
произвольной пространственной системы
сил к одному центру. Главный вектор и
главный момент. Условия эквивалентности
систем сил, приложенных к твердому телу.
Зависимость главного момента от выбора
центра приведения, статические
инварианты.
1.2. Равновесие тела и
системы тел.
Уравнения
равновесия твердого тела. Статически
определимые и статически неопределимые
задачи равновесия системы твердых тел.
Плоская система сил.
1.3.
Трение. скольжения, трения качения.
Трение,
основные
модели, равновесие при наличии сил
трения,
трение скольжения и трение качения.
Угол трения.
1.4.
Центр тяжести .
Центр
параллельных сил и его свойство. Центр
тяжести тела, координаты центра тяжести
объёма, поверхности, линии.
Дополнительные
вопросы,
включаемые по согласованию с выпускающими
кафедрами:
Частные
случаи приведения системы сил. Условия
равновесия при наличии сухого трения.
Задача опрокидывания тела, трение
качения. Трение
верчения,
Равновесие
гибких нерастяжимых нитей. Геометрическая
производная вектора по скалярному
аргументу. Натуральный триэдр осей,
Формула Френе, кривизна, радиус кривизны.
Векторное уравнение равновесия нити,
его проекция в декартовых и естественных
осях. Формула Эйлера для ленточного
тормоза. Дифференциальные уравнения
равновесия прямого тонкого стержня.
Закон Гука, задача растяжения и сжатия
стержня.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Центр удара – это точка на протяженном массивном объекте, прикрепленном к оси вращения, где перпендикулярный удар не вызовет реактивного удара в шарнире. Поступательные и вращательные движения отменяются в точке поворота, когда импульсный удар наносится по центру удара. Центр удара часто обсуждается в контексте биты, ракетки, двери, меча или другого протяженного объекта, удерживаемого за один конец.
Эта же точка называется центром колебаний для объекта, подвешенного на оси в виде маятника, что означает, что простой маятник со всей своей массой сосредоточен в этой точке. точка будет иметь тот же период колебаний, что и составной маятник.
В спорте центр удара битой или ракеткой связан с так называемым «сладким пятном », но последнее также связано с колебательным изгибом объекта.
Содержание
- 1 Пояснение
- 2 Расчет центра удара
- 3 Центр удара однородного луча
- 4 Некоторые приложения
- 5 Ссылки
Пояснение
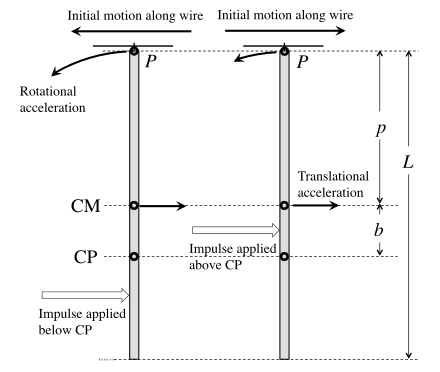 Влияние удар по подвесной балке. CP – это центр удара, а CM – это центр масс балки.
Влияние удар по подвесной балке. CP – это центр удара, а CM – это центр масс балки.
Представьте жесткую балку, подвешенную на проволоке с помощью приспособления, которое может свободно скользить по проволоке в точке P, как показано на рисунке. Импульсный удар наносится слева. Если он находится ниже центра масс (CM), это приведет к тому, что луч будет вращаться вокруг CM против часовой стрелки, а также приведет к перемещению CM вправо. Центр перкуссии (ЦП) находится ниже ЦМ. Если удар падает выше CP, поступательное движение вправо будет больше, чем вращательное движение влево в точке P, в результате чего чистое начальное движение приспособления будет направлено вправо. Если удар падает ниже CP, произойдет обратное: вращательное движение в точке P будет больше, чем поступательное движение, и приспособление сначала переместится влево. Только если удар падает точно на CP, два компонента движения компенсируются, чтобы произвести нулевое чистое начальное движение в точке P.
Когда скользящее приспособление заменяется осью, которая не может перемещаться влево или вправо, Импульсный удар в любом месте, кроме точки CP, приводит к возникновению начальной реактивной силы на оси.
Расчет центра удара
Для свободного жесткого луча импульс F dt { displaystyle Fdt}


- F = M dvcmdt, { displaystyle F = M { frac {dv_ {cm}} {dt}},}
где M { displaystyle M}

- F b = I d ω dt, { displaystyle Fb = I { frac {d omega} {dt}},}
где I { displaystyle I}
Для любой точки P, находящейся на расстоянии p { displaystyle p}
- dvnet = dvcm – pd ω { displaystyle dv_ {net} = dv_ {cm} -pd omega ,}
где p { displaystyle p}
- d v n e t d t = (1 M – p b I) F. { displaystyle { frac {dv_ {net}} {dt}} = left ({ frac {1} {M}} – { frac {pb} {I}} right) F.}
Когда это ускорение равно нулю, b { displaystyle b}

- b = I p M. { displaystyle b = { frac {I} {pM}}.}
Обратите внимание, что P, ось вращения, не обязательно должна находиться на конце балки, но ее можно выбрать на любом расстоянии p { displaystyle p}
Длина b + p { displaystyle b + p}
Центр удара однородного луча
Для частного случая луча однородного плотность длины L { displaystyle L}
- I = 1 12 ML 2 { displaystyle I = { frac {1} {12 }} ML ^ {2}}
(см. момент инерции для доказательства),
и для вращения вокруг оси в конце,
- p = L / 2 { displaystyle p = L / 2}
.
Это приводит к:
- b = L 2 12 p = 1 6 L { displaystyle b = { frac {L ^ {2}} {12p}} = { frac {1} {6}} L}
.
Отсюда следует, что CP составляет 2/3 длины равномерного луча L { displaystyle L}
Некоторые приложения
Например, распашная дверь, которую останавливает дверной упор, расположенный на 2/3 ширины двери, выполнит свою работу с минимальным встряхиванием двери, потому что откидной конец не подвергается действию чистой реактивной силы. (Эта точка также является узлом второй колебательной гармоники, что также минимизирует вибрацию.)
зона наилучшего восприятия на бейсбольной бите обычно определяется как точка при котором удар ощущается лучше всего. Центр удара определяет место, где, если летучая мышь ударяет по мячу и руки бьющего находятся в точке поворота, бэттер не чувствует внезапной силы реакции. Однако, поскольку летучая мышь не является жестким объектом, вибрации, возникающие при ударе, также играют роль. Кроме того, точка поворота качелей не может находиться в том месте, где находятся руки отбивающего. Исследования показали, что доминирующий физический механизм в определении зоны наилучшего восприятия возникает из расположения узлов в колебательных режимах летучей мыши, а не из расположения центра удара.
Концепция центра удара может применяться к мечам. Это гибкие объекты, поэтому «золотая середина» для такого режущего оружия зависит не только от центра удара, но и от характеристик изгиба и вибрации.
Ссылки
- ^Дэниел А. Рассел (16 июня 2005 г.). «Что такое КС и какое это имеет значение?». Физика и акустика бейсбольных и софтбольных бит. Государственный университет Пенсильвании. Архивировано с оригинального 5 апреля 2009 г. Получено 24 мая 2012 г.
- ^Род Кросс (2004). «Центр ударного действия ручных орудий» (PDF ). Американский журнал физики. 72(5): 622–630. Bibcode : 2004AmJPh..72..622C. doi : 10,1119 / 1,1634965.
- ^Джордж Тернер (1999). «Движения и удары меча: расследование и анализ». Ассоциация боевых искусств эпохи Возрождения. Проверено 24 мая 2012 г.
- ^Гейсслер, Роберт (2014). «О динамике мечей». HROARR. Проверено 18 января 2015 г.





