Как найти центр в многоугольнике

В математике барице́нтр, или геометри́ческий центр, двумерной фигуры — это среднее арифметическое положений всех точек данной фигуры. Определение распространяется на любой объект в n-мерном пространстве. Радиус-вектор барицентра в трёхмерном случае вычисляется как

,

где интегрирование выполняется по объёму тела. Другое название барицентра в этом значении — центроид.

Неформально, геометрический барицентр есть точка равновесия фигуры, вырезанной из картона, в предположении, что картон имеет постоянную плотность, а внешнее гравитационное поле однородно.

В физике термин «барицентр» — синоним понятия «центр масс», используемый, в основном, в задачах космической механики. Центр масс объекта является средним арифметическим всех его точек с учётом локальной плотности массы. Для физических объектов с постоянной плотностью центр масс совпадает с барицентром фигуры той же формы.

Ниже барицентр рассматривается в математическом (геометрическом) смысле, о барицентре в физике см. статью Центр масс.

Свойства[править | править код]

Геометрический барицентр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь барицентр, лежащий вне фигуры. Барицентр кольца или миски, например, лежат вне фигуры.

Если барицентр известен, он является фиксированной точкой группы изометрии симметрий фигуры. Барицентр объекта лежит на пересечении всех его гиперплоскостей симметрии. Барицентры многих фигур (правильного многоугольника, правильного многогранника, цилиндра, прямоугольника, ромба, окружности, сферы, эллипса, эллипсоида, суперэллипса, суперэллипсоида и т. д.) можно найти исходя исключительно из этого принципа.

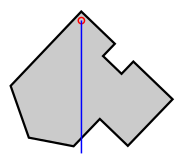
В частности, барицентром треугольника является точка пересечения его медиан (см. рисунок). Барицентром параллелограмма является точка пересечения его диагоналей, но это неверно для других четырёхугольников.

Барицентр объекта с трансляционной симметрией не определён (или лежит вне пространства фигуры), поскольку сдвиг не имеет фиксированной точки.

Центроид треугольника[править | править код]

• Барицентр треугольника называется центроидом и лежит на пересечении трёх медиан, также лежит на прямой Эйлера (проходящей и через другие ключевые точки, включая ортоцентр и центр описанной окружности)^[1][2].

• Если в вершины треугольника поместить равные массы, то центр масс (барицентр) полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой массой также находится в центроиде.

^[3].

• Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин треугольника:

^[3].

• Центр масс сторон треугольника совпадает с центром вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера. Если стороны треугольника сделать из тонкой проволоки одинакового сечения, то центр масс (барицентр) полученной системы будет совпадать с инцентром дополнительного треугольника, или с центром Шпикера.
• О других свойствах центроида треугольника смотрите ниже.

Минимаксные свойства центроида треугольника[править | править код]

• Центроид или точка пресечения медиан треугольника является единственной точкой треугольника такой, что проведенные через неё три чевианы разделяют своими концами стороны треугольника на шесть отрезков. При этом произведение длин трёх из этих шести отрезков, не имеющих общих концов, максимально^[4].
• Центроид или точка пересечения трёх медиан является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).

Центроид четырёх точек (вершин четырёхугольника)[править | править код]

Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие — середины противолежащих сторон. Точка пересечения делит все три отрезка пополам.

Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в одной точке (центроиде вершин четырёхугольника) и делятся ею в отношении 3:1, считая от вершины.

Центр масс вершин четырёхугольника не обязан совпадать с центром масс самого четырёхугольника как плоской фигуры.

Определение местоположения барицентра[править | править код]

Определение местоположения барицентра однородной плоской фигуры методом отвеса[править | править код]

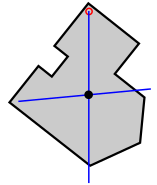
Барицентр однородной плоской фигуры, такой как фигура (a) на рисунке, можно найти экспериментально с использованием отвеса и булавки путём нахождения центра масс тонкой пластины однородной плотности, имеющей ту же форму. Пластина удерживается булавкой, вставленной ближе к периметру так, чтобы пластина могла свободно вращаться. Отмечаем на пластине прямую, которую образует отвес, прикреплённый к булавке (b). Проделываем то же самое с другим положением булавки. Пересечение двух прямых даст барицентр (c).

Этот метод можно распространить (в теории) на вогнутые фигуры, когда барицентр лежит вне их, а также тела (постоянной плотности), но положение линии отвеса придётся отмечать каким-то иным способом.

Определение местоположения барицентра выпуклой двумерной фигуры методом балансировки[править | править код]

Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например, на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.

Определение местоположения барицентра для конечного множества точек[править | править код]

Барицентр конечного множества из точек в находится по формуле

^[5].

Полученная точка такая, что сумма квадратов расстояний между ней и точками множества является минимальной.

Определение местоположения барицентра с помощью геометрического разложения[править | править код]

Барицентр плоской фигуры можно вычислить, разделив её на конечное число более простых фигур , найдя положение барицентров и площадей каждой части, а затем вычислив

Дыры в фигуре , наложения частей, или части, выступающие за фигуру, можно рассматривать как фигуры с отрицательной площадью . А именно, знак площади нужно выбирать так, чтобы сумма знаков для всех частей, включающих точку , была равна 1, если принадлежит , и 0 в противном случае.

Например, фигуру (a) на рисунке легко разделить на квадрат и треугольник с положительным знаком, круглое отверстие с отрицательным (b).

Барицентр каждой части легко найти в любом списке барицентров простых фигур (c). Затем вычисляется барицентр фигуры, как средневзвешенное трёх точек. Горизонтальное положение барицентра, считая от левого края фигуры, равно

Вертикальное положение вычисляется аналогично.

Та же формула применима для любого трёхмерного объекта, только обозначают уже объёмы частей тела , а не площади. Формула верна также для пространства любой размерности при замене площади -мерными мерами частей.

Определение местоположения барицентра интегрированием[править | править код]

Барицентр подмножества X пространства можно вычислить с помощью интеграла

где интегрирование ведётся по всему пространству , а g является характеристической функцией подмножества, принимающей 1 внутри X и 0 вне его^[6]. Заметим, что знаменатель равен мере множества X. Формула неприменима к множеству нулевой меры, а также к множествам, для которых интеграл расходится.

Другая формула для вычисления координат барицентра:

где G_k является k-й координатой G, а S_k(z) — мера пересечения X с гиперплоскостью, определяемой уравнением x_k = z. Снова знаменатель — это мера множества X.

Для плоской фигуры координатами барицентра будут

где A — площадь фигуры X, S_y(x) — длина пересечения^{[неизвестный термин]} X с вертикальной прямой с абциссой x, S_x(y) — аналогичная величина при обмене осей.

Определение местоположения барицентра для области, ограниченной графиками непрерывных функций[править | править код]

Координаты барицентра области, ограниченной графиками непрерывных функций и , таких что на интервале , , задаются выражениями

^[6].

^[7]

где  — площадь области (вычисляемая по формуле )^[8][9].

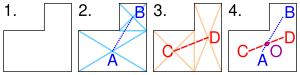
Определение местоположения барицентра объекта, имеющего форму буквы L[править | править код]

Метод нахождения барицентра фигуры, имеющей форму буквы L.

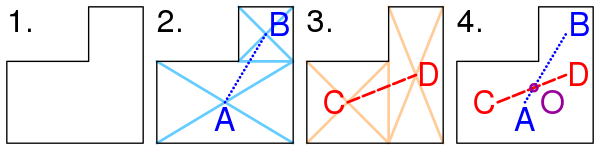
1. Фигуру делят на два прямоугольника (см. фигуру (2) на рисунке). Находят барицентры A и B этих двух прямоугольников как пересечение диагоналей. Рисуют отрезок AB, соединяющий барицентры. Барицентр фигуры должен лежать на этом отрезке AB.
2. Делят фигуру на два прямоугольника другим способом (см. фигуру (3) на рисунке). Находят барицентры C и D этих двух прямоугольников. Проводят отрезок CD, соединяющий барицентры. Барицентр фигуры должен лежать на отрезке CD.
3. Поскольку барицентр должен лежать как на отрезке AB, так и на отрезке CD, очевидно, что он является точкой пересечения этих двух отрезков — точкой O. Точка O не обязана лежать внутри фигуры.

Барицентры треугольника и тетраэдра[править | править код]

Барицентр треугольника совпадает с пересечением медиан. Барицентр разбивает каждую медиану в отношении 2:1, то есть барицентр находится на расстоянии ⅓ от стороны до противоположной вершины (см. рисунок). Его декартовыми координатами является среднее координат трёх вершин. То есть, если вершинами треугольника являются , и , то координаты барицентра вычисляются по формуле

.

Таким образом, барицентр имеет барицентрические координаты .

В трилинейных координатах барицентр можно получить одним из эквивалентных способов^[10]:

Барицентр является также физически центром масс треугольника, сделанного из однородного листового материала, а также, если вся масса сконцентрирована в вершинах и одинаково разделена между ними. Если же масса распределена равномерно вдоль периметра, то центр масс лежит в точке Шпикера (инцентре серединного треугольника), который (в общем случае) не совпадает с центроидом всего треугольника.

Площадь треугольника равна 3/2 длины любой стороны, умноженной на расстояние от центроида до стороны^[11].

Центроид треугольника лежит на прямой Эйлера между его ортоцентром и центром его описанной окружности , ровно вдвое ближе ко второму, чем к первому:

.

Кроме того, для инцентра и центра девяти точек , мы имеем

,

,

,

,

.

Аналогичными свойствами обладает тетраэдр — его барицентр является пересечением отрезков, соединяющих вершины с барицентрами противоположных граней. Эти отрезки делятся барицентром в отношении 3:1. Результат может быть обобщён на любой -мерный симплекс. Если вершины симплекса обозначить и рассматривать вершины как вектора, центроид равен

.

Геометрический барицентр совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как равных масс.

Изогональным сопряжением центроида треугольника является точка пересечения его симедиан.

Барицентр тетраэдра[править | править код]

Тетраэдр является телом в трёхмерном пространстве, имеющим четыре треугольника в качестве граней. Отрезок, соединяющий вершину тетраэдра с барицентром противоположной грани, называется медианой, а отрезок, соединяющий середины двух противоположных сторон, называется бимедианой. Таким образом, имеется четыре медианы и две бимедианы. Эти шесть отрезков пересекаются в барицентре тетраэдра^[12]. Барицентр тетраэдра лежит посередине между точкой Монжа и центром описанной сферы. Эти точки задают прямую Эйлера тетраэдра, являющуюся аналогом прямой Эйлера треугольника.

Барицентр многоугольника[править | править код]

Барицентром самонепересекающегося замкнутого многоугольника, заданного вершинами , , , , является точка , где

;

и где является площадью многоугольника (со знаком):

^[13].

В этой формуле предполагается, что вершины пронумерованы вдоль периметра многоугольника. Кроме того, вершина считается той же самой, что и .
Заметим, что если точки пронумерованы по часовой стрелке, площадь , вычисленная выше, будет отрицательной, но координаты барицентра подкорректируют этот случай.

Барицентры конуса и пирамиды[править | править код]

Барицентр конуса или пирамиды расположен на отрезке, соединяющем вершину тела с барицентром основания. Для целого конуса или пирамиды барицентр находится на расстоянии 1/4 от основания к вершине. Для поверхности конуса или пирамиды (боковая поверхность без внутренности и без основания) центроид находится на 1/3 расстояния от основания до вершины.

См. также[править | править код]

• Центр масс
• Центроид треугольника
• Центр тяжести
• Центр Чебышева^[en]
• Среднее Фреше^[en]
• k-means
• Список барицентров
• Теоремы Паппа — Гульдина
• Замечательные точки треугольника

Примечания[править | править код]

Литература[править | править код]

• Зетель, С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е изд/. — М. : Учпедгиз, 1962. — С. 12.
• Leung Kam-tim, Suen Suk-nam. Vectors, matrices and geometry. — Hong Kong University Press, 1994.

• Nathan Altshiller-Court. College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. — 2nd. — New York: Barnes & Noble, 1925.
• Paul Bourke. Calculating the area and centroid of a polygon. — 1997.
• Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007.
• David C. Kay. College Geometry. — New York: Holt, Rinehart and Winston, 1969.
• Roland E. Larson, Robert P. Hostetler, Bruce H. Edwards. Calculus of a Single Variable. — 6th. — Houghton Mifflin Company, 1998.
• Murray H. Protter, Charles B. Morrey Jr. College Calculus with Analytic Geometry. — 2nd. — Reading: Addison-Wesley, 1970.

Ссылки[править | править код]

• Characteristic Property of Centroid at cut-the-knot
• Barycentric Coordinates at cut-the-knot
• Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge
• Experimentally finding the medians and centroid of a triangle at Dynamic Geometry Sketches, an interactive dynamic geometry sketch using the gravity simulator of Cinderella.

Here are six different approaches I have tried.

1. cv2 based center of mass (get_center_of_mass)
2. shapely based representative point (get_representative_point)
3. cv2 + skimage.skeleton based center of mass of the skeletonized shape (get_skeleton_center_of_mass)
4. scipy based furthest distance to border (get_furthest_point_from_edge)
5. cv2 based version of the previous furthest distance to border -algorithm (get_furthest_point_from_edge_cv2)
6. the “center point of half-area line” algorithm proposed in this thread by @T.Austin (get_center_of_half_area_line)

Let’s begin with imports and some helper functions

import numpy as np
import cv2
from shapely.geometry import Polygon, LineString, MultiLineString, Point, MultiPoint, GeometryCollection
from skimage.morphology import skeletonize, medial_axis
from scipy.optimize import minimize_scalar
from scipy.ndimage.morphology import distance_transform_edt
import matplotlib.pyplot as plt

H, W = 300, 300

def get_random_contour():
    xs = np.random.randint(0, W, 4)
    ys = np.random.randint(0, H, 4)
    cnt = np.array([[x,y] for x,y in zip(xs,ys)])
    mask = draw_contour_on_mask((H,W), cnt)
    cnt, _ = cv2.findContours(mask, 1, 2)
    cnt = cnt[0]
    return cnt

def draw_contour_on_mask(size, cnt, color:int = 255):
    mask = np.zeros(size, dtype='uint8')
    mask = cv2.drawContours(mask, [cnt], -1, color, -1)
    return mask

def get_center_of_mass(cnt):
    M = cv2.moments(cnt)
    cx = int(M['m10']/M['m00'])
    cy = int(M['m01']/M['m00'])
    return cx, cy

def split_mask_by_line(mask, centroid:tuple, theta_degrees:float, eps:float = 1e-4):
    h, w = mask.shape[:2]
    mask = mask[..., None]
    cx, cy = centroid
    # convert theta first to radians and then to line slope(s)
    theta_degrees = np.atleast_1d(theta_degrees)
    theta_degrees = np.clip(theta_degrees, -90+eps, 90-eps)
    theta_rads = np.radians(theta_degrees)
    slopes = np.tan(theta_rads)[:, None]
    # define the line(s)
    x = np.arange(w, dtype="int32")
    y = np.int32(slopes * (x - cx) + cy)
    _y = np.arange(h, dtype="int32")
    # split the input mask into two halves by line(s)
    m = (y[..., None] <= _y).T
    m1 = (m * mask).sum((0,1))
    m2 = ((1 - m) * mask).sum((0,1))
    m2 = m2 + eps if m2==0 else m2
    # calculate the resultant masks ratio
    ratio = m1/m2
    return (x.squeeze(), y.squeeze()), ratio

def get_half_area_line(mask, centroid: tuple, eps: float = 1e-4):
    # find the line that splits the input mask into two equal area halves
    minimize_fun = lambda theta: abs(1. - split_mask_by_line(mask, centroid, theta, eps=eps)[1].item())
    bounds = np.clip((-90, 90), -90 + eps, 90 - eps)
    res = minimize_scalar(minimize_fun, bounds=bounds, method='bounded')
    theta_min = res.x
    line, _ = split_mask_by_line(mask, centroid, theta_min)
    return line

Now let’s define the functions for finding the visual center

def get_representative_point(cnt):
    poly = Polygon(cnt.squeeze())
    cx = poly.representative_point().x
    cy = poly.representative_point().y
    return cx, cy

def get_skeleton_center_of_mass(cnt):
    mask = draw_contour_on_mask((H,W), cnt)
    skel = medial_axis(mask//255).astype(np.uint8) #<- medial_axis wants binary masks with value 0 and 1
    skel_cnt,_ = cv2.findContours(skel,1,2)
    skel_cnt = skel_cnt[0]
    M = cv2.moments(skel_cnt) 
    if(M["m00"]==0): # this is a line
        cx = int(np.mean(skel_cnt[...,0]))
        cy = int(np.mean(skel_cnt[...,1]))
    else:
        cx = int(M['m10']/M['m00'])
        cy = int(M['m01']/M['m00'])
    return cx, cy

def get_furthest_point_from_edge(cnt):
    mask = draw_contour_on_mask((H,W), cnt)
    d = distance_transform_edt(mask)
    cy, cx = np.unravel_index(d.argmax(), d.shape)
    return cx, cy

def get_furthest_point_from_edge_cv2(cnt):
    mask = draw_contour_on_mask((H,W), cnt)
    dist_img = cv2.distanceTransform(mask, distanceType=cv2.DIST_L2, maskSize=5).astype(np.float32)
    cy, cx = np.where(dist_img==dist_img.max())
    cx, cy = cx.mean(), cy.mean()  # there are sometimes cases where there are multiple values returned for the visual center
    return cx, cy

def get_center_of_half_area_line(cnt):
    mask = draw_contour_on_mask((H,W), cnt, color=1)
    # get half-area line that passes through centroid
    cx, cy = get_center_of_mass(mask)
    line = get_half_area_line(mask, centroid=(cx, cy))
    line = LineString(np.array(list(zip(line))).T.reshape(-1, 2))
    # find the visual center
    contours, _ = cv2.findContours(mask, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
    contours = [c for c in contours if cv2.contourArea(c) > 5]
    polys = [Polygon(c.squeeze(1)) for c in contours if len(c) >= 3]  # `Polygon` must have at least 3 points
    cpoint = Point(cx, cy)
    points = []
    for poly in polys:
        isect = poly.intersection(line)
        if isect.is_empty:
            # skip when intersection is empty: this can happen for masks that consist of multiple disconnected parts
            continue
        if isinstance(isect, (MultiLineString, GeometryCollection)):
            # take the line segment intersecting with `poly` that is closest to the centroid point
            isect = isect.geoms[np.argmin([g.distance(cpoint) for g in isect.geoms])]
        if isinstance(isect, Point):
            # sometimes the intersection can be a singleton point
            points.append(isect)
            continue
        isect = isect.boundary
        if poly.intersects(cpoint):
            points = [isect]
            break
        else:
            points.append(isect)

    if len(points) == 0:
        # multiple reasons for this one:
        # - if len(polys)==0
        # - if len(polys)==1, but for some reason the line does not intersect with polygon
        # - if the above search does not match with any points

        return cx, cy

    points = points[np.argmin([p.distance(cpoint) for p in points])]
    if isinstance(points, Point):
        return np.array(points.xy)
    
    points = [np.array(p.xy).tolist() for p in points.geoms]
    visual_center = np.average(points, (0, 2))
    return visual_center

Here’s my analysis on the topic:

• get_center_of_mass is the fastest but, as mentioned in this thread, the center of mass can be located outside the shape for non-convex shapes.
• get_representative_point is also fast but the identified point, although always guaranteed to stay inside the shape (or with minor edits even multiple disconnected shapes!), does not have much if anything to do with the center of the object
• get_skeleton_center_of_mass returns a perceptually nice center point, but is slow and requires logic for disconnected shapes
• get_furthest_point_from_edge is relatively fast, generalizes easily to disconnected shapes and the center point is visually pleasing
• get_furthest_point_from_edge_cv performs otherwise similarly as get_furthest_point_from_edge but is an order of magnitude faster
• get_center_of_half_area_line performs neatly: the result is usually closest to where I myself would annotate the visual center. Unfortunately, at least my implementation is quite slow.

rows = 4
cols = 4
markers = ['x', '+', "*", "o", '^', "v"]
colors = ['r','b','g','orange', 'purple', 'lime']
functions = [
    get_center_of_mass, 
    get_representative_point, 
    get_skeleton_center_of_mass, 
    get_furthest_point_from_edge,
    get_furthest_point_from_edge_cv2,
    get_center_of_half_area_line
]

plt.figure(figsize=(2*cols, 2*rows, ))
for i in range(rows*cols): 
    cnt = get_random_contour()
    mask = draw_contour_on_mask((H,W), cnt)
    
    plt.subplot(cols,rows, i+1)
    plt.imshow(mask, cmap='gray')
    for c, m, f in zip(colors, markers, functions):
        l = f.__name__
        cx, cy = f(cnt)
        plt.scatter(cx, cy, c=c, s=100, label=l, marker=m, alpha=0.7)

plt.tight_layout()    
plt.legend(loc=3)
plt.show()

Here’s how the algorithms, run on 100 random examples, compare in speed:

N_EXAMPLES = 100
cnts = [get_random_contour() for _ in range(N_EXAMPLES)]

for fn in functions:
    print(fn.__name__+":")
    %time _ = [fn(cnt) for cnt in cnts]
    print("~ "*40)

get_center_of_mass:
CPU times: user 2.35 ms, sys: 777 µs, total: 3.13 ms
Wall time: 1.91 ms
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 
get_representative_point:
CPU times: user 15.7 ms, sys: 0 ns, total: 15.7 ms
Wall time: 14.8 ms
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 
get_skeleton_center_of_mass:
CPU times: user 6.52 s, sys: 104 ms, total: 6.62 s
Wall time: 6.62 s
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 
get_furthest_point_from_edge:
CPU times: user 413 ms, sys: 63 µs, total: 413 ms
Wall time: 413 ms
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 
get_furthest_point_from_edge_cv2:
CPU times: user 47.8 ms, sys: 0 ns, total: 47.8 ms
Wall time: 47.8 ms
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 
get_center_of_half_area_line:
CPU times: user 1.66 s, sys: 0 ns, total: 1.66 s
Wall time: 1.66 s
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 

Как найти центр вписанной окружности в правильном многоугольнике

Ключевые слова: многоугольник, правильный многоугольник, сторона, угол, вписанная, описанная окружность

Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.

Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.

Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.

См. также:
Вписанная окружность, Описанная окружность, Выпуклый четырёхугольник, Произвольный выпуклый многоугольник

Геометрия

План урока:

Понятие правильного многоугольника

У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.

Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.

Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны. Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник. Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными.

Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:

Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:

Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:

Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?

Решение. Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:

Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?

Решение. В формулу

Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?

Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:

Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.

Описанная и вписанная окружности правильного многоугольника

Докажем важную теорему о правильном многоуг-ке.

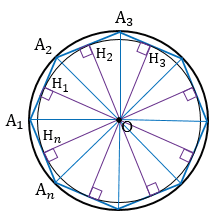
Для доказательства обозначим вершины произвольного правильного n-угольника буквами А₁, А₂, А₃…А_n. Далее проведем биссектрисы углов ∠А₁ и ∠А₂. Они пересекутся в некоторой точке О. Соединим О с другими вершинами многоуг-ка отрезками ОА₃, ОА₄ и т. д.

∠А₁ и ∠А₂ одинаковы по определению правильного многоуг-ка:

Из этого факта вытекает два равенства:

Получается, что ОА₃ – это также биссектриса ∠А₃. Тогда, повторив все предыдущие рассуждения, мы можем доказать равенство, аналогичное (1):

Это равенство означает, что точка О равноудалена от вершин многоуг-ка. Значит, можно построить окружность с центром в О, на которой будут лежать все вершины многоуг-ка:

Естественно, существует только одна такая описанная окружность, ведь через любые три точки, в частности, через А₁, А₂ и А₃, можно провести только одну окружность, ч. т. д.

Продолжим рассматривать выполненное нами построение с описанной окружностью. Ясно, что ∆ОА₁А₂, ∆ОА₂А₃, ∆ОА₃А₄, …, равны, ведь у них одинаковы по 3 стороны. Опустим из О высоты ОН₁, ОН₂, ОН₃… на стороны многоуг-ка.

Так как высоты проведены в равных треуг-ках, то и сами они равны:

Теперь проведем окружность, центр которой находится в О, а радиус – это отрезок ОН₁. Он должен будет пройти и через точки Н₂, Н₃, … Н_n. Причем отрезки ОН₁, ОН₂, ОН₃ окажутся радиусами. Так как они перпендикулярны сторонам многоуг-ка, то эти самые стороны будут касательными к окружности (по признаку касательной). Стало быть, эта окружность является вписанной:

Ясно, что такая окружность будет единственной вписанной. Если бы существовала вторая вписанная окружность, то ее центр был бы равноудален от сторон многоуг-ка, а потому лежал бы в точке пересечения биссектрис углов ∠А₁, ∠А₂, ∠А₃, то есть в точке О. Так как расстояние от О до А₁А₂ – это отрезок ОН₁, то именно такой радиус был бы у второй окружности. Получается, что вторая окружность полностью совпала бы с первой, так как их центр находился бы в одной точке, и радиусы были одинаковы.

Примечание. Точка, которая центром и вписанной, и описанной окружности, именуется центром правильного многоуг-ка.

Ещё раз вернемся к приведенному доказательству и заметим, что высоты ОН₁, ОН₂, ОН₃,… проведены в равнобедренных треуг-ках∆ОА₁А₂, ∆ОА₂А₃, ∆ОА₃А₄,… Следовательно, эти высоты являются ещё и медианами, то есть точки Н₁, Н₂, Н₃,… – это середины сторон многоуг-ка.

Задание. Могут ли две биссектрисы, проведенные в правильном многоуг-ке, быть параллельными друг другу?

Решение. Центр правильного многоуг-ка находится в точке пересечения всех его биссектрис. То есть любые две биссектрисы будут иметь хотя бы одну общую точку. Параллельные же прямые общих точек не имеют. Получается, что биссектрисы не могут быть параллельными.

Примечание. Аналогичное утверждение можно доказать и для серединных перпендикуляров, проведенных к сторонам правильного многоуг-ка.

Формулы для правильного многоугольника

Правильный многоуг-к, как и любая другая плоская фигура, имеет площадь (она обозначается буквой S) и периметр (обозначается как Р). Длина стороны многоуг-ка традиционно обозначается буквой a_n, где n– число сторон у многоуг-ка. Например a₄– это сторона квадрата, a₆– сторона шестиугольника. Наконец, мы выяснили, что для каждого правильного многоуг-ка можно построить описанную и вписанную окружность. Радиус описанной окружности обозначается большой буквой R, а вписанной – маленькой буквой r.

Оказывается, все эти величины взаимосвязаны друг с другом. Ранее мы уже получили формулу

для многоуг-ка, в который вписана окружность. Подходит она и для правильного многоуг-ка.

Для вывода остальных формул правильного многоугольника построим n-угольники соединим две его вершины с центром:

Теперь у нас есть формула, связывающая друг с другом Rи r. Наконец, прямо из определения периметра следует ещё одна формула:

С их помощью, зная только один из параметров правильного n-угольника, легко найти и все остальные параметры (если известно и число n).

Задание. Докажите, что сторона правильного шестиугольника равна радиусу описанной около него окружности.

Решение. Запишем следующую формулу:

Это равенство как раз и надо было доказать в этом задании.

Задание. Около окружности описан квадрат. В свою очередь и около квадрата описана окружность радиусом 4. Найдите длину стороны квадрата и радиус вписанной окружности.

Решение. Запишем формулу:

Задание. Вычислите площадь правильного многоугольника с шестью углами, длина стороны которого составляет единицу.

Найдем периметр шестиугольника:

Задание. Около правильного треугольника описана окружность. В ту же окружность вписан и квадрат. Какова длина стороны этого квадрата, если периметр треугольника составляет 18 см?

Решение. Зная периметр треуг-ка, легко найдем и его сторону:

Далее вычисляется радиус описанной около треугольника окружности:

Задание. Необходимо изготовить болт с шестигранной головкой, причем размер под ключ (так называется расстояние между двумя параллельными гранями головки болта) должен составлять 17 мм. Из прутка какого диаметра может быть изготовлен такой болт, если диаметр прутков измеряется целым числом?

Решение. Здесь надо найти диаметр окружности, описанной около шестиугольника. Ранее мы уже доказывали, что у шестиугольника длина этого радиуса совпадает с длиной его стороны:

Осталось найти сторону шестиугольника. Для этого соединим две его вершины (обозначим их А и С) так, как это показано на рисунке:

Отрезок АС как раз и будет расстоянием между двумя параллельными гранями, что легко доказать. Каждый угол шестиугольника будет составлять 120°:

В частности ∠АВС = 120°. Так как АВ = ВС, то ∆АВС – равнобедренный, и углы при его основании одинаковы:

Аналогично можно показать, что и ∠ACD – прямой. Таким образом, АС перпендикулярен сторонам AF и CD, а значит является расстоянием между ними, и по условию равно 17 мм:

∆АВС – равнобедренный. Опустим в нем высоту НВ, которая одновременно будет и медианой. Тогда АН окажется вдвое короче АС:

AH = AC/2 = 17/2 = 8,5 мм

Теперь сторону АВ можно найти из ∆АВН, являющегося прямоугольным:

Здесь мы округлили ответ до ближайшего большего целого числа, так как по условию можно использовать лишь пруток с целым диаметром.

Построение правильных многоугольников

При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:

Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.

Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:

На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а₆. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а₆. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):

Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.

Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.

Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.

Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:

Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.

Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.

В этом уроке мы узнали о правильных многоуг-ках и их свойствах. Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности.

Окружность, вписанная в правильный многоугольник

Теорема

В любой правильный многоугольник можно вписать окружность, и притом только одну.

Доказательство

Доказать: в многоугольник А₁А₂А₃. А_n можно вписать окружность, и притом только одну.

Доказательство:

А₁ОА₂ = А₂ОА₃ = . = А₁ОА_n по трем сторонам (ОА₁ = ОА₂ = . = ОА_n, как радиусы описанной окружности и А₁А₂ = А₂А₃ = . = А_nА₁, как стороны правильного многоугольника), тогда и высоты этих треугольников, проведенные из вершины О, также будут равны: ОН₁ = ОН₂ = . = ОН_n. Следовательно, окружность с центром О и радиусом ОН₁ проходит через точки Н₁, Н₂, . , Н_n и касается сторон многоугольника в этих точках, т.е. эта окружность вписана в данный правильный многоугольник А₁А₂А₃. А_n.

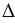
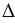
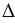
Докажем, что вписать можно только одну окружность.

Пусть существует окружность с центром О₁, вписанная в многоугольник А₁А₂А₃. А_n, отличная от окружности с центром О и радиусом ОН₁. Тогда ее центр О₁ равноудален от сторон многоугольника, т.е. точка О₁ лежит на каждой из биссектрис углов многоугольника А₁А₂А₃. А_n и, следовательно, совпадает с точкой О пересечения этих биссектрис (смотри теорему об окружности, описанной около правильного многоугольника). Радиус этой окружности равен расстоянию от точки О до сторон многоугольника,т.е. равен ОН₁. Значит, получаем, что вторая окружность совпадает с первой. Следовательно, наше предположение неверно, и в правильный многоугольник вписать можно только одну окружность. Теорема доказана.

Следствие 1

Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.

Следствие 2

Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

Эта точка называется центром правильного многоугольника.

Поделись с друзьями в социальных сетях:

[spoiler title=”источники:”]

http://100urokov.ru/predmety/pravilnye-mnogougolniki

http://budu5.com/manual/chapter/3571

[/spoiler]

На карте отобразил условный контур и теперь хотел бы в него вывести балун. Создать балун не проблема, не поместить его в центр полигона — проблема.

В математике есть довольно сложные формулы для расчёта центра масс многоугольника, ими я не умею пользоваться. но в яндекс апи есть poly.geometry.getBounds(), который берёт максимально большой контур и находит центр. У меня тоже не получается его применить потому что полигон я создал не стандартным способом( new ymaps.Polygon()), а через map.geoObjects.add(objectManager);

Помогите пожалуйста получить координаты центра полигона.

Если нужно, то вот фиддл, который демонстрирует getBounds().

Медиана треугольника есть диаметр, делящий пополам хорды, параллельные основанию, поэтому на ней лежит центр тяжести (п° 217) площади треугольника. Следовательно, три медианы треугольника, пересекаясь, определяют центр тяжести площади треугольника.

Элементарные соображения показывают, что медианы треугольника пересекаются в точке, отстоящей на две трети длины каждой из них от соответствующей вершины. Поэтому центр тяжести площади треугольника лежит на любой его медиане на расстоянии двух третей ее длины от вершины.

219. Четырехугольник.

Центр тяжести площади четырехугольника определяется пересечением двух прямых, которые мы получаем, применяя распределительное свойство центров тяжести (п° 213).

Сначала делим четырехугольник диагональю на два треугольника. Центр тяжести четырехугольника лежит на прямой, соединяющей центры тяжести этих треугольников. Эта прямая и есть первая из двух искомых прямых.

Вторую прямую получим таким же способом, разбивая четырехугольник на два треугольника (отличных от предыдущих) посредством другой диагонали.

220. Многоугольник.

Мы знаем способы нахождения центров тяжести площади треугольника и четырехугольника. Чтобы определить центр тяжести площади многоугольника с произвольным числом сторон, предположим, что мы умеем находить центр тяжести площади многоугольника с меньшим числом сторон.

Тогда можно поступить так же, как в случае четырехугольника. Площадь данного многоугольника делят на две части двумя разными способами проведением диагоналей. В каждом из двух случаев соединяют прямой центры тяжести отдельных частей. Эти две прямые пересекаются в искомом центре тяжести.

221. Дуга окружности.

Пусть требуется определить центр тяжести дуги окружности АВ длины s. Отнесем окружность к двум взаимно перпендикулярным диаметрам ОХ и OY, из которых первый проходит через середину С дуги АВ. Центр тяжести лежит на оси ОХ, являющейся осью симметрии. Достаточно поэтому определить 5. Для этого имеем формулу:

Пусть будут: а — радиус окружности, с — длина хорды АВ, — угол между осью ОХ и радиусом, проведенным к элементу значения , соответствующие концам дуги АВ. Имеем:

Тогда, принимая В за переменную интегрирования и выполняя интегрирование вдоль дуги АВ, получим:

Следовательно, центр тяжести дуги окружности лежит на радиусе, проведенном через середину дуги, в точке, расстояние которой от центра окружности есть четвертая пропорциональная длины дуги, радиуса и хорды.

222. Круговой сектор.

Сектор, заключенный между дугой окружности и двумя радиусами ОА и ОВ, может быть разложен промежуточными радиусами на бесконечно малые равные между собою секторы. Эти элементарные секторы можно рассматривать как бесконечно узкие треугольники; центр тяжести каждого из них, по предыдущему, лежит на радиусе, проведенном через середину элементарной дуги этого сектора, на расстоянии двух третей длины радиуса от центра окружности. Равные между собою массы всех элементарных треугольников, сосредоточенные в их центрах тяжести, образуют однородную дугу окружности, радиус которой равен двум третям радиуса дуги сектора. Рассматриваемый случая приводится, таким образом, к отысканию центра тяжести этой однородной дуги, т. е. к задаче, решенной в предыдущем п°.

223. Тетраэдр.

Определим центр тяжести объема тетраэдра. Плоскость, проходящая через одно из ребер и через середину противоположного ребра, есть диаметральная плоскость, которая делит пополам хорды, параллельные этому последнему ребру: она содержит поэтому центр тяжести объема тетраэдра. Следовательно, шесть плоскостей, тетраэдра, из которых каждая проходит через одно из ребер и через середину противоположного ребра, пересекаются в одной точке, представляющей собой центр тяжести объема тетраэдра.

Рассмотрим тетраэдр ABCD (фиг. 37); соединим вершину А с центром тяжести I основания BCD; прямая AI есть пересечение диаметральных плоскостей, проходящих

через ребра АВ и поэтому она содержит искомый центр тяжести. Точка находится на расстоянии двух третей медианы ВН от вершины В. Точно так же возьмем на медиане АН точку К на расстоянии двух третей ее длины от вершины . Прямая В К пересечет прямую А в центре тяжести тетраэдра. Проведем из подобия треугольников АВН и ЮН видно, что IK есть третья часть АВ) далее, из подобия треугольников и ВГА заключаем, что есть третья часть .

Следовательно, центр тяжести объема тетраэдра лежит на отрезке, соединяющем любую вершину тетраэдра с центром тяжести противоположной грани, на расстоянии трех четвертей длины этого отрезка от вершины.

Заметим еще, что прямая, соединяющая середины Я и L двух противоположных ребер (фиг. 38) есть пересечение диаметральных плоскостей, проходящих через эти ребра, она также проходит через центр тяжести тетраэдра. Таким образом, три прямые, соединяющие середины противоположных ребер тетраэдра, пересекаются в его центре тяжести.

Пусть Н и — середины одной пары противоположных ребер (фиг. 38) и М, N — середины двух других противоположных ребер. Фигура HNLM есть параллелограм, стороны которого соответственно параллельны остальным

двум ребрам. Прямые HL и MN, соединяющие середины двух противоположных ребер, суть диагонали этого параллелограма, а значит, они в точке пересечения делятся пополам. Таким образом, центр тяжести тетраэдра лежит в середине отрезка, соединяющего середины двух противоположных ребер тетраэдра.

224. Пирамида с многоугольным основанием.

Центр тяжести пирамиды лежит на отрезке, соединяющем вершину пирамиды с центром тяжести основания на расстоянии трех четвертей длины этого отрезка от вершины.

Чтобы доказать эту теорему, разложим пирамиду на тетраэдры плоскостями, проведенными через вершину пирамиды и через диагонали основания ABCD (например BD на фиг. 39).

Проведем плоскость пересекающую ребра на расстоянии трех четвертей их длины от вершины. Эта плоскость содержит центры тяжести тетраэдров, а следовательно, и пирамиды. Массы тетраэдров, которые мы предполагаем сосредоточенными в их центрах тяжести, пропорциональны их объемам, следовательно и площадям из оснований (фиг. 39) или также площадям треугольников bad, bed. подобных предыдущим и расположенным в секущей плоскости abcd. Таким образом, искомый центр тяжести совпадает с центром тяжести многоугольника abcd. Последний же лежит на прямой, соединяющей вершину S пирамиды с центром тяжести (подобно расположенным) многоугольника основания.

225. Призма. Цилиндр. Конус.

На основании симметрии, центры тяжести призмы и цилиндра лежат на середине отрезка, соединяющего центры тяжести оснований.

Рассматривая конус, как предел вписанной в него пирамиды с той же вершиной, убеждаемся, что центр тяжести конуса лежит на отрезке, соединяющем вершину конуса с центром тяжести основания, на расстоянии трех четвертей длины этого отрезка от вершины. Можно также сказать, что центр тяжести конуса совпадает с центром тяжести сечения конуса плоскостью, параллельной основанию и проведенной на расстоянии одной четверти высоты конуса от основания.

Понятие “центр тяжести многоугольника” можно интерпретировать тремя различными способами:

1. Масса находится только в вершинах, причем каждая вершина “весит” одинаково
2. Масса равномерно распределена по границе многоугольника
3. Масса равномерно распределена по области, ограниченной многоугольником.

Рассмотрим все три интерпретации в порядке возрастания сложности алгоритма.

1. Масса находится только в вершинах, причем каждая вершина весит одинаково

В этом случае координаты центра тяжести выражаются по формулам:

Таким образом для нашего частного случая имеем:

2. Масса равномерно распределена по границе многоугольника

В этом случае масса ребра пропорциональна его длине. Таким образом каждое ребро мы можем заменить на точечную массу (пропорциональную длине ребра). Затем применяя те же формулы для определения центра тяжести получаем:

Ниже представлена программа, реализующая описанный алгоритм:

3. Масса равномерно распределена по области, ограниченной многоугольником.

Этот случай уже не является столь тривиальным, как два предыдущих. Для построения алгоритма понадобится следующий факт:

Предложение 1
Пусть фигура Ф есть объединение двух других фигур Ф1 и Ф2 (пересекающихся только по границе).
Тогда центр тяжести фигуры Ф выражается так:

(Это утверждение очевидно следует из определения центра тяжести произвольной фигуры и свойства аддитивности интеграла)

Кроме того для треугольника центр тяжести определяется так:

Разобьем наш многоугольник на треугольники. Для каждого треугольника найдем его центр тяжести (Xci, Yci) и площадь (Si). После этого, согласно Предложению 1, координаты центра тяжести многоугольника можно найти следующим образом:

Остается вопрос, как разбить многоугольник на треугольники. Если многоугольник выпуклый, а вершины перечислены в порядке обхода по или против часовой стрелки, то достаточно просто найти одну точку внутри многоугольника (Xm,Ym), а затем разбить многоугольник на N следующих треугольников:

Если же многоугольник выпуклый, но вершины перечислены не в порядке обхода, то их придется упорядочить. Сделать это можно, например, отсортировав вершины по углу между положительной полуосью ОХ и вектором (Xi-Xm, Yi-Ym).

Невыпуклый многоугольник всегда можно разбить на несколько выпуклых. А затем, применив описанный алгоритм для каждой выпуклой части, и используя Предложение 1, найти центр тяжести всего многоугольника. Задача о разбиении произвольного многоугольника на выпуклые части является самостоятельной задачей, которая рассмотрена в соответствующем разделе. Поэтому представленная ниже реализация алгоритма работает только для выпуклых многоугольников.

Ниже представлен пример реализации описанного алгоритма на языке С для нахождения центра тяжести выпуклого многоугольника, вершины которого перечислены в порядке обхода по или против часовой стрелки:

Среднее («среднее») положение всех точек в форме Центроид треугольника

В математика и физика, центроид или геометрический центр плоской фигуры – это среднее арифметическое положение всех точек на рисунке. Неформально, это точка, в которой вырез формы может быть идеально сбалансирован на кончике булавки.

Определение распространяется на любой объект в n- мерном пространстве : его центроид – это среднее положение всех точек во всех направлениях координат.

В то время как в геометрии слово барицентр является синонимом центроида, в астрофизике и астрономии барицентр – это центр масс двух или более тел, вращающихся по орбите друг с другом. В физике центр масс – это среднее арифметическое всех точек , взвешенных по локальной плотности или удельному весу. Если физический объект имеет однородную плотность, его центр масс совпадает с центроидом его формы.

В geography центроид радиальной проекции области земной поверхности на уровень моря – это географический центр региона.

Содержание

• 1 История
• 2 Свойства
• 3 Примеры
• 4 Расположение
  • 4.1 Метод отвеса
  • 4.2 Метод балансировки
  • 4.3 Из конечного набора точек
  • 4.4 Путем геометрического разложения
  • 4.5 По интегральной формуле
  • 4.6 Ограниченной области
  • 4.7 L-образного объекта
  • 4.8 Треугольника
  • 4.9 Многоугольника
  • 4.10 Конуса или пирамиды
  • 4.11 Тетраэдра и n -мерный симплекс
  • 4.12 Полушария
• 5 См. также
• 6 Примечания
• 7 Ссылки
• 8 Внешние ссылки

История

Термин «центроид» появился недавно чеканка (1814 г.). Он используется в качестве замены старых терминов «центр тяжести » и «центр масс », когда необходимо подчеркнуть чисто геометрические аспекты этой точки. Термин свойственен английскому языку. Французы чаще всего используют «центр притяжения», а другие используют термины схожего значения.

Центр тяжести, как следует из названия, возник в механике, скорее всего, в связи со строительством. Когда, где и кем он был изобретен, неизвестно, так как эта концепция, вероятно, пришла в голову многим людям индивидуально с небольшими различиями.

Хотя возможно Евклид все еще был активен в Александрии в детстве Архимеда (287–212 до н.э.), несомненно, что когда Архимед посетил Александрия, Евклида там больше не было. Таким образом, Архимед не мог усвоить теорему о том, что медианы треугольника пересекаются в точке – центре тяжести треугольника непосредственно от Евклида, поскольку этого утверждения нет в Элементах Евклида. Первое явное утверждение этого предположения принадлежит Герону Александрийскому (возможно, I век н.э.) и встречается в его «Механике». Между прочим, можно добавить, что это положение не входило в учебники по геометрии плоскости до XIX века.

Хотя Архимед прямо не заявляет об этом утверждении, он косвенно ссылается на него, предполагая, что он был с ним знаком. Однако Жан Этьен Монтукла (1725–1799), автор первой истории математики (1758), категорически заявляет (т. I, стр. 463), что центр тяжести твердых тел является предметом Архимеда не трогал.

В 1802 году Шарль Босу (1730–1813) опубликовал двухтомный Essai sur l’histoire générale des mathématiques. Эта книга была высоко оценена современниками, судя по тому, что уже через два года после публикации она была переведена на итальянский (1802–03), английский (1803) и немецкий (1804) языки. Боссут считает, что Архимед обнаружил центроид плоских фигур, но ничего не говорит о твердых телах.

Свойства

Геометрический центроид выпуклого объекта всегда лежит в объект. У невыпуклого объекта центр тяжести может находиться за пределами самой фигуры. Центроид кольца кольца или чаши, например, лежит в центральной пустоте объекта.

Если центроид определен, он является фиксированной точкой всех изометрий в его группе симметрии. В частности, геометрический центр тяжести объекта лежит на пересечении всех его гиперплоскостей симметрии . Центроид многих фигур (правильный многоугольник, правильный многогранник, цилиндр, прямоугольник, ромб, круг, сфера, эллипс, эллипсоид, суперэллипс, суперэллипсоид и т. д.) может определяться только этим принципом.

В частности, центр тяжести параллелограмма является точкой пересечения его двух диагоналей . Это не относится к другим четырехугольникам .

. По той же причине центроид объекта с трансляционной симметрией не определен (или находится за пределами ограничивающего пространства), поскольку сдвиг не имеет фиксированной точки..

Примеры

Центроид треугольника – это пересечение трех медиан треугольника (каждая медиана соединяет вершину с серединой противоположной стороны).

Другие свойства центроида треугольника см. В ниже.

Определение местоположения

Метод отвесной линии

Центроид равномерно плотной плоской пластинки, например, на рисунке (а) ниже, может быть определено экспериментально с использованием отвеса и штифта для нахождения совмещенного центра масс тонкого тела однородной плотности, имеющего такую ​​же форму. Корпус удерживается штифтом, вставленным в точку за пределами предполагаемого центра тяжести, таким образом, что он может свободно вращаться вокруг штифта; затем отвес снимается со штифта (рисунок b). Положение отвеса отслеживается на поверхности, и процедура повторяется со шпилькой, вставленной в любой другой точке (или в нескольких точках) за пределами центроида объекта. Единственной точкой пересечения этих линий будет центроид (рисунок c). При условии, что тело имеет однородную плотность, все линии, построенные таким образом, будут включать центроид, и все линии будут пересекаться в одном и том же месте.

Этот метод может быть расширен (теоретически) на вогнутые формы, где центр тяжести может лежать вне формы, и фактически к твердым телам (опять же с однородной плотностью), где центр тяжести может находиться внутри тела. (Виртуальные) положения отвесов должны быть записаны другими способами, кроме их рисования по форме.

Метод балансировки

Для выпуклых двумерных форм центр тяжести может быть найден путем уравновешивания формы на меньшей форме, такой как вершина узкого цилиндра. Центроид находится где-то в пределах диапазона контакта между двумя формами (и точно в точке, где форма будет балансировать на штифте). В принципе, для определения центра тяжести с произвольной точностью можно использовать все более узкие цилиндры. На практике воздушные потоки делают это невозможным. Однако, отмечая диапазон перекрытия нескольких весов, можно достичь значительного уровня точности.

конечного набора точек

Центроид конечного набора k { displaystyle k}точек x 1, x 2, …, Xk { displaystyle mathbf {x} _ {1}, mathbf {x} _ {2}, ldots, mathbf {x} _ {k}}в R п { displaystyle mathbb {R} ^ {n}}равно

C = x 1 + x 2 + ⋯ + xkk { displaystyle mathbf {C} = { frac { mathbf {x} _ {1} + mathbf {x} _ {2} + cdots + mathbf {x} _ {k}} {k}}}.

Эта точка минимизирует сумму квадратов евклидовых расстояний между собой и каждая точка в наборе.

Путем геометрического разложения

Центроид плоской фигуры X { displaystyle X}можно вычислить, разделив его на конечное число более простых фигур X 1, X 2,…, X n { displaystyle X_ {1}, X_ {2}, dots, X_ {n}}, вычисление центроида C i { displaystyle C_ {i}}и области A i { displaystyle A_ {i}}каждой части, а затем вычисление

C x = ∑ C ix A я ∑ A я, С Y знак равно ∑ С iy A я ∑ A я { displaystyle C_ {x} = { frac { sum C_ {i_ {x}} A_ {i}} { sum A_ {i}} }, C_ {y} = { frac { sum C_ {i_ {y}} A_ {i}} { sum A_ {i}}}}

Отверстия на рисунке X { displaystyle X }, перекрытия между частями или части, выходящие за пределы рисунка, могут быть обработаны с использованием отрицательных областей A i { displaystyle A_ {i}}. А именно, меры A i { displaystyle A_ {i}}следует принимать с положительными и отрицательными знаками таким образом, чтобы сумма знаков A i { displaystyle A_ {i}}для всех частей, которые окружают данную точку p { displaystyle p}равно 1, если p { displaystyle p}принадлежит X { displaystyle X}, иначе 0.

Например, рисунок ниже (а) легко разделить на квадрат и треугольник, оба с положительной площадью; и круглое отверстие с отрицательной площадью (b).

(a) 2D-объект (b) Объект, описанный с использованием более простых элементов (c) Центроиды элементов объекта

Центроид каждой части можно найти в любом списке центроидов простых форм (в). Тогда центроид фигуры – это средневзвешенное значение трех точек. Горизонтальное положение центроида от левого края рисунка

x = 5 × 10 2 + 13,33 × 1 2 10 2 – 3 × π 2,5 2 10 2 + 1 2 10 2 – π 2,5 2 ≈ 8,5 единицы измерения. { displaystyle x = { frac {5 times 10 ^ {2} +13,33 times { frac {1} {2}} 10 ^ {2} -3 times pi 2,5 ^ {2}} {10 ^ {2} + { frac {1} {2}} 10 ^ {2} – pi 2,5 ^ {2}}} приблизительно 8,5 { mbox {units}}.}

Вертикальное положение центроид находится точно так же.

Та же формула верна для любых трехмерных объектов, за исключением того, что каждый A i { displaystyle A_ {i}}должен быть объемом X i { displaystyle X_ {i}}, а не его площадь. Это также справедливо для любого подмножества R d { displaystyle mathbb {R} ^ {d}}, для любого измерения d { displaystyle d}с областями, замененными на d { displaystyle d}-размерные меры частей.

По интегральной формуле

Центроид подмножества X из R n { displaystyle mathbb {R} ^ {n}}также может быть вычислен интегралом

C = ∫ xg (x) dx ∫ g (x) dx { displaystyle C = { frac { int xg (x) ; dx} { int g (x) ; dx}}}

где интегралы берутся по всему пространству R n { displaystyle mathbb {R} ^ {n}}, а g – характеристика функция подмножества, которая равна 1 внутри X и 0 вне его. Обратите внимание, что знаменатель – это просто мера множества X. Эта формула не может быть применена, если у множества X есть нулевая мера или если любой интеграл расходится.

Другая формула для центроида:

C k = ∫ z S k (z) dz ∫ S k (z) dz { displaystyle C_ {k} = { frac { int zS_ {k } (z) ; dz} { int S_ {k} (z) ; dz}}}

где C k – это k-я координата C, а S k (z) – это мера пересечения X с гиперплоскостью, определяемая уравнением x k = z. И снова знаменатель – это просто мера X.

Для плоской фигуры, в частности, координаты центра масс:

C x = ∫ x S y (x) dx A { displaystyle C _ { mathrm {x}} = { frac { int xS _ { mathrm {y}} (x) ; dx} {A}}}

C y = ∫ y S x (y) dy A { displaystyle C _ { mathrm {y}} = { frac { int yS _ { mathrm {x}} (y) ; dy} {A}}}

где A – площадь фигуры X; S y (x) – длина пересечения X с вертикальной линией на абсциссе x; и S x (y) – аналогичная величина для поменяемых местами осей.

ограниченной области

Центроид (x ¯, y ¯) { displaystyle ({ bar {x}}, ; { bar {y}}) }области, ограниченной графиками непрерывных функций f { displaystyle f}и g { displaystyle g}такое, что f (x) ≥ g (x) { displaystyle f (x) geq g (x)}на интервале [a, b] { displaystyle [a, b]}, a ≤ x ≤ b { displaystyle a leq x leq b}, задается как

x ¯ = 1 A ∫ abx [f (х) – g (x)] dx { displaystyle { bar {x}} = { frac {1} {A}} int _ {a} ^ {b} x [f (x) -g ( х)] ; dx}

y ¯ = 1 A ∫ ab [f (x) + g (x) 2] [f (x) – g (x)] dx, { displaystyle { bar {y }} = { frac {1} {A}} int _ {a} ^ {b} left [{ frac {f (x) + g (x)} {2}} right] [f ( x) -g (x)] ; dx,}

где A { displaystyle A}– площадь региона (заданная как ∫ ab [f (x) – g (x)] dx { displaystyle int _ {a} ^ {b} [f (x) -g (x)] ; dx}).

L-образного объекта

Это метод определения ce ntroid L-образного объекта.

1. Разделите фигуру на два прямоугольника, как показано на рис. 2. Найдите центроиды этих двух прямоугольников, нарисовав диагонали. Нарисуйте линию, соединяющую центроиды. Центроид фигуры должен лежать на этой линии AB.
2. Разделите фигуру на два других прямоугольника, как показано на рис. 3. Найдите центроиды этих двух прямоугольников, нарисовав диагонали. Нарисуйте линию, соединяющую центроиды. Центроид L-образной формы должен лежать на этой прямой CD.
3. Поскольку центр тяжести формы должен лежать как вдоль AB, так и вдоль CD, он должен быть на пересечении этих двух линий в точке O. точка O может находиться внутри или снаружи L-образного объекта.

треугольника

Центроид треугольника – это точка пересечения его медиан (линии соединение каждой вершины со средней точкой противоположной стороны). Центроид делит каждую из медиан в соотношении 2: 1, то есть находится на расстояния от каждой стороны до противоположной вершины (см. Рисунки справа). Его декартовы координаты – это означает координат трех вершин. То есть, если три вершины равны L = (x L, y L), { displaystyle L = (x_ {L}, y_ {L}),}M = (x M, y M), { displaystyle M = (x_ {M}, y_ {M}),}и N = (x N, y N), { displaystyle N = (x_ {N}, y_ {N}),}, то центроид (обозначенный здесь C, но чаще всего обозначаемый G в геометрии треугольника ) равен

C = 1 3 (L + M + N) = (1 3 (x L + x M + x N), 1 3 (y L + y M + y N)). { displaystyle C = { frac {1} {3}} (L + M + N) = left ({ frac {1} {3}} (x_ {L} + x_ {M} + x_ {N) }), ; ; { frac {1} {3}} (y_ {L} + y_ {M} + y_ {N}) right).}

Следовательно, центроид находится в 1 3: 1 3: 1 3 { displaystyle { tfrac {1} {3}}: { tfrac {1} {3}}: { tfrac {1} {3}}}дюйм барицентрические координаты.

В трилинейных координатах центроид может быть выражен любым из этих эквивалентных способов с точки зрения длин сторон a, b, c и углов при вершинах L, M, N:

C = 1 a: 1 b: 1 c = bc: ca: ab = csc ⁡ L: csc ⁡ M: csc ⁡ N = cos ⁡ L + cos ⁡ M ⋅ cos ⁡ N: cos ⁡ M + cos ⁡ N ⋅ cos ⁡ L: cos ⁡ N + cos ⁡ L ⋅ cos ⁡ M = sec ⁡ L + sec ⁡ M ⋅ sec ⁡ N: sec ⁡ M + sec ⁡ N ⋅ sec ⁡ L: sec ⁡ N + sec ⁡ L ⋅ sec ⁡ М. { displaystyle { begin {align} C = { frac {1} {a}}: { frac {1} {b}}: { frac {1} {c}} = bc: ca: ab = csc L: csc M: csc N \ [6pt] = cos L + cos M cdot cos N: cos M + cos N cdot cos L: cos N + cos L cdot cos M \ [6pt] = sec L + sec M cdot sec N: sec M + sec N cdot sec L: sec N + sec L cdot sec M. end {выровнено }}}

Центроид также является физическим центром масс, если треугольник сделан из однородного листа материала; или если вся масса сосредоточена в трех вершинах и поровну разделена между ними. С другой стороны, если масса распределена по периметру треугольника с равномерной линейной плотностью, то центр масс находится в центре Шпикера (центр среднего треугольника ), который (в общем случае) не совпадает с геометрическим центром тяжести полного треугольника.

Площадь треугольника в 1,5 раза превышает длину любой стороны, умноженную на перпендикулярное расстояние от стороны до центроида.

Центроид треугольника лежит на его прямой Эйлера между его ортоцентром H и его центром описанной окружности O, ровно в два раза ближе к последнему, чем к первому:

CH ¯ = 2 CO ¯. { displaystyle { overline {CH}} = 2 { overline {CO}}.}

Кроме того, для инцентратора I и центра по девяти точкам N, имеем

CH ¯ = 4 CN ¯ CO ¯ = 2 CN ¯ IC ¯ < H C ¯ I H ¯ < H C ¯ I C ¯ < I O ¯ {displaystyle {begin{aligned}{overline {CH}}=4{overline {CN}}\[5pt]{overline {CO}}=2{overline {CN}}\[5pt]{overline {IC}}<{overline {HC}}\[5pt]{overline {IH}}<{overline {HC}}\[5pt]{overline {IC}}<{overline {IO}}end{aligned}}}

Если G – центр тяжести треугольника ABC, то:

(Площадь △ ABG) = (Площадь △ ACG) = (Площадь △ BCG) = 1 3 (Площадь △ ABC) { displaystyle displaystyle ({ text {Площадь}} треугольник mathrm {ABG}) = ({ text {Площадь}} треугольник mathrm {ACG}) = ({ text {Площадь}} треугольник mathrm {BCG}) = { frac {1} {3}} ({ text {Площадь}} треугольник mathrm {ABC })}

изогонально сопряженным центроиду треугольника является его симедианная точка.

Любая из трех медиан, проходящих через центроид, делит площадь треугольника пополам. Это неверно для других линий, проходящих через центроид; наибольшее отклонение от деления на равные площади происходит, когда линия, проходящая через центр тяжести, параллельна стороне треугольника, образуя меньший треугольник и трапецию ; в этом случае площадь трапеции равна 5/9 площади исходного треугольника.

Пусть P – любая точка на плоскости треугольника с вершинами A, B, C и центроидом G. Тогда сумма Квадрат расстояний P от трех вершин превышает сумму квадратов расстояний от центроида G до вершин в три раза больше квадрата расстояния между P и G:

PA 2 + PB 2 + PC 2 = GA 2 + GB 2 + GC 2 + 3 PG 2. { displaystyle PA ^ {2} + PB ^ {2} + PC ^ {2} = GA ^ {2} + GB ^ {2} + GC ^ {2} + 3PG ^ {2}.}

сумма квадратов сторон треугольника равна троекратной сумме квадратов расстояний от центроида до вершин:

AB 2 + BC 2 + CA 2 = 3 (GA 2 + GB 2 + GC 2). { displaystyle AB ^ {2} + BC ^ {2} + CA ^ {2} = 3 (GA ^ {2} + GB ^ {2} + GC ^ {2}).}

Центроид треугольника равен точка, которая максимизирует произведение ориентированных расстояний от точки до сторон треугольника.

Пусть ABC – треугольник, пусть G – его центр тяжести, а D, E и F – середины BC, CA и AB соответственно. Для любой точки P в плоскости ABC тогда

P A + P B + P C ≤ 2 (P D + P E + P F) + 3 P G. { displaystyle PA + PB + PC leq 2 (PD + PE + PF) + 3PG.}

многоугольника

Центроид несамопересекающегося замкнутого многоугольника, определяемое n вершинами (x 0,y0), (x 1,y1),…, (x n − 1, y n − 1), является точкой ( C x, C y), где

C x = 1 6 A ∑ i = 0 n – 1 (xi + xi + 1) (xiyi + 1 – xi + 1 yi), { displaystyle C _ { mathrm {x}} = { frac {1} {6A}} sum _ {i = 0} ^ {n-1} (x_ {i} + x_ {i + 1}) (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}),}и

C y = 1 6 A ∑ i = 0 п – 1 (yi + yi + 1) (xiyi + 1 – xi + 1 yi), { displaystyle C _ { mathrm {y}} = { frac {1} {6A}} sum _ {i = 0 } ^ {n-1} (y_ {i} + y_ {i + 1}) (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}),}

и где A – подписанная площадь многоугольника, как описано формулой шнурка :

A = 1 2 ∑ i = 0 n – 1 (xiyi + 1 – xi + 1 yi). { displaystyle A = { frac {1} {2}} sum _ {i = 0} ^ {n-1} (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}).}

В этих формулах предполагается, что вершины пронумерованы в порядке их появления по периметру многоугольника; кроме того, вершина (x n, y n) предполагается такой же, как (x 0, y 0), значение i + 1 { displaystyle i + 1}в последнем случае должно выполняться в цикле до i = 0 { displaystyle i = 0}. (Если точки пронумерованы по часовой стрелке, площадь A, вычисленная, как указано выше, будет отрицательной; однако координаты центроида будут правильными даже в этом случае.)

Конуса или пирамиды

Центроид конуса или пирамиды расположен на отрезке линии, который соединяет вершину с центроидом основания. Для твердого конуса или пирамиды центр тяжести составляет 1/4 расстояния от основания до вершины. Для конуса или пирамиды, представляющих собой просто оболочку (полую) без основания, центроид составляет 1/3 расстояния от плоскости основания до вершины.

тетраэдра и n-мерного симплекса

A тетраэдр представляет собой объект в трехмерном пространстве, имеющий четыре треугольника в качестве его граней. Отрезок, соединяющий вершину тетраэдра с центром тяжести противоположной грани, называется срединной, а отрезок, соединяющий середины двух противоположных ребер, называется бимедианой. Следовательно, есть четыре медианы и три бимедианы. Эти семь отрезков пересекаются в центре тетраэдра. Медианы делятся на центроид в соотношении 3: 1. Центроид тетраэдра – это середина между его точкой Монжа и центром описанной области (центром описанной сферы). Эти три точки определяют линию Эйлера тетраэдра, которая аналогична прямой Эйлера треугольника.

Эти результаты обобщаются на любой n-мерный симплекс следующим образом. Если набор вершин симплекса равен v 0,…, vn { displaystyle {v_ {0}, ldots, v_ {n}}}, то рассматриваемые вершины как векторов, центроид равен

C = 1 n + 1 ∑ i = 0 nvi. { displaystyle C = { frac {1} {n + 1}} sum _ {i = 0} ^ {n} v_ {i}.}

Геометрический центроид совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как n + 1 равных масс.

полушария

Центроид твердого полушария (т.е. половина твердого шара) делит отрезок прямой, соединяющий центр шара с полюсом полушария в соотношении 3: 5 (т.е. лежит на 3/8 пути от центра до полюса). Центроид полого полушария (то есть половина полой сферы) делит отрезок прямой, соединяющий центр сферы с полюсом полушария пополам.

См. Также

• Центр Чебышева
• Среднее Фреше
• Алгоритм k-средних
• Список центроидов
• Определение центра масс
• Медоид
• Теорема Паппа о центроидах
• Спектральный центроид
• Центр треугольника

Примечания

Ссылки

• Альтшиллер-Корт, Натан (1925), Геометрия колледжа: Введение в современную геометрию треугольника и круга (2-е изд..), Нью-Йорк: Barnes Noble, LCCN 52013504
• Бурк, Пол (июль 1997 г.). «Расчет площади и центра тяжести многоугольника».
• Джонсон, Роджер А. (2007), Advanced Euclidean Geometry, Dover
• Kay, David C. (1969), College Geometry, Нью-Йорк : Holt, Rinehart and Winston, LCCN 69012075
• Larson, Roland E.; Хостетлер, Роберт П.; Эдвардс, Брюс Х. (1998), Исчисление одной переменной (6-е изд.), Houghton Mifflin Company
• Protter, Murray H.; Морри, младший, Чарльз Б. (1970), College Calculus with Analytic Geometry (2-е изд.), Чтение: Addison-Wesley, LCCN 76087042

External ссылки

• Энциклопедия центров треугольников Кларка Кимберлинга. Центроид индексируется как X (2).
• Характеристическое свойство центроида в точке срезать узел
• Барицентрические координаты в точке разрезать узел
• Интерактивный анимация, показывающая Центроид треугольника и Построение центроида с компасом и линейкой
• Экспериментальное определение медиан и центроида треугольника в Эскизы динамической геометрии, интерактивный эскиз динамической геометрии с использованием симулятора гравитации Золушки.