Как найти центр в своем теле

Описан способ определения положения центров масс (центров тяжести, ЦТ) звеньев тела человека по Вильгельму Брауне и Отто Фишеру. Приведен пример определения ЦТ звеньев тела спортсмена в статическом положении при выполнении силовых упражнений.

Определение положения центров масс (центров тяжести) звеньев тела человека

Введение

Определение положения центров масс, а в нашем случае центров тяжести (ЦТ) звеньев тела человека необходимо для того, чтобы знать место приложения силы тяжести и рассчитать плечи силы тяжести. Это, в свою очередь, позволяет оценить моменты силы тяжести, действующие относительно центров суставов тела человека.

Другими словами, для определения направленности упражнения (то есть выявления групп мышц, которые работают при выполнении упражнения) необходимо знать, где расположены ЦТ звеньев тела человека.

Существует несколько способов определения положения ЦТ звеньев тела человека. Опишем один из них.

Способ определения ЦТ звеньев тела человека

В конце XIX биомеханики осознали, что для расчета сил, действующих относительно суставов в теле человека, нужно знать массы звеньев и расположение ЦТ звеньев тела человека. В предыдущих записях я рассказала о том, каким способом, зная массу тела человека рассчитать массу звеньев человека. Теперь поговорим о том, как определить положение ЦТ звена.

С этой целью нужно помнить следующее определение ЦТ твердого тела.

Понятие ЦТ твердого тела

Центр тяжести твердого тела – это точка, относительно которой сумма моментов силы тяжести, действующих по часовой стрелке равна сумме моментов силы тяжести, действующих против часовой стрелки.

История разработки способа определения ЦТ звеньев тела человека

На основе этого понятия Вильгельм Брауне и Отто Фишер (W. Braune, O. Fisher, 1889) предложили метод нахождения положения ЦТ звеньев тела человека. С этой целью они расчленяли замороженные трупы на отдельные звенья. После этого ученые уравновешивали звенья тела человека на острие призмы. И таким образом определяли точку равновесия, которая и являлась ЦТ звена. В результате этих экспериментов В. Брауне и О. Фишер нашли коэффициенты, использование которых позволяет определить локализацию ЦТ звеньев тела человека.

В таблице 1 представлено положение ЦТ звеньев тела по В. Брауне и О. Фишеру (1889).

Таблица 1 – Расположение ЦТ звеньев тела человека (W. Braune, O. Fisher, 1889)

Звено	Измерение длины звена или положение ЦТ звена	Положение ЦТ звена	Относительное расстояние ЦТ звена от проксимального конца звена
Голова		ЦТ расположен над верхним краем наружного слухового отверстия
Туловище	от центра плечевого сустава до центра тазобедренного сустава		0,44
Плечо	от центра плечевого сустава до центра локтевого сустава		0,47
Предплечье	от центра локтевого сустава до центра лучезапястного сустава		0,42
Кисть (с полусогнутыми пальцами		ЦТ расположен в области пястно-фалангового сустава третьего пальца
Бедро	от центра тазобедренного сустава до центра коленного сустава		0,44
Голень	от центра коленного сустава до центра голеностопного сустава		0,42
Стопа (пальца	от пяточного бугра до конца большого пальца		0,44

Чтобы понять, как использовать коэффициенты, полученные В. Брауне и О. Фишером для определения положения ЦТ звена, рассмотрим следующий пример.

Пример

Найти положение ЦТ тяжести звеньев тела человека по его фотографии (рисунок 1) на основе коэффициентов, рассчитанных В. Брауне и О. Фишером (1889) и представленных в таблице 1.

Решение

1. Вначале нужно сфотографировать статическое положение человека при выполнении упражнения и распечатать эту фотографию. На фотографии отметить центры вращения в суставах (на рисунке 1 они отмечены точками).
2. После этого соединить прямой линией центры суставов:

• плечевого и локтевого (для измерения длины плеча);
• локтевого и лучезапястного (для измерения длины предплечья);
• плечевого и тазобедренного (для измерения длины туловища);
• тазобедренного и коленного (для измерения длины бедра);
• коленного и голеностопного (для измерения длины голени);
• пяточного бугра и носка стопы (для измерения длины стопы) (рисунок 2).

1. Измерить длину звеньев (например, в мм) и занести полученные значения в столбец 2 таблицы 2.

Например, длина туловища, измеренная по фотографии равна 40 мм, а длина плеча – 20 мм и т.д. (таблица 2). Хочу отметить, что при распечатке фотографии из примера в другом масштабе могут быть другие значения длины звеньев тела человека, но это никак не повлияет на итоговые результаты.

1. После этого умножить значения длины звеньев (столбец 2) на коэффициенты К (столбец 3), найденные В. Брауне и О. Фишером.
2. Полученные значения отложить на прямой, соединяющей центры суставов, начиная от проксимального сустава (рисунок 3).

Например, при определении ЦТ туловища значение R=17,6 мм нужно отложить от плечевого сустава; при определении ЦТ бедра R=13,2 мм нужно отложить от тазобедренного сустава и т.д. В таблице 2 в столбце 5 указано, какой сустав считать проксимальным при определении значения R.

Таблица 2 – Пример определения ЦТ звеньев тела человека, изображенного на рисунке 1.

Звено	L, мм	К	R=LK, мм	Проксимальный сустав
1	2	3	4	5
Голова	—	—	ЦТ расположен над верхним краем наружного слухового отверстия	—
Туловище	40	0,44	17,6	Плечевой
Плечо	20	0,47	9,4	Плечевой
Предплечье	13	0,42	5,46	Локтевой
Кисть	—	—	—	—
Бедро	30	0,44	13,2	Тазобедренный
Голень	30	0,42	12,6	коленный
Стопа	25	0,44	11	Пяточный бугор

Обозначения: L – длина звена; k – коэффициент; R – расстояние от проксимального сустава до ЦТ звена

Следует заметить, что положение ЦТ туловища определяется по-разному в зависимости от того, выпрямлено оно или находится в согнутом состоянии.

При прямом положении туловища (рисунок 1), для определения положения его ЦТ нужно соединить прямой линией плечевой и тазобедренный суставы. После этого отложить на прямой линии, соединяющей плечевой и тазобедренный суставы значение R для туловища (таблица 2). Проксимальным считать плечевой сустав.

Если тело человека сильно изогнуто, например, при использовании «моста» при жиме штанги лежа, или при выполнении гимнастического «моста», после нахождения положения ЦТ на прямой, соединяющей плечевой и тазобедренный суставы, необходимо через середину туловища провести дугу, которая будет соответствовать изгибу тела. Из точки на прямой восстановить перпендикуляр, пересекающий дугу. Место пересечения дуги и перпендикуляра считать ЦТ туловища (рисунок 4).

Конечно, в настоящее время существуют более точные методы определения ЦТ звеньев тела человека. Например, тот, который описан в книге «Биомеханика двигательного аппарата человека» (В.М. Зациорский, А.С. Аруин, В.Н. Селуянов, 1980). Однако для практических расчетов вполне подходит и способ расчета В. Брауне и О. Фишера.

Если Вам нужно определить положение ОЦТ (общего центра тяжести) тела человека, воспользуйтесь предлагаемой программой расчета положения ОЦТ.

Литература

1. Зациорский В.М., Аруин А.С., Селуянов В.Н. Биомеханика двигательного аппарата человека. – М.: Физкультура и спорт, 1981. – 144 с.
2. Котельникова Е.Г. Биомеханика. Методические указания к практическим занятиям. – Л. ГДОИФК, 1974. – 60 с.
3. Braune W. Fisher O.  In: Abhandlunger der mathermatishchphysischen Class der Konigl Sachsischen Gesellschaft der Wissenschaften . – 1889. – Bd. 26. – S. 561–672.

С уважением, А.В.Самсонова

Похожие записи:

---

Мышечно-сухожильный комплекс

Приведена рецензия на книгу  В.Т.Тураева и В.В. Тюпа «Мышечно-сухожильный комплекс: анатомия, биомеханика, спортивная практика» зав. кафедрой биомеханики НГУ…

---

Сила тяжести

Дано определение силы тяжести. Показано, что сила тяжести является частным случаем силы гравитации. Описаны факторы, определяющие силу тяжести:…

---

Сила

Дано определение силы в механике. Описаны факторы, определяющие действие на тело силы: направление, точка приложения и численное значение.

---

Типы телосложения (соматотип) по Башкирову

Описана краткая биография П.Н. Башкирова и его научные труды. Дается классификация типов телосложения человека: долихоморфного (астенического), мезоморфного…

---

Типы телосложения (конституции) по Э. Кречмеру

Описана биография Эрнста Кречмера – немецкого психиатра и психолога, разработавшего типологию тела человека. Дано описание типов телосложения…

---

Типы конституции женщин по И.Б. Галанту

Описана биография известного советского психиатра И.Б.Галанта, предложившего естественную систему конституциональных типов женщин. Дана характеристика предложенных И.Б.Галантом  конституциональных…

Вы можете прожить всю жизнь, не зная, где он находится. Но однажды разберетесь в этом — и многое станет более понятным. Центр обычно является самой чувствительной частью тела, при этом он хорошо просматривается как в статике, так и в динамике.

В статических позах — сидя, стоя или лежа, человек закрывает центр руками или поворотом туловища в некомфортных ситуациях, и выделяет, открывает в комфортных и безопасных. Например, все мы любим спать в какой-то определенной позе. В ней мы закрываем центр, как бы защищая его от неожиданного вторжения. Если центром является живот или грудь — люди спят на животе или в позе эмбриона, если спина — на спине, если голова — люди подкладывают руки под голову или свертываются калачиком.

Движение человека, как правило, начинается с центра и как бы закручивается вокруг него. Понаблюдайте внимательно и наверняка заметите, что один человек идет, горделиво неся вперед свою голову, кто-то движется, закручиваясь вокруг своей оси, кто-то основательно переступает ногами. При этом видно, какую часть тела человек несет, а какие просто тащит за собой.

Центр тела человек и украшать любит. Нередко мы особенно привязаны к какой-то части гардероба. Имеем по десять юбок или брюк, или кучу перчаток. Части гардероба тоже связаны с частями тела. Брюки у женщин связаны с ногами, а юбки с тазом, перчатки с руками и социальными контактами, шляпы и головные уборы с головой, шарфы — с шеей.

Если для человека главным в жизни являются контакты с другими людьми, его руки будут очень подвижными. Он будет постоянно привлекать внимание разнообразными жестами, потиранием, хрустом пальцев, сложным маникюром, кольцами и перстнями.

Всевозможные аксессуары, кажется, специально придуманы только для этого.

С годами центр тела может меняться. Решается какая-то проблема, уходит потребность в чем-либо, и тогда один центр уступает место другому. Плохо, когда центр остается всегда один. Обычно это означает, что человек мало совершенствовался, недостаточно изменился, обладает стандартным мышлением.

С изменением центра меняется быстрота движения, скорость, грация и пластика. В разных ситуациях центр может быть разным. Нормально, когда на работе человек центрируется на зоне головы, но настораживает, если «включается» живот. Можно предположить, что человек боится потерять работу или находится в постоянном стрессе.

К центру проще всего «подключиться», поэтому именно он оказывается особенно уязвим в случае энергетической агрессии. Наверное, вы замечали: в некомфортной ситуации у одних начинает болеть голова, у других сердце, у кого-то — живот. Это тоже один из критериев центра. В целях защиты его закрывают всевозможными амулетами.

Для чего нужно знать свой центр тела? Он одновременно и сила, и слабость человека. Пока человек находится в зоне своего центра, он эффективен и действует правильно. Стоит оказаться в не свойственной среде — и все буквально рассыпается. Это как играть в футбол на своем поле. Кроме того, центр — это еще система аргументации. Зная, каков центр тела у вашего оппонента, вы сможете легко говорить с ним на одном языке.

Человеку, который живет из головы, бесполезно говорить — «почувствуйте». Обращаясь к нему, апеллируйте к его логике, смело аргументируйте, выводите формулы, взвешивайте плюсы и минусы.

Устраиваясь на работу к начальнику, живущему из зоны рук, расскажите ему, как много для вас значит возможность работать в хорошем, сплоченном коллективе. Если перед вами основательный и крепко стоящий на ногах человек — опирайтесь на то, как ваш опыт и способности увеличат прибыль фирмы.

Чтобы узнать, что является центром тела человека, достаточно недолго понаблюдать, как он двигается, сидит, встает, ведет себя по отношению к пространству.

Какие же центры тела существуют и чаще всего встречаются у людей? Если центр — голова, перед вами человек мыслящий, логичный, пытающийся во всем найти свой смысл и действовать, все взвесив и продумав. Во всем он любит представить план действий. Изменения переносит с трудом. Отвергает любые проявления чувств, если они не подкреплены логикой. На все свои действия и действия других людей накладывает цензуру правильности. Общаясь с ним, обращайтесь к его логике, доказывайте свою правоту трезвым рассудком.

Шея. Этот человек постоянно находится в поиске нового — возможности, знакомства, встречи, ситуации. Он достаточно чувствителен к собственной выгоде. Хитер и изворотлив. Но при этом умен и может пережить любые кризисы и невзгоды легко и безболезненно, как барон Мюнхгаузен. С ним достаточно легко и интересно. Пытаясь заинтересовать такого человека, предложите нестандартное решение или то, что он еще никогда не делал, или просто выложите все карты. Такие люди очень любят выбирать.

Плечи. Люди с центром тела в них очень ответственны и терпеливы. Обычно жизнь такого человека — бесконечный груз и заботы за всех окружающих. Чаще это старшие дети в многодетных семьях, которые, вырастив младших, потом терпеливо тащат свои семьи, взрослых детей, да еще умудряются занимать ответственные посты на работе. Они довольно спокойны и рассудительны, но их рассудок «выключается», когда вы задаете им вопрос, почему, собственно, они так живут? Добиться чего-либо от них не сложно. Достаточно произнести сакраментальную фразу: «Ты же не можешь меня подвести? Я так рассчитывал на тебя!» Если такую фразу часто произносят в ваш адрес, подумайте, не слишком ли тяжела ноша на ваших плечах?

Руки. Самым важным в жизни является общение и взаимодействие с другими людьми. Общаясь с таким человеком, старайтесь подчеркивать вашу общность. Местоимение «мы» для этого человека звучит слаще, чем «я». Это превосходные люди команды. В жизни они многого достигают благодаря коммуникабельности. Слабость этого центра проявляется тогда, когда контакт с другими по каким-то причинам затруднен.

Грудь. Этот человек живет чувствами и только ими. Пока не иссушится поток чувств, ему везде и всегда будет комфортно. При этом неважно, какие чувства — хорошие или плохие, негативные или положительные. Ему хорошо просто от того, что они есть. Логика для него — пустой звук. Он внимательно выслушает ваши аргументы, но все равно сделает по-своему. Он способен многое создать и многое разрушить. Чем более эмоциональна ваша речь, тем более понятны вы будете такому собеседнику.

Спина. Люди с центровкой на спине очень нуждаются в поддержке. Они готовы свернуть горы, если чувствуют, что кто-то прикрывает сзади, но не способны сделать и шаг, если внезапно теряют это. Главным их мотивом в работе и в жизни является стремление заслужить чье-то одобрение. Желая добиться чего-то от таких людей, скажите им: «Давай, действуй, я прикрою!».

Таз. Люди, живущие из этой части тела, очень трепетно относятся к свободе, своей и окружающих. Они многое позволяют себе, действуя из собственной логики, замешанной на представлении о том, как оно должно быть. Их девиз: «Я делаю то, что хорошо мне!». Несмотря на эгоцентризм, они уважают свободу других. Они чувственны, сексуальны, раскованны, иногда даже невоздержанны. Гедонисты и эстеты по убеждению. Обращаясь к ним, играйте на тонких струнах их души, но не в коем случае не пытайтесь ограничить их свободу. Совершенно не выносят жестких рамок. Контрактные или договорные отношения для них не приемлемы, законы и правила написаны не для них, бухгалтерия — утомляет, а необходимость оплачивать счета повергает в ужас.

Ноги. Эти люди очень солидны, основательны, степенны и содержательны. Самым главным в их жизни является накопление капитала материального и духовного. В отличие от людей «шеи», они не мыслят сиюминутной выгоды, но строят отношения на века. Очень подвержены влиянию рода или клана. Обожают предметы роскоши. Предпочитают получать серьезное образование в лучших вузах и строят дома для внуков и правнуков, еще не обзаведясь детьми.

Люди такого типа очень падки на любые гарантии. Это любимые клиенты страховых агентов и солидных компаний. Вся их жизнь — создание своей базы. Их девиз: «Я сделал. Я построил. Мои внуки будут мной гордится». С ними можно иметь дело, они надежны и этого же требуют от других.

Центр тяжести треугольника

Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин

Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.

Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.

Как определить центр треугольника?

Как найти середину у треугольника?

Пересекающиеся медианы Найдите середину одной стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой A.

Как найти центр тяжести в треугольнике?

Центроид треугольника (также барицентр треугольника и центр тяжести треугольника) — точка пересечения медиан в треугольнике. . Центроид треугольника относится к замечательным точкам треугольника и он перечислен в энциклопедии центров треугольника Кларка Кимберлинга, как точка X(2).

Как найти центр тяжести в прямоугольном треугольнике?

Как найти координаты центра тяжести треугольника?

1. Рисуем треугольник ABC.
2. Ставим точку M – середина BC.
3. Ставим точку H – середина AC.
4. Пересечение BH и AM – и есть центр тяжести треугольника ABC.
5. Найдем его координаты (координаты точки O (xo, yo, zo) )

Как найти Инцентр?

Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник. Инцентр лежит ближе к вершине, расположенной напротив большей стороны треугольника.

Как найти центр тяжести тела неправильной формы?

Центр тяжести тела неправильной формы можно определить так: подвесить его за любую точку, и провести вертикальную линию по отвесу. Затем повернуть тело и повторить операцию. Точка пересечения двух прямых и есть центр тяжести тела.

Где находится центр тяжести призмы?

Так, центр тяжести призмы и цилиндра лежит на середине линии, соединяющей центры тяжести оснований. Центр тяжести шара совпадает с его геометрическим центром. Центр тяжести пирамиды (рис. 18, а) лежит на прямой, соединяющей центр тяжести площади основания с противоположной вершиной на расстоянии /4 высоты от основания.

Где находится центр тяжести у кольца?

Так, центр тяжести однородных диска и шара расположен в их центре, однородного цилиндра в точке на середине его оси; однородного параллелепипеда на пересечении его диагоналей и т, д. У всех однородных тел центр тяжести совпадает с центром симметрии. Центр тяжести может находиться вне тела, например, у кольца.

Как найти Центроид фигуры?

Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие – середины противополежащих сторон. Точка пересечения делит все три отрезка пополам.

Где находится центр тяжести однородного треугольника?

Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан, которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.

Где находится центр тяжести у трапеции?

Для произвольной трапеции (то есть она может быть прямоугольной, тупоугольной, равнобокой или любой другой) справедливо то, что центр ее тяжести лежит на прямой, которая соединяет середины оснований трапеции.

Как найти центр масс треугольника?

Как найти центр треугольника

Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.

Как найти длину медианы в прямоугольном треугольнике?

Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

Где находится центр круга?

Центр вписанной окружности треугольника (инцентр) — одна из замечательных точек треугольника, точка пересечения биссектрис треугольника. Центр вписанной в треугольник окружности также иногда называют инцентром.

Где лежит центр равнобедренного треугольника?

В равнобедренном треугольнике высота, проведенная к основанию, является серединным перпендикуляром. Следовательно, центр описанной около равнобедренного треугольника окружности будет лежать на серединном перпендикуляре, который является и высотой, и медианой, и биссектрисой угла при вершине.

Где лежит центр окружности?

Окружность, проходящая через все три вершины треугольника, называется его описанной окружностью. Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника.

Центры тяжести многоугольников и многогранников

Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.

Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.

В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.

Двумерный случай: многоугольники

На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:

• Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
• Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
• Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.

Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.

Центр масс системы точек

Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:

где — массы точек, — их радиус-векторы (задающие их положение относительно начала координат), и — искомый радиус-вектор центра масс.

В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:

Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке , в которой сумма моментов всех сил равна нулю. В данном случае это превращается в условие того, чтобы сумма радиус-векторов всех точек относительно точки , домноженных на массы соответствующих точек, равнялась нулю:

и, выражая отсюда , мы и получаем требуемую формулу.

Центр масс каркаса

Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.

Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.

Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:

где — точка-середина -ой стороны многоугольника, — длина -ой стороны, — периметр, т.е. сумма длин сторон.

Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).

Центр масс сплошной фигуры

Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.

Случай треугольника

Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:

Случай треугольника: доказательство

Приведём здесь элементарное доказательство, не использующее теорию интегралов.

Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian “Finding Centroids the Easy Way”.

Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.

Разобьём данный треугольник на четыре, соединив середины сторон, как показано на рисунке:

Четыре получившихся треугольника подобны треугольнику с коэффициентом .

Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого лежит в точке пересечения его диагоналей (поскольку это фигура, симметричная относительно обеих диагоналей, а, значит, её центр масс обязан лежать на каждой из двух диагоналей). Точка находится посередине общей стороны треугольников №1 и №2, а также лежит на медиане треугольника :

Пусть теперь вектор — вектор, проведённый из вершины к центру масс треугольника №1, и пусть вектор — вектор, проведённый из к точке (которая, напомним, является серединой стороны, на которой она лежит):

Наша цель — показать, что вектора и коллинеарны.

Обозначим через и точки, являющиеся центрами масс треугольников №3 и №4. Тогда, очевидно, центром масс совокупности этих двух треугольников будет точка , являющаяся серединой отрезка . Более того, вектор от точки к точке совпадает с вектором .

Искомый центр масс треугольника лежит посередине отрезка, соединяющего точки и (поскольку мы разбили треугольник на две части равных площадей: №1-№2 и №3-№4):

Таким образом, вектор от вершины к центроиду равен . С другой стороны, т.к. треугольник №1 подобен треугольнику с коэффициентом , то этот же вектор равен . Отсюда получаем уравнение:

Таким образом, мы доказали, что вектора и коллинеарны, что и означает, что искомый центроид лежит на медиане, исходящей из вершины .

Более того, попутно мы доказали, что центроид делит каждую медиану в отношении , считая от вершины.

Случай многоугольника

Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.

Окончательная формула получается следующей:

где — центроид -го треугольника в триангуляции заданного многоугольника, — площадь -го треугольника триангуляции, — площадь всего многоугольника.

Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники , где .

Случай многоугольника: альтернативный способ

С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка , а затем суммируются знаковые площади треугольников, образованных этой точкой и точками многоугольника: . Аналогичный приём можно применить и для поиска центра масс: только теперь мы будем суммировать центры масс треугольников , взятых с коэффициентами, пропорциональными их площадям, т.е. итоговая формула для центра масс такова:

где — произвольная точка, — точки многоугольника, — центроид треугольника , — знаковая площадь этого треугольника, — знаковая площадь всего многоугольника (т.е. ).

Трёхмерный случай: многогранники

Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:

• Центр масс системы точек — вершин многогранника.
• Центр масс каркаса — рёбер многогранника.
• Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
• Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.

Центр масс системы точек

Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:

который в случае равных масс превращается в среднее арифметическое координат всех точек.

Центр масс каркаса многогранника

Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.

Центр масс поверхности многогранника

Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.

Центр масс сплошного многогранника

Случай тетраэдра

Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.

Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).

Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.

Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:

(это можно вывести из того факта, что центроид делит медианы в отношении )

Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.

Случай произвольного многогранника

Перейдём теперь к общему случаю — случаю произвольного многогранника.

Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.

[spoiler title=”источники:”]

http://topobzor10.ru/kak-opredelit-tsentr-treugolnika

http://e-maxx.ru/algo/gravity_center

[/spoiler]

Анатомия и физиология позвоночника

Позвоночник человека – это очень непростой механизм, правильная работа которого влияет на функционирование всех остальных механизмов организма.

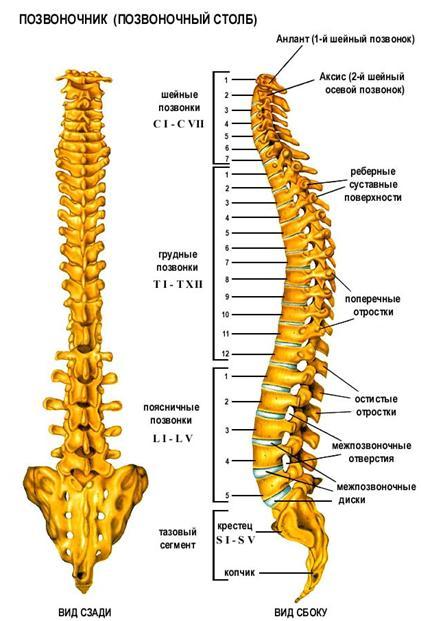
Позвоночник (от лат. «columna vertebralis», синоним – позвоночный столб) состоит из 32 – 33 позвонков (7 шейных, 12 грудных, 5 поясничных, 5 крестцовых, соединенных в крестец, и 3 – 4 копчиковых), между которыми расположены 23 межпозвоночных диска.

Связочно-мышечный аппарат, межпозвоночные диски, суставы соединяют позвонки между собой. Они позволяют удерживать его в вертикальном положении и обеспечивают необходимую свободу движения. При ходьбе, беге и прыжках эластичные свойства межпозвоночных дисков, значительно смягчают толчки и сотрясения, передаваемые на позвоночник, спинной и головной мозг.

Физиологические изгибы тела создают позвоночнику дополнительную упругость и помогают смягчать нагрузку на позвоночный столб.

Позвоночник является главной опорной структурой нашего тела. Без позвоночника человек не мог бы ходить и даже стоять. Другой важной функцией позвоночника является защита спинного мозга. Большая частота заболеваний позвоночника у современного человека обусловлена, главным образом, его «прямохождением», а также высоким уровнем травматизма.

Отделы позвоночника: В позвоночнике различают шейный, грудной, поясничный отделы, крестец и копчик. В процессе роста и развития позвоночника формируется шейный и поясничный лордозы, грудной и крестцово – копчиковый кифозы, превращающие позвоночник в «пружинящую систему», противостоящую вертикальным нагрузкам. В медицинской терминологии, для краткости, для обозначения шейных позвонков используется латинская буква «С» – С1 – С7, для обозначения грудных позвонков – «Th» – Th1 – Th12, поясничные позвонки обозначаются буквой «L» – L1 – L5.

Шейный отдел. Это самый верхний отдел позвоночного столба. Он отличается особой подвижностью, что обеспечивает такое разнообразие и свободу движения головы. Два верхних шейных позвонка с красивыми названиями атлант и аксис, имеют анатомическое строение, отличное от строения всех остальных позвонков. Благодаря наличию этих позвонков, человек может совершать повороты и наклоны головы.

Грудной отдел. К этому отделу прикрепляются 12 пар рёбер. Грудной отдел позвоночника участвует в формировании задней стенки грудной клетки, которая является вместилищем жизненно важных органов. В связи с этим грудной отдел позвоночника малоподвижен.

Поясничный отдел. Этот отдел состоит из самых массивных позвонков, так как на них лежит самая большая нагрузка. У некоторых людей встречается шестой поясничный позвонок. Это явление врачи называют люмбализацией. Но в большинстве случаев такая аномалия не имеет клинического значения. 8-10 позвонков срастаются, образуя крестец и копчик.

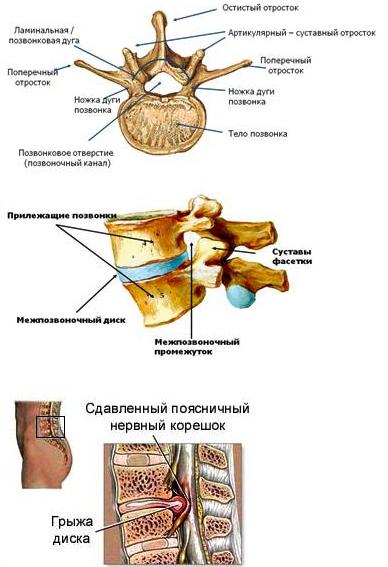Позвонок состоит из тела, дуги, двух ножек, остистого, двух поперечных и четырёх суставных отростков. Между дугой, телом и ножками позвонков находятся позвонковые отверстия, из которых формируется позвоночный канал.  Между телами двух смежных позвонков располагается межпозвонковый диск, состоящий из фиброзного кольца и пульпозного ядра и выполняющий 3 функции: амортизация, удержание смежных позвонков, обеспечение подвижности тел позвонков. Вокруг ядра располагается многослойное фиброзное кольцо, которое удерживает ядро в центре и препятствует сдвиганию позвонков в сторону относительно друг друга. Фиброзное кольцо имеет множество слоев и волокон, перекрещивающихся в трех плоскостях. В нормальном состоянии фиброзное кольцо образовано очень прочными волокнами. Однако в результате дегенеративного заболевания дисков (остеохондроза) происходит замещение волокон фиброзного кольца на рубцовую ткань. Волокна рубцовой ткани не обладают такой прочностью и эластичностью как волокна фиброзного кольца. Это ведет к ослаблению межпозвоночного диска и при повышении внутридискового давления может приводить к разрыву фиброзного кольца. Значительное повышение давления внутри межпозвоночных дисков может привести к разрыву фиброзного кольца и выходу части пульпозного ядра за пределы диска. Так формируется грыжа диска, которая может приводить к сдавлаванию нервных структур, что вызывает, в свою очередь появление болевого синдрома и неврологических нарушений.

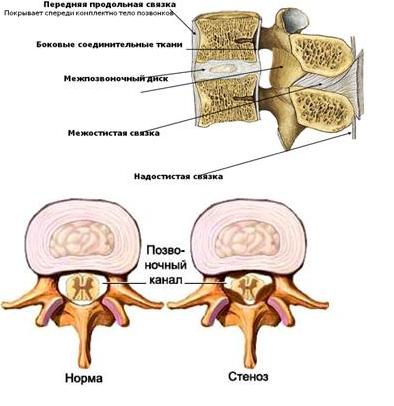Связочный аппарат представлен передней и задней продольными, над – и межостистыми связками, жёлтыми, межпоперечными связками и капсулой межпозвонковых суставов. Два позвонка с межпозвоночным диском и связочным аппаратом представляют позвоночный сегмент. При разрушении межпозвоночных дисков и суставов связки стремятся компенсировать повышенную патологическую подвижность позвонков (нестабильность), в результате чего происходит гипертрофия связок.Этот процесс ведет к уменьшению просвета позвоночного канала, в этом случае даже маленькие грыжи или костные наросты (остеофиты) могут сдавливать спинной мозг и корешки. Такое состояние получило название стеноза позвоночного канала. Для расширения позвоночного канала производится операция декомпрессии нервных структур.

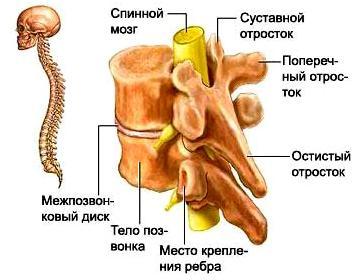В позвоночном канале расположен спинной мозг и корешки «конского хвоста». Спинной мозг начинается от головного мозга и заканчивается на уровне промежутка между первым и вторым поясничными позвонками коническим заострением. Далее от спинного мозга в канале проходят спинномозговые нервные корешки, которые формируют так называемый «конский хвост». Спинной мозг окружён твёрдой, паутинной и мягкой оболочками и фиксирован в позвоночном канале корешками и клетчаткой. Твердая мозговая оболочка формирует герметичный соединительнотканный мешок (дуральный мешок), в котором расположены спинной мозг и несколько сантиметров нервных корешков.Спинной мозг в дуральном мешке омывает спинномозговая жидкость (ликвор).  От спинного мозга отходит 31 пара нервных корешков. Из позвоночного канала нервные корешки выходят через межпозвоночные (фораминарные) отверстия, которые образуются ножками и суставными отростками соседних позвонков. У человека, так же как и у других позвоночных, сохраняется сегментарная иннервация тела. Это значит, что каждый сегмент спинного мозга иннервирует определенную область организма. Например, сегменты шейного отдела спинного мозга иннервируют шею и руки, грудного отдела – грудь и живот, поясничного и крестцового – ноги, промежность и органы малого таза (мочевой пузырь, прямую кишку).

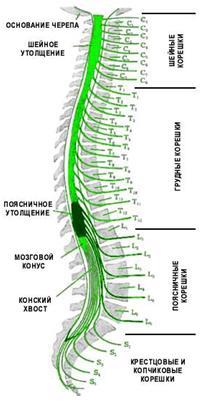По периферическим нервам нервные импульсы поступают от спинного мозга ко всем органам нашего тела для регуляции их функции. Информация от органов и тканей поступает в центральную нервную систему по чувствительным нервным волокнам. Большинство нервов нашего организма имеют в своем составе чувствительные, двигательные и вегетативные волокна. Спинной мозг имеет два утолщения: шейное и поясничное. Поэтому межпозвоночные грыжи шейного отдела позвоночника более опасны, чем поясничного. Врач, определяя в какой области тела, появились расстройства чувствительности или двигательной функции, может предположить, на каком уровне произошло повреждение спинного мозга.