Правильный многоугольник
- формулы, признаки и свойства правильного многоугольника
- формулы правильного n-угольника
- правильный треугольник
- правильный четырехугольник
- правильный шестиугольник
- правильный восьмиугольник
Формулы, признаки и свойства правильного многоугольника
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.
a1=a2=a3=…=an-1=an
,
α1=α2=α3=…=αn-1=αn
где a1…an — длины сторон правильного многоугольника,
α1…αn — внутренние углы между стронами правильного многоугольника.
Основные свойства правильного многоугольника
- Все стороны равны:
a1=a2=a3=…=an-1=an - Все углы равны:
α1=α2=α3=…=αn-1=αn - Центр вписанной окружности Oв совпадает с центром описанной окружности Oо, что и образуют центр многоугольника O.
- Сумма всех углов n-угольника равна:180°·n-2
- Сумма всех внешних углов n-угольника равна 360°: β1+β2+β3+…+βn-1+βn=360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: Dn = n·n-32
- В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π4·a2
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O.
Формулы правильного n-угольника
Формулы длины стороны правильного n-угольника
Формула стороны правильного n-угольника через радиус вписанной окружности
a = 2·r·tg180°n
(через градусы),
a = 2·r·tgπn
(через радианы)
Формула стороны правильного n-угольника через радиус описанной окружности
a = 2·R·sin180°n
(через градусы),
a = 2·R·sinπn
(через радианы)
Формулы радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны
r = a:2·tg180°n
(через градусы),
r = a:2·tgπn
(через радианы)
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны
R = a:2·sin180°n
(через градусы),
R = a:2·sinπn
(через радианы)
Формулы площади правильного n-угольника
Формула площади n-угольника через длину стороны
S = n·a24·ctg180°n
Формула площади n-угольника через радиус вписанной окружности
S = n·r2·tg180°n
Формула площади n-угольника через радиус описанной окружности
S = n·R22·sin360°n
Формула периметра правильного многоугольника
Формула периметра правильного n-угольника
Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.
P = n·a
Формула определения угла между сторонами правильного многоугольника
Формула угла между сторонами правильного n-угольника
αn = n-2n·180°
Правильный треугольник
Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
Формулы правильного треугольника
Формула стороны правильного треугольника через радиус вписанной окружности
Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.
a = 2·r·3
Формула стороны правильного треугольника через радиус описанной окружности
Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.
a = R·3
r = a·36
R = a·33
Формула площади правильного треугольника через длину стороны
S = a2·34
Формула площади правильного треугольника через радиус вписанной окружности
S = r2·3·3
Формула площади правильного треугольника через радиус описанной окружности
S = R2·3·34
Углы между сторонами правильного треугольника
α1=α2=α3=60°
Правильный четырехугольник
Правильный четырехугольник — это квадрат.
Формулы правильного четырехугольника
Формула стороны правильного четырехугольника через радиус вписанной окружности
Сторона правильного четырехугольника равна двум радиусам вписанной окружности.
a = 2·r
Формула стороны правильного четырехугольника через радиус описанной окружности
Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.
a = R·2
Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.
r = a2
Формула радиуса описанной окружности правильного четырехугольника через длину стороны
Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.
R = a·22
Формула площади правильного четырехугольника через длину стороны
Площадь правильного четырехугольника равна квадрату стороны четырехугольника.
S = a2
Формула площади правильного четырехугольника через радиус вписанной окружности
Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.
S = 4·r2
Формула площади правильного четырехугольника через радиус описанной окружности
Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.
S = 2·R2
Углы между сторонами правильного четырехугольника
α1=α2=α3=α4=90°
Правильный шестиугольник
Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.
Формулы правильного шестиугольник
Формула стороны правильного шестиугольника через радиус вписанной окружности
a = 2·r·33
Формула стороны правильного шестиугольника через радиус описанной окружности
Длина стороны правильного шестиугольника равна радиусу описанной окружности.
a = R
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
r = a·32
Формула радиуса описанной окружности правильного шестиугольника через длину стороны
R = a
Формула площади правильного шестиугольника через длину стороны
S = a2·3·32
Формула площади правильного шестиугольника через радиус вписанной окружности
S = r2·2·3
Формула площади правильного шестиугольника через радиус описанной окружности
S = R2·3·32
Углы между сторонами правильного шестиугольника
α1=α2=α3=α4=α5=α6=120°
Правильный восьмиугольник
Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.
Формулы правильного восьмиугольника
Формула стороны правильного восьмиугольника через радиус вписанной окружности
a = 2·r·2-1
Формула стороны правильного восьмиугольника через радиус описанной окружности
a = R·2-2
Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны
r = a·2+12
Формула радиуса описанной окружности правильного восьмиугольника через длину стороны
R = a·4+222
Формула площади правильного восьмиугольника через длину стороны
S = a2·2·2+1
Формула площади правильного восьмиугольника через радиус вписанной окружности
S = r2·8·2-1
Формула площади правильного восьмиугольника через радиус описанной окружности
S = R2·2·2
Углы между сторонами правильного восьмиугольника
α1=α2=α3=α4=α5=α6=α7=α8=135°
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Длина окружности и площадь круга
- Окружность, вписанная в правильный многоугольник
Теорема
Доказательство
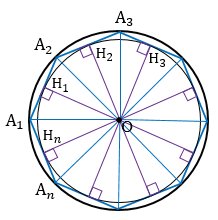
Дано: А1А2А3…Аn – правильный многоугольник.
Доказать: в многоугольник А1А2А3…Аn можно вписать окружность, и притом только одну.
Доказательство:
А1А2А3…Аn – правильный многоугольник, значит, мы можем описать около него окружность. Пусть окружность с центром О описана около многоугольника А1А2А3…Аn.
Докажем, что вписать можно только одну окружность.
Пусть существует окружность с центром О1, вписанная в многоугольник А1А2А3…Аn, отличная от окружности с центром О и радиусом ОН1. Тогда ее центр О1 равноудален от сторон многоугольника, т.е. точка О1 лежит на каждой из биссектрис углов многоугольника А1А2А3…Аn и, следовательно, совпадает с точкой О пересечения этих биссектрис (смотри теорему об окружности, описанной около правильного многоугольника). Радиус этой окружности равен расстоянию от точки О до сторон многоугольника,т.е. равен ОН1. Значит, получаем, что вторая окружность совпадает с первой. Следовательно, наше предположение неверно, и в правильный многоугольник вписать можно только одну окружность. Теорема доказана.
Следствие 1
Следствие 2
Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.
Эта точка называется центром правильного многоугольника.
Советуем посмотреть:
Правильный многоугольник
Окружность, описанная около правильного многоугольника
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Построение правильных многоугольников
Длина окружности
Площадь круга
Площадь кругового сектора
Длина окружности и площадь круга
Правило встречается в следующих упражнениях:
7 класс
Задание 1086,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1087,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1089,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1130,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1140,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1215,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1239,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1285,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Понятие правильного многоугольника
Определение 1
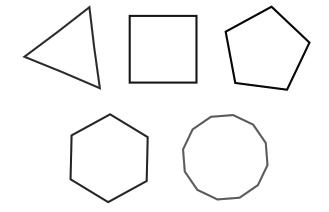
Правильный многоугольник — выпуклый многоугольник, у которого все стороны и все углы равны между собой (Рис. 1).
Рисунок 1. Правильные многоугольники
Как мы знаем, сумма углов многоугольника находится по формуле$(n-2)cdot {180}^0$
Значит, градусная мера одного угла правильного многоугольника равняется
Теорема об описанной около правильного многоугольника окружности
Доказательство.
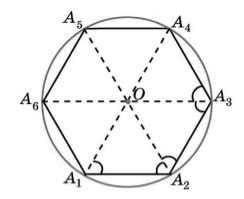
Существование. Пусть нам дан правильный многоугольник $A_1A_2A_3dots A_n$. Пусть биссектрисы углов $A_1 и A_2$ пересекаются в точке $O$. Соединим с этой точкой все остальные вершины правильного многоугольника (Рис. 2).
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Рисунок 2. Описанная вокруг правильного многоугольника окружность
Так как углы $A_1 и A_2$ равны и $A_1O и A_2O$ — биссектрисы, то угол $OA_1A_2$ равен углу $O{A_2A}_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.
Так как $A_1A_2=A_2A_3$, $angle O{A_2A}_1=angle O{A_2A}_3$ и сторона $A_2O$ – общая, то треугольники $O{A_2A}_1$ и $O{A_2A}_3$ равны. Следовательно, $OA_2=OA_3$.
Аналогично доказывают другие равенства. В результате, будем иметь
То есть точка $O$ равноудалена от всех вершин многоугольника, а, значит, точка $O$ – центр описанной вокруг правильного многоугольника окружности.
Единственность. Рассмотрим три вершины многоугольника. Очевидно, что через них проходит только одна окружность, следовательно, вокруг правильного многоугольника можно описать только одну окружность.
«Правильные многоугольники» 👇
Теорема доказана.
Теорема вписанной в правильный многоугольник окружности
Теорема 2
В любой правильный многоугольник можно вписать единственную окружность.
Доказательство.
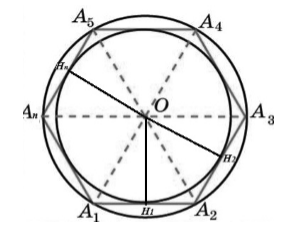
Пусть нам дан правильный многоугольник $A_1A_2A_3dots A_n$. Пусть точка $O$ – центр описанной вокруг данного многоугольника окружности (Рис. 3).
Рисунок 3. Вписанная в правильный многоугольник окружность
Так как углы $A_1 и A_2$ равны и $A_1O и A_2O$ — биссектрисы, то угол $OA_1A_2$ равен углу $O{A_2A}_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.
Так как $A_1A_2=A_2A_3$, $angle O{A_2A}_1=angle O{A_2A}_3$ и сторона $A_2O$ – общая, то треугольники $O{A_2A}_1$ и $O{A_2A}_3$ равны.
Аналогично доказывается равенство других треугольников. То есть, мы получим
Значит и высоты этих треугольников равны между собой
Тогда окружность с центром в точке $O$ и радиусом, равным ${OH}_1$ проходит через точки $H_1, H_2,dots ,H_n$, то есть касается всех сторон данного многоугольника. Следовательно. Является вписанной для правильного многоугольника.
Единственность. Предположим противное. Пусть существует еще одна вписанная в этот многоугольник окружность. Обозначим её центр $O’$. Тогда $O’$ равноудалена от всех сторон многоугольника, а значит лежит в точке пересечения биссектрис его углов. Но тогда точка $O’$ совпадает с точкой $O$ и, следовательно, эти окружности также совпадают.
Теорема доказана.
Из этих двух теорем можно сформулировать следующие следствия:
Следствие 1: Вписанная в правильный многоугольник окружность касается его в серединах его сторон.
Следствие 2: Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот же правильный многоугольник. Этот центр называется центром правильного многоугольника.
Формулы для правильного многоугольника
Дадим теперь несколько формул, относящихся к понятию правильного многоугольника (без их вывода).
Введем следующие обозначения. Пусть $S$ — площадь правильного многоугольника, $P$ — периметр правильного многоугольника, $a$ – сторона правильного многоугольника, $r$ – радиус вписанной в правильный многоугольник окружности, $R$ – радиус описанной около правильного многоугольника окружности. Тогда
Пример задачи на понятие правильного многоугольника
Пример 1
Чему равна сумма внешних углов правильного $n$-угольника. Если при каждой вершине взят только один внешний угол.
Решение.
Очевидно, что все внешние углы будут равны между собой и их количество равно $n$. Найдем один из них. Внешний угол $beta $ многоугольника будет смежным с внутренним углом многоугольника. Используя формулу нахождения угла правильного $n$-угольника $alpha =frac{{180}^0(n-2)}{n}$, получим
[beta ={180}^0-frac{{180}^0(n-2)}{n}={180}^0left(1-frac{n-2}{n}right)=frac{{360}^0}{n}]
Значит, сумма всех внешних углов равна
[frac{{360}^0}{n}cdot n={360}^0]
Ответ: ${360}^0.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
На этом уроке мы вспомним, какую окружность называют
вписанной в многоугольник. Докажем теорему об окружности, вписанной в
правильный многоугольник. А также рассмотрим следствия из этой теоремы.
Для начала давайте вспомним определение правильного
многоугольника. Итак, правильным многоугольником называется выпуклый
многоугольник, у которого все углы равны и все стороны равны. Так как у правильного многоугольника все
углы равны, то угол правильного n-угольника
можно вычислить по формуле: альфа энное равно 180 градусов умножить на эн минус
два деленное на н, где n – количество сторон (углов) правильного n-угольника.
И вспомним
еще определение вписанной окружности.
Определение. Окружность называется вписанной в
многоугольник, если все стороны многоугольника касаются этой окружности.
При этом многоугольник называется описанным около этой окружности.
Ранее мы с вами рассматривали касание прямой и
окружности.
Напомню, что если задана окружность с центром в точке О
и радиусом r, и точка А – общая точка прямой и
окружности, то такая точка единственная. Прямая p,
которая проходит через точку касания, называется касательной. Радиус OA, проведенный в точку касания, перпендикулярен касательной p.
Теорема. Отрезки касательных к окружности,
проведенные из одной точки, равны и составляют равные углы с прямой, проходящей
через эту точку и центр окружности.
Значит, точка О – центр окружности – лежит на
биссектрисе угла. Таким образом, имеем окружность, вписанную в угол.
Докажем
теорему об окружности, вписанной в правильный многоугольник.
Теорема.
В любой правильный
многоугольник можно вписать окружность, и притом только одну.
Доказательство.
Пусть – правильный многоугольник.
по двум сторонам и углу между ними.
Отсюда,.
Т.е. .
Следовательно,
точка равноудалена от всех сторон
многоугольника.
Если
провести окружность с центром и
, то все стороны многоугольника будут
касаться окружности в этих точках.
Значит, в
данный многоугольник можно вписать окружность.
Теперь
докажем, что вписанная окружность только одна.
Предположим,
что в то же время с окружностью с центром и радиусом
существует и другая окружность.
Тогда ее
центр лежит на каждой из биссектрис углов
многоугольника.
Следовательно,
ее центр совпадает с точкой
пересечения этих биссектрис.
Радиус этой
окружности равен расстоянию от точки до сторон многоугольника. Т.е. равен
.Значит, вторая окружность совпадает с
первой.
Теорема
доказана.
Из этой
теоремы вытекают следствия. Рассмотрим их.
Следствие
1. Окружность,
вписанная в правильный многоугольник, касается сторон
многоугольника в их серединах.
Доказательство.
Пусть – правильный многоугольник.
– радиус вписанной в него окружности.
Рассмотрим .
Значит, – равнобедренный.
– по свойству касательной к окружности.
– высота
.
– медиана
по свойствам равнобедренного
треугольника.
Следовательно,
.
Что и
требовалось доказать.
Следствие
2. Центр окружности,
описанной около правильного многоугольника, совпадает с центром окружности,
вписанной в тот же многоугольник.
Задача. В правильный четырехугольник вписана
окружность. Определите ее радиус, если периметр правильного четырехугольника
равен см.
Решение.
Так
как , то
– квадрат.
.
Значит,
(см).
(см).
(см).
Ответ: (см).
Подведем
итоги урока. На этом уроке мы доказали теорему об окружности, вписанной в
правильный многоугольник. А именно, доказали, что в любой правильный
многоугольник можно вписать окружность, и притом только одну. А также вывели
следствия из этой теоремы. Первое следствие: окружность, вписанная в правильный
многоугольник, касается сторон многоугольника в их серединах. Второе
следствие: центр окружности, описанной около правильного многоугольника,
совпадает с центром окружности, вписанной в тот же многоугольник. Эта точка
называется центром правильного многоугольника.
В любой правильный многоугольник можно вписать окружность. Центр вписанной окружности совпадает с центром описанной окружности и называется центром правильного многоугольника.
Выясним, какой радиус вписанной окружности имеют описанные правильные многоугольники в общем случае и в некоторых частных случаях.

O — его центр.
AB=a.
Соединим точку O с точками A и B и проведем 
OF=r — радиус вписанной окружности.
OA=OB=R- радиусы описанной окружности.
Треугольник AOB — равнобедренный с основанием AB. Следовательно, OF — его высота, медиана и биссектриса.
Угол AOB — центральный угол данного правильного многоугольника. Если n — количество сторон многоугольника, то
Рассмотрим прямоугольный треугольник AOF.
По определению тангенса,
Таким образом, формула радиуса вписанной в правильный многоугольник окружности —
где a — сторона многоугольника, n — количество его сторон.
В частности, при n=3 формула радиуса вписанной в правильный треугольник окружности
так как
При n=4 формула радиуса вписанной в правильный четырехугольник окружности
При n=6 формула радиуса вписанной в правильный шестиугольник окружности
так как






![Rendered by QuickLaTeX.com [r = frac{a}{{2tgfrac{{{{180}^o}}}{6}}} = frac{a}{{2tg{{30}^o}}} = frac{a}{{2 cdot frac{1}{{sqrt 3 }}}} = frac{{asqrt 3 }}{2}.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-a1944a94e2050496d1173a83060e7ae4_l3.png)
