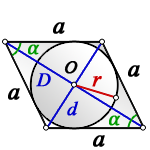
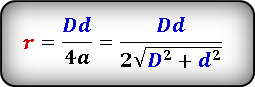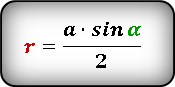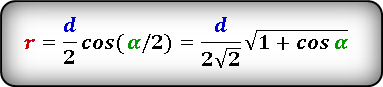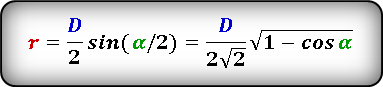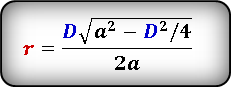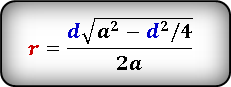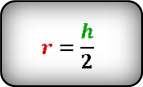Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac<1><2>(a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac<1><2>(a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
a, b, c – стороны треугольника,
S – площадь,
r – радиус вписанной окружности,
p – полупериметр

a – сторона равностороннего треугольника,
r – радиус вписанной окружности
| Фигура | Рисунок | Формула | Обозначения |
| Произвольный треугольник |  |
||
| Равнобедренный треугольник |  |
||
| Равносторонний треугольник |  |
||
| Прямоугольный треугольник |  |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр
где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр
где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности
| Произвольный треугольник |
 |
| Равнобедренный треугольник |
 |
| Равносторонний треугольник |
 |
| Прямоугольный треугольник |
 |
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр
где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр
Равнобедренный треугольник
Равносторонний треугольник
где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности
Прямоугольный треугольник
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
Описанные и вписанные окружности – формулы, свойства и определение с примерами решения
Содержание:
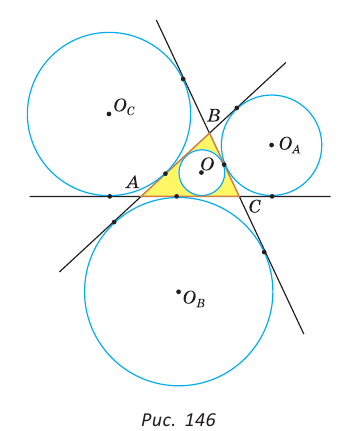
Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью треугольника. На рисунке 146 изображен треугольник АВС и три его вневписанные окружности с центрами
Вневписанные окружности обладают рядом интересных свойств:
1. Центры вписанной и вневписанной окружностей лежат на биссектрисе соответствующего внутреннего угла треугольника.
2. 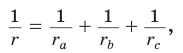
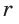
3. 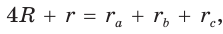
Попробуйте доказать некоторые из этих свойств.
Найдем радиус 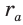
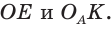
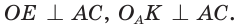
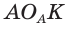
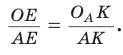
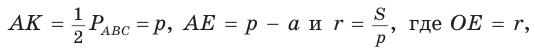
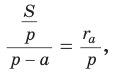
Пример:
Вычислим, используя данную формулу, радиус вневписанной окружности прямоугольного треугольника с катетами 3 и 4, которая касается гипотенузы:
Описанная и вписанная окружности треугольника
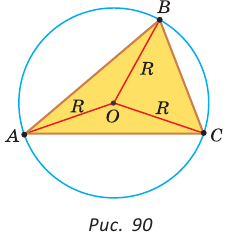
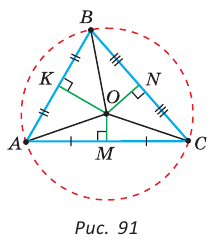
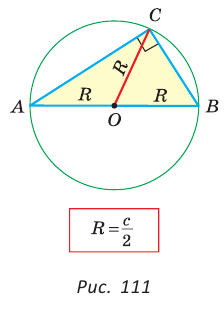
Определение. Окружность называется описанной около треугольника, если она проходит через все его вершины.
На рисунке 90 изображена окружность с радиусом R и центром 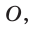
Так как ОА = ОВ = ОС = R, то центр описанной окружности равноудален от вершин треугольника.
Вместо слов «окружность, описанная около треугольника АВС», также говорят «окружность, описанная вокруг треугольника АВС», или «описанная окружность треугольника АВС».
Теорема (об окружности, описанной около треугольника).
Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения серединных перпендикуляров к сторонам треугольника.
Рассмотрим произвольный треугольник АВС (рис. 91). Пусть О — точка пересечения серединных перпендикуляров к его сторонам. Проведем отрезки ОА, ОВ и ОС. По свойству серединного перпендикуляра ОА = ОС, ОС = ОВ. Так как точка О равноудалена от всех вершин треугольника АВС, то окружность с центром в точке О и радиусом ОА проходит через все вершины треугольника АВС, т. е. является его описанной окружностью. Единственность описанной окружности докажите самостоятельно.
Замечание. Так как все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, то для нахождения центра описанной окружности достаточно построить точку пересечения любых двух из них.
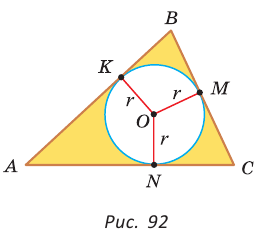
Определение. Окружность называется вписанной в треугольник, если она касается всех его сторон.
На рисунке 92 изображена окружность с центром О и радиусом 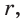
Так как 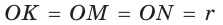
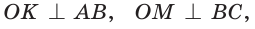
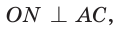
Вместо слов «окружность, вписанная в треугольник АВС», также говорят «вписанная окружность треугольника АВС».
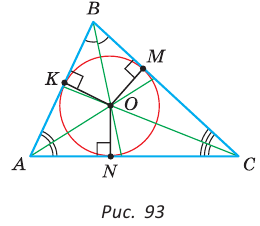
Теорема (об окружности, вписанной в треугольник).
В любой треугольник можно вписать окружность, причем только одну, ее центр находится в точке пересечения биссектрис треугольника.
Рассмотрим произвольный треугольник АВС (рис. 93). Пусть О — точка пересечения его биссектрис. Проведем из точки О перпендикуляры ОК, ОМ и ON соответственно к сторонам АВ, ВС и АС. По свойству биссектрисы угла ОК = ON, ON = ОМ. Окружность с центром в точке О и радиусом ОК будет проходить через точки К, М и N и касаться сторон АВ, ВС и АС в указанных точках по признаку касательной.
Следовательно, эта окружность является вписанной в треугольник АВС. Единственность вписанной окружности докажите самостоятельно.
Замечание. Так как все три биссектрисы треугольника пересекаются в одной точке, то для нахождения центра вписанной окружности достаточно построить точку пересечения любых двух из них.
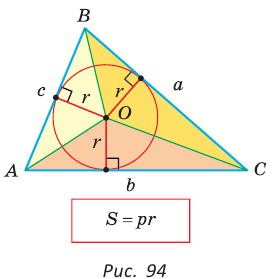
Теорема. Площадь треугольника можно найти по формуле 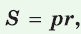
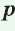
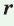
Пусть дан треугольник АВС со сторонами 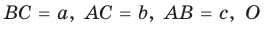
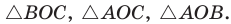
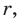
Следствие:
Радиус окружности, вписанной в треугольник, можно найти по формуле
Одной из важнейших задач данной темы является задача нахождения радиуса описанной и радиуса вписанной окружностей данного треугольника.
Пример:
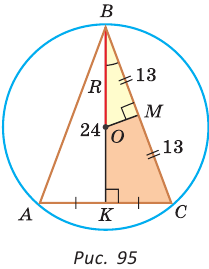
Найти радиус окружности, описанной около равнобедренного треугольника АВС, у которого АВ = ВС = 26 см, высота ВК = 24 см
(рис. 95).
Решение:
Способ 1 (метод подобия). Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. Проведем серединные перпендикуляры к сторонам АС и ВС, которые пересекутся в точке О — центре описанной окружности. Так как в равнобедренном треугольнике высота, проведенная к основанию, является медианой, то ВК — серединный перпендикуляр к стороне АС. Пусть МО — серединный перпендикуляр к стороне ВС. Тогда ВМ = 13 см, ВО = R -— искомый радиус. Поскольку 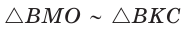
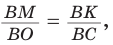
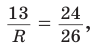
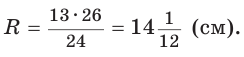
Способ 2 (тригонометрический метод). Из 
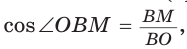
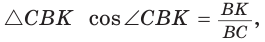
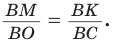
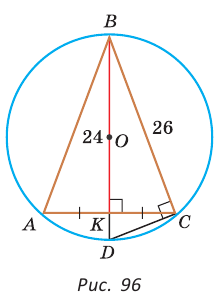
Способ 3* (среднее пропорциональное). Продлим высоту ВК до пересечения с описанной окружностью в точке D (рис. 96). Так как центр описанной окружности равнобедренного треугольника лежит на прямой ВК (см. способ 1), то BD = 2R — диаметр данной окружности. В прямоугольном треугольнике BCD 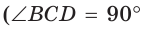
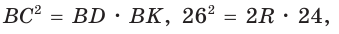
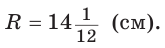
Ответ: 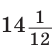
Замечание. Из решения ключевой задачи 1 следует свойство: «Центр окружности, описанной около равнобедренного треугольника, лежит на его высоте, проведенной к основанию, или на ее продолжении».
Верно и обратное утверждение: «Если центр окружности, описанной около треугольника, лежит на высоте треугольника или на ее продолжении, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Полезно запомнить!
Если в ключевой задаче 1 боковую сторону обозначить 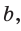
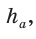
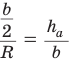
Отсюда следует удобная формула для нахождения радиуса окружности, описанной около равнобедренного треугольника:
Пример:
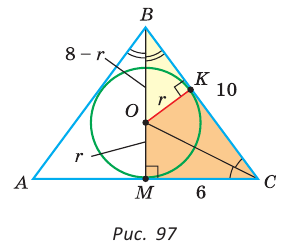
Найти радиус окружности, вписанной в равнобедренный треугольник АВС, у которого АВ = ВС = 10 см, АС = 12 см.
Решение:
Способ 1 (метод подобия). Центр вписанной окружности находится в точке пересечения биссектрис треугольника. Проведем в треугольнике АВС биссектрисы из вершин В и С, которые пересекутся в точке О — центре вписанной окружности (рис. 97). Биссектриса ВМ, проведенная к основанию равнобедренного треугольника АВС, будет его высотой и медианой, луч СО — биссектриса угла С, 
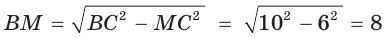
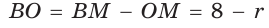
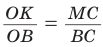
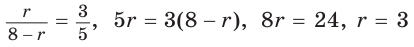
Способ 2 (тригонометрический метод). Из 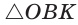
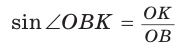
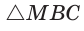
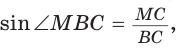
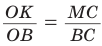
Способ 3 (свойство биссектрисы треугольника). СО — биссектриса 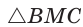
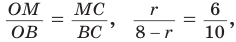
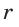
Способ 4 (формула 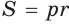
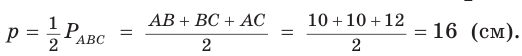
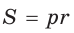
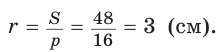
Ответ: 3 см.
Замечание. Из решения ключевой задачи 2 следует свойство: «Центр окружности, вписанной в равнобедренный треугольник, лежит на его высоте, проведенной к основанию».
Верно и обратное утверждение: «Если центр окружности, вписанной в треугольник, лежит на высоте треугольника, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
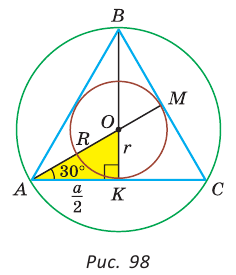
Пример:
Дан равносторонний треугольник со стороной а. Найти радиус R его описанной окружности и радиус 
Решение:
Способ 1 (тригонометрический метод).Так как в равностороннем треугольнике биссектрисы являются и высотами, и медианами, то его биссектрисы лежат на серединных перпендикулярах к сторонам треугольника. Поэтому в равностороннем треугольнике центры описанной и вписанной окружностей совпадают.
Рассмотрим равносторонний треугольник АВС со стороной а, у которого высоты AM и ВК пересекаются в точке О — центре описанной и вписанной окружностей (рис. 98). Тогда ОА = OB = R — радиусы описанной, 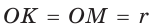
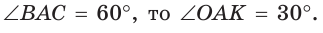
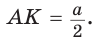
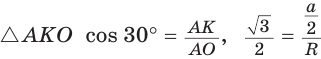
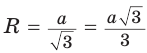
В 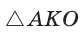
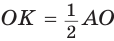
Способ 2 (свойство медиан). Поскольку AM и ВК — медианы треугольника АВС (см. рис. 98), то по свойству медиан 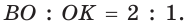
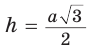
Ответ:
Полезно запомнить!
Поскольку радиус описанной окружности равностороннего треугольника 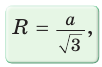
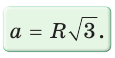
треугольника в 
Чтобы найти радиус R описанной окружности равностороннего треугольника, нужно сторону 
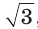
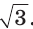
Прямоугольный треугольник и его описанная и вписанная окружности
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а ее радиус равен половине гипотенузы, т. е. 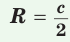
Проведем в прямоугольном треугольнике АВС медиану СО к гипотенузе АВ (рис. 111). Так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы, то ОС = ОА = ОВ.
Тогда середина гипотенузы — точка О — равноудалена от точек А, В и С и поэтому является центром описанной окружности треугольника АВС. Радиус этой окружности 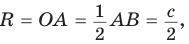
Теорема доказана.
Замечание. Также можно доказать, что серединные перпендикуляры к катетам прямоугольного треугольника пересекаются на середине гипотенузы.
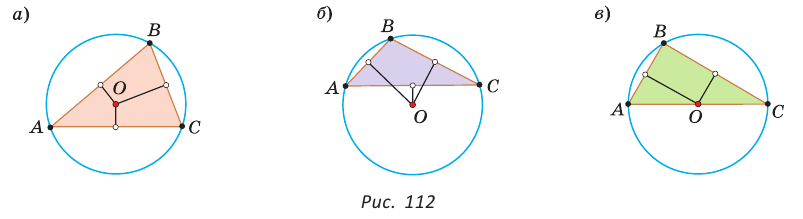
Отметим, что у остроугольного треугольника центр описанной окружности лежит внутри треугольника (рис. 112, а), у тупоугольного — вне треугольника (рис. 112, б), у прямоугольного — на середине гипотенузы (рис. 112, в). Обоснуйте первые два утверждения самостоятельно.
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле 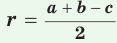
Рассмотрим прямоугольный треугольник АВС с катетами и гипотенузой . Пусть вписанная в треугольник окружность с центром О и радиусом касается сторон треугольника в точках М, N и К (рис. 113).
Проведем радиусы в точки касания и получим: Четырехугольник CMON — квадрат, так как у него все углы прямые и . Тогда Так как отрезки касательных, проведенных из одной точки к окружности, равны между собой, то Но , т. е. , откуда
Следствие: где р — полупериметр треугольника.
Преобразуем формулу радиуса вписанной окружности:
Формула в сочетании с формулами и дает возможность решать многие задачи, связанные с прямоугольным треугольником, алгебраическим методом.
Пример. Дан прямоугольный треугольник, Найти .
Решение:
Так как то
Из формулы следует . По теореме Виета (обратной) — посторонний корень.
Ответ: = 2.
Пример:
Найти радиус окружности, описанной около прямоугольного треугольника, у которого один из катетов равен 6, а радиус вписанной окружности равен 2.
Решение:
Способ 1 (геометрический). Пусть в треугольнике АВС, где — радиус вписанной окружности (рис. 114). Проведем из центра О вписанной окружности перпендикуляры ОК, ОМ и ON к сторонам треугольника, которые будут радиусами вписанной окружности. Так как — квадрат, то
По свойству касательных
Тогда По теореме Пифагора
Следовательно,
Радиус описанной окружности
Способ 2 (алгебраический). Подставив в формулу значения получим По теореме Пифагора , т. е. Тогда
Ответ: 5.
Пример:
Гипотенуза прямоугольного треугольника радиус вписанной в него окружности Найти площадь треугольника.
Решение:
Способ 1 (геометрический). Пусть в гипотенуза АВ – = с = 18,0 — центр вписанной окружности, ОК, ОМ, ON — ее радиусы, проведенные в точки касания (рис. 115). Так как
, то CMON — квадрат co стороной, равной радиусу вписанной окружности, — высота . Поскольку отрезки касательных, проведенных из одной точки к окружности, равны между собой, то АК = AM, ВК = BN.
Отсюда по катету и гипотенузе.
Площадь равна сумме удвоенной площади и площади квадрата CMON, т. е.
Способ 2 (алгебраический). Из формулы следует Возведем части равенства в квадрат: Так как и
Способ 3 (алгебраический). Из формулы следует, что Из формулы следует, что
Ответ: 40.
Реальная геометрия:
Есть два листа ДСП (древесно-стружечной плиты). Один из них имеет форму равностороннего треугольника со стороной 1 м, другой — форму прямоугольного равнобедренного треугольника с катетами, равными 1 м (рис. 120). Из каждого листа необходимо вырезать по одному кругу наибольшего диаметра. Определите, из какого листа будет вырезан круг большего диаметра и каким в этом случае будет процент отходов, если известно, что площадь круга можно найти по формуле
Вписанные и описанные четырехугольники
Определение. Окружность называется описанной около многоугольника, если она проходит через все его вершины. При этом многоугольник называется вписанным в окружность.
Окружность называется вписанной в многоугольник, если она касается всех его сторон. При этом много угольник называется описанным около окружности.
Пятиугольник ABCDE (рис. 121, а) является вписанным в окружность а четырехугольник MNPK (рис. 121, б) — описанным около окружности.
Центр описанной окружности многоугольника находится в точке пересечения серединных перпендикуляров к его сторонам, а центр вписанной — в точке пересечения биссектрис его углов.
Обоснуйте эти утверждения самостоятельно.
Теорема (свойство вписанного четырехугольника).
Сумма противоположных углов четырехугольника, вписанного в окружность, равна 180°.
Пусть ABCD — четырехугольник, вписанный в окружность (рис. 122). Его углы А, В, С и D являются вписанными в окружность. Так как вписанный угол равен половине дуги, на которую он опирается, то Дуги BCD и BAD дополняют друг друга до окружности, и поэтому сумма их градусных мер равна 360°. Отсюда
Аналогично доказывается, что 180°. Теорема доказана.
Теорема (признак вписанного четырехугольника).
Если сумма противоположных углов четырехугольника равна то около него можно описать окружность.
Рассмотрим четырехугольник ABCD, у которого (рис. 123). Через вершины А, В и D проведем окружность (около любого треугольника можно описать окружность). Если бы вершина С не лежала на данной окружности, а находилась вне ее в положении или внутри нее в положении то в первом случае угол С был бы меньше, а во втором — больше половины градусной меры дуги BAD (по свойству угла между секущими и угла между пересекающимися хордами).
Тогда сумма не была бы равна 180°. Следовательно, вершина С лежит на данной окружности. Теорема доказана.
Замечание. Так как сумма углов четырехугольника равна 360°, то для того чтобы около четырехугольника можно было описать окружность, достаточно, чтобы сумма любой пары его противоположных углов была равна 180°.
Следствия.
1. Около параллелограмма можно описать окружность, только если этот параллелограмм — прямоугольник (рис. 124, а). Центр этой окружности лежит в точке пересечения диагоналей прямоугольника.
2. Около ромба можно описать окружность, только если этот ромб — квадрат (рис. 124, б).
3. Около трапеции можно описать окружность, только если она равнобедренная (рис. 124, в).
Докажите эти следствия самостоятельно.
Теорема (свойство описанного четырехугольника ).
Суммы противоположных сторон описанного четырехугольника равны между собой.
Пусть ABCD — описанный четырехугольник, М, N, Р и К — точки касания его сторон с окружностью (рис. 125). Так как отрезки касательных, проведенных к окружности из одной точки, равны между собой, то AM = АК = а, ВМ = BN = b, СР = CN = с, DP = DK = d. Тогда
откуда AD + ВС = AB + CD.
Теорема доказана.
Следствие:
Периметр описанного четырехугольника равен удвоенной сумме длин любой пары его противоположных сторон:
Теорема (признак описанного четырехугольника).
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Пусть для выпуклого четырехугольника ABCD справедливо, что
(1)
Проведем окружность, которая касается прямых AD, АВ и ВС (рис. 126). Такая окружность существует, ее центр находится в точке пересечения биссектрис углов А и В. Если окружность не касается стороны CD, то либо прямая CD не имеет с окружностью общих точек, либо является секущей. Рассмотрим первый случай. Проведем отрезок который касается окружности. По свойству описанного четырехугольника
(2)
Отняв почленно от равенства (1) равенство (2), получим что противоречит неравенству треугольника.
Рассмотрев случай, когда прямая DC — секущая, также придем к противоречию (сделайте это самостоятельно). Следовательно, данная окружность касается стороны CD и в четырехугольник ABCD можно вписать окружность. Теорема доказана.
Следствия.
1. В параллелограмм можно вписать окружность, только если этот параллелограмм — ромб. Центр этой окружности лежит в точке пересечения диагоналей ромба, а ее диаметр равен высоте ромба (рис. 127, а).
2. В прямоугольник можно вписать окружность, только если этот прямоугольник — квадрат (рис. 127, б).
3. Диаметр окружности, вписанной в трапецию, равен ее высоте (рис. 127, в).
Докажите эти следствия самостоятельно.
Для описанного многоугольника справедлива формула , где S — его площадь, р — полупериметр, — радиус вписанной окружности.
Доказательство аналогично приведенному в § 8 для треугольника. Выполните его самостоятельно, используя рисунок 128.
Пример:
Найти радиус окружности, вписанной в ромб с периметром 24 см и острым углом, равным 45°.
Решение:
Способ 1 (решение прямоугольного треугольника). Пусть ABCD — ромб (рис. 129), О — центр вписанной в ромб окружности. Известно, что высота ВК ромба равна диаметру EF вписанной окружности, т. е. Так как у ромба все стороны равны , то (см).
Из прямоугольного треугольника АВК находим. что откуда Искомый радиус вписанной окружности (см).
Способ 2 (метод площадей). Ромб — параллелограмм. По формуле площади параллелограмма найдем площадь данного ромба: С другой стороны , площадь ромба можно найти по формуле площади описанного многоугольника Поскольку (см), то Отсюда (см).
Ответ: см.
Пример:
Окружность, вписанная в прямоугольную трапецию ABCD, где делит точкой касания большую боковую сторону CD на отрезки СК = 1, KD = 4. Найти площадь трапеции (рис. 130).
Решение:
Способ 1. Площадь трапеции находится по формуле Необходимо найти сумму оснований и высоту трапеции. Проведем высоту трапеции, проходящую через центр О вписанной окружности. По свойству касательных, проведенных из одной точки к окружности, CF = СК = 1, DH = DK = 4. Проведем высоту СМ. Так как HFCM — прямоугольник (все углы прямые), то НМ = FC = 1, MD = 3. В прямоугольном треугольнике CMD по теореме Пифагора Тогда По свойству описанного четырехугольника Отсюда
Способ 2*. Центр О вписанной окружности лежит на пересечении биссектрис углов и Так как как внутренние односторонние углы при и секущей CD, то (рис. 131). Тогда — прямоугольный, радиус является его высотой, проведенной к гипотенузе CD. Высота прямоугольного треугольника, проведенная к гипотенузе, — есть среднее пропорциональное между проекциями катетов на гипотенузу. Поэтому или Высота описанной трапеции равна диаметру вписанной окружности, откуда Так как по свойству описанного четырехугольника то
Ответ: 18.
Замечание. Полезно запомнить свойство: «Боковая сторона описанной трапеции видна из центра вписанной окружности под углом 90°».
Пример:
Внутри острого угла А взята точка М, из которой опущены перпендикуляры МВ и МС на стороны угла А, Найти величину угла ВАС (рис. 132, а).
Решение:
Так как в четырехугольнике АВМС сумма углов В и С равна 180°, то около него можно описать окружность. Проведем в ней хорду AM (рис. 132, б). Поскольку как вписанные углы, опирающиеся на одну и ту же дугу МС, то и прямоугольный треугольник АМС является равнобедренным, В прямоугольном треугольнике ABM откуда
Окружность, вписанная в треугольник
Пример:
Окружность вписана в треугольник АВС со сторонами ВС = а, АС = Ь, АВ = с. Вывести формулу для нахождения длин отрезков, на которые точки касания окружности со сторонами делят каждую сторону треугольника.
Решение:
Пусть К, М и N — точки касания вписанной окружности соответственно со сторонами АС, АВ и ВС треугольника АВС (рис. 140). Известно, что отрезки касательных, проведенных из одной точки к окружности, равны между собой.
Тогда, если то Так как АВ = AM + МВ, то откуда т. е. . После преобразований получим: Аналогично:
Ответ:
Замечание. Если (рис. 141), то (см. c. 69). Формула радиуса окружности, вписанной в прямоугольный треугольник, — частный случай результата задачи 1.
Описанная трапеция
Пример:
Найти площадь описанной равнобедренной трапеции с основаниями а и Ь.
Решение:
Площадь трапеции можно найти по формуле Пусть в трапеции ABCD основания — боковые стороны, — высота (рис. 142). По свойству описанного четырехугольника АВ + CD = AD + ВС, откуда . Известно, что в равнобедренной трапеции (можно опустить высоту СК и убедиться в этом). Из прямоугольного треугольника АНВ получаем: Отсюда Ответ:
Замечание. Площадь описанной равнобедренной трапеции равна произведению среднего арифметического и среднего геометрического ее оснований.
Полезно запомнить!
Для описанной равнобедренной трапеции с основаниями боковой стороной с, высотой h, средней линией и радиусом вписанной окружности (см. рис. 142) справедливы равенства:
Дополнительные свойства и признаки вписанного четырехугольника
Теорема.
Около четырехугольника можно описать окружность тогда и только тогда, когда угол между его стороной и диагональю равен углу между противоположной стороной и другой диагональю.
Рис. 143
1. Если четырехугольник ABCD вписан в окружность (рис. 143), то как вписанные углы, опирающиеся на одну и ту же дугу.
2. Докажем, что если в некотором четырехугольнике ABCD то около него можно описать окружность.
Опишем около треугольника ABD окружность.
В 8-м классе (В. В. Казаков. «Геометрия, 8», с. 186) было доказано свойство:
«Геометрическим местом точек плоскости, из которых данный отрезок AD виден под углом а, является объединение двух дуг окружностей: дуги ABD и ей симметричной относительно прямой AD, исключая точки » . Данное свойство гарантирует, что вершины всех углов, равных углу ABD и лежащих по одну сторону от прямой AD, расположены на дуге ABD окружности. Поэтому окружность, описанная около треугольника ABD, пройдет и через вершину С. Теорема доказана.
Обобщенная теорема Пифагора
В прямоугольном треугольнике проведена высота СН, которая делит его на треугольники АСН и СВН, подобные между собой и подобные треугольнику (рис. 148). Тогда теорема Пифагора может звучать так: сумма квадратов гипотенуз треугольников СВН и АСН равна квадрату гипотенузы треугольника АВС. И вообще, если – соответствующие линейные элементы то можно сформулировать обобщенную теорему Пифагора:
Действительно, из подобия указанных треугольников откуда
Пример:
Пусть (см. рис. 148). Найдем По обобщенной теореме Пифагора отсюда
Ответ: = 39.
Формула Эйлера для окружностей
Для вписанной и описанной окружностей треугольника с радиусами и расстоянием d между их центрами (рис. 149) справедлива формула Эйлера
Проверим справедливость этой формулы на примере равнобедренного треугольника АВС, у которого АВ = ВС = 10, АС = 12 (рис. 150).
Вначале найдем расстояние между центрами указанных окружностей традиционным способом.
Проведем высоту ВН, длина которой будет равна 8 (пифагорова тройка 6, 8, 10). Центры описанной и вписанной окружностей — соответственно точки , и — лежат на прямой ВН (свойство равнобедренного треугольника). Тогда— расстояние между указанными центрами. Для нахождения радиуса описанной окружности воспользуемся формулой где b — боковая сторона, — высота, проведенная к основанию равнобедренного треугольника. Получим Радиус вписанной окружности Так как то Искомое расстояние
А теперь найдем d по формуле Эйлера:
откуда Как видим, формула Эйлера достаточно эффективна.
Запомнить:
- Центр описанной окружности треугольника (многоугольника) лежит в точке пересечения серединных перпендикуляров к его сторонам.
- Центр вписанной окружности треугольника (многоугольника) лежит в точке пересечения биссектрис его углов.
- Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, а ее радиус равен половине гипотенузы:
- Радиус вписанной окружности прямоугольного треугольника находится по формуле
- Если четырехугольник вписан в окружность, то суммы его противоположных углов равны 180°. И обратно.
- Если четырехугольник описан около окружности, то суммы его противоположных сторон равны между собой. И обратно.
- Площадь треугольника и описанного многоугольника можно найти по формуле где — полупериметр, — радиус вписанной окружности.
Справочная информация по описанной и вписанной окружности треугольника
Определение. Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.
На рисунке 298 изображена окружность, описанная около треугольника. В этом случае также говорят, что треугольник вписан в окружность. Очевидно, что центр описанной окружности треугольника равноудален от всех его вершин. На рисунке 298 точка — центр окружности, описанной около треугольника , поэтому .
Теорема 21.1. Вокруг любого треугольника можно описать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника существует точка , равноудаленная от всех его вершин. Тогда точка будет центром описанной окружности, а отрезки , и — ее радиусами.
На рисунке 299 изображен произвольный треугольник . Проведем серединные перпендикуляры и сторон и соответственно. Пусть точка — точка пересечения этих прямых. Поскольку точка принадлежит серединному перпендикуляру , то . Так как точка принадлежит серединному перпендикуляру , то . Значит, , т. е. точка равноудалена от всех вершин треугольника.
Заметим, что вокруг треугольника можно описать только одну окружность. Это следует из того, что серединные перпендикуляры и (рис. 299) имеют только одну точку пересечения. Следовательно, существует только одна точка, равноудаленная от всех вершин треугольника.
Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.
Следствие 2. Центр описанной окружности треугольника — это точка пересечения серединных перпендикуляров его сторон.
Определение. Окружность называют вписанной в треугольник, если она касается всех его сторон.
На рисунке 300 изображена окружность, вписанная в треугольник. В этом случае также говорят, что треугольник описан около окружности.
Точка (рис. 300) — центр вписанной окружности треугольника , отрезки , , — радиусы, проведенные в точки касания, . Понятно, что центр вписанной окружности треугольника равноудален от всех его сторон.
Теорема 21.2. В любой треугольник можно вписать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника существует точка , удаленная от каждой его стороны на некоторое расстояние г. Тогда в силу следствия из теоремы 20.4 точка будет центром окружности радиуса г, которая касается сторон .
На рисунке 301 изображен произвольный треугольник . Проведем биссектрисы углов и , — точка их пересечения. Так как точка принадлежит биссектрисе угла , то она равноудалена от сторон и (теорема 19.2). Аналогично, так как точка принадлежит биссектрисе угла , то она равноудалена от сторон и . Следовательно, точка равноудалена от всех сторон треугольника.
Заметим, что в треугольник можно вписать только одну окружность. Это следует из того, что биссектрисы углов и (рис. 301) пересекаются только в одной точке. Следовательно, существует только одна точка, равноудаленная от сторон треугольника.
Следствие 1. Биссектрисы углов треугольника пересекаются в одной точке.
Следствие 2. Центр вписанной окружности треугольника — это точка пересечения его биссектрис.
Докажите, что радиус окружности, вписанной в прямоугольный треугольник, определяется по формуле , где — радиус вписанной окружности, и — катеты, — гипотенуза.
Решение:
В треугольнике (рис. 302) , , , , точка — центр вписанной окружности, , и — точки касания вписанной окружности со сторонами , и соответственно.
Отрезок — радиус окружности, проведенный в точку касания. Тогда .
Так как точка — центр вписанной окружности, то — биссектриса угла и . Тогда — равнобедренный прямоугольный, . Используя свойство отрезков касательных, проведенных к окружности из одной точки, получаем:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Первый признак равенства треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://www.resolventa.ru/uslugi/uslugischoolrost.htm
http://www.evkova.org/opisannyie-i-vpisannyie-okruzhnosti
[/spoiler]
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 февраля 2023 года; проверки требуют 2 правки.
Окружность, вписанная в многоугольник ABCDE
Окружность называют вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех его сторон.
В многоугольнике[править | править код]
- Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех внутренних углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
В треугольнике[править | править код]
Окружность, вписанная в треугольник со сторонами a, b, c.
Свойства вписанной окружности:
где 

- где
— площадь треугольника, а
— его полупериметр.
,
— полупериметр треугольника (Теорема котангенсов).
- Если прямая, проходящая через точку I параллельно стороне
, пересекает стороны
и
в точках
и
, то
.
- Если точки касания вписанной в треугольник
окружности соединить отрезками с его сторонами, то получится треугольник
со свойствами:
- Биссектрисы T являются серединными перпендикулярами T1
- Пусть T2 — ортотреугольник T1. Тогда его стороны параллельны сторонам исходного треугольника T.
- Пусть T3 — серединный треугольник T1. Тогда биссектрисы T являются высотами T3.
- Пусть T4 — ортотреугольник T3, тогда биссектрисы T являются биссектрисами T4.
- Радиус вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c окружности равен
.
- Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны, равно
.
- Расстояние от вершины C до центра вписанной окружности равно
, где
— радиус вписанной окружности, а γ — угол вершины C.
- Расстояние от вершины C до центра вписанной окружности может также быть найдено по формулам
и
- Теорема о трезубце или теорема трилистника: Если D — точка пересечения биссектрисы угла A с описанной окружностью треугольника ABC, I и J — соответственно центры вписанной и вневписанной окружности, касающейся стороны BC, тогда
.
Полувписанная окружность и центр гомотетии G для вписанной и описанной окружностей с радиусами соответственно r и R. Лемма Веррьера: Центр вписанной окружности лежит на отрезке, соединяющем точки касания сторон треугольника и окружности Веррьера (полувписанной окружности)
- Теорема Фейербаха. Окружность девяти точек касается всех трёх вневписанных окружностей, а также вписанной окружности. Точка касания окружности Эйлера и вписанной окружности известна как точка Фейербаха.
Связь вписанной и описанной окружностей[править | править код]
[4]
,
где 

- Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности[5].
- Для треугольника можно построить полувписанную окружность, или окружность Варьера. Это окружность, касающаяся двух сторон треугольника и его описанной окружности внутренним образом. Отрезки, соединяющие вершины треугольника и соответствующие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке. Эта точка служит центром гомотетии с положительным коэффициентом, переводящей описанную окружность во вписанную.
- Центр вписанной окружности лежит на отрезке, соединяющем точки касания сторон треугольника и полувписанной окружности.
Полувписанная окружность и центр гомотетии G для вписанной и описанной окружностей с радиусами соответственно r и R
Связь центра вписанной окружности и середин высот треугольника[править | править код]
- Теорема Ригби. Если к любой стороне остроугольного треугольника провести высоту и касающуюся ее с другой стороны вневписанную окружность, то точка касания последней с этой стороной, середина упомянутой высоты, а также инцентр лежат на одной прямой.[6].
- Из теоремы Ригби следует, что 3 отрезка, соединяющих середину каждой из 3 высот треугольника с точкой касания вневписанной окружности, проведенной к той же стороне, что и высота, пересекаются в инцентре.
В четырёхугольнике[править | править код]
- Описанный четырёхугольник, если у него нет самопересечений («простой»), должен быть выпуклым.
- Некоторые (но не все) четырёхугольники имеют вписанную окружность. Они называются описанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важным является то, что суммы противоположных сторон равны. Это утверждение называется теоремой Пито.
- Иными словами, в выпуклый четырёхугольник ABCD можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны:
.
- Во всяком описанном четырёхугольнике две середины диагоналей и центр вписанной окружности лежат на одной прямой (теорема Ньютона). На ней же лежит середина отрезка с концами в точках пересечения продолжений противоположных сторон четырёхугольника (если они не параллельны). Эта прямая называется прямой Ньютона. На рисунке она зелёная, диагонали красные, отрезок с концами в точках пересечения продолжений противоположных сторон четырёхугольника тоже красный.
- Центр описанной около четырёхугольника окружности — точка пересечения высот треугольника с вершинами в точке пересечения диагоналей и точках пересечения противоположных сторон (теорема Брокара).
В сферическом треугольнике[править | править код]
Вписанная окружность для сферического треугольника — это окружность, касающаяся всех его сторон.
- Тангенс радиуса[7] вписанной в сферический треугольник окружности равен[8]:73-74
- Вписанная в сферический треугольник окружность принадлежит сфере. Радиус, проведенный из центра сферы через центр вписанной окружности пересечет сферу в точке пересечения биссектрис углов (дуг больших кругов сферы, делящих углы пополам) сферического треугольника[8]:20-21.
Обобщения[править | править код]
- Вписанной сферой называется сфера, касающаяся всех граней многогранника.
- Эллипс Штейнера — вписанный в треугольник эллипс.
См. также[править | править код]
- Вневписанная окружность
- Внеописанный четырёхугольник
- Вписанная и вневписанные в треугольник окружности
- Вписанные и описанные фигуры для треугольника
- Замечательные прямые треугольника
- Замечательные точки треугольника
- Вписанное коническое сечение[en]
- Описанная окружность
- Описанный четырёхугольник
- Ортоцентр
- Степень точки относительно окружности
- Теорема Мансиона
- Теорема о трезубце
- Теорема Тебо 2 и 3
- Теорема Фейербаха
- Теорема Харкорта
- Точки Аполлония
- Треугольник
- Центроид
- Центроид треугольника
Примечания[править | править код]
- ↑ Altshiller-Court, 1925, p. 79.
- ↑ Ефремов Д. Новая геометрия треугольника. — Одесса, 1902. — С. 130. — 334 с. Архивная копия от 4 марта 2016 на Wayback Machine
- ↑ Ефремов Д. Новая геометрия треугольника. Изд. 2. Серия: Физико-математическое наследие (репринтное воспроизведение издания).. — Москва: Ленанд, 2015. — 352 с. — ISBN 978-5-9710-2186-5. Архивная копия от 22 июля 2020 на Wayback Machine
- ↑ Longuet-Higgins, Michael S., «On the ratio of the inradius to the circumradius of a triangle», Mathematical Gazette 87, March 2003, 119—120.
- ↑ Мякишев А. Г. Элементы геометрии треугольника. Серия: «Библиотека „Математическое просвещение“». М.: МЦНМО, 2002. c. 11, п. 5
- ↑ Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: The Mathematical Association of America, 1996, ISBN 978-0883856390. p. 30, Figure 34, §3. An Unlikely Collinearity.
- ↑ Здесь радиус окружности измеряется по сфере, то есть представляет собой градусную меру дуги большого круга, соединяющей точку пересечения радиуса сферы, проведенного из центра сферы через центр окружности, со сферой и точку касания окружностью стороны треугольника.
- ↑ 1 2 Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.
Литература[править | править код]
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 89. — 383 с. — ISBN 5-09-001287-3.
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 52-53. — ISBN 5-94057-170-0.
- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble
Вписанная окружность — в какую фигуру нельзя вписать
Для решения геометрических задач можно использовать различные формулы и приемы, которые помогут облегчить поиск искомых показателей. Один из способов найти различные неизвестные в многогранной фигуре – сделать это через вписанную окружность.
Вписанная окружность — окружность, которая лежит внутри угла и касается его сторон. Касание происходит в одной точке с каждой стороны.
Вписанная в фигуру окружность, например, в треугольник или многоугольник, будет касаться всех его сторон. Это главное свойство окружности, которая будет называться вписанной. Сама фигура в таком случае называется описанной вокруг окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Следствие
Из этого следует, что вписанная окружность не будет таковой, если не будет касаться всех сторон фигуры.
Окружность точно можно вписать в следующие геометрические фигуры:
- треугольник;
- выпуклый правильный многоугольник;
- квадрат;
- равнобедренная трапеция;
- ромб.
При этом окружность в данные фигуры может быть вписана лишь единожды.
Четырехугольник является неоднозначной фигурой при процессе вписывания в нее окружности. Для того, чтобы окружность была вписанной в четырехугольник, суммы длин его противоположных сторон должны быть равны.
Окружность точно нельзя вписать в следующие геометрические фигуры:
- прямоугольник;
- параллелограмм (если он не является ромбом).
Ни один из видов данных фигур не сможет иметь вписанную окружность, так как она не сможет соприкасаться со всеми их сторонами, что является главным признаком вписанной окружности.
Теорема о вписанной окружности
Теорема о вписанной окружности гласит, что в любой треугольник и в любой выпуклый многоугольник и четырехугольник с равными суммами длин противоположных сторон можно вписать окружность, но только одну.
Правило о центре вписанной окружности
Центр окружности при этом будет находиться в точке пересечения биссектрис фигуры. Чтобы определить центр, нужно построить биссектрисы из каждого угла и найти пересечение.
Формула нахождения радиуса вписанной окружности
Вычисление радиуса вписанной окружности ведется по формулам, которые зависят от фигуры и известных данных. Главным условием является тот факт, что фигура должна подходить под список тех, в которые можно вписать окружность.
Радиус — перпендикуляр, соединяющий центр окружности с любой точкой, лежащей на окружности. По длине радиус составляет половину диаметра.
Треугольник
Формула нахождения радиуса окружности, вписанной в треугольник через все стороны:
(r=sqrt{frac{left(p-aright)left(p-bright)left(p-cright)}p},)
где r — радиус,
a, b и c — стороны треугольника,
p — полупериметр, (p=frac{a+b+c}2.)
Формула нахождения радиуса окружности, вписанной в треугольник через сторону и высоту:
(r=frac{btimes h}{b+sqrt{4times h^2+b^2}},)
(r=frac{htimessqrt{a^2-h^2}}{a+sqrt{a^2-h^2}},)
где r — радиус,
a и b — стороны треугольника,
h — высота.
Равносторонний треугольник
Формула нахождения радиуса окружности, вписанной в равносторонний треугольник:
(r=frac a{2sqrt3},)
где r — радиус,
a — сторона треугольника.
Равнобедренный треугольник
Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через значения сторон:
(r=frac b2sqrt{frac{2a-b}{2a+b}},)
где r — радиус,
a и b — стороны треугольника.
Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через сторону и угол:
(r=Atimesfrac{sinleft(aright)timescosleft(aright)}{1+cosleft(aright)}= Atimescosleft(aright)timestanleft(frac a2right),)
(r=frac b2timesfrac{sinleft(aright)}{1+cosleft(aright)}=frac b2timestanleft(frac a2right),)
где r — радиус,
A и b — стороны треугольника,
a — угол при основании.
Прямоугольный треугольник
Формула нахождения радиуса окружности, вписанной в прямоугольный треугольник:
(r=frac{atimes b}{a+b+c}=frac{a+b-c}2,)
где r — радиус,
a и b — катеты треугольника,
c — гипотенуза.
Равнобедренная трапеция
Формула нахождения радиуса окружности, вписанной в равнобедренную трапецию:
(r=frac h2=frac{sqrt{ctimes b}}2,)
где r — радиус,
с — нижнее основание,
b — верхнее,
а — боковые стороны,
h — высота.
Квадрат
Формула нахождения радиуса окружности, вписанной в квадрат:
(r=frac a2,)
где r — радиус,
а — сторона квадрата.
Ромб
Формула нахождения радиуса окружности, вписанной в ромб через значения диагоналей:
(r=frac{Dtimes d}{4times a}=frac{Dtimes d}{2sqrt{D^2+d^2}}.)
Формула нахождения радиуса окружности, вписанной в ромб через значения стороны и угла:
(r=frac{atimessinleft(aright)}2.)
Формула нахождения радиуса окружности, вписанной в ромб через диагональ и угол:
(r=frac d2timescosleft(frac a2right)=frac d{2sqrt2}timessqrt{1+cosleft(aright)},)
(r=frac D2timessinleft(frac a2right)=frac D{2sqrt2}timessqrt{1-cosleft(aright)}.)
Формула нахождения радиуса окружности, вписанной в ромб через диагональ и сторону:
(r=frac{Dsqrt{a^2-{displaystylefrac{D^2}4}}}{2a},)
(r=frac{dsqrt{a^2-{displaystylefrac{d^2}4}}}{2a}.)
Формула нахождения радиуса окружности, вписанной в ромб через высоту:
(r=frac h2,)
где r — радиус,
а — сторона ромба,
D — большая диагональ,
d — меньшая диагональ,
a — острый угол,
h — высота.
Многоугольник
Формула нахождения радиуса окружности, вписанной в правильный многоугольник:
(r=frac a{2timestanleft({displaystylefrac{180^circ}N}right)},)
где r — радиус,
N — количество сторон многоугольника.
Шестиугольник
Формула нахождения радиуса окружности, вписанной в шестиугольник:
(r=frac{sqrt3}2times a,)
где r — радиус,
a — сторона шестиугольника.
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
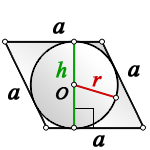
a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
a – сторона ромба
h – высота
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :
Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106).
Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107).
Свойства вписанной окружности
1. Окружность можно вписать в любой треугольник.
2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны.
Например, на рисунке 8.106 
Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.
Свойства описанной окружности
1. Окружность можно описать около любого треугольника.
2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны.
Например, на рисунке 8.107 
Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.
Расположение центров окружностей, описанных около треугольника:
1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;
2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:
а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);
б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);
3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);
4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).
Расположение центров окружностей, вписанных в треугольник:
1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);
2) центром окружности является точка пересечения биссектрис треугольника;
3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.
Формулы для вычисления радиусов вписанной и описанной окружностей
Радиус окружности, описанной около многоугольника, как правило, обозначают 

1) для равностороннего треугольника со стороной 


2) для произвольного треугольника со сторонами 



3) для прямоугольного треугольника с катетами 



4) для квадрата со стороной 



5) для прямоугольника с диагональю 

6) для ромба с высотой 

7) для трапеции с высотой 

Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами 


8) для правильного шестиугольника со стороной 


Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка 
Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна 
Решение. Так как площадь круга радиуса 




А так как 





Ответ: 
Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.
Решение. Площадь прямоугольника со смежными сторонами 


Пусть 

Получим: 




По теореме Пифагора найдем диагональ прямоугольника: 


Ответ: 
Пример 3. Найдите радиус окружности, вписанной в ромб, если его диагонали равны 6 и 8.
Решение. По теореме Пифагора найдем сторону ромба (рис. 8.119):



По формуле 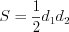

Но площадь ромба можно найти и по формуле 




Ответ: 2,4.
Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна 
Решение. Площадь правильного треугольника со стороной 
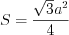
Зная площадь треугольника, найдем его сторону: 


По формуле 8.35 найдем радиус окружности, вписанной в этот треугольник: 
По формуле 8.30 найдем длину окружности: 
Ответ: 
Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.
Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой 

Так как треугольник равнобедренный, то его катеты 




Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае 

Ответ: 
Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.
Решение. Рассмотрим прямоугольный треугольник 

Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат 



Пусть отрезок 


Тогда по теореме Пифагора 



Найдем катет 

Найдем площадь треугольника: 

Ответ: 60.
Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).
Решение. Согласно свойству биссектрисы треугольника запишем: 

Радиус окружности, вписанной в треугольник, найдем по формуле 8.37.
В свою очередь по формуле Герона 


Тогда 
Ответ: 
Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.
Решение. Согласно условию задачи и рисунку 8.122, запишем: 

По свойству четырехугольника, описанного около окружности, получим: 


Согласно формуле 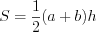

Ответ: 45.
Пример 9. Длины оснований равнобедренной трапеции относятся как 
Решение. Рассмотрим равнобедренную трапецию 
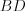
Радиус окружности, описанной около треугольника 


Зная, что 



Так как длина средней линии трапеции равна высоте трапеции, то 



Поскольку четырехугольник 


Согласно теореме Пифагора запишем:




По формуле 8.36 найдем радиус окружности, описанной около треугольника 


Согласно формуле 8.32 найдем площадь круга: 
Ответ: 
Пример 10. В правильный шестиугольник вписана окружность и около него описана окружность. Найдите площадь образовавшегося кольца, если сторона шестиугольника равна 
Решение. По формуле 8.45 найдем радиус окружности, описанной около правильного шестиугольника: 
По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как 

Площадь круга находят по формуле 8.32. Тогда 

Найдем площадь кольца: 

Ответ: 
1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.
2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.
3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.
4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.
5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.
Длину окружности радиуса 

Площадь круга радиуса 






























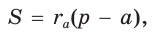
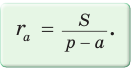
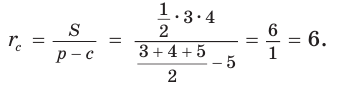
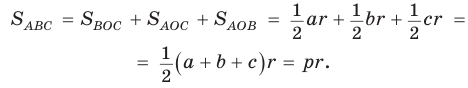
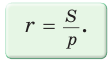
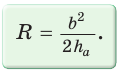
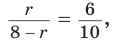
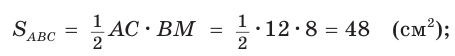
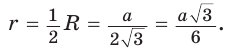
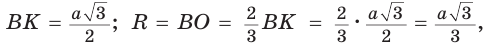
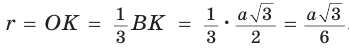
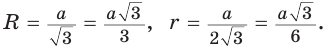
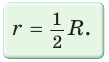








![{displaystyle |OI|^{2}={frac {a,b,c,}{a+b+c}}left[{frac {a,b,c,}{(a+b-c),(a-b+c),(-a+b+c)}}-1right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a7061fb1c7aeaee79ac8298cd2023d35d364e5a)