Мгновенный центр вращения:
Для двух бесконечно близких положений плоской фигуры вместо центра конечного вращения получим так называемый мгновенный центр вращения. Любое плоское перемещение фигуры можно приближенно заменить последовательностью вращательных перемещений вокруг своих центров конечного вращения. В пределе плоское перемещение фигуры можно заменить бесконечной последовательностью элементарных мгновенных поворотов вокруг мгновенных центров вращений, расположенных в определенной последовательности.
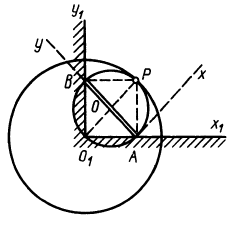
Рис. 71
Отсюда следует, что любое плоское движение фигуры можно заменить последовательностью мгновенных вращений, совершаемых за тот же промежуток времени, что и рассматриваемое плоское движение. Можно ввести угловую скорость вращения вокруг мгновенного центра вращения или, точнее, вокруг мгновенной оси, проходящей через мгновенный центр вращения и перпендикулярной плоскости движения.
При плоском движении фигуры мгновенный центр вращения перемещается как в неподвижной, так и в подвижной плоскости, скрепленной с движущейся плоской фигурой. Геометрическое место мгновенных центров вращения на неподвижной плоскости называют неподвижной центроидой, а геометрическое место этих же мгновенных центров вращения на подвижной плоскости, скрепленной с движущейся фигурой,— подвижной центроидой. Для каждого плоского движения фигуры существуют свои две центроиды: подвижная и неподвижная. Очевидно, что точка плоской фигуры, с которой в рассматриваемый момент совпадает мгновенный центр вращения, имеет скорость, равную нулю; следовательно, она является в то же время мгновенным центром скоростей.
При плоском движении фигуры подвижная центроида катится без скольжения по неподвижной центроиде. Эта теорема позволяет плоское движение твердого тела рассматривать как качение без скольжения одной плоской кривой по другой.
Центроиды нашли применение в некоторых вопросах кинематики механизмов. Рассмотрим пример нахождения центроид.
Пример:
Стержень 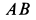
Решение. Скорость точки 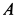 может быть направлена только по
может быть направлена только по 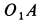 , а точки
, а точки 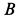 —только по
—только по 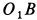 , так как траекториями этих точек являются указанные прямые. Восстанавливая перпендикуляры в точках
, так как траекториями этих точек являются указанные прямые. Восстанавливая перпендикуляры в точках 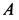 и
и 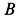 к этим направлениям, получаем положение точки
к этим направлениям, получаем положение точки 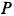 , которая и будет мгновенным центром скоростей на подвижной плоскости, скрепленной со стрежнем, и мгновенным центром вращения на неподвижной плоскости. Из рисунка видно, что
, которая и будет мгновенным центром скоростей на подвижной плоскости, скрепленной со стрежнем, и мгновенным центром вращения на неподвижной плоскости. Из рисунка видно, что 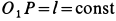 во все время движения, как диагональ прямоугольника. Следовательно, неподвижная центроида является окружностью радиусом
во все время движения, как диагональ прямоугольника. Следовательно, неподвижная центроида является окружностью радиусом 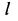 с центром в точке
с центром в точке 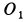 .
.
На подвижной плоскости 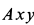 , скрепленной со стрежнем
, скрепленной со стрежнем 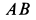 , точка
, точка 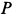 обладает аналогичным геометрическим свойством, так как
обладает аналогичным геометрическим свойством, так как 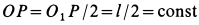 , поэтому подвижной центроидой является окружность радиуса
, поэтому подвижной центроидой является окружность радиуса 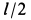 с центром в точке
с центром в точке 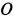 .
.
При качении подвижной окружности по неподвижной концы 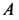 и
и 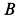 диаметра окружности движутся прямолинейно соответственно по прямым
диаметра окружности движутся прямолинейно соответственно по прямым 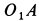 и
и 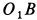 . Повернув на произвольный угол вокруг точки
. Повернув на произвольный угол вокруг точки 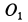 в плоскости чертежа оси координат
в плоскости чертежа оси координат 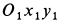 и рассмотрев этот случай после закрепления осей координат в новом положении, можно убедиться, что центроидами являются те же окружности. Следовательно, другие две точки подвижной окружности движутся прямолинейно.
и рассмотрев этот случай после закрепления осей координат в новом положении, можно убедиться, что центроидами являются те же окружности. Следовательно, другие две точки подвижной окружности движутся прямолинейно.
- Заказать решение задач по теоретической механике
Таким образом убеждаемся, что все точки подвижной окружности движутся по прямым линиям, проходящим через центр неподвижной окружности  . Это свойство точек подвижной окружности можно использовать для преобразования вращательного движения в прямолинейное поступательное движение.
. Это свойство точек подвижной окружности можно использовать для преобразования вращательного движения в прямолинейное поступательное движение.
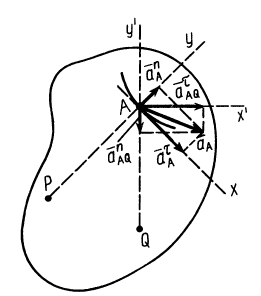
Рис. 72
В общем случае движения плоской фигуры мгновенный центр скоростей— точка 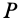 — и мгновенный центр ускорений —точка
— и мгновенный центр ускорений —точка 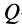 — являются различными точками этой фигуры (рис. 72). Эти точки совпадают, если плоское движение вырождается во вращательное движение вокруг неподвижной оси.
— являются различными точками этой фигуры (рис. 72). Эти точки совпадают, если плоское движение вырождается во вращательное движение вокруг неподвижной оси.
Выберем точку 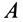 плоской фигуры и отметим точки
плоской фигуры и отметим точки 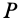 и
и 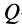 . Поставим задачу — указать формулы, по которым можно вычислить проекции ускорения точки
. Поставим задачу — указать формулы, по которым можно вычислить проекции ускорения точки 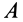 на оси
на оси 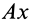 и
и 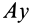 ,
, 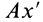 и
и 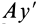 . Ось
. Ось 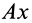 перпендикулярна оси
перпендикулярна оси 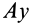 и
и 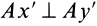 . Точка
. Точка 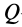 является мгновенным центром ускорений. Следовательно, ускорение
является мгновенным центром ускорений. Следовательно, ускорение
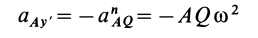
и 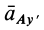 направлено всегда к точке
направлено всегда к точке 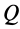 ; проекция ускорения на перпендикулярное направление
; проекция ускорения на перпендикулярное направление 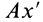
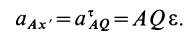
Точка 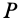 является мгновенным центром скоростей. Скорость точки
является мгновенным центром скоростей. Скорость точки 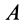 перпендикулярна
перпендикулярна 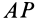 , а скорость всегда направлена по касательной к траектории. Следовательно, ось
, а скорость всегда направлена по касательной к траектории. Следовательно, ось 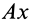 есть касательная к траектории и проекция ускорения на нее является касательным ускорением и вычисляется по формуле для касательного ускорения
есть касательная к траектории и проекция ускорения на нее является касательным ускорением и вычисляется по формуле для касательного ускорения
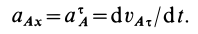
Ось 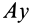 перпендикулярна касательной; следовательно, это главная нормаль траектории. Проекция ускорения на это направление вычисляется по формуле для нормального ускорения
перпендикулярна касательной; следовательно, это главная нормаль траектории. Проекция ускорения на это направление вычисляется по формуле для нормального ускорения
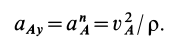
Если 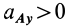 , то траектория точки обращена выпуклостью к точке
, то траектория точки обращена выпуклостью к точке 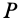 ; если
; если 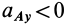 , то вогнутостью.
, то вогнутостью.
Кажется, что у точки 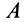 два различных нормальных и касательных ускорения. Но
два различных нормальных и касательных ускорения. Но 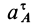 и
и 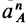 — касательное и нормальное ускорения абсолютного движения точки
— касательное и нормальное ускорения абсолютного движения точки 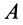 по отношению к неподвижной системе координат (на рис. 72 не показана), a
по отношению к неподвижной системе координат (на рис. 72 не показана), a 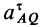 и
и 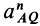 — соответственно касательное и нормальное ускорения относительного движения точки
— соответственно касательное и нормальное ускорения относительного движения точки 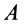 по отношению к подвижной системе координат, движущейся поступательно относительно неподвижной вместе с точкой
по отношению к подвижной системе координат, движущейся поступательно относительно неподвижной вместе с точкой 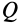 . Переносное ускорение точки
. Переносное ускорение точки 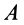 совпадает с абсолютным ускорением точки
совпадает с абсолютным ускорением точки 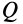 , а оно равно нулю, так как эта точка фигуры является мгновенным центром ускорений.
, а оно равно нулю, так как эта точка фигуры является мгновенным центром ускорений.
- Вращение твердого тела вокруг неподвижной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
|
|
Макеты страниц
(задачи 542, 544—549, 552, 553)
Геометрическое место мгновенных центров вращения на неподвижной плоскости, в которой движется плоская фигура, называется неподвижной центроидой, а геометрическое место мгновенных центров скоростей на плоскости самой движущейся фигуры называется подвижной центроидой.
В каждый данный момент подвижная и неподвижная центроиды касаются друг друга, и точка касания этих кривых является в данный момент мгновенным центром вращения (мгновенным центром скоростей) движущейся плоской фигуры.
Данное движение плоской фигуры в ее плоскости можно осуществить, построив подвижную и неподвижную центроиды и заставив первую катиться без скольжения по второй с соответствующей угловой скоростью.
Задачи, в которых требуется найти неподвижную и подвижную центроиды, решаются двумя способами: аналитическим и геометрическим.
При аналитическом способе определения центроид текущие координаты мгновенного центра вращения в неподвижной системе координат и текущие координаты того же центра в подвижной системе координат, неизменно связанной с движущейся фигурой, нужно выразить как функции времени, или другого переменного параметра (например, угла поворота фигуры); исключив затем этот переменный параметр, получим соответственно уравнения подвижной и неподвижной центроид (см. задачи 552, 553).
При геометрическом способе определения центроид искомые центроиды находят, исходя из геометрических соображений. Например, если расстояние мгновенного центра вращения от данной неподвижной точки оказывается постоянным, то неподвижная центроида есть окружность; если сумма расстояний мгновенного центра вращения от двух данных точек подвижной плоскости, т. е. плоскости самой движущейся фигуры, есть величина постоянная, то подвижная центроида есть эллипс, фокусы которого находятся в этих точках подвижной плоскости, и т. п. (см. задачи 542, 547, 548).
Пример 77. Стержень  концами скользит по двум прямым ОА и
концами скользит по двум прямым ОА и  , образующим между собой угол
, образующим между собой угол  45°. Найти подвижную и неподвижную центроиды (рис. 106).
45°. Найти подвижную и неподвижную центроиды (рис. 106).
Решение. 1-й способ (геометрический). Так как скорости точек А и В направлены соответственно по прямым ОА и ОВ, то мгновенный центр вращения  стержня АВ находим как точку пересечения перпендикуляров, восставленных из точек А и В к прямым ОА и ОВ. Поэтому углы
стержня АВ находим как точку пересечения перпендикуляров, восставленных из точек А и В к прямым ОА и ОВ. Поэтому углы  и АРВ равны как углы с перпендикулярными сторонами, т. е.
и АРВ равны как углы с перпендикулярными сторонами, т. е.  . Отсюда следует, что подвижная центроида есть геометрическое место таких точек, из которых отрезок АВ виден под одним и тем же углом, равным 45°.
. Отсюда следует, что подвижная центроида есть геометрическое место таких точек, из которых отрезок АВ виден под одним и тем же углом, равным 45°.
Как известно из геометрии, таким геометрическим местом является дуга АРВ окружности, описанной около треугольника АРВ; так как сумма углов АРВ и АОВ равна 180°, то эта окружность проходит и через точку О. Но сторона треугольника равна диаметру описанного круга, умноженному на синус угла, противолежащего этой стороне, поэтому, обозначая радиус подвижной центроиды через R, имеем:

откуда

Так как  90°, то отрезок ОР является диаметром подвижной центроиды, а потому
90°, то отрезок ОР является диаметром подвижной центроиды, а потому  , т. е. расстояние мгновенного центра вращения
, т. е. расстояние мгновенного центра вращения  от неподвижной точки О постоянно; отсюда следует, что неподвижная центроида есть окружность радиуса
от неподвижной точки О постоянно; отсюда следует, что неподвижная центроида есть окружность радиуса  с центром в точке О.
с центром в точке О.

Рис. 106.
2-й способ (аналитический). Построим две системы координатных осей: неподвижную  и подвижную
и подвижную  , неизменно связанную со стержнем АВ, как указано на рис. 106; начало
, неизменно связанную со стержнем АВ, как указано на рис. 106; начало  подвижной системы возьмем в середине отрезка АВ. Если обозначим координаты точки
подвижной системы возьмем в середине отрезка АВ. Если обозначим координаты точки  в неподвижной системе
в неподвижной системе  через
через  и
и  , а в подвижной системе
, а в подвижной системе  — через
— через  и
и  , то
, то

Обозначим далее переменный угол ОАВ через  и выразим координаты х и у через этот угол. Из треугольников ОАВ и АРВ по теореме синусов имеем:
и выразим координаты х и у через этот угол. Из треугольников ОАВ и АРВ по теореме синусов имеем:

отсюда находим:

Чтобы найти геометрическое место точек  на неподвижной плоскости, т. е. получить уравнение неподвижной центроиды, нужно из этих уравнений исключить параметр
на неподвижной плоскости, т. е. получить уравнение неподвижной центроиды, нужно из этих уравнений исключить параметр  . Для этого достаточно возвести каждое из этих уравнений в квадрат и затем их сложить. Тогда получим:
. Для этого достаточно возвести каждое из этих уравнений в квадрат и затем их сложить. Тогда получим:

или

Отсюда видим, что неподвижная центроида есть окружность радиуса  с центром в начале координат О.
с центром в начале координат О.
Чтобы выразить теперь через угол  координаты
координаты  и
и  точки
точки  в подвижной системе осей, рассмотрим треугольники АСР и ВСР, из которых имеем:
в подвижной системе осей, рассмотрим треугольники АСР и ВСР, из которых имеем:

и

или

и

Освобождаясь во втором уравнении от знаменателя, получим:

Чтобы найти геометрическое место точек  на подвижной плоскости, т. е. найти подвижную центроиду, нужно из этих двух уравнений исключить
на подвижной плоскости, т. е. найти подвижную центроиду, нужно из этих двух уравнений исключить  . Из первого уравнения имеем:
. Из первого уравнения имеем:

Подставляя это значение  во второе уравнение, получим:
во второе уравнение, получим:

или

или

отсюда видим, что подвижная центроида есть окружность радиуса  с центром в точке
с центром в точке  .
.
Пример 78. Стержень, согнутый в виде прямого угла ABC, перемещается так, что точка А движется по оси  , а сторона ВС все время проходит через неподвижную точку D на оси у. Найти уравнения подвижной и неподвижной центроид, если
, а сторона ВС все время проходит через неподвижную точку D на оси у. Найти уравнения подвижной и неподвижной центроид, если  (рис. 107).
(рис. 107).
Решение.  способ (геометрический). Скорость точки А направлена по оси
способ (геометрический). Скорость точки А направлена по оси  , а скорость точки D — вдоль стержня ВС.
, а скорость точки D — вдоль стержня ВС.
Мгновенный центр вращения Р стержня ABC находится в точке пересечения перпендикуляров, восставленных из точек А и D к скоростям этих точек.

Рис. 107.
Так как прямоугольные треугольники АВЕ и OED, в которых  , равны, то
, равны, то  , а потому из равенства треугольников АРЕ и DPE заключаем, что
, а потому из равенства треугольников АРЕ и DPE заключаем, что  . Но, как известно из аналитической
. Но, как известно из аналитической  , геометрическое место точек, расстояния от которых до данной неподвижной точки (точки D) и до данной неподвижной прямой (прямой
, геометрическое место точек, расстояния от которых до данной неподвижной точки (точки D) и до данной неподвижной прямой (прямой  ) равны между собой, есть парабола. Поэтому неподвижная центроида есть парабола, для которой прямая
) равны между собой, есть парабола. Поэтому неподвижная центроида есть парабола, для которой прямая  является директрисой, а точка D — фокусом. Точно так же рассматривая геометрическое место точек
является директрисой, а точка D — фокусом. Точно так же рассматривая геометрическое место точек  на подвижной плоскости, связанной со стержнем ABC, из равенства
на подвижной плоскости, связанной со стержнем ABC, из равенства  заключаем, что подвижная центроида есть парабола, для которой директрисой является прямая ВС, а фокусом — точка А.
заключаем, что подвижная центроида есть парабола, для которой директрисой является прямая ВС, а фокусом — точка А.
2-й способ (аналитический). Если построим координаты х и у точки  в неподвижной системе
в неподвижной системе  , то
, то

Из треугольника PDK имеем:

или, принимая во внимание, что  ,
,

Следовательно, неподвижная центроида есть парабола с осью  и с вершиной в точке
и с вершиной в точке  .
.
Построив теперь координаты  и
и  точки
точки  в подвижной системе осей
в подвижной системе осей  неизменно связанных со стержнем АВС, имеем:
неизменно связанных со стержнем АВС, имеем:

Чтобы найти зависимость между  и
и  , проведем отрезок. AL, параллельный
, проведем отрезок. AL, параллельный  .
.
Тогда

и

или

т. е.

или

Следовательно, подвижная центроида есть парабола с осью  и с вершиной в точке
и с вершиной в точке  .
.
Оглавление
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Представим
твердое тело как систему материальных
точек, разбив его на элементарные массы
![]() .
.
Каждая масса![]() может
может
находиться под воздействием внутренних
сил![]() и внешних
и внешних![]() .
.
По второму закону Ньютона
![]() .
.
Сложив
эти уравнения для всех частиц тела,
получаем
![]() .
.
Сумма
всех внутренних сил, действующих в
системе, равна нулю, тогда
![]() .
.
Сумму,
стоящую в левой части, можно заменить
произведением массы системы на ускорение
центра масс![]() ,
,
поэтому
![]() .
.
-
ц
 ентр
ентр
масс (инерции) твердого тела движется
так, как двигалась бы материальная
точка с массой, равной массе тела, под
действием всех приложенных к телу сил,
на ускорение центра масс (см. главу 2).
5.3. Вращение тела вокруг неподвижной оси
Рассмотрим твердое
тело, которое может вращаться вокруг
неподвижной вертикальной оси (рис.5.3).
Чтобы удержать ось от перемещений в
пространстве, заключим ее в подшипники.
Абсолютно
твердое тело – это система материальных
точек с неизменным расстоянием между
ними, и для всех его частиц (материальных
точек) справедливо уравнение:![]() .
.
Это уравнение справедливо и для твердого
тела. При этом под![]() следует понимать момент импульса тела,
следует понимать момент импульса тела,
а![]() есть сумма моментов всех внешних сил,
есть сумма моментов всех внешних сил,![]() .
.![]()
Возьмем на оси вращения точку О
и будем характеризовать положение
образующих тело частиц радиус-векторами
![]() ,
,
проведенными и з
з
этой точки (на рис.5.3 показана![]() -я
-я
частица с массой![]() ).
).
Момент импульса![]() -той
-той
частицы относительно точкиО
равен
![]() Векторы
Векторы![]() и
и![]() для всех частиц тела взаимно перпендикулярны,
для всех частиц тела взаимно перпендикулярны,
поэтому модуль вектора![]() равен
равен
![]() .
.
 Направление
Направление
вектора
![]() показано на рис.5.4, его модуль пропорционален
показано на рис.5.4, его модуль пропорционален
угловой скорости![]() .
.
Направление![]() не
не
зависит от![]() ,
,
так как![]() лежит в плоскости, проходящей через ось
лежит в плоскости, проходящей через ось
вращения и частицу![]() ,
,
и перпендикулярен![]() .
.
Проекция вектора![]() на
на
ось вращения![]() ,
,
как следует из рис.5.4 , равна
![]() .
.
Очевидно,
для однородного тела вращения суммарный
момент импульса направлен по оси
вращения в ту же сторону, что и
![]() (рис.5.5). Действительно, разобьем тело
(рис.5.5). Действительно, разобьем тело
на пары равных по массе и расположенных
симметрично частиц (на рис. 5.5
показаны пары![]() –
–![]() и
и![]() ).
).
Сумма моментов каждой пары![]() и
и![]() направлена вдоль вектора
направлена вдоль вектора![]() ,
,
поэтому суммарный момент![]() также
также
будет совпадать по направления с![]() ,
,
и модуль вектора![]() равен
равен
его проекции на ось![]()
![]() .
.
(5.1)
Величина
![]() ,
,
равная сумме произведений элементарных
масс на квадраты их расстояний до
некоторой оси, называется моментом
инерции тела относительно этой оси:
![]() .
.
(5.2)
Тогда
выражение (5.1) принимает вид:
![]() .
.
(5.3)
Так
как векторы
![]() и
и![]() имеют
имеют
одинаковые направления, в векторной
форме
получаем:
![]() (5.4)
(5.4)
Это
выражение справедливо только для
однородного тела, вращающегося вокруг
оси симметрии. В общем случае оно не
выполняется.
 Для
Для
несимметричного или неоднородного тела
момент импульса
![]() не
не
совпадает по направлению с вектором![]() .
.
На рис.5.6 пунктиром выделена та часть
несимметричного однородного тела,
которая симметрична относительно оси
вращения. Суммарный момент импульса
этой части направлен вдоль![]() .
.
Момент![]() каждой
каждой
частицы, не входящей в симметричную
часть, отклонен от оси вращения ( вправо
для ситуации, представленной на рис.5.6).
Полный момент импульса всего тела будет
отклонен в ту же сторону (рис.5.7). При
вращении тела вектор![]() поворачивается
поворачивается
вместе с ним, описывая конус. За время![]() вектор
вектор![]() получает
получает
приращение![]() .
.
Если вектор![]() не
не
изменяется по величине, то вектор![]() направлен
направлен
за чертеж на рис.5.7, так же направлен и
вектор![]() .
.
На этом рисунке момент внешних сил
создается силами тяжести![]() (сила приложена в центре масс тела С),
(сила приложена в центре масс тела С),
бокового давления подшипников на ось![]() и
и![]() ,
,
а также давления бортика подшипника на
фланец![]() .
.
Силы трения отсутствуют.
Момент
импульса относительно оси вращения для
любого тела равен
![]()
 (5.5)
(5.5)
В
отличие от (5.4) эта формула выполняется
для любого тела. Тогда
![]() .
.
(5.6)
Подставив
(5.5) в выражение (5.6), получаем
![]() ,
,
(5.7)
г де
де![]() – проекция углового ускорения на ось
– проекция углового ускорения на ось![]() .
.
Уравнение (5.7) аналогично второму закону
Ньютона![]() .
.
Роль массы играет момент инерции, роль
линейного ускорения – угловое ускорение,
роль суммарной силы – суммарный момент
внешних сил. Поэтому (5.7) описывает
динамику тела, вращающегося вокруг
неподвижной оси, и называется основным
уравнением динамики вращающегося тела.
В
случае вращения однородного симметричного
тела силы бокового давления на подшипники
не возникают (рис.5.8). В этом случае при
отсутствии силы тяжести ось сохраняет
свое положение в пространстве. Ось,
положение которой в пространстве
остается неизменным при вращении вокруг
не тела в отсутствие внешних сил,
называется свободной осью тела.
 Для тела любой
Для тела любой
формы с произвольным распределением
массы существуют три взаимно
перпендикулярные, проходящие через
центр масс тела оси, которые являются
свободными осями. Они называются главными
осями инерции тела.
У
однородного параллелепипеда (рис.5.9)
главными осями инерции являются оси
![]() ,
,
проходящие через центры противоположных
граней.
 У тела, обладающего
У тела, обладающего
осевой симметрией, например, у цилиндра
(рис.5.10) одной из главных осей является
ось симметрии, две другие – любые две
взаимно перпендикулярные оси, лежащие
в плоскости, перпендикулярной к оси
симметрии и проходящие через центр
масс тела. Таким образом, у тела с осевой
симметрией фиксирована только одна из
главных осей инерции.
У
тела с центральной симметрией (шар)
главными осями инерции являются любые
три взаимно перпендикулярные оси,
проходящие через центр масс, т.е. ни одна
из главных осей не фиксирована.
 Моменты
Моменты
инерции относительно главных осей
называются главными моментами инерции
тела. В общем случае эти моменты различны:
![]() .
.
Для тела с осевой симметрией два главных
момента одинаковы, а третий от них
отличен,![]() .
.
Такие тела называются симметричными
волчками. У тел с центральной симметрией
все три главных момента инерции одинаковы,
эти тела называют шаровыми волчками.
Важной
особенностью главных осей является то,
что при вращении
тела вокруг любой из них его момент
импульса
![]()
совпадает
по направлению с угловой скоростью
![]()
и определяется
как
![]() ,где
,где
![]() – момент инерции тела относительно
– момент инерции тела относительно
данной главнойоси
(Заметим,
что последнее соотношение справедливо
и относительно осей, параллельных
главным осям тела и не проходящих через
его центр масс).
Причем
![]()
не зависит от выбора точки, относительно
которой
его определяют (здесь предполагается,
что ось вращения неподвижна).
Если
твердое тело привести во вращение и
затем предоставить
самому себе, то направление оси вращения
в пространстве, вообще
говоря, будет меняться. Для того чтобы
произвольная ось
вращения тела сохраняла свое направление
неизменным, к ей
необходимо приложить определенные
силы. Рассмотрим
этот вопрос более подробно на следующем
примере. Пусть середина С
однородного
стержня жестко скреплена
с осью вращения так, что угол между
стержнем и осью равен
![]() (рис. 5. 11). Найдем момент
(рис. 5. 11). Найдем момент![]() внешних сил, которые необходимо
внешних сил, которые необходимо
приложить к оси вращения, чтобы
при вращении стержня с угловой скоростью
![]() ее направление не менялось.Согласно
ее направление не менялось.Согласно
основному уравнению динамики вращательного
движения,
![]() .Таким
.Таким
образом, чтобы определить
![]() ,
,
сначала
надо найти момент импульса стержня
![]() ,
,
а затем его производную по времени. Момент
импульса
![]()
проще всего определить относительно
точки С.
Мысленно выделим элемент стержня массы
![]() ,
,
находящейся
на расстоянии r
от точки С.
Его
момент импульса относительно
этой точки
![]() ,
,
где
![]() – скорость элемента. Легко
– скорость элемента. Легко
видеть, что вектор
![]() направлен перпендикулярно стержню
направлен перпендикулярно стержню
(рис. 5.11), причем его направление не
зависит от выбора элемента![]() .
.
Поэтому суммарный момент импульса
![]()
стержня совпадает
по направлению с вектором
![]() .
.
Заметим,
что в данном случае вектор
![]() не
не
совпадает по
направлению с вектором
![]() !
!
При
вращении стержня вектор
![]()
будет также вращаться с угловой
скоростью
![]() .
.
За промежуток времени
![]() вектор
вектор
![]()
получает
приращение
![]() ,
,
модуль которого, как видно из (рис.
5.11) равен
![]() ,
,
или в векторной форме![]() .
.
Поделив
обе части последнего
выражения на
![]() ,
,
получим
![]() .
.
Таким
образом, действительно, для удержания
оси вращения
в неизменном направлении к ней необходимо
в данном случае
приложить момент
![]() некоторых внешних сил
некоторых внешних сил![]() (они показаны
(они показаны
на рис. 5.11). Однако нетрудно видеть, что
если
![]() ,
,
товектор
![]()
совпадает по направлению с вектором
![]() ,
,
и в этом случае
![]() ,
,
т. е. направление оси вращения будет
оставаться неизменным
без внешнего воздействия.
Наиболее
просто убедиться в справедливости
![]() можно
можно
для
случая однородного тела с осевой
симметрией. Действительно,
момент импульса твердого тела относительно
оси вращения
![]() (
(![]() -это
-это
проекция
вектора
![]() ,
,
определенного относительно любой точки
на этой
оси). Но если тело симметрично относительно
оси вращения, то из соображения
симметрии сразу следует, что вектор![]() совпадает
совпадает
по направлению с вектором
![]() и, значит,
и, значит,
![]() .
.
В
общем случае (ось вращения не совпадает
ни с одной из главных осей, хотя и проходит
через центр
масс тела) направление вектора
![]()
не совпадает с вектором
![]() ,
,
и связь между этими векторами носит
сложный характер.
Это обстоятельство является причиной
сложного поведения
вращающихся твердых тел.
Соседние файлы в папке Физика лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Динамика механической системы
- Геометрия масс
- Механическая система. Центр масс механической системы
- Порядок решения задач на определение центра масс механической системы
- Примеры решения задач на тему: Определение центра масс механической системы
- Моменты инерции твердого тела относительно оси
- Моменты инерции некоторых однородных тел
- Примеры решения задач на тему: Моменты инерции твердого тела относительно оси
- Теорема о движении центра масс механической системы
- Закон сохранения движения центра масс
- Порядок решения задач на применение теоремы о движении центра масс
- Примеры решения задач на тему: Теорема о движении центра масс механической системы
- Теорема об изменении количества движения точки и механической системы
- Импульс силы
- Теорема об изменении количества движения точки и системы
- Закон сохранения количества движения системы
- Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
- Примеры решения задач на тему: Теорема об изменении количества движения точки и механической системы
- Теорема об изменении момента количества движения точки и механической системы
- Дифференциальное уравнение вращательного движения тела вокруг неподвижной оси
- Порядок решения задач на применение теоремы об изменении момента количества движения точки и механической системы
- Примеры решения задач на тему: Теорема об изменении момента количества движения точки и механической системы
- Теорема об изменении кинетической энергии механической системы
- Кинетическая энергия механической системы
- Определение кинетической энергии твердого тела в различных случаях его движения
- Порядок решения задач на использование теоремы об изменении кинетической энергии механической системы
- Примеры решения задач на тему: Теорема об изменении кинетической энергии механической системы
Динамика механической системы – изучает движение совокупности материальных точек и твердых тел, объединяемых общими законами.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Динамика механической системы
В предыдущей главе рассматривались задачи, связанные с движением материальной точки, которая находится под действием приложенных к ней сил. Однако часто приходится встречаться с такими случаями, когда движение одной точки невозможно рассматривать изолированно от движения других материальных точек. Это заставляет нас перейти к изучению движения совокупности материальных точек, или механических систем.
В механике под механической системой материальных точек или тел имеют в виду такую их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения или движения всех других.
Совокупность тел, между которыми отсутствуют силы взаимодействия и движение которых никаким образом не связано друг с другом, механическую систему не создают. Механические системы бывают свободными и несвободными.
Система материальных точек, движение которых не ограничено никакими связями, а определяется только действующими на эти точки силами, называется системой свободных точек.
Система материальных точек, движение которых ограничивается наложенными на точки связями, называется системой несвободных точек.
Решение задач динамики механической системы базируется на теоремах динамики и некоторых принципах, которые будут рассмотрены в данной главе.
Геометрия масс
Геометрия точки масс, в просторечии известная как точки масс , является проблемой геометрии – метод решения , который применяет физический принцип центра масс к геометрическим задачам, включающим треугольники и пересекающиеся чевианы . Все задачи, которые могут быть решены с использованием геометрии материальных точек, также могут быть решены с использованием аналогичных треугольников, векторов или соотношений площадей, но многие студенты предпочитают использовать массовые точки.
Механическая система. Центр масс механической системы
В механике под механической системой подразумевают совокупность взаимодействующих между собой материальных точек или тел.
Частным случаем механической системы является абсолютно твердое тело.
Массой механической системы называется сумма масс всех точек, входящих в систему:

где  – масса материальной точки с номером
– масса материальной точки с номером  ,
,
 – число всех точек системы.
– число всех точек системы.
Центром масс (центром инерции) механической системы называется точка  (рис.5.1), радиус-вектор
(рис.5.1), радиус-вектор  которой определяется по формуле:
которой определяется по формуле:

где  – масса системы материальных точек;
– масса системы материальных точек;
 – радиус-вектор точки с массой
– радиус-вектор точки с массой  .
.
Декартовы координаты центра масс системы материальных точек определяются по зависимостям:

Здесь  – координаты
– координаты  -ой материальной точки.
-ой материальной точки.

Для твердого тела центр масс совпадает с центром тяжести.
Порядок решения задач на определение центра масс механической системы
Решение задач, в которых необходимо определить положение центра масс и уравнение его траектории, рекомендуется проводить в следующей последовательности:
Выбрать систему координат.
Записать координаты центров тяжести каждой из масс системы, выразив их в виде функций времени:

Определить координаты центра масс системы по формулам (5.1), при этом  будут функциями времени, то есть, полученные выражения будут параметрическими уравнениями движения центра масс.
будут функциями времени, то есть, полученные выражения будут параметрическими уравнениями движения центра масс.
Для нахождения уравнений траектории центра масс надо с последних выражений (пункт 3) исключить время.
Примеры решения задач на тему: Определение центра масс механической системы
Задача № 1
Определить положение центра масс центробежного регулятора, изображенного на рис.5.2, если вес каждого из шаров  и
и  равен
равен  , вес муфты
, вес муфты  равен
равен  . Пули
. Пули  и
и  считать материальными точками. Массой стержней пренебречь.
считать материальными точками. Массой стержней пренебречь.
Решение. Система координат, относительно которой необходимо определить положение центра масс, изображена на рис.5.2.
Для определения положения центра масс системы надо определить его координаты по формулам (5.1):

где 
 – координаты центра масс пуль
– координаты центра масс пуль  ,
,  и муфты
и муфты  .
.
Следовательно,

Находим координаты центров масс:
пули  :
: 
пули  :
: 
муфты  :
: 
Тогда:

поскольку


Ответ: 
Задача № 2
Найти уравнение движения центра масс шарнирного параллелограмма  а также уравнение траектории его центра масс при вращении кривошипа
а также уравнение траектории его центра масс при вращении кривошипа  с постоянной угловой скоростью
с постоянной угловой скоростью  . Звенья параллелограмма – однородные стержни (рис.5.3), и
. Звенья параллелограмма – однородные стержни (рис.5.3), и 

Решение. Начало системы координат свяжем с шарниром  кривошипа
кривошипа  . Ось
. Ось  направим справа по линии
направим справа по линии  а ось
а ось  – перпендикулярно линии
– перпендикулярно линии  .
.
Поскольку звенья 1,2,3 параллелограмма однородны, то центры масс их лежат посередине звеньев (точки  ).
).
Из размеров звеньев вытекает: 
Определим координаты центров масс звеньев механизма как функции угла поворота  (рис.5.3):
(рис.5.3):

Для определения координат центра масс шарнирного параллелограмма  воспользуемся зависимостью (5.1):
воспользуемся зависимостью (5.1):


Для определения уравнения траектории центра масс (точки  ) исключим параметр
) исключим параметр  из уравнений (1) и (2). С этой целью выполним следующие преобразования:
из уравнений (1) и (2). С этой целью выполним следующие преобразования:

Сложим, соответственно, левые и правые части этих уравнений:

Таким образом, траекторией центра масс шарнирного параллелограмма является окружность:
с радиусом, равным  , с центром в точке
, с центром в точке  с координатами
с координатами 
Ответ: 

Задача № 3
Определить траекторию центра масс механизма эллипсографа (рис.5.4), который состоит из муфт  и
и  весом
весом  каждая, кривошипа
каждая, кривошипа  весом
весом  и линейки
и линейки  весом
весом  , если
, если 

Считать, что линейка и кривошип есть однородные стержни, а муфты – точечные массы.
Решение. Механизм состоит из 4 подвижных звеньев. Для удобства решения задачи пронумеруем звенья соответственно рис.5.4.
Система координат, относительно которой будет определяться траектория центра масс механизма показана на рисунке.
Сначала определим координаты центров масс всех звеньев механизма:

Для определения координат центра масс механизма эллипсографа воспользуемся формулой (5.1):

Следовательно, координаты центра масс эллипсографа имеют значения:

Для нахождения уравнения траектории центра масс в явном виде необходимо из этих уравнений исключить угол  . Решив оба уравнения относительно
. Решив оба уравнения относительно  и
и  , возводя их затем к квадрату и сложив, получим:
, возводя их затем к квадрату и сложив, получим:

Траекторией центра масс является окружность с центром в точке  и радиусом
и радиусом  , который равен:
, который равен:

Ответ: 
Задача № 4
Определить зависимость от угла поворота кривошипа  координат центра масс кривошипно-ползунного механизма, что изображено на рис.5.5. Длина кривошипа
координат центра масс кривошипно-ползунного механизма, что изображено на рис.5.5. Длина кривошипа  , его вес
, его вес  , длина шатуна
, длина шатуна  , его вес
, его вес  , вес ползуна
, вес ползуна  .
.
Решение. Выберем систему координат  как показано на рис.5.5. Рассмотрим механизм в произвольном положении, которое определяется углом
как показано на рис.5.5. Рассмотрим механизм в произвольном положении, которое определяется углом  (для любого положения
(для любого положения  , так как
, так как  ).
).
Применяя формулу (5.1), получим:

где  – координаты центров тяжести тел, составляющих систему,
– координаты центров тяжести тел, составляющих систему,
 – масса всей системы.
– масса всей системы.
С рис.5.5 находим:

Масса всей системы в данном случае равна:

Подставляя в выражения (1) и (2) значения координат центров масс тел механической системы и величину массы системы  , получим:
, получим:

Ответ: 
Задача № 5
Определить уравнение траектории центра масс кулисного механизма (рис.5.6), если вес кривошипа  равен
равен  , вес ползуна
, вес ползуна  равен
равен  , а вес кулисы и штанги
, а вес кулисы и штанги  равен
равен  . Кривошип, который вращается с постоянной угловой скоростью
. Кривошип, который вращается с постоянной угловой скоростью  , считать тонким однородным стержнем, а ползун
, считать тонким однородным стержнем, а ползун  – точечной массой. Центр тяжести кулисы и штанги расположен в точке
– точечной массой. Центр тяжести кулисы и штанги расположен в точке  , причем
, причем  . При расчетах принять:
. При расчетах принять:

Будем считать, что в начальный момент ползун  занимал крайнее правое положение.
занимал крайнее правое положение.
Решение. Выберем оси декартовых координат, как показано на рисунке, где положение кулисного механизма соответствует моменту времени  . Так как кривошип вращается равномерно, то его угол поворота равен
. Так как кривошип вращается равномерно, то его угол поворота равен 
Для определения положения центра масс системы  необходимо найти его координаты
необходимо найти его координаты  и
и  по формуле (5.1).
по формуле (5.1).
Поскольку механическая система состоит из трех тел – кривошипа  , ползуна
, ползуна  и кулисы со штангой
и кулисы со штангой  , то:
, то:

Индекс 1 соответствует кривошипу, индекс 2 – ползуну  , индекс 3 – кулисе со штангой.
, индекс 3 – кулисе со штангой.

Из рисунка видно:

Подставим значения  в формулы для определения
в формулы для определения  и
и  .
.

Исключим время  в уравнениях, которые определяют движение центра масс.
в уравнениях, которые определяют движение центра масс.
Для этого решим оба уравнения относительно  и
и  :
:

Возведем эти уравнения к квадрату и добавим:

Таким образом, траекторией центра масс кулисного механизма является эллипс с полуосями  и
и 
Центр эллипса лежит на оси  и отдален от начала координат
и отдален от начала координат  вправо на расстояние
вправо на расстояние 
Ответ: 
Моменты инерции твердого тела относительно оси
Влияние собственных свойств тела на вращательное движение значительно сложнее, чем в поступательном движении.
Также как масса тела является мерой инертности тела при его поступательном движении, так и момент инерции тела относительно данной оси является мерой инертности тела при его вращательном движении.
Как мера инертности тела момент инерции входит во все формулы вращательного движения. Не зная момента инерции тела, не умея его определить, нельзя решать задачи, которые связаны с вращательным или сложным движением тела, частью которого является вращательное движение.
Момент инерции тела (системы) относительно оси, например  , обозначим
, обозначим  (индекс указывает на ось, относительно которой определяется момент инерции).
(индекс указывает на ось, относительно которой определяется момент инерции).
Моментом инерции тела относительно оси, например  , называется скалярная величина, равная сумме произведений масс точек тела на квадраты их расстояний к оси:
, называется скалярная величина, равная сумме произведений масс точек тела на квадраты их расстояний к оси:

Если тело сплошное, то под  необходимо понимать массу элементарной частицы тела
необходимо понимать массу элементарной частицы тела  , тогда момент инерции будет выражаться интегралом:
, тогда момент инерции будет выражаться интегралом:

где  – расстояние доли
– расстояние доли  от оси.
от оси.
Этот интеграл берется по всей массе тела. Очевидно, что величина момента инерции зависит от размеров и формы тела , а также от закона распределения массы в теле.
Момент инерции измеряется в системе СИ – в  , в технической системе – в
, в технической системе – в  .
.
Для тел правильной геометрической формы определение моментов инерции делается с помощью интегрального вычисления. Если тело имеет неправильную форму, то момент инерции его определяется либо приблизительно, путем разбития тела на несколько тел, которые имеют правильную геометрическую форму, либо экспериментально.
Для однородного тела, при плотности  :
:

где интеграл берется по всему объему тела.
Для однородной материальной поверхности:

где  – масса единицы плоскости поверхности и интеграл берется по всей плоскости поверхности.
– масса единицы плоскости поверхности и интеграл берется по всей плоскости поверхности.
Для однородной материальной линии:

где  – масса единицы длины линии. Интеграл берется по длине
– масса единицы длины линии. Интеграл берется по длине  .
.
Для одной материальной точки, которая находится на расстоянии  от оси, момент инерции равен:
от оси, момент инерции равен:

Иногда при определении момента инерции тела пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси, например  , называется линейная величина
, называется линейная величина  , определяемая равенством:
, определяемая равенством:

где  – масса тела.
– масса тела.
Следовательно, радиус инерции определяет расстояние от оси  к точке, в которой необходимо сосредоточить всю массу
к точке, в которой необходимо сосредоточить всю массу  тела, чтобы момент инерции точки относительно этой оси равнялся моменту инерции тела.
тела, чтобы момент инерции точки относительно этой оси равнялся моменту инерции тела.
Момент инерции системы относительно начала координат равен

Моменты инерции относительно координатных осей (осевые моменты) выражаются зависимостями:

Существует простая зависимость между моментами инерции тела относительно параллельных осей, одна из которых проходит через его центр масс (теорема Гюйгенса-Штейнера).
Момент инерции тела относительно любой оси равен моменту инерции тела относительно оси, проходящей через центр масс тела параллельно данной оси, плюс произведение массы тела на квадрат расстояния между осями:

где  – момент инерции тела относительно оси, которая проходит через центр масс и параллельна данной;
– момент инерции тела относительно оси, которая проходит через центр масс и параллельна данной;
 – момент инерции тела относительно данной оси;
– момент инерции тела относительно данной оси;
 – расстояние между осями.
– расстояние между осями.
Из выражения (5.4) вытекает, что наименьшим момент инерции тела будет относительно той оси, которая проходит через центр его масс.
Моменты инерции некоторых однородных тел
| Форма тела. | Схема тела. | Момент инерции. |
| Тонкий прямолинейный стержень |  |
 |
| -„- |  |
 |
| Круглая пластинка малой толщины |  |
 |
| Кольцо (материальная окружность) |  |
 |
| Круглый цилиндр |  |
 |
| Прямоугольный параллелепипед |  |
 |
| Полый шар со стенками малой толщины |  |
 |
| Шар |  |
 |
Примеры решения задач на тему: Моменты инерции твердого тела относительно оси
Задача №1
Маятник, изображенный на рис. 5.7, состоит из тонкого однородного стержня длиной  и массой
и массой  и круглого однородного диска с радиусом
и круглого однородного диска с радиусом  и массой
и массой 

Определить момент инерции  относительно оси его вращения
относительно оси его вращения  (ось
(ось  направлена перпендикулярно плоскости рисунка).
направлена перпендикулярно плоскости рисунка).
Решение. Маятник состоит из двух тел: стержня и диска, поэтому

где  и
и  моменты инерции относительно оси
моменты инерции относительно оси  стержня и диска, соответственно.
стержня и диска, соответственно.
Момент инерции стержня равен (см. 5.5):

Момент инерции диска найдем по формуле (5.4):

где  – момент инерции диска относительно оси, которая проходит параллельно оси
– момент инерции диска относительно оси, которая проходит параллельно оси  через его центр масс, точку
через его центр масс, точку  , а расстояние от центра масс к оси
, а расстояние от центра масс к оси  –
– 
Итак

Пользуясь выражениями для моментов инерции стержня (2) и диска (3), найдем момент инерции маятника относительно оси  :
:

После подстановки в выражение (4) числовых данных, получим:

Ответ: 
Задача №2.
Определить момент инерции  стального вала радиуса
стального вала радиуса  см и массой
см и массой  относительно его образующей. Вал считать однородным сплошным цилиндром (рис.5.8).
относительно его образующей. Вал считать однородным сплошным цилиндром (рис.5.8).

Решение. Для определения момента инерции стального вала относительно оси  , надо воспользоваться формой Гюйгенса-Штейнера
, надо воспользоваться формой Гюйгенса-Штейнера

где  – момент инерции относительно оси
– момент инерции относительно оси  , которая проходит через центр масс тела.,
, которая проходит через центр масс тела.,
 – масса вала,
– масса вала,
 – расстояние между осями, равное радиусу вала.
– расстояние между осями, равное радиусу вала.

Тогда

Ответ: 
Задача № 3
Определить осевые моменты инерции  и
и  изображенной на рис.5.9 однородной прямоугольной пластинки весом
изображенной на рис.5.9 однородной прямоугольной пластинки весом  .
.

Решение. Определим момент инерции пластинки относительно оси  . Для этого выделим на расстоянии
. Для этого выделим на расстоянии  полоску шириной
полоску шириной  .
.
Момент инерции этой тонкой полоски относительно оси  равен:
равен:

где  – масса полоски.
– масса полоски.
Масса полоски равна:

где  – площадь полоски;
– площадь полоски;
 – масса единицы площади поверхности пластинки.
– масса единицы площади поверхности пластинки.
Тогда:

а момент инерции всей пластинки будет равен сумме моментов инерции всех полосок, на которые можно разбить пластинку:

При предельном переходе, то есть, когда 

Итак,

Вычислим массу пластинки:

Таким образом

Момент инерции пластинки относительно оси  находим аналогичным путем и получим:
находим аналогичным путем и получим:

Ответ: 
Задача №4
Определить момент инерции относительно оси 
 однородного прямоугольного параллелепипеда весом
однородного прямоугольного параллелепипеда весом  (рис.5.10).
(рис.5.10).
Решение. Выделим элементарный параллелепипед со сторонами основания  и высотой
и высотой  Расстояние элементарного параллелепипеда от осей
Расстояние элементарного параллелепипеда от осей  и
и  равно
равно  и
и  соответственно.
соответственно.
Момент инерции элементарного параллелепипеда относительно оси  равен:
равен:

где:  – масса элементарного параллелепипеда, равна:
– масса элементарного параллелепипеда, равна:


Тогда, 
а момент инерции всего параллелепипеда

При предельном переходе, то есть при  то сумма, которая стоит справа, переходит в двойной интеграл:
то сумма, которая стоит справа, переходит в двойной интеграл:

Вычислим двойной интеграл:

Масса параллелепипеда:

Следовательно,

Ответ: 
Задача №5
Определить момент инерции относительно оси  тонкой однородной параболической пластинки (рис.5.11) массой
тонкой однородной параболической пластинки (рис.5.11) массой  . Предельная прямая пластинки параллельна оси
. Предельная прямая пластинки параллельна оси  и удалена от нее на расстояние
и удалена от нее на расстояние  . Уравнение параболы, которая ограничивает пластинку, имеет вид
. Уравнение параболы, которая ограничивает пластинку, имеет вид 

Решение. Проведем на пластинке (рис.5.11) две прямые, параллельные оси  и удаленные от нее на расстоянии
и удаленные от нее на расстоянии  и
и 
Вычислим момент инерции относительно оси  элементарной полоски, которая ограничена этими прямыми и параболическим контуром пластинки (заштрихована на рисунке):
элементарной полоски, которая ограничена этими прямыми и параболическим контуром пластинки (заштрихована на рисунке):

где  – элементарная масса плоскости, которая равна:
– элементарная масса плоскости, которая равна:

Здесь  – плотность пластинки,
– плотность пластинки,
 – площадь пластинки.
– площадь пластинки.
Итак,

Из уравнения  вытекает
вытекает 
Таким образом

Момент инерции пластинки относительно оси  равен:
равен:

Масса пластинки 
где площадь пластинки 
Тогда

Следовательно,

Ответ: 
Задача №6
Определить для тонкого равнобедренного треугольника  , основание которого равно
, основание которого равно  , высота
, высота  и масса
и масса  (рис.5.12), его моменты инерции относительно основания и относительно высоты.
(рис.5.12), его моменты инерции относительно основания и относительно высоты.

Решение. С серединой  основания равнобедренного треугольника свяжем начало системы координат
основания равнобедренного треугольника свяжем начало системы координат  ; ось
; ось  проведем по основанию
проведем по основанию  , а ось
, а ось  – перпендикулярно основанию.
– перпендикулярно основанию.
Для определения момента инерции треугольника относительно основания (относительно оси  ) выделим на расстоянии
) выделим на расстоянии  элементарную полоску шириной
элементарную полоску шириной  .
.
Момент инерции этой полоски относительно оси  составит:
составит:

где  , масса полоски длиной
, масса полоски длиной  , равна:
, равна:

Тогда момент инерции элементарной полоски относительно основания будет равен:

Найдем зависимость между координатой  и длиной полоски
и длиной полоски  . Из сходства треугольников
. Из сходства треугольников  и
и  (рис.5.12) следует:
(рис.5.12) следует:
 или
или 
откуда

Подставив (2) у (1’), получим:

а момент инерции треугольника  относительно основания определится как
относительно основания определится как

или

В интеграле (3) границы координаты  меняются от
меняются от  к
к  .
.
Высчитаем интеграл (3):

Выразим момент инерции  через массу
через массу  треугольника
треугольника  :
:

Преобразуем выражение (4):

или

Перейдем к определению момента инерции треугольника  относительно его высоты
относительно его высоты  .
.
Поскольку у треугольника  высота
высота  является осью симметрии, то достаточно определить момент инерции относительно этой оси для прямоугольного треугольника
является осью симметрии, то достаточно определить момент инерции относительно этой оси для прямоугольного треугольника  , тогда
, тогда

где  – момент инерции треугольника
– момент инерции треугольника  ;
;
 – момент инерции треугольника
– момент инерции треугольника  .
.
Расчетная схема для определения момента инерции  приведена на рис.5.13.
приведена на рис.5.13.

Выделим элементарную полоску на расстоянии  от оси
от оси  , ширина полоски –
, ширина полоски –  , длина –
, длина –  .
.
Определим момент инерции этой полоски относительно оси  :
:

где  – масса элементарной полоски.
– масса элементарной полоски.
Определим зависимость между длиной полоски  и координатой
и координатой  . Из сходства треугольников
. Из сходства треугольников  и
и  получается:
получается:
 или
или 
откуда

Подставив (6) у (5), получим:

Момент инерции треугольника  относительно оси
относительно оси  (относительно высоты
(относительно высоты  ), равен:
), равен:

или

Определим интеграл (7):

Окончательно,

Тогда, момент инерции треугольника  относительно высоты
относительно высоты  будет равен:
будет равен:

Ответ: 
Задачи, которые рекомендуются для самостоятельной работы: 34.9, 34.12, 34.16 [2].
Теорема о движении центра масс механической системы
Силы, действующие на механическую систему, можно условно поделить на внешние и внутренние.
Силы, которые действуют на точки данной механической системы со стороны точек или тел, не входящих в эту систему, называются внешними.
Силы, действующие на точки механической системы со стороны точек данной системы, называются внутренними.
Внешние силы обозначаются верхним индексом  , внутренние –
, внутренние –  :
:  -внешняя сила,
-внешняя сила,  – внутренняя сила.
– внутренняя сила.
Внутренние силы обладают следующими свойствами:
а) геометрическая сумма (главный вектор) внутренних сил равна нулю:

б) геометрическая сумма моментов (главный момент) всех внутренних сил относительно любого центра  или оси равна нулю:
или оси равна нулю:


Теорема о движении центра масс механической системы формулируется следующим образом:
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех внешних сил, действующих на систему.

где  – масса системы;
– масса системы;
 – ускорение центра масс;
– ускорение центра масс;
 – сумма внешних сил, которые действуют на систему.
– сумма внешних сил, которые действуют на систему.
Из сравнения приведенной выше формулы со вторым законом динамики, который, как известно, записан для материальной точки:

можно сделать следующий вывод:
Центр масс механической системы движется как материальная точка, в которой сосредоточено массу всей системы и к которой приложены те же внешние силы, действующие на систему.
Теорема о движении центра масс системы, если ее записать в проекциях на оси декартовой системы координат, имеет вид:

где  – координаты центра масс механической системы.
– координаты центра масс механической системы.
Из приведенных уравнений следует, что внутренние силы непосредственно не влияют на движение центра масс. Теорема позволяет исключить из рассмотрения все ранее неизвестные внутренние силы.
Задачи динамики поступательного движения твердого тела решаются с помощью теоремы о движении центра масс системы материальных точек.
Действительно, применив эту теорему, мы определим уравнение траектории, скорость и ускорение центра тяжести твердого тела. При поступательном движении твердого тела траектории всех его точек одинаковы, одинаковы и их скорости и ускорения.
Закон сохранения движения центра масс
Из теоремы о движении центра масс вытекает несколько следствий:
а) если геометрическая сумма всех внешних сил, действующих на систему, равна нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно.
Пусть  , тогда
, тогда
 или
или  , поэтому
, поэтому 
Если изначально центр масс был в покое, то он и останется в покое. Если же начальная скорость не равна нулю, то центр масс движется прямолинейно и равномерно с этой скоростью;
б) если геометрическая сумма внешних сил, действующих на систему, не равна нулю, но сумма их проекций на какую-нибудь ось (например, ось  ) равна нулю, то центр масс системы вдоль этой оси или не движется, или движется равномерно.
) равна нулю, то центр масс системы вдоль этой оси или не движется, или движется равномерно.
Если  , то:
, то:
 или
или  , поэтому
, поэтому 
Если при этом равна нулю начальная скорость, то есть  , то
, то  , то есть
, то есть 
Таким образом видим, что в этом случае координата центра масс  механической системы во время ее движения остается неизменной.
механической системы во время ее движения остается неизменной.
При  проекция центра масс на ось
проекция центра масс на ось  движется равномерно.
движется равномерно.
Все эти результаты выражают законы сохранения движения центра масс системы.
Порядок решения задач на применение теоремы о движении центра масс
Рекомендуется такая последовательность решения задач:
Изобразить на рисунке все внешние силы, действующие на систему;
Выбрать систему координат;
Записать теорему о движении центра масс в векторной форме;
Спроектировать это векторное уравнение на оси координат;
Высчитать суммы проекций всех внешних сил на оси координат и подставить их в проекции уравнения движения;
Решить полученные уравнения и определить искомые величины.
Примеры решения задач на тему: Теорема о движении центра масс механической системы
Задача № 1
Определить главный вектор внешних сил, действующих на колесо весом  , которое скатывается без скольжения с наклонной плоскости, если его центр масс
, которое скатывается без скольжения с наклонной плоскости, если его центр масс  движется по закону
движется по закону  (рис.6.1).
(рис.6.1).

Решение. Покажем внешние силы, которые действуют на колесо: силу тяжести  и реакцию поверхности
и реакцию поверхности  , которые проходят через центр масс колеса
, которые проходят через центр масс колеса  .
.
Запишем теорему о движении центра масс в векторной форме:

Выбираем систему координат  и спроектируем уравнение (1) на оси
и спроектируем уравнение (1) на оси  и
и  :
:

Поскольку  . то
. то  и
и  . То есть, главный вектор внешних сил является параллельным оси
. То есть, главный вектор внешних сил является параллельным оси  :
:

Найдем проекцию ускорения центра масс на ось  :
:

Итак,

Ответ: 
Задача №2
Колесо весом  и радиусом
и радиусом  катится со скольжением по прямолинейной горизонтальной рейке в результате действия постоянной силы
катится со скольжением по прямолинейной горизонтальной рейке в результате действия постоянной силы  , которая приложена к его центру тяжести
, которая приложена к его центру тяжести  (рис.6.2).
(рис.6.2).

Определить скорость центра масс колеса, если в начальный момент оно находилось в покое. Коэффициент трения скольжения равен  .
.
Решение. На колесо действуют внешние силы:  – сила тяжести колеса,
– сила тяжести колеса,  – движущая сила,
– движущая сила,  – нормальная реакция рейки,
– нормальная реакция рейки,  – сила трения скольжения, которая направлена вдоль рельса в сторону, противоположную силе
– сила трения скольжения, которая направлена вдоль рельса в сторону, противоположную силе  .
.
Запишем теорему о движении центра масс колеса в векторной форме:

где  – ускорение центра масс колеса.
– ускорение центра масс колеса.
Спроектируем это уравнение на оси координат  :
:

Во время движения колеса  Итак
Итак  из второго уравнения (1) получаем:
из второго уравнения (1) получаем:

Поскольку при качении колеса со скольжением сила трения достигает своего максимального значения, то

Подставим (3) в первое из уравнений (1) и получим:

Поскольку

то

Согласно начальным условиям при  с тех пор находим, что произвольная постоянная
с тех пор находим, что произвольная постоянная 
Итак, закон изменения скорости центра масс колеса  имеет вид:
имеет вид:

Ответ: 
Задача №3
На однородную призму  , которая лежит на горизонтальной плоскости, положили однородную призму
, которая лежит на горизонтальной плоскости, положили однородную призму  (рис.6.3,а), поперечные сечения призм – прямоугольные треугольники, вес призмы
(рис.6.3,а), поперечные сечения призм – прямоугольные треугольники, вес призмы  втрое больше веса призмы
втрое больше веса призмы  . Необходимые размеры показаны на рисунке.
. Необходимые размеры показаны на рисунке.
Определить длину  , на которую передвинется призма
, на которую передвинется призма  , когда призма
, когда призма  , спускаясь по поверхности призмы
, спускаясь по поверхности призмы  , дойдет к горизонтальной плоскости. Предположить, что все поверхности, которые соприкасаются, идеально гладкие.
, дойдет к горизонтальной плоскости. Предположить, что все поверхности, которые соприкасаются, идеально гладкие.
Решение. Рассмотрим движение механической системы, состоящей из 2-х призм  и
и  . Призма
. Призма  , спускаясь по призме
, спускаясь по призме  справа, как будто выжимает ее, отодвигает налево (рис.6.3, б).
справа, как будто выжимает ее, отодвигает налево (рис.6.3, б).
Для решения этой задачи применим теорему о движении центра масс.
На систему действуют внешние силы: тяжести  призмы
призмы  , тяжести
, тяжести  призмы
призмы  , нормальная реакция плоскости
, нормальная реакция плоскости  (рис.6.3). Внешняя сила трения призм по идеально гладкой поверхности равна нулю.
(рис.6.3). Внешняя сила трения призм по идеально гладкой поверхности равна нулю.
Таким образом, все внешние силы системы вертикальны. Внутренние силы системы (давление призмы  на призму
на призму  , реакция на это давление, а также силы трения между призмами
, реакция на это давление, а также силы трения между призмами  и
и  ), нас не интересуют.
), нас не интересуют.
Введем систему координат  , ось
, ось  направим по горизонтали справа и запишем теорему о движении центра масс системы в проекции на ось
направим по горизонтали справа и запишем теорему о движении центра масс системы в проекции на ось  :
:

Поскольку внешние силы перпендикулярны оси  , то
, то

Тогда

где  – постоянная интегрирования.
– постоянная интегрирования.
В начальный момент времени система находилась в состоянии покоя, то есть скорость центра масс  Итак,
Итак, 
Из этого следует, что  , то есть, абсцисса центра масс, независимо от перемещения призм, остается постоянной.
, то есть, абсцисса центра масс, независимо от перемещения призм, остается постоянной.

Запишем выражение для определения координаты центра масс в начале движения:

где  – абсцисса центра масс призмы
– абсцисса центра масс призмы  ,
,
 – абсцисса центра масс призмы
– абсцисса центра масс призмы  .
.
Выражение для определения координаты центра масс системы, когда призма  опускается по боковой грани призмы
опускается по боковой грани призмы  к горизонтальной плоскости:
к горизонтальной плоскости:

где  – новое значение абсциссы центра масс призмы
– новое значение абсциссы центра масс призмы  ,
,
 – новое значение абсциссы центра масс призмы
– новое значение абсциссы центра масс призмы  .
.
Поскольку  , то
, то

или

Перепишем это уравнение следующим образом:

Найдем перемещение центров масс призм  и
и  :
:

Присутствие слагаемого ( ) в последнем уравнении учитывает перемещение призмы
) в последнем уравнении учитывает перемещение призмы  вместе с призмой
вместе с призмой  слева на величину
слева на величину  .
.
Подставим значение перемещений в уравнение (1):
 .
.
Решим это уравнение относительно  , имея в виду, что
, имея в виду, что  :
:

Ответ: 
Задача №4
Три груза (рис.6.4), весом  соединенные невесомой нитью, которая не растягивается, и которая перекинута через неподвижные блоки
соединенные невесомой нитью, которая не растягивается, и которая перекинута через неподвижные блоки  и
и  . Во время опускания груза 1 вниз груз 2 перемещается по верхнему основанию четырехугольной усеченной пирамиды
. Во время опускания груза 1 вниз груз 2 перемещается по верхнему основанию четырехугольной усеченной пирамиды  весом
весом  справа, а груз 3 поднимается по боковой грани
справа, а груз 3 поднимается по боковой грани  вверх. Пренебрегая трением между срезанной пирамидой
вверх. Пренебрегая трением между срезанной пирамидой  и полом, определить перемещение
и полом, определить перемещение  усеченной пирамиды
усеченной пирамиды  относительно пола, если груз
относительно пола, если груз  опустится на
опустится на 
Решение. Изобразим все внешние силы, которые приложены к материальной системе, состоящей из пирамиды и трех грузов (рис.6.4). Внешними силами являются:  – сила тяжести пирамиды;
– сила тяжести пирамиды;  – силы тяжести грузов;
– силы тяжести грузов;  – нормальная реакций
– нормальная реакций

горизонтальной плоскости. Направим ось  по горизонтали справа и запишем теорему о движении центра масс системы материальных точек в проекции на эту ось:
по горизонтали справа и запишем теорему о движении центра масс системы материальных точек в проекции на эту ось:

Поскольку все внешние силы перпендикулярны оси  , то
, то 
Следовательно, 
тогда

В начальный момент времени система была в состоянии покоя, то есть  , поэтому
, поэтому 
Поскольку

то

Таким образом, абсцисса центра масс системы не зависит от перемещений грузов, входящих в систему, и остается неизменной относительно неподвижной системы координат  .
.
Запишем выражение для определения  для начального момента времени, когда грузы находились в состоянии покоя:
для начального момента времени, когда грузы находились в состоянии покоя:

где  – абсциссы центров масс пирамиды
– абсциссы центров масс пирамиды  и грузов 1,2 и 3.
и грузов 1,2 и 3.
Если груз 1 опустится на величину  при неподвижной пирамиде, то координата
при неподвижной пирамиде, то координата  при этом не изменится. Тогда груз 2 переместится вправо на величину
при этом не изменится. Тогда груз 2 переместится вправо на величину  и координата его центра масс будет равна
и координата его центра масс будет равна  . Груз 3 тоже подвинется по наклонной поверхности
. Груз 3 тоже подвинется по наклонной поверхности  на величину
на величину  , при этом по направлению оси
, при этом по направлению оси  его положение изменится на величину
его положение изменится на величину  и координата центра масс будет
и координата центра масс будет  . То есть, относительно пирамиды центр масс системы изменит свое положение, но не изменит его относительно неподвижной системы координат, поскольку должен выполняться закон сохранения движения центра масс. И тогда пирамида должна переместиться налево на некоторую величину
. То есть, относительно пирамиды центр масс системы изменит свое положение, но не изменит его относительно неподвижной системы координат, поскольку должен выполняться закон сохранения движения центра масс. И тогда пирамида должна переместиться налево на некоторую величину  .
.
Грузы 1,2 и 3 вместе с пирамидой также переместятся влево на расстояние  , и новые координаты всех центров масс будут равны:
, и новые координаты всех центров масс будут равны:

Запишем выражение для определения положения абсциссы центра масс для нового положения системы:

Поскольку  то
то

После приведения подобных получим:

или

Окончательно

После подстановки числовых величин, получим:

Ответ: 
Задача № 5
Электрический двигатель весом  с горизонтальным валом без всяких креплений установлен на гладком горизонтальном фундаменте.
с горизонтальным валом без всяких креплений установлен на гладком горизонтальном фундаменте.
На валу электродвигателя (рис.6.5) под прямым углом закреплен одним концом однородный стержень  длиной
длиной  и весом
и весом  , на второй конец стержня насажен точечный груз
, на второй конец стержня насажен точечный груз  весом
весом  ; угловая скорость вала равна
; угловая скорость вала равна  .
.
Определить:
Закон горизонтального движения электродвигателя;
Угловую скорость вала электродвигателя, при которой электродвигатель будет «подскакивать» над фундаментом;
Наибольшее горизонтальное усилие  , которое действует на болты, если ими закреплен корпус электродвигателя на фундаменте.
, которое действует на болты, если ими закреплен корпус электродвигателя на фундаменте.
Решение. Будем рассматривать электромотор, стержень и груз как одну механическую систему. Внешними силами, которые действуют на эту систему, являются: сила тяжести электродвигателя  , сила тяжести стержня
, сила тяжести стержня  , сила тяжести груза
, сила тяжести груза  , а также реакции фундамента
, а также реакции фундамента  и
и  . Все эти силы вертикальны.
. Все эти силы вертикальны.

Начало неподвижной системы координат возьмем в точке  , соответствующей положению центра вала электродвигателя, когда стержень направлен вертикально вверх (рис.6.5, а).
, соответствующей положению центра вала электродвигателя, когда стержень направлен вертикально вверх (рис.6.5, а).
Поскольку проекция на ось  главного вектора действующих на систему внешних сил равна нулю, то дифференциальное уравнение движения центра масс системы вдоль оси
главного вектора действующих на систему внешних сил равна нулю, то дифференциальное уравнение движения центра масс системы вдоль оси  имеет вид:
имеет вид:

где  – масса системы.
– масса системы.
В нашем случае  или
или

Тогда дифференциальное уравнение движения центра масс (1) приводится к виду:

откуда 
Предполагая, что в начальный момент скорость центра масс системы равна нулю, то есть, при пуске электродвигателя он был неподвижным, получим 
Следовательно,  , то есть, центр масс системы не перемещается вдоль оси
, то есть, центр масс системы не перемещается вдоль оси  .
.
Поскольку в начальный момент времени центр масс системы находится на оси  (то есть,
(то есть,  ), то и в любой момент времени
), то и в любой момент времени 
При вращении стержня координаты центров масс электрического двигателя, стержня и груза  будут варьироваться.
будут варьироваться.
Предположим, что в некоторый момент времени  координата центра масс мотора станет равной
координата центра масс мотора станет равной  , тогда координаты центров масс стержня и груза
, тогда координаты центров масс стержня и груза  будут равны
будут равны  и
и  (рис.6.5,b).
(рис.6.5,b).
Поскольку все время  , то
, то

где  На рисунке 6.5,b показан момент, когда координата
На рисунке 6.5,b показан момент, когда координата  отрицательна.
отрицательна.
Тогда

откуда

и, следовательно:

Таким образом, центр электродвигателя совершает гармонические колебания вдоль оси  с амплитудой, равной:
с амплитудой, равной:

и периодом

Определим угловую скорость вала, при которой электродвигатель будет «подскакивать» над фундаментом.
Для этого составим дифференциальное уравнение движения центра масс системы вдоль оси  :
:

или

где  – суммарная реакция фундамента.
– суммарная реакция фундамента.
Значение  найдем из выражения для координаты центра масс:
найдем из выражения для координаты центра масс:

поскольку

Последнее уравнение перепишем в виде:

Возьмем из обеих частей равенства вторую производную по времени

Из уравнений (2) и (3) вытекает, что

итак,

Минимальное значение реакции фундамента будет при  :
:

Если  , то это значит, что электромотор не прижимается к фундаменту. Итак, искомое значение угловой скорости, при которой электродвигатель начинает “подскакивать” над фундаментом, найдем из условия
, то это значит, что электромотор не прижимается к фундаменту. Итак, искомое значение угловой скорости, при которой электродвигатель начинает “подскакивать” над фундаментом, найдем из условия

откуда

В завершение определим наибольшее горизонтальное усилие  , которое действует на болты, если ими будет закреплен корпус электродвигателя на фундаменте.
, которое действует на болты, если ими будет закреплен корпус электродвигателя на фундаменте.
На рис.6.5 штрих-пунктирными линиями показаны оси болтов и горизонтальные реакции болтов  и
и  .
.
В этом случае дифференциальное уравнение движения центра масс системы вдоль оси  будет:
будет:

Значение  найдем по формуле:
найдем по формуле:

или

Тогда

При этом уравнение (4) принимает вид:

Из последнего уравнения выходит:

Таким образом, максимальное горизонтальное усилие, действующее на болты, будет при  :
:

Ответ:

Задачи, которые рекомендуются для самостоятельной работы: 35.1; 35.6; 35.10; 35.20 [2].
Теорема об изменении количества движения точки и механической системы
Теорема об изменении количества движения (импульса) системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает количество движения с импульсом внешних сил, действующих на тела, составляющие систему.
Импульс силы
Для характеристики действия силы за некоторый промежуток времени вводится понятие импульса силы.
Если сила  – постоянная, то импульс силы
– постоянная, то импульс силы  равен
равен

Направление импульса силы  совпадает с направлением
совпадает с направлением  .
.
Единица измерения импульса в системе СИ –  , в системе МкГс –
, в системе МкГс –  .
.
Если сила  переменная, то импульс силы за конечный промежуток времени
переменная, то импульс силы за конечный промежуток времени  определяется как интеграл:
определяется как интеграл:

Импульс силы – сложная физическая величина, которая одновременно учитывает влияние модуля, направления и времени действия силы на изменение состояния движения тела.
Модуль импульса силы можно определить через его проекции на оси координат:

где  – проекции силы;
– проекции силы;
 – проекции импульса на оси координат.
– проекции импульса на оси координат.
Углы между вектором  и осями координат определяются из следующих соотношений:
и осями координат определяются из следующих соотношений:

Теорема об изменении количества движения точки и системы
Одной из мер движения точки является количество ее движения.
Количеством движения точки называется вектор  , который равен произведению массы
, который равен произведению массы  точки на ее скорость
точки на ее скорость  и направлен по вектору скорости:
и направлен по вектору скорости:
 .
.
Понятие количества движения было введено в механику Декартом и положено в основу механики Ньютоном.
Единица измерения количества движения в системе СИ –  , в системе МкГс –
, в системе МкГс –  .
.
Если спроектировать вектор количества движения на оси координат, то ее проекции определяются следующим образом:

Теорема об изменении количества движения точки в дифференциальной форме имеет вид:

Производная по времени от количества движения материальной точки равна геометрической сумме всех сил, действующих на эту точку.
Теорема об изменении количества движения точки в интегральной форме:

Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех сил, которые приложены к точке.
Векторному уравнению (7.1) соответствуют три уравнения в проекциях на оси координат:

Большинство практических задач решается с использованием выражения (7.2).
Количеством движения механической системы называется векторная величина  , равная геометрической сумме (главному вектору) количеств движения всех точек этой системы.
, равная геометрической сумме (главному вектору) количеств движения всех точек этой системы.

Найти  можно путем построения многоугольника количеств движения всех точек системы (рис.7.1).
можно путем построения многоугольника количеств движения всех точек системы (рис.7.1).
Замыкающая сторона векторного многоугольника будет представлять собой вектор  .
.
Величина  может быть какой угодно, даже равняться нулю, когда многоугольник, построенный из векторов
может быть какой угодно, даже равняться нулю, когда многоугольник, построенный из векторов  , оказывается замкнутым.
, оказывается замкнутым.

Формулу (7.3) можно записать в виде:

где  – масса всей системы;
– масса всей системы;
 – скорость центра масс системы.
– скорость центра масс системы.
Из этой формулы следует, что количество движения системы равно нулю, когда скорость центра масс равна нулю. Например, если тело вращается вокруг неподвижной оси, которая проходит через его центр масс, то количество движения тела равно нулю.
В случае, когда колесо катится, вектор  характеризует только поступательную часть плоского движения колеса.
характеризует только поступательную часть плоского движения колеса.
Теорема об изменении количества движения системы в дифференциальной форме выразится формулой:

где  – главный вектор всех внешних сил, которые действуют на механическую систему.
– главный вектор всех внешних сил, которые действуют на механическую систему.
Производная по времени от количества движения механической системы равна геометрической сумме всех действующих на точки системы внешних сил.
В проекциях на оси координат уравнение (7.5) соответствует уравнениям:

В интегральной форме теорема об изменении количества движения системы имеет вид:

где  – количество движения системы в начальный момент времени.
– количество движения системы в начальный момент времени.
 – количество движения системы в конечный момент времени.
– количество движения системы в конечный момент времени.
Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, которые действуют на систему за тот же промежуток времени.
Векторному уравнению (7.7) соответствуют три уравнения в проекциях на оси координат:

Практическая ценность теоремы заключается в том, что она позволяет исключить из рассматривания неизвестные внутренние силы.
Закон сохранения количества движения системы
Выводы из теоремы об изменении количества движения системы, которые еще имеют название законов сохранения количества движения:
1. Если главный вектор внешних сил, действующих на систему, равен нулю, то вектор количества движения системы не меняется:
если 
то  и
и 
2. Если сумма проекций внешних сил на какую-либо ось, например  , равна нулю, то проекция количества движения системы на эту ось сохраняется постоянной:
, равна нулю, то проекция количества движения системы на эту ось сохраняется постоянной:
если 
то  и
и 
Эти результаты выражают законы сохранения количества движения системы. Из них вытекает, что внутренние силы не могут изменить количество движения системы.
Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
Для материальной точки:
Изобразить на рисунке все силы, приложенные к материальной точке, то есть активные силы и реакции связей.
Выбрать систему координат.
Записать теорему об изменении количества движения точки в векторной форме.
Спроектировать это векторное уравнение на оси выбранной системы координат.
Решить полученные уравнения и определить искомые величины.
Для механической системы:
Изобразить на рисунке все внешние силы.
Выбрать систему координат.
Записать теорему об изменении количества движения системы в векторной форме.
Спроектировать это векторное уравнение на оси выбранной системы координат.
Решить полученные уравнения и определить искомые величины.
Примеры решения задач на тему: Теорема об изменении количества движения точки и механической системы
Задача № 1
Железнодорожный поезд движется по горизонтальному и прямолинейному участку пути (рис.7.2). Во время торможения до полной остановки развивается сила сопротивления, равная  веса поезда. В момент начала торможения скорость
веса поезда. В момент начала торможения скорость  поезда составляла 72 км/ч.
поезда составляла 72 км/ч.

Определить время  и путь
и путь  торможения.
торможения.
Решение. Изобразим силы, действующие на поезд во время торможения: сила тяжести поезда  , нормальная реакция пути
, нормальная реакция пути  , сила сопротивления
, сила сопротивления  , которая по величине равна
, которая по величине равна 
Выберем систему координат. Поскольку движение прямолинейное и горизонтальное, достаточно рассмотреть движение по направлению оси  .
.
Запишем теорему об изменении количества движения поезда (рассматривая его как материальную точку) в интегральной форме:

где  – масса поезда,
– масса поезда,
 – конечная и начальная скорость поезда,
– конечная и начальная скорость поезда,
 – сумма импульсов сил
– сумма импульсов сил  ,
,  ,
,  которые действуют на поезд во время торможения.
которые действуют на поезд во время торможения.
Спроектируем векторное уравнение (1) на ось  :
:

Проекции импульсов сил  и
и  на ось
на ось  равны нулю, поскольку векторы
равны нулю, поскольку векторы  и
и  перпендикулярны оси.
перпендикулярны оси.
Сила сопротивления  во время торможения по величине не изменяется, следовательно, ее импульс равен:
во время торможения по величине не изменяется, следовательно, ее импульс равен:

Скорость в конце участка торможения равна нулю, то есть 
Окончательно, уравнение импульсов (2) в проекции на ось  приобретет вид:
приобретет вид:

или

откуда

С учетом числовых значений величин  и
и  имеем:
имеем:

Путь торможения определим из формулы для равнопеременного движения:

В этом случае ускорение поезда определяется из формулы:

то есть,

Тогда

Ответ: 
Задача № 2
По шероховатой наклонной плоскости, которая составляет с горизонтом угол  , спускается тяжелое тело без начальной скорости.
, спускается тяжелое тело без начальной скорости.
Определить время  , за которое тело пройдет путь длиной
, за которое тело пройдет путь длиной  , если коэффициент трения
, если коэффициент трения  и
и  .
.
Решение. Во время движения на тело действуют сила тяжести тела  , нормальная реакция поверхности
, нормальная реакция поверхности  и сила трения
и сила трения  , которая направлена в сторону, противоположную движению(рис.7.3).
, которая направлена в сторону, противоположную движению(рис.7.3).

Направим ось  вдоль наклонной поверхности вниз и запишем теорему об изменении количества движения в векторной форме:
вдоль наклонной поверхности вниз и запишем теорему об изменении количества движения в векторной форме:

Спроектируем ровность (1) на ось  :
:

Проекция импульса нормальной реакции  на ось
на ось  равна нулю, поскольку сила
равна нулю, поскольку сила  перпендикулярна
перпендикулярна  .
.
Учитывая, что во время движения сила тяжести  и сила трения
и сила трения  не меняются , то
не меняются , то

Кроме того

Итак, уравнение импульса (2) примет вид:

Вычислим силу трения:

Тогда уравнение (3) примет вид:

или 
откуда

Поскольку

то

Используя полученную зависимость, сначала подсчитаем ускорение тела, а после этого – время движения.
Поскольку

то
 и
и 
Из формулы  , учитывая, что при
, учитывая, что при  получим
получим 
Из этой формулы находим время движения  :
:

Ответ: 
Задача № 3
На полигоне пушка, которая наклонена под углом  к горизонту, делает выстрел в мишень. Сила тяжести ствола пушки –
к горизонту, делает выстрел в мишень. Сила тяжести ствола пушки – 
 Сила тяжести снаряда равна
Сила тяжести снаряда равна  Скорость снаряда у дульного среза
Скорость снаряда у дульного среза 
Определить скорость  свободного отката ствола пушки в момент вылета снаряда.
свободного отката ствола пушки в момент вылета снаряда.
Решение. В задаче рассматривается движение материальной системы, состоящей из ствола и снаряда (рис.7.4).

На систему действуют внешние силы: тяжести ствола  и тяжести снаряда
и тяжести снаряда  . Внутренние силы определяются давлением пороховых газов
. Внутренние силы определяются давлением пороховых газов  . Эти силы необходимо исключить из рассмотрения, согласно теореме о количестве движения механической системы.
. Эти силы необходимо исключить из рассмотрения, согласно теореме о количестве движения механической системы.
Применим теорему об изменении количества движения системы:

где  – количество движения системы в конечный момент времени;
– количество движения системы в конечный момент времени;
 – количество движения системы в начальный момент времени;
– количество движения системы в начальный момент времени;
 – сумма импульсов всех внешних сил (
– сумма импульсов всех внешних сил ( ,
,  ).
).
Ось  направим перпендикулярно векторам внешних сил
направим перпендикулярно векторам внешних сил  и
и  .
.
Спроектируем уравнение (1) на ось  :
:

Поскольку проекции сил  и
и  на ось
на ось  равны нулю, то и проекции импульсов
равны нулю, то и проекции импульсов  и
и  также равны нулю. Итак:
также равны нулю. Итак:
 или
или 
Таким образом, проекция количества движения системы на ось  в конечный момент времени равна проекции количества движения системы в начальный момент времени.
в конечный момент времени равна проекции количества движения системы в начальный момент времени.
В начальный момент времени (до выстрела) снаряд и ствол были неподвижны, следовательно, их количества движения равнялись нулю и

В момент вылета снаряда проекция количества движения системы на ось равна:

или

Поскольку

то

откуда
 и
и 
С учетом числовых значений:

Знак минус показывает, что скорость ствола направлена в сторону, противоположную скорости снаряда.
Ответ: 
Задача № 4
Буксирный пароход весом  набрал скорость
набрал скорость  , после чего натянулся буксирный канат, и баржа весом
, после чего натянулся буксирный канат, и баржа весом  двинулась вслед за пароходом.
двинулась вслед за пароходом.
Определить общую скорость парохода и баржи  , считая, что движущая сила и сила сопротивления воды уравновешиваются, то есть, (
, считая, что движущая сила и сила сопротивления воды уравновешиваются, то есть, ( )
)  дв =
дв =  соп (
соп ( ).
).
Решение. Для определения скорости  применим теорему об изменении количества движения системы.
применим теорему об изменении количества движения системы.
На систему, которая состоит из парохода и баржи, действуют внешние силы: силы тяжести  и
и  , силы выталкивания
, силы выталкивания  и
и  , которые приложены к баржи и буксиру, а также движущая сила
, которые приложены к баржи и буксиру, а также движущая сила  дв и сила сопротивления воды
дв и сила сопротивления воды  соп (рис.7.5).
соп (рис.7.5).

Внутренняя сила – натяжение буксирного каната  – неизвестна.
– неизвестна.
Ось  направим горизонтально, вправо.
направим горизонтально, вправо.
Запишем теорему об изменении количества движения данной системы в интегральной форме:

где  – количество движения системы баржа-буксир в тот момент времени, когда они начинают двигаться с одинаковой скоростью;
– количество движения системы баржа-буксир в тот момент времени, когда они начинают двигаться с одинаковой скоростью;
 – количество движения этой системы в начальный момент времени;
– количество движения этой системы в начальный момент времени;
 – сумма импульсов всех внешних сил.
– сумма импульсов всех внешних сил.
Спроектируем уравнение (1) на ось  :
:

Поскольку по условиям  дв =
дв =  соп, а направлены они в разные стороны, то
соп, а направлены они в разные стороны, то

Кроме того, проекции на ось  сил тяжести парохода и баржи, а также выталкивающих сил
сил тяжести парохода и баржи, а также выталкивающих сил  и
и  , равны нулю. Следовательно, проекции импульсов этих сил на ось
, равны нулю. Следовательно, проекции импульсов этих сил на ось  тоже равны нулю. Таким образом уравнение проекций принимает вид:
тоже равны нулю. Таким образом уравнение проекций принимает вид:
 или
или 
Подсчитаем количество движения парохода и баржи в начальный момент времени, когда скорость парохода равна  , а скорость баржи
, а скорость баржи  .
.

Совместимое движение парохода и баржи происходит с одинаковой скоростью  , поэтому количество движения системы в это время
, поэтому количество движения системы в это время

Поскольку

то 
Отсюда имеем

Ответ: 
Задача № 5
Механическая система состоит из грузов 1 и 2 массами  и
и  соответственно, а также прямоугольной вертикальной плиты 3 массой
соответственно, а также прямоугольной вертикальной плиты 3 массой  которая движется вдоль горизонтальных направляющих( рис.7.6). В момент времени
которая движется вдоль горизонтальных направляющих( рис.7.6). В момент времени  , когда скорость плиты
, когда скорость плиты  груз под действием внутренних сил начинают двигаться по желобам плиты. Груз 1 движется по дуге окружности с радиусом
груз под действием внутренних сил начинают двигаться по желобам плиты. Груз 1 движется по дуге окружности с радиусом  по закону
по закону  , где
, где  выражено в радианах,
выражено в радианах,  – в секундах (ось, от которой ведется положительное направление отсчета угла
– в секундах (ось, от которой ведется положительное направление отсчета угла  показано на рисунке). Груз 2 движется от точки
показано на рисунке). Груз 2 движется от точки  прямолинейно по закону
прямолинейно по закону  , где
, где  выражено в метрах,
выражено в метрах,  – в секундах (на рисунке груз 2 изображен в положении положительного отсчета координаты
– в секундах (на рисунке груз 2 изображен в положении положительного отсчета координаты  ), угол
), угол  .
.
Определить зависимость  , то есть, скорость движения плиты как функцию времени, считая грузы материальными точками и пренебрегая всеми силами сопротивления движения.
, то есть, скорость движения плиты как функцию времени, считая грузы материальными точками и пренебрегая всеми силами сопротивления движения.
Решение. Рассмотрим механическую систему в произвольном положении (рис.7.6).
Изобразим все внешние силы, действующие на систему: силы тяжести  ,
,  ,
,  и реакцию направляющей
и реакцию направляющей  .
.
Проведем координатные оси  так, чтобы ось
так, чтобы ось  проходила через точку
проходила через точку  , где находится центр масс плиты
, где находится центр масс плиты  в начальный момент времени
в начальный момент времени 
Определим  с помощью теоремы об изменении количества движения
с помощью теоремы об изменении количества движения  механической системы в проекции на ось
механической системы в проекции на ось  .
.
Поскольку все внешние силы, действующие на систему, вертикальны, то  и, согласно (7.10), имеем:
и, согласно (7.10), имеем:
 или
или  , (1)
, (1)
где  – проекция количества движения системы в момент времени
– проекция количества движения системы в момент времени 
 – проекция количества движения системы в произвольный момент времени
– проекция количества движения системы в произвольный момент времени  .
.
Определим количества движения  и
и  :
:

где 
Выразим координаты  и
и  через координату
через координату  .
.
С рис.7.6 видно, что в произвольный момент времени абсцисса первого груза

а абсцисса второго груза

Тогда


Подставляя полученные выражения для  и
и  в (3), получим:
в (3), получим:

Поскольку  то
то

В соответствии с (1), выражения (2) и (4) равны, то есть:

Отсюда окончательно получим:

Ответ: 
Задачи, которые рекомендуются для самостоятельной работы: 28.3; 28.7; 36.9; 36.11; 36.16 [2].
Теорема об изменении момента количества движения точки и механической системы
Наряду с количеством движения, как векторной меры поступательного движения, для вращательного движения можно ввести момент количества движения.
Для материальной точки массой  , которая имеет скорость
, которая имеет скорость  , момент количества движения
, момент количества движения  относительно любого центра
относительно любого центра  определяется из выражения (рис.8.1):
определяется из выражения (рис.8.1):


Вектор момента количества движения прикладывается в точке  , относительно которой он вычисляется. Если спроектировать обе части уравнения (8.1) на оси декартовой системы координат, получим моменты количества движения точки относительно осей координат:
, относительно которой он вычисляется. Если спроектировать обе части уравнения (8.1) на оси декартовой системы координат, получим моменты количества движения точки относительно осей координат:

Кинетическим моментом  или главным моментом количества движения механической системы относительно данного центра называется вектор, равный геометрической сумме моментов количеств движения всех материальных точек системы относительно этого же центра:
или главным моментом количества движения механической системы относительно данного центра называется вектор, равный геометрической сумме моментов количеств движения всех материальных точек системы относительно этого же центра:

Подобно тому, как количество движения системы является характеристикой поступательного движения, кинетический момент является характеристикой вращательного движения системы.
Кинетический момент твердого тела, которое вращается относительно оси  с угловой скоростью
с угловой скоростью  , равной произведению угловой скорости тела на его момент инерции относительно оси вращения:
, равной произведению угловой скорости тела на его момент инерции относительно оси вращения:

Производная по времени от момента количества движения точки, взятого относительно любого неподвижного центра  равна моменту силы, действующей на эту точку, относительно того же центра:
равна моменту силы, действующей на эту точку, относительно того же центра:

Спроектировав это уравнение на оси координат, получим:

Если рассматривать движение системы, на которую действуют внешние  и внутренние силы
и внутренние силы  , то производная по времени от кинетического момента механической системы относительно некоторого центра равна геометрической сумме моментов всех внешних сил относительно того же центра:
, то производная по времени от кинетического момента механической системы относительно некоторого центра равна геометрической сумме моментов всех внешних сил относительно того же центра:

Проектируя обе части уравнения на неподвижные оси  и учитывая, что проекция вектора, который изображает момент силы относительно точки на ось, равна моменту силы относительно этой оси, получим:
и учитывая, что проекция вектора, который изображает момент силы относительно точки на ось, равна моменту силы относительно этой оси, получим:

Теорема об изменении кинетического момента позволяет изучать вращательное движение твердого тела вокруг оси и точки, или вращательную часть движения тела в общем случае движения свободного твердого тела.
Практическая ценность теоремы заключается еще и в том, что она позволяет при изучении движения системы исключить из рассмотрения неизвестные внутренние силы.
Из теорем об изменении кинетического момента системы (8.7)-(8.8) вытекают важные выводы:
Если сумма моментов относительно центра  всех внешних сил, действующих на систему, равна нулю, то кинетический момент системы
всех внешних сил, действующих на систему, равна нулю, то кинетический момент системы  относительно той же точки является постоянным по величине и направлению, то есть,
относительно той же точки является постоянным по величине и направлению, то есть,
если  , то
, то  и
и 
Если сумма моментов всех внешних сил, действующих на систему, относительно некоторой оси, например  , равна нулю, то проекция кинетического момента на эту же ось является постоянной по величине, то есть,
, равна нулю, то проекция кинетического момента на эту же ось является постоянной по величине, то есть,
если  . то
. то  и
и 
Дифференциальное уравнение вращательного движения тела вокруг неподвижной оси
Кинетический момент тела относительно оси вращения по уравнению (8.4) , если ось  является осью вращения тела, равен:
является осью вращения тела, равен:

Следовательно,

Сумма моментов внешних сил  относительно оси вращения называется вращательным моментом и обозначается
относительно оси вращения называется вращательным моментом и обозначается

Таким образом, дифференциальное уравнение вращательного движения тела имеет вид:

Из (8.9) следует, что произведение момента инерции тела относительно оси вращения на угловое ускорение тела равно вращательному моменту

Это уравнение позволяет решать следующие задачи:
– если заданы уравнения вращения тела  и его момент инерции
и его момент инерции  , то можно определить вращательный момент:
, то можно определить вращательный момент:

– если заданы внешние силы, приложенные к телу, начальные условия вращения  и
и  , момент инерции
, момент инерции  тела, то можно найти уравнение вращения тела
тела, то можно найти уравнение вращения тела  :
:

– определить момент инерции тела  относительно оси вращения, если известны величины
относительно оси вращения, если известны величины  и
и  :
:

Из уравнения  вытекают отдельные случаи:
вытекают отдельные случаи:
1. Если  , то
, то  , а если
, а если  , то и
, то и  . В этом случае тело вращается равномерно.
. В этом случае тело вращается равномерно.
2. Если  , то
, то  , а если
, а если  то и
то и  . Итак, твердое тело вращается равнопеременно.
. Итак, твердое тело вращается равнопеременно.
Порядок решения задач на применение теоремы об изменении момента количества движения точки и механической системы
Задачи, которые относятся к этой теме, можно разделить на следующие четыре основных типа:
Вычисление кинетического момента.
Изучение движения конкретной точки механической системы, если эта точка участвует во вращательном движении системы.
Изучение вращательного движения твердого тела.
Изучение движения механической системы, в которую входят тела, совершающие как поступательные, так и вращательные движения.
Задачи первого типа могут быть решены с помощью общих формул (8.4), (8.5).
Порядок решения задач второго типа может быть следующим:
- Выбрать систему координат.
- Изобразить все внешние силы, приложенные к материальной точке; в случае произвольной точки к этим силам добавить реакции внешних связей.
- Записать в скалярной форме выражение теоремы об изменении момента количества движения точки.
- Высчитать сумму моментов сил, которые приложены к материальной точке.
- Определить количество движения материальной точки и его момент относительно осей.
- Подставить данные пунктов 4 и 5 в уравнения (8.6) теоремы об изменении момента количества движения материальной точки.
- Решить, в соответствии с условием, прямую или обратную задачу динамики точки.
При решении задач третьего типа сохранять рекомендации первых двух пунктов, а далее делать следующим образом:
- Записать дифференциальное уравнение вращательного движения тела вокруг неподвижной оси (8.9).

- Определить момент инерции твердого тела относительно неподвижной оси.
- Подсчитать сумму моментов всех внешних сил относительно оси вращения.
- Величины, полученные в п. п. 4 и 5, подставить в уравнение (8.9).
- Записать начальные условия.
- Решить уравнение п. 6 в зависимости от условия, как прямую или обратную задачу.
При решении задач четвертого типа необходимо предварительно расчленить заданную систему на отдельные твердые тела, и к каждому из них, в зависимости от характера движения, применить одну из теорем: об изменении количества движения – в случае поступательного движения тел расчлененной системы; об изменении кинетического момента – при наличии тел, которые совершают вращательные движения.
Примеры решения задач на тему: Теорема об изменении момента количества движения точки и механической системы
Задача №1
Однородный круглый диск весом  и с радиусом
и с радиусом  катится без скольжения по горизонтальной плоскости, делая вокруг собственной оси 60 об/мин (рис.8.2).
катится без скольжения по горизонтальной плоскости, делая вокруг собственной оси 60 об/мин (рис.8.2).

Определить главный момент количеств движения диска  относительно оси
относительно оси  , которая проходит через центр диска перпендикулярно плоскости движения.
, которая проходит через центр диска перпендикулярно плоскости движения.
Решение. Главный момент количеств движения системы (кинетический момент) относительно оси вращения равен (8.6):

где  – момент инерции тела относительно оси вращения,
– момент инерции тела относительно оси вращения,
 – угловая скорость вращения.
– угловая скорость вращения.
В данном случае кинетический момент относительно оси, проходящей через центр диска  , равен:
, равен:


Ответ: 
Задача №2
Во время вращения барабана 1 весом  и радиусом
и радиусом  вокруг неподвижной оси
вокруг неподвижной оси  на его боковую поверхность наматывается невесомая и нерастяжимая нить, что вызывает движение груза 2 весом
на его боковую поверхность наматывается невесомая и нерастяжимая нить, что вызывает движение груза 2 весом  , который скользит по неподвижной гладкой горизонтальной плоскости (рис.8.3).
, который скользит по неподвижной гладкой горизонтальной плоскости (рис.8.3).

Определить главный момент количества движения (кинетический момент) системы относительно оси  и выразить его как зависимость от угловой скорости. Барабан считать однородным круглым цилиндром. Ось
и выразить его как зависимость от угловой скорости. Барабан считать однородным круглым цилиндром. Ось  направлена перпендикулярно рисунку.
направлена перпендикулярно рисунку.
Решение. В состав механической системы входят два твердых тела: барабан 1 и груз 2.
Следовательно, кинетический момент системы равен:

где  – кинетический момент барабана;
– кинетический момент барабана;
 – кинетический момент груза относительно неподвижной оси
– кинетический момент груза относительно неподвижной оси  .
.
Кинетический момент барабана равен (8.5):

где

тогда

Главный момент количества движения груза, который движется поступательно, определяется как момент количества движения материальной точки, то есть:

поскольку

то

Окончательно

Ответ: 
Задача №3
Шарик  , который находится в сосуде с жидкостью и прикреплен к концу стержня
, который находится в сосуде с жидкостью и прикреплен к концу стержня  длиной
длиной  , приводится в вращение вокруг вертикальной оси
, приводится в вращение вокруг вертикальной оси  с начальной угловой скоростью
с начальной угловой скоростью  (рис.8.4, а). Сила сопротивления жидкости пропорциональна угловой скорости вращения
(рис.8.4, а). Сила сопротивления жидкости пропорциональна угловой скорости вращения  :
:  , где
, где  – масса шарика,
– масса шарика,  – коэффициент пропорциональности.
– коэффициент пропорциональности.

Определить, через какой промежуток времени  угловая скорость вращения станет вдвое меньше начальной, а также число оборотов
угловая скорость вращения станет вдвое меньше начальной, а также число оборотов  , которое сделает стержень с шариком за этот промежуток времени. Массу шарика считать сосредоточенной в ее центре, массой стержня пренебречь.
, которое сделает стержень с шариком за этот промежуток времени. Массу шарика считать сосредоточенной в ее центре, массой стержня пренебречь.
Решение. Ось  направим вдоль оси вращения
направим вдоль оси вращения  и покажем силы, действующие на вал с шариком: силу сопротивления
и покажем силы, действующие на вал с шариком: силу сопротивления  , которая направлена в сторону, противоположную вращению (рис.8.4, б), силу тяжести шарика
, которая направлена в сторону, противоположную вращению (рис.8.4, б), силу тяжести шарика  , реакции
, реакции  подшипника
подшипника  и
и  подпятника
подпятника  .
.
Все силы указаны на рисунках, направления сил  и
и  изображены произвольно.
изображены произвольно.
Запишем дифференциальное уравнение вращательного движения шарика относительно оси  :
:

где момент инерции шарика

Поскольку момент силы тяжести  относительно оси
относительно оси  равен нулю (
равен нулю (  параллельна оси
параллельна оси  ), то вращательный момент
), то вращательный момент  равен моменту силы сопротивления
равен моменту силы сопротивления  относительно оси
относительно оси  (как известно, момент силы сопротивления всегда отрицательный):
(как известно, момент силы сопротивления всегда отрицательный):

Следовательно, дифференциальное уравнение вращательного движения имеет вид:

или

Разделим переменные и проинтегрируем:

Произвольную постоянную  определим по начальным условиям: при
определим по начальным условиям: при  .
.

Следовательно,

Высчитаем, через какой промежуток времени  угловая скорость вращения станет вдвое меньше начальной, то есть,
угловая скорость вращения станет вдвое меньше начальной, то есть,  .
.

Откуда:

Для определения числа оборотов, которые сделает стержень с шариком за промежуток времени  , необходимо найти зависимость угла поворота
, необходимо найти зависимость угла поворота  от времени
от времени  :
:

Следовательно,

Разделим переменные и проинтегрируем это дифференциальное уравнение:

Произвольную постоянную  определим по начальным условиям: при
определим по начальным условиям: при  .
.

Итак закон изменения угла поворота  по времени имеет вид:
по времени имеет вид:

или

При  , угол поворота
, угол поворота  равен
равен

Поскольку за 1 оборот шарик обернется на  , то количество оборотов
, то количество оборотов  составит
составит

Ответ: 
Задача №4
Для определения момента трения в цапфах, на вал насажен маховик весом  , радиус инерции маховика
, радиус инерции маховика  Маховику придана угловая скорость, соответствующая
Маховику придана угловая скорость, соответствующая  об/мин. Без внешнего воздействия на него, он остановился через
об/мин. Без внешнего воздействия на него, он остановился через  мин.
мин.
Определить момент трения  , считая его постоянным.
, считая его постоянным.
Решение. Направим ось  вдоль неподвижной оси вращения. Изобразим на рис.8.5 внешние нагрузки, действующие на вал и маховик: силу тяжести маховика
вдоль неподвижной оси вращения. Изобразим на рис.8.5 внешние нагрузки, действующие на вал и маховик: силу тяжести маховика  , реакции опор
, реакции опор  и
и  и момент сил трения
и момент сил трения  .
.
Запишем теорему об изменении кинетического момента относительно оси вращения:

Поскольку мы рассматриваем вращение твердого тела, то

Найдем вращательный момент внешних сил относительно оси вращения  , если учтем, что момент сил
, если учтем, что момент сил  ,
,  и
и  относительно оси
относительно оси  равны нулю, поскольку эти силы пересекают ось. Следовательно, вращательный момент равен моменту сил трения и направлен в сторону, противоположную вращению маховика.
равны нулю, поскольку эти силы пересекают ось. Следовательно, вращательный момент равен моменту сил трения и направлен в сторону, противоположную вращению маховика.
Таким образом

Высчитаем величины, которые входят в это уравнение:

где  – угловая скорость маховика в момент остановки,
– угловая скорость маховика в момент остановки,  ,
,
 – угловая скорость в начальный момент времени.
– угловая скорость в начальный момент времени.
Поскольку  то
то 
С учетом значений  и
и  получим:
получим:

Ответ: 
Задача №5
Однородный цилиндр (рис.8.6) радиусом  вращается вокруг своей геометрической оси
вращается вокруг своей геометрической оси  угловой скоростью
угловой скоростью  .
.

Определить, как изменится угловая скорость  цилиндра, если ось вращения перейдет в положение
цилиндра, если ось вращения перейдет в положение  , которое совпадает с образующей цилиндра?
, которое совпадает с образующей цилиндра?
Решение. На цилиндр действует сила тяжести  , которая направлена вертикально вниз.
, которая направлена вертикально вниз.
Запишем теорему об изменении кинетического момента цилиндра:

где  – момент инерции цилиндра,
– момент инерции цилиндра,
 – сумма моментов внешних сил относительно оси вращения.
– сумма моментов внешних сил относительно оси вращения.
Поскольку сила  параллельна оси вращения, то
параллельна оси вращения, то
 и
и 
Итак,  , тогда
, тогда

где  – момент инерции цилиндра относительно оси
– момент инерции цилиндра относительно оси  ,
,
 – момент инерции цилиндра относительно оси
– момент инерции цилиндра относительно оси  ,
,
По теореме Гюйгенса-Штейнера

где  – масса цилиндра.
– масса цилиндра.
Из формулы (1) получим:

Вычислим  и
и  :
:

Следовательно,

Угловая скорость уменьшилась в три раза, поскольку в три раза увеличился момент инерции.
Ответ: 
Задача №6
Молотильный барабан начинает вращаться из состояния покоя ( ) под действием постоянного момента
) под действием постоянного момента 
Определить, пренебрегая трением, частоту вращения барабана после того, как он начнет вращаться и сделает  оборотов (рис.8.7), зная, что момент инерции барабана относительно оси вращения
оборотов (рис.8.7), зная, что момент инерции барабана относительно оси вращения 

Решение. Для определения угловой скорости барабана воспользуемся формулой:

где  – начальная угловая скорость вращения,
– начальная угловая скорость вращения,
 – конечная угловая скорость вращения,
– конечная угловая скорость вращения,
 – угол, на который поворачивается барабан.
– угол, на который поворачивается барабан.
Из (1) вытекает:
 где
где 
Следовательно,

Таким образом, для определения угловой скорости необходимо знать угловое ускорение  .
.
Для определения  воспользуемся теоремой об изменении кинетического момента:
воспользуемся теоремой об изменении кинетического момента:

где  – сумма моментов всех внешних сил относительно оси вращения.
– сумма моментов всех внешних сил относительно оси вращения.
На барабан действуют следующие внешние нагрузки:  – сила тяжести барабана;
– сила тяжести барабана;  ,
,
 – реакции подшипников
– реакции подшипников  и
и  ;
;  – вращательный момент.
– вращательный момент.
С учетом действующих сил уравнение (2) будет иметь вид:

При этом  , поскольку силы
, поскольку силы  ,
,  и
и
 пересекают ось
пересекают ось  и моментов не образуют. Итак,
и моментов не образуют. Итак,

Тогда,

Ответ: 
Задача №7
Груз весом  подвешен на канате, который навитый на цилиндрический барабан, ось вращения которого горизонтальна (рис.8.8).
подвешен на канате, который навитый на цилиндрический барабан, ось вращения которого горизонтальна (рис.8.8).

Определить угловое ускорение барабана  во время опускания груза
во время опускания груза  , пренебрегая весом каната, сопротивлением воздуха, трением в подшипниках. Барабан считать однородным цилиндром весом
, пренебрегая весом каната, сопротивлением воздуха, трением в подшипниках. Барабан считать однородным цилиндром весом  и радиусом
и радиусом 
Решение. Для определения углового ускорения  барабана будем рассматривать движение системы, в которую включим следующие тела: барабан весом
барабана будем рассматривать движение системы, в которую включим следующие тела: барабан весом  , груз весом
, груз весом  и канат, натяжение которого заранее неизвестно.
и канат, натяжение которого заранее неизвестно.
Если применить теорему об изменении кинетического момента системы относительно оси, то натяжение каната, являющегося внутренней силой, в уравнение не войдет.
Относительно оси, которая проходит через точку  , эта теорема имеет вид:
, эта теорема имеет вид:

На систему действуют следующие внешние силы:  – вес груза,
– вес груза,  – вес барабана,
– вес барабана,  – реакция опоры
– реакция опоры  .
.
Силы  и
и  не создают моментов относительно оси
не создают моментов относительно оси  , потому что они ее пересекают. Только сила
, потому что они ее пересекают. Только сила  создает момент относительно оси
создает момент относительно оси  , который равен:
, который равен:

Итак,

Определим кинетический момент системы относительно оси вращения  :
:

где  – кинетический момент барабана,
– кинетический момент барабана,
 – кинетический момент груза.
– кинетический момент груза.

где  – момент инерции барабана относительно оси вращения
– момент инерции барабана относительно оси вращения  ;
;

поскольку 
Тогда кинетический момент системы равен:

Подставим полученные результаты в уравнение (1):

Знак момента силы  взят положительным, поскольку направление вращения барабана совпадает с направлением момента силы
взят положительным, поскольку направление вращения барабана совпадает с направлением момента силы  .
.
Решаем уравнение (2) и определяем угловое ускорение  .
.
Выносим из под знака дифференциала в левой части уравнения (2) постоянные величины:

или

С учетом числовых значений угловое ускорение  равно:
равно:

Ответ: 
Теорема об изменении кинетической энергии механической системы
Теорема о кинетической энергии системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему.
Кинетическая энергия механической системы
Кинетической энергией  материальной точки называется скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости:
материальной точки называется скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости:

Кинетической энергией  механической системы называется арифметическая сумма кинетических энергий всех точек механической системы:
механической системы называется арифметическая сумма кинетических энергий всех точек механической системы:

Кинетическая энергия системы не зависит от направлений скоростей точек.
Кинетическая энергия может равняться нулю, если скорости всех точек системы равны нулю.
Кинетическая энергия системы характеризует и поступательное, и вращательное движения системы. Поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач.
Единицей кинетической энергии в системе СИ является Джоуль (Дж).
Определение кинетической энергии твердого тела в различных случаях его движения
Поступательное движение твердого тела:
При поступательном движении твердого тела скорости всех его точек (в том числе скорость  центра масс тела) в каждый момент времени равны между собой; то есть, для любой точки
центра масс тела) в каждый момент времени равны между собой; то есть, для любой точки  . Итак
. Итак

Кинетическая энергия твердого тела при поступательном движении равна половине произведения массы тела  на квадрат скорости его центра масс.
на квадрат скорости его центра масс.
Вращательное движение твердого тела:
Скорость любой точки твердого тела, которое вращается с угловой скоростью  , равна
, равна

где  – расстояние от точки к оси вращения.
– расстояние от точки к оси вращения.
Тогда кинетическая энергия тела определяется согласно зависимости:

Поскольку

то

Следовательно кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
Плоскопараллельное движение твердого тела:
При плоскопараллельном движении скорости всех точек тела в каждый момент времени распределены так, будто тело вращается вокруг оси, которая перпендикулярна плоскости движения и которая проходит через мгновенный центр скоростей  .
.
В этом случае кинетическую энергию тела можно определить по формуле:

где  – момент инерции тела относительно оси, которая проходит через мгновенный центр скоростей.
– момент инерции тела относительно оси, которая проходит через мгновенный центр скоростей.
Поскольку (согласно теореме Штейнера-Гюйгенса)

где  – момент инерции относительно оси, которая проходит через центр масс тела и параллельна мгновенной оси вращения, то
– момент инерции относительно оси, которая проходит через центр масс тела и параллельна мгновенной оси вращения, то

Поскольку  , то окончательно
, то окончательно

Таким образом,
в случае плоскопараллельного движения тела кинетическая энергия состоит из кинетических энергий поступательного движения вместе со скоростью центра масс и вращательного движения вокруг оси, которая проходит через центр масс перпендикулярно плоскости движения.
Теорема об изменении кинетической энергии механической системы:
Дифференциальная форма:
Дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему:

Производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних и внутренних сил, действующих на систему:

Интегральная форма:
Изменение кинетической энергии механической системы при конечном перемещении ее из положения (1) в положение (2) равно сумме работ на этом перемещении всех внешних и внутренних сил, действующих на эту систему

Если механическая система неизменна, то сумма работ внутренних сил равна нулю и теорема запишется так:

Порядок решения задач на использование теоремы об изменении кинетической энергии механической системы
Решение задач с помощью теоремы об изменении кинетической энергии в интегральной форме рекомендуется проводить в следующей последовательности:
а) изобразить на рисунке все внешние силы системы;
б) высчитать сумму работ всех внешних сил на перемещении точек системы;
в) вычислить кинетическую энергию системы материальных точек в начальном и конечном ее состояниях;
г ) пользуясь результатами подсчетов по пунктам б) и в) записать теорему об изменении кинетической энергии механической системы и определить искомую величину.
Примеры решения задач на тему: Теорема об изменении кинетической энергии механической системы
Задача № 1
Механизм эллипсографа (рис.10.1) состоит из ползунов  и
и  весом
весом  каждый, кривошипа
каждый, кривошипа  весом
весом  , и линейки
, и линейки  весом
весом  . Кривошип
. Кривошип  вращается вокруг неподвижной оси
вращается вокруг неподвижной оси  , которая перпендикулярна плоскости чертежа с угловой скоростью
, которая перпендикулярна плоскости чертежа с угловой скоростью  .
.
Определить кинетическую энергию механизма эллипсографа, полагая, что линейка  и кривошип
и кривошип  – однородные тонкие стержни, а ползуны
– однородные тонкие стержни, а ползуны  и
и  – материальные точки, а также, что
– материальные точки, а также, что 

Решение. Заданная механическая система состоит из четырех тел: кривошипа 1 и линейки 2, ползунов 3 и 4.
Кинетическая энергия всей системы равна:

где  – кинетическая энергия кривошипа 1,
– кинетическая энергия кривошипа 1,
 – кинетическая энергия линейки 2,
– кинетическая энергия линейки 2,
 – кинетическая энергия ползунов 3 и 4.
– кинетическая энергия ползунов 3 и 4.
Кривошип  совершает вращательное движение вокруг неподвижной оси
совершает вращательное движение вокруг неподвижной оси  , которая перпендикулярна оси рисунка. В этом случае кинетическая энергия тела равна
, которая перпендикулярна оси рисунка. В этом случае кинетическая энергия тела равна

Тогда

Линейка 2 движется плоскопараллельно. Ее кинетическая энергия равна

где  – скорость точки С, которая является центром масс линейки 2,
– скорость точки С, которая является центром масс линейки 2,
 – угловая скорость линейки 2,
– угловая скорость линейки 2,
 – момент инерции линейки относительно оси
– момент инерции линейки относительно оси  , которая проходит через центр масс линейки
, которая проходит через центр масс линейки  .
.
Для определения угловой скорости  линейки 2 используем понятие мгновенного центра скоростей. Как известно, мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям двух точек тела, движущихся плоскопараллельно. Тогда в нашем случае он будет расположен в точке
линейки 2 используем понятие мгновенного центра скоростей. Как известно, мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям двух точек тела, движущихся плоскопараллельно. Тогда в нашем случае он будет расположен в точке  , и скорость точки
, и скорость точки  определится:
определится:

С другой стороны, точка  принадлежит звену 1, и ее скорость равна
принадлежит звену 1, и ее скорость равна

Тогда, учитывая, что  получим:
получим:

Момент инерции линейки относительно оси  равен:
равен:

С учетом полученных значений  кинетическая энергия линейки 2 равна:
кинетическая энергия линейки 2 равна:

Подсчитаем кинетическую энергию ползунов 3 и 4, которые двигаются поступательно:
 .
.
Скорости точек  можно определить, учитывая положение мгновенного центра скоростей линейки 2:
можно определить, учитывая положение мгновенного центра скоростей линейки 2:

Тогда

Подставляя найденные выражения (2), (4), (5) в (1), получим:

Ответ: 
Задача № 2
На рисунке 10.2 изображен подъемный механизм лебедки. Груз  весом
весом  поднимается с помощью невесомого и нерастяжимого троса, который переброшен через блок
поднимается с помощью невесомого и нерастяжимого троса, который переброшен через блок  и намотан на барабан
и намотан на барабан  радиусом
радиусом  и весом
и весом  . К барабану приложен вращательный момент, который пропорционален квадрату угла поворота
. К барабану приложен вращательный момент, который пропорционален квадрату угла поворота  барабану:
барабану:

где  – постоянный коэффициент.
– постоянный коэффициент.

Определить скорость груза  в момент, когда он поднимется на высоту
в момент, когда он поднимется на высоту  . Массу барабана
. Массу барабана  считать равномерно распределенной вдоль его обода. Блок
считать равномерно распределенной вдоль его обода. Блок  – сплошной диск весом
– сплошной диск весом  . В начальный момент система находилась в покое.
. В начальный момент система находилась в покое.
Решение. Изобразим на рисунке все внешние силы, действующие на барабан  , блок
, блок  и груз
и груз  : силы тяжести
: силы тяжести  ,
,  ,
,  ; вращательный момент, а также реакции шарниров
; вращательный момент, а также реакции шарниров  и
и  . Внутренней силой является натяжение троса
. Внутренней силой является натяжение троса  .
.
Запишем теорему об изменении кинетической энергии системы:

где  – кинетическая энергия системы в конечном положении;
– кинетическая энергия системы в конечном положении;
 – кинетическая энергия системы в исходном положении;
– кинетическая энергия системы в исходном положении;
 – сумма работ всех внешних сил на перемещении
– сумма работ всех внешних сил на перемещении  ;
;
 – сумма работ всех внутренних сил на перемещении
– сумма работ всех внутренних сил на перемещении  .
.
Поскольку в начальный момент времени система находилась в состоянии покоя, то

В связи с тем, что трос не растягивается и при движении системы находится в натянутом состоянии, сумма работ внутренних сил системы равна нулю, следовательно

При поднятии груза  на высоту
на высоту  сумма работ равна:
сумма работ равна:

Поскольку точки приложения сил  и
и  – неподвижны, то
– неподвижны, то

Работа силы  равна:
равна:

Работа вращательного момента в случае, когда он не меняется

где  – угол поворота тела под действием момента.
– угол поворота тела под действием момента.
Поскольку в нашем случае вращательный момент меняется, то его работа определится следующим образом:

Определим угол  , на который вернулся барабан
, на который вернулся барабан  при подъеме груза
при подъеме груза  на высоту
на высоту  :
:

Следовательно,

Таким образом,

Перейдем к подсчету кинетической энергии системы в конечном положении:

где  – кинетическая энергия груза
– кинетическая энергия груза  ;
;
 – кинетическая энергия диска
– кинетическая энергия диска  ;
;
 – кинетическая энергия барабана
– кинетическая энергия барабана  .
.
Груз  движется поступательно и его кинетическая энергия равна:
движется поступательно и его кинетическая энергия равна:

Диск  совершает вращательное движение, его кинетическая энергия определяется из выражения:
совершает вращательное движение, его кинетическая энергия определяется из выражения:
где  – момент инерции диска относительно оси вращения;
– момент инерции диска относительно оси вращения;
 – угловая скорость диска.
– угловая скорость диска.
Поскольку диск  – сплошной, то
– сплошной, то  равен:
равен:

где  – радиус диска.
– радиус диска.
Поскольку линейная скорость обода диска равна скорости груза, угловая скорость вращения  :
:

Итак,

Кинетическая энергия барабана  , поскольку он совершает вращательное движение, равна:
, поскольку он совершает вращательное движение, равна:

Поскольку масса барабана  распределена по ободу, то:
распределена по ободу, то:

Угловую скорость барабана высчитаем из условия равенства линейных скоростей на ободах диска и барабана:

Откуда

Таким образом

Кинетическая энергия системы в конечном положении равна

Итак, теорема об изменении кинетической энергии системы имеет вид:

Решая это уравнение относительно  , находим скорость груза
, находим скорость груза  после того, как он пройдет путь
после того, как он пройдет путь  :
:

Ответ: 
Задача № 3
Груз  (рис.10.3) весом
(рис.10.3) весом  , опускаясь вниз с помощью перекинутого через неподвижный блок
, опускаясь вниз с помощью перекинутого через неподвижный блок  невесомого и нерастяжимого троса, поднимает вверх груз
невесомого и нерастяжимого троса, поднимает вверх груз  весом
весом  , который закреплен к оси подвижного блока
, который закреплен к оси подвижного блока  . Блоки
. Блоки  и
и  считать однородными сплошными дисками весом
считать однородными сплошными дисками весом  каждый.
каждый.

Определить скорость груза  в момент, когда он опустится на высоту
в момент, когда он опустится на высоту  . Скольжением на ободах блоков и силами сопротивления пренебречь.
. Скольжением на ободах блоков и силами сопротивления пренебречь.
В начальный момент система находилась в состоянии покоя.
Решение. Изобразим внешние силы, которые действуют на систему: силы тяжести  ; реакцию шарнира
; реакцию шарнира  и реакцию в точке
и реакцию в точке  –
–  . Внутренней силой является натяжение троса
. Внутренней силой является натяжение троса  .
.
Запишем теорему об изменении кинетической энергии системы:

В начальный момент времени система находилась в покое, следовательно,  . Работа внутренней силы натяжения троса, равна нулю. Итак,
. Работа внутренней силы натяжения троса, равна нулю. Итак,

Сумма работ внешних сил при перемещении системы в конечное положение составляет:

Работа сил  равна нулю, поскольку точки приложения сил 3
равна нулю, поскольку точки приложения сил 3  неподвижны.
неподвижны.
Итак,

Работа силы  при опускании груза
при опускании груза  на высоту
на высоту  равна:
равна:

Работу силы тяжести  блока
блока  определим следующим образом. При опускании груза
определим следующим образом. При опускании груза  на высоту
на высоту  точка
точка  блока
блока  поднимается вверх на расстояние
поднимается вверх на расстояние  , которая равна
, которая равна  , а центр блока
, а центр блока  на величину
на величину  , так как точка
, так как точка  – мгновенный центр скоростей блока
– мгновенный центр скоростей блока  .
.
Таким образом,

Груз  поднимается вверх так же на величину
поднимается вверх так же на величину  . Тогда работа силы тяжести груза
. Тогда работа силы тяжести груза  будет равна:
будет равна:

Итак,

Вычислим кинетическую энергию системы в конечном положении:

Груз  перемещается поступательно и его кинетическая энергия равна
перемещается поступательно и его кинетическая энергия равна

где  – скорость груза
– скорость груза  в конце перемещения.
в конце перемещения.
Блок  осуществляет плоскопараллельное движение. В этом случае:
осуществляет плоскопараллельное движение. В этом случае:

Кинетическая энергия поступательного движения блока  равна:
равна:

Поскольку точка  – мгновенный центр скоростей блока
– мгновенный центр скоростей блока  , а скорость точки
, а скорость точки  равна скорости груза
равна скорости груза  , то скорость вращения блока
, то скорость вращения блока  :
:

Тогда

Таким образом,

Кинетическая энергия вращательного движения блока  определяется из равенства:
определяется из равенства:

где  – момент инерции блока
– момент инерции блока  относительно оси, которая проходит через центр масс
относительно оси, которая проходит через центр масс  . Блок
. Блок  – сплошной однородный диск, поэтому
– сплошной однородный диск, поэтому

Тогда

Таким образом, кинетическая энергия блока  равна:
равна:

Блок  совершает вращательное движение и его кинетическая энергия:
совершает вращательное движение и его кинетическая энергия:

то есть

Груз  совершает поступательное движение со скоростью точки
совершает поступательное движение со скоростью точки  то есть со скоростью
то есть со скоростью  . Поэтому
. Поэтому

Следовательно, кинетическая энергия системы  в конечном положении:
в конечном положении:

Таким образом, теорема об изменении кинетической энергии системы имеет вид:

Находим скорость груза  , решая это уравнение относительно
, решая это уравнение относительно  :
:

Ответ: 
Задача № 4
Прямоугольная пластинка  (рис.10.4) со сторонами
(рис.10.4) со сторонами  и
и  , и весом
, и весом  вращается вокруг вертикальной оси
вращается вокруг вертикальной оси  с начальной угловой скоростью
с начальной угловой скоростью  . Каждый элемент пластинки несет при этом сопротивление воздуха, направление которого перпендикулярно плоскости пластинки, а величина пропорциональна площади элемента и квадрату его скорости. Коэффициент пропорциональности равен
. Каждый элемент пластинки несет при этом сопротивление воздуха, направление которого перпендикулярно плоскости пластинки, а величина пропорциональна площади элемента и квадрату его скорости. Коэффициент пропорциональности равен  .
.

Определить, сколько оборотов сделает пластинка к тому мгновению, когда ее угловая скорость станет вдвое меньше начальной?
Решение. Поскольку силы сопротивления, приложенные к пластинке, не постоянные, а зависят от скорости, то для решения задачи воспользуемся теоремой об изменении кинетической энергии системы в дифференциальной форме:

Высчитаем дифференциал кинетической энергии пластинки. Поскольку пластинка вращается вокруг неподвижной оси, то ее кинетическая энергия равна:

откуда:

где  – момент инерции пластинки относительно оси
– момент инерции пластинки относительно оси  .
.
Перейдем к определению суммы элементарных работ внешних сил, которые действуют на пластинку. Это такие силы (рис.10.4):
– сила тяжести пластинки  ;
;
– реакции в опорах  и
и  :
:  и
и  ;
;
– сила сопротивления воздуха  .
.
Итак,

где  – элементарная работа силы тяжести пластинки;
– элементарная работа силы тяжести пластинки;
 – элементарные работы реакций подшипников;
– элементарные работы реакций подшипников;
 – элементарная работа силы сопротивления
– элементарная работа силы сопротивления  .
.
Работы реакций  и
и  равны нулю, ибо точки их приложения неподвижны. Работа силы тяжести
равны нулю, ибо точки их приложения неподвижны. Работа силы тяжести  тоже равна нулю в связи с тем, что высота центра тяжести пластинки не меняется.
тоже равна нулю в связи с тем, что высота центра тяжести пластинки не меняется.
Таким образом,

Для вычета работы сил сопротивления воспользуемся формулой для работы сил, которые приложены к вращающемуся твердому телу:

где  – сумма моментов всех приложенных к телу сил относительно оси вращения;
– сумма моментов всех приложенных к телу сил относительно оси вращения;
 – элементарный угол поворота.
– элементарный угол поворота.
Чтобы определить  , разобьем пластинку на элементарные прямоугольники со сторонами
, разобьем пластинку на элементарные прямоугольники со сторонами  и
и  . Тогда сила сопротивления, приложенная к элементарному прямоугольнику, будет равняться:
. Тогда сила сопротивления, приложенная к элементарному прямоугольнику, будет равняться:

и

Следовательно,

или

и
 .
.
Таким образом, уравнение (1) принимает вид:

Разделим переменные и проинтегрируем:

Момент инерции пластинки составляет:

Тогда

Откуда находим:

Число оборотов  составляет:
составляет:

Ответ: 
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки

