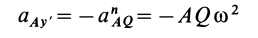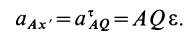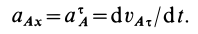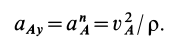Мгновенный центр вращения:
Для двух бесконечно близких положений плоской фигуры вместо центра конечного вращения получим так называемый мгновенный центр вращения. Любое плоское перемещение фигуры можно приближенно заменить последовательностью вращательных перемещений вокруг своих центров конечного вращения. В пределе плоское перемещение фигуры можно заменить бесконечной последовательностью элементарных мгновенных поворотов вокруг мгновенных центров вращений, расположенных в определенной последовательности.
Рис. 71
Отсюда следует, что любое плоское движение фигуры можно заменить последовательностью мгновенных вращений, совершаемых за тот же промежуток времени, что и рассматриваемое плоское движение. Можно ввести угловую скорость вращения вокруг мгновенного центра вращения или, точнее, вокруг мгновенной оси, проходящей через мгновенный центр вращения и перпендикулярной плоскости движения.
При плоском движении фигуры мгновенный центр вращения перемещается как в неподвижной, так и в подвижной плоскости, скрепленной с движущейся плоской фигурой. Геометрическое место мгновенных центров вращения на неподвижной плоскости называют неподвижной центроидой, а геометрическое место этих же мгновенных центров вращения на подвижной плоскости, скрепленной с движущейся фигурой,— подвижной центроидой. Для каждого плоского движения фигуры существуют свои две центроиды: подвижная и неподвижная. Очевидно, что точка плоской фигуры, с которой в рассматриваемый момент совпадает мгновенный центр вращения, имеет скорость, равную нулю; следовательно, она является в то же время мгновенным центром скоростей.
При плоском движении фигуры подвижная центроида катится без скольжения по неподвижной центроиде. Эта теорема позволяет плоское движение твердого тела рассматривать как качение без скольжения одной плоской кривой по другой.
Центроиды нашли применение в некоторых вопросах кинематики механизмов. Рассмотрим пример нахождения центроид.
Пример:
Стержень
Решение. Скорость точки 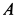
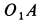
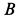
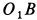
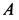
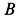
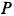
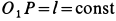
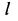
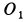
На подвижной плоскости 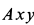
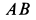
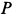
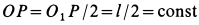
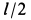
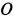
При качении подвижной окружности по неподвижной концы 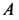
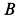
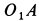
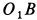
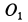
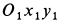
- Заказать решение задач по теоретической механике
Таким образом убеждаемся, что все точки подвижной окружности движутся по прямым линиям, проходящим через центр неподвижной окружности 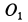
Рис. 72
В общем случае движения плоской фигуры мгновенный центр скоростей— точка 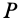
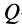
Выберем точку 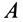
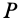
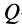
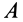
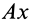
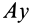
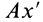
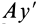
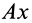
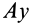
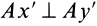
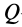
и 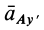
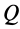
Точка 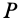
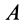
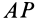
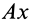
Ось 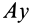
Если 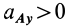
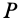
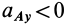
Кажется, что у точки 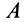
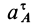
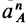
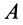
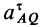
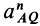
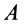
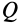
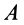
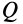
- Вращение твердого тела вокруг неподвижной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
Для кинематического описания процесса вращения твердого тела нужно ввести такие понятия как угловое перемещение Δφ, угловое ускорение ε и угловая скорость ω:
ω=∆φ∆t, (∆t→0),ε=∆φ∆t, (∆t→0).
Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.
Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.
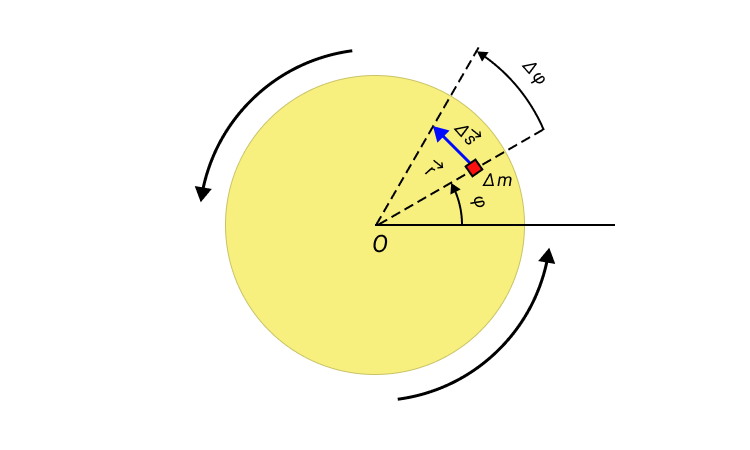
Рисунок 1. Вращение диска относительно оси, проходящей через его центр O.
Если угловое перемещение Δφ мало, то модуль вектора линейного перемещения ∆s→ некоторого элемента массы Δm вращающегося твердого тела можно выразить соотношением:
∆s=r∆ϕ,
в котором r – модуль радиус-вектора r→.
Между модулями угловой и линейной скоростей можно установить связь посредством равенства
v=rω.
Модули линейного и углового ускорения также взаимосвязаны:
a=aτ=rε.
Векторы v→ и a→=aτ→ направлены по касательной к окружности радиуса r.
Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.
Модуль ускорения выражается формулой:
an=v2r=ω2r.
Если разделить вращающееся тело на небольшие фрагменты Δmi, обозначить расстояние до оси вращения через ri, а модули линейных скоростей через vi, то запись формулы кинестетической энергии вращающегося тела будет иметь вид:
Ek=∑iνmvi22=∑i∆m(riω)22=ω22∑i∆miri2.
Физическая величина ∑i∆miri2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:
I=∑i∆miri2.
В пределе при Δm→0 эта сумма переходит в интеграл. Единица измерения момента инерции в СИ – килограмм–метр в квадрате (кг·м2). Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:
Ek=Iω22.
В отличие от выражения, которое мы использовали для описания кинестетической энергии поступательно движущегося тела mv22, вместо массы m в формулу входит момент инерции I. Также мы принимаем во внимание вместо линейной скорости v угловую скорость ω.
Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.
В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.
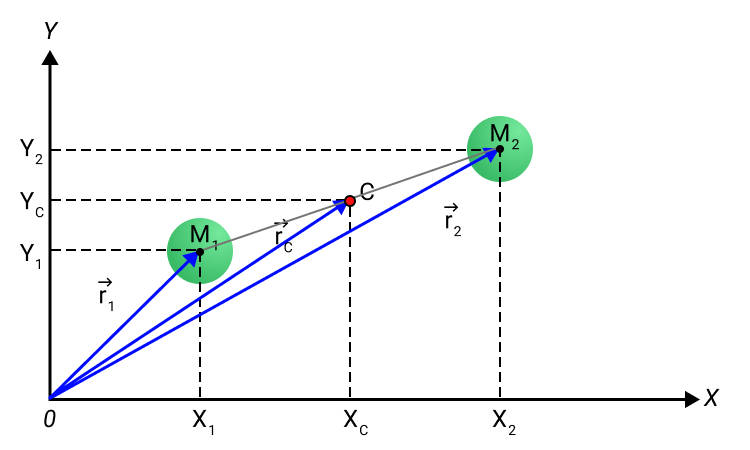
Положение xC, yC центра масс для простого случая системы из двух частиц с массами m1 и m2, расположенными в плоскости XY в точках с координатами x1, y1 и x2, y2 определяется выражениями:
xC=m1x1+m2x2m1+m2, yC=m1y1+m2y2m1+m2.
Рисунок 2. Центр масс C системы из двух частиц.
В векторной форме это соотношение принимает вид:
rC→=m1r1→+m2r2→m1+m2.
Аналогично, для системы из многих частиц радиус-вектор rC→ центра масс определяется выражением
rC→=∑miri→∑mi.
Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для rC→ необходимо заменить интегралами.
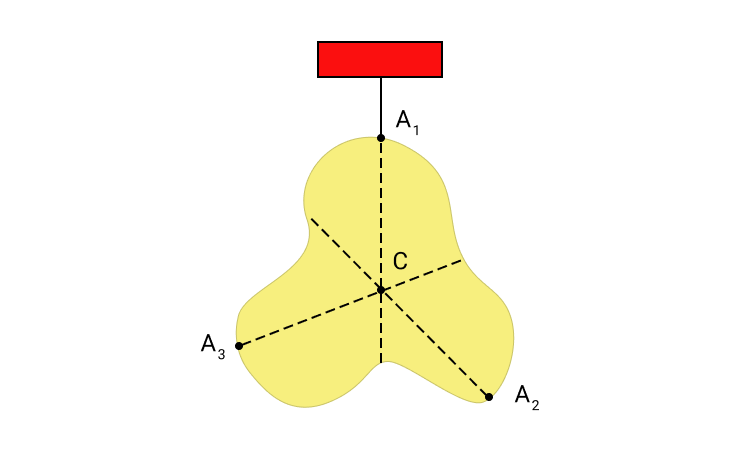
Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.
Рисунок 3. Определение положения центра масс C тела сложной формы. A1, A2, A3 точки подвеса.
На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.
Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.
Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.
Теорема о движении центра масс
Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:
Ek=mvC22+ICω22,
где m – полная масса тела, IC – момент инерции тела относительно оси, проходящей через центр масс.
Рисунок 4. Качение колеса как сумма поступательного движения со скоростью vC→ и вращения с угловой скоростью ω=vCR относительно оси O, проходящей через центр масс.
В механике используется теорема о движении центра масс.
Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.
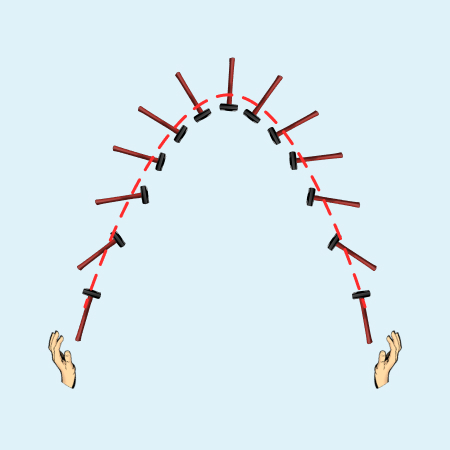
На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.
Рисунок 5. Движение твердого тела под действием силы тяжести.
Теорема Штейнера о параллельном переносе оси вращения
Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции IC этого тела относительно оси, проходящей через центр масс тела и параллельной первой.
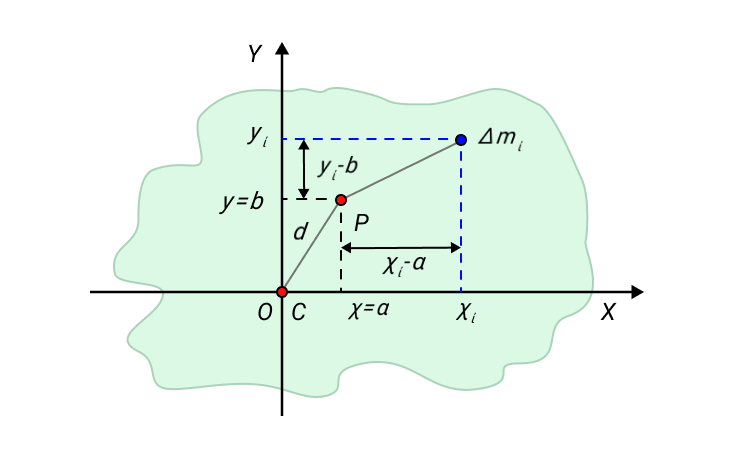
Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.
Для примера возьмем твердое тело, форма которого произвольна. Обозначим центр масс С. Выберем систему координат ХУ с началом координат 0. Совместим центр масс и начало координат.
Одна из осей проходит через центр масс С. Вторая ось пересекает произвольно выбранную точку Р, которая расположена на расстоянии d от начала координат. Выделим некоторый малый элемент массы данного твердого тела Δmi.
По определению момента инерции:
IC=∑∆mi(xi2+yi2),IP=∑mi(xi-a)2+yi-b2
Выражение для IP можно переписать в виде:
IP=∑∆mi(xi2+yi2)+∑∆mi(a2+b2)-2a∑∆mixi-2b∑∆miyi.
Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.
Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.
Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.
IP=IC+md2,
где m – полная масса тела.
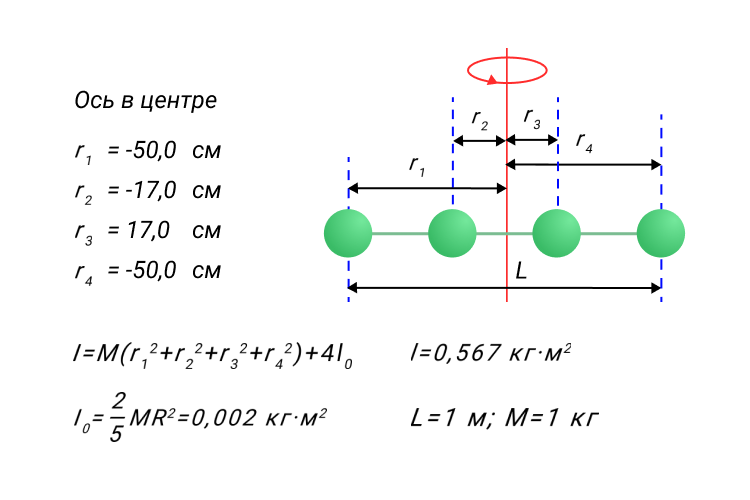
Рисунок 7. Модель момента инерции.
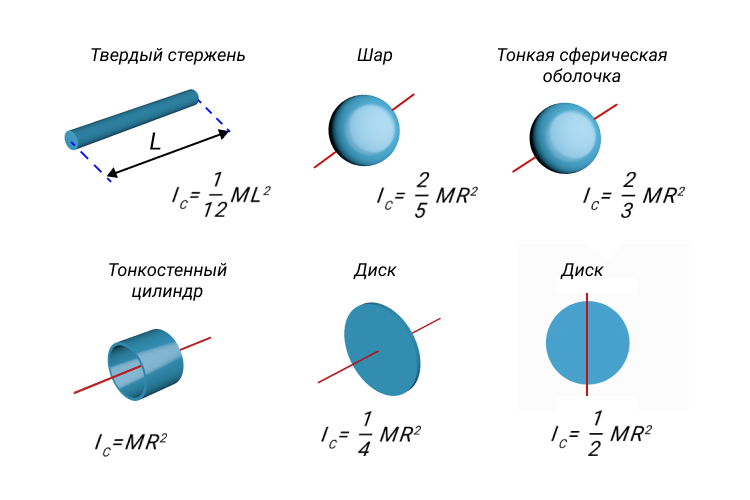
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
Рисунок 8. Моменты инерции IC некоторых однородных твердых тел.
Основное уравнение динамики вращательного движения твердого тела
В тех случаях, когда мы имеем дело с твердым телом, которое вращается относительно неподвижной оси, мы можем обобщить второй закон Ньютона. На рисунке ниже мы изобразили твердое тело произвольной формы, вращающееся относительно некоторой оси, проходящей через точку О. Ось вращения расположена перпендикулярно плоскости рисунка.
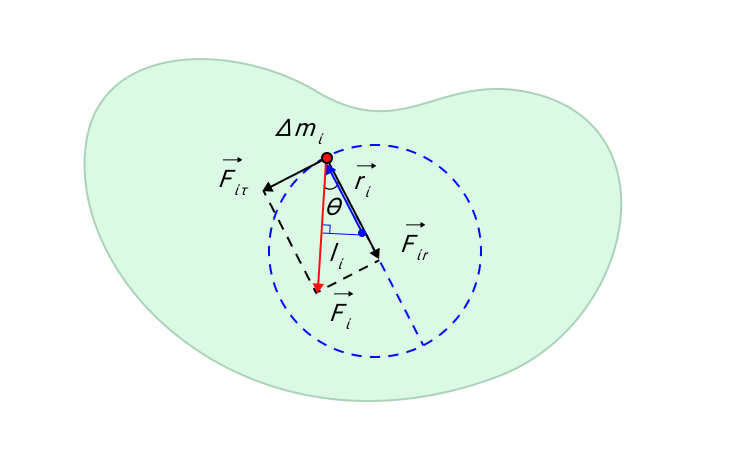
Δmi – это произвольный малый элемент массы, на который оказывают воздействие внешние и внутренние силы. Равнодействующая всех сил есть Fi→. Ее можно разложить на две составляющие: касательную составляющую Fiτ→ и радиальную Fir→. Радиальная составляющая Fir→ создает центростремительное ускорение an.
Рисунок 9. Касательная Fiτ→ и радиальная Fir→ составляющие силы Fi→ действующей на элемент Δmi твердого тела.
Касательная составляющая Fiτ→ вызывает тангенциальное ускорение aiτ→ массы Δmi. Второй закон Ньютона, записанный в скалярной форме, дает
∆miaiτ=Fiτsin θ или ∆miriε=Fisin θ,
где ε=aiτri – угловое ускорение всех точек твердого тела.
Если обе части написанного выше уравнения умножить на ri, то мы получим:
∆miri2ε=Firisin θ=Fili=Mi.
Здесь li – плечо силы, Fi,→Mi – момент силы.
Теперь нужно аналогичные соотношения записать для всех элементов массы Δmi вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:
∑∆miri2ε=∑Mi.
Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.
∑M=∑Miвнешн+∑Miвнутр.
Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M. Так мы получили основное уравнение динамики вращательного движения твердого тела.
Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.
Iε=M
Обычно за положительное направление вращения принимают направление против часовой стрелки.
Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω→, ε→, M→ определяются как векторы, направленные по оси вращения.
Закон сохранения момента импульса
В разделе, посвященном поступательному движению тела, мы ввели понятие импульса тела p→. По аналогии с поступательным движением для вращательного движения мы вводим понятие момента импульса.
Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.
Для обозначения момента импульса используется латинская буква L.
L=lω
Поскольку ε=∆ω∆t; ∆t→0, уравнение вращательного движения можно представить в виде:
M=Iε=I∆ω∆t или M∆t=I∆ω=∆L.
Получаем:
M=∆L∆t; (∆t→0).
Мы получили это уравнение для случая, когда I = const. Но оно будет справедливо и тогда, когда момент инерции тела будет изменяться в процессе движения.
Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L=Iω относительно данной оси сохраняется: ∆L=0, если M=0.
Следовательно,
L=lω=const.
Так мы пришли к закону сохранения момента импульса.
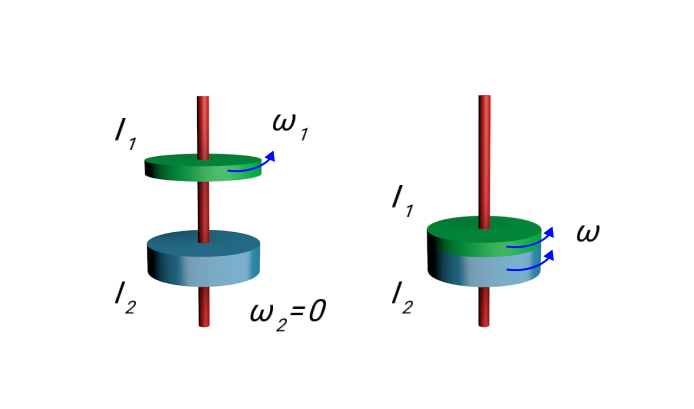
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.
Рисунок 10. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I1ω1=(I1+I2)ω.
Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.
Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.
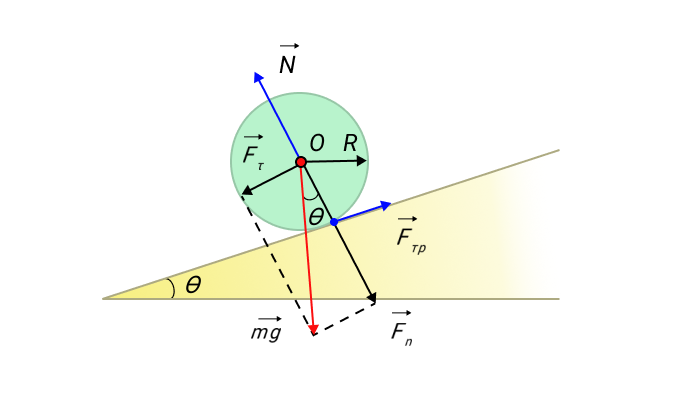
Рисунок 11. Качение симметричного тела по наклонной плоскости.
Ось вращения O проходит через центр масс тела. Моменты силы тяжести mg→ и силы реакции N→ относительно оси O равны нулю. Момент M создает только сила трения: M = FтрR.
Уравнение вращательного движения:
ICε=ICaR=M=FтрR,
где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, IC – момент инерции относительно оси O, проходящей через центр масс.
Второй закон Ньютона для поступательного движения центра масс записывается в виде:
ma=mg sin α-Fтр.
Исключая из этих уравнений Fтр, получим окончательно:
α=mg sin θICR2+m.
Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара IC=25mR2, а у сплошного однородного цилиндра IC=12mR2. Следовательно, шар будет скатываться быстрее цилиндра.
From Wikipedia, the free encyclopedia
Sketch 1: Instantaneous center P of a moving plane
The instant center of rotation (also, instantaneous velocity center,[1] instantaneous center, or instant center) is the point fixed to a body undergoing planar movement that has zero velocity at a particular instant of time. At this instant, the velocity vectors of the other points in the body generate a circular field around this point which is identical to what is generated by a pure rotation.
Planar movement of a body is often described using a plane figure moving in a two-dimensional plane. The instant center is the point in the moving plane around which all other points are rotating at a specific instant of time.
The continuous movement of a plane has an instant center for every value of the time parameter. This generates a curve called the moving centrode. The points in the fixed plane corresponding to these instant centers form the fixed centrode.
The generalization of this concept to 3-dimensional space is that of a twist around a screw. The screw has an axis which is a line in 3D space (not necessarily through the origin), and the screw also has a finite pitch (a fixed translation along its axis corresponding to a rotation about the screw axis).
Pole of a planar displacement[edit]
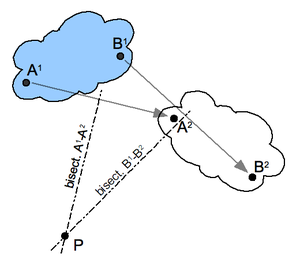
Sketch 2: Pole of a planar displacement
The instant center can be considered the limiting case of the pole of a planar displacement.
The planar displacement of a body from position 1 to position 2 is defined by the combination of a planar rotation and planar translation. For any planar displacement there is a point in the moving body that is in the same place before and after the displacement. This point is the pole of the planar displacement, and the displacement can be viewed as a rotation around this pole.
Construction for the pole of a planar displacement: First, select two points A and B in the moving body and locate the corresponding points in the two positions; see the illustration. Construct the perpendicular bisectors to the two segments A1A2 and B1B2. The intersection P of these two bisectors is the pole of the planar displacement. Notice that A1 and A2 lie on a circle around P. This is true for the corresponding positions of every point in the body.
If the two positions of a body are separated by an instant of time in a planar movement, then the pole of a displacement becomes the instant center. In this case, the segments constructed between the instantaneous positions of the points A and B become the velocity vectors VA and VB. The lines perpendicular to these velocity vectors intersect in the instant center.
The algebraic construction of the Cartesian coordinates 

has the Cartesian coordinates
and the midpoint between 

The two angles from 



taking the correct branches of the tangent. Let the center 



Rewrite this as a 4 × 4 inhomogeneous system of linear equations with 4 unknowns (the two distances 

The coordinates of the center of the rotation are the first two components of the solution vector
Pure translation[edit]
If the displacement between two positions is a pure translation, then the perpendicular bisectors of the segments A1B1 and A2B2 form parallel lines. These lines are considered to intersect at a point on the line at infinity, thus the pole of this planar displacement is said to “lie at infinity” in the direction of the perpendicular bisectors.
In the limit, pure translation becomes planar movement with point velocity vectors that are parallel. In this case, the instant center is said to lie at infinity in the direction perpendicular to the velocity vectors.
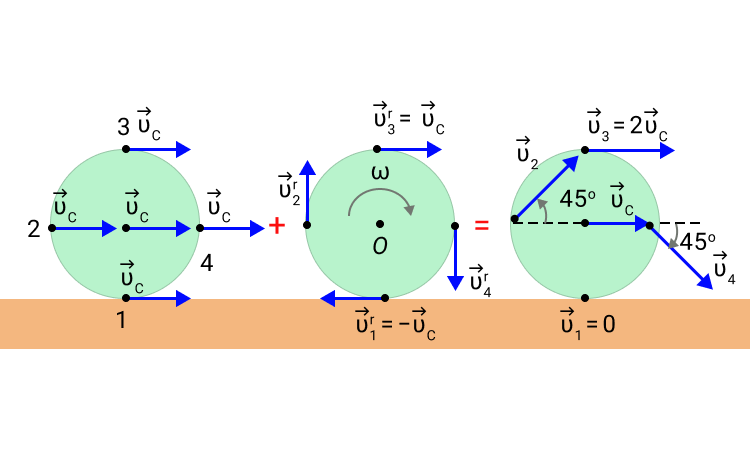
Instant center of a wheel rolling without slipping[edit]
Instant centre of rotation of a rolling wheel broken down into points. By breaking down the rolling wheel into several points, it can be more easily seen how all points of the wheel rotate around a single point at each instant. This point is the instant centre of rotation, shown in black.
Consider the planar movement of a circular wheel rolling without slipping on a linear road; see sketch 3. The wheel rotates around its axis M, which translates in a direction parallel to the road. The point of contact P of the wheel with road does not slip, which means the point P has zero velocity with respect to the road. Thus, at the instant the point P on the wheel comes in contact with the road it becomes an instant center.
The set of points of the moving wheel that become instant centers is the circle itself, which defines the moving centrode. The points in the fixed plane that correspond to these instant centers is the line of the road, which defines the fixed centrode.
The velocity vector of a point A in the wheel is perpendicular to the segment AP and is proportional to the length of this segment. In particular, the velocities of points in the wheel are determined by the angular velocity of the wheel in rotation around P. The velocity vectors of a number of points are illustrated in sketch 3.
The further a point in the wheel is from the instant center P, the proportionally larger its speed. Therefore, the point at the top of the wheel moves in the same direction as the center M of the wheel, but twice as fast, since it is twice the distance away from P. All points that are a distance equal to the radius of the wheel ‘r’ from point P move at the same speed as the point M but in different directions. This is shown for a point on the wheel that has the same speed as M but moves in the direction tangent to the circle around P.
Relative center of rotation for two contacting planar bodies[edit]
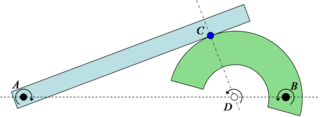
Sketch 4: Example relative center of rotation. Two bodies in contact at C, one rotating about A and the other about B must have a relative center of rotation somewhere along the line AB. Since the parts cannot interpenetrate the relative rotation center must also be along the normal direction to the contact and through C. The only possible solution is if the relative center is at D.
If two planar rigid bodies are in contact, and each body has its own distinct center of rotation, then the relative center of rotation between the bodies has to lie somewhere on the line connecting the two centers. As a result, since pure rolling can only exist when the center of rotation is at the point of contact (as seen above with the wheel on the road), it is only when the point of contact goes through the line connecting the two rotation centers that pure rolling can be achieved. This is known in involute gear design as the pitch point, where there is no relative sliding between the gears. In fact, the gearing ratio between the two rotating parts is found by the ratio of the two distances to the relative center. In the example in Sketch 4 the gearing ratio is 
Instant center of rotation and mechanisms[edit]
Sketch 1 above shows a four-bar linkage where a number of instant centers of rotation are illustrated. The rigid body noted by the letters BAC is connected with links P1-A and P2-B to a base or frame.
The three moving parts of this mechanism (the base is not moving) are: link P1-A, link P2-B, and body BAC. For each of these three parts an instant center of rotation may be determined.
Considering first link P1-A: all points on this link, including point A, rotate around point P1. Since P1 is the only point not moving in the given plane it may be called the instant center of rotation for this link. Point A, at distance P1-A from P1, moves in a circular motion in a direction perpendicular to the link P1-A, as indicated by vector VA.
The same applies to link P2-B: point P2 is the instant center of rotation for this link and point B moves in the direction as indicated by vector VB.
For determining the instant center of rotation of the third element of the linkage, the body BAC, the two points A and B are used because its moving characteristics are known, as derived from the information about the links P1-A and P2-B.
The direction of speed of point A is indicated by vector VA. Its instant center of rotation must be perpendicular to this vector (as VA is tangentially located on the circumference of a circle). The only line that fills the requirement is a line colinear with link P1-A. Somewhere on this line there is a point P, the instant center of rotation for the body BAC.
What applies to point A also applies to point B, therefore this instant center of rotation P is located on a line perpendicular to vector VB, a line colinear with link P2-B. Therefore, the instant center of rotation P of body BAC is the point where the lines through P1-A and P2-B cross.
Since this instant center of rotation P is the center for all points on the body BAC for any random point, say point C, the speed and direction of movement may be determined: connect P to C. The direction of movement of point C is perpendicular to this connection. The speed is proportional to the distance to point P.
Continuing this approach with the two links P1-A and P2-B rotating around their own instant centers of rotation the centrode for instant center of rotation P may be determined. From this the path of movement for C or any other point on body BAC may be determined.
Examples of application[edit]
In biomechanical research the instant center of rotation is observed for the functioning of the joints in the upper and lower extremities.[2]
For example, in analysing the knee,[3][4][5]
ankle,[6] or shoulder joints.[7][8]
Such knowledge assists in developing artificial joints and prosthesis, such as elbow [9] or finger joints.[10]
Study of the joints of horses: “…velocity vectors determined from the instant centers of rotation indicated that the joint surfaces slide on each other.”[11]
Studies on turning a vessel moving through water.[12]
The braking characteristics of a car may be improved by varying the design of a brake pedal mechanism.[13]
Designing the suspension of a bicycle,[14] or of a car.[15]
In the case of the coupler link in a four-bar linkage, such as a double wishbone suspension in front view, the perpendiculars to the velocity lie along the links joining the grounded link to the coupler link. This construction is used to establish the kinematic roll center of the suspension.
See also[edit]
- Angular velocity
- Burmester’s theory
- Centrode
- Rigid body
- Roll center
- Rotation around a fixed axis
- Screw axis
References[edit]
- ^ Illustrated Dictionary of Mechanical Engineering: English, German, French, Dutch, Russian (Springer Science & Business Media, 17 Apr. 2013 – 422 pages)
- ^ “Muscle Physiology — Joint Moment Arm”.
- ^ Knee joint motion description and measurement[permanent dead link]
- ^ Moorehead JD, Montgomery SC, Harvey DM (Sep 2003). “Instant center of rotation estimation using the Reuleaux technique and a Lateral Extrapolation technique”. J Biomech. 36 (9): 1301–7. doi:10.1016/S0021-9290(03)00156-8. PMID 12893038.
- ^ Hollman JH, Deusinger RH, Van Dillen LR, Matava MJ (Aug 2003). “Gender differences in surface rolling and gliding kinematics of the knee”. Clin Orthop Relat Res. 413 (413): 208–21. doi:10.1097/01.blo.0000072902.36018.fe. PMID 12897612. S2CID 45191914.
- ^ Maganaris CN, Baltzopoulos V, Sargeant AJ (Aug 1998). “Changes in Achilles tendon moment arm from rest to maximum isometric plantarflexion: in vivo observations in man”. Journal of Physiology. 510 (Pt 3): 977–85. doi:10.1111/j.1469-7793.1998.977bj.x. PMC 2231068. PMID 9660906. Archived from the original on 2012-09-08.
- ^ Biomechanics of shoulder
- ^ Poppen NK, Walker PS (Mar 1976). “Normal and abnormal motion of the shoulder”. J Bone Joint Surg Am. 58 (2): 195–201. doi:10.2106/00004623-197658020-00006. PMID 1254624.
- ^ US 5030237 Elbow prosthesis
- ^ “Pyrocarbon Finger Joint Implant” (PDF). Archived from the original (PDF) on 2011-07-21. Retrieved 2008-08-22.
- ^ Colahan P, Piotrowski G, Poulos P (Sep 1988). “Kinematic analysis of the instant centers of rotation of the equine metacarpophalangeal joint”. Am J Vet Res. 49 (9): 1560–5. PMID 3223666.
- ^ “PART VI Vessel Navigation and Manoeuvering” (PDF). Archived from the original (PDF) on 2009-12-15. Retrieved 2008-08-22.
- ^ GB 1443270 Variable Mechanical Ratio Brake Pedal Mounts – General Motors, 1976
- ^ US 7100930 Bicycle rear suspension system
- ^ Reza N. Jazar (2008). Vehicle Dynamics: Theory and Application. Berlin: Springer. ISBN 978-0-387-74243-4.
Мгновенный центр вращения
2017-02-17
Когда колесо катится без проскальзывания, его движение складывается из поступательного и вращательного. Скорость нижней точки колеса в таком движении всегда равна нулю, и эта точка является мгновенным центром вращения.
Другие видеоуроки по физика:
- Видео
- Конспект
- Задачи
Измерить вес тела можно также пружинными весами (рис. 3). Груз давит на дно чаши и сжимает пружину внутри весов. Чем больше вес тела, тем больше сжатие пружины. Чтобы измерять вес, пружинные весы нужно предварительно проградуировать, используя эталонные грузы.
Как возникает действие груза на пружинные весы? Известно, что все тела притягиваются Землей силой тяжести. Груз давит на чашу весов силой, равной по величине силе тяжести, которая уравновешивается пружиной. Эту силу называют весом тела.
Мгновенный центр вращения. Центроиды
- Получает так называемый мгновенный центр вращения для двух почти бесконечных положений на плоской фигуре, а не в центре конечного вращения. Плоское смещение фигуры может быть почти заменено серией вращательных смещений вокруг конечного центра вращения. В пределе, плоское движение формы может быть заменено бесконечной последовательностью основных мгновенных вращений вокруг центра мгновенного вращения в определенной последовательности. Рисунок 71. Таким образом, плоское движение на фигуре может быть заменено последовательностью мгновенных вращений, которые выполняются в течение того же периода, что и рассматриваемое плоское движение.
Вы можете ввести мгновенную угловую скорость или, точнее, угловую скорость вокруг мгновенной оси, которая проходит через мгновенный центр вращения и перпендикулярна плоскости движения. В плоском движении фигуры Центр вращения вены движется как в неподвижной, так и в подвижной плоскостях и соединяется с подвижным планом. Геометрическое положение мгновенного центра вращения на неподвижной плоскости называется неподвижным центроидом, а геометрическое положение этого же мгновенного центра вращения на движущейся плоскости, связанной с движущейся фигурой, называется движущимся центроидом. , Движение каждой плоскости фигуры имеет два центра тяжести: подвижный и неподвижный.
Когда все силы инерции точек системы исчезают по принципу возможного смещения статики, только в случае равновесия системы, до сих пор нет проблем с устойчивостью системы.
Людмила Фирмаль
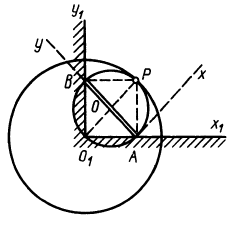
Очевидно, что скорость точки на плане, где мгновенный центр вращения совпадает в момент задачи, равна нулю. Следовательно, это также мгновенный центр скорости. Благодаря плоскому движению фигуры, движущийся центр тяжести вращается без скольжения вдоль неподвижного центра тяжести. Эта теорема позволяет рассматривать движение сплошной плоскости как катящееся без скольжения одной плоской кривой вдоль другой. Центр тяжести был применен к нескольким задачам в механике кинематики. Рассмотрим пример нахождения центра тяжести. Пример. Стержень I длины I скользит по двум прямым линиям, которые перпендикулярны друг другу (Рисунок 71). Это движение находит центр тяжести стержня AB.
Решения. Поскольку показанная линия является траекторией этих точек, скорость точки A направлена только вдоль O, A и точки B. Восстановление нормалей точек A и B в этих направлениях дает точку P. Центр скорости на плоскости, приклеенной к стержню, Мгновенный центр вращения на фиксированной плоскости. Из рисунка видно, что OtP = l = const в течение всего движения, как прямоугольная диагональ. Таким образом, фиксированный центр тяжести представляет собой круг с радиусом I с центром в точке Ot. Соединен со стержнем AB с подвижной поверхностью Ahu. Поскольку OP равен O, PI2 = ll2 = const, точка P имеет аналогичные геометрические характеристики, поэтому движущийся центр тяжести представляет собой круг с радиусом 1/2 с центром в точке O.
- При прокатке круга, который движется вдоль неподвижного конца, концы A и B диаметра круга перемещаются линейно по прямым линиям 0,4, 0 и d соответственно. Повернут на произвольный угол вокруг точки O координатной плоскости 0, x, y на плоскости рисования, и этот случай был рассмотрен после исправления Размещая оси координат в новых положениях, вы можете сделать центр тяжести таким же кругом. В результате две другие точки движущегося круга движутся линейно. Таким образом, мы видим, что вес точки движущейся окружности движется по прямой, проходящей через центр неподвижной окружности O |.
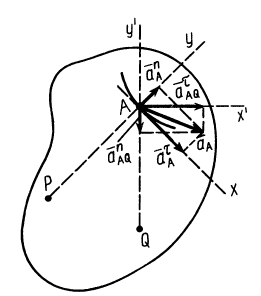
Это характеристика вращательного линейного перевода В общем случае движения плоской фигуры центр мгновенной скорости — точка P — и центр мгновенного ускорения — точка Q — это разные точки этой фигуры (рис. 72). Эти очки соответствуют и Когда плоское движение сводится к вращательному движению вокруг неподвижной оси. Выберите точку A на плане этажа и отметьте точки P и Q. Поднимите проблему. Вот выражение, которое может вычислить проекцию ускорения точки A на оси Ax и Au, Ax ‘и Au’. Ось Ax перпендикулярна осям Au и Ax’LAy ‘. Точка Q является центром мгновенного ускорения. Отсюда ускорение Всегда направлено на точку Q. Вертикальное ускорение проекция Ах ‘ ^ ax ‘- ^ aq-AQ. Точка P является центром мгновенной скорости. Скорость точки A перпендикулярна AR, а скорость всегда направлена по касательной к траектории.
Поэтому система отсчета, в которой материальная точка покоится, должна иметь соответствующую систему отсчета для материальной точки, поскольку относительная скорость и ускорение равны нулю.
Людмила Фирмаль
Следовательно, ось Ax является касательной к траектории, а проекция ускорения на ось является тангенциальным ускорением, рассчитанным по формуле тангенциального ускорения. Ось Au перпендикулярна касательной. Следовательно, это главная норма орбиты. Проекция ускорения в этом направлении рассчитывается по формуле нормального ускорения Если aLy> 0, точечная траектория является выпуклой относительно точки P. Если aAy <0, он вогнутый. Кажется, что точка А имеет два разных вертикальных и тангенциальных ускорения. Где и apl — тангенциальные и нормальные ускорения абсолютного движения точки А.
Для фиксированной системы координат (не показана на рисунке 72) 0 и «AQ — это касательное и нормальное ускорение точки A относительно движущейся системы координат, которая не перемещается относительно точки Q. Точка A Соответствует абсолютному ускорению в точке Q. Поскольку эта точка является центром мгновенного ускорения, она равна нулю.
Смотрите также:
Задачи по теоретической механике
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.