
The frequency axis of this symbolic diagram may be linearly or logarithmically scaled. Except in special cases, the peak response will not align precisely with the center frequency.
In electrical engineering and telecommunications, the center frequency of a filter or channel is a measure of a central frequency between the upper and lower cutoff frequencies. It is usually defined as either the arithmetic mean or the geometric mean of the lower cutoff frequency and the upper cutoff frequency of a band-pass system or a band-stop system.
Typically, the geometric mean is used in systems based on certain transformations of lowpass filter designs, where the frequency response is constructed to be symmetric on a logarithmic frequency scale.[1] The geometric center frequency corresponds to a mapping of the DC response of the prototype lowpass filter, which is a resonant frequency sometimes equal to the peak frequency of such systems, for example as in a Butterworth filter.
The arithmetic definition is used in more general situations, such as in describing passband telecommunication systems, where filters are not necessarily symmetric but are treated on a linear frequency scale for applications such as frequency-division multiplexing.[2]
References[edit]
- ^ John T. Taylor and Qiuting Huang (1997). CRC Handbook of Electrical Filters. CRC Press. ISBN 0-8493-8951-8.
- ^ Julie K. Petersen (2003). Fiber Optics Illustrated Dictionary. CRC Press. ISBN 0-8493-1349-X.
External links[edit]
- Calculations and comparisons between the geometric mean and the arithmetic mean
Центральная частота f 0 является средним геометрическим для нижней f 1 и верхней f 2 предельной частоты ( частоты кроссовера) полосы частот с определенной полосой пропускания фильтра , также известной под термином « полоса пропускания» .
Основы
Центральная частота полосы пропускания фильтра B = f 2 – f 1 вычисляется по формуле:
Среднее арифметическое часто вычисляется неправильно , хотя частоты в полосах частот логарифмически связаны. Например, центральная частота звуковых частот телефона от 300 Гц до 3400 Гц равна не (3400 Гц + 300 Гц) / 2 Гц = 1850 Гц, а квадратному корню из 300 Гц x 3400 Гц = 1010 Гц.
Тем не менее центральная частота линейно расположенных спектров, например, в антенной технике, должна рассчитываться как среднее арифметическое:

характеристики
Из-за определения центральной частоты отношения предельных частот к центральной частоте одинаковы:
Если f 1 , f 0 и f 2 отмечены на логарифмической шкале частот, то f 0 находится посередине:
Использовать как приближение
Полоса пропускания f 2 – f 1 часто мала по сравнению с центральной частотой. Затем вы можете использовать среднее арифметическое для расчета в качестве хорошего приближения:
Со многими средневолновыми передатчиками z. Б. Полоса пропускания всего 9 кГц. Передатчик, который указан как 1500 кГц, передает здесь в диапазоне от 1495,5 кГц до 1504,5 кГц. Формула аппроксимации дает
в то время как точная формула используется для определения:
Значение, вычисленное по формуле приближения, всегда слишком велико. Если обозначить полосу пропускания буквой B , отклонение формулы аппроксимации составляет примерно
в приведенном примере это менее 7 Гц.
литература
- Майкл Дикрайтер, Фолькер Диттель, Вольфганг Хог, Мартин Вёр (ред.), “Handbuch der Tonstudiotechnik”, 8-е, исправленное и расширенное издание, 2 тома, издатель: Вальтер де Грюйтер, Берлин / Бостон, 2014, ISBN 978-3-11 -028978-7 или e- ISBN 978-3-11-031650-6
- Грегор Хеберле, Хайнц Хеберле, Томас Кляйбер: опыт работы в радио, телевидении и радиоэлектронике. 3-е издание, Verlag Europa-Lehrmittel, Haan-Gruiten, 1996, ISBN 3-8085-3263-7
- Карл Герман Хубер: Фильтрация и просеивание звуковых частот. 1-е издание, Frech Verlag, Штутгарт, 1974, ISBN 3-7724-0162-7
- Уоррен Л. Штутцман: теория и конструкция антенн . 3-е издание, Wiley Verlag, Weinheim, 2012, ISBN 978-0470576649
Смотри тоже
- Распределительная ленточная технология
веб ссылки
- Центральная частота как среднее геометрическое предельных частот – по сравнению со средним арифметическим
- Преобразование: «полоса пропускания в октавах» N в добротности Q и добротность Q в «полосе пропускания в октавах» N
Центральная частота – полоса – пропускание
Cтраница 1
Центральная частота полосы пропускания / ц – значение частоты, равное полусумме нижней и верхней граничных частот полосы пропускания микросхемы.
[1]
Центральная частота полосы пропускания определяется частотой движения глазного века.
[2]
Центральная частота полосы пропускания / д – значение частоты, равное полусумме нижней и верхней граничных частот полосы пропускания микросхемы.
[3]
Центральная частота полосы пропускания fa – значение частоты, равное полусумме нижней и верхней граничных частот полосы пропускания микросхемы.
[4]
Центральная частота полосы пропускания fo, обычно совпадающая с несущей частотой в усилителях модулированного сигнала, зависит от назначения усилителя и составляет 0 1 – 200 МГц. Значение полосы пропускания определяется шириной спектра усиливаемого сигнала и составляет для полосовых усилителей величину от нескольких сотен герц до нескольких десятков магагерц. По относительной ширине полосы пропускания Afyc / / o усилители можно условно разделит.
[5]
Обозначения, принятые в программе: El, E2, ЕЗ – модули упругости материалов диска, связки, сердечника; Р0 – объемная плотность материалов диска и связок; Р – резонансное входное сопротивление; РЗ – объемная плотность материала сердечника; С – диаметр связки; С2, СЗ – скорости распространения механических колебаний в материале связки и сердечника; F0 – центральная частота полосы пропускания; F1 – ширина полосы пропускания; F2 – резонансная частота звена; F3 – нормированная резонансная частота; F8 – минимально допустимая рабочая частота фильтра; F9 – максимально допустимая рабочая частота фильтра; А – параметр, равный D / ta; A0 – уровень отсчета, на котором определяется коэффициент прямоугольное характеристики затухания фильтра; А1 – число крайних связок; А9 – допустимая неравномерность затухания фильтра в полосе пропускания; К – коэффициент связи резонаторов; К1 – коэффициент прямоугольное; Q – требуемая добротность фильтра; Q1 – рассчитанное значение добротности фильтра; N0 – код нагрузки фильтра: 1 – разнотипная; 2 – однотипная; W – вспомогательный параметр; Wl – W5 – коды вопросов; W6 – код материала сердечника преобразователя; 1 – сплав 50 КФ; 2 – никель марки НП2; D – относительные полосы пропускания и прозрачности; D7, D8 – диаметры диска резонатора и сердечника; Н, Н0 – приведенная добротность и округленное ее значение; М – число звеньев фильтра; S – обобщенная расстройка; Т – толщина диска-резонатора; Л, J2 – вспомогательные параметры; V – относительная резонансная частота дискового резонатора; Y – число узловых окружностей колебаний диска; R – резонансное сопротивление нагрузки; R1 – характеристическое сопротивление диска; Z – коэффициент трансформации; L2, L3 – длина связки и сердечника; X – отношение характеристических сопротивлений внутренних и крайних связок; XI, Х2 – вспомогательные коэффициенты.
[6]
Некоторые виды искажений могут быть скомпенсированы. Сдвиг центральной частоты полосы пропускания можно практически исключить при настройке усилителя, из-неине коэффициента усиления можно устранить выбором необходимого запаса п введением установочной регулировки усиления. Поэтому обычно Ау выбирается исходя из допустимого значения некомпенсируемых искажений полосы пропускания п асимметрии частотных характеристик.
[7]
Влияние использования центральной частоты полосы пропускания приемника при расчете величин и и v для всех частот внутри полосы обсуждается в разд. Измеренная функция видности будет спадать слишком быстро по и и v и центральный пик функции видности будет слишком узким. Поэтому ширина изображения по / и т будет слишком большая. Таким образом, если источник излучает радиолинию на голубом крыле полосы, его угловые размеры могут быть переоценены, и наоборот, недооценены на красном краю полосы. Этот эффект называется хроматической аберрацией.
[8]
Нормируем это сопротивление по величине, поделив на некоторое сопротивление Л о ( 0м) и затем нормируем по частоте wo ( рад / с), введя нормированную частоту х – ш / ( оо. Если речь идет о фильтрах, то шо берут равной либо частоте среза НЧ-фильтра, либо центральной частоте полосы пропускания ПП-фильтра.
[9]
Таким образом, в амплитудно-частотном методе экспериментально находят э и Аник. Отметим, что в случае небольшого различия Л ин при э выше и ниже центральной частоты полосы пропускания целесообразно использовать прием усреднения экспериментально находимых величин Лмии.
[10]
Таким образом, в реальных конструкциях фильтров на ДР используются частотно-избирательные структуры в виде нескольких резонаторов, связанных друг с другом и с линиями передачи. Коэффициенты, оценивающие количественно степень этих связей, определяют вид АЧХ коэффициентов передачи и отражения. На рис. 10.4 приведен вид обобщенной АЧХ коэффициента передачи ПФ; принятые здесь обозначения имеют следующий смысл: / о – центральная частота полосы пропускания 2Д / П фильтра, в которой потери равны Аи, неравномерность вносимых фильтром потерь равна АЛп.
[12]
Мы видим, что предельная избирательность п-каскадного усилителя очень мала. Это объясняется тем, что при неограниченном увеличении числа каскадов для сохранения заданной полосы пропускания усилителя Af необходимо увеличивать эквивалентное затухание колебательного контура каждого каскада, вследствие чего форма резонансной кривой быстро ухудшается. Это обстоятельство приводит в конечном счете к весьма незначительному увеличению избирательности всего усилителя. Бблылую избирательность от – каскадного усилителя с одиночными контурами в каждом каскаде можно получить, если колебательные контуры каскадов симметрично попарно расстроить относительно центральной частоты полосы пропускания.
[13]
Страницы:
1
Глава 1 Введение
Цель данной книги — сформировать базовые знания о супергетеродинных анализаторах спектра и рассказать о недавних достижениях в развитии их возможностей.
В самых общих чертах анализатор спектра можно описать как частотно-избирательный вольтметр, реагирующий на амплитуду и настроенный так, чтобы отображать среднеквадратичное значение синусоидальной волны. Важно осознавать, что анализатор спектра не является измерителем мощности, несмотря на то, что он способен напрямую отображать значение мощности. Если нам известен какой-нибудь параметр синусоидальной волны (например, пиковое или среднее значение) и известно сопротивление, через которое мы измеряем это значение, мы можем настроить наш вольтметр на отображение мощности. С преимуществами цифровой технологии, современные анализаторы спектра обладают куда более широкими возможностями. В данной книге будут рассмотрены простейшие анализаторы спектра, а также множество дополнительных возможностей, предоставленных развитием цифровой технологии и цифровой обработки сигналов.
Частотная область против временной области
Прежде чем начать подробно рассматривать анализатор спектра, зададимся вопросом: «А что же такое вообще спектр, и зачем нам его измерять и анализировать?» Обычной и естественной системой отсчета для нас является время. Мы замечаем, когда происходит то или иное событие. Это включает и события электрического характера. Можно использовать осциллограф и наблюдать мгновенное значение величины какого-то электрического явления (или любого другого явления, переведенного в вольты посредством надлежащего преобразователя) в зависимости от времени. Иными словами, мы используем осциллограмму для наблюдения формы сигнала во временной области
Теория Фурье1 гласит, что любое электрическое явление во временной области состоит из одной или нескольких синусоидальных волн с соответствующими частотами, амплитудами и фазами. То есть можно преобразовать сигнал во временной области в его эквивалент в частотной области. Измерения в частотной области способны показать, сколько энергии имеется на каждой конкретной частоте. При надлежащей фильтрации такой сигнал, как на Рис. 1-1, может быть разложен на отдельные синусоидальные волны, или спектральные составляющие, которые затем можно оценить независимо друг от друга. Каждая такая волна описывается амплитудой и фазой. Если сигнал, который мы хотим исследовать, — периодический (как в нашем случае), то по теории Фурье составляющие его синусоидальные волны будут разнесены в частотной области на 1/Т, где Т – это период сигнала2.
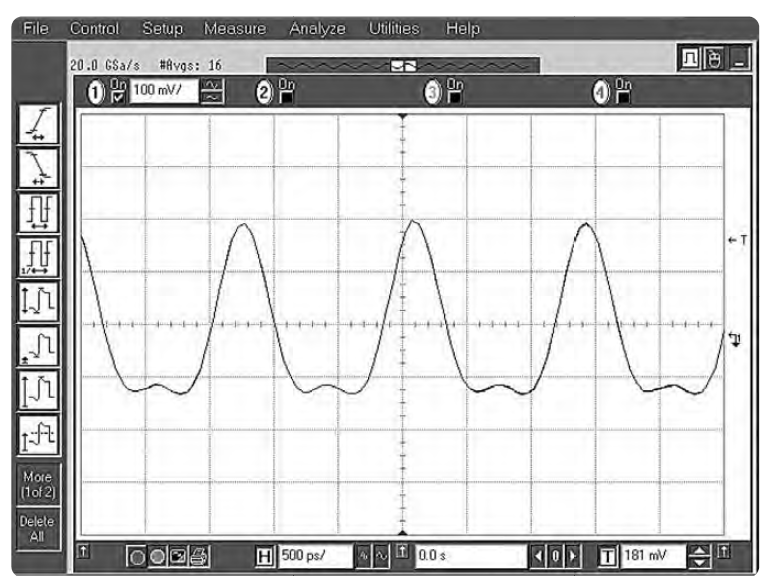
- Жан Баптист Фурье, 1768 – 1830, французский математик и физик, открывший, что периодические функции могут быть представлены последовательностью синусов и косинусов.
- Если же сигнал появляется лишь раз, то его спектральным представлением будет непрерывное множество синусоидальных волн.
Некоторые измерения требуют получения полной информации о сигнале – частоты, амплитуды и фазы. Такого рода анализ называется векторным анализом сигнала и рассматривается в документе Agilent Application Note 150-15, Vector Signal Analysis Basics. Современные анализаторы спектра способны проводить различного рода векторные измерения сигнала. Однако, другая обширная группа измерений не включает определения фазовых соотношений между синусоидальными составляющими. Такой тип анализа сигнала называется спектральным анализом. Поскольку спектральный анализ более прост для понимания и одновременно необычайно полезен на практике, мы сперва рассмотрим то, как анализаторы спектра осуществляют измерения для спектрального анализа, начиная с Главы 2.
Теоретически, чтобы осуществить преобразование из временной области в частотную область, сигнал должен быть оценен на всем промежутке времени, то есть до ± бесконечности. Однако, на практике мы всегда ограничиваемся каким-то конечным периодом, когда проводим измерение. Преобразование Фурье также может быть осуществлено и из частотной области во временную. В этом случае, опять же, теоретически нам надо знать все спектральные составляющие в диапазоне частот до ± бесконечности. На самом же деле, производя измерения только в той области частот, в которой содержится наибольшая часть энергии сигнала, можно получить вполне приемлемые результаты. При преобразовании Фурье из частотной области очень важно знать фазу индивидуальных составляющих. Например, прямоугольный периодический сигнал, переведенный в частотную область и обратно, может превратиться в пилообразный, если не были зафиксированы фазы.
Что такое спектр?
Так чем же является спектр в контексте нашего обсуждения? Спектр – это набор синусоидальных волн, которые, будучи надлежащим образом скомбинированы, дают изучаемый нами сигнал во временной области. На Рис. 1-1 показана волновая форма сложного сигнала. Давайте предположим, что мы ожидали увидеть чисто синусоидальный сигнал. И хотя форма явно демонстрирует нам, что сигнал не является чистой синусоидой, она не дает определенного ответа на вопрос о причинах данного явления. На Рис. 1-2 показан наш сложный сигнал во временной и в частотной области. В частотной области показана амплитуда для каждой синусоидальной волны в спектре в зависимости от частоты. Как видно, в данном случае спектр состоит лишь из двух волн. Теперь мы знаем, отчего наш сигнал не является чистой синусоидой: в нем содержится еще одна волна, вторая гармоника в нашем случае. Означает ли это, что измерения во временной области можно вообще не проводить? Отнюдь. Временная область является предпочтительной для многих измерений, а для некоторых является единственно возможной. К примеру, только во временной области можно измерить длительность фронта и спада импульса, выбросы и биения.
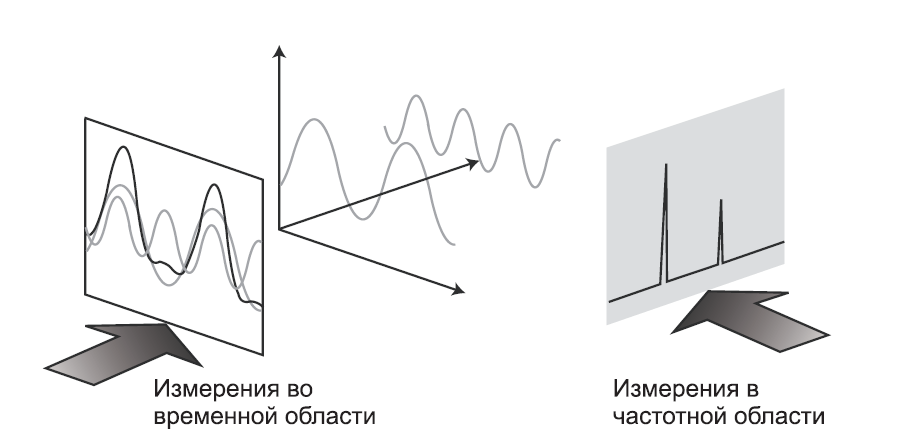
Для чего измерять спектр?
У частотной области есть свои плюсы в плане измерений. Мы уже видели на Рис. 1-1 и 1-2, что частотная область гораздо удобнее для определения гармонического состава сигнала. Те, кто занимаются беспроводной связью, очень заинтересованы в определении внеполосного и паразитного излучения. Например, сотовые радиосистемы должны проверяться на наличие гармоник несущего сигнала, которые могут вносить помехи в работу других систем, оперирующих на той же частоте, что и гармоники. Инженеры и техники также часто обеспокоены искажением сообщений, модулирующих несущий сигнал. Интермодуляция третьего порядка (то есть две составляющие сложного сигнала, модулирующие друг друга) может причинить много хлопот, поскольку продукты искажений могут попасть в интересуемую полосу частот и не будут надлежащим образом отфильтрованы.
Наблюдение за спектром – еще одна важная сторона измерений в частотной области. Государственные регулирующие структуры распределяют различные частоты для различных радио-служб: телевизионное и радиовещание, сотовая связь, связь правоохранительных органов и спасательных служб, а также множество иных организаций и приложений. Крайне важно, чтобы каждая служба работала только на предназначенной для нее частоте и оставалась в пределах выделенной полосы канала. Передатчики и другие излучатели зачастую могут работать на очень близко расположенных соседних частотах. Для усилителей мощности и других узлов таких систем ключевым параметром для измерения является количество энергии сигнала, просачивающейся в соседние каналы и порождающей интерференцию.
Электромагнитная интерференция (EMI) – это термин, применяемый к нежелательному излучению от преднамеренных и случайных излучателей. Поводом для беспокойства тут служит тот факт, что это нежелательное излучение, будучи передано в эфир или по проводам, может затруднить работу других систем. При разработке и производстве практически любой электрической или электронной продукции необходимо исследовать уровни излучения в зависимости от частоты, и приводить их в соответствие с нормами, устанавливаемыми правительственными органами или индустриальными стандартами. На Рис. с 1-3 по 1-6 показаны некоторые из такого рода измерений.
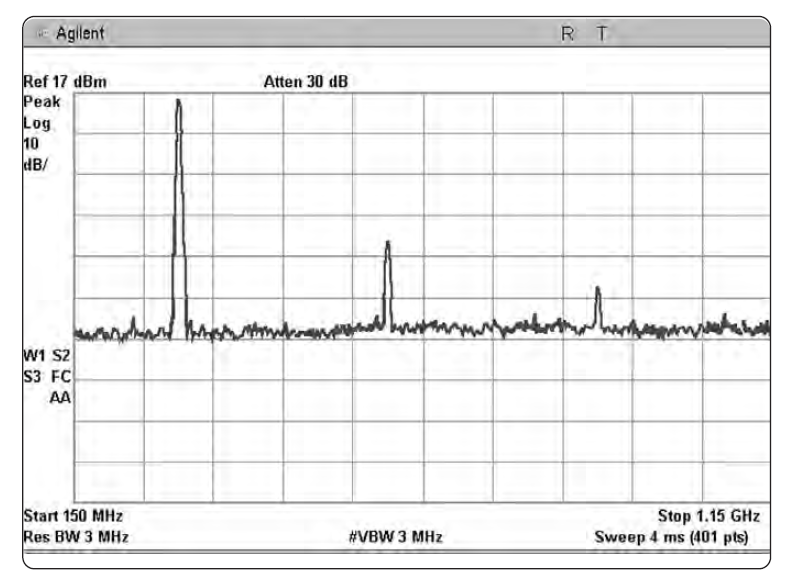

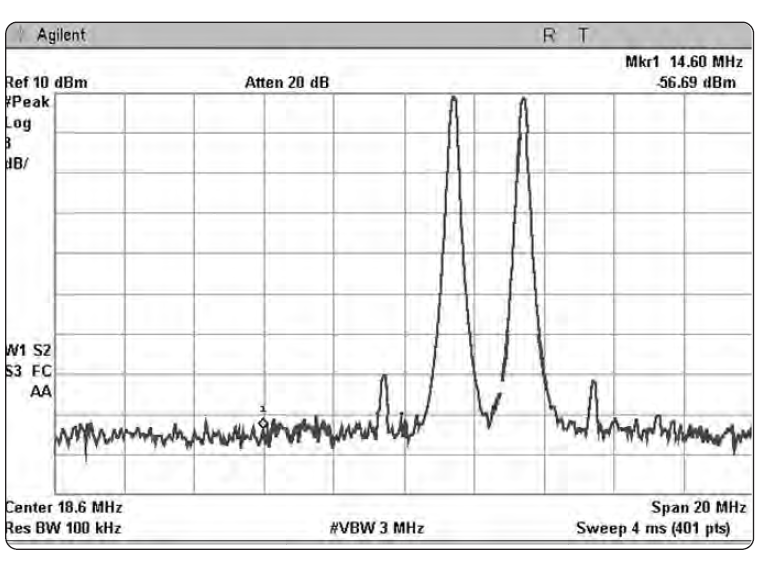
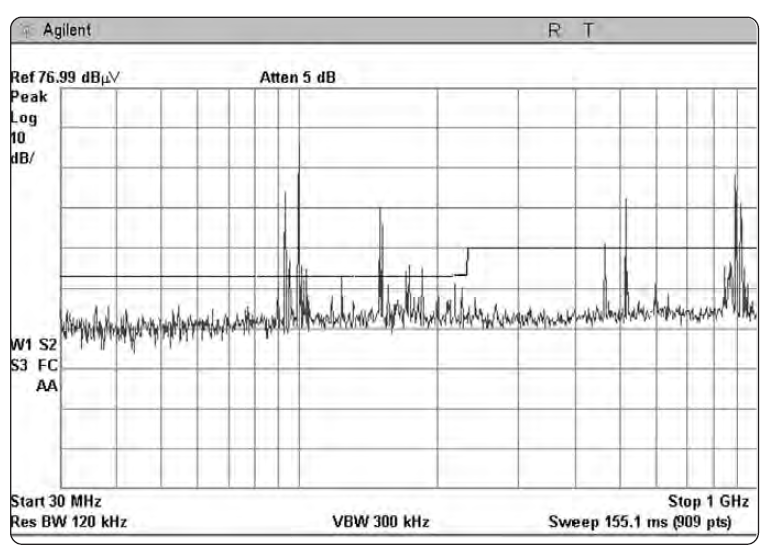
Типы измерений
Чаще всего с помощью анализаторов спектра измеряют частоту, мощность, модуляцию, искажения и шум. Знание спектрального состава сигнала очень важно, особенно в системах с полосой частот ограниченной ширины. Переданная мощность также является важным измеряемым параметром. Слишком малая мощность означает, что сигнал не сможет достичь точки назначения. Слишком большая мощность может быстро истощить заряд батарей, создать искажения и чрезмерно повысить рабочую температуру системы.
Измерение качества модуляции может быть важным для того, чтобы обеспечить нормальную работу системы и быть уверенным в том, что информация передается корректно. Измерения коэффициента модуляции, амплитуды боковых полос (частот), качества модуляции и заполнения полосы частот – это примеры самых распространенных измерений при аналоговой модуляции. В случае цифровой модуляции измеряются модуль вектора погрешности, дисбаланс IQ, зависимость неопределенности фазы от времени и ряд других параметров. Более подробно об этих видах измерений рассказано в документе Agilent Application Note 150-15, Vector Signal Analysis Basics.
В сфере коммуникаций и связи измерение искажений очень важно как для приемников, так и для передатчиков. Излишние гармонические искажения на выходе передатчика могут создавать помехи на других коммуникационных частотах. В блоках предусилителей приемника не должно быть интермодуляции, чтобы избежать перекрестного наложения сигнала. Хороший пример – интермодуляция несущих сигналов кабельного телевидения, которые при распространении по распределительной системе вносят искажения в другие каналы этого же кабеля. Распространенными измерениями искажений являются измерения интермодуляции, гармоник и паразитного излучения.
Часто бывает нужно измерить и шум как сигнал. Любая активная цепь или устройство будет генерировать шум. Измерения коэффициента шума и отношения сигнал/шум (С/Ш) являются важными для описания показателей устройства и его вклада в общие показатели системы.
Виды анализаторов сигнала
Хотя в этом руководстве мы концентрируемся на перестраиваемом супергетеродинном анализаторе спектра, существуют и другие архитектуры. Важный не супергетеродинный тип анализатора – тот, что оцифровывает сигнал во временной области, использует методы цифровой обработки сигнала, выполняет быстрое преобразование Фурье (БПФ) и показывает сигнал в частотной области. Одно преимущество подхода с БПФ в том, что появляется возможность характеризовать одновспышечные явления. Другое – в том, что кроме амплитуды можно измерить и фазу. Однако, БПФ-машины имеют некоторые ограничения в сравнении с супергетеродинными анализаторами спектра, в частности — по диапазону частот, чувствительности и динамическому диапазону.
Векторные анализаторы сигнала тоже оцифровывают сигнал во временной области, как и БПФ-машины, но их возможности при этом распространяются и на область СВЧ при помощи понижающих преобразователей, включенных перед АЦП. Такие анализаторы позволяют провести быстрые измерения спектра с хорошим разрешением, демодуляцию и расширенный анализ во временной области. Они особенно полезны для описания сложных сигналов – всплесков, переходного или модулированного сигнала в системах связи, телевещания, радиовещания, в сонарах, а также в приложениях ультразвукового зондирования.
Хотя мы определили анализ спектра и векторный анализ сигнала как отдельные виды измерений, цифровые технологии и цифровая обработка сигналов делают это различие весьма размытым. Здесь критичным является то, на каком этапе сигнал был оцифрован. Раньше, когда цифровые преобразователи были ограничены десятками килогерц, оцифровывался только видео-сигнал анализаторов спектра. Поскольку видео-сигнал не нес никакой информации о фазе, на дисплей выводились только данные об амплитуде. Но даже такое ограниченное использование цифровой технологии давало значительные преимущества: немерцающий дисплей медленных разверток, экранные маркеры, различные виды усреднений, а также вывод данных на компьютеры и принтеры.
Поскольку сигналы, которые требуется измерять, со временем становятся все более и более сложными, последние поколения анализаторов спектра обладают многими возможностями векторного анализа, которые ранее были присущи только БПФ-машинам и векторным анализаторам сигнала. Анализатор спектра может оцифровать сигнал практически непосредственно на входе, либо после некоторого усиления, либо после одной или нескольких ступеней понижающих преобразований. В любом из этих случаев сохраняются относительная фаза и амплитуда. Вдобавок к вышеперечисленным преимуществам, можно провести и истинные векторные измерения. Так что возможности инструмента определяются возможностями цифровой обработки сигнала, присущей непосредственно прибору или дополнительному программному обеспечению, работающему в составе прибора или на компьютере, подсоединенном к анализатору извне. На Рис. 1-7 показан пример такой способности. Отметьте, что символы квадратурной фазовой манипуляции (QPSK) отображаются как скопления ( а не как одиночные точки), индицирующие ошибки в модуляции измеряемого сигнала.
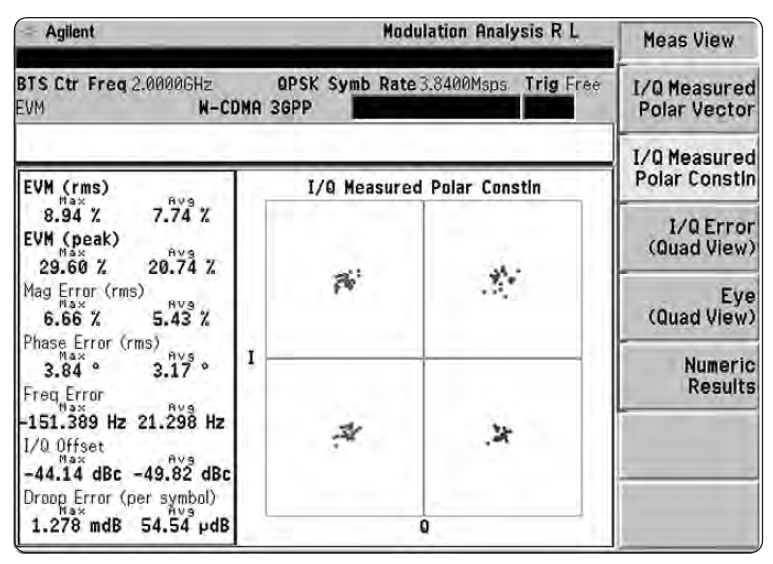
Глава 2 Основные принципы работы анализатора спектра
В этой главе мы сфокусируемся на теоретических основаниях работы анализатора спектра. И хотя современные технологии позволяют заменить множество аналоговых цепей современными цифровыми их воплощениями, весьма полезно будет изучить архитектуру классического анализатора спектра и использовать ее как отправную точку дальнейших обсуждений. Позже мы еще рассмотрим возможности и плюсы спектрального анализа при наличии цифровых узлов. В Главе 3 будут рассмотрены цифровые архитектуры современных анализаторов спектра.
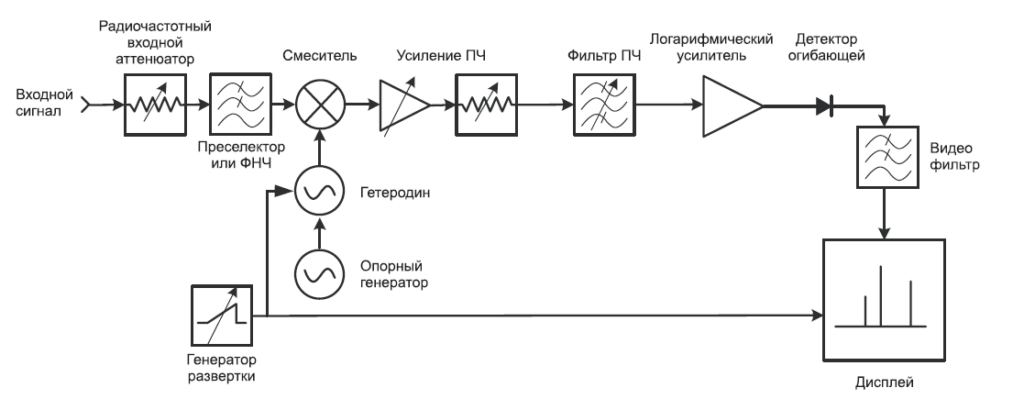
Рис. 2-1 представляет собою упрощенную структурную схему супергетеродинного анализатора спектра. «Гетеродинировать» — означает смешивать, то есть переносить частоту, а «супер» относится к супераудио-частотам или частотам выше звукового диапазона*. Исходя из структурной схемы на Рис. 2-1, видно, что входной сигнал проходит через аттенюатор, а затем через фильтр нижних частот (позже мы поймем, зачем здесь фильтр) на смеситель, где он смешивается с сигналом от гетеродина (локального осциллятора, LO). Поскольку смеситель – нелинейный элемент, на его выходе будут не только два первоначальных сигнала, но и их гармоники, а также суммы и разности первоначальных частот и их гармоник. Если какой-то из продуктов смешения попадает в полосу фильтра промежуточной частоты (ПЧ), то далее он обрабатывается (усиливается и, возможно, сжимается по логарифмической шкале). Он выпрямляется детектором огибающей, оцифровывается и выводится на дисплей. Генератор пилообразного напряжения создает горизонтальное движение по дисплею слева направо, а также перестраивает гетеродин таким образом, что его частота изменяется пропорционально напряжению «пилы».
Если вы знакомы с супергетеродинными АМ-приемниками — теми, что принимают обычные сигналы радиовещания, — вы заметите сильное сходство между ними и структурной схемой на Рис. 2-1. Разница только в том, что сигнал с выхода спектроанализатора подается на дисплей, а не на динамик, и что гетеродин перестраивается электронно, а не вручную.
Раз выходной сигнал анализатора спектра – это кривая в X-Y-плоскости дисплея, давайте посмотрим, какую информацию мы можем из нее получить. Дисплей разграфлен масштабной сеткой на 10 главных горизонтальных полос и, обычно, на 10 главных вертикальных полос. Горизонтальная ось калибруется по частоте, которая увеличивается линейно слева направо. Установка частоты обычно двухэтапный процесс. Сначала мы подгоняем частоту центральной линии масштабной сетки с помощью блока управления центральной частоты. Затем мы подгоняем обзор, приходящийся на все 10 горизонтальных полос, с помощью блока управления полосой обзора. Эти блоки управления независимы, так что если мы меняем центральную частоту, полоса обзора не меняется. Как вариант, мы можем устанавливать начальную и конечную частоты вместо установки центральной частоты и полосы обзора. В любом случае, мы можем определять абсолютную частоту любого сигнала, отображенного на дисплее, и частотную разность двух любых сигналов.
Вертикальная ось калибруется по амплитуде. Обычно предлагается выбор между линейной шкалой, калиброванной в вольтах, и логарифмической шкалой, калиброванной в децибелах. Логарифмическая шкала используется намного чаще, чем линейная, так как позволяет отображать намного больший динамический диапазон. Логарифмическая шкала позволяет одновременно отображать сигналы с перепадом в 70 – 100 дБ (отношения напряжений 3100 – 100000, отношения мощностей 107 – 1010). С другой стороны, линейную шкалу можно использовать для сигналов, отличающихся не более чем на 20 – 30 дБ (отношение напряжений 10 – 32). В любом случае, мы задаем верхнюю линию калибровочной сетки, уровень отсчета, опорный уровень, абсолютную величину с точностью до калибровки1 и используем цену деления горизонтальной полосы, чтобы найти величину другого значения по вертикали. Так мы можем измерить как абсолютную величину сигнала, так и разность амплитуд двух сигналов.
Калибровка шкал по частоте и амплитуде показывается в виде информационной надписи на дисплее. На Рис. 2-2 показан дисплей типичного анализатора спектра. А теперь снова обратим внимание на Рис. 2-1.
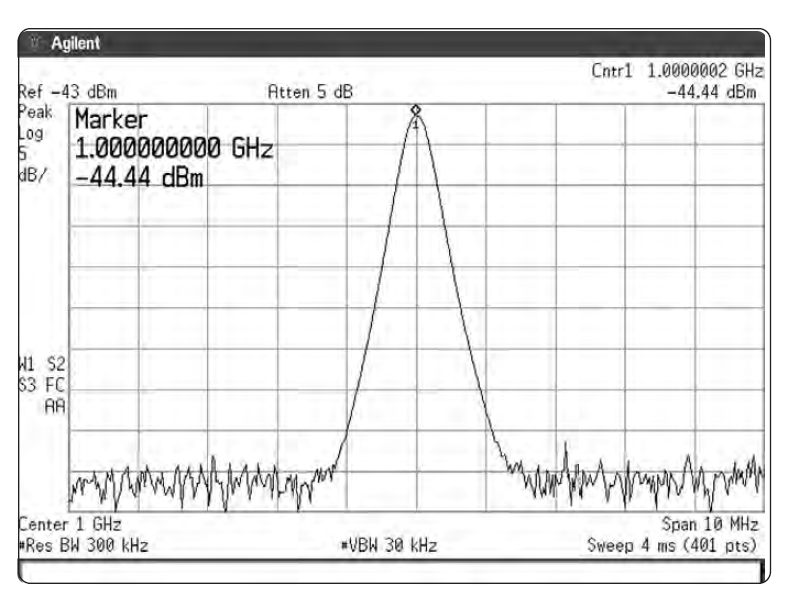
- см. Главу 4 Амплитудная и частотная точность
Радиочастотный аттенюатор
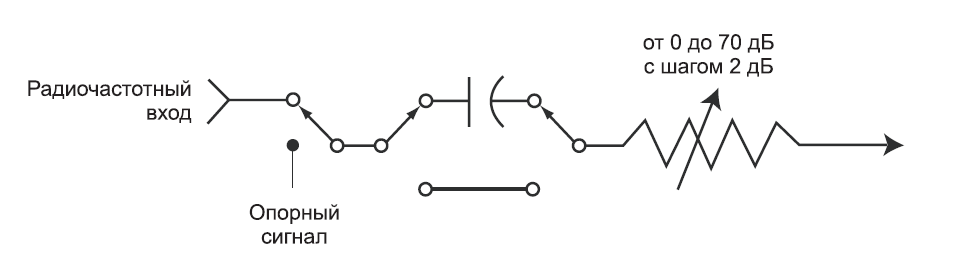
Первым элементом нашего анализатора является входной радиочастотный аттенюатор. Его назначение – обеспечить подачу на смеситель сигнала приемлемого уровня, дабы избежать перегрузки, сжатия усиления и искажений. Поскольку ослабление – это защитная цепь анализатора, обычно оно устанавливается автоматически, в зависимости от опорного уровня. Однако ручная установка ослабления также доступна – с шагом 10, 5, 2 и даже 1 дБ. На изображенной ниже схеме показан пример цепи аттенюатора с максимальным ослаблением 70 дБ и шагом 2 дБ. Блокирующий конденсатор используется для предотвращения повреждения анализатора сигналом постоянного тока или смещением постоянной составляющей сигнала. К сожалению, он заодно ослабляет и низкочастотные сигналы, чем повышает минимальную начальную частоту анализатора до 100 Гц в случае одних анализаторов и до 9 кГц в случае иных.
В некоторых анализаторах опорный сигнал может быть подведен так, как показано на Рис. 2-3, обеспечивая сигнал с точной амплитудой и частотой, которым анализатор пользуется для автокалибровки.
Низкочастотный фильтр или преселектор
Низкочастотный фильтр блокирует доступ высокочастотных сигналов в смеситель. Это предотвращает смешение внеполосных сигналов с сигналом гетеродина и дальнейшее появление нежелательных откликов на промежуточной частоте. В микроволновых анализаторах спектра низкочастотный фильтр заменяется преселектором, который является настраиваемым фильтром и отсеивает все частоты кроме тех, которые нам в данный момент нужны. В Главе 7 мы подробнее рассмотрим работу и назначение фильтрации на входе.
Настройка анализатора
Нам нужно знать, как настроить наш анализатор спектра на нужный нам диапазон частот. Настройка есть функция центральной частоты фильтра ПЧ, частотного диапазона гетеродина, и диапазона частот, которые разрешено подавать на смеситель из внешнего мира (тех, которым разрешено проходить через фильтр нижних частот). Из всех продуктов, поступающих со смесителя, два имеют наибольшую амплитуду и поэтому наиболее желательны: это продукт на частоте разности частот гетеродина и сигнала и продукт на частоте суммы этих частот. Если мы сможем сделать так, чтобы интересующий нас сигнал лежал выше или ниже частоты гетеродина на величину ПЧ, то один из нужных нам продуктов смешения попадет в полосу пропускания фильтра ПЧ, будет продетектирован и создаст амплитудный отклик на дисплее.
Как нам выбрать частоту гетеродина и ПЧ, чтобы создать анализатор с желаемым диапазоном частот? Предположим, что мы хотим настроить диапазон 0 – 3 ГГц. Какую ПЧ нужно выбрать? Давайте попробуем выбрать 1 ГГц. Поскольку эта частота находится внутри частотного диапазона настройки, мы можем иметь входной сигнал на частоте 1 ГГц. И поскольку выход смесителя также включает исходные входные сигналы, входной сигнал на частоте 1 ГГц должен давать нам постоянный выход смесителя на ПЧ. Таким образом, сигнал 1 ГГц будет проходить сквозь систему, и давать постоянный амплитудный отклик на дисплее, независимо от настройки гетеродина. В результате будет «дыра» в частотном диапазоне, в которой мы не сможем правильно изучать сигналы, поскольку амплитудный отклик будет независим от частоты гетеродина. Поэтому ПЧ 1 ГГц нам не подходит.
Значит, мы должны выбрать вместо такой ПЧ более высокую частоту, на которую мы должны настраиваться. В анализаторах спектра фирмы Agilent, настраиваемых до частоты 3 ГГц, ПЧ выбирается около 3.9 ГГц. Теперь, если мы желаем настраиваться от 0 Гц (в действительности от некоторой малой частоты, поскольку мы не можем наблюдать сигнал нулевой частоты из-за архитектуры прибора) до 3 ГГц, в каком диапазоне должен перестраиваться гетеродин? Если он стартует с ПЧ (fLO — fIF=0) и перестраивается до частоты, большей, чем ПЧ на 3 ГГц, мы можем покрыть диапазон частот fLO — fIF. Используя эти рассуждения, можем записать уравнение настройки:

Если мы желаем определить частоту гетеродина, необходимую для настройки анализатора на низкую, среднюю и высокую частоты сигнала (скажем, 1 кГц, 1.5 ГГц, 3 ГГц), мы должны сначала переписать уравнение настройки в терминах fLO:
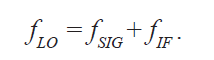
Затем мы должны вставить значения частот сигнала и ПЧ:

На Рис. 2-4 проиллюстрирован процесс настройки анализатора. Здесь fLO недостаточно высока, чтобы продукт смешения с результирующей частотой fLO — fSIG попадал в полосу ПЧ, поэтому не будет отклика на дисплее. Однако если мы подгоним генератор пилообразного напряжения так, чтобы настраивать гетеродин на более высокие частоты, этот продукт смешения попадет в полосу ПЧ в некоторой точке «пилы» (развертки), и мы увидим отклик на дисплее.
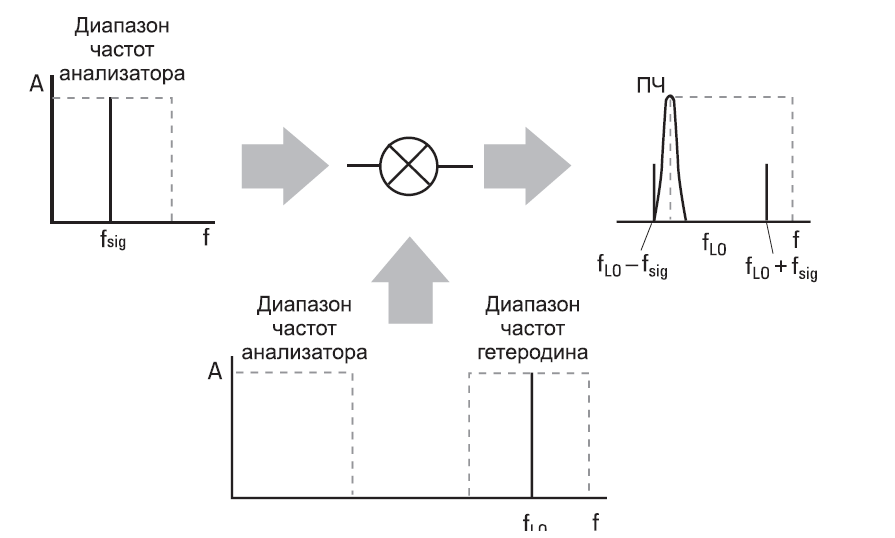
Поскольку генератор «пилы» контролирует как горизонтальную позицию луча на дисплее, так и частоту гетеродина, мы можем теперь калибровать горизонтальную ось дисплея в терминах частоты входного сигнала.
Пока мы еще не совсем покончили с настройкой. Что случится, если частота входного сигнала будет 8.2 ГГц? Когда гетеродин перестраивается в своем диапазоне 3.9 – 7.0 ГГц, он достигает частоты (4.3 ГГц), в которой он отличается от 8.2-ГГц сигнала на величину ПЧ. И снова мы имеем продукт смешения на частоте ПЧ, создающий изображение на экране дисплея. Другими словами, уравнение настройки вполне могло бы иметь вид fSIG = fLO — fIF .
Это уравнение говорит, что архитектура на Рис. 2-1 может также привести к диапазону настройки 7.8 – 10.9 ГГц, но только если мы позволим сигналам этого диапазона достичь смесителя. Задачей фильтра нижних частот на Рис. 2-1 является предотвращение попадания сигналов этих высоких частот на смеситель. Мы также желаем не пускать сигналы на самой ПЧ в смеситель, как описано выше, так что фильтр нижних частот должен хорошенько ослаблять сигналы частоты 3.9 ГГц, а также в диапазоне 7.8 – 10.9 ГГц.
В результате, мы можем сказать, что для ВЧ анализатора спектра, полоса обзора которого перекрывается одной перестройкой гетеродина, мы должны выбирать ПЧ больше самой высокой частоты диапазона настройки, делая диапазон перестройки гетеродина от ПЧ до ПЧ плюс верхний предел диапазона настройки, и включать фильтр нижних частот перед смесителем, чтобы вырезать частоты ниже ПЧ.
Чтобы разделить тесно расположенные сигналы (см. далее подпункт Разрешение сигналов), некоторые анализаторы спектра имеют по ПЧ узкую полосу пропускания 1 кГц, другие – 10 Гц, а некоторые даже 1 Гц. Столь узкие фильтры трудно изготовить на центральной частоте 3.9 ГГц. Поэтому мы должны добавить дополнительные каскады смешения, обычно от двух до четырех, для преобразования частот вниз от начальной до конечной. Рис. 2-5 показывает возможную последовательность промежуточных частот, основанную на архитектуре типичного анализатора спектра. Полное уравнение настройки для этого прибора:
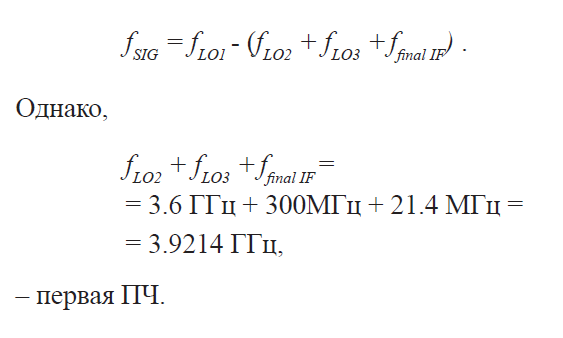
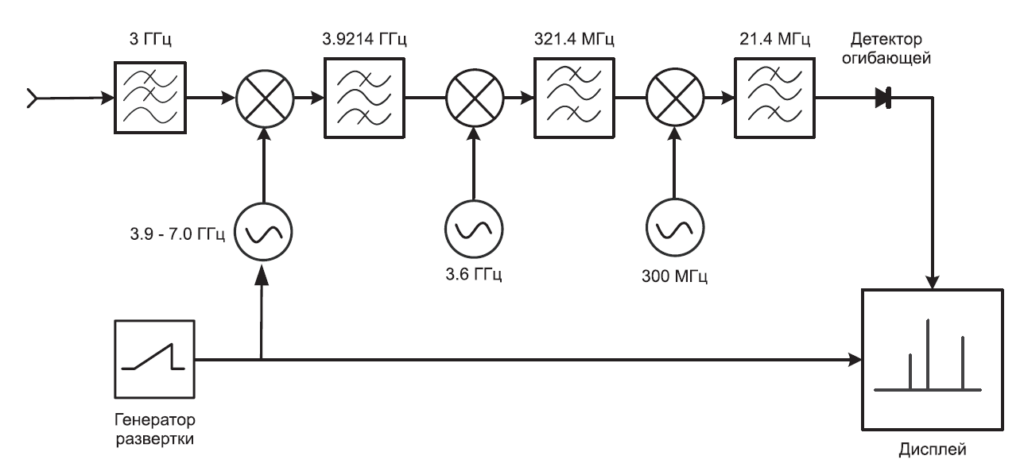
Так, упрощая уравнение настройки путем использования только первой ПЧ, приходим к тем же верным ответам. Хотя на рисунке показаны только пассивные фильтры, действительное воплощение включает усиление в более узкополосном каскаде ПЧ. Последняя секция содержит дополнительные узлы – например, логарифмический усилитель или АЦП, в зависимости от конструкции конкретного анализатора.
В большинстве анализаторов радиочастотного спектра нижняя частота гетеродина бывает равна первой ПЧ и даже ниже. Поскольку изоляция между гетеродинным и ПЧ портами смесителя конечна, колебания гетеродина проникают на выход смесителя. Когда частота гетеродина равна ПЧ, сигнал гетеродина обрабатывается системой и появляется на дисплее в виде отклика, как если бы это был сигнал на частоте 0 Гц. Этот отклик, называемый сквозное гетеродинное просачивание, может скрыть сигналы на очень низких частотах, поэтому не все анализаторы включают в отображаемый диапазон частоту 0 Гц.
Усиление ПЧ
Снова взглянув на Рис. 2-1, видим, что следующим узлом структурной схемы является усилитель с переменным коэффициентом усиления. Он используется для подстройки вертикального положения сигнала на дисплее без воздействия на уровень сигнала во входном смесителе. Когда изменяется уровень усиления ПЧ, соответственно изменяется значение опорного уровня, чтобы поддерживать корректное отображение амплитуды сигналов. Обычно, нам вовсе не нужно, чтобы опорный уровень менялся при изменении входного ослабления, поэтому установки ПЧ-усиления и входного аттенюатора сопряжены. Изменение во входном аттенюаторе автоматически вызывает изменение в усилении ПЧ, чтобы устранить эффект изменения входного ослабления и оставить сигнал на том же месте на дисплее, где он и был.
Разрешение сигналов
Следом за усилителем ПЧ в схеме идет секция, состоящая из аналоговых и/или цифровых разрешающих фильтров.
Аналоговые фильтры
Частотное разрешение – это способность анализатора спектра разделять две входные синусоиды на два отдельных отклика. По теории Фурье, вся энергия сигнала чистой синусоидальной волны находится на одной частоте, так что, вроде бы, никаких проблем с разрешением возникать не должно – ведь два сигнала, неважно, насколько близкие друг к другу по частоте, должны отображаться на дисплее в виде двух отдельных линий. Но, внимательно приглядевшись к нашему супергетеродинному приемнику, мы увидим, почему у отображаемых на дисплее сигналов есть вполне ощутимая ширина. На выходе смесителя имеются два исходных сигнала (входной и ПЧ), а также их сумма и разность. Полосовой фильтр определяет промежуточную частоту, и он же пропускает нужный продукт смешения, а остальные сигналы отсеивает. Поскольку входной сигнал – фиксированный, а сигнал гетеродина – качается по частоте, то продукты смешения также будут качаться. Если при этой перестройке или развертке продукт смешения будет проходить через частоту, соответствующую ПЧ, то на дисплее будет отображаться характеристическая кривая полосового фильтра. Взгляните на Рис. 2-6. Самый узкополосный фильтр в последовательности будет определять всю отображаемую ширину полосы, а в архитектуре на Рис. 2-5 это фильтр на ПЧ 21.4 МГц.
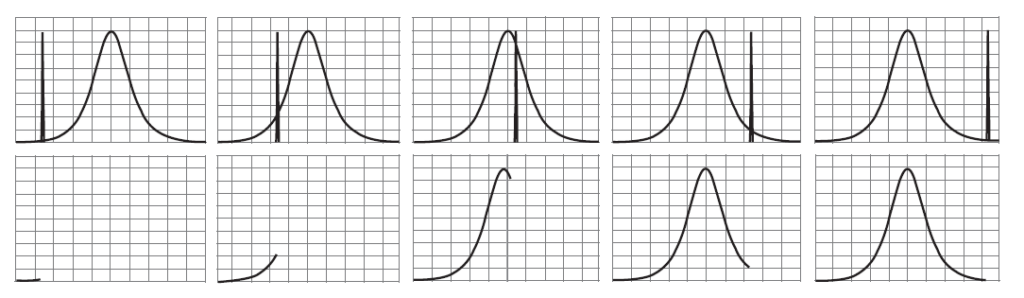
Так что два сигнала должны отстоять друг от друга довольно значительно, а иначе их отображения будут накладываться друг на друга и отображаться как один единственный отклик. К счастью, в анализаторах спектра можно переключаться между несколькими полосовыми фильтрами (ПЧ), поэтому обычно имеется возможность выбрать один достаточно узкополосный для того, чтобы различить близкие по частоте сигналы.
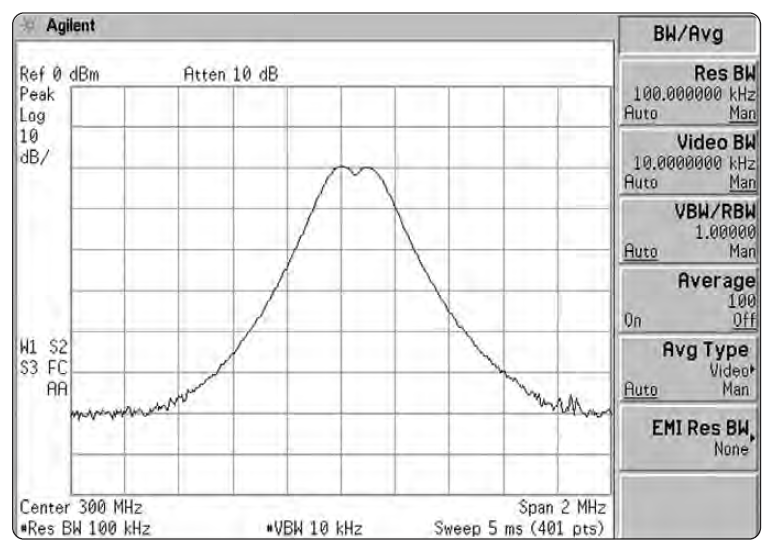
В документации на приборы фирмы Agilent разрешающая способность заявлена указанием полос по уровню 3 дБ доступных фильтров ПЧ. Такой вид требования показывает, насколько близко могут находиться друг к другу сигналы – и при этом все еще быть различимы. В данном случае это будет провал приблизительно в 3 дБ между двумя пиками отображаемых сигналов. Судя по Рис. 2-7, сигналы могут находиться и еще ближе друг к другу, прежде чем их отклики начнут полностью сливаться, но полоса по уровню 3 дБ – это хорошее практическое правило для разделения сигналов одинаковой амплитуды 3.
3. Если вы экспериментируете с разрешением на анализаторе спектра с использованием нормального режима (режима розенфелл) детектора (см. Типы детекторов далее в этой главе), то используйте достаточную видео-фильтрацию для создания гладкой кривой. Иначе будет смазывание изображения из-за взаимодействия двух сигналов. И хотя смазанная кривая ясно показывает наличие более чем одного сигнала, амплитуды индивидуальных сигналов определить весьма трудно. Анализаторы с положительно-пиковым режимом, установленного в качестве режима детектора по умолчанию, могут не показывать эффект смазывания. В этом случае смазывание можно наблюдать, включив режим детектора выборки.
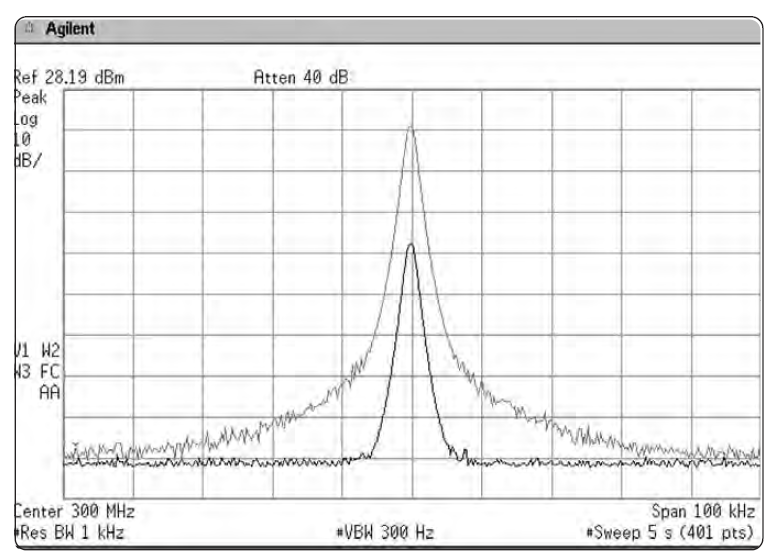
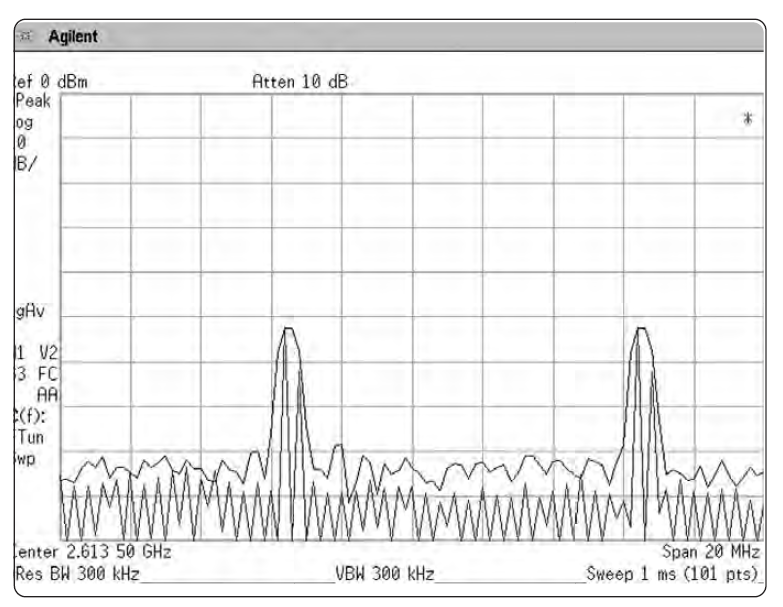
Гораздо чаще мы имеем дело с синусоидами, не равными между собой по амплитуде. В таком случае меньшая синусоида запросто может потеряться под «юбкой» отклика синусоиды с большей амплитудой. Этот эффект показан на Рис. 2-8. Верхний отклик выглядит как единичный сигнал, но на самом деле здесь присутствуют два сигнала: один на частоте 300 МГц (0 дБм), а другой – на 300.005 МГц (-30 дБм). Нижний отклик показан после того, как убран сигнал 300 МГц.
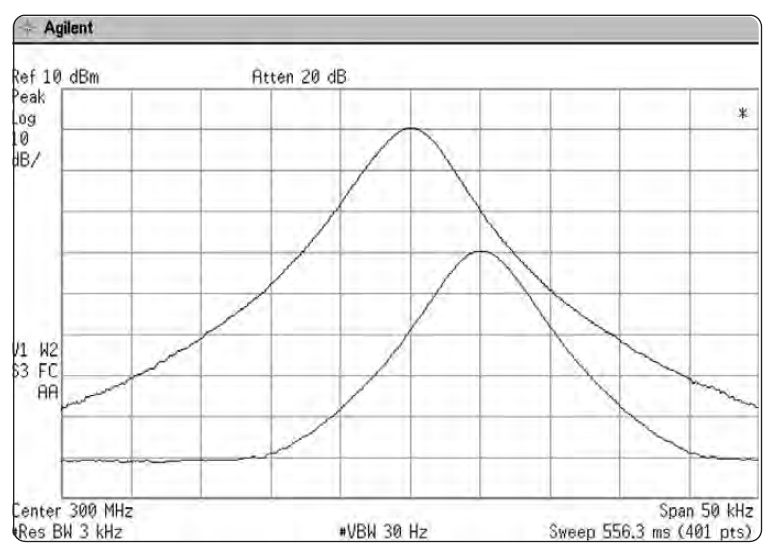
Для разрешающих фильтров указывают и другую характеристику: полосовую избирательность (избирательность или коэффициент прямоугольности). Полосовая избирательность помогает оценить разрешающую способность по отношению к неодинаковым синусоидам. Для анализаторов фирмы Agilent полосовая избирательность обычно определяется отношением полосы на уровне 60 дБ к полосе на уровне 3 дБ, как показано на Рис. 2-9. Аналоговые фильтры в анализаторах Agilent имеют четырехполюсную синхронно-настроенную схему с формой АЧХ близкой к гауссовой 4. Такого типа фильтры демонстрируют полосовую избирательность приблизительно 12.7:1.
4. Некоторые старые анализаторы спектра использовали пятиполюсные фильтры для самой узкой полосы разрешения, чтобы достичь улучшенной избирательности примерно 10:1. Современные схемы способны достичь даже лучших значений полосовой избирательности при помощи цифровых фильтров.
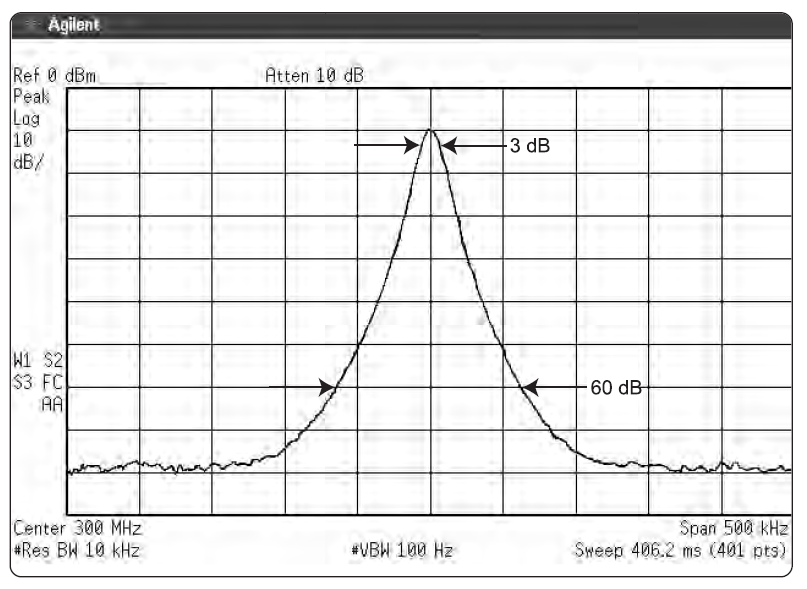
Например, какую полосу разрешения следует нам выбрать, чтобы различить сигналы, отличающиеся на 4 кГц и 30 дБ друг от друга, с учетом полосовой избирательности в 12,7:1? Поскольку нас интересует ослабление большего сигнала при анализаторе, настроенном на меньший сигнал, нам нет нужды рассматривать всю полосу, а только лишь частотную разность от центральной частоты фильтра до «юбки» АЧХ. Для определения того, насколько низко находится край АЧХ при заданной отстройке, используем следующее уравнение:

Для нашего примера, N=4, а Δf=4000. Давайте для начала попробуем фильтр с полосой разрешения 3 кГц. Сначала вычислим f0:
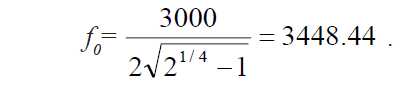
Теперь можно определить подавление фильтра на отстройке в 4 кГц:
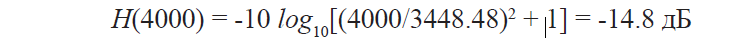
Этого недостаточно, чтобы мы смогли увидеть меньший из 2х сигнал. Давайте, снова рассчитаем H(Δf) для фильтра с полосой 1 кГц:
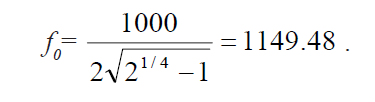
Это дает нам подавление фильтра:
Таким образом, фильтр с разрешением по полосе в 1 кГц способен выделить меньший сигнал. Это показано на Рис. 2-10.
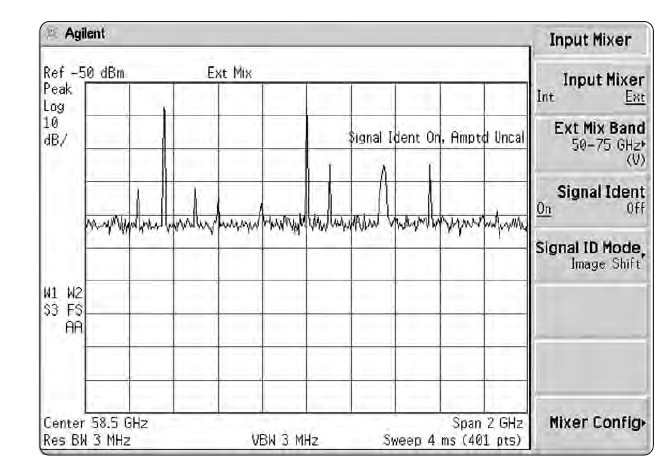
Цифровые фильтры
В некоторых анализаторах спектра используются цифровые технологии для реализации разрешающих фильтров. Цифровые фильтры предоставляют ряд важных преимуществ, к примеру – значительно улучшенную полосовую избирательность. Анализаторы серии PSA фирмы Agilent задают все полосы разрешения исключительно цифровым способом. В других же моделях – например, в серии ESA-E фирмы Agilent – применяется гибридный подход, используя аналоговые фильтры для широких полос, а цифровые фильтры – для полос в 300 Гц и менее. В Главе 3 будет дано больше информации о цифровых фильтрах.
Остаточная частотная модуляция
Ширина полосы фильтра – это не единственный фактор, влияющий на частотное разрешение анализатора спектра. Стабильность гетеродина анализатора, в особенности первого гетеродина, также вносит свой вклад. Обычно, первый гетеродин – это ЖИГ-перестраиваемый генератор, настраиваемый где-то в диапазоне от 3 до 7 ГГц. В ранних конструкциях анализаторов спектра у этих генераторов имелась остаточная ЧМ в 1 кГц или более. Эта нестабильность передавалась любым продуктам смешения гетеродина, и впоследствии было невозможно определить, что является источником нестабильности: входной сигнал или гетеродин.
Минимальная полоса разрешения определяется — по крайней мере, частично — стабильностью первого гетеродина. Анализаторы, в которых не принято никаких мер по устранению внутренней остаточной ЧМ ЖИГ-генераторов, обычно могут иметь минимальную полосу разрешения в 1 кГц. Однако в современных анализаторах значительно уменьшена остаточная ЧМ. Например, у анализаторов Agilent серии PSA это значение равняется 1-4 Гц, а у серии ESA – 2-8 Гц, что, в принципе, позволяет сузить полосу разрешения до 1 Гц. Так что на сегодняшний день, если мы наблюдаем какую-то нестабильность на анализаторе спектра, это нестабильность входного сигнала.
Фазовый шум
Хотя мы можем и не видеть существующий частотный джиттер гетеродина анализатора спектра, все равно имеется проявление частотной или фазовой нестабильности, которое можно наблюдать: фазовый шум (также называемый односторонним шумом). Нет генераторов с идеальной стабильностью. Все они в какой-то степени частотно- или фазово-модулированы случайным процессом. Как отмечено выше, всякая нестабильность гетеродина переносится в любой продукт смешения гетеродина и входного сигнала. Поэтому боковая полоса, обязанная фазово-шумовой модуляции гетеродина, присутствует вокруг любой спектральной компоненты на дисплее, которая достаточно велика в сравнении с широкополосным остаточным шумом системы (Рис. 2-11). Амплитудная разница между изображаемой на дисплее спектральной компонентой и фазовым шумом есть функция стабильности гетеродина. Чем более стабилен гетеродин, тем ниже фазовый шум. Амплитудная разница есть также функция полосы разрешения. Если мы уменьшим полосу разрешения в десять раз, уровень фазовых шумов уменьшится на 10 дБ 5
5. Этот эффект подобен поведению широкополосного шума; см. далее Главу 5 Чувствительность и шум.
Форма фазово-шумового спектра зависит от конструкции анализатора, конкретнее – от сложности реализации схемы ФАПЧ гетеродина. В некоторых анализаторах спектр фазового шума – относительно плоский пьедестал до полосы стабилизирующей петли. В других фазовый шум может затухать как функция отстройки от сигнала. Фазовый шум приводится в размерности дБн, то есть дБ относительно несущей, и нормализуется к 1 Гц полосе мощности шума. Иногда он определяется на конкретных частотных отстройках. Иной же раз приводится кривая, чтобы показать характеристики фазового шума в целом диапазоне отстроек.
В общем, мы можем видеть собственный фазовый шум анализатора только в самых узких разрешающих фильтрах, когда он скрывает нижние области кривой АЧХ этих фильтров. Использование цифровых фильтров, упомянутых выше, не меняет этот эффект. Для более широких фильтров фазовый шум невидим под нижней кромкой АЧХ фильтра, так же как в случае двух неравных синусоид, рассмотренном ранее.
Современные анализаторы спектра позволяют пользователям выбирать различные режимы стабилизации гетеродина для оптимизации фазового шума под разные условия измерений. К примеру, серия измерителей PSA предлагает три режима:
- Оптимизация фазового шума для частотных отстроек <50 кГц от несущей. В этом режиме фазовый шум гетеродина оптимизируется для близкой области около несущей, ценой ухудшения фазового шума за пределами 50 кГц отстройки.
- Оптимизация фазового шума для частотных отстроек >50 кГц от несущей. В этом режиме фазовый шум оптимизируется для отстроек более 50 кГц от несущей, особенно для области 70-300 кГц. При этом страдают более близкие области около несущей, и падает скорость обработки при измерении.
- Оптимизация гетеродина на быструю перестройку. В данном режиме фазовый шум гетеродина повышается на всех отстройках от несущей вплоть до приблизительно 2 МГц. Однако при этом минимизируется время измерения и максимально увеличивается скорость обработки при изменении центральной частоты или полосы обзора.
Оптимизацию фазового шума анализаторов серии PSA также можно установить в автоматический режим, при котором прибор самостоятельно будет изменять свое поведение и оптимизировать скорость или динамический диапазон для различных условий работы. При обзоре ≥10.5 МГц или при разрешающей полосе >200 кГц выбирается режим быстрой перестройки. Для обзоров >141.4 кГц и разрешающих полос >9.1 кГц авто-режим оптимизирует шум для отстроек > 50 кГц. Во всех остальных случаях анализатор оптимизируется для отстроек <50 кГц. Три этих режима показаны на Рис. 2-12а.
Анализаторы серии ESA используют более простую схему оптимизации, предлагая пользователю два режима на выбор: оптимизацию для наилучшего показателя фазового шума и оптимизацию гетеродина для быстрой перестройки, а также режим автоматического переключения между этими двумя.
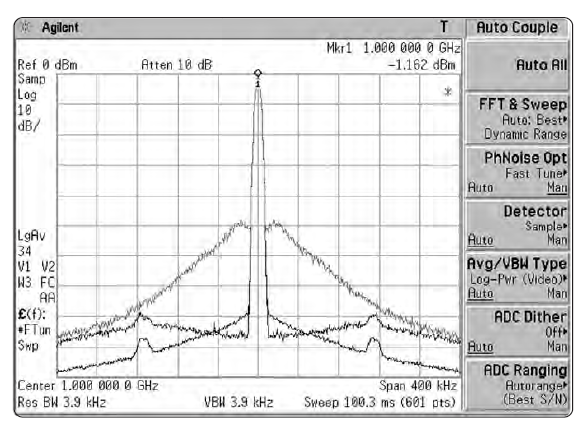
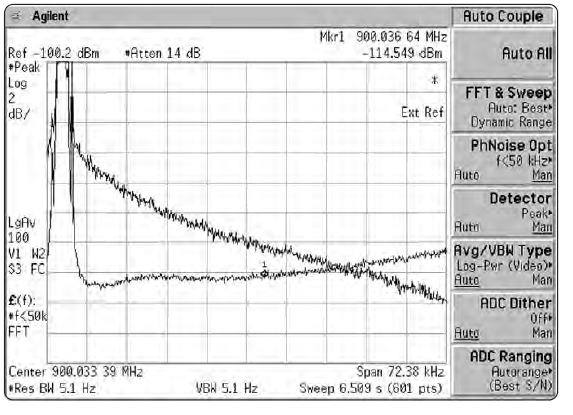
В любом случае, фазовый шум является принципиальным ограничением способности анализатора различать сигналы с неравными амплитудами. Как видно из Рис. 2-13, мы вполне можем столкнуться с ситуацией, когда мы можем разрешить два сигнала при данных полосе разрешения и избирательности, но обнаружить, что меньший сигнал потерялся под уровнем фазового шума гетеродина.
Время развертки
Аналоговые разрешающие фильтры
Если бы разрешающая способность была единственным критерием, по которому оценивалось качество анализатора спектра, мы бы просто строили анализаторы с наиболее узкими из возможных разрешающими фильтрами ПЧ, и на этом бы успокоились. Но разрешение влияет на время развертки, а оно нам весьма небезразлично. Время развертки напрямую влияет на то, как долго будет проводиться измерение.
Разрешение вступает в игру потому, что фильтры ПЧ – это цепи с ограничением по полосе, которым требуется определенное время на заряд и разряд. Если продукты смешения перестраиваются по частоте через фильтр слишком быстро, происходит потеря в величине отображаемой амплитуды, как видно на Рис. 2-14. (См. Детектор огибающей далее в этой главе, где будет описан иной подход к времени отклика ПЧ). Если подумать о том, как долго продукт смешения находится в полосе пропускания фильтра ПЧ, то окажется, что это время прямо пропорционально ширине полосы и обратно пропорционально развертке в Гц на единицу времени, то есть:
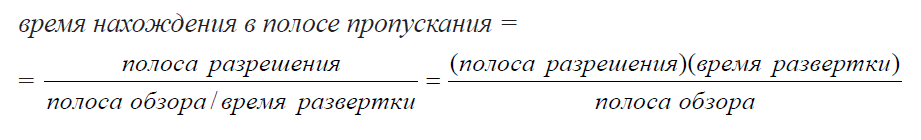
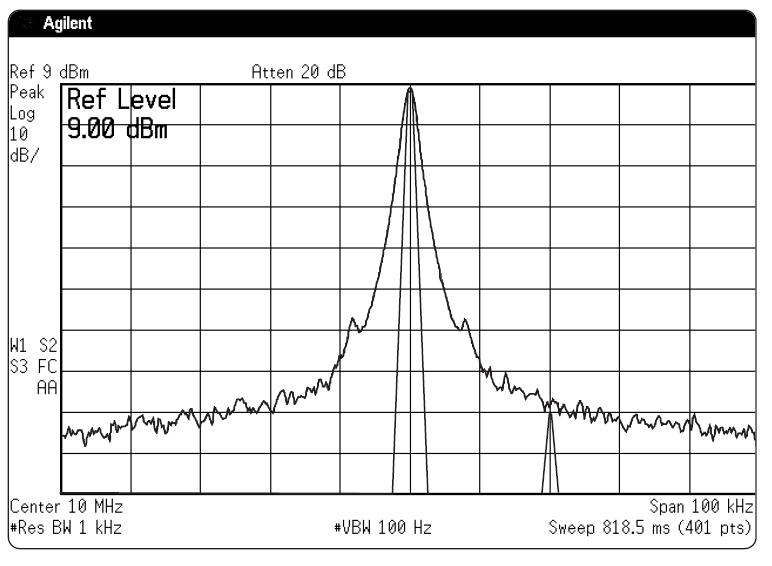
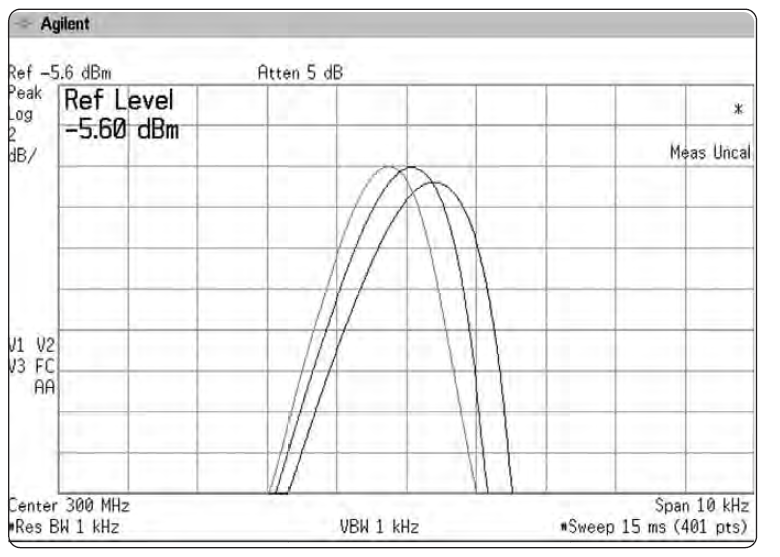
С другой стороны, время роста (длительность переднего фронта) фильтра обратно пропорционально ширине его полосы, и если мы введем коэффициент пропорциональности k, то:
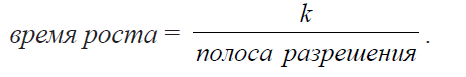
Если приравнять эти два времени и разрешить полученное уравнение относительно времени развертки, то получим:

Значение k лежит в диапазоне от 2 до 3 для синхронно-настроенных окологауссовских фильтров, которые используются в большинстве анализаторов Agilent.
Важным наблюдением является то, что любое изменение в разрешающей способности окажет сильнейшее влияние на время развертки. Большинство анализаторов Agilent обеспечивают величины в последовательности 1, 3, 10 или же в отношениях с шагами, приблизительно равными квадратному корню из десяти. Так что время развертки изменяется примерно в 10 раз с каждым шагом изменения разрешения. Серия приборов PSA предоставляет шаг по полосе всего в 10%, что улучшает компромисс между обзором, разрешением и временем развертки.
Анализаторы спектра автоматически связывают время развертки с обзором и с установкой полосы разрешения. Время развертки подстраивается для поддержания калиброванной картинки на дисплее. Если время анализа превышает максимально доступное, то анализатор выводит сообщение о том, что дисплей не откалиброван. При возникновении необходимости пользователю предоставляется возможность отключить автоматическую установку и выставить время анализа вручную.
Цифровые разрешающие фильтры
Цифровые разрешающие фильтры влияют на время развертки несколько по-иному, нежели аналоговые разрешающие фильтры, о которых только что шла речь. Для анализов с разверткой частоты, применение цифровых фильтров может улучшить скорость измерения в 2-4 раза. Цифровые БПФ-фильтры могут дать даже еще большую разницу. А разница эта появляется из-за того, что анализируемый сигнал обрабатывается частотными блоками, которые варьируются в зависимости от конкретного анализатора. Например, если блок частоты будет 1 кГц, то при выборе полосы разрешения в 10 Гц наш анализатор одновременно обработает данные по каждому 1-килогерцовому блоку через 100 смежных 10-герцовых фильтров. Если бы цифровая обработка была мгновенной, то можно было бы ожидать улучшения времени развертки в 100 раз. На самом деле коэффициент улучшения гораздо меньше, но все равно весьма значителен. Более подробно о преимуществах цифровой обработки будет рассказано в Главе 3.
Детектор огибающей6
6. Не следует путать детектор огибающей с детекторами дисплея. Более подробно см. Типы детекторов далее в этой главе. Дополнительную информацию о детекторах огибающей можно найти в документе Agilent Application Note 1303, Spectrum Analyzer Measurements and Noise.
Анализатор спектра обычно преобразует сигнал ПЧ в видео-сигнал7 при помощи детектора огибающей. В простейшей своей форме, детектор огибающей – это диод, резистивная нагрузка и фильтр НЧ, как показано на Рис. 2-15. Сигнал на выходе тракта ПЧ, в данном примере амплитудно-модулированная синусоидальная волна, поступает на вход детектора. Отклик детектора повторяет изменения в огибающей сигнала ПЧ, но не в мгновенном значении амплитуды самой синусоидальной волны ПЧ.
7. Сигнал с частотой от постоянного тока до некоторой более высокой частоты, определяемой элементами цепи. Исторически, анализаторы спектра с аналоговыми дисплеями напрямую использовали этот сигнал для управления вертикальным отклонением луча ЭЛТ-дисплея. Отсюда и термин видео-сигнал.
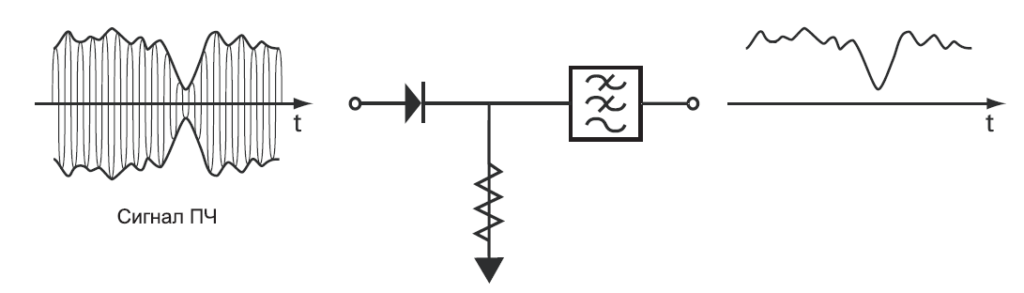
Для большинства измерений мы выбираем полосу разрешения достаточно узкой, чтобы разрешить индивидуальные спектральные компоненты входного сигнала. Если мы зафиксируем частоту гетеродина так, чтобы наш анализатор был настроен на одну спектральную компоненту сигнала, сигнал на выходе тракта ПЧ будет устойчивой синусоидой с постоянной огибающей. Тогда сигнал на выходе детектора огибающей будет постоянным напряжением, и не будет вариаций огибающей, за которыми следовал бы детектор.
Однако случается, что мы сами намеренно выбираем разрешающую полосу настолько широкой, чтобы она включала две или более спектральные компоненты. Иногда у нас даже нет иного выбора. Спектральные компоненты могут быть так тесно расположены по частоте, что не могут быть разделены самым узким разрешающим фильтром. Если предположить, что в полосе пропускания находятся только две спектральные компоненты, то мы получим две взаимодействующие синусоиды, создающие биения, и огибающая сигнала на ПЧ меняется тогда так, как показано на Рис. 2-16, по мере изменения мгновенной разности фаз синусоид.
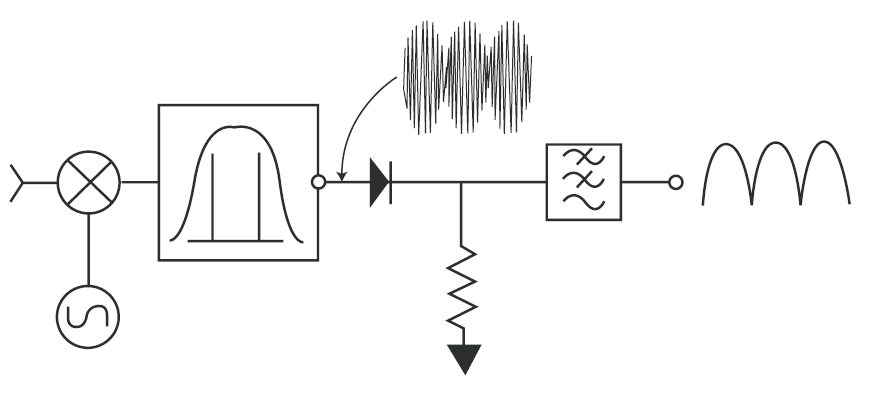
Ширина полосы разрешающего фильтра ПЧ определяет максимальную скорость, с которой может меняться огибающая сигнала ПЧ. Эта полоса определяет, как далеко могут быть разнесены две входные синусоиды, чтобы после смешения они одновременно оказались внутри полосы фильтра. Если предположить, что последняя ПЧ равна 21.4 МГц, а полоса равна 100 кГц, то два входных сигнала, разнесенные между собой на 100 кГц, будут давать продукты смешения на 21.35 и 21.45 МГц, и поэтому удовлетворять критерию. См. Рис. 2-16. Детектор должен быть способен следовать за изменениями огибающей, созданными этими двумя сигналами, но не за самим сигналом промежуточной частоты 21.4 МГц.
Детектор огибающей — это то, что делает анализатор спектра вольтметром. Если мы повторим рассмотренную выше ситуацию и предположим два равных по амплитуде сигнала в полосе пропускания ПЧ в один момент времени, что мы ожидаем увидеть на дисплее? Измеритель мощности показал бы уровень мощности 3 дБ над каждым сигналом, то есть полную мощность двух сигналов. Предположим, что два сигнала так тесно расположены, что анализатор, настроенный на середину частотного интервала между ними, имеет на их частотах пренебрежимо малое ослабление за счет отклонения их частот от центральной частоты фильтра8. Тогда дисплей анализатора покажет кривую, меняющуюся между двойным напряжением каждого (6 дБ) и нулем (минус бесконечность в логарифмической шкале). Мы должны помнить, что два сигнала есть синусоиды (векторы) на различных частотах, и поэтому они непрерывно меняются по фазе друг относительно друга. В один момент времени они складываются точно в фазе, в другой – точно в противофазе.
8. Для данного предположения мы принимаем, что фильтр – идеально прямоугольный.
Итак, детектор огибающей следует за изменениями амплитудных пиков сигнала ПЧ, но не за мгновенными значениями этого сигнала, что выливается в потерю информации о фазе. Это дает анализатору его характеристики как вольтметра.
В случае цифрового воплощения полосы разрешения, аналоговый детектор огибающей не применяется. Вместо этого численно высчитывается корень квадратный из суммы квадратов данных I и Q, что является математическим эквивалентом детектора огибающей. Более подробно о цифровой архитектуре рассказано в Главе 3.
Дисплеи
До середины 70-х годов анализаторы спектра были исключительно аналоговыми устройствами. Отображаемая на дисплее кривая представляла собой непрерывную индикацию огибающей сигнала, и никакой информации при этом не терялось. Однако, у аналоговых дисплеев были свои недостатки. Главной проблемой была необходимость применения долгой развертки при использовании узких полос разрешения. В самых худших случаях на экране отображалась лишь точка, медленно ползущая по экрану ЭЛТ, визуально не дававшая никакой кривой на дисплее. Так что информативной картинки при длительных временах развертки достичь было невозможно.
Agilent Technologies (в то время – часть Hewlett-Packard) ввела в обиход накопительную ЭЛТ с переменным свечением, на дисплее которой можно было регулировать скорость угасания изображения. При надлежащей настройке старая кривая угасала как раз в том месте, где начинала отображаться новая. Изображение было непрерывным, без мерцания и без сбивающих с толку наложений. Новинка работала достаточно хорошо, но требовала перенастройки интенсивности свечения и скорости угасания для каждого нового измерения. Когда в середине 70-х годов стала доступна цифровая схемотехника, она быстро нашла свое применение в анализаторах спектра. Теперь, как только кривая оцифровывалась и записывалась в память, она становилась доступной для постоянного отображения на дисплее. Обновлять картинку на дисплее в режиме без мерцаний, без ранее сопутствующих этому размытия и блеклости, стало проще простого. Данные в памяти обновлялись со скоростью развертки, и, поскольку содержимое памяти отображалось на дисплее в режиме без мерцания, можно было следить за этими обновлениями одновременно с тем, как анализатор проходил по установленной полосе обзора частот, — совсем как на аналоговых приборах.
Типы детекторов
При использовании цифровых дисплеев нам нужно было решить, какое значение должно отображаться в каждой его точке? Неважно, сколько точек отображения мы используем на дисплее – каждая из них должна представлять то, что появилось в рамках некоторого частотного диапазона и (хоть мы, обычно, и не мыслим в терминах времени, когда работаем с анализатором спектра) в течение некоторого интервала времени.
Это как если данные за каждый временной интервал заключить в один блок, а затем математически извлечь нужный нам кусочек информации из нашего входного сигнала. Это значение помещается в память и отображается на дисплее. Такой подход обладает большой гибкостью. Здесь мы с вами рассмотрим шесть различных видов детекторов.
На Рис. 2-18 каждый блок содержит данные из частотного и временного интервала, определяемые следующими выражениями:

Частота дискретизации будет различна для разных приборов, но наибольшей точности можно достичь за счет уменьшения полосы обзора и/или увеличения времени развертки, поскольку количество отсчетов в каждом блоке будет увеличиваться в любом из этих случаев. У анализаторов с цифровой ПЧ реализуются в цифровом виде те же операции, что и в АС с аналоговой ПЧ, и обеспечивается такая же непрерывная во времени обработка данных.
Понятие «блока» очень важно, так как оно поможет нам различать шесть типов детекторов:

Первые три упомянутых детектора – выборки, пиковый и минимально-пиковый, — достаточно просты для понимания и визуально представлены на Рис. 2-19. Нормальный, детектор среднего и квази-пиковый – более сложны, и их мы обсудим чуть позже.
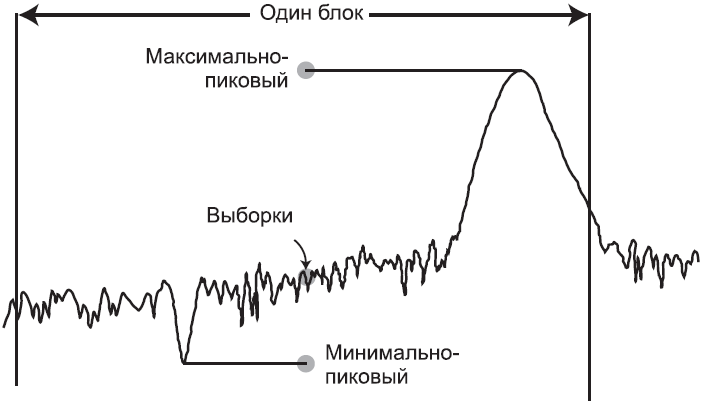
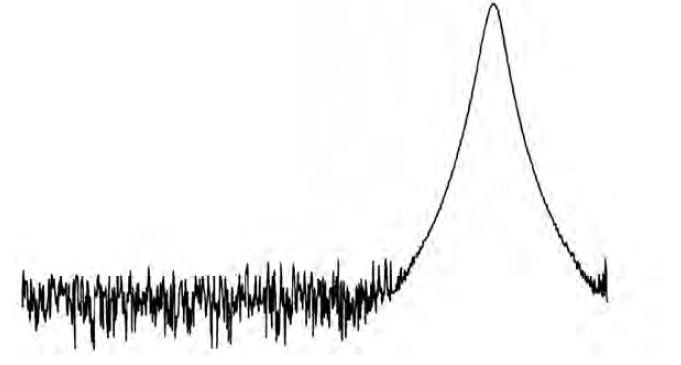
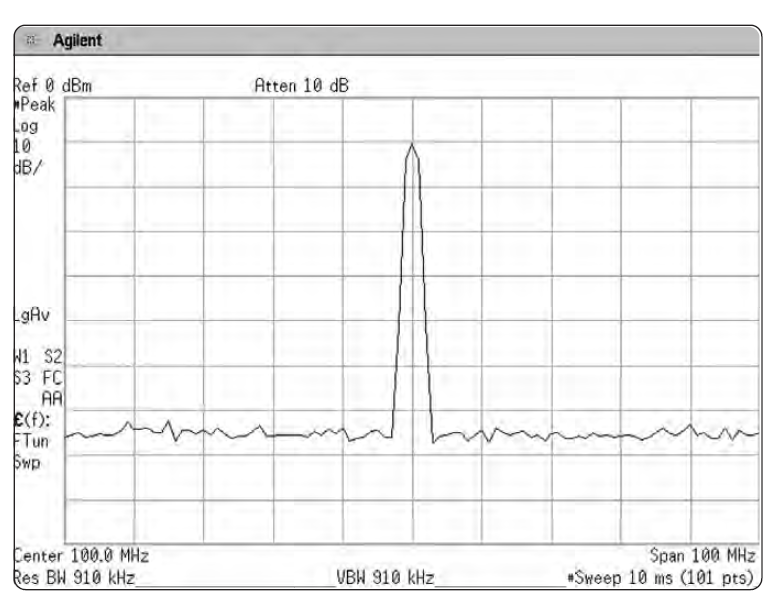
Давайте вернемся к вопросу о том, как нам отобразить аналоговые показания наиболее правдиво при помощи цифровых технологий. Представим себе ситуацию, изображенную на Рис. 2-17, где у нас на дисплее есть только шум и один-единственный сигнал гармонического колебания.
Детектирование выборки
Для первого метода давайте просто изберем в качестве точки данных мгновенный уровень в центре каждого блока (см. Рис. 2-19). Это и будет метод детектирования выборки. Чтобы наша кривая была непрерывной, создадим систему, которая будет соединять наши точки отрезками. Из сравнения Рис. 2-17 и 2-20 очевидно, что картинка у нас получается достаточно правдоподобная. Разумеется, чем больше точек на кривой, тем лучше будет воспроизведение оригинального аналогового сигнала. Количество доступных для отображения точек на дисплее различно для разных анализаторов. На приборах серии ESA и PSA количество точек дисплея для кривых в частотной области может быть установлено от минимальных 101 до максимальных 8192 точек. Как показано на Рис. 2-21, увеличение количества точек, несомненно, приближает нашу картинку к аналоговому оригиналу.

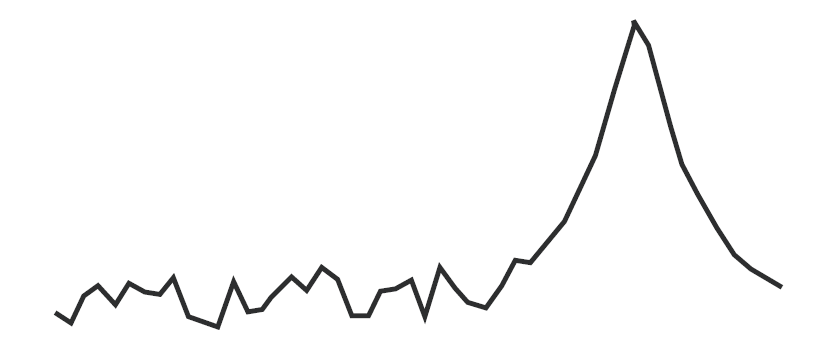
Хотя метод детектирования выборки хорошо справляется с индикацией случайности шума, в этом режиме неудобно проводить анализ синусоидального сигнала. Если бы мы собрались смотреть 100-МГц гребенку при помощи анализатора Agilent ESA E4407B, его полосу обзора можно установить от 0 до 26.5 ГГц. Даже при 1001 доступной точке дисплея, каждая точка тогда будет представлять блок в 26.5 МГц, что гораздо шире полосы максимального разрешения в 5 МГц.
В результате, истинное значение амплитуды гребенки будет отображаться только в том случае, если продукт смешения случайно попадает точно в центр ПЧ, когда производится взятие точки для отображения. На Рис. 2-22а показана полоса обзора в 5 ГГц с полосой разрешения 1 МГц, отображаемая в режиме детектирования выборки. Зубцы гребенки должны бы быть относительно одинаковы по амплитуде, как показано на Рис. 2-22б (где используется режим пикового детектирования). Следовательно, режим выборки не улавливает все сигналы, и не обязательно отражает истинное пиковое значение отображаемых сигналов. Когда полоса разрешения уже, чем интервал выборки (то есть ширина блока), то выборочный режим может давать ошибочные результаты.
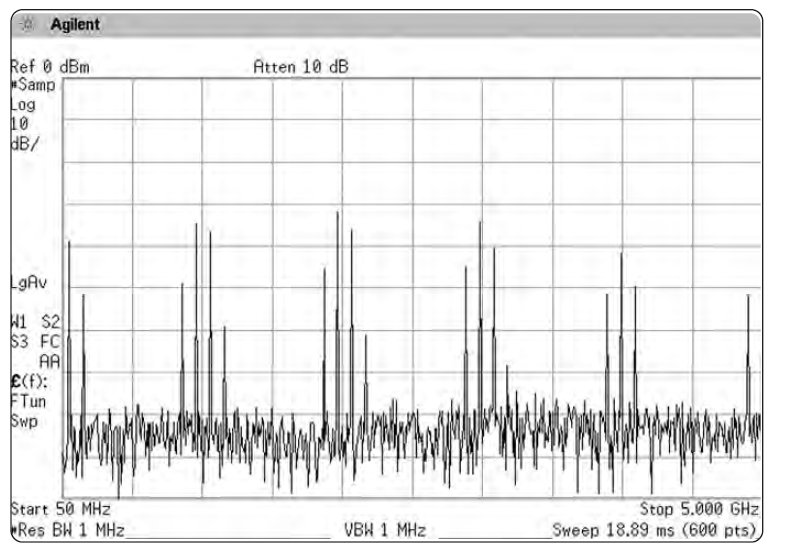
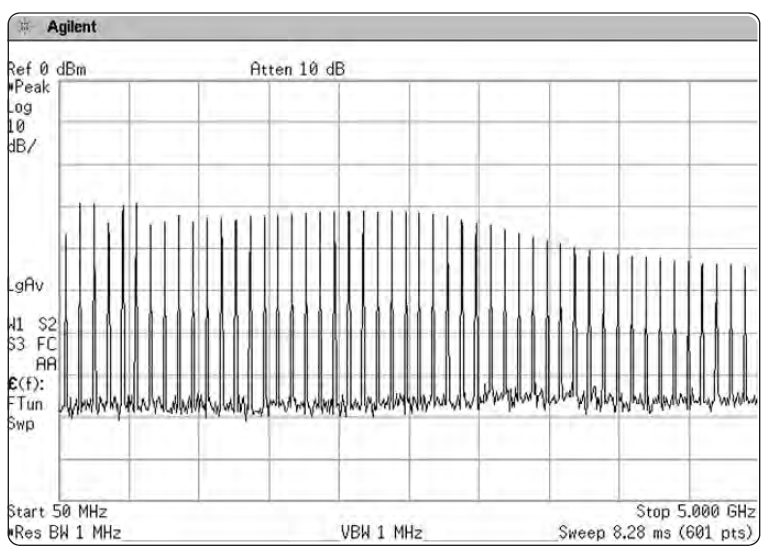
Пиковое детектирование (максимально-пиковое)
Одним из способов гарантировать то, что все синусоиды отобразятся со своими реальными амплитудами, является отображение максимальной величины, находящейся в каждом блоке. Это – максимально-пиковый режим детектирования, или просто пиковый режим. Его результат проиллюстрирован на Рис. 2-22б. Пиковый режим является установленным по умолчанию во многих анализаторах, поскольку он гарантирует, что ни одна синусоида не будет пропущена, вне зависимости от соотношения между полосой разрешения и шириной блока. Однако, в отличие от метода выборки, пиковый режим не дает хорошего отображения случайного шума, поскольку он выделяет только максимальное значение в каждом блоке и игнорирует истинную случайность шума. Поэтому анализаторы спектра, использующие пиковый режим по умолчанию, обычно предоставляют режим выборки в качестве альтернативного.
Минимально-пиковое детектирование
Минимально-пиковый режим отображает минимальное значение из каждого блока. Обычно он присутствует в большинстве анализаторов, хотя и не используется так часто, как другие способы детектирования. Отделение гармонических сигналов от импульсных при тестах на электромагнитную совместимость – вот одно из применений минимально-пикового режима. Позже мы еще рассмотрим, как этот режим применяется в процессе идентификации сигналов при использовании внешних смесителей для высокочастотных измерений.
Рисунок 2-23. Сравнение нормального режима дисплейного детектирования и режима выборки при измерении шума
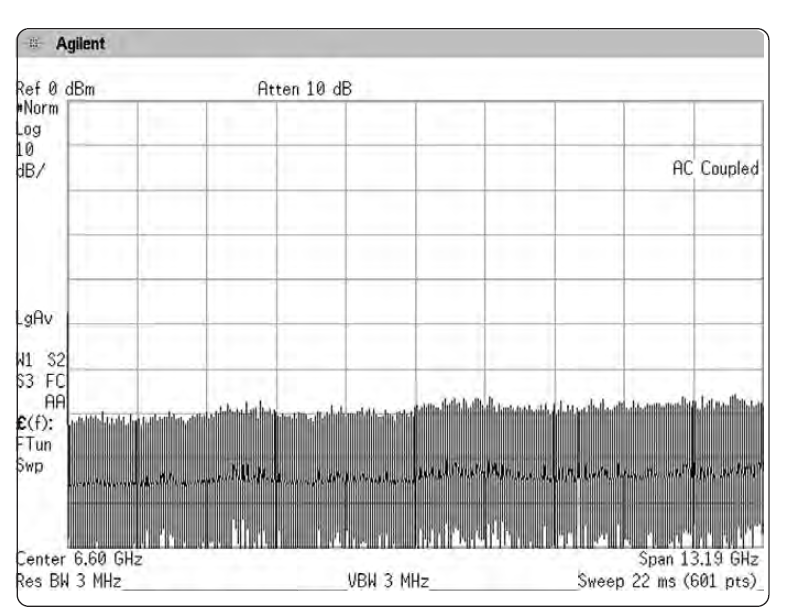
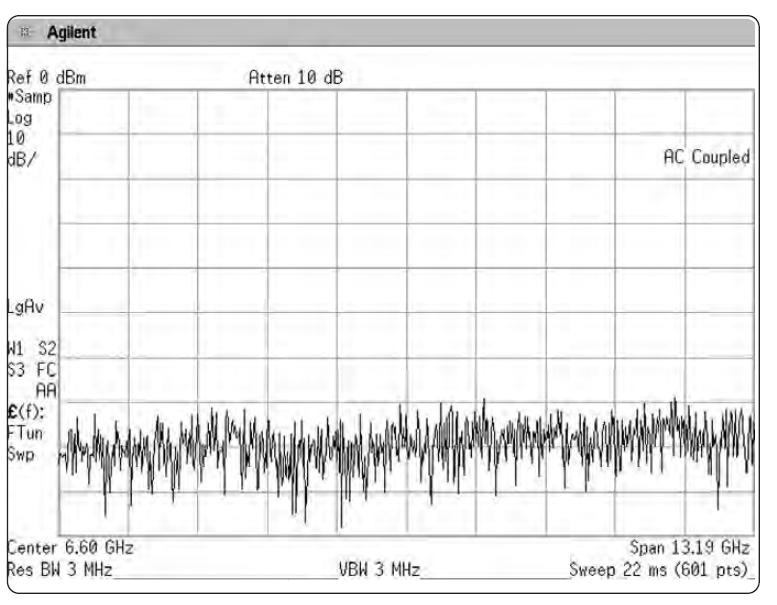
Нормальное детектирование
Для того чтобы отображать случайный шум лучше, чем это делает пиковый режим, и одновременно избегать проблемы с пропущенными сигналами, как в случае с режимом выборки, во многих анализаторах спектра предлагается режим нормального детектирования, неформально также называемый «розенфелл»9. Если сигнал в рамках одного блока и рос, и падал, что было бы продетектировано максимально- и минимально-пиковым режимами, то алгоритм классифицирует данный сигнал как шум. В таком случае в нечетной точке отображается максимальное значение, а в четной – минимальное, взятое из соответствующих этим точкам блоков (см. Рис. 2-25). На Рис. 2-23а и 2-23б сравниваются нормальный режим и режим выборки.10
- Розенфелл – это не имя человека, а описание алгоритма, который определяет, рос (rose) и спадал (fell) ли сигнал в рамках одного блока, представленного точкой на дисплее; иногда может встречаться в текстах как «rose’n’fell».
- Из-за своей пригодности для измерения шума, детектор выборки обычно используют в приложениях шумового маркера. Аналогично, измерение мощности канала и мощности соседнего канала требует детектор такого типа, который мог бы выдавать результаты, не искаженные пиковым детектированием. Для анализаторов без усредняющих детекторов, детектор выборки – это наилучший вариант.
Что же будет, если нам попадется синусоидальный сигнал? Мы знаем, что при перестройке продукта смешения через фильтр ПЧ на дисплее отображается кривая АЧХ этого фильтра. Если эта кривая распространяется на множество точек дисплея, то мы сталкиваемся с ситуацией, когда отображаемый сигнал только растет, пока продукт смешения приближается к центральной частоте, а затем только спадает, когда продукт смешения удаляется от центральной частоты. В любом из этих случаев максимально- и минимально-пиковый детекторы обнаружат изменение амплитуды только в одном направлении, и, исходя из алгоритма нормального детектирования, для каждого блока будет отображаться только максимальное значение (см. Рис. 2-24).
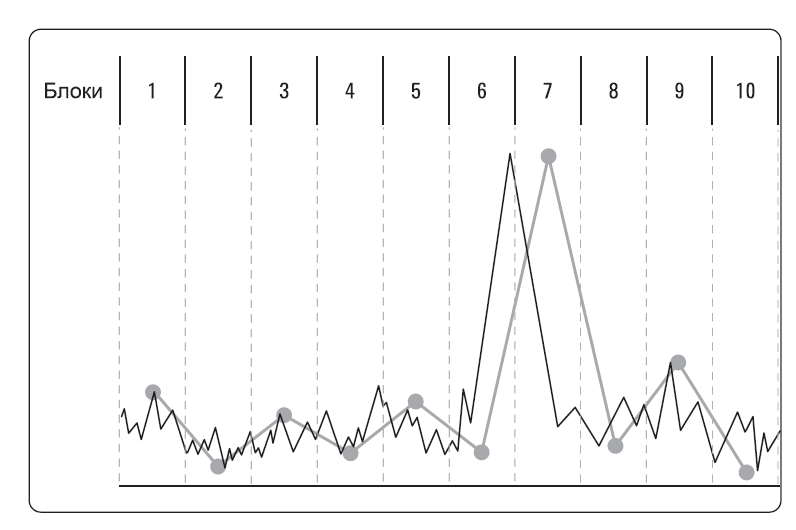
Что произойдет, когда полоса разрешения будет узкой относительно ширины блока? Сигнал в рамках блока будет и расти, и спадать. Если блоку случится быть нечетным, то все в порядке. Максимальное значение из этого блока будет построено на экране в качестве следующей точки данных. Однако же, если блок будет четным, то отобразится минимальное значение, взятое из него. В зависимости от соотношения величин полосы пропускания и ширины блока, это минимальное значение может отличаться от истинного пикового значения (того, которое бы мы хотели видеть на дисплее) как незначительно, так и очень сильно. В самом худшем случае, когда ширина блока гораздо больше полосы разрешения, разница между максимумом и минимумом в рамках одного блока будет полной разностью между пиком сигнала и шумом. Это рассмотрено в примере на Рис. 2-25. Взгляните на блок под номером 6. Пиковое значение предыдущего блока всегда сравнивается с таковым из текущего блока. Наибольшее из этих двух значений отображается, если блок – нечетный, как в случае с блоком номер 7. Пик сигнала на самом деле появляется в блоке 6, но не отображается до блока 7.
Алгоритм нормального детектирования:
Если сигнал растет и спадает в рамках блока:
Четные блоки отображают минимум (отрицательный пик). Максимум запоминается.
Нечетные блоки отображают максимум (положительный пик), определяемый сравнением пика текущего блока с пиком предыдущего (запомненным).
Если сигнал только растет или только спадает в рамках блока, отображается пик. См. Рис. 2-25.
Этот процесс может привести к тому, что максимум на дисплее может быть сдвинут вправо на одну точку, однако этот сдвиг в процентном отношении от всего обзора дисплея – малая величина. Некоторые анализаторы спектра, например, приборы серии PSA от Agilent, компенсируют этот потенциальный эффект сдвигом начальной и конечной частоты гетеродина.
Другой вид ошибки – это отображение двух пиков вместо одного реального. На Рис. 2-26 показано, что происходит в таком случае. Контур двух пиков показан с применением пикового детектирования с более широкой полосой разрешения.
Итак, пиковое детектирование наилучшим образом справляется с отделением гармонических сигналов от шума. Режим выборки больше всего пригоден для наблюдения шума, а нормальный режим – для наблюдения сигналов и шума одновременно.
Детектирование среднего
Хотя характеристики современных цифровых схем модуляции шумоподобны, детектирование выборки не всегда может предоставить нам всю необходимую информацию. Например, при измерении мощности канала сигнала W-CDMA, необходимо интегрирование среднеквадратичных значений. Это измерение связано с суммированием мощностей по целому диапазону частотных блоков анализатора. Режим детектирования выборки такого обеспечить не может.
В то время как анализаторы спектра обычно определяют амплитуду много раз в рамках одного частотного блока, детектирование выборки сохраняет только одно из них и отбрасывает остальные. С другой стороны, детектор среднего использует все данные, собранные в рамках временного (и частотного) интервала блока. Оцифровав данные, и зная условия, при которых они были оцифрованы, можно так или иначе манипулировать этими значениями, чтобы добиться желаемых результатов.
В некоторых анализаторах спектра детектор среднего называется среднеквадратичным детектором, когда он усредняет мощность (основываясь на среднеквадратичном значении напряжения). В анализаторах серий PSA и ESA фирмы Agilent присутствует режим детектирования среднего с возможностью усреднять мощность, напряжение или логарифм сигнала благодаря возможности независимого от других настроек выбора типа усреднения:
Усреднение мощности (среднеквадратичное) – усредняет среднеквадратичные уровни путем вычисления квадратного корня из суммы квадратов данных по напряжению на протяжении интервала одного блока, приведенного к характеристическому входному сопротивлению анализатора спектра (обычно 50 Ом). Усреднение мощности вычисляет реальное значение средней мощности и лучше всего подходит для измерения мощности сложных сигналов.
Усреднение напряжения – усредняет линейные данные по напряжению сигнала детектора огибающей, измеренные за интервал одного блока. Часто используется при исследованиях электромагнитных помех для измерения узкополосных сигналов (подробнее об этом будет рассказано далее). Усреднение напряжения также полезно при наблюдении поведения роста и спада амплитудно-модулированных или импульсно-модулированных сигналов радаров или TDMA (time-division multiple access — множественный доступ с временным разделением, МДВУ) передатчиков.
Логарифмическое (видео) усреднение – усредняет логарифмические значения амплитуды (дБ) сигнала детектора огибающей, измеренные за интервал одного блока. Логарифмическое усреднение отлично подходит для наблюдения синусоидальных сигналов, особенно околошумовых11.
11. см. Главу 5 Чувствительность и шум.
Так, использование детектора среднего в режиме усреднения мощности дает истинное значение средней мощности, основанное на среднеквадратичном значении напряжения. А в режиме усреднения напряжения работает как усредняющий детектор общего назначения. Для режима же логарифмического усреднения другого эквивалента не существует.
Детектирование среднего – это улучшение по сравнению с использованием детектирования выборки для определения мощности. Детектирование выборки требует нескольких разверток для сбора достаточного количества точек данных, чтобы предоставить нам точную информацию о средней мощности. Детектирование среднего превращает измерение мощности канала из суммирования между блоками в интегрирование по временному интервалу, представляющему диапазон частот в анализаторе с разверткой частоты. В анализаторах, основанных на быстром преобразовании Фурье (БПФ-машины),12 эта операция превращается из суммирования по блокам дисплея в суммирование по частотным отсчетам БПФ. И в случае развертки частоты, и в случае БПФ интегрирование захватывает всю доступную информацию о мощности, а не только ту, что выбрана детектором выборки. В результате, детектор среднего обеспечивает результаты с меньшей неопределенностью за то же время. В случае анализа с разверткой частоты он также позволяет уменьшить неопределенность за счет простого увеличения времени развертки.
12. В БПФ-машинах математические вычисления осуществляются в рамках множества частотных блоков одновременно, что улучшает скорость измерения. Подробнее см. Главу 3.
Детекторы электромагнитных помех: детектирование среднего и квази-пиковое
Важной областью применения детектирования среднего является исследование устройств на электромагнитную совместимость. В этом случае усреднение напряжения, как было сказано в предыдущем пункте, используется для измерения узкополосных сигналов, которые могут быть скрыты наличествующим широкополосным импульсным шумом. Детектирование среднего, используемое в соответствующих приборах, берет сигнал детектора огибающей и пропускает его через фильтр низких частот с шириной полосы гораздо меньшей, чем полоса разрешения. Фильтр интегрирует (усредняет) высокочастотные компоненты – такие, как шум. Чтобы осуществить такой тип детектирования на анализаторе спектра старой модели, где нет встроенного усреднения напряжения, установите анализатор в линейный режим и выберите видеофильтр с частотой среза ниже минимальной частоты повторения измеряемого сигнала.
Квази-пиковые детекторы также применяются при исследованиях электромагнитной совместимости. Это, по сути, взвешенная форма пикового детектирования. Измеренная в таком режиме величина спадает при снижении повторяемости измеряемого сигнала. Таким образом, импульсный сигнал заданной амплитуды и с повторяемостью импульса 10 Гц будет иметь меньшее квази-пиковое значение, чем сигнал с той же амплитудой, но с повторяемостью
1 кГц. Взвешивание сигнала осуществляется при помощи цепей с определенными постоянными зарядаразряда и времени отображения, которые устанавливаются в стандарте CISPR13.
13. CISPR — Особая Международная Комиссия по Радиосовместимости, основанная в 1934 году группой международных организаций для регулирования радиопомех. Это негосударственная организация, чьи рекомендуемые стандарты обычно принимаются в качестве базовых стандартов радиосовместимости государственными управляющими агентствами по всему миру.
Квази-пиковое детектирование является способом измерения и исчисления так называемого «фактора раздражения» сигнала. Представьте, что вы слушаете радиостанцию, страдающую от помех. Если вы иногда слышите случайный щелчок из-за шума каждые, допустим, несколько секунд, вы продолжите слушать передачу без каких-либо особых неудобств. Если же этот щелчок начнет повторяться 60 раз в секунду, с той же амплитудой, он станет очень раздражающим, и передачу слушать будет просто невозможно.
Процессы усреднения
В анализаторе спектра есть несколько обработок, сглаживающих вариации в амплитуде огибающей. Первый такой метод – детектирование среднего – мы рассмотрели ранее. Теперь рассмотрим еще два способа: видеофильтрацию и межкадровое усреднение.14
14. Четвертый метод – шумовой маркер – рассмотрен в Главе 5 Шум и чувствительность. Более подробно о нем можно прочитать в документе Agilent Application Note 1303, Spectrum Analyzer Measurements and Noise.
Видеофильтрация
Разглядеть сигнал, близкий к шуму, — это серьезная проблема при проведении измерений электромагнитной совместимости. Анализатор спектра отображает сигналы плюс свой собственный внутренний шум, как показано на Рис. 2-27. Чтобы уменьшить влияние шума на амплитуду изображаемого сигнала, мы часто сглаживаем или усредняем изображаемые данные, как показано на Рис. 2-28. Анализаторы спектра для этой цели включают переменный видеофильтр. Это фильтр нижних частот, расположенный за детектором и задающий полосу видеосигнала, который потом будет оцифрован для получения данных об амплитуде. Частота среза видеофильтра может быть уменьшена до такой степени, когда она становится меньше, чем полоса выбранного разрешающего фильтра ПЧ. Если это произойдет, видеосистема больше не сможет следовать за более быстрыми вариациями огибающей сигналов, проходящих через цепь ПЧ. В результате получается усреднение или сглаживание изображаемого сигнала.
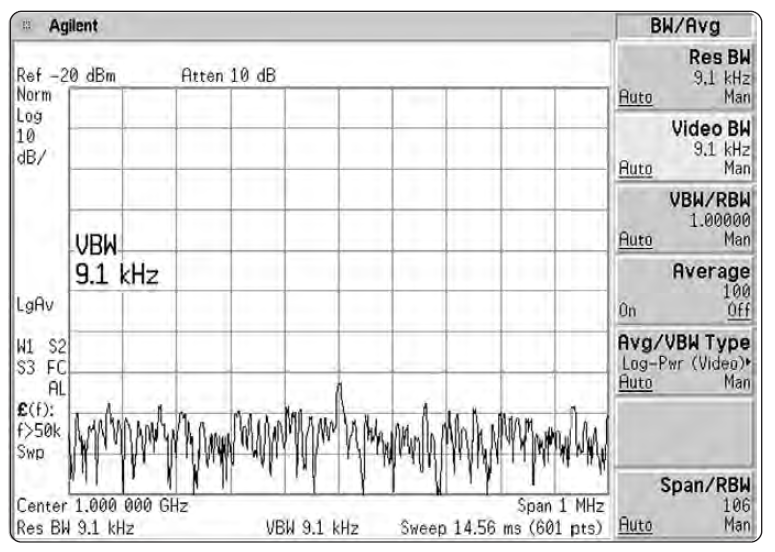
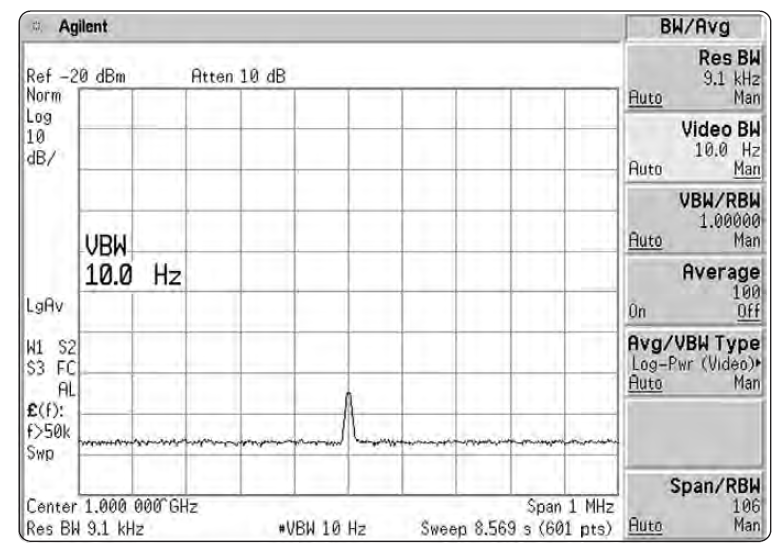
Эффект этот наиболее заметен при измерении шума, — в частности, когда используется широкая разрешающая полоса. Когда мы уменьшаем видеополосу, размах вариаций амплитуды шума уменьшается. Как показано на Рис. 2-29, степень уменьшения (степень усреднения или сглаживания) есть функция отношения видеополосы к полосе разрешения. Когда отношение равно 0.01 или меньше, сглаживание очень хорошее; при больших отношениях сглаживание ухудшается. Та часть трассы, которая уже гладка – например, синусоида, хорошо различимая на фоне шума – не подвержена влиянию видеофильтра.
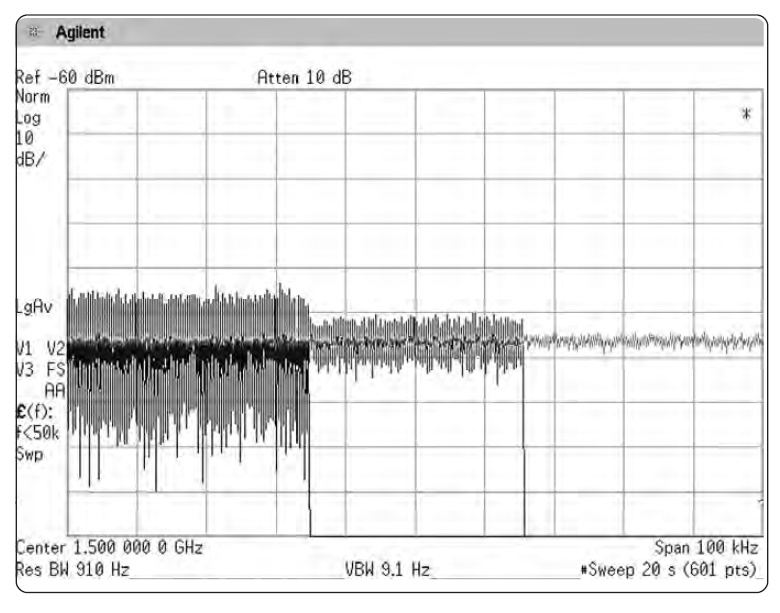
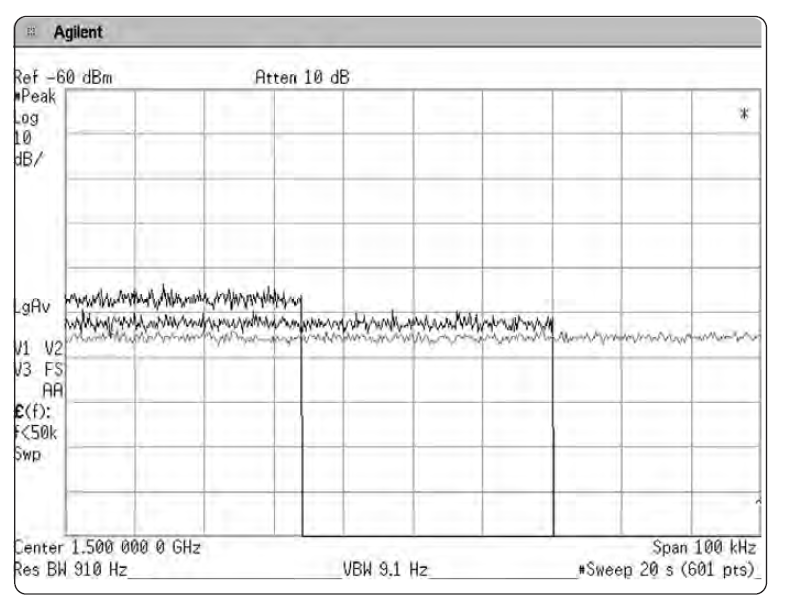
Если переключить анализатор в режим пикового детектирования, можно заметить две вещи. Первое: если видеополоса больше полосы разрешения, то изменение ширины полосы разрешения не приводит к заметным изменениям в пиковом размахе флуктуаций шума. Второе: если видеополоса меньше полосы разрешения, то изменение ширины видеополосы заметно влияет на пиковые значения шума. Однако, уровень шума тоже изменяется с изменением ширины видеополосы, поскольку изменяется усреднение (сглаживание), что изменяет в свою очередь пиковые значения сглаженной огибающей шума. См. Рис. 2-30а. Если мы выберем детектирование среднего, мы увидим, что средний уровень шума останется постоянным. См. Рис. 2-30б.
Поскольку у видеофильтра есть свое собственное время переходных процессов, время развертки увеличивается приблизительно обратно-пропорционально ширине видеополосы, когда видеополоса меньше полосы разрешения. Таким образом, время развертки можно описать как:
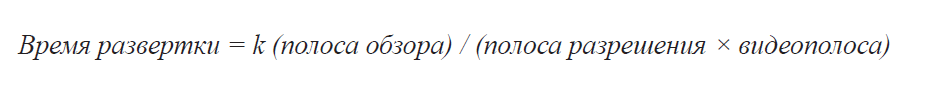
Анализатор автоматически выставляет время развертки так, чтобы учитывать видеополосу, так же как и полосу обзора, и полосу разрешения.
Межкадровое усреднение
Цифровые дисплеи предлагают другой способ сглаживания изображения: межкадровое усреднение. Это процесс, совершенно отличный от того способа, который осуществляется при помощи детектирования среднего. Здесь усреднение проводится поточечно, за две или более развертки. В каждой точке дисплея новое значение усредняется с предыдущим усредненным значением:

Таким образом, картинка на дисплее постепенно сходится к среднему за несколько проходов. Как и при видеофильтрации, можно устанавливать степень усреднения и сглаживания. Делается это выбором количества проходов развертки, за которое происходит усреднение. На Рис. 2-31 показано межкадровое усреднение для различного количества проходов. Хотя межкадровое усреднение и не влияет на время развертки, все равно, чтобы достичь желаемого уровня сглаживания, требуется времени примерно столько же, как и при видеофильтрации, потому что необходимо несколько проходов развертки.
Во многих случаях совершенно не важно, какой из способов сглаживания кривых на экране мы выберем. Если сигнал – это шум, или низкоуровневая синусоида, близкая к шуму, мы получим одинаковые результаты, как при видеофильтрации, так и при межкадровом усреднении. Однако, существует и значительная разница между этими способами. Видеофильтрация осуществляет усреднение в режиме реального времени. То есть, мы наблюдаем полный эффект усреднения в каждой точке дисплея по мере прохода развертки. Каждая точка усредняется лишь один раз, за время, примерно равное 1/видеополоса, при каждом проходе развертки. Межкадровое усреднение, с другой стороны, требует нескольких проходов развертки, чтобы достичь полной степени усреднения, и усреднение в каждой точке имеет место лишь за полный период времени, требующегося для совершения нескольких проходов.
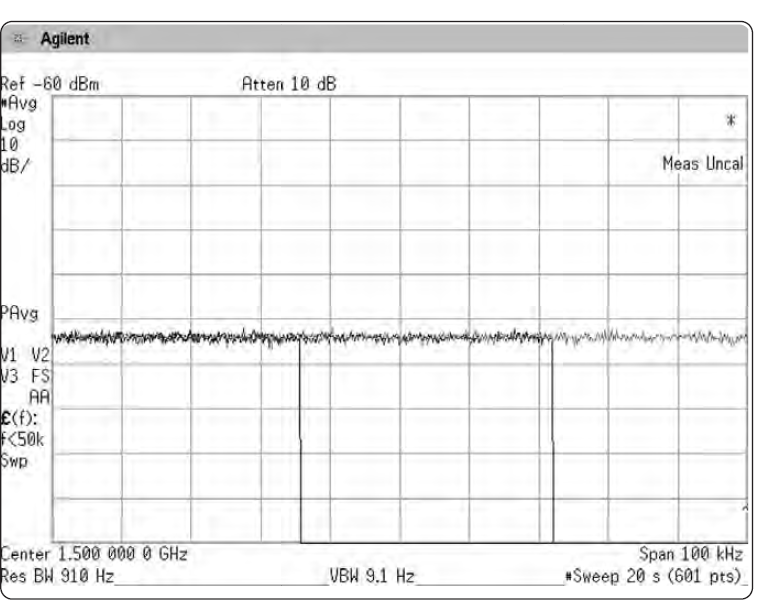
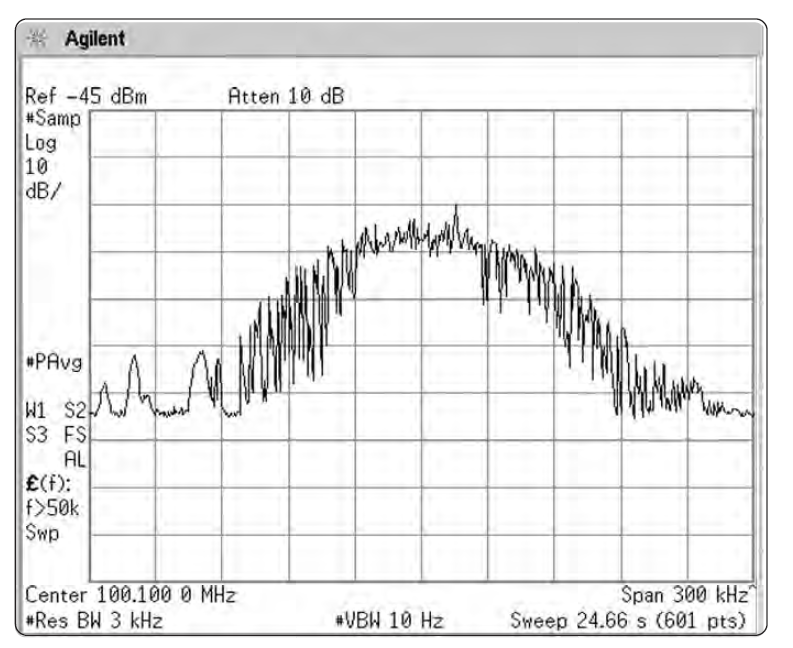
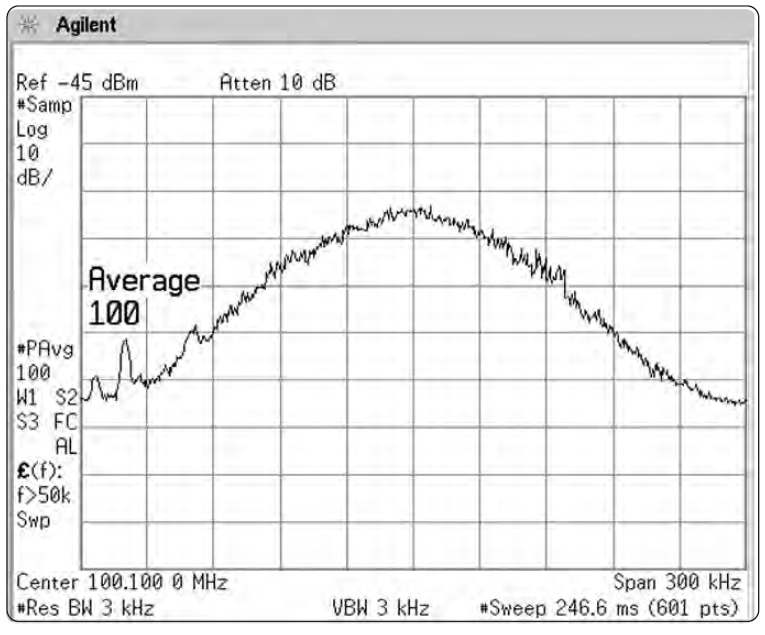
Поэтому мы можем получить значительно отличающиеся результаты для некоторых сигналов при использовании разных методов усреднения. Например, сигнал с переменным во времени спектром может показывать разное среднее значение при каждом проходе развертки, когда мы используем видеофильтрацию. Если же мы используем межкадровое усреднение за много проходов, мы получим значение, гораздо точнее соответствующее реальному среднему. См. Рис. 2-32а и 2-32б.
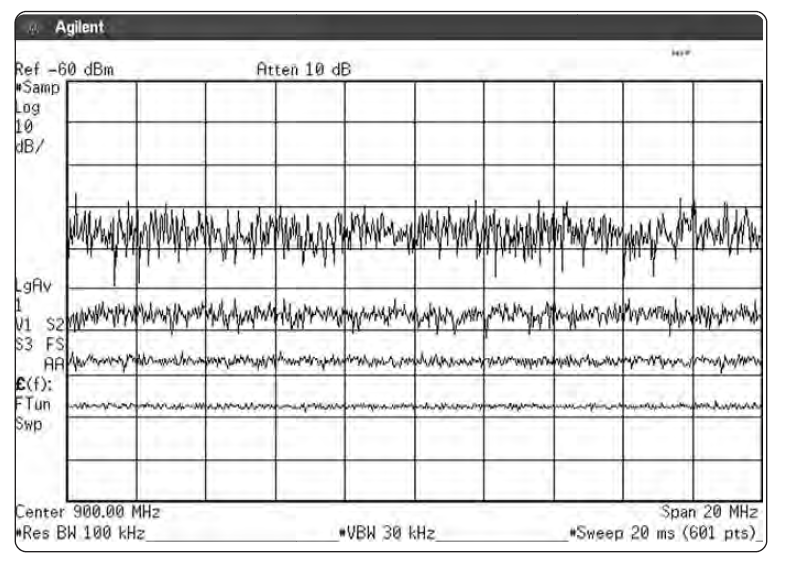
Рисунок 2-32. Видеофильтрация и межкадровое усреднение по-разному отражаются на сигнале ФМ-вещания
Временное стробирование
Анализ спектра с временным стробированием позволяет получать информацию о спектре сигналов, занимающих одну область частотного спектра, но разделенных во временной области. При помощи внешнего триггерного сигнала, координирующего разделение исследуемых сигналов, можно осуществлять следующие операции:
- измерение любого из нескольких сигналов, разделенных во времени; например,можно разделить спектры двух радиосигналов, делящих во времени одну частоту
- измерение спектра сигнала в одной временной ячейке TDMA-системы
- выделение спектра сигналов-помех, которые существуют какое-то ограниченное время — например, переходные процессы фронтов периодических импульсов
Для чего нужно временное стробирование
Традиционный анализ спектра в частотной области предоставляет ограниченную информацию о некоторых сигналах. Примерами таких сложных для анализа сигналов являются следующие типы:
- импульсный радиочастотный сигнал
- с временным мультиплексированием
- многостанционный доступ с временным разделением каналов (TDMA)
- перемежающиеся или уплотненные импульсные
- модулированные всплеском
Иногда возможность временного стробирования позволяет проводить измерения, которые в ином случае были бы затруднены, если не невозможны вовсе. Например, взгляните на Рис. 2-33а, где показан упрощенный цифровой сигнал мобильной радиосвязи: два источника, #1 и #2, делят во времени один и тот же частотный канал. Каждый источник передает отдельный всплеск длительностью 1 мс, а затем отключается, чтобы другой тоже передал свою 1 мс. Измерить уникальный частотный спектр каждого передатчика – задача не из тривиальных.
К сожалению, традиционные анализаторы спектра с такой задачей справиться не могут. Они просто демонстрируют суммарный спектр, как показано на Рис. 2-33б. Используя возможности временного стробирования и внешний сигнал-триггер, можно увидеть спектр только передатчика #1 (или передатчика #2, если пожелаете), и, вдобавок, идентифицировать его как источник паразитного сигнала, как видно на Рис. 2-33в.
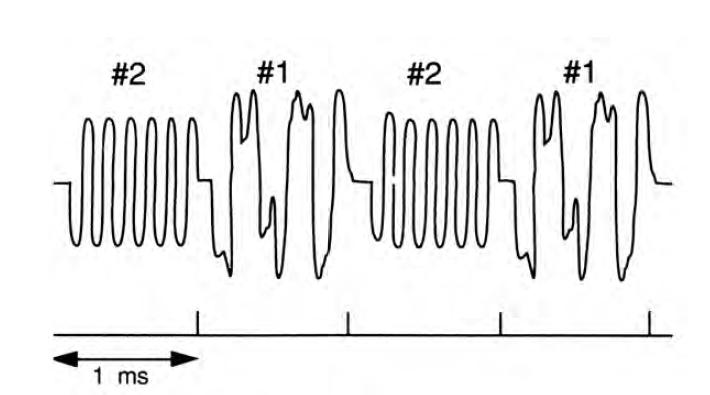
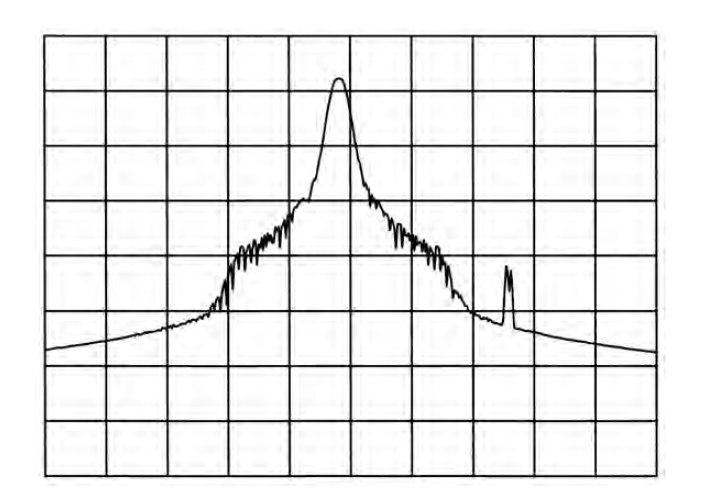
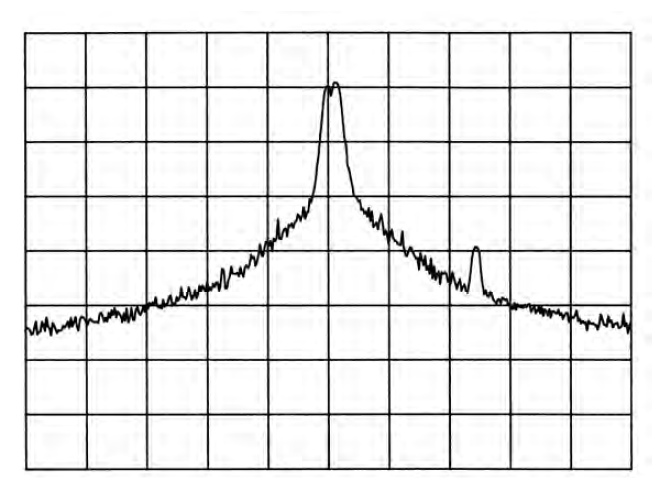
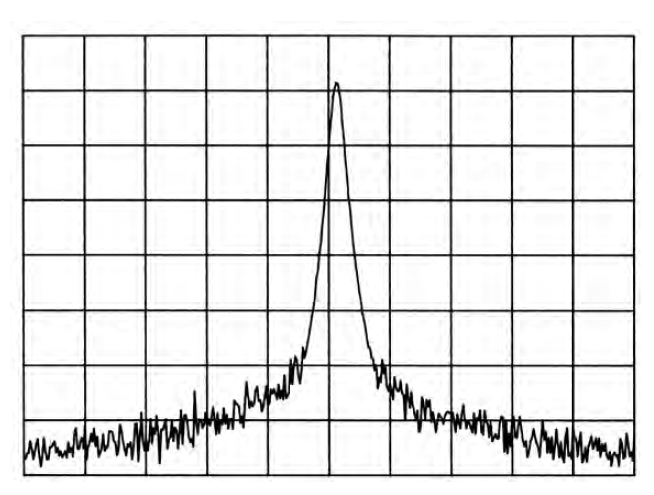
Временное стробирование можно осуществить тремя различными способами, которые мы подробно рассмотрим чуть позже. Однако, существуют определенные общие концепции временного стробирования, применимые к любому способу его воплощения. В частности, вам будет необходимо обеспечить четыре следующие вещи:
- внешний сигнал-триггер стробирования
- управление стробированием или режим триггера (по фронту или по уровню)
- установка задержки стробирования, которая определит, как скоро после включения триггера наступит активность наблюдаемого сигнала
- установка длительности стробирования, которая определит, как долго будет наблюдаться сигнал
Управление этими параметрами позволит нам наблюдать спектр сигнала в течение заданного периода времени. Если вам посчастливится обеспечить стробирующий сигнал, который является ненулевым только в желаемый период времени, то вы можете осуществить стробирование по уровню, как показано на Рис. 2-34. Однако, во многих случаях стробирующий сигнал не будет идеально совпадать с тем временем, в которое бы нам хотелось измерить спектр. Поэтому более гибким подходом будет использование триггера по фронту, в сочетании с определенной задержкой и длительностью стробирования для точного задания временного периода, в котором необходимо замерять сигнал.
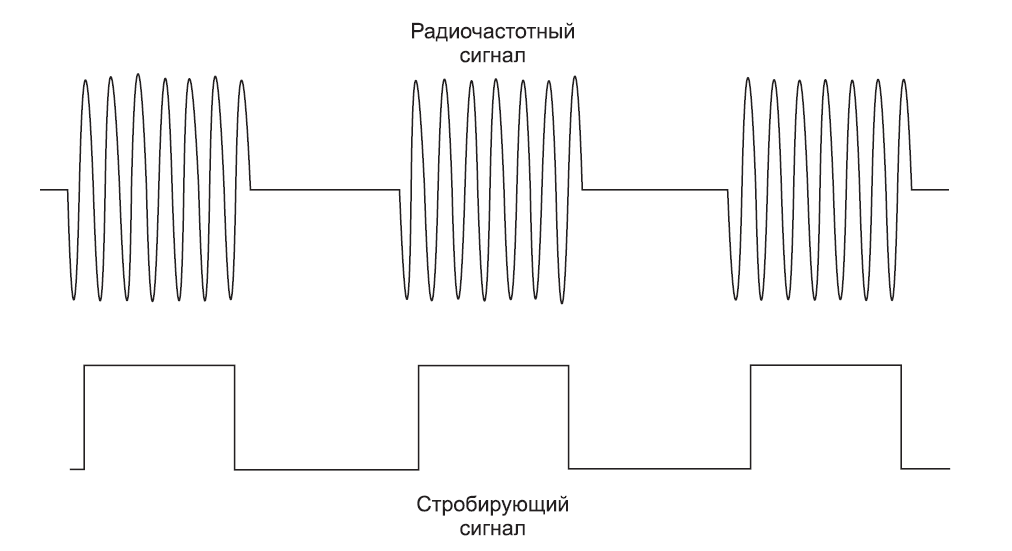
Возьмем, к примеру, сигнал мобильной связи с восемью временными ячейками, показанный на Рис. 2-35. Каждый всплеск длится 0.57 мс, а полный кадр – 4.615 мс. Нас вполне может интересовать спектр сигнала в рамках одной определенной временной ячейки. Для нашего примера предположим, что мы используем только две из восьми доступных временных ячеек, как показано на Рис. 2-36. Если мы посмотрим на этот сигнал в частотной области (Рис. 2-37), мы заметим наличие нежелательного паразитного сигнала в спектре. Чтобы разобраться с этой проблемой и найти источник этой помехи, нам надо определить ту временную ячейку, в которой она появляется. Если мы хотим посмотреть на ячейку номер 2, мы устанавливаем стробирование на включение триггером по фронту роста всплеска номер 0, затем задаем задержку в 1.3 мс и длительность стробирования в 0.3 мс, как показано на Рис. 2-38. Задержка стробирования гарантирует, что мы измерим только спектр ячейки номер 2, когда ее мощность будет полностью включена. Обратите внимание, что задержка стробирования тщательно подобрана таким образом, чтобы избежать фронта подъема всплеска, поскольку нам нужно обеспечить какое-то время, чтобы установился отфильтрованный разрешающей полосой сигнал, прежде чем мы осуществим непосредственно измерение. Соответственно, длительность стробирования подобрана так, чтобы избежать фронта спада всплеска. На Рис. 2-39 изображен спектр временной ячейки номер 2, на котором видно, что источником помехи данный всплеск НЕ является.
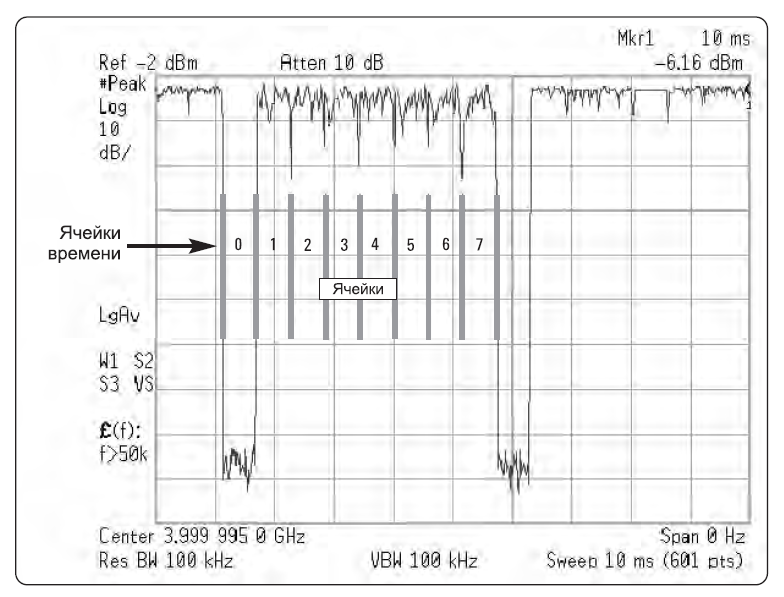
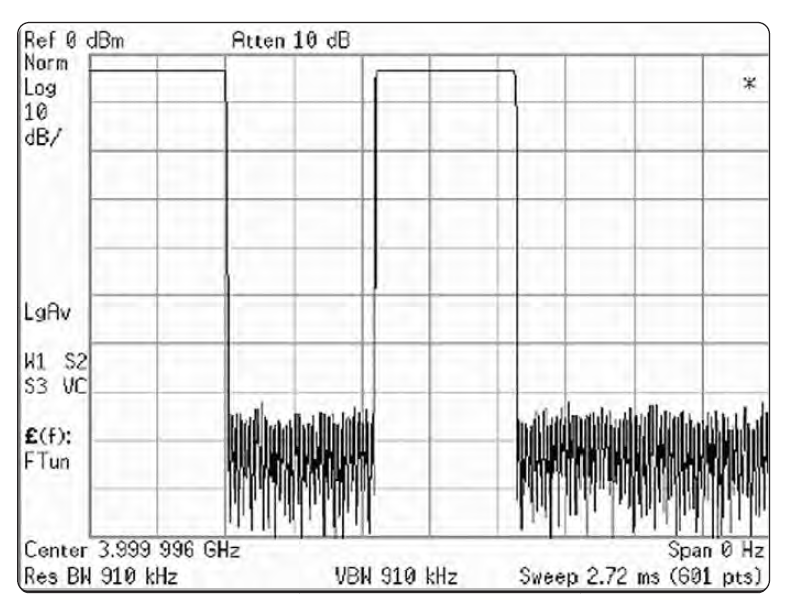
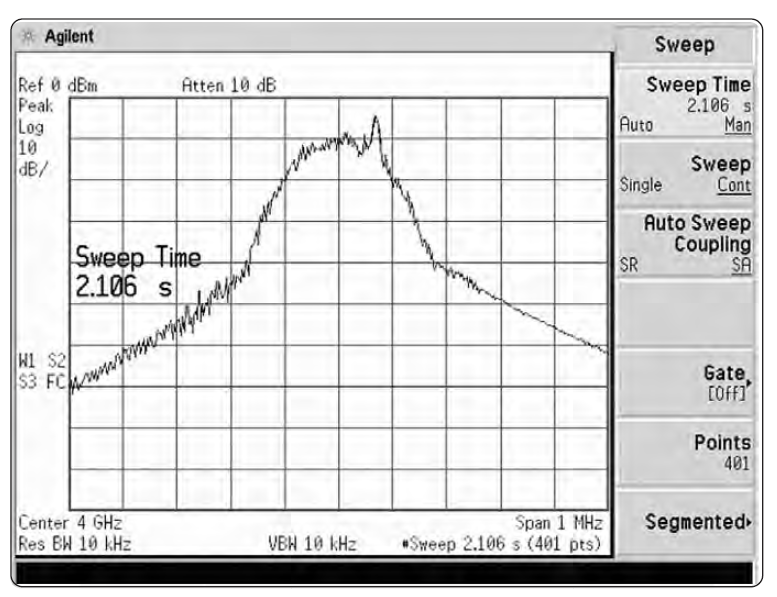
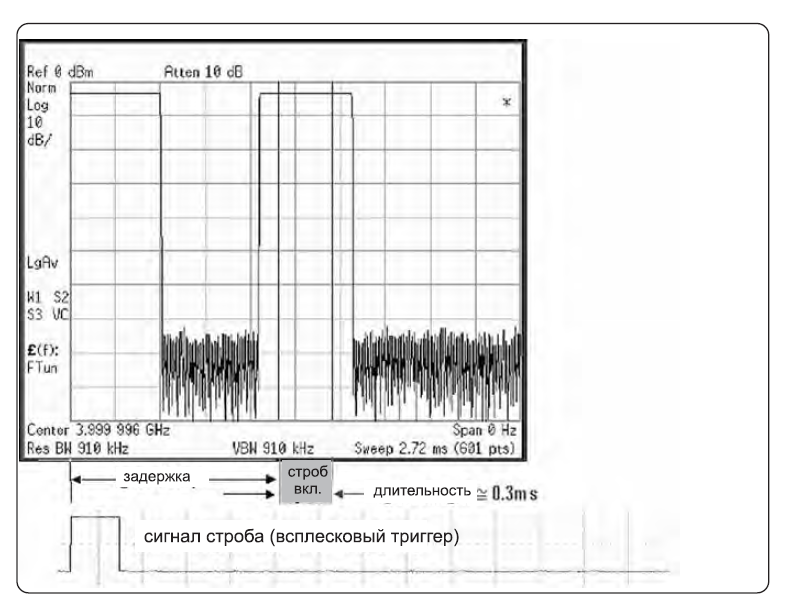
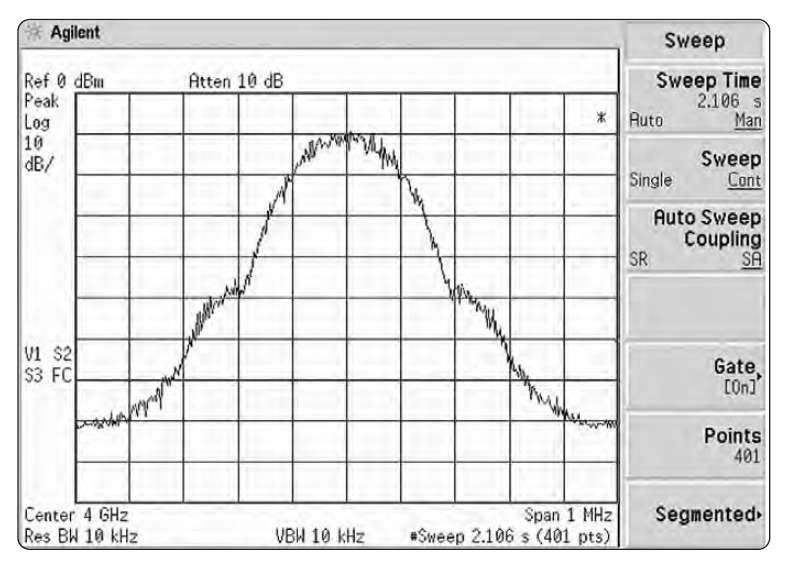
Существуют три распространенных метода для осуществления временного стробирования:
- стробированное БПФ
- стробированное видео
- стробированная развертка
Стробированное БПФ
У некоторых анализаторов спектра, например, у серии PSA фирмы Agilent, есть встроенные возможности быстрого преобразования Фурье. В этом режиме данные для БПФ-обработки оцифровываются спустя выбранное время задержки после появления триггер-сигнала. Сигнал ПЧ оцифровывается и захватывается в течение времени, равного 1.83/величина полосы разрешения. БПФ-вычисления производятся, основываясь на этих полученных данных, и результаты преобразования отображаются в виде спектра. Таким образом, спектр получается в определенный момент и за определенный временной промежуток. Это – самый быстрый способ временного стробирования, если только полоса обзора не превышает максимальную полосу одноразового анализа БПФ, которая для PSA имеет значение 10 МГц.
Чтобы добиться максимального разрешения по частоте, выберите максимально узкую полосу разрешения, чье время захвата укладывается в рамки интересующего нас временного промежутка. Потребность в этом есть не всегда, и можно выбирать более широкие разрешающие полосы, с соответствующей укороченной длительностью стробирования. Минимальная достижимая полоса разрешения в приложениях стробированного БПФ всегда меньше, чем она же при других способах стробирования, потому что сигнал ПЧ должен полностью установиться за время измеряемого радио-импульса, что занимает времени больше, чем отношение числа 1.83 к полосе разрешения.
Стробированное видео
Стробированное видео – это техника анализа, применяемая в ряде анализаторов спектра, в том числе Agilent 8650, 8590 и приборах серии ESA. Здесь напряжение видеосигнала выключается, или сводится к «минус бесконечности децибел», на тот период времени, когда стробирование находится в неактивном состоянии. Детектор устанавливается в пиковый режим. Время развертки должно быть установлено так, чтобы стробирование осуществлялось хотя бы один раз на каждую точку дисплея (или блок), чтобы пиковый детектор мог получить реальные данные за этот промежуток времени. Иначе будут присутствовать точки без данных, что выльется в отображение неполного спектра. Поэтому минимальное время развертки должно быть: «N блоков дисплея умножить на длительность импульса». В примере с сигналом мобильной связи полный кадр длится 4.615 мс. Для прибора ESA, с установленной по умолчанию 401 дисплейной точкой, минимальное время развертки для измерения мобильного сигнала со стробированным видео будет 401 умножить на 4.615 мс, или 1.85 с. У некоторых TDMA форматов полный кадр длится 90 мс, что потребует очень большого времени развертки при использовании стробированного видео.
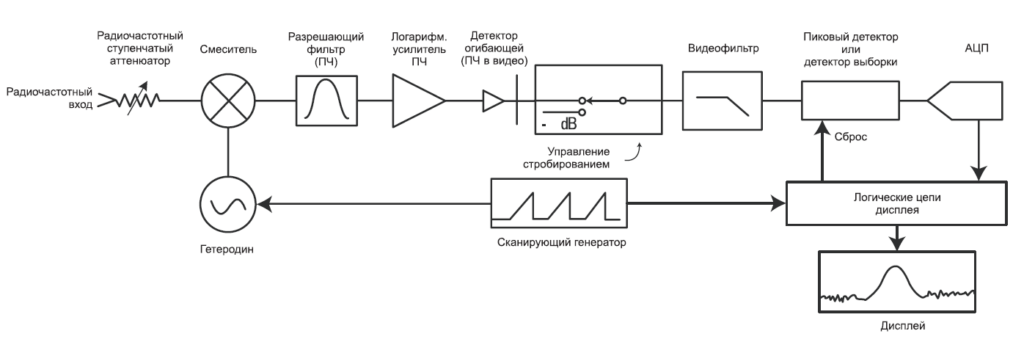
Стробированная развертка
Последний из методов – стробированная развертка, иногда называется «стробированный гетеродин». В режиме стробированной развертки мы управляем линейным ростом напряжения в генераторе развертки, которым перестраивается гетеродин. Это показано на Рис. 2-41. Когда стробирование активно, гетеродин увеличивает частоту, как в любом другом анализаторе спектра. Когда стробирование выключается, напряжение генератора развертки фиксируется, и гетеродин перестает увеличивать частоту. Такой способ может быть гораздо более быстрым, нежели стробированное видео, поскольку для одного всплеска может быть измерено несколько блоков. Для примера обратимся снова к описанному ранее сигналу цифровой мобильной связи. Если использовать анализатор серии PSA, то обычная нестробированная развертка пройдет полосу обзора в 1 МГц за 14.6 мс, как показано на Рис. 2-42. С длительностью стробирования 0.3 мс, развертка анализатора должна разбиться на 49 стробированных отрезков (14.6 разделить на 0.3). Если полный кадр мобильного сигнала составляет 4.615 мс, то полное время измерения будет 49 отрезков по 4.615 мс – то есть 226 мс. Ускорение измерения, по сравнению с 1.85 с в случае стробированного видео с 401 точкой данных, весьма значительно. Режим стробированной развертки присутствует на анализаторах серии PSA.
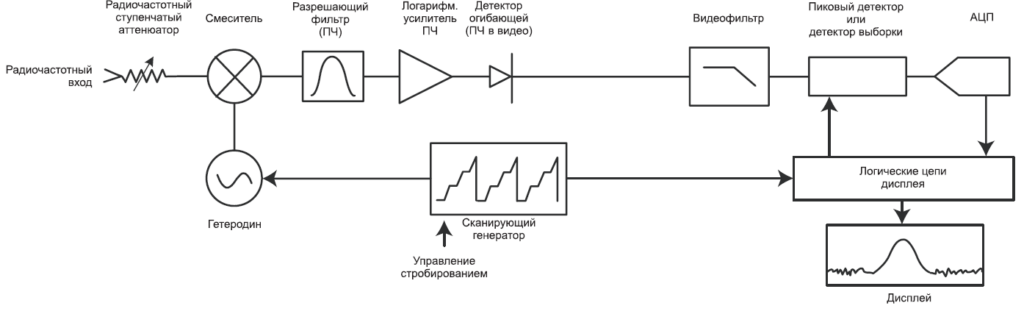
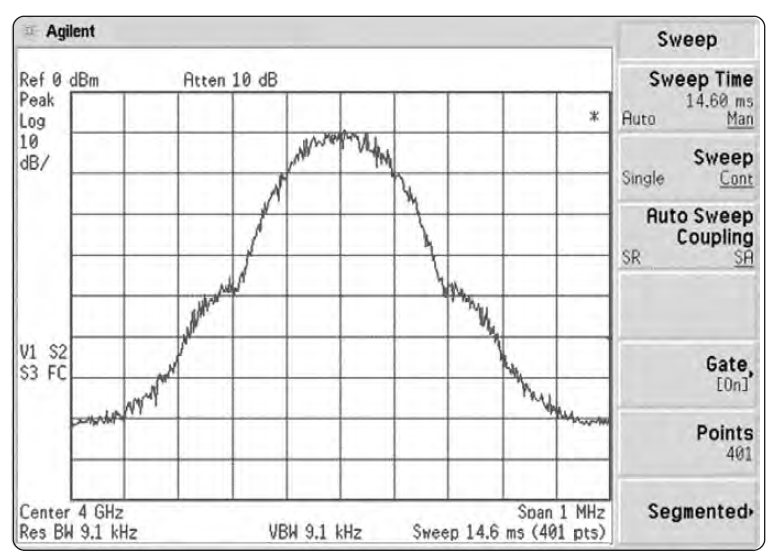
Глава 3 Обзор цифровой ПЧ
Начиная с 80-х годов прошлого века одним из самых значительных изменений в анализе спектра стало применение цифровой технологии для замены узлов приборов, которые до этого имели исключительно аналоговое воплощение. С появлением высокопроизводительных АЦП, новые анализаторы спектра стали способны оцифровывать входящий сигнал гораздо быстрее, чем приборы, созданные буквально за пару лет до этого. Наиболее грандиозные улучшения произошли в секции ПЧ анализаторов спектра. Цифровая ПЧ1 произвела сильный эффект улучшения в скорости, точности и способности измерять сложные сигналы, благодаря использованию передовых технологий цифровой обработки сигналов.
- Строго говоря, как только сигнал оцифрован, он уже не находится на промежуточной частоте, или ПЧ. С этого момента сигнал представлен цифровыми значениями. Однако, мы используем термин «цифровая ПЧ» для описания тех цифровых процессов, которые пришли на смену аналоговой секции ПЧ, существовавшей в традиционных анализаторах спектра.)
Цифровые фильтры
Частичное цифровое воплощение цепей ПЧ имеет место в анализаторах Agilent серии ESA-E. Если полосы разрешения в 1 кГц и шире обычно можно обеспечить традиционными аналоговыми LC-фильтрами и кварцевыми фильтрами, то самые узкие полосы разрешения (от 1 Гц до 300 Гц) реализуются цифровыми способами. Как показано на Рис. 3-1, линейный аналоговый сигнал преобразуется вниз на частоту ПЧ 8.5 кГц и затем пропускается через полосовой фильтр шириной всего 1 кГц. Этот сигнал ПЧ усиливается, затем запоминается в устройстве выборки и хранения (УВХ) и оцифровывается с частотой 11.3 кГц.
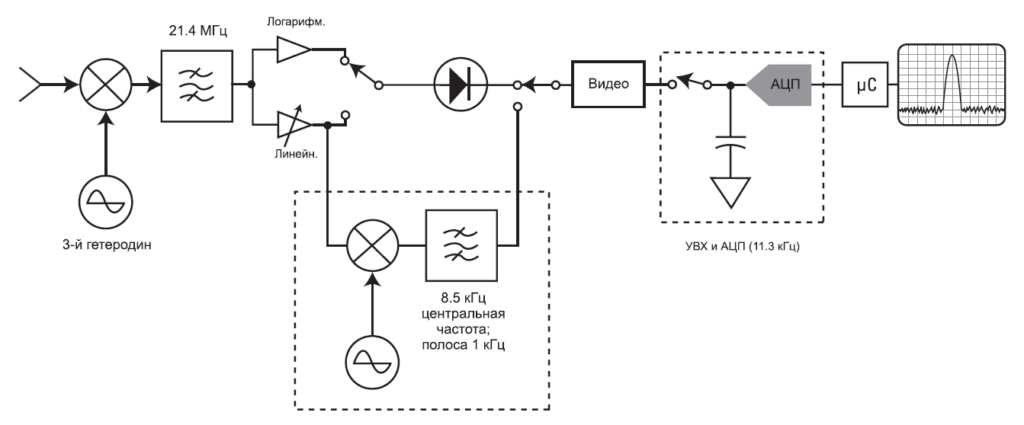
Как только сигнал оцифрован, над ним выполняется операция БПФ. Чтобы преобразовать подходящий сигнал, анализатор должен быть в состоянии фиксированной настройки (без развертки). То есть, преобразование должно быть осуществлено над сигналом временной области. Поэтому в анализаторах серии ESA-E вместо непрерывной развертки в режиме цифровых разрешающих полос используется ступенчатая развертка с шагом 900 Гц. Такая ступенчатая настройка может наблюдаться на дисплее, который обновляется шагами по 900 Гц, по мере выполнения цифровой обработки.
Как мы вскоре увидим, другие анализаторы спектра – например, приборы серии PSA, — используют полностью цифровую ПЧ, и все их разрешающие фильтры имеют цифровое исполнение.
Ключевым преимуществом цифровой обработки, осуществляемой этими анализаторами, является полосовая избирательность примерно 4:1. Такая избирательность доступна на самых узкополосных фильтрах – тех, которые нам нужны для разделения наиболее близко расположенных сигналов.
В Главе 2 мы провели расчет избирательности для двух сигналов, разнесенных на 4 кГц, при использовании 3-килогерцового аналогового фильтра. Давайте повторим этот расчет для случая цифровой фильтрации. Хорошей моделью избирательности цифрового фильтра будет около-гауссовская модель:
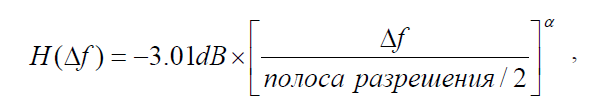

Подставляя значения из нашего примера в это уравнение, получим:
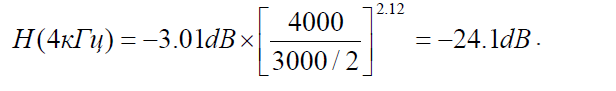
На отстройке 4 кГц, 3-килогерцовый цифровой фильтр подавляет до -24.1 дБ, по сравнению с аналоговым фильтром, который подавлял всего -14.8 дБ. Благодаря своей превосходящей избирательности, цифровой фильтр может различить гораздо более близко расположенные сигналы.
Полностью цифровая ПЧ
В анализаторах спектра серии PSA фирмы Agilent впервые было совмещено несколько цифровых технологий, чтобы создать полностью цифровой блок ПЧ. Чисто цифровая ПЧ обеспечивает целый букет преимуществ для пользователя. Комбинация БПФ-анализа для узких и анализа с разверткой для широких полос обзора оптимизирует развертку для обеспечения наибыстрейших измерений*. Архитектурно АЦП передвинулся ближе ко входному порту, что стало возможным благодаря усовершенствованиям в аналогово-цифровых преобразователях и другом цифровом оборудовании. Давайте начнем с рассмотрения структурной схемы полностью цифровой ПЧ анализатора серии PSA, изображенной на Рис. 3-2.
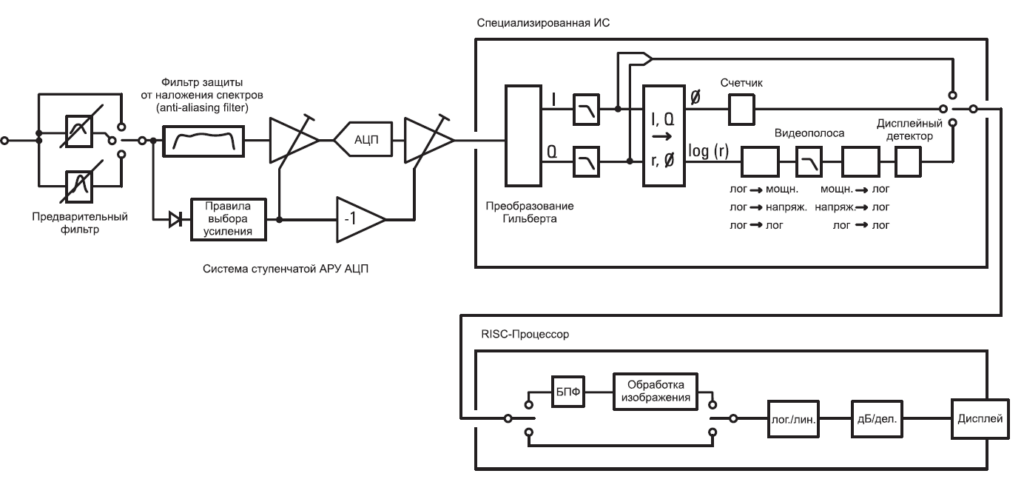
Здесь все 160 полос разрешения реализованы цифровым способом. Хотя присутствуют и аналоговые цепи перед АЦП, начиная с нескольких ступеней преобразования «вниз» и заканчивая парой однополюсных предварительных фильтров (один LC-фильтр и один кварцевый фильтр). Предварительный фильтр помогает предотвратить попадание искажений третьего порядка в последующую цепь, точно так же, как и в аналоговой реализации ПЧ. Вдобавок, он делает возможным расширение динамического диапазона за счет ступенчатой автоматической регулировки усиления (АРУ). Сигнал с выхода однополюсного предварительного фильтра поступает на детектор АРУ и на фильтр защиты от наложения спектров (anti-aliasing filter).
Как и в случае любой архитектуры ПЧ, основанной на БПФ, фильтр защиты от наложения спектров необходим для устранения наложений (вклада внеполосных сигналов в выборку данных АЦП). Этот фильтр – многополюсный, поэтому обладает значительной групповой задержкой. Даже очень резко возрастающий радиочастотный всплеск, перенесенный вниз на ПЧ, испытает задержку на более чем три такта АЦП (30 МГц) при проходе через него. Задержка дает время распознать поступающий большой сигнал до того, как он вызовет перегрузку АЦП. Логическая цепь, управляемая детектором АРУ, уменьшит усиление перед АЦП, до того, как сигнал туда поступит, чем предотвратит ограничение амплитуды импульса. Если огибающая сигнала будет оставаться низкой продолжительное время, система АРУ увеличит усиление, понизив эффективный шум на входе. Цифровое усиление после АЦП также изменяется, чтобы компенсировать аналоговое усиление перед АЦП. Результат – АЦП с «плавающей точкой», очень широким динамическим диапазоном при включенной АРУ в режиме развертки.
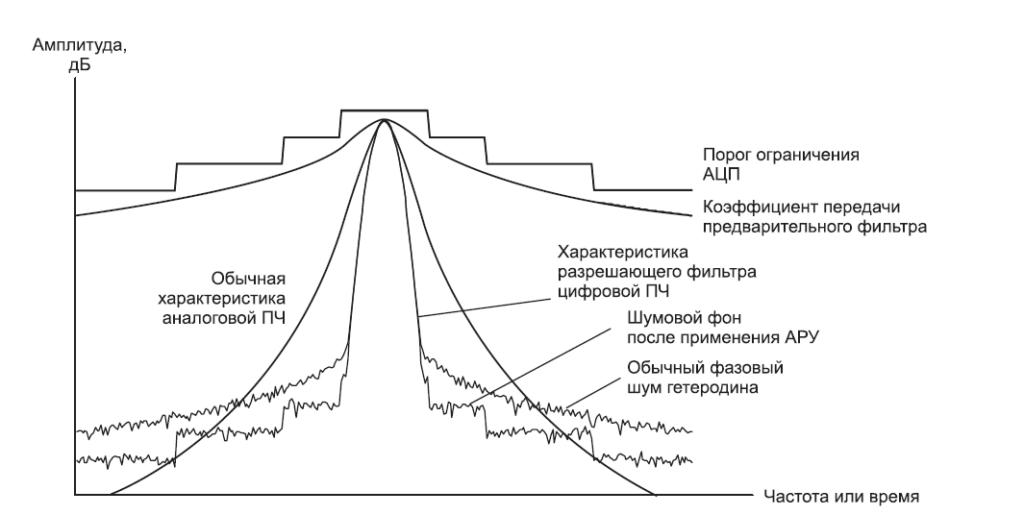
На Рис. 3-3 показано поведение анализатора серии PSA при развертке. Однополюсный предварительный фильтр позволяет увеличить усиление, пока анализатор настроен далеко от несущей частоты. По мере приближения к несущей усиление уменьшается и шум квантования АЦП растет. Уровень шума будет зависеть от уровня сигнала и его частотной отстройки от несущей, поэтому он будет выглядеть как ступенчатый фазовый шум. Но фазовый шум отличен от этого «шума автоподстройки». Фазового шума в анализаторах спектра избежать нельзя. Однако уменьшение ширины предварительной фильтрации помогает снизить «шум автоподстройки» на большинстве частотных отстроек от несущей. Поскольку ширина полосы предварительной фильтрации примерно в 2.5 раза больше ширины полосы разрешения, уменьшение полосы разрешения понижает «шум автоподстройки».
Специализированная ИС обработки сигнала
Вернемся к структурной схеме цифровой ПЧ (Рис. 3-2). После аналогового усиления до АЦП и его компенсации цифровым усилением, специализированная ИС начинает обработку выборки. Сначала 30-мегагерцовые отсчеты ПЧ разбиваются на I и Q пары с половинным шагом (15 миллионов пар в секунду). Пары I и Q затем получают высокочастотную коррекцию при помощи цифрового фильтра первого порядка, коэффициент передачи которого обратен и фаза примерно противоположна таковым у аналогового однополюсного предварительного фильтра. Потом пары I и Q фильтруются ФНЧ с линейной фазовой характеристикой и почти идеальной гауссовой частотной характеристикой. Гауссовские фильтры всегда были самыми подходящими для анализа с разверткой частоты, благодаря оптимальному компромиссу между поведением в частотной области (коэффициент прямоугольности) и во временной области (отклик на быструю развертку). С уменьшенной шириной полосы сигнала, пары I и Q теперь могут быть прорежены и отправлены на процессор для БПФ-обработки или демодуляции. Хотя БПФ может быть выполнено для части полосы обзора шириной до 10 МГц (полоса пропускания фильтра защиты от наложения спектров), то даже при БПФ в более узкой полосе частот 1 кГц, с узкой полосой разрешения в 1 Гц, для расчета потребуется 20 миллионов точек данных. Использование прореживания данных при более узких полосах обзора значительно уменьшает количество требуемых для БПФ точек данных и ускоряет вычисления.
Для анализа с разверткой частоты, отфильтрованные пары I и Q преобразуются в пары амплитуды и фазы. В традиционном анализе с разверткой частоты сигнал с детектора огибающей фильтруется видеофильтром, а затем оцифровывается для системы детекторов дисплея. Выбор режима отображения «логарифмический/линейный» и масштабирование «дБ/единицы» производится в процессоре, так что результат отображается в любом из масштабов без проведения повторных измерений.
Дополнительные возможности видеообработки
Обычно, видеофильтр сглаживает логарифм амплитуды сигнала, но у него есть немало дополнительных возможностей. Он может преобразовывать логарифм амплитуды огибающей в напряжение перед фильтрацией, и переводить обратно перед детектированием дисплея, для согласованности показаний.
Фильтрация амплитуды в масштабе линейного напряжения желательна для наблюдения огибающих импульсных радиосигналов при нулевом обзоре. Сигнал с логарифмической амплитудой также может быть пересчитан в мощность (квадрат амплитуды) перед фильтрацией, а затем обратно. Фильтрация мощности позволяет анализатору дать такой же средний отклик на шумободобные сигналы (сигналы цифровой связи), как и на сигналы гармонических колебаний с таким же среднеквадратичным напряжением. В наше время все чаще требуется измерять полную мощность в канале или во всем диапазоне частот. При таких измерениях, точка на дисплее может показывать среднюю мощность за то время, которое гетеродин проходит через эту точку. Видеофильтр может быть перенастроен в режим накапливающего сумматора для осуществления усреднения в масштабе логарифма, напряжения или мощности.
Счет частоты
В анализаторах спектра с разверткой частоты обычно есть счетчик частоты. Он отсчитывает количество пересечений нуля в сигнале ПЧ и пересчитывает результат расчета на известные величины отстройки от гетеродинов на остальном участке цепи преобразования. Если счет будет идти 1 секунду, можно получить разрешение по частоте в 1 Гц.
Благодаря использованию синтезаторов частот в качестве гетеродинов и полностью цифровой реализации полосы разрешения, присущая анализаторам серии PSA точность (установки) частоты очень высокая (0.1% от полосы обзора). Вдобавок, в PSA есть счетчик частоты, который отслеживает не только пересечения нуля, но и изменения фазы. Поэтому он может разрешать частоты в десятки миллигерц за 0.1 секунды. С такой конструкцией способность определять изменения частоты ограничена уже не анализатором спектра, а, скорее, зашумленностью исследуемого сигнала.
Другие преимущества полностью цифровой ПЧ
Мы уже рассмотрели ряд особенностей приборов серии PSA: фильтрация логарифма/напряжения/мощности, счет частоты с высоким разрешением, переключение логарифмического/линейного масштаба хранящихся в памяти данных, превосходный коэффициент прямоугольности, режим детектора усреднения данных в точке отображения, 160 различных полос разрешения, и, конечно же, режим последовательного анализа или режим БПФ. При анализе спектра фильтрация разрешающими фильтрами вносит неопределенность в измерения амплитуды и фазы, являющихся функциями скорости развертки. При определенном фиксированном уровне таких неопределенностей, разрешающие фильтры чисто цифровой ПЧ с линейной фазовой характеристикой допускают более высокие скорости развертки частоты, чем аналоговые фильтры. Цифровое воплощение также обеспечивает известные компенсации при снятии данных частоты и амплитуды, допуская тем самым скорости развертки обычно вдвое большие, чем у более старых анализаторов, и демонстрирует отличные показатели даже при учетверенной скорости развертки.
Реализованное в цифровом виде логарифмическое усиление отличается высокой точностью. Типичные неопределенности, характерные для анализатора в целом, гораздо меньше неопределенностей измерения, с помощью которых производитель оценивает достоверность логарифмического представления. Значение достоверности логарифмического представления задано +0.07 дБ для сигнала уровня до -20 дБм на входном смесителе анализатора. Диапазон логарифмического усиления не ограничивает уровня достоверности логарифмического представления на низких уровнях, как это было бы при аналоговой ПЧ; диапазон ограничен только шумом (пересчитанным на входной смеситель) порядка -155 дБм. Из-за сжатия однотонового сигнала в последующих цепях на более высоких мощностях, параметр достоверности ухудшается до ±0.13 дБ для уровней сигналов до -10 дБм на входном смесителе. Для сравнения, аналоговый логарифмический усилитель обычно характеризуется допусками порядка ±1 дБ.
Влияние других источников неопределенностей,связанных с ПЧ, также уменьшилось. Предварительный фильтр ПЧ – аналоговый, и должен быть настроен как любой аналоговый фильтр, так что он подвержен неопределенностям настройки. Но он все равно лучше, чем прочие аналоговые фильтры. При том, что для него нужно изготовить всего одно звено, его можно сделать гораздо более стабильным, чем в случае 4- и 5-звенных фильтров, которые используются в анализаторах с аналоговой ПЧ. В результате, перепады усиления между разрешающими фильтрами удается удержать в рамках величины ±0.03 дБ, что в десять раз лучше, чем для чисто аналоговых конструкций.
Точность полосы ПЧ определяется ограничениями размещаемости в цифровой части фильтрации и неопределенностью калибровки в аналоговом предварительном фильтре. И снова, предварительный фильтр — весьма стабилен, и привносит лишь 20% от той неопределенности, которая бы присутствовала в аналоговой реализации полосы разрешения, состоящей из пяти таких звеньев. В результате, большинство разрешающих полос укладываются в 2 процента от своей заявленной ширины, в отличие от 10-20 процентов в случае анализаторов с аналоговой ПЧ.
Самый важный аспект точности полосы пропускания – это минимизация неопределенности измерения мощности в канале и подобных измерений. Полоса шума разрешающих фильтров имеет спецификацию гораздо лучше, чем допуск в 2 процента на установочные процессы, а шумовые маркеры и измерение мощности в канале имеют допуск в ±0.5%. Таким образом, неопределенности полосы пропускания дают вклад всего ±0.022 дБ в неопределенность измерения плотности мощности шума и мощности в канале.
И, наконец, при полном отсутствии аналоговых звеньев усиления, зависящих от опорного уровня, вообще не существует неопределенности «усиления ПЧ». Суммарное значение всех этих улучшений таково, что чисто цифровая ПЧ обеспечивает значительное улучшение в точности анализатора спектра. Также появляется возможность изменять настройки анализатора без сколько-нибудь значительного влияния на точность измерения. В следующей главе мы поговорим об этом подробнее.
Глава 4 Амплитудная и частотная точность
Теперь, когда мы спокойно можем наблюдать наш сигнал на дисплее, давайте обратимся к амплитудной точности, или, скорее, к амплитудной неопределенности. Большинство анализаторов спектра описываются в терминах как абсолютной, так и относительной точности. Однако, относительные характеристики имеют влияние на оба вида точности, так что давайте сначала рассмотрим факторы, определяющие относительную неопределенность.
Но сперва снова взглянем на структурную схему аналогового анализатора спектра с разверткой по частоте, изображенную на Рис. 4-1, и посмотрим, какие узлы дают вклад в неопределенность. Чуть позже в этой главе мы рассмотрим, как цифровая ПЧ и различные методы калибровки могут значительно снизить неопределенность измерений.
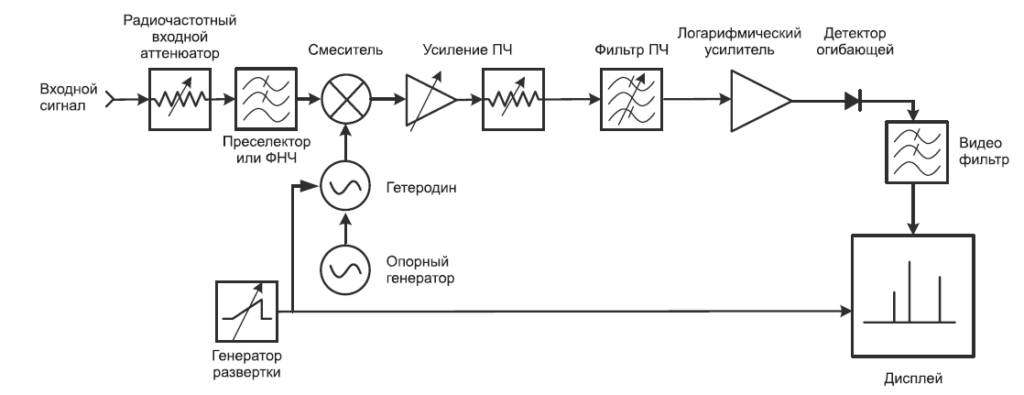
Итак, узлы, дающие вклад в неопределенность:
- Входной соединитель (рассогласование)
- Входной радиочастотный аттенюатор
- Смеситель и входной фильтр (равномерность)
- Усиление/ослабление ПЧ (опорный уровень)
- Разрешающие фильтры
- Достоверность масштаба
- Калибратор (не показан)
Важным фактором, дающим вклад в неопределенность измерений, которому очень часто не придают должного значения, является рассогласование импеданса. Входной импеданс анализаторов не идеален, выходной импеданс источников сигнала – тоже. При наличии рассогласования, векторы падающего и отраженного сигналов могут складываться, увеличивая или уменьшая результирующий вектор. Поэтому сигнал, пришедший на анализатор, может быть больше или меньше истинного сигнала. В большинстве случаев, неопределенность за счет рассогласования относительно мала. Однако следует отметить, что в то время как общая точность анализаторов в последнее время значительно возросла, доля «незначительной» неопределенности рассогласования теперь составляет заметную часть общей неопределенности измерений. В любом случае, улучшая согласование источника или анализатора, можно снизить общую неопределенность1.
- Подробнее см. документ Agilent PSA Performance Spectrum Analyzer Series Amplitude Accuracy Product Note.
Основное выражение для расчета максимальной неопределенности рассогласования в дБ:
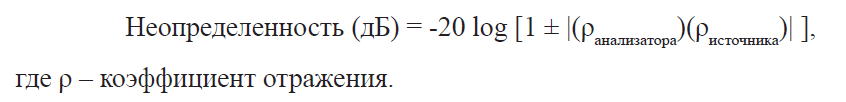
В документации анализаторов спектра обычно указывается входной коэффициент стоячей волны по напряжению (КСВН). Зная КСВН, можно вычислить ρ следующим способом:
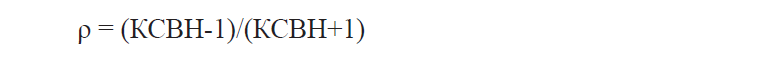
Для примера, положим входной КСВН анализатора равным 1.2 и возьмем исследуемое устройство (ИУ) с КСВН 1.4 на выходном порту. Результирующая неопределенность рассогласования будет ±0.13 дБ.
Поскольку самый худший случай согласования анализатора имеет место при установке его входного аттенюатора на 0 дБ, по возможности следует избегать такой установки. В качестве альтернативы, можно присоединить хорошо согласованный аттенюатор ко входу анализатора, и тем самым значительно уменьшить значение рассогласования как фактора. Добавление ослабления – это прием снижения неопределенности измерений, который хорошо работает в случае, если исследуемый нами сигнал значительно возвышается над уровнем шума. При низком же отношении сигнал/шум (обычно ≤7 дБ), добавление ослабления, наоборот, увеличит неопределенность измерения, поскольку мощность шума даст вклад в мощность сигнала, что выльется в ошибочно высокие показания.
Обратимся ко входному аттенюатору. Некоторые относительные измерения производятся с различными установками аттенюатора. В таких случаях мы должны учитывать неопределенность переключения входного ослабления. Поскольку радиочастотный входной аттенюатор должен работать во всем частотном диапазоне анализатора, его точность установки ослабления зависит от частоты. Аттенюатор также вносит вклад в общую частотную характеристику. Так, на частоте 1 ГГц показатели аттенюатора ожидаемо хороши; на частоте 26 ГГц они заведомо хуже.
Следующий узел на пути прохождения сигнала – это входной фильтр. В анализаторах спектра используется фиксированный низкочастотный фильтр в нижнем поддиапазоне, и перестраиваемый полосовой фильтр, именуемый преселектором (подробнее речь о нем пойдет в Главе 7), в верхнем поддиапазоне. У ФНЧ частотная характеристика лучше, чем у преселектора, и вклад его в неопределенность частотной характеристики мал. Преселектор – обычно перестраиваемый ЖИГ-фильтр – обладает более значительными изменениями частотной характеристики в диапазоне от 1.5 дБ до 3 дБ на частотах миллиметровых волн.
Следом за входным фильтром идут смеситель и гетеродин, оба они вносят вклад в неопределенность частотной характеристики. На Рис. 4-2 показано, как может выглядеть частотная характеристика в одной частотной полосе. Частотную характеристику обычно описывают как ±Х дБ относительно средней точки между экстремумами*. Частотная характеристика анализатора спектра представляет собой характеристику всей системы, складывающуюся из равномерности характеристик и взаимодействия между различными узлами тракта сигнала вплоть до первого смесителя включительно. Анализаторы спектра СВЧ сигналов используют более одной частотной полосы для достижения частот выше 3 ГГц. Это осуществляется благодаря использованию высшей гармоники гетеродина, что будет подробнее рассмотрено в Главе 7. При проведении относительных измерений между сигналами в разных полосах частот, необходимо складывать частотные характеристики каждой полосы, чтобы определить суммарную неопределенность частотной характеристики. Вдобавок, у некоторых анализаторов есть еще и неопределенность переключения между полосами, которую также нужно добавлять в общую неопределенность измерений.
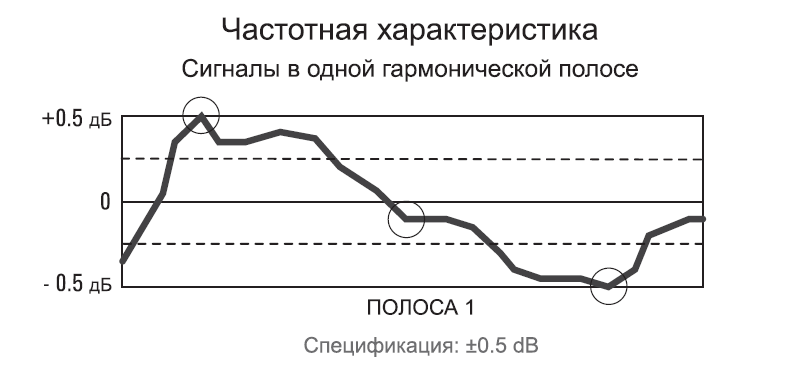
После того, как входной сигнал преобразован в сигнал ПЧ, он проходит через усилитель ПЧ и аттенюатор ПЧ, которые настроены так, чтобы скомпенсировать изменения в установках радиочастотного аттенюатора и потери преобразования смесителя. Таким образом, амплитуды входного сигнала соотносятся с верхней отметкой координатной сетки дисплея, известной как опорный уровень. Усилитель и аттенюатор ПЧ работают только на одной частоте, и, потому, не вносят вклада в частотную характеристику. Однако всегда есть некоторая амплитудная неопределенность, обусловленная точностью их настройки на желаемое значение. Эта неопределенность называется неопределенностью опорного уровня.
Другой параметр, который мы можем изменять во время измерений, — это полоса разрешения. У разных фильтров значение вносимых потерь разное. В общем случае, наибольшую разницу можно увидеть при переключении от LC-фильтров (используемых для широких полос разрешения) к кварцевым фильтрам (применяющимся при узких полосах). Это является источником неопределенности переключения полос разрешения.
Чаще всего сигнал на анализаторе спектра отображают в логарифмическом масштабе амплитуды, например, 10 дБ на деление или 1 дБ на деление. Это значит, что обычно сигнал ПЧ проходит через логарифмический усилитель. Передаточная характеристика логарифмического усилителя лишь аппроксимирует логарифмическую кривую. Так что любое отклонение от идеальной логарифмической характеристики дает вклад в неопределенность амплитуды. Аналогично, когда анализатор спектра находится в режиме линейной шкалы, характеристика усилителя так же не идеально линейная. Этот тип неопределенности называется достоверностью масштаба отображения.
Относительная неопределенность
Когда мы проводим относительные измерения входного сигнала, мы используем либо какую-то часть этого же сигнала, либо другой сигнал в качестве опорного. Например, когда мы проводим измерения гармонических искажений второго порядка, мы используем сигнал основной частоты в качестве опорного сигнала. Абсолютные значения в расчет не принимаются; нас интересует лишь то, насколько вторая гармоника отличается от сигнала основной частоты по амплитуде.
В худшем возможном случае при относительном измерении, сигнал основной частоты может находиться в наивысшей точке частотной характеристики, в то время как гармоника, которую мы хотим измерить, находится в низшей ее точке. Равновероятна и обратная ситуация. Поэтому, если величина относительной частотной характеристики равна ±0.5 дБ, как показано на Рис. 4-2, то суммарная неопределенность будет вдвое больше, то есть ±1 дБ.
Может случиться, что два исследуемых сигнала окажутся в разных частотных полосах анализатора спектра. В этом случае тщательный анализ суммарной неопределенности должен учитывать сумму неопределенностей равномерности обеих частотных полос.
Другими неопределенностями – такими, как неопределенность переключения полос разрешения, — можно пренебречь при проведении относительных измерений, поскольку они одинаково воздействуют на оба сигнала.
Абсолютная точность измерения амплитуды
Почти все анализаторы спектра обладают встроенным калиброванным источником, который обеспечивает опорный сигнал заданной частоты и амплитуды. Затем мы уже полагаемся на относительную точность анализатора, переносящего абсолютную калибровку опорного сигнала на другие частоты и амплитуды. В спецификациях анализаторов часто указана величина абсолютной частотной характеристики, где нулевая точка на кривой равномерности соотносится с этим калибровочным сигналом. Во многих анализаторах фирмы Agilent используется опорный сигнал в 50 МГц. На этой частоте заявленная абсолютная точность измерения амплитуды чрезвычайно хороша: ±0.34 дБ для серии ESA-E и ±0.24 дБ для серии PSA.
Лучше всего всегда рассматривать все известные неопределенности, и только потом решать, какими из них можно пренебречь при определенных типах измерений. Набор значений в Табл. 4-1 представляет собой заявленные спецификации нескольких различных анализаторов спектра.
Некоторые из этих спецификаций – например, частотная характеристика, — зависят от диапазона частот. 3-гигагерцовый радиочастотный анализатор может иметь частотную характеристику ±0.38 дБ, в то время как СВЧ-анализатор, работающий до 26 ГГц, может иметь частотную характеристику ±2.5 дБ или даже больше. С другой стороны, некоторые источники неопределенностей, такие как переключение полос разрешения, одинаково применимы ко всем частотам.

Уменьшение общей неопределенности
Взглянув первый раз на общую неопределенность измерений, мы можем не на шутку встревожиться, суммируя значения неопределенностей. Самый неблагоприятный случай предполагает, что все источники неопределенностей вашего анализатора вносят самый свой максимальный вклад, действуют одновременно и с одинаковым знаком. Но поскольку источники неопределенности можно считать независимыми переменными, то скорее всего, некоторые неопределенности будут положительными, в то время как другие — отрицательными. Поэтому обычно вычисляют среднеквадратичную ошибку.
Независимо от того, находим ли мы среднеквадратичную ошибку или ошибку самого худшего случая, есть несколько способов улучшить ситуацию с неопределенностями. Во-первых, мы должны изучить спецификации нашего конкретного анализатора. Эти заявленные спецификации вполне могут оказаться приемлемыми в том диапазоне, в котором мы собираемся измерять. Если же нет, то Табл. 4-1 может нам помочь улучшить точность.
Прежде чем снимать какие-то данные, можно мысленно пройтись по этапам нашего измерения и выяснить, какие настройки могут обойтись без переключений. Мы вполне можем обнаружить, что возможно провести измерение без изменения установок радиочастотного аттенюатора, полосы разрешения или опорного уровня. Если так, то все неопределенности, связанные с изменением данных настроек, не учитываются. Мы вполне можем пожертвовать точностью опорного уровня в угоду достоверности отображения и наоборот, используя то, что в данном случае обеспечит высшую точность, и пренебрегая остальным как источником неопределенности вообще. Мы даже можем обойти неопределенность частотной характеристики, если не сочтем за труд промерить и охарактеризовать наш конкретный анализатор2. Осуществить это можно при помощи измерителя мощности, сравнивая показания анализатора спектра на интересующих нас частотах и показания измерителя мощности.
2. Если мы это проделаем, то может возрасти роль неопределенности входного рассогласования.
То же самое относится к калибратору. Если у нас есть более точный калибратор, или более близкий к интересующей нас частоте, мы вполне можем воспользоваться им, а не встроенным калибратором. Наконец, у многих нынешних анализаторов есть процедура автокалибровки. Эта процедура генерирует коэффициенты неопределенностей (например, изменение амплитуды в зависимости от полосы разрешения), которые в дальнейшем используются анализатором для коррекции полученных данных. В результате, автокалибровка позволяет проводить хорошие амплитудные измерения и дает больше свободы в изменении настроек анализатора во время измерений.
Спецификации, типичные технические характеристики и номинальные значения
При оценке точности анализатора спектра, очень важно понимать значение различных величин, указанных в документации прибора. Agilent Technologies определяет три класса данных о характеристиках прибора:
Спецификации: описывают параметры, которые покрываются гарантийными обязательствами при работе прибора в диапазоне температур от 0° до +55°С (если не указано иное). Каждый прибор протестирован на предмет соответствия спецификации, причем в расчет берется неопределенность измерения того оборудования, с помощью которого проводится тестирование. 100% протестированных приборов будут отвечать требованиям спецификации.
Некоторые производители измерительного оборудования используют подход
«2 сигма», или доверительный инетрвал 95% в оценке некоторых спецификаций прибора. Поэтому при сравнении данных документации от приборов различных производителей очень важно убедиться, что вы сравниваете одинаково оцененные производителями параметры, прежде чем делать выводы.
Типичные технические характеристики: содержат дополнительные данные о рабочих параметрах продукта, которые не покрываются гарантийным обязательством. Это рабочие параметры, лежащие за пределами заявленных в спецификации значений, которыми будут обладать 80% приборов с 95% вероятностью, при уровне температур от +20° до +30°С. Типичные технические характеристики не включают в себя неопределенности измерений. При производстве все приборы проверяются на типичные характеристики.
Номинальные значения: указывают ожидаемые характеристики, либо описывают показатели прибора, знать которые при его использовании полезно, но не покрываемые гарантийным обязательством. Тестов номинальных значений при производстве приборов обычно не осуществляют.
Цифровая секция ПЧ
Как было показано ранее, цифровая архитектура ПЧ устраняет или минимизирует многие из неопределенностей, свойственных аналоговым анализаторам спектра. Как то:
Точность опорного уровня (неопределенность усиления ПЧ)
Анализаторы спектра с полностью цифровой ПЧ, такие как приборы серии PSA от Agilent, не имеют усиления ПЧ, которое изменяет опорный уровень. Поэтому в данном случае такой неопределенности просто нет.
Достоверность масштаба отображения
Цифровая архитектура ПЧ не включает в себя логарифмический усилитель. Вместо этого функция логарифмирования осуществляется математически, и традиционной неопределенности достоверности логарифмического представления нет. Однако в неопределенность масштаба отображения вносят вклад иные факторы: радиочастотное сжатие (особенно для входных сигналов выше -20 дБм), точность расположения диапазона усиления АЦП и линейность АЦП (или ошибка квантования). Ошибку квантования можно улучшить добавлением шума, который сглаживает среднее значение передаточной функции АЦП. Этот дополнительный шум называют дифер (или подмешиваемый сигнал). Добавление шума улучшает линейность, но при этом слегка ухудшает отображаемый средний уровень шума. При использовании приборов серии PSA обычно рекомендуется сглаживание, если у измеряемого сигнала соотношение сигнал/шум больше или равно 10 дБ. Если это соотношение меньше 10 дБ, ухудшение точности любого единичного измерения (то есть без усреднения) из-за поднятия уровня шума становится значительнее, чем проблема линейности, которую таким способом решают, поэтому сглаживание лучше выключить.
Неопределенность переключения полос разрешения
Цифровая ПЧ у приборов серии PSA включает в себя аналоговый предварительный фильтр с полосой в 2.5 раза шире, чем желаемая полоса разрешения. У этого предварительного фильтра есть неопределенность ширины полосы, усиления и центральной частоты как функции установки полосы разрешения. Остальная фильтрация по полосе разрешения происходит уже в цифровом формате в специализированной ИС в цифровой секции ПЧ. Хотя цифровые фильтры не идеальны, они, тем не менее, отличаются высокой повторяемостью. Вдобавок, применяется некоторая компенсация для минимизации ошибки. Все это выражается в значительном общем улучшении неопределенности переключения полос разрешения по сравнению с аналоговыми приборами.
Примеры
Давайте рассмотрим некоторые амплитудные неопределенности на примерах различных измерений. Допустим, нам нужно измерить радиочастотный сигнал 1 ГГц с амплитудой -20 дБм. Если мы работаем с анализатором E4402B серии ESA-E с установками: ослабление = 10 дБ, полоса разрешения = 1 кГц, видеополоса = 1 кГц, полоса обзора = 20 кГц, опорный уровень = -20 дБм, включен логарифмический масштаб отображения, используется автоматическая установка времени развертки, а окружающая температура лежит в пределах от +20° до +30°С, то, исходя из спецификаций, абсолютная неопределенность измерения будет ±0.54 дБ плюс модуль частотной характеристики. У анализатора E4440A серии PSA при измерении того же сигнала с теми же установками неопределенность будет равна ±0.24 дБ плюс модуль частотной характеристики. Эти значения сведены в Табл. 4-2.
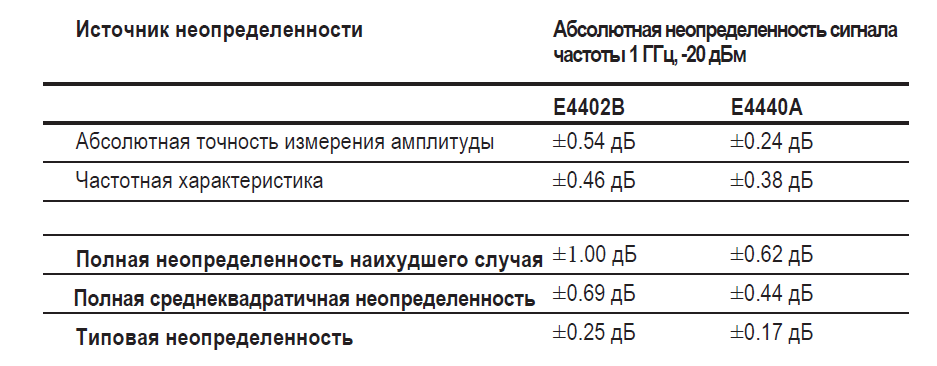
С ростом частоты возрастают и неопределенности. В этом примере мы хотим измерить сигнал на частоте 10 ГГц с амплитудой -10 дБм. Вдобавок, мы хотим измерить вторую гармонику на частоте 20 ГГц. Предположим, что условия измерения следующие: окружающая температура от 0° до +55°С, полоса разрешения = 300 кГц, ослабление = 10 дБ, опорный уровень = -10 дБм. В Табл. 4-3 приводится сравнение абсолютной и относительной амплитудных неопределенностей двух анализаторов спектра от фирмы Agilent: 8563EC (аналоговая ПЧ) и E4440A PSA (цифровая ПЧ).
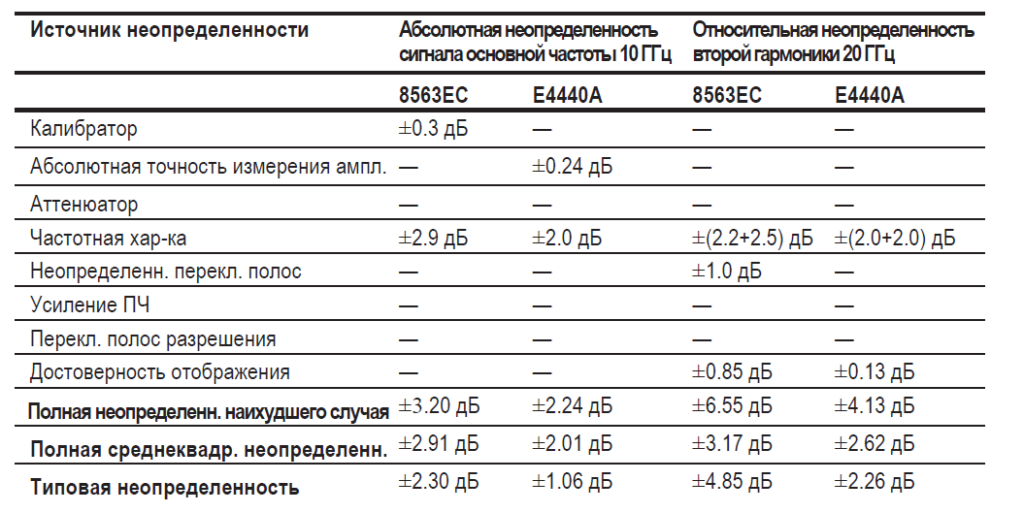
Точность измерения частоты
До сих пор мы говорили практически только об амплитудных измерениях. Что же насчет измерений частоты? Тут мы снова можем выделить две основные категории: абсолютные и относительные измерения частоты. Абсолютные измерения проводятся с целью узнать частоты конкретных сигналов. Как, например, когда мы хотим измерить сигнал радиовещания, чтобы убедиться, что станция передает на предписанной ей частоте. Абсолютные измерения также применяются для анализа нежелательных сигналов, например, при исследовании паразитной помехи. Относительные измерения, с другой стороны, удобны для того, чтобы узнать, как далеко друг от друга отстоят спектральные компоненты, или какова частота модуляции.
До конца 70-х годов абсолютная неопределенность частоты измерялась в мегагерцах, поскольку первыми гетеродинами были высокочастотные генераторы, работавшие выше радиочастотного диапазона анализатора, и попыток связать гетеродин с более точным опорным генератором не предпринималось. Современные анализаторы спектра в качестве гетеродина используют синтезаторы частот, что обеспечивает более высокую точность. Абсолютная неопределенность частоты обычно описывается как спецификация точности замера частоты, и относится к центральной, начальной, конечной частотам и частотам маркеров.
С появлением прибора Agilent 8568А в 1977 году, впервые в инструментах общего назначения стала доступна счетчикоподобная точность частоты, а для уменьшения дрейфа стали применяться термостатированные генераторы. С течением времени в приборах всех ценовых диапазонов появились кварцевые опорные генераторы и гетеродины с различными формами косвенного синтеза. Самое общее определение косвенного синтеза — это некий способ задания частоты генератора при помощи опорного генератора. Сюда входят такие технологии как фазовая автоподстройка частоты, частотная дискриминация и автоподстройка с помощью счетчика.
Что нас интересует – так это эффект, который все эти изменения произвели на частотную точность (и дрейф). Типичная точность показаний может быть определена следующим образом:
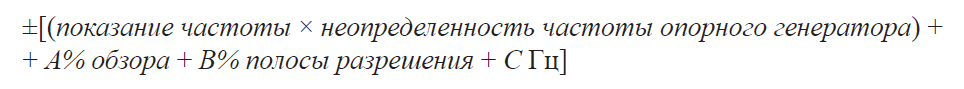
Обратите внимание, что мы не можем определить конкретную неопределенность частоты без хоть какой-нибудь информации очастоте опорного генератора. В большинстве случаев нам известна годовая степень старения, например, ±1·10-7 в год, хотя иногда старение определяют за более короткий период (±5·10-10 в день). Вдобавок, мы должны знать, когда последний раз подстраивался генератор и как близко он был установлен к своей номинальной частоте (обычно 10 МГц). Есть и другие факторы, которые мы обычно упускаем из виду, когда определяем неопределенность частоты: например, то, как долго генератор находится в рабочем состоянии. Многим генераторам требуется от 24 до 72 часов работы, чтобы достичь заявленного в спецификации уровня дрейфа. Чтобы минимизировать этот эффект, некоторые анализаторы спектра подают питание на свои опорные генераторы все то время, которое прибор подключен к сети электропитания. В этом случае прибор не «отключен», а, скорее, находится в режиме «ожидания». Также следует иметь в виду температурную стабильность, поскольку она может быть хуже, чем уровень дрейфа. Короче говоря, существует множество факторов, которые надо принимать в расчет при определении частотной неопределенности.
На производстве обычно имеется лабораторный стандарт частоты, который возможно трассировать вплоть до национального стандарта. Большинство анализаторов со встроенными опорными генераторами имеют возможность подключения внешних источников опорного сигнала. В таком случае, в нижеприведенном выражении неопределенность частоты опорного генератора становится ошибкой производственного стандарта.
При проведении относительных измерений в игру вступает точность полосы обзора. Для анализаторов фирмы Agilent точность обзора означает неопределенность в отображении на дисплее расстояния между двумя любыми спектральными компонентами. Для примера, положим точность полосы обзора в 0.5% от ширины обзора, и пусть два сигнала разделены между собой двумя делениями при обзоре в 1 МГц (100кГц на деление). Неопределенность разнесения сигналов будет 5 кГц. Неопределенность будет той же, если использовать дельта-маркеры, и разница их показаний будет 200 кГц. Поэтому результатом измерения будет 200 кГц ±5 кГц.
При проведении измерений в полевых условиях мы обычно хотели бы включить анализатор, выполнить измерения, и сняться с места как можно скорее. В таких случаях полезно знать, как ведет себя опорный генератор при условии короткого времени разогрева. Например, портативные приборы серии ESA-E фирмы Agilent приходят в соответствие с заявленными спецификациями после пяти минут прогрева.
В большинстве анализаторов спектра есть маркеры, которые могут быть установлены на отображаемый сигнал, чтобы дать нам абсолютную амплитуду и абсолютную частоту. Однако, отображаемая частота маркера является функцией частотной калибровки дисплея, положения маркера на дисплее и выбранного количества дисплейных точек. Вдобавок, чтобы добиться максимальной точности частоты, мы должны поместить маркер строго на пик отклика спектральной компоненты. Если мы установим маркер на какую-то другую точку отображаемого отклика, то получим другое значение частоты. Для повышения точности мы можем сузить полосу обзора и полосу разрешения, чтобы минимизировать их влияние, и тогда поместить маркер на пик отклика станет проще.
У многих анализаторов есть режимы маркера, в которых задействованы схемы внутренних счетчиков для устранения влияния полосы обзора и полосы разрешения на частотную точность. Счетчик не считает непосредственно входной сигнал, а вместо этого считает сигнал ПЧ и, возможно, один или несколько сигналов гетеродина, а процессор уже вычисляет частоту входного сигнала. Чтобы устранить шум как фактор при счете, требуется минимальное отношение «сигнал/шум». Счет сигнала на ПЧ также устраняет необходимость помещения маркера непосредственно на пик экранного отклика. Если используется функция отсчета маркера, то достаточно расположить маркер в любом месте отклика, значительно отличающемся от шума. Точность счета маркера можно выразить как:

С неопределенностью частоты опорного генератора все равно приходится иметь дело, как указывалось ранее. Разрешение счетчика подразумевает наименьший значимый разряд в значении счета – фактор, присущий любому простому частотному счетчику. Некоторые анализаторы допускают использование режима со счетом с дельта-маркерами. В этом случае влияние разрешения счетчика и фиксированной частоты удваивается.
Глава 5 Чувствительность и шум
Чувствительность
Одно из основных применений анализаторов спектра – выделить и измерить сигнал низкого уровня. Ограничением при такого рода измерениях является шум, генерируемый внутри самого анализатора. Этот шум, порождаемый случайным движением электронов внутри различных элементов цепей, увеличивается несколькими ступенями усиления анализатора и, в конце концов, отображается на дисплее как шумовой сигнал. В терминах анализатора спектра этот шум обычно называют средним уровнем собственных шумов (отображаемым средним уровнем шума, DANL)1. И хотя существуют методики, позволяющие измерить сигналы, находящиеся даже чуть ниже этого уровня, по большому счету мощность этого шума является непреодолимым ограничением нашей возможности проводить измерения сигналов с низким уровнем.
- Термин «средний уровень собственных шумов» иногда путают с «чувствительностью». Хоть эти два понятия и связаны, смысл у них все же различен. Чувствительность – это мера минимального уровня сигнала, дающего заданное отношение сигнал/шум или заданный коэффициент битовой ошибки. Спецификации анализаторов спектра всегда даются в терминах среднего уровня собственных шумов.
Давайте допустим, что ко входу анализатора спектра подключена 50-омная нагрузка, чтобы предотвратить попадание в анализатор любых нежелательных сигналов. Эта пассивная нагрузка генерирует небольшое количество шумовой энергии, равное kTB ,

Поскольку полная мощность шума зависит от полосы измерения, это значение обычно нормируют на 1 Гц полосы. Таким образом, при комнатной температуре плотность мощности шума равна -174 дБм/Гц. Когда этот шум достигает первой ступени усиления анализатора, усилитель увеличивает шум и добавляет немного своего собственного. По мере прохождения шумового сигнала через систему значение его амплитуды остается довольно значительным, так что шум, генерируемый в последующих ступенях усиления, дает очень малый вклад в полную мощность шума. Следует отметить, что между входным разъемом анализатора и первой ступенью усиления есть входной аттенюатор и один или несколько смесителей, и все эти узлы также генерируют шум. Однако, значение генерируемого ими шума либо равно, либо достаточно близко к абсолютному минимуму -174 дБм/Гц, поэтому значительного влияния на уровень шума, поступающего на первую ступень усиления, они не оказывают.
Хотя входной аттенюатор, смеситель и другие элементы цепи между входным разъемом анализатора и первой ступенью усиления очень слабо влияют на фактический шум системы, они, тем не менее, серьезно влияют на способность анализатора отображать сигналы низкого уровня, поскольку они ослабляют входной сигнал. Таким образом, они уменьшают соотношение сигнал/шум и тем самым ухудшают чувствительность.
Мы можем определить уровень собственных шумов, просто глядя на уровень, отображаемый на дисплее, когда вход анализатора нагружен на 50 Ом. Этот уровень есть уровень собственных шумов анализатора. Сигналы более низкого уровня скрываются шумом, и увидеть их нельзя. Однако уровень собственных шумов не является фактическим уровнем шума на входе, а представляет собой скорее эффективный шумовой уровень. Дисплей анализатора настроен на отображение уровня сигнала на входе анализатора, так что уровень собственных шумов представляет некий фиктивный – или эффективный – шумовой фон на входе.
Фактический шум системы на входе зависит от входного сигнала. И конечно же, иногда сам шум и является интересующим нас сигналом. Как и любой другой сигнал, шумовой сигнал гораздо легче измерить, если он находится намного выше эффективного (собственного) шумового фона. Эффективный шумовой фон включает в себя потери, вносимые входным аттенюатором, потери при смешении, и потери в прочих элементах цепи, стоящих до первой ступени усиления. С потерями преобразования смесителя мы ничего не можем поделать, зато мы можем изменить входной радиочастотный аттенюатор. Это дает нам возможность управлять уровнем входного сигнала, поступающего на первый смеситель, и тем самым менять отображаемое соотношение сигнал/шум. Разумеется, наименьшее значение уровня собственных шумов мы получим, избрав минимальное (нулевое) радиочастотное ослабление.
Поскольку входной аттенюатор никак не влиял на фактический шум, генерируемый в системе, у некоторых ранних моделей анализаторов отображаемый средний уровень шума просто оставался в одном и том же положении, независимо от установки входного ослабления. То есть усиление ПЧ оставалось постоянным. В этом случае входной аттенюатор влиял на положение истинного входного сигнала на дисплее. По мере увеличения входного ослабления, уменьшающего уровень входного сигнала, положение сигнала на дисплее опускалось ниже, в то время как шум оставался на своем месте.
Начиная с конца 70-х годов, конструкторы анализаторов спектра применили иной подход. В новых анализаторах внутренний микропроцессор изменяет усиление ПЧ, чтобы компенсировать изменения во входном аттенюаторе. Таким образом, сигнал, поступающий на вход анализатора, не меняет своего положения на дисплее при изменении входного ослабления, в то время как отображаемый средний уровень шума движется вверх-вниз. В этом случае опорный уровень остается неизменным. Это проиллюстрировано на Рис. 5-1. При увеличении ослабления от 5 до 15 и 25 дБ, отображаемый шум поднимается, а сигнал -30 дБ остается неизменным. В любом случае, наилучшее соотношение сигнал/шум мы получим, избрав наименьшее входное ослабление.
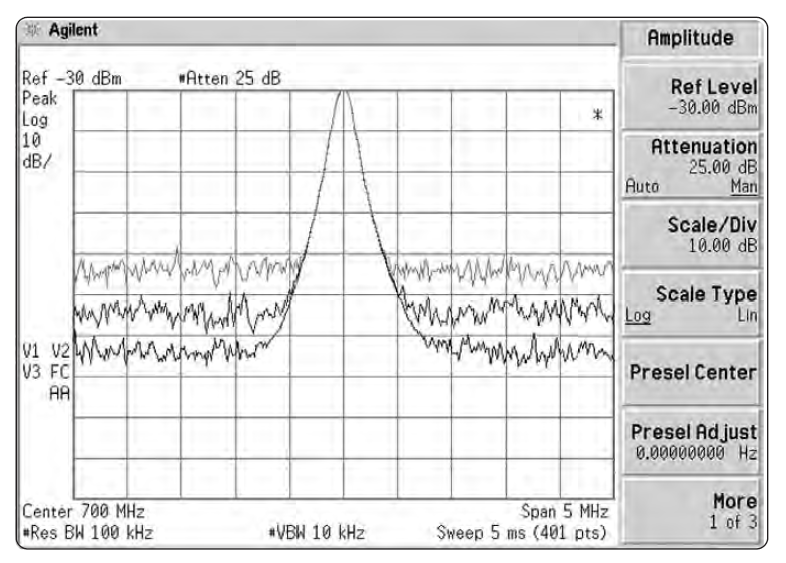
Полоса разрешения тоже влияет на отношение сигнал/шум, или на чувствительность. Внутренний шум анализатора, случаен и обладает постоянной амплитудой в широком диапазоне частот. Поскольку разрешающие фильтры, или фильтры ПЧ, установлены после первой ступени усиления, полная мощность шума, проходящая через фильтры, определяется шириной полос этих фильтров. Далее этот шумовой сигнал детектируется и отображается на дисплее. Случайная природа шумового сигнала заставляет отображаемый уровень изменяться как

Так, если мы изменим полосу разрешения в десять раз, отображаемый средний уровень шума изменится на 10 дБ, как показано на Рис. 5-2. Для гармонических сигналов мы получим наилучшее отношение сигнал/шум, или наилучшую чувствительность, используя минимальную полосу разрешения из доступных в нашем анализаторе2.
2. Широкополосные импульсные сигналы могут демонстрировать совершенно обратное поведение, когда отношение сигнал/шум будет расти с увеличением полосы.)
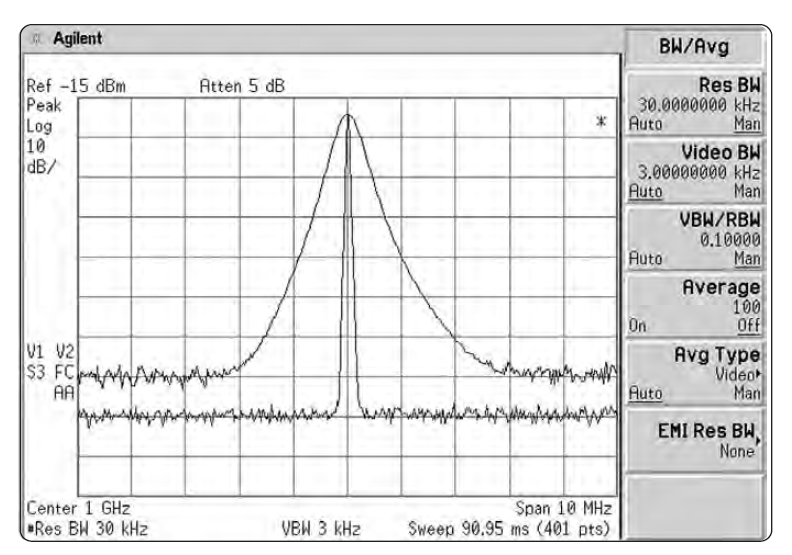
Анализатор спектра отображает сумму шума и сигнала, и поэтому при малом отношении сигнал/шум становится очень трудно различить собственно сигнал. Ранее мы отмечали, что можно использовать видеофильтр для уменьшения флуктуаций амплитуды зашумленных сигналов, не оказывая при этом особого влияния на постоянный сигнал. Рис. 5-3 иллюстрирует то, как видеофильтр может помочь нам различить низкоуровневый сигнал. Следует отметить, что видеофильтр не оказывает влияния на средний уровень собственных шумов и потому не влияет на чувствительность анализатора.
В итоге, наилучшей чувствительности по отношению к узкополосным сигналам можно достичь выбором минимальной полосы разрешения и минимального входного ослабления. Также можно выбрать минимальную видеополосу, чтобы различить сигнал, находящийся на уровне шума или близко к нему3. Разумеется, выбор узкой полосы разрешения и видеополосы увеличивает время развертки.
3. О влиянии шума на точность см. Динамический диапазон в зависимости от неопределенности измерения в Главе 6.
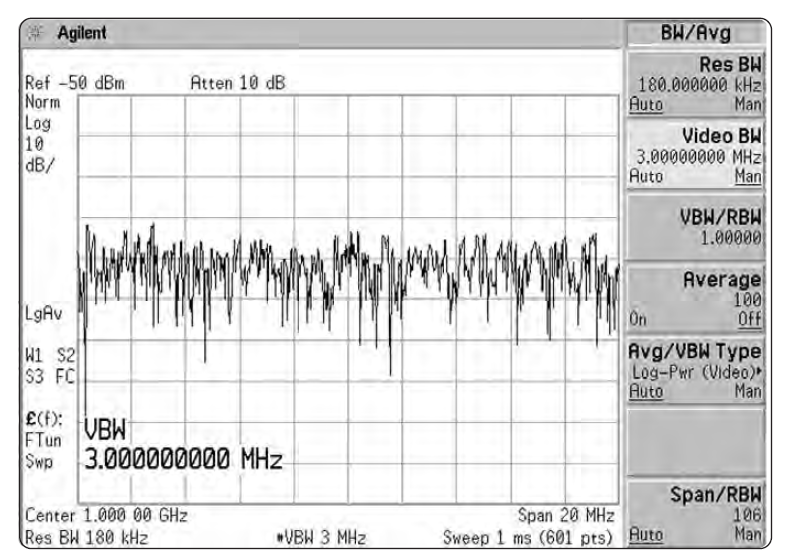
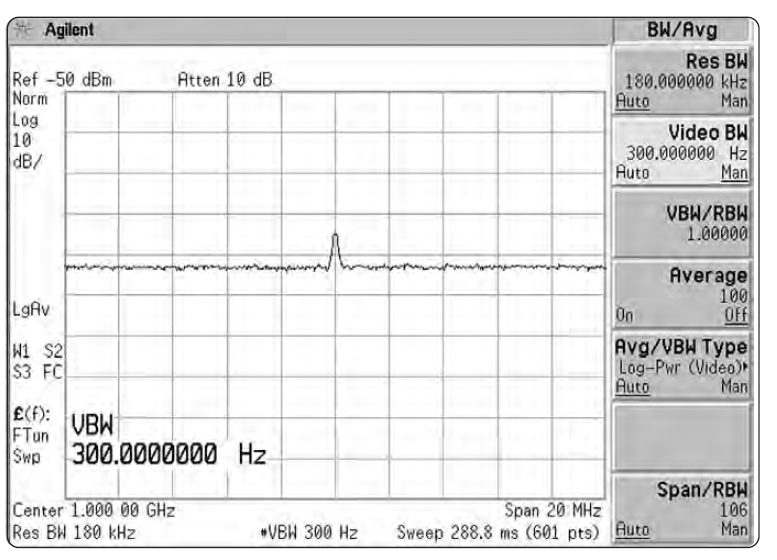
Коэффициент шума
Многие производители описывают эффективность своих приемников в терминах коэффициента шума, а не чувствительности. Как мы увидим, оба эти способа эквивалентны. Анализатор спектра — это приемник, поэтому мы рассмотрим его коэффициент шума на примере синусоидального входного сигнала.
Коэффициент шума можно определить как ухудшение отношения сигнал-шум при прохождении сигнала через прибор, в нашем случае – через анализатор. Мы можем выразить коэффициент шума как

Это выражение можно упростить для случая анализатора спектра. Во-первых, выходной сигнал равен входному, умноженному на коэффициент усиления анализатора. Во-вторых, усиление нашего анализатора есть единица, поскольку уровень сигнала на выходе (показанный на дисплее) тот же, что и на входе (на входном разъеме). Поэтому в нашем случае, после подстановки, приведения подобных и упорядочивания, коэффициент шума становится таким:

Это выражение говорит нам, что все, что мы должны сделать, чтобы определить коэффициент шума, это сравнить уровень шума, как он считывается с дисплея, с истинным (не эффективным) шумовым уровнем на входном разъеме.
Коэффициент шума обычно выражается в терминах дБ, то есть:
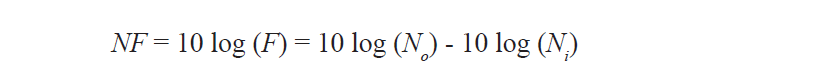
Мы используем истинный шумовой уровень на входе, а не эффективный шумовой уровень, поскольку наше отношение сигнал-шум было основано на истинном входном шуме. Как мы определили ранее, когда вход нагружен на 50 Ом, уровень kTB шума при комнатной температуре в полосе 1 Гц равен -174 дБм.
Мы знаем, что средний уровень собственных шумов анализатора меняется с полосой. Поэтому все, что мы должны сделать, чтобы определить коэффициент шума нашего спектроанализатора, это измерить шумовую мощность в некоторой полосе и пересчитать ее на полосу в один Гц, используя вышеприведенную формулу 10 log (BW2/BW1), а затем сравнить результат с величиной –174 дБм.
Например, если мы измерили –110 дБм при разрешающей полосе 10 кГц, мы имеем:

Коэффициент шума не зависит от полосы4. Выбери мы другую полосу разрешения, результат у нас получился бы все равно тот же самый. Например, если бы мы выбрали полосу разрешения в 1 кГц, измеренный шум был бы -120 дБм, а 10 log(RBW/1) был бы 30. Подставив эти значения, мы получим -120 – 30 + 174 = 24 дБ, тот же коэффициент, что и прежде.
4. Не для всякого анализатора это утверждение безоговорочно верно из-за различного способа распределения секций разрешающих фильтров и усиления в цепи ПЧ.
Коэффициент шума в 24 дБ в нашем примере говорит нам, что синусоидальный сигнал должен быть на 24 дБ выше kTB , чтобы сравняться со средним уровнем собственных шумов на этом конкретном анализаторе. Таким образом мы можем использовать коэффициент шума для определения среднего уровня собственных шумов для заданной полосы, или чтобы сравнить средние уровни собственных шумов разных анализаторов в одной полосе5.
5. Вычисленный подобным образом коэффициент шума нельзя непосредственно сравнивать с коэффициентом шума приемника, поскольку «измеренный шум» в уравнении меньше действительного шума на 2.5 дБ. См. пункт Шум как сигнал далее в этой главе.
Предусилители
Одна из причин введения коэффициента шума состоит в том, что он помогает определить, как много выгоды мы можем получить от использования предусилителя. Несмотря на то, что коэффициент шума 24 дБ хорош для анализатора спектра, он не очень хорош для соответствующего приемника. Однако, помещая подходящий предусилитель до анализатора спектра, мы можем получить систему (предусилитель/анализатор), коэффициент шума которой ниже, чем у только анализатора. В той мере, в какой мы понижаем коэффициент шума, мы также улучшаем чувствительность системы.
Когда мы выше вводили коэффициент шума, мы делали это на примере синусоидального входного сигнала. Мы изучим выгоды от предусилителя на этом же примере. Однако предусилитель также усиливает шум, и его выходной шум может быть выше, чем эффективный уровень входного шума анализатора. Как мы увидим ниже в разделе Шум как сигнал, анализатор спектра с усреднением логарифма мощности отображает случайный шумовой сигнал на 2.5 дБ ниже действительной величины. Когда мы рассматриваем предусилители, мы должны учесть эти 2.5 дБ там, где необходимо.
Вместо выведения множества формул для определения выгоды, даваемой предусилителем, давайте взглянем на два крайних случая и посмотрим, когда каждый из них может применяться. Во-первых, если шумовая мощность на выходе предусилителя (в полосе равной той, что у анализатора спектра) хотя бы на 15 дБ выше, чем отображаемый средний шумовой уровень анализатора, то коэффициент шума системы примерно на 2.5 дБ ниже коэффициента шума предусилителя. Как мы можем установить, что именно этот случай имеет место? Нужно просто подключить предусилитель к анализатору и отметить, что случилось с шумом на экране. Если шум поднялся на 15 или более дБ, то это и есть указанный случай.
С другой стороны, если шумовая мощность на выходе предусилителя (снова в той же полосе, что у анализатора) на 10 или более дБ меньше, чем средний отображаемый на дисплее анализатора шумовой уровень, то коэффициент шума системы меньше коэффициента шума анализатора на коэффициент усиления предусилителя. Снова мы можем провести проверку. Подключите предусилитель к анализатору; если отображаемый шум не изменится, то это тот случай.
Но тестирование экспериментальным путем предусматривает, что мы имеем нужное оборудование на руках. Нам не надо беспокоиться о цифрах. Мы просто подключаем предусилитель к анализатору, отмечаем средний отображаемый шумовой уровень и вычитаем коэффициент усиления предусилителя. Тогда мы получаем чувствительность системы.
Что мы в действительности хотим, так это знать заранее, что предусилитель для нас сделает. Мы можем сформулировать разобранные выше два случая следующим образом:

Используя эти выражения, мы увидим, как предусилитель влияет на чувствительность. Предположим, что наш анализатор имеет коэффициент шума 24 дБ, а предусилитель обладает коэффициентом усиления 36 дБ и коэффициентом шума 8 дБ. Все, что нам надо сделать, это сравнить усиление плюс коэффициент шума предусилителя с коэффициентом шума анализатора. Усиление плюс коэффициент шума предусилителя равно 44 дБ, и это более чем на 15 дБ превосходит коэффициент шума анализатора, так что коэффициент шума комбинации предусилитель/анализатор тот же, что у предусилителя, но на 2.5 дБ меньше, то есть 5.5 дБ. При полосе разрешения 10 кГц комбинация предусилитель/анализатор имеет чувствительность
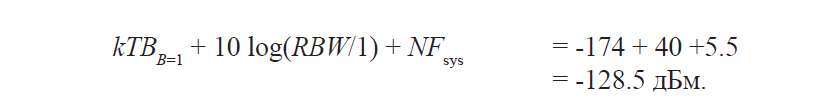
Это дает нам улучшение на 18.5 дБ по сравнению с шумовым фоном в -110 дБм в случае без предусилителя.
Однако, могут быть и отрицательные стороны применения предусилителя в зависимости от конечной цели проведения измерения. Если мы желаем достичь наилучшей чувствительности, но без потерь диапазона измерений, то предусилитель – это неправильный выбор. Рис. 5-4 иллюстрирует этот тезис. Анализатор с коэффициентом шума 24 дБ будет иметь отображаемый средний уровень шума –110 дБм при полосе разрешения 10 кГц. Если 1-дБ точка сжатия для этого анализатора есть 0 дБм, то измерительный динамический диапазон 110 дБ 6. Когда мы подключим предусилитель, мы должны уменьшить максимальный входной сигнал системы в число раз, равное коэффициенту усиления предусилителя, до –36 дБм. Однако когда мы подключаем предусилитель, средний уровень отображаемого шума поднимется на 17.5 дБ, поскольку шумовая мощность на выходе предусилителя именно на столько больше, чем собственный шум анализатора, даже после учета фактора 2.5 дБ. Теперь коэффициент усиления предусилителя надо вычитать именно из этого возросшего уровня шума. При подключенном предусилителе динамический диапазон измерений составляет 92.5 дБ, то есть на 17.5 дБ меньше, чем без предусилителя. Потери измерительного динамического диапазона равны изменению отображаемого на дисплее шума при подключении предусилителя.
6. См. пункт Сжатие смесителя.
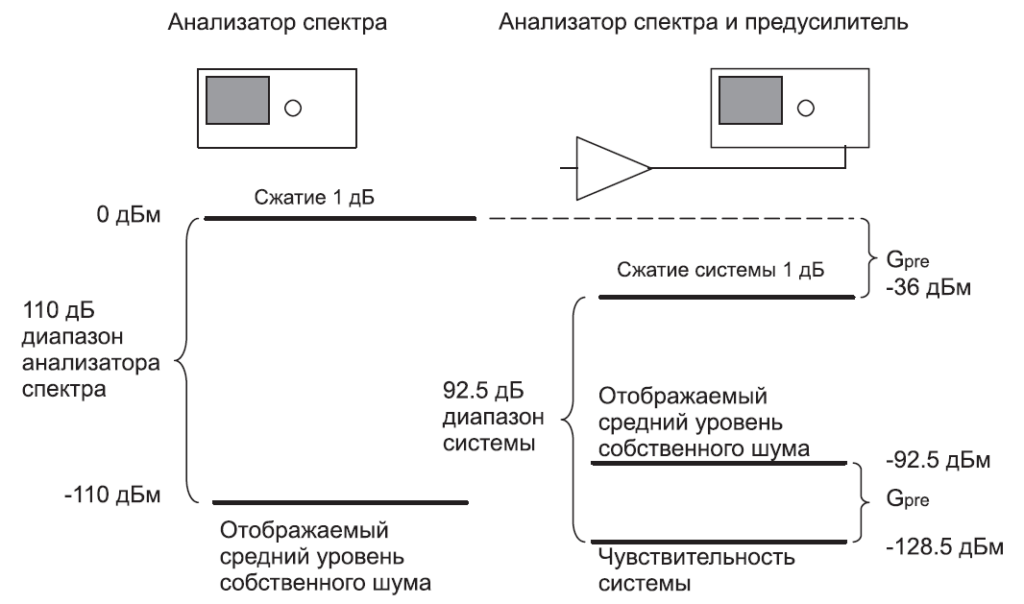
Желание подобрать такой предусилитель, который даст нам улучшение в чувствительности без потери части динамического диапазона измерений, диктует нам необходимость удовлетворения второму из критериев, перечисленных ранее: сумма собственного усиления и коэффициента шума предусилителя должна быть примерно на 10 дБ меньше коэффициента шума анализатора. В этом случае шумовой фон не будет заметно меняться, когда мы подключаем предусилитель, так что, хоть мы и сдвигаем весь диапазон измерения вниз на усиление предусилителя, в конце концов мы остаемся с тем полным динамическим диапазоном, что и вначале.
Чтобы выбрать правильный предусилитель, мы должны оценить наши измерительные нужды. Если мы хотим абсолютно наилучшей чувствительности и не очень беспокоимся по поводу измерительного диапазона, мы должны выбрать предусилитель с высоким усилением и малым коэффициентом шума, так чтобы наша система получила коэффициент шума предусилителя минус 2.5 дБ. Если мы желаем иметь чувствительность получше, но не можем себе позволить потерять никакую часть динамического диапазона, мы должны выбрать предусилитель с более низким усилением.
Достаточно интересно то, что мы можем использовать входной аттенюатор спектроанализатора для эффективного уменьшения его коэффициента шума (или, если хотите, для уменьшения усиления предусилителя). Например, если мы нуждаемся в чуть-чуть лучшей чувствительности, но не хотим жертвовать динамическим диапазоном, мы можем использовать вышеупомянутый предусилитель и радиочастотное ослабление в 30 дБ на входном аттенюаторе анализатора. Это ослабление увеличивает коэффициент шума анализатора с 24 до 54 дБ. Теперь усиление плюс коэффициент шума предусилителя (36+8) на 10 дБ меньше, чем коэффициент шума анализатора, и мы отмечаем выполнение условий второго критерия. Теперь коэффициент шума системы:
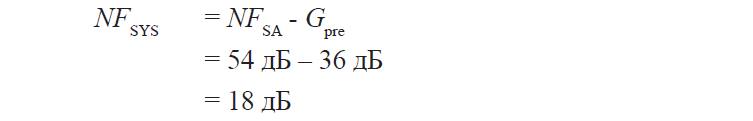
Это дает улучшение коэффициента шума на 6 дБ по сравнению со случаем использования одного только анализатора и 0 дБ входного ослабления. Так мы улучшили на 6 дБ чувствительность и практически не пожертвовали динамическим диапазоном.
Конечно, есть предусилители, которые попадают в промежуток между этими двумя крайними случаями. Рис. 5-5 поможет нам определить коэффициент шума системы, если мы знаем коэффициенты шума анализатора и предусилителя и коэффициент усиления предусилителя. Обратимся к графику на Рис. 5-5, определяя NFpre + Gpre — NFsa . Если значение меньше нуля, мы находим соответствующую точку на пунктирной кривой и смотрим коэффициент шума системы на левой оси ординат, в дБ над уровнем NFsa — Gpre. Если NFpre + Gpre — NFsa величина положительная, мы ищем соответствующую точку на сплошной кривой и смотрим значение коэффициента шума системы на правой оси ординат, выраженное в дБ относительно значения NFpre. Давайте для начала проверим два наших крайних случая.
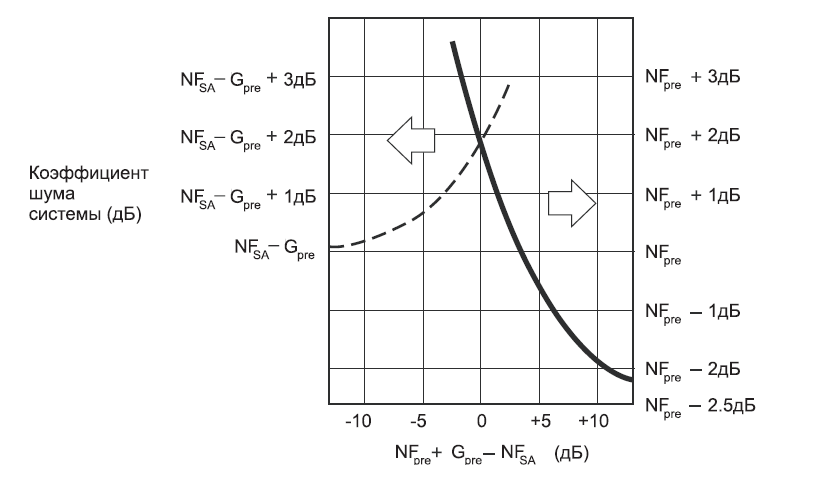
Когда NFpre + Gpre — NFsa становится меньше -10 дБ, мы видим, что коэффициент шума системы асимптотически стремится к NFsa — Gpre. Когда та же величина становится больше +15 дБ, коэффициент шума системы асимптотически приближается к NFpre минус 2.5 дБ.
Теперь давайте рассмотрим два численных примера. Ранее мы предположили, что коэффициент шума нашего анализатора равен 24 дБ. Каков будет коэффициент шума системы, если мы подключим еще и Agilent 8447D, предусилитель с коэффициентом шума примерно 8 дБ и коэффициентом усиления 26 дБ? Сначала определим, что NFpre + Gpre — NFsa равно +10 дБ. Из графика на Рис. 5-5 находим, что коэффициент шума системы примерно NFpre – 1.8 дБ, или около 8 — 1.8 = 6.2 дБ. На графике уже учтен фактор 2.5 дБ. С другой стороны, если усиление предусилителя всего 10 дБ, то NFpre + Gpre — NFpre будет -6 дБ. В этом случае по графику определяем коэффициент шума системы NFsa — Gpre + 0.6 дБ, или 24 – 10 + 0.6 = 14.6 дБ 7. (При определении коэффициента шума отдельного анализатора, проведенном ранее, фактор 2.5 дБ не вводился, поскольку измеренный шум мы снимали непосредственно с дисплея, а отображаемый шум уже учитывает эти 2.5 дБ.)
7. Более подробно о коэффициенте шума см. в документе Agilent Application Note 57-1 “Fundamentals of RF and Microvave Noise Figure Measurements”.
Многие современные анализаторы спектра имеют опциональные встроенные предусилители. По сравнению с подключаемыми предусилителями, встроенные предусилители упрощают измерительное оборудование и исключают необходимость в дополнительных кабелях. Амплитудные измерения гораздо удобнее проводить с использованием встроенного предусилителя, поскольку комбинация предусилитель/анализатор калибруется одновременно как система, и отображаемые на экране амплитудные значения будут соответствующим образом откорректированы. В случае с внешним предусилителем будет необходимо скорректировать показания анализатора путем изменения опорного уровня на величину усиления предусилителя. Многие современные анализаторы спектра позволяют произвести ввод значения усиления предусилителя со своей передней панели. Затем анализатор применяет это введенное значение к отображаемому опорному уровню, так что можно непосредственно наблюдать скорректированные результаты измерения на экране.
Шум как сигнал
Пока что мы рассматривали внутренний шум измерительной системы (анализатор или предусилитель/анализатор). Мы описали, как средний отображаемый средний уровень шума системы ограничивает ее общую чувствительность. Однако, порой тем сигналом, который мы хотим измерить, является случайный шум. Из-за природы шума, супергетеродинный анализатор спектра показывает значение, меньшее, чем истинное значение шума. Давайте посмотрим, почему это так, и что можно сделать, чтобы внести коррекцию.
Под случайным шумом мы понимаем сигнал, чье мгновенное значение во времени имеет гауссово распределение вероятностей, как показано на Рис. 5-6. Например, тепловой шум, или шум Джонсона, обладает таким распределением.
Подобный сигнал не имеет дискретных спектральных компонент, поэтому мы не можем выбрать какую-то конкретную компоненту и измерить ее, чтобы получить представление о величине сигнала. На самом деле, мы должны определить, что мы считаем величиной сигнала. Если мы замерим сигнал в произвольный момент времени, теоретически мы можем получить любую величину. Нам нужна некоторая мера, которая выразит шумовой уровень, усредненный по времени. Мощность и среднее квадратичное отклонение оба удовлетворяют этому требованию.
Мы уже видели, что и видео-фильтрация и видео-усреднение уменьшают размах флуктуаций сигнала и могут дать нам ровную величину. Мы должны приравнять эту величину или к мощности или к среднеквадратичному напряжению. Среднеквадратичная величина гауссовского распределения равна его стандартному отклонению σ.
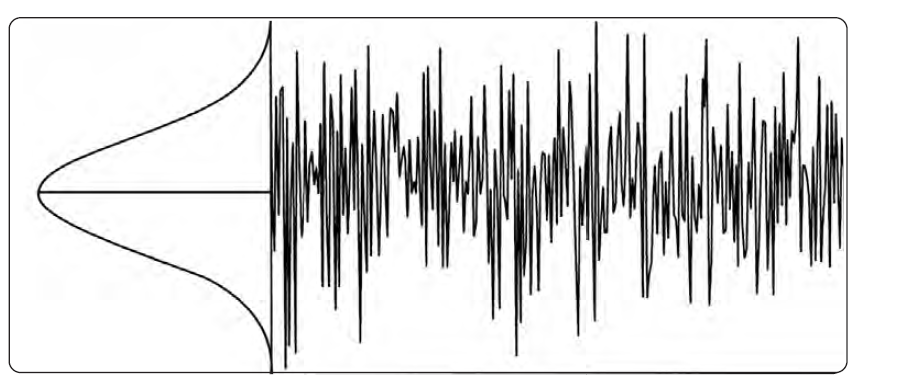
Давайте начнем с анализатора с линейным масштабом дисплея. Гауссовский шум на входе ограничен по полосе после прохождения через цепь ПЧ, и его огибающая принимает форму релеевского распределения (Рис. 5-7).
Шум, который мы видим на дисплее, то есть сигнал с выхода детектора огибающей, есть распределенная по Релею огибающая входного шумового сигнала. Чтобы получить стабильное среднее значение, мы используем видео-фильтрацию для усреднения. Среднее значение распределения Релея равно 1.253 σ.
Но наш анализатор – это пиковый вольтметр, настроенный на отображение среднеквадратичного значения синусоидальной волны. Для перевода пиковых значений в среднеквадратичные, наш анализатор масштабирует свои показания в 0.707 раз (-3 дБ). Среднее значение распределенного по Релею шума масштабируется в той же пропорции, давая нам значение 0.886 σ (1.05 дБ ниже σ). Чтобы приравнять среднее значение, демонстрируемое на дисплее, к среднеквадратичному напряжению входного шумового сигнала, мы должны учесть ошибку в отображаемой величине. Заметим, что ошибка эта не является неопределенностью; это постоянная ошибка, которую можно скорректировать добавлением 1.05 дБ к отображаемой величине.
В большинстве анализаторов спектра масштаб дисплея (логарифмический или линейный по напряжению) определяет масштаб, в котором будет проведено усреднение шумового распределения при помощи видеофильтра или межкадрового усреднения. Обычно анализатор спектра используется с логарифмическим масштабом дисплея, и этот режим вносит добавку в ошибку измерения шума. Усиление логарифмического усилителя является функцией амплитуды сигнала, так что высокие уровни шумового сигнала не усиливаются в одинаковой пропорции с низкими уровнями шумового сигнала. В результате на выходе детектора огибающей будет скошенное распределение Релея, и его среднее значение, полученное видео-фильтрацией или усреднением, будет еще на 1.45 дБ ниже. Получается, что в логарифмическом режиме средний уровень шума отображается на 2.5 дБ ниже. И снова эта ошибка не есть неопределенность, и ее всегда можно скорректировать8.
8. В приборах серии ESA и PSA усреднение может быть переключено в режим усреднения видео, напряжения или мощности (среднеквадратичное), независимо от выбранного режима дисплея. При использовании усреднения мощности поправка не требуется, поскольку среднеквадратичный уровень определяется квадратом амплитуды сигнала, а не логарифмом или огибающей напряжения.
Это и есть тот фактор 2.5 дБ, который мы встретили при недавнем обсуждении предусилителей, в случае, когда выходная мощность шума предусилителя равна или больше величины собственного шума анализатора.
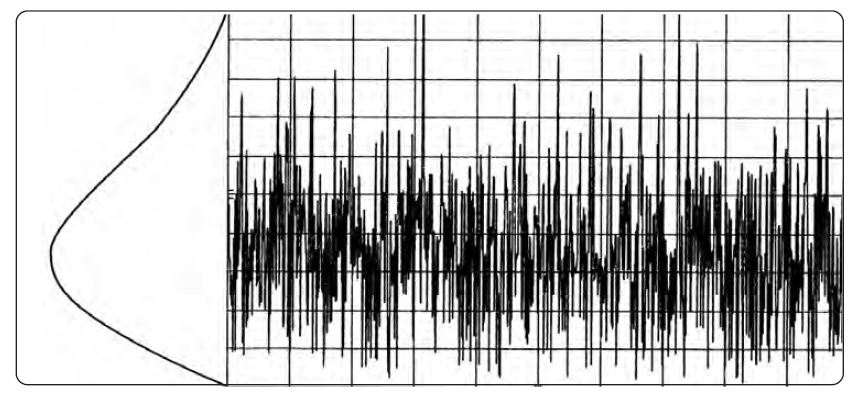
Другим фактором, влияющим на измерения шумовых сигналов, является полоса, в которой производятся измерения. Мы видели, как изменение полосы разрешения влияет на отображаемый уровень внутреннего шума анализатора. Полоса влияет на внешний шумовой сигнал подобным же образом. Чтобы сравнить измерения, сделанные на различных анализаторах, мы должны знать полосу, использованную в каждом случае.
Не только полоса анализатора по уровню 3 дБ (или 6 дБ) влияет на измеряемый шумовой уровень, но и форма АЧХ разрешающего фильтра* также играет некоторую роль. Чтобы сделать сравнения возможными, мы определяем стандартную шумовую полосу: ширину прямоугольного фильтра, который пропускает ту же шумовую мощность, что и фильтр нашего анализатора. Для окологауссовских фильтров анализаторов фирмы Agilent эффективная шумовая полоса в 1.05 – 1.13 раз шире полосы по уровню 3 дБ, в зависимости от полосовой избирательности. Например, разрешающий фильтр с полосой 10 кГц по уровню 3 дБ имеет эффективную шумовую полосу 10.5 – 11.3 кГц.
Если мы используем формулу 10 log(BW2/BW1) для подгонки отображаемого шумового уровня к тому, который мы должны измерить в эффективной шумовой полосе, соответствующей полосе по уровню 3 дБ, мы находим, что подгоночная величина меняется от
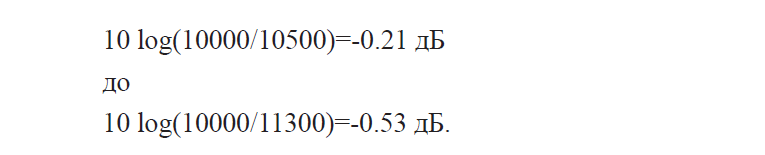
Другими словами, если мы вычитаем нечто между 0.21 и 0.53 дБ из отображаемого шумового уровня, мы получим шумовой уровень в эффективной шумовой полосе, который удобен для расчетов. Для нижеследующих примеров мы используем величину 0.5 дБ в качестве разумного компромисса для коррекции полосы9.
9. Анализаторы серии ESA калибруют каждую полосу разрешения во время процедуры установки ПЧ, чтобы определить эквивалентную шумовую полосу. Анализаторы серии PSA имеют заявленную в спецификации точность эффективной шумовой полосы в рамках 1% (±0.044 дБ).
Давайте рассчитаем суммарную коррекцию для различных видов усреднения:
Линейное усреднение (напряжения):
Распределение Релея (линейный режим): 1.05 дБ
Отношение полосы по уровню 3 дБ к эффективной шумовой полосе: -0.5 дБ
Суммарная коррекция: 0.55 дБ
Логарифмическое усреднение:
Логарифм распределения Релея: 2.5 дБ
Отношение полосы по уровню 3 дБ к эффективной шумовой полосе: -0.5 дБ
Суммарная коррекция: 2 дБ
Усреднение мощности (среднеквадратичное):
Распределение мощности: 0 дБ
Отношение полосы по уровню 3 дБ к эффективной шумовой полосе: -0.5 дБ
Суммарная коррекция: -0.5 дБ
Многие современные анализаторы с микропроцессорным управлением позволяют использовать шумовой маркер. При этом микропроцессор переключает анализатор в режим усреднения мощности, рассчитывает среднее значение по некоторому количеству дисплейных точек маркера10, нормализует и корректирует значение к 1 Гц эффективной шумовой полосы, и отображает нормализованное значение.
10. Например, приборы серии ESA и PSA рассчитывают среднее за половину деления, независимо от количества дисплейных точек.
Анализатор сам делает тяжелую часть работы. А перевести значение шумового маркера в другие полосы уже легко. Например, если мы хотим знать полную мощность шума в канале связи 4 МГц, мы добавляем 10log(4000000/1) или 66 дБ к значению шумового маркера11.
11. Многие современные анализаторы делают эти вычисления еще проще при помощи функции «Мощность Канала». Пользователь вводит полосу интегрирования канала и помещает сигнал в центр дисплея. Функция «Мощность Канала» вычисляет полную мощность сигнала в канале.
Предусилитель для измерения шума
Поскольку обычно шумовые сигналы имеют низкий уровень, мы часто нуждаемся в предусилителе, чтобы получить подходящую чувствительность для их измерения. Однако, сперва мы должны пересчитать чувствительность нашего анализатора. Выше мы определили чувствительность как уровень синусоидального сигнала, который равен отображаемому среднему шумовому фону. Поскольку анализатор калибруется так, чтобы показать правильную амплитуду синусоиды, никаких поправок для сигнала не нужно. Но шум располагается на 2.5 дБ ниже, поэтому входной шумовой сигнал должен быть на 2.5 дБ выше шумового фона анализатора, чтобы быть на том же уровне к моменту отображения на дисплее.
Внутренний и внешний шумовые сигналы складываются по мощности, так что отображаемый шум увеличивается на 3 дБ, то есть в 2 раза по мощности. Поэтому мы можем определить коэффициент шума нашего анализатора для шумового сигнала как:
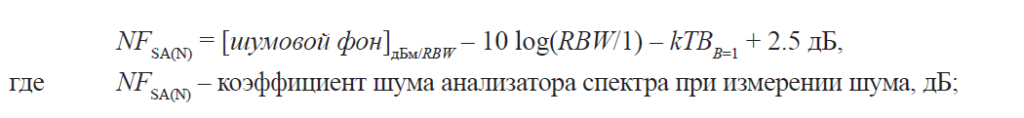
Если использовать тот же шумовой фон, что и прежде, -110 дБ в полосе разрешения 10 кГц, то получим:
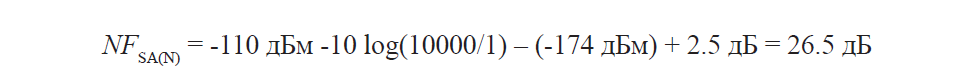
Как и в случае с синусоидальным сигналом, NFSA(N) не зависит от полосы разрешения, и показывает нам, насколько выше над kTB должен быть шумовой сигнал, чтобы сравняться с шумовым фоном нашего анализатора.
Когда мы добавляем предусилитель к нашему анализатору, коэффициент шума системы улучшается. Однако мы уже учли фактор 2.5 дБ в нашем определении NFSA(N), так что график коэффициента шума системы становится таким, как показано на Рис. 5-8. Коэффициент шума для шумового сигнала определяется точно так же, как и в предыдущем случае с синусоидальным сигналом.
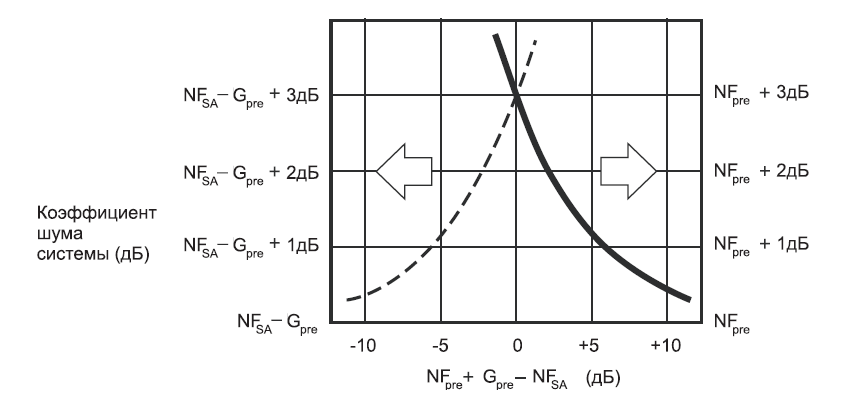
Глава 6 Динамический диапазон
Определение
Динамический диапазон обычно понимают, как возможность анализатора измерять гармонически связанные сигналы и взаимодействия двух или более сигналов; например, измерять гармонические искажения второго и третьего порядков или интермодуляции третьего порядка. Имея дело с подобными измерениями, нужно помнить, что входной смеситель анализатора спектра – устройство нелинейное, и поэтому всегда генерирует собственные искажения. Для нелинейности смесителя имеется причина. Он должен быть нелинейным, чтобы преобразовывать входной сигнал на желаемую ПЧ. Но нежелательные продукты искажения, генерируемые в смесителе, попадают на те же частоты, на которых находятся те продукты искажений, которые мы желаем измерить для изучения входного сигнала.
Поэтому мы можем определить динамический диапазон следующим образом: это есть отношение, выраженное в дБ, наибольшего и наименьшего сигналов, одновременно присутствующих на входе анализатора спектра, которое допускает измерение наименьшего сигнала с заданной степенью неопределенности.
Заметим, что точность измерения есть часть определения. Ниже мы увидим, как внутренний шум и искажения влияют на точность.
Зависимость динамического диапазона от внутренних искажений
Чтобы определить зависимость динамического диапазона от искажения, мы должны вначале точно определить поведение входного смесителя. Большинство анализаторов, в частности те, что применяют гармоническое смешение для расширения своего диапазона перестройки1, используют диодные смесители. Другие типы смесителей ведут себя подобным же образом.
- см. Главу 7 Расширение частотного диапазона.
Ток через идеальный диод можно выразить так:

Мы можем разложить это выражение в ряд:
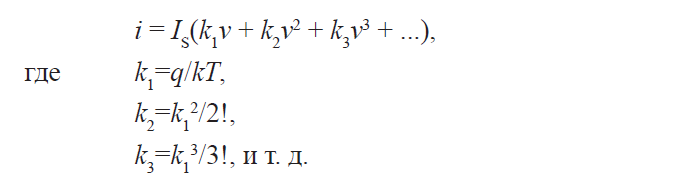
Приложим теперь к смесителю два сигнала. Один будет входным сигналом, который мы хотим анализировать, другой – сигналом гетеродина, необходимым для перевода сигнала на ПЧ:

Легко математически найти желаемый продукт смешения на промежуточной частоте:

Кроме того, генерируется другой член:
но когда мы обсуждали уравнение настройки, мы обнаружили, что хотим иметь частоту гетеродина выше ПЧ, поэтому частота ωLO + ω1 также всегда выше ПЧ.
При постоянном уровне гетеродина сигнал на выходе смесителя линеен относительно уровня входного сигнала. На практике это верно до тех пор, пока входной сигнал более чем на 15 – 20 дБ ниже уровня гетеродина. Здесь есть также члены, включающие гармоники входного сигнала:
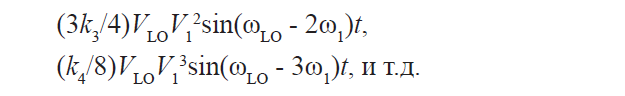
Эти члены говорят нам, что динамический диапазон благодаря внутренним искажениям зависит от уровня сигнала на входе смесителя. Посмотрим, как это работает, используя для нашего определения динамического диапазона разность в дБ между основной частотой и внутренне генерируемым искажениями.
Аргумент синуса в первом члене включает 2ω1, поэтому он представляет вторую гармонику входного сигнала. Уровень этой гармоники есть функция квадрата амплитуды основной частоты, V12. Этот факт говорит нам, что на каждый дБ сигнала на основной частоте приходится два дБ второй гармоники. См. Рис. 6-1. Второй член включает 3ω1, третью гармонику, пропорциональную кубу амплитуды входного сигнала, V13. Поэтому на 1 дБ изменения на основной частоте на входе смесителя приходится 3 дБ изменения внутренне генерируемой третьей гармоники.
Искажения часто описываются их порядком. Порядок можно определить обозначением коэффициента, связанного с частотой сигнала, или показателем экспоненты, связанной с амплитудой. Поэтому искажения типа второй гармоники есть искажения второго порядка, а третья гармоника – искажения третьего порядка. Порядок также показывает изменение внутренне генерируемых искажений относительно изменения на основной частоте, которая создает эти искажения.
Теперь добавим второй входной сигнал:
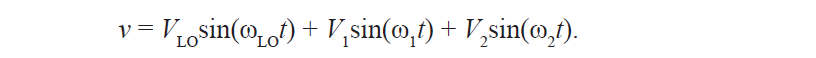
На этот раз можем получить математически:
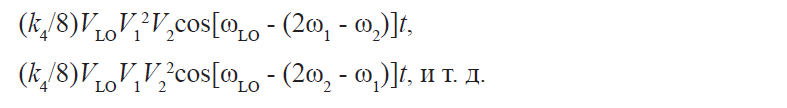
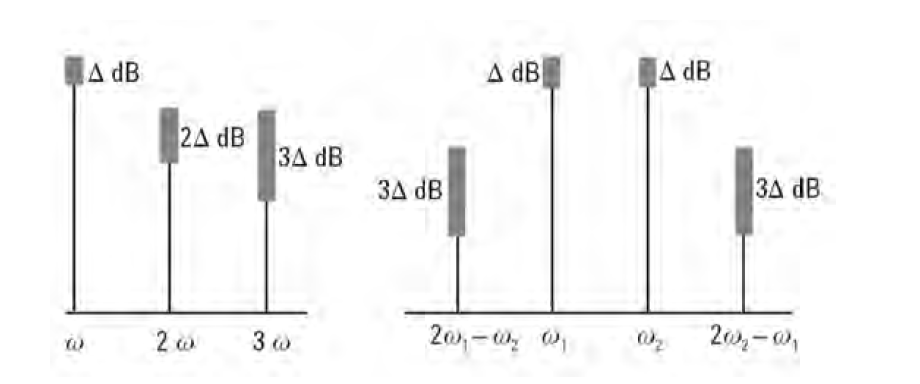
Здесь представлены интермодуляционные искажения, получаемые при взаимодействии двух входных сигналов между собой. Продукт искажений, находящийся ниже частот входных сигналов, располагается на частоте 2ω1-ω2, и попадает ниже ω1 на разностную частоту сигналов ω2-ω1. Продукт искажений, находящийся выше частот входных сигналов, располагается на частоте 2ω2-ω1, и попадает выше частоты ω2 на ту же разность. См. Рис. 6-1.
Снова напомним, что динамический диапазон зависит от уровня сигналов на входе смесителя. Внутренне генерируемые искажения изменяются как продукты V12 и V2 в первом случае, как продукты V1 и V22 – во втором случае. Если V1 и V2 имеют одинаковые амплитуды, обычный случай при проведении измерения искажений, мы можем трактовать их продукты как кубические члены (V13 или V23). Поэтому для каждого дБ одновременного изменения двух входных сигналов, будет 3 дБ изменения продуктов искажений, как показано на Рис. 6-1.
Это та же степень изменения, которую мы видели при гармонических искажениях третьего порядка. И это, на самом деле, тоже искажения третьего порядка. В этом случае мы можем определить степень искажений, суммируя коэффициенты при ω1 и при ω2 (то есть 2ω1-1ω2 дает 2+1=3) или показатели экспонент при V1 и при V2.
Все это говорит о том, что динамический диапазон зависит от уровня сигнала на смесителе. Откуда мы знаем, какой уровень необходим на смесителе для проведения конкретного измерения? В документацию на большинство анализаторов включаются графики, чтобы сказать нам как меняется динамический диапазон. Однако если никаких графиков нет, мы можем построить свои собственные2.
2. Более подробно о том, как построить собственные графики динамического диапазона, см. документ Agilent PSA Performance Spectrum Analyzer Series Product Note, Optimizing Dynamic Range for Distortion Measurements.
Нам нужна отправная точка, и ее мы можем получить из документации. Вначале посмотрим на искажения второго порядка. Предположим, в документации указано, что гармонические искажения второго порядка на 75 дБ ниже сигнала -40 дБм на входе смесителя. Поскольку измерение искажений относится к относительным измерениям и (по крайней мере, в данный момент) мы называем динамическим диапазоном разность в дБ между сигналом основной частоты и внутренне генерируемыми искажениями, мы получили нашу отправную точку. Внутренне генерируемый искажения второго порядка 75 дБ, поэтому мы можем измерять искажения ниже 75 дБ. Наносим эту точку на график, где по осям нанесены искажения (дБн — дБ по отношению к несущей) – по вертикальной оси, в зависимости от уровня на смесителе (уровень на входном разъеме минус установка входного аттенюатора). См. Рис. 6-2. Что случится, если уровень сигнала на входе смесителя упадет до –50 дБм? Как отмечено на Рис. 6-1, для каждого дБ изменения уровня сигнала на входе смесителя на основной частоте будет 2 дБ изменения внутренне генерируемой второй гармоники. Но для измерительных целей мы интересуемся только относительным изменением, то есть тем, что случится с нашим измерительным диапазоном. В этом случае, для каждого дБ, на который сигнал основной частоты изменится на входе смесителя, измерительный диапазон изменится также на 1 дБ. Тогда в нашем примере со второй гармоникой, когда уровень сигнала на входе смесителя изменится от –40 дБм до –50 дБм, внутренние искажения, а значит, измерительный диапазон, изменятся от –75 дБн до –85 дБн. Действительно, эти точки попадают на линию с угловым коэффициентом 1, которая описывает динамический диапазон для любого входного уровня на смесителе.
Мы можем построить подобную линию и для искажений третьего порядка. Например, в документации указано, что искажения третьего порядка, скажем, -85 дБн для сигнала уровня –30 дБм на входе смесителя. Снова, это наша начальная точка, и мы отметим на графике точку, показанную на Рис. 6-2. Если мы теперь снизим уровень сигнала на смесителе до –40 дБм, что случится? Обращаясь снова к Рис. 6-1, мы видим, что и искажения, связанные с третьей гармоникой, и интермодуляционные искажения третьего порядка падают на 3 дБ за каждый дБ, на который падает сигнал на основной частоте. И снова нам важна только разность. Если уровень сигнала на входе смесителя изменяется от –30 дБм до –40 дБм, разность между сигналом основной частоты и внутренне генерируемыми искажениями изменяется на 20 дБ. Так что величина внутренних искажений будет -105 дБн. Эти две точки попадают на линию, имеющую угловой коэффициент 2, давая нам поведение искажений третьего порядка для любого уровня на смесителе.
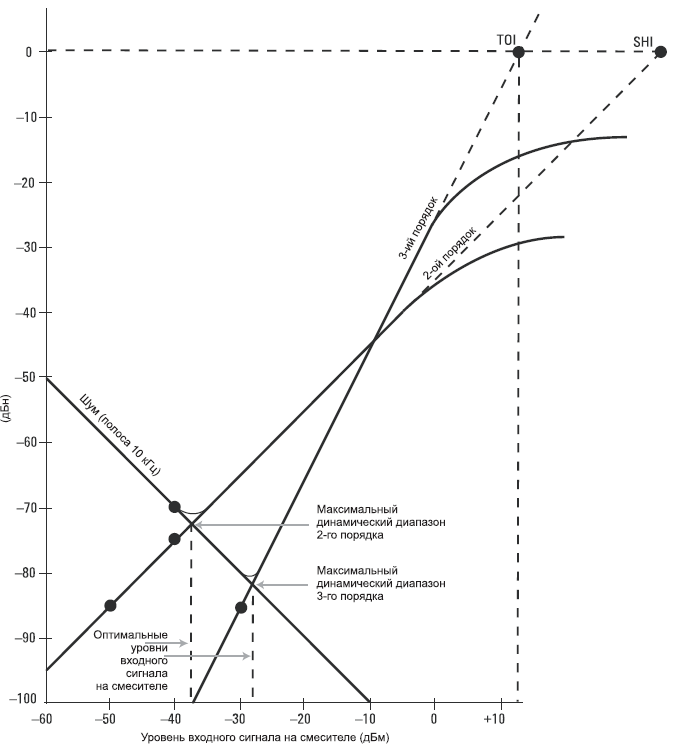
Иногда поведение интермодуляционных искажений третьего порядка дается в терминах TOI (Third Order Intercept, точка пересечения третьего порядка). Это уровень на смесителе, при котором внутренне генерируемые искажения третьего порядка должны быть равными основным, или 0 дБн. Эта ситуация невозможна на практике, поскольку при этом смеситель должен быть глубоко в насыщении. Однако с математической точки зрения TOI есть исключительно удобная точка, поскольку мы знаем наклон линии. Поэтому даже с TOI как стартовой точкой мы можем определить степень внутренне генерируемых искажений при заданном уровне сигнала на входе смесителя.
Мы можем рассчитать TOI из информации, указанной в документации прибора. Поскольку динамический диапазон третьего порядка меняется на 2 дБ на каждый дБ изменения уровня сигнала на основной частоте на входе смесителя, мы получим TOI, вычитая половину указанного в спецификации динамического диапазона в дБ из уровня на основной частоте:

Используя величины из выше проведенного обсуждения, получаем:
Проверка аттенюатором
Понимание графика искажений важно, но мы можем провести несложную проверку для определения того, являются ли отображаемые продукты искажений истинными входными сигналами, или внутренне генерируемыми сигналами. Измените входное ослабление. Если отображаемая величина продуктов искажений останется той же, компоненты есть часть входного сигнала. Если отображаемая величина изменилась, продукты искажений есть внутренне генерируемые или сумма внешних и внутренне генерируемых сигналов. Продолжаем изменять ослабление до тех пор, пока отображаемые продукты искажений не перестанут изменяться, и затем завершаем измерение.
Шум
Есть и другое ограничение динамического диапазона, и это – шумовой фон нашего анализатора. Возвращаясь к нашему определению динамического диапазона как отношения наибольшего и наименьшего измеряемого сигналов, понимаем, что средний шум устанавливает предел наименьшему сигналу. Поэтому динамический диапазон зависит от шума и становится отношением сигнал/шум, в котором сигнал основной частоты становится тем объектом, искажения которого мы хотим измерить.
Нанести шум на график динамического диапазона довольно просто. Например, предположим, что в документации на анализатор его отображаемый средний шум задан спецификацией в –110 дБм в полосе разрешения 10 кГц. Если наш сигнал на основной частоте имеет уровень –40 дБм на смесителе, то это на 70 дБ выше среднего шума, поэтому мы имеем отношение сигнал/шум 70 дБ. На каждый дБ, на который мы снижаем уровень сигнала на входе смесителя, мы теряем 1 дБ отношения сигнал/шум. Наша шумовая кривая есть прямая линия, имеющая угловой коэффициент –1, как показано на Рис. 6-2.
Если мы на какое-то время пренебрежем соображениями точности измерения, то наилучший динамический диапазон будет на пересечении подходящей кривой искажений и кривой шума. Рис. 6-2 показывает нам, что наш максимальный динамический диапазон для искажений второго порядка есть 72.5 дБ; для искажений третьего порядка – 81.7 дБ. На практике пересечение кривых шума и искажений не является четко определенной точкой, потому что шум дает вклад в продукты искажений, снижая динамический диапазон на 2 дБ при использовании логарифмического масштаба с логарифмическим усреднением.
На Рис. 6-2 показан динамический диапазон для одной полосы разрешения. Мы, конечно, можем улучшить динамический диапазон путем сужения полосы разрешения, но здесь нет взаимно однозначного соответствия между сниженным шумовым уровнем и улучшением динамического диапазона. Для искажений второго порядка улучшение есть половина изменения шумового уровня; для искажений третьего порядка улучшение есть две трети изменения шумового уровня. См. Рис. 6-3.
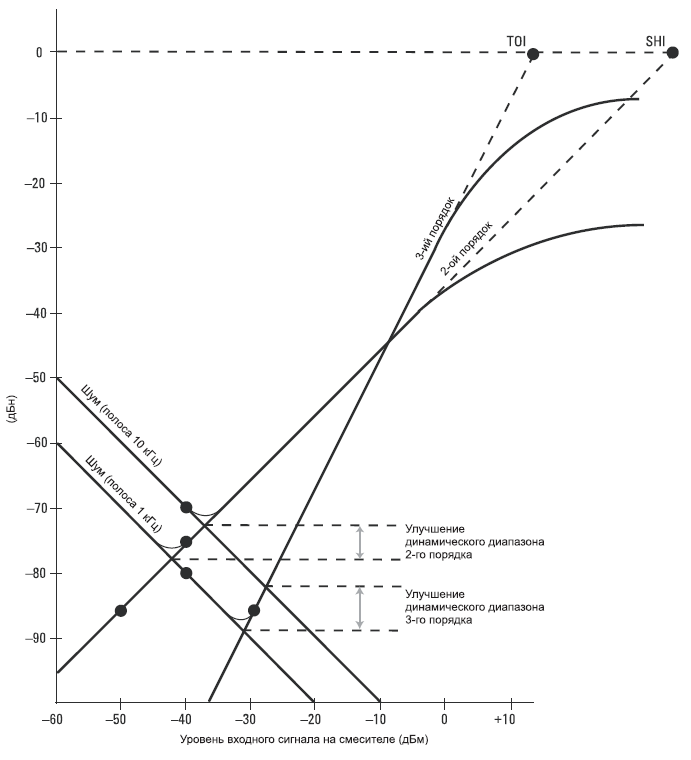
Окончательный ограничитель динамического диапазона — это фазовый шум гетеродина анализатора спектра, и он влияет только на измерения искажений третьего порядка. Например, предположим, что мы проводим измерения интермодуляционных искажений третьего порядка на усилителе, и наши подаваемые частоты разделены на 10 кГц. Продукты искажений третьего порядка будут отделены от подаваемых частот также на 10 кГц. Для этих измерений мы можем использовать полосу разрешения в 1 кГц. Глядя на Рис. 6-3 и допуская уменьшение шумовой кривой на 10 дБ, мы обнаружим максимальный динамический диапазон порядка 88 дБ. Предположим, однако, что на отстройке в 10 кГц наш фазовый шум всего -80 дБн. Тогда 80 дБ становятся непреодолимым ограничением динамического диапазона для нашего измерения, как показано на Рис. 6-4.
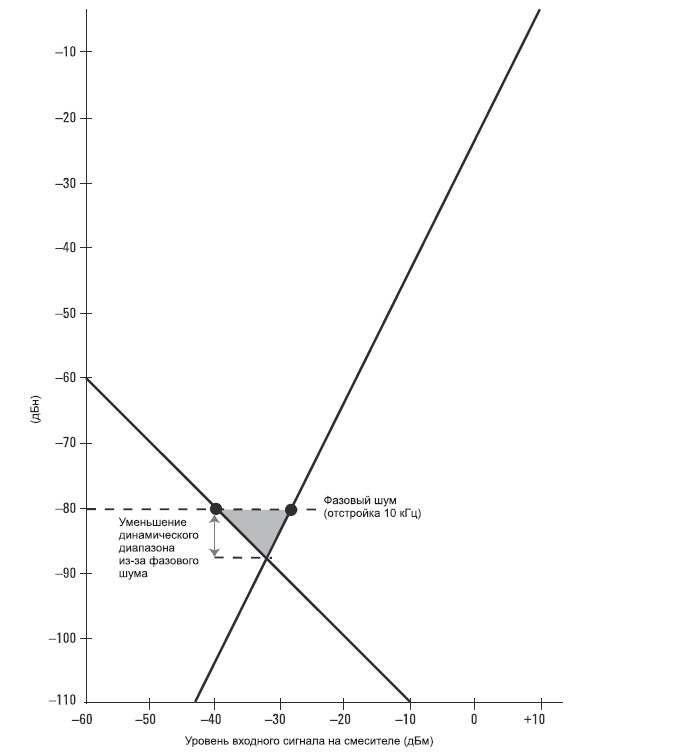
Окончательно, можно сказать, что динамический диапазон анализатора спектра ограничен тремя факторами: искажениями во входном смесителе; широкополосным шумовым уровнем (чувствительностью) системы и фазовым шумом гетеродина.
Динамический диапазон в зависимости от неопределенности измерений
В наших предыдущих обсуждениях амплитудной точности мы рассматривали только те пункты, которые перечислены в Табл. 4-1, плюс рассогласование. Мы не обсудили возможности того, что внутренне генерируемый продукт искажений (синусоида) может быть на той же частоте, что и внешний сигнал, который мы хотим измерить. Однако внутренне генерируемые продукты искажений попадают точно на те же частоты, что и продукты искажений, которые мы хотим измерить у внешних сигналов. Проблема здесь в том, что нет способа узнать фазовые соотношения между внешними и внутренними сигналами. Поэтому мы только можем определить потенциальный диапазон неопределенности:

Взглянем на Рис. 6-5. Например, если мы обеспечим условия, когда внутренне генерируемые искажения равной по амплитуде искажениям входящего сигнала, ошибка измерения может быть от +6 дБ (два сигнала точно в фазе) до минус бесконечности (два сигнала точно в противофазе и поэтому взаимно уничтожаются). Подобная неопределенность в большинстве случаев неприемлема. Если мы установим предел на неопределенность измерения в ±1 дБ, то Рис. 6-5 показывает нам, что внутренне генерируемый продукт искажений должен быть примерно на 18 дБ ниже продукта искажений, который мы хотим измерить. Чтобы построить кривые динамического диапазона для измерений второго и третьего порядков с неопределенностью измерения не более чем 1 дБ, мы должны сместить кривые на Рис. 6-2 на 18 дБ, как показано на Рис. 6-6.
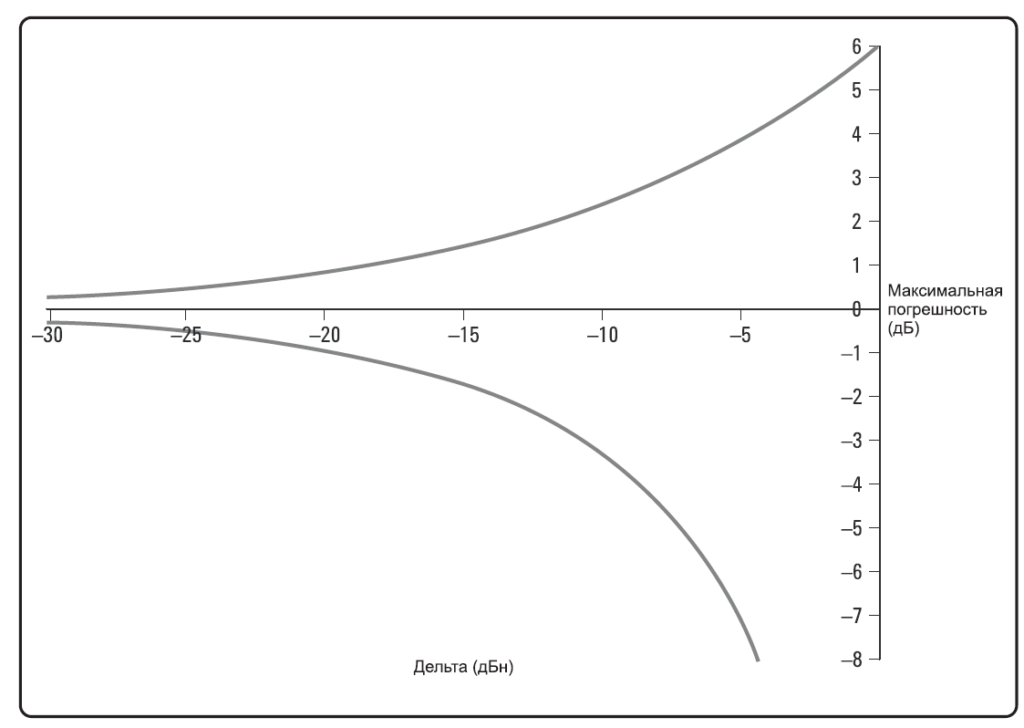
Далее рассмотрим неопределенность из-за низкого отношения сигнал/шум. Продукты искажений, которые мы хотим измерить, есть, как мы надеемся, низкоуровневые сигналы, и часто они находятся на шумовом уровне анализатора или близки к нему. В подобных случаях мы обычно используем видеофильтр, чтобы сделать эти низкоуровневые сигналы более различимыми. Рис. 6-7 показывает ошибку отображаемого уровня сигнала в зависимости от отношения сигнал/шум для обычного анализатора спектра. Заметим, что ошибка имеется только одного знака, поэтому мы можем корректировать ее. Однако обычно мы не делаем этого. Поэтому для измерения динамического диапазона примем, что ошибка за счет шума составляет 0.3 дБ, и сместим шумовую кривую на 5 дБ, как показано на Рис. 6-6. Там, где кривая искажений и шумовая кривая пересекаются, максимально возможная ошибка должна быть менее 1.3 дБ.
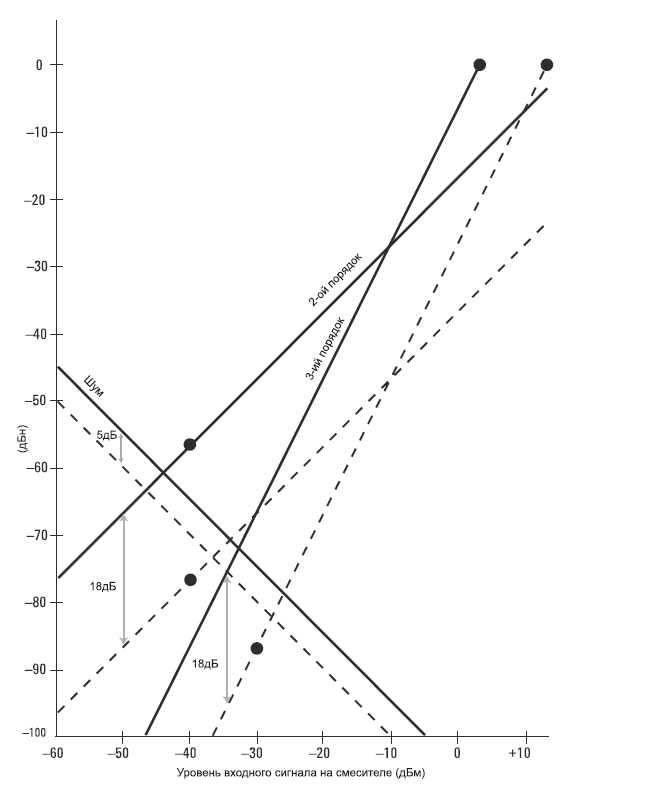
Посмотрим, что случится с динамическим диапазоном в результате нашей обеспокоенности неопределенностью измерений. Как показано на Рис. 6-6, динамический диапазон искажений второго порядка изменяется с 72.5 дБ до 61 дБ, с разницей в 11.5 дБ. Это – половина полного сдвига двух кривых (18 дБ для искажений, 5 дБ для шума). Искажений третьего порядка изменяются с 81.7 дБ до примерно 72.7 дБ с разницей примерно в 9 дБ. В последнем случае изменение – это одна треть от 18-дБ сдвига кривой искажений плюс две трети от 5-дБ сдвига кривой шума.
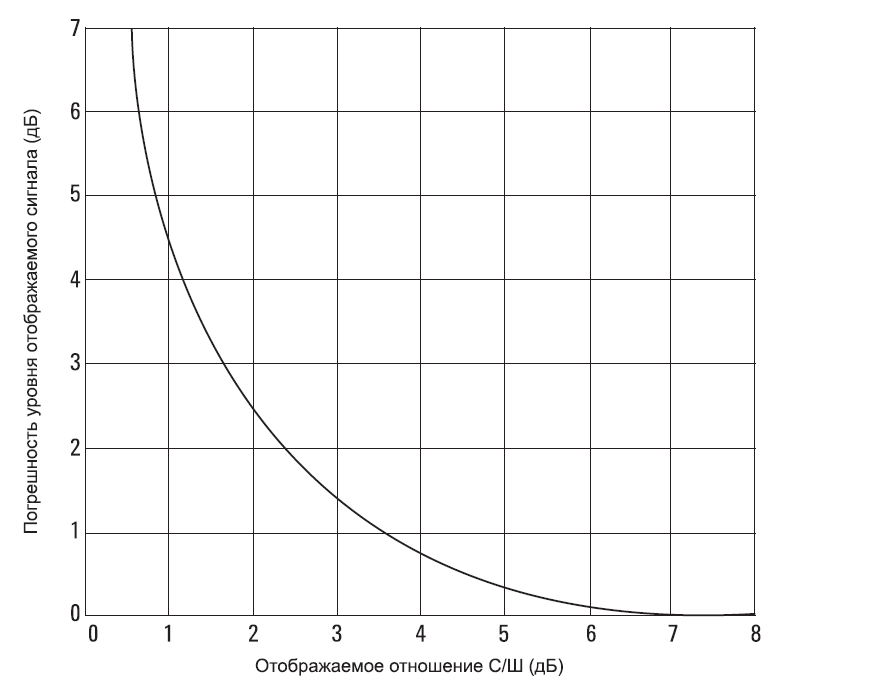
Сжатие усиления
При обсуждении динамического диапазона мы до сих пор не задумывались, насколько точно отображается больший тон, даже в относительном смысле. При увеличении уровня входного синусоидального сигнала, уровень сигнала на входе смесителя, в конце концов, становится настолько высоким, что желаемый выходной продукт смешения уже не изменяется линейно по отношению к амплитуде входного сигнала. Смеситель достигает насыщения и отображаемая амплитуда сигнала становится слишком мала. Насыщение – процесс скорее постепенный, нежели мгновенный. Чтобы помочь нам работать не в режиме насыщения, обычно задается точка сжатия 1 дБ. Обычно сжатие усиления начинается при уровне сигнала на входе смесителя в диапазоне от -5 до +5 дБм. Поэтому мы можем определить установку входного аттенюатора для проведения точного измерения сигналов высокого уровня3. Анализаторы спектра с цифровой секцией ПЧ в случае выхода за рамки диапазона АЦП выведут на экран сообщение о перегрузке ПЧ.
3. Многие анализаторы внутренне контролируют комбинированную установку входного аттенюатора и усиления по ПЧ, так что появление на входе смесителя сигнала, равного уровню сжатия, создает отклонение от верхней линии масштабной сетки. Поэтому мы не можем нечаянно провести неправильные измерения.
На самом деле, существуют три различных метода оценки сжатия. Традиционный метод, называемый однотоновым сжатием, измеряет изменение усиления прибора (усилителя, или смесителя, или системы), когда мощность входного сигнала увеличивается. Это тот метод, который мы только что описали. Отметим, что точка однотонового сжатия значительно выше, чем уровни сигналов основной частоты, указанные выше даже для динамического диапазона средней величины. Поэтому мы были правы, когда не волновались по поводу возможного сжатия больших сигналов.
Второй метод, названный сжатием двухтонового сигнала, измеряет изменение усиления системы для малых сигналов, пока мощность больших сигналов увеличивается. Сжатие двухтонового сигнала применяется при измерении многих CW-сигналов, таких как боковые полосы и независимые сигналы. Порог сжатия для этого метода обычно на несколько дБ ниже, чем таковой в однотоновом методе. Этот метод используется фирмой Agilent Technologies для определения сжатия усиления анализаторов спектра.
Третий метод, называемый сжатием импульстного сигнала, измеряет изменение усиления системы узкого (широкополосного) радиочастотного импульса, когда мощность импульса увеличивается. Когда измеряются импульсы, мы часто используем полосу разрешения намного более узкую, чем полоса частот спектра импульса, поэтому наш анализатор отображает уровень сигнала гораздо ниже пиковой мощности импульса. В результате, мы можем не знать о том, что полная мощность сигнала выше порога сжатия смесителя. Высокий порог улучшает отношение сигнал/шум для высокомощного ультра-узкого импульса или импульса с линейной модуляцией частоты. Порог при этом примерно на 12 дБ выше, чем для сжатия двутонового сигнала в анализаторах Agilent 8560EC. Тем не менее, поскольку различные механизмы влияют на методы однотонового, двутонового и импульсного сжатия по-разному, любой порог сжатия может быть ниже, чем какой-то другой.
Дисплейный диапазон и диапазон измерений
Есть два дополнительных диапазона, которые часто путают с динамическим диапазоном: дисплейный диапазон и измерительный диапазон. Дисплейный диапазон, часто называемый дисплейным динамическим диапазоном, имеет отношение к калиброванному амплитудному диапазону дисплея анализатора. Например, дисплей с десятью делениями будет, очевидно, иметь дисплейный диапазон 100 дБ, когда мы выбираем 10 дБ на деление. Это абсолютно верно для современных анализаторов с цифровой секцией ПЧ, например, приборов серии PSA. Это также верно и для серии ESA-E при использовании узких (от 10 до 300 Гц) полос разрешения. Однако, анализаторы спектра с аналоговой секцией ПЧ обычно калибруются лишь на первые 85 или 90 дБ вниз от опорного уровня. В этом случае нижняя линия сетки обозначает сигнал с нулевой амплитудой, поэтому нижняя часть дисплея представляет собой область диапазона от -85 или -90 дБ до минус бесконечности относительно опорного уровня.
Другой ограничивающий фактор, в случае анализаторов с аналоговой частью ПЧ – это диапазон логарифмического усилителя. Например, в приборах серии ESA-L используется 85-дБ логарифмический усилитель. Поэтому измерения только до 85 дБ вниз от опорного уровня могут быть верными.
Вопрос состоит в том, можем ли мы использовать полный дисплейный диапазон? Из проведенного выше обсуждения динамического диапазона мы знаем, что в общем случае ответ «да». На самом деле, динамический диапазон часто даже превосходит дисплейный диапазон или диапазон логарифмического усилителя*. Чтобы перевести меньшие сигналы на калиброванную область дисплея, мы должны увеличить усиление ПЧ. Но при этом мы двигаем большие сигналы за верхний предел дисплея, выше опорного уровня. Некоторые анализаторы фирмы Agilent – например, приборы серии PSA, — позволяют провести измерения сигналов, когда они выше опорного уровня, без изменения точности, с которой отображаются меньшие сигналы. Это показано на Рис. 6-8. Поэтому мы действительно можем пользоваться преимуществом полного динамического диапазона анализатора даже тогда, когда динамический диапазон превосходит дисплейный диапазон. На Рис. 6-8, несмотря на то, что опорный уровень изменился с -8 дБм до -53 дБм, и сигнал ушел далеко за верхний предел экрана, показания маркера не изменились.
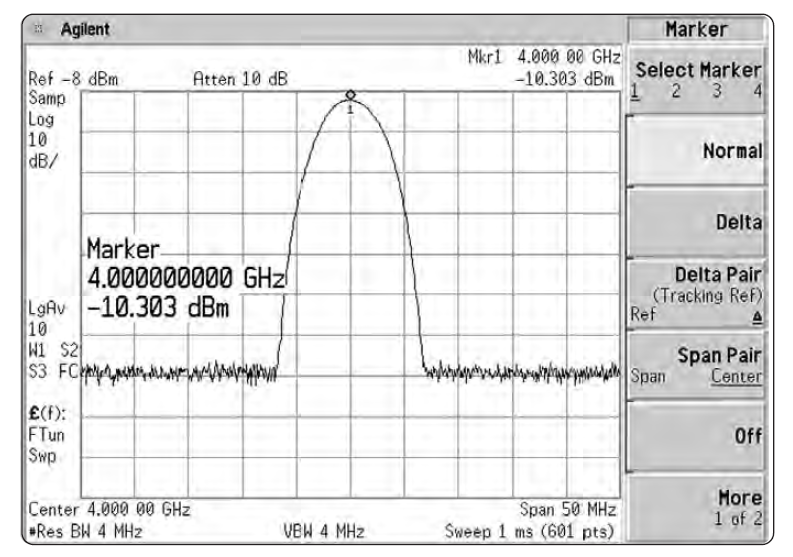
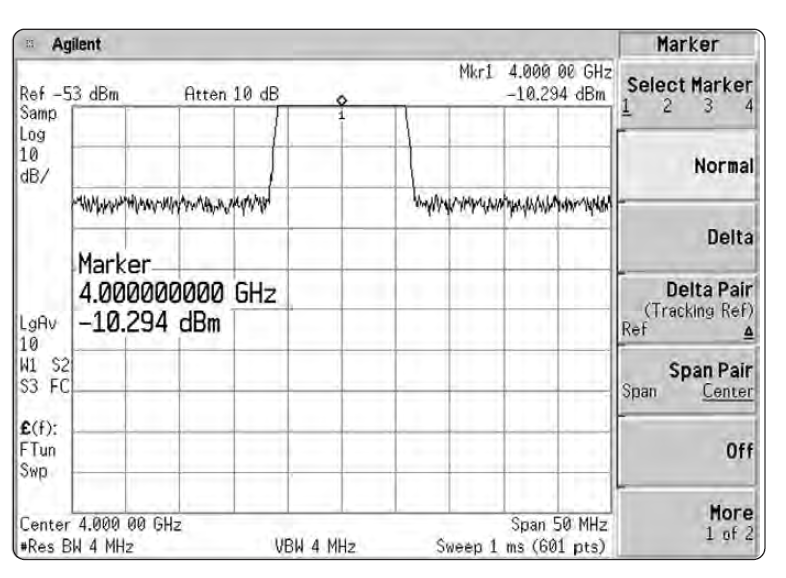
Измерительный диапазон есть отношение наибольшего сигнала к наименьшему сигналу, которые можно измерить в любых обстоятельствах. Верхний предел определяется максимально безопасным входным уровнем, +30 дБм (1 Ватт) для большинства анализаторов. У этих анализаторов есть входные аттенюаторы, которые могут устанавливаться до 60 или 70 дБ, так что мы можем уменьшать сигналы уровня +30 дБм до уровня, существенно более низкого, чем точка сжатия входного смесителя, и качественно измерять их. Отображаемый средний уровень собственных шумов устанавливает противоположный предел диапазона. В зависимости от минимальной полосы разрешения конкретного анализатора, уровень собственных шумов обычно лежит в диапазоне от –115 дБм до –170 дБм. Таким образом, измерительный диапазон может варьироваться в пределах от 145 дБ до 20 дБ. Конечно, мы не можем видеть сигнал –170 дБм, пока сигнал +30 дБм также присутствует на входе.
Измерение мощности в соседнем канале
TOI, SOI, 1-дБ сжатие усиления и отображаемый средний уровень собственных шумов – все это классические показатели качества анализатора спектра. Однако, с гигантским развитием цифровых систем связи, и другие меры динамического диапазона становятся не менее важными. Например, при измерении мощности соседних каналов, которое часто проводится для систем связи, основанных на CDMA (Code Division Multiple Access – множественный доступ с кодовым разделением каналов), необходимо определить количество мощности сигнала, просачивающейся или «перетекающей» в соседние или дополнительные каналы,
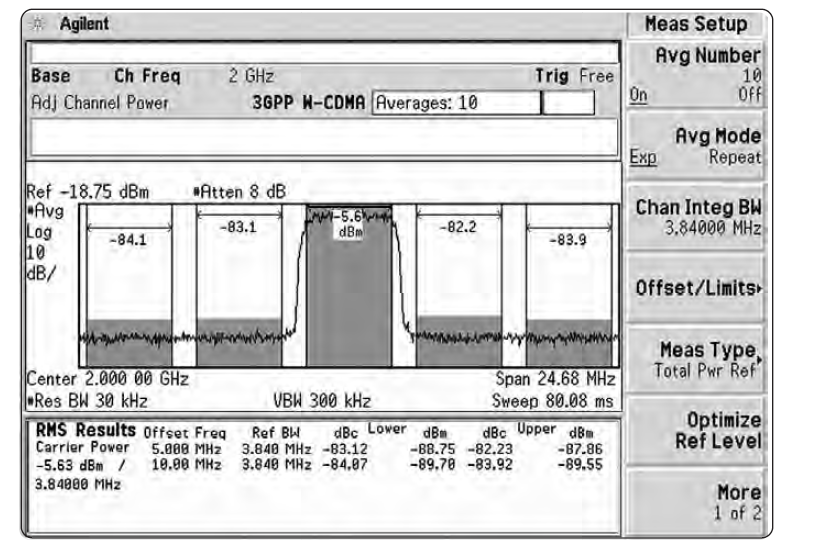
расположенные ниже и выше несущей. Пример такого измерения показан на
Рис. 6-9.
Обратите внимание на различия в мощности основного канала и соседних и дополнительных каналов. Одновременно может быть измерено до шести каналов с каждой стороны от основного.
Обычно нас интересует относительное различие между мощностью сигнала в основном канале и мощностью сигнала в соседнем или дополнительном канале. В зависимости от конкретного стандарта связи, эти измерения часто именуют измерением относительной мощности соседнего канала или относительной утечки соседнего канала. Поскольку сигналы с цифровой модуляцией, а также генерируемые ими искажения, по своему характеру очень шумоподобны, производственные стандарты обычно определяют еще и полосу канала, по которой интегрируется мощность сигнала.
Чтобы точно измерить показатель мощности в соседних каналах у исследуемого устройства (например, усилителя мощности), показатель мощности в соседних каналах самого анализатора должен быть лучше, чем у ИУ. Поэтому динамический диапазон относительной мощности соседнего канала у анализатора спектра стал ключевым параметром для измерений цифровых систем связи.
Глава 7 Расширение частотного диапазона
По мере того, как все больше и больше новых беспроводных услуг разрабатывается и становится доступными, частотный спектр становится все более и более плотно заселенным. Поэтому существует определенная тенденция разрабатывать новые продукты и услуги, работающие на более высоких частотах. Вдобавок, новые СВЧ технологии продолжают успешно развиваться, создавая растущую потребность в измерениях СВЧ диапазона. Конструкторы анализаторов спектра ответили на этот вызов созданием приборов, способных производить измерения по коаксиальному входу до 50 ГГц. А при использовании внешних смесителей, можно измерять и более высокие частоты. В этой главе мы рассмотрим методы, которые позволяют использовать анализаторы спектра на таких высоких частотах.
Внутреннее гармоническое смешение
В Главе 2 мы описали анализатор спектра с одним диапазоном частот, который перестраивается до 3 ГГц. Теперь мы хотим иметь перестройку до более высокой частоты. Наиболее практичный путь достижения подобного расширения диапазона – гармоническое смешение.
Но давайте не будем спешить. При выводе уравнения перестройки в Главе 2 мы обнаружили, что нуждаемся в фильтре нижних частот, изображенном на схеме Рис. 2-1, чтобы предотвратить попадание высокочастотных сигналов на смеситель. В результате получился анализатор с одним диапазоном частот с однозначной характеристикой, который перестраивается до 3 ГГц. Сейчас мы хотим обозревать и измерять более высокочастотные сигналы, поэтому фильтр нижних частот надо убрать.
Другими факторами, которые мы обнаружили при выводе уравнения перестройки, были выбор диапазона частот гетеродина и промежуточных частот. Мы решили, что ПЧ не должна быть внутри полосы интересующих нас частот, поскольку она создает дыру в диапазоне перестройки, в которой мы не можем производить измерения. Поэтому мы выбрали 3.6 ГГц, сдвинув ПЧ выше максимальной частоты диапазона перестройки (3 ГГц). Поскольку наш новый диапазон перестройки будет выше 3 ГГц, логично сдвинуть новую ПЧ до частоты ниже 3 ГГц. Обычная первая ПЧ для этого диапазона более высоких частот в спектральных анализаторах Agilent равна 321.4 МГц. Мы будем использовать эту частоту в наших примерах. В итоге, для нижнего поддиапазона, до 3 ГГц, наша первая ПЧ равна 3.6 ГГц. Для верхнего поддиапазона мы должны переключиться на первую ПЧ, равную 321.4 МГц. Заметим, что на Рис. 7-1 вторая ПЧ уже равна 321.4 МГц, так что все, что нам надо сделать, когда мы захотим настроиться на более высокий диапазон, это обойти первую ПЧ.
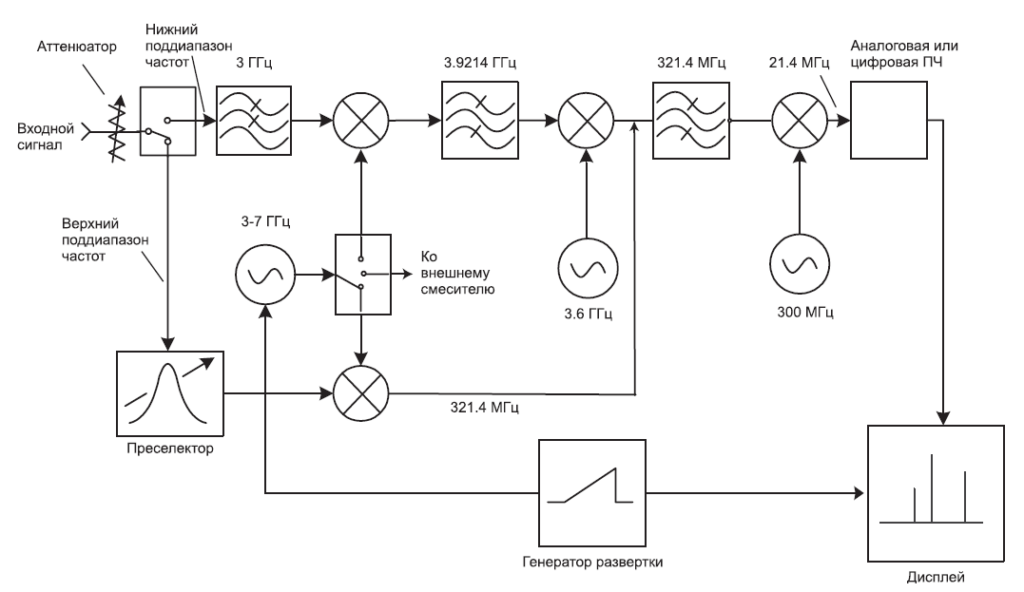
В Главе 2 мы использовали математический подход, чтобы заключить, что мы нуждаемся в фильтре нижних частот. Как мы увидим, в этой ситуации все становится гораздо сложнее, поэтому мы будем использовать графический подход как более легкий наглядный метод увидеть, что же происходит. Нижний поддиапазон частот — это более простой случай, поэтому начнем с него. Во всех наших графиках, мы будем отсчитывать частоту гетеродина вдоль горизонтальной оси, а частоту сигнала — вдоль вертикальной оси, как показано на Рис. 7-2. Поскольку мы знаем, что получим продукт смешения, равный ПЧ (и, следовательно, отклик на дисплее), когда входной сигнал отличается от гетеродина на величину ПЧ. Поэтому мы можем определить частоту, на которую анализатор настраивается, просто прибавив ПЧ к частоте гетеродина, или вычтя ее из частоты гетеродина. Чтобы определить наш диапазон настройки, мы начинаем с вычерчивания частоты гетеродина относительно оси частоты сигнала, как показано пунктирной линией на Рис. 7-2. Вычитание ПЧ из пунктирной линии дает нам диапазон настройки от 0 до 3 ГГц, — диапазон, который мы рассматривали в Главе 2. Отметим, что эта линия на Рисунке 7-2 обозначена «1-», чтобы показать смешение на основной частоте и использование знака «минус» в уравнении перестройки. Мы можем использовать график для определения того, какая частота гетеродина требуется, чтобы принять конкретный сигнал (чтобы отобразить сигнал частоты 1 ГГц, гетеродин должен быть настроен на 4.9 ГГц), или чтобы узнать, на какой сигнал анализатор настроен при данной частоте гетеродина (при частоте гетеродина 6 ГГц спектральный анализатор настроен на прием сигнала частоты 2.1 ГГц). В нашем тексте мы округляем первую ПЧ до первого десятичного знака; точное значение ПЧ указано на структурной схеме.
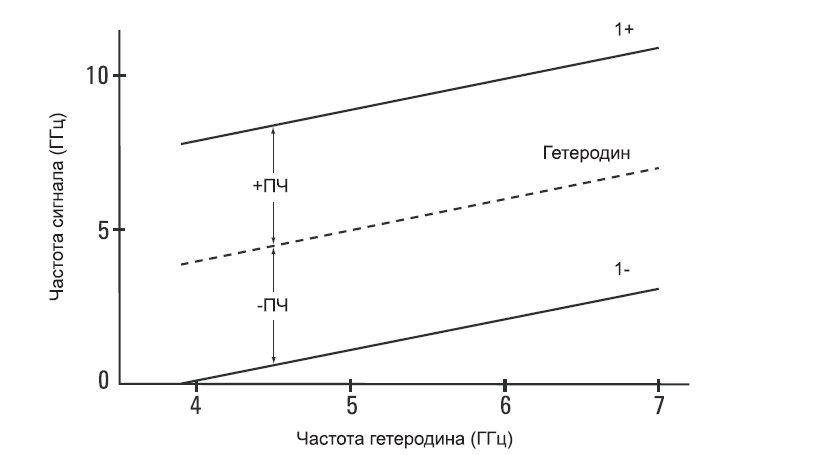
Теперь добавим другую полосу смешения на основной частоте путем суммирования ПЧ и линии гетеродина на Рис. 7-2. Это дает нам сплошную верхнюю линию, помеченную 1+, которая представляет собой диапазон настройки от 7.8 ГГц до 10.9 ГГц. Отметим, что для конкретной частоты гетеродина, две частоты, на которые настраивается анализатор, разделены между собой на двойное значение ПЧ. Предполагая, что при проведении измерений сигналов в нижнем поддиапазоне на входе у нас будет фильтр низких частот, беспокоиться о наличии сигналов в диапазоне частот 1+ нам не надо.
Теперь посмотрим, насколько гармоническое смешение усложняет ситуацию. Гармоническое смешение происходит из-за того, что гетеродин подает на смеситель сигнал большой мощности, необходимый для эффективного смешения, и поскольку смеситель – нелинейный прибор, он генерирует гармоники сигнала гетеродина. Входящие сигналы могут смешиваться с гармониками гетеродина, а также с основной частотой, и любой продукт смешения с частотой, равной ПЧ, порождает отклик на дисплее. Другими словами, наше уравнение перестройки теперь становится таким:

Добавим преобразование на второй гармонике на наш график на Рис. 7-3 и посмотрим, насколько это усложнит нашу измерительную процедуру. Как и раньше, вначале откладываем частоту гетеродина относительно оси частоты сигнала. Умножая частоту гетеродина на два, получаем верхнюю пунктирную линию на Рис. 7-3. Так же, как мы делали это для смешения на основной частоте, просто вычтем ПЧ (3.9 ГГц) из нее, и прибавим ее к кривой второй гармоники гетеродина, чтобы получить настроечные диапазоны 2- и 2+. Поскольку они не перекрываются с желаемым настраиваемым диапазоном 1-, мы можем снова считать, что они на самом деле не усложняют измерительный процесс. Другими словами, сигналы в диапазоне 1- производят уникальные, недвусмысленные отклики на дисплее анализатора. Тот же самый фильтр низких частот, что применялся в случае смешения на основной частоте, точно так же может избавить нас и от тех откликов, что появляются в результате гармонического смешения.
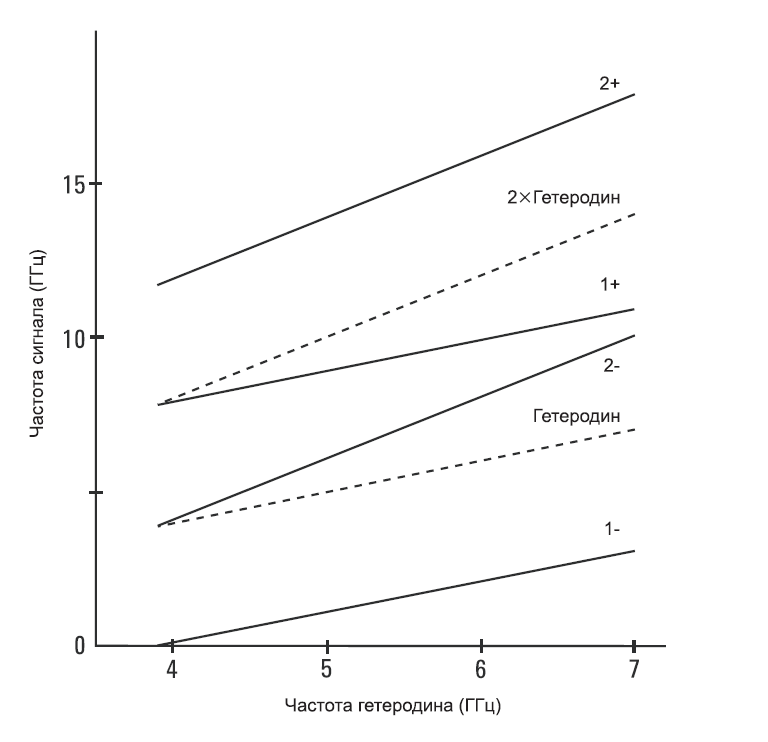
Значительно отличается ситуация в случае верхнего поддиапазона частот и низкой ПЧ. Как и раньше, мы начинаем с построения первой гармоники частоты гетеродина рядом с осью частот сигнала, а затем добавляем и вычитаем ПЧ, получая результаты, показанные на Рис. 7-4. Заметим, что диапазоны настройки 1- и 1+ теперь располагаются значительно ближе друг к другу и они в действительности перекрываются, поскольку ПЧ много ниже, в данном случае 321.4 МГц. Усложняется ли измерительный процесс тем, что диапазоны настройки стали близко расположены? И да и нет. Прежде всего, наша система может быть калибрована только на один диапазон настройки. В этом случае мы должны выбрать настройку 1-, что даст нам частоту 2.7 ГГц на нижней границе так, чтобы мы имели некоторое перекрытие с частотой 3 ГГц на верхней границе нашего диапазона настройки в нижнем поддиапазоне частот. Тогда что же мы можем увидеть на дисплее? Если посмотреть на график частот гетеродина на отметке 5 ГГц, то мы обнаружим две возможных частоты сигнала, которые дадут нам отклики в одной и той же точке на дисплее: 4.7 и 5.3 ГГц (это снова округленные числа). С другой стороны, если мы взглянем на ось частот сигнала в точке 5.3 ГГц, то увидим, что, вдобавок к отклику 1+ на частоте гетеродина в 5 ГГц, мы можем также получить отклик 1-. Это произойдет, если мы позволим гетеродину достроиться до 5.6 ГГц, то есть на два значения ПЧ выше 5 ГГц. Также, если мы посмотрим на график частоты сигнала в точке 4.7 ГГц, мы обнаружим отклик 1+ на частоте гетеродина около 4.4 ГГц (на две ПЧ ниже 5 ГГц) вдобавок к отклику 1- на частоте гетеродина в 5 ГГц. Таким образом, для каждого полезного отклика диапазона настройки 1- будет существовать второй отклик, расположенный на два значения ПЧ ниже по частоте. Эти пары откликов называют множественными откликами.
При таком преобразовании сигналов вполне возможен случай, когда сигналы на разных частотах произведут отклик в одной и той же точке на дисплее, то есть, на одинаковой ПЧ. Как видно на Рис. 7-4, входные сигналы 4.7 ГГц и 5.3 ГГц дают отклик на ПЧ, когда частота гетеродина равна 5 ГГц. Эти сигналы называются зеркальными частотами, и они разнесены также на двойную величину ПЧ.
Ясно, что нам необходим способ разделения откликов, генерируемых на настроечной кривой 1-, для которой анализатор калиброван, и откликов, производимых на настроечной кривой 1+. Однако, прежде чем рассмотреть решение проблемы разделения сигналов, добавим кривые гармонического смешения на 26.5 ГГц и посмотрим, есть здесь какие-либо дополнительные факторы, которые мы должны учесть в процессе идентификации сигналов.
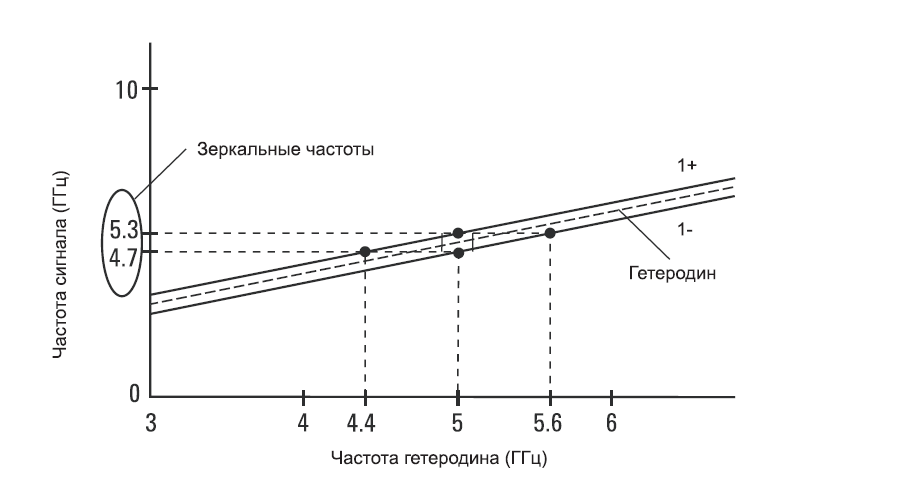
При внимательном рассмотрении Рис. 7-5 можно обнаружить некоторые дополнительные сложности. Здесь анализатор спектра настроен для работы в нескольких полосах настройки. В зависимости от частоты, на которую настроен анализатор, его дисплей калибруется по частоте для конкретной гармоники гетеродина. Например, для диапазона входных частот от 6.2 до 13.2 ГГц, анализатор спектра калиброван для настроечной кривой 2-. Предположим, что на вход подается сигнал 11 ГГц. По мере развертки гетеродина по частоте, этот сигнал произведет отклики на частоте ПЧ на настроечных кривых 3+, 3-, 2+ и 2-. Нужный нам отклик на настроечной кривой 2- появится, когда частота гетеродина будет удовлетворять уравнению настройки:

Аналогично, мы можем рассчитать, что отклик на настроечной кривой 2+ появится, когда частота гетеродина будет 5.35 ГГц, что даст нам отображаемый сигнал на частоте 10.4 ГГц.
Сигналы на дисплее, созданные откликами на настроечных кривых 3+ и 3-, называются внутриполосными множественными откликами. Поскольку они появляются при настройке гетеродина на частоты 3.57 ГГц и 3.77 ГГц, на экране они порождают ложные отклики, выглядящие как сигналы на частотах 6.84 ГГц и 7.24 ГГц.
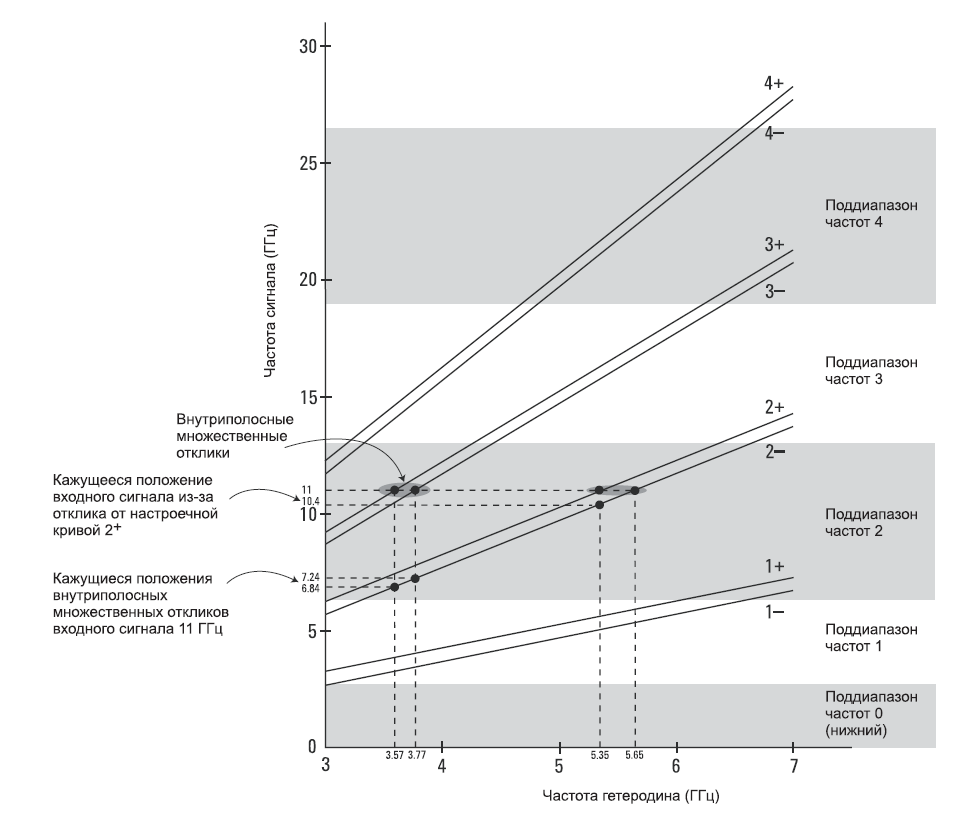
В другой ситуации возможно появление внеполосных множественных откликов. Например, пусть мы наблюдаем в полосе 1- — 1+ сигнал с частотой 5 ГГц, у которого есть третья гармоника высокого уровня на частоте 15 ГГц (полоса 3- — 3+). Вдобавок к ожидаемой паре множественных откликов, порождаемой 5-ГГц сигналом на настроечных кривых 1+ и 1-, мы получим еще отклики, генерируемые 15-ГГц сигналом на настроечных кривых 4+, 4-, 3+ и 3-. Поскольку эти отклики появляются, когда гетеродин настроен соответственно на 3.675, 3.825, 4.9 и 5.1 ГГц, то на экране отобразятся ложные сигналы на частотах 3.375, 3.525, 4.6 и 4.8 ГГц, как показано на Рис. 7-6.
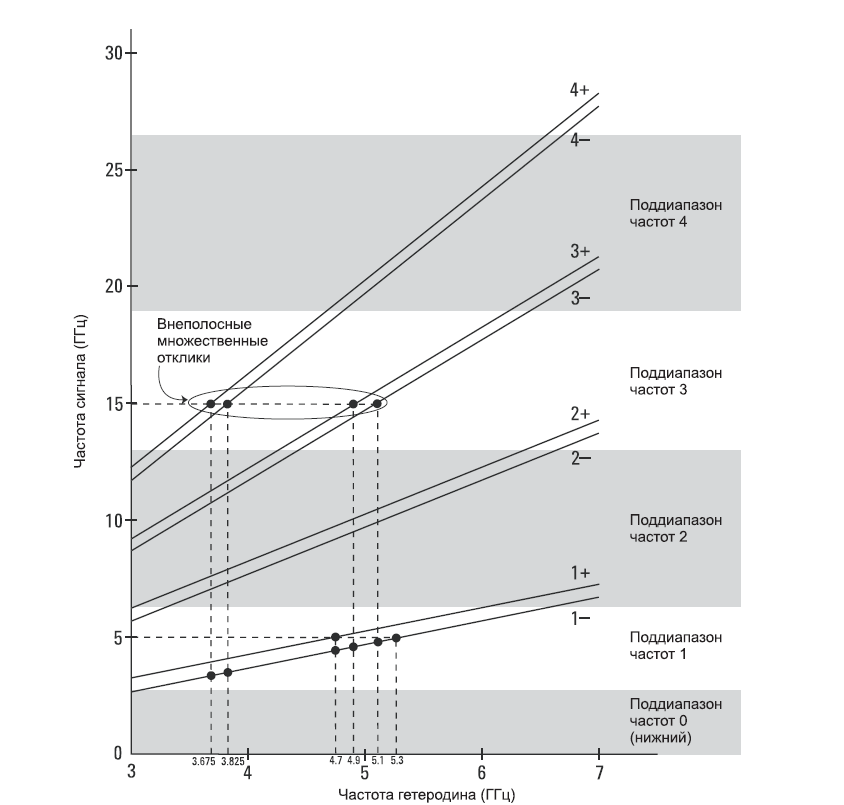
Множественные отклики обычно проявляются парно1, продукт смешения с «плюсом» и продукт смешения с «минусом». Когда мы используем верный номер смешения на гармониках для данной полосы настройки, отклики будут разнесены на 2fIF. Поскольку наклон каждой пары настроечных кривых линейно увеличивается с ростом номера гармоники N, множественные пары от любого другого номера гармоники будут разнесены на:
- Часто их называют «зеркальными парами», однако такая терминология не вполне верна: за всеми зеркальными откликами стоят два или больше реальных сигналов, присутствующих на входе анализатора, которые порождают ПЧ-отклики на одной и той же частоте гетеродина.)

Можно ли в результате всего вышеизложенного заключить, что анализаторы спектра с гармоническим смешением непрактичны? Вовсе не обязательно. В случаях, когда частота сигнала известна, можно настроиться непосредственно на сигнал, зная, что анализатор выберет подходящий режим смешения, для которого он откалиброван. В случае контролируемых процессов, при наличии только одного или двух сигналов, довольно легко отделить реальный сигнал от зеркального или от множественных откликов. Однако есть множество ситуаций, когда мы и понятия не имеем, сколько сигналов участвует в процессе или каковы могут быть их частоты. Например, мы можем выискивать неизвестные паразитные сигналы, проводить наблюдение за состоянием местности в рамках мониторинга частотной заселенности, или осуществлять ЭМС-тестирование для измерения нежелательных излучений устройства. Во всех этих случаях мы можем находиться в поиске совершенно неизвестного нам сигнала в, возможно, весьма плотно заселенном спектральном окружении. И если проводить некую процедуру распознавания по отношению к каждому отклику, то наши измерения затянутся на неимоверно долгое время.
К счастью, есть способ существенно устранить зеркальные и множественные отклики путем предварительной фильтрации сигнала. Этот метод называется преселекцией.
Преселекция
Каким образом должна осуществляться преселекция? Вновь обратившись к Рис. 7-4, предположим, что у нас на входе анализатора есть два сигнала с частотами 4.7 и 5.3 ГГц. Если бы нас интересовал конкретно один из этих сигналов, то достаточно было бы использовать полосовой фильтр, чтобы пропустить в анализатор нужный нам сигнал и подавить второй. Однако фиксированный фильтр не устраняет множественные отклики; поэтому если спектр густо заселен, все равно есть вероятность путаницы. Еще более важным является ограничение, которое фиксированный фильтр накладывает на гибкость всего анализатора. Если мы проводим какие-то широкополосные измерения, нам точно не захочется постоянно менять полосовые фильтры.
Решением является настраиваемый фильтр, построенный так, что он автоматически следит за частотой подходящего режима смешения. На Рис. 7-7 проиллюстрировано действие такого преселектора. Здесь мы используем преимущество того факта, что наш супергетеродинный анализатор спектра не проводит анализ в реальном времени; то есть он настраивается только на одну частоту в один момент времени. Пунктирная линия на Рис. 7-7 представляет собой полосу следящего преселектора. Сигналы за штриховой линией подавляются.
Предположим, у нас есть сигналы на 4.7 ГГц и 5.3 ГГц на входе анализатора. Если мы установим центральную частоту 5 ГГц и полосу обзора 2 ГГц, то давайте посмотрим, что случится, когда анализатор будет перестраиваться через этот диапазон. Когда гетеродин проходит через 4.4 ГГц (частота, на которой он может смешиваться с входным сигналом 4.7 ГГц в режиме смешения 1+ ), преселектор настраивается на 4.1 ГГц и, таким образом, подавляет сигнал 4.7 ГГц.
Поскольку входной сигнал не достигает смесителя, никаких смешений не происходит, и никакого отклика на дисплее не появляется. Как только гетеродин минует 5 ГГц, преселектор позволяет сигналу 4.7 ГГц достичь смесителя, и мы видим соответствующий отклик на дисплее. Сигнал на частоте зеркального канала 5.3 ГГц подавляется, поэтому он не создает продукт смешения, который складывался бы с продуктом смешения от 4.7 ГГц и приводил к появлению отклика неправильной амплитуды. И, наконец, когда гетеродин проходит 5.6 ГГц, преселектор позволяет сигналу 5.3 ГГц достичь смесителя, и мы видим его верное отображение на дисплее. На Рис. 7-7 видно, что различные режимы смешения не пересекаются. Так что, до тех пор, пока полоса преселектора достаточно узка (она обычно меняется от 35 МГц на низких частотах до 80 МГц на высоких частотах), он будет значительно ослаблять все зеркальные и множественные отклики.
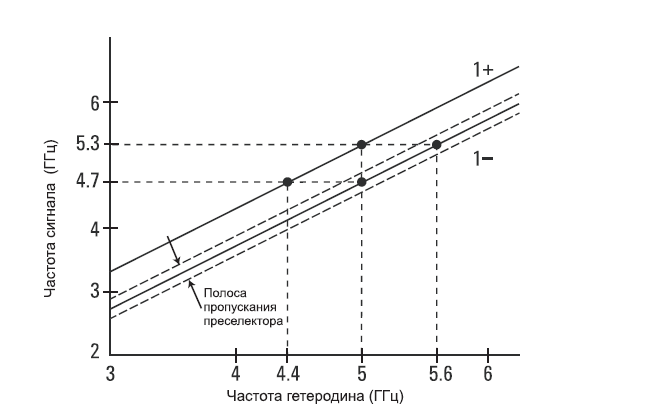
Слово «устранять» может быть преувеличением. Подавление у преселектора не бесконечное. Граница его проходит скорее где-то на уровне 70-80 дБ. Так что, если мы исследуем очень низкоуровневые сигналы при одновременном наличии сигналов с очень высоким уровнем, то мы можем увидеть низкоуровневые зеркальные и множественные отклики высокоуровневых сигналов.
А что насчет нижнего поддиапазона частот? Ведь большинство следящих преселекторов основано на ЖИГ-технологии, а ЖИГ-фильтры не очень хорошо работают на низких частотах. К счастью, решение есть. Как мы видели на Рис. 7-3, ни один другой режим смешения не перекрывает режим 1- в случае низких частот и высокой ПЧ. Поэтому простой фильтр низких частот поможет нам ослабить и зеркальные, и множественные отклики. На Рис. 7-8 изображена схема обычного анализатора спектра СВЧ.
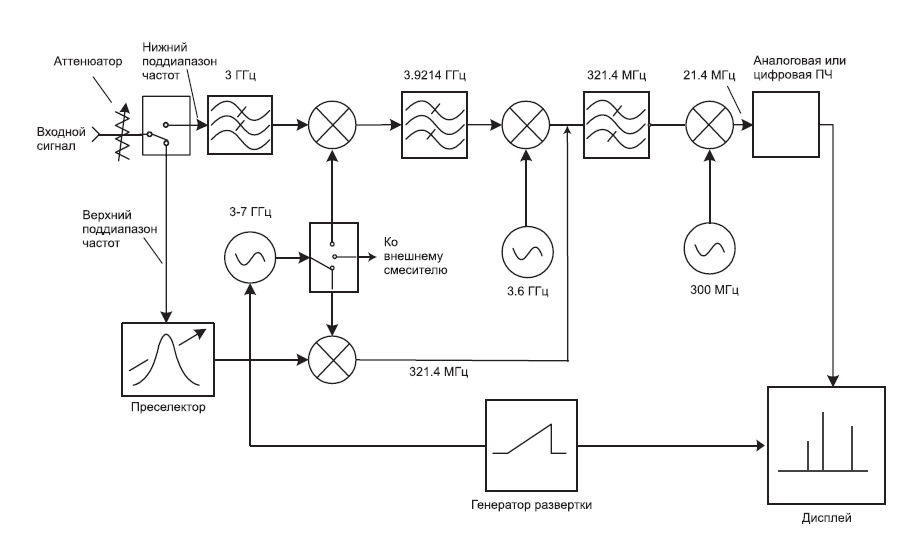
Амплитудная калибровка
До сих пор мы рассматривали то, как анализатор спектра с гармоническим смешением реагирует на различные входные частоты. А как насчет амплитуд?
Потери преобразования в смесителе – это функция номера гармоники, и потери эти увеличиваются с ростом номера. Это означает, что сигналы одинаковой амплитуды будут отображаться на разных уровнях на дисплее, если они смешиваются на разных гармониках. Так что надо что-то предпринять, чтобы сохранить калибровку по амплитуде. В анализаторах фирмы Agilent, например, изменяется усиление ПЧ. Увеличение потерь преобразования на более высоких гармониках гетеродина выливается в снижение чувствительности, точно так же как если бы мы увеличили входную аттенюацию. А поскольку изменение усиления ПЧ происходит уже после потерь преобразования, то изменение усиления отображается соответствующим изменением уровня шума на экране. Так что мы можем определить чувствительность анализатора в диапазонах смешения на гармониках, отмечая средний уровень собственных шумов, точно так же, как мы делали это в случае смешения на основной частоте.
В старых анализаторах спектра увеличение отображаемого среднего уровня шумов с каждой новой гармонической полосой было довольно заметным. Новые модели фирмы Agilent обладают двойным балансным смесителем на гармониках гетеродина с подавлением зеркального канала, что минимизирует увеличение потерь преобразования при использовании более высоких гармоник. Таким образом эффект «лестничных ступенек» при отображении среднего уровня собственных шумов сменился на плавное наклонное увеличение с ростом частоты. Наглядно это можно увидеть на Рис. 7-9.
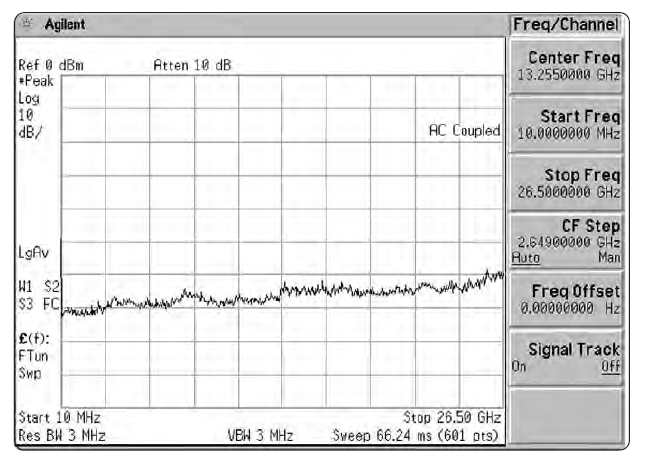
Фазовый шум
В Главе 2 мы отметили, что нестабильность гетеродина анализатора проявляется в виде фазового шума вокруг сигналов, которые достаточно сильно возвышаются над отображаемым средним уровнем шума. Также мы говорили, что этот фазовый шум ограничивает нашу способность разделять близко отстоящие друг от друга сигналы с неодинаковыми амплитудами. Уровень фазового шума показывает угловые, или фазовые, отклонения в сигнале гетеродина. Что происходит с фазовым шумом, когда гармоника гетеродина участвует в процессе смешения? Относительно смешения на основной частоте, фазовый шум (в децибелах) увеличивается как 20log(N), где N – номер гармоники гетеродина.
Для примера положим, что основная частота гетеродина имеет размах отклонений в 10 Гц. Вторая гармоника – размах в 20 Гц, третья – в 30 Гц и т.д. Поскольку фазовый шум указывает на наличие сигнала (в данном случае – шумового), производящего модуляцию, то уровень фазового шума должен быть выше, чтобы вызвать более значительные отклонения. Когда степень модуляции очень мала, как в нашем случае, амплитуда боковых полос модуляции прямо пропорциональна отклонениям несущей (гетеродина). Если отклонения удваиваются, то уровень боковых полос также должен удвоиться по амплитуде; то есть, увеличиться на 6 дБ или 20log(2). В результате, способность нашего анализатора измерять близко расположенные сигналы разных амплитуд уменьшается с ростом номера гармоники гетеродина, участвующей в смешении. Рис. 7-10 иллюстрирует разницу фазового шума при смешении на основной частоте 5-ГГц сигнала и смешении на четвертой гармонике 20-ГГц сигнала.
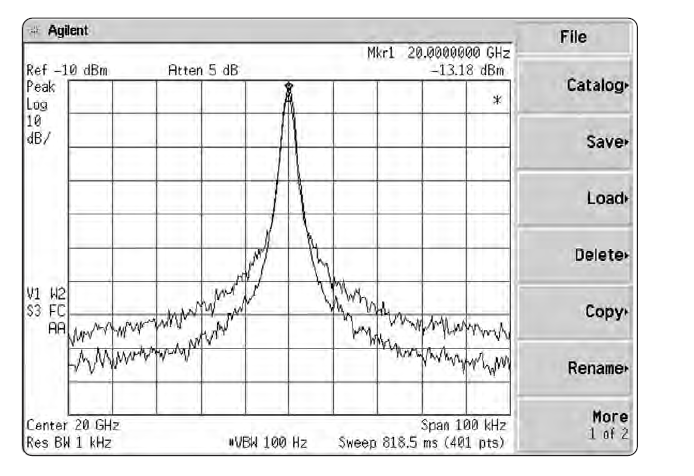
Улучшенный динамический диапазон
Преселектор улучшает динамический диапазон, если наш сигнал достаточно отстоит по частоте. При обсуждении динамического диапазона в Главе 6 было сделано допущение, что и большой, и маленький сигналы постоянно подаются на смеситель, и что их амплитуды не изменяются в течение времени измерения. Но, как мы видели, если сигналы достаточно далеко отстоят друг от друга, преселектор пропускает лишь один, подавляя остальные. К примеру, если бы мы тестировали СВЧ-генератор на наличие гармоник, то преселектор подавил бы основную моду при настройке анализатора на одну из гармоник.
Давайте рассмотрим динамический диапазон на примере тестирования второй гармоники 3-ГГц генератора. Пользуясь примером из Главы 6, допустим, что сигнал величиной -40 дБм в смесителе порождает вторую гармонику -75 дБн. Нам также известно из наших предыдущих обсуждений, что на каждый дБ изменения уровня основной моды в смесителе, диапазон измерений также изменяется на 1 дБ. Кривая искажений второй гармоники показана на Рис. 7-11. Для нашего примера предположим, что от генератора поступает значительная мощность, и установим входной аттенюатор так, чтобы при измерении основной частоты генератора уровень на смесителе был -10 дБм, то есть ниже точки сжатия 1 дБ.
Из графика нам видно, что сигнал -10 дБм на смесителе создаст продукт искажений второй гармоники -45 дБн. Теперь мы настроим анализатор на вторую гармонику частотой 6 ГГц. Если подавление преселектора будет 70 дБ, то сигнал основной частоты на смесителе опустится до -80 дБм. На Рис. 7-11 показано, что для сигнала -80 дБм на смесителе внутреннее генерируемые искажения будут -115 дБн, то есть на 115 дБ ниже нового уровня сигнала основной частоты -80 дБм. Это помещает абсолютный уровень гармоники на отметку -195 дБм. Так что разница между основной частотой гетеродина, когда мы на нее настраиваемся, и внутренне сгенерированной второй гармоникой, при настройке на нее, будет 185 дБ! Совершенно ясно, что для измерения гармонических искажений динамический диапазон ограничен со стороны низких уровней сигналов (гармоник) только уровнем шума (чувствительностью) анализатора.
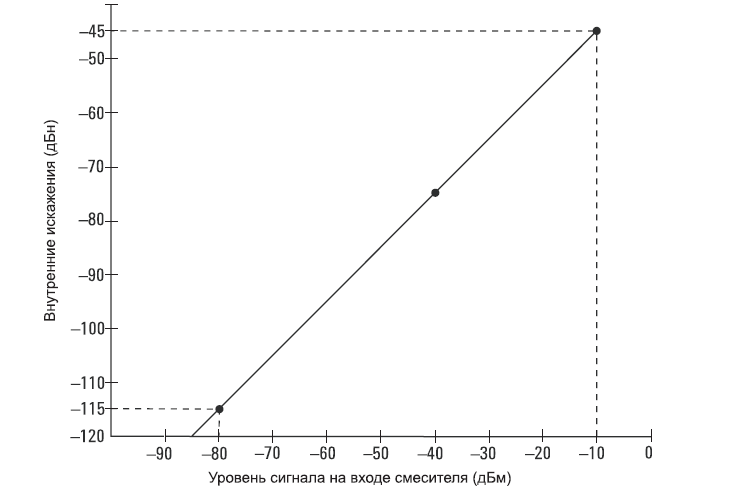
Что же насчет верхней, высокоуровневой части диапазона? При измерении основной частоты генератора нам надо ограничить мощность, идущую на вход смесителя, чтобы получить точные показания уровня сигнала. Можно воспользоваться внутренним или подключаемым аттенюатором, чтобы ослабить сигнал основной частоты на смесителе до некоторого уровня ниже точки сжатия 1 дБ. Однако, поскольку преселектор значительно ослабляет сигнал основной частоты, когда мы настроены на вторую гармонику, то можно и уменьшить аттенюацию, если нам нужна чувствительность получше, чтобы измерить гармонику. Уровень сигнала основной частоты порядка +20 дБм на преселекторе не должен слишком повлиять на нашу способность измерить его гармонику.
Любое улучшение в динамическом диапазоне для измерений интермодуляционных искажений третьего порядка зависит от соотношения разделения подаваемых частот и полосы пропускания преселектора. Как было сказано ранее, полоса обычного преселектора примерно равна 35 МГц в нижнем поддиапазоне частот и 80 МГц в верхнем поддиапазоне частот. В качестве ограничивающего значения можно использовать крутизну обычного ЖИГ-преселектора в 18 дБ на октаву полосы пропускания ниже точки ослабления 3 дБ. Так что для определения улучшения динамического диапазона, нам надо узнать, насколько ослабляется каждый сигнал основной частоты и как это влияет на внутренне генерируемые искажения. Из уравнений для интермодуляции третьего порядка из Главы 6 мы имеем:
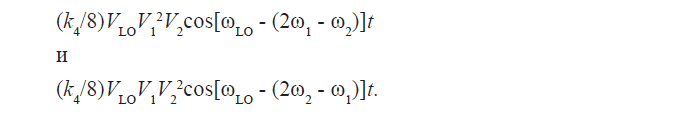
Глядя на эти выражения, видно, что что для продукта искажений (2ω1 – ω2) амплитуда изменяется пропорционально квадрату V1 и первой степени V2. С другой стороны, для продукта искажений (2ω2 – ω1) амплитуда изменяется пропорционально квадрату V2 и первой степени V1. Однако, в зависимости от частот сигнала и их разделения, преселектор может ослабить эти два основных сигнала не в равной степени.
Представим себе ситуацию, изображенную на Рис. 7-12, когда мы настроены на нижний продукт искажений, а два основных сигнала разделены на половину полосы преселектора. В этом случае тестовый тон нижней частоты лежит у самого края полосы пропускания преселектора и ослабляется на 3 дБ. Тестовый тон верхней частоты лежит выше нижнего продукта искажений на величину, равную полной полосе преселектора, и ослабляется примерно на 21 дБ. Поскольку мы настроены на нижний продукт искажений, внутренне генерируемые искажения на этой частоте понижаются в два раза относительно ослабления V1 (2 × 3 дБ = 6 дБ) и на столько же, на сколько ослабляется V2 (21 дБ). Улучшением динамического диапазона будет сумма 6 дБ и 21 дБ, то есть 27 дБ. Как и в случае искажений второй гармоники, уровень собственных шумов анализатора тоже должен быть учтен. Для тестовых тонов, очень близко расположенных по частоте, преселектор не дает никакого улучшения, и динамический диапазон будет таким же, как и вовсе без преселектора.
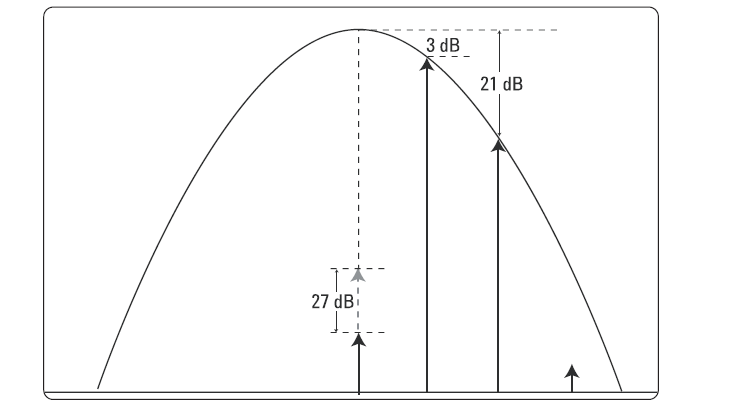
Обсуждение динамического диапазона в Главе 6 относится к случаю, когда мы ведем измерение в нижнем поддиапазоне, фильтруемом ФНЧ. Исключения возникают только тогда, когда определенная гармоника сигнала нижнего поддиапазона попадает в диапазон преселектора. Например, если мы измеряем вторую гармонику от сигнала на частоте 2.5 ГГц, преселектор нам становится полезен, когда мы настраиваемся на гармонику с частотой 5 ГГц.
Плюсы и минусы преселекции
Плюсы преселекции мы с вами уже увидели: это упрощение пользования анализатором, не загроможденная картинка на дисплее, улучшенный динамический диапазон, широкие полосы обзора. Однако, по сравнению с анализаторами без преселекции, есть также и некоторые отрицательные стороны.
Во-первых, преселектор обладает вносимыми потерями, обычно от 6 до 8 дБ. Эти потери вносятся до первой ступени усиления, поэтому чувствительность системы ухудшается на полную величину этих потерь. Вдобавок, когда преселектор присоединен непосредственно к смесителю, взаимодействие рассогласования преселектора и рассогласования смесителя может ухудшить частотную характеристику. Для компенсации этой волнистости необходимо применять определенные калибровочные методы. Другим способом решения этой проблемы может быть включение согласующей прокладки (фиксированного аттенюатора) или изолятора между преселектором и смесителем. В этом случае чувствительность ухудшится на полное значение потерь в аттенюаторе или изоляторе.
В некоторых архитектурах анализаторов спектра устраняется необходимость в согласующем переходе или изоляторе. По мере увеличения электрической длины между преселектором и смесителем, скорость изменения фазы отраженного и переотраженного сигналов увеличивается при заданном изменении входной частоты. Результатом будет более выраженный эффект волнистости. Архитектуры, подобные тем, что используются в приборах серий ESA и PSA, включают в себя смесительные диоды, как составную часть сборки преселектор/смеситель. В такой конструкции обеспечивается минимальная электрическая длина между преселектором и смесителем. В таких архитектурах устраняется волнистость частотной характеристики и улучшается чувствительность системы из-за отсутствия согласующего перехода или изолятора.
Даже помимо взаимодействий со смесителем, преселектор сам несколько ухудшает частотную характеристику. Полоса пропускания преселектора не является идеально ровной, а всегда имеет некоторую волнистость. В большинстве конструкций, развертка подстроечного напряжения подается на преселектор и на гетеродин из одного источника, но механизма обратной связи, чтобы убедиться, что преселектор в точности отслеживает настройку анализатора, нет. Другой причиной посленастроечного дрейфа является собственный нагрев из-за тока в цепи преселектора. Положение центра полосы пропускания преселектора будет зависеть от температуры и градиентов температуры. А это будет в свою очередь зависеть от истории настройки преселектора. В результате, наилучшей равномерности можно добиться, центруя преселектор на каждом сигнале. Функция центровки обычно обеспечивается встроенными средствами анализатора, и включается либо вручную с панели управления при проведении измерения, либо программно в автоматизированных измерительных системах. При активации функция центровки подправляет настроечный ЦАП преселектора, чтобы поместить центр полосы пропускания на сигнал. Спецификации частотной характеристики большинства СВЧ-анализаторов соответствуют реальности только после центровки преселектора, поэтому на практике лучше всего пользоваться этой функцией до проведения амплитудных измерений микроволновых сигналов, чтобы избежать эффекта посленастроечного дрейфа.
Внешнее гармоническое смешение
Мы рассмотрели процесс настройки на высокие частоты, происходящий внутри анализатора. Для внутреннего гармонического смешения анализаторы серий ESA и PSA используют вторую гармонику (N=2-) для настройки до 13.2 ГГц, и четвертую (N=4-) для настройки до 26.5 ГГц. Что же делать, если мы хотим провести измерение, лежащее выше максимальной частоты настройки анализатора? В некоторых анализаторах спектра предусмотрен способ обхода внутреннего первого смесителя и преселектора для использования внешнего подключаемого смесителя, дающего возможность проводить более высокочастотные измерения2. При внешнем смешении мы можем использовать более высокие гармоники первого гетеродина. Обычно, у анализатора спектра, который поддерживает возможность внешнего смешения, есть два дополнительных разъема на панели. Порт «Выход гетеродина» поставляет сигнал внутреннего первого гетеродина на внешний смеситель, который использует его высокие гармоники для смешения с высокочастотными сигналами. Выход ПЧ внешнего смесителя подключается к порту «Вход ПЧ» анализатора. И пока внешний смеситель использует ту же ПЧ, что и анализатор, сигнал может быть обработан и отображен внутренними средствами анализатора, точно как и любой другой сигнал, поступающий от внутреннего первого смесителя. На Рис. 7-13 изображена структурная схема использования внешнего смесителя в связке с анализатором спектра.
2. Более подробно о внешнем смешении см. документ Agilent Application Note 1485, External Waveguide Mixing and Millimeter Wave Measurements with Agilent PSA Spectrum Analyzers.
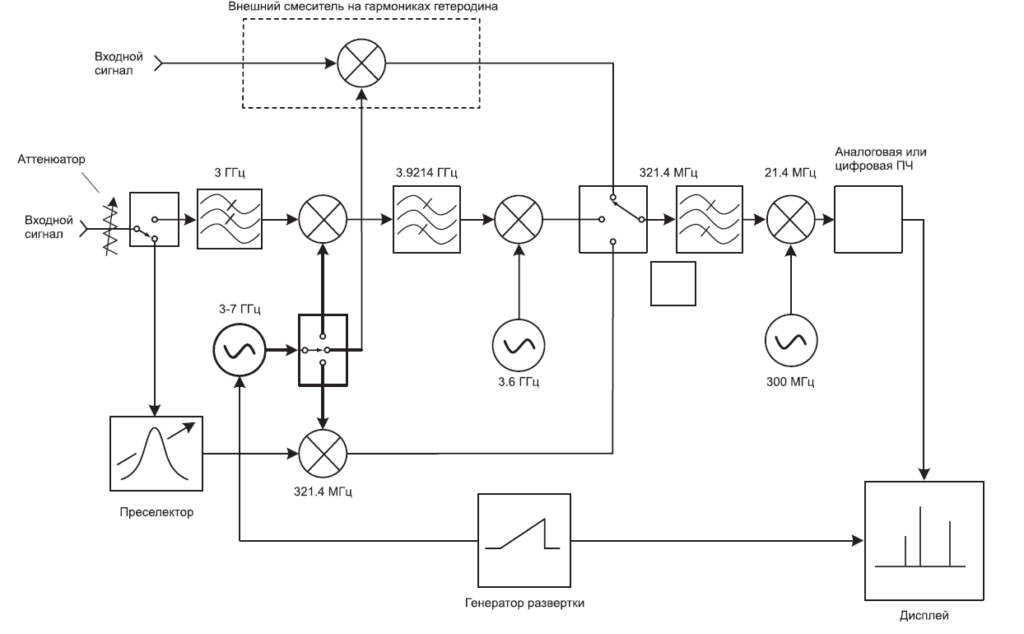
В Табл. 7-1 перечислены режимы гармонического смешения, используемые анализаторами ESA и PSA в различных полосах миллиметровых волн. Смеситель выбирается в зависимости от частотного диапазона. Обычно это стандартные волноводные диапазоны. Существует два вида внешних смесителей на гармониках: с преселекцией и без. Компания Agilent предлагает смесители без преселекции в шести частотных диапазонах: 18 – 26.5 ГГц, 26.5 – 40 ГГц, 33 – 50 ГГц, 40 – 60 ГГц, 50 – 75 ГГц и 75 – 110 ГГц. С преселектором доступны четыре модели в диапазонах до 75 ГГц. Для частот свыше 110 ГГц существуют модели других производителей, позволяющие работать до частот 325 ГГц.
Некоторым внешним смесителям от других производителей требуется ток смещения для того, чтобы установить диоды смесителя на требуемую рабочую точку. Анализаторы спектра серий ESA и PSA могут обеспечить подачу постоянного тока до ±10 mA через порт «Выход ПЧ», чтобы обеспечить смещение и максимально облегчить подготовку к измерению.
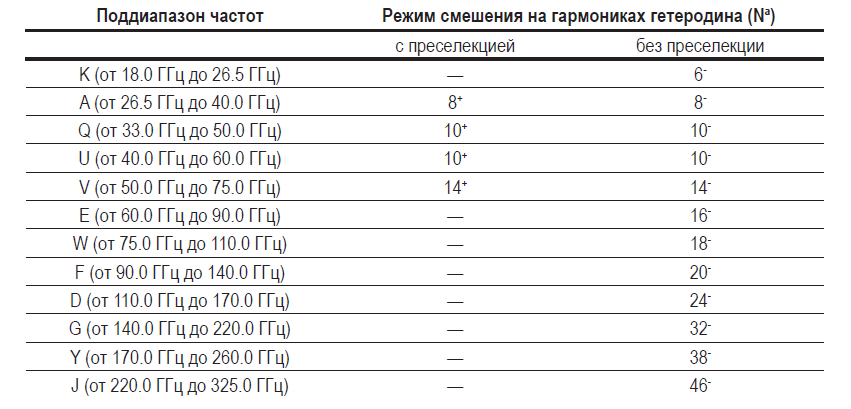
Происходит ли смешение на внутреннем смесителе или на внешнем – проблемы в любом случае одинаковы. Сигнал гетеродина и его гармоники смешиваются не только с радиочастотным входным сигналом, но и с любым сигналом, который может присутствовать на входе. Так могут появиться продукты смешения, попадающие на ПЧ и обрабатывающиеся наряду с другими, нужными сигналами. Есть два способа борьбы с этими нежелательными сигналами. Преселектор, встроенный во внешний смеситель, осуществляет те же самые функции настраиваемого фильтра, что и в анализаторе спектра, только в рамках интересующего частотного диапазона. На Рис. 7-14 показан анализатор спектра и внешний смеситель со встроенным преселектором. Преимущества и недостатки внешнего смесителя с преселекцией практически идентичны таковым в случае преселектора, встроенного в анализатор спектра. Наиболее явным недостатком смесителей с преселекцией является увеличение вносимых потерь из-за фильтра, что выражается в снижении чувствительности измерения. Смесители с преселектором также значительно дороже, чем без него. По этим причинам в возможности самого анализатора спектра включается другой способ работы с нежелательными сигналами. Эта функция называется «идентификация сигнала».
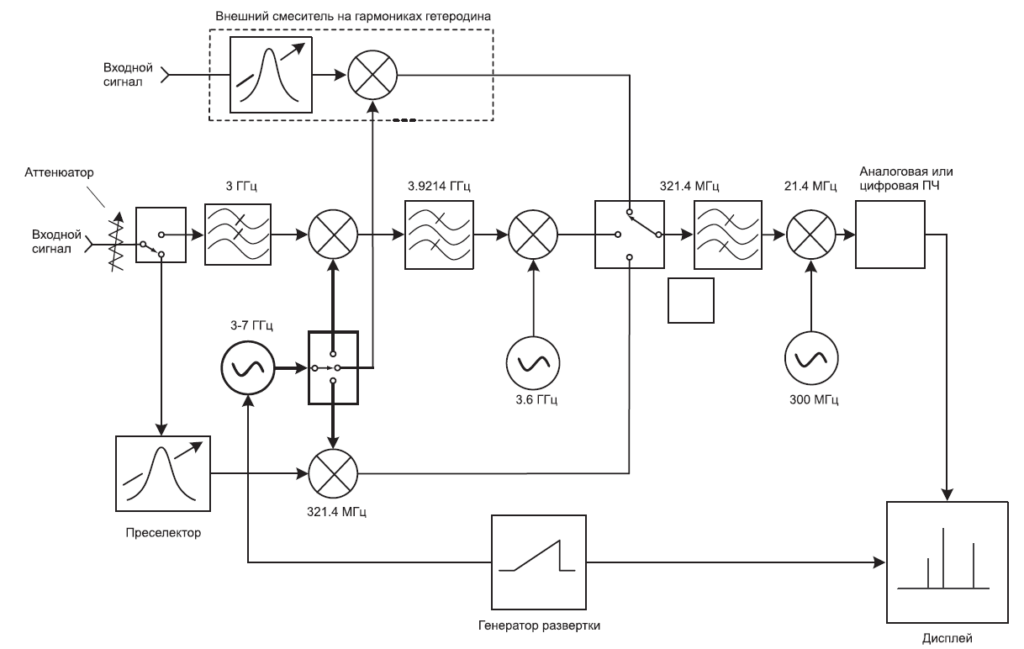
Идентификация сигнала
Даже при использовании смесителя без преселекции и при работе в тщательно контролируемом окружении бывают ситуации, когда нам приходится иметь дело с неизвестными сигналами. В таких случаях вполне вероятно, что отклик, наблюдаемый на экране, был сгенерирован на гармонике гетеродина или в режиме смешения, отличном от того, на который настроен и калиброван дисплей. Так что у нашего анализатора должен быть способ поведать нам о том, калиброван ли дисплей для этого отклика или же нет. Для примера давайте предположим, что мы пользуемся фильтром Agilent 11970V без преселекции для диапазона 50 – 75 ГГц, который использует режим смешения 14-. Часть этого миллиметрового диапазона можно увидеть на Рис. 7-15.
Анализатор спектра Agilent E4407B серии ESA-E предлагает два метода идентификации сигнала: сдвиг изображения и подавление изображения. Для начала рассмотрим метод сдвига изображения. Изучая Рис. 7-16, давайте предположим, что мы настроили анализатор на частоту 58.5 ГГц. 14-ая гармоника гетеродина порождает пару откликов, и продукт смешения 14- появляется на экране в правильной точке 58.5 ГГц, а продукт смешения 14+ дает отклик с частотой 57.8572 ГГц, что на 2fIF ниже реального отклика. Поскольку ПЧ анализатора серии ESA равна 321.4 МГц, то пара откликов будет разнесена по частоте на 642.8 МГц.
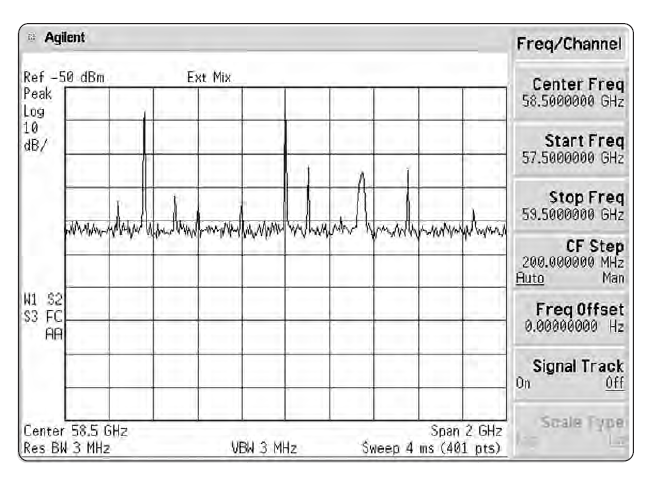
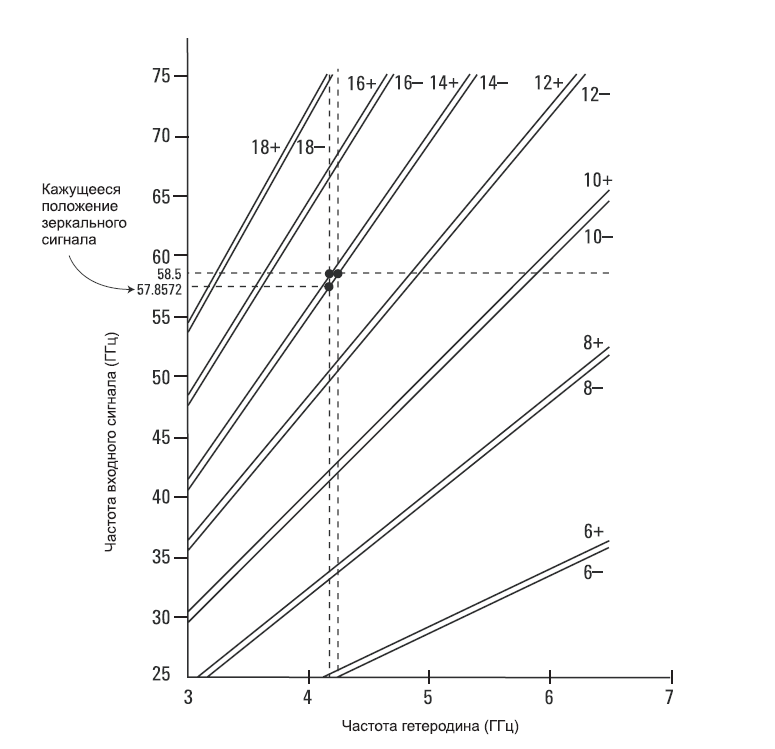
Предположим, что некоторое представление о характеристиках нашего сигнала мы все же имеем, но точную частоту не знаем. Как нам определить, какой из сигналов верный? Процедура сдвига изображения перенастраивает основную частоту гетеродина на величину равную 2fIF/N. Благодаря этому гармоника с номером N смещается на 2fIF. Если мы настроены на реальный сигнал, его соответствующая пара займет на экране то положение, которое он занимал при предыдущем цикле развертки. Если мы настроены на другую множественную пару, сгенерированную какой-то другой гармоникой, то сигнал на дисплее окажется сдвинут по частоте. Анализатор ESA смещает гетеродин в поочередных циклах развертки, что дает две картинки, изображенные на Рис. 7-17а и 7-17б. На Рис. 7-17а реальный сигнал (продукт смешения на 14-) настроен в центр экрана. На Рис. 7-17б показано, как функция сдвига изображения смещает соответствующую пару (продукт смешения 14+) в центр экрана.
Рисунок 7-17. Два разных прохода развертки, снятые с использованием функции сдвига изображения

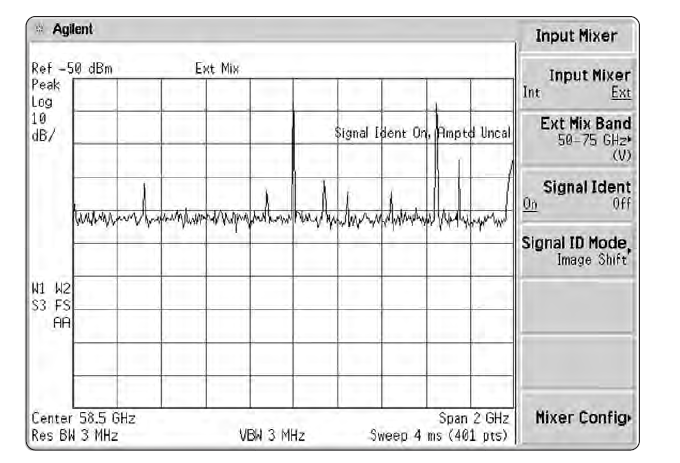
Теперь давайте разберем второй метод идентификации сигнала, называемый подавлением изображения. В этом режиме берутся два последовательных цикла развертки с функцией MIN HOLD, которая запоминает меньшее из значений для каждой точки отображения (или блока) за оба прохода развертки. Первый проход развертки осуществляется при обычных значениях настройки гетеродина. При втором проходе основная частота гетеродина смещается на величину равную 2fIF/N. Как мы видели в предыдущем методе, при этом второй продукт смешения на нужной гармонике попадет точно в то место, где при первом проходе находился отклик реального сигнала. Поэтому здесь трасса сохранит высокое амплитудное значение. Любой ложный отклик, смещенный по частоте, будет заменен на более низкое значение в данной точке. Таким образом, все зеркальные и неправильные множественные отклики отобразятся на экране как шум. Это проиллюстрировано на Рис. 7-18.
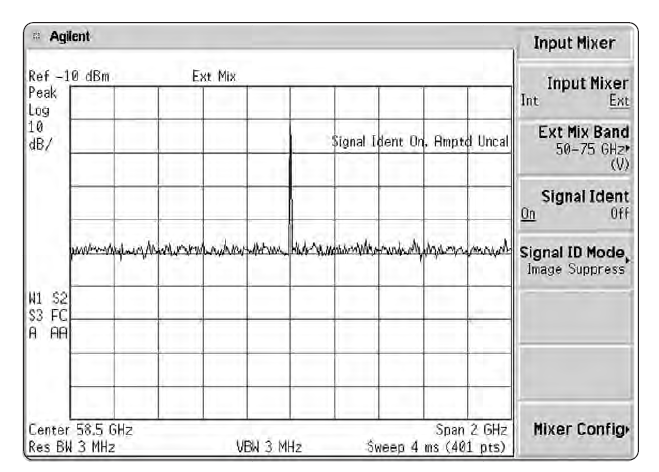
Следует отметить, что оба метода идентификации сигнала используются только для идентификации верных частот. Во время включенной функции идентификации сигнала не следует предпринимать попыток провести амплитудные измерения. На Рис. 7-17 и 7-18 видно экранное сообщение, уведомляющее пользователя об этом факте. Как только мы определим интересующий нас реальный сигнал, функцию идентификации мы выключаем и приближаем изображение сигнала, уменьшая полосу обзора. Теперь можно измерять частоту и амплитуду сигнала. См. Рис. 7-19.
Для проведения точных амплитудных измерений очень важно сперва ввести калибровочные данные для внешнего смесителя. Обычно эти данные поставляются производителем смесителя и представляют собой таблицу потерь преобразования в смесителе, в дБ, определенную для некоторого количества точек частоты в соответствующем диапазоне. Таблица для заполнения вызывается клавишей [AMPLITUDE] и последующим выбором в меню [More], [Corrections], [Other] и [Edit]. После внесения данных потерь преобразования, корректировка применяется путем нажатия [Correction On]. Теперь опорный уровень анализатора откалиброван для сигналов на входе внешнего смесителя. Если присутствуют другие элементы с потерями или усилением, включенные между источником сигнала и смесителем (антенны, кабели, предусилители), частотные характеристики этих элементов следует также внести в таблицу поправок амплитуды.
Глава 8 Современные анализаторы спектра
На протяжении предыдущих глав мы разобрали основную архитектуру анализатора спектра и получили основные понятия о проведении измерений в частотной области. На практике, современные анализаторы спектра должны уметь справляться со многими дополнительными задачами, чтобы удовлетворять всем требованиям современных измерений. Эти задачи включают в себя:
- обеспечение измерений в специфичных задачах: мощности соседних каналов, коэффициента шума, фазовых шумов;
- обеспечение измерений для анализа цифровой модуляции в соответствии с индустриальными или регулирующими стандартами (GSM, cdma2000, 802.11, Bluetooth);
- проведение векторного анализа сигналов;
- сохранение данных;
- вывод данных на печать;
- передача данных через шину ввода/вывода в компьютер;
- обеспечение возможности дистанционного управления посредством GPIB, LAN, Internet;
- предоставление возможности обновления вшитых программ для включения новых возможностей или устранения дефектов;
- обеспечение возможности самокалибровки, устранения неисправностей, диагностики и починки;
- совместимость и возможность работы с опциональным оборудованием и/или программным обеспечением для расширения возможностей.
Специфические измерительные задачи
Вдобавок к измерениям основных характеристик сигнала – частоты и амплитуды – зачастую возникает потребность в проведении специфического измерения определенных параметров сигнала. Это, к примеру, может быть измерение мощности в канале и измерение мощности в соседних каналах, которое было рассмотрено нами в Главе 6. У многих сегодняшних анализаторов спектра эти функции являются уже встроенными. Нам нужно только задать полосу каналов и разнесение между ними, а затем запустить автоматическое измерение простым нажатием кнопки.
Дополнительная интегральная функция распределения (CCDF), показывающая статистику мощности, — еще один пример измерительной возможности, которая все чаще встречается в современных анализаторах спектра. Это проиллюстрировано на Рис. 8-1. CCDF-измерения предоставляют статистическую информацию, показывающую процент времени, которое мгновенная мощность сигнала превышает средний уровень мощности на заданное количество дБ. Эта информация полезна при разработке, к примеру, усилителей мощности, где важно обрабатывать мгновенные пики сигнала с минимальным искажением, одновременно минимизируя стоимость, массу и энергопотребление устройства.
Другими примерами встроенных измерительных функций могут служить измерения занимаемой полосы, гармонических искажений и искажений пересечения третьего порядка (TOI), а также паразитного излучения. Настройки прибора – центральная частота, полоса обзора, полоса разрешения — для этих измерений зависят от определенных радио-стандартов, в соответствии с которыми исследуется конкретное устройство. У большинства современных анализаторов спектра эти настройки хранятся в памяти, так что пользователь может просто выбрать необходимый радио-стандарт из списка (GSM/EDGE, cdma2000, W-CDMA, 802.11a/b/g и т.п.) и провести измерения надлежащим образом.
Конструкторы СВЧ-устройств часто заинтересованы в знании коэффициента шума своих устройств, поскольку он напрямую влияет на чувствительность приемников и других систем. У некоторых анализаторов спектра – например, у моделей серий PSA и ESA-E, — есть дополнительная возможность измерения коэффициента шума. Эта опция предоставляет возможность управления источником шума, который необходимо подключить к входу исследуемого устройства, а также использовать программные средства, требуемые для автоматизирования процесса измерения и вывода результатов. На Рис. 8-2 показаны обычные результаты подобного измерения, содержащие коэффициент шума исследуемого устройства (верхняя трасса) и усиление (нижняя трасса) в зависимости от частоты. Для более подробной информации об измерениях коэффициента шума см. документ Agilent Application Note 1439, Measuring Noise Figure with a Spectrum Analyzer.
Аналогично, измерение фазовых шумов – обычная процедура при исследовании работы генераторов. В системах связи с цифровой модуляцией фазовый шум может негативно повлиять на значение коэффициента битовых ошибок. Фазовый шум также способен снизить способность доплеровских радарных систем улавливать и обрабатывать импульсы, отраженные от цели. Многие анализаторы фирмы Agilent, включая модели серий ESA, PSA и 8560, могут предложить опциональные возможности измерения фазового шума. Они предоставляют программные средства для управления измерением и выводом результатов измерений фазового шума в зависимости от частотной отстройки от несущей, как показано на Рис. 8-3.
Анализ цифровой модуляции
У обычных систем беспроводной связи, используемых нынче по всему миру, есть предписанные методы измерения параметров, установленные организациями, разрабатывающими стандарты, или же государственными органами регулирования. И в анализаторах спектра сегодня обычно можно встретить опциональные возможности по проведению ключевых измерений для различных форматов связи. Например, если нам надо протестировать передатчик на предмет соответствия стандарту беспроводной связи Bluetooth, нам нужно измерить такие параметры, как:
- среднюю/пиковую выходную мощность
- модуляционные характеристики
- начальный частотный допуск несущей
- дрейф частоты несущей
- полосу/канал слежения
- обзор модуляции
- полосу по уровню 20 дБ
- мощность соседних каналов
Такие измерения возможно провести на приборах серии ESA-E с соответствующими опциями. Для более подробной информации об измерениях в рамках стандарта Bluetooth см. документ Agilent Application Note 1333, Performing Bluetooth RF Measurements Today. Опции для проведения измерений по другим стандартам связи доступны для приборов серии ESA-E, включая стандарты cdmaOne и GSM/GPRS/EDGE.
Измерительные возможности для широкого ассортимента стандартов беспроводной связи также доступны для анализаторов серии PSA, включая:
- GSM/EDGE
- W-CDMA
- HSDPA
- cdma2000
- 1xEV-DO
- 1xEV-DV
- cdmaOne
- NADC and PDC
- TD-SCDMA
На Рис. 8-4 показано измерение модуля вектора погрешности, проводимое для сигнала GSM/EDGE. Этот тест помогает провести диагностику модуляционных искажений или искажений усиления, которые ведут к битовым ошибкам в приемнике.

Не все системы цифровой связи основаны на подробно сформулированных индустриальных стандартах. Инженерам, работающим с нестандартными запатентованными системами или с системами еще только разрабатывающихся стандартов, необходимо больше гибкости для анализа векторно-модулированных сигналов в изменяющихся условиях. Обеспечить это можно двумя способами. Во-первых, во многих анализаторах спектра имеются возможности встроенного анализа модуляции. Во-вторых, более обширный анализ можно провести при помощи программного обеспечения, установленного на внешний компьютер. Например, программное обеспечение для векторных анализаторов сигнала серии Agilent 89600 может быть использовано с анализаторами спектра серий ESA и PSA для обеспечения многостороннего и гибкого векторного анализа сигнала. В этом случае анализатор спектра работает как радиочастотный понижающий преобразователь и аналого-цифровой преобразователь. Программное обеспечение работает с анализатором спектра посредством соединения GPIB или LAN, и передает IQ-данные в компьютер, где и производится векторный анализ сигнала. Измерительные настройки – тип модуляции, скорость передачи, фильтрация, время запуска и длительность регистрации – можно изменять по необходимости, в зависимости от конкретного исследуемого сигнала.
Сохранение и печать данных
По окончании измерения вполне закономерно желание как-то зафиксировать и сохранить полученные данные. Возможно, нам будет достаточно просто сделать быструю распечатку с дисплея прибора. В зависимости от конкретных моделей анализатора и принтера, соединить их можно по параллельному порту, RS-232 или GPIB.
Очень часто нам важнее сохранить результаты измерения в виде файла данных — либо в собственную память анализатора, либо на универсальный внешний накопитель (например, гибкий диск). В таком случае нас могут заинтересовать различные формы представления данных, которые мы желаем сохранить. Это включает:
- Графическое изображения на дисплее – Желательно, в распространенном формате файла, вроде BMP, gif или Windows metafile.
- Данные трассы – Сохраняются в виде пар координат X-Y, представляющих точки частоты и амплитуды на экране. Количество пар данных может варьироваться. Современные анализаторы спектра – например, приборы серии ESA и PSA, — позволяют выбирать разрешение экрана, устанавливая от минимум 2 до максимум 8192 дисплейных точек на экране. Такой формат данных хорошо подходит для использования в электронных таблицах при работе на компьютере.
- Состояние прибора – Необходимо для протоколирования настроек анализатора спектра: центральной частоты, полосы обзора, опорного уровня и т.п., которые использовались при проведении измерения. Совпадение измерительных настроек очень важно для проведения повторяемых измерений по прошествии некоторого времени.
Большинство анализаторов спектра фирмы Agilent поставляются с копией программного обеспечения Agilent’s IntuiLink. Оно позволяет переводить данные о трассе или о настройках прибора непосредственно в электронную таблицу Microsoft Excel или в документ Word.
Передача данных и дистанционное управление прибором
В 1977 году компания Agilent Technologies (в то время еще в составе Hewlett-Packard) создала первый в мире анализатор спектра, управляемый по GPIB – модель 8568А. Интерфейс GPIB (также известный как HP-IB или IEEE-488) сделал возможным управление всеми главными функциями анализатора с внешнего компьютера и передачу данных трассы на компьютер. Это новшество проложило путь множеству автоматизированных измерений спектра, которые оказались более быстрыми, чем измерения с ручным управлением, и обладали более высокой повторяемостью. А данные измерений, передаваемые на компьютер, можно было сохранять на диск, анализировать, корректировать и обрабатывать всевозможными способами.
Сегодня автоматическое контрольно-измерительное оборудование стало нормой, и практически все современные анализаторы спектра поставляются со множеством встроенных интерфейсов. Самым распространенным так и остался GPIB, но в последние годы значительно возросла популярность подключения по Ethernet LAN, поскольку оно обеспечивает высокую скорость передачи данных на большое расстояние, а также легко интегрируется в любое окружение с компьютерной сетью — например, производственные помещения. Да и другие стандартные интерфейсы, которые широко применяются в компьютерной индустрии, скорее всего, найдут воплощение в составе анализаторов спектра в будущем, что облегчит соединение прибора и компьютера.
Доступен ряд коммерческих программных продуктов для обеспечения управления анализатором спектра удаленно через шину ввода/вывода. Также можно написать и собственное программное обеспечение для управления прибором, причем несколькими разными способами. Один из методов – это посылать программирующие команды напрямую в анализатор. Старые модели обычно использовали собственные фирменные наборы команд, но новые инструменты – например, серии Agilent ESA и PSA, — используют команды общего промышленного стандарта SCPI («стандартные команды для программируемых приборов»). Более распространенный способ – использовать стандартные программные драйверы, например VXI plug&play, которые позволяют пользоваться функциональными командами высокого уровня без необходимости подробного знания составных команд SCPI. Не так давно появилось новое поколение драйверов, независимых от языка, под названием IVI-COM («взаимозаменяемый виртуальный инструмент»), которые можно использовать в работе с моделями серий ESA и PSA. Драйверы IVI-COM основаны на стандарте Microsoft Component Object Model и работают в ряде PC-приложений и сред разработки, таких как Agilent T&M Programmers Toolkit и Microsoft Visual Studio .NET.
Некоторые задачи требуют, чтобы управление анализатором спектра и сбор данных с него проводились с очень большого расстояния. Например, может возникнуть потребность в слежении за спутниковыми сигналами, когда оператор находится в центре управления, а данные собираются с удаленных станций слежения, находящихся за сотни, а то и тысячи километров от центра. Анализаторы спектра серий ESA и PSA имеют программные опции, которые позволяют управлять прибором, захватывать изображение с экрана и передавать данные трассы по сети Internet посредством стандартного web-браузера.
Обновление встроенного ПО
Внутри современных анализаторов спектра содержится намного больше программного обеспечения, чем в приборах, созданных буквально несколько лет назад. И по мере добавления новых возможностей в программы или исправления ошибок, очень желательно обновить прошивки уже готовых приборов, чтобы воспользоваться преимуществами проделанных улучшений.
Свежайшие версии прошивок для анализаторов спектра можно найти на веб-сайте Agilent Technologies. Оттуда их можно сохранить на компьютер в виде файла. Простейший метод перенести новые прошивки в анализатор – это скопировать их при помощи гибких дисков. Некоторые модели, включая приборы серии PSA, позволяют записать новые прошивки непосредственно в анализатор через порт Ethernet LAN.
Рекомендуется периодически заглядывать на веб-страничку, посвященную вашей модели анализатора спектра, и проверять, не обновились ли версии прошивки.
Калибровка, устранение неисправностей, диагностика и ремонт
Анализаторы спектра нуждаются в периодической калибровке, которая обеспечивает уверенность в том, что прибор соответствует всем своим заявленным спецификациям. Обычно ее проводят раз в год. Однако, помимо этих ежегодных калибровок, прибор надлежит периодически настраивать, чтобы скомпенсировать тепловой дрейф и эффекты старения. Современные анализаторы спектра, такие как приборы серий ESA и PSA, обладают встроенными процедурами такой настройки, которые активируются при включении прибора, во время обратной трассировки через определенные интервалы времени, или при изменении внутренней температуры прибора. Эти процедуры постоянно подстраивают прибор, поддерживая его заявленные технические характеристики. Раньше приходилось включать анализаторы в условиях неизменной температуры и держать включенными минимум тридцать минут, чтобы прибор достиг своих заявленных спецификаций. Автоподстроечные процедуры позволяют современным инструментам выйти на заявленный рабочий режим уже через пять минут после включения.
Современные анализаторы спектра обычно имеют программное сервисное меню. С его помощью можно осуществлять полезные диагностические функции, например, проверку органов управления передней панели. Также можно выводить на экран подробности процесса автоподстройки или список опциональных встроенных возможностей измерения, установленных в приборе. Когда возникает необходимость установить новую персонализированную настройку для определенного рода измерений, фирма Agilent предоставляет уникальный лицензионный ключ для нее, привязанный к серийному номеру прибора. Этот ключ вводится с клавиатуры передней панели и активирует вшитую опциональную измерительную возможность.
Заключение
Целью данной книги является предоставить читателю широкий обзор основных концепций и понятий об анализаторах спектра. Однако, вполне предсказуемо желание ознакомиться подробнее со многими другими темами, связанными со спектральным анализом. Подходящим местом, с которого можно начать, является веб-сайт Agilent Technologies по адресу www.agilent.com, на котором можно воспользоваться функцией поиска по теме «анализатор спектра».
Источник: www.agilent.com
Изобретение относится к области оптических измерений, в частности к способам и устройствам для определения центральной частоты симметричной оптической структуры. При реализации способов определения центральной частоты симметричной оптической структуры генерируют одночастотное зондирующее излучение, преобразуют его в двухчастотное, подают его на вход и принимают с выхода симметричной оптической структуры. Далее перестраивают частоту зондирующего излучения в диапазоне измерений, лежащую в области полосы пропускания симметричной оптической структуры, регистрируют изменения его параметров, по которым вычисляют центральную частоту симметричной оптической структуры. При этом при реализации способа по первому варианту разностную частоту выбирают не превышающей полуширины склонов симметричной оптической структуры. В ходе перестройки частоты одночастотного оптического излучения запоминают первое значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m1 и фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения fCP = fCP1. Далее в ходе перестройки частоты одночастотного оптического излучения запоминают второе значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m2=m1 и фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения fCP = fCP2. После чего вычисляют центральную частоту симметричной оптической структуры по формуле fЦ = (fCP1 + fCP2)/2. При реализации способа по второму варианту в ходе перестройки частоты одночастотного оптического излучения регистрируют данные двух соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m3<1, а во втором m=m4=1, и запоминают значение средней частоты двухчастотного зондирующего излучения fCP = fCP4 для второго из них. Далее в ходе перестройки регистрируют данные двух других соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m5=1, а во втором m=m6<1, и запоминают значение средней частоты двухчастотного зондирующего излучения fCP = fCP5 для первого из них, по которым вычисляют центральную частоту симметричной оптической структуры как fЦ = (fCP4 + fCP5)/2. Устройство для определения центральной частоты симметричной оптической структуры состоит из последовательно соединенных перестраиваемого по частоте источника одночастотного оптического излучения, преобразователя одночастотного оптического излучения в двухчастотное, циркулятора, первого волоконно-оптического кабеля, один конец которого соединен с первым выходом циркулятора, а второй конец – с входом симметричной оптической структуры, второго волоконно-оптического кабеля, один конец которого соединен с выходом симметричной оптической структуры, а второй конец – со вторым входом циркулятора, детектора, перестраиваемого фильтра разностной частоты, а также контроллера управления и измерения центральной частоты симметричных оптических структур. Причем перестраиваемый по частоте источник одночастотного оптического излучения, преобразователь одночастотного оптического излучения в двухчастотное, перестраиваемый фильтр разностной частоты и контроллер управления и измерения центральной частоты имеют входы/выходы управления, объединенные в шину управления. Технический результат изобретения заключается в повышении точности определения центральной частоты как узкополосной, так и широкополосной симметричной оптической структуры. 3 н.п. ф-лы, 4 ил.
Техническое решение относится к способам и устройствам оптических измерений, в частности, к способам и устройствам для определения центральной частоты симметричной оптической структуры, значение которой строго регламентируется ITU в телекоммуникационных системах и определяет качество связи, в сенсорных системах является величиной однозначно несущей информацию о величине внешнего воздействия некоторого физического поля или определяет центральное положение области частот радиосигналов обрабатываемых в оптическом диапазоне в радиофотонных системах. Объектом указанных измерений являются симметричные оптические структуры, условно имеющие при линейной аппроксимации трапецеидальную форму: два симметричных склона и плоскую вершину. При этом симметричные оптические структуры будем считать узкополосными, если спектральная протяженность вершины равна нулю, и широкополосными, если больше нуля. Примером первых являются классические волоконно-оптические решетки Брэгга, интерферометры Фабри-Перо, упорядоченные волоконные решетки, тонкопленочные фильтры и т.п., примером вторых – перестраиваемые оптические мультиплексоры ввода-вывода, чипированные решетки Брэгга, полосовые оптические фильтры и т.п.
Известны способы для определения центральной частоты симметричных оптических структур и устройства для их реализации, основанные на использовании широкополосного или одночастотного сканирующего излучения для зондирования оптических полосовых структур на базе оптических анализаторов спектра или векторных и скалярных анализаторов сетей. Данные способы и устройства позволяют определять центральную частоту как узкополосных, так и широкополосных симметричных оптических структур.
Недостатком указанных способов для определения центральной частоты симметричных оптических структур и устройств для их реализации является необходимость использования сложного дорогостоящего блока зондирования симметричных оптических структур и фотоприемного блока для регистрации спектрального смещения центральной частоты. Оптоэлектронная обработка сигналов с выделением центральной частоты из широкого спектра сигналов зондирования, также представляется сложной, и требует наличия либо перестраиваемых лазерных излучателей, либо сложных систем спектральной фильтрациии, либо нескольких фотоприемников, либо, как вариант, системы матричных ПЗС-приемников. Все это приводит к появлению дополнительных источников погрешностей измерения центральной частоты симметричных оптических структур, снижению их точности и невозможности использования указанных устройств в полевых условиях.
Известен способ для определения центральной частоты симметричных оптических структур (описанный в работе Wang Y, Zhang J, Coutinho О, Yao J. «Interrogation of a linearly chirped fiber Bragg grating sensor with high resolution using a linearly chirped optical waveform», Opt Lett. 2015 Nov 1; 40(21)), заключающийся в том, что генерируют одночастотное ЛЧМ оптическое излучение, подают его на вход и принимают с выхода оптической структуры, регистрируют параметры биений зондирующего и отраженного сигналов, по которым далее вычисляют центральную частоту оптической структуры fЦ.
Устройство, реализующее данный способ, содержит последовательно соединенные источник ЛЧМ оптического излучения, контроллер, преобразователь оптического излучения, циркулятор, фотоприемник, контроллер управления и измерения характеристик симметричных оптических структур, волоконно-оптический кабель и оптическую структуру.
Описанный выше способ для определения центральной частоты симметричных оптических структур и устройство для его реализации используют оборудование, применимое в полевых условиях. Данный способ и устройство позволяют определять центральную частоту как узкополосных, так и широкополосных симметричных оптических структур. Их использование позволяет избавиться от применения сложной дорогостоящей спектральной аппаратуры или аппаратуры для векторного или скалярного анализа. Кроме того, применение для анализа центральной частоты симметричных оптических структур биений зондирующего и отраженного сигналов, и перенос информации на частоту биений позволяет избавиться от флуктуаций низкочастотной природы.
Однако недостатком данного способа для определения центральной частоты симметричных оптических структур и устройства для его реализации является наличие паразитной амплитудной модуляции при формировании одночастотного ЛЧМ оптического излучения и малая величина частоты биений, на которой производится анализ центральной частоты, лежащей в области максимальных шумов фотоприемника, что снижает чувствительность, отношение сигнал/шум и точность измерений. Малая величина частоты биений определяется обязательным наличием второй, рядом расположенной опорной решетки, не подверженной воздействию внешних физических полей, что усложняет конструкцию устройства и требования к его эксплуатации в полевых условиях.
Прототипом технического решения для двух вариантов предлагаемого способа является способ для определения центральной частоты симметричных оптических структур (Патент РФ №2512616 С2 на изобретение «Способ измерения параметров физических полей и устройство для его осуществления», МПК G01K 11/32, 10.04.2014), заключающийся в том, генерируют одночастотное оптическое излучение с частотой ![]() , формируют из него двухчастотное зондирующее излучение с двумя составляющими равной амплитуды соответственно на частотах
, формируют из него двухчастотное зондирующее излучение с двумя составляющими равной амплитуды соответственно на частотах ![]() и
и ![]() , со средней
, со средней ![]() и разностной частотами
и разностной частотами ![]() , лежащими в области полосы пропускания симметричной оптической структуры, подают его на вход и принимают с выхода симметричной оптической структуры, при этом частоту одночастотного оптического излучения
, лежащими в области полосы пропускания симметричной оптической структуры, подают его на вход и принимают с выхода симметричной оптической структуры, при этом частоту одночастотного оптического излучения ![]() перестраивают в диапазоне измерений, соответствующем полосе частот симметричного оптического фильтра, при чем в ходе перестройки
перестраивают в диапазоне измерений, соответствующем полосе частот симметричного оптического фильтра, при чем в ходе перестройки ![]() оставляют неизменной, регистрируют изменения параметров двухчастотного зондирующего излучения, а именно, средней частоты двухчастотного зондирующего излучения
оставляют неизменной, регистрируют изменения параметров двухчастотного зондирующего излучения, а именно, средней частоты двухчастотного зондирующего излучения ![]() и коэффициента модуляции т огибающей биений между составляющими двухчастотного зондирующего излучения на выходе симметричной оптической структуры, по которым далее определяют центральную частоту
и коэффициента модуляции т огибающей биений между составляющими двухчастотного зондирующего излучения на выходе симметричной оптической структуры, по которым далее определяют центральную частоту ![]() симметричной оптической структуры.
симметричной оптической структуры.
Устройство, выбранное в качестве прототипа и реализующее данный способ, содержит последовательно соединенные перестраиваемый по частоте источник одночастотного оптического излучения, преобразователь одночастотного оптического излучения в двухчастотное, циркулятор, первый волоконно-оптический кабель, узкополосную симметричную оптическую структуру, второй волоконно-оптический кабель, выход которого через второй вход и второй выход циркулятора соединен с детектором, а также контроллер управления и измерения центральной частоты узкополосных симметричных оптических структур, причем перестраиваемый по частоте источник одночастотного оптического излучения, преобразователь одночастотного оптического излучения в двухчастотное, циркулятор, контроллер управления и измерения центральной частоты узкополосных оптических структур имеют входы/выходы управления, объединенные в шину управления.
Описанный выше способ и устройство, выбранное в качестве прототипа, используют оборудование, применимое в полевых условиях. Его использование, также, как и в приведенном аналоге, позволяет избавиться от применения сложной дорогостоящей спектральной аппаратуры или аппаратуры для векторного или скалярного анализа, а также от шумов низкочастотной природы. Применение для анализа центральной частоты симметричных оптических фильтров биений компонент двухчастотного зондирующего излучения, и перенос информации на частоту биений, которая лежит в области минимальных шумов фотоприемника позволяет повысить чувствительность, отношение сигнал/шум и точность измерений по сравнению с аналогом.
Однако недостатком данного способа и устройства, выбранного в качестве прототипа, является использование широкополосного детектора, ширина полосы пропускания которого может достигать десятков ГГц и определяется полосой пропускания симметричного оптического фильтра и значением большей разностной частоты двухчастотного зондирующего излучения. Данная полоса пропускания больше чем у аналога, и в этом случае интегральный вклад шумов при обработке сигнала на выходе детектора будет значительным.
Вторым недостатком указанных способа и устройства, выбранного в качестве прототипа, является его фактическое назначение для работы с узкополосными симметричными оптическими структурами. Возможность работы с широкополосными оптическими структурами определяется ситуацией, когда разностная частота двухчастотного зондирующего излучения больше, чем спектральная ширина плоской вершины симметричной оптической структуры. В противном случае невозможно определение центральной частоты широкополосных симметричных оптических структур, поскольку при определенных разностной частоте и шаге сканирования возможна ситуация, при которой коэффициент модуляции огибающей биений между компонентами двухчастотного зондирующего излучения будет равен 1 неоднократно, также как и будут равны амплитуды принятых составляющих при ряде последовательных измерений, что противоречит условиям реализации способа.
Решаемая техническая задача (технический результат) для двух вариантов предлагаемого способа и предлагаемого устройства заключается в повышении точности измерений определения центральной частоты как узкополосной, так и широкополосной симметричной оптической структуры.
Решаемая техническая задача в способе для определения центральной частоты симметричной оптической структуры, по его первому варианту, заключающемся в том, что генерируют одночастотное оптическое излучение с частотой ![]() , формируют из него двухчастотное зондирующее излучение с двумя составляющими равной амплитуды соответственно на частотах
, формируют из него двухчастотное зондирующее излучение с двумя составляющими равной амплитуды соответственно на частотах ![]() и
и ![]() , со средней
, со средней ![]() и разностной частотами
и разностной частотами ![]() , лежащими в области полосы пропускания симметричной оптической структуры, подают его на вход и принимают с выхода симметричной оптической структуры, при этом частоту одночастотного оптического излучения
, лежащими в области полосы пропускания симметричной оптической структуры, подают его на вход и принимают с выхода симметричной оптической структуры, при этом частоту одночастотного оптического излучения ![]() перестраивают в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры, при чем в ходе перестройки
перестраивают в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры, при чем в ходе перестройки ![]() оставляют неизменной, регистрируют изменения параметров двухчастотного зондирующего излучения, а именно, средней частоты двухчастотного зондирующего излучения
оставляют неизменной, регистрируют изменения параметров двухчастотного зондирующего излучения, а именно, средней частоты двухчастотного зондирующего излучения ![]() и коэффициента модуляции m огибающей биений между составляющими двухчастотного зондирующего излучения на выходе симметричной оптической структуры, по которым далее определяют центральную частоту
и коэффициента модуляции m огибающей биений между составляющими двухчастотного зондирующего излучения на выходе симметричной оптической структуры, по которым далее определяют центральную частоту ![]() симметричной оптической структуры, достигается тем, что разностную частоту
симметричной оптической структуры, достигается тем, что разностную частоту ![]() выбирают достаточно малой, чтобы не превысить полуширины склонов симметричной оптической структуры, в ходе перестройки частоты одночастотного оптического излучения
выбирают достаточно малой, чтобы не превысить полуширины склонов симметричной оптической структуры, в ходе перестройки частоты одночастотного оптического излучения ![]() запоминают некоторое значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m1, причем m∈[0,5;1] и фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения
запоминают некоторое значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m1, причем m∈[0,5;1] и фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения ![]() , далее в ходе перестройки запоминают значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m2=m1 и фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения
, далее в ходе перестройки запоминают значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m2=m1 и фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения ![]() , завершают перестройку частоты одночастотного оптического излучения
, завершают перестройку частоты одночастотного оптического излучения ![]() вычисляют центральную частоту симметричной оптической структуры как
вычисляют центральную частоту симметричной оптической структуры как ![]() .
.
Решаемая техническая задача в способе для определения центральной частоты симметричной оптической структуры, по его второму варианту, заключающемся в том, что генерируют одночастотное оптическое излучение с частотой ![]() , формируют из него двухчастотное зондирующее излучение с двумя составляющими равной амплитуды соответственно на частотах
, формируют из него двухчастотное зондирующее излучение с двумя составляющими равной амплитуды соответственно на частотах ![]() и
и ![]() , со средней
, со средней ![]() и разностной частотами
и разностной частотами ![]() , лежащими в области полосы пропускания симметричной оптической структуры, подают двухчастотное зондирующее излучение на вход и принимают с выхода симметричной оптической структуры, при этом частоту
, лежащими в области полосы пропускания симметричной оптической структуры, подают двухчастотное зондирующее излучение на вход и принимают с выхода симметричной оптической структуры, при этом частоту ![]() одночастотного оптического излучения перестраивают в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры, при чем в ходе перестройки разностную частоту
одночастотного оптического излучения перестраивают в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры, при чем в ходе перестройки разностную частоту ![]() оставляют неизменной, регистрируют изменения параметров двухчастотного зондирующего излучения, а именно, средней частоты двухчастотного зондирующего излучения
оставляют неизменной, регистрируют изменения параметров двухчастотного зондирующего излучения, а именно, средней частоты двухчастотного зондирующего излучения ![]() и коэффициента модуляции m огибающей биений между составляющими двухчастотного зондирующего излучения на выходе симметричной оптической структуры, по которым далее определяют центральную частоту
и коэффициента модуляции m огибающей биений между составляющими двухчастотного зондирующего излучения на выходе симметричной оптической структуры, по которым далее определяют центральную частоту ![]() симметричной оптической структуры, достигается тем, что в ходе перестройки частоты одночастотного оптического излучения
симметричной оптической структуры, достигается тем, что в ходе перестройки частоты одночастотного оптического излучения ![]() регистрируют данные двух соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m3<1, а во втором m=m4=1, и запоминают значение средней частоты двухчастотного зондирующего излучения
регистрируют данные двух соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m3<1, а во втором m=m4=1, и запоминают значение средней частоты двухчастотного зондирующего излучения ![]() для второго из них, далее в ходе перестройки регистрируют данные двух других соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m5=1, а во втором m=m6<1, и запоминают значение средней частоты двухчастотного зондирующего излучения
для второго из них, далее в ходе перестройки регистрируют данные двух других соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m5=1, а во втором m=m6<1, и запоминают значение средней частоты двухчастотного зондирующего излучения ![]() для первого из них, по которым вычисляют центральную частоту симметричной оптической структуры как
для первого из них, по которым вычисляют центральную частоту симметричной оптической структуры как ![]() .
.
Решаемая техническая задача в устройстве для определения центральной частоты симметричной оптической структуры, содержащем последовательно соединенные перестраиваемый по частоте источник одночастотного оптического излучения, преобразователь одночастотного оптического излучения в двухчастотное, циркулятор, первый волоконно-оптический кабель, один конец которого соединен с первым выходом циркулятора, а второй конец – с входом симметричной оптической структуры, второй волоконно-оптический кабель, один конец которого соединен с выходом симметричной оптической структуры, а второй конец – со вторым входом циркулятора, циркулятор вторым выходом соединен с детектором, а также контроллер управления и измерения центральной частоты симметричных оптических структур, причем перестраиваемый по частоте источник одночастотного оптического излучения, преобразователь одночастотного оптического излучения в двухчастотное, контроллер управления и измерения центральной частоты симметричных оптических структур имеют входы/выходы управления, объединенные в шину управления, достигается тем, что в него дополнительно введен перестраиваемый фильтр разностной частоты, вход которого подключен к выходу детектора, а выход – к входу контроллера управления и измерения центральной частоты симметричных оптических структур, который выполнен как контроллер управления и измерения центральной частоты узкополосных и широкополосных симметричных оптических структур, при этом перестраиваемый фильтр разностной частоты имеет вход/выход управления, подключенный к шине управления.
На фиг. 1 изображена структурная схема устройства, реализующего предложенные способы для определения центральной частоты симметричной оптической структуры (по первому и второму вариантам).
На фиг. 2 и фиг. 3 показано спектральное расположение двухчастотного зондирующего излучения (для первого и второго вариантов предлагаемого способа соответственно) относительно симметричной оптической структуры в случае совпадения их средней частоты с резонансной частотой, где ![]() – частоты составляющих зондирующего излучения на выходе преобразователя одночастотного оптического излучения в двухчастотное,
– частоты составляющих зондирующего излучения на выходе преобразователя одночастотного оптического излучения в двухчастотное, ![]() – средняя частота двухчастотного зондирующего излучения,
– средняя частота двухчастотного зондирующего излучения, ![]() – центральная (резонансная) частота, m – коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения
– центральная (резонансная) частота, m – коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения
На фиг. 4 показана относительная обобщенная расстройка полосы пропускания симметричной оптической структуры, на которой отображена зависимость коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения, полученного на выходе преобразователя одночастотного оптического излучения в двухчастотное, прошедшего через симметричную оптическую структуру и зарегистрированного на выходе перестраиваемого фильтра разностной частоты, от относительной обобщенной расстройки полосы пропускания симметричной оптической структуры.
В приложении 1 и приложении 2 представлены алгоритмы работы контроллера управления и измерения центральной частоты симметричных оптических структур для осуществления измерений (для первого и второго варианта предлагаемого способа соответственно).
Устройство для определения центральной частоты симметричной оптической структуры (фиг. 1), содержит последовательно соединенные перестраиваемый по частоте источник одночастотного оптического излучения 1, преобразователь одночастотного оптического излучения в двухчастотное 2, циркулятор 3, первый волоконно-оптический кабель 4, один конец которого соединен с первым выходом циркулятора 3, а второй конец – с входом симметричной оптической структуры 5, второй волоконно-оптический кабель 6, один конец которого соединен с выходом симметричной оптической структуры 5, а второй конец – со вторым входом циркулятора 3, циркулятор 3 вторым выходом соединен с детектором 7, а также контроллер управления и измерения центральной частоты симметричных оптических структур 8, причем перестраиваемый по частоте источник одночастотного оптического излучения 1, преобразователь одночастотного оптического излучения в двухчастотное 2, контроллер управления и измерения центральной частоты симметричных оптических структур 8 имеют входы/выходы управления, объединенные в шину управления 9, достигается тем, что в него дополнительно введен перестраиваемый фильтр разностной частоты 10, вход которого подключен к выходу детектора 7, а выход – к входу контроллера управления и измерения центральной частоты симметричных оптических структур 8, который выполнен как контроллер управления и измерения центральной частоты узкополосных и широкополосных симметричных оптических структур, при этом перестраиваемый фильтр разностной частоты 10 имеет вход/выход управления, подключенный к шине управления.
Изображенными на фиг. 1 штриховыми линиями условно показаны первая 4 и вторая 6 линии передачи, выполненные на основе волоконно-оптического кабеля. Соединения между перестраиваемым по частоте источником одночастотного оптического излучения 1, преобразователем одночастотного оптического излучения в двухчастотное 2, циркулятором 3 и детектором 7 также показаны штриховыми линиями, поскольку имеют отношения к оптическим блокам. Тип используемых соединений условно не показан, поскольку они могут быть выполнены в любом исполнении, в том числе и в интегральном виде при интегральном объединении всех блоков устройства для определения центральной частоты симметричной оптической структуры. Система электропитания блоков, входящих в состав, условно не показана.
На фиг. 2 и фиг. 3 показано спектральное расположение двухчастотного зондирующего излучения (для первого и второго вариантов предлагаемого способа соответственно) относительно симметричной оптической структуры в случае совпадения их средней частоты ![]() с резонансной частотой
с резонансной частотой ![]() .
.
Изображенные на фиг. 2 составляющие двухчастотного зондирующего излучения ![]() и их расположение показаны в случае совпадения их средней частоты
и их расположение показаны в случае совпадения их средней частоты ![]() с резонансной частотой
с резонансной частотой ![]() . Сигнал, зондирующий симметричную оптическую структуру, в отличие от существующих аналогов и прототипа, представляет собой двухчастотное зондирующее излучение соответственно с составляющими
. Сигнал, зондирующий симметричную оптическую структуру, в отличие от существующих аналогов и прототипа, представляет собой двухчастотное зондирующее излучение соответственно с составляющими ![]() и
и ![]() , со средней
, со средней ![]() и разностной частотами
и разностной частотами ![]() . Исходные амплитуды составляющих на выходе преобразователя одночастотного оптического излучения в двухчастотное 2 равны.
. Исходные амплитуды составляющих на выходе преобразователя одночастотного оптического излучения в двухчастотное 2 равны.
Изображенные на фиг. 3 составляющие двухчастотного зондирующего излучения ![]() и их расположение показаны в случае совпадения их средней частоты
и их расположение показаны в случае совпадения их средней частоты ![]() с резонансной частотой
с резонансной частотой ![]() . Сигнал, зондирующий симметричную оптическую структуру, в отличие от существующих аналогов и прототипа, представляет собой двухчастотное зондирующее излучение соответственно с составляющими
. Сигнал, зондирующий симметричную оптическую структуру, в отличие от существующих аналогов и прототипа, представляет собой двухчастотное зондирующее излучение соответственно с составляющими ![]() и
и ![]() , со средней
, со средней ![]() и разностной частотами
и разностной частотами ![]() . Исходные амплитуды составляющих на выходе преобразователя одночастотного оптического излучения в двухчастотное 2 равны.
. Исходные амплитуды составляющих на выходе преобразователя одночастотного оптического излучения в двухчастотное 2 равны.
На фиг. 4 показана относительная обобщенная расстройка полосы пропускания симметричной оптической структуры 5, на которой отображена зависимость коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения, полученного на выходе преобразователя одночастотного оптического излучения в двухчастотное 2, прошедшего через симметричную оптическую структуру 5 и зарегистрированного на выходе перестраиваемого фильтра разностной частоты 10, от относительной обобщенной расстройки полосы пропускания симметричной оптической структуры 5.
Изображенная на фиг. 4 зависимость коэффициента модуляции огибающей биений двухчастотного зондирующего излучения m на разностной частоте ![]() от относительной обобщенной расстройки полосы пропускания симметричной оптической структуры 5 представлена для случая, когда разностная частота
от относительной обобщенной расстройки полосы пропускания симметричной оптической структуры 5 представлена для случая, когда разностная частота ![]() достаточно мала, чтобы не превысить полуширины склонов симметричной оптической структуры 5. Характерной точкой данной зависимости является точка нулевой относительной обобщенной расстройки, которая соответствует равенству средней частоты
достаточно мала, чтобы не превысить полуширины склонов симметричной оптической структуры 5. Характерной точкой данной зависимости является точка нулевой относительной обобщенной расстройки, которая соответствует равенству средней частоты ![]() зондирующего излучения резонансной частоте
зондирующего излучения резонансной частоте ![]() . В этом случае коэффициент модуляции m1 огибающей биений двухчастотного зондирующего излучения на разностной частоте
. В этом случае коэффициент модуляции m1 огибающей биений двухчастотного зондирующего излучения на разностной частоте ![]() , зарегистрированный на выходе перестраиваемого фильтра разностной частоты 10 будет равен значению «1».
, зарегистрированный на выходе перестраиваемого фильтра разностной частоты 10 будет равен значению «1».
Все сказанное выше относится и к зависимости коэффициента модуляции m2-m6 огибающей биений двухчастотного зондирующего излучения с разностной частотой ![]() .
.
Факт равенства коэффициентов модуляции m1 и m2 значения «1» для огибающей биений двухчастотного зондирующего излучения с разностной частотой ![]() , зарегистрированных на выходе перестраиваемого фильтра разностной частоты 10 используется для принятия решения об определении резонансной частоты
, зарегистрированных на выходе перестраиваемого фильтра разностной частоты 10 используется для принятия решения об определении резонансной частоты ![]() .
.
Рассмотрим осуществление способов и работу устройства для определения центральной частоты симметричной оптической структуры (для первого и второго варианта предлагаемого способа).
Рассмотрим осуществление способа и работу устройства для определения центральной частоты симметричной оптической структуры для первого варианта предлагаемого способа.
Для начала работы с устройством производят включение блоков к сети электропитания согласно их нормируемому напряжению.
Для измерения характеристик симметричной оптической структуры с помощью перестраиваемого по частоте источника одночастотного оптического излучения в двухчастотное 1 генерируют исходное одночастотное оптическое излучение, из которого формируют двухчастотное зондирующее излучение с двумя составляющими равной амплитуды в преобразователе одночастотного оптического излучения в двухчастотное 2.
Для этого с контроллера управления и измерения центральной частоты симметричных оптических структур 8 через шину управления 9 подается команда управления параметрами генерации перестраиваемого по частоте источника одночастотного оптического излучения 1, преобразования в преобразователе одночастотного оптического излучения в двухчастотное 2 и настройки перестраиваемого фильтра разностной частоты 10. Алгоритм работы контроллера управления и измерения центральной частоты симметричных оптических структур 8 для осуществления измерений представлен в Приложении 1 (по первому варианту предлагаемого способа).
В соответствии с алгоритмом работы с поданной командой зондирующий сигнал в преобразователе одночастотного оптического излучения в двухчастотное 2 формируют двухчастотным, состоящим из двух одночастотных сигналов равной амплитуды соответственно на частотах ![]() и
и ![]() . Для его формирования в перестраиваемом по частоте источнике одночастотного оптического излучения 1 генерируют среднюю частоту равную
. Для его формирования в перестраиваемом по частоте источнике одночастотного оптического излучения 1 генерируют среднюю частоту равную ![]() . Средняя частота поступает в преобразователь одночастотного оптического излучения в двухчастотное 2, в котором по полученной команде задают разностную частоту между формируемыми двухчастотного зондирующего излучения
. Средняя частота поступает в преобразователь одночастотного оптического излучения в двухчастотное 2, в котором по полученной команде задают разностную частоту между формируемыми двухчастотного зондирующего излучения ![]() , лежащей в области полосы пропускания симметричной оптической структуры 5. При этом сама средняя частота подавляется. На сформированную разностную частоту
, лежащей в области полосы пропускания симметричной оптической структуры 5. При этом сама средняя частота подавляется. На сформированную разностную частоту ![]() производится настройка перестраиваемого фильтра разностной частоты 10, причем разностную частоту
производится настройка перестраиваемого фильтра разностной частоты 10, причем разностную частоту ![]() выбирают достаточно малой, чтобы не превысить полуширины склонов симметричной оптической структуры 5 и оставляют неизменной в ходе перестройки средней частоты
выбирают достаточно малой, чтобы не превысить полуширины склонов симметричной оптической структуры 5 и оставляют неизменной в ходе перестройки средней частоты ![]() .
.
Затем передают двухчастотное зондирующее излучение к симметричной оптической структуре 5 через циркулятор 3 и первый волоконно-оптический кабель 4. В двухчастотном зондирующем излучении, проходящем через симметричную оптическую структуру 5, происходит изменение амплитуд составляющих зондирующего излучения – они становятся равными в зависимости от взаимного положения его средней частоты ![]() и резонансной частоты
и резонансной частоты ![]() симметричной оптической структуры 5.
симметричной оптической структуры 5.
Далее принимают двухчастотное излучение после воздействия на симметричную оптическую структуру 5 на детекторе 7. В соответствии с алгоритмом работы включают циркулятор 3 по команде с контроллера управления и измерения центральной частоты симметричных оптических структур 8 в режим «двойного Т-моста» так, что прошедшее через симметричную оптическую структуру 5 выходное двухчастотное излучение через второй волоконно-оптический кабель 6 и второй вход циркулятора 3 поступает на второй выход циркулятора 3 и потом на детектор 7.
На выходе детектора 7 образуется сигнал, прошедший через симметричную оптическую структуру 5, соответствующий биениям двухчастотного сигнала на разностной частоте ![]() , который выделяется перестраиваемым фильтром разностной частоты 10.
, который выделяется перестраиваемым фильтром разностной частоты 10.
Далее в соответствии с алгоритмом работы подают команду по шине управления 9 с контроллера управления и измерения центральной частоты симметричных оптических структур 8 на перестраиваемый по частоте источник одночастотного оптического излучения 1 для перестройки средней частоты ![]() двухчастотных излучений с заданным шагом в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры 5 и на преобразователь одночастотного оптического излучения в двухчастотное 2 для сохранения постоянной в ходе перестройки разностной частоты
двухчастотных излучений с заданным шагом в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры 5 и на преобразователь одночастотного оптического излучения в двухчастотное 2 для сохранения постоянной в ходе перестройки разностной частоты ![]() .
.
В ходе перестройки средней частоты ![]() одночастотного оптического излучения в контроллере управления и измерения центральной частоты симметричных оптических структур 8 запоминают некоторое значение коэффициента модуляции огибающей биений между составляющими двухчастотного излучения m=m1, причем m∈[0,5;1] и фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения
одночастотного оптического излучения в контроллере управления и измерения центральной частоты симметричных оптических структур 8 запоминают некоторое значение коэффициента модуляции огибающей биений между составляющими двухчастотного излучения m=m1, причем m∈[0,5;1] и фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения ![]() . Далее в ходе перестройки запоминают значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m2=m1 и фиксируют соответствующее ему значение средней частоты
. Далее в ходе перестройки запоминают значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m2=m1 и фиксируют соответствующее ему значение средней частоты ![]() . После чего завершают перестройку частоты одночастотного оптического излучения
. После чего завершают перестройку частоты одночастотного оптического излучения ![]() и вычисляют центральную частоту симметричной оптической структуры как
и вычисляют центральную частоту симметричной оптической структуры как ![]() .
.
Алгоритм работы контроллера управления и измерения центральной частоты симметричной оптической структуры 8 для осуществления измерений для заявки на изобретение по первому варианту предлагаемого способа представлен в Приложении 1.
Рассмотрим осуществление способа и работу устройства для определения центральной частоты симметричной оптической структуры для второго варианта предлагаемого способа.
Для начала работы с устройством производят включение блоков к сети электропитания согласно их нормируемому напряжению.
Для измерения характеристик симметричной оптической структуры с помощью перестраиваемого по частоте источника одночастотного оптического излучения в двухчастотное 1 генерируют исходное одночастотное оптическое излучение, из которого формируют двухчастотное зондирующее излучение с двумя составляющими равной амплитуды в преобразователе одночастотного оптического излучения в двухчастотное 2.
Для этого с контроллера управления и измерения центральной частоты симметричных оптических структур 8 через шину управления 9 подается команда управления параметрами генерации перестраиваемого по частоте источника одночастотного оптического излучения 1, преобразования в преобразователе одночастотного оптического излучения в двухчастотное 2 и настройки перестраиваемого фильтра разностной частоты 10. Алгоритм работы контроллера управления и измерения центральной частоты симметричных оптических структур 8 для осуществления измерений представлен в Приложении 2 (по второму варианту предлагаемого способа).
В соответствии с алгоритмом работы с поданной командой зондирующий сигнал в преобразователе одночастотного оптического излучения в двухчастотное 2 формируют двухчастотным, состоящим из двух одночастотных сигналов равной амплитуды соответственно на частотах ![]() и
и ![]() . Для его формирования в перестраиваемом по частоте источнике одночастотного оптического излучения 1 генерируют среднюю частоту равную
. Для его формирования в перестраиваемом по частоте источнике одночастотного оптического излучения 1 генерируют среднюю частоту равную ![]() . Средняя частота поступает в преобразователь одночастотного оптического излучения в двухчастотное 2, в котором по полученной команде задают разностную частоту между формируемыми двухчастотного зондирующего излучения
. Средняя частота поступает в преобразователь одночастотного оптического излучения в двухчастотное 2, в котором по полученной команде задают разностную частоту между формируемыми двухчастотного зондирующего излучения ![]() , лежащей в области полосы пропускания симметричной оптической структуры 5. При этом сама средняя частота подавляется. На сформированную разностную частоту
, лежащей в области полосы пропускания симметричной оптической структуры 5. При этом сама средняя частота подавляется. На сформированную разностную частоту ![]() производится настройка перестраиваемого фильтра разностной частоты 10, причем разностную частоту
производится настройка перестраиваемого фильтра разностной частоты 10, причем разностную частоту ![]() выбирают достаточно малой, чтобы не превысить полуширины склонов симметричной оптической структуры 5 и оставляют неизменной в ходе перестройки средней частоты
выбирают достаточно малой, чтобы не превысить полуширины склонов симметричной оптической структуры 5 и оставляют неизменной в ходе перестройки средней частоты ![]() .
.
Затем передают двухчастотное зондирующее излучение к симметричной оптической структуре 5 через циркулятор 3 и первый волоконно-оптический кабель 4. В двухчастотном зондирующем излучении, проходящем через симметричную оптическую структуру 5, происходит изменение амплитуд составляющих зондирующего излучения – они становятся равными в зависимости от взаимного положения его средней частоты ![]() и резонансной частоты
и резонансной частоты ![]() симметричной оптической структуры 5.
симметричной оптической структуры 5.
Далее принимают двухчастотное излучение после воздействия на симметричную оптическую структуру 5 на детекторе 7. В соответствии с алгоритмом работы включают циркулятор 3 по команде с контроллера управления и измерения центральной частоты симметричных оптических структур 8 в режим «двойного Т-моста» так, что прошедшее через симметричную оптическую структуру 5 выходное двухчастотное излучение через второй волоконно-оптический кабель 6 и второй вход циркулятора 3 поступает на второй выход циркулятора 3 и потом на детектор 7.
На выходе детектора 7 образуется сигнал, прошедший через симметричную оптическую структуру 5, соответствующий биениям двухчастотного сигнала на разностной частоте ![]() , который выделяется перестраиваемым фильтром разностной частоты 10.
, который выделяется перестраиваемым фильтром разностной частоты 10.
Далее в соответствии с алгоритмом работы подают команду по шине управления 9 с контроллера управления и измерения центральной частоты симметричных оптических структур 8 на перестраиваемый по частоте источник одночастотного оптического излучения 1 для перестройки средней частоты ![]() двухчастотных излучений с заданным шагом в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры 5 и на преобразователь одночастотного оптического излучения в двухчастотное 2 для сохранения постоянной в ходе перестройки разностной частоты
двухчастотных излучений с заданным шагом в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры 5 и на преобразователь одночастотного оптического излучения в двухчастотное 2 для сохранения постоянной в ходе перестройки разностной частоты ![]() .
.
В ходе перестройки средней частоты одночастотного оптического излучения ![]() регистрируют данные двух соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m3<1, а во втором m=m4=1, и запоминают значение средней частоты зондирующего излучения
регистрируют данные двух соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m3<1, а во втором m=m4=1, и запоминают значение средней частоты зондирующего излучения ![]() для второго из них. Далее в ходе перестройки регистрируют данные двух других соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m5=1, а во втором m=m6<1, и запоминают значение средней частоты двухчастотного зондирующего излучения
для второго из них. Далее в ходе перестройки регистрируют данные двух других соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m5=1, а во втором m=m6<1, и запоминают значение средней частоты двухчастотного зондирующего излучения ![]() для первого из них, по которым вычисляют центральную частоту симметричной оптической структуры как
для первого из них, по которым вычисляют центральную частоту симметричной оптической структуры как ![]() .
.
Алгоритм работы контроллера управления и измерения центральной частоты симметричной оптической структуры 8 для осуществления измерений для заявки на изобретение по второму варианту предлагаемого способа представлен в Приложении 2.
На фиг. 2 и фиг. 3 показано спектральное расположение двухчастотного зондирующего излучения (для первого и второго вариантов предлагаемого способа соответственно) относительно симметричной оптической структуры в случае совпадения их средней частоты ![]() с резонансной частотой
с резонансной частотой ![]() .
.
Изображенные на фиг. 2 составляющие двухчастотного зондирующего излучения ![]() и их расположение показаны в случае совпадения их средней частоты
и их расположение показаны в случае совпадения их средней частоты ![]() с резонансной частотой
с резонансной частотой ![]() . Исходные амплитуды составляющих на выходе преобразователя одночастотного оптического излучения в двухчастотное 2 равны.
. Исходные амплитуды составляющих на выходе преобразователя одночастотного оптического излучения в двухчастотное 2 равны.
Изображенные на фиг. 3 составляющие двухчастотного зондирующего излучения ![]() и их расположение показаны в случае совпадения их средней частоты
и их расположение показаны в случае совпадения их средней частоты ![]() с резонансной частотой
с резонансной частотой ![]() . Исходные амплитуды составляющих на выходе преобразователя одночастотного оптического излучения в двухчастотное 2 равны.
. Исходные амплитуды составляющих на выходе преобразователя одночастотного оптического излучения в двухчастотное 2 равны.
Изображенная на фиг. 4 зависимость коэффициента модуляции огибающей биений двухчастотного зондирующего излучения m на разностной частоте ![]() от относительной обобщенной расстройки полосы пропускания симметричной оптической структуры 5 представлена для случая, когда разностная частота
от относительной обобщенной расстройки полосы пропускания симметричной оптической структуры 5 представлена для случая, когда разностная частота ![]() достаточно мала, чтобы не превысить полуширины склонов симметричной оптической структуры 5. Характерной точкой данной зависимости является точка нулевой относительной обобщенной расстройки, которая соответствует равенству средней частоты
достаточно мала, чтобы не превысить полуширины склонов симметричной оптической структуры 5. Характерной точкой данной зависимости является точка нулевой относительной обобщенной расстройки, которая соответствует равенству средней частоты ![]() зондирующего излучения резонансной частоте
зондирующего излучения резонансной частоте ![]() . В этом случае коэффициент модуляции m1 огибающей биений двухчастотного зондирующего излучения на разностной частоте
. В этом случае коэффициент модуляции m1 огибающей биений двухчастотного зондирующего излучения на разностной частоте ![]() , зарегистрированный на выходе перестраиваемого фильтра разностной частоты 10 будет равен значению «1».
, зарегистрированный на выходе перестраиваемого фильтра разностной частоты 10 будет равен значению «1».
Все сказанное выше относится и к зависимости коэффициента модуляции m2-m6 огибающей биений двухчастотного зондирующего излучения с разностной частотой ![]() .
.
Факт равенства коэффициентов модуляции m1 и m2 значения «1» для огибающей биений двухчастотного зондирующего излучения с разностной частотой ![]() , зарегистрированных на выходе перестраиваемого фильтра разностной частоты 10 используется для принятия решения об определении резонансной частоты
, зарегистрированных на выходе перестраиваемого фильтра разностной частоты 10 используется для принятия решения об определении резонансной частоты ![]() .
.
Перестраиваемый фильтр разностной частоты 10 выполнен перестраиваемым для выполнения условия по соответствию значения разностной частоты ![]() , которое должно быть достаточно малым, чтобы не превысить полуширины склонов симметричной оптической структуры.
, которое должно быть достаточно малым, чтобы не превысить полуширины склонов симметричной оптической структуры.
Устройство для определения центральной частоты симметричной оптической структуры может быть реализовано на следующих элементах, рассчитанных на работу на длине волны 1550 нм (возможны и другие длины волн):
– перестраиваемый по частоте источник одночастотного оптического излучения 1 – одночастотный лазерный перестраиваемый диод с диапазоном перестройки до 40 нм, определяемым шириной полосы пропускания симметричной оптической структуры, например, Phoenix-1000, фирмы Luna;
– преобразователь одночастотного оптического излучения в двухчастотное 2 – электрооптический модулятор Маха-Цендера, например, MX-LN-10, фирмы IXBLUE;
– циркулятор 3 – циркулятор РМОС-4-15, фирмы DK Photonics Technology Limited, на четыре вывода;
– первый и второй волоконно-оптический кабели 4 и 6 – эталонные шнуры или кабели на волокне SMF-28 фирмы Corning;
– симметричная оптическая структура 5 – исследуемые решетки и фильтры;
– детектор 7 – детектор огибающий ADL5511 или ADL6010 фирмы Analog Devices;
– контроллер управления и измерения спектральных характеристик оптических структур 8 – микропроцессорный контроллер на базе чипов фирм Atmel, Microchip и т.д.;
– шина управления 9 – шины реализующие передачу сигналов управления и данных по протоколам Modbus, RS и других.
– перестраиваемый фильтр разностной частоты 10 – фирма Agilent, K&L, Магнетон.
При реализации устройства для определения центральной симметричных оптических структур все указанные блоки генерации, приема и обработки сигналов могут быть выполнены на едином кристалле в интегральном исполнении.
По сравнению с существующими способами и устройствами (включая прототип) для определения центральной частоты симметричной оптической структуры, которая характеризуются изменениями коэффициента модуляции в зависимости от изменения электрофизических параметров материалов, предложенный способ (по двум вариантам предлагаемого способа) и устройство с двухчастотным зондированием и измерением коэффициентов модуляции указанного двухчастотного оптического излучения после прохождения через него с дальнейшим вычислением характеристик не требует применения широкополосного приема, а позволяет обрабатывать сигнал на частотах биений компонент двухчастотных сигналов, равных разностным частотам между ними, и выделенных перестраиваемым фильтром разностной частоты, что существенно сужает полосу пропускания приемной части устройства и, соответственно, повышает отношение сигнал/шум измерений. Кроме того полоса пропускания перестраиваемых фильтров разностной частоты находится в области минимальных шумов детектора, что, соответственно, также повышает отношение сигнал/шум измерений.
При прямом детектировании собственные шумы детектора излучения превалируют над внешними и определяют пороговую мощность принимаемого сигнала. Выигрыш по отношению сигнал/шум можно вычислить с помощью следующего выражения:
![]()
где ![]() – спектральная плотность шума детектора.
– спектральная плотность шума детектора.
При этом выигрыш будет определяться в основном различной природой и уровнем шумов в различных частотных диапазонах, несмотря на некоторое увеличение требуемой полосы пропускания.
Для прямого детектирования диапазона ![]() в детекторе – это токовые шумы с распределением вида
в детекторе – это токовые шумы с распределением вида ![]() и другие мощные шумы и флуктуации низкочастотной природы.
и другие мощные шумы и флуктуации низкочастотной природы.
Для диапазона ![]() детектора – это дробовой шум малой интенсивности, где
детектора – это дробовой шум малой интенсивности, где ![]() – полоса пропускания детектора, необходимая для регистрации амплитуды зондирующего излучения после его взаимодействия с симметричной оптической структурой. Для измерений в оптическом диапазоне выигрыш может составить 1-2 порядка.
– полоса пропускания детектора, необходимая для регистрации амплитуды зондирующего излучения после его взаимодействия с симметричной оптической структурой. Для измерений в оптическом диапазоне выигрыш может составить 1-2 порядка.
Кроме того, при реализации способа и устройства из алгоритмов работы его блоками и измерения характеристик резонансных структур, отраженных в Приложении 1 и Приложении 2, были исключены операции, связанные с перестройкой разностной частоты, что позволило упростить их структуру по сравнению с прототипом.
Испытания показали, что использование зондирования двухчастотными излучениями симметричной оптической структуры и регистрация средней частоты и коэффициентов модуляции огибающих биений его компонент на выходе перестраиваемого фильтра разностной частоты, позволило достичь отношения сигнал/шум измерений ~ 60 дБ.
Все это позволяет говорить о достижении решения поставленной технической задачи (технического результата) для двух вариантов предлагаемого способа – повышение точности измерений определения центральной частоты как узкополосной, так и широкополосной симметричной оптической структуры.


1. Способ определения центральной частоты симметричной оптической структуры, заключающийся в том, что генерируют одночастотное оптическое излучение с частотой ![]() , формируют из него двухчастотное зондирующее излучение с двумя составляющими равной амплитуды соответственно на частотах
, формируют из него двухчастотное зондирующее излучение с двумя составляющими равной амплитуды соответственно на частотах ![]() и
и ![]() , со средней
, со средней ![]() и разностной частотами
и разностной частотами ![]() , лежащими в области полосы пропускания симметричной оптической структуры, подают двухчастотное зондирующее излучение на вход и принимают с выхода симметричной оптической структуры, при этом частоту
, лежащими в области полосы пропускания симметричной оптической структуры, подают двухчастотное зондирующее излучение на вход и принимают с выхода симметричной оптической структуры, при этом частоту ![]() одночастотного оптического излучения перестраивают в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры, причем в ходе перестройки разностную частоту
одночастотного оптического излучения перестраивают в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры, причем в ходе перестройки разностную частоту ![]() оставляют неизменной, регистрируют изменения параметров двухчастотного зондирующего излучения, а именно средней частоты двухчастотного зондирующего излучения
оставляют неизменной, регистрируют изменения параметров двухчастотного зондирующего излучения, а именно средней частоты двухчастотного зондирующего излучения ![]() и коэффициента модуляции m огибающей биений между составляющими двухчастотного зондирующего излучения на выходе симметричной оптической структуры, по которым далее определяют центральную частоту
и коэффициента модуляции m огибающей биений между составляющими двухчастотного зондирующего излучения на выходе симметричной оптической структуры, по которым далее определяют центральную частоту ![]() симметричной оптической структуры, отличающийся тем, что разностную частоту
симметричной оптической структуры, отличающийся тем, что разностную частоту ![]() выбирают не превышающей полуширины склонов симметричной оптической структуры, в ходе перестройки частоты
выбирают не превышающей полуширины склонов симметричной оптической структуры, в ходе перестройки частоты ![]() одночастотного оптического излучения запоминают первое значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m1, в пределах m∈[0,5; 1], и фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения
одночастотного оптического излучения запоминают первое значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m1, в пределах m∈[0,5; 1], и фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения ![]() , далее в ходе перестройки частоты
, далее в ходе перестройки частоты ![]() одночастотного оптического излучения запоминают второе значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m2=m1, и
одночастотного оптического излучения запоминают второе значение коэффициента модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m2=m1, и
фиксируют соответствующее ему значение средней частоты двухчастотного зондирующего излучения ![]() , завершают перестройку частоты
, завершают перестройку частоты ![]() одночастотного оптического излучения и вычисляют центральную частоту симметричной оптической структуры как
одночастотного оптического излучения и вычисляют центральную частоту симметричной оптической структуры как ![]() .
.
2. Способ определения центральной частоты симметричной оптической структуры, заключающийся в том, что генерируют одночастотное оптическое излучение с частотой ![]() , формируют из него двухчастотное зондирующее излучение с двумя составляющими равной амплитуды соответственно на частотах
, формируют из него двухчастотное зондирующее излучение с двумя составляющими равной амплитуды соответственно на частотах ![]() и
и ![]() , со средней
, со средней ![]() и разностной частотами
и разностной частотами ![]() , лежащими в области полосы пропускания симметричной оптической структуры, подают двухчастотное зондирующее излучение на вход и принимают с выхода симметричной оптической структуры, при этом частоту
, лежащими в области полосы пропускания симметричной оптической структуры, подают двухчастотное зондирующее излучение на вход и принимают с выхода симметричной оптической структуры, при этом частоту ![]() одночастотного оптического излучения перестраивают в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры, причем в ходе перестройки разностную частоту
одночастотного оптического излучения перестраивают в диапазоне измерений, соответствующем полосе частот симметричной оптической структуры, причем в ходе перестройки разностную частоту ![]() оставляют неизменной, регистрируют изменения параметров двухчастотного зондирующего излучения, а именно средней частоты двухчастотного зондирующего излучения
оставляют неизменной, регистрируют изменения параметров двухчастотного зондирующего излучения, а именно средней частоты двухчастотного зондирующего излучения ![]() и коэффициента модуляции m огибающей биений между составляющими двухчастотного зондирующего излучения на выходе симметричной оптической структуры, по которым далее определяют центральную частоту
и коэффициента модуляции m огибающей биений между составляющими двухчастотного зондирующего излучения на выходе симметричной оптической структуры, по которым далее определяют центральную частоту ![]() симметричной оптической структуры, отличающийся тем, что в ходе перестройки частоты одночастотного оптического излучения
симметричной оптической структуры, отличающийся тем, что в ходе перестройки частоты одночастотного оптического излучения ![]() регистрируют данные двух соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m3<1, а во втором m=m4=1, и запоминают значение средней частоты двухчастотного зондирующего излучения
регистрируют данные двух соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m3<1, а во втором m=m4=1, и запоминают значение средней частоты двухчастотного зондирующего излучения ![]() для второго из них, далее в ходе перестройки регистрируют данные двух других соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m5=1, а во втором m=m6<1, и запоминают значение средней частоты двухчастотного зондирующего излучения
для второго из них, далее в ходе перестройки регистрируют данные двух других соседних измерений, в первом из которых коэффициент модуляции огибающей биений между составляющими двухчастотного зондирующего излучения m=m5=1, а во втором m=m6<1, и запоминают значение средней частоты двухчастотного зондирующего излучения ![]() для первого из них, по которым вычисляют центральную частоту симметричной оптической структуры как
для первого из них, по которым вычисляют центральную частоту симметричной оптической структуры как ![]() .
.
3. Устройство для определения центральной частоты симметричной оптической структуры, содержащее последовательно соединенные перестраиваемый по частоте источник одночастотного оптического излучения, преобразователь одночастотного оптического излучения в двухчастотное, циркулятор, первый волоконно-оптический кабель, один конец которого соединен с первым выходом циркулятора, а второй конец – с входом симметричной оптической структуры, второй волоконно-оптический кабель, один конец которого соединен с выходом симметричной оптической структуры, а второй конец – со вторым входом циркулятора, циркулятор вторым выходом соединен с детектором, а также контроллер управления и измерения центральной частоты симметричных оптических структур, причем перестраиваемый по частоте источник одночастотного оптического излучения, преобразователь одночастотного оптического излучения в двухчастотное, контроллер управления и измерения центральной частоты симметричных оптических структур имеют входы/выходы управления, объединенные в шину управления, отличающееся тем, что в него дополнительно введен перестраиваемый фильтр разностной частоты, вход которого подключен к выходу детектора, а выход – к входу контроллера управления и измерения центральной частоты симметричных оптических структур, который выполнен как контроллер управления и измерения центральной частоты узкополосных и широкополосных симметричных оптических структур, при этом перестраиваемый фильтр разностной частоты имеет вход/выход управления, подключенный к шине управления.







