Как найти центральную точку треугольника

Центроид треугольника
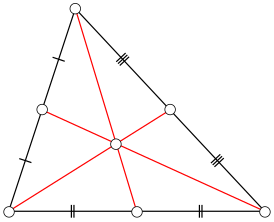Медианы и центроид треугольника
Барицентрические координаты	1 : 1 : 1
Трилинейные координаты	${displaystyle {frac {1}{a}}:{frac {1}{b}}:{frac {1}{c}}}$
Код ЭЦТ	X(2)
Связанные точки
Изогонально сопряженная	точка Лемуана
Изотомически сопряженная	она же
Дополнительная^[es]	она же
Антидополнительная^[es]	она же

Центроид треугольника (также барицентр треугольника и центр тяжести треугольника) — точка пересечения медиан в треугольнике^[1].

Центроид традиционно обозначается латинской буквой . Центроид треугольника относится к замечательным точкам треугольника и он перечислен в энциклопедии центров треугольника Кларка Кимберлинга, как точка X(2).

Свойства[править | править код]

Центроид делит каждую медиану в отношении 2:1, считая от вершины.
Центроид лежит на отрезке, соединяющем ортоцентр и центр описанной окружности, и делит его в отношении 2:1 (см. прямая Эйлера).
Если в вершины треугольника поместить равные массы, то центр масс (барицентр) полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой внутри массой также находится в центроиде.
Если — центроид треугольника то для любой точки верно равенство

${displaystyle {overrightarrow {OM}}={frac {1}{3}}({overrightarrow {OA}}+{overrightarrow {OB}}+{overrightarrow {OC}})}$ .
Центроид является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).
Три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника (равной площади).
Три отрезка прямых, соединяющих середины сторон треугольника с центроидом, разбивают данный треугольник на три равновеликих четырёхугольника (равной площади).
При изогональном сопряжении центроид переходит в точку Лемуана (в точку пересечения трех симедиан треугольника).
Построим две прямые, каждая из которых проходит через точку Аполлония и точку Торричелли, отличную от изогонально сопряжённой ей. Такие прямые пересекутся в центроиде треугольника.
Пусть — треугольник на плоскости. Окружность, проходящая через центроид и две точки Аполлония треугольника , называется окружностью Парри треугольника .
Три чевианы, проведённые через произвольную точку внутри треугольника, делят своими концами стороны треугольника на шесть отрезков. Произведение длин трёх из этих шести отрезков, не имеющих общих концов, максимально, если точка совпадает с центроидом^[2].
Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин:

$AB^{2}+BC^{2}+CA^{2}=3(GA^{2}+GB^{2}+GC^{2})$

.^[3]

${displaystyle {frac {q_{a}}{q_{b}}}={frac {b}{a}},quad {frac {q_{b}}{q_{c}}}={frac {c}{b}},quad {frac {q_{a}}{q_{c}}}={frac {c}{a}}}$

${displaystyle q_{a}cdot a=q_{b}cdot b=q_{c}cdot c={frac {2}{3}}S}$

где

— площадь треугольника.

История[править | править код]

Факт того, что три медианы пересекаются в одной точке, был доказан ещё Архимедом.

Вариации и обобщения. Центроиды в четырёхугольнике[править | править код]

Центроид (барицентр или центр масс) произвольного четырёхугольника лежит в точке пересечения средних линий четырёхугольника и отрезка, соединяющего середины диагоналей, и делит все три отрезка пополам.

Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершины

Если во вписанном в окружность четырёхугольнике провести диагональ, а в полученные два треугольника вписать две окружности, затем аналогично поступить, проведя вторую диагональ, тогда центроиды этих четырёх треугольников лежат на одной окружности^[5].
У выпуклого четырёхугольника, вписанного в окружность, «центроид площади» или центр масс его площади G_a, вершинный центроид или центр масс четырёх его вершин G_v и точка пересечения его диагоналей P коллинеарны. Расстояния между этими точками удовлетворяют формуле^[6]

$PG_{a}={tfrac {4}{3}}PG_{v}.$

См. также[править | править код]

Барицентр
Центр тяжести
Центр масс
Ортоцентр
Инцентр
Замечательные точки треугольника
Геометрия треугольника

Примечания[править | править код]

↑ Е. Смирнова. Планиметрия: виды задач и методы их решений. Элективный курс для учащихся 9—11 классов. — Litres, 2017-09-05. — С. 165. — 417 с.
↑ Зетель, 1962, с. 12.
↑ Altshiller-Court (1925, pp. 70–71)
↑ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ. Co., 2007
↑ Andreescu, Titu & Enescu, Bogdan (2004), 2.3 Cyclic quads, Mathematical Olympiad Treasures, Springer, с. 44–46, 50, ISBN 978-0-8176-4305-8
↑ Bradley, Christopher (2011), Three Centroids created by a Cyclic Quadrilateral, <http://people.bath.ac.uk/masgcs/Article141.pdf>

Литература[править | править код]

Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 80-81. — ISBN 5-94057-170-0.
Дм. Ефремов. Новая геометрия треугольника 1902 год
Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М: Учпедгиз, 1962. 153 с.
Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble

Источник

Загрузить PDF

Центр тяжести треугольника (центроид) – это точка центра масс. Представьте себе треугольную линейку, положенную на кончик карандаша. Линейка будет балансировать, если кончик карандаша будет находиться в ее центре тяжести. Расположение центроида, которое легко находится с помощью геометрии, необходимо знать при работе над дизайнерским или инженерным проектом.

1
Найдите середину одной стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой A.
- Например, если сторона треугольника равна 10 см, то середина находится на расстоянии 5 см () от вершины треугольника.
2
Найдите середину второй стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой В.
- Например, если вторая сторона треугольника равна 12 см, то середина находится на расстоянии 6 см () от вершины треугольника.
3
Соедините середины сторон с противолежащими вершинами. Вы получите две медианы.^[1]
- Вершина – это точка, в которой сходятся две стороны треугольника.
4
Отметьте точку пересечения двух медиан. Эта точка является центром тяжести треугольника.^[2]^[3]
- Центр тяжести находится на пересечении трех медиан, но так как медианы всегда пересекаются в одной точке, можно работать только с двумя медианами.
Реклама

1

Проведите медиану. Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны. Можно работать с любой медианой.
2
Измерьте длину медианы. Сделайте это аккуратно и точно.
- Например, медиана равна 3,6 см.
3
Найдите третью часть (треть) медианы. Для этого разделите длину медианы на три. Сделайте это аккуратно и точно. Округлив полученное значение, вы не найдете центроид.
- В нашем примере медиана равна 3,6 см. Поэтому разделите 3,6 на 3:
  . Таким образом, треть медианы равна 1,2 см.
4
Треть медианы отметьте точкой. Эта точка является центроидом, потому что он всегда делит медиану треугольника в отношении 2:1. То есть центр тяжести находится на расстоянии, которое равно ⅓ длины медианы, от середины стороны, или на расстоянии, которое равно ⅔ длины медианы, от вершины треугольника.^[4]
- Например, если медиана равна 3,6 см, то центроид находится на расстоянии 1,2 см от середины стороны.
Реклама

1
Определите координаты трех вершин треугольника. Координаты могут быть даны; в противном случае будет дан треугольник, построенный на координатной плоскости. Координаты представляются в виде .
- Например, дан треугольник PQR, вершины которого имеют следующие координаты: P (3,5), Q (4,1), R (1,0).
2
Сложите значения координат «х». Не забудьте сложить все три значения. Вы не найдете центр тяжести, если будете работать только с двумя значениями.
- Например, если координаты «х» равны 3, 4 и 1, сложите эти значения: .
3
Сложите значения координат «у». Не забудьте сложить все три значения.
- Например, если координаты «у» равны 5, 1 и 0, сложите эти значения: .
4

Найдите средние значения сумм координат «х» и «у». Полученные значения будут соответствовать центру тяжести треугольника.^[5] Чтобы найти среднее значение, разделите каждую сумму на 3.
5
Нанесите точку центра тяжести на треугольник. Центр тяжести находится в точке, координаты которой равны средним значениям сумм координат «х» и «у».
- В нашем примере центр тяжести – это точка с координатами .
Реклама

Советы

Не имеет значения, с какой стороной треугольника вы работаете – центр тяжести будет находится в одной и той же точке. Если построить медианы для всех трех сторон, они пересекутся в одной точке.

Об этой статье

Эту страницу просматривали 145 291 раз.

Была ли эта статья полезной?

Источник

Центр треугольника

Центр треугольника является центром симметрии одной из наиболее распространенных в машиностроении и строительстве формы деталей. Важным практическим применением вычисления данного параметра является потребность знать, в каком месте будет находиться центр тяжести того или иного элемента бетонной или металлической конструкции.

Центр треугольника, центр тяжести, центр симметрии находятся в одной точке. Именно на нее, точку пересечения трех медиан, приходится вес всей однородной детали треугольной формы. При выявлении значения центра треугольника G с помощью онлайнового калькулятора необходимо задать координаты его вершин:
o (x1, y1);
o (x2, y2);
o (x3, y3).

Важным направлением ряда инженерных расчетов является определение статических моментов в отношении тех или иных сложных по форме деталей. Следует иметь в виду, что любую фигуру можно представить совокупностью простых фигур, к которым относятся треугольник, прямоугольник и пр.

Статический момент сложной детали может быть определен как сумма статических моментов входящих в нее элементов. Отсюда вытекает важность умения быстро находить значения центра треугольника (центра тяжести), прямоугольника и пр.

Центр треугольника

Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.

Существует несколько понятий центра для треугольника.

Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.

Ортоцентр — точка пересечения его высот.

Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.

Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).

Как найти центр треугольника

Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.

Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.

Центр равностороннего треугольника является также центром вписанной и описанной окружности.

Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.

Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:

ввести в поле калькулятора координаты вершин треугольника;
нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности	Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов
Площадь треугольника
Радиус описанной окружности

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

[spoiler title=”источники:”]

Центр треугольника

http://www.resolventa.ru/spr/planimetry/otcircle.htm

[/spoiler]

Источник

Download Article

The center of gravity, or centroid, is the point at which a triangle’s mass will balance. To help visualize this, imagine you have a triangular tile suspended over the tip of a pencil. The tile will balance if the pencil tip is placed at its center of gravity. Finding the centroid might be necessary in various design and engineering applications, and can be found by using simple geometry.

1
Find the midpoint of one side of the triangle. To find the midpoint, measure the side, and divide the length in half. Label the midpoint A.
- For example, if one side of the triangle is 10 cm long, the midpoint will be at 5 cm, since .
2
Find the midpoint of a second side of the triangle. Measure the length of the side, and divide the length in half. Label the midpoint B.^[1]
- For example, if the side of the triangle is 12 cm long, the midpoint will be at 6 cm, since .
Advertisement
3
Draw a line from the midpoint of each side to its opposite vertex. These two lines are the median of each side.^[2]
- A vertex is the point at which two sides of a triangle meet.
4
Draw a point where the two medians intersect. This point is the triangle’s center of gravity, also called the centroid, or center of mass.^[3]
- The center of gravity is where the three medians intersect, but since the medians only intersect in one point, you can use a shortcut and find the center of gravity by only finding the intersection of two medians.

1

Draw a median of your triangle. Remember, the median is a line drawn from the midpoint of a side to the opposite vertex. You can use any median in the triangle.
2
Measure the length of the median. Make sure the measurement is exact.
- For example, you might have a median that is 3.6 cm long.
3
Divide the length of the median into thirds. To do this, divide the length by three. Again, make an exact calculation. If you round, you will not find the center of gravity.
- For example, if your median is 3.6 cm long, you would divide 3.6 by 3:
  , so ⅓ of the median is 1.2 cm.
4
Mark a point on the median ⅓ from the midpoint. This point is the triangle’s centroid, which will always divide a median into a 2:1 ratio; that is, the centroid is ⅓ the median’s distance from the midpoint, and ⅔ the median’s distance from the vertex.^[4]
- For example, on a median that is 3.6 cm long, the centroid will be 1.2 cm up from the midpoint.

1
Determine the coordinates of the three vertices of the triangle. This method only works if you are working with a coordinate plane. The coordinates may already be given, or you may have a triangle drawn on a graph without the coordinates labeled. Remember that coordinates should be listed .^[5]
- For example, you might be given triangle PQR, and you need to find and label point P (3, 5), point Q (4, 1), and R (1, 0).
2
Add the value of the x-coordinates. Remember to add all three coordinates. You will not calculate the correct center of gravity if you only use two coordinates.^[6]
- For example, if your three x-coordinates are 3, 4, and 1, add these three values together: .
3
Add the value of the y-coordinates. Remember to add all three coordinates.^[7]
- For example, if your three y-coordinates are 5, 1, and 0, add these three values together: .
4

Find the average of the x- and y-coordinates. These coordinates will correspond to the triangle’s center of gravity, also known as the centroid or center of mass.^[8] To find the average, divide the sum of the coordinates by 3.
5
Plot the center of gravity on the triangle. The center of gravity, or centroid, is the average of the x- and y-coordinates.^[9]
- In the example problem, the center of gravity is the point .

Add New Question

Question

The length of a rectangle is x units and the width is x-5. How do I find an equation for the perimeter and area of the rectangle?

For the perimeter, add the four sides together and simplify. For the area, multiply the length by the width.
Question

Is the center of gravity of triangular cardboard outside or on the body?

The center of gravity is always inside the triangle.
Question

How can I determine the center of gravity of an Isoceles triangle without knowing the mass?

The horizontal coordinate will be half of the base, and the vertical will be one third of the height.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

It does not matter which side you select, the center of gravity will be at the same point. If you perform this process on all three sides, the lines will cross at a single point.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate the center of gravity of a triangle, start by drawing a line from the midpoint of any 1 of the sides to the opposite vertex to create a median. Next, measure the median and divide it into thirds. For example, if the median is 3.6 cm long, mark the spots that are 1.2 cm and 2.4 cm along the median, starting from the midpoint. The spot that’s 1.2 inches from the midpoint is the centroid, or the center of gravity of the triangle. To learn more, like how to find the center of gravity of a triangle using intersecting medians, scroll down.

Did this summary help you?

Thanks to all authors for creating a page that has been read 274,249 times.

Did this article help you?

Источник

Центр треугольника

Точка, прямая, плоскость

Существует несколько понятий центра для треугольника.

Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.

Ортоцентр — точка пересечения его высот.

Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.

Как найти центр треугольника

Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.

Центр равностороннего треугольника является также центром вписанной и описанной окружности.

Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:

ввести в поле калькулятора координаты вершин треугольника;
нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.

Источник

Свойства[править | править код]

История[править | править код]

Вариации и обобщения. Центроиды в четырёхугольнике[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Центр треугольника

Центр треугольника

Как найти центр треугольника

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

Окружность, описанная около треугольника

Свойства описанной около треугольника окружности. Теорема синусов

Доказательства теорем о свойствах описанной около треугольника окружности

Video

References

About This Article

Did this article help you?

Центр треугольника

Как найти центр треугольника

Добавить комментарий Отменить ответ

Свойства[править | править код]

История[править | править код]

Вариации и обобщения. Центроиды в четырёхугольнике[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Центр треугольника

Центр треугольника

Как найти центр треугольника

Окружность, описанная около треугольника.Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

Окружность, описанная около треугольника

Свойства описанной около треугольника окружности. Теорема синусов

Доказательства теорем о свойствах описанной около треугольника окружности

Video

References

About This Article

Did this article help you?

Центр треугольника

Как найти центр треугольника

Вам также может понравиться

Как можно найти площадь ромба по формуле

Заговор как найти то что потерял дома

Как найти силу архимеда пример

Добавить комментарий Отменить ответ

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов