Начальные и центральные моменты случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Начальные моменты
Начальным моментом порядка
случайной величины
называют математическое ожидание величины
:
В
частности:
Пользуясь
этими моментами, формулу для вычисления дисперсии
можно записать так:
Центральные моменты
Кроме
моментов случайной величины
целесообразно рассматривать моменты отклонения
.
Центральным моментом порядка
случайной величины
называют математическое ожидание величины
:
В
частности,
Взаимосвязь центральных и начальных моментов
Легко
выводятся соотношения, связывающие начальные и центральные моменты:
Моменты
более высоких порядков применяются редко.
Формулы для вычисления моментов дискретных и непрерывных случайных величин
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Нетрудно
заметить, что при
первый
начальный момент случайной величины
есть ее
математическое ожидание, то есть
, при
второй
центральный момент – дисперсия, то есть
.
Асимметрия и эксцесс случайной величины
Третий центральный момент
служит для
характеристики асимметрии (скошенности) распределения. Он имеет размерность
куба случайной величины. Чтобы получить безразмерную величину, ее делят на
, где
– среднее
квадратическое отклонение случайной величины
. Полученная величина
называется
коэффициентом асимметрии случайной величины:
Если распределение симметрично относительно
математического ожидания, то коэффициент асимметрии
.
Четвертый центральный момент
служит для
характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом (или коэффициентом
эксцесса) случайной величины называется число
Число 3 вычитается из отношения
потому, что для
наиболее часто встречающегося нормального распределения отношение
. Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные – отрицательным
эксцессом.
Смежные темы решебника:
- Асимметрия и эксцесс распределения
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Дискретная
случайная величина X задана законом распределения:
|
|
1 | 3 | 4 | 5 |
|
|
0,2 | 0,3 | 0,1 | 0,4 |
Найти начальные моменты первого, второго и третьего
порядков.
Решение
Найдем
начальный момент 1-го порядка:
Начальный
момент 2-го порядка:
Начальный
момент 3-го порядка:
Ответ:
.
Пример 2
Дискретная
случайная величина X задана законом распределения:
|
|
0 | 3 | 5 | 6 |
|
|
0,3 | 0,2 | 0,3 | 0,2 |
Найти центральные моменты первого, второго,
третьего и четвертого порядков.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Центральный
момент первого порядка равен нулю:
Для
вычисления центральных моментов удобно воспользоваться формулами, выражающими
центральные моменты через начальные, поэтому предварительно найдем начальные
моменты:
Начальный
момент 2-го порядка:
Начальный
момент 3-го порядка:
Начальный
момент 4-го порядка:
Найдем центральные моменты:
Ответ:
.
Пример 3
Непрерывная случайная
величина X задана плотностью распределения:
Найти
математическое ожидание, дисперсию, асимметрию и эксцесс.
Решение
Математическое
ожидание (начальный момент первого порядка):
Начальный
момент второго порядка:
Дисперсия
(центральный момент второго порядка):
Среднее
квадратическое отклонение:
Начальный
момент третьего порядка:
Начальный
момент четвертого порядка:
Вычисляем
центральные моменты третьего и четвертого порядков:
Коэффициент
асимметрии:
Эксцесс:
Ответ:
.
- Краткая теория
- Примеры решения задач
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 февраля 2020 года; проверки требуют 19 правок.
Моме́нт случа́йной величины́ — числовая характеристика распределения данной случайной величины.
Происхождение понятия[править | править код]
Момент в математике — прямая аналогия с понятием момента в физике и механике. В математике моменты функции — это количественные измерения, связанные с формой графика функции. Например, если функция представляет собой распределение вероятностей, то первый момент — это ожидаемое значение, второй центральный момент (англ.) — это дисперсия, третий стандартизированный момент (англ.) — это асимметрия, а четвертый стандартизированный момент — это эксцесс. Если функция описывает плотность массы, то нулевой момент — это полная масса, первый момент (нормализованный по полной массе) — это центр масс, а второй момент — это момент инерции.
Определения[править | править код]
Если дана случайная величина 
-
- если математическое ожидание
в правой части этого равенства определено;
-
и
- если математическое ожидание в правой части этого равенства определено.[1]
Абсолютные моменты могут быть определены не только для целых, но и для любых положительных действительных чисел 
Замечания[править | править код]
Геометрический смысл некоторых моментов[править | править код]
-
- называется коэффициентом асимметрии.
показывает, насколько тяжелые у распределения хвосты. Величина
-
- называется коэффициентом эксцесса распределения
Вычисление моментов[править | править код]
- Моменты могут быть вычислены напрямую через определение путём интегрирования соответствующих степеней случайной величины. В частности, для абсолютно непрерывного распределения с плотностью
имеем:
если 
- а для дискретного распределения с функцией вероятности
если 
- Также моменты случайной величины могут быть вычислены через её характеристическую функцию
:
- Если распределение таково, что для него в некоторой окрестности нуля определена производящая функция моментов
то моменты могут быть вычислены по следующей формуле:
Обобщения[править | править код]
Можно также рассматривать нецелые значения 

Можно рассматривать моменты многомерной случайной величины. Тогда первый момент будет вектором той же размерности, второй — тензором второго ранга (см. матрица ковариации) над пространством той же размерности (хотя можно рассматривать и след этой матрицы, дающий скалярное обобщение дисперсии). И т. д.
См. также[править | править код]
- Момент изображения
Примечания[править | править код]
- ↑ Г. Крамер. Математические методы статистики. — 2-е изд. — М.: Мир, 1975. — С. 196-197, 284. — 648 с.
Начальным
моментом k-го
порядка
случайной величины X
называется математическое ожидание
величины
Xk:
![]() .
.
(5.10)
В частности,
![]()
Центральным
моментом k-го
порядка
случайной величины X
называется математическое ожидание
величины
[X–M(X)]k:
![]() .
.
(5.11)
В частности,
![]()
Воспользовавшись
определениями и свойствами математического
ожидания и дисперсии, можно получить,
что
![]() ,
,
![]() ,
,
![]() .
.
Моменты более
высоких порядков применяются редко.
Предположим,
что распределение случайной величины
симметрично относительно математического
ожидания. Тогда все центральные нечетного
порядка равны нулю. Это можно объяснить
тем, что для каждого положительного
значения отклонения X–M[X]
найдется (в силу симметричности
распределения) равное ему по абсолютной
величине отрицательное значение, причем
их вероятности будут одинаковыми. Если
центральный момент равен нечетного
порядка не равен нулю, то это говорит
об асимметричности распределения и чем
больше момент, тем больше асимметрия.
Поэтому в качестве характеристики
асимметрии распределения разумнее
всего взять какой-нибудь нечетный
центральный момент. Так как центральный
момент 1-го порядка всегда равен нулю,
то целесообразно для этой цели использовать
центральный момент 3-го порядка. Однако
принять этот момент для оценки
асимметричности неудобно потому, что
его величина зависит от единиц, в которых
измеряется случайная величина. Чтобы
устранить этот недостаток, 3
делят на 3
и таким образом получают характеристику.
Коэффициентом
асимметрии
A
называется
величина
![]() .
.
(5.12)

Рис.
5.1
Если коэффициент асимметрии
отрицателен, то это говорит о большом
влиянии на величину3
отрицательных отклонений. В этом случае
кривые распределения более пологи слева
от M[X].
Если коэффициент A
положителен, то кривая более пологи
справа.
Как
известно, дисперсия (2-й центральный
момент) служит для характеристики
рассеивания значений случайной величины
вокруг математического ожидания. Чем
больше дисперсия, тем более полога
соответствующая кривая распределения.
Однако нормированный момент 2-го порядка
2/2
не может служить характеристикой
“плосковершинности” или
“островершинности” распределения
потому, что для любого распределения
D[x]/2=1.
В этом случае используют центральный
момент 4-го порядка.
Эксцессом
E
называется
величина
![]() .
.
(5.13)
Ч

Рис.
5.2
исло 3 здесь выбрано потому, что для
наиболее распространенного нормального
закона распределения4/4=3.
Поэтому эксцесс служит для сравнения
имеющихся распределений с нормальным,
у которого эксцесс равен нулю. Это
означает, что если у распределения
эксцесс положителен, то соответствующая
кривая распределения более “островершина”
по сравнению с кривой нормального
распределения; если у распределения
эксцесс отрицателен, то соответствующая
кривая более “плосковершина”.
Пример
5.6. ДСВ
X
задана следующим законом распределения:
|
X |
1 |
3 |
5 |
7 |
9 |
|
P |
0,1 |
0,4 |
0,2 |
0,2 |
0,1 |
Найти коэффициент
асимметрии и эксцесс.
 Рис.
Рис.
5.4
Решение.
Предварительно найдем начальные моменты
до 4-го порядка
![]()
![]()
![]()
![]()
Теперь вычислим
центральные моменты:
![]()
![]()
![]()
Таким образом,
![]()
Пример
5.7. НСВ
X
задана следующей плотностью распределения:

Найти коэффициент
асимметрии и эксцесс.
 Рис.
Рис.
5.5
Решение.
Предварительно найдем начальные моменты
до 4-го порядка
![]()
![]()
![]()
![]()
Теперь вычислим
центральные моменты:
![]()
![]()
![]() .
.
Таким
образом,
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Примеры с решением
Моменты случайной величины
Определение и основные свойства
Мы уже видели в предыдущей главе, какое большое значение имеют такие числовые характеристики распределения, как математическое ожидание и дисперсия. Обобщением этих понятий являются начальные и центральные моменты.
Определение. Начальным моментом порядка  случайной величины
случайной величины  называют математическое ожидание
называют математическое ожидание  степени
степени 

Из определения ясно, что начальный момент первого порядка совпадает с математическим ожиданием.

Для дискретных случайных величин с законом распределения  формула для начального момента порядка
формула для начального момента порядка  выглядит следующим образом:
выглядит следующим образом:

для абсолютно непрерывных случайных величин с плотностью 

если ряд (6.3) и интеграл (6.4) сходятся абсолютно.
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Определение. Центральным моментом порядка  случайной величины
случайной величины  называют математическое ожидание
называют математическое ожидание  степени отклонения
степени отклонения  где
где  математическое ожидание
математическое ожидание 
 Мы уже видели, что первый центральный момент равен нулю, а второй центральный момент совпадает с дисперсией случайной величины
Мы уже видели, что первый центральный момент равен нулю, а второй центральный момент совпадает с дисперсией случайной величины 

Для дискретных случайных величин формула для центрального момента порядка  выглядит следующим образом:
выглядит следующим образом:

для непрерывных случайных величин

Возможно вам будут полезны данные страницы:
Разлагая бином  и пользуясь свойствами математического ожидания, нетрудно получить формулы, выражающие центральные моменты через начальные. Например,
и пользуясь свойствами математического ожидания, нетрудно получить формулы, выражающие центральные моменты через начальные. Например,

откуда


так что

Полученная формула полностью идентична с уже известной формулой для дисперсии. Аналогично получаются следующие формулы, вывод которых предоставляется читателю:

Отметим следующие свойства третьего и четвертого центральных моментов. Свойство. Если величины  независимы, то
независимы, то

Доказательство. Используя формулу куба суммы и свойство математического ожидания, имеем

По теореме умножения математического ожидания для независимых величин получим

Поскольку центральные моменты первого порядка равны нулю, то формула (6.12) отсюда следует непосредственно.
Доказанная формула непосредственно обобщается на произвольное число независимых слагаемых:

Для моментов четвертого порядка аналогичное свойство выглядит более сложным образом.
Свойство. Для независимых случайных величин  выполняется формула
выполняется формула

Доказательство полностью аналогично предыдущему и оставляется читателю. Для произвольного числа независимых слагаемых формула (6.14) приобретает следующий вид:

Рассмотрим ряд примеров нахождения моментов высших порядков для типичных законов распределения.
Примеры с решением
Пример 1:
Найти все центральные моменты до четвертого порядка включительно для случайной величины  распределенной по биномиальному закону с параметрами
распределенной по биномиальному закону с параметрами 
Решение:
Что касается нахождения центральных моментов первого и второго порядка, то ответ нам известен:

Чтобы найти  воспользуемся формулой (6.13) и представлением случайной величины
воспользуемся формулой (6.13) и представлением случайной величины  виде суммы индикаторов появления события
виде суммы индикаторов появления события  испытании:
испытании:

Для каждого слагаемого  третий центральный момент находится непосредственно
третий центральный момент находится непосредственно

Поэтому

Для нахождения центрального момента четвертого порядка воспользуемся формулой (6.15). Вначале найдем моменты для каждого слагаемого:

Отсюда

откуда окончательно получаем

Для нахождения всех начальных моментов непрерывной случайной величины проще использовать производящую функцию моментов.
Определение. Производящей функцией моментов случайной величины  называют математическое ожидание случайной величины
называют математическое ожидание случайной величины  где
где  действительный параметр:
действительный параметр:

Производящая функция моментов позволяет находить все начальные моменты случайной величины X. Справедлива следующая теорема.
Теорема 6.1. Если случайная величина  имеет начальный момент порядка
имеет начальный момент порядка  то производящая функция
то производящая функция  раз дифференцируема по
раз дифференцируема по  и для всех
и для всех  выполняется соотношение
выполняется соотношение

Если оставить в стороне вопрос о дифференцируемости данной функции, то соотношение (6.20) получается формально дифференцированием соотношения (6.19)  раз по
раз по 

Подставляя в последнее соотношение  получим
получим

откуда непосредственно вытекает равенство (6.19).
Сравнивая разложение производящей функции моментов в ряд Маклорена с равенствами (6.19), получим ее разложение в ряд с использованием начальных моментов:

Пример 2:
Найти производящую функцию моментов для случайной величины  распределенной по нормальному закону
распределенной по нормальному закону 
Решение:
Имеем по определению

Для вычисления этого интеграла рассмотрим отдельно показатель экспоненты, стоящей под знаком интеграла. Имеем

Выделим в числителе последней дроби полный квадрат по  После небольшого числа тождественных преобразований получим:
После небольшого числа тождественных преобразований получим:

Таким образом, выражение для характеристической функции приобретет вид:

Поскольку первый множитель равен 1 как интеграл от плотности нормальной случайной величины  то окончательное выражение для характеристической функции нормального закона имеет вид:
то окончательное выражение для характеристической функции нормального закона имеет вид:

Особенно простой вид имеет характеристическая функция стандартного нормального закона 

Теперь нам будет нетрудно найти все начальные моменты стандартной нормальной случайной величины. Вместо того чтобы дифференцировать функцию (6.22), можно разложить ее в ряд и сравнить с рядом (6.20):

откуда имеем выражения для начальных моментов:



Лекции:
- Моменты высших порядков
- Метод моментов
- Функции случайных величин
- Случайный вектор распределения
- Системы случайных величин
- Математическая дисперсия случайной величины
- Дисперсия суммы случайных величин
- Дисперсия формула
- Математическое ожидание: пример решения
- Законы распределения случайных величин
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности: 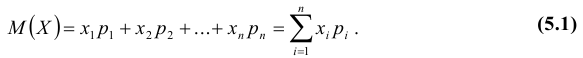
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся 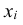
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
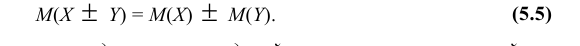
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:

- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:

Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим 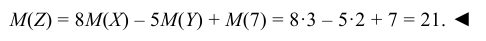
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания: 
Для дискретной случайной величины X эта формула принимает вид: 
Для непрерывной случайной величины: 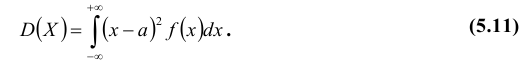 На практике для вычисления дисперсии часто удобно пользоваться следующей теоремой.
На практике для вычисления дисперсии часто удобно пользоваться следующей теоремой.
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:  Для дискретной случайной величины X эта формула принимает вид:
Для дискретной случайной величины X эта формула принимает вид:  Для непрерывной случайной величины:
Для непрерывной случайной величины: 
Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:

- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.

- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.

- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.

Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим 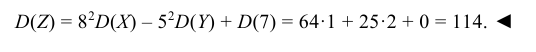
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину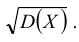
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии: 
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 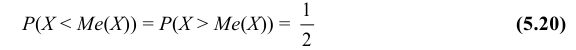 т. е. вероятность того, что случайная величина Х примет значение, меньшее медианы или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая х = Ме(Х), проходящая через точку с абсциссой, равной Ме(Х), делит площадь фигуры под кривой распределения на две равные части. Очевидно, что в точке х = Ме(Х) функция распределения равна 1/2.
т. е. вероятность того, что случайная величина Х примет значение, меньшее медианы или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая х = Ме(Х), проходящая через точку с абсциссой, равной Ме(Х), делит площадь фигуры под кривой распределения на две равные части. Очевидно, что в точке х = Ме(Х) функция распределения равна 1/2.
Пример №2
Найти моду, медиану случайной величины Х с плотностью вероятности 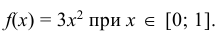
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 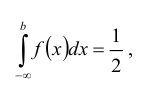 или
или 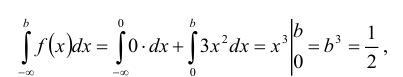 откуда
откуда 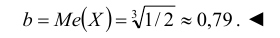
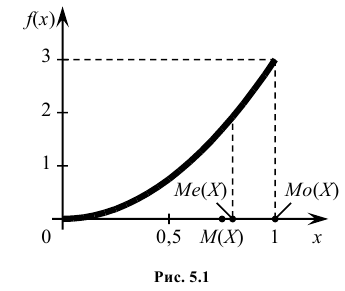
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е. 
Пример №3
По данным примера 5.3 найти квантиль 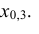
Решение:
Находим функцию распределения 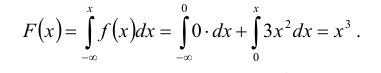
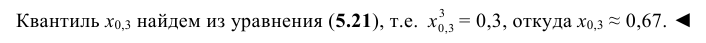
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины:  Для дискретной случайной величины формула начального момента имеет вид:
Для дискретной случайной величины формула начального момента имеет вид:  Для непрерывной случайной величины:
Для непрерывной случайной величины: 
Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания: 
Для дискретной случайной величины формула центрального момента имеет вид:

Для непрерывной случайной величины:  Нетрудно заметить, что при k = 1 первый начальный момент случайной величины Х есть ее математическое ожидание
Нетрудно заметить, что при k = 1 первый начальный момент случайной величины Х есть ее математическое ожидание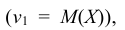 при k = 2 второй центральный момент – дисперсия
при k = 2 второй центральный момент – дисперсия 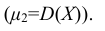
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 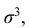 , где σ – среднее квадратическое отклонение случайной величины Х.
, где σ – среднее квадратическое отклонение случайной величины Х.
Полученная величина А называется коэффициентом асимметрии случайной величины:  Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии равен нулю А = 0.
Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии равен нулю А = 0.
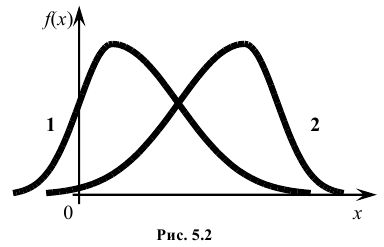
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число  (Число 3 вычитается из отношения потому, что для нормального распределения, которое встречается наиболее часто, отношение
(Число 3 вычитается из отношения потому, что для нормального распределения, которое встречается наиболее часто, отношение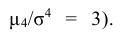 Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом.
Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом.
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 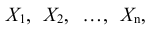 которые имеют одинаковые распределения, а следовательно, одинаковые характеристики (математическое ожидание, дисперсию и др.). Наибольший интерес представляют числовые характеристики среднего арифметического этих величин.
которые имеют одинаковые распределения, а следовательно, одинаковые характеристики (математическое ожидание, дисперсию и др.). Наибольший интерес представляют числовые характеристики среднего арифметического этих величин.
Обозначим среднее арифметическое n взаимно независимых случайных величин через 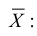
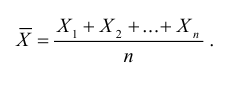
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 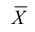 и соответствующими характеристиками каждой отдельной величины.
и соответствующими характеристиками каждой отдельной величины.
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:

- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
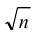 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: 
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:

Пример:
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
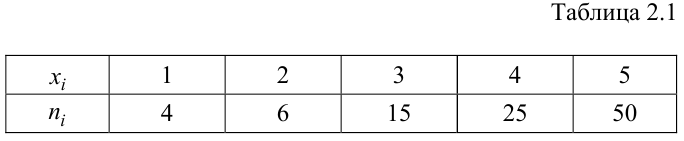
Решение. Определяем объем выборки: 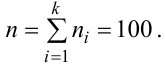
Определяем относительные частоты вариант (табл. 2.2):
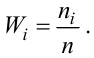
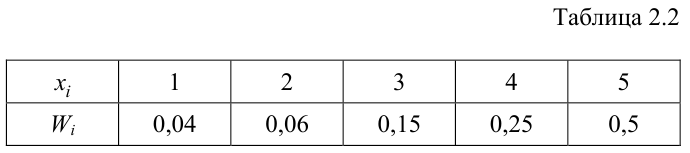
Так как значение 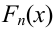 есть сумма относительных частот вариант
есть сумма относительных частот вариант 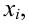 попадающих в интервал
попадающих в интервал 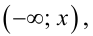 запишем эмпирическую функцию распределения:
запишем эмпирическую функцию распределения:
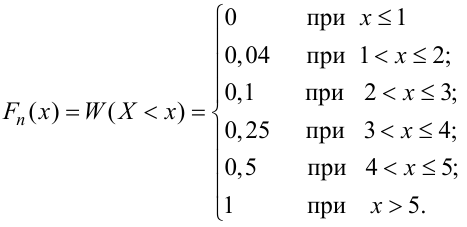
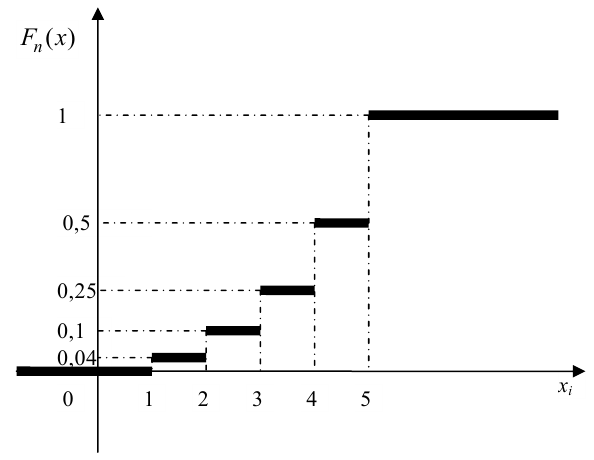
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
![{displaystyle nu _{k}=mathbb {M} left[X^{k}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e859ee783c97df459238a867977268a1be057c96)
![{displaystyle mu _{k}=mathbb {M} left[(X-mathbb {M} X)^{k}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b84dc1582c641c508b1faf8c8671c4165dbc2559)
![{displaystyle mu _{k}=mathbb {M} left[|X-mathbb {M} X|^{k}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc700a97bd94d34a22ba2a2961c50de7f9525e38)
![{displaystyle mu _{k}=mathbb {M} left[X(X-1)...(X-k+1)right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f7dae2d81aadb91a59d1903f5e4e1e9c6b78524)








