Как найти центральный угол правильного многоугольника формула

Определение.

Центральный угол правильного многоугольника — это угол, под которым сторона многоугольника видна из его центра.

Например,

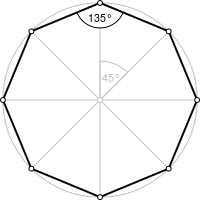
∠AOB — центральный угол правильного восьмиугольника.

Около любого правильного многоугольника можно описать окружность, центр которой совпадает с центром этого многоугольника. Если у многоугольника n сторон, то центральных углов у него также n и все они равны между собой.

Градусная мера всей окружности — 360º, следовательно, градусная мера каждой дуги окружности, на которую окружность разбивают вершины n-угольника, равна

$[frac{{{{360}^o}}}{n}]$

Так как центральный угол равен дуге, на которую от опирается, то и каждый из центральных углов равен 360º:n.

Примеры

Центральный угол правильного треугольника

равен 360º:3=120º.

Центральный угол квадрата

равен 360º:4=90º.

Центральный угол правильного шестиугольника

равен 360º:6=60º.

Центральный угол правильного восьмиугольника

равен 360º:8=45º.

Источник

Углы правильного многоугольника делятся на :

центральный угол;
внутренний угол;
внешний угол.

Углы многоугольника

Сумма внутреннего и внешнего угла равна (180°).

Сумма внутренних углов правильного многоугольника с (n) сторонами равна:

((n – 2)180°)

Для нахождения внутреннего угла используют формулу:

(alpha = frac{{{{180}^o}(n – 2)}}{n})

(n)– число сторон

Для нахождения внешнего угла используют формулу:

(varphi = frac{{{{360}^o}}}{n})

(n)– число сторон

Для нахождения центрального угла используют формулу:

(beta = frac{{{{360}^o}}}{n})

(n)– число сторон

Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Источник

Правильный многоугольник
Правильный восьмиугольник
Тип	Многоугольник
Символ Шлефли
Вид симметрии	Диэдрическая группа ${displaystyle (mathrm {D} _{5})}$
Площадь	${displaystyle S={frac {n}{4}} a^{2}operatorname {ctg} {frac {pi }{n}}}$
Внутренний угол	${displaystyle (n-2)*180^{circ }}$
Свойства
выпуклый, вписанный, равносторонний, равноугольный^[en], изотоксальный
Медиафайлы на Викискладе

Пра́вильный многоуго́льник — выпуклый многоугольник, у которого равны все стороны и все углы между смежными сторонами.

Определение правильного многоугольника может зависеть от определения многоугольника: если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны.

Связанные определения[править | править код]

Центром правильного многоугольника называется его центр масс, совпадающий с центрами его вписанной и описанной окружностей.

Свойства[править | править код]

Координаты[править | править код]

Пусть $x_{C}$ и $y_{C}$ — координаты центра, а — радиус описанной вокруг правильного многоугольника окружности, ${phi }_{0}$ — угловая координата первой вершины относительно центра, тогда декартовы координаты вершин правильного n-угольника определяются формулами:

$x_{i}=x_{C}+Rcos left({phi }_{0}+{frac {2pi i}{n}}right)$

$y_{i}=y_{C}+Rsin left({phi }_{0}+{frac {2pi i}{n}}right)$

где принимает значения от до n-1 .

Размеры[править | править код]

Правильный многоугольник, вписанный и описанный около окружности

Пусть — радиус описанной вокруг правильного многоугольника окружности, тогда радиус вписанной окружности равен

$r=Rcos {frac {pi }{n}}$

а длина стороны многоугольника равна

$a=2Rsin {frac {pi }{n}}=2r{mathop {{mathrm {tg}}}},{frac {pi }{n}}$

Площадь[править | править код]

Площадь правильного многоугольника с числом сторон и длиной стороны составляет:

$S={frac {n}{4}} a^{2}{mathop {{mathrm {}}}},operatorname {ctg}{frac {pi }{n}}$

Площадь правильного многоугольника с числом сторон , вписанного в окружность радиуса , составляет:

$S={frac {n}{2}}R^{2}sin {frac {2pi }{n}}$

Площадь правильного многоугольника с числом сторон , описанного вокруг окружности радиуса , составляет:

$S=nr^{2}{mathop {{mathrm {tg}}}},{frac {pi }{n}}$

Площадь правильного многоугольника с числом сторон равна

${displaystyle S={frac {nra}{2}}={frac {1}{2}}Pr}$

где — радиус вписанной окружности многоугольника, — длина его стороны, а – его периметр.

Периметр[править | править код]

Если нужно вычислить длину стороны a_n правильного n-угольника, вписанного в окружность, зная длину окружности можно вычислить длину одной стороны многоугольника:

— длина стороны правильного n-угольника.

${displaystyle a_{n}=sin {Big (}{frac {pi }{n}}{Big )}cdot {frac {L}{pi }}}$

Периметр $P_{n}$ равен

$P_{n}=a_{n}cdot n$

где — число сторон многоугольника.

Свойства диагоналей правильных многоугольников[править | править код]

Максимальное количество диагоналей правильного -угольника, пересекающихся в одной точке, не являющейся его вершиной или центром, равно:

Существуют лишь три исключения: данное число равно

в треугольнике,

в шестиугольнике и

в двенадцатиугольнике.^[3].

При чётном

в центре многоугольника пересекается n/2

диагонали.

Введём функцию ${displaystyle delta _{m}(n)}$ , равную в случае, если делится на , и равную в противном случае. Тогда:

Количество точек пересечения диагоналей правильного -угольника равно

${displaystyle {begin{array}{l}C_{n}^{4}+left(-5n^{3}+45n^{2}-70n+24right)/24cdot delta _{2}(n)-(3n/2)cdot delta _{4}(n)+\+left(-45n^{2}+262nright)/6cdot delta _{6}(n)+42ncdot delta _{12}(n)+60ncdot delta _{18}(n)+\+35ncdot delta _{24}(n)-38ncdot delta _{30}(n)-82ncdot delta _{42}(n)-330ncdot delta _{60}(n)-\-144ncdot delta _{84}(n)-96ncdot delta _{90}(n)-144ncdot delta _{120}(n)-96ncdot delta _{210}(n)end{array}}}$

Где ${displaystyle C_{n}^{4}}$

– число сочетаний из

по

^[3].

Количество частей, на которые правильный -угольник делят его диагонали, равно

${displaystyle {begin{array}{l}left(n^{4}-6n^{3}+23n^{2}-42n+24right)/24+\+left(-5n^{3}+42n^{2}-40n-48right)/48cdot delta _{2}(n)-(3n/4)cdot delta _{4}(n)+\+left(-53n^{2}+310nright)/12cdot delta _{6}(n)+(49n/2)cdot delta _{12}(n)+32ncdot delta _{18}(n)+\+19ncdot delta _{24}(n)-36ncdot delta _{30}(n)-50ncdot delta _{42}(n)-190ncdot delta _{60}(n)-\-78ncdot delta _{84}(n)-48ncdot delta _{90}(n)-78ncdot delta _{120}(n)-48ncdot delta _{210}(n)end{array}}}$

^[3].

Применение[править | править код]

Правильными многоугольниками по определению являются грани правильных многогранников.

Древнегреческие математики (Антифонт, Брисон Гераклейский, Архимед и др.) использовали правильные многоугольники для вычисления числа π. Они вычисляли площади вписанных в окружность и описанных вокруг неё многоугольников, постепенно увеличивая число их сторон и получая таким образом оценку площади круга.^[4]

История[править | править код]

Построение циркулем и линейкой правильного многоугольника с сторонами оставалось проблемой для математиков вплоть до XIX века. Такое построение идентично разделению окружности на равных частей, так как, соединив между собой точки, делящие окружность на части, можно получить искомый многоугольник.

Евклид в своих «Началах» занимался построением правильных многоугольников в книге IV, решая задачу для . Кроме этого, он уже определил первый критерий построимости многоугольников: хотя этот критерий и не был озвучен в «Началах», древнегреческие математики умели построить многоугольник с $2^{m}$ сторонами (при целом m>1 ), имея уже построенный многоугольник с числом сторон ${displaystyle 2^{m-1}}$ : пользуясь умением разбиения дуги на две части, из двух полуокружностей мы строим квадрат, потом правильный восьмиугольник, правильный шестнадцатиугольник и так далее. Кроме этого, в той же книге Евклид указывает и второй критерий построимости: если известно, как строить многоугольники с и сторонами, и и взаимно простые, то можно построить и многоугольник с сторонами. Это достигается построением многоугольника с сторонами и многоугольника с сторонами так, чтобы они были вписаны в одну окружность и чтобы одна вершина у них была общей – в таком случае некоторые две вершины этих многоугольников будут являться соседними вершинами -угольника. Синтезируя эти два способа, можно прийти к выводу, что древние математики умели строить правильные многоугольники с ${displaystyle 2^{m}cdot 3}$ , ${displaystyle 2^{m}cdot 5}$ и ${displaystyle 2^{m}cdot 3cdot 5}$ сторонами при любом целом неотрицательном .

Средневековая математика почти никак не продвинулась в этом вопросе. Лишь в 1796 году Карлу Фридриху Гауссу удалось доказать, что если число сторон правильного многоугольника равно простому числу Ферма, то его можно построить при помощи циркуля и линейки. На сегодняшний день известны следующие простые числа Ферма: . Вопрос о наличии или отсутствии других таких чисел остаётся открытым. Гаусс, в частности, первым смог доказать возможность построения правильного -угольника, а под конец жизни завещал выбить его на своём надгробии, однако скульптор отказался выполнять столь сложную работу.^[5]

Из результата Гаусса мгновенно следовало, что правильный многоугольник возможно построить, если число его сторон равно ${displaystyle 2^{k}{p_{1}}{p_{2}}cdots {p_{s}}}$ , где {k} — целое неотрицательное число, а ${p_{j}}$ — попарно различные простые числа Ферма. Гаусс подозревал, что это условие является не только достаточным, но и необходимым, но впервые это было доказано Пьером-Лораном Ванцелем в 1836 году. Итоговая теорема, совмещающая оба результата, называется Теоремой Гаусса-Ванцеля.

Последними результатами в области построения правильных многоугольников являются явные построения 17-, 257- и 65537-угольника. Первое было найдено Йоханнесом Эрхингером в 1825 году, второе — Фридрихом Юлиусом Ришело в 1832 году, а последнее — Иоганном Густавом Гермесом в 1894 году.

См. также[править | править код]

Правильный многогранник

Примечания[править | править код]

↑ МАТВОКС
↑ treugolniki.ru. Дата обращения: 12 мая 2020. Архивировано 2 июля 2020 года.
↑ ¹ ² ³ Bjorn Poonen and Michael Rubinstein “The number of intersection points made by thediagonals of a regular polygon”. Дата обращения: 16 июля 2020. Архивировано 17 июля 2020 года.
↑ А. В. Жуков. О числе π. — М.: МЦНМО, 2002. ISBN 5-94057-030-5.
↑ Лабуда

Источник

Профи

(587),
закрыт

7 лет назад

Захар Полторак

Мыслитель

(9959)

8 лет назад

Рассмотрим треугольник АВО, образованный радиусами описанной окружности, проведенными к одной из сторон многоугольника,
где О центр многоугольника, АВ – сторона многоугольника, ОА = ОВ = R – радиусы описанной окружности.
Опустим перпендикуляр ОД на сторону АВ. ОД = r – радиус вписанной окружности.
Угол АОВ – центральный угол многоугольника, ОД – делит этот угол пополам, то есть угол АОВ = 2*(угол АОД).
Треугольник ОАД – прямоугольный. По условию задачи ОД/ОА = r/R = 1/2 = cos(угол АОД).
Отсюда угол АОД = 60 гр, угол АОВ = 2*60 = 120 гр.
Количество сторон многоугольника = 360/120 = 3. Многоугольник этот – треугольник.
Ответ: центральный угол = 120 гр.

Источник

��

�� : ��, �� , ��, ��, ��, ��

�� ��, �� .

�� ��  �� , �� .

��  ��  �� , �� .

�� .

��
�� , ��
�� .
�� a_n
�� n-�� R �� $$a_{n} = 2Rsinfrac{180^circ}{n}= 2Rsinfrac{pi}{n}$$.
�� n-�� .

bid

��

�� R — �� , �� $$r = R cdot cosfrac{pi}{n}$$, � �� $$a = 2R cdot sinfrac{pi}{n}$$.
�� n � �� a �� $$S = frac{n}{4}a^{2} cdot ctgfrac{pi}{n}$$.
�� n, �� R �� $$S = frac{n}{2}R^{2} cdot sinfrac{2pi}{n}$$.
�� n, �� r �� $$S = nr^{2} cdot tgfrac{pi}{n}$$.

��. ��:
�� ,
�� ,
�� ң��,
��

Источник

Связанные определения[править | править код]

Свойства[править | править код]

Координаты[править | править код]

Размеры[править | править код]

Площадь[править | править код]

Периметр[править | править код]

Свойства диагоналей правильных многоугольников[править | править код]

Применение[править | править код]

История[править | править код]

См. также[править | править код]

Примечания[править | править код]

���������� �������������

Вам также может понравиться

Как можно найти приемных родителей

Как найти машину в хорошем состоянии

Западение спинки носа как исправить

Добавить комментарий Отменить ответ

��