Радиус и угол сектора круга

Свойства
Сектор круга является его частью, ограниченной двумя радиусами. Поскольку радиус является неизменным показателем для круга и его сектора, то сам сектор будет зависеть от длины дуги или центрального угла сектора, измеренного в градусах. Зная радиус и угол сектора круга, вычислить площадь сектора круга представляется возможным, разделив площадь самого круга на 360 градусов и умножив на данный угол. S=πr^2 α/〖360〗^° =(r^2 α)/2
Теперь через площадь сектора круга можно найти и длину дуги, разделив удвоенное значение на радиус. После подстановки приведенной для площади формулы сокращается радиус и число π, и остается произведение радиуса на угол сектора круга. p=2S/r=2πr α/〖360〗^° =rα
Центральный угол сектора круга. Калькулятор и формулы
Этот калькулятор позволит быстро найти центральный угол сектора круга! Для того чтобы им воспользоваться, вначале нужно заполнить любую ячейку первого калькулятора – калькулятора окружности. После этого ввести любое известное значение из следующих: периметр, длина дуги, площадь сектора круга в слот калькулятора сектора окружности и нажать на кнопку расчета.
Также калькулятор рассчитывает величины сегмента, если известно какое-либо одно значение из следующих: угол сегмента, длина дуги, длина хорды или высота сегмента, а также радиус окружности.

Калькулятор окружности:
Достаточно заполнить только одну ячейку — остальное калькулятор посчитает сам.
Центральные и вписанные углы

О чем эта статья:
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly
[/spoiler]
Информация по назначению калькулятора
Сектор круга – это часть окружности внутри круга, состоящая из дуги вместе с ее двумя радиусами. Часть окружности (также известная как дуга) и 2 радиуса окружности встречаются в обеих конечных точках дуги, образуя сектор. Форма сектора круга выглядит как кусочек пиццы или пирога. В геометрии круг – одна из самых совершенных фигур. Форма сектора окружности – самая простая форма в геометрии. У него есть свои собственные различные части. Например, диаметр, радиус, окружность, сегмент, сектор.
Круг разделен на два сектора, и разделенные части известны как второстепенные сектора и главные сектора.
Большая часть круга является основным сектором, в то время как меньшая часть является второстепенным сектором.
В случае полукругов окружность делится на два сектора одинакового размера.
2 радиуса встречаются в части окружности круга, известной как дуга, образуя сектор окружности.
Онлайн калькулятор предназначен для нахождения параметров сектора круга, таких как:
- Площадь сектора
- Длина дуги
- Радиус
- Периметр сектора
- Центральный угол сектора в градусах и радианах
– это объем пространства, занимаемого в пределах границы сектора круга. Сектор всегда начинается с центра круга. Полукруг также является сектором круга, в данном случае круг имеет два сектора одинакового размера.
Можно найти зная радиус и центральный угол в градусах (Ssek = ( α / 360° ) * πr2)
– находится путем умножения радиуса на центральный угол сектора в радианах (L = r * α)
– равен сумме длины дуги и двум радиусам (Psek = L + r + r)
Этот калькулятор позволит быстро найти центральный угол сектора круга! Для того чтобы им воспользоваться, вначале нужно заполнить любую ячейку первого калькулятора – калькулятора окружности. После этого ввести любое известное значение из следующих: периметр, длина дуги, площадь сектора круга в слот калькулятора сектора окружности и нажать на кнопку расчета.
Также калькулятор рассчитывает величины сегмента, если известно какое-либо одно значение из следующих: угол сегмента, длина дуги, длина хорды или высота сегмента, а также радиус окружности.
Калькулятор окружности:
Достаточно заполнить только одну ячейку — остальное калькулятор посчитает сам.
Периметр или длина окружности (P)
Калькулятор сектора окружности:
Достаточно ввести только одно значение и указать радиус окружности — остальное калькулятор посчитает сам.
Центральный угол сектора в градусах (α)
Площадь сектора окружности (S1)
Калькулятор сегмента окружности:
Достаточно ввести только одно* значение и указать радиус окружности — остальное калькулятор посчитает сам.
Исключения:
* – при известном периметре (P2) нужно дополнительно указать длину дуги (l1) или хорды (c).
* – при известной площади (S2) нужно дополнительно указать длину хорды (c) или высоты (h).
Угол сегмента в градусах (α1)
Площадь сегмента окружности (S2)
Округление:
* – обязательно заполнить
Как найти центральный угол
Начертив в любом круге два несовпадающих радиуса, вы обозначите в нем два центральных угла. Эти углы определят, соответственно, и две дуги на окружности. Каждая дуга, в свою очередь, зададут две хорды, два круговых сегмента и два сектора. Размеры всего перечисленного связаны между собой, что позволяет найти нужную величину по известным значениям связанных параметров.
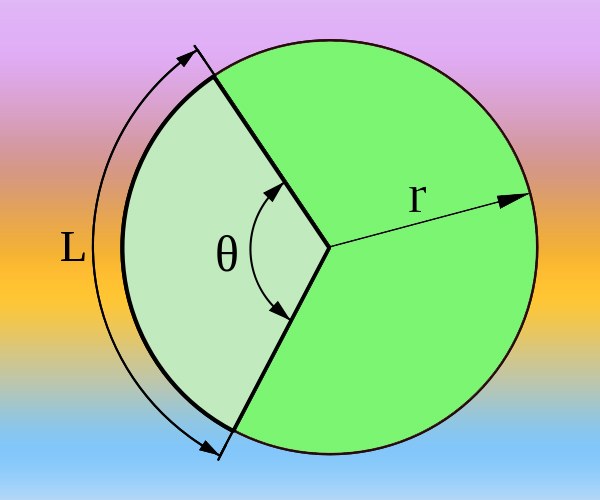
Инструкция
Если известны радиус (R) круга и длина дуги (L), соответствующая искомому центральному углу (θ), рассчитать его можно как в градусах, так и в радианах. Полная длина окружности определяется формулой 2*π*R и соответствует центральному углу в 360° или двум числам Пи, если вместо градусов использовать радианы. Поэтому исходите из пропорции 2*π*R/L = 360°/θ = 2*π/θ. Выразите из нее центральный угол в радианах θ = 2*π/(2*π*R/L) = L/R или градусах θ = 360°/(2*π*R/L) = 180*L/(π*R) и рассчитайте ответ по полученной формуле.
По длине хорды (m), соединяющей точки окружности, которые определяет центральный угол (θ), его величину тоже можно рассчитать, если известен радиус (R) круга. Для этого рассмотрите треугольник, образованный двумя радиусами и хордой. Это равнобедренный треугольник, все стороны которого известны, а найти нужно угол, лежащий напротив основания. Синус его половины равен отношению длины основания – хорды – к удвоенной длине боковой стороны – радиуса. Поэтому используйте для вычислений обратную синусу функцию – арксинус: θ = 2*arcsin(½*m/R).
Знание площади сектора круга (S), ограниченного радиусами (R) центрального угла (θ) и дугой окружности, тоже позволит вычислить величину этого угла. Чтобы это сделать, удвойте соотношение между площадью и возведенным в квадрат радиусом: θ = 2*S/R².
Центральный угол может быть задан и в долях от полного оборота или от развернутого угла. Например, если нужно найти центральный угол, соответствующей четверти полного оборота, разделите 360° на четверку: θ = 360°/4 = 90°. Эта же величина в радианах должна быть равна 2*π/4 ≈ 3,14/2 ≈ 1,57. Развернутый угол равен половине полного оборота, поэтому, например, центральный угол, соответствующий четверти от него будет вдвое меньше рассчитанных выше значений как в градусах, так и в радианах.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
28
Авг 2013
Категория: 01 ГеометрияПланиметрия
01. Круг
2013-08-28
2022-09-11
![]()
Видео к теме 1; 2; 3; 4
Задача 1. Найдите площадь круга, длина окружности которого равна

Решение: + показать
Задача 2. Площадь круга равна . Найдите длину его окружности.

Решение: + показать
Задача 3. Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны и
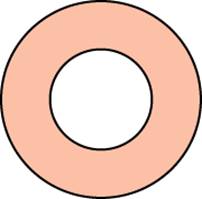
Решение: + показать
Задача 4. На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры. Видеорешение*

Решение: + показать
Задача 5. На клетчатой бумаге с клетками размером 1 см x 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите . Видео*
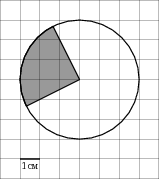
Решение: + показать
Задача 6. Найдите площадь сектора круга радиуса 6, длина дуги которого равна 3.
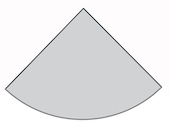
Решение: + показать
Задача 7. Площадь сектора круга радиуса 3 равна 15. Найдите длину его дуги.

Решение: + показать
Задача 8. Найдите центральный угол сектора круга радиуса , площадь которого равна 96. Ответ дайте в градусах.

Решение: + показать
Задача 9. На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 56?

Решение: + показать
Задача 10. На клетчатой бумаге с клетками размером 1 см x 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите . Видео
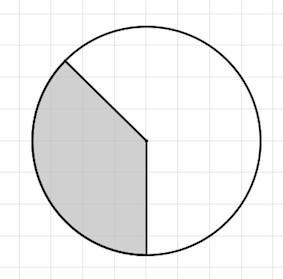
Решение: + показать
Задача 11. На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите радиус описанной около него окружности.
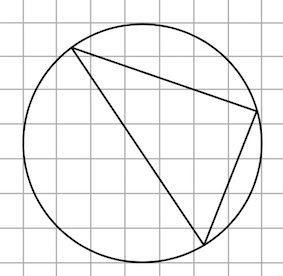
Решение: + показать
Задача 12. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC Ответ дайте в градусах.
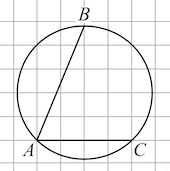
Решение: + показать

Вы можете пройти тест
Автор: egeMax |
комментариев 14
