Как найти центроид прямоугольника

Как найти центроид прямоугольника

Centroid of rectangle is defined as the center point where all the diagonals intersect each other. The diagonals of the rectangle intersect at width b/2 from x – axis and at height h/2 from y – axis. It can also be termed as the geometric center. Centroid can be located in the shape or figure using various methods like plumb line method, balancing methodn etc., Make use of this online centroid of rectangle calculator to find the centroid value of the rectangle shape with its length and width.

Centroid of rectangle is defined as the center point where all the diagonals intersect each other. The diagonals of the rectangle intersect at width b/2 from x – axis and at height h/2 from y – axis. It can also be termed as the geometric center. Centroid can be located in the shape or figure using various methods like plumb line method, balancing methodn etc., Make use of this online centroid of rectangle calculator to find the centroid value of the rectangle shape with its length and width.

Code to add this calci to your website Expand embed code Minimize embed code

Formula:

Centroid on X-axis = Length / 2
Centroid on Y-axis = Width / 2

Example:

What is the centroid of a rectangle with length 10 cm and width 6 cm.

Solution:

Centroid on X-axis = 10 / 2
= 5
Centroid on Y-axis = 6/2
=3

Источник

Среднее («среднее») положение всех точек в форме Центроид треугольника

В математика и физика, центроид или геометрический центр плоской фигуры – это среднее арифметическое положение всех точек на рисунке. Неформально, это точка, в которой вырез формы может быть идеально сбалансирован на кончике булавки.

Определение распространяется на любой объект в n- мерном пространстве : его центроид – это среднее положение всех точек во всех направлениях координат.

В то время как в геометрии слово барицентр является синонимом центроида, в астрофизике и астрономии барицентр – это центр масс двух или более тел, вращающихся по орбите друг с другом. В физике центр масс – это среднее арифметическое всех точек , взвешенных по локальной плотности или удельному весу. Если физический объект имеет однородную плотность, его центр масс совпадает с центроидом его формы.

В geography центроид радиальной проекции области земной поверхности на уровень моря – это географический центр региона.

Содержание

  • 1 История
  • 2 Свойства
  • 3 Примеры
  • 4 Расположение
    • 4.1 Метод отвеса
    • 4.2 Метод балансировки
    • 4.3 Из конечного набора точек
    • 4.4 Путем геометрического разложения
    • 4.5 По интегральной формуле
    • 4.6 Ограниченной области
    • 4.7 L-образного объекта
    • 4.8 Треугольника
    • 4.9 Многоугольника
    • 4.10 Конуса или пирамиды
    • 4.11 Тетраэдра и n -мерный симплекс
    • 4.12 Полушария
  • 5 См. также
  • 6 Примечания
  • 7 Ссылки
  • 8 Внешние ссылки

История

Термин «центроид» появился недавно чеканка (1814 г.). Он используется в качестве замены старых терминов «центр тяжести » и «центр масс », когда необходимо подчеркнуть чисто геометрические аспекты этой точки. Термин свойственен английскому языку. Французы чаще всего используют «центр притяжения», а другие используют термины схожего значения.

Центр тяжести, как следует из названия, возник в механике, скорее всего, в связи со строительством. Когда, где и кем он был изобретен, неизвестно, так как эта концепция, вероятно, пришла в голову многим людям индивидуально с небольшими различиями.

Хотя возможно Евклид все еще был активен в Александрии в детстве Архимеда (287–212 до н.э.), несомненно, что когда Архимед посетил Александрия, Евклида там больше не было. Таким образом, Архимед не мог усвоить теорему о том, что медианы треугольника пересекаются в точке – центре тяжести треугольника непосредственно от Евклида, поскольку этого утверждения нет в Элементах Евклида. Первое явное утверждение этого предположения принадлежит Герону Александрийскому (возможно, I век н.э.) и встречается в его «Механике». Между прочим, можно добавить, что это положение не входило в учебники по геометрии плоскости до XIX века.

Хотя Архимед прямо не заявляет об этом утверждении, он косвенно ссылается на него, предполагая, что он был с ним знаком. Однако Жан Этьен Монтукла (1725–1799), автор первой истории математики (1758), категорически заявляет (т. I, стр. 463), что центр тяжести твердых тел является предметом Архимеда не трогал.

В 1802 году Шарль Босу (1730–1813) опубликовал двухтомный Essai sur l’histoire générale des mathématiques. Эта книга была высоко оценена современниками, судя по тому, что уже через два года после публикации она была переведена на итальянский (1802–03), английский (1803) и немецкий (1804) языки. Боссут считает, что Архимед обнаружил центроид плоских фигур, но ничего не говорит о твердых телах.

Свойства

Геометрический центроид выпуклого объекта всегда лежит в объект. У невыпуклого объекта центр тяжести может находиться за пределами самой фигуры. Центроид кольца кольца или чаши, например, лежит в центральной пустоте объекта.

Если центроид определен, он является фиксированной точкой всех изометрий в его группе симметрии. В частности, геометрический центр тяжести объекта лежит на пересечении всех его гиперплоскостей симметрии . Центроид многих фигур (правильный многоугольник, правильный многогранник, цилиндр, прямоугольник, ромб, круг, сфера, эллипс, эллипсоид, суперэллипс, суперэллипсоид и т. д.) может определяться только этим принципом.

В частности, центр тяжести параллелограмма является точкой пересечения его двух диагоналей . Это не относится к другим четырехугольникам .

. По той же причине центроид объекта с трансляционной симметрией не определен (или находится за пределами ограничивающего пространства), поскольку сдвиг не имеет фиксированной точки..

Примеры

Центроид треугольника – это пересечение трех медиан треугольника (каждая медиана соединяет вершину с серединой противоположной стороны).

Другие свойства центроида треугольника см. В ниже.

Определение местоположения

Метод отвесной линии

Центроид равномерно плотной плоской пластинки, например, на рисунке (а) ниже, может быть определено экспериментально с использованием отвеса и штифта для нахождения совмещенного центра масс тонкого тела однородной плотности, имеющего такую ​​же форму. Корпус удерживается штифтом, вставленным в точку за пределами предполагаемого центра тяжести, таким образом, что он может свободно вращаться вокруг штифта; затем отвес снимается со штифта (рисунок b). Положение отвеса отслеживается на поверхности, и процедура повторяется со шпилькой, вставленной в любой другой точке (или в нескольких точках) за пределами центроида объекта. Единственной точкой пересечения этих линий будет центроид (рисунок c). При условии, что тело имеет однородную плотность, все линии, построенные таким образом, будут включать центроид, и все линии будут пересекаться в одном и том же месте.

Этот метод может быть расширен (теоретически) на вогнутые формы, где центр тяжести может лежать вне формы, и фактически к твердым телам (опять же с однородной плотностью), где центр тяжести может находиться внутри тела. (Виртуальные) положения отвесов должны быть записаны другими способами, кроме их рисования по форме.

Метод балансировки

Для выпуклых двумерных форм центр тяжести может быть найден путем уравновешивания формы на меньшей форме, такой как вершина узкого цилиндра. Центроид находится где-то в пределах диапазона контакта между двумя формами (и точно в точке, где форма будет балансировать на штифте). В принципе, для определения центра тяжести с произвольной точностью можно использовать все более узкие цилиндры. На практике воздушные потоки делают это невозможным. Однако, отмечая диапазон перекрытия нескольких весов, можно достичь значительного уровня точности.

конечного набора точек

Центроид конечного набора k { displaystyle k}k точек x 1, x 2, …, Xk { displaystyle mathbf {x} _ {1}, mathbf {x} _ {2}, ldots, mathbf {x} _ {k}} mathbf {x} _ {1}, mathbf {x} _ {2}, ldots, mathbf {x } _ {k} в R п { displaystyle mathbb {R} ^ {n}} mathbb {R} ^ {n} равно

C = x 1 + x 2 + ⋯ + xkk { displaystyle mathbf {C} = { frac { mathbf {x} _ {1} + mathbf {x} _ {2} + cdots + mathbf {x} _ {k}} {k}}} mathbf {C} = { frac { mathbf {x} _ {1} + mathbf {x} _ {2} + cdots + mathbf {x} _ {k}} {k}} .

Эта точка минимизирует сумму квадратов евклидовых расстояний между собой и каждая точка в наборе.

Путем геометрического разложения

Центроид плоской фигуры X { displaystyle X}Xможно вычислить, разделив его на конечное число более простых фигур X 1, X 2,…, X n { displaystyle X_ {1}, X_ {2}, dots, X_ {n}}X_ {1}, X_ {2}, dots, X_ {n} , вычисление центроида C i { displaystyle C_ {i}}C_ {i} и области A i { displaystyle A_ {i}}A_ {i} каждой части, а затем вычисление

C x = ∑ C ix A я ∑ A я, С Y знак равно ∑ С iy A я ∑ A я { displaystyle C_ {x} = { frac { sum C_ {i_ {x}} A_ {i}} { sum A_ {i}} }, C_ {y} = { frac { sum C_ {i_ {y}} A_ {i}} { sum A_ {i}}}}C_ {x} = { frac { sum C_ {i_ {x}} A_ {i}} { sum A_ {i} }}, C_ {y} = { frac { sum C_ {i_ {y}} A_ {i}} { sum A_ {i}}}

Отверстия на рисунке X { displaystyle X }X, перекрытия между частями или части, выходящие за пределы рисунка, могут быть обработаны с использованием отрицательных областей A i { displaystyle A_ {i}}A_ {i} . А именно, меры A i { displaystyle A_ {i}}A_ {i} следует принимать с положительными и отрицательными знаками таким образом, чтобы сумма знаков A i { displaystyle A_ {i}}A_ {i} для всех частей, которые окружают данную точку p { displaystyle p}p равно 1, если p { displaystyle p}p принадлежит X { displaystyle X}X, иначе 0.

Например, рисунок ниже (а) легко разделить на квадрат и треугольник, оба с положительной площадью; и круглое отверстие с отрицательной площадью (b).

(a) 2D-объект (b) Объект, описанный с использованием более простых элементов (c) Центроиды элементов объекта

Центроид каждой части можно найти в любом списке центроидов простых форм (в). Тогда центроид фигуры – это средневзвешенное значение трех точек. Горизонтальное положение центроида от левого края рисунка

x = 5 × 10 2 + 13,33 × 1 2 10 2 – 3 × π 2,5 2 10 2 + 1 2 10 2 – π 2,5 2 ≈ 8,5 единицы измерения. { displaystyle x = { frac {5 times 10 ^ {2} +13,33 times { frac {1} {2}} 10 ^ {2} -3 times pi 2,5 ^ {2}} {10 ^ {2} + { frac {1} {2}} 10 ^ {2} – pi 2,5 ^ {2}}} приблизительно 8,5 { mbox {units}}.}x = { frac {5 times 10 ^ {2} +13,33 times { frac {1} {2}} 10 ^ {2} -3 times pi 2,5 ^ {2} } {10 ^ {2} + { frac {1} {2}} 10 ^ {2} - pi 2,5 ^ {2}}} приблизительно 8,5 { mbox {units}}.

Вертикальное положение центроид находится точно так же.

Та же формула верна для любых трехмерных объектов, за исключением того, что каждый A i { displaystyle A_ {i}}A_ {i} должен быть объемом X i { displaystyle X_ {i}}X_ {i} , а не его площадь. Это также справедливо для любого подмножества R d { displaystyle mathbb {R} ^ {d}} mathbb {R} ^ {d} , для любого измерения d { displaystyle d}d с областями, замененными на d { displaystyle d}d -размерные меры частей.

По интегральной формуле

Центроид подмножества X из R n { displaystyle mathbb {R} ^ {n}} mathbb {R} ^ {n} также может быть вычислен интегралом

C = ∫ xg (x) dx ∫ g (x) dx { displaystyle C = { frac { int xg (x) ; dx} { int g (x) ; dx}}}C = { frac { int xg (x) ; dx} { int g (x) ; dx}}

где интегралы берутся по всему пространству R n { displaystyle mathbb {R} ^ {n}} mathbb {R} ^ {n} , а g – характеристика функция подмножества, которая равна 1 внутри X и 0 вне его. Обратите внимание, что знаменатель – это просто мера множества X. Эта формула не может быть применена, если у множества X есть нулевая мера или если любой интеграл расходится.

Другая формула для центроида:

C k = ∫ z S k (z) dz ∫ S k (z) dz { displaystyle C_ {k} = { frac { int zS_ {k } (z) ; dz} { int S_ {k} (z) ; dz}}}C_ {k} = { frac { int zS_ {k} (z) ; dz } { int S_ {k} (z) ; dz}}

где C k – это k-я координата C, а S k (z) – это мера пересечения X с гиперплоскостью, определяемая уравнением x k = z. И снова знаменатель – это просто мера X.

Для плоской фигуры, в частности, координаты центра масс:

C x = ∫ x S y (x) dx A { displaystyle C _ { mathrm {x}} = { frac { int xS _ { mathrm {y}} (x) ; dx} {A}}}C _ { mathrm {x}} = { frac { int xS _ { mathrm {y}} (x) ; dx} {A}}
C y = ∫ y S x (y) dy A { displaystyle C _ { mathrm {y}} = { frac { int yS _ { mathrm {x}} (y) ; dy} {A}}}C _ { mathrm {y}} = { frac { int yS _ { mathrm {x}} (y) ; dy} {A}}

где A – площадь фигуры X; S y (x) – длина пересечения X с вертикальной линией на абсциссе x; и S x (y) – аналогичная величина для поменяемых местами осей.

ограниченной области

Центроид (x ¯, y ¯) { displaystyle ({ bar {x}}, ; { bar {y}}) }({ bar {x} }, ; { bar {y}}) области, ограниченной графиками непрерывных функций f { displaystyle f}f и g { displaystyle g}g такое, что f (x) ≥ g (x) { displaystyle f (x) geq g (x)}f (x) geq g (x) на интервале [a, b] { displaystyle [a, b]}[a,b provided, a ≤ x ≤ b { displaystyle a leq x leq b}а leq x leq b , задается как

x ¯ = 1 A ∫ abx [f (х) – g (x)] dx { displaystyle { bar {x}} = { frac {1} {A}} int _ {a} ^ {b} x [f (x) -g ( х)] ; dx}{ bar {x}} = { frac {1} {A}} int _ {a} ^ {b} x [f (x) -g (x)] ; dx
y ¯ = 1 A ∫ ab [f (x) + g (x) 2] [f (x) – g (x)] dx, { displaystyle { bar {y }} = { frac {1} {A}} int _ {a} ^ {b} left [{ frac {f (x) + g (x)} {2}} right] [f ( x) -g (x)] ; dx,}{ bar {y}} = { frac {1} {A}} int _ {a} ^ {b} left [{ frac {f (x) + g (x)} {2}} right] [f (x) -g (x)] ; dx,

где A { displaystyle A}A – площадь региона (заданная как ∫ ab [f (x) – g (x)] dx { displaystyle int _ {a} ^ {b} [f (x) -g (x)] ; dx} int _ {a} ^ {b} [f (x) -g (x)] ; dx ).

L-образного объекта

Это метод определения ce ntroid L-образного объекта.

CoG of L shape.svg

  1. Разделите фигуру на два прямоугольника, как показано на рис. 2. Найдите центроиды этих двух прямоугольников, нарисовав диагонали. Нарисуйте линию, соединяющую центроиды. Центроид фигуры должен лежать на этой линии AB.
  2. Разделите фигуру на два других прямоугольника, как показано на рис. 3. Найдите центроиды этих двух прямоугольников, нарисовав диагонали. Нарисуйте линию, соединяющую центроиды. Центроид L-образной формы должен лежать на этой прямой CD.
  3. Поскольку центр тяжести формы должен лежать как вдоль AB, так и вдоль CD, он должен быть на пересечении этих двух линий в точке O. точка O может находиться внутри или снаружи L-образного объекта.

треугольника

Центроид треугольника – это точка пересечения его медиан (линии соединение каждой вершины со средней точкой противоположной стороны). Центроид делит каждую из медиан в соотношении 2: 1, то есть находится на расстояния от каждой стороны до противоположной вершины (см. Рисунки справа). Его декартовы координаты – это означает координат трех вершин. То есть, если три вершины равны L = (x L, y L), { displaystyle L = (x_ {L}, y_ {L}),}L = (x_ {L}, y_ {L}), M = (x M, y M), { displaystyle M = (x_ {M}, y_ {M}),}M = (x_ {M}, y_ {M}), и N = (x N, y N), { displaystyle N = (x_ {N}, y_ {N}),}N = (x_ {N}, y_ {N}), , то центроид (обозначенный здесь C, но чаще всего обозначаемый G в геометрии треугольника ) равен

C = 1 3 (L + M + N) = (1 3 (x L + x M + x N), 1 3 (y L + y M + y N)). { displaystyle C = { frac {1} {3}} (L + M + N) = left ({ frac {1} {3}} (x_ {L} + x_ {M} + x_ {N) }), ; ; { frac {1} {3}} (y_ {L} + y_ {M} + y_ {N}) right).}C = { frac {1} {3}} (L + M + N) = left ({ frac {1} {3}} ( x_ {L} + x_ {M} + x_ {N}), ; ; { frac {1} {3}} (y_ {L} + y_ {M} + y_ {N}) right).

Следовательно, центроид находится в 1 3: 1 3: 1 3 { displaystyle { tfrac {1} {3}}: { tfrac {1} {3}}: { tfrac {1} {3}}}{ tfrac {1} {3}}: { tfrac {1} {3}}: { tfrac {1} {3}} дюйм барицентрические координаты.

В трилинейных координатах центроид может быть выражен любым из этих эквивалентных способов с точки зрения длин сторон a, b, c и углов при вершинах L, M, N:

C = 1 a: 1 b: 1 c = bc: ca: ab = csc ⁡ L: csc ⁡ M: csc ⁡ N = cos ⁡ L + cos ⁡ M ⋅ cos ⁡ N: cos ⁡ M + cos ⁡ N ⋅ cos ⁡ L: cos ⁡ N + cos ⁡ L ⋅ cos ⁡ M = sec ⁡ L + sec ⁡ M ⋅ sec ⁡ N: sec ⁡ M + sec ⁡ N ⋅ sec ⁡ L: sec ⁡ N + sec ⁡ L ⋅ sec ⁡ М. { displaystyle { begin {align} C = { frac {1} {a}}: { frac {1} {b}}: { frac {1} {c}} = bc: ca: ab = csc L: csc M: csc N \ [6pt] = cos L + cos M cdot cos N: cos M + cos N cdot cos L: cos N + cos L cdot cos M \ [6pt] = sec L + sec M cdot sec N: sec M + sec N cdot sec L: sec N + sec L cdot sec M. end {выровнено }}}{ displaystyle { begin {align} C = { frac {1} {a}}: { frac {1} {b}}: { frac {1} {c}} = bc: ca: ab = csc L: csc M: csc N \ [6pt] = cos L + cos M cdot cos N: cos M + cos N cdot cos L: cos N + cos L cdot cos M \ [6pt] = sec L + sec M cdot sec N: sec M + sec N cdot sec L: sec N + sec L cdot sec M. end {выровнено} }}

Центроид также является физическим центром масс, если треугольник сделан из однородного листа материала; или если вся масса сосредоточена в трех вершинах и поровну разделена между ними. С другой стороны, если масса распределена по периметру треугольника с равномерной линейной плотностью, то центр масс находится в центре Шпикера (центр среднего треугольника ), который (в общем случае) не совпадает с геометрическим центром тяжести полного треугольника.

Площадь треугольника в 1,5 раза превышает длину любой стороны, умноженную на перпендикулярное расстояние от стороны до центроида.

Центроид треугольника лежит на его прямой Эйлера между его ортоцентром H и его центром описанной окружности O, ровно в два раза ближе к последнему, чем к первому:

CH ¯ = 2 CO ¯. { displaystyle { overline {CH}} = 2 { overline {CO}}.}{ displaystyle { overline {CH}} = 2 { overline {CO}}.}

Кроме того, для инцентратора I и центра по девяти точкам N, имеем

CH ¯ = 4 CN ¯ CO ¯ = 2 CN ¯ IC ¯ < H C ¯ I H ¯ < H C ¯ I C ¯ < I O ¯ {displaystyle {begin{aligned}{overline {CH}}=4{overline {CN}}\[5pt]{overline {CO}}=2{overline {CN}}\[5pt]{overline {IC}}<{overline {HC}}\[5pt]{overline {IH}}<{overline {HC}}\[5pt]{overline {IC}}<{overline {IO}}end{aligned}}}{ displaystyle { begin {align} { overline {CH}} = 4 { overline {CN}} \ [5pt] { overline { CO}} = 2 { overline {CN}} \ [5pt] { overline {IC}} <{ overline { HC}} \ [5pt] { overline {IH}} <{ overline {HC}} \ [5pt] { overline {IC}} <{ overline {IO}} end {выровнено} }}

Если G – центр тяжести треугольника ABC, то:

(Площадь △ ABG) = (Площадь △ ACG) = (Площадь △ BCG) = 1 3 (Площадь △ ABC) { displaystyle displaystyle ({ text {Площадь}} треугольник mathrm {ABG}) = ({ text {Площадь}} треугольник mathrm {ACG}) = ({ text {Площадь}} треугольник mathrm {BCG}) = { frac {1} {3}} ({ text {Площадь}} треугольник mathrm {ABC })}{ displaystyle displaystyle ({ text {Площадь}} треугольник mathrm {ABG}) = ({ text { Площадь}} треугольник mathrm {ACG}) = ({ text {Площадь}} треугольник mathrm {BCG}) = { frac {1} {3}} ({ text {Площадь}} треугольник mathrm {ABC})}

изогонально сопряженным центроиду треугольника является его симедианная точка.

Любая из трех медиан, проходящих через центроид, делит площадь треугольника пополам. Это неверно для других линий, проходящих через центроид; наибольшее отклонение от деления на равные площади происходит, когда линия, проходящая через центр тяжести, параллельна стороне треугольника, образуя меньший треугольник и трапецию ; в этом случае площадь трапеции равна 5/9 площади исходного треугольника.

Пусть P – любая точка на плоскости треугольника с вершинами A, B, C и центроидом G. Тогда сумма Квадрат расстояний P от трех вершин превышает сумму квадратов расстояний от центроида G до вершин в три раза больше квадрата расстояния между P и G:

PA 2 + PB 2 + PC 2 = GA 2 + GB 2 + GC 2 + 3 PG 2. { displaystyle PA ^ {2} + PB ^ {2} + PC ^ {2} = GA ^ {2} + GB ^ {2} + GC ^ {2} + 3PG ^ {2}.}PA ^ {2} + PB ^ {2} + PC ^ {2} = GA ^ {2} + GB ^ {2} + GC ^ {2} + 3PG ^ {2}.

сумма квадратов сторон треугольника равна троекратной сумме квадратов расстояний от центроида до вершин:

AB 2 + BC 2 + CA 2 = 3 (GA 2 + GB 2 + GC 2). { displaystyle AB ^ {2} + BC ^ {2} + CA ^ {2} = 3 (GA ^ {2} + GB ^ {2} + GC ^ {2}).}AB ^ {2} + BC ^ {2} + CA ^ {2} = 3 (GA ^ {2} + GB ^ {2} + GC ^ {2}).

Центроид треугольника равен точка, которая максимизирует произведение ориентированных расстояний от точки до сторон треугольника.

Пусть ABC – треугольник, пусть G – его центр тяжести, а D, E и F – середины BC, CA и AB соответственно. Для любой точки P в плоскости ABC тогда

P A + P B + P C ≤ 2 (P D + P E + P F) + 3 P G. { displaystyle PA + PB + PC leq 2 (PD + PE + PF) + 3PG.}{ display стиль PA + PB + PC leq 2 (PD + PE + PF) + 3PG.}

многоугольника

Центроид несамопересекающегося замкнутого многоугольника, определяемое n вершинами (x 0,y0), (x 1,y1),…, (x n − 1, y n − 1), является точкой ( C x, C y), где

C x = 1 6 A ∑ i = 0 n – 1 (xi + xi + 1) (xiyi + 1 – xi + 1 yi), { displaystyle C _ { mathrm {x}} = { frac {1} {6A}} sum _ {i = 0} ^ {n-1} (x_ {i} + x_ {i + 1}) (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}),}{ displaystyle C _ { mathrm {x}} = { frac {1} {6A}} sum _ {i = 0} ^ {n-1} (x_ {i} + x_ {i + 1}) (x_ { i} y_ {i + 1} -x_ {i + 1} y_ {i}),} и
C y = 1 6 A ∑ i = 0 п – 1 (yi + yi + 1) (xiyi + 1 – xi + 1 yi), { displaystyle C _ { mathrm {y}} = { frac {1} {6A}} sum _ {i = 0 } ^ {n-1} (y_ {i} + y_ {i + 1}) (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}),}{ displaystyle C _ { mathrm {y}} = { frac {1} {6A}} sum _ {i = 0} ^ {n-1} (y_ {i} + y_ {i + 1}) ( x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}),}

и где A – подписанная площадь многоугольника, как описано формулой шнурка :

A = 1 2 ∑ i = 0 n – 1 (xiyi + 1 – xi + 1 yi). { displaystyle A = { frac {1} {2}} sum _ {i = 0} ^ {n-1} (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}).}{ displaystyle A = { frac {1} {2}} sum _ {i = 0} ^ {n-1} (x_ {i} y_ {i + 1 } -x_ {i + 1} y_ {i}).}

В этих формулах предполагается, что вершины пронумерованы в порядке их появления по периметру многоугольника; кроме того, вершина (x n, y n) предполагается такой же, как (x 0, y 0), значение i + 1 { displaystyle i + 1}i +1 в последнем случае должно выполняться в цикле до i = 0 { displaystyle i = 0}i = 0 . (Если точки пронумерованы по часовой стрелке, площадь A, вычисленная, как указано выше, будет отрицательной; однако координаты центроида будут правильными даже в этом случае.)

Конуса или пирамиды

Центроид конуса или пирамиды расположен на отрезке линии, который соединяет вершину с центроидом основания. Для твердого конуса или пирамиды центр тяжести составляет 1/4 расстояния от основания до вершины. Для конуса или пирамиды, представляющих собой просто оболочку (полую) без основания, центроид составляет 1/3 расстояния от плоскости основания до вершины.

тетраэдра и n-мерного симплекса

A тетраэдр представляет собой объект в трехмерном пространстве, имеющий четыре треугольника в качестве его граней. Отрезок, соединяющий вершину тетраэдра с центром тяжести противоположной грани, называется срединной, а отрезок, соединяющий середины двух противоположных ребер, называется бимедианой. Следовательно, есть четыре медианы и три бимедианы. Эти семь отрезков пересекаются в центре тетраэдра. Медианы делятся на центроид в соотношении 3: 1. Центроид тетраэдра – это середина между его точкой Монжа и центром описанной области (центром описанной сферы). Эти три точки определяют линию Эйлера тетраэдра, которая аналогична прямой Эйлера треугольника.

Эти результаты обобщаются на любой n-мерный симплекс следующим образом. Если набор вершин симплекса равен v 0,…, vn { displaystyle {v_ {0}, ldots, v_ {n}}}{v_ {0}, ldots, v_ {n}} , то рассматриваемые вершины как векторов, центроид равен

C = 1 n + 1 ∑ i = 0 nvi. { displaystyle C = { frac {1} {n + 1}} sum _ {i = 0} ^ {n} v_ {i}.}C = { frac {1} {n + 1}} sum _ {i = 0} ^ {n} v_ {i}.

Геометрический центроид совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как n + 1 равных масс.

полушария

Центроид твердого полушария (т.е. половина твердого шара) делит отрезок прямой, соединяющий центр шара с полюсом полушария в соотношении 3: 5 (т.е. лежит на 3/8 пути от центра до полюса). Центроид полого полушария (то есть половина полой сферы) делит отрезок прямой, соединяющий центр сферы с полюсом полушария пополам.

См. Также

  • Центр Чебышева
  • Среднее Фреше
  • Алгоритм k-средних
  • Список центроидов
  • Определение центра масс
  • Медоид
  • Теорема Паппа о центроидах
  • Спектральный центроид
  • Центр треугольника

Примечания

Ссылки

  • Альтшиллер-Корт, Натан (1925), Геометрия колледжа: Введение в современную геометрию треугольника и круга (2-е изд..), Нью-Йорк: Barnes Noble, LCCN 52013504
  • Бурк, Пол (июль 1997 г.). «Расчет площади и центра тяжести многоугольника».
  • Джонсон, Роджер А. (2007), Advanced Euclidean Geometry, Dover
  • Kay, David C. (1969), College Geometry, Нью-Йорк : Holt, Rinehart and Winston, LCCN 69012075
  • Larson, Roland E.; Хостетлер, Роберт П.; Эдвардс, Брюс Х. (1998), Исчисление одной переменной (6-е изд.), Houghton Mifflin Company
  • Protter, Murray H.; Морри, младший, Чарльз Б. (1970), College Calculus with Analytic Geometry (2-е изд.), Чтение: Addison-Wesley, LCCN 76087042

External ссылки

  • Энциклопедия центров треугольников Кларка Кимберлинга. Центроид индексируется как X (2).
  • Характеристическое свойство центроида в точке срезать узел
  • Барицентрические координаты в точке разрезать узел
  • Интерактивный анимация, показывающая Центроид треугольника и Построение центроида с компасом и линейкой
  • Экспериментальное определение медиан и центроида треугольника в Эскизы динамической геометрии, интерактивный эскиз динамической геометрии с использованием симулятора гравитации Золушки.
Источник

Расчет центроида сложных форм методом геометрической декомпозиции - Образование

Расчет центроида сложных форм методом геометрической декомпозиции – Образование

Содержание

  • Что такое центроид?
  • Что такое геометрическая декомпозиция?
  • Пошаговая процедура решения центроида составных форм
  • Центроид для общих форм
  • Проблема 1: Центроид C-образных форм
  • Проблема 2: Центроид неправильных фигур
  • Момент инерции неправильной или сложной формы
  • Вопросы и Ответы

Что такое центроид?

Центроид – это центральная точка фигуры, также называемая геометрическим центром. Это точка, которая соответствует центру тяжести определенной формы. Это точка, которая соответствует среднему положению всех точек на рисунке. Центроид – это термин для двумерных форм. Центр масс – это термин для трехмерных фигур. Например, центр тяжести круга и прямоугольника находится посередине. Центроид прямоугольного треугольника находится на 1/3 снизу и от прямого угла. Но как насчет центроида сложных форм?

Что такое геометрическая декомпозиция?

Геометрическая декомпозиция

CИкс = Cix Аix / Аix

Cу = Ciy Аiy / Аiy

Пошаговая процедура решения центроида составных форм

Вот серия шагов в поиске центроида любой составной формы.

1. Разделите данную составную фигуру на различные первичные фигуры. Эти основные фигуры включают прямоугольники, круги, полукруги, треугольники и многое другое. При разделении составной фигуры включайте детали с отверстиями. Эти отверстия следует рассматривать как твердые компоненты, но с отрицательными значениями. Убедитесь, что вы разбили каждую часть составной формы, прежде чем переходить к следующему шагу.

2. Найдите площадь каждой разделенной фигуры. Таблица 1-2 ниже показывает формулы для различных основных геометрических фигур. После определения области дайте название каждой области (область один, область два, область три и т. Д.). Сделайте отрицательную область для обозначенных областей, которые действуют как отверстия.

3. На данной фигуре должны быть оси абсцисс и оси ординат. Если оси x и y отсутствуют, нарисуйте оси наиболее удобным способом. Помните, что ось X – это горизонтальная ось, а ось Y – это вертикальная ось. Вы можете расположить оси посередине, слева или справа.

4. Получите расстояние центроида каждой разделенной основной фигуры от оси x и оси y. В таблице 1-2 ниже показаны центроиды для различных основных форм.

Центроид для общих форм

Таблица 1-2: Центроид для общих форм. X-bar – это расстояние от центроида до оси y. Полоса Y – это расстояние от центроида до оси x.

Форма Площадь X-бар Y-образная штанга

Прямоугольник

бх

Би 2

d / 2

Треугольник

(bh) / 2

–

ч / 3

Прямоугольный треугольник

(bh) / 2

ч / 3

ч / 3

Полукруг

(пи (г ^ 2)) / 2

0

(4r) / (3 (пи))

Четверть круга

(пи (г ^ 2)) / 4

(4r) / (3 (пи))

(4r) / (3 (пи))

Круговой сектор

(г ^ 2) (альфа)

(2рсин (альфа)) / 3 (альфа)

0

Сегмент дуги

2r (альфа)

(rsin (альфа)) / альфа

0

Полукруглая дуга

(пи) (г)

(2r) / пи

0

Площадь под навесом

(bh) / (n + 1)

б / (п + 2)

(hn + h) / (4n + 2)

5. Создание таблицы всегда упрощает вычисления. Постройте таблицу, подобную приведенной ниже.

Таблица 1-1: Формат таблицы. X – расстояние центроида от оси y. Y – расстояние центроида от оси x.

Название области Площадь (А) Икс у Топор Ау

Площадь 1

–

–

–

Ax1

Ay1

Площадь 2

–

–

–

Ax2

Ay2

Площадь n

–

–

–

Axn

Айн

Всего

(Общая площадь)

–

–

(Суммирование топора)

(Суммирование Ay)

6. Умножьте площадь «A» каждой базовой формы на расстояние между центроидами «x» и осью y. Тогда получим суммирование ΣAx. См. Формат таблицы выше.

7. Умножьте площадь «A» каждой основной формы на расстояние между центроидами «y» и осью x. Тогда получим суммирование ΣAy. См. Формат таблицы выше.

8. Найдите общую площадь ΣA всей фигуры.

9. Найдите центроид CИксвсей фигуры путем деления суммы ΣAx на общую площадь фигуры ΣA. Результирующий ответ – это расстояние от центра тяжести всей фигуры до оси ординат.

10. Найдите центроид Cу всей фигуры путем деления суммы ΣAy на общую площадь фигуры ΣA. В результате получается расстояние от центра тяжести всей фигуры до оси абсцисс.

Вот несколько примеров получения центроида.

Проблема 1: Центроид C-образных форм

Решение 1

а. Разделите сложную фигуру на основные фигуры. В этом случае C-образная форма состоит из трех прямоугольников. Назовите три подразделения как Зона 1, Зона 2 и Зона 3.

б. Решите для площади каждого подразделения. Прямоугольники имеют размеры 120 x 40, 40 x 50, 120 x 40 для области 1, области 2 и области 3 соответственно.

Площадь 1 = bxh Площадь 1 = 120,00 мм x 40,00 мм Площадь 1 = 4800,00 квадратных миллиметров Площадь 2 = bxh Площадь 2 = 40,00 мм x 50,00 мм Площадь 2 = 2000 квадратных миллиметров Площадь 3 = bxh Площадь 3 = 120,00 мм x 40,00 мм Площадь 3 = 4800,00 квадратных миллиметров A = 4800 + 2000 + 4800 A = 11600,00 квадратных миллиметров

c. Расстояния X и Y каждой области. Расстояния по X – это расстояния от центроида каждой области до оси y, а расстояния по Y – это расстояния от центроида каждой области от оси x.

Площадь 1: x = 60,00 миллиметров y = 20,00 миллиметров Площадь 2: x = 100,00 миллиметров y = 65,00 миллиметров Область 3: x = 60 миллиметров y = 110 миллиметров

d. Найдите значения Ax. Умножьте площадь каждой области на расстояния от оси Y.

Ax1 = 4800,00 квадратных мм x 60,00 мм Ax1 = 288000 кубических миллиметров Ax2 = 2000,00 квадратных мм x 100,00 мм Ax2 = 200000 кубических миллиметров Ax3 = 4800,00 квадратных мм x 60,00 мм Ax3 = 288000 кубических миллиметров Ax = 776000 кубических миллиметров

е. Найдите значения Ay. Умножьте площадь каждой области на расстояния от оси абсцисс.

Ay1 = 4800,00 квадратных мм x 20,00 мм Ay1 = 96000 кубических миллиметров Ay2 = 2000,00 квадратных мм x 65,00 мм Ay2 = 130000 кубических миллиметров Ay3 = 4800,00 квадратных мм x 110,00 мм Ay3 = 528000 кубических миллиметров Ay = 754000 кубических миллиметров

Все единицы указаны в миллиметрах.

Название области Площадь (А) Икс у Топор Ау

Площадь 1

4800

60

20

288000

96000

Площадь 2

2000

100

65

200000

130000

Зона 3

4800

60

110

288000

528000

Всего

11600

776000

754000

f. Наконец, найдите центроид (CИкс, Су) разделив Ax на A и Ay на A.

Cx = ΣAx / ΣA Cx = 776000/11600 Cx = 66,90 миллиметров Cy = ΣAy / ΣA Cy = 754000/11600 Cy = 65,00 миллиметров

Центроид сложной фигуры находится на расстоянии 66,90 миллиметра от оси y и 65,00 миллиметра от оси x.

Проблема 2: Центроид неправильных фигур

Решение 2

а. Разделите сложную фигуру на основные фигуры. В этом случае неправильная форма имеет полукруг, прямоугольник и прямоугольный треугольник. Назовите три подразделения как Зона 1, Зона 2 и Зона 3.

б. Решите для площади каждого подразделения. Размеры прямоугольника 250 x 300, прямоугольного треугольника 120 x 120, а полукруга – 100. Обязательно инвертируйте значения для прямоугольного треугольника и полукруга, потому что это отверстия.

Площадь 1 = bxh Площадь 1 = 250,00 мм x 300,00 мм Площадь 1 = 75000,00 квадратных миллиметров Площадь 2 = 1/2 (bh) Площадь 2 = 1/2 (120 мм) (120 мм) Площадь 2 = – 7200 квадратных миллиметров Площадь 3 = ((pi) r ^ 2) / 2 Площадь 3 = ((pi) (100) ^ 2) / 2 Площадь 3 = – 5000pi квадратных миллиметров A = 75000.00 – 7200 – 5000pi A = 52092,04 квадратных миллиметра

c. Расстояния X и Y каждой области. Расстояния по X – это расстояния от центроида каждой области до оси y, а расстояния по y – это расстояния от центроида каждой области от оси x. Учтите ориентацию осей x и y. Для квадранта I значения x и y положительны. Для квадранта II x отрицателен, а y положителен.

Площадь 1: x = 0 y = 125,00 миллиметров Площадь 2: x = 110,00 миллиметров y = 210,00 миллиметров Область 3: x = – 107,56 миллиметров y = 135 миллиметров

d. Найдите значения Ax. Умножьте площадь каждой области на расстояния от оси Y.

Ax1 = 75000,00 квадратный мм x 0,00 мм Ax1 = 0 Ax2 = – 7200,00 квадратный мм x 110,00 мм Ax2 = – 792000 кубических миллиметров Ax3 = – 5000pi квадратный мм x – 107,56 мм Ax3 = 1689548,529 кубических миллиметров Ax = 897548,529 кубических миллиметров

е. Найдите значения Ay. Умножьте площадь каждой области на расстояния от оси абсцисс.

Ay1 = 75000,00 квадратный мм x 125,00 мм Ay1 = 9375000 кубических миллиметров Ay2 = – 7200,00 квадратных мм x 210,00 мм Ay2 = – 1512000 кубических миллиметров Ay3 = – 5000pi квадратный мм x 135,00 мм Ay3 = – 2120575,041 кубических миллиметров Ay = 5742424,959 кубических миллиметров

Все единицы указаны в миллиметрах.

Название области Площадь (А) Икс у Топор Ау

Площадь 1

75000

0

125

0

9375000

Площадь 2

– 7200

110

210

-792000

-1512000

Зона 3

– 5000 пикселей

– 107.56

135

1689548.529

-2120575.041

Всего

52092.04

897548.529

5742424.959

f. Наконец, найдите центроид (CИкс, Су) разделив Ax на A и Ay на A.

Cx = ΣAx / ΣA Cx = 897548,529 / 52092,04 Cx = 17,23 миллиметра Cy = ΣAy / ΣA Cy = 5742424,959 / 52092,04 Cy = 110,24 миллиметра

Центроид сложной фигуры находится на расстоянии 17,23 миллиметра от оси y и 110,24 миллиметра от оси x.

Момент инерции неправильной или сложной формы

  • Как найти момент инерции неправильных или сложных форм
    Это полное руководство по решению момента инерции сложных или неправильных форм. Знать основные необходимые шаги и формулы и владеть решающим моментом инерции.

Вопросы и Ответы

Вопрос: Есть ли какой-либо альтернативный метод решения для центроида, кроме этого геометрического разложения?

Отвечать: Да, есть метод, использующий ваш научный калькулятор для определения центроида.

Вопрос: в области два треугольника в задаче 2 … как получилось 210 мм стержня y?

Отвечать: Это расстояние y центра тяжести прямоугольного треугольника от оси x.

y = 130 мм + (2/3) (120) мм

y = 210 мм

Вопрос: Как Y-образная штанга для области 3 стала 135 миллиметров?

Отвечать: Я очень сожалею о путанице с вычислением Y-бара. На рисунке должно быть не хватает каких-то размеров. Но если вы понимаете процесс решения проблем с центроидом, то вам не о чем беспокоиться.

Вопрос: Как вы рассчитываете центр тяжести w-луча?

Отвечать: W-образные балки – это двутавровые балки. Вы можете начать решение центра тяжести W-образной балки, разделив всю площадь поперечного сечения балки на три прямоугольные области – верхнюю, среднюю и нижнюю. Затем вы можете приступить к выполнению описанных выше шагов.

Вопрос: Почему в задаче 2 квадрант расположен посередине, а в задаче 1 – нет?

Отвечать: В большинстве случаев положение квадрантов показано на данном рисунке. Но в случае, если вас просят сделать это самостоятельно, вы должны поместить ось в положение, в котором вы можете решить проблему наиболее простым способом. В случае проблемы номер два размещение оси Y посередине даст более простое и короткое решение.

Вопрос: Что касается Q1, есть графические методы, которые можно использовать во многих простых случаях. Вы видели игровое приложение, Pythagorean?

Отвечать: Смотрится интересно. В нем говорится, что Pythagorea – это набор геометрических головоломок разного типа, которые можно решить без сложных построений или вычислений. Все объекты нарисованы на сетке, ячейки которой – квадраты. Многие уровни можно решить, используя только вашу геометрическую интуицию или найдя законы природы, регулярность и симметрию. Это действительно может быть полезно.

Источник

Центроид треугольника — точка пересечения его медиан

В математике барице́нтр, или геометри́ческий центр, двумерной фигуры — это среднее арифметическое положений всех точек данной фигуры. Определение распространяется на любой объект в n-мерном пространстве. Радиус-вектор барицентра в трёхмерном случае вычисляется как

{displaystyle {vec {r}}_{b}=V^{-1}int _{V}{vec {r}}dV},

где интегрирование выполняется по объёму тела. Другое название барицентра в этом значении — центроид.

Неформально, геометрический барицентр есть точка равновесия фигуры, вырезанной из картона, в предположении, что картон имеет постоянную плотность, а внешнее гравитационное поле однородно.

В физике термин «барицентр» — синоним понятия «центр масс», используемый, в основном, в задачах космической механики. Центр масс объекта является средним арифметическим всех его точек с учётом локальной плотности массы. Для физических объектов с постоянной плотностью центр масс совпадает с барицентром фигуры той же формы.

Ниже барицентр рассматривается в математическом (геометрическом) смысле, о барицентре в физике см. статью Центр масс.

Свойства[править | править код]

Геометрический барицентр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь барицентр, лежащий вне фигуры. Барицентр кольца или миски, например, лежат вне фигуры.

Если барицентр известен, он является фиксированной точкой группы изометрии симметрий фигуры. Барицентр объекта лежит на пересечении всех его гиперплоскостей симметрии. Барицентры многих фигур (правильного многоугольника, правильного многогранника, цилиндра, прямоугольника, ромба, окружности, сферы, эллипса, эллипсоида, суперэллипса, суперэллипсоида и т. д.) можно найти исходя исключительно из этого принципа.

В частности, барицентром треугольника является точка пересечения его медиан (см. рисунок). Барицентром параллелограмма является точка пересечения его диагоналей, но это неверно для других четырёхугольников.

Барицентр объекта с трансляционной симметрией не определён (или лежит вне пространства фигуры), поскольку сдвиг не имеет фиксированной точки.

Центроид треугольника[править | править код]

  • Барицентр треугольника называется центроидом и лежит на пересечении трёх медиан, также лежит на прямой Эйлера (проходящей и через другие ключевые точки, включая ортоцентр и центр описанной окружности)[1][2].
  • Если в вершины треугольника поместить равные массы, то центр масс (барицентр) полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой массой также находится в центроиде.
MA^{2}+MB^{2}+MC^{2}=GA^{2}+GB^{2}+GC^{2}+3MG^{2}[3].
  • Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин треугольника:
AB^{2}+BC^{2}+CA^{2}=3(GA^{2}+GB^{2}+GC^{2})[3].
  • Центр масс сторон треугольника совпадает с центром вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера. Если стороны треугольника сделать из тонкой проволоки одинакового сечения, то центр масс (барицентр) полученной системы будет совпадать с инцентром дополнительного треугольника, или с центром Шпикера.
  • О других свойствах центроида треугольника смотрите ниже.

Минимаксные свойства центроида треугольника[править | править код]

  • Центроид или точка пресечения медиан треугольника является единственной точкой треугольника такой, что проведенные через неё три чевианы разделяют своими концами стороны треугольника на шесть отрезков. При этом произведение длин трёх из этих шести отрезков, не имеющих общих концов, максимально[4].
  • Центроид или точка пересечения трёх медиан является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).

Центроид четырёх точек (вершин четырёхугольника)[править | править код]

Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие — середины противолежащих сторон. Точка пересечения делит все три отрезка пополам.

Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в одной точке (центроиде вершин четырёхугольника) и делятся ею в отношении 3:1, считая от вершины.

Центр масс вершин четырёхугольника не обязан совпадать с центром масс самого четырёхугольника как плоской фигуры.

Определение местоположения барицентра[править | править код]

Определение местоположения барицентра однородной плоской фигуры методом отвеса[править | править код]

Барицентр однородной плоской фигуры, такой как фигура (a) на рисунке, можно найти экспериментально с использованием отвеса и булавки путём нахождения центра масс тонкой пластины однородной плотности, имеющей ту же форму. Пластина удерживается булавкой, вставленной ближе к периметру так, чтобы пластина могла свободно вращаться. Отмечаем на пластине прямую, которую образует отвес, прикреплённый к булавке (b). Проделываем то же самое с другим положением булавки. Пересечение двух прямых даст барицентр (c).

Этот метод можно распространить (в теории) на вогнутые фигуры, когда барицентр лежит вне их, а также тела (постоянной плотности), но положение линии отвеса придётся отмечать каким-то иным способом.

Определение местоположения барицентра выпуклой двумерной фигуры методом балансировки[править | править код]

Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например, на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.

Определение местоположения барицентра для конечного множества точек[править | править код]

Барицентр конечного множества из {k} точек {displaystyle mathbf {x} _{1},mathbf {x} _{2},ldots ,mathbf {x} _{k}} в mathbb {R} ^{n} находится по формуле

{displaystyle mathbf {G} ={frac {mathbf {x} _{1}+mathbf {x} _{2}+cdots +mathbf {x} _{k}}{k}}}[5].

Полученная точка {mathbf {G}} такая, что сумма квадратов расстояний между ней и точками множества является минимальной.

Определение местоположения барицентра с помощью геометрического разложения[править | править код]

(b) Разложение фигуры на простые элементы

(c) Барицентры элементов объекта

Барицентр плоской фигуры X можно вычислить, разделив её на конечное число более простых фигур {displaystyle X_{1},X_{2},dots ,X_{n}}, найдя положение барицентров G_{i} и площадей A_{i} каждой части, а затем вычислив

{displaystyle G_{x}={frac {sum G_{i_{x}}A_{i}}{sum A_{i}}},G_{y}={frac {sum G_{i_{y}}A_{i}}{sum A_{i}}}.}

Дыры в фигуре X, наложения частей, или части, выступающие за фигуру, можно рассматривать как фигуры с отрицательной площадью A_{i}. А именно, знак площади A_{i} нужно выбирать так, чтобы сумма знаков A_{i} для всех частей, включающих точку p, была равна 1, если p принадлежит X, и 0 в противном случае.

Например, фигуру (a) на рисунке легко разделить на квадрат и треугольник с положительным знаком, круглое отверстие с отрицательным (b).

Барицентр каждой части легко найти в любом списке барицентров простых фигур (c). Затем вычисляется барицентр фигуры, как средневзвешенное трёх точек. Горизонтальное положение барицентра, считая от левого края фигуры, равно

{displaystyle x={frac {5times 10^{2}+13.33times {frac {1}{2}}10^{2}-3times pi 2.5^{2}}{10^{2}+{frac {1}{2}}10^{2}-pi 2.5^{2}}}approx 8.5.}

Вертикальное положение вычисляется аналогично.

Та же формула применима для любого трёхмерного объекта, только A_{i} обозначают уже объёмы частей тела X_{i}, а не площади. Формула верна также для пространства mathbb {R} ^{d} любой размерности d при замене площади d-мерными мерами частей.

Определение местоположения барицентра интегрированием[править | править код]

Барицентр подмножества X пространства mathbb {R} ^{n} можно вычислить с помощью интеграла

{displaystyle G={frac {int xg(x);dx}{int g(x);dx}},}

где интегрирование ведётся по всему пространству mathbb {R} ^{n}, а g является характеристической функцией подмножества, принимающей 1 внутри X и 0 вне его[6]. Заметим, что знаменатель равен мере множества X. Формула неприменима к множеству нулевой меры, а также к множествам, для которых интеграл расходится.

Другая формула для вычисления координат барицентра:

{displaystyle G_{k}={frac {int zS_{k}(z);dz}{int S_{k}(z);dz}},}

где Gk является k-й координатой G, а Sk(z) — мера пересечения X с гиперплоскостью, определяемой уравнением xk = z. Снова знаменатель — это мера множества X.

Для плоской фигуры координатами барицентра будут

{displaystyle G_{mathrm {x} }={frac {int xS_{mathrm {y} }(x);dx}{A}};}
{displaystyle G_{mathrm {y} }={frac {int yS_{mathrm {x} }(y);dy}{A}},}

где A — площадь фигуры X, Sy(x) — длина пересечения[неизвестный термин] X с вертикальной прямой с абциссой x, Sx(y) — аналогичная величина при обмене осей.

Определение местоположения барицентра для области, ограниченной графиками непрерывных функций[править | править код]

Координаты барицентра {displaystyle ({bar {x}},;{bar {y}})} области, ограниченной графиками непрерывных функций f и g, таких что f(x)geq g(x) на интервале [a,b], aleq xleq b, задаются выражениями

{displaystyle {bar {x}}={frac {1}{A}}int _{a}^{b}xleft[f(x)-g(x)right];dx}[6].
{displaystyle {bar {y}}={frac {1}{A}}int _{a}^{b}left[{frac {f(x)+g(x)}{2}}right]left[f(x)-g(x)right];dx,}[7]

где A — площадь области (вычисляемая по формуле {displaystyle int _{a}^{b}left[f(x)-g(x)right];dx})[8][9].

Определение местоположения барицентра объекта, имеющего форму буквы L[править | править код]

Метод нахождения барицентра фигуры, имеющей форму буквы L.


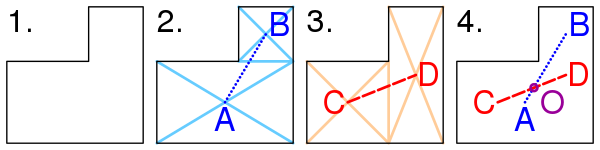
CoG of L shape.svg

  1. Фигуру делят на два прямоугольника (см. фигуру (2) на рисунке). Находят барицентры A и B этих двух прямоугольников как пересечение диагоналей. Рисуют отрезок AB, соединяющий барицентры. Барицентр фигуры должен лежать на этом отрезке AB.
  2. Делят фигуру на два прямоугольника другим способом (см. фигуру (3) на рисунке). Находят барицентры C и D этих двух прямоугольников. Проводят отрезок CD, соединяющий барицентры. Барицентр фигуры должен лежать на отрезке CD.
  3. Поскольку барицентр должен лежать как на отрезке AB, так и на отрезке CD, очевидно, что он является точкой пересечения этих двух отрезков — точкой O. Точка O не обязана лежать внутри фигуры.

Барицентры треугольника и тетраэдра[править | править код]

Точка пересечения медиан (барицентр) делит каждую медиану в отношении 2:1. То есть, расстояние от стороны до барицентра равно 1/3 длины проведённой к стороне высоты

В прямоугольном треугольнике расстояние от одного катета до барицентра равно 1/3 длины другого катета

Барицентр треугольника совпадает с пересечением медиан. Барицентр разбивает каждую медиану в отношении 2:1, то есть барицентр находится на расстоянии ⅓ от стороны до противоположной вершины (см. рисунок). Его декартовыми координатами является среднее координат трёх вершин. То есть, если вершинами треугольника являются {displaystyle a=(x_{a},y_{a})}, {displaystyle b=(x_{b},y_{b})} и {displaystyle c=(x_{c},y_{c})}, то координаты барицентра вычисляются по формуле

{displaystyle G={frac {1}{3}}(a+b+c)=left({frac {1}{3}}(x_{a}+x_{b}+x_{c}),{frac {1}{3}}(y_{a}+y_{b}+y_{c})right)}.

Таким образом, барицентр имеет барицентрические координаты {tfrac {1}{3}}:{tfrac {1}{3}}:{tfrac {1}{3}}.

В трилинейных координатах барицентр можно получить одним из эквивалентных способов[10]:

{displaystyle G={frac {1}{a}}:{frac {1}{b}}:{frac {1}{c}}=bc:ca:ab=csc A:csc B:csc C}

{displaystyle =cos A+cos Bcdot cos C:cos B+cos Ccdot cos A:cos C+cos Acdot cos B}
{displaystyle =sec A+sec Bcdot sec C:sec B+sec Ccdot sec A:sec C+sec Acdot sec B.}

Барицентр является также физически центром масс треугольника, сделанного из однородного листового материала, а также, если вся масса сконцентрирована в вершинах и одинаково разделена между ними. Если же масса распределена равномерно вдоль периметра, то центр масс лежит в точке Шпикера (инцентре серединного треугольника), который (в общем случае) не совпадает с центроидом всего треугольника.

Площадь треугольника равна 3/2 длины любой стороны, умноженной на расстояние от центроида до стороны[11].

Центроид треугольника лежит на прямой Эйлера между его ортоцентром H и центром его описанной окружности O, ровно вдвое ближе ко второму, чем к первому:

{displaystyle GH=2GO}.

Кроме того, для инцентра I и центра девяти точек N, мы имеем

{displaystyle GH=4GN},
{displaystyle GO=2GN},
{displaystyle IG<HG},
{displaystyle IH<HG},
{displaystyle IG<IO}.

Аналогичными свойствами обладает тетраэдр — его барицентр является пересечением отрезков, соединяющих вершины с барицентрами противоположных граней. Эти отрезки делятся барицентром в отношении 3:1. Результат может быть обобщён на любой n-мерный симплекс. Если вершины симплекса обозначить {displaystyle v_{0},ldots ,v_{n}} и рассматривать вершины как вектора, центроид равен

{displaystyle G={frac {1}{n+1}}sum _{i=0}^{n}v_{i}}.

Геометрический барицентр совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как n равных масс.

Изогональным сопряжением центроида треугольника является точка пересечения его симедиан.

Барицентр тетраэдра[править | править код]

Тетраэдр является телом в трёхмерном пространстве, имеющим четыре треугольника в качестве граней. Отрезок, соединяющий вершину тетраэдра с барицентром противоположной грани, называется медианой, а отрезок, соединяющий середины двух противоположных сторон, называется бимедианой. Таким образом, имеется четыре медианы и две бимедианы. Эти шесть отрезков пересекаются в барицентре тетраэдра[12]. Барицентр тетраэдра лежит посередине между точкой Монжа и центром описанной сферы. Эти точки задают прямую Эйлера тетраэдра, являющуюся аналогом прямой Эйлера треугольника.

Барицентр многоугольника[править | править код]

Барицентром самонепересекающегося замкнутого многоугольника, заданного n вершинами (x_{0},y_{0}), (x_{1},y_{1}), ldots , {displaystyle (x_{n-1},y_{n-1})}, является точка {displaystyle (G_{x},G_{y})}, где

{displaystyle G_{x}={frac {1}{6A}}sum _{i=0}^{n-1}(x_{i}+x_{i+1})(x_{i}y_{i+1}-x_{i+1}y_{i})};
{displaystyle G_{y}={frac {1}{6A}}sum _{i=0}^{n-1}(y_{i}+y_{i+1})(x_{i}y_{i+1}-x_{i+1}y_{i})}

и где A является площадью многоугольника (со знаком):

{displaystyle A={frac {1}{2}}sum _{i=0}^{n-1}(x_{i}y_{i+1}-x_{i+1}y_{i})}[13].

В этой формуле предполагается, что вершины пронумерованы вдоль периметра многоугольника. Кроме того, вершина {displaystyle (x_{n},y_{n})} считается той же самой, что и (x_{0},y_{0}).
Заметим, что если точки пронумерованы по часовой стрелке, площадь A, вычисленная выше, будет отрицательной, но координаты барицентра подкорректируют этот случай.

Барицентры конуса и пирамиды[править | править код]

Барицентр конуса или пирамиды расположен на отрезке, соединяющем вершину тела с барицентром основания. Для целого конуса или пирамиды барицентр находится на расстоянии 1/4 от основания к вершине. Для поверхности конуса или пирамиды (боковая поверхность без внутренности и без основания) центроид находится на 1/3 расстояния от основания до вершины.

См. также[править | править код]

  • Центр масс
  • Центроид треугольника
  • Центр тяжести
  • Центр Чебышева[en]
  • Среднее Фреше[en]
  • k-means
  • Список барицентров
  • Теоремы Паппа — Гульдина
  • Замечательные точки треугольника

Примечания[править | править код]

  1. ↑ Altshiller-Court, 1925, с. 101.
  2. ↑ Kay, 1969, с. 18,189,225–226.
  3. ↑ 1 2 Altshiller-Court, 1925, с. 70–71.
  4. ↑ Зетель, 1962.
  5. ↑ Protter, Morrey, 1970, с. 520.
  6. ↑ 1 2 Protter, Morrey, 1970, с. 526.
  7. ↑ Protter, Morrey, 1970, с. 527.
  8. ↑ Protter, Morrey, 1970.
  9. ↑ Larson, Hostetler, Edwards, 1998, с. 458–460.
  10. ↑ Encyclopedia of Triangle Centers Архивная копия от 19 апреля 2012 на Wayback Machine by Clark Kimberling. The centroid is indexed as X(2).
  11. ↑ Johnson, 2007, с. 173.
  12. ↑ Kam-tim, Suk-nam, 1994, с. 53–54.
  13. ↑ Bourke, 1997.

Литература[править | править код]

  • Зетель, С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е изд/. — М. : Учпедгиз, 1962. — С. 12.
  • Leung Kam-tim, Suen Suk-nam. Vectors, matrices and geometry. — Hong Kong University Press, 1994.
  • Nathan Altshiller-Court. College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. — 2nd. — New York: Barnes & Noble, 1925.
  • Paul Bourke. Calculating the area and centroid of a polygon. — 1997.
  • Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007.
  • David C. Kay. College Geometry. — New York: Holt, Rinehart and Winston, 1969.
  • Roland E. Larson, Robert P. Hostetler, Bruce H. Edwards. Calculus of a Single Variable. — 6th. — Houghton Mifflin Company, 1998.
  • Murray H. Protter, Charles B. Morrey Jr. College Calculus with Analytic Geometry. — 2nd. — Reading: Addison-Wesley, 1970.

Ссылки[править | править код]

  • Characteristic Property of Centroid at cut-the-knot
  • Barycentric Coordinates at cut-the-knot
  • Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge
  • Experimentally finding the medians and centroid of a triangle at Dynamic Geometry Sketches, an interactive dynamic geometry sketch using the gravity simulator of Cinderella.
Источник

ТЕМА № 10. Элементарный пространственный анализ.

Слайд 2. Точечные объекты высокого уровня.

Помимо обычных точек, линий и полигонов в пространственном анализе и моделировании используют особые точечные, линейные и полигональные объекты, которые называют «геометрическими объектами высокого уровня», подчеркивая их особенности и важность для анализа. Рассмотрим их по отдельности

Точечные объекты высокого уровня. Существует два основных типа точечных объектов высокого уровня: центроиды и узлы.

Узел – это особая точка, в которой соединяются 2 или более дуг. Узел – один из основных элементов топологических моделей векторных данных.

Центроид (centroid) обычно определяется как точка, находящаяся в точном географическом центре области или полигона.

Слайд 3. Центроиды.

Определение центроида просто для простых многоугольников, таких как прямоугольники. Для многоугольников процедура определения положения центроида более сложная. Географические центроиды в векторном случае вычисляются по правилу четырехугольников (trapezoidal rule), которое делит многоугольник на некоторое число перекрывающихся четырехугольников. Затем вычисляются центроиды, или центральные координаты, каждого четырехугольника, затем – их взвешенное среднее.

Слайд 4. Центроиды (продолжение).

Существуют и другие способы построения центроидов. Например, центроидом может считаться центр прямоугольника, описанного вокруг полигона.

Каноническим для ГИС центроидом является центр эллипса, наиболее близкого по форме к контуру полигона. Кроме того, оно позволяет использовать большую ось эллипса для определения ориентации полигона.

Центроид может быть нужен, когда вы создаете карту поверхности по значениям, определенным в разных ее областях. Например, вам нужно создать карту, показывающую уровень добычи нефти за период 1999-2001 гг. При этом вы располагаете данными, собранными на уровне НГДУ (обобщенные сведения об объемах добычи за отчетный период). Т.к. каждое НГДУ имеет компактную ограниченную территорию добычи, то вам необходимо рассчитать центроиды для территории каждого НГДУ. Затем, через

интерполяцию, на основе этих точек могут быть построены изолинии или поверхности. Другой пример. Предположим, что у вас есть карта крупного масштаба, которую

вы желаете использовать для региональных исследований. На крупномасштабной карте отдельно стоящие здания и промышленные объекты представлены полигонами. При переходе к более мелкому масштабу эти полигональные объекты отображаются некорректно (наезжают друг на друга и другие объекты, мешают чтению карты). Наиболее простым решением этой проблемы будет замена полигональных объектов точечными, а именно, центроидами.

Таким образом, центроид выполняет функцию точечного объекта, к которому при известных обстоятельствах можно отнести данные полигона.

Слайд 5. Центроиды – центры распределения точек.

Центроиды могут также помещаться в центре распределения некоторого явления, а не в абсолютном географическом центре многоугольника. Эта точка, называемая центром масс, требует раздельного усреднения координат Х и Y по всем точкам. Конечным результатом будет одна пара координат, представляющая центральную точку этого распределения точек. Координаты центра масс определяются как частные от деления сумм координат Х и Y на число точек.

Если в распределении не все точки одинаково важны в отображении изучаемого явления, то им можно назначить весовые коэффициенты: например, точки могут указывать и местоположения, и объемы продаж каждого магазина. В этом случае положение центроида рассчитывается с учетом весового фактора. Определение такого взвешенного центра масс требует перемножения каждой координаты на взвешивающий коэффициент (в последнем примере – объем продаж), суммирования одноименных координат и деления сумм на общую массу (сумму коэффициентов). В результате получаем пару координат центра распределения с учетом весовых коэффициентов.

Следует отметить, что растровые ГИС не приспособлены к процедуре расчета центроидов. Во многих случаях даже векторные ГИС не имеют соответствующей функции. В системе ArcGIS реализованы возможности определения центральных точек и для полигональных объектов, и для точечных распределений.

Слайд 6. Линейные объекты высокого уровня.

Два типа линий особенно важны и оправдывают свое название объектов высокого уровня: границы и сети.

Первый упоминался при обсуждении отношений между атрибутами линий и прилежащих к ним полигонов. Линии называются границами, если при их пересечении происходит существенное изменение одного или многих атрибутов местности. Другими словами, важность границ обусловлена их функцией по отношению к прилежащим полигонам.

Линии могут также становиться объектами высокого уровня, когда они связаны друг с другом некоторыми отношениями. В таких случаях это не просто изображения линейных объектов или границ между полигонами, а особые структуры, которые вместе с узлами образуют сети (networks).

Сети могут быть определены как набор соединенных линейных объектов, вдоль которых возможно движение от одного узла к другому.

Сети позволяют моделировать множество видов потока: движение автомобилей и поездов, транспортировку грузов, перекачку нефти, газа, воды, и даже миграции животных по миграционным коридорам.

Сети состоят из двух основных компонентов: ребер и соединений. Ребро– это тип элемента сети, который имеет определенную длину и через который движется поток определенного предмета потребления. Линии электропередач, трубопроводы и русла потоков могут служить примерами ребер. Соединение имеет место на пересечении двух и более ребер и обеспечивает передачу потока между ребрами. Примерами могут служить предохранители, трансформаторы, служебные втулки и переходники, точки слияния потоков. Ребра соединяются друг с другом в соединениях, поток из одних ребер сети переходит в другие ребра через соединения.

Чтобы иметь возможность проводить операции на сетях, элементы сети должны иметь специальные атрибуты, необходимые для анализа этих потоков (ограничения скорости, сопротивление, запрет на въезд, открытая или закрытая задвижка и т.д.). Кроме того, элементам сети могут быть сопоставлены правила поведения: например, 50-ти дюймовая и 20-ти дюймовая трубы могут быть соединены только через переходник.

По конфигурации сети или их части разделяют на прямолинейные, как автомагистраль; древовидные, как речная сеть; контуры, как ведущая в исходную точку комбинация улиц или кольцевые объездные дороги вокруг крупных городов.

Сети также различаются на направленные или ненаправленные. В направленной сети поток может иметь только одно направление. Например, реки при нормальных обстоятельствах текут только вниз по склону. Аналогично, на улицах с односторонним движением запрещено движение в одном из направлений.

В ненаправленных сетях поток может двигаться в любом направлении, хотя, в общем случае, сопротивление движению во встречных направлениях может быть

неодинаковым.

Растровые ГИС не подходят для работы с сетями, так как в них нет средств явного определения сетей.

Слайд 7. Площадные объекты высокого уровня.

Как и точки и линии, области также могут быть объектами высокого уровня. Полигоны высокого уровня называются регионами. Регионы создаются на основе атрибутов: в один регион объединяются полигоны с одинаковым значением какого-либо атрибута. Например, мы могли бы определить регион, отобрав все полигоны, в которых главным растительным компонентом является лес. Это даст нам “лесной” регион.

Регионы различаются не только атрибутами, но и своей конфигурацией в пространстве. Имеются три основных вида регионов: сплошные, фрагментированные и перфорированные. Сплошной регион образуется из смежных полигонов. Фрагментированный регион составлен из двух или более полигональных фигур, разделенных пространством, которое не относится к этому региону. Например, лесной регион может выглядеть как некоторое число полигонов, разбросанных по карте, имеющих при этом единый набор видов деревьев. Для фрагментированных регионов нет ограничений на расстояние между образующими их полигонами, пока сохраняется сходство атрибутов. Перфорированный регион, в отличие от фрагментированного, не состоит из отдельных полигонов, а исключает их. То есть, такой регион представляет собой связную область, из которой исключены некоторые внутренние полигоны, называемые отверстиями или островами. Очевидно, что между перфорированными и фрагментированными регионами может быть взаимосвязь. Если полигоны, содержащиеся внутри перфорированного региона, имеют общие между собой атрибуты, то они могут образовывать фрагментированный регион.

Слайд 8. Измерения. Измерение длин линейных объектов.

Основу пространственного анализа также составляют различные измерения. Кроме измерения расстояний и линейных размеров пространственных объектов, можно также измерять такие пространственные характеристики как форма объектов, их ориентация в пространстве, направленность объектов и др.

Измерения длин линейных объектов. Измерения длин линейных объектов различно при использовании растровых и векторных моделей данных. Определение длины вертикальных или горизонтальных линий в растре проводится подсчетом числа ячеек, через которые линия проходит, и умножением его на линейный размер одной

ячейки (разрешение) растра. Если линия занимает 15 ячеек по вертикали при разрешении растра 50 метров, то ее общая длина составит 15х 50 = 750 метров. Аналогично – для горизонтали.

Но если линия ориентирована не точно по горизонтали или вертикали, метод будет неточным. Например, если линия проходит точно по диагоналям ячеек, то ее длина будет очевидно больше (в данном случае (примерно 1.414) раз), чем произведение разрешения на число ячеек. То есть, для таких линий нужно использовать разрешение растра, умноженное на √2. Тем менее, оказывается, что многие простые растровые системы только лишь подсчитывают число ячеек растра и используют это число в качестве длины, оставляя за пользователем вычисление реальной длины.

Более сложная проблема возникает, когда мы имеем дело с извилистой линией, проходящей случайным образом по растру. В зависимости от разрешения растра и извилистости линии, вполне возможно, что целые петли могут быть представлены лишь одной ячейкой растра; в таком случае длина будет преуменьшена независимо от метода ее определения. Поэтому, если проводимый вами анализ активно использует измерение линейных объектов, то, по возможности, следует использовать векторную структуру данных.

Определение длины линейного объекта в векторной системе гораздо более точно (как и само представление линии), чем подсчет ячеек растра. Для каждого прямого отрезка из образующих линию система хранит координаты крайних точек, из которых может быть получена по теореме Пифагора длина этого отрезка. Просто сложив длины всех отрезков линии, мы получим точное значение ее общей длины. Нужно только помнить, что векторное представление линейных объектов также использует своего рода дискретизацию, когда кривые участки линии аппроксимируются прямыми отрезками, и чем больше таких отрезков используется, тем точнее представление объекта в этой структуре данных и тем точнее будет полученное значение общей длины линии.

Определение периметра. Измерение периметра полигонов производится таким же образом, что и измерение длин линий.

Слайд 9. Вычисление площадей полигонов.

Вычисление площадей для растрового и векторного способов представления данных также различно. В растре площадь подсчитывается простым умножением площади ячейки (а это есть разрешение в квадрате) на количество ячеек, занимаемых областью.

Для векторного представления данных наиболее простое решение состоит в делении сложного полигона на несколько простых фигур, площади которых легко определяются по формулам, после чего эти числа суммируются. Во многих векторных ГИС площади полигонов подсчитываются при их вводе и заносятся в таблицы атрибутов, так что в дальнейшем определение площади требует только выборки соответствующего значения из БД.

Слайд 10. Меры формы: измерение извилистости

Существует тесная взаимосвязь между формой (очертаниями) и такими мерами, как периметр и площадь для полигонов и длина для линейных объектов. Во многих случаях очертания полигонов и меры извилистости линейных объектов обеспечивают понимание взаимоотношений между объектами и их окружением. Например, извилистость реки связана с такими функциями, как объем переносимого осадка, уклон и расход воды (дебит). В свою очередь, эти функциональные отношения существенно связаны с состоянием реки: происходит ли намыв осадка, находится ли река в состоянии баланса или деградирует. Гидрологи, геоморфологи и другие специалисты используют эти величины в общем анализе состояния региона.

Измерение извилистости. Существуют две простые меры извилистости, которые могут использоваться для характеристики линий. Перваяэто отношение суммарной длины отрезков, составляющих линию, к расстоянию между ее крайними точками. Чем ближе это значение к единице, тем менее извилиста линия, для прямой линии это отношение составляет ровно единицу.

Но часто о форме кривой линии требуется знать больше. Например, очень резкие изгибы дороги с большей вероятностью могут стать причиной аварий. А острая излучина реки вызывает активную эрозию внешнего берега и нанос осадка на внутреннем берегу. По этой причине полезно знать радиус изгиба линейного объекта. Чтобы определить его, мы принимаем, что изгиб является по сути круговым, хотя так может быть не всегда. Затем мы вписываем окружность в каждое закругление и измеряем ее радиус. Если река представлена полигоном, то появляется возможность измерить еще и отношение радиуса к ширине реки, которое дает еще одну полезную характеристику формы.

Как в растровых, так и в векторных системах измерение радиуса кривизны обычно требует участия оператора. Многие ГИС не имеют адекватных средств для таких измерений, но многие специальные системы позволяют проводить такие измерения средствами внешних программ, которые возвращают данные обратно в систему для дальнейшего анализа. Чаше всего пользователю приходится самому вписывать

окружности, что может быть довольно утомительно. Поэтому вам нужно оценить важность таких измерений для ваших задач и способность вашей системы производить их.

Слайд 11. Меры формы полигонов.

Существует несколько подходов для измерения формы полигона. Одни из них основаны на изучение пространственной целостности полигонов, другие используют меры выпуклости или отношение периметр/площадь, третьи изучают форму границ.

Слайд 12. Меры формы полигонов: функция Эйлера.

Первый подход основан на идеи перфорированных и фрагментированных регионов и имеет общее название пространственной целостности. Наиболее распространенной мерой пространственной целостности является функция Эйлера.

Функция Эйлера представляет численное выражение степени фрагментированности и перфорированности. На слайде изображены три возможные конфигурации полигонов. Функция Эйлера сопоставляет с каждой из них одно число, называемое числом Эйлера, которое определяется так:

E = H-(F- 1),

где Е – число Эйлера, Н – суммарное количество отверстий во всех полигонах региона, F – количество полигонов во фрагментированном регионе.

Рассмотрим три различные конфигурации и связанные с ними числа Эйлера: 1) 4 отверстия в одном сплошном регионе: E=4+(1-1)=4; 2) два фрагмента, по 2 отверстия в каждом : E=4 –(2-1) = 3; 3) три фрагмента, два с двумя отверстиями, третий – с одним: E=5-(3-1)= 3. Заметьте, что во втором и третьем случаях число Эйлера одно и то же, несмотря на то, что конфигурации различны.

Слайд 13. Меры формы полигонов (продолжение).

Другая

группа

мер

полигонов,

относящихся к

их

границам,

довольно

многочисленна.

Большинство этих

мер

связано с

отношением периметра

к площади,

которое

является наиболее сжатой характеристикой формы, мерой сложности полигона. Наименьшее такое отношение из всех фигур имеет круг, в то время как вытянутые узкие полигоны имеют большее значение этого отношения. Многие задачи, особенно связанные

с природными ресурсами, часто используют отношение периметр/площадь. Например, чем меньше это отношение для участка леса, тем больше вероятность обнаружения в нём животных, предпочитающих внутренние области для обитания, что может быть важно для сохранения этого вида. И наоборот, если вы хотите заняться разработкой приозерной территории для туризма, то чем выше это отношение для озера, тем больше длина пляжей, которые можно предложить потенциальным покупателям участков.

Отношение периметр/площадь дает общее представление об объекте, однако, оно не описывает реальную геометрическую форму объекта. Вместо простого отношения было бы неплохо иметь некоторую более “формообразную” меру. Для этого мы чаше всего сравниваем имеющиеся полигональные фигуры с более знакомыми фигурами, которые можем легко описать. Например, мы могли бы сравнивать их с параллелограммами, трапециями и треугольниками. Но даже эти фигуры очень разнообразны, в то время как круг является наиболее простой, компактной и легко определимой фигурой. По этой причине основным методом измерения формы является сравнение ее с кругом.

В связи с использованием круга как сравнительной фигуры, мы можем говорить, что эта мера является также и мерой выпуклости или вогнутости полигона. Круг является наиболее выпуклой фигурой: как известно, все другие геометрические фигуры имеют большую длину периметра при том же значении площади. Сравнение имеющегося многоугольника с кругом, по сути, – то же, что рассмотрение величины выпуклости этого полигона по сравнению с выпуклостью круга. Общая формула выпуклости в векторных ГИС такова: CI – k Р/S, где: CI – индекс выпуклости, к – некоторая константа, Р – периметр, S – площадь.

Здесь мы имеем отношение периметра к площади, умноженное на некоторую константу. Эта константа определяется размером круга, описанного вокруг многоугольника, так что индекс принимает значения в диапазоне 1…99, причем большее значение соответствуют большему сходству с кругом, а 100 получается, если мы возьмем идеальный круг.

Слайд 14. Меры формы полигонов: развитость границ.

Имеется еще одна мера конфигурации границ полигонов, называемая развитостью границ. Для расчета этой меры используется оконная функция. Возьмем окно размером 3×3 ячейки, которое скользит по области изучения с шагом в одну ячейку и в каждом положении рассчитывает индекс границ. При каждом положении окна каждой ячейке

матрицы мы присваиваем единицу, если она имеет тот же атрибут, что и край, который нас интересует, и ноль, – если она имеет атрибуты любого другого объекта покрытия. Индекс границ получается простым подсчетом числа ячеек с единицами. Чем больше единиц, тем меньше границ и тем больше внутренней области мы имеем. Поэтому, значение 7 на слайде указывает на малую развитость границы. Значение 9 соответствует внутренней области полигона, где все ячейки растра соединены и вообще нет границ. И наоборот, значение 2 показывает, что только небольшое число нужных ячеек растра имеется в окне, а остальные относятся к фону. Оно указывает на небольшой узкий выступ в окружение. Иначе говоря, во втором случае окно покрывает большое количество краев.

Слайд 15. Простое и функциональное расстояния.

Измерение расстояния между объектами является одной из канонических задач ГИС. Измерение расстояний между объектами важно не только для дальнейшего анализа отношений между ними, но и как непосредственная оценка движения к ним, от них и вокруг них.

На первый взгляд может показаться, что измерение расстояния представляет собой ту же самую задачу, что и измерение длин линейный объектов. Это так, если речь идет о простом физическом расстоянии между двумя выбранными точками. Но, кроме того, измерение расстояния может учитывать стоимость продвижения по пересеченной местности или подорожной сети в противоположность движения напрямую, или в обход барьеров, которые препятствуют движению. Эти меры называются функциональными расстояниями.

Измерение Простого расстояния, известного также как эвклидово расстояние, относительно просто и в растровых, и в векторных ГИС. В растровых системах простое расстояние измеряется количеством ячеек между точками, умноженным на величину разрешения растра. В векторной системе расстояния определяются по теореме Пифагора.

Кроме такого способа определения расстояния между точками, существует и другой, при котором заранее просчитываются расстояния от определенной точки до всех других возможных точек покрытия. В растре это делается созданием набора концентрических окружностей с центром в заданной точке, каждая последующая из которых имеет радиус на одну ячейку больше. В результате образуется изотропная поверхность. Во всех направлениях от выбранной точки скорость движения одинаковая (скорость на слайде показана синими векторами): расстояние между изолиниями в любом

направлении одно и тоже. Другими словами в любом направлении за одно и тоже время можно продвинуться на одно и тоже расстояние.

Функциональное расстояние. С другой стороны, нашу способность двигаться по прямой часто ограничивают препятствия или сложная местность. Например, мы можем быть ограничены либо использованием сетей, таких как авто- и железные дороги, либо потому, что местность слишком пересеченная, образуя поверхность с препятствиями, либо из-за ограждений, окружающих промежуточное пространство, которые действуют как барьеры на нашем пути. Поверхности с сопротивлением (фрикционные поверхности)- это области, которые замедляют наше продвижение, увеличивая время достижения заданной точки по сравнению с поверхностью без сопротивления (изотропные поверхности). На слайде показано, что для поверхности с сопротивлением скорость движение в различных направлениях будет разной: при движении на север поверхность оказывает максимальное сопротивление, при движении на юг – минимальное.

Слайд 16. Функциональное расстояние: барьеры.

Барьеры бывают двух типов: абсолютные, движение через которые невозможно (скалы, огражденная территория, озеро и т.д.), и условные, которые идентичны фрикционным поверхностям, но занимают лишь небольшие участки покрытия. Примерами условных барьеров могут быть холмистая местность, мелкие реки, преодолимые внедорожными машинами, или участки леса, которые тормозят, но не останавливают полностью движение стада животных.

Абсолютные барьеры останавливают или отклоняют движение, в то время как относительные барьеры и фрикционные поверхности налагают некоторую стоимость на передвижение, замедляя его или требуя большего расхода энергии. Подойдя к барьеру, мы должны приложить больше усилий (выражаемых количеством бензина, времени, или потерей скорости движения) на преодоление участка пути, принадлежащего барьеру, чтобы попасть за него. Если посмотреть на график затрат, то до барьера (в случае относительного барьера) график затрат выглядел бы как прямая линия, в месте барьера объем затрат увеличивается. В случае абсолютного барьера на этом графике появится вертикальный скачок, указывающий на бесконечно большой объем затрат.

Слайд 17. Карты расстояний: простое расстояние и аллокация.

Составляя карты расстояний, вы можете получить такую информацию, как расстояние от места происшествия до ближайшей больницы для выбора пути вертолета

Соседние файлы в папке ГИТ лекционный курс

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Добавить комментарий