Как найти центроид сложной фигуры - Сайт, где вы сможете решить свои вопросы

Что такое центроид?

Центроид – это центральная точка фигуры, также называемая геометрическим центром. Это точка, которая соответствует центру тяжести определенной формы. Это точка, которая соответствует среднему положению всех точек на рисунке. Центроид – это термин для двумерных форм. Центр масс – это термин для трехмерных фигур. Например, центр тяжести круга и прямоугольника находится посередине. Центроид прямоугольного треугольника находится на 1/3 снизу и от прямого угла. Но как насчет центроида сложных форм?

Что такое геометрическая декомпозиция?

Геометрическая декомпозиция – один из методов, используемых для получения центроида сложной формы. Это широко используемый метод, потому что вычисления просты и требуют только основных математических принципов. Это называется геометрической декомпозицией, потому что расчет состоит из разложения фигуры на простые геометрические фигуры. В геометрической декомпозиции деление комплексной фигуры Z является основным шагом в вычислении центроида. Учитывая фигуру Z, получите центр тяжести C _i и площадь A _i каждой части Z _{n, в} которой все отверстия, выходящие за пределы составной формы, должны рассматриваться как отрицательные значения. Наконец, вычислите центроид по формуле:

С _x = ∑C _ix A _ix / ∑A _ix

C _y = ∑C _iy A _iy / ∑A _iy

Пошаговая процедура решения центроида составных форм

Вот серия шагов в поиске центроида любой составной формы.

1. Разделите данную составную фигуру на различные первичные фигуры. Эти основные фигуры включают прямоугольники, круги, полукруги, треугольники и многое другое. При разделении составной фигуры включите детали с отверстиями. Эти отверстия следует рассматривать как твердые компоненты, но с отрицательными значениями. Прежде чем переходить к следующему шагу, убедитесь, что вы разбили каждую часть составной формы.

2. Найдите площадь каждой разделенной фигуры. В таблице 1-2 ниже показаны формулы для различных основных геометрических фигур. После определения области дайте название каждой области (первая, вторая, третья и т. Д.). Сделайте отрицательную область для обозначенных областей, которые действуют как отверстия.

3. На данном рисунке должны быть оси абсцисс и ось у. Если оси x и y отсутствуют, нарисуйте оси наиболее удобным способом. Помните, что ось X – это горизонтальная ось, а ось Y – это вертикальная ось. Вы можете расположить оси посередине, слева или справа.

4. Получите расстояние центроида каждой разделенной основной фигуры от оси x и оси y. В таблице 1-2 ниже показаны центроиды для различных основных форм.

Центроид для общих форм

Таблица 1-2: Центроид для общих форм. X-bar – это расстояние от центроида до оси y. Полоса Y – это расстояние от центроида до оси x.


Форма	Площадь	X-бар	Y-образный стержень
Прямоугольник	бх	Би 2	d / 2
Треугольник	(bh) / 2	–	ч / 3
Прямоугольный треугольник	(bh) / 2	ч / 3	ч / 3
Полукруг	(пи (г ^ 2)) / 2	0	(4r) / (3 (пи))
Четверть круга	(пи (г ^ 2)) / 4	(4r) / (3 (пи))	(4r) / (3 (пи))
Круговой сектор	(г ^ 2) (альфа)	(2рсин (альфа)) / 3 (альфа)	0
Сегмент дуги	2r (альфа)	(rsin (альфа)) / альфа	0
Полукруглая дуга	(пи) (г)	(2r) / пи	0
Площадь под навесом	(bh) / (n + 1)	б / (п + 2)	(hn + h) / (4n + 2)

Центроиды простых геометрических форм

Джон Рэй Куэвас

5. Создание таблицы всегда упрощает вычисления. Постройте таблицу, подобную приведенной ниже.

Таблица 1-1: Формат таблицы. X – расстояние центроида от оси y. Y – это расстояние центроида от оси x.


Название области	Площадь (А)	Икс	y	Топор	Ау
Площадь 1	–	–	–	Ax1	Ay1
Площадь 2	–	–	–	Ax2	Ay2
Площадь n	–	–	–	Axn	Айн
Всего	(Общая площадь)	–	–	(Суммирование топора)	(Суммирование Ay)

6. Умножьте площадь «A» каждой базовой формы на расстояние между центроидами «x» и осью y. Тогда получим суммирование ΣAx. См. Формат таблицы выше.

7. Умножьте площадь «A» каждой базовой формы на расстояние между центроидами «y» и осью x. Тогда получим суммирование ΣAy. См. Формат таблицы выше.

8. Найдите общую площадь ΣA всей фигуры.

9. Найдите центроид C _x всей фигуры, разделив сумму ΣAx на общую площадь фигуры ΣA. Результирующий ответ – это расстояние от центра тяжести всей фигуры до оси y.

10. Найдите центроид C _y всей фигуры, разделив сумму ΣAy на общую площадь фигуры ΣA. В результате получается расстояние от центра тяжести всей фигуры до оси абсцисс.

Вот несколько примеров получения центроида.

Проблема 1: Центроид С-образных форм

Центроид для сложных фигур: C-образные формы

Джон Рэй Куэвас

Решение 1

а. Разделите сложную фигуру на основные фигуры. В этом случае C-образная форма состоит из трех прямоугольников. Назовите три подразделения как Зона 1, Зона 2 и Зона 3.

б. Решите для площади каждого подразделения. Прямоугольники имеют размеры 120 x 40, 40 x 50, 120 x 40 для области 1, области 2 и области 3 соответственно.

Area 1 = b x h Area 1 = 120.00 mm x 40.00 mm Area 1 = 4800.00 square millimeters Area 2 = b x h Area 2 = 40.00 mm x 50.00 mm Area 2 = 2000 square millimeters Area 3 = b x h Area 3 = 120.00 mm x 40.00 mm Area 3 = 4800.00 square millimeters ∑A = 4800 + 2000 + 4800 ∑A = 11600.00 square millimeters

c. Расстояния X и Y каждой области. Расстояния по X – это расстояния от центроида каждой области до оси y, а расстояния по Y – это расстояния от центроида каждой области от оси x.

Центроид для C-образных форм

Джон Рэй Куэвас

Area 1: x = 60.00 millimeters y = 20.00 millimeters Area 2: x = 100.00 millimeters y = 65.00 millimeters Area 3: x = 60 millimeters y = 110 millimeters

d. Найдите значения Ax. Умножьте площадь каждой области на расстояния от оси Y.

Ax1 = 4800.00 square mm x 60.00 mm Ax1 = 288000 cubic millimeters Ax2 = 2000.00 square mm x 100.00 mm Ax2 = 200000 cubic millimeters Ax3 = 4800.00 square mm x 60.00 mm Ax3 = 288000 cubic millimeters ∑Ax = 776000 cubic millimeters

е. Найдите значения Ay. Умножьте площадь каждой области на расстояния от оси абсцисс.

Ay1 = 4800.00 square mm x 20.00 mm Ay1 = 96000 cubic millimeters Ay2 = 2000.00 square mm x 65.00 mm Ay2 = 130000 cubic millimeters Ay3 = 4800.00 square mm x 110.00 mm Ay3 = 528000 cubic millimeters ∑Ay = 754000 cubic millimeters

Все единицы указаны в миллиметрах.


Название области	Площадь (А)	Икс	y	Топор	Ау
Площадь 1	4800	60	20	288000	96000
Площадь 2	2000 г.	100	65	200000	130000
Зона 3	4800	60	110	288000	528000
Всего	11600			776000	754000

f. Наконец, найдите центроид (C _x, C _y), разделив ∑Ax на ∑A и ∑Ay на ∑A.

Cx = ΣAx / ΣA Cx = 776000 / 11600 Cx = 66.90 millimeters Cy = ΣAy / ΣA Cy = 754000 / 11600 Cy = 65.00 millimeters

Центроид сложной фигуры находится на расстоянии 66,90 миллиметра от оси y и 65,00 миллиметра от оси x.

Центроид для C-образной формы

Джон Рэй Куэвас

Проблема 2: Центроид неправильных фигур

Центроид для сложных фигур: неправильные фигуры

Джон Рэй Куэвас

Решение 2

а. Разделите сложную фигуру на основные фигуры. В этом случае неправильная форма состоит из полукруга, прямоугольника и прямоугольного треугольника. Назовите три подразделения как Зона 1, Зона 2 и Зона 3.

б. Решите для площади каждого подразделения. Размеры прямоугольника 250 x 300, прямоугольного треугольника 120 x 120, полукруга – 100. Обязательно инвертируйте значения для прямоугольного треугольника и полукруга, потому что это отверстия.

Area 1 = b x h Area 1 = 250.00 mm x 300.00 mm Area 1 = 75000.00 square millimeters Area 2 = 1/2 (bh) Area 2 = 1/2 (120 mm) (120 mm) Area 2 = - 7200 square millimeters Area 3 = ((pi) r^2) / 2 Area 3 = ((pi) (100)^2) / 2 Area 3 = - 5000pi square millimeters ∑A = 75000.00 - 7200 - 5000pi ∑A = 52092.04 square millimeters

c. Расстояния X и Y каждой области. Расстояния по X – это расстояния от центроида каждой области от оси y, а расстояния по y – это расстояния от центроида каждой области от оси x. Учтите ориентацию осей x и y. Для квадранта I значения x и y положительны. Для квадранта II x отрицателен, а y положителен.

Решение для неправильной формы

Джон Рэй Куэвас

Area 1: x = 0 y = 125.00 millimeters Area 2: x = 110.00 millimeters y = 210.00 millimeters Area 3: x = - 107.56 millimeters y = 135 millimeters

d. Найдите значения Ax. Умножьте площадь каждой области на расстояния от оси Y.

Ax1 = 75000.00 square mm x 0.00 mm Ax1 = 0 Ax2 = - 7200.00 square mm x 110.00 mm Ax2 = - 792000 cubic millimeters Ax3 = - 5000pi square mm x - 107.56 mm Ax3 = 1689548.529 cubic millimeters ∑Ax = 897548.529 cubic millimeters

е. Найдите значения Ay. Умножьте площадь каждой области на расстояния от оси абсцисс.

Ay1 = 75000.00 square mm x 125.00 mm Ay1 = 9375000 cubic millimeters Ay2 = - 7200.00 square mm x 210.00 mm Ay2 = - 1512000 cubic millimeters Ay3 = - 5000pi square mm x 135.00 mm Ay3 = - 2120575.041 cubic millimeters ∑Ay = 5742424.959 cubic millimeters

Все единицы указаны в миллиметрах.


Название области	Площадь (А)	Икс	y	Топор	Ау
Площадь 1	75000	0	125	0	9375000
Площадь 2	– 7200	110	210	-792000	-1512000
Зона 3	– 5000 пикселей	– 107,56	135	1689548,529	-2120575.041
Всего	52092,04			897548,529	5742424,959

f. Наконец, найдите центроид (C _x, C _y), разделив ∑Ax на ∑A и ∑Ay на ∑A.

Cx = ΣAx / ΣA Cx = 897548.529 / 52092.04 Cx = 17.23 millimeters Cy = ΣAy / ΣA Cy = 5742424.959 / 52092.04 Cy = 110.24 millimeters

Центроид сложной фигуры находится на расстоянии 17,23 миллиметра от оси y и 110,24 миллиметра от оси x.

Окончательный ответ на неправильную форму

Джон Рэй Куэвас

Момент инерции неправильной или сложной формы

Как вычислить
момент инерции сложных или сложных форм Это полное руководство по вычислению момента инерции сложных или неправильных форм. Знать основные необходимые шаги и формулы и владеть решающим моментом инерции.

Вопросы и Ответы

Вопрос: Есть ли какой-либо альтернативный метод решения для центроида, кроме этого геометрического разложения?

Ответ: Да, существует методика, использующая ваш научный калькулятор для определения центроида.

Вопрос: в области два треугольника в задаче 2… как получилось 210 мм y стержня?

Ответ: Это расстояние y центра тяжести прямоугольного треугольника от оси x.

y = 130 мм + (2/3) (120) мм

y = 210 мм

Вопрос: Как Y-образная штанга для области 3 стала 135 миллиметров?

Ответ: Прошу прощения за путаницу с вычислением Y-бара. На рисунке должно быть не хватает каких-то размеров. Но если вы понимаете процесс решения проблем с центроидом, то вам не о чем беспокоиться.

Вопрос: Как рассчитать центроид w-луча?

Ответ: W-балки – это двутавровые балки. Вы можете начать решение центра тяжести W-образной балки, разделив всю площадь поперечного сечения балки на три прямоугольные области – верхнюю, среднюю и нижнюю. Затем вы можете приступить к выполнению описанных выше шагов.

Вопрос: Почему в задаче 2 квадрант расположен посередине, а в задаче 1 – нет?

Ответ: Чаще всего положение квадрантов показано на данном рисунке. Но в случае, если вас просят сделать это самостоятельно, вы должны поместить ось в положение, в котором вы сможете решить проблему наиболее простым способом. В случае проблемы номер два размещение оси Y посередине даст более простое и быстрое решение.

Вопрос: Что касается Q1, то есть графические методы, которые можно использовать во многих простых случаях. Вы видели игровое приложение Pythagorean?

Ответ: Выглядит интересно. В нем говорится, что Pythagorea – это набор геометрических головоломок разного типа, которые можно решить без сложных построений или вычислений. Все объекты нарисованы на сетке, ячейки которой – квадраты. Многие уровни можно решить, используя только вашу геометрическую интуицию или найдя законы природы, регулярность и симметрию. Это действительно может быть полезно.

Источник

Расчет центроида сложных форм методом геометрической декомпозиции – Образование

Содержание

Что такое центроид?
Что такое геометрическая декомпозиция?
Пошаговая процедура решения центроида составных форм
Центроид для общих форм
Проблема 1: Центроид C-образных форм
Проблема 2: Центроид неправильных фигур
Момент инерции неправильной или сложной формы
Вопросы и Ответы

Что такое центроид?

Что такое геометрическая декомпозиция?

Геометрическая декомпозиция

C_Икс = C_ix А_ix / А_ix

C_у = C_iy А_iy / А_iy

Пошаговая процедура решения центроида составных форм

Вот серия шагов в поиске центроида любой составной формы.

1. Разделите данную составную фигуру на различные первичные фигуры. Эти основные фигуры включают прямоугольники, круги, полукруги, треугольники и многое другое. При разделении составной фигуры включайте детали с отверстиями. Эти отверстия следует рассматривать как твердые компоненты, но с отрицательными значениями. Убедитесь, что вы разбили каждую часть составной формы, прежде чем переходить к следующему шагу.

2. Найдите площадь каждой разделенной фигуры. Таблица 1-2 ниже показывает формулы для различных основных геометрических фигур. После определения области дайте название каждой области (область один, область два, область три и т. Д.). Сделайте отрицательную область для обозначенных областей, которые действуют как отверстия.

3. На данной фигуре должны быть оси абсцисс и оси ординат. Если оси x и y отсутствуют, нарисуйте оси наиболее удобным способом. Помните, что ось X – это горизонтальная ось, а ось Y – это вертикальная ось. Вы можете расположить оси посередине, слева или справа.

Центроид для общих форм

Форма	Площадь	X-бар	Y-образная штанга
Прямоугольник	бх	Би 2	d / 2
Треугольник	(bh) / 2	–	ч / 3
Прямоугольный треугольник	(bh) / 2	ч / 3	ч / 3
Полукруг	(пи (г ^ 2)) / 2	0	(4r) / (3 (пи))
Четверть круга	(пи (г ^ 2)) / 4	(4r) / (3 (пи))	(4r) / (3 (пи))
Круговой сектор	(г ^ 2) (альфа)	(2рсин (альфа)) / 3 (альфа)	0
Сегмент дуги	2r (альфа)	(rsin (альфа)) / альфа	0
Полукруглая дуга	(пи) (г)	(2r) / пи	0
Площадь под навесом	(bh) / (n + 1)	б / (п + 2)	(hn + h) / (4n + 2)

5. Создание таблицы всегда упрощает вычисления. Постройте таблицу, подобную приведенной ниже.

Таблица 1-1: Формат таблицы. X – расстояние центроида от оси y. Y – расстояние центроида от оси x.

Название области	Площадь (А)	Икс	у	Топор	Ау
Площадь 1	–	–	–	Ax1	Ay1
Площадь 2	–	–	–	Ax2	Ay2
Площадь n	–	–	–	Axn	Айн
Всего	(Общая площадь)	–	–	(Суммирование топора)	(Суммирование Ay)

7. Умножьте площадь «A» каждой основной формы на расстояние между центроидами «y» и осью x. Тогда получим суммирование ΣAy. См. Формат таблицы выше.

8. Найдите общую площадь ΣA всей фигуры.

9. Найдите центроид C_Иксвсей фигуры путем деления суммы ΣAx на общую площадь фигуры ΣA. Результирующий ответ – это расстояние от центра тяжести всей фигуры до оси ординат.

10. Найдите центроид C_у всей фигуры путем деления суммы ΣAy на общую площадь фигуры ΣA. В результате получается расстояние от центра тяжести всей фигуры до оси абсцисс.

Вот несколько примеров получения центроида.

Проблема 1: Центроид C-образных форм

Решение 1

Площадь 1 = bxh Площадь 1 = 120,00 мм x 40,00 мм Площадь 1 = 4800,00 квадратных миллиметров Площадь 2 = bxh Площадь 2 = 40,00 мм x 50,00 мм Площадь 2 = 2000 квадратных миллиметров Площадь 3 = bxh Площадь 3 = 120,00 мм x 40,00 мм Площадь 3 = 4800,00 квадратных миллиметров A = 4800 + 2000 + 4800 A = 11600,00 квадратных миллиметров

Площадь 1: x = 60,00 миллиметров y = 20,00 миллиметров Площадь 2: x = 100,00 миллиметров y = 65,00 миллиметров Область 3: x = 60 миллиметров y = 110 миллиметров

d. Найдите значения Ax. Умножьте площадь каждой области на расстояния от оси Y.

Ax1 = 4800,00 квадратных мм x 60,00 мм Ax1 = 288000 кубических миллиметров Ax2 = 2000,00 квадратных мм x 100,00 мм Ax2 = 200000 кубических миллиметров Ax3 = 4800,00 квадратных мм x 60,00 мм Ax3 = 288000 кубических миллиметров Ax = 776000 кубических миллиметров

е. Найдите значения Ay. Умножьте площадь каждой области на расстояния от оси абсцисс.

Ay1 = 4800,00 квадратных мм x 20,00 мм Ay1 = 96000 кубических миллиметров Ay2 = 2000,00 квадратных мм x 65,00 мм Ay2 = 130000 кубических миллиметров Ay3 = 4800,00 квадратных мм x 110,00 мм Ay3 = 528000 кубических миллиметров Ay = 754000 кубических миллиметров

Все единицы указаны в миллиметрах.

Название области	Площадь (А)	Икс	у	Топор	Ау
Площадь 1	4800	60	20	288000	96000
Площадь 2	2000	100	65	200000	130000
Зона 3	4800	60	110	288000	528000
Всего	11600			776000	754000

f. Наконец, найдите центроид (C_Икс, С_у) разделив Ax на A и Ay на A.

Cx = ΣAx / ΣA Cx = 776000/11600 Cx = 66,90 миллиметров Cy = ΣAy / ΣA Cy = 754000/11600 Cy = 65,00 миллиметров

Центроид сложной фигуры находится на расстоянии 66,90 миллиметра от оси y и 65,00 миллиметра от оси x.

Проблема 2: Центроид неправильных фигур

Решение 2

а. Разделите сложную фигуру на основные фигуры. В этом случае неправильная форма имеет полукруг, прямоугольник и прямоугольный треугольник. Назовите три подразделения как Зона 1, Зона 2 и Зона 3.

б. Решите для площади каждого подразделения. Размеры прямоугольника 250 x 300, прямоугольного треугольника 120 x 120, а полукруга – 100. Обязательно инвертируйте значения для прямоугольного треугольника и полукруга, потому что это отверстия.

Площадь 1 = bxh Площадь 1 = 250,00 мм x 300,00 мм Площадь 1 = 75000,00 квадратных миллиметров Площадь 2 = 1/2 (bh) Площадь 2 = 1/2 (120 мм) (120 мм) Площадь 2 = – 7200 квадратных миллиметров Площадь 3 = ((pi) r ^ 2) / 2 Площадь 3 = ((pi) (100) ^ 2) / 2 Площадь 3 = – 5000pi квадратных миллиметров A = 75000.00 – 7200 – 5000pi A = 52092,04 квадратных миллиметра

c. Расстояния X и Y каждой области. Расстояния по X – это расстояния от центроида каждой области до оси y, а расстояния по y – это расстояния от центроида каждой области от оси x. Учтите ориентацию осей x и y. Для квадранта I значения x и y положительны. Для квадранта II x отрицателен, а y положителен.

Площадь 1: x = 0 y = 125,00 миллиметров Площадь 2: x = 110,00 миллиметров y = 210,00 миллиметров Область 3: x = – 107,56 миллиметров y = 135 миллиметров

d. Найдите значения Ax. Умножьте площадь каждой области на расстояния от оси Y.

Ax1 = 75000,00 квадратный мм x 0,00 мм Ax1 = 0 Ax2 = – 7200,00 квадратный мм x 110,00 мм Ax2 = – 792000 кубических миллиметров Ax3 = – 5000pi квадратный мм x – 107,56 мм Ax3 = 1689548,529 кубических миллиметров Ax = 897548,529 кубических миллиметров

е. Найдите значения Ay. Умножьте площадь каждой области на расстояния от оси абсцисс.

Ay1 = 75000,00 квадратный мм x 125,00 мм Ay1 = 9375000 кубических миллиметров Ay2 = – 7200,00 квадратных мм x 210,00 мм Ay2 = – 1512000 кубических миллиметров Ay3 = – 5000pi квадратный мм x 135,00 мм Ay3 = – 2120575,041 кубических миллиметров Ay = 5742424,959 кубических миллиметров

Все единицы указаны в миллиметрах.

Название области	Площадь (А)	Икс	у	Топор	Ау
Площадь 1	75000	0	125	0	9375000
Площадь 2	– 7200	110	210	-792000	-1512000
Зона 3	– 5000 пикселей	– 107.56	135	1689548.529	-2120575.041
Всего	52092.04			897548.529	5742424.959

f. Наконец, найдите центроид (C_Икс, С_у) разделив Ax на A и Ay на A.

Cx = ΣAx / ΣA Cx = 897548,529 / 52092,04 Cx = 17,23 миллиметра Cy = ΣAy / ΣA Cy = 5742424,959 / 52092,04 Cy = 110,24 миллиметра

Центроид сложной фигуры находится на расстоянии 17,23 миллиметра от оси y и 110,24 миллиметра от оси x.

Момент инерции неправильной или сложной формы

Как найти момент инерции неправильных или сложных форм
Это полное руководство по решению момента инерции сложных или неправильных форм. Знать основные необходимые шаги и формулы и владеть решающим моментом инерции.

Вопросы и Ответы

Отвечать: Да, есть метод, использующий ваш научный калькулятор для определения центроида.

Вопрос: в области два треугольника в задаче 2 … как получилось 210 мм стержня y?

Отвечать: Это расстояние y центра тяжести прямоугольного треугольника от оси x.

y = 130 мм + (2/3) (120) мм

y = 210 мм

Вопрос: Как Y-образная штанга для области 3 стала 135 миллиметров?

Отвечать: Я очень сожалею о путанице с вычислением Y-бара. На рисунке должно быть не хватает каких-то размеров. Но если вы понимаете процесс решения проблем с центроидом, то вам не о чем беспокоиться.

Вопрос: Как вы рассчитываете центр тяжести w-луча?

Отвечать: W-образные балки – это двутавровые балки. Вы можете начать решение центра тяжести W-образной балки, разделив всю площадь поперечного сечения балки на три прямоугольные области – верхнюю, среднюю и нижнюю. Затем вы можете приступить к выполнению описанных выше шагов.

Вопрос: Почему в задаче 2 квадрант расположен посередине, а в задаче 1 – нет?

Отвечать: В большинстве случаев положение квадрантов показано на данном рисунке. Но в случае, если вас просят сделать это самостоятельно, вы должны поместить ось в положение, в котором вы можете решить проблему наиболее простым способом. В случае проблемы номер два размещение оси Y посередине даст более простое и короткое решение.

Вопрос: Что касается Q1, есть графические методы, которые можно использовать во многих простых случаях. Вы видели игровое приложение, Pythagorean?

Отвечать: Смотрится интересно. В нем говорится, что Pythagorea – это набор геометрических головоломок разного типа, которые можно решить без сложных построений или вычислений. Все объекты нарисованы на сетке, ячейки которой – квадраты. Многие уровни можно решить, используя только вашу геометрическую интуицию или найдя законы природы, регулярность и симметрию. Это действительно может быть полезно.

Источник

Центроид треугольника — точка пересечения его медиан

В математике барице́нтр, или геометри́ческий центр, двумерной фигуры — это среднее арифметическое положений всех точек данной фигуры. Определение распространяется на любой объект в n-мерном пространстве. Радиус-вектор барицентра в трёхмерном случае вычисляется как

${displaystyle {vec {r}}_{b}=V^{-1}int _{V}{vec {r}}dV}$

где интегрирование выполняется по объёму тела. Другое название барицентра в этом значении — центроид.

Неформально, геометрический барицентр есть точка равновесия фигуры, вырезанной из картона, в предположении, что картон имеет постоянную плотность, а внешнее гравитационное поле однородно.

В физике термин «барицентр» — синоним понятия «центр масс», используемый, в основном, в задачах космической механики. Центр масс объекта является средним арифметическим всех его точек с учётом локальной плотности массы. Для физических объектов с постоянной плотностью центр масс совпадает с барицентром фигуры той же формы.

Ниже барицентр рассматривается в математическом (геометрическом) смысле, о барицентре в физике см. статью Центр масс.

Свойства[править | править код]

Геометрический барицентр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь барицентр, лежащий вне фигуры. Барицентр кольца или миски, например, лежат вне фигуры.

Если барицентр известен, он является фиксированной точкой группы изометрии симметрий фигуры. Барицентр объекта лежит на пересечении всех его гиперплоскостей симметрии. Барицентры многих фигур (правильного многоугольника, правильного многогранника, цилиндра, прямоугольника, ромба, окружности, сферы, эллипса, эллипсоида, суперэллипса, суперэллипсоида и т. д.) можно найти исходя исключительно из этого принципа.

В частности, барицентром треугольника является точка пересечения его медиан (см. рисунок). Барицентром параллелограмма является точка пересечения его диагоналей, но это неверно для других четырёхугольников.

Барицентр объекта с трансляционной симметрией не определён (или лежит вне пространства фигуры), поскольку сдвиг не имеет фиксированной точки.

Центроид треугольника[править | править код]

Барицентр треугольника называется центроидом и лежит на пересечении трёх медиан, также лежит на прямой Эйлера (проходящей и через другие ключевые точки, включая ортоцентр и центр описанной окружности)^[1]^[2].

Если в вершины треугольника поместить равные массы, то центр масс (барицентр) полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой массой также находится в центроиде.

$MA^{2}+MB^{2}+MC^{2}=GA^{2}+GB^{2}+GC^{2}+3MG^{2}$

^[3].

Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин треугольника:

$AB^{2}+BC^{2}+CA^{2}=3(GA^{2}+GB^{2}+GC^{2})$

^[3].

Центр масс сторон треугольника совпадает с центром вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера. Если стороны треугольника сделать из тонкой проволоки одинакового сечения, то центр масс (барицентр) полученной системы будет совпадать с инцентром дополнительного треугольника, или с центром Шпикера.
О других свойствах центроида треугольника смотрите ниже.

Минимаксные свойства центроида треугольника[править | править код]

Центроид или точка пресечения медиан треугольника является единственной точкой треугольника такой, что проведенные через неё три чевианы разделяют своими концами стороны треугольника на шесть отрезков. При этом произведение длин трёх из этих шести отрезков, не имеющих общих концов, максимально^[4].
Центроид или точка пересечения трёх медиан является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).

Центроид четырёх точек (вершин четырёхугольника)[править | править код]

Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие — середины противолежащих сторон. Точка пересечения делит все три отрезка пополам.

Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в одной точке (центроиде вершин четырёхугольника) и делятся ею в отношении 3:1, считая от вершины.

Центр масс вершин четырёхугольника не обязан совпадать с центром масс самого четырёхугольника как плоской фигуры.

Определение местоположения барицентра[править | править код]

Определение местоположения барицентра однородной плоской фигуры методом отвеса[править | править код]

Барицентр однородной плоской фигуры, такой как фигура (a) на рисунке, можно найти экспериментально с использованием отвеса и булавки путём нахождения центра масс тонкой пластины однородной плотности, имеющей ту же форму. Пластина удерживается булавкой, вставленной ближе к периметру так, чтобы пластина могла свободно вращаться. Отмечаем на пластине прямую, которую образует отвес, прикреплённый к булавке (b). Проделываем то же самое с другим положением булавки. Пересечение двух прямых даст барицентр (c).

Этот метод можно распространить (в теории) на вогнутые фигуры, когда барицентр лежит вне их, а также тела (постоянной плотности), но положение линии отвеса придётся отмечать каким-то иным способом.

Определение местоположения барицентра выпуклой двумерной фигуры методом балансировки[править | править код]

Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например, на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.

Определение местоположения барицентра для конечного множества точек[править | править код]

Барицентр конечного множества из {k} точек ${displaystyle mathbf {x} _{1},mathbf {x} _{2},ldots ,mathbf {x} _{k}}$ в $mathbb {R} ^{n}$ находится по формуле

${displaystyle mathbf {G} ={frac {mathbf {x} _{1}+mathbf {x} _{2}+cdots +mathbf {x} _{k}}{k}}}$

^[5].

Полученная точка такая, что сумма квадратов расстояний между ней и точками множества является минимальной.

Определение местоположения барицентра с помощью геометрического разложения[править | править код]

(b) Разложение фигуры на простые элементы

Барицентр плоской фигуры можно вычислить, разделив её на конечное число более простых фигур ${displaystyle X_{1},X_{2},dots ,X_{n}}$ , найдя положение барицентров $G_{i}$ и площадей $A_{i}$ каждой части, а затем вычислив

${displaystyle G_{x}={frac {sum G_{i_{x}}A_{i}}{sum A_{i}}},G_{y}={frac {sum G_{i_{y}}A_{i}}{sum A_{i}}}.}$

Дыры в фигуре , наложения частей, или части, выступающие за фигуру, можно рассматривать как фигуры с отрицательной площадью $A_{i}$ . А именно, знак площади $A_{i}$ нужно выбирать так, чтобы сумма знаков $A_{i}$ для всех частей, включающих точку , была равна 1, если принадлежит , и 0 в противном случае.

Например, фигуру (a) на рисунке легко разделить на квадрат и треугольник с положительным знаком, круглое отверстие с отрицательным (b).

Барицентр каждой части легко найти в любом списке барицентров простых фигур (c). Затем вычисляется барицентр фигуры, как средневзвешенное трёх точек. Горизонтальное положение барицентра, считая от левого края фигуры, равно

${displaystyle x={frac {5times 10^{2}+13.33times {frac {1}{2}}10^{2}-3times pi 2.5^{2}}{10^{2}+{frac {1}{2}}10^{2}-pi 2.5^{2}}}approx 8.5.}$

Вертикальное положение вычисляется аналогично.

Та же формула применима для любого трёхмерного объекта, только $A_{i}$ обозначают уже объёмы частей тела $X_{i}$ , а не площади. Формула верна также для пространства $mathbb {R} ^{d}$ любой размерности при замене площади -мерными мерами частей.

Определение местоположения барицентра интегрированием[править | править код]

Барицентр подмножества X пространства $mathbb {R} ^{n}$ можно вычислить с помощью интеграла

${displaystyle G={frac {int xg(x);dx}{int g(x);dx}},}$

где интегрирование ведётся по всему пространству $mathbb {R} ^{n}$ , а g является характеристической функцией подмножества, принимающей 1 внутри X и 0 вне его^[6]. Заметим, что знаменатель равен мере множества X. Формула неприменима к множеству нулевой меры, а также к множествам, для которых интеграл расходится.

Другая формула для вычисления координат барицентра:

${displaystyle G_{k}={frac {int zS_{k}(z);dz}{int S_{k}(z);dz}},}$

где G_k является k-й координатой G, а S_k(z) — мера пересечения X с гиперплоскостью, определяемой уравнением x_k = z. Снова знаменатель — это мера множества X.

Для плоской фигуры координатами барицентра будут

${displaystyle G_{mathrm {x} }={frac {int xS_{mathrm {y} }(x);dx}{A}};}$

${displaystyle G_{mathrm {y} }={frac {int yS_{mathrm {x} }(y);dy}{A}},}$

где A — площадь фигуры X, S_y(x) — длина пересечения^{[неизвестный термин]} X с вертикальной прямой с абциссой x, S_x(y) — аналогичная величина при обмене осей.

Определение местоположения барицентра для области, ограниченной графиками непрерывных функций[править | править код]

Координаты барицентра области, ограниченной графиками непрерывных функций и , таких что на интервале [a,b] , , задаются выражениями

${displaystyle {bar {x}}={frac {1}{A}}int _{a}^{b}xleft[f(x)-g(x)right];dx}$

^[6].

${displaystyle {bar {y}}={frac {1}{A}}int _{a}^{b}left[{frac {f(x)+g(x)}{2}}right]left[f(x)-g(x)right];dx,}$

^[7]

где — площадь области (вычисляемая по формуле ${displaystyle int _{a}^{b}left[f(x)-g(x)right];dx}$ )^[8]^[9].

Определение местоположения барицентра объекта, имеющего форму буквы L[править | править код]

Метод нахождения барицентра фигуры, имеющей форму буквы L.

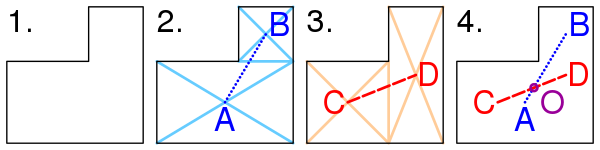
Фигуру делят на два прямоугольника (см. фигуру (2) на рисунке). Находят барицентры A и B этих двух прямоугольников как пересечение диагоналей. Рисуют отрезок AB, соединяющий барицентры. Барицентр фигуры должен лежать на этом отрезке AB.
Делят фигуру на два прямоугольника другим способом (см. фигуру (3) на рисунке). Находят барицентры C и D этих двух прямоугольников. Проводят отрезок CD, соединяющий барицентры. Барицентр фигуры должен лежать на отрезке CD.
Поскольку барицентр должен лежать как на отрезке AB, так и на отрезке CD, очевидно, что он является точкой пересечения этих двух отрезков — точкой O. Точка O не обязана лежать внутри фигуры.

Барицентры треугольника и тетраэдра[править | править код]

Точка пересечения медиан (барицентр) делит каждую медиану в отношении 2:1. То есть, расстояние от стороны до барицентра равно 1/3 длины проведённой к стороне высоты

В прямоугольном треугольнике расстояние от одного катета до барицентра равно 1/3 длины другого катета

Барицентр треугольника совпадает с пересечением медиан. Барицентр разбивает каждую медиану в отношении 2:1, то есть барицентр находится на расстоянии ⅓ от стороны до противоположной вершины (см. рисунок). Его декартовыми координатами является среднее координат трёх вершин. То есть, если вершинами треугольника являются ${displaystyle a=(x_{a},y_{a})}$ , ${displaystyle b=(x_{b},y_{b})}$ и ${displaystyle c=(x_{c},y_{c})}$ , то координаты барицентра вычисляются по формуле

${displaystyle G={frac {1}{3}}(a+b+c)=left({frac {1}{3}}(x_{a}+x_{b}+x_{c}),{frac {1}{3}}(y_{a}+y_{b}+y_{c})right)}$

Таким образом, барицентр имеет барицентрические координаты ${tfrac {1}{3}}:{tfrac {1}{3}}:{tfrac {1}{3}}$ .

В трилинейных координатах барицентр можно получить одним из эквивалентных способов^[10]:

${displaystyle G={frac {1}{a}}:{frac {1}{b}}:{frac {1}{c}}=bc:ca:ab=csc A:csc B:csc C}$

{displaystyle =cos A+cos Bcdot cos C:cos B+cos Ccdot cos A:cos C+cos Acdot cos B}

{displaystyle =sec A+sec Bcdot sec C:sec B+sec Ccdot sec A:sec C+sec Acdot sec B.}

Барицентр является также физически центром масс треугольника, сделанного из однородного листового материала, а также, если вся масса сконцентрирована в вершинах и одинаково разделена между ними. Если же масса распределена равномерно вдоль периметра, то центр масс лежит в точке Шпикера (инцентре серединного треугольника), который (в общем случае) не совпадает с центроидом всего треугольника.

Площадь треугольника равна 3/2 длины любой стороны, умноженной на расстояние от центроида до стороны^[11].

Центроид треугольника лежит на прямой Эйлера между его ортоцентром и центром его описанной окружности , ровно вдвое ближе ко второму, чем к первому:

Кроме того, для инцентра и центра девяти точек , мы имеем

Аналогичными свойствами обладает тетраэдр — его барицентр является пересечением отрезков, соединяющих вершины с барицентрами противоположных граней. Эти отрезки делятся барицентром в отношении 3:1. Результат может быть обобщён на любой -мерный симплекс. Если вершины симплекса обозначить ${displaystyle v_{0},ldots ,v_{n}}$ и рассматривать вершины как вектора, центроид равен

${displaystyle G={frac {1}{n+1}}sum _{i=0}^{n}v_{i}}$

Геометрический барицентр совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как равных масс.

Изогональным сопряжением центроида треугольника является точка пересечения его симедиан.

Барицентр тетраэдра[править | править код]

Тетраэдр является телом в трёхмерном пространстве, имеющим четыре треугольника в качестве граней. Отрезок, соединяющий вершину тетраэдра с барицентром противоположной грани, называется медианой, а отрезок, соединяющий середины двух противоположных сторон, называется бимедианой. Таким образом, имеется четыре медианы и две бимедианы. Эти шесть отрезков пересекаются в барицентре тетраэдра^[12]. Барицентр тетраэдра лежит посередине между точкой Монжа и центром описанной сферы. Эти точки задают прямую Эйлера тетраэдра, являющуюся аналогом прямой Эйлера треугольника.

Барицентр многоугольника[править | править код]

Барицентром самонепересекающегося замкнутого многоугольника, заданного вершинами $(x_{0},y_{0})$ , $(x_{1},y_{1})$ , ldots , ${displaystyle (x_{n-1},y_{n-1})}$ , является точка ${displaystyle (G_{x},G_{y})}$ , где

${displaystyle G_{x}={frac {1}{6A}}sum _{i=0}^{n-1}(x_{i}+x_{i+1})(x_{i}y_{i+1}-x_{i+1}y_{i})}$

;

${displaystyle G_{y}={frac {1}{6A}}sum _{i=0}^{n-1}(y_{i}+y_{i+1})(x_{i}y_{i+1}-x_{i+1}y_{i})}$

и где является площадью многоугольника (со знаком):

${displaystyle A={frac {1}{2}}sum _{i=0}^{n-1}(x_{i}y_{i+1}-x_{i+1}y_{i})}$

^[13].

В этой формуле предполагается, что вершины пронумерованы вдоль периметра многоугольника. Кроме того, вершина ${displaystyle (x_{n},y_{n})}$ считается той же самой, что и $(x_{0},y_{0})$ .
Заметим, что если точки пронумерованы по часовой стрелке, площадь , вычисленная выше, будет отрицательной, но координаты барицентра подкорректируют этот случай.

Барицентры конуса и пирамиды[править | править код]

Барицентр конуса или пирамиды расположен на отрезке, соединяющем вершину тела с барицентром основания. Для целого конуса или пирамиды барицентр находится на расстоянии 1/4 от основания к вершине. Для поверхности конуса или пирамиды (боковая поверхность без внутренности и без основания) центроид находится на 1/3 расстояния от основания до вершины.

См. также[править | править код]

Центр масс
Центроид треугольника
Центр тяжести
Центр Чебышева^[en]
Среднее Фреше^[en]
k-means
Список барицентров
Теоремы Паппа — Гульдина
Замечательные точки треугольника

Примечания[править | править код]

↑ Altshiller-Court, 1925, с. 101.
↑ Kay, 1969, с. 18,189,225–226.
↑ ¹ ² Altshiller-Court, 1925, с. 70–71.
↑ Зетель, 1962.
↑ Protter, Morrey, 1970, с. 520.
↑ ¹ ² Protter, Morrey, 1970, с. 526.
↑ Protter, Morrey, 1970, с. 527.
↑ Protter, Morrey, 1970.
↑ Larson, Hostetler, Edwards, 1998, с. 458–460.
↑ Encyclopedia of Triangle Centers Архивная копия от 19 апреля 2012 на Wayback Machine by Clark Kimberling. The centroid is indexed as X(2).
↑ Johnson, 2007, с. 173.
↑ Kam-tim, Suk-nam, 1994, с. 53–54.
↑ Bourke, 1997.

Литература[править | править код]

Зетель, С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е изд/. — М. : Учпедгиз, 1962. — С. 12.
Leung Kam-tim, Suen Suk-nam. Vectors, matrices and geometry. — Hong Kong University Press, 1994.

Nathan Altshiller-Court. College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. — 2nd. — New York: Barnes & Noble, 1925.
Paul Bourke. Calculating the area and centroid of a polygon. — 1997.
Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007.
David C. Kay. College Geometry. — New York: Holt, Rinehart and Winston, 1969.
Roland E. Larson, Robert P. Hostetler, Bruce H. Edwards. Calculus of a Single Variable. — 6th. — Houghton Mifflin Company, 1998.
Murray H. Protter, Charles B. Morrey Jr. College Calculus with Analytic Geometry. — 2nd. — Reading: Addison-Wesley, 1970.

Ссылки[править | править код]

Characteristic Property of Centroid at cut-the-knot
Barycentric Coordinates at cut-the-knot
Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge
Experimentally finding the medians and centroid of a triangle at Dynamic Geometry Sketches, an interactive dynamic geometry sketch using the gravity simulator of Cinderella.

Источник

Главная
Список секций
Математика
ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ЦЕНТРОВ СЛОЖНЫХ ФИГУР

ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ЦЕНТРОВ СЛОЖНЫХ ФИГУР

Авторы
Руководители
Файлы работы
Наградные документы

Сенагатуллина А.К. 1

1МБОУ “Биляр-Озерская СОШ” Нурлатского МР РТ

Токарева Е.Г. 1

1МБОУ “Биляр-Озерская СОШ”

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение.

«Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.» Эти слова принадлежат М.И. Калинину.

И действительно, это так, на сегодняшний день, в век инновационных технологий эта крылатая фраза имеет еще большое значение в современной жизни человека. Лишь математика как самый надежный инструмент может представить истину познания человеку в абсолютно любой области.

Тема определения центров областей, губерний, республик не нова. Многие территориальные образования уже давно обзавелись стелами, памятными камнями, обозначающими географический центр. Над этим работали и студенты, и научные работники и обучающиеся школ. И я тоже задалась проблемой определения центра неправильной фигуры, в первую очередь методов, понятных и доступных для большинства обучающихся, также проверки этого метода всеми возможными способами, ну и конечно, определение самого центра, для исследования которого взяла город Нурлат.

Цель проекта: найти центр г. Нурлат

Задачи проекта:Рассмотреть приемы исследовательской деятельности, методы, формы и способы научного исследования, научного познания.Формировать мотивацию исследовательской деятельности.Формировать творческую активность.Развивать самостоятельность.

Ожидаемые результаты:

Узнать методы и приемы определения центра сложных фигур, в частности географического центра города Нурлат;ощутить себя в роли экспериментатора, провести простые, но поучительные опыты по определению центров различных фигур;

закрепить вычислительные навыки, навыки вычисления площадей геометрических фигур, что позволит успешно сдать экзамены по математике.

План работы:

1. Выбор направления и темы работы2. Постановка цели и задач3. Изучение теории4. Поиск и подготовка материалов5 Проверка точности теоретических вычислений опытным путем.

6. Выводы7. Оформление работы и Презентация.

Историческая справка

Центр тяжести – неизменно связанная с твердым телом точка, через которую проходит равнодействующая сил тяжести, действующих на частицы этого тела при любом положении тела в пространстве. У однородного тела, имеющего центр симметрии (круг, шар, куб и т. д.), центр тяжести находится в центре симметрии тела.

Понятие о центре тяжести было впервые изучено примерно 2200 лет назад греческим геометром Архимедом, величайшим математиком древности. С тех пор это понятие стало одним из важнейших в механике, а также позволило сравнительно просто решать некоторые геометрические задачи.

У каждого предмета есть центр тяжести. Изучение этого свойства тел необходимо для понимания понятия равновесия тел, при решении конструкторских задач, расчете устойчивости сооружений и во многих других случаях.

Теоретическая часть

1. Понятие о центре тяжести

Каждое тело можно представить как систему материальных частиц, взаимодействующих с Землей. Суммарный результат этого взаимодействия — равнодействующая элементарных сил тяжести. Точка приложения этой равнодействующей называется центром тяжести тела. Поскольку элементарные силы тяжести образуют систему параллельных сил, то центр тяжести обладает всеми свойствами центра параллельных сил. Следовательно, при любом положении тела в пространстве положение центра тяжести остается неизменным.

2. Определение центра тяжести плоских фигур

Положение центра тяжести плоских фигур (т. е. весьма тонких тел) можно определить аналитически и экспериментально.

Аналитически центр тяжести находится как центр параллельных сил. При этом возможны три случая:

фигура имеет две оси симметрии — центр тяжести находится на пересечении осей;

фигура имеет одну ось симметрии — центр тяжести лежит на этой оси, необходимо отыскать одну координату;

фигура не имеет осей симметрии — положение центра тяжести заранее неизвестно, надо определить две координаты.

Заданную фигуру разбивают на простейшие, положение центров тяжести которых вполне определенно, и затем подсчитывают искомые координаты по следующим формулам:

х_с= ;

(1)

y_c= ,

где х₁, х₂, …,хn и у_1,,у₂,…, уn – координаты центров тяжести простейших фигур;

S₁, S₂,…, Sn – площади простейших фигур.

3. Центр тяжести простых фигур

Отрезок – его середина;

Параллелограмм – точка пересечения диагоналей;

Треугольник – точка пересечения медиан;

Круг – его центр.

4. Центр тяжести сложной фигуры

Задача 1. Определить координаты центра тяжести однородной пластинки, изображенной на рисунке, зная, чтоАН=2см, HG=1,5см, AB=3см, BK=10см, EF=4см, ED=2см.

Решение. Фигура не имеет осей симметрии, следовательно, для определения центра тяжести надо найти две его координаты. Проводим оси Ох и Оу и разбиваем пластину на три прямоугольника: AHGL, LRKB и EDRF (линии разреза показаны на рисунке). Вычисляем координаты центров тяжести каждого из прямоугольников и их площади:

Для прямоугольника AHGL S₁=AH∙HG; x₁= ; y₁=LB+.

Так как LB=AB-HG=3-1,5=1,5см, то S₁=2∙1,5=3 см²; x₁==1 см; y₁= 1,5+=1,5+0,75=2,25 см .

Для прямоугольника LRKB S₂=BK∙LB; x₂= ; y₂=,

т.е. S₂=10∙1,5=15 см²; x₂==5 см; y₂==0,75 см.

Для прямоугольника EDRF S₃=BD∙EF; x₃=BK-; y₃=LB+,

т.е. S₃=2∙4=8 см²; x₃=10-=9 см; y₃= 1,5+=3,5 см.

По формулам (1) получаем:

X_c==5 см; Y_c==1 см.

5. Координаты центра тяжести площади треугольника.

Разобьем площадь треугольника ABD на бесконечно тонкие элементарные полоски, параллельные основанию AB. Центр тяжести каждой такой полоски расположен в ее середине. Геометрическое место центров тяжести всех полосок есть медиана OE. На ней поэтому и должен лежать центр тяжести всего треугольника. Так как такое же рассуждение справедливо и для двух других медиан, то центр тяжести треугольника лежит в точке пересечения его медиан. При задании вершин треугольника их координатами получим

X_C=(x_A+xB+x_D); (2)

Y_C=(y_A+yB+y_D)

Экспериментальный способ основан на том, что при любом положении тела линия действия силы тяжести проходит через центр тяжести и заключается в последовательном подвешивании тела (плоской фигуры) за любые две точки. На пересечении отвесов, проходящих через эти точки, и будет находиться центр тяжести. Проверить это можно, если на остриё карандаша поместить фигуру в найденном центре тяжести. Она окажется в равновесии.

Практическая часть.

Изначально был найден центр Нурлатского района, он находится вблизи села Тюрнясево. А я задумала найти центр города Нурлат. Сейчас эта тема достаточно популярна. Я в своей работе сделала возможным найти приблизительные координаты этого исторического места, и тем не менее считаю работу выполненной. Положительный момент, который мне помог в вычислениях – это относительно ровный ландшафт, а сложность в том, что конфигурация территории города извилистая. Не каждое территориальное образование имеет географический центр, например, центр территории России невозможно найти, т.к. она имеет острова и Калининградскую область, расположенные обособленно.

Перед началом работы я разобрала теоретические вопросы, изучила методы и приемы определения центра различных фигур. Опробовала эти методы на простейших фигурах, затем перешла к более сложным фигурам, центр тяжести которых определяется методом группировки.

Определение центра города Нурлат Нурлатского района республики Татарстан

1. Для определения границ Нурлата я воспользовалась генеральным планом-схемой, которая размещена на сайте Нурлатского муниципального района http://nurlat.tatarstan.ru/rus/generalniy-plan-goroda-nurlat.htm .(Рис.1)

2. Далее увеличенное изображение карты перенесла на миллиметровую бумагу, т.к. требовалась работа с координатами.(Рис.2)

3. Затем разбила территорию города на множество простейших фигур, координаты центров которых определить относительно легко.(Рис.2)

4. Затем по формулам, описанным выше, вычислила координаты центра.(см Таблица)

5. Для подтверждения результата я применила физические методы исследования, используя простейшие приемы из статики. Для этого я перенесла карту на плоский картон, вырезала изображение по контуру и проверила точку центра, используя метод подвесов и вертикальный упор. Все полученные результаты совпали. (см. Фото3,4)

Центром города Нурлат является точка, которая расположена в области железнодорожного вокзала.

Заключение.

Тема вынашивалась давно, но реализовать ее раньше не удавалось по причине того, что практически ежегодно вносились изменения в границы города. Сначала к территории города были присоединены близлежащие поселки Ключи, Верхний Нурлат, Нижний Нурлат, позже с выделением земельных участков для многодетных семей, к территории города были присоединены новые площади, которые изменили границы города. Последняя версия карты с границами нашего районного центра размещена на сайте Нурлатского муниципального района.

Методы, которые я использовала, с успехом можно применять для определения подобных точек различных территориальных образований. Ожидаемые результаты осуществлены.

Литература и информационные ресурсы:

1. Геометрия. 7-9 классы: учеб. Для общеобразоват. Организаций/[Л.С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др.].- 2-еизд. – М.:Просвещение, 2014. – 383с.

2. Гольдин, И. И. Основные сведения по технической механике: Учеб.пособие для сред.ПТУ / И. И. Гольдин. – 3-е изд.,перераб.и доп. – М. : Высшая школа, 1986. – 96с.

3. https://ru.wikipedia.org/wiki

4. http://nwpi-fsap.narod.ru/lists/statika/5.htm.

5.http://freemath.ru/publ/istorija_matematiki/vyskazyvanija_o_matematike/vyskazyvanija_o_matematike/19-1-0-36

Приложение

Рис.1 Рис.2

Таблица. Координаты центров и площади простейших фигур

i	x_i	y_i	S_i	X_i∙S_i	y_i∙S_i
Для прямоугольников
1	25	30	600	15000	18000
2	21,1	48,5	85,4	1801,94	4141,9
3	31,8	45,7	9,75	310,05	445,575
4	37,3	44,4	22,09	823,957	980,796
5	37,4	41	9,2	344,08	377,2
6	37,5	37,5	25	937,5	937,5
7	37,5	32,5	25	937,5	812,5
8	41	35,5	2	82	71
9	40,7	33,6	3,64	148,148	122,304
10	37,3	26,9	27,6	1029,48	742,44
11	35,8	23,5	1,5	53,7	35,25
12	36,3	20,8	11,7	424,71	243,36
13	39,25	22,25	0,25	9,8125	5,5625
14	38,4	20,8	3,52	135,168	73,216
15	38,9	19,1	3,12	121,368	59,592
16	38,5	11,75	94,5	3638,25	1110,375
17	43,7	12,1	27,06	1182,522	327,426
18	45,65	12,55	6,12	279,378	76,806
19	43	7	4	172	28
20	37	4,4	4,8	177,6	21,12
21	34,3	4,4	3,15	108,045	13,86
22	33	4,1	1,7	56,1	6,97
23	31,15	8,1	0,84	26,166	6,804
24	32,35	12,1	30,74	994,439	371,954
25	25,3	13,55	26,1	660,33	353,655
26	27,5	11,5	2,4	66	27,6
27	21,75	11,7	1,12	24,36	13,104
28	20,65	13,95	0,35	7,2275	4,8825
29	19,2	14,6	2,88	55,296	42,048
30	14,3	13,8	5,5	78,65	75,9
31	12,65	14,1	1,62	20,493	22,842
32	7,85	13,75	22	172,7	302,5
33	10,15	12,25	1,05	10,6575	12,8625
34	8	11,05	0,7	5,6	7,735
35	2,9	14,5	1,3	3,77	18,85
36	10	20	100	1000	2000
37	3,75	18	15	56,25	270
38	4	22	4	16	88
39	4,5	23,75	1,5	6,75	35,625
40	6,75	25,75	5,25	35,4375	135,1875
41	7,35	26,5	2,2	16,17	58,3
42	9,5	27,7	10,8	102,6	299,16
43	12,75	30	45	573,75	1350
44	12,5	40,3	52,5	656,25	2115,75
45	7,6	40,35	32,16	244,416	1297,656
46	8,9	34,25	4,65	41,385	159,2625
47	8,35	36	6,6	55,11	237,6
48	6,1	36,5	1,2	7,32	43,8
49	14,35	46,75	3,25	46,6375	151,9375
50	14,75	48,45	0,45	6,6375	21,8025
51	40	27,4	1,55	62	42,47
52	23,5	2,7	0,54	12,69	1,458
53	29,6	11,6	0,12	3,552	1,392
Для треугольников
1	27,63	47,3	45,5	1257,165	2152,15
2	28,4	46	0,225	6,39	10,35
3	39,8	43,7	0,72	28,656	31,464
4	39,8	40,66	0,6	23,88	24,396
5	40,66	37,33	4	162,64	149,32
6	41.5	34,6	0,36	14,94	12,456
7	41,6	32,73	0,72	29,952	23,5656
8	40,73	31,46	2,42	98,5666	76,1332
9	39.85	29,9	0,045	1,79325	1,3455
10	39,85	29,2	0,165	6,57525	4,818
11	40,43	28,8	0,385	15,56555	11,088
12	40,46	28,7	0,13	5,2598	3,731
13	40,63	27,13	0,78	31,6914	21,1614
14	40,26	27,66	0,3	12,078	8,298
15	39,86	25,73	0,125	4,9825	3,21625
16	39,83	25,03	0,28	11,1524	7,0084
17	39,3	24,93	0,09	3,537	2,2437
18	37,9	23,6	1,44	54,576	33,984
19	37	23,33	0,75	27,75	17,4975
20	37,7	22,66	0,15	5,655	3,399
21	39,3	21,76	0,105	4,1265	2,2848
22	39,3	21,23	0,135	5,3055	2,86605
23	39,4	19,33	0,21	8,274	4,0593
24	40,8	18,4	1,08	44,064	19,872
25	43,1	16,96	5,775	248,9025	97,944
26	45,86	15,46	0,935	42,8791	14,4551
27	47,8	12,83	6,15	293,97	78,9045
28	48,7	14,71	1	48,7	14,71
29	48,98	14,1	1,035	50,6943	14,5935
30	45,86	9,3	1,6	73,376	14,88
31	44,43	7,36	1,235	54,87105	9,0896
32	42,6	5,7	0,9	38,34	5,13
33	39,96	3,93	1,74	69,5478	6,8382
34	37,6	3,6	0,77	28,952	2,772
35	35.6	3,7	0,27	9,612	0,999
36	32,3	4	0,43	13,889	1,72
37	33,3	5,2	0,15	4,995	0,78
38	34,1	5,8	0,6	20,46	3,48
39	33,5	8	8,3	278,05	66,4
40	30,6	8,7	0,2	6,12	1,74
41	29,6	9,7	0,3	8,88	2,91
42	28,7	12	0,1	2,87	1,2
43	26,9	10,8	0,18	4,842	1,944
44	25,7	11,6	0,12	3,084	1,392
45	24,6	11,	1,53	37,638	16,83
46	23,4	1,7	0,29	6,786	0,493
47	22,6	11,9	0,18	4,068	2,142
48	21,9	11,2	0,17	3,723	1,904
49	20,9	13,4	0,12	2,508	1,608
50	17,8	14	0,39	6,942	5,46
51	17	14	0,98	16,66	13,72
52	16	14,2	2,25	36	31,95
53	14,2	12,4	0,36	5,112	4,464
54	4,4	12,3	0,25	1,1	3,075
55	11,3	11,8	0,18	2,034	2,124
56	8,6	11,2	0,12	1,032	1,344
57	8,4	11,8	0,9	7,56	10,62
58	8,1	12,1	1,38	11,178	16,698
59	3,3	13	0,45	1,485	5,85
60	2,4	15,9	0,54	1,296	8,586
61	5,7	21,4	0,17	0,969	3,638
62	3,7	23,4	0,54	1,998	12,636
63	4,7	25,1	0,81	3,807	20,331
64	5,6	26,6	0,24	1,344	6,384
65	8	28,1	1,23	9,84	34,563
66	10,4	36,5	0,62	6,448	22,63
67	9,7	33,3	0,21	2,037	6,993
68	7,2	34,5	0,49	3,528	16,905
69	6,5	35,7	0,3	1,95	10,71
70	5,4	36,7	0,18	0,972	6,606
71	5	41,4	1,35	6,75	55,89
72	4,9	42,9	0,88	4,312	37,752
73	8,4	44,3	4,47	37,548	198,021
74	12,5	46	2,59	32,375	119,14
75	14,3	48,3	0,3	4,29	14,49
Для окружностей
1	10,7	11,4	0,785	8,3995	8,949
2	12,7	12	0,785	9,9695	9,42
3	19,8	13,7	0,785	15,543	10,7545
Сумма		1473,8	36306,77	41894,16

Расчеты координат центра карты в рассмотренной системе координат

Фото 1 Фото 2.

Просмотров работы: 2779

Источник

Как найти Центроид фигуры?

Центроид треугольника находится в точке пересечения его медиан. Если у фигуры есть центр симметрии, то он является ее центроидом. Если фигура имеет ось симметрии, то её центроид лежит на этой оси. Центроид фигуры из двух частей, лежит на отрезке, соединяющем центроиды этих частей.

Как определить Центроид?

Центроид четырёх точек (вершин четырёхугольника) Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие — середины противополежащих сторон. Точка пересечения делит все три отрезка пополам.

Что пересекается в центре треугольника?

Центроид треугольника (также барицентр треугольника и центр тяжести треугольника) — точка пересечения медиан в треугольнике.

Что такое Центроид графа?

centroid) называется такая вершина дерева , после удаления которой дерево разбивается на несколько поддеревьев , таких что для каждого : , то есть размер каждого поддерева не превосходит половины размера исходного дерева.

Как найти центр сложной фигуры?

Вычисляешь массу каждого треугольника (если тело однородно, то m/M=s/S, где m и M массы, а s и S площади каждого треугольника и всей фигуры). Затем считаешь каждый центр масс материальной точкой и находишь для этих материальных точек центр тяжести.

Как найти центр многогранника?

Чтобы найти координаты центра (ну или еще говорят центра тяжести) многоугольника, нужно сложить соответствующие координаты его вершин и разделить на число вершин.

Как найти геометрический центр треугольника?

Отметьте точку пересечения двух медиан. Эта точка является центром тяжести треугольника. Центр тяжести находится на пересечении трех медиан, но так как медианы всегда пересекаются в одной точке, можно работать только с двумя медианами.

Где находится центр масс Солнечной системы?

В Солнце сосредоточена подавляющая часть всей массы системы (около 99,866 %), оно удерживает своим тяготением планеты и прочие тела, принадлежащие к Солнечной системе.

Что проходит через центр окружности?

Точки касания окружностей Веррьера (полувписанных окружностей) со сторонами лежат на прямой, которая проходит через центр вписанной окружности (инцентр) (См.

На чем лежит центр вписанной окружности?

Окружность называют вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла. Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех его сторон.

Как работает алгоритм Дейкстры?

Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены. Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности.

Как определить центр графа?

Центр (или центр Жордана) графа — это множество всех вершин с минимальным эксцентриситетом. То есть множество всех вершин A, для которой максимальное расстояние d(A,B) до других вершин B минимально. Эквивалентно, это множество вершин с эксцентриситетом, равным радиусу графа.

Как найти координаты центра тяжести круга?

Круг. Так как круг имеет две оси симметрии, то его центр тяжести находится на пересечении осей симметрии. Полукруг. Полукруг имеет одну ось симметрии, то центр тяжести лежит на этой оси.

Как найти положение центра тяжести системы?

Способы определения координат центра тяжести

Аналитический (путем интегрирования).
Метод симметрии. …
Экспериментальный. …
Разбиение. …
Дополнение (Метод отрицательных площадей или объемов).

Как найти геометрический центр сложной фигуры?

Как вычислить центр тяжести фигуры?

Существует 5 способов:

Аналитический (путем интегрирования).
Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Экспериментальный. …
Разбиение. …
Дополнение (Метод отрицательных площадей или объемов).

Как найти центр масс в треугольнике?

Источник

Что такое центроид?

Что такое геометрическая декомпозиция?

Пошаговая процедура решения центроида составных форм

Центроид для общих форм

Проблема 1: Центроид С-образных форм

Проблема 2: Центроид неправильных фигур

Момент инерции неправильной или сложной формы

Вопросы и Ответы

Содержание

Что такое центроид?

Что такое геометрическая декомпозиция?

Пошаговая процедура решения центроида составных форм

Центроид для общих форм

Проблема 1: Центроид C-образных форм

Проблема 2: Центроид неправильных фигур

Момент инерции неправильной или сложной формы

Вопросы и Ответы

Свойства[править | править код]

Центроид треугольника[править | править код]

Минимаксные свойства центроида треугольника[править | править код]

Центроид четырёх точек (вершин четырёхугольника)[править | править код]

Определение местоположения барицентра[править | править код]

Определение местоположения барицентра однородной плоской фигуры методом отвеса[править | править код]

Определение местоположения барицентра выпуклой двумерной фигуры методом балансировки[править | править код]

Определение местоположения барицентра для конечного множества точек[править | править код]

Определение местоположения барицентра с помощью геометрического разложения[править | править код]

Определение местоположения барицентра интегрированием[править | править код]

Определение местоположения барицентра для области, ограниченной графиками непрерывных функций[править | править код]

Определение местоположения барицентра объекта, имеющего форму буквы L[править | править код]

Барицентры треугольника и тетраэдра[править | править код]

Барицентр тетраэдра[править | править код]

Барицентр многоугольника[править | править код]

Барицентры конуса и пирамиды[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ЦЕНТРОВ СЛОЖНЫХ ФИГУР

Как найти Центроид фигуры?

Как определить Центроид?

Что пересекается в центре треугольника?

Что такое Центроид графа?

Как найти центр сложной фигуры?

Как найти центр многогранника?

Как найти геометрический центр треугольника?

Где находится центр масс Солнечной системы?

Что проходит через центр окружности?

На чем лежит центр вписанной окружности?

Как работает алгоритм Дейкстры?

Как определить центр графа?

Как найти координаты центра тяжести круга?

Как найти положение центра тяжести системы?

Как найти геометрический центр сложной фигуры?

Как вычислить центр тяжести фигуры?

Как найти центр масс в треугольнике?

Вам также может понравиться

Как найти игру по логотипу

Как составить регламент то оборудования

Как найти певца по голосу

Добавить комментарий Отменить ответ