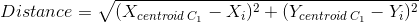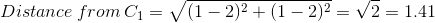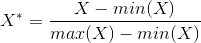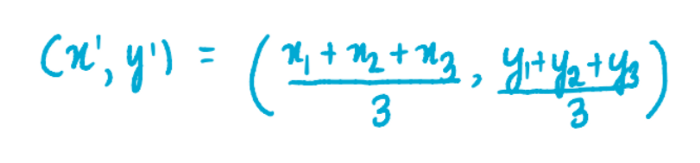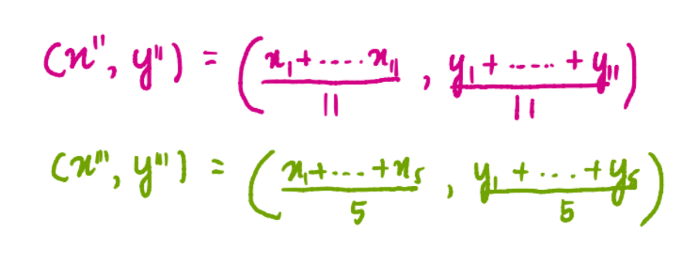Время на прочтение
4 мин
Количество просмотров 48K
Мы знаем, что Земля – это одна из 8 планет, которые вращаются вокруг Солнца. Солнце – это всего лишь звезда среди порядка 200 миллиардов звезд в галактике Млечный Путь. Очень тяжело осознать это число. Зная это, можно сделать предположение о количестве звезд во вселенной – приблизительно 4X10^22. Мы можем видеть около миллиона звезд на небе, хотя это всего лишь малая часть от всего фактического количества звезд. Итак, у нас появилось два вопроса:
- Что такое галактика?
- И какая связь между галактиками и темой статьи (кластерный анализ)
Галактика – это скопление звезд, газа, пыли, планет и межзвездных облаков. Обычно галактики напоминают спиральную или эдептическую фигуру. В пространстве галактики отделены друг от друга. Огромные черные дыры чаще всего являются центрами большинства галактик.
Как мы будем обсуждать в следующем разделе, есть много общего между галактиками и кластерным анализом. Галактики существуют в трехмерном пространстве, кластерный анализ – это многомерный анализ, проводимый в n-мерном пространстве.
Заметка: Черная дыра – это центр галактики. Мы будем использовать похожую идею в отношении центроидов для кластерного анализа.
Кластерный анализ
Предположим вы глава отдела по маркетингу и взаимодействию с потребителями в телекоммуникационной компании. Вы понимаете, что все потребители разные, и что вам необходимы различные стратегии для привлечения различных потребителей. Вы оцените мощь такого инструмента как сегментация клиентов для оптимизации затрат. Для того, чтобы освежить ваши знания кластерного анализа, рассмотрим следующий пример, иллюстрирующий 8 потребителей и среднюю продолжительность их разговоров (локальных и международных). Ниже данные:
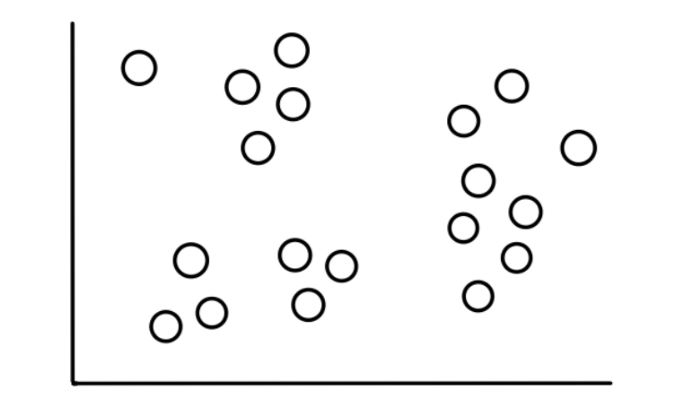
Для лучшего восприятия нарисуем график, где по оси x будет откладываться средняя продолжительность международных разговоров, а по оси y — средняя продолжительность локальных разговоров. Ниже график:
Заметка: Это похоже на анализ расположения звезд на ночном небе (здесь звезды заменены потребителями). В дополнение, вместо трехмерного пространства у нас двумерное, заданное продолжительностью локальных и международных разговоров, в качестве осей x и y.
Сейчас, разговаривая в терминах галактик, задача формулируется так – найти положение черных дыр; в кластерном анализе они называются центроидами. Для обнаружения центроидов мы начнем с того, что возьмем произвольные точки в качестве положения центроидов.
Евклидово расстояние для нахождения Центроидов для Кластеров
В нашем случае два центроида (C1 и C2) мы произвольным образом поместим в точки с координатами (1, 1) и (3, 4). Почему мы выбрали именно эти два центроида? Визуальное отображение точек на графике показывает нам, что есть два кластера, которые мы будем анализировать. Однако, впоследствии мы увидим, что ответ на этот вопрос будет не таким уж простым для большого набора данных.
Далее, мы измерим расстояние между центроидами (C1 и C2) и всеми точками на графике использую формулу Евклида для нахождения расстояния между двумя точками.
Примечание: Расстояние может быть вычислено и по другим формулам, например,
- квадрат евклидова расстояния – для придания веса более отдаленным друг от друга объектам
- манхэттенское расстояние – для уменьшения влияния выбросов
- степенное расстояние – для увеличения/уменьшения влияния по конкретным координатам
- процент несогласия – для категориальных данных
- и др.
Колонка 3 и 4 (Distance from C1 and C2) и есть расстояние, вычисленное по этой формуле. Например, для первого потребителя
Принадлежность к центроидам (последняя колонка) вычисляется по принципу близости к центроидам (C1 и C2). Первый потребитель ближе к центроиду №1 (1.41 по сравнению с 2.24) следовательно, принадлежит к кластеру с центроидом C1.
Ниже график, иллюстрирующий центроиды C1 и C2 (изображенные в виде голубого и оранжевого ромбика). Потребители изображены цветом соответствующего центроида, к кластеру которого они были отнесены.
Так как мы произвольным образом выбрали центроиды, вторым шагом мы сделать этот выбор итеративным. Новая позиция центроидов выбирается как средняя для точек соответствующего кластера. Так, например, для первого центроида (это потребители 1, 2 и 3). Следовательно, новая координата x для центроида C1 э то средняя координат x этих потребителей (2+1+1)/3 = 1.33. Мы получим новые координаты для C1 (1.33, 2.33) и C2 (4.4, 4.2).Новый график ниже:
В конце концов, мы поместим центроиды в центр соответствующего кластера. График ниже:
Позиции наших черных дыр (центров кластеров) в нашем примере C1 (1.75, 2.25) и C2(4.75, 4.75). Два кластера выше подобны двум галактикам, разделенным в пространстве друг от друга.
Итак, рассмотрим примеры дальше. Пусть перед нами стоит задача по сегментации потребителей по двум параметрам: возраст и доход. Предположим, что у нас есть 2 потребителя с возрастом 37 и 44 лет и доходом в $90,000 и $62,000 соответственно. Если мы хотим измерить Евклидово расстояние между точками (37, 90000) и (44, 62000), мы увидим, что в данном случае переменная доход «доминирует» над переменной возраст и ее изменение сильно сказывается на расстоянии. Нам необходима какая-нибудь стратегия для решения данной проблемы, иначе наш анализ даст неверный результат. Решение данной проблемы это приведение наших значений к сравнимым шкалам. Нормализация – вот решение нашей проблемы.
Нормализация данных
Существует много подходов для нормализации данных. Например, нормализация минимума-максимума. Для данной нормализации используется следующая формула
в данном случае X* — это нормализованное значение, min и max – минимальная и максимальная координата по всему множеству X
(Примечание, данная формула располагает все координаты на отрезке [0;1])
Рассмотрим наш пример, пусть максимальный доход $130000, а минимальный — $45000. Нормализованное значение дохода для потребителя A равно
Мы сделаем это упражнение для всех точек для каждых переменных (координат). Доход для второго потребителя (62000) станет 0.2 после процедуры нормализации. Дополнительно, пусть минимальный и максимальный возрасты 23 и 58 соответственно. После нормализации возрасты двух наших потребителей составит 0.4 и 0.6.
Легко увидеть, что теперь все наши данные расположены между значениями 0 и 1. Следовательно, у нас теперь есть нормализованные наборы данных в сравнимых шкалах.
Запомните, перед процедурой кластерного анализа необходимо произвести нормализацию.
Статью нашел kuznetsovin
Данная статья является переводом. Ссылка на оригинал.
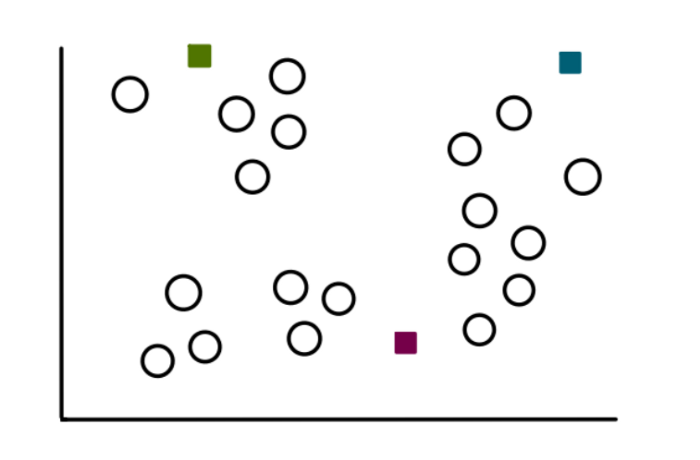
Перед тем как начнем изучать алгоритм, давайте разберемся – что же такое кластеризация. Под кластеризацией понимается обнаружение естественных группировок в данных. Обычно, когда нам даны данные, которые мы можем визуализировать (2- или 3-мерные данные), человеческий глаз может легко формировать различные кластеры. Но для машин это делать несколько сложнее. Но тут на помощь и приходят алгоритмы кластеризации, способные находить кластеры в пространстве с ещё большим количеством измерений, чего не может делать даже глаз человека. Теперь, когда мы знаем, что мы хотим сделать, воспользуемся K-means здесь.
Представьте, что у нас есть набор данных из 19 значений, которые выглядят примерно так:
Теперь предположим, что мы знаем, что эти данные разбиваются на 3, относительно очевидные, категории и выглядеть это будет так:
Наша задача – использовать алгоритм кластеризации K-means, чтобы произвести эту категоризацию.
Шаг 1: Выбираем число кластеров, k
Число кластеров, которые мы хотим распознать, это и есть k в K-means. В нашем случае, так как мы предположили, что всего 3 кластера, k = 3.
Шаг 2: Выбираем k случайных значений
Процесс обнаружения кластеров мы начинаем с выбора 3 случайно выбранных значений (не обязательно, чтобы они были нашими данными). Эти точки будут сейчас работать как центроиды или центры кластеров, которые мы собираемся сгруппировать:
Шаг 3: Создать k кластеров
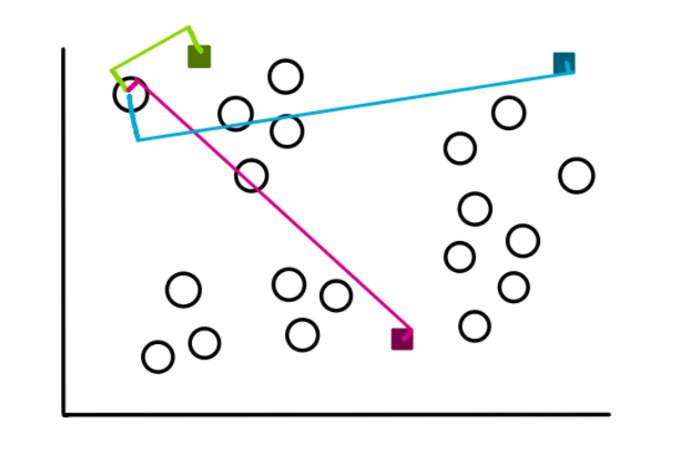
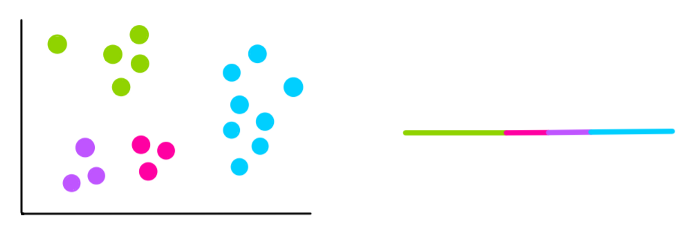
Чтобы создать кластеры, мы начнем измерять расстояние между каждым значением наших данных до каждого из трех центроидов, а затем добавляем его к наиболее близкому кластеру. Для значения, взятого в качестве примера, расстояния будут выглядеть примерно так:
Смотря на рисунок, мы понимаем, что расстояние от значения до зеленого центроида наименьшее, поэтому мы и добавляем значение в зеленый кластер.
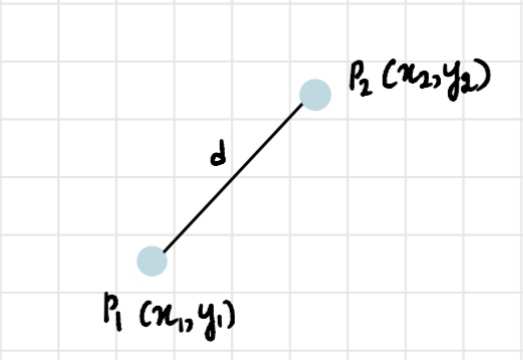
В 2-мерном пространстве для нахождения расстояния между двумя точками используется формула:
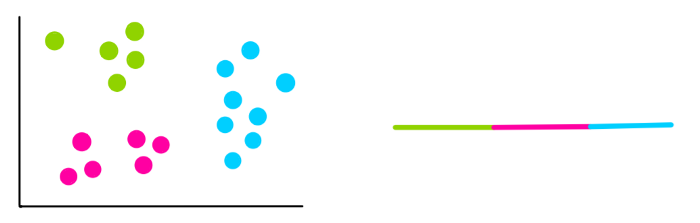
Используя эту формулу, мы повторяем процесс с оставшимися значениями, после этого кластеры будут выглядеть следующим образом:
Шаг 4: Вычисляем новый центроид каждого кластера
Теперь, когда у нас есть все три кластера, мы находим новые центроиды для каждого из них. Например, ниже изображена формула для нахождения координат синего кластера:
где x1, x2 и x3 – это координаты по оси x каждого из трех значений синего кластера, а y1, y2 и y3 – координаты соответствующих точек по оси y. Мы разделили сумму координат на 3, потому что 3 значения содержится в кластере. Аналогично, координаты центроид розового и зеленого кластеров будут равны:
Так, новые центроиды будут иметь вид:
Шаг 5: Оценить качество каждого кластера
Так как k-means не может видеть кластеры так, как это делаем мы, он измеряет качество, находя среднее отклонение внутри всех кластеров. Основная идея, лежащая в основе k-means, заключается в определении таких кластеров, что отклонения внутри каждого кластера минимальны. Чтобы оценить отклонение, мы вычислим такую величину, как WCSS (within-cluster sum of squares) – cумму квадратов внутрикластерных расстояний до центра кластера.
Где С – это кластерные центроиды, а d – значения данных в каждом кластере
Но в целях упрощения, давайте представим, что отклонение визуально выглядит так:
Шаг 6: повторяем шаги 3-5
Итак, мы получили кластеры и отклонение, и … Мы начинаем все сначала.
Но теперь мы используем центроиды, которые были вычислены ранее, чтобы создать 3 новых кластера, пересчитать центры новых кластеров и вычислить сумму расстояний внутри каждого кластера.
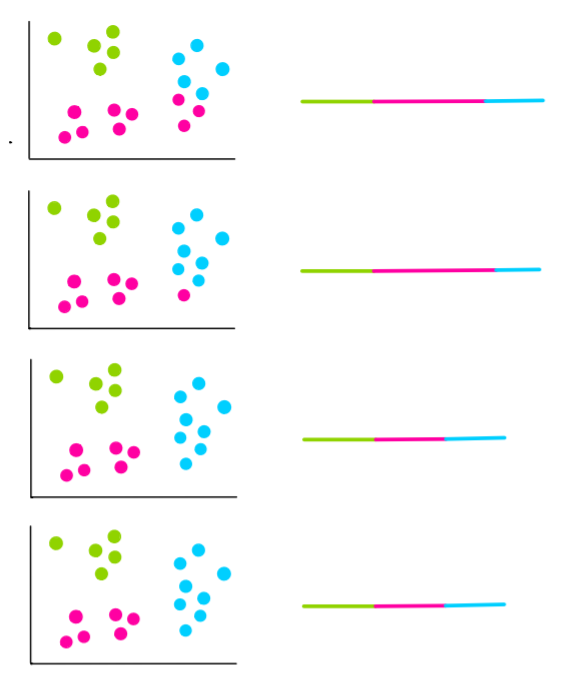
Давайте предположим, что следующие 4 итерации будут выглядеть так:
На двух последних итерациях мы видим, что кластеры не меняются. Это значит, что алгоритм сошелся и мы останавливаем процесс. Затем мы выбираем кластеры с наименьшим WCSS. Это будут кластеры на последних 2 итерациях, поэтому они и становятся нашими финальными кластерами.
Как выбирать k?
В нашем примере мы знали, что нам нужно 3 кластера. Но что, если мы не знаем, какое количество кластеров мы имеем, тогда как нам выбрать k?
В этом случае мы пытаемся использовать различные значения k и считать WCSS.
k=1:
k=2:
k=3:
k=4:
Вы можете заметить, что каждый раз, когда мы добавляем новый кластер, общее отклонение внутри каждого кластера становится все меньше и меньше. В конце настанет случай, когда на каждое значение данных будет приходиться отдельный кластер, и тогда отклонение будет равно 0.
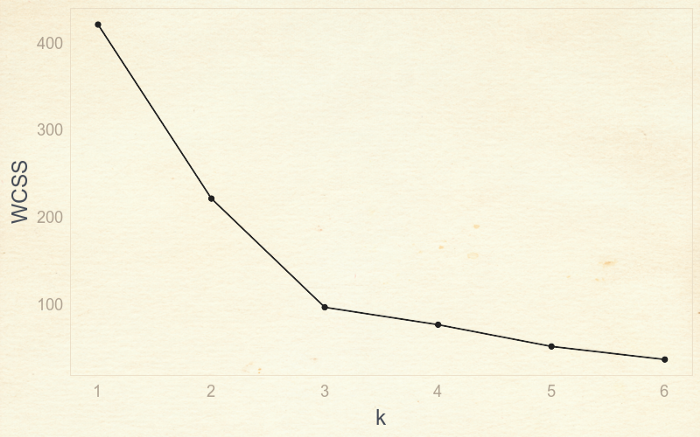
Нам нужно использовать подход, называемый «метод локтя», чтобы найти наилучшее значение k. Для этого мы строим график зависимости WCSS от количества кластеров, или k.
Подход называется «метод локтя», потому что мы можем найти оптимальное значение k, когда найдем «согнутый локоть» графика, что находится в точке с k=3. Вы можете заметить, что до 3 наблюдается быстрое уменьшение отклонения, но потом отклонение перестает падать также быстро.
Что ж, а на этом все. Вот такой он, k-means – простой, но эффективный алгоритм кластеризации! Подведем краткий итог. Сегодня из этой статьи мы узнали, что же такое k-means, как он работает при решении задач кластеризации, а также как находить количество кластеров, когда это неизвестно. Надеюсь, что статья вам понравилось. До новых встреч.
Мне нужно оперативно освоить алгоритмы и структуры данных. Что делать?
Если хотите подтянуть или освежить знания по алгоритмам и структурам данных, загляните на наш курс «Алгоритмы и структуры данных», на котором вы:
- углубитесь в решение практических задач;
- научитесь применять алгоритмы и структуры данных при разработке программ;
- изучите сленг, на котором говорят все разработчики независимо от языка программирования: язык алгоритмов и структур данных;
- узнаете все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Вы также будете на связи с преподавателем и другими студентами. В итоге будете браться за сложные проекты и повысите чек за свою работу. Курс подходит как junior, так и middle-разработчикам.
Кластеризация K-средних – один из наиболее широко используемых алгоритмов неконтролируемого машинного обучения, который формирует кластеры данных на основе сходства между экземплярами данных. Для работы этого конкретного алгоритма необходимо заранее определить количество кластеров. K в K-средних означает количество кластеров.
Алгоритм K-средних начинается со случайного выбора значения центроида для каждого кластера. После этого алгоритм итеративно выполняет три шага:
- (i) Найти евклидово расстояние между каждым экземпляром данных и центроидами всех кластеров.
- (ii) Назначьте экземпляры данных кластеру центроида с ближайшим расстоянием.
- (iii) Вычислить новые значения центроидов на основе средних значений координат всех экземпляров данных из соответствующего кластера.
Пример
Давайте попробуем увидеть, как работает алгоритм K-средних, на собственном примере, прежде чем реализовывать алгоритм в Scikit-Learn. Для реализации алгоритма кластеризации K-средних в Scikit-Learn требуется три строки кода. Однако, чтобы понять, как это работает на самом деле, давайте сначала решим проблему с помощью K-средних «на бумаге».
Предположим, у нас есть набор следующих двухмерных экземпляров данных с именем D.
D = { (5,3), (10,15), (15,12), (24,10), (30,45), (85,70), (71,80), (60,78), (55,52), (80,91) }
Мы хотим разделить эти данные на два кластера, C1 и C2, на основе сходства между точками данных.
Первым шагом является случайная инициализация значений центроидов обоих кластеров. Назовем центроиды кластеров C1 и C2 c1 и c2 и инициализируем их значениями первых двух точек данных, то есть (5, 3) и (10, 15).
Теперь нужно приступить к итерациям.
Итерация 1
| S.No | Точки данных | Евклидово расстояние от центроида скопления c1 = (5,3) | Евклидово расстояние от центроида скопления c2 = (10,15) | Назначенный кластер |
|---|---|---|---|---|
| 1 | (5,3) | 0 | 13 | C1 |
| 2 | (10,15) | 13 | 0 | C2 |
| 3 | (15,12) | 13,45 | 5,83 | C2 |
| 4 | (24,10) | 20,24 | 14,86 | C2 |
| 5 | (30,45) | 48,87 | 36 | C2 |
| 6 | (85,70) | 104,35 | 93 | C2 |
| 7 | (71,80) | 101,41 | 89 | C2 |
| 8 | (60,78) | 93 | 80 | C2 |
| 9 | (55,52) | 70 | 58 | C2 |
| 10 | (80,91) | 115,52 | 103,32 | C2 |
В приведенной выше таблице второй столбец содержит все точки данных. Третий столбец содержит евклидово расстояние между всеми точками данных и центроидом c1. Точно так же четвертый столбец содержит расстояние между центроидом c2 и точками данных. Наконец, в пятом столбце мы показываем, какому кластеру назначена точка данных на основе евклидова расстояния между двумя центроидами кластера. Например, посмотрите на третью точку данных (15, 12), он имеет расстояние 13,45 единиц от c1 и 5,83 единиц от c2, поэтому он был сгруппирован в C2.
После присвоения точек данных соответствующим кластерам следующим шагом является вычисление новых значений центроида. Эти значения вычисляются путем нахождения средних значений координат точек данных, принадлежащих определенному кластеру.
Для кластера C1 в настоящее время существует только одна точка, т.е. (5,3), поэтому среднее значение координат останется таким же, и новое значение центроида для c1 также будет (5,3).
Для C2 в настоящее время имеется 9 точек данных. Мы называем координаты точек данных, как x и y. Новое значение для координаты x центроида c2 можно вычислить, определив среднее значение координат x всех 9 точек, принадлежащих кластеру C2, как показано ниже:
c2(x) = (10 + 15 + 24 + 30 + 85 + 71 + 60 + 55 + 80) / 9 = 47.77
Новое значение координаты y центроида c2 можно вычислить, определив среднее значение всех координат y всех 9 точек, принадлежащих кластеру C2.
c2(y) = (15 + 12 + 10 + 45 + 70 + 80 + 78 + 52 + 91) / 9 = 50.33
Обновленное значение центроида для c2 теперь будет {47,77, 50,33}.
Для следующей итерации будут использоваться новые значения центроидов для c1 и c2, и весь процесс будет повторен. Итерации продолжаются до тех пор, пока значения центроидов не перестанут обновляться. Следующие итерации выглядят следующим образом.
Итерация 2
| S.No | Точки данных | Евклидово расстояние от центроида скопления c1 = (5,3) | Евклидово расстояние от центра скопления c2 = (47,77,50,33) | Назначенный кластер |
|---|---|---|---|---|
| 1 | (5,3) | 0 | 63,79 | C1 |
| 2 | (10,15) | 13 | 51,71 | C1 |
| 3 | (15,12) | 13,45 | 50,42 | C1 |
| 4 | (24,10) | 20,24 | 46,81 | C1 |
| 5 | (30,45) | 48,87 | 18,55 | C2 |
| 6 | (85,70) | 104,35 | 42,10 | C2 |
| 7 | (71,80) | 101,41 | 37,68 | C2 |
| 8 | (60,78) | 93 | 30,25 | C2 |
| 9 | (55,52) | 70 | 7,42 | C2 |
| 10 | (80,91) | 115,52 | 51,89 | C2 |
c1(x) = (5, 10, 15, 24) / 4 = 13.5 c1(y) = (3, 15, 12, 10) / 4 = 10.0
Обновлен c1 до (13.5, 10.0).
c2(x) = (30 + 85 + 71 + 60 + 55 + 80) / 6 = 63.5 c2(y) = (45 + 70 + 80 + 78 + 52 +91) / 6 = 69.33
Обновлен c2 до (63.5, 69.33).
Итерация 3
| S.No | Точки данных | Евклидово расстояние от центра скопления c1 = (13,5,10) | Евклидово расстояние от центра скопления c2 = (63,5,69,33) | Назначенный кластер |
|---|---|---|---|---|
| 1 | (5,3) | 11.01 | 88,44 | C1 |
| 2 | (10,15) | 6.10 | 76,24 | C1 |
| 3 | (15,12) | 2,5 | 75,09 | C1 |
| 4 | (24,10) | 10,5 | 71,27 | C1 |
| 5 | (30,45) | 38,69 | 41,40 | C1 |
| 6 | (85,70) | 93,33 | 21,51 | C2 |
| 7 | (71,80) | 90,58 | 13.04 | C2 |
| 8 | (60,78) | 82,37 | 9,34 | C2 |
| 9 | (55,52) | 59,04 | 19.30 | C2 |
| 10 | (80,91) | 104,80 | 27,23 | C2 |
c1(x) = (5, 10, 15, 24, 30) / 5 = 16.8 c1(y) = (3, 15, 12, 10, 45) / 5 = 17.0
Обновлен c1 до (16.8, 17.0).
c2(x) = (85 + 71 + 60 + 55 + 80) / 5 = 70.2 c2(y) = (70 + 80 + 78 + 52 + 91) / 5 = 74.2
Обновлен c2 до (70.2, 74.2).
Итерация 4
| S.No | Точки данных | Евклидово расстояние от центра скопления c1 = (16,8,17) | Евклидово расстояние от центра скопления c2 = (70,2,74,2) | Назначенный кластер |
|---|---|---|---|---|
| 1 | (5,3) | 18.30 | 96,54 | C1 |
| 2 | (10,15) | 7,08 | 84,43 | C1 |
| 3 | (15,12) | 5,31 | 83,16 | C1 |
| 4 | (24,10) | 10.04 | 79,09 | C1 |
| 5 | (30,45) | 30,95 | 49,68 | C1 |
| 6 | (85,70) | 86,37 | 15,38 | C2 |
| 7 | (71,80) | 83,10 | 5,85 | C2 |
| 8 | (60,78) | 74,74 | 10,88 | C2 |
| 9 | (55,52) | 51,80 | 26,90 | C2 |
| 10 | (80,91) | 97,31 | 19,44 | C2 |
c1(x) = (5, 10, 15, 24, 30) / 5 = 16.8 c1(y) = (3, 15, 12, 10, 45) / 5 = 17.0
Обновлен c1 до (16.8, 17.0).
c2(x) = (85 + 71 + 60 + 55 + 80) / 5 = 70.2 c2(y) = (70 + 80 + 78 + 52 + 91) / 5 = 74.2
Обновлен c2 до (70.2, 74.2).
В конце четвертой итерации обновленные значения C1 и C2 такие же, как и в конце третьей итерации. Это означает, что данные больше не могут быть кластеризованы. c1 и c2 – центроиды для C1 и C2. Чтобы классифицировать новую точку данных, вычисляется расстояние между точкой данных и центроидами кластеров. Точка данных назначается кластеру, центроид которого находится ближе всего к точке данных.
Теперь, когда мы знаем, как на самом деле работает алгоритм кластеризации K-средних, давайте посмотрим, как мы можем реализовать его с помощью Scikit-Learn.
Для запуска следующего скрипта вам потребуются библиотеки matplotlib, numpy и scikit-learn. По следующим ссылкам можно найти инструкции по загрузке и установке этих библиотек:
- matplotlib;
- Numpy;
- Scikit-Learn.
Начнем наш скрипт с импорта необходимых библиотек:
import matplotlib.pyplot as plt %matplotlib inline import numpy as np from sklearn.cluster import KMeans
Подготовка данных
Следующим шагом является подготовка данных, которые мы хотим кластеризовать. Давайте создадим массив из 10 строк и 2 столбцов. Строка содержит те же точки данных, которые мы использовали в нашем примере ручной кластеризации K-средних в последнем разделе. Мы создаем массив точек данных, потому что библиотека Scikit-Learn может работать с входными данными типа массивов без предварительной обработки.
X = np.array([[5,3],
[10,15],
[15,12],
[24,10],
[30,45],
[85,70],
[71,80],
[60,78],
[55,52],
[80,91],])
Визуализация данных
Вы можете видеть, что это те же точки данных, которые мы использовали в предыдущем примере. Давайте нарисуем эти точки и проверим, можем ли мы взглянуть на какие-либо кластеры. Для этого выполните следующую строку:
plt.scatter(X[:,0],X[:,1], label='True Position')
Приведенный выше код просто отображает все значения в первом столбце массива X относительно всех значений во втором столбце. График будет выглядеть так:

Невооруженным глазом, если нам нужно сформировать два кластера из вышеуказанных точек данных, мы, вероятно, сделаем один кластер из пяти точек в нижнем левом углу и один из пяти точек в правом верхнем углу. Посмотрим, делает ли наш алгоритм кластеризации K-средних то же самое или нет.
Создание кластеров
Чтобы создать кластер K-средних из двух кластеров, просто введите следующий скрипт:
kmeans = KMeans(n_clusters=2) kmeans.fit(X)
Да, это всего лишь две строчки кода. В первой строке вы создаете объект KMeans и передаете ему 2 в качестве значения параметра n_clusters. Затем вам просто нужно вызвать метод fit для kmeans и передать данные, которые вы хотите кластеризовать, в данном случае это массив X, который мы создали ранее.
Теперь посмотрим, какие значения центроидов алгоритм сгенерировал для конечных кластеров.
print(kmeans.cluster_centers_)
На выходе будет двумерный массив формы 2 x 2.
[[ 16.8 17. ] [ 70.2 74.2]]
Здесь первая строка содержит значения для координат первого центроида, т.е. (16.8, 17), а вторая строка содержит значения для координат другого центроида, то есть (70.2, 74.2). Вы можете видеть, что эти значения аналогичны тем, которые мы вычислили вручную для центроидов c1 и c2 в предыдущем разделе.
Чтобы увидеть метки для точки данных, выполните следующий скрипт.
print(kmeans.labels_)
Результатом является одномерный массив из 10 элементов, соответствующих кластерам, назначенным нашим 10 точкам данных.
[0 0 0 0 0 1 1 1 1 1]
Здесь первые и последние пять точек сгруппированы вместе. Здесь 0 и 1 используются только для представления идентификаторов кластера и не имеют математического значения. Если бы кластеров было три, третий кластер был бы представлен цифрой 2.
Давайте снова нанесем точки данных на график и визуализируем, как данные были сгруппированы. На этот раз мы построим график данных вместе с присвоенной им меткой, чтобы мы могли различать кластеры. Выполните следующий скрипт:
plt.scatter(X[:,0],X[:,1], c=kmeans.labels_, cmap='rainbow')
Здесь мы сопоставляем первый столбец массива X со вторым столбцом, однако в этом случае мы также передаем kmeans.labels_ в качестве значения для параметра c, соответствующего меткам. Параметр cmap = ‘rainbow’ передается для выбора типа цвета для различных точек данных. Выходной график должен выглядеть так:

Как и ожидалось, первые пять точек в левом нижнем углу были сгруппированы вместе (отображаются синим цветом), а остальные точки в правом верхнем углу были сгруппированы вместе (отображаются красным цветом).
Теперь давайте выполним алгоритм K-средних с тремя кластерами и посмотрим на выходной график.

Вы можете видеть, что близкие друг к другу точки снова сгруппированы вместе.
Теперь давайте нанесем точки вместе с координатами центроида каждого кластера, чтобы увидеть, как положение центроида влияет на кластеризацию. Снова мы будем использовать три кластера, чтобы увидеть эффект центроидов. Выполните следующий скрипт, чтобы нарисовать график:
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_, cmap='rainbow') plt.scatter(kmeans.cluster_centers_[:,0] ,kmeans.cluster_centers_[:,1], color='black')
В этом случае мы наносим точки данных в цвета радуги, а центроиды – в черный цвет. Результат выглядит так:

В случае трех кластеров две точки в середине (отображаются красным цветом) имеют расстояние ближе к центроиду в середине (отображается черным цветом между двумя красными) по сравнению с центроидами в нижнем левом или верхнем правом углу. Однако, если бы было два кластера, не было бы центроида в центре, поэтому красные точки должны были бы быть сгруппированы вместе с точками в нижнем левом или верхнем правом кластерах.
Заключение
Кластеризация K-средних – это простой, но очень эффективный алгоритм неконтролируемого машинного обучения для кластеризации данных. Он группирует данные на основе евклидова расстояния между точками данных. Алгоритм кластеризации K-средних имеет множество применений для группировки текстовых документов, изображений, видео и многого другого.
Cluster analysis is a method of organizing data into representative groups based upon similar characteristics. Each member of the cluster has more in common with other members of the same cluster than with members of the other groups. The most representative point within the group is called the centroid. Usually, this is the mean of the values of the points of data in the cluster.
- Calculator
- Graph paper
-
If the centroid has to be a particular point of data instead of a midpoint between the data, then the median may be used to determine it, instead of the mean.
Organize the data. If the data consists of a single variable, a histogram might be appropriate. If two variables are involved, graph the data on a coordinate plane. For example, if you were looking at the height and weight of school children in a classroom, plot the points of data for each child on a graph, with the weight being the horizontal axis and the height being the vertical axis. If more than two variables are involved, matrices may be needed to display the data.
Group the data into clusters. Each cluster should consist of the points of data closest to it. In the height and weight example, group any points of data that appear to be close together. The number of clusters, and whether every point of data has to be in a cluster, may depend upon the purposes of the study.
For each cluster, add the values of all members. For example, if a cluster of data consisted of the points (80, 56), (75, 53), (60, 50), and (68,54), the sum of the values would be (283, 213).
Divide the total by the number of members of the cluster. In the example above, 283 divided by four is 70.75, and 213 divided by four is 53.25, so the centroid of the cluster is (70.75, 53.25).
Plot the cluster centroids and determine whether any points are closer to a centroid of another cluster than they are to the centroid of their own cluster. If any points are closer to a different centroid, redistribute them to the cluster containing the closer centroid.
Repeat Steps 3, 4 and 5 until all points of data are in the cluster containing the centroid to which they are closest.
Things You’ll Need
Tips
Кластеризация неразмеченных данных можно выполнить с помощью модуля sklearn.cluster.
Каждый алгоритм кластеризации имеет два варианта: класс, реализующий fit метод изучения кластеров на данных поезда, и функция, которая, учитывая данные поезда, возвращает массив целочисленных меток, соответствующих различным кластерам. Для класса метки над обучающими данными можно найти в labels_ атрибуте.
2.3.1. Обзор методов кластеризации
| Название метода | Параметры | Масштабируемость | Использование | Геометрия (используемая метрика) |
|---|---|---|---|---|
| К-средник | число кластеров | Очень большое значение n симплов среднее n_clusters вместе с Мини батчи K-средних | Универсальный, любой размер кластеров, плоская геометрия, не слишком много кластеров | Дистанция между точками |
| Афинное распространение | дамфинг, предпочтение выборки | Не масштабируется с помощью n_clusters | Много кластеров, не равномерный размер кластера, неплоская геометрия | Дистанция графа (например граф ближайших соседей) |
| Средний сдвиг | пропускная способность | Не масштабируется с помощью n_clusters | Много кластеров, не равномерный размер кластера, неплоская геометрия | Дистанция между точками |
| Спектральная кластеризация | число кластеров | Средняя n симплов маленькое n_clasters | Мало кластеров, или размер кластера, неплоская геометрия | Дистанция графа (например граф ближайших соседей) |
| Иерархическая кластеризация | чилсо кластеров или порог расстояния | Большое n симплов и n_clasters | Мало кластеров, возможно ограничене связей | Дистанция между точками |
| Агломеративная кластеризация | число кластеров, порог дистанции, тип связи, дистанция | Большое n симплов и n_clasters | Мало кластеров, возможно ограничене связей и не Евклидовое расстояние | Любая попарная дистанция |
| DBSCAN | размер окрестности | Очень большое n симплов и среднее n_clasters | не плоская геометрия, неравномерный размер кластеров | Дистанция между ближайшими точками |
| OPTICS | Минимальное количество элементов в кластере | Очень большое n симплов и большое n_clasters | не плоская геометрия, неравномерный размер кластеров, переменная плотность кластеров | Дистанция между точками |
| Гауссовская Смешаянная модель | много параметров | не масштабируемо | плоская геометрия, подходит для оценки плотности | Расстояния до центров Махаланобиса |
| Birch | факторы ветвления, порог, не обязательный глобальный кластер | Большое n симплов и n_clasters | Большой объем данных, удаление выбросов, сокращение данных | Евклидовое расстояние между точками |
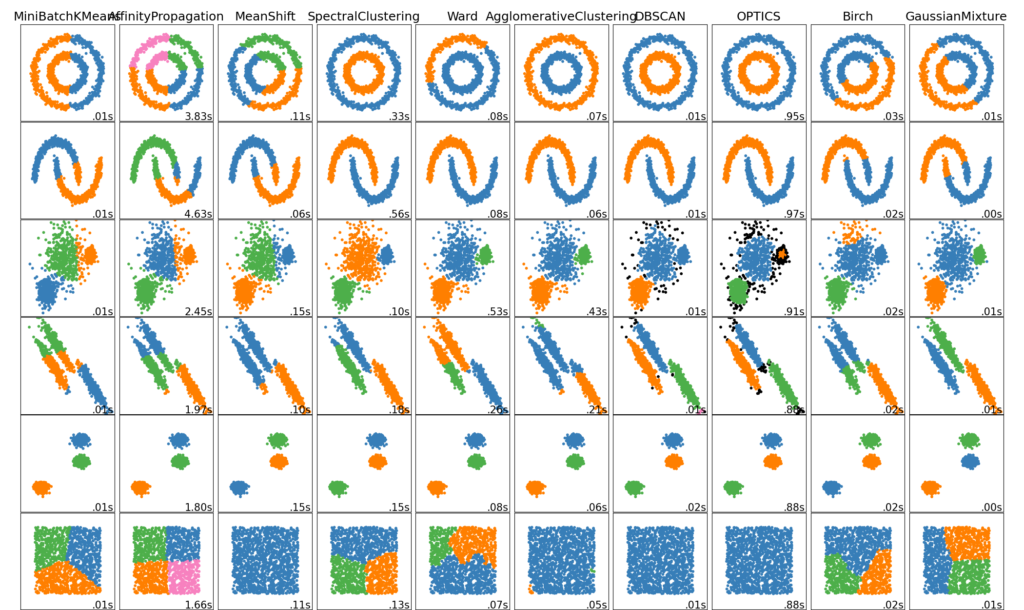
Неплоская геометрия кластеризации полезно когда кластеры имеют специфичную форму, то есть многообразие и стандартное евклидовое расстояние в качестве метрики не подходят. Это случай возникает в двух верхних строках рисунка.
Гауссовская Смешаянная модель полезна для кластеризации описанные в другой статье документации, посвященная смешанным моделям. Метод K-средних можно расматривать как частный случай Гауссовской смешанной модели с равной ковариации для каждого компонента.
Методы трансдуктивной кластеризации (в отличие отметодов индуктивной кластеризации) не предназначены для применения к новым, невидимым данным.
2.3.2. K-средних
Эти KMeans данные алгоритмы кластеров пытаются отдельными образцы в п групп одинаковой дисперсии, сводя к минимуму критерия , известный как инерция или внутри-кластера сумм квадратов (см ниже). Этот алгоритм требует указания количества кластеров. Он хорошо масштабируется для большого количества образцов и используется в широком диапазоне областей применения во многих различных областях.
Алгоритм k-средних делит набор $N$ образцы $X$ в $K$ непересекающиеся кластеры $C$, каждый из которых описывается средним $mu_j$ образцов в кластере. Средние значения обычно называют «центроидами» кластера; обратите внимание, что это, как правило, не баллы из $X$, хотя они живут в одном пространстве.
Алгоритм K-средних нацелен на выбор центроидов, которые минимизируют инерцию или критерий суммы квадратов внутри кластера : $$sum_{i=0}^{n}min_{mu_j in C}(||x_i — mu_j||^2)$$
Инерцию можно определить как меру того, насколько кластеры внутренне связаны. Он страдает различными недостатками:
- Инерция предполагает, что кластеры выпуклые и изотропные, что не всегда так. Он плохо реагирует на удлиненные кластеры или коллекторы неправильной формы.
- Инерция — это не нормализованная метрика: мы просто знаем, что более низкие значения лучше, а ноль — оптимально. Но в очень многомерных пространствах евклидовы расстояния имеют тенденцию становиться раздутыми (это пример так называемого «проклятия размерности»). Выполнение алгоритма уменьшения размерности, такого как анализ главных компонентов (PCA) перед кластеризацией k-средних, может облегчить эту проблему и ускорить вычисления.
K-средних часто называют алгоритмом Ллойда. В общих чертах алгоритм состоит из трех шагов. На первом этапе выбираются начальные центроиды, а самый простой метод — выбрать $k$ образцы из набора данных $X$. После инициализации K-средних состоит из цикла между двумя другими шагами. Первый шаг присваивает каждой выборке ближайший центроид. На втором этапе создаются новые центроиды, взяв среднее значение всех выборок, назначенных каждому предыдущему центроиду. Вычисляется разница между старым и новым центроидами, и алгоритм повторяет эти последние два шага, пока это значение не станет меньше порогового значения. Другими словами, это повторяется до тех пор, пока центроиды не переместятся значительно.
K-средних эквивалентно алгоритму максимизации ожидания с маленькой, все равной диагональной ковариационной матрицей.
Алгоритм также можно понять через концепцию диаграмм Вороного. Сначала рассчитывается диаграмма Вороного точек с использованием текущих центроидов. Каждый сегмент на диаграмме Вороного становится отдельным кластером. Во-вторых, центроиды обновляются до среднего значения каждого сегмента. Затем алгоритм повторяет это до тех пор, пока не будет выполнен критерий остановки. Обычно алгоритм останавливается, когда относительное уменьшение целевой функции между итерациями меньше заданного значения допуска. В этой реализации дело обстоит иначе: итерация останавливается, когда центроиды перемещаются меньше допуска.
По прошествии достаточного времени K-средние всегда будут сходиться, однако это может быть локальным минимумом. Это сильно зависит от инициализации центроидов. В результате вычисление часто выполняется несколько раз с разными инициализациями центроидов. Одним из способов решения этой проблемы является схема инициализации k-means++, которая была реализована в scikit-learn (используйте init='k-means++'параметр). Это инициализирует центроиды (как правило) удаленными друг от друга, что, вероятно, приводит к лучшим результатам, чем случайная инициализация, как показано в справочнике.
K-means++ также может вызываться независимо для выбора начальных значений для других алгоритмов кластеризации, sklearn.cluster.kmeans_plusplus подробности и примеры использования см. В разделе .
Алгоритм поддерживает выборочные веса, которые могут быть заданы параметром sample_weight. Это позволяет присвоить некоторым выборкам больший вес при вычислении центров кластеров и значений инерции. Например, присвоение веса 2 выборке эквивалентно добавлению дубликата этой выборки в набор данных $X$.
Метод K-средних может использоваться для векторного квантования. Это достигается с помощью метода преобразования обученной модели KMeans.
2.3.2.1. Низкоуровневый параллелизм
KMeans преимущества параллелизма на основе OpenMP через Cython. Небольшие порции данных (256 выборок) обрабатываются параллельно, что, кроме того, снижает объем памяти. Дополнительные сведения о том, как контролировать количество потоков, см. В наших заметках о параллелизме .
Примеры:
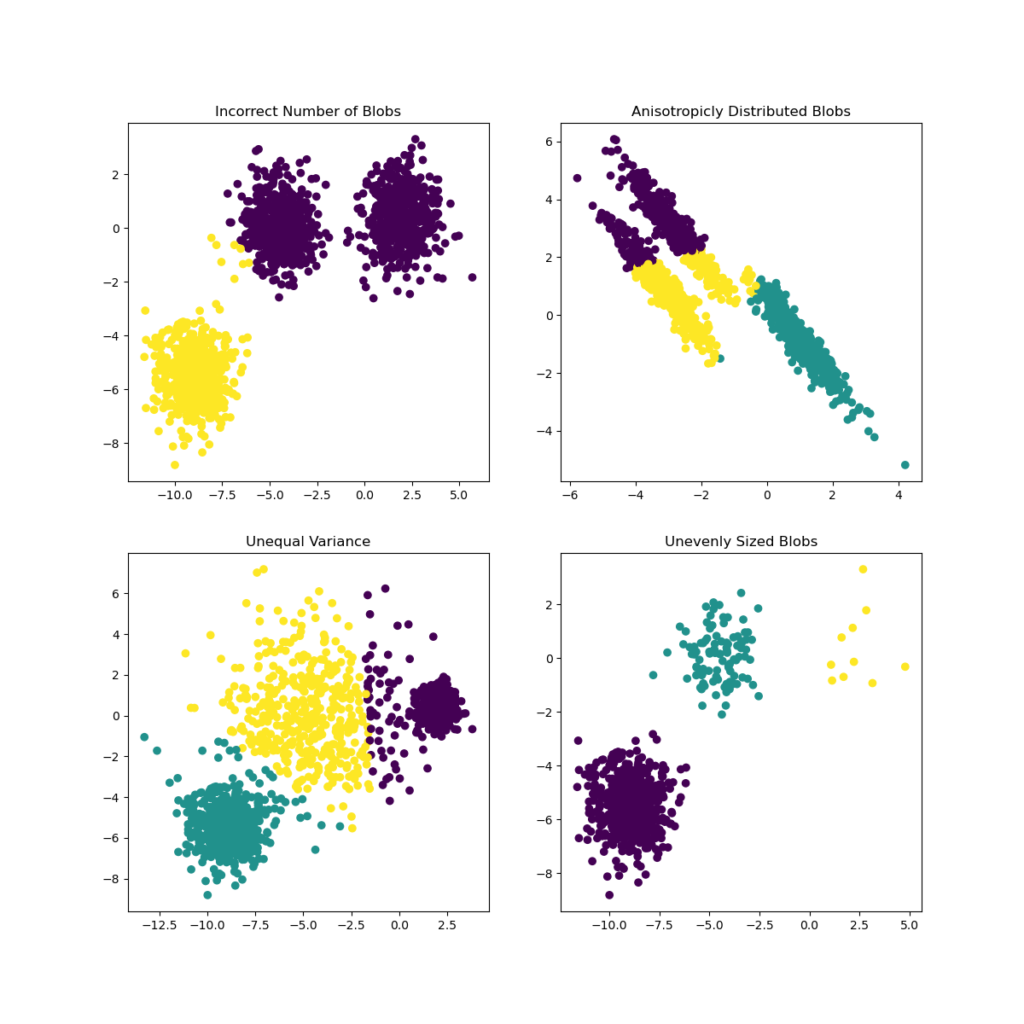
- Демонстрация предположений k-средних : демонстрация того, когда k-средних работает интуитивно, а когда нет
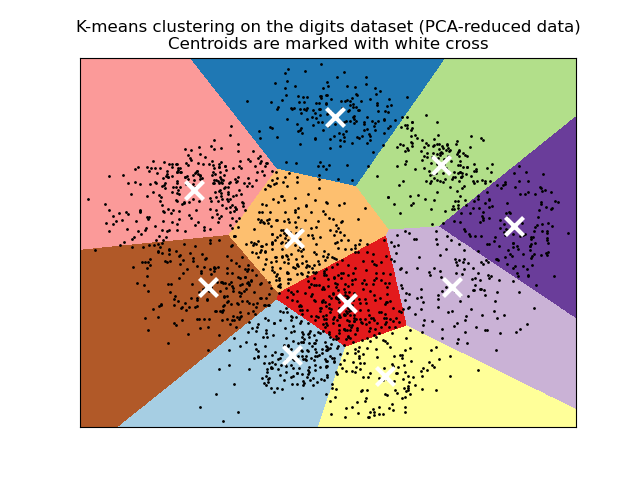
- Демонстрация кластеризации K-средних на данных рукописных цифр : Кластеризация рукописных цифр
Рекомендации:
- «K-means ++: преимущества тщательного посева» Артур, Дэвид и Сергей Васильвицкий, Труды восемнадцатого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам , Общество промышленной и прикладной математики (2007)
2.3.2.2. Мини-партия K-средних
Это MiniBatchKMeans вариант KMeans алгоритма, который использует мини-пакеты для сокращения времени вычислений, но при этом пытается оптимизировать ту же целевую функцию. Мини-пакеты — это подмножества входных данных, которые выбираются случайным образом на каждой итерации обучения. Эти мини-пакеты резко сокращают объем вычислений, необходимых для схождения к локальному решению. В отличие от других алгоритмов, которые сокращают время сходимости k-средних, мини-пакетные k-средние дают результаты, которые, как правило, лишь немного хуже, чем стандартный алгоритм.
Алгоритм повторяется между двумя основными шагами, аналогично обычным k-средним. На первом этапе $b$ образцы выбираются случайным образом из набора данных, чтобы сформировать мини-пакет. Затем они присваиваются ближайшему центроиду. На втором этапе обновляются центроиды. В отличие от k-средних, это делается для каждой выборки. Для каждой выборки в мини-пакете назначенный центроид обновляется путем взятия среднего потокового значения выборки и всех предыдущих выборок, назначенных этому центроиду. Это приводит к снижению скорости изменения центроида с течением времени. Эти шаги выполняются до тех пор, пока не будет достигнута сходимость или заранее определенное количество итераций.
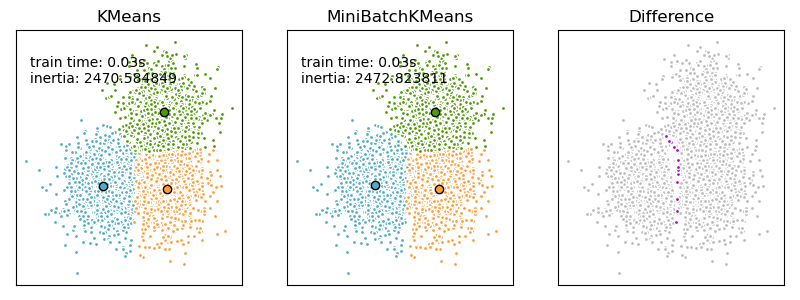
MiniBatchKMeans сходится быстрее, чем KMeans, но качество результатов снижается. На практике эта разница в качестве может быть довольно небольшой, как показано в примере и цитированной ссылке.
Примеры:
- Сравнение алгоритмов кластеризации K-средних и MiniBatchKMeans : сравнение KMeans и MiniBatchKMeans
- Кластеризация текстовых документов с использованием k-средних : кластеризация документов с использованием разреженных MiniBatchKMeans
- Онлайн обучение словаря частей лиц
2.3.3. Распространения близости (Affinity Propagation)
AffinityPropagation создает кластеры, отправляя сообщения между парами образцов до схождения. Затем набор данных описывается с использованием небольшого количества образцов, которые определяются как наиболее репрезентативные для других образцов. Сообщения, отправляемые между парами, представляют пригодность одного образца быть образцом другого, который обновляется в ответ на значения из других пар. Это обновление происходит итеративно до сходимости, после чего выбираются окончательные образцы и, следовательно, дается окончательная кластеризация.
Метод Распространения близости может быть интересным, поскольку он выбирает количество кластеров на основе предоставленных данных. Для этой цели двумя важными параметрами являются предпочтение , которое контролирует, сколько экземпляров используется, и коэффициент демпфирования, который снижает ответственность и сообщения о доступности, чтобы избежать числовых колебаний при обновлении этих сообщений.
Главный недостаток метода Распространения близости — его сложность. Алгоритм имеет временную сложность порядка $O(N^2 T)$, где $N$ количество образцов и $T$ — количество итераций до сходимости. Далее, сложность памяти порядка $O(N^2)$ если используется плотная матрица подобия, но может быть сокращена, если используется разреженная матрица подобия. Это делает метод Распространения близости наиболее подходящим для наборов данных малого и среднего размера.
Примеры:
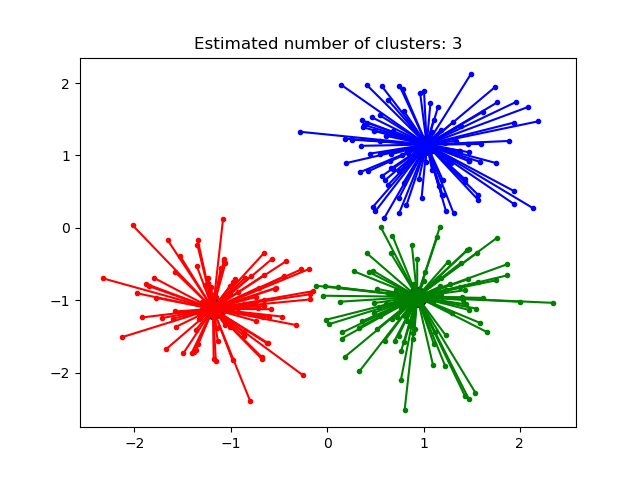
- Демонстрация алгоритма кластеризации распространения близости: метода Распространения близости на синтетических наборах данных 2D с 3 классами.
- Визуализация структуры фондового рынка Финансовые временные ряды метода Распространения близости для поиска групп компаний
Описание алгоритма: сообщения, отправляемые между точками, относятся к одной из двух категорий. Во-первых, это ответственность $r(i,k)$, которое является накопленным свидетельством того, что образец $k$ должен быть образцом для образца $i$. Второе — доступность $a(i,k)$ что является накопленным свидетельством того, что образец $i$ следует выбрать образец $k$ быть его образцом, и учитывает значения для всех других образцов, которые $k$ должен быть образцом. Таким образом, образцы выбираются по образцам, если они (1) достаточно похожи на многие образцы и (2) выбираются многими образцами, чтобы быть репрезентативными.
Более формально ответственность за образец $k$ быть образцом образца i дан кем-то: $$r(i, k) leftarrow s(i, k) — max [ a(i, k’) + s(i, k’) forall k’ neq k ]$$
Где $s(i,k)$ сходство между образцами $i$ а также $k$. Наличие образца $k$ быть образцом образца $i$ дан кем-то: $$a(i, k) leftarrow min [0, r(k, k) + sum_{i’~s.t.~i’ notin {i, k}}{r(i’, k)}]$$
Начнем с того, что все значения для $r$ и $a$ aустановлены в ноль, и расчет каждой итерации повторяется до сходимости. Как обсуждалось выше, чтобы избежать числовых колебаний при обновлении сообщений, коэффициент демпфирования $lambda$ вводится в итерационный процесс: $$r_{t+1}(i, k) = lambdacdot r_{t}(i, k) + (1-lambda)cdot r_{t+1}(i, k)$$ $$a_{t+1}(i, k) = lambdacdot a_{t}(i, k) + (1-lambda)cdot a_{t+1}(i, k)$$
где $t$ указывает время итерации.
2.3.4. Средний сдвиг
MeanShift кластеризация направлена на обнаружение капель в образцах с плавной плотностью. Это алгоритм на основе центроидов, который работает, обновляя кандидатов в центроиды, чтобы они были средними точками в данном регионе. Затем эти кандидаты фильтруются на этапе постобработки, чтобы исключить почти дубликаты и сформировать окончательный набор центроидов.
Учитывая центроид кандидата $x_i$ для итерации $t$, кандидат обновляется в соответствии со следующим уравнением: $$x_i^{t+1} = m(x_i^t)$$
Где $N(x_i)$ это соседство образцов на заданном расстоянии вокруг $x_i$ а также $m$ — вектор среднего сдвига, который вычисляется для каждого центроида, который указывает на область максимального увеличения плотности точек. Это вычисляется с использованием следующего уравнения, эффективно обновляющего центроид до среднего значения выборок в его окрестности: $$m(x_i) = frac{sum_{x_j in N(x_i)}K(x_j — x_i)x_j}{sum_{x_j in N(x_i)}K(x_j — x_i)}$$
Алгоритм автоматически устанавливает количество кластеров, вместо того, чтобы полагаться на параметр bandwidth, который определяет размер области для поиска. Этот параметр можно установить вручную, но можно оценить с помощью предоставленной estimate_bandwidth функции, которая вызывается, если полоса пропускания не задана.
Алгоритм не отличается высокой масштабируемостью, так как он требует многократного поиска ближайшего соседа во время выполнения алгоритма. Алгоритм гарантированно сходится, однако алгоритм прекратит итерацию, когда изменение центроидов будет небольшим.
Маркировка нового образца выполняется путем нахождения ближайшего центроида для данного образца.
Примеры:
- Демонстрация алгоритма кластеризации среднего сдвига: кластеризация среднего сдвига на синтетических наборах данных 2D с 3 классами.
Рекомендации:
- «Средний сдвиг: надежный подход к анализу пространства признаков». Д. Команичиу и П. Меер, IEEE Transactions on Pattern Analysis and Machine Intelligence (2002)
2.3.5. Спектральная кластеризация
SpectralClustering выполняет низкоразмерное встраивание матрицы аффинности между выборками с последующей кластеризацией, например, с помощью K-средних, компонентов собственных векторов в низкоразмерном пространстве. Это особенно эффективно с точки зрения вычислений, если матрица аффинности является разреженной, а amgрешатель используется для проблемы собственных значений (обратите внимание, amg что решающая программа требует, чтобы был установлен модуль pyamg ).
Текущая версия SpectralClustering требует, чтобы количество кластеров было указано заранее. Это хорошо работает для небольшого количества кластеров, но не рекомендуется для многих кластеров.
Для двух кластеров SpectralClustering решает выпуклую релаксацию проблемы нормализованных разрезов на графе подобия: разрезание графа пополам так, чтобы вес разрезаемых рёбер был мал по сравнению с весами рёбер внутри каждого кластера. Этот критерий особенно интересен при работе с изображениями, где вершинами графа являются пиксели, а веса ребер графа подобия вычисляются с использованием функции градиента изображения.
Предупреждение:
Преобразование расстояния в хорошее сходство
Обратите внимание, что если значения вашей матрицы подобия плохо распределены, например, с отрицательными значениями или с матрицей расстояний, а не с подобием, спектральная проблема будет сингулярной, а проблема неразрешима. В этом случае рекомендуется применить преобразование к элементам матрицы. Например, в случае матрицы расстояний со знаком обычно применяется тепловое ядро:
similarity = np.exp(-beta * distance / distance.std()) См. Примеры такого приложения.
Примеры:
- Спектральная кластеризация для сегментации изображения : сегментирование объектов на шумном фоне с использованием спектральной кластеризации.
- Сегментирование изображения греческих монет по регионам : спектральная кластеризация для разделения изображения монет по регионам.
2.3.5.1. Различные стратегии присвоения меток
Могут использоваться различные стратегии присвоения меток, соответствующие assign_labels параметру SpectralClustering. "kmeans" стратегия может соответствовать более тонким деталям, но может быть нестабильной. В частности, если вы не контролируете random_state, он может не воспроизводиться от запуска к запуску, так как это зависит от случайной инициализации. Альтернативная "discretize" стратегия воспроизводима на 100%, но имеет тенденцию создавать участки довольно ровной и геометрической формы.
2.3.5.2. Графики спектральной кластеризации
Спектральная кластеризация также может использоваться для разбиения графов через их спектральные вложения. В этом случае матрица аффинности является матрицей смежности графа, а SpectralClustering инициализируется с помощью affinity='precomputed':
>>> from sklearn.cluster import SpectralClustering >>> sc = SpectralClustering(3, affinity='precomputed', n_init=100, ... assign_labels='discretize') >>> sc.fit_predict(adjacency_matrix)
Рекомендации:
- «Учебное пособие по спектральной кластеризации» Ульрике фон Люксбург, 2007 г.
- «Нормализованные разрезы и сегментация изображения» Джианбо Ши, Джитендра Малик, 2000 г.
- «Случайный взгляд на спектральную сегментацию» Марина Мейла, Цзяньбо Ши, 2001
- «О спектральной кластеризации: анализ и алгоритм» Эндрю Й. Нг, Майкл И. Джордан, Яир Вайс, 2001 г.
- «Предварительно обусловленная спектральная кластеризация для задачи потокового графа стохастического разбиения блоков» Давид Жужунашвили, Андрей Князев
2.3.6. Иерархическая кластеризация
Иерархическая кластеризация — это общее семейство алгоритмов кластеризации, которые создают вложенные кластеры путем их последовательного слияния или разделения. Эта иерархия кластеров представлена в виде дерева (или дендрограммы). Корень дерева — это уникальный кластер, который собирает все образцы, а листья — это кластеры только с одним образцом. См. Страницу в Википедии для получения более подробной информации.
В AgglomerativeClustering объекте выполняет иерархическую кластеризацию с использованием подхода снизу вверх: каждый начинает наблюдения в своем собственном кластере, и кластеры последовательно объединены вместе. Критерии связывания определяют метрику, используемую для стратегии слияния:
- Ward минимизирует сумму квадратов разностей во всех кластерах. Это подход с минимизацией дисперсии, и в этом смысле он аналогичен целевой функции k-средних, но решается с помощью агломеративного иерархического подхода.
- Максимальное (Maximum) или полное связывание (complete linkage) сводит к минимуму максимальное расстояние между наблюдениями пар кластеров.
- Среднее связывание (Average linkage) минимизирует среднее расстояние между всеми наблюдениями пар кластеров.
- Одиночная связь (Single linkage) минимизирует расстояние между ближайшими наблюдениями пар кластеров.
AgglomerativeClustering может также масштабироваться до большого количества выборок, когда он используется вместе с матрицей связности, но требует больших вычислительных затрат, когда между выборками не добавляются ограничения связности: он рассматривает на каждом шаге все возможные слияния.
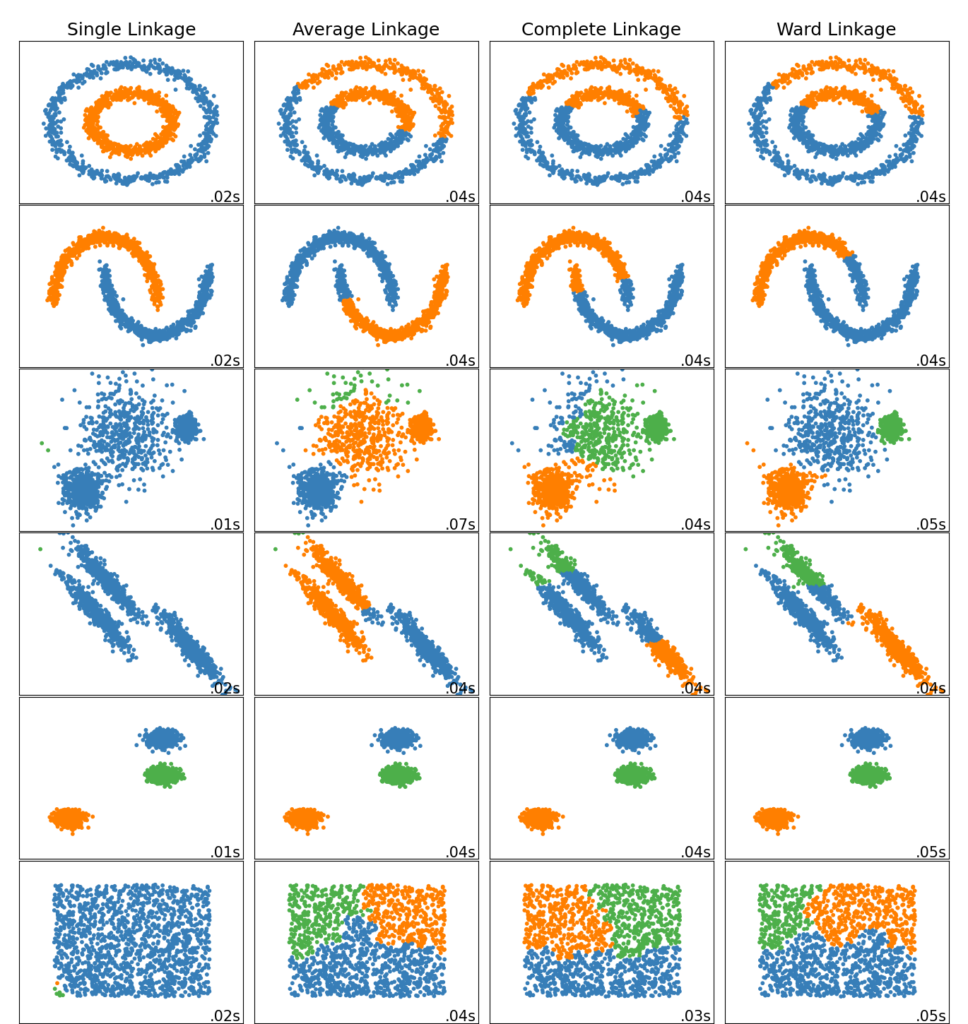
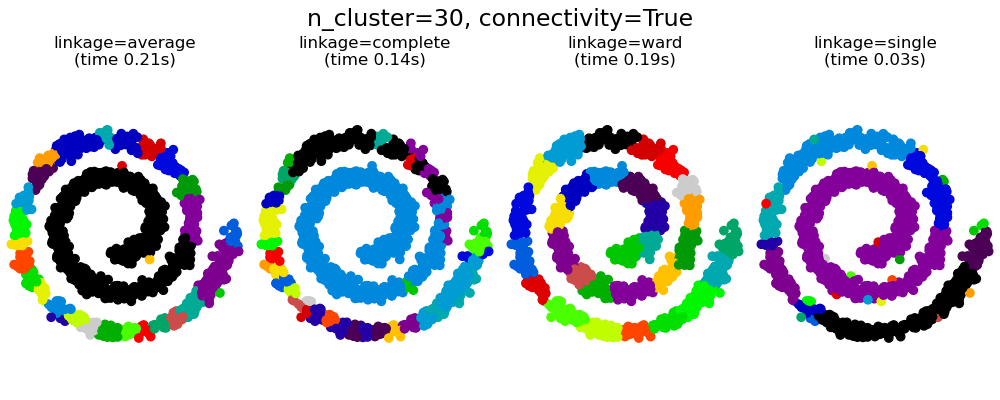
2.3.6.1. Различные типы связи: Ward, полный, средний и одиночный связь
AgglomerativeClustering поддерживает стратегии Ward, одиночного, среднего и полного связывания.
Агломеративный кластер ведет себя по принципу «богатый становится богатее», что приводит к неравномерному размеру кластера. В этом отношении одинарная связь — худшая стратегия, и Ward дает самые обычные размеры. Однако сродство (или расстояние, используемое при кластеризации) нельзя изменять с помощью Уорда, поэтому для неевклидовых показателей хорошей альтернативой является среднее связывание. Одиночная связь, хотя и не устойчива к зашумленным данным, может быть вычислена очень эффективно и поэтому может быть полезна для обеспечения иерархической кластеризации больших наборов данных. Одиночная связь также может хорошо работать с неглобулярными данными.
Примеры:
- Различная агломеративная кластеризация по двумерному встраиванию цифр : изучение различных стратегий связывания в реальном наборе данных.
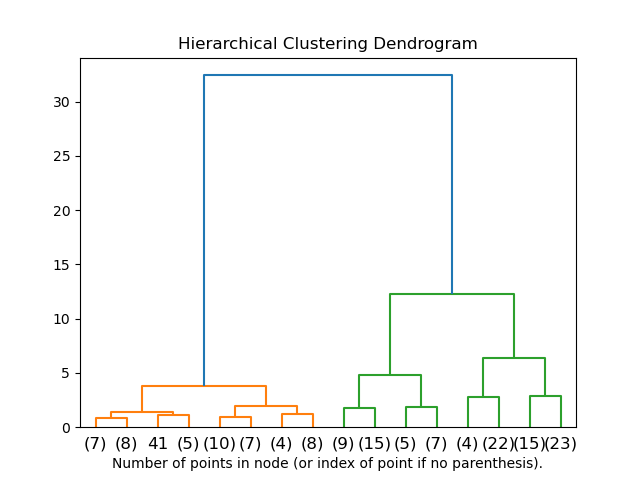
2.3.6.2. Визуализация кластерной иерархии
Можно визуализировать дерево, представляющее иерархическое слияние кластеров, в виде дендрограммы. Визуальный осмотр часто может быть полезен для понимания структуры данных, особенно в случае небольших размеров выборки.
2.3.6.3. Добавление ограничений связи
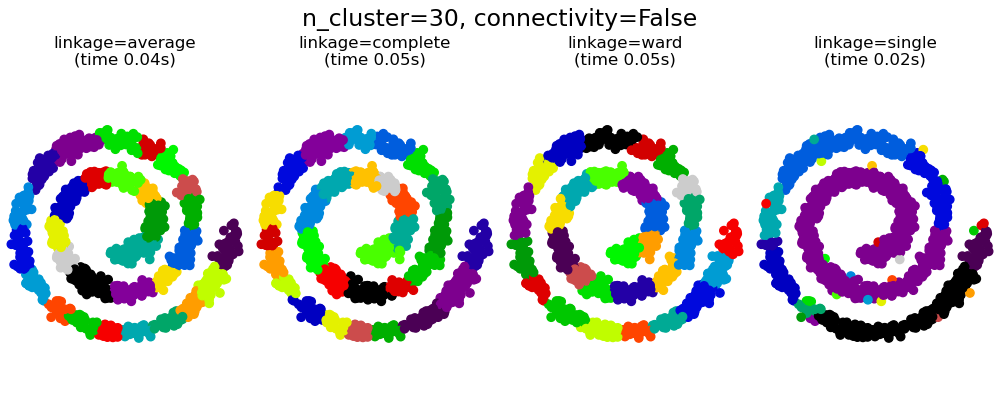
Интересным аспектом AgglomerativeClustering является то, что к этому алгоритму могут быть добавлены ограничения связности (только соседние кластеры могут быть объединены вместе) через матрицу связности, которая определяет для каждой выборки соседние выборки, следующие заданной структуре данных. Например, в приведенном ниже примере швейцарского рулона ограничения связности запрещают объединение точек, которые не являются смежными на швейцарском рулоне, и, таким образом, избегают образования кластеров, которые проходят через перекрывающиеся складки рулона.
Эти ограничения полезны для наложения определенной локальной структуры, но они также ускоряют алгоритм, особенно когда количество выборок велико.
Ограничения связности накладываются через матрицу связности: scipy разреженную матрицу, которая имеет элементы только на пересечении строки и столбца с индексами набора данных, которые должны быть связаны. Эта матрица может быть построена из априорной информации: например, вы можете захотеть сгруппировать веб-страницы, объединяя только страницы со ссылкой, указывающей одну на другую. Это также можно узнать из данных, например, используя sklearn.neighbors.kneighbors_graph для ограничения слияния до ближайших соседей, как в этом примере , или с помощью, sklearn.feature_extraction.image.grid_to_graphчтобы разрешить слияние только соседних пикселей на изображении, как в примере с монетой.
Примеры:
- Демонстрация структурированной иерархической кластеризации Варда на изображении монет : Кластеризация Варда для разделения изображения монет на регионы.
- Иерархическая кластеризация: структурированная и неструктурированная палата : пример алгоритма Уорда в швейцарской системе, сравнение структурированных подходов и неструктурированных подходов.
- Агломерация признаков против одномерного выбора: пример уменьшения размерности с агломерацией признаков на основе иерархической кластеризации Уорда.
- Агломеративная кластеризация со структурой и без нее
Предупреждение Ограничения по подключению с одиночным, средним и полным подключением
Ограничения связности и одиночная, полная или средняя связь могут усилить аспект агломеративной кластеризации «богатый становится еще богаче», особенно если они построены на sklearn.neighbors.kneighbors_graph. В пределе небольшого числа кластеров они имеют тенденцию давать несколько макроскопически занятых кластеров и почти пустые. (см. обсуждение в разделе «Агломеративная кластеризация со структурой и без нее» ). Одиночная связь — самый хрупкий вариант связи в этом вопросе.
2.3.6.4. Варьируя метрику
Одиночная, средняя и полная связь может использоваться с различными расстояниями (или сходствами), в частности евклидовым расстоянием ( l2 ), манхэттенским расстоянием (или Cityblock, или l1 ), косинусным расстоянием или любой предварительно вычисленной матрицей аффинности.
- Расстояние l1 часто хорошо для разреженных функций или разреженного шума: то есть многие из функций равны нулю, как при интеллектуальном анализе текста с использованием вхождений редких слов.
- косинусное расстояние интересно тем, что оно инвариантно к глобальному масштабированию сигнала.
Рекомендации по выбору метрики — использовать метрику, которая максимизирует расстояние между выборками в разных классах и минимизирует его внутри каждого класса.
2.3.7. DBSCAN
Алгоритм DBSCAN рассматривает кластеры , как участки высокой плотности , разделенных районах с низкой плотностью. Из-за этого довольно общего представления кластеры, обнаруженные с помощью DBSCAN, могут иметь любую форму, в отличие от k-средних, которое предполагает, что кластеры имеют выпуклую форму. Центральным компонентом DBSCAN является концепция образцов керна , то есть образцов, находящихся в областях с высокой плотностью. Таким образом, кластер представляет собой набор образцов керна, каждый из которых находится близко друг к другу (измеряется с помощью некоторой меры расстояния), и набор образцов, не относящихся к керну, которые близки к образцу керна (но сами не являются образцами керна). В алгоритме есть два параметра, min_samples и eps, которые формально определяют, что мы имеем в виду, когда говорим «плотный» . Выше min_samples или ниже eps указывают на более высокую плотность, необходимую для формирования кластера.
Более формально мы определяем образец керна как образец в наборе данных, так что существуют min_samples другие образцы на расстоянии eps, которые определены как соседи образца керна. Это говорит нам о том, что основной образец находится в плотной области векторного пространства. Кластер — это набор образцов керна, который можно построить путем рекурсивного взятия образца керна, поиска всех его соседей, которые являются образцами керна, поиска всех их соседей, которые являются образцами керна, и т. Кластер также имеет набор неосновных выборок, которые представляют собой выборки, которые являются соседями керновой выборки в кластере, но сами не являются основными выборками. Интуитивно эти образцы находятся на периферии кластера.
Любой образец керна по определению является частью кластера. Любая выборка, не являющаяся образцом керна и находящаяся по крайней мере eps на расстоянии от любой выборки керна, считается алгоритмом выбросом.
Хотя параметр в min_samples первую очередь контролирует устойчивость алгоритма к шуму (на зашумленных и больших наборах данных может быть желательно увеличить этот параметр), параметр epsимеет решающее значение для правильного выбора для набора данных и функции расстояния и обычно не может быть оставлен на значение по умолчанию. Он контролирует локальное окружение точек. Если выбран слишком маленький размер, большая часть данных вообще не будет кластеризована (и помечена как -1 для «шума»). Если выбран слишком большой, близкие кластеры будут объединены в один кластер, и в конечном итоге весь набор данных будет возвращен как единый кластер. Некоторые эвристики для выбора этого параметра обсуждались в литературе, например, на основе перегиба на графике расстояний до ближайших соседей (как обсуждается в ссылках ниже).
На рисунке ниже цвет указывает на принадлежность к кластеру, а большие кружки обозначают образцы керна, найденные алгоритмом. Меньшие кружки — это неосновные образцы, которые все еще являются частью кластера. Более того, выбросы обозначены ниже черными точками.
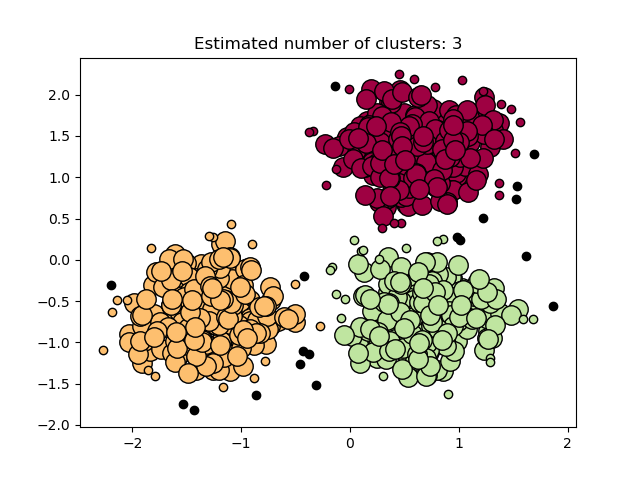
Выполнение
Алгоритм DBSCAN является детерминированным, всегда генерируя одни и те же кластеры, когда им предоставляются одни и те же данные в одном порядке. Однако результаты могут отличаться, если данные предоставляются в другом порядке. Во-первых, даже если основные образцы всегда будут назначаться одним и тем же кластерам, метки этих кластеров будут зависеть от порядка, в котором эти образцы встречаются в данных. Во-вторых, что более важно, кластеры, которым назначены неосновные выборки, могут различаться в зависимости от порядка данных. Это может произойти, если образец неосновного керна находится на расстоянии меньше, чем epsдва образца керна в разных кластерах. Согласно треугольному неравенству эти два образца керна должны быть дальше, чемepsдруг от друга, иначе они были бы в одном кластере. Неосновная выборка назначается тому кластеру, который сгенерирован первым при передаче данных, поэтому результаты будут зависеть от порядка данных.
Текущая реализация использует шаровые деревья и kd-деревья для определения окрестности точек, что позволяет избежать вычисления полной матрицы расстояний (как это было сделано в версиях scikit-learn до 0.14). Сохранена возможность использования пользовательских метрик; подробности см NearestNeighbors.
Потребление памяти для больших размеров выборки
Эта реализация по умолчанию неэффективна с точки зрения памяти, поскольку она строит полную матрицу попарного сходства в случае, когда нельзя использовать kd-деревья или шаровые деревья (например, с разреженными матрицами). Эта матрица будет потреблять $n^2$ плавает. Вот несколько способов обойти это:
- Используйте кластеризацию OPTICS вместе с
extract_dbscanметодом. Кластеризация OPTICS также вычисляет полную попарную матрицу, но сохраняет в памяти только одну строку (сложность памяти n). - График окрестностей с разреженным радиусом (где предполагается, что отсутствующие записи находятся вне eps) можно предварительно вычислить эффективным с точки зрения памяти способом, и dbscan можно обработать с помощью
metric='precomputed'. Смотритеsklearn.neighbors.NearestNeighbors.radius_neighbors_graph. - Набор данных можно сжать, удалив точные дубликаты, если они встречаются в ваших данных, или используя BIRCH. Тогда у вас будет относительно небольшое количество представителей для большого количества точек. Затем вы можете
sample_weightуказать при установке DBSCAN.
Рекомендации:
- «Алгоритм на основе плотности для обнаружения кластеров в больших пространственных базах данных с шумом» Эстер, М., Х. П. Кригель, Дж. Сандер и X. Сюй, в материалах 2-й Международной конференции по открытию знаний и интеллектуальному анализу данных, Портленд, штат Орегон , AAAI Press, стр. 226–231. 1996 г.
- «Новый взгляд на DBSCAN: почему и как вы должны (по-прежнему) использовать DBSCAN. Шуберт, Э., Сандер, Дж., Эстер, М., Кригель, HP, и Сюй, X. (2017). В транзакциях ACM в системах баз данных (TODS), 42 (3), 19.
2.3.8. ОПТИКА
В OPTICS акции алгоритма много общих с DBSCAN алгоритмом, и можно рассматривать как обобщение DBSCAN, что расслабляет epsтребование от одного значения до диапазона значений. Ключевое различие между DBSCAN и OPTICS заключается в том, что алгоритм OPTICS строит граф достижимости , который назначает каждой выборке reachability_ расстояние и точку в ordering_ атрибуте кластера ; эти два атрибута назначаются при подборе модели и используются для определения принадлежности к кластеру. Если OPTICS запускается со значением по умолчанию inf, установленным для max_eps, то извлечение кластера в стиле DBSCAN может выполняться повторно за линейное время для любого заданного eps значения с использованием этого cluster_optics_dbscan метода. Параметр max_eps более низкое значение приведет к сокращению времени выполнения, и его можно рассматривать как максимальный радиус окрестности от каждой точки для поиска других потенциальных достижимых точек.
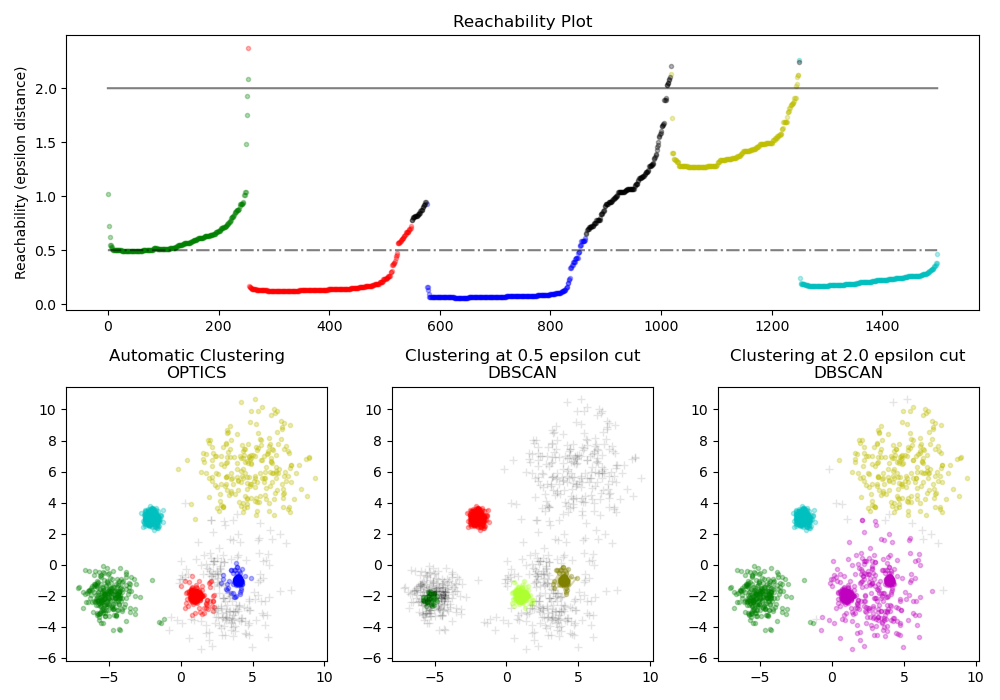
Расстояния достижимости, генерируемые OPTICS, позволяют извлекать кластеры с переменной плотностью в пределах одного набора данных. Как показано на приведенном выше графике, объединение расстояний достижимости и набора данных ordering_ дает график достижимости , где плотность точек представлена на оси Y, а точки упорядочены таким образом, что соседние точки являются смежными. «Вырезание» графика достижимости по одному значению дает результаты, подобные DBSCAN; все точки над «вырезом» классифицируются как шум, и каждый раз, когда есть перерыв при чтении слева направо, означает новый кластер. При извлечении кластеров по умолчанию с помощью OPTICS анализируются крутые уклоны на графике, чтобы найти кластеры, и пользователь может определить, что считается крутым уклоном, используя параметр xi. Существуют также другие возможности для анализа на самом графике, такие как создание иерархических представлений данных с помощью дендрограмм графика достижимости, а иерархия кластеров, обнаруженных алгоритмом, может быть доступна через cluster_hierarchy_ параметр. Приведенный выше график имеет цветовую кодировку, поэтому цвета кластеров в плоском пространстве соответствуют кластерам линейных сегментов на графике достижимости. Обратите внимание, что синий и красный кластеры находятся рядом на графике достижимости и могут быть иерархически представлены как дочерние элементы более крупного родительского кластера.
Сравнение с DBSCAN
Результаты cluster_optics_dbscan метода OPTICS и DBSCAN очень похожи, но не всегда идентичны; в частности, маркировка периферийных и шумовых точек. Отчасти это связано с тем, что первые образцы каждой плотной области, обработанной OPTICS, имеют большое значение достижимости, будучи близкими к другим точкам в своей области, и поэтому иногда будут помечены как шум, а не периферия. Это влияет на соседние точки, когда они рассматриваются как кандидаты на то, чтобы их пометить как периферию или как шум.
Обратите внимание, что для любого отдельного значения eps DBSCAN будет иметь более короткое время выполнения, чем OPTICS; однако для повторных запусков с разными eps значениями один запуск OPTICS может потребовать меньше совокупного времени выполнения, чем DBSCAN. Также важно отметить , что выход ОПТИКА» близок к DBSCAN, только если epsи max_eps близки.
Вычислительная сложность
Деревья пространственной индексации используются, чтобы избежать вычисления полной матрицы расстояний и обеспечить эффективное использование памяти для больших наборов выборок. С помощью metric ключевого слова можно указать различные метрики расстояния .
Для больших наборов данных аналогичные (но не идентичные) результаты можно получить с помощью HDBSCAN. Реализация HDBSCAN является многопоточной и имеет лучшую алгоритмическую сложность во время выполнения, чем OPTICS, за счет худшего масштабирования памяти. Для очень больших наборов данных, которые исчерпывают системную память с помощью HDBSCAN, OPTICS будет поддерживатьn (в отличие от $n^2$) масштабирование памяти; тем не менее, max_eps для получения решения в разумные сроки, вероятно, потребуется настройка параметра.
Рекомендации:
- «ОПТИКА: точки упорядочивания для определения структуры кластеризации». Анкерст, Михаэль, Маркус М. Бройниг, Ханс-Петер Кригель и Йорг Зандер. В ACM Sigmod Record, vol. 28, вып. 2. С. 49-60. ACM, 1999.
2.3.9. BIRCH (сбалансированное итеративное сокращение и кластеризация с использованием иерархий — balanced iterative reducing and clustering using hierarchies)
Для Birch заданных данных он строит дерево, называемое деревом функций кластеризации (CFT). Данные по существу сжимаются с потерями до набора узлов Clustering Feature (CF Nodes). Узлы CF имеют ряд подкластеров, называемых подкластерами функций кластеризации (подкластеры CF), и эти подкластеры CF, расположенные в нетерминальных узлах CF, могут иметь узлы CF в качестве дочерних.
Подкластеры CF содержат необходимую информацию для кластеризации, что избавляет от необходимости хранить все входные данные в памяти. Эта информация включает:
- Количество образцов в подкластере.
- Линейная сумма — n-мерный вектор, содержащий сумму всех выборок.
- Squared Sum — сумма квадратов нормы L2 всех выборок.
- Центроиды — чтобы избежать пересчета линейной суммы / n_samples.
- Квадратная норма центроидов.
Алгоритм BIRCH имеет два параметра: порог и коэффициент ветвления. Фактор ветвления ограничивает количество подкластеров в узле, а порог ограничивает расстояние между входящей выборкой и существующими подкластерами.
Этот алгоритм можно рассматривать как экземпляр или метод сокращения данных, поскольку он сокращает входные данные до набора подкластеров, которые получаются непосредственно из конечных точек CFT. Эти сокращенные данные могут быть дополнительно обработаны путем подачи их в глобальный кластеризатор. Этот глобальный кластеризатор может быть установлен с помощью n_clusters. Если n_clusters установлено значение None, подкластеры из листьев считываются напрямую, в противном случае шаг глобальной кластеризации помечает эти подкластеры в глобальные кластеры (метки), а выборки сопоставляются с глобальной меткой ближайшего подкластера.
Описание алгоритма:
- Новый образец вставляется в корень дерева CF, который является узлом CF. Затем он объединяется с подкластером корня, который имеет наименьший радиус после объединения, ограниченный пороговыми условиями и условиями фактора ветвления. Если у подкластера есть дочерний узел, то это повторяется до тех пор, пока он не достигнет листа. После нахождения ближайшего подкластера в листе свойства этого подкластера и родительских подкластеров рекурсивно обновляются.
- Если радиус подкластера, полученного путем слияния новой выборки и ближайшего подкластера, больше квадрата порога, и если количество подкластеров больше, чем коэффициент ветвления, то для этой новой выборки временно выделяется пространство. Берутся два самых дальних подкластера, и подкластеры делятся на две группы на основе расстояния между этими подкластерами.
- Если у этого разбитого узла есть родительский подкластер и есть место для нового подкластера, то родительский подкластер разбивается на два. Если места нет, то этот узел снова делится на две части, и процесс продолжается рекурсивно, пока не достигнет корня.
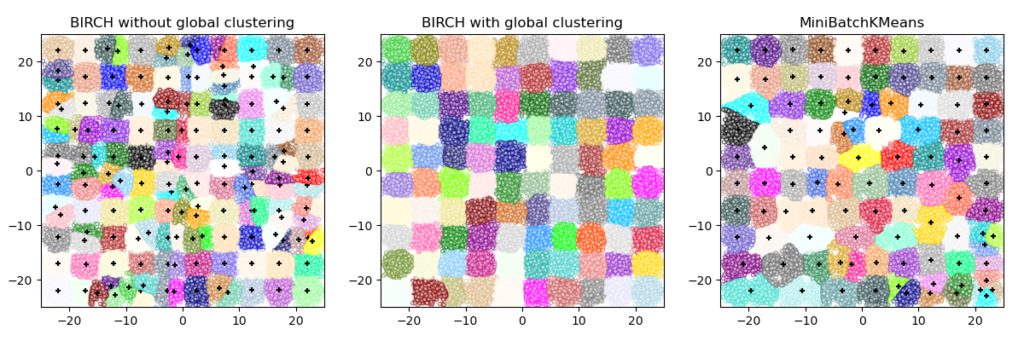
BIRCH или MiniBatchKMeans?
- BIRCH не очень хорошо масштабируется для данных большого размера. Как правило, если
n_featuresоно больше двадцати, лучше использовать MiniBatchKMeans. - Если количество экземпляров данных необходимо уменьшить или если требуется большое количество подкластеров в качестве этапа предварительной обработки или иным образом, BIRCH более полезен, чем MiniBatchKMeans.
Как использовать partial_fit?
Чтобы избежать вычисления глобальной кластеризации, при каждом обращении partial_fit пользователя рекомендуется
- Установить
n_clusters=Noneизначально - Обучите все данные несколькими вызовами partial_fit.
- Установите
n_clustersнеобходимое значение с помощьюbrc.set_params(n_clusters=n_clusters. - Вызов,
partial_fitнаконец, без аргументов, т.е.brc.partial_fit()который выполняет глобальную кластеризацию.
Рекомендации:
- Тиан Чжан, Рагху Рамакришнан, Марон Ливни БЕРЕЗА: эффективный метод кластеризации данных для больших баз данных. https://www.cs.sfu.ca/CourseCentral/459/han/papers/zhang96.pdf
- Роберто Пердиши JBirch — Java-реализация алгоритма кластеризации BIRCH https://code.google.com/archive/p/jbirch
2.3.10. Оценка эффективности кластеризации
Оценка производительности алгоритма кластеризации не так тривиальна, как подсчет количества ошибок или точности и отзыва контролируемого алгоритма классификации. В частности, любая метрика оценки должна учитывать не абсолютные значения меток кластера, а, скорее, если эта кластеризация определяет разделения данных, аналогичные некоторому основному набору истинных классов или удовлетворяющему некоторому предположению, так что члены, принадлежащие к одному классу, более похожи чем члены разных классов в соответствии с некоторой метрикой сходства.
2.3.10.1. Индекс Rand
Учитывая знания о назначениях базовых классов истинности labels_true и назначениях нашим алгоритмом кластеризации одних и тех же выборок labels_pred, (скорректированный или нескорректированный) индекс Рэнда — это функция, которая измеряет сходство двух назначений, игнорируя перестановки:
>>> from sklearn import metrics >>> labels_true = [0, 0, 0, 1, 1, 1] >>> labels_pred = [0, 0, 1, 1, 2, 2] >>> metrics.rand_score(labels_true, labels_pred) 0.66...
Индекс Rand не гарантирует получение значения, близкого к 0,0 при случайной маркировке. Скорректированный индекс Rand вносит поправку на случайность и дает такую основу.
>>> metrics.adjusted_rand_score(labels_true, labels_pred) 0.24...
Как и в случае со всеми метриками кластеризации, можно переставить 0 и 1 в предсказанных метках, переименовать 2 в 3 и получить ту же оценку:
>>> labels_pred = [1, 1, 0, 0, 3, 3] >>> metrics.rand_score(labels_true, labels_pred) 0.66... >>> metrics.adjusted_rand_score(labels_true, labels_pred) 0.24...
Более того, оба rand_score adjusted_rand_score они симметричны : замена аргумента не меняет оценок. Таким образом, их можно использовать в качестве критериев консенсуса:
>>> metrics.rand_score(labels_pred, labels_true) 0.66... >>> metrics.adjusted_rand_score(labels_pred, labels_true) 0.24...
Идеальная маркировка оценивается в 1,0:
>>> labels_pred = labels_true[:] >>> metrics.rand_score(labels_true, labels_pred) 1.0 >>> metrics.adjusted_rand_score(labels_true, labels_pred) 1.0
Плохо согласованные ярлыки (например, независимые ярлыки) имеют более низкие оценки, а для скорректированного индекса Rand оценка будет отрицательной или близкой к нулю. Однако для нескорректированного индекса Rand оценка, хотя и ниже, не обязательно будет близка к нулю:
>>> labels_true = [0, 0, 0, 0, 0, 0, 1, 1] >>> labels_pred = [0, 1, 2, 3, 4, 5, 5, 6] >>> metrics.rand_score(labels_true, labels_pred) 0.39... >>> metrics.adjusted_rand_score(labels_true, labels_pred) -0.07...
2.3.10.1.1. Преимущества
- Интерпретируемость : нескорректированный индекс Рэнда пропорционален количеству пар выборок, метки которых одинаковы в обоих
labels_predи /labels_trueили различаются в обоих. - Случайные (единообразные) присвоения меток имеют скорректированный балл индекса Rand, близкий к 0,0 для любого значения
n_clustersиn_samples(что не относится, например, к нескорректированному индексу Rand или V-мере). - Ограниченный диапазон : более низкие значения указывают на разные маркировки, аналогичные кластеры имеют высокий (скорректированный или нескорректированный) индекс Rand, 1,0 — это оценка идеального соответствия. Диапазон оценок составляет [0, 1] для нескорректированного индекса Rand и [-1, 1] для скорректированного индекса Rand.
- Не делается никаких предположений о структуре кластера: (скорректированный или нескорректированный) индекс Rand может использоваться для сравнения всех видов алгоритмов кластеризации и может использоваться для сравнения алгоритмов кластеризации, таких как k-средних, который предполагает изотропные формы капли с результатами спектрального анализа. алгоритмы кластеризации, которые могут найти кластер со «сложенными» формами.
2.3.10.1.2. Недостатки
- Вопреки инерции, (скорректированный или нескорректированный) индекс Рэнда требует знания основных классов истинности, что почти никогда не доступно на практике или требует ручного назначения аннотаторами-людьми (как в условиях контролируемого обучения). Однако (скорректированный или нескорректированный) индекс Rand также может быть полезен в чисто неконтролируемой настройке в качестве строительного блока для консенсусного индекса, который может использоваться для выбора модели кластеризации (TODO).
- Нескорректированный индекс Rand часто близко к 1,0 , даже если самим кластеризациям существенно различаются. Это можно понять, интерпретируя индекс Рэнда как точность маркировки пар элементов, полученную в результате кластеризации: на практике часто существует большинство пар элементов, которым присваивается
differentметка пары как при прогнозируемой, так и при базовой кластеризации истинности, что приводит к высокой доля парных меток, которые согласны, что впоследствии приводит к высокой оценке.
Примеры:
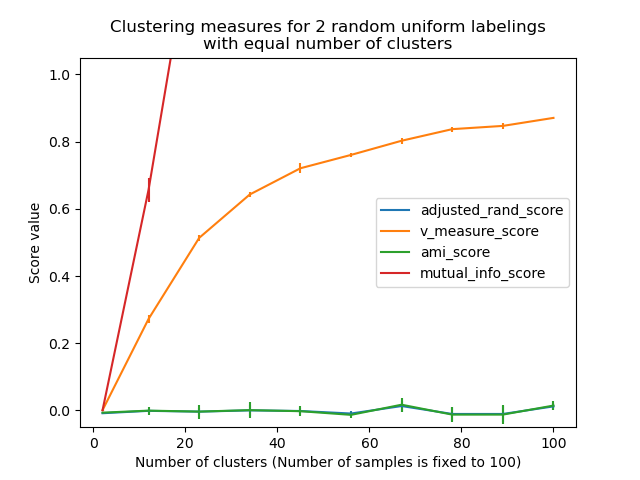
- Поправка на случайность при оценке производительности кластеризации : анализ влияния размера набора данных на значение показателей кластеризации для случайных назначений.
2.3.10.1.3. Математическая постановка
Если C — это наземное присвоение класса истинности, а K — кластеризация, давайте определим $a$ и $b$ в виде:
- $a$, количество пар элементов, которые находятся в одном наборе в C и в одном наборе в K
- $b$, количество пар элементов, которые находятся в разных наборах в C и в разных наборах в K
Затем нескорректированный индекс Рэнда рассчитывается следующим образом: $$text{RI} = frac{a + b}{C_2^{n_{samples}}}$$
где $C_2^{n_{samples}}$ — общее количество возможных пар в наборе данных. Не имеет значения, выполняется ли расчет для упорядоченных пар или неупорядоченных пар, если расчет выполняется последовательно.
Однако индекс Rand не гарантирует, что случайные присвоения меток получат значение, близкое к нулю (особенно, если количество кластеров имеет тот же порядок величины, что и количество выборок).
Чтобы противостоять этому эффекту, мы можем дисконтировать ожидаемый RI. $E[text{RI}]$ случайных маркировок путем определения скорректированного индекса Rand следующим образом: $$text{ARI} = frac{text{RI} — E[text{RI}]}{max(text{RI}) — E[text{RI}]}$$
Рекомендации
- Сравнение разделов Л. Хуберт и П. Араби, Журнал классификации 1985 г.
- Свойства скорректированного индекса Рэнда Хьюберта- Араби Д. Стейнли, Психологические методы, 2004 г.
- Запись в Википедии для индекса Rand
- Запись в Википедии о скорректированном индексе Рэнда
2.3.10.2. Оценки на основе взаимной информации
Учитывая знания о назначениях базовых классов истинности labels_true и назначениях нашим алгоритмом кластеризации одних и тех же выборок labels_pred, взаимная информация — это функция, которая измеряет согласованность двух назначений, игнорируя перестановки. Доступны две различные нормализованные версии этой меры: нормализованная взаимная информация (NMI) и скорректированная взаимная информация (AMI) . NMI часто используется в литературе, в то время как AMI был предложен совсем недавно и нормируется на случайность :
>>> from sklearn import metrics >>> labels_true = [0, 0, 0, 1, 1, 1] >>> labels_pred = [0, 0, 1, 1, 2, 2] >>> metrics.adjusted_mutual_info_score(labels_true, labels_pred) 0.22504...
Можно переставить 0 и 1 в предсказанных метках, переименовать 2 в 3 и получить тот же результат:
>>> labels_pred = [1, 1, 0, 0, 3, 3] >>> metrics.adjusted_mutual_info_score(labels_true, labels_pred) 0.22504...
Все, mutual_info_score, adjusted_mutual_info_scoreи normalized_mutual_info_scoreявляется симметричным: замена аргумента не меняет рейтинг. Таким образом, их можно использовать в качестве меры консенсуса :
>>> metrics.adjusted_mutual_info_score(labels_pred, labels_true) 0.22504...
Идеальная маркировка оценивается в 1,0:
>>> labels_pred = labels_true[:] >>> metrics.adjusted_mutual_info_score(labels_true, labels_pred) 1.0 >>> metrics.normalized_mutual_info_score(labels_true, labels_pred) 1.0
Это неверно mutual_info_score, поэтому судить о них труднее:
>>> metrics.mutual_info_score(labels_true, labels_pred) 0.69...
Плохие (например, независимые маркировки) имеют отрицательные оценки:
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1] >>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2] >>> metrics.adjusted_mutual_info_score(labels_true, labels_pred) -0.10526...
2.3.10.2.1. Преимущества
- Случайные (унифицированные) присвоения меток имеют оценку AMI, близкую к 0,0 для любого значения
n_clustersиn_samples(что не относится, например, к необработанной взаимной информации или V-мере). - Верхняя граница 1 : значения, близкие к нулю, указывают на два назначения меток, которые в значительной степени независимы, а значения, близкие к единице, указывают на значительное согласие. Кроме того, AMI, равный ровно 1, указывает, что два присвоения меток равны (с перестановкой или без нее).
2.3.10.2.2. Недостатки
- Вопреки инерции, меры на основе MI требуют знания основных классов истинности, хотя на практике они почти никогда не доступны или требуют ручного назначения аннотаторами-людьми (как в условиях контролируемого обучения).
Однако показатели на основе MI также могут быть полезны в чисто неконтролируемой настройке в качестве строительного блока для согласованного индекса, который можно использовать для выбора модели кластеризации
- NMI и MI не подвергаются случайной корректировке.
Примеры:
- Поправка на случайность при оценке производительности кластеризации: анализ влияния размера набора данных на значение показателей кластеризации для случайных назначений. Этот пример также включает скорректированный индекс ранда.
2.3.10.2.3. Математическая постановка
Предположим, что два присвоения метки (одних и тех же N объектов), $U$ а также $V$. Их энтропия — это величина неопределенности для набора разбиений, определяемая следующим образом:
$$H(U) = — sum_{i=1}^{|U|}P(i)log(P(i))$$
где $P(i) = |U_i| / N$ вероятность того, что объект выбран наугад из $U$ попадает в класс $U_i$. Аналогично дляV:
$$H(V) = — sum_{j=1}^{|V|}P'(j)log(P'(j))$$
С участием $P'(j) = |V_j| / N$. Взаимная информация (MI) между $U$ и $V$ рассчитывается по:
$$text{MI}(U, V) = sum_{i=1}^{|U|}sum_{j=1}^{|V|}P(i, j)logleft(frac{P(i,j)}{P(i)P'(j)}right)$$
где $P(i, j) = |U_i cap V_j| / N$ вероятность того, что случайно выбранный объект попадает в оба класса $U_i$ а также $V_j$.
Это также может быть выражено в формулировке множества элементов:
$$text{MI}(U, V) = sum_{i=1}^{|U|} sum_{j=1}^{|V|} frac{|U_i cap V_j|}{N}logleft(frac{N|U_i cap V_j|}{|U_i||V_j|}right)$$
Нормализованная взаимная информация определяется как
$$text{NMI}(U, V) = frac{text{MI}(U, V)}{text{mean}(H(U), H(V))}$$
Это значение взаимной информации, а также нормализованного варианта не скорректировано на случайность и будет иметь тенденцию к увеличению по мере увеличения количества различных меток (кластеров), независимо от фактического количества «взаимной информации» между назначениями меток.
Ожидаемое значение для взаимной информации можно рассчитать с помощью следующего уравнения [VEB2009] . В этом уравнении $a_i = |U_i|$ (количество элементов в $U_i$) а также $b_j = |V_j|$ (количество элементов в $V_j$).
$$E[text{MI}(U,V)]=sum_{i=1}^{|U|} sum_{j=1}^{|V|} sum_{n_{ij}=(a_i+b_j-N)^+ }^{min(a_i, b_j)} frac{n_{ij}}{N}log left( frac{ N.n_{ij}}{a_i b_j}right) frac{a_i!b_j!(N-a_i)!(N-b_j)!}{N!n_{ij}!(a_i-n_{ij})!(b_j-n_{ij})! (N-a_i-b_j+n_{ij})!}$$
Используя ожидаемое значение, скорректированная взаимная информация может быть затем рассчитана с использованием формы, аналогичной форме скорректированного индекса Rand:
$$text{AMI} = frac{text{MI} — E[text{MI}]}{text{mean}(H(U), H(V)) — E[text{MI}]}$$
Для нормализованной взаимной информации и скорректированной взаимной информации нормализующее значение обычно представляет собой некоторое обобщенное среднее энтропий каждой кластеризации. Существуют различные обобщенные средства, и не существует твердых правил предпочтения одного по сравнению с другим. Решение в основном принимается отдельно для каждого поля; например, при обнаружении сообществ чаще всего используется среднее арифметическое. Каждый метод нормализации обеспечивает «качественно похожее поведение» [YAT2016] . В нашей реализации это контролируется average_methodпараметром.
Vinh et al. (2010) назвали варианты NMI и AMI методом их усреднения [VEB2010] . Их средние «sqrt» и «sum» являются средними геометрическими и арифметическими; мы используем эти более общие имена.
2.3.10.3. Однородность, полнота и V-мера
Зная о назначении основных классов истинности выборкам, можно определить некоторую интуитивно понятную метрику, используя условный энтропийный анализ.
В частности, Розенберг и Хиршберг (2007) определяют следующие две желательные цели для любого кластерного задания:
- однородность : каждый кластер содержит только членов одного класса.
- полнота : все члены данного класса относятся к одному кластеру.
Мы можем превратить эти концепции в партитуры homogeneity_score и completeness_score. Оба ограничены снизу 0,0 и выше 1,0 (чем выше, тем лучше):
>>> from sklearn import metrics >>> labels_true = [0, 0, 0, 1, 1, 1] >>> labels_pred = [0, 0, 1, 1, 2, 2] >>> metrics.homogeneity_score(labels_true, labels_pred) 0.66... >>> metrics.completeness_score(labels_true, labels_pred) 0.42...
Их гармоническое среднее значение, называемое V-мерой , вычисляется по формуле v_measure_score:
>>> metrics.v_measure_score(labels_true, labels_pred) 0.51...
Формула этой функции выглядит следующим образом:
$$v = frac{(1 + beta) times text{homogeneity} times text{completeness}}{(beta times text{homogeneity} + text{completeness})}$$
beta по умолчанию используется значение 1.0, но для использования значения менее 1 для бета-версии:
>>> metrics.v_measure_score(labels_true, labels_pred, beta=0.6) 0.54...
больший вес будет приписан однородности, а использование значения больше 1:
>>> metrics.v_measure_score(labels_true, labels_pred, beta=1.8) 0.48...
больший вес будет приписан полноте.
V-мера фактически эквивалентна описанной выше взаимной информации (NMI), при этом функция агрегирования является средним арифметическим [B2011] .
Однородность, полнота и V-мера могут быть вычислены сразу, используя homogeneity_completeness_v_measure следующее:
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred) (0.66..., 0.42..., 0.51...)
Следующее назначение кластеризации немного лучше, поскольку оно однородное, но не полное:
>>> labels_pred = [0, 0, 0, 1, 2, 2] >>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred) (1.0, 0.68..., 0.81...)
Примечание:
v_measure_score является симметричным : его можно использовать для оценки соответствия двух независимых присвоений одному и тому же набору данных.
Это не относится к completeness_score и homogeneity_score: оба связаны отношениями:
homogeneity_score(a, b) == completeness_score(b, a)
2.3.10.3.1. Преимущества
- Ограниченные баллы : 0,0 — это настолько плохо, насколько это возможно, 1,0 — идеальный балл.
- Интуитивная интерпретация: кластеризацию с плохой V-мерой можно качественно проанализировать с точки зрения однородности и полноты, чтобы лучше понять, какие «ошибки» допускаются при задании.
- Не делается никаких предположений о структуре кластера : может использоваться для сравнения алгоритмов кластеризации, таких как k-среднее, которое предполагает изотропные формы капли, с результатами алгоритмов спектральной кластеризации, которые могут находить кластер со «сложенными» формами.
2.3.10.3.2. Недостатки
- Ранее введенные метрики не нормализованы в отношении случайной маркировки : это означает, что в зависимости от количества выборок, кластеров и основных классов истинности полностью случайная маркировка не всегда будет давать одинаковые значения для однородности, полноты и, следовательно, v-меры.
В частности, случайная маркировка не даст нулевых оценок, особенно когда количество кластеров велико. Эту проблему можно спокойно игнорировать, если количество выборок больше тысячи, а количество кластеров меньше 10. Для меньших размеров выборки или большего количества кластеров безопаснее использовать скорректированный индекс, такой как Скорректированный индекс ранда (ARI) .
- Эти метрики требуют знания основных классов истинности, хотя почти никогда не доступны на практике или требуют ручного назначения аннотаторами-людьми (как в условиях контролируемого обучения).
Примеры:
- Поправка на случайность при оценке производительности кластеризации : анализ влияния размера набора данных на значение показателей кластеризации для случайных назначений.
2.3.10.3.3. Математическая постановка
Оценки однородности и полноты формально даются по формуле:
$$h = 1 — frac{H(C|K)}{H(C)}$$
$$c = 1 — frac{H(K|C)}{H(K)}$$
где $H(C|K)$ является условной энтропией классов с учетом кластерных назначений и определяется выражением:
$$H(C|K) = — sum_{c=1}^{|C|} sum_{k=1}^{|K|} frac{n_{c,k}}{n} cdot logleft(frac{n_{c,k}}{n_k}right)$$
а также $H(C)$ — энтропия классов и определяется выражением:
$$H(C) = — sum_{c=1}^{|C|} frac{n_c}{n} cdot logleft(frac{n_c}{n}right)$$
с участием n общее количество образцов, $n_c$ а также $n_k$ количество образцов, соответственно принадлежащих к классу c и кластер $k$, и наконец $n_{c, k}$ количество образцов из класса c назначен кластеру k.
Условная энтропия кластеров данного класса $H(C|K)$ и энтропия кластеров $H(K)$ определены симметричным образом.
Розенберг и Хиршберг далее определяют V-меру как гармоническое среднее однородности и полноты:
$$v = 2 cdot frac{h cdot c}{h + c}$$
2.3.10.4. Результаты Фаулкса-Мэллоуса
Индекс Фаулкса-Мэллоуса ( sklearn.metrics.fowlkes_mallows_score) может использоваться, когда известны наземные присвоения классов истинности выборкам. FMI по шкале Fowlkes-Mallows определяется как среднее геометрическое для попарной точности и отзыва:
$$text{FMI} = frac{text{TP}}{sqrt{(text{TP} + text{FP}) (text{TP} + text{FN})}}$$
Где TP— количество истинных положительных результатов (True Positive) (т.е. количество пар точек, принадлежащих одним и тем же кластерам как в истинных, так и в предсказанных метках), FP— это количество ложных положительных результатов (False Positive) (то есть количество пар точек, принадлежащих к одинаковые кластеры в истинных метках, а не в предсказанных метках) и FN является количеством ложно-отрицательных (False Negative) (т. е. количеством пар точек, принадлежащих одним и тем же кластерам в предсказанных метках, а не в истинных метках).
Оценка варьируется от 0 до 1. Высокое значение указывает на хорошее сходство между двумя кластерами.
>>> from sklearn import metrics >>> labels_true = [0, 0, 0, 1, 1, 1] >>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred) 0.47140...
Можно переставить 0 и 1 в предсказанных метках, переименовать 2 в 3 и получить тот же результат:
>>> labels_pred = [1, 1, 0, 0, 3, 3] >>> metrics.fowlkes_mallows_score(labels_true, labels_pred) 0.47140...
Идеальная маркировка оценивается в 1,0:
>>> labels_pred = labels_true[:] >>> metrics.fowlkes_mallows_score(labels_true, labels_pred) 1.0
Плохие (например, независимые маркировки) имеют нулевые баллы:
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1] >>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2] >>> metrics.fowlkes_mallows_score(labels_true, labels_pred) 0.0
2.3.10.4.1. Преимущества
- Случайное (единообразное) присвоение меток имеет оценку FMI, близкую к 0,0 для любого значения
n_clustersиn_samples(что не относится, например, к необработанной взаимной информации или V-мере). - Верхний предел — 1 : значения, близкие к нулю, указывают на два назначения меток, которые в значительной степени независимы, а значения, близкие к единице, указывают на значительное согласие. Кроме того, значения ровно 0 указывают на чисто независимые присвоения меток, а FMI ровно 1 указывает, что два назначения меток равны (с перестановкой или без нее).
- Не делается никаких предположений о структуре кластера : может использоваться для сравнения алгоритмов кластеризации, таких как k-среднее, которое предполагает изотропные формы капли, с результатами алгоритмов спектральной кластеризации, которые могут находить кластер со «сложенными» формами.
2.3.10.4.2. Недостатки
- Вопреки инерции, меры, основанные на FMI, требуют знания основных классов истинности, хотя почти никогда не доступны на практике или требуют ручного назначения аннотаторами-людьми (как в условиях контролируемого обучения).
Рекомендации
- EB Fowkles и CL Mallows, 1983. «Метод сравнения двух иерархических кластеров». Журнал Американской статистической ассоциации. http://wildfire.stat.ucla.edu/pdflibrary/fowlkes.pdf
- Запись в Википедии об Индексе Фаулкса-Маллоуза
2.3.10.5. Коэффициент силуэта
Если наземные метки достоверности неизвестны, оценка должна выполняться с использованием самой модели. Коэффициент силуэта ( sklearn.metrics.silhouette_score) является примером такой оценки, где более высокий показатель коэффициента силуэта относится к модели с лучше определенными кластерами. Коэффициент силуэта определяется для каждого образца и состоит из двух баллов:
- a : Среднее расстояние между образцом и всеми другими точками того же класса.
- b : Среднее расстояние между образцом и всеми другими точками в следующем ближайшем кластере .
Тогда коэффициент силуэта s для одного образца определяется как:
$$s = frac{b — a}{max(a, b)}$$
Коэффициент силуэта для набора образцов дается как среднее значение коэффициента силуэта для каждого образца.
>>> from sklearn import metrics >>> from sklearn.metrics import pairwise_distances >>> from sklearn import datasets >>> X, y = datasets.load_iris(return_X_y=True)
При обычном использовании коэффициент силуэта применяется к результатам кластерного анализа.
>>> import numpy as np >>> from sklearn.cluster import KMeans >>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X) >>> labels = kmeans_model.labels_ >>> metrics.silhouette_score(X, labels, metric='euclidean') 0.55...
Рекомендации
- Питер Дж. Руссеу (1987). «Силуэты: графическое средство для интерпретации и проверки кластерного анализа». Вычислительная и прикладная математика 20: 53–65. DOI: 10.1016 / 0377-0427 (87) 90125-7 .
2.3.10.5.1. Преимущества
- Оценка ограничена от -1 за неправильную кластеризацию до +1 за высокоплотную кластеризацию. Баллы около нуля указывают на перекрывающиеся кластеры.
- Оценка выше, когда кластеры плотные и хорошо разделенные, что относится к стандартной концепции кластера.
2.3.10.5.2. Недостатки
- Коэффициент силуэта обычно выше для выпуклых кластеров, чем для других концепций кластеров, таких как кластеры на основе плотности, подобные тем, которые получены с помощью DBSCAN.
Примеры:
- Выбор количества кластеров с анализом силуэта в кластеризации KMeans : в этом примере анализ силуэта используется для выбора оптимального значения для n_clusters.
2.3.10.6. Индекс Калински-Харабаса
Если наземные метки достоверности неизвестны, индекс Калински-Харабаса ( sklearn.metrics.calinski_harabasz_score) — также известный как критерий отношения дисперсии — можно использовать для оценки модели, где более высокий балл Калински-Харабаса относится к модели с более определенными кластерами.
Индекс представляет собой отношение суммы дисперсии между кластерами и дисперсии внутри кластера для всех кластеров (где дисперсия определяется как сумма квадратов расстояний):
>>> from sklearn import metrics >>> from sklearn.metrics import pairwise_distances >>> from sklearn import datasets >>> X, y = datasets.load_iris(return_X_y=True)
При обычном использовании индекс Калински-Харабаса применяется к результатам кластерного анализа:
>>> import numpy as np >>> from sklearn.cluster import KMeans >>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X) >>> labels = kmeans_model.labels_ >>> metrics.calinski_harabasz_score(X, labels) 561.62...
2.3.10.6.1. Преимущества
- Оценка выше, когда кластеры плотные и хорошо разделенные, что относится к стандартной концепции кластера.
- Счет быстро подсчитывается.
2.3.10.6.2. Недостатки
- Индекс Калински-Харабаса обычно выше для выпуклых кластеров, чем для других концепций кластеров, таких как кластеры на основе плотности, подобные тем, которые получены с помощью DBSCAN.
2.3.10.6.3. Математическая постановка
Для набора данных $E$ размера $n_E$ который был сгруппирован в $k$ кластеры, оценка Калински-Харабаса $s$ определяется как отношение средней дисперсии между кластерами и дисперсии внутри кластера:
$$s = frac{mathrm{tr}(B_k)}{mathrm{tr}(W_k)} times frac{n_E — k}{k — 1}$$
где $tr(B_k)$ является следом межгрупповой дисперсионной матрицы и $tr(W_k)$ является следом матрицы дисперсии внутри кластера, определяемой следующим образом:
$$W_k = sum_{q=1}^k sum_{x in C_q} (x — c_q) (x — c_q)^T$$
$$B_k = sum_{q=1}^k n_q (c_q — c_E) (c_q — c_E)^T$$
с участием $C_q$ набор точек в кластере $q$, $c_q$ центр кластера $q$, $c_E$ центр $E$, а также $n_q$ количество точек в кластере $q$.
Рекомендации
- Калински Т. и Харабаш Дж. (1974). «Дендритный метод кластерного анализа» . Коммуникации в теории статистики и методах 3: 1-27. DOI: 10.1080 / 03610927408827101 .
2.3.10.7. Индекс Дэвиса-Болдина
Если наземные метки истинности неизвестны, для оценки модели можно использовать индекс Дэвиса-Болдина (sklearn.metrics.davies_bouldin_score), где более низкий индекс Дэвиса-Болдина относится к модели с лучшим разделением между кластерами.
Этот индекс означает среднее «сходство» между кластерами, где сходство — это мера, которая сравнивает расстояние между кластерами с размером самих кластеров.
Ноль — это наименьший возможный результат. Значения, близкие к нулю, указывают на лучшее разделение.
При обычном использовании индекс Дэвиса-Болдина применяется к результатам кластерного анализа следующим образом:
>>> from sklearn import datasets >>> iris = datasets.load_iris() >>> X = iris.data >>> from sklearn.cluster import KMeans >>> from sklearn.metrics import davies_bouldin_score >>> kmeans = KMeans(n_clusters=3, random_state=1).fit(X) >>> labels = kmeans.labels_ >>> davies_bouldin_score(X, labels) 0.6619...
2.3.10.7.1. Преимущества
- Вычисление Дэвиса-Боулдина проще, чем оценка Силуэта.
- В индексе вычисляются только количества и характеристики, присущие набору данных.
2.3.10.7.2. Недостатки
- Индекс Дэвиса-Боулдинга обычно выше для выпуклых кластеров, чем для других концепций кластеров, таких как кластеры на основе плотности, подобные тем, которые получены из DBSCAN.
- Использование центроидного расстояния ограничивает метрику расстояния евклидовым пространством.
2.3.10.7.3. Математическая постановка
Индекс определяется как среднее сходство между каждым кластером. $C_i$ для $i=1, …, k$ и его самый похожий $C_j$. В контексте этого индекса сходство определяется как мера $R_{ij}$ что торгуется:
- $s_i$, среднее расстояние между каждой точкой кластера $i$ и центроид этого кластера — также известный как диаметр кластера.
- $d_{ij}$, расстояние между центрами скоплений $i$ а также $j$.
Простой выбор для построения $R_{ij}$ так что он неотрицателен и симметричен:
$$R_{ij} = frac{s_i + s_j}{d_{ij}}$$
Тогда индекс Дэвиса-Болдина определяется как:
$$DB = frac{1}{k} sum_{i=1}^k max_{i neq j} R_{ij}$$
Рекомендации
- Дэвис, Дэвид Л .; Боулдин, Дональд В. (1979). «Мера разделения кластеров» IEEE-транзакции по анализу шаблонов и машинному интеллекту. ПАМИ-1 (2): 224-227. DOI: 10.1109 / TPAMI.1979.4766909 .
- Халкиди, Мария; Батистакис, Яннис; Вазиргианнис, Михалис (2001). «О методах кластеризации валидации» Журнал интеллектуальных информационных систем, 17 (2-3), 107-145. DOI: 10,1023 / А: 1012801612483 .
- Запись в Википедии для индекса Дэвиса-Болдина .
2.3.10.8. Матрица непредвиденных обстоятельств
Матрица непредвиденных обстоятельств ( sklearn.metrics.cluster.contingency_matrix) сообщает мощность пересечения для каждой истинной / прогнозируемой пары кластеров. Матрица непредвиденных обстоятельств обеспечивает достаточную статистику для всех метрик кластеризации, где выборки независимы и одинаково распределены, и нет необходимости учитывать некоторые экземпляры, которые не были кластеризованы.
Вот пример:
>>> from sklearn.metrics.cluster import contingency_matrix
>>> x = ["a", "a", "a", "b", "b", "b"]
>>> y = [0, 0, 1, 1, 2, 2]
>>> contingency_matrix(x, y)
array([[2, 1, 0],
[0, 1, 2]])
Первая строка выходного массива указывает, что есть три образца, истинный кластер которых равен «a». Из них два находятся в предсказанном кластере 0, один — в 1 и ни один — в 2. И вторая строка указывает, что есть три выборки, истинный кластер которых равен «b». Из них ни один не находится в прогнозируемом кластере 0, один — в 1, а два — в 2.
Матрица неточностей для классификации является квадратной матрицей непредвиденной где порядок строк и столбцов соответствует списку классов.
2.3.10.8.1. Преимущества
- Позволяет изучить распространение каждого истинного кластера по прогнозируемым кластерам и наоборот.
- Вычисленная таблица непредвиденных обстоятельств обычно используется при вычислении статистики сходства (как и другие, перечисленные в этом документе) между двумя кластерами.
2.3.10.8.2. Недостатки
- Матрицу непредвиденных обстоятельств легко интерпретировать для небольшого количества кластеров, но становится очень трудно интерпретировать для большого количества кластеров.
- Он не дает ни одной метрики для использования в качестве цели для оптимизации кластеризации.
2.3.10.9. Матрица неточности пар
Матрица смешения пар ( sklearn.metrics.cluster.pair_confusion_matrix) представляет собой матрицу подобия 2×2
$$begin{split}C = left[begin{matrix}
C_{00} & C_{01}
C_{10} & C_{11}
end{matrix}right]end{split}$$
между двумя кластерами, вычисленными путем рассмотрения всех пар выборок и подсчета пар, которые назначены в один и тот же или в разные кластеры в рамках истинной и прогнозируемой кластеризации.
В нем есть следующие записи:
$C_{00}$: количество пар с обеими кластерами, в которых образцы не сгруппированы вместе
$C_{10}$: количество пар с истинной кластеризацией меток, в которых образцы сгруппированы вместе, но в другой кластеризации образцы не сгруппированы вместе
$C_{01}$: количество пар с истинной кластеризацией меток, в которых образцы не сгруппированы вместе, а другая кластеризация содержит образцы, сгруппированные вместе
$C_{11}$: количество пар с обеими кластерами, имеющими образцы, сгруппированные вместе
Если рассматривать пару образцов, сгруппированных вместе как положительную пару, то, как и в бинарной классификации, количество истинных отрицательных значений равно $C_{00}$, ложноотрицательные $C_{10}$, истинные положительные стороны $C_{11}$ а ложные срабатывания $C_{01}$.
Идеально совпадающие метки имеют все ненулевые записи на диагонали независимо от фактических значений меток:
>>> from sklearn.metrics.cluster import pair_confusion_matrix
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 1])
array([[8, 0],
[0, 4]])
>>> pair_confusion_matrix([0, 0, 1, 1], [1, 1, 0, 0])
array([[8, 0],
[0, 4]])
Метки, которые назначают все члены классов одним и тем же кластерам, являются полными, но не всегда могут быть чистыми, следовательно, наказываются и имеют некоторые недиагональные ненулевые записи:
>>> pair_confusion_matrix([0, 0, 1, 2], [0, 0, 1, 1])
array([[8, 2],
[0, 2]])
Матрица не симметрична:
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 2])
array([[8, 0],
[2, 2]])
Если члены классов полностью разделены по разным кластерам, назначение полностью неполное, следовательно, матрица имеет все нулевые диагональные элементы:
>>> pair_confusion_matrix([0, 0, 0, 0], [0, 1, 2, 3])
array([[ 0, 0],
[12, 0]])
Рекомендации
- Л. Хьюберт и П. Араби, Сравнение разделов, журнал классификации 1985 < https://link.springer.com/article/10.1007%2FBF01908075 > _