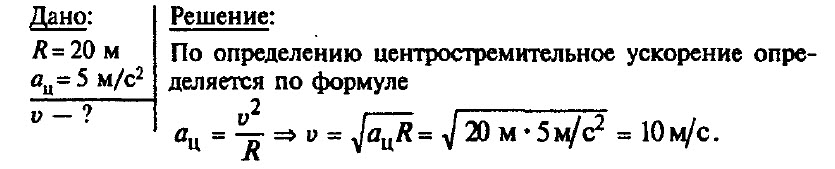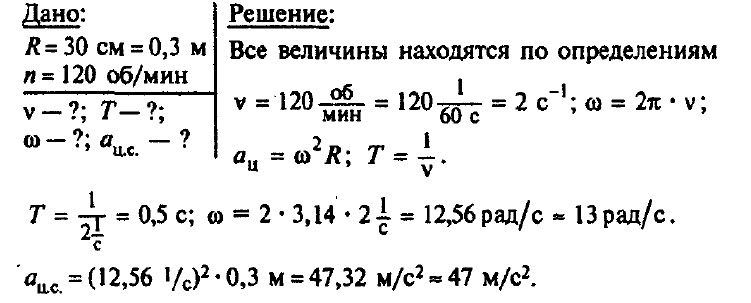Всего: 9 1–9
Добавить в вариант
Центростремительное ускорение при движении по окружности (в м/c2 ) можно вычислить по формуле где
— угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
Центростремительное ускорение (в м/c2) вычисляется по формуле α = ω2R, где ω — угловая скорость (в с–1), R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 10 с–1, а центростремительное ускорение равно 54 м/c2.
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a = ω2R, где ω — угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 4 с−1, а центростремительное ускорение равно 48 м/с2. Ответ дайте в метрах.
Из формулы центростремительного ускорения a = ω2R найдите R (в метрах), если ω = 4 с−1 и a = 64 м/с2.
Центростремительное ускорение (в м/c2) вычисляется по формуле α = ω2R, где ω — угловая скорость (в с–1), R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 5 с–1, а центростремительное ускорение равно 35 м/c2.
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a = ω2R, где ω — угловая скорость (в с −1), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с−1, а центростремительное ускорение равно 289 м/с2.
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a = ω2R, где ω — угловая скорость (в с −1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 9 с−1, а центростремительное ускорение равно 648 м/с2.
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a = ω2R, где ω — угловая скорость (в с −1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 5,5 с−1, а центростремительное ускорение равно 60,5 м/с2.
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a = ω2R, где ω — угловая скорость (в с −1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 4 с−1, а центростремительное ускорение равно 64 м/с2.
Всего: 9 1–9
Центростремительное движение по окружности огэ
Задача 8. (Центростремительное ускорение)
(Приведено решение в общем виде, с выводом конечной формулы)
Материальная точка вращается по окружности радиусом ( R=2 м ), с периодом (T=6,28 с )
Найти центростремительное ускорение этой точки.
Принять ( pi=3,14 )
Показать ответ Показать решение Видеорешение
Ответ: ( a_<цс>= 2 м/с^2 )
Приведено решение для тех, кто хочет научиться решать сложные задачи
Длина окружности рассчитывается по формуле:
Пройденный путь рассчитывается по формуле:
За время равное периоду (T ) точка совершает один оборот, то есть проходит расстояние, равное длине окружности (l)
( a_<цс>= dfrac<4 pi^2 R> = 4R left( dfrac< pi > right )^2= 4 cdot 2 cdot left( dfrac< 3,14 > <6,28>right )^2= 2 м/с^2 )
Ответ: ( a_<цс>= 2 м/с^2 )
Задача 10. (Центростремительное ускорение)
(Приведено простенькое решение для тех, кому тяжело разобраться) Ниже будет разобрана эта же задача в общем виде.
Найти центростремительное ускорение крайней точки секундной стрелки настенных часов, если ее длина составляет 10 сантиметров . Принять ( pi=3,14 )
Дать ответ в системе СИ, округлить до тысячных.
Показать ответ Показать решение Видеорешение
Ответ: ( a_<цс>= 0,001 м/с^2 )
Секундная стрелка совершает полный оборот за 60 секунд, поэтому период ( T=60 с )
Длина окружности рассчитывается по формуле:
Пройденный путь рассчитывается по формуле:
За время равное периоду (T ) точка совершает один оборот, то есть проходит расстояние, равное длине окружности (l)
( a_<цс>=dfrac< (0,0104(6) м/с) ^2> <0,1 м>approx 0,00109551 м/с^2 approx 0,001 м/с^2 )
Центростремительное движение по окружности огэ
Задание 12. Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле 
Выразим из формулы ускорения радиус, получим:
Подставим сюда числовые значения и вычислим радиус:

- Вариант 1
- Вариант 1. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
- Решения заданий по номерам
- 1-5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- Вариант 2
- Вариант 2. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
- Решения заданий по номерам
- 1-5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- Вариант 3
- Вариант 3. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
- Решения заданий по номерам
- 1-5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- Вариант 4
- Вариант 4. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
- Решения заданий по номерам
- 1-5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- Вариант 5
- Вариант 5. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
- Решения заданий по номерам
-
Внимание! Нумерация заданий в сборнике 2021 отличается от сборника 2020
- Вариант 7
- Задания 1-5 полностью совпадают с Вариант 5. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 1. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 8
- Задания 1-5 полностью совпадают с Вариант 5. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 2. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 9
- Задания 1-5 полностью совпадают с Вариант 19. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 3. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 10
- Задания 1-5 полностью совпадают с Вариант 20. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 4. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 11
- Задания 1-5 полностью совпадают с Вариант 13. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 5. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 12
- Задания 1-5 полностью совпадают с Вариант 14. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 6. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 13
- Задания 1-5 полностью совпадают с Вариант 11. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 7. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 14
- Задания 1-5 полностью совпадают с Вариант 12. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 8. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 15
- Задания 1-5 полностью совпадают с Вариант 35. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 9. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 16
- Задания 1-5 полностью совпадают с Вариант 36. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 10. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 17
- Задания 6-25 полностью совпадают с Вариант 11. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 1-5
- 14
- Вариант 18
- Задания 6-25 полностью совпадают с Вариант 12. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 1-5
- 14
- Вариант 19
- Задания 1-5 полностью совпадают с Вариант 15. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 13. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 20
- Задания 1-5 полностью совпадают с Вариант 16. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 14. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 21
- Задания 1-5 полностью совпадают с Вариант 29. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 15. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 22
- Задания 1-5 полностью совпадают с Вариант 30. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 16. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 23
- Задания 1-5 полностью совпадают с Вариант 31. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 17. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 24
- Задания 1-5 полностью совпадают с Вариант 32. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 18. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 25
- Задания 1-5 полностью совпадают с Вариант 27. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 19. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 26
- Задания 1-5 полностью совпадают с Вариант 28. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 20. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 27
- Задания 1-5 полностью совпадают с Вариант 1. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 21. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 28
- Задания 1-5 полностью совпадают с Вариант 2. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 22. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 29
- Задания 6-25 полностью совпадают с Вариант 23. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 1-5
- 8
- 14
- Вариант 30
- Задания 6-25 полностью совпадают с Вариант 24. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 1-5
- 8
- 14
- Вариант 31
- Задания 1-5 полностью совпадают с Вариант 23. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 25. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 32
- Задания 1-5 полностью совпадают с Вариант 24. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 26. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 33
- Задания 1-5 полностью совпадают с Вариант 4. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 31. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 34
- Задания 1-5 полностью совпадают с Вариант 21. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 32. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 14
- Вариант 35
- Задания 1-5 полностью совпадают с Вариант 17. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 33. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
- Вариант 36
- Задания 1-5 полностью совпадают с Вариант 18. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Задания 6-25 полностью совпадают с Вариант 34. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
- Кроме заданий:
- 8
- 14
Равномерное движение по окружности.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.
Равномерное движение по окружности – это достаточно простой пример движения с вектором ускорения, зависящим от времени.
Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.
Период обращения – это время одного полного оборота. Для периода имеем очевидную формулу:
Частота обращения – это величина, обратная периоду:
Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).
Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.
Угловая скорость.
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1 ).
 |
| Рис. 1. Равномерное движение по окружности |
Пусть – начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .
Отношение угла поворота ко времени называется угловой скоростью вращения точки:
Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому
Сопоставляя формулы (1) и (3) , получаем связь линейной и угловой скоростей:
Закон движения.
Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1 , что
Но из формулы (2) имеем: . Следовательно,
Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.
Центростремительное ускорение.
Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5) :
С учётом формул (5) имеем:
Полученные формулы (6) можно записать в виде одного векторного равенства:
где – радиус-вектор вращающейся точки.
Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1 ). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.
Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:
Выразим угловую скорость из (4)
и подставим в (8) . Получим ещё одну формулу для центростремительного ускорения:
[spoiler title=”источники:”]
http://self-edu.ru/oge2021_36.php?id=2_12
http://ege-study.ru/ru/ege/materialy/fizika/ravnomernoe-dvizhenie-po-okruzhnosti/
[/spoiler]
Движение по окружности. Простые механизмы. Колебания и волны. Движение тела под действием силы тяжести.
Для успешного решения задания №4 необходимо знание тем и разделов, приведенных в заглавии. Т.е. это материалы частично из раздела динамики (криволинейное движение, силы в природе), частично из раздела статики. Кроме того, для решения может потребоваться понимание колебательных процессов. Полезные сведения даны в разделе теории.
Теория к заданию №4 ОГЭ по физике
Равномерное движение по окружности
Движение тела по окружности можно свести к движению по очень коротким прямым линиям (хордам), которые складываются в замкнутую криволинейную траекторию. Такой подход позволяет рассматривать движение в каждый момент времени как прямолинейное и говорить о перемещении, скорости и ускорении такого движения в привычном их понимании.
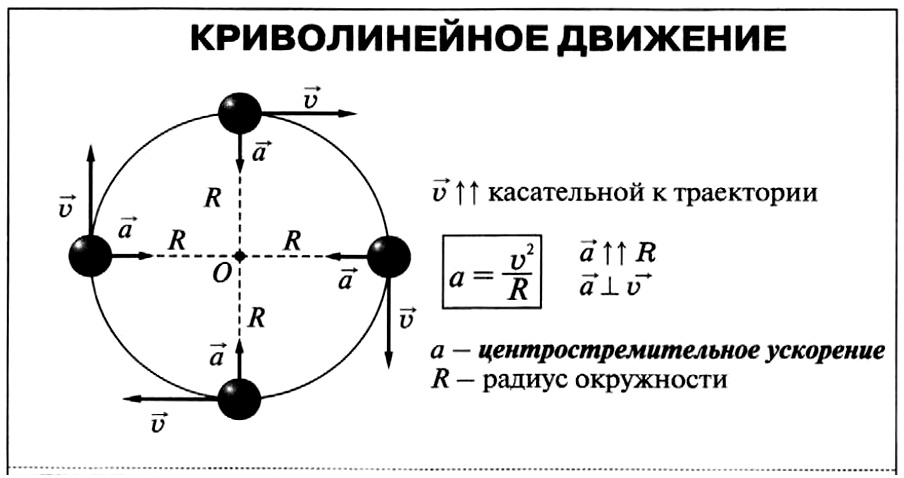
В каждой точке окружности тело имеет мгновенную скорость, вектор которой совпадает с вектором перемещения в этой точке и, следовательно, направлен по касательной к окружности. При этом модуль скорости не изменяется, что и делает движение равномерным.
Ускорение в каждой точке окружности направлено к ее центру. Т.е. при движении по окружности с постоянной скоростью тело испытывает ускорение. В этом особенность такого движения, которая и обеспечивает соответствующую траекторию. Связана она с тем, что векторы скорости и ускорения имеют между собой прямой угол, и их результирующая (определяемая по правилу треугольника) удерживает тело от движения по касательной, заставляя его смещаться и держаться на одинаковом расстоянии от центра окружности.
Центростремительное ускорение может быть вычислено по формуле:
,
где R – радиус окружности.
Блоки
Блок в физике – это простой механизм, обеспечивающий возможность регулирования силы, действующей на связанные с ним тела. Блок представляет собой колесо некоторой толщины с выемкой (желобом) по своей окружности. Обязательное условие для блока – возможность вращаться вокруг своей оси. По желобу проходит ремень (цепь, канат, веревка и т.д.), контакт с которым и обеспечивает вращение блока.
Блок может быть неподвижным и подвижным. Первый имеет неподвижную (зафиксированную) ось вращения, второй – подвижную.
Всякий блок – это рычаг, причем неподвижный является равноплечим рычагом, а подвижный имеет плечи, длины которых относятся между собой как 1:2. Из того, что блоки это рычаги, следует, что для них справедливо правило: проигрыш в расстоянии обеспечивает равную величину выигрыша в усилии (т.е. в силе).
Условие равновесия тела (правило моментов)
Если тело имеет неподвижную ось вращения, то оно находится в равновесии при условии, что сумма (алгебраическая) всех моментов сил, приложенных к телу, равна нулю относительно данной неподвижной оси.
Математическое выражение условия равновесия:
.
Момент силы при этом можно вычислить по формуле:
,
где F – приложенная сила, l – плечо силы (кратчайшее расстояния от прямой, на которой находится до оси вращения).
Движение тела по вертикали
Речь в данном случае идет о движении тел, брошенных вертикально вверх или опускающихся вертикально вниз. И в первом, и во втором случае имеется в виду, что на тела действует только сила тяжести, а сопротивление воздуха отсутствует.
Если тела движутся исключительно под действием силы тяжести, то это движение является равноускоренным, причем ускорение всегда одинаково. Это – ускорение своб.падения g. Величина ускорения для Земли: . Если тело движется вверх, то
, если падает вниз, то
.
При таком движении тела скорость и высота могут быть найдены по формулам:
,
.
Знак «–» в формулах перед g соответствует ситуации, когда тело движется вверх, поскольку в этом случае направления векторов скорости и ускорения противоположны.
Движение тела вниз под действием силы тяжести без начальной скорости (т.е. в ситуации, когда его просто отпускают, а не бросают), называют свободным падением.
Период колебания маятника
В механике различают маятники математические и пружинные. Разница между ними заключается в том, что в первом случае тело скреплено с пружиной, а во втором – подвешено на тонкой неупругой нити. Соответственно, в пружинном маятнике тело колеблется по прямой линии, то удаляясь от положения равновесия, то возвращаясь в него, а в математическом – колеблется по дуге влево и вправо от положения равновесия.
Период колебания в пружинном маятнике вычисляется так:
.
где m – масса тела, k – жесткость пружины.
Период колебаний математического маятника:
,
где l – длина нити, на которой подвешено тело.
Волны
В самом общем случае под волной понимают распространение колебаний от частицы к частице и от точки к точке. Различают волны механические, звуковые и др. Параметрами, описывающими характер распространения волны, являются ее длина (λ), частота ( ), период (Т), амплитуда (А). Кроме того, говорят о скорости распространения (v) волн. Эти величины связаны между собой различными соотношениями, например:
Разбор типовых вариантов заданий №4 ОГЭ по физике
Демонстрационный вариант 2018
[su_note note_color=”#defae6″]
Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью υ0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Полная механическая энергия тела на некоторой промежуточной высоте h равна
[/su_note]
Алгоритм решения:
- Записываем уравнение з-на сохранения энергии. Используя его, анализируем его и определяем полную энергию в граничных точках – в момент броска и при достижении телом максимальной высоты.
- Определяем полную энергию для тела в произвольный промежуточный момент времени, т.е. после того, как тело уже подброшено, но еще не достигло максимальной высоты.
- Записываем ответ.
Решение:
- Поскольку в условии есть оговорка о том, что сопротивлением воздуха можно пренебречь, то можно использовать з-н сохранения энергии. Полная энергия тела в любой момент времени, согласно закону, равна:
. Т.к. изначально тело бросают с поверхности земли с ненулевой скоростью (по условию – со скоростью v0), то в нач.момент времени
, т.е. имеет максимальную кинетич.энергию и равную нулю потенциальную. Когда тело достигает максимальной высоты, это значит, что его движение остановилось (
) и тело находится в покое на некоторой высоте над землей. В этот момент тело имеет максимальную потенц.энергию при нулевой кинетической:
.
- В процессе подъема тело одновременно находится в движении (его скорость уже не равна v0, а имеет меньшее значение v) и в то же время является телом, поднятым над землей на некую высоту h. Это значит, что полная энергия на промежуточной высоте должна быть выражена уравнением:
. Такого варианта ответа среди предложенных нет. Однако среди них есть вариант 2:
. Он содержит выражение для полной энергии в момент максимального подъема тела. Поскольку по з-ну сохранения энергии ее значение одинаково в любой момент времени, то это значит, что вариант 2 хотя и не содержит подробной расчетной формулы для вычисления полной энергии на высоте h, но отражает ее правильное количественное значение. А следовательно, именно вариант 2 является единственно правильным в данном случае.
Ответ: 2
Первый вариант (Камзеева, № 3)
[su_note note_color=”#defae6″]
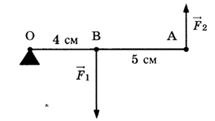
Легкий рычаг находится в равновесии под действием двух сил (см. рис.)
Отношение модуля силы F1 к модулю силы F2 равно
- 1,25
- 2,25
- 1,8
- 0,8
[/su_note]
Алгоритм решения:
- Переведем в СИ величины ОВ и ВА.
- Записываем ур-ние равновесия рычага.
- Записываем формулу для вычисления момента. Преобразуем ее для М1 и М2.
- Находим искомое отношение сил, используя ур-ние равновесия рычага (1).
- Записываем ответ.
Решение:
- Переведем в СИ данные в условии расстояния: ОВ=4 см=0,04 м; ВА=5 см=0,05 м.
- Согласно условию равновесия, имеем:
. Здесь М1 и М2 – соответственно моменты для F1 и F2. Примем, что положительным будет момент, направленный по часовой стрелке. Тогда получаем, что
(можно и наоборот).
- Момент силы определяется по формуле:
. Т.к.
, то
.
- Подставим выражения для моментов в (1). Получим:
. Отсюда:
.
Ответ: 2
Второй вариант (Камзеева, № 7)
[su_note note_color=”#defae6″]
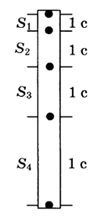
Для тела, свободно падающего из состояния покоя у поверхности некоторой планеты, измерялись расстояния, проходимые телом за последовательные равные промежутки времени (см. рис.). Чему равно ускорение свободного падения на планете, если S2=30 м? Сопротивление атмосферы пренебрежимо мало.
- 5 м/с2
- 10 м/с2
- 20 м/с2
- 40 м/с2
[/su_note]
Алгоритм решения:
- Выражаем S1 через S2. Находим S1.
- Записываем формулу для S1 через ускорение. Выражаем из нее искомое ускорение. Вычисляем ускорение.
- Записываем ответ.
Решение:
- Известно, что при равноускоренном движении пути, проходимые телом за одинаковые временные промежутки относятся как ряд нечетных натуральных чисел, а именно:
. Исходя из этого:
.
- Поскольку тела начинает двигаться из состояния покоя (
), то
. Отсюда:
. Т.к. S1 – это путь за первую секунду, то t=1c. Тогда получаем:
.
Ответ: 3
Третий вариант (Камзеева, № 11)
[su_note note_color=”#defae6″]
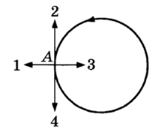
Тело движется равномерно по окружности против часовой стрелки (см. рис.). Какое направление имеет вектор ускорения в точке А?
- 1
- 2
- 3
- 4
[/su_note]
Алгоритм решения:
- Анализируем условие. Определяем вид ускорения. Находим правильный вариант ответа.
- Записываем ответ.
Решение:
Поскольку имеет место равномерное движение тела по окружности, то оно испытывает единственное ускорение – центростремительное. Его вектор всегда направлен к центру окружности. Следовательно, в т.А правильное направление – под номером 3.
Ответ: 3
Даниил Романович | Просмотров: 4.2k
Задачи на движение по окружности .
Центростремительное ускорение:
( a_{цс}=dfrac{v^2}{R} )
(v) – линейная скорость тела
(R)-радиус
Задача 1. (Центростремительное ускорение)
Найти центростремительное ускорение
мотоциклиста, если он движется по круговой трассе с радиусом (R=100 м ), со скоростью (v=10 м/с . )
Показать ответ
Показать решение
Видеорешение
Задача 2. (Центростремительное ускорение)
Найти центростремительное ускорение крайних точек колеса автомобиля, если он движется со скоростью (v=10 м/с , )
а радиус его колес равен (0,4 м )
Показать ответ
Показать решение
Видеорешение
Задача 3. (Центростремительное ускорение)
Один конец веревки длиной 0,5 метра привязали к потолку, после чего к другому ее концу был привязан груз.
Груз отвели в сторону и отпустили. Когда груз проходил нижнюю точку траектории, его скорость составляла (v=4 м/с. )
Вычислить центростремительное ускорение груза в нижней точке траектории.
Показать ответ
Показать решение
Видеорешение
Задача 4. (Центростремительное ускорение)
Спутник земли движется со скоростью (v=1000 м/с ) по круговой орбите радиусом (R=5 cdot 10^6 м .)
Вычислить его центростремительное ускорение.
Показать ответ
Показать решение
Видеорешение
Задача 5. (Центростремительное ускорение)
Найти линейную скорость (v ) мальчика, который катается на каруселях, если его центростремительное ускорение
(a_{цс}=4 м/с^2 ) , а расстояние между ним и осью вращения каруселей равно ( 2,25 м )
Показать ответ
Показать решение
Видеорешение
Задача 6. (Центростремительное ускорение)
Девочка качается на качелях. С какой скоростью она движется в нижней точке траектории, если ее центростремительное ускорение в этой точке
(a_{цс}=2,88 м/с^2 ), а расстояние от нее до точки подвеса качелей составляет 2 метра?
Показать ответ
Показать решение
Видеорешение
Задача 7. (Центростремительное ускорение)
На какую максимальную высоту (H ) можно подняться в колесе обозрения, если линейная скорость его кабинок (v= 0,8 м/с ) , а их центростремительное ускорение (a_{цс}=0,05 м/с^2 )
Показать ответ
Показать решение
Видеорешение
Задача 8. (Центростремительное ускорение)
(Приведено простенькое решение для тех, кому тяжело разобраться)
Ниже будет разобрана эта же задача в общем виде.
Материальная точка вращается по окружности радиусом ( R=2 м ), с периодом (T=6,28 с )
Найти центростремительное ускорение этой точки.
Принять ( pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 8. (Центростремительное ускорение)
(Приведено решение в общем виде, с выводом конечной формулы)
Материальная точка вращается по окружности радиусом ( R=2 м ), с периодом (T=6,28 с )
Найти центростремительное ускорение этой точки.
Принять ( pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 10. (Центростремительное ускорение)
(Приведено простенькое решение для тех, кому тяжело разобраться)
Ниже будет разобрана эта же задача в общем виде.
Найти центростремительное ускорение крайней точки секундной стрелки настенных часов, если ее длина составляет 10 сантиметров .
Принять ( pi=3,14 )
Дать ответ в системе СИ, округлить до тысячных.
Показать ответ
Показать решение
Видеорешение
Задача 10. (Центростремительное ускорение)
(Приведено решение в общем виде, с выводом конечной формулы)
Найти центростремительное ускорение крайней точки секундной стрелки настенных часов, если ее длина составляет 10 сантиметров .
Принять ( pi=3,14 )
Дать ответ в системе СИ, округлить до тысячных.
Показать ответ
Показать решение
Видеорешение
Центростремительное ускорение при движении по окружности…
Условие задачи:
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a=w^2*R где w — угловая скорость (в с-1), a R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 4 с-1, а центростремительное ускорение равно 64 м/с2.
Решение:
Ответ: 4
- 1
- 2
- 3
- 4
- 5
Оценка: 5.0 из 1
Комментарии
Всего комментариев
: 0

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Основные формулы центростремительного ускорения
Центростремительное ускорение, которое также называют нормальным ускорением, всегда направлено к центру окружности, по которой движется точка.
Модуль центростремительного ускорения определяется формулой:
Модуль остается постоянным, однако направление вектора
все время меняется, поэтому движение по окружности не является равноускоренным.
Центростремительное ускорение также можно определить через угловую скорость:
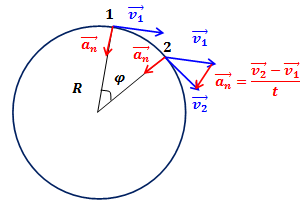
Рис.1. Центростремительное ускорение при равномерном движении точки по окружности
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Скрыть
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Красочные наградные
материалы для всех участников
низкий оргвзнос: от 19 руб.
Принять участие
успейте подать заявку
Скрыть
Высшее образование
в московском вузе
- Онлайн
формат - Диплом
гособразца - Помощь в трудоустройстве
Подобрать ВУЗ
Наши услуги
для Вас бесплатны!
Скрыть
репетиторы онлайн от проекта «ИнфоУрок»
Онлайн-репетиторы
Подберем педагога для Вас и запишем на бесплатное вводное занятие!
- подготовка к ЕГЭ/ОГЭ и ВПР
- по всем предметам 1-11 классов
Цена занятия единая и не зависит от их количества в пакете
от 490₽
Узнать подробнее
Рекордно низкая стоимость занятий!

Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
72 ч.
от 1900 ₽
от 470 ₽
Смотреть курс
- Сейчас обучается 864 человека из 78 регионов

Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
36 ч.
от 1500 ₽
от 370 ₽
Смотреть курс
- Сейчас обучается 46 человек из 22 регионов

Курс профессиональной переподготовки
Физика: теория и методика преподавания в образовательной организации
Учитель физики
300/600 ч.
от 4900 ₽
от 1220 ₽
Смотреть курс
- Сейчас обучается 366 человек из 73 регионов
Скрыть
онлайн конференция
идёт регистрация
«Профессиональный имидж педагога: стереотипы и методы их преодоления»
Свидетельство и скидка на обучение каждому участнику
Рычкова Анжела
Еремия Татьяна
Зарегистрироваться
19–21 апреля 2022 г.
Скрыть
Международный конкурс
«Лига эрудитов»
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам

Принять участие
Скачать материал
Скачать тест к материалу
Скрыть
Московский институт профессиональной
переподготовки и повышения квалификации
педагогов
Дистанционные курсы для педагогов
179 курсов профессиональной
переподготовки
484 курса повышения
квалификации
Выбрать курс со скидкой
Выдаём документы
установленного образца
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 836 795 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
- Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Физика», Перышкин А.В., Гутник Е.М.
Тема
§ 18 Движение тела по окружности с постоянной по модулю скоростью
Больше материалов по этой теме
Скрыть
Ищем педагогов
в команду «Инфоурок»
- ЗП до 91 000 руб.
- Гибкий график
- Удаленная работа
Хочу в команду!
Скрыть
онлайн семинар
идёт регистрация
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
Каштанов Роман
Зарегистрироваться
27 апреля 2022 г.
Скачать материал
Скачать тест к материалу
Скрыть
Ищем студентов
для работы онлайн
в проекте «Инфоурок»
Хочу в команду!
Другие материалы
pptx
-
Физика
-
9 класс
-
Презентации
Презентация по физике «Из чего состоит Солнце» (9 класс)
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: § 66 Строение, излучения и эволюция Солнца и звёзд
- 11.02.2018
- 1718
- 17

rar
-
Физика
-
9 класс
-
Презентации
Презентация о первом космонавте Земли
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: § 21 Реактивное движение. Ракеты
- 11.02.2018
- 1524
- 20

docx
-
Физика
-
9 класс
-
Тесты
Полугодовая КР по физике 9 класс
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: Глава 1. Законы взаимодействия и движения тел
Рейтинг:
2 из 5
- 11.02.2018
- 17349
- 332

pptx
-
Физика
-
9 класс
-
Презентации
Презентация по физике по теме «Движение тела, брошенного вертикально вверх» (9 класс)
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: § 14 Движение тела, брошенного вертикально вверх. Невесомость
Рейтинг:
5 из 5
- 11.02.2018
- 6529
- 737

pptx
-
Физика
-
9 класс
-
Видеоуроки
Урок «Законы сохранения в механике». Подготовка к сдаче ОГЭ по физике
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: § 22 Вывод закона сохранения механической энергии
- 11.02.2018
- 1120
- 5

docx
-
Физика
-
9 класс
-
Конспекты
Урок физики в 9 классе по теме : » Решение задач по теме : «Сила Ампера. Сила Лоренца»»
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: § 36 Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки
Рейтинг:
4 из 5
- 11.02.2018
- 17259
- 666

docx
-
Физика
-
9 класс
-
Другие методич. материалы
Дидактический материал к уроку по теме:»Криволинейное движение. Движение тела по окружности»
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: § 18 Движение тела по окружности с постоянной по модулю скоростью
- 22.11.2017
- 1142
- 8

docx
-
Физика
-
9 класс
-
Тесты
Задачи «Движение по окружности»
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: § 18 Движение тела по окружности с постоянной по модулю скоростью
- 20.11.2017
- 1542
- 1

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс профессиональной переподготовки «Физика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Основы религиозных культур и светской этики: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Экономика и право: налоги и налогообложение»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС технических направлений подготовки»
-
Курс повышения квалификации «Маркетинг в организации как средство привлечения новых клиентов»
-
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
-
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
-
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
-
Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»
-
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
-
Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
-
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»
Оставьте свой комментарий
Авторизуйтесь,
чтобы задавать вопросы.
Задачи на Движение тела по окружности с решениями
Формулы, используемые на уроках «Задачи на Движение тела по окружности».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Какова линейная скорость тела, движущегося по окружности радиусом 40 м с ускорением 2,5 м/с2 ?
Задача № 2.
С какой наибольшей скоростью может двигаться автомобиль массой 1 т на повороте радиусом 100 м, чтобы его не «занесло», если максимальная сила трения 4 кН?
Задача № 3.
Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.
Задача № 4.
Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Задача № 5.
Велосипедист ехал со скоростью 25,2 км/ч. Сколько оборотов совершило колесо диаметром 70 см за 10 мин?
Задача № 6.
Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.
Задача № 7.
Автомобиль движется по закруглению дороги, радиус которой равен 20 м. Определите скорость автомобиля, если центростремительное ускорение равно 5 м/с2.
Задача № 8.
Шкив радиусом 30 см имеет частоту вращения 120 об/мин. Определите частоту, период обращения, угловую скорость шкива и центростремительное ускорение точек шкива, наиболее удаленных от оси вращения.
Задача № 9.
Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли. Радиус Земли считайте равным 6370 км.
Задача № 10.
ОГЭ
Точка движется равномерно по окружности. Как изменится её центростремительное ускорение, если скорость возрастёт вдвое, а радиус окружности вдвое уменьшится?
Задача № 11.
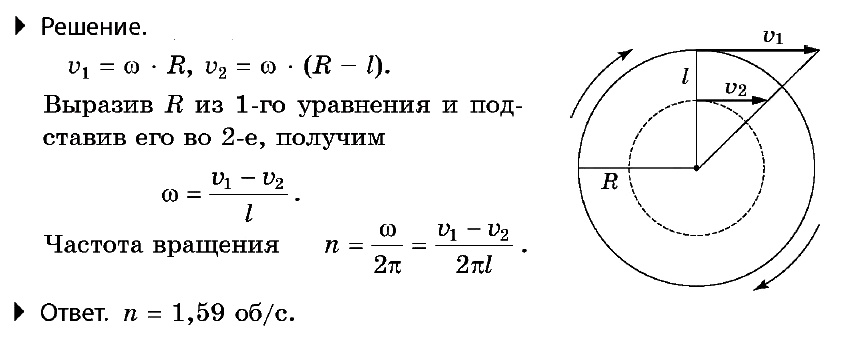
ЕГЭ
Линейная скорость точек обода вращающегося диска v1 = 3 м/с, а точек, находящихся на l = 10 см ближе к оси вращения, v2 = 2 м/с. Найти частоту вращения диска.
Краткая теория для решения Задачи на Движение тела по окружности.
Это конспект по теме «ЗАДАЧИ на Движение тела по окружности». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Искусственные спутники планет.
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Задание:
Задача на расчет центростремительного ускорения при движении тела по окружности с постоянной скоростью.
Условие задачи: Рассчитайте центростремительное ускорение предмета, расположенного на экваторе Земли.
Решение:
υ = 2πR/ T = 2 • 3,14 • 6370 • 103 м / (24 • 3600 c) = 463 м/с.
aц.с. = υ2 / R = (463 м/с)2 / (6370 • 103 м) = 0,034 м/с2.
Ответ: 0,034 м/с2.