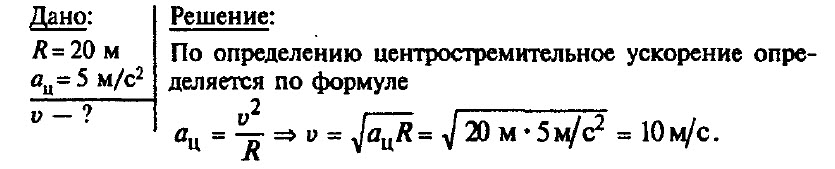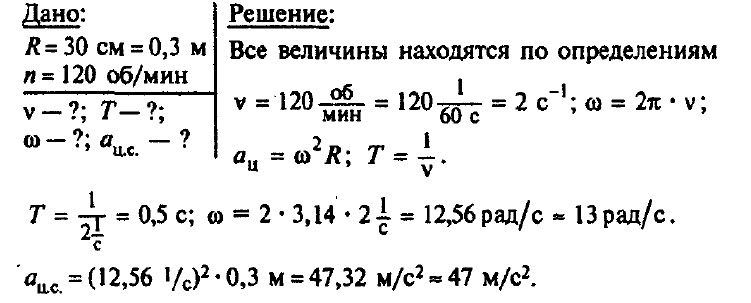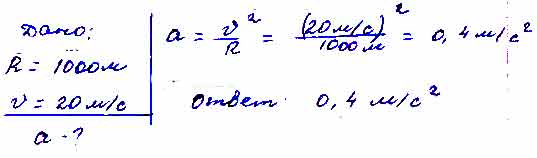- Учебники
- 7 класс
- Физика 👍
- Марон
- №1629
авторы: Марон, Позойский.
издательство: “Дрофа”
Раздел:
- 9 КЛАСС
- ЗАКОНЫ ВЗАИМОДЕЙСТВИЯ И ДВИЖЕНИЯ ТЕЛ
- Движение по окружности
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Движение по окружности. Номер №1629
- Предыдущее
- Следующее
Рассчитайте центростремительное ускорение, с которым по закруглению радиусом 250 м движется поезд со скоростью 36 км/ч.
reshalka.com
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Движение по окружности. Номер №1629
Решение
Дано:
R = 250 м;
v = 36 км/ч.
Найти:
a
ц
− ?
СИ:
v = 10 м/с.
Решение:
a
ц
=
v
2
R
;
a
ц
=
10
2
250
=
0
,
4
м
/
с
2
.
Ответ: 0,4
м
/
с
2
.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Задачи на Движение тела по окружности с решениями
Формулы, используемые на уроках «Задачи на Движение тела по окружности».
Название величины |
Обозначение |
Единица измерения |
Формула |
Радиус окружности |
r |
м |
|
Линейная скорость (модуль) |
v |
м/с |
|
Центростремительное ускорение (модуль) |
a |
м/с2 |
|
Центростремительная сила (модуль) |
F |
Н |
|
Масса тела |
m |
кг |
|
Угловая скорость при равномерном вращении |
ω |
рад/с |
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Какова линейная скорость тела, движущегося по окружности радиусом 40 м с ускорением 2,5 м/с2 ?
Задача № 2.
С какой наибольшей скоростью может двигаться автомобиль массой 1 т на повороте радиусом 100 м, чтобы его не «занесло», если максимальная сила трения 4 кН?
Задача № 3.
Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.
Задача № 4.
Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Задача № 5.
Велосипедист ехал со скоростью 25,2 км/ч. Сколько оборотов совершило колесо диаметром 70 см за 10 мин?
Задача № 6.
Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.
Задача № 7.
Автомобиль движется по закруглению дороги, радиус которой равен 20 м. Определите скорость автомобиля, если центростремительное ускорение равно 5 м/с2.
Задача № 8.
Шкив радиусом 30 см имеет частоту вращения 120 об/мин. Определите частоту, период обращения, угловую скорость шкива и центростремительное ускорение точек шкива, наиболее удаленных от оси вращения.
Задача № 9.
Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли. Радиус Земли считайте равным 6370 км.
Задача № 10.
ОГЭ
Точка движется равномерно по окружности. Как изменится её центростремительное ускорение, если скорость возрастёт вдвое, а радиус окружности вдвое уменьшится?
Задача № 11.
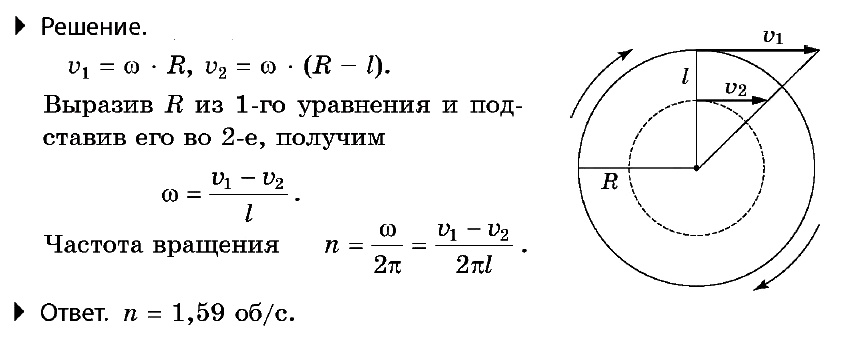
ЕГЭ
Линейная скорость точек обода вращающегося диска v1 = 3 м/с, а точек, находящихся на l = 10 см ближе к оси вращения, v2 = 2 м/с. Найти частоту вращения диска.
Задача № 12.
Груз, привязанный к шнуру длиной l = 50 см, описывает окружность в горизонтальной плоскости. Какой угол φ образует шнур с вертикалью, если частота вращения n = 1 с-1 ?
Рассуждение: На схеме покажем груз, подвешенный на нити и движущийся по окружности некого радиуса R в горизонтальной плоскости так, что нить составляет с вертикалью угол φ. На груз действуют две силы: 1) сила тяжести mg; 2) сила натяжения нити T. Так как груз не движется вдоль оси y, то запишем первый закон Ньютона в проекции на эту ось: T⋅• cos φ = mg. Поскольку груз описывается окружность, то второй закон Ньютона запишется так: T⋅• sin φ = ma.
Ответ: 60º.
Краткая теория для решения Задачи на Движение тела по окружности.
Это конспект по теме «ЗАДАЧИ на Движение тела по окружности». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Искусственные спутники планет.
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
UCHEES.RU – помощь студентам и школьникам
В 5:36 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Определите центростремительное ускорение автомобиля, движущегося по закруглённому участку дороги радиусом 1 км, если скорость автомобиля постоянна и равна 20 м/с.
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике “ЕГЭ (школьный)”. Ваш вопрос звучал следующим образом: Определите центростремительное ускорение автомобиля, движущегося по закруглённому участку дороги радиусом 1 км, если скорость автомобиля постоянна и равна 20 м/с.
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
ответ к заданию по физике
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Соколова Малика Геннадиевна – автор студенческих работ, заработанная сумма за прошлый месяц 50 392 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
РАЗДЕЛЫ САЙТА
Ответы на вопросы – в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.
Полезные статьи – раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.
Красивые высказывания – цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.
ЗАДАТЬ ВОПРОС
НОВЫЕ ОТВЕТЫ
- Абадзехская стоянка, Даховская пещера. ..
- По закону сохранения заряда каждый шарик после соприкасl..
- 2)прогудел первый мохнатый шмель 3) Зазвенела Прогудел 4) ..
- В мілкій траві ворушаться сліди веселих, сполоханих доще
..
ПОХОЖИЕ ВОПРОСЫ
- Сравните силы притяжения, действующие на тела у поверхности Земли, со стороны Земли и Солнца.
- С какой силой лётчик-космонавт притягивается к Земле, находясь на высоте 300 км от её поверхности? Масса космонавта 80 кг. Сравните полученное
- Вентилятор вращается со скоростью 600 оборотов за 1 мин. После выключения он вращается равнозамедленно и делает 86 оборотов. За какое время он
- Диск циркулярной пилы имеет диаметр 30 см. Вместе с диском на ось циркулярной пилы насажен шкив диаметром 6 см, который соединён посредством
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
2020 – 2023 – UCHEES.RU
Оливия Соловьева
29 мая, 17:40
0
R = 100 м.
V = 10 м/с.
a – ?
Так как при движении по закругленной траектории изменяется направление скорости, автомобиль имеет центростремительное ускорение. Центростремительное ускорение а определяется формулой: a = V² / R, где V – скорость движения, R – радиус закругления траектории.
а = (10 м/с) ² / 100 м = 1 м/с².
Ответ: автомобиль движется с центростремительным ускорением а = 1 м/с².
- Комментировать
- Жалоба
- Ссылка
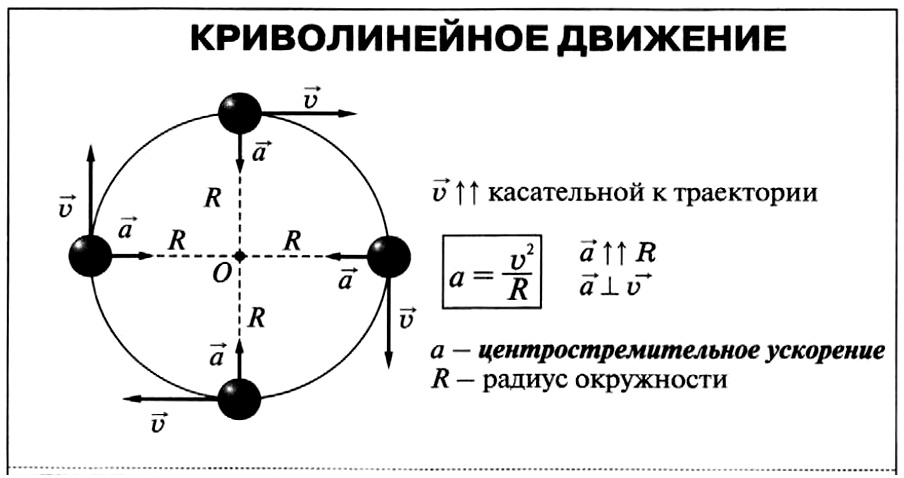
Центростремительное ускорение при движении по окружности
Центростремительное ускорение при движении по окружности
Равномерное движение по окружности
Рассмотрим равномерное движение материальной точки по окружности. При равномерном движении величина скорости постоянна ($v=const$). Однако ускорение точки при этом не равно нулю, так как скорость при движении по окружности постоянно изменяет свое направление. Вектор скорости является касательным к траектории, по которой движется точка, то есть является касательной к окружности в рассматриваемой точке
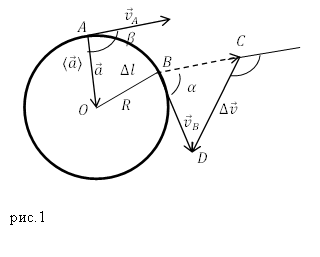
Рассмотрим точки A и B лежащие на окружности по которой движется точка. Вектор изменения скорости при перемещении частицы из А в B равен:
[Delta overline{v}={overline{v}}_B-{overline{v}}_Aleft(1right).]
При бесконечно малом времени движения частицы, между точками A и B, дуга AB примерно равна длине хорды AB. Треугольники AOB и BCD подобны, поэтому получим:
[frac{Delta v}{v}=frac{Delta l}{R}=alpha left(2right),]
где R – радиус окружности.
Величину среднего ускорения определим как:
[leftlangle arightrangle =frac{Delta v}{Delta t}=frac{vDelta l}{RDelta t}left(3right).]
Модуль мгновенного ускорения получаем, переходя к пределу при $Delta tto 0 $ в выражении (3):
[a={mathop{lim }_{Delta tto 0} leftlangle arightrangle }={mathop{lim }_{Delta tto 0} frac{vDelta l}{RDelta t}=frac{v}{r} }mathop{{rm lim}}_{Delta tto 0}frac{Delta l}{Delta t}=frac{v}{R}v=frac{v^2}{R}left(4right).]
Из формулы (4) следует, что при равномерном движении по окружности величина центростремительного ускорения не изменяется.
Вектор $overline{leftlangle arightrangle }$ имеет с $overline{v} $угол равный$ beta $:
[beta =frac{pi +alpha }{2}left(5right).]
При $Delta tto 0 $ угол $alpha to 0.$ Получаем, что угол между вектором мгновенного ускорения и скорости при равномерном движении по окружности равен $90{}^circ $.
И так, материальная точка, движущаяся с постоянной скоростью по окружности, обладает ускорением, направленным к центру окружности (перпендикулярное вектору скорости), его модуль равен скорости в квадрате, деленной на радиус окружности. Такое ускорение называют центростремительным или нормальным, обозначают его обычно ${overline{a}}_n$.
[a_n=frac{v^2}{R}={omega }^2R left(6right),]
где $omega $ – угловая скорость движения материальной точки ($v=omega cdot R$).
Определение центростремительного ускорения
Определение
Центростремительное ускорение – это компонента полного ускорения материальной точки, движущейся по криволинейной траектории,
характеризующая, быстроту изменения направления вектора скорости.
Центростремительное ускорение можно определить как:
[{overline{a}}_n=frac{v^2}{R^2}overline{R }left(7right).]
Неравномерное движение материальной точки по окружности
Если точка движется по окружности неравномерно, то ее полное ускорение ($overline{a}$) рассматривают как состоящее из двух частей. Одна из частей – это центростремительное ускорение. Другой составляющей полного ускорения при криволинейном движении служит тангенциальное ускорение (${overline{a}}_{tau }$), оно отвечает за изменение величины скорости.
[overline{a}={overline{a}}_{tau }+{overline{a}}_nleft(8right).]
[a=sqrt{a^2_n+a^2_{tau }}left(9right).]
Тангенциальное ускорение определяют как:
[{overline{a}}_{tau }=frac{doverline{v}}{dt}left(10right).]
Впервые верные формулы для центростремительного ускорения были получены Х. Гюйгенсом.
Единицей измерения центростремительного ускорения в Международной системе единиц является метр, деленный на секунду в квадрате:
[left[a_nright]=frac{м}{с^2}.]
Примеры задач на центростремительное ускорения
Пример 1
Задание. Каким будет нормальное ускорение материальной точки движущейся по окружности радиуса $R=3$м, в момент времени, равный $t=1$ c, если путь ($s$) от времени зависит как $s(t)=0,4 t^2+0,1t (м)$?
Решение. Основой для решения задачи служит определение центростремительного ускорения в виде:
[a_n=frac{v^2}{R}left(1.1right).]
Используя уравнение $sleft(tright)=0,4 t^2+0,1t и$ уравнение, связывающее мгновенное значение скорости и перемещения:
[v=frac{ds}{dt} left(1.2right),]
найдем величину скорости в момент времени $t=1$ с:
[vleft(tright)=frac{d}{dt}left(0,4 t^2+0,1tright)=0,8t+0,1to vleft(t=1 cright)=0,9 frac{м}{с}.]
Подставим величину скорости и радиус в (1.1) найдем величину нормального ускорения:
[a_n=frac{{0,9}^2}{3}=0,27 left(frac{м}{с^2}right).]
Ответ. $a_n=0,27frac{м}{с^2}$
Пример 2
Задание. Материальная точка перемещается по окружности радиуса R. Тангенциальное ускорение этой точки равно $a_{tau }=A=const$. В какой момент времени вектор полного ускорения образует с вектором скорости угол равный $alpha $?
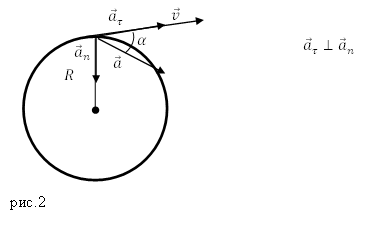
Решение. Сделаем рисунок.
Из рис.2 следует, что:
[tg alpha =frac{a_n}{a_{tau }}left(2.1right).]
Величина тангенциального ускорения равна:
[a_{tau }=frac{dv}{dt}=Аleft(2.2right).]
По условию тангенциальное ускорение постоянно и равно постоянной A. Выразим из (2.2) модуль скорости:
[v=intlimits^{t_1}_0{Adt=At_1left(2.3right).}]
Центростремительное ускорение движения точки по окружности равно:
[a_n=frac{v^2}{R}left(2.4right).]
Используя (2.3) имеем:
[a_n=frac{{(At_1)}^2}{R} left(2.5right).]
Подставим правые части выражений (2.5) и (2.2) в формулу (2.1) [tg alpha =frac{{(At_1)}^2}{R}frac{1}{A}=frac{At^2_1}{R} left(2.6right).]
Выразим искомое время из (2.6), имеем:
[t_1=sqrt{frac{R tg alpha }{A}}.]
Ответ. $t_1=sqrt{frac{R tg alpha }{A}}$
Читать дальше: циклическая частота.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!