Макеты страниц
Мы видели, что кривизна к окружности есть величина, обратная ее радиусу 
Чем больше радиус окружности, тем меньше ее кривизна. По аналогии вводится понятие радиуса кривизны кривой в данной точке.
Определение. Радиусом кривизны R в данной точке кривой называется величина, обратная кривизне 
Так как кривизна кривой, вообще говоря, изменяется при переходе от данной ее точки к другой, то и радиус кривизны является переменной величиной.
Если кривая задана уравнением 
то ее радиус кривизны 
как величина, обратная кривизне, определяется следующей формулой:
Если же кривая задана параметрически, то ее радиус кривизны выражается формулой
Пример. Найти радиус кривизны кривой 
в точке М (1; 0).
Решение. Находим 
. По формуле (78) получим
Построим теперь в данной точке М кривой отрезок МР, направленный по нормали к кривой в сторону ее вогнутости и равный по величине радиусу кривизны кривой в точке М:
(рис. 201). Окружность с центром в точке Р и радиусом, равным радиусу кривизны кривой в данной точке 
, называется кругом кривизны. Центр Р этого круга называется центром кривизны. Очевидно, данная кривая и ее круг кривизны в точке М имеют общую касательную (рис. 201).
Рис. 201
Рис. 202
Покажем, как найти координаты центра кривизны кривой, заданной уравнением 
.
Пусть 
– точка данной кривой и 
– соответствующий ее центр кривизны (рис. 202). Уравнение нормали к кривой в точке 
имеет вид
Так как точка 
лежит на нормали, то ее координаты удовлетворяют этому уравнению:
Кроме того, расстояние между точками 
равно радиусу кривизны R кривой:
откуда
Решая совместно систему уравнений
и заменяя R его выражением по формуле (78), найдем
Предположим для определенности, что 
. Тогда кривая вогнута и 
(см. рис. 202), т. е. в правой части формулы (80) для 
следует взять знак «плюс», и, следовательно, в правой части формулы для 
– знак «минус». При этом, поскольку 
для координат 
центра кривизны мы получим следующие формулы:
Можно показать, что в случае 
формулы (81) сохраняют свой вид.
-
Радиус, центр и круг кривизны. Эволюта и эвольвента
Радиусом
кривизны называется величина, обратная
кривизне, т. е.
.
Если
плоская кривая отнесена к прямоугольной
системе координат и задана уравнением
,
то радиус кривизны
выражается формулой
.
Eсли
плоская кривая отнесена к прямоугольной
системе координат и задана параметрически
системой уравнений
, то радиус кривизны
выражается формулой
,
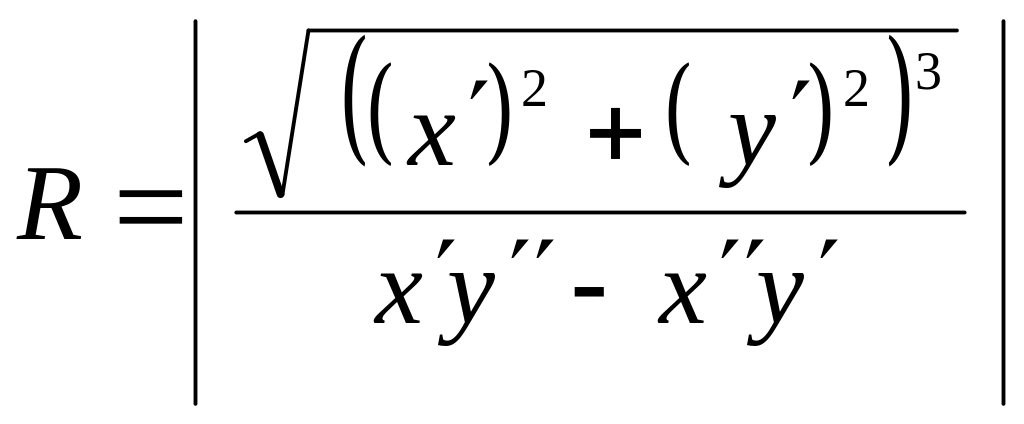
где
,
,
,
.
Если
плоская кривая отнесена к полярной
системе координат и задана уравнением
,
то радиус кривизны
выражается формулой
,
где
,
.
Окружностью
кривизны данной линии её точке А
называется
предельное положение окружности,
проходящей через три точки A,
B,
C
кривой, когда
и
.
Радиус
окружности кривизны равен радиусу
кривизны. Центр окружности кривизны
называется центром кривизны и находится
на нормали к линии, проведенной в точке
А
в сторону вогнутости этой линии.
Координаты
и
центра кривизны линии
вычисляются по формулам:
,
.
Эволютой
линии называется множество её центров
кривизны, а сама линия относительно
своей эволюты называется эвольвентой.
Формулы
для координат центра кривизны можно
рассматривать как параметрические
уравнения эволюты, где параметром
является абсцисса х
исходной линии.
Данная
линия может иметь лишь одну эволюту, но
у данной эволюты существует бесконечное
множество эвольвент.
Пример.
Найти
радиус кривизны линии
в
точке с абсциссой
.
Решение.
Найдем значения производных первого и
второго порядков функции
в точке с абсциссой
:
,
.
Подставим
найденные значения
и
в
формулу
:
.
Следовательно,
радиус кривизны
линии
в
точке с абсциссой
.
Пример.
Найти
радиус кривизны линии
в
точке
.
Решение.
Дифференцируя по t,
получим
,
,
,
.
Вычислим
значения производных в
точке
:
,
.
Подставляя
найденные значения
,
в
формулу
,
имеем
Следовательно,
радиус кривизны
линии
в
точке с абсциссой
Пример.
Найти
радиус кривизны кардиоиды
в
любой её точке.
Решение.
Найдем
и
:
.
Подставим
найденные выражения в формулу
:
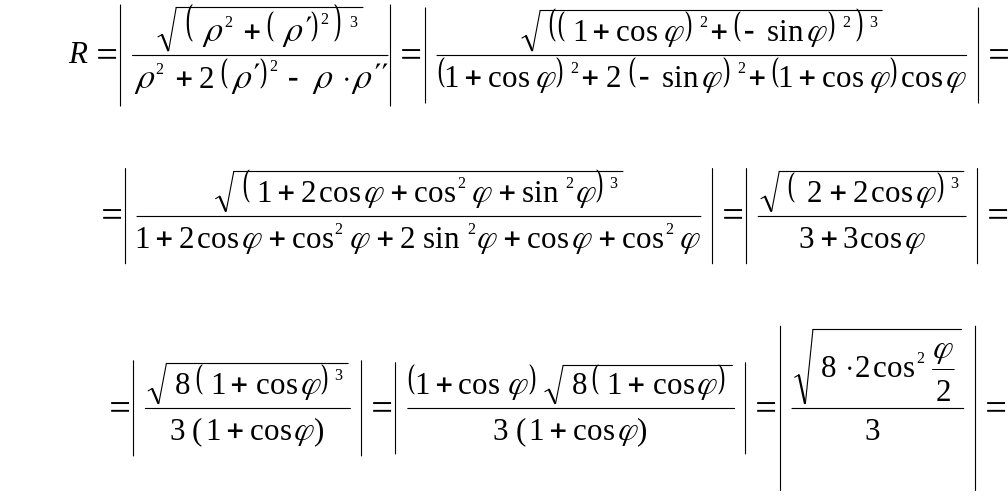
Следовательно,
радиус кривизны
кардиоиды
в
любой её точке
Пример.
Найти
координаты
и
центра кривизны линии
в
точке
.
Решение.
Найдем значения производных первого
и второго порядков функции
в точке с абсциссой
:
,
.
Подставим
значения
,
и найденные
значения
и
в
формулы
,
:
,
Следовательно,
координаты
центра кривизны линии
в
точке
и
Пример.
Составить
уравнение эволюты кривой
.
Решение.
Продифференцируем дважды уравнение
параболы:
;
.
Так
как
,
то
.
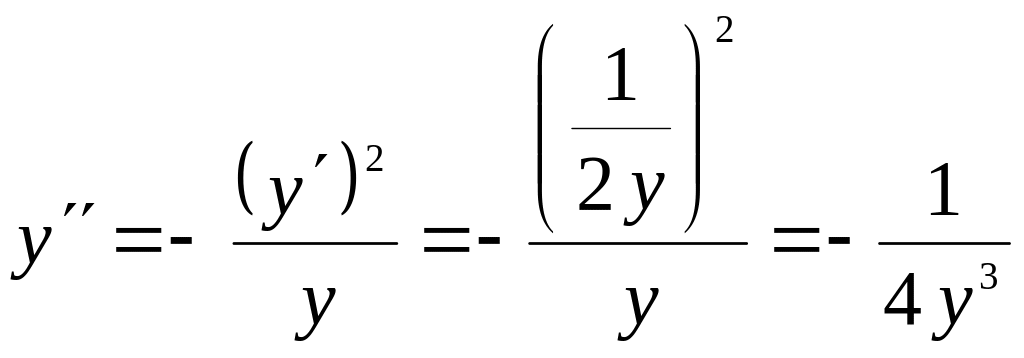
Найдем
координаты
и
центра кривизны линии ,
предварительно выразив х
из уравнения
:
.
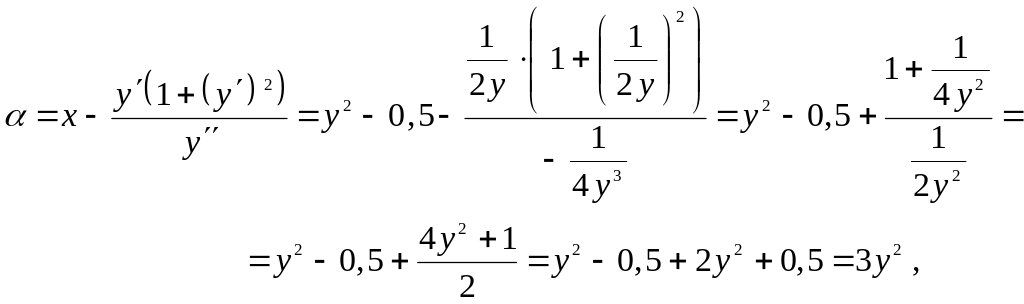
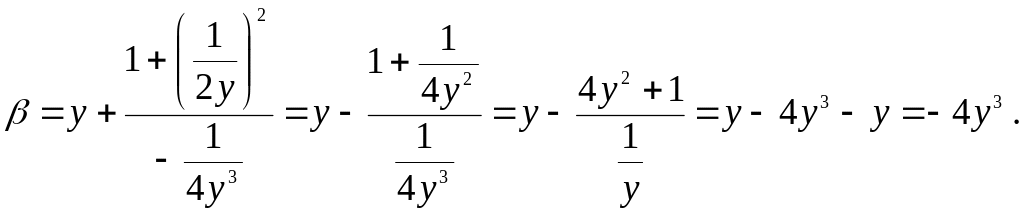
Имеем
–
уравнение эволюты в параметрической
форме. Выразим параметр у
из
и
:
;
.
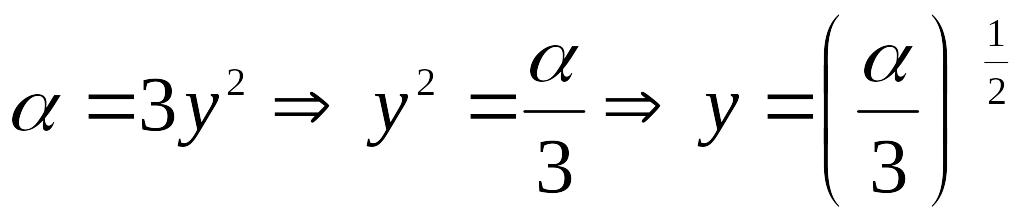
Окончательно
получаем,
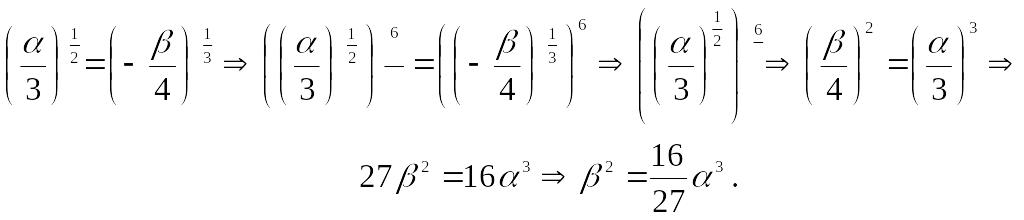
Следовательно,
уравнение
эволюты кривой
имеет вид
(уравнение
полукубической параболы).
Упражнения
1.
Найти радиус кривизны линии
в
точке A:
а)
,
A
(
2; 2 ), б)
,
A
(
0; 1 ) .
2.
Найти радиус кривизны трехлепестковой
розы
, при
.
3.
Найти координаты
и
центра кривизны линии
в
точке A:
а)
,
A
(
1; 1 ), б)
,
A
(
1; 0 ) .
4.
Составить уравнение эволюты кривой
:
а)
,
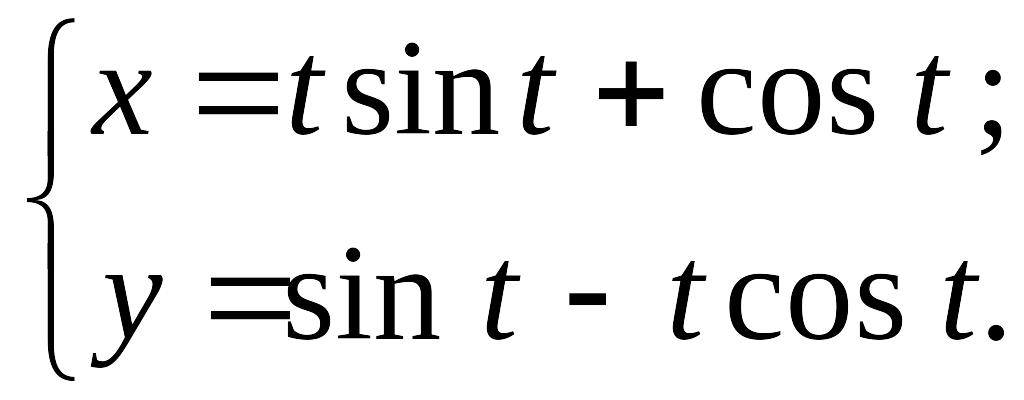
б)
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример 3. Найти координаты центра кривизны и построить кривую и круг кривизны кривой:
1) в ее вершине;
2) в точке, где
.
Решение. 1) Данное уравнение определяет параболу, ось которой параллельна оси . Найдем ее вершину как точку, где касательная параллельна оси
, т. е. где
:
при
Далее по формулам
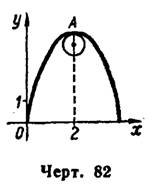
находим координаты центра кривизны данной параболы в ее вершине (2; 4)
и строим параболу и круг кривизны в ее вершине (рис. 82).
2) Находим производные , их значения при
:
и по формулам (2) координаты центра кривизны
Затем строим данную циклоиду, ее точку , где
, найденный центр кривизны
и круг кривизны (рис. 83).
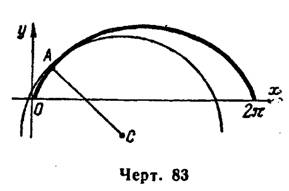
Пример 4. В каких точках параболы радиус кривизны равен единице?
Решение. Находим производные и по формуле (1)
радиус кривизны параболы в любой ее точке с абсциссой :
Полагая , получим абсциссы искомых точек
$
Пример 5. В какой точке кривая имеет наибольшую кривизну?
Решение. Находим производные и кривизну данной кривой в любой точке:
Далее ищем наибольшее значение функции , которая определена и непрерывна на всей числовой оси:
при
т.е. в единственной точке . Определяя знаки
слева и справа от этой критической точки:
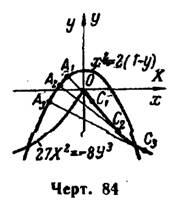
Это параметрические уравнения эволюты. Исключая из них параметр , получим
— уравнение полукубической параболы. Данная парабола и найденная ее эволюта изображены на рис. 84.
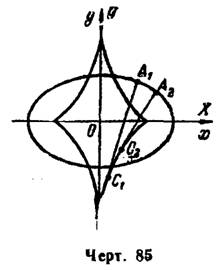
2) Из уравнений эллипса найдем производные и по формулам (2) получим, после упрощений, параметрические уравнения эволюты эллипса
где
Эллипс и его эволюта построены на рис. 85.
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Смысл понятий радиуса, круга и центра кривизны
В технических приложениях часто оказывается удобным использовать окружности для приближенной замены кривой в окрестностях рассматриваемых точек. Это существенно упрощает решение целого ряда задач за счет применения более удобных выражений.
Наиболее употребительными характеристиками любой кривой являются касательная и нормаль. Касательная — предельное положение секущей $MN$ при неограниченном приближении точки $N$ к точке $M$ вдоль кривой. Нормаль — прямая, проходящая через точку касания перпендикулярно касательной.
Уравнение касательной в точке $Mleft(x_{0} ,y_{0} right)$ к кривой $y=fleft(xright)$ имет вид $y-y_{0} =y’left(x_{0} right)cdot left(x-x_{0} right)$, уравнение нормали $y-y_{0} =-frac{1}{y’left(x_{0} right)} cdot left(x-x_{0} right)$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Задача 1
Записать уравнения касательной и нормали к кривой $y=3cdot x^{2} -x+2$ в заданной точке $x_{0} =1$.
Значение функции в заданной точке: $y_{0} =yleft(x_{0} right)=yleft(1right)=3cdot 1^{2} -1+2=4$.
Значение производной в заданной точке:
[y’=left(3cdot x^{2} -x+2right)^{{‘} } =6cdot x-1; y’left(x_{0} right)=y’left(1right)=6cdot 1-1=5.]
Уравнение касательной: $y-4=5cdot left(x-1right)$ или $5cdot x-y-1=0$.
Уравнение нормали: $y-4=-frac{1}{5} cdot left(x-1right)$ или $x+5cdot y-21=0$.
Определение
Радиус кривизны — это параметр кривой, значение которого обратно значению кривизны $R=frac{1}{K} $. Следовательно, это такая же переменная величина, как и кривизна.
Если в данной точке $M$ построить нормаль к кривой и отложить на ней в сторону вогнутости кривой отрезок, равный по длине радиусу кривизны кривой в этой точке, то получим точку — центр кривизны. Окружность с центром в полученной точке и радиусом, равным радиусу кривизны — это круг кривизны. Так как данная кривая и её круг кривизны касаются в данной точке, то они имеют в данной точке общую касательную. Кроме того, значения кривизны кривой и круга кривизны в данной точке совпадают.
Важным свойством круга кривизны является то, что он является соприкасающимся кругом, то есть предельным положением круга, проходящего через три точки кривой, стремящимся к совпадению в данной.
Если некоторая точка перемещается вдоль кривой, то и соответствующий ей центр кривизны также описывает некоторую кривую. Геометрическое место центров кривизны данной кривой называется её эволютой. При этом данная кривая по отношению к своей эволюте называется её эвольвентой.
Вычисление радиуса и определение центра круга кривизны
Формулы для радиуса кривизны получить легко, если известны формулы для вычисления кривизны кривой.
При произвольном параметрическом задании кривой $x=xleft(tright)$ и $y=yleft(tright)$ имеем $R=frac{sqrt{left(left(x’_{t} right)^{2} +left(y’_{t} right)^{2} right)^{3} } }{y”_{tt} cdot x’_{t} -x”_{tt} cdot y’_{t} } $.
Если кривая задана в явном виде $y=fleft(xright)$, то $R=frac{sqrt{left(1+left(y’right)^{2} right)^{3} } }{y”} $.
Если кривая задана в полярных координатах $rho =rho left(phi right)$, то $R=frac{sqrt{left(rho ^{2} +left(rho ‘_{phi } right)^{2} right)^{3} } }{rho ^{2} +2cdot left(rho ‘_{phi } right)^{2} -rho cdot rho ”_{phi phi } } $.
«Радиус, круг и центр кривизны» 👇
Задача 2
Найти радиус кривизны экспоненты $y=e^{x} $ при $x=0$.
Находим производные: $y’=e^{x} $; $y”=e^{x} $.
По формуле для радиуса кривизны получаем:
[R=frac{sqrt{left(1+left(y’right)^{2} right)^{3} } }{y”} =frac{sqrt{left(1+left(e^{x} right)^{2} right)^{3} } }{e^{x} } =frac{sqrt{left(1+e^{2cdot x} right)^{3} } }{e^{x} } .]
Вычисляем радиус кривизны экспоненты при $x=0$:
[Rleft(0right)=frac{sqrt{left(1+e^{2cdot 0} right)^{3} } }{e^{0} } =2cdot sqrt{2} . ]
Задача 3
Найти радиус кривизны кардиоиды $rho =1+cos phi $.
Находим производные: $rho ‘=-sin phi $; $rho ”=-cos phi $.
Вычисляем:
[rho ^{2} +rho ‘^{2} =left(1+cos phi right)^{2} +left(-sin phi right)^{2} =2cdot left(1+cos phi right);]
[rho ^{2} +2cdot rho ‘^{2} -rho cdot rho ”=left(1+cos phi right)^{2} +2cdot left(-sin phi right)^{2} -left(1+cos phi right)cdot left(-cos phi right)=]
[=3cdot left(1+cos phi right).]
По формуле для радиуса кривизны получаем:
[R=frac{sqrt{left(rho ^{2} +left(rho ‘_{phi } right)^{2} right)^{3} } }{rho ^{2} +2cdot left(rho ‘_{phi } right)^{2} -rho cdot rho ”_{phi phi } } =frac{sqrt{left(2cdot left(1+cos phi right)right)^{3} } }{3cdot left(1+cos phi right)} =frac{2}{3} cdot sqrt{2cdot left(1+cos phi right)} =frac{4}{3} cdot cos frac{phi }{2} .]
Найдем координаты центра кривизны $Pleft(x_{C} ;y_{C} right)$ кривой $y=fleft(xright)$.
Координаты центра кривизны для точки $Mleft(x;yright)$ удовлетворяют уравнению нормали $y_{C} -y=-frac{1}{y’left(xright)} cdot left(x_{C} -xright)$.
Уравнение круга кривизны: $left(x-x_{C} right)^{2} +left(y-y_{C} right)^{2} =R^{2} $.
Решив систему $left{begin{array}{c} {y_{C} -y=-frac{1}{y’left(xright)} cdot left(x_{C} -xright)} \ {left(x-x_{C} right)^{2} +left(y-y_{C} right)^{2} =R^{2} } end{array}right. $, получим искомые координаты центра кривизны: $left{begin{array}{c} {x_{C} =x-frac{y’cdot left(1+y’^{2} right)}{y”} } \ {y_{C} =y+frac{1+y’^{2} }{y”} } end{array}right. $.
Координаты центра кривизны по существу являются параметрическими уравнения эволюты.
Задача 4
Найти эволюту параболы $y=x^{2} $. Результаты представить графически.
Находим производные: $y’=2cdot x$; $y”=2$.
По формулам $left{begin{array}{c} {x_{C} =x-frac{y’cdot left(1+y’^{2} right)}{y”} } \ {y_{C} =y+frac{1+y’^{2} }{y”} } end{array}right. $ находим координаты центра кривизны для произвольной точки $Mleft(x;yright)$.
Получаем:
[x_{C} =x-frac{2cdot xcdot left(1+left(2cdot xright)^{2} right)}{2} =-4cdot x^{3} ;]
[y_{C} =y+frac{1+left(2cdot xright)^{2} }{2} =3cdot x^{2} +frac{1}{2} .]
Полученные выражения фактически представляют собой параметрические уравнения эволюты, в которых $x$ является параметром. Если исключить параметр $x$ из этих уравнений, то может быть получено уравнение вида $Fleft(x_{C} ;y_{C} right)=0$, которое непосредственно связывает координаты эволюты.
Совмещенный график эвольвенты $y=x^{2} $ и её эволюты:
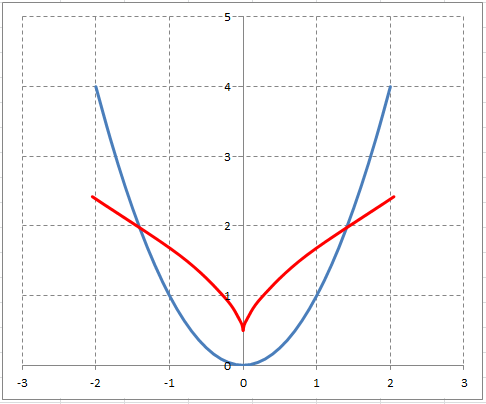
На графике синей линией изображена парабола $y=x^{2} $, а красной линией — её эволюта. Эволюта представляет собой полукубическую параболу.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Если в механизме с низшими парами точка звена на некотором участке траектории описывает приближенно дугу окружности (рис. 13.1) или прямую, то это обстоятельство можно использовать для получения механизма с остановкой ведомого звена при непрерывном движении начального звена. Действительно, если в точке звена, приближенно описывающей дугу окружности, шарнирно присоединить первое звено АВ двухповодковой группы, длина 1ав которого равна радиусу кривизны дуги окружности, а второе звено ВС этой группы присоединить к неподвижному, то при совпадении центра В внутреннего шарнира группы с центром О кривизны дуги этот центр шарнира остановится, следовательно, второе звено ВС группы будет также неподвижным все время, пока внешний шарнир А группы перемещается по дуге окружности. Неподвижный центр С шарнира необходимо всегда располагать на дуге радиуса 1вс с центром в точке О. [c.323]
Представим себе дугу окружности радиуса R (черт. 161). Возьмем на дуге две точки Ж и Mj и проведем в них нормали к дуге. Эги нормали совпадают с радиусами дуги и пересекаю 1ся в центре дуги О. Если мы будем приближать точку Aij к точке М, точка пересечения нормалей будет оставаться неизменной. Значит, и предельное ее положение, т. е. центр кривизны дуги, будет совпадать с центром дуги О. [c.169]
Для передачи движения с постоянным передаточным отношением широкое распространение получили предложенные еще Л. Эйлером (см. прил.) профили, являющиеся дугами эвольвент окружностей. Геометрическое место центров кривизны любой кривой (эвольвенты) называется эволютой. Эвольвенту и эволюту характеризуют следующие геометрические свойства эвольвента является разверткой эволюты, т. е. она описывается точкой прямой, которая перекатывается по эволюте без скольжения, поэтому радиус кривизны эвольвенты равен длине соответствующей дуги эволюты касательная к эволюте является нормалью к эвольвенте точка касания с эволютой нор.мали к эвольвенте является центром ее кривизны. [c.94]
Определим приращение вектора t на участке dZ (рис. 1.4). Можно строго показать, что при стремлении точки 2 к точке 1 отрезок траектории между ними стремится к дуге окружности с центром в некоторой точке О. Эту точку называют центром кривизны траектории в данной точке, а радиус р соответствующей окружности — радиусом кривизны траектории в той же точке. [c.15]
Радиус кривизны эвольвенты в точке 52 равен длине дуги 8аВ основной окружности. Центр кривизны эвольвенты в данной точке находится на основной окружности. [c.104]
При этом получают точки 1 —10, через которые проводят касательные к соответствующим основным окружностям. Как сказано выше, эти точки являются центрами кривизны эвольвент в определенных точках последних. Известно также, что длина радиуса кривизны равна длине развернутой дуги эволюты. На этом основании получим соответствующие точки эвольвент (9, 1, 2,. .., 10, отложив от точек касания О, 1, 2,. .., 10 отрезки, равные сум.марной длине такого количества долей, которое равно порядковому номеру точек. Так, например, чтобы определить точку 7 эвольвенты /(j, необходимо от точки 7 окружности F на соответствующей касательной отложить отрезок 7 —7, длина которого равна семи долям отрезка РВ. Полученные точки О, [c.288]
Передаточное отнощение от вала 1 к зубчатому колесу И равно четырем. Профиль кулачка 9 в пределах четырех равных участков очерчен дугами окружностей разных радиусов с плавным переходом на границах этих участков. Таким образом, за один оборот вала 1 кулачок 9 получает четверть оборота и устанавливает ползун 4 с роликом 8 на определенном расстоянии от центра вала, которое соответствует данному радиусу кривизны профиля кулачка 9. Высота выступающей части ползуна 4 определяет ход толкателя 7. [c.288]
Пользуясь третьим свойством эвольвенты, гласящим, что точки окружности Го являются центрами кривизны эвольвенты, дугу эвольвенты, проходящую через точку Р на участке между двумя [c.415]
Указанный способ построения при помощи дуг окружности не является единственным. Часто пользуются приемом построения, в котором центры дуг заменяющих окружностей выбирают в точках пересечения касательных к окружности Tq. Этот способ удовлетворяет условию плавного сопряжения дуг (чего нельзя сказать о способе, рассмотренном выще), но неточность его будет связана с тем, что центры кривизны отдельных участков кривой будут располагаться вне основной окружности, в то время как у действительной эвольвенты центры кривизны лежат на самой основной окружности. Мы будем в дальнейшем пользоваться изложенным выще приемом. Самым точным приемом графического построения эвольвенты является построение по координатам, вычисленным по уравнению эвольвенты, составленному на основании ее геометрических свойств и отнесенному к той или иной координатной системе (прямоугольной или полярной). [c.416]
Перейдем к выяснению профиля рейки, соответствующей эволь-вентному зацеплению, так называемой эвольвентной рей-к е. Переход от эвольвентного зубчатого колеса к эвольвентной рейке можно себе представить следующим образом. Пусть на рис. 427 будет представлено эвольвентное колесо с начальной окружностью т и углом зацепления а и основной окружностью Гц. Эвольвентный профиль около полюса зацепления Я в первом приближении может быть представлен как дуга окружности центра р, поскольку р является центром кривизны эвольвенты в точке Я. [c.423]
Так как направления касательной и, следовательно, нормали в начальной точке известны, можно найти положение центра кривизны. Радиусом е,со проводим небольшую дугу окружности и получаем точку Ai (фиг. 7). Определяем координаты точки Ai (фх, i) и tg 01, по которым вычисляем q j, находим новый центр кривизны и т. д. [c.206]
Торовый вариатор (рис. 10.8). Имеет на входном и выходном валах торовые чашки 7 и 2, между которыми вращаются два или три ролика 3. Рабочий профиль чашек очерчен дугами окружности с общим центром кривизны О. Частота вращения регулируется изменением угла наклона осей вращения роликов 3. [c.228]
Схема зацепления М. Л. Новикова показана на рис. 42. Рабочая часть профиля ведущего зуба 1 очерчена по дуге окружности радиуса Рх с центром в полюсе зацепления Р ведомый зуб 2 имеет вогнутый в торцовом сечении профиль с радиусом кривизны Р2>Р1- Обычно принимают — я [c.217]
Для иллюстрации результатов 11.3 — 11.5 рассмотрим устойчивость части тора, имеющей отрицательную гауссову кривизну, под действием осевой силы Р и крутящего момента М, приложенных к торцам и оболочки (рис. 11.1). Тор образован вращением дуги окружности радиуса R вокруг оси 00. Пусть — расстояние от центра С этой окружности до [c.225]
Здесь rfA —длина дуги, соответствующая углу (50 и охватывающая угол ( ф для мгновенного центра кривизны. Обозначим через а, h, р и Р соответственно окружное сжимающее [c.53]
НОСТИ (точке возврата) касательная к эвольвенте направлена по нормали к окружности. Отрезки прямой между точкой, образующей эвольвенту, и точкой касания этой прямой с окружностью представляют собой мгновенные радиусы кривизны эвольвенты. Например, в точке VII эвольвента имеет радиус кривизны д, определяемый длиной отрезка VII—7 с центром кривизны в точке 7. Поскольку кривая образуется обкатыванием прямой д по окружности, длина д всегда равна длине дуги [c.274]
Фиг, 1632. Шарнирный механизм для движения с остановками. Центр кривизны траектории точки Е шатуна ВС шарнирного четырехзвенника АВСО находится в точке Р, за время движения которой по приближенной дуге окружности радиуса ЕР коромысло НР будет почти неподвижно. [c.525]
Определение положений центров кривизны и радиусов очерчивающей кривой не встречает особых затруднений, когда кулачок очерчен дугами окружностей, отрезками прямой или участками эллипсов, парабол и т. п. Если же кулачок очерчен сложными кривыми, то приходится ограничиваться приближенными значениями радиусов. [c.151]
При отклонении клещевого рычага (если считать отрезок 0 0 у жестко с ним скрепленным) точка Оу перемещается по дуге окружности с радиусом = ОгО]. Таким образом, дуга 0 0 является геометрическим местом центров кривизны рабочего профиля клещевого рычага при центральном захватывании им заготовок различного диаметра. [c.201]
Переменное по дуге угловой части распределение деформаций, а следовательно, и переменное по дуге значение конечной толщины приводит к тому, что если внутренняя поверхность при штамповке получает форму и размеры, соответствующие размерам рабочей части пуансона, то наружная поверхность — некоторую естественную форму, зависящую от характера изменения толщины по дуге. Если при гибке по цилиндрической внутренней поверхности аппроксимировать наружную поверхность дугой окружности, то наружная и внутренняя поверхности будут иметь разные центры кривизны, а не один, как при гибке моментом. Это приводит к необходимости при конструировании деталей, получаемых гибкой, назначать размеры по внутренней поверхности угловых участков (по пуансону), а не по наружной. [c.116]
Отгибание бортов выполняется на штамповочных прессах или вручную на оправках. При ручном отгибании бортов с криволинейных листов используется оправка с очертанием, подобным кривизне листа. Отдельные участки листа нагреваются в горне, затем быстро закрепляются на оправке и фланцуются (отгибаются) также отдельными участками. При отбортовке листов, очерченных по дуге окружности большого диаметра, применяют оправку со штырем. В центре листа сверлят отверстие для центрирования и быстрого решения листа на штыре оправки. [c.152]
Теоретический профиль кулачка 1 описан на участке аЬ по прямой, на участке Ьс – по дуге окружности с центром Oj и, наконец, на участке са — по кривой переменной кривизны. Тогда на участке пЬ заменяющий механизм будет кулисным механизмом с ведущей кулисой X X, принадлежащей кулачку I, и фиктивным ползуном 3. На участке Ьс заменяющий механизм будет четырёхшарнирным механизмом 010 2 2, у которого кривошип 0 0-i принадлежит кулачку 1, а звено 5 будет фиктивным. Наконец, на участке са заменяющий механизм будет четырёхшарнирным механизмом O1O3B3/I.1 с переменными размерами кривошипа О] 63, принадлежащего кулачку У, и шатуна О3 В3. [c.23]
Если соблюдатся условие (12) для массы свободного ролика, равнодействующая сил 5 направлена касательно к гиперболе и инерционная центробежная сила очень мала из-за малого значения массы, то оказывается, что компенсаторная сила должна быть то же направлена по касательной к гиперболе. В действительности фокус А 2 перемещается по дуге окружности с радиусом и траектория отличается от гиперболы. Графически легко изобразить эту кривую. При конструировании для получения приблизительного движения по оптимальной траектории можно найти средний радиус кривизны и связать ролик с центром кривизны так, чтобы он двигался по окружности. Радиус кривизны определяется из зависимости [c.158]
Вычислив по этой формуле радиус кривизны меридиана в точке р имеем возможность провести следующую дугу окружности ргрз (с центром в m2 при m pi = = i T) и т. д. [c.114]
Кроме того, вводится таблица сведений 1= Ц, о характеристиках линий геометрическом виде линий (прямая, окружность, кривая), типе линий (контурная, невидимого контура, осевая, размерная), сведения о координатах центров кривизны, длин радиуссЗв, длин дуг. [c.68]
Всякий достаточно малый участок любой криволинейной траектории можно заменить дугой соответствующей окружности и, следовательно, представить себе эту криволинейную траекторию состоящей из дуг окружностей, описанных различными радиусами и из различных центров. Отсюда следует, что для определения нормального ускорения точки в любом ее криволинейном движении можно пользоваться установленной выше формулой, если только подставлять в нее вместо радиуса окружности радиус кривизны траектории в соответствующей ее точке. Таким образом, формуле для модуля а нормального ускорения можно придать следующую словесную формулировку нормальное ускорение точки равно квадрату скорости точки, деленному на радиус кривизны траектории в соответствующей ее точт кривой – [c.184]
Так как i охватывает окружность L в плоскости то контур на плоскости г, в который переходит окружность L, будет ох ватывать дугу BD , но при этом, подходя к точке В с двух сто рон, он будет касаться дуги BD (по теореме о сохранени углов). Полученный таким образом контур носит название ро филя Жуковского. При заданном расстоянии 4с в плоскости z профили, получаемые применением преобразования Жуковского к окружностям Li, характеризуются двумя параметрами. Параметр k, равный расстоянию по мнимой оси до центра основной окружности L, в плоскости z характеризует изгиб или кривизну профиля (его скелетной дужки). Параметр е, равный сдвигу F G по радиусу центра новой охватывающей окружности L относительно центра основной окружности L, характеризует толщину профиля (его телесность). Таким образом, профили Жуковского образуют двупараметрическое семейство, зависящее от параметров k и е/с. [c.163]
Горизонтальное сечение в виде круга, центр которого Су, будет перпендикулярно оси АС. Соседние горизонтальные сечения дают на поверхности оболочки окружности (широтные параллели), при этом элементарная длина дуги кривой АВ между соседними параллелями будет а кривизна дуги в данной точке равна 1/р1, где р1 — радиус кривизны меридиональной кривой АВ (в плоскости меридионального сечения). Если меридиональная кривая — прямая (цилиндрический резервуар, конический сосуд), то р1 = со. Два соседних меридиана АВ и АВ” и два соседних широтных круга вырезают на поверхности оболочки элемент 1—2—3—4 размерами с1з1 Хс182, где 52 — длина дуги кривой 1—2 в горизонтальном сечении (рис. 40). Радиус кривизны этой кривой в направлении, нормальном к кривой 1—3, в данной точке обозначаем через рз при этом следует иметь в виду, что для произвольного направления меридиональной кривой радиус этот не совпадает с г и равен р2 = г/з1па1, где угол — угол между осью АС и радиусом рг (в случае цилиндрического сосуда = 90°). Элемент, выделенный двумя соседними меридианами и соседними параллелями, изображен на рис. 40. По сечениям его 1—2 и 3—4 приложим по касательным в точках а и 6 к меридиональной кривой аЬ элементарные продольные меридиональные усилия [c.74]
Дисковый генератор схема-конструкция — рис. 6.12, а, б. Радиус дисков К принимают больше радиуса кривизны гибкого колеса, растянутого двумя силами. При этом гибкое колесо располагается по окружности ролика на некоторой дуге 2у. Радиусы дисков и расстояние между их центрами 2 е подбирают такими, чтобы угол у достигал 20-ь–Ь-40°. Гибкое колесо получает опору по всей зоне зацепления, что способствует сохранению формы деформации под нагрузкой. В этом преимущество перед четырехроликовым генератором. Отсутствие специальных подшипников и кулачка специального профиля упрощает конструкцию по сравнению с кулачковым генератором, что имеет значение главным образом для индивидуального и мелкосерийного производств. Для массового производства кулачковый генератор проще и дешевле. Кроме того, форма деформации по дуге окружности менее благоприятна по сравнению с формой по закону четырех сил (см, рис 6.2). Момент инерции и окружные скорости подшипников у дискового генератора значительно меньше, чем у кулачкового. Это может оказаться решающим при выборе типа генератора для передач, к которым предъявляют требо 5ния малой инерционности. Смещенное положение дисков 186 [c.186]
Подбором соотношения длин звеньев движение ведомого звена с периодической остановкой можно осуществить также при помощи рычажных механизмов, один из которых показан на рис. 48. В рычажном четырехзвенном шарнирном механизме ОАСО точка Е шатуна описывает траекторию, показанную на схеме штриховой линией. На некотором участке эта траектория мало отличается от дуги окружности с центром в Р. Если теперь к четырехзвенному механизму присоединить группу звеньев ЕРН, причем длину звена ЕР принять равной радиусу кривизны траектории на участке, описываемом дугой окружности, то при движении точки Е по этому участку траектории звено PH будет неподвижным. [c.25]
c.146
]
Курс теоретической механики Том1 Изд3 (1979) — [
c.140
]
