Как найти центры точек сопряжения

Как найти центры точек сопряжения

Сопряжения

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

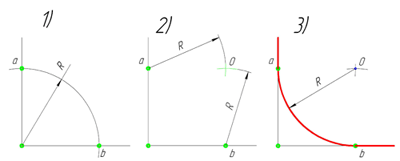
Сопряжение прямого угла

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

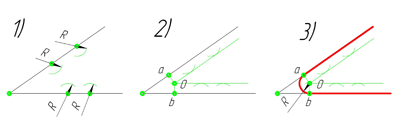
Сопряжение острого угла

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

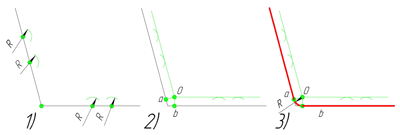
Сопряжение тупого угла

Сопряжение параллельных прямых линий

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Сопряжение паралельных прямых линий

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

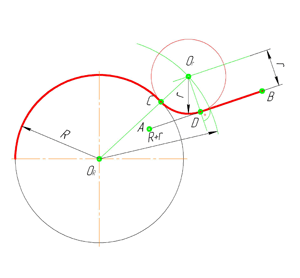
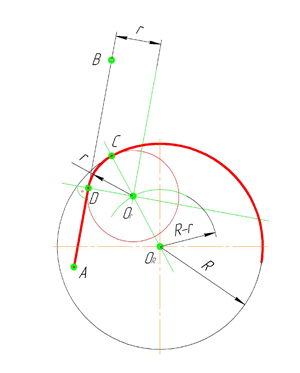
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.

Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внешнее сопряжение прямой линии с дугой окружности

Внутреннее сопряжение прямой линии с дугой

По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r. Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой окружности

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

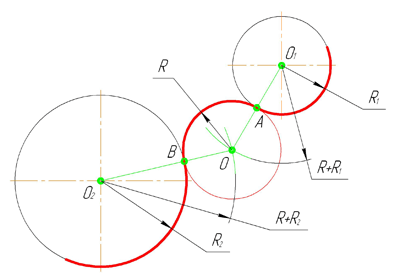
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внешнее сопряжение дуг окружностей

Внутреннее сопряжение дуг окружностей

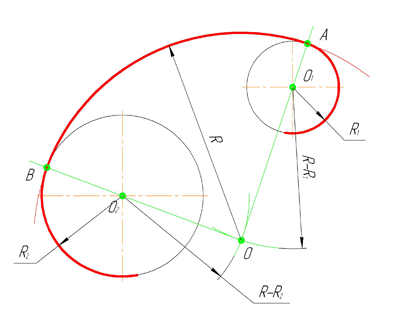
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Внутреннее сопряжение дуг окружностей

Смешанное сопряжение дуг окружностей

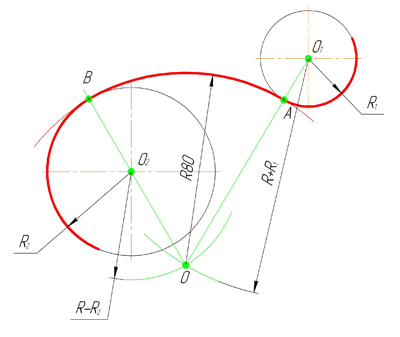
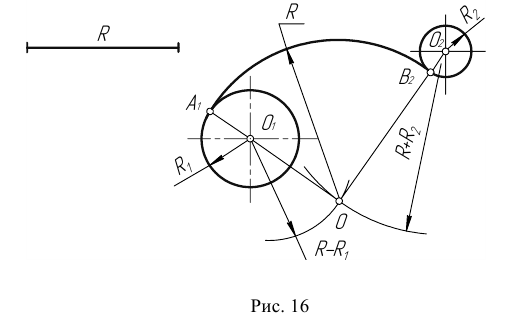
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Смешанное сопряжение дуг окружностей

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Сопряжения в инженерной графике на чертежах с примерами

Содержание:

В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход  одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.

  1. Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный  в точку касания К, перпендикулярен к касательной прямой.
  2. Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).

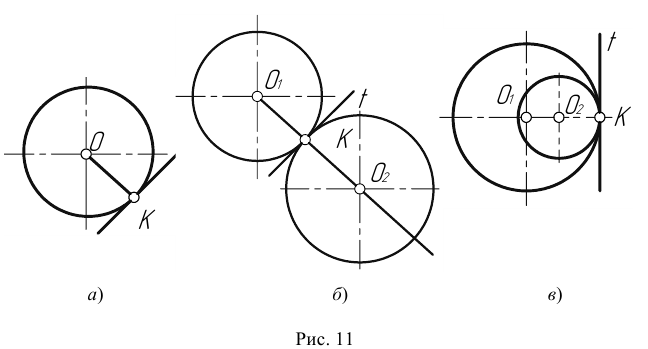
Сопряжения в инженерной графике на чертежах с примерами

Точка касания К и центры  окружностей 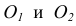Сопряжения в инженерной графике на чертежах с примерами

  • Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
  • Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
  • Дуга сопряжения АВ  – это дуга окружности, с помощью которой  выполняется сопряжение (рис. 12).
  • Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).

Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения;  2) центр сопряжения; 3) точки сопряжения.

Сопряжение двух пересекающихся прямых линий

Пусть  даны две пересекающиеся прямые m, n  и  радиус  сопряжения  R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.

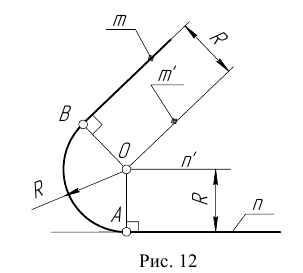
Сопряжения в инженерной графике на чертежах с примерами

Выполним следующие построения:

  1. Построим множество точек центров сопряжения, удаленных от прямой n   на расстояние радиуса R сопряжения. Таким множеством является прямая 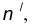Сопряжения в инженерной графике на чертежах с примерами параллельная данной прямой n  и отстоящая от неё на расстояние R.
  2. Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая 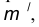Сопряжения в инженерной графике на чертежах с примерами  параллельная m и отстоящая от последней на расстояние R.
  3. В пересечении построенных прямых 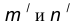Сопряжения в инженерной графике на чертежах с примерами найдем центр сопряжения О.
  4. Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.

Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.

Сопряжения прямой с окружностью

Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.  

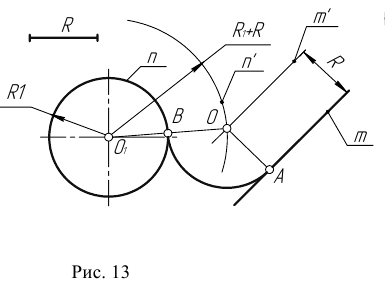
Пример 1. Пусть задана окружность радиусом R с центром в точке 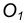Сопряжения в инженерной графике на чертежах с примерами и прямая m. Требуется построить сопряжение окружности с прямой дугой окружности заданного радиуса R (рис. 13).

Для решения задачи выполним следующие построения:

  1. Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает  прямая 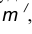Сопряжения в инженерной графике на чертежах с примерами параллельная m  и отстоящая от неё на расстояние R.
  2. Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность 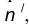 Сопряжения в инженерной графике на чертежах с примерами проведенная радиусом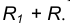 Сопряжения в инженерной графике на чертежах с примерами
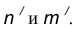
  3. Центр сопряжения О находим как точку пересечения линий Сопряжения в инженерной графике на чертежах с примерами
  4. Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров 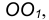Сопряжения в инженерной графике на чертежах с примерами т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
  5. Проведем дугу сопряжения АВ.

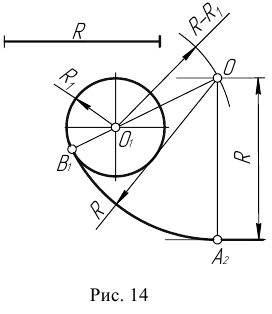
Сопряжения в инженерной графике на чертежах с примерами  Сопряжения в инженерной графике на чертежах с примерами

Пример 2.  При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 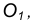Сопряжения в инженерной графике на чертежах с примерами , радиусом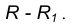  Сопряжения в инженерной графике на чертежах с примерами

  • Заказать чертежи

Сопряжение двух окружностей

Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.  

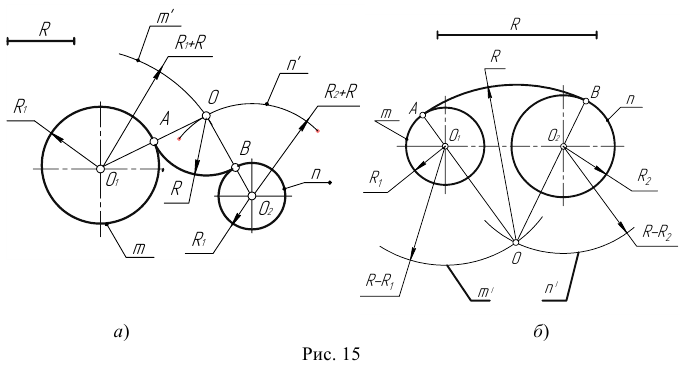
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n  с радиусами 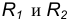Сопряжения в инженерной графике на чертежах с примерами  дугой заданного радиуса R (рис. 15а).

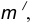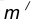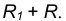
  1. Для нахождения центра сопряжения О  проведем окружность Сопряжения в инженерной графике на чертежах с примерами удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности Сопряжения в инженерной графике на чертежах с примерами равен Сопряжения в инженерной графике на чертежах с примерами
  2. Радиусом 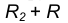Сопряжения в инженерной графике на чертежах с примерами  проведем окружность 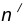Сопряжения в инженерной графике на чертежах с примерами, удаленную от данной окружности n на расстояние R.
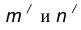  3. Найдем центр сопряжения О как точку пересечения окружностей  Сопряжения в инженерной графике на чертежах с примерами .
  4. Найдем точку сопряжения А как пересечение линии центров 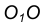Сопряжения в инженерной графике на чертежах с примерами с дугой m.
  5. Аналогично найдем точку В как пересечение линии центров 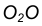Сопряжения в инженерной графике на чертежах с примерами с дугой n .
  6. Проведем дугу сопряжения   АВ.

Сопряжения в инженерной графике на чертежах с примерами

Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m  и n   с радиусами 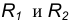Сопряжения в инженерной графике на чертежах с примерами  дугой радиусом   R  (рис. 15б).

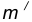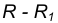  1. Для нахождения центра сопряжения О проведем окружность Сопряжения в инженерной графике на чертежах с примерами  на расстоянии Сопряжения в инженерной графике на чертежах с примерами от данной окружности m.
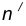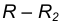  2. Проведем окружность Сопряжения в инженерной графике на чертежах с примерами  на расстоянии Сопряжения в инженерной графике на чертежах с примерами от данной окружности n.
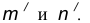
  3. Центр сопряжения О найдем  как точку пересечения  окружностей Сопряжения в инженерной графике на чертежах с примерами
  4. Точку сопряжения А найдем как точку пересечения линии центров 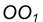  Сопряжения в инженерной графике на чертежах с примерами  с заданной   окружностью m.
  5. Точку сопряжения В найдем как точку  пересечения линии центров 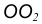  Сопряжения в инженерной графике на чертежах с примерамиc заданной окружностью n.
  6. Проведем дугу сопряжения AВ с центром в точке O.  

Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.

Сопряжения в инженерной графике на чертежах с примерами

Построение касательных

Пример 1. Дана окружность с центром в точке 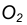Сопряжения в инженерной графике на чертежах с примерами и точка 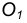Сопряжения в инженерной графике на чертежах с примерами  вне её. Через данную точку 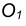Сопряжения в инженерной графике на чертежах с примерами провести касательную к данной окружности (рис. 17).

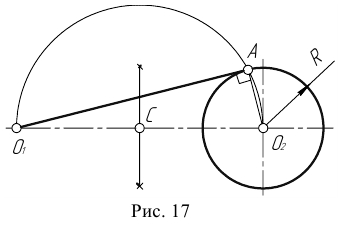
Сопряжения в инженерной графике на чертежах с примерами

Для решения задачи выполним следующие построения.

  1. Соединим точку 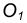Сопряжения в инженерной графике на чертежах с примерами с центром окружности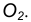 Сопряжения в инженерной графике на чертежах с примерами
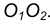
  2. Находим середину С отрезка Сопряжения в инженерной графике на чертежах с примерами
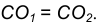
  3. Из точки С, как из центра, проведем вспомогательную окружность радиусом Сопряжения в инженерной графике на чертежах с примерами
  4. В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку 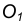Сопряжения в инженерной графике на чертежах с примерами с точкой А.  

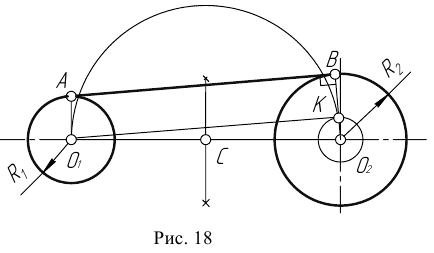
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 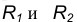Сопряжения в инженерной графике на чертежах с примерами  (рис. 18).

Сопряжения в инженерной графике на чертежах с примерами

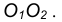
  1. Находим середину С отрезка Сопряжения в инженерной графике на чертежах с примерами
  2. Из точки С, как из центра, радиусом 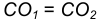Сопряжения в инженерной графике на чертежах с примерами проведем вспомогательную окружность.
  3. Из центра большей  окружности 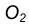Сопряжения в инженерной графике на чертежах с примерами  проведем вторую вспомогательную окружность радиусом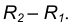 Сопряжения в инженерной графике на чертежах с примерами
  4. Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус 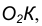Сопряжения в инженерной графике на чертежах с примерами идущий в точку касания В. 5. Для построения второй точки касания А проведем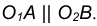 Сопряжения в инженерной графике на чертежах с примерами
  5. Соединим точки А и В отрезком прямой линии.
  • Нанесение размеров на чертежах
  • Резьба на чертеже
  • Соединения разъемные и неразъемные в инженерной графике
  • Виды конструкторских документов
  • Виды в инженерной графике
  • Разрезы в инженерной графике
  • Сечения в инженерной графике
  • Выносные элементы в инженерной графике
Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ ПЛОСКИХ ФИГУР (А.Ю. Горячкина, И.А. Горюнова) (книга).pdf

Скачиваний:

143

Добавлен:

10.02.2015

Размер:

16.47 Mб

Скачать

Рис. 28

построения соответственно семи-, восьми-, девятиугольника и т. д. с заданной стороной AB. Радиусами проводимых при этом окружностей являются расстояния от точки A до соответствующих центров.

4.1.Алгоритм построения cопряжений

Сопряжение — плавный переход одной линии в другую либо непосредственно, либо с помощью промежуточных дуг окружностей, называемых дугами сопряжения, радиусы в этом случае называют радиусами сопряжения.

Точка сопряжения — общая точка двух сопрягающихся линий, в которой одна линия переходит в другую и через которую проходит их общая касательная.

Центр сопряжения — центр дуги окружности, сопрягающей две линии. Его находят на пересечении двух геометрических фигур, каждая из которых является множеством точек плоскости, равноудаленных на заданное расстояние от одной из сопрягаемых линий.

Построения сопряжений с непосредственным переходом одной линии в другую являются не чем иным, как построением касательных: прямой, касательной к окружности, и окружности, касательной к другой окружности.

Рассмотрим переходы:

а) прямой в дугу окружности (или дуги окружности в прямую) (рис. 29). Точкой сопряжения K является точка касания, она находится в основании перпендикуляра, опущенного из центра O окружности на данную прямую. Где бы ни была проведена окружность радиуса R, плавно переходящая в данную прямую, всегда расстояние от ее центра O до заданной прямой равно R, т. е. геометрическим множеством центров O является прямая, проведенная параллельно данной прямой на расстоянии радиуса R;

б) одной дуги окружности внешнего касания в другую (рис. 30). Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной. Точкой сопряжения K является точка касания, она находится на пересечении сопрягаемых дуг линией их центров OO1. Где бы ни была проведена дуга

13

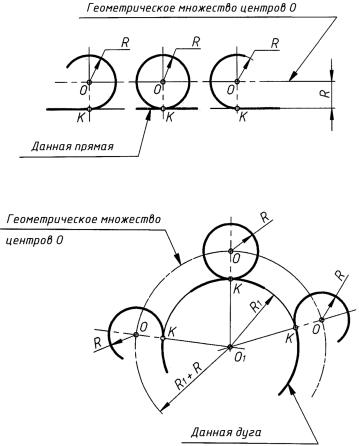
Рис. 29

Рис. 30

окружности радиуса R, расположенная с внешней стороны данной дуги окружности радиуса R1 и плавно переходящая в данную дугу, всегда расстояние от ее центра O до данной дуги равно ее радиусу R. Следовательно, геометрическим множеством центров O таких дуг окружностей будет концентрическая дуга окружности, расположенная с внешней стороны данной дуги на расстоянии радиуса R. Радиус этой дуги, а следовательно и расстояние между центрами O и O1, равен сумме радиусов R1 + R сопрягаемых дуг;

в) одной дуги окружности внутреннего касания в другую (рис. 31). Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной. Точкой K сопряжения является точка касания сопрягаемых дуг, она находится на пересечении этих дуг линией, являющейся продолжением линии центров OO1. Где бы ни была проведена дуга окружности радиуса R, расположенная внутри данной дуги окружности радиуса R1 и плавно переходящая в данную дугу, всегда расстояние от ее центра O до данной дуги равно ее радиусу R. Следовательно, геометрическим множеством центров O таких дуг будет концентрическая дуга окружности, расположенная внутри данной дуги и отстоящая от нее на величину радиуса R, т. е. радиус этой дуги (а следовательно, и расстояние между центрами O1 и O) будет равен разности радиусов R1 − R.

На основании изложенного можно сформулировать алгоритм построения сопряжения двух линий при заданном радиусе сопряжения:

1) построение множества точек, находящихся на расстоянии радиуса сопряжения от первой из сопрягаемых линий;

14

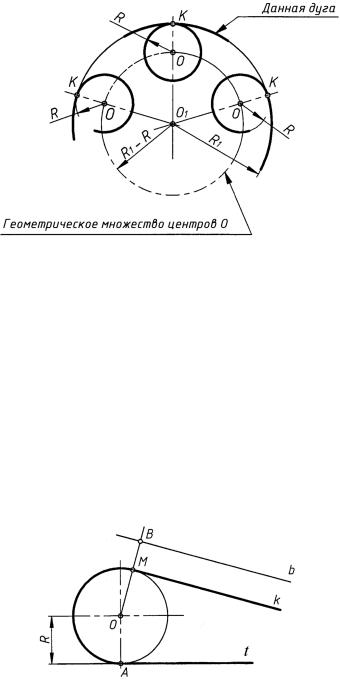
Рис. 31

2)построение множества точек, находящихся на расстоянии радиуса сопряжения от второй из сопрягаемых линий;

3)определение центра сопряжения на пересечении этих множеств;

4)определение точек сопряжения на сопрягаемых линиях; проведение дуги сопряжения между точками сопряжения.

4.2. Построение прямой, касательной к окружности

Прямая, касательная к окружности, составляет угол 90◦ с радиусом, проведенным

вточку касания. Таким образом, для построения прямой t, касающейся окружности

взаданной точке A, надо провести искомую прямую перпендикулярно радиусу OA (рис. 32).

Рис. 32

Для проведения касательной к окружности, параллельной заданной прямой b, достаточно найти точку сопряжения M на пересечении заданной окружности с перпендикуляром к прямой, опущенным из центра O: b OB; k OB; k||b.

4.3. Сопряжение пересекающихся прямых с помощью дуги окружности заданного радиуса R

Для нахождения центра O сопрягающей окружности (рис. 33) строим геометрическое множество точек, отстоящее от прямой m на расстояние R. Строим геометрическое множество точек, отстоящее от прямой n на расстояние R. На пересечении двух множеств находим точку O — центр дуги сопряжения. Точки сопряжения A и B лежат в

15

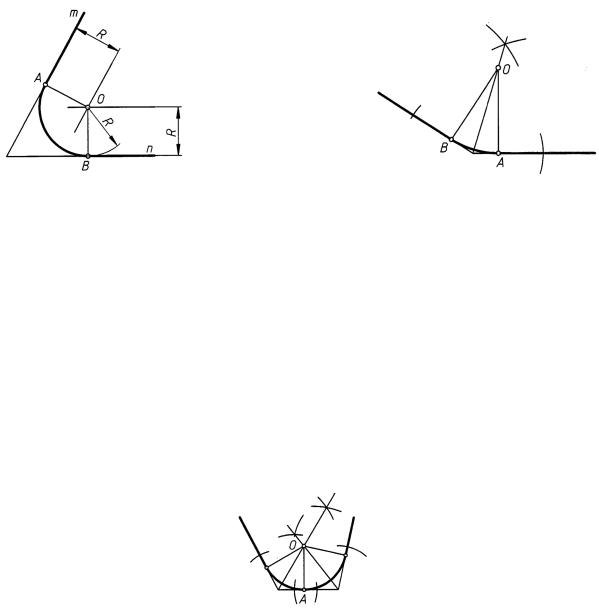
основании перпендикуляров, проведенных к исходным прямым, и ограничивают дугу сопряжения.

Если положение одной из точек сопряжения задано (рис. 34, точка A), а радиус сопряжения не указан, то искомый центр O находится на пересечении перпендикуляра к прямой, проведенного из точки A, и биссектрисы угла, образованного заданными прямыми (построение биссектрисы см. на рис. 13).

4.4. Сопряжение трех пересекающихся прямых

Положение центра сопрягаемой окружности (рис. 35) определяется точкой пересечения биссектрис углов. Радиус окружности (дуги´ сопряжения) равен длине перпендикуляра, опущенного из центра O на любую из трех заданных прямых.

Рис. 35

4.5. Сопряжение окружности и прямой с помощью дуги окружности заданного радиуса R

Внешнее касание (рис. 36, а). Центр O дуги сопряжения находится на пересечении двух геометрических множеств точек: вспомогательной прямой, отстоящей от заданной прямой на величину радиуса R, и дуги´ радиуса R1 + R, проведенного из центра O1. Точки сопряжения K и M находятся соответственно в основании перпендикуляра OK и на пересечении прямой O1O с основной окружностью.

Внутреннее касание (рис. 36, б). Центр O дуги сопряжения находится на пересечении двух геометрических множеств точек: вспомогательной прямой, отстоящей от заданной прямой на величину радиуса R, и дуги´ радиуса R1 −R, проведенной из центра O. Точки сопряжения K и M находятся соответственно в основании перпендикуляра OK и на пересечении продолжения луча O1O с основной окружностью.

16

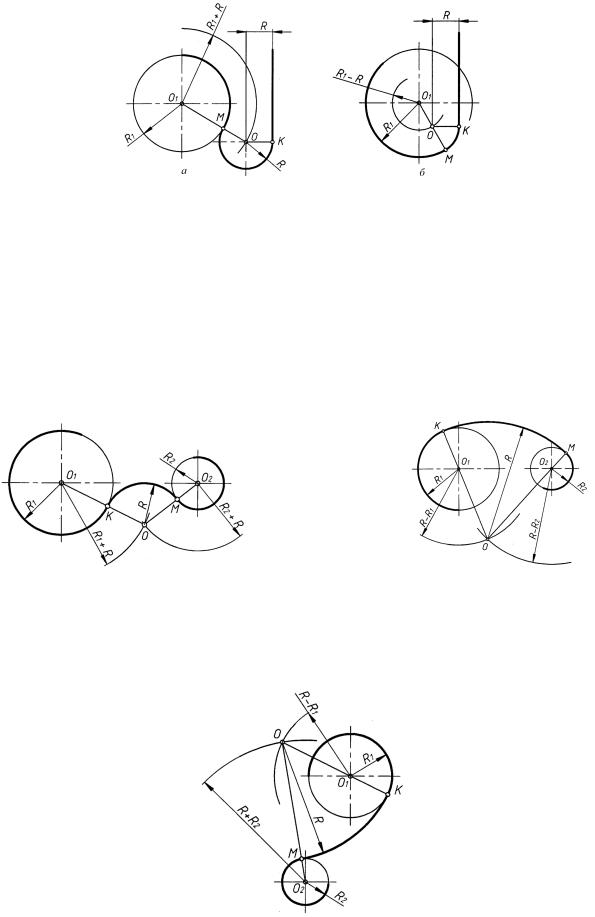
Рис. 36

4.6. Сопряжение двух окружностей с помощью дуги окружности заданного радиуса R

Внешнее касание (рис. 37). Центр O искомой дуги радиуса R находится на пересечении двух геометрических множеств точек — двух вспомогательных окружностей,

описанных из центров O1 и O2 соответствующими радиусами R1 + R и R2 + R. Внутреннее касание (рис. 38). Центр O искомой дуги радиуса R находится на пере-

сечении двух геометрических множеств точек — двух вспомогательных окружностей, описанных из центров O1 и O2 соответствующими радиусами R − R1 и R − R2.

Рис. 37 Рис. 38

Смешанное касание (внешнее и внутреннее) (рис. 39). Центр O искомой дуги радиуса R находится на пересечении двух геометрических множеств точек — двух вспомогательных окружностей, описанных из центров O1 и O2 соответствующими

Рис. 39

17

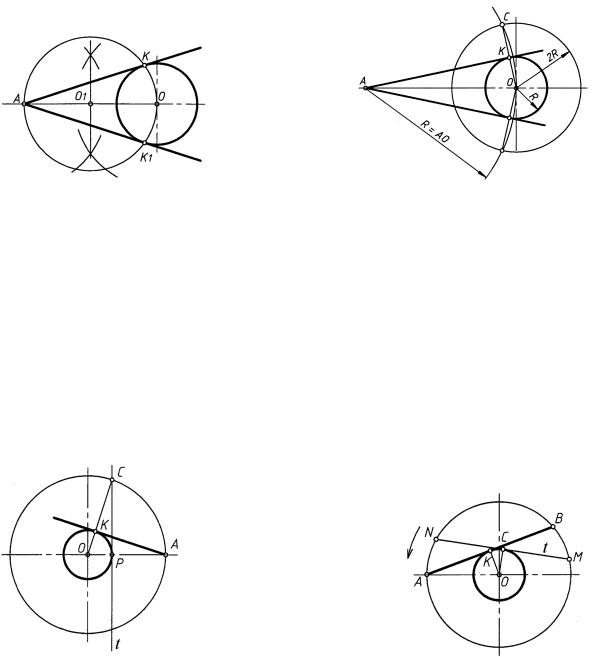
радиусами R − R1 и R + R2. Для всех случаев точки сопряжения K и M лежат на линиях, соединяющих центры сопрягаемых окружностей.

4.7. Построение касательной к окружности, проведенной через заданную точку, лежащую вне окружности

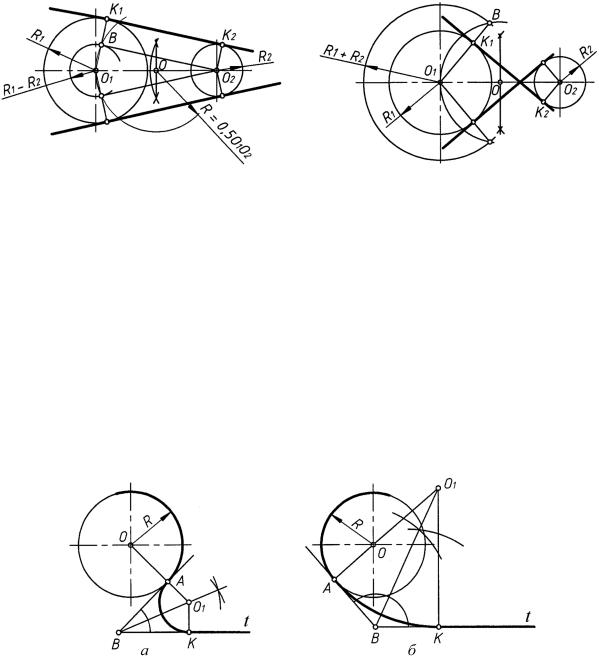
Способ 1 (рис. 40). Точки сопряжения K и K1 расположены на окружности при ее пересечении со вспомогательной окружностью, диаметр которой равен AO (вписанный в окружность угол равен половине центрального угла, следовательно, угол OKA прямой, AK — касательная).

Способ 2 (рис. 41). Точка сопряжения К расположена на окружности при ее пересечении с отрезком OC. Точка C — точка пересечения первой вспомогательной окружности с центром в точке O, радиус которой в 2 раза больше радиуса заданной окружности, и второй вспомогательной окружности с центром в точке A радиуса AO (точка K является серединой отрезка OC основания равнобедренного треугольника CAO, следовательно, угол OKA прямой, AK — касательная).

Способ 3 (рис. 42). Точка сопряжения K расположена на окружности при ее пересечении с отрезком OC. Точка C — точка пересечения вспомогательной окружности с центром в точке O радиуса OA с касательной t (треугольники OPC и OKA конгруэнтны, так как имеют общий угол при вершине O, заключенный между равными сторонами OP = OK, OC = OA, но треугольник OPC прямоугольный (угол при вершине P = 90◦), поэтому угол К = 90◦, AK — касательная).

Рис. 42 Рис. 43

Способ 4 (рис. 43). Точка сопряжения K получена вращением вокруг точки O касательной t в произвольной точке С заданной окружности до совмещения точки N с точкой A. Точка С займет положение точки K; AK — касательная.

18

4.8. Построение касательной к двум окружностям

Эта задача сводится к задаче на построение касательной к окружности, проведенной через заданную точку, лежащую вне окружности (см. разд. 4.7).

Внешнее касание (рис. 44). Из центра O1 большей окружности построить вспомогательную окружность радиуса R1 − R2. Разделить отрезок O1O2 пополам в точке O и провести вторую вспомогательную окружность радиуса R = OO1. Точка B пересечения вспомогательных окружностей определяет направление радиуса O1K1, где K1 — искомая точка сопряжения для окружности радиуса R1. Для построения точки сопряжения K2 для окружности радиуса R2 достаточно из центра O2 провести радиус O2K2 параллельно радиусу O1K1 до пересечения с окружностью радиуса R2.

Внутреннее касание (рис. 45). Из центра O1 большей окружности построить вспомогательную окружность радиуса R1 +R2. Далее выполнить построения в соответствии

срис. 44.

4.9.Сопряжение окружности и прямой при условии, что дуга сопряжения

проходит через заданную точку на окружности

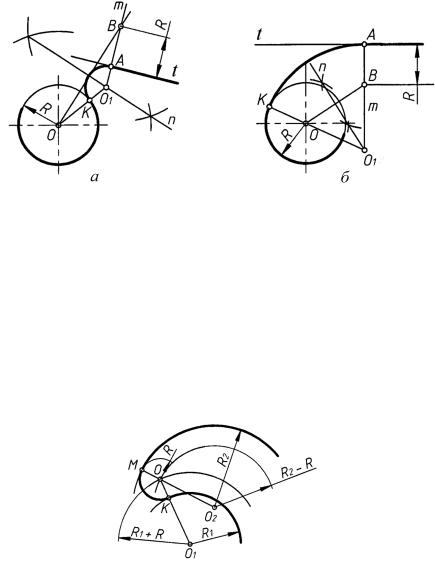
Центр дуги сопряжения O1 (рис. 46, а — внешнее касание; рис. 46, б — внутреннее касание) определяется точкой пересечения прямой OA, проведенной через точку сопряжения A и центр O заданной окружности, и биссектрисы угла ABK, образованного касательной AB в точке сопряжения A и заданной прямой t. Радиус сопрягающей дуги равен расстоянию O1A; O1K t, где точка K — точка сопряжения на прямой t.

Рис. 46

19

4.10. Сопряжение окружности и прямой при условии, что дуга сопряжения проходит через точку на прямой

Центр дуги сопряжения O1 (рис. 47, а — внешнее касание; рис. 47, б — внутреннее касание) определяется точкой пересечения перпендикуляров m и n; m — перпендикуляр к прямой t, проведенный через точку A; n — серединный перпендикуляр к отрезку OB (отрезок AB равен радиусу R заданной окружности). Поскольку точка касания двух окружностей находится на линии, соединяющей их центры, то точка K — точка сопряжения; O1K — радиус дуги сопряжения.

Рис. 47

4.11. Сопряжение двух неконцентрических дуг окружностей третьей дугой заданного радиуса R

Даны две дуги, описанные из центров O1 и O2 радиусами R1 и R2. Для сопряжения их дугой заданного радиуса R (рис. 48) проведем из тех же центров две вспомогательные дуги радиусов R1 + R и R2 − R. Пересечение этих дуг позволяет определить искомый центр сопряжения — точку O. Точки сопряжения K и M лежат на линиях, соединяющих центр сопряжения и соответствующие центры дуг.

Рис. 48

4.12. Сопряжение окружности в заданной точке с окружностью, проходящей через заданную точку

Центр О1 дуги сопряжения (рис. 49, а — внешнее касание; рис. 49, б — внутреннее касание) определяется точкой пересечения прямой, проведенной через центр O и заданную точку сопряжения B, с перпендикуляром, восстановленным из середины хорды AB; O1B — радиус искомой окружности.

20

Рис. 49

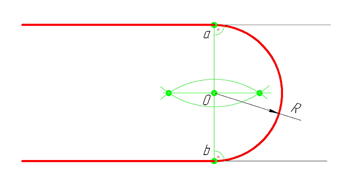
4.13. Сопряжение двух параллельных прямых двумя дугами при заданных точках сопряжения

Для построения центров сопряжения O1 и O2 (рис. 50) заданные точки сопряжения A и B соединены отрезком AB. На отрезке AB выбрана произвольная точка M. Восстановлены серединные перпендикуляры к отрезкам AM и MB. Искомые центры сопряжения O1 и O2 находятся в точках пересечения серединных перпендикуляров с соответствующими перпендикулярами, проведенными к заданным прямым из точек сопряжения A и B. Радиусы сопрягаемых дуг: R1 = O1A; R2 = O2B. Касание дуг происходит в точке M, находящейся на линии центров O1O2. Если AM = MB, то

R1 = R2.

Рис. 50

Примеры использования сопряжений в инженерной практике представлены на рис. 51 и 52.

Рис. 51

21

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #

    10.02.201533.89 Mб41Гидравлика и гидропневмоприводы 2010.pdf

Источник

При изучении дисциплины «Начертательная геометрия и
инженерная графика» студенты должны усвоить правила и последовательность
выполнения геометрических построений и сопряжений. В этом отношении лучшим
способом приобретения навыков построения являются задания по вычерчиванию
контуров сложных деталей.

Прежде чем приступить к выполнению контрольного задания,
нужно изучить технику выполнения геометрических построений и сопряжений по
методическому пособию.

Сопряжения линий

Сопряжением называется
плавный переход от одной линии к другой. Для построения любого сопряжения дугой
заданного радиуса нужно найти:

  1. Центр
    сопряжения – центр, из которого проводят дугу;
  2. Точки
    сопряжения (касания) – точки, в которых одна линия переходит в другую.

Центр сопряжения
находится от точек сопряжения на одинаковых расстояниях, равных радиусу
сопряжения R.  Переход от прямой к
окружности будет плавным в том случае, если прямая касается к окружности. Точка
сопряжения К лежит на перпендикуляре, опущенном из центра О окружности к прямой
(рис.
1)

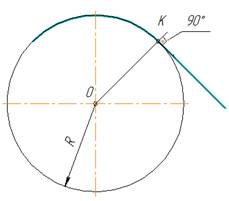
рис. 1

Переход от одной
окружности к другой будет плавным, если окружности касаются.

Различают два случая
касания дуг окружностей: внешнее (рис.
2)  и внутреннее (рис.3).

При внешнем касании
центры окружностей лежат по разные стороны от их общей касательной L (рис. 2). Расстояние между их центрами ОО1 равно
сумме радиусов окружностей R+R1 и точка касания лежит на прямой ОО1,
соединяющей их центры.

При внутреннем касании
центры окружностей лежат по одну сторону от их общей касательной L. Расстояние
между их центрами ОО1 равно разности их радиусов  R-R1 и точка касания К окружностей
лежит на продолжении прямой ОО1 (рис.
3).

рис. 2

рис. 3

Касание дуг окружностей:

рис. 2 – сопряжение двух окружностей (внешнее касание)

рис. 3 – сопряжение двух окружностей (внутреннее касание)

Сопряжение двух пересекающихся прямых 

Даны
пересекающиеся  под прямым, острым и
тупым углами прямые линии.

Требуется построить сопряжения этих прямых дугой заданного
радиуса R.

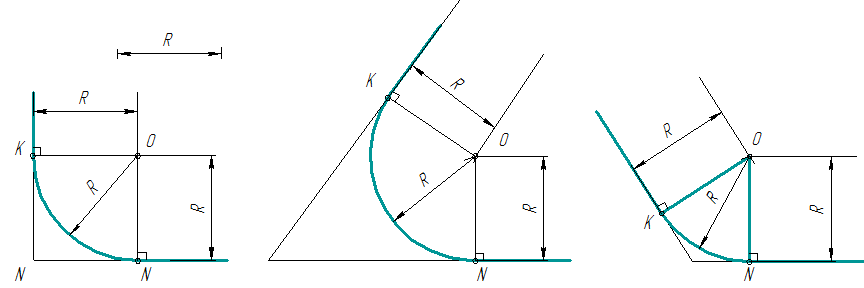
рис. 4

  1. Для
    нахождения центра сопряжения проводят вспомогательные прямые, параллельные
    данным на расстоянии равном радиусу R. Точка пересечения этих прямых т.О и
    будет центом дуги сопряжения (рис.
    4).
  2. Перпендикуляры,
    опущенные из центра дуги сопряжения т.О на данные прямые, определяют точки
    касания К и N.
  3. Из
    точки О, как центра, описывают дугу заданного радиуса R.

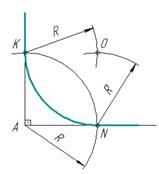
рис. 5

Примечание.Для
прямых углов центр сопряжения удобнее находить с помощью циркуля (рис. 5).

Сопряжение дуги окружности и прямой
линии дугой заданного радиуса.

Внешнее касание

Дана окружность радиуса
R  и прямая АВ. Требуется соединить их дугой
радиусом  R1.

 

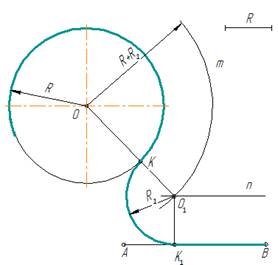
 рис. 6 

  1. Для
    нахождения центра сопряжения из центра О заданной окружности проводят дугу m радиуса R + R1 и
    на расстоянии R1 – прямую n // AB. Точка  О1  пересечения прямой n и дуги m будет центром
    сопряжения.
  2. Для
    получения точек сопряжения: К и К1  проводят линию центров ОО1 и
    восстанавливают к прямой АВ перпендикуляр ОК1.
  3. Из
    центра сопряжения О1 между точками К и К1  проводят дугу сопряжения радиусом  R1

Внутреннее касание

В случае внутреннего
касания выполняют те же построения, но дугу m 
вспомогательной окружности проводят радиусом R – R1.

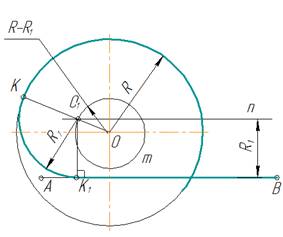
рис. 7

Сопряжение двух окружностей дугой
заданного радиуса

Заданы две окружности
радиусом R1 и R2. Требуется построить сопряжение дугой
заданного радиуса R.

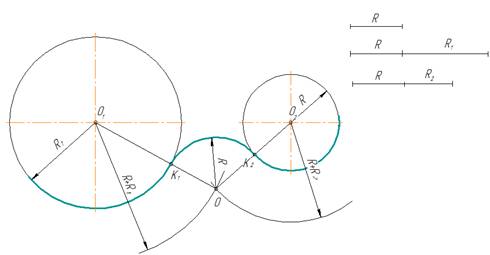
рис. 8

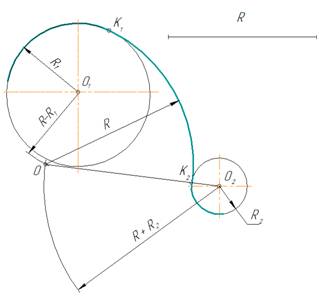
Внешнее касание

  1. Для
    определения центра сопряжения О проводят вспомогательные дуги: из центра О1окружности радиусом  R + R1  и из центра О2 окружности радиуса R
    + R2. Точка О пересечения этих дуг является центом сопряжения.
  2. Соединяя
    центры О и О1, а так же О и О2 , определяют точки
    сопряжения (касания) К1  и  К2.
  3. Из
    центра О радиусом R проводят дугу сопряжения между точками  К1 
    и К2

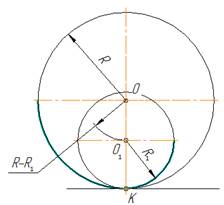
Внутреннее касание

При внутреннем касании
выполняют те же построения, но дуги проводят радиусами

R -R1  и R – R2.

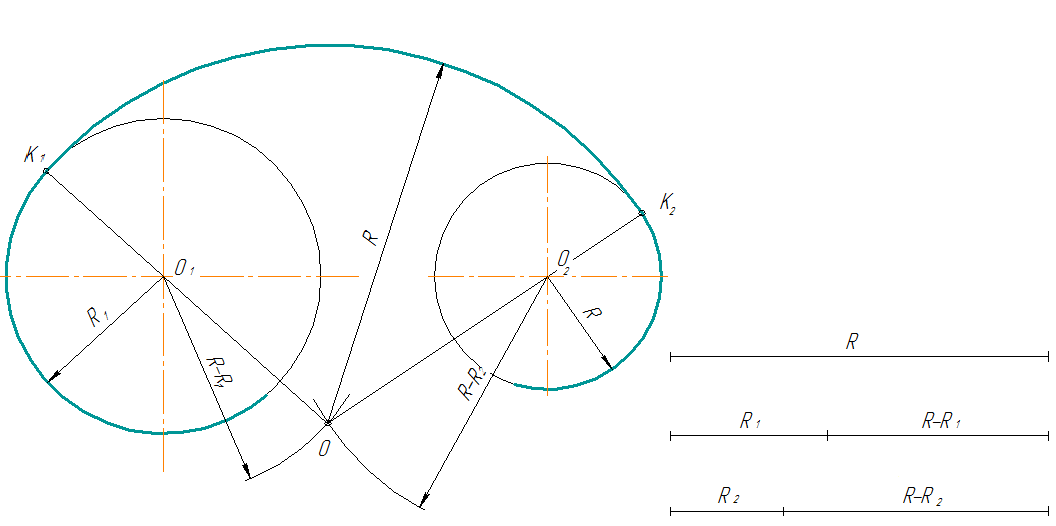
рис. 9

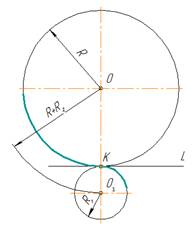
Смешанное касание


рис. 10

Центр сопряжения О
находится в пересечении двух дуг, описанных из центра О1 радиусом R
– R1 и из центра О2 радиусом R + R2

Примечание. При
смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри
сопрягающей дуги радиуса R , а центр О2 другой дуги – вне ее.

Частные случаи

Нахождение
центра дуги заданного радиуса.

Задана дуга радиусом R,
соединяющая две параллельные прямые mи n и проходящая через точку А ∈ m (рис. 11). Требуется найти центр О заданной дуги.

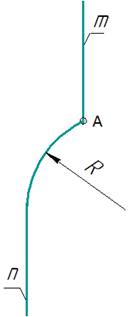
рис. 11

В основу построения положено нахождение
точки О, равноудаленной от заданных прямых (рис.
11).

  1. Из
    точки А ∈ m, как из центра, проводят дугу
    вспомогательной окружности с заданным радиусом R.   
  2. Проводят
    вспомогательную прямую l,
    параллельную прямой n, на
    расстоянии, равном заданному радиусу R.
  3. Точка О – точка пересечения этих
    вспомогательных линий является центром заданной дуги. (рис. 12)

 

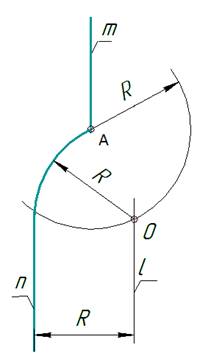
рис. 12

Литература

  1. Боголюбов
    С.К. Инженерная графика: Учебник для средних специальных учебных заведений. –
    3-е изд., испр. И доп. – М.: Машиностроение, 2006. – с.392:  ил.
  2. Куприков
    М.Ю. Инженерная графика: учебник для ССУЗов – М.: Дрофа, 2010 – 495 с.: ил.
  3. Федоренко
    В.А., Шошин А.И. Справочник по машиностроительному черчению Л.: Машиностроение.
    1976. 336 с.
Источник

Обновлено: 23 нояб. 2020 г.

Графические работы ПР.01.02., ПР.01.03. Раздел “Геометрические построения”.


Если Вы пропустили занятие с разбором данной темы и не знаете как выполнить задание, то прочитайте этот пост.

Для выполнения работы необходимо знать следующие темы:

– рамка и основная надпись;

– типы линий;

– правила нанесения размеров на чертежи;

– геометрические построения.

Задание на ПР.01.02.

На формате А4, расположенном вертикально, вычертить рамку и основную надпись. Выполнить работу как в примере, используя знания по делению окружностей на равные части.

Сопряжения

Часто в черчении возникает необходимость в скруглении прямых. Для этого необходимо знать алгоритм выполнения сопряжений.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

1. Сопряжение прямого угла.

Построение сопряжения прямого угла заданным радиусом сопряжения R. Примем R=15 мм. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R=15 мм до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R=15 мм до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

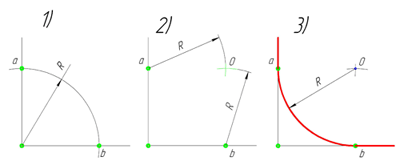
2. Сопряжение острого угла.

Для построения сопряжения острого угла раствором циркуля, равным радиусу сопряжения R=15 мм, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R=15 мм, соединив точки сопряжения a и b. Сопряжение острого угла построено.

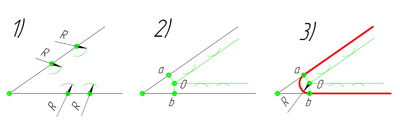
3. Сопряжение тупого угла.

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R=15 мм проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. После чего опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R=15 мм, полученные точки a и b.

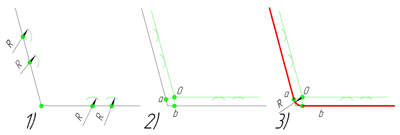
При построении сопряжения двух окружностей дугой третьей окружности заданного радиуса возможны три варианта: внешнее сопряжение, внутренне сопряжение и сочетание внешнего и внутреннего сопряжений.

Разберем по порядку каждый вариант сопряжения двух окружностей.

4. Внешнее сопряжение окружностей дугой заданного радиуса R.

Сопрягающая дуга касается заданных окружностей внешней стороной. Центр О сопрягающей дуги должен отстоять от окружностей на одном и том же расстоянии, равном R. Чтобы построить центр О сопрягающей сопрягающей дуги, из центров окружностей О1 и О2 проведем две вспомогательные дуги радиусами (R+R1) и (R+R2) до их взаимного пересечения. Точки сопряжения лежат на линиях, соединяющих центры окружностей.

В данном примере R=30 мм, R1=25 мм, R2=15 мм. Расстояние между центрами окружностей – О1-О2=60 мм.

5. Внутренне сопряжение окружностей дугой заданного радиуса R.

Сопрягающая дуга касается заданных окружностей внутренней стороной. Центр О сопрягающей дуги определяется пересечением дуг вспомогательных окружностей, радиусы которых равны разностям (R-R1) и (R-R2).

В данном примере R=80 мм, R1=25 мм, R2=15 мм. Расстояние между центрами окружностей – О1-О2=60 мм.

6. Сочетание внешнего и внутреннего сопряжений окружностей дугой заданного радиуса R.

Одна из заданных окружностей находится внутри сопрягающей окружности. Центр О сопрягающей дуги определяется в точке пересечения вспомогательных окружностей, проведенных для внешнего сопряжения радиусом (R+R1), а для внутреннего – радиусом (R-R2).

В данном примере R=70 мм, R1=25 мм, R2=15 мм. Расстояние между центрами окружностей – О1-О2=60 мм.

Задание и пример выполнения практической работы 01.03 представлены ниже.

На формате А4, расположенном вертикально, вычертить рамку (5 мм сверху, снизу и справа, 20 мм слева) и основную надпись. Выполнить работу как в примере, используя знания по выполнению сопряжений.

Выполненные работы сдать на проверку преподавателю.

Источник

Добавить комментарий