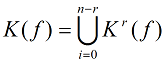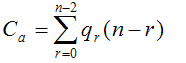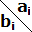Цена покрытия.
Цена
r-куба
представляет собой количество несвязанных
координат.
Sr=n*r
Для
оценки качества покрытия используют
два вида цены покрытия :
m
-
Sa=åSrNr,
где
Nr
–
количество r-кубов,
входящих в по-
r=0
крытие,
m
–
максимальная размерность куба.
Цена Sa
представляет
собой сумму цен кубов,
входящих в покрытие.
-
Sb=Sa+k,
где
k
– количество кубов,
входящих в покрытие
m
m
Sa
=å(n-r)
Nr
;
Sb=å(n-r)(Nr+1)
r=0
r=0
Под
минимальным покрытием понимают покрытие,
обладающее минимальной ценой Sa
по сравнению с любым другим покрытием
этой функции.
Можно
показать,
что покрытие,
обладающее минимальной ценой Sa
обладает также и минимальной ценой
Sb.
Пример
:
f3(x)=V(0,1,4,6,7)
(f=1)
C0(f)=K0(f)
; Sa=5*3=15
; Sb=Sa+5=20
C1(f)=K1(f)
; Sa=4*2=8
; Sb=Sa+4=12
Cmin(f)
: Sa=3*2=6
; Sb=9
Цена
покрытия Sa
представляет собой количество букв,
входящих в ДНФ,
которая соответствует данному покрытию.
Цена
Sb
представляет для ДНФ сумму количества
букв и количества термов.
Цена
покрытия хорошо согласуется с ценой
схемы по Квайну,
которая строится по нормальной форме,
соответствующей этому покрытию.
Для
приведенной схемы цена по Квайну SQ=9=Sb
(9-число
входов).
В
принципе,
между SQ
и ценами
Sa
и Sb
существует соотношение Sa
£
SQ
£
Sb
Это неравенство имеет место при следующих
допущениях по комбинационной схеме :
1)Схема
строится по нормальной форме (ДНФ или
КНФ).
2)Схема
строится на элементах булевого базиса
(И,
ИЛИ).
3)На
входы схемы можно подавать как прямые,
так и инверсные значения входных
переменных,
представляющие собой значения аргументов
булевой функции (схема с парафазными
входами).
Элементы
НЕ (инвертора в схеме отсутствуют.
Нулевое покрытие булевой функции и получение минимальной кнф.
Выше
было рассмотрено покрытие булевой
функции на наборах аргументов для
которых функция равна единице.
Такие
покрытия можно назвать единичными.
Наряду с единичными
покрытиями существуют и нулевые,
для которых покрываются наборы аргументов,
на которых функция равна нулю,
то есть покрытие реализуется для
существенных вершин,
но не самой функции,
а ее отрицания (инверсии).
Нулевое
покрытие строится также как и единичное,
но только для отрицания исходной функции.
f3(x)=V(0,1,4,6,7)
f3(x)=&(2,3,5)
(f=1)
(f=0)
|010
K0(`f
)=|011
|101
C0(`f
)= K0(`f
) Sa=9
Sb=12
K1(`f
)=|01x Z(`f
)=Cmin(`f
)=|01x Sa=5
Sb=7
|101
Цена
минимального нулевого покрытия оказалась
меньше цены минимального единичного
покрытия.
Так
как заранее предсказать невозможно,
какое из минимальных покрытий данной
функции,
единичное
или нулевое,
будет иметь меньшую цену,
то для построения схемы,
обладающей минимальной ценой по Квайну,
целесообразно решать задачу минимзации
в отношении обоих покрытий.
Импликанты булевой функции. Системы импликант.
Решение
задачи минимизации булевой функции
методом Квайна и усовершенствованным
методом Квайна-МакКласски базируется
на понятиях импликант и их систем.
Определение
:
Булева функция g(x)
называется импликантой булевой функции
f(x),
если для любого набора аргументов,
на
которых g(x)=1,
f(x) также
равна единице.
~
~
~
g(
x )=1 => f( x )=1,
где х
– некоторый
набор аргументов.
Свойства
импликант
:
-
Между
импликантой и самой функцией существует
отношение включения g(x)Ìf(x). -
Можно
утверждать,
что для любого набора аргументов,
на котором функция равна нулю,
ее импликанта также равна нулю. -
Если
g(x)
и j(x)
являются
импликантами функции f(x),
то их дизъюнкция также является
импликантой этой функции.
Простейшими
примерами импликант могут служить
конъюнктивные термы,
входящие в ДНФ данной функции.
Пример
:
для f3(x)=V(0,1,4,6,7)
(#)
(f=1)
импликантами
являются `х1`х2х3;
х1х2`х3;
х1х2;…
Произвольная
дизъюнкция этих термов также является
импликантой функции.
Определение
:
Простой (первичной) импликантой булевой
функции называется конъюнктивный терм,
который сам является импликантой этой
функции,
но никакая его собственная часть уже
не является импликантой этой функции.
Под
собственной частью терма понимается
новый терм,
полученный
из исходного,
путем вычеркивания произвольного числа
букв.
Для
данного примера функции (#)
простыми импликантами
являются
:
`х1`х2х3;
х1х2`х3;
х1х2;…
Множеству
простых импликант можно поставить в
соответствие множество максимальных
кубов.
Определение
:
Дизъюнкция всех простых импликант
булевой функции представляет собой ДНФ
этой функции,
которая называется сокращенной – СДНФ.
Для
функции (#)
из
приведенного примера
СДНФ
:
y=
х1х2v
`х1`х2v`х2`х3v
х1`х3
Понятие
«сокращенное»
присвоено ДНФ в том смысле,
что она,
как правило,
содержит меньшее количество букв и
термов по сравнению с КДНФ.
Для
нашего примера КДНФ содержит 15 букв и
5 термов,
а СДНФ – 8 букв и 4 терма.
Обратимся ко второму общему методу разработки аппроксимирующих алгоритмов: методу назначения цены. Для знакомства с этим методом будет рассмотрена версия задачи о вершинном покрытии. Как было показано в главе 8, задача о вершинном покрытии является частным случаем задачи покрытия множества, поэтому сначала мы рассмотрим возможность применения сведения при разработке аппроксимирующих алгоритмов. После этого мы разработаем алгоритм с улучшенными гарантиями аппроксимации по сравнению с обобщенной границей, полученной для задачи покрытия множества в предыдущем разделе.
Задача
Напомним, что вершинным покрытием в графе G = (V, E) называется такое множество S ⊆ V, что по крайней мере один конец каждого ребра принадлежит S. В версии задачи, которая рассматривается здесь, каждой вершине i ∈ V назначается вес wi ≥ 0, а вес множества вершин S обозначается Требуется найти вершинное покрытие S, для которого значение w(S) минимально. В стандартной версии задачи о вершинном покрытии все веса равны 1, и требуется принять решение о том, существует ли вершинное покрытие с весом не более k.
Аппроксимация посредством сведения
Прежде чем переходить к разработке алгоритма, мы обсудим один интересный вопрос: задача о вершинном покрытии легко сводится к задаче покрытия множества, для которой мы только что рассмотрели аппроксимирующий алгоритм. Какие выводы можно сделать относительно аппроксимируемости вершинного покрытия? При рассмотрении этого вопроса проявляются некоторые неочевидные аспекты взаимодействия результатов аппроксимации со сведениями с полиномиальным временем.
Начнем с частного случая, в котором все веса равны 1, — иначе говоря, ищется вершинное покрытие минимального размера. Назовем этот случай невзвешенным. Вспомните, что для доказательства NР-полноты задачи покрытия множества использовалось сведение от невзвешенной версии задачи о вершинном покрытии с принятием решения, то есть
Вершинное покрытие ≤р Покрытие множества
Это сведение означает: “Если бы у нас был алгоритм с полиномиальным временем, решающий задачу покрытия множества, то мы могли бы использовать этот алгоритм для решения задачи о вершинном покрытии за полиномиальное время”. Теперь у нас есть алгоритм с полиномиальным временем, возвращающий приближенное решение для задачи покрытия множества. Означает ли это, что алгоритм может использоваться для формулировки аппроксимирующего алгоритма для задачи о вершинном покрытии?
(11.12) Аппроксимирующий алгоритм задачи покрытия множества может использоваться для получения Н(d)-аппроксимирующего алгоритма для взвешенной задачи о вершинном покрытии, где d — максимальная степень графа.
Доказательство. Оно базируется на сведении, которое демонстрировало, что Вершинное покрытие ≤р Покрытие множества; оно также распространяется на взвешенную версию. Рассмотрим экземпляр взвешенной задачи о вершинном покрытии, заданный графом G = (V, E). Экземпляр задачи покрытия множества определяется следующим образом: используемое множество U равно E. Для каждого узла i определяется множество Si, состоящее из всех ребер, инцидентных узлу i, и этому множеству назначается вес wi. Совокупности множеств, покрывающие U, точно соответствуют вершинным покрытиям. При этом максимальный размер любого множества Si точно совпадает с максимальной степенью d.
Следовательно, аппроксимирующий алгоритм для задачи покрытия множества может использоваться для нахождения вершинного покрытия, вес которого лежит в пределах множителя H(d) от минимума. ■
Эта Н(d)-аппроксимация достаточно хороша при малых d; но с ростом d она ухудшается, приближаясь к границе, логарифмической по количеству вершин. Позднее мы разработаем усиленный аппроксимирующий алгоритм, отличающийся от оптимума не более чем в 2 раза.
Но прежде чем заниматься 2-аппроксимирующим алгоритмом, мы должны отметить один факт: при использовании сведений для разработки аппроксимирующих алгоритмов необходимо действовать очень осторожно. В (11.12) такой подход сработал, но мы специально обосновали, почему он сработал; это вовсе не значит, что любое сведение с полиномиальным временем приводит к аналогичному выводу для аппроксимирующего алгоритма.
Рассмотрим поучительный пример: мы использовали задачу о независимом множестве, чтобы доказать NР-полноту задачи о вершинном покрытии. А именно, мы доказали
Независимое множество ≤р Вершинное покрытие
Это означает: “Если бы у нас был алгоритм с полиномиальным временем, решающий задачу о вершинном покрытии, то мы могли бы использовать этот алгоритм для решения задачи о независимом множестве за полиномиальное время”. Сможем ли мы использовать аппроксимирующий алгоритм для вершинного покрытия с минимальным размером для разработки соизмеримо хорошего аппроксимирующего алгоритма для независимого множества с максимальным размером?
Ответ — нет. Вспомните, что множество I вершин называется независимым в том, и только в том случае, если его дополнение S = V – 1 является вершинным покрытием. Для заданного вершинного покрытия S* с минимальным размером мы получим независимое множество с максимальным размером, вычисляя дополнение I* = V – S. Теперь предположим, что мы используем аппроксимирующий алгоритм задачи о вершинном покрытии для получения приближенного минимального вершинного покрытия S. Дополнение I = V – S действительно является независимым множеством — здесь проблем нет. Проблемы появляются тогда, когда мы пытаемся определить коэффициент аппроксимации для задачи о независимом множестве; I может быть очень далеко от оптимума. Предположим, например, что оптимальное вершинное покрытие S* и оптимальное независимое множество I* оба имеют размер |V|/2. Если выполнить 2-аппроксимирующий алгоритм для задачи о вершинном покрытии, вполне возможно, что мы вернемся к множеству S = V. Но в этом случае “приближенное максимальное независимое множество” I = V – S не содержит элементов.
Разработка алгоритма: метод назначения цены
Хотя (11.12) предоставляет аппроксимирующий алгоритм с доказуемыми гарантиями, это не лучший вариант. Следующее описание хорошо демонстрирует применение метода назначения цены при разработке аппроксимирующих алгоритмов.
Применение метода назначения цены для минимизации стоимости
Метод назначения цены (также называемый прямо-двойственным методом) основан на экономических представлениях. Для задачи о вершинном покрытии веса мы будем рассматривать веса узлов как стоимости, а каждое ребро — как необходимость оплаты его “доли” в стоимости найденного вершинного покрытия. На самом деле мы уже видели пример подобного анализа в жадном алгоритме для покрытия множества из раздела 11.3; он тоже может рассматриваться как алгоритм назначения цены. Жадный алгоритм покрытия множества определял значения cs — стоимости, оплачиваемые алгоритмом за покрытие элемента s. Значение cs может рассматриваться как “доля” элементам в стоимости. Утверждение (11.9) показывает, что модель долевого участия csочень естественна, так как сумма долей равна стоимости покрытия множества С, возвращаемой алгоритмом,
Ключом к доказательству того, что алгоритм является H(d*)-аппроксимирующим, было некоторое приближенное свойство “справедливости” долей стоимости: (11.10) показывает, что оплата за элементы множества Sk превосходит стоимость покрытия их множеством Sk не более чем в H(|Sk|) раз.
В этом разделе мы воспользуемся методом назначения цены на другом примере — на примере задачи о вершинном покрытии. И снова вес wi вершины i будет рассматриваться как стоимость использования i в покрытии. Каждое ребро e будет рассматриваться как отдельный “агент”, желающий “заплатить” что-то покрывающему его узлу. Алгоритм будет не только находить вершинное покрытие S, но и определять цены pe ≥ 0 для каждого ребра e ∈ E, так что если каждое ребро e ∈ E платит цену pe, в сумме это приблизительно покроет стоимость S. Цены peявляются аналогами cs из алгоритма о покрытии множества.
Интерпретация ребер как “агентов” предполагает некоторые естественные правила “справедливости” цен, аналогичные свойству, доказанному (11.10). Прежде всего, выбор вершины iпокрывает все ребра, инцидентные i, поэтому будет “несправедливо” взимать за эти инцидентные ребра оплату, в сумме превосходящую стоимость вершины i. Цены pe будут называться справедливыми, если для каждой вершины i за ребра, смежные с i, не приходится платить больше стоимости вершины: Обратите внимание: свойство, доказанное (11.10) для задачи покрытия множества, является приближенным условием справедливости, тогда как в алгоритме вершинного покрытия будет использоваться точная концепция справедливости, определенная здесь. Полезная особенность справедливых цен заключается в том, что они всегда предоставляют нижнюю границу стоимости любого решения.
(11.13) Для каждого вершинного покрытия S* и любых неотрицательных и справедливых цен ре выполняется
Доказательство. Рассмотрим вершинное покрытие S*. По определению справедливости имеем для всех узлов i ∈ S*. Суммируя эти неравенства по всем узлам S*, получаем
Теперь выражение в левой части представляет собой сумму слагаемых, каждое из которых представляет собой некоторую цену ребра pe. Поскольку S* является вершинным покрытием, каждое ребро e вносит как минимум одно слагаемое pe в левую часть. Оно может внести в сумму более одного экземпляра pe, потому что может покрываться S* с обоих концов; но цены неотрицательные, поэтому сумма в левой части по крайней мере не меньше суммы всех цен pe. А значит,
Объединяя с предыдущим неравенством, получаем:
как и требовалось. ■
Алгоритм
Целью аппроксимирующего алгоритма является поиск вершинного покрытия одновременно с назначением цен. Алгоритм можно рассматривать как жадный в отношении того, как он назначает цены. Затем цены используются для управления выбором узлов вершинного покрытия.
Узел i называется насыщенным (или “оплаченным”), если
Для примера рассмотрим выполнение алгоритма для экземпляра на рис. 11.8. Изначально плотных узлов нет; алгоритм решает выбрать ребро (a, b). Он может поднять цену, оплачиваемую (a, b), до 3; в этот момент узел b становится плотным и повышение останавливается. Затем алгоритм выбирает ребро (a, d). Оно может поднять цену только на 1, так как в этот момент узел становится насыщенным (так как вес узла a равен 4 и он уже инцидентен ребру с оплатой 3). Наконец, алгоритм выбирает ребро (c, d). Он может поднять цену, оплачиваемую (c, d), на 2, когда узел d становится насыщенным. В возникшей ситуации у каждого ребра имеется хотя бы один насыщенный конец, поэтому алгоритм завершается. Насыщенными являются узлы a, b и d; это и есть полученное вершинное покрытие. (Обратите внимание: это вершинное покрытие не минимально; для получения минимального покрытия следовало бы выбрать a и c.)
Рис. 11.8. Части (a)-(d) представляют шаги выполнения алгоритма назначения цены в экземпляре взвешенной задачи о вершинном покрытии. Числа в узлах обозначают веса; числа у ребер обозначают цены, выплачиваемые в ходе выполнения алгоритма
Анализ алгоритма
На первый взгляд может показаться, что вершинное покрытие S полностью оплачивается ценами: все узлы в S насыщенны, а следовательно, ребра, прилегающие к узлу i в S, могут оплачивать стоимость i. Но дело в том, что ребро e может прилегать к более чем одному узлу вершинного покрытия (если оба конца e принадлежат покрытию), и возможно, e придется “платить” более чем за один узел. Например, так обстоит дело с ребрами (a, b) и (a, d) в конце выполнения алгоритма на рис. 11.8.
Однако заметьте, что если взять ребра, для которых оба конца принадлежат вершинному покрытию и мы взимаем их цену дважды, то мы в точности оплачиваем вершинное покрытие. (В примере стоимость вершинного покрытия складывается из стоимости узлов a, b и d, которая равна 10. Эта стоимость складывается из двукратной оплаты (a, b) и (a, d) и однократной оплаты (c, d).) Действительно, для некоторых ребер это несправедливо, но величина несправедливости может быть ограничена: каждое ребро оплачивается не более двух раз (по одному для каждого конца).
Формализуем этот аргумент:
(11.14) Для множества S и цен р, возвращаемых алгоритмом, выполняется неравенство
Доказательство. Все узлы в S являются насыщенными, поэтому для всех i ∈ S. Суммируя по всем узлам в S, получаем
Ребро e = (i, j) может входить в сумму в правой части не более двух раз (если i и j входят в S), поэтому мы получаем
как и было заявлено. ■
Наконец, этот множитель 2 переходит в утверждение, дающее гарантии аппроксимации.
(11.15) Множество S, возвращаемое алгоритмом, является вершинным покрытием, а его стоимость не более чем вдвое превышает стоимость минимального вершинного покрытия.
Доказательство. Сначала докажем, что S действительно является вершинным покрытием. Предположим от обратного, что S не покрывает ребро e = (i, j). Из этого следует, что ни i, ни jненасыщенны, а это противоречит тому факту, что цикл Пока в алгоритме завершился.
Чтобы получить заявленную границу аппроксимации, достаточно объединить (11.14) с (11.13). Пусть р — цены, заданные алгоритмом, a S* — оптимальное вершинное покрытие. Согласно (11.14), имеем а по (11.13) –
Другими словами, сумма цен ребер является нижней границей для веса любого вершинного покрытия, а удвоенная сумма цен ребер является верхней границей веса нашего вершинного покрытия:
На стоимость покрытия для детской площадки влияют различные факторы:
1. Стоимость исходных материалов
резиновая или каучуковая крошка, а также клей и их страна производитель.
2. Травмобезопасность
Требования к качеству таких покрытий определяются техническим регламентом Евразийского экономического союза ТР ЕАЭС 042/2017 “О безопасности оборудования для детских игровых площадок”. Они должны учитывать возрастную категорию и критическую высоту падения: чем выше высота устанавливаемого на площадке оборудования, тем больше должна быть толщина используемого покрытия.
3. Уровень квалификации исполнителей
4. Площадь будущего объекта
5. Транспортные затраты при выезде рабочих и оборудования на объект.
Немаловажным фактором при покрытии является их срок службы и прочность. Бывает так, что выбирая недорогое бесшовное покрытие , Вы снижаете первоначальные затраты, но не учитываете того, что через два-три года Вам придётся предпринимать меры для его ремонта, а следовательно это новые вложения и затраты. Под воздействием ультрафиолетового излучения и агрессивных погодных условий, покрытия из менее дорогостоящих материалов блекнут и теряют упругость, просаживаются и разрушаются.
Поэтому стоимость укладки покрытия почти всегда индивидуальна!
Наши менеджеры проконсультируют Вас по телефону, либо ответят на Ваши запросы по электронной почте, помогут вам выбрать оптимальный вариант по цене и качеству в зависимости от ваших пожеланий и бюджета. Бригада квалифицированных рабочих быстро и в срок осуществит монтаж, а также обеспечит гарантией на долгие годы вперёд.
Калькулятор
Метод Квайна
В основе две операции:
где под p понимается некоторая элементарная конъюнкция.
Теорема.
Если в СДНФ какой-либо переключательной функции выполнить все возможные операции неполного попарного склеивания и элементарного поглощения, то в результате получится СкДНФ(сокращенная дизъюнктивная нормальная форма), эквивалентная исходной функции.
Итерационый алгоритм. Задача в нахождении по полной системе импликант (конституэнт единицы) полной системы простых импликант.
Алгоритм:
- Исходным является множество конституэнт единицы функции – импликанты нулевого ранга.
- Выполняются все возможные операции неполного попарного склеивания для элементарных конъюнкций длины n. (где n-кол-во аргументов).
Согласно соотношениям “a.” и “b.” результат – дополнительная импликанта p.
- Выполняются все возможные операции элементарного поглощения для элементарных конъюнкций длины n-1. (общая часть “p” имеет длину n-1)
- В результате получилось множество элементарных конъюнкций, разделяемых на два подмножества(по длине):
- подмножество элементарных конъюнкций длины n (оставшиеся)
- подмножество элементарных конъюнкций длины n-1
Элементарные конъюнкции длины n не участвовали в склеивания, а, следовательно, и в поглощении (т.к. поглощаются собственной частью те, которые участвовали в склеивании).
Следовательно, подмножество элементарных конъюнкций длины n входит в множество простых импликант (импликант нулевого ранга). - Если множество элементарных конъюнкций длины n-1 не пусто, то выполняются шаги со второго для конъюнкций длины n-1 и т.д.
Алгоритм завершается, когда подмножество является пустым, либо нельзя выполнить ни одной операции неполного попарного склеивания.
Таким образом, получаем систему простых импликант функции.
Нахождение тупиковых ДНФ
Стратегическая задача нахождения приведенной системы простых импликант заключается в нахождении наилучших покрытий единиц функции простыми импликантами.
Для системы простых импликант для заданной функции может быть получено несколько приведенных систем. Следует считать, что среди них есть такая, которая дает тупиковую нормальную форму минимальной длины.
Алгоритм нахождения приведенных систем простых импликант также является переборным. Задача в том, чтобы обеспечить направленный перебор. Для этого алгоритм строится в виде итерационной процедуры, которая содержит следующие шаги:
- Находятся такие единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант (для каждой единицы считаем сколько ее покрывает импликант и отмечаем их).
Этим импликанты образуют, так называемое, ядро функции. Такие импликанты будут входить в приведенную систему простых импликант. Следовательно, конъюнкции будут входить во все ТДНФ( в том числе минимальные).
- Исключаются из рассмотрения все единицы функции, покрываемые ядром.
- Осталось множество непокрытых ядром единицы функции и множество простых импликант, которые не вошли в ядро.
Повторяем шаг 1 и шаг 2 для оставшихся множеств (находится псевдоядро). Но перед повторением должен быть дополнительный шаг, который уменьшает перебор. (выкидываем из тех, которые покрывают одни и те же единицы(из оставшихся) ту импликанту, которая имеет наибольшую длину)
И так далее до тех пор, пока не будут покрыты все единицы функции.
Велика вероятность, что на каком-то шаге не найдется ни одной единицы функции, которая покрывается одной импликантой. В этом случае ищется наилучшее (наименьшей длины) покрытие оставшихся единиц функции методом перебора:
Если единица функции покрывается импликантами A,B,C,…
- Пусть A входит в ТДНФ, а B,C,… нет.
- Пусть В входит в ТДНФ, а A,C,… нет.
- Пусть C входит в ТДНФ, а A,B,… нет.
- …
Таким образом, получаем множество ТДНФ. Затем выбираем из них ДНФ наименьшей длины – получаем {МДНФ}.
Пример минимизации переключательной функции методом Квайна
Функция задана вектором: 883F. Запишем 16-ричное число 883F в двоичной виде в столбец значений функции таблицы истинности.
| Набор> | Значение исходной функции | Набор> | Значение исходной функции |
| 0000 | 1 | 1000 | 0 |
| 0001 | 0 | 1001 | 0 |
| 0010 | 0 | 1010 | 1 |
| 0011 | 0 | 1011 | 1 |
| 0100 | 1 | 1100 | 1 |
| 0101 | 0 | 1101 | 1 |
| 0110 | 0 | 1110 | 1 |
| 0111 | 0 | 1111 | 1 |
Цена ДНФ является суммой длин всех входящих в нее конъюнкций.
Минимизация функции методом Квайна.
На данном шаге все импликанты участвовали в операциях попарного неполного склеивания и были поглощены своими собственными частями. Поэтому простые импликанты на этом шаге не получены.
В результате на данном шаге получаем простые импликанты: ,
В результате на данном шаге получаем простые импликанты: ,
СкДНФ: v
v
v
Нахождение тупиковых форм.
Обозначения:
- Единицы ДНФ, покрываемые импликантами СкДНФ, обозначаются “+”.Импликанты, попадающие в ядро помечаются “*”.
- Единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант, помечаются “>”.
- Единицы функции, покрываемые ядром, но не покрываемые только какой-то одной импликантой из системы простых импликант, помечаются “>>”.
| > |
>> |
> |
> |
>> |
> |
>> |
>> |
|
| + | + | |||||||
| + | + | |||||||
| + | + | + | + | |||||
| + | + | + | + |
Ядро: v
v
МДНФ: v
v
, цена=7
Графический метод минимизации – Карты Карно
Карты Карно – это графическое представление операций попарного неполного склеивания и элементарного поглощения.
Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции.
Карты Карно – определенная плоская развертка n-мерного булева куба.
Строится таблица истинности функции определенным образом. Каждая клетка таблицы соответствует вполне определенной вершине булева куба. Нулевые значения не записываются.
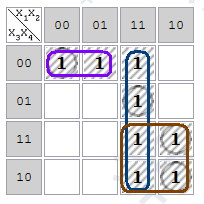
Карта Карно для функции 4-х переменных:
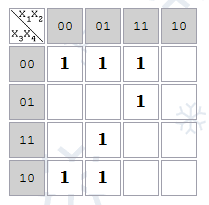
Карта Карно рассматривается как поверхность фигуры под названием тор (“бублик”).
p-клетки – клетки карты Карно, соответствующие единичному значению функции.
Соседние наборы – наборы, которые различаются только одним аргументом (одной орбитой).
Любой паре соседних наборов в Карте Карно соответствуют соседние клетки.
Две соседние p-клетки на карте Карно дают импликанту первого ранга. Например, клетки 1100 и 1101 отличаются только значением переменной x3, следовательно, они дают импликанту 1
2
4.
Две соседние импликанты первого ранга образуют импликанту второго ранга.
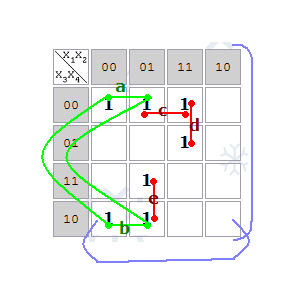
На этой карте соседние клетки образуют импликанты a,b,c,d,e. При этом импликанты a и b являются соседними, поэтому они образуют импликанту второго ранга.
Если функция имеет 5 переменных, то рисуются 2 Карты Карно: для x5=0 и для x5=1. Если 6 переменных – 4 Карты, так чтобы в соседних картах соседние клетки имели одинаковые координаты:
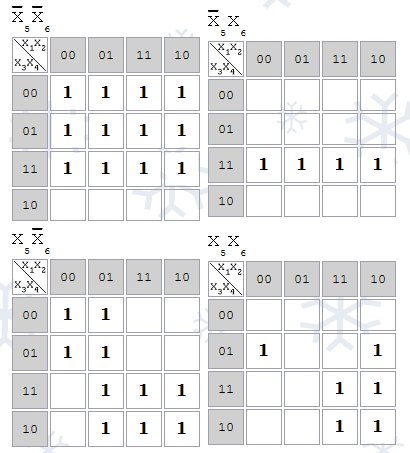
Соседние p-клетки, соответствующие импликанте образуют компактную группу.
Количество p-клеток в компактной группе является степенью двойки.
Задача минимизации переключательной функции с помощью карт Карно заключается в нахождении импликант высшего ранга (соответствующих компактным группам наибольшей размерности), покрывающих p-клетки функции наилучшим образом.
Если на картах Карно выделить все компактные группы наибольшей размерности, то дизъюнкция соответствующих конъюнкций даст СкДНФ.
Пример минимизации функции 4-х переменных методом Карт Карно
Компактных групп размера 4 – 2
Компактных групп размера 2 – 2
Нахождение тупиковых форм.
Обозначения:
Цветом выделены компактные группы наибольшей размерности, вошедшие в ядро.
Ядро: v
v
МДНФ: v
v
, цена=7
Машинно-ориентированные методы минимизации переключательных функций.
Основаны на применении соответствующих алгебр(или соответствующих алгебраический преобразований).
Вопрос 1. Интервальная форма задания функции. Постановка задачи минимизации.
Геометрический представление: (отображение функции на n-мерный булев куб)
Любому набору значений аргументов соответствует элементарная конъюнкция, содержащая все эти переменные – конституента единицы.
Те вершины n-мерного булева куба, в которых функция принимает единичное значение называются 0-кубами.
Два 0-куба образуют 1-куб, если соответствующие булевы вектора(их координаты) отличаются между собой значением только одной координаты(или одной компоненты). Эти координаты носят название свободной координаты. Обозначение x, остальные координаты 0-куба называются связанными и имеют либо 1, либо 0 значение. 0-кубы, образующие 1-куб называются его гранями. Два 1-куба образуют 2-куб, если свободная координата у них одинакова и они различаются значением только одной связанной компоненты.( 1-кубы – грани соответствующего 2-куба).
…
И так далее до n-куба( в случае тавтологии).
В общем случае, r-куб-это такой куб в булевом пространстве, у которого r свободных компонент и n-r связанных компонент.
Пример:
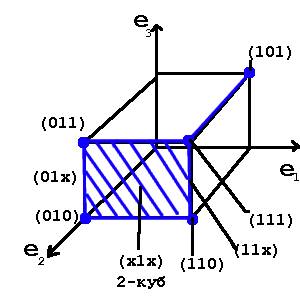
(1x1xx1) – 3-куб
(1x1x01),(1x1x11)- два 2-куба. Они являются гранями этого 3-куба(образуют его).
Если для какой-то функции взять все возможные кубы одинаковой размерности, то получаем множество кубов(или комплекс кубов).
Kr(f) – комплекс r-кубов функции f/
Для некоторой функции всегда есть комплекс
(Если Kn(f) содержит куб, то f – константа 1
оператор граней:
Cr=(a1a2…an-1an)-куб,
где a∈{0,1,x}, тогда для этого куба можно вычислить грани этого куба. Грани куба:
| ∂ip(a1a2…an-1an)= | a1a2…ai-1 p ai+1…an-1an, ai=x, p∈{0;1} | |
| ∅, ai ≠ x |
где C-получаемый куб.
При ai=x есть две грани (вместо i-ой либо 0, либо 1).
Оператор сограней
позволяет вычислить куб большей размерности, гранью которого может быть этот куб.
| δi(a1a2…an-1an)= | a1a2…ai-1 x ai+1…an-1an, ai≠x, Cr+1⊆K(f) | |
| ∅, ai=x, Cr+1⊄K(f) |
Подмножество вершин булева куба, соответствующие кубу размерности r называется интервалом булева пространства ранга r. (интервал 1 ранга – 1×1, интервал 2 ранга – x1x)
Для нашего примера:
K0(f)={101,110,111,010,011}
K1(f)={01x,11x,1×1,x11,x10}
K2(f)={x1x}
В общем случае комплекс кубов определенного ранга не является покрытием исходной функции(за исключением K0).
В нашем примере K2 не является покрытием, хотя K1 – покрытие.
K(f)=K0∪K1∪K2 – для нашей функции
Куб большей размерности покрывает кубы меньшей размерности, если они могут быть получены из него последовательным применением оператора граней.
(x1x) имеет грани (01x) и (11x), которые имеют грани : (010),(011) и (110),(111)
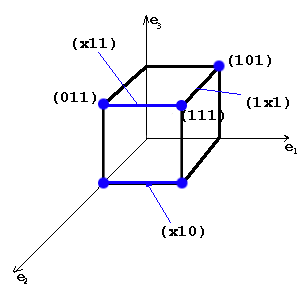
Если взять интервал булева пространства, то аналитически его можно описать в виде соответствующих элементарных конъюнкций.
Некоторый комплекс кубов – L, таких, что каждая вершина из комплекса K0(f) включена по крайней мер в один из кубов комплекса L, называется покрытием комплекса K функции f.
Каждое покрытие комплекса K(f) определяет некоторую ДНФ переключательной функции.
Покрытие можно рассматривать (с точки зрения реализации), как двухуровневую схему.
| Аргументы (0-ой уровень) | конъюнктивные члены(элементарные конъюнкции) (1-ый уровень) | дизъюнкция (2-ой уровень) |
Не учитывается инверсия аргументов на нулевом уровне.
Минимизация
Цена r-куба: c=n-r – число связанных переменных, количество символов в элементарной конъюнкции(совпадает с ценой в смысле Квайне)
–цена покрытия, где qr-количество кубов размерности r в покрытии L.
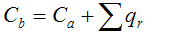
Задача минимизации: Найти такое покрытие L комплекса K(f), цена которого будет минимальна – минимизация в смысле Квайне.
Задача решается алгебраически, вводится свой математический аппарат. Это аппарат исчисления кубических комплексов (задает операции над кубами).
Каждая операция проходит в два этапа:
I Этап. Предварительное вычисление путем покоординатной обработки кубов по правилам, задаваемым с помощью таблиц покоординатной обработки.
II Этап. Окончательный.
Зададим операции над кубами:
a = (a1 a2 … an)
b = (b1 b2 … bn)
- Операция *: c=a*b
По содержанию * – это нахождение куба некоторой размерности r, грани которого содержаться в кубах a и b.
ci=ai*bi 0 1 x 0 0 y 0 1 y 1 1 x 0 1 x a*b = ∅, если ∑αici>1 c, если ∑αici≤1 где αici = 0, ci≠y 1, ci=y c = ([a1*b1] … [an*bn]).
При чем, если результат операции – y, то y заменяется на x.
(101)*(111)
после предварительной обработки:
=(1y1)
Окончательный вариант:
=(1×1)(x11)*(101)=(1×1)
(x10) (101) (1yy) ∅ – нет общих граней - Операция пересечения кубов.
c = a ∩ b
покоординатно!
ci=ai∩bi 0 1 x 0 0 ∅ 0 1 ∅ 1 1 x 0 1 x a ∩ b = ∅, если ∃i (ai∩bi = ∅ c в противном случае Пересечение – нахождение общей части булева пространства, покрываемой этими кубами (т.е. куба или грани какого-то уровня)
(1×1)∩(x1x)=(111) - Операция вычитания кубов (#).
ci=ai#bi 0 1 x 0 z y z 1 y z z x 1 0 z * и ∪ обладают свойством коммутативности, но a#b ≠ b#a !
Операция вычитания кубов удаляет из куба a общую часть кубов уменьшаемого и вычитаемого (т.е. пересечение кубов a и b).
В результате вычитания можем иметь несколько кубов.
Если куб a входит в куб b, то результат – ∅
Пример:
a#b = (1×1)#(x11) = (z0z) = (101)
c#b = (1xx)#(x11) = (z00) = {(10x),(1×0)}
Нахождение множества простых импликант
K(f)=K0∪K1∪…∪Ki∪…∪Kn-1 – комплекс K функции f
z⊆K является простой импликантой этого комплекса, если δi(z)=∅ (δi – оператор сограней), то есть не существует какого-либо другого куба, который бы включал в себя исходный куб z.
Z(f)={z} – множество импликант для функции f
Необходимо получить весь комплекс K функции f, используя операторы граней и сограней.
Берем куб z из K и проверяем, есть ли какой-то куб, гранью которого является рассматриваемый.
Операция *(“звездочка”) позволяет получить множество Z – кубов, соответствующих простым импликантам функции.
Алгоритм (*) – нахождение множества кубов, соответствующих простым импликантам функции.
Предположим есть некоторый комплекс Ĉ0, являющийся покрытием комплекса K(f), т.е.
- Ĉ0(f) – неупорядоченное покрытие
причем одна и та же единица функции может покрываться несколькими кубами - C0 = Ĉ0 – {c1 | c1 ∈ Ĉ0 ∧ c2 ∈ Ĉ0 ∧ c1 ⊆ c2}
(тоже, что и поглощение в методе Квайне) - C0*C0 попарно
- в результате 3) находится множество 0-кубов:
Z0 = { c0 | c0 * C0 не содержит никаких 1-кубов }
– это такие кубы, которые в результате операции * не дают никаких 1-кубов - вычисляется Ĉ1:
Ĉ1 = C0 ∪ (C0*C0) - C1 = Ĉ1 – { c | c ⊆ d, c,d∈Ĉ1 } – {0-кубы, получившиеся в результате операции *, и Z0}
( (1×1)*(x11)= (111) ) - C1 * C1
- Z1
- Ĉ2
- C2 (удаляем 0-кубы и 1-кубы)
и так далее (итерационный процесс)
Ĉ0(f) – исходное покрытие K(f)
C1(f) и т.д. в общем случае покрытием функции не являются
C1(f) ∪ Z0 ⊆ K – является покрытием K(f)
Алгоритм заканчивается, когда на каком-то шаге получаем множество C, содержащее один куб.
Результат – множество Z – множество простых импликант.
Z = ∪Zi
Алгоритм извлечения
ИЗ множества простых импликант извлечь те (выбрать такое подмножество кубов) простые импликанты, которые:
- Является покрытием исходного множества кубов функции;
- С минимальной ценой покрытия, если покрытий несколько.
Для решения этой задачи исходные данные фактически – исходный комплекс функции, то есть некоторый исходный комплекс K0(f) и Z(f).
Определение: возьмем некоторую вершину d∈K0. Говорят, что эта вершина является обособленной вершиной комплекса на множестве простых импликант Z, если существует такой куб z∈Z, что вершина d накрывается только этой импликантой z.
Такая импликанта будет простая. Вершина d называется различающей. А импликанта получила название экстремаль.
Любое минимальное покрытие содержит экстремали нулевого ранга.
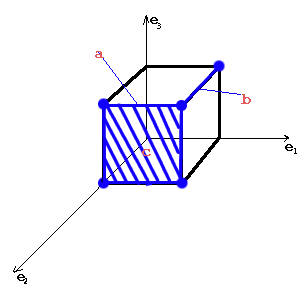
Пример:
Различающие вершины: (0;0;1) и (0;1;0)
E0={ a, d}, осталось покрыть одну вершину – (1;1;1)
Задача минимизации: необходимо найти все обособленные вершины и выделить импликанты, накрывающие эти обособленные вершины.
Такие импликанты образуют множество экстремалей.
Задача решается, если известно K0(f), то есть все вершины.
В общем случае задачи минимизации функция задана некоторым комплексом K(f), который состоит не только из 0-кубов. Тогда можно найти все 0-кубы и решить задачу, а можно и не находить.
- Некоторая простая импликанта e∈Z является экстремалью, если e∩K ≠ e∩U'(e,Z)∩K, а e∩K ≠ ∅,
U'(e,Z) = U(e,Z) – e,
U(e,Z) = { z | z∈Z, Z∩e ≠ ∅}.
Z – множество простых импликант,
U(e,Z) – окрестность куба e, т.е. все простые импликанты из Z, которые имеют общие части с импликантой e.
U'(e,Z) – окрестность без самой импликанты.Функция может быть не полностью определена:
L – комплекс, где функция определена и равна 1,
D – комплекс, где значение функции не определено,
тогда K=L∪D.
но чаще экстремали вычисляют по одному соотношению:
- [e#(Z-e)]∩K≠∅
e#(Z-e) – те вершины булева куба, которые накрываются только e и не накрываются всех оставшейся частью Z.
+ эти вершины присутствуют в комплексе K (или L для неполностью определенной функции)Если из простой импликанты e удалить все подкубы (Z-e), и остается, по крайней мере, одна вершина булева куба, которая содержится в исходном комплексе функции, то оставшиеся вершины является выделенными, или отмеченными.
Алгоритм нахождения экстремалей также итерационный.
Нахождение множества экстремалей
- Каждая простая импликанта проверяется на наличие в ней выделенной вершины, т.е. вычисляется e#(Z-e), если результат вычитания кубов не пустой, то такая импликанта может быть экстремалью.
Как правило, вычитание e#(Z-e) сводится в таблицу.
- Каждый кандидат на экстремаль проверяется на пересечение с комплексом единичных значений функции.
Если результат пересечения не пустой, значит в L (комплексе единичных значений) имеются обособленные вершины, а e является экстремалью.
Получаем множество экстремалей нулевого ранга – E0 = {e}. В смысле Квайна оно соответствует ядру функции.
- Находим
1 = Z0 – E0
Т.е. из множества простых импликант удаляем множество экстремалей нулевого ранга.
Находим L1 = L0 # E0, т.е. находятся все вершины, не покрытые экстремалями.
1 – оставшаяся часть множества простых импликант, неупорядоченное множество простых импликант.
Операция, которая позволяет сократить в последующем перебор и исключить из
i не максимальные кубы – упорядочивание.
Пусть u∈
1, v∈
1. Говорят, что u1 удовлетворяет условию u∩L1 ⊆ v∩L1.
( вершины из L1, покрываемые u, покрываются и кубов v )В этом случае из кубов u,v выбираем при упорядочивание куб v.
Если кубы разной размерности, а вершины покрывают одинаковые – то оставляем куб большей размерности ( цена = n – r ).
Таким образом,
1 => Z1 (находится Z1 – упорядоченной множество оставшихся простых импликант), применением процедуры упорядочивания.
- Остались Z1 и L1
(Z1,L1) => E1 по тому же алгоритму.
Затем
2 => Z2; L2 = L1#E1; (Z2,L2) => E2 и т.д.
Два варианта окончания алгоритма:
- L = ∅ => покрытие единственное
E = ∪Ei - L ≠ ∅ Если проверка на экстремальность не дает результата, т.е. ни одна простая импликанта не содержит квазеопорных вершин, а операция упорядочивания не дает результата.
Пример:
В этом случае не остается никакого другого варианта решения, кроме волюнтаристского.
Берется любая простая импликанта, для которой выдвигается две гипотезы (Алгоритм ветвления):
- простая импликанта входит в минимальное покрытие
e∈E
находим Li+1=Li#{e}, упорядочиваем Z и вновь применяем алгоритм извлечения (возможно еще ветвление). - простая импликанта не входит в минимальное покрытие
e∉E
удаляем e из Zi (находимi+1), упорядочиваем
i+1 => Zi+1
Li+1 = Li
И применяем алгоритм извлечения.
Таким образом, при ветвление получаем множество покрытий, сравниваем по цене и выбираем наименьшей.
- простая импликанта входит в минимальное покрытие
Все вычисления в ручном варианте сводятся к вычислениям над таблицами.
Минимизация функции методом кубических покрытий.
Рассмотрим комплекс кубов К(f) = L D, где L – множество единичных наборов, D – множество наборов, на которых ДНФ не определена.
Будем выполнять операцию “*” для получения множества простых импликант.
| 0000 | 0010 | 0100 | 0110 | 1010 | 1100 | 1101 | 1110 | |
| 0000 | – | 00×0 | 0x00 | Ø | Ø | Ø | Ø | Ø |
| 0010 | 00×0 | – | Ø | 0x10 | x010 | Ø | Ø | Ø |
| 0100 | 0x00 | Ø | – | 01×0 | Ø | x100 | Ø | Ø |
| 0110 | Ø | 0x10 | 01×0 | – | Ø | Ø | Ø | x110 |
| 1010 | Ø | x010 | Ø | Ø | – | Ø | Ø | 1×10 |
| 1100 | Ø | Ø | x100 | Ø | Ø | – | 110x | 11×0 |
| 1101 | Ø | Ø | Ø | Ø | Ø | 110x | – | Ø |
| 1110 | Ø | Ø | Ø | x110 | 1×10 | 11×0 | Ø | – |
Z0=Ø
Ĉ1=C0∪(C0*C0)
C1=>
| 00×0 | 0x00 | 0x10 | x010 | 01×0 | x100 | x110 | 1×10 | 110x | 11×0 | |
| 00×0 | – | 0000 | 0010 | 0010 | 0xx0 | 0x00 | 0x10 | x010 | Ø | Ø |
| 0x00 | 0000 | – | 0xx0 | 00×0 | 0100 | 0100 | 01×0 | Ø | x100 | x100 |
| 0x10 | 0010 | 0xx0 | – | 0010 | 0110 | 01×0 | 0110 | xx10 | Ø | x110 |
| x010 | 0010 | 00×0 | 0010 | – | 0x10 | Ø | xx10 | 1010 | Ø | 1×10 |
| 01×0 | 0xx0 | 0100 | 0110 | 0x10 | – | 0100 | 0110 | x110 | x100 | x1x0 |
| x100 | 0x00 | 0100 | 01×0 | Ø | 0100 | – | x1x0 | 11×0 | 1100 | 1100 |
| x110 | 0x10 | 01×0 | 0110 | xx10 | 0110 | x1x0 | – | 1110 | 11×0 | 1110 |
| 1×10 | x010 | Ø | xx10 | 1010 | x110 | 11×0 | 1110 | – | 11×0 | 1110 |
| 110x | Ø | x100 | Ø | Ø | x100 | 1100 | 11×0 | 11×0 | – | 1100 |
| 11×0 | Ø | x100 | x110 | 1×10 | x1x0 | 1100 | 1110 | 1110 | 1100 | – |
Z1=
Ĉ2=C1∪(C1*C1)
C2=>
| 0xx0 | xx10 | x1x0 | |
| 0xx0 | – | 0x10 | 01×0 |
| xx10 | 0x10 | – | x110 |
| x1x0 | 01×0 | x110 | – |
Z2=
Ĉ3=C2∪(C2*C2)
C3=>Ø
Z = Z0∪Z1∪Z2
Z=>
Нахождение тупиковых форм.
| 110x | 0xx0 | xx10 | x1x0 | ||
|
110x |
– |
110x |
110x |
1101 |
v |
|
0xx0 |
0xx0 |
– |
0x00 |
0000 |
v |
|
xx10 |
xx10 |
1×10 |
– |
1010 |
v |
|
x1x0 |
x110 |
1110 |
Ø | – |
E0:
L1=L0#E0
| 110x | 0xx0 | xx10 | |
|
0000 |
0000 |
1010 |
Ø |
L1:Ø


Z1:
E:
МДНФ: v
v
, цена=7
Содержание
- Постановка задачи
- Решение задачи
- Анализ переключательной функции
- Метод Квайна
- Карты Карно
- Кубические покрытия
- Анализ полученных результатов
- Список литературы
1. Постановка задачи
Минимизировать переключательную функцию шести аргументов. Функция задана в виде наборов, на которых значения функции равны единице либо не определены. Наборы задаются в шестнадцатеричной системе счисления. В скобках заданы наборы, на которых значение функции не определено:
y => (2) v (3B) v (20) v (21) v (1D) v (6) v (1B) v (D) v (24) v (2C) v (23) v (B) v 36 v 1C v 3A v 7 v A v 8 v 10 v 38 v 12 v 15 v 5 v 1F v 3F v 1A v 17 v 3E v 3D v 39 v 9 v 37 v 19 v 2A v 11 v 18 v 4 v 3C v 2E v 29 v 0 v 2D v 28 v 25 v 14 v 1E
Необходимо выполнить следующие задачи:
- Доопределить функцию нулями, минимизировать полученную функцию методом Квайна;
- Доопределить функцию единицами и произвести минимизацию, используя карты Карно;
- Минимизировать исходную функцию методом кубических покрытий;
- Проанализировать полученные результаты;
2. Решение задачи
2.1 Анализ переключательной функции
Представим исходную последовательность в виде таблицы истинности.
Исходная последовательность:
(2) v (3B) v (20) v (21) v (1D) v (6) v (1B) v (D) v (24) v (2C) v (23) v (B) v 36 v 1C v 3A v 7 v A v 8 v 10 v 38 v 12 v 15 v 5 v 1F v 3F v 1A v 17 v 3E v 3D v 39 v 9 v 37 v 19 v 2A v 11 v 18 v 4 v 3C v 2E v 29 v 0 v 2D v 28 v 25 v 14 v 1E
| Набор | Значение исходной функции | Набор | Значение исходной функции |
|---|---|---|---|
| x1x2x3x4x5x6 | x1x2x3x4x5x6 | ||
| 000000 | 1 | 100000 | ? |
| 000001 | 0 | 100001 | ? |
| 000010 | ? | 100010 | 0 |
| 000011 | 0 | 100011 | ? |
| 000100 | 1 | 100100 | ? |
| 000101 | 1 | 100101 | 1 |
| 000110 | ? | 100110 | 0 |
| 000111 | 1 | 100111 | 0 |
| 001000 | 1 | 101000 | 1 |
| 001001 | 1 | 101001 | 1 |
| 001010 | 1 | 101010 | 1 |
| 001011 | ? | 101011 | 0 |
| 001100 | 0 | 101100 | ? |
| 001101 | ? | 101101 | 1 |
| 001110 | 0 | 101110 | 1 |
| 001111 | 0 | 101111 | 0 |
| 010000 | 1 | 110000 | 0 |
| 010001 | 1 | 110001 | 0 |
| 010010 | 1 | 110010 | 0 |
| 010011 | 0 | 110011 | 0 |
| 010100 | 1 | 110100 | 0 |
| 010101 | 1 | 110101 | 0 |
| 010110 | 0 | 110110 | 1 |
| 010111 | 1 | 110111 | 1 |
| 011000 | 1 | 111000 | 1 |
| 011001 | 1 | 111001 | 1 |
| 011010 | 1 | 111010 | 1 |
| 011011 | ? | 111011 | ? |
| 011100 | 1 | 111100 | 1 |
| 011101 | ? | 111101 | 1 |
| 011110 | 1 | 111110 | 1 |
| 011111 | 1 | 111111 | 1 |
‘?’ обозначено значение наборов, на которых функция не определена.
Цена ДНФ является суммой длин всех входящих в нее конъюнкций.
2.2 Минимизация функции методом Квайна.
Доопределим функцию нулями, получим конституэнты единицы, затем выполним операции попарного неполного склеивания и элементарного поглощения.
|
|
На данном шаге все импликанты участвовали в операциях попарного неполного склеивания и были поглощены своими собственными частями. Поэтому простые импликанты на этом шаге не получены.
|
|
В результате на данном шаге получаем простые импликанты:
x2x3x4x5x6 , x1x2x4x5x6
|
|
В результате на данном шаге получаем простые импликанты:
x1x3x5x6 , x1x4x5x6 , x1x3x4x5 , x1x3x4x6 , x1x2x3x5 , x1x2x4x5 , x1x2x4x6 , x1x2x5x6 , x2x4x5x6 , x2x3x4x5 , x1x3x5x6 , x1x3x5x6 , x1x2x4x5 , x1x2x3x5 , x1x2x3x4
|
В результате на данном шаге получаем простые импликанты:
x3x4x5 , x3x4x6 , x2x3x6
СкДНФ:
x2x3x4x5x6 v x1x2x4x5x6 v x1x3x5x6 v x1x4x5x6 v x1x3x4x5 v x1x3x4x6 v x1x2x3x5 v x1x2x4x5 v x1x2x4x6 v x1x2x5x6 v x2x4x5x6 v x2x3x4x5 v x1x3x5x6 v x1x3x5x6 v x1x2x4x5 v x1x2x3x5 v x1x2x3x4 v x3x4x5 v x3x4x6 v x2x3x6
Нахождение тупиковых форм.
Обозначения:
- Единицы ДНФ, покрываемые импликантами СкДНФ, обозначаются “+”.Импликанты, попадающие в ядро помечаются “*”.
- Единицы функции, которые покрываются только какой-то одной импликантой из системы простых импликант, помечаются “>”.
- Единицы функции, покрываемые ядром, но не покрываемые только какой-то одной импликантой из системы простых импликант, помечаются “>>”.
|
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6>> |
|
| x2x3x4x5x6 | + | + | ||||||||||||||||||||||||||||||||
| x1x2x4x5x6 | + | + | ||||||||||||||||||||||||||||||||
| x1x3x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x4x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x4x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x4x6* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x3x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x4x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x4x6* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x2x4x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x2x3x4x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x5x6 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x3x5x6* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x4x5* | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x3x5 | + | + | + | + | ||||||||||||||||||||||||||||||
| x1x2x3x4 | + | + | + | + | ||||||||||||||||||||||||||||||
| x3x4x5* | + | + | + | + | + | + | + | + | ||||||||||||||||||||||||||
| x3x4x6* | + | + | + | + | + | + | + | + | ||||||||||||||||||||||||||
| x2x3x6 | + | + | + | + | + | + | + | + |
Ядро: x1x3x4x6 v x1x2x4x6 v x1x3x5x6 v x1x2x4x5 v x3x4x5 v x3x4x6
До упорядочивания:
|
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
|
| x2x3x4x5x6 | + | ||||||||||
| x1x2x4x5x6 | + | + | |||||||||
| x1x3x5x6 | + | + | + | ||||||||
| x1x4x5x6 | + | ||||||||||
| x1x3x4x5 | + | + | |||||||||
| x1x2x3x5 | + | + | |||||||||
| x1x2x4x5 | + | ||||||||||
| x1x2x5x6 | + | + | |||||||||
| x2x4x5x6 | + | ||||||||||
| x2x3x4x5 | + | + | |||||||||
| x1x3x5x6 | + | + | |||||||||
| x1x2x3x5 | + | + | |||||||||
| x1x2x3x4 | + | + | |||||||||
| x2x3x6 | + | + | + |
После упорядочивания:
|
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6> |
x1x2x3x4x5x6>> |
x1x2x3x4x5x6 |
x1x2x3x4x5x6 |
|
| x1x2x4x5x6* | + | + | |||||||||
| x1x3x5x6* | + | + | + | ||||||||
| x1x2x3x5* | + | + | |||||||||
| x1x2x5x6 | + | + | |||||||||
| x2x3x4x5* | + | + | |||||||||
| x1x3x5x6 | + | + | |||||||||
| x1x2x3x5 | + | + | |||||||||
| x2x3x6 | + | + | + |
Псевдоядро: x1x2x4x5x6 v x1x3x5x6 v x1x2x3x5 v x2x3x4x5
До упорядочивания:
| x1x2x3x4x5x6 | x1x2x3x4x5x6 | x1x2x3x4x5x6 | |
| x1x2x5x6 | + | ||
| x1x3x5x6 | + | ||
| x1x2x3x5 | + | + | |
| x2x3x6 | + | + |
После упорядочивания:
| x1x2x3x4x5x6> | x1x2x3x4x5x6>> | x1x2x3x4x5x6> | |
| x1x2x3x5* | + | + | |
| x2x3x6* | + | + |
Псевдоядро: x1x2x3x5 v x2x3x6
МДНФ: x1x3x4x6 v x1x2x4x6 v x1x3x5x6 v x1x2x4x5 v x3x4x5 v x3x4x6 v x1x2x4x5x6 v x1x3x5x6 v x1x2x3x5 v x2x3x4x5 v x1x2x3x5 v x2x3x6, цена=46
2.3 Минимизация функции методом Карт Карно.
Дополним функцию единицами и построим Карты Карно.
Компактных групп размера 16 – 1
Компактных групп размера 8 – 9
Компактных групп размера 4 – 13
Компактных групп размера 2 – 1
Нахождение тупиковых форм.
Обозначения:
Ядро: x1x2x3x4x6 v x1x2x4x5 v x1x4x6 v x1x3x4 v x1x2x5 v x1x3x6 v x2x3
Псевдоядро: x1x2x3x4 v x1x3x4x6
Псевдоядро: x1x2x5
Псевдоядро: x3x5x6
МДНФ: x1x2x3x4x6 v x1x2x4x5 v x1x4x6 v x1x3x4 v x1x2x5 v x1x3x6 v x2x3 v x1x2x3x4 v x1x3x4x6 v x1x2x5 v x3x5x6, цена=37
2.4 Минимизация функции методом кубических покрытий.
Рассмотрим комплекс кубов К(f) = L D, где L – множество единичных наборов, D – множество наборов, на которых ДНФ не определена.
Будем выполнять операцию “*” для получения множества простых импликант.
| K(f) = |
|
=> C0 => |
|
| 000000 | 000010 | 000100 | 000101 | 000110 | 000111 | 001000 | 001001 | 001010 | 001011 | 001101 | 010000 | 010001 | 010010 | 010100 | 010101 | 010111 | 011000 | 011001 | 011010 | 011011 | 011100 | 011101 | 011110 | 011111 | 100000 | 100001 | 100011 | 100100 | 100101 | 101000 | 101001 | 101010 | 101100 | 101101 | 101110 | 110110 | 110111 | 111000 | 111001 | 111010 | 111011 | 111100 | 111101 | 111110 | 111111 | |
| 000000 | – | 0000×0 | 000×00 | Ø | Ø | Ø | 00×000 | Ø | Ø | Ø | Ø | 0x0000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000010 | 0000×0 | – | Ø | Ø | 000×10 | Ø | Ø | Ø | 00×010 | Ø | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000100 | 000×00 | Ø | – | 00010x | 0001×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000101 | Ø | Ø | 00010x | – | Ø | 0001×1 | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000110 | Ø | 000×10 | 0001×0 | Ø | – | 00011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000111 | Ø | Ø | Ø | 0001×1 | 00011x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001000 | 00×000 | Ø | Ø | Ø | Ø | Ø | – | 00100x | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001001 | Ø | Ø | Ø | Ø | Ø | Ø | 00100x | – | Ø | 0010×1 | 001×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001010 | Ø | 00×010 | Ø | Ø | Ø | Ø | 0010×0 | Ø | – | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×1 | 00101x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001101 | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 001×01 | Ø | Ø | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010000 | 0x0000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 01000x | 0100×0 | 010×00 | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01000x | – | Ø | Ø | 010×01 | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010010 | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0100×0 | Ø | – | Ø | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010100 | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×00 | Ø | Ø | – | 01010x | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010101 | Ø | Ø | Ø | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×01 | Ø | 01010x | – | 0101×1 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010111 | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0101×1 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 011000 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | – | 01100x | 0110×0 | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 011001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | 01100x | – | Ø | 0110×1 | Ø | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø |
| 011010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | 0110×0 | Ø | – | 01101x | Ø | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø |
| 011011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | – | Ø | Ø | Ø | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø |
| 011100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | 011×00 | Ø | Ø | Ø | – | 01110x | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø |
| 011101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | 011×01 | Ø | Ø | 01110x | – | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø |
| 011110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 0111×0 | Ø | – | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | Ø |
| 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | 011×11 | Ø | 0111×1 | 01111x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 |
| 100000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 10000x | Ø | 100×00 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10000x | – | 1000×1 | Ø | 100×01 | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1000×1 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100100 | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | Ø | Ø | – | 10010x | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100101 | Ø | Ø | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | Ø | 10010x | – | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 101000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | Ø | Ø | Ø | Ø | – | 10100x | 1010×0 | 101×00 | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 101001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | 10100x | – | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø |
| 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | Ø | – | Ø | Ø | 101×10 | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø |
| 101100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | 101×00 | Ø | Ø | – | 10110x | 1011×0 | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø |
| 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×101 | Ø | 101×01 | Ø | 10110x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø |
| 101110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×10 | 1011×0 | Ø | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | Ø |
| 110110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 11011x | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | Ø |
| 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11011x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×111 |
| 111000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 11100x | 1110×0 | Ø | 111×00 | Ø | Ø | Ø |
| 111001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | 11100x | – | Ø | 1110×1 | Ø | 111×01 | Ø | Ø |
| 111010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø | 1110×0 | Ø | – | 11101x | Ø | Ø | 111×10 | Ø |
| 111011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | 11101x | – | Ø | Ø | Ø | 111×11 |
| 111100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | 111×00 | Ø | Ø | Ø | – | 11110x | 1111×0 | Ø |
| 111101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | 11110x | – | Ø | 1111×1 |
| 111110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 11×110 | Ø | Ø | Ø | 111×10 | Ø | 1111×0 | Ø | – | 11111x |
| 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×111 | Ø | Ø | Ø | 111×11 | Ø | 1111×1 | 11111x | – |
Z0=Ø
Ĉ1=C0∪(C0*C0)
C1=>
| 0000×0, 000×00, 00×000 0x0000, x00000, 000×10 00×010, 0x0010, 00010x 0001×0, 0x0100, x00100 0001×1, 00×101, 0x0101 x00101, 00011x, 0x0111 00100x, 0010×0, 0x1000 x01000, 0010×1, 001×01 0x1001, x01001, 00101x 0x1010, x01010, 0x1011 0x1101, x01101, 01000x 0100×0, 010×00, 01×000 010×01, 01×001, 01×010 01010x, 01×100, 0101×1 01×101, 01×111, x10111 01100x, 0110×0, 011×00 x11000, 0110×1, 011×01 x11001, 01101x, 011×10 x11010, 011×11, x11011 01110x, 0111×0, x11100 0111×1, x11101, 01111x x11110, x11111, 10000x 100×00, 10×000, 1000×1 100×01, 10×001, 10010x 10×100, 10×101, 10100x 1010×0, 101×00, 1×1000 101×01, 1×1001, 101×10 1×1010, 10110x, 1011×0 1×1100, 1×1101, 1×1110 11011x, 11×110, 11×111 11100x, 1110×0, 111×00 1110×1, 111×01, 11101x 111×10, 111×11, 11110x 1111×0, 1111×1, 11111x |
| 0000×0 | 000×00 | 00×000 | 0x0000 | x00000 | 000×10 | 00×010 | 0x0010 | 00010x | 0001×0 | 0x0100 | x00100 | 0001×1 | 00×101 | 0x0101 | x00101 | 00011x | 0x0111 | 00100x | 0010×0 | 0x1000 | x01000 | 0010×1 | 001×01 | 0x1001 | x01001 | 00101x | 0x1010 | x01010 | 0x1011 | 0x1101 | x01101 | 01000x | 0100×0 | 010×00 | 01×000 | 010×01 | 01×001 | 01×010 | 01010x | 01×100 | 0101×1 | 01×101 | 01×111 | x10111 | 01100x | 0110×0 | 011×00 | x11000 | 0110×1 | 011×01 | x11001 | 01101x | 011×10 | x11010 | 011×11 | x11011 | 01110x | 0111×0 | x11100 | 0111×1 | x11101 | 01111x | x11110 | x11111 | 10000x | 100×00 | 10×000 | 1000×1 | 100×01 | 10×001 | 10010x | 10×100 | 10×101 | 10100x | 1010×0 | 101×00 | 1×1000 | 101×01 | 1×1001 | 101×10 | 1×1010 | 10110x | 1011×0 | 1×1100 | 1×1101 | 1×1110 | 11011x | 11×110 | 11×111 | 11100x | 1110×0 | 111×00 | 1110×1 | 111×01 | 11101x | 111×10 | 111×11 | 11110x | 1111×0 | 1111×1 | 11111x | |
| 0000×0 | – | 000000 | 000000 | 000000 | 000000 | 000010 | 000010 | 000010 | 000×00 | 000xx0 | 000×00 | 000×00 | Ø | Ø | Ø | Ø | 000×10 | Ø | 00×000 | 00x0x0 | 00×000 | 00×000 | Ø | Ø | Ø | Ø | 00×010 | 00×010 | 00×010 | Ø | Ø | Ø | 0x0000 | 0x00x0 | 0x0000 | 0x0000 | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000×00 | 000000 | – | 000000 | 000000 | 000000 | 000xx0 | 0000×0 | 0000×0 | 000100 | 000100 | 000100 | 000100 | 00010x | 00010x | 00010x | 00010x | 0001×0 | Ø | 00×000 | 00×000 | 00×000 | 00×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0000 | 0x0000 | 0x0x00 | 0x0000 | Ø | Ø | Ø | 0x0100 | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00x00 | x00000 | Ø | Ø | Ø | x00100 | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00×000 | 000000 | 000000 | – | 000000 | 000000 | 0000×0 | 00x0x0 | 0000×0 | 000×00 | 000×00 | 000×00 | 000×00 | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 001000 | 001000 | 001000 | 00100x | 00100x | 00100x | 00100x | 0010×0 | 0010×0 | 0010×0 | Ø | Ø | Ø | 0x0000 | 0x0000 | 0x0000 | 0xx000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 0x1000 | 0x1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x0x000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0000 | 000000 | 000000 | 000000 | – | 000000 | 0000×0 | 0000×0 | 0x00x0 | 000×00 | 000×00 | 0x0x00 | 000×00 | Ø | Ø | Ø | Ø | Ø | Ø | 00×000 | 00×000 | 0xx000 | 00×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010000 | 010000 | 010000 | 010000 | 01000x | 01000x | 0100×0 | 010×00 | 010×00 | Ø | Ø | Ø | Ø | 01×000 | 01×000 | 01×000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00000 | 000000 | 000000 | 000000 | 000000 | – | 0000×0 | 0000×0 | 0000×0 | 000×00 | 000×00 | 000×00 | x00x00 | Ø | Ø | Ø | Ø | Ø | Ø | 00×000 | 00×000 | 00×000 | x0x000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0000 | 0x0000 | 0x0000 | 0x0000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | 100000 | 100000 | 10000x | 10000x | 10000x | 100×00 | 100×00 | Ø | 10×000 | 10×000 | 10×000 | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 000×10 | 000010 | 000xx0 | 0000×0 | 0000×0 | 0000×0 | – | 000010 | 000010 | 0001×0 | 000110 | 0001×0 | 0001×0 | 00011x | Ø | Ø | Ø | 000110 | 00011x | Ø | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | 00×010 | 00×010 | 00×010 | Ø | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00×010 | 000010 | 0000×0 | 00x0x0 | 0000×0 | 0000×0 | 000010 | – | 000010 | Ø | 000×10 | Ø | Ø | Ø | Ø | Ø | Ø | 000×10 | Ø | 0010×0 | 001010 | 0010×0 | 0010×0 | 00101x | Ø | Ø | Ø | 001010 | 001010 | 001010 | 00101x | Ø | Ø | Ø | 0x0010 | Ø | Ø | Ø | Ø | 0xx010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0x1010 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | x01010 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0010 | 000010 | 0000×0 | 0000×0 | 0x00x0 | 0000×0 | 000010 | 000010 | – | Ø | 000×10 | Ø | Ø | Ø | Ø | Ø | Ø | 000×10 | Ø | Ø | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | 00×010 | 0xx010 | 00×010 | Ø | Ø | Ø | 0100×0 | 010010 | 0100×0 | 0100×0 | Ø | Ø | 010010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | Ø | Ø | 01×010 | 01×010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00010x | 000×00 | 000100 | 000×00 | 000×00 | 000×00 | 0001×0 | Ø | Ø | – | 000100 | 000100 | 000100 | 000101 | 000101 | 000101 | 000101 | 0001xx | 0001×1 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 00×101 | Ø | Ø | 0x0100 | Ø | 0x0101 | Ø | Ø | 0x010x | 0x0100 | 0x0101 | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | x00101 | Ø | x0010x | x00100 | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0001×0 | 000xx0 | 000100 | 000×00 | 000×00 | 000×00 | 000110 | 000×10 | 000×10 | 000100 | – | 000100 | 000100 | 0001xx | 00010x | 00010x | 00010x | 000110 | 00011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | 0x0100 | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | x00100 | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0100 | 000×00 | 000100 | 000×00 | 0x0x00 | 000×00 | 0001×0 | Ø | Ø | 000100 | 000100 | – | 000100 | 00010x | 00010x | 0x010x | 00010x | 0001×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×00 | 010×00 | 010100 | 010×00 | 01010x | Ø | Ø | 010100 | 010100 | 01010x | 01010x | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | 01×100 | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | x00100 | Ø | Ø | Ø | Ø | x00100 | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00100 | 000×00 | 000100 | 000×00 | 000×00 | x00x00 | 0001×0 | Ø | Ø | 000100 | 000100 | 000100 | – | 00010x | 00010x | 00010x | x0010x | 0001×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0100 | Ø | Ø | Ø | Ø | 0x0100 | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | 100100 | 100×00 | Ø | 10010x | Ø | 100100 | 100100 | 10010x | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | 10×100 | 10×100 | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0001×1 | Ø | 00010x | Ø | Ø | Ø | 00011x | Ø | Ø | 000101 | 0001xx | 00010x | 00010x | – | 000101 | 000101 | 000101 | 000111 | 000111 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 00×101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | 0x0101 | Ø | 0x01x1 | 0x0101 | 0x0111 | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | x00101 | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00×101 | Ø | 00010x | Ø | Ø | Ø | Ø | Ø | Ø | 000101 | 00010x | 00010x | 00010x | 000101 | – | 000101 | 000101 | 0001×1 | 0001×1 | 001×01 | Ø | Ø | Ø | 001×01 | 001101 | 001×01 | 001×01 | Ø | Ø | Ø | Ø | 001101 | 001101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | 0x0101 | Ø | 0x0101 | 0xx101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1101 | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | x00101 | Ø | x0x101 | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | x01101 | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0101 | Ø | 00010x | Ø | Ø | Ø | Ø | Ø | Ø | 000101 | 00010x | 0x010x | 00010x | 000101 | 000101 | – | 000101 | 0001×1 | 0x01x1 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 0xx101 | 00×101 | 010×01 | Ø | 01010x | Ø | 010101 | 010×01 | Ø | 010101 | 01010x | 010101 | 010101 | 0101×1 | 0101×1 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | 01×101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | x00101 | Ø | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00101 | Ø | 00010x | Ø | Ø | Ø | Ø | Ø | Ø | 000101 | 00010x | 00010x | x0010x | 000101 | 000101 | 000101 | – | 0001×1 | 0001×1 | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | x0x101 | Ø | Ø | Ø | Ø | 0x0101 | Ø | Ø | 0x0101 | Ø | 0x0101 | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | 10010x | Ø | 100×01 | 100101 | 100×01 | 100101 | 10010x | 100101 | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | 10×101 | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00011x | 000×10 | 0001×0 | Ø | Ø | Ø | 000110 | 000×10 | 000×10 | 0001xx | 000110 | 0001×0 | 0001×0 | 000111 | 0001×1 | 0001×1 | 0001×1 | – | 000111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | 0x0111 | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0111 | Ø | Ø | Ø | Ø | Ø | 00011x | Ø | Ø | 0001×1 | 00011x | Ø | Ø | 000111 | 0001×1 | 0x01x1 | 0001×1 | 000111 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0101×1 | Ø | Ø | 0101×1 | Ø | 010111 | 0101×1 | 010111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | 01×111 | Ø | 01×111 | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00100x | 00×000 | 00×000 | 001000 | 00×000 | 00×000 | Ø | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | – | 001000 | 001000 | 001000 | 001001 | 001001 | 001001 | 001001 | 0010xx | 0010×0 | 0010×0 | 0010×1 | 001×01 | 001×01 | Ø | Ø | Ø | 0x1000 | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x100x | 0x1000 | 0x1000 | 0x1000 | 0x1001 | 0x1001 | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | x01001 | Ø | Ø | Ø | x0100x | x01000 | x01000 | x01000 | x01001 | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0010×0 | 00x0x0 | 00×000 | 001000 | 00×000 | 00×000 | 00×010 | 001010 | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | – | 001000 | 001000 | 0010xx | 00100x | 00100x | 00100x | 001010 | 001010 | 001010 | 00101x | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x10x0 | 0x1000 | 0x1000 | Ø | Ø | Ø | 0x1010 | 0x1010 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x010x0 | x01000 | x01000 | Ø | Ø | x01010 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x1000 | 00×000 | 00×000 | 001000 | 0xx000 | 00×000 | Ø | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 001000 | – | 001000 | 00100x | 00100x | 0x100x | 00100x | 0010×0 | 0x10x0 | 0010×0 | Ø | Ø | Ø | 01×000 | 01×000 | 01×000 | 011000 | Ø | 01100x | 0110×0 | Ø | 011×00 | Ø | Ø | Ø | Ø | 011000 | 011000 | 011000 | 011000 | 01100x | 01100x | 01100x | 0110×0 | 0110×0 | 0110×0 | Ø | Ø | 011×00 | 011×00 | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | xx1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x01000 | 00×000 | 00×000 | 001000 | 00×000 | x0x000 | Ø | 0010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 001000 | 001000 | – | 00100x | 00100x | 00100x | x0100x | 0010×0 | 0010×0 | x010x0 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 0x1000 | xx1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | 10×000 | 101000 | Ø | Ø | 10100x | Ø | 101×00 | Ø | 101000 | 101000 | 101000 | 101000 | 10100x | 10100x | 1010×0 | 1010×0 | 101×00 | 101×00 | 101×00 | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1×1000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0010×1 | Ø | Ø | 00100x | Ø | Ø | Ø | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | 001001 | 0010xx | 00100x | 00100x | – | 001001 | 001001 | 001001 | 001011 | 00101x | 00101x | 001011 | 001×01 | 001×01 | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | 0x10x1 | 0x1001 | 0x1001 | 0x1011 | Ø | Ø | 0x1011 | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | x01001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 001×01 | Ø | Ø | 00100x | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 00×101 | 001101 | 00×101 | 00×101 | Ø | Ø | 001001 | 00100x | 00100x | 00100x | 001001 | – | 001001 | 001001 | 0010×1 | Ø | Ø | 0010×1 | 001101 | 001101 | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1001 | Ø | Ø | Ø | 0x1001 | 0x1x01 | 0x1001 | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1101 | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | x01101 | x01001 | Ø | Ø | Ø | x01x01 | x01001 | Ø | Ø | x01101 | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x1001 | Ø | Ø | 00100x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | 001001 | 00100x | 0x100x | 00100x | 001001 | 001001 | – | 001001 | 0010×1 | Ø | Ø | 0x10x1 | 0x1x01 | 001×01 | 01×001 | Ø | Ø | 01100x | 01×001 | 011001 | Ø | Ø | Ø | Ø | 011×01 | Ø | Ø | 011001 | 01100x | 01100x | 01100x | 011001 | 011001 | 011001 | 0110×1 | Ø | Ø | 0110×1 | 0110×1 | 011×01 | Ø | Ø | 011×01 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | Ø | Ø | Ø | x01001 | xx1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x11001 | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x01001 | Ø | Ø | 00100x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 001×01 | Ø | Ø | Ø | Ø | 001001 | 00100x | 00100x | x0100x | 001001 | 001001 | 001001 | – | 0010×1 | Ø | Ø | 0010×1 | 001×01 | x01x01 | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | Ø | Ø | 0x1001 | 0x1001 | xx1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | 10100x | 10×001 | 10×001 | 101001 | Ø | Ø | 101×01 | 101001 | 10100x | 10100x | 10100x | 101001 | 101001 | Ø | Ø | 101×01 | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00101x | 00×010 | Ø | 0010×0 | Ø | Ø | 00×010 | 001010 | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010xx | 001010 | 0010×0 | 0010×0 | 001011 | 0010×1 | 0010×1 | 0010×1 | – | 001010 | 001010 | 001011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | 0x1011 | Ø | Ø | 0x101x | 0x1010 | 0x1010 | 0x1011 | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | x01010 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x1010 | 00×010 | Ø | 0010×0 | Ø | Ø | 00×010 | 001010 | 0xx010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 001010 | 0x10x0 | 0010×0 | 00101x | Ø | Ø | Ø | 001010 | – | 001010 | 0x101x | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0110×0 | 011010 | 0110×0 | 0110×0 | 01101x | Ø | Ø | 011010 | 011010 | 011010 | 01101x | 01101x | Ø | 011×10 | Ø | Ø | Ø | 011×10 | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | x01010 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | x11010 | x11010 | Ø | Ø | Ø | Ø | Ø |
| x01010 | 00×010 | Ø | 0010×0 | Ø | Ø | 00×010 | 001010 | 00×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 001010 | 0010×0 | x010x0 | 00101x | Ø | Ø | Ø | 001010 | 001010 | – | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0x1010 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | 101010 | 1010×0 | 1010×0 | Ø | Ø | 101010 | 101010 | Ø | 101×10 | Ø | Ø | 101×10 | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | 1×1010 | 1×1010 | Ø | Ø | Ø | Ø | Ø |
| 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | 00101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0010×1 | 00101x | Ø | Ø | 001011 | 0010×1 | 0x10x1 | 0010×1 | 001011 | 0x101x | 00101x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | Ø | Ø | Ø | Ø | 011×11 | Ø | 0110×1 | 01101x | Ø | Ø | 011011 | 0110×1 | 0110×1 | 011011 | 01101x | 01101x | 011011 | 011011 | Ø | Ø | Ø | 011×11 | Ø | 011×11 | Ø | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | x11011 | Ø | x11011 | Ø | Ø | Ø | Ø |
| 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 00×101 | 001101 | 0xx101 | 00×101 | Ø | Ø | 001×01 | Ø | Ø | Ø | 001×01 | 001101 | 0x1x01 | 001×01 | Ø | Ø | Ø | Ø | – | 001101 | Ø | Ø | Ø | Ø | 01×101 | 011×01 | Ø | 01×101 | 01110x | 01×101 | 011101 | 0111×1 | Ø | 011×01 | Ø | 01110x | Ø | 011×01 | 011101 | 011×01 | Ø | Ø | Ø | 0111×1 | Ø | 011101 | 01110x | 01110x | 011101 | 011101 | 0111×1 | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | Ø | x01101 | Ø | Ø | Ø | x01101 | Ø | Ø | xx1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø |
| x01101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | Ø | Ø | Ø | 00×101 | 001101 | 00×101 | x0x101 | Ø | Ø | 001×01 | Ø | Ø | Ø | 001×01 | 001101 | 001×01 | x01x01 | Ø | Ø | Ø | Ø | 001101 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | Ø | Ø | 0x1101 | xx1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×101 | 101×01 | 10×101 | 10110x | 101101 | 101×01 | Ø | 10110x | Ø | 101101 | 101×01 | Ø | Ø | 101101 | 10110x | 10110x | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø |
| 01000x | 0x0000 | 0x0000 | 0x0000 | 010000 | 0x0000 | Ø | Ø | 0100×0 | Ø | Ø | 010×00 | Ø | Ø | Ø | 010×01 | Ø | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 010000 | 010000 | 010000 | 010001 | 010001 | 0100×0 | 010x0x | 010×00 | 010×01 | 010×01 | Ø | Ø | 01x00x | 01×000 | 01×000 | 01×000 | 01×001 | 01×001 | 01×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0100×0 | 0x00x0 | 0x0000 | 0x0000 | 010000 | 0x0000 | 0x0010 | 0x0010 | 010010 | Ø | Ø | 010×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | 01×010 | Ø | Ø | Ø | Ø | 010000 | – | 010000 | 010000 | 01000x | 01000x | 010010 | 010×00 | 010×00 | Ø | Ø | Ø | Ø | 01×000 | 01x0x0 | 01×000 | 01×000 | Ø | Ø | Ø | 01×010 | 01×010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010×00 | 0x0000 | 0x0x00 | 0x0000 | 010000 | 0x0000 | Ø | Ø | 0100×0 | 0x0100 | 0x0100 | 010100 | 0x0100 | Ø | Ø | 01010x | Ø | Ø | Ø | Ø | Ø | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010000 | 010000 | – | 010000 | 010x0x | 01000x | 0100×0 | 010100 | 010100 | 01010x | 01010x | Ø | Ø | 01×000 | 01×000 | 01xx00 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | 01×100 | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×000 | 0x0000 | 0x0000 | 0xx000 | 010000 | 0x0000 | Ø | Ø | 0100×0 | Ø | Ø | 010×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 011000 | 0x1000 | Ø | Ø | 01100x | Ø | Ø | 0110×0 | Ø | Ø | Ø | Ø | 010000 | 010000 | 010000 | – | 01000x | 01x00x | 01x0x0 | 010×00 | 01xx00 | Ø | Ø | Ø | Ø | 011000 | 011000 | 011000 | 011000 | 01100x | 01100x | 01100x | 0110×0 | 0110×0 | 0110×0 | Ø | Ø | 011×00 | 011×00 | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 010×01 | Ø | Ø | Ø | 01000x | Ø | Ø | Ø | Ø | 0x0101 | Ø | 01010x | Ø | 0x0101 | 0x0101 | 010101 | 0x0101 | Ø | 0101×1 | Ø | Ø | Ø | Ø | Ø | Ø | 01×001 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 010001 | 01000x | 010x0x | 01000x | – | 010001 | Ø | 010101 | 01010x | 010101 | 010101 | 0101×1 | 0101×1 | 01×001 | Ø | Ø | Ø | 01×001 | 01xx01 | 01×001 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | 01×101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×001 | Ø | Ø | Ø | 01000x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×01 | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x1001 | 0x1001 | 011001 | 0x1001 | Ø | Ø | Ø | 0110×1 | 011×01 | Ø | 010001 | 01000x | 01000x | 01x00x | 010001 | – | Ø | 010×01 | Ø | 010×01 | 01xx01 | Ø | Ø | 011001 | 01100x | 01100x | 01100x | 011001 | 011001 | 011001 | 0110×1 | Ø | Ø | 0110×1 | 0110×1 | 011×01 | Ø | Ø | 011×01 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x11001 | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×010 | 0x0010 | Ø | Ø | 0100×0 | Ø | 0x0010 | 0xx010 | 010010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 011010 | 0x1010 | 01101x | Ø | Ø | 0100×0 | 010010 | 0100×0 | 01x0x0 | Ø | Ø | – | Ø | Ø | Ø | Ø | Ø | Ø | 0110×0 | 011010 | 0110×0 | 0110×0 | 01101x | Ø | Ø | 011010 | 011010 | 011010 | 01101x | 01101x | Ø | 011×10 | Ø | Ø | Ø | 011×10 | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | x11010 | x11010 | Ø | Ø | Ø | Ø | Ø |
| 01010x | Ø | 0x0100 | Ø | 010×00 | Ø | Ø | Ø | Ø | 0x010x | 0x0100 | 010100 | 0x0100 | 0x0101 | 0x0101 | 010101 | 0x0101 | Ø | 0101×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 010x0x | 010×00 | 010100 | 010×00 | 010101 | 010×01 | Ø | – | 010100 | 010101 | 010101 | 0101×1 | 0101×1 | Ø | Ø | 01×100 | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | 01x10x | 01×100 | 01×100 | 01×101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×100 | Ø | 0x0100 | Ø | 010×00 | Ø | Ø | Ø | Ø | 0x0100 | 0x0100 | 010100 | 0x0100 | Ø | Ø | 01010x | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01110x | Ø | 010×00 | 010×00 | 010100 | 01xx00 | 01010x | Ø | Ø | 010100 | – | 01010x | 01x10x | Ø | Ø | 011×00 | 011×00 | 011100 | 011×00 | Ø | 01110x | Ø | Ø | 0111×0 | Ø | Ø | Ø | 011100 | 011100 | 011100 | 01110x | 01110x | 0111×0 | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | x11100 | x11100 | Ø | Ø |
| 0101×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0101 | Ø | 01010x | Ø | 0x01x1 | 0x0101 | 010101 | 0x0101 | 0x0111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 010×01 | Ø | 01010x | Ø | 010101 | 010×01 | Ø | 010101 | 01010x | – | 010101 | 010111 | 010111 | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | Ø | Ø | Ø | 01×111 | Ø | 01×101 | Ø | Ø | 01x1x1 | 01×101 | 01×111 | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0101 | Ø | 01010x | Ø | 0x0101 | 0xx101 | 010101 | 0x0101 | Ø | 0101×1 | Ø | Ø | Ø | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | Ø | 011101 | 0x1101 | 010×01 | Ø | 01010x | Ø | 010101 | 01xx01 | Ø | 010101 | 01x10x | 010101 | – | 01x1x1 | 0101×1 | 011×01 | Ø | 01110x | Ø | 011×01 | 011101 | 011×01 | Ø | Ø | Ø | 0111×1 | Ø | 011101 | 01110x | 01110x | 011101 | 011101 | 0111×1 | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø |
| 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | 0101×1 | Ø | 0x0111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | Ø | Ø | Ø | 0101×1 | Ø | Ø | 0101×1 | Ø | 010111 | 01x1x1 | – | 010111 | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | 011×11 | 01111x | Ø | 011111 | 011×11 | 0111×1 | 01111x | Ø | 011111 | 0111×1 | 011111 | 01111x | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x1x111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | Ø | Ø | x11111 | x11111 |
| x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | Ø | 0101×1 | Ø | 0x0111 | 010111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0101×1 | Ø | Ø | 0101×1 | Ø | 010111 | 0101×1 | 010111 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | 01×111 | Ø | 01×111 | Ø | x1x111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 110111 | 11011x | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×111 | Ø | Ø | 11×111 | 11×111 |
| 01100x | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x100x | 0x1000 | 011000 | 0x1000 | 0x1001 | 0x1001 | 011001 | 0x1001 | Ø | 0110×0 | Ø | 0110×1 | 011×01 | Ø | 01x00x | 01×000 | 01×000 | 011000 | 01×001 | 011001 | 0110×0 | Ø | 011×00 | Ø | 011×01 | Ø | Ø | – | 011000 | 011000 | 011000 | 011001 | 011001 | 011001 | 0110xx | 0110×0 | 0110×0 | 0110×1 | 0110×1 | 011x0x | 011×00 | 011×00 | 011×01 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | x11000 | x11000 | x11001 | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0110×0 | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x10x0 | 011000 | 0x1000 | Ø | Ø | 01100x | Ø | 0x1010 | 011010 | 0x1010 | 01101x | Ø | Ø | 01×000 | 01x0x0 | 01×000 | 011000 | Ø | 01100x | 011010 | Ø | 011×00 | Ø | Ø | Ø | Ø | 011000 | – | 011000 | 011000 | 0110xx | 01100x | 01100x | 011010 | 011010 | 011010 | 01101x | 01101x | 011×00 | 011xx0 | 011×00 | Ø | Ø | 011×10 | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x110x0 | x11000 | Ø | Ø | x11010 | x11010 | Ø | Ø | Ø | Ø | Ø |
| 011×00 | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 011000 | 0x1000 | Ø | Ø | 01100x | Ø | Ø | 0110×0 | Ø | Ø | 01110x | Ø | 01×000 | 01×000 | 01xx00 | 011000 | Ø | 01100x | 0110×0 | 01×100 | 011100 | Ø | 01110x | Ø | Ø | 011000 | 011000 | – | 011000 | 01100x | 011x0x | 01100x | 0110×0 | 011xx0 | 0110×0 | Ø | Ø | 011100 | 011100 | 011100 | 01110x | 01110x | 0111×0 | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11x00 | Ø | Ø | Ø | Ø | Ø | x11100 | x11100 | Ø | Ø |
| x11000 | Ø | Ø | 0x1000 | 01×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | 011000 | xx1000 | Ø | Ø | 01100x | Ø | Ø | 0110×0 | Ø | Ø | Ø | Ø | 01×000 | 01×000 | 01×000 | 011000 | Ø | 01100x | 0110×0 | Ø | 011×00 | Ø | Ø | Ø | Ø | 011000 | 011000 | 011000 | – | 01100x | 01100x | x1100x | 0110×0 | 0110×0 | x110x0 | Ø | Ø | 011×00 | 011×00 | x11x00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1×1000 | 1×1000 | 111000 | Ø | 11100x | Ø | 1110×0 | Ø | Ø | 111×00 | Ø | Ø | Ø | Ø | Ø | 111000 | 111000 | 111000 | 11100x | 11100x | 1110×0 | 1110×0 | Ø | 111×00 | 111×00 | Ø | Ø |
| 0110×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x10x1 | 0x1001 | 011001 | 0x1001 | 0x1011 | 01101x | Ø | 011011 | 011×01 | Ø | 01×001 | Ø | Ø | 01100x | 01×001 | 011001 | 01101x | Ø | Ø | Ø | 011×01 | 011×11 | Ø | 011001 | 0110xx | 01100x | 01100x | – | 011001 | 011001 | 011011 | 01101x | 01101x | 011011 | 011011 | 011×01 | Ø | Ø | 011xx1 | 011×01 | 011×11 | Ø | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x110x1 | x11001 | x11011 | Ø | x11011 | Ø | Ø | Ø | Ø |
| 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x1001 | 0x1x01 | 011001 | 0x1001 | Ø | Ø | Ø | 0110×1 | 011101 | 0x1101 | 01×001 | Ø | Ø | 01100x | 01xx01 | 011001 | Ø | 01×101 | 01110x | 01×101 | 011101 | 0111×1 | Ø | 011001 | 01100x | 011x0x | 01100x | 011001 | – | 011001 | 0110×1 | Ø | Ø | 011xx1 | 0110×1 | 011101 | 01110x | 01110x | 011101 | 011101 | 0111×1 | Ø | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | x11001 | x11x01 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø |
| x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1001 | Ø | 01100x | Ø | 0x1001 | 0x1001 | 011001 | xx1001 | Ø | Ø | Ø | 0110×1 | 011×01 | Ø | 01×001 | Ø | Ø | 01100x | 01×001 | 011001 | Ø | Ø | Ø | Ø | 011×01 | Ø | Ø | 011001 | 01100x | 01100x | x1100x | 011001 | 011001 | – | 0110×1 | Ø | Ø | 0110×1 | x110x1 | 011×01 | Ø | Ø | 011×01 | x11x01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | 1×1001 | Ø | Ø | 11100x | 1×1001 | 111001 | Ø | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | Ø | Ø | 111001 | 11100x | 11100x | 111001 | 111001 | 1110×1 | Ø | 1110×1 | 111×01 | Ø | 111×01 | Ø |
| 01101x | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | 0x1011 | Ø | 0110×1 | Ø | 0x101x | 011010 | 0x1010 | 011011 | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | 0110×1 | 011010 | Ø | Ø | Ø | Ø | 011×11 | Ø | 0110xx | 011010 | 0110×0 | 0110×0 | 011011 | 0110×1 | 0110×1 | – | 011010 | 011010 | 011011 | 011011 | Ø | 011×10 | Ø | 011×11 | Ø | 011x1x | 011×10 | 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | x11011 | Ø | x1101x | x11010 | x11011 | Ø | Ø | Ø | Ø |
| 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 011010 | 0x1010 | 01101x | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | Ø | 011010 | Ø | 0111×0 | Ø | Ø | 01111x | Ø | 0110×0 | 011010 | 011xx0 | 0110×0 | 01101x | Ø | Ø | 011010 | – | 011010 | 011x1x | 01101x | 0111×0 | 011110 | 0111×0 | 01111x | Ø | 011110 | 011110 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | x11110 | Ø | x11110 | Ø | Ø | x11010 | Ø | Ø | Ø | x11010 | x11x10 | Ø | Ø | x11110 | Ø | x11110 |
| x11010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | Ø | Ø | Ø | Ø | 0x1010 | 011010 | xx1010 | 01101x | Ø | Ø | Ø | 01×010 | Ø | 0110×0 | Ø | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0110×0 | 011010 | 0110×0 | x110x0 | 01101x | Ø | Ø | 011010 | 011010 | – | 01101x | x1101x | Ø | 011×10 | Ø | Ø | Ø | 011×10 | x11x10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | 1110×0 | Ø | Ø | 1×1010 | 111010 | Ø | Ø | Ø | Ø | 111×10 | Ø | 111×10 | Ø | 1110×0 | 111010 | 1110×0 | 11101x | Ø | 111010 | 111010 | 11101x | Ø | 111×10 | Ø | 111×10 |
| 011×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | 0x1011 | Ø | 0110×1 | Ø | 0x1011 | 01101x | Ø | 011011 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | Ø | Ø | 01×111 | 0111×1 | 011111 | 01×111 | 0110×1 | 01101x | Ø | Ø | 011011 | 011xx1 | 0110×1 | 011011 | 011x1x | 01101x | – | 011011 | 0111×1 | 01111x | Ø | 011111 | 0111×1 | 011111 | 01111x | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | Ø | Ø | Ø | x11011 | Ø | x11011 | Ø | x11x11 | Ø | Ø | x11111 | x11111 |
| x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1011 | Ø | 0110×1 | Ø | 0x1011 | 01101x | Ø | 011011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0110×1 | 01101x | Ø | Ø | Ø | Ø | 011×11 | Ø | 0110×1 | 01101x | Ø | Ø | 011011 | 0110×1 | x110x1 | 011011 | 01101x | x1101x | 011011 | – | Ø | Ø | Ø | 011×11 | Ø | 011×11 | Ø | x11x11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | Ø | 11101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 111×11 | 1110×1 | 11101x | Ø | 111011 | 1110×1 | 111011 | 11101x | 111011 | Ø | Ø | 111×11 | 111×11 |
| 01110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | Ø | 011101 | 0x1101 | Ø | Ø | 01×100 | 011×00 | 01×101 | 011×01 | Ø | 01x10x | 011100 | 01×101 | 011101 | 0111×1 | Ø | 011x0x | 011×00 | 011100 | 011×00 | 011×01 | 011101 | 011×01 | Ø | 0111×0 | Ø | 0111×1 | Ø | – | 011100 | 011100 | 011101 | 011101 | 0111xx | 0111×0 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | x11101 | Ø | Ø | Ø | x1110x | x11100 | x11101 | Ø |
| 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | 01110x | Ø | Ø | Ø | 01×100 | 011×00 | Ø | Ø | 011×10 | 01×100 | 011100 | Ø | 01110x | 01111x | Ø | 011×00 | 011xx0 | 011100 | 011×00 | Ø | 01110x | Ø | 011×10 | 011110 | 011×10 | 01111x | Ø | 011100 | – | 011100 | 0111xx | 01110x | 011110 | 011110 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | x11110 | Ø | x11110 | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | x11110 | Ø | x11100 | x111x0 | Ø | x11110 |
| x11100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01110x | Ø | Ø | Ø | 01×100 | 011×00 | Ø | Ø | Ø | 01×100 | 011100 | Ø | 01110x | Ø | Ø | 011×00 | 011×00 | 011100 | x11x00 | Ø | 01110x | Ø | Ø | 0111×0 | Ø | Ø | Ø | 011100 | 011100 | – | 01110x | x1110x | 0111×0 | x111x0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1100 | 111×00 | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | 111100 | 11110x | 1111×0 | Ø | 1111×0 | Ø | 111×00 | 111×00 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | 111100 | 111100 | 11110x | 1111×0 |
| 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | 011×11 | 011101 | 0x1101 | Ø | Ø | Ø | Ø | 01×101 | 011×01 | Ø | 01×101 | 01110x | 01x1x1 | 011101 | 011111 | 01×111 | 011×01 | Ø | 01110x | Ø | 011xx1 | 011101 | 011×01 | 011×11 | 01111x | Ø | 011111 | 011×11 | 011101 | 0111xx | 01110x | – | 011101 | 011111 | 01111x | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | x11111 | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | x11111 | x11101 | Ø | x111x1 | x11111 |
| x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x1101 | 011×01 | Ø | Ø | Ø | Ø | Ø | 011101 | xx1101 | Ø | Ø | Ø | Ø | 01×101 | 011×01 | Ø | 01×101 | 01110x | 01×101 | 011101 | 0111×1 | Ø | 011×01 | Ø | 01110x | Ø | 011×01 | 011101 | x11x01 | Ø | Ø | Ø | 0111×1 | Ø | 011101 | 01110x | x1110x | 011101 | – | 0111×1 | Ø | x111x1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | 1×1101 | 111×01 | Ø | Ø | 1×1101 | Ø | 11110x | 111101 | Ø | Ø | Ø | 1111×1 | 111×01 | Ø | 11110x | 111×01 | 111101 | Ø | Ø | 1111×1 | 111101 | 11110x | 111101 | 1111×1 |
| 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 011×11 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 0111×0 | 01×111 | 0111×1 | 011111 | 01×111 | Ø | 011×10 | 0111×0 | Ø | 011×11 | 0111×1 | Ø | 011x1x | 011110 | 011×10 | 011111 | 011×11 | 0111xx | 011110 | 0111×0 | 011111 | 0111×1 | – | 011110 | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | Ø | x11110 | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | x11111 | Ø | x11110 | x11111 | x1111x |
| x11110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | 0111×0 | Ø | Ø | 01111x | Ø | Ø | 011×10 | 0111×0 | Ø | Ø | Ø | Ø | 011×10 | 011110 | x11x10 | 01111x | Ø | 0111×0 | 011110 | x111x0 | 01111x | Ø | 011110 | – | x1111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | Ø | 1×1110 | 1111×0 | Ø | 111110 | 11×110 | 111110 | 11111x | Ø | 111×10 | 1111×0 | Ø | Ø | 111×10 | 111110 | 11111x | 1111×0 | 111110 | 11111x | 111110 |
| x11111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×111 | 0111×1 | 011111 | x1x111 | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | 011×11 | 01111x | Ø | 011111 | x11x11 | 0111×1 | 01111x | Ø | 011111 | x111x1 | 011111 | x1111x | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1111×1 | 11111x | 11×111 | 11111x | 111111 | Ø | Ø | Ø | 111×11 | 1111×1 | 111×11 | 11111x | 111111 | 1111×1 | 11111x | 111111 | 111111 |
| 10000x | x00000 | x00000 | x00000 | x00000 | 100000 | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | Ø | Ø | Ø | 100×01 | Ø | Ø | Ø | Ø | Ø | 10×000 | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 100000 | 100000 | 100001 | 100001 | 100001 | 100x0x | 100×00 | 100×01 | 10x00x | 10×000 | 10×000 | 10×000 | 10×001 | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100×00 | x00000 | x00x00 | x00000 | x00000 | 100000 | Ø | Ø | Ø | x00100 | x00100 | x00100 | 100100 | Ø | Ø | Ø | 10010x | Ø | Ø | Ø | Ø | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | – | 100000 | 10000x | 100x0x | 10000x | 100100 | 100100 | 10010x | 10×000 | 10×000 | 10xx00 | 10×000 | Ø | Ø | Ø | Ø | 10×100 | 10×100 | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10×000 | x00000 | x00000 | x0x000 | x00000 | 100000 | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | 101000 | Ø | Ø | Ø | 10100x | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | 100000 | – | 10000x | 10000x | 10x00x | 100×00 | 10xx00 | Ø | 101000 | 101000 | 101000 | 101000 | 10100x | 10100x | 1010×0 | 1010×0 | 101×00 | 101×00 | 101×00 | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1×1000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 1000×1 | Ø | Ø | Ø | Ø | 10000x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100001 | 10000x | 10000x | – | 100001 | 100001 | 100×01 | Ø | 100×01 | 10×001 | Ø | Ø | Ø | 10×001 | 10×001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 100×01 | Ø | Ø | Ø | Ø | 10000x | Ø | Ø | Ø | x00101 | Ø | Ø | 10010x | x00101 | x00101 | x00101 | 100101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×001 | Ø | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100001 | 100x0x | 10000x | 100001 | – | 100001 | 100101 | 10010x | 100101 | 10×001 | Ø | Ø | Ø | 10xx01 | 10×001 | Ø | Ø | 10×101 | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10×001 | Ø | Ø | Ø | Ø | 10000x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×01 | Ø | Ø | x01001 | Ø | Ø | 10100x | x01001 | x01001 | x01001 | 101001 | Ø | Ø | Ø | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100001 | 10000x | 10x00x | 100001 | 100001 | – | 100×01 | Ø | 10xx01 | 101001 | 10100x | 10100x | 10100x | 101001 | 101001 | Ø | Ø | 101×01 | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10010x | Ø | x00100 | Ø | Ø | 100×00 | Ø | Ø | Ø | x0010x | x00100 | x00100 | 100100 | x00101 | x00101 | x00101 | 100101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100x0x | 100100 | 100×00 | 100×01 | 100101 | 100×01 | – | 100100 | 100101 | Ø | Ø | 10×100 | Ø | 10×101 | Ø | Ø | Ø | 10x10x | 10×100 | 10×100 | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10×100 | Ø | x00100 | Ø | Ø | 100×00 | Ø | Ø | Ø | x00100 | x00100 | x00100 | 100100 | Ø | Ø | Ø | 10010x | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | Ø | 100×00 | 100100 | 10xx00 | Ø | 10010x | Ø | 100100 | – | 10x10x | 101×00 | 101×00 | 101100 | 101×00 | 10110x | Ø | 1011×0 | Ø | 101100 | 101100 | 101100 | 10110x | 1011×0 | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | Ø | Ø |
| 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00101 | Ø | Ø | 10010x | x00101 | x0x101 | x00101 | 100101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 101×01 | Ø | Ø | Ø | Ø | x01101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 100×01 | 10010x | Ø | 100×01 | 100101 | 10xx01 | 100101 | 10x10x | – | 101×01 | Ø | 10110x | Ø | 101101 | 101×01 | Ø | Ø | 101101 | 10110x | 10110x | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø |
| 10100x | Ø | Ø | x01000 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x0100x | x01000 | x01000 | 101000 | x01001 | x01001 | x01001 | 101001 | Ø | Ø | 1010×0 | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10x00x | 10×000 | 101000 | 10×001 | 10×001 | 101001 | Ø | 101×00 | 101×01 | – | 101000 | 101000 | 101000 | 101001 | 101001 | 1010×0 | 1010×0 | 101x0x | 101×00 | 101×00 | 101×01 | Ø | Ø | Ø | Ø | 1x100x | 1×1000 | 1×1000 | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 1010×0 | Ø | Ø | x01000 | Ø | 10×000 | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x010x0 | x01000 | 101000 | Ø | Ø | Ø | 10100x | x01010 | x01010 | 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | 10×000 | 101000 | Ø | Ø | 10100x | Ø | 101×00 | Ø | 101000 | – | 101000 | 101000 | 10100x | 10100x | 101010 | 101010 | 101×00 | 101xx0 | 101×00 | Ø | 101×10 | Ø | Ø | Ø | 1×1000 | 1x10x0 | 1×1000 | Ø | Ø | 1×1010 | 1×1010 | Ø | Ø | Ø | Ø | Ø |
| 101×00 | Ø | Ø | x01000 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | x01000 | 101000 | Ø | Ø | Ø | 10100x | Ø | Ø | 1010×0 | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | Ø | Ø | 10×000 | 10xx00 | 101000 | Ø | Ø | 10100x | 10×100 | 101100 | 10110x | 101000 | 101000 | – | 101000 | 101x0x | 10100x | 101xx0 | 1010×0 | 101100 | 101100 | 101100 | 10110x | 1011×0 | Ø | Ø | Ø | 1×1000 | 1×1000 | 1x1x00 | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | Ø | Ø |
| 1×1000 | Ø | Ø | x01000 | Ø | 10×000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01000 | x01000 | xx1000 | 101000 | Ø | Ø | Ø | 10100x | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | 111000 | Ø | Ø | 11100x | Ø | Ø | 1110×0 | Ø | Ø | Ø | Ø | 111×00 | Ø | Ø | Ø | Ø | Ø | 10×000 | 10×000 | 101000 | Ø | Ø | 10100x | Ø | 101×00 | Ø | 101000 | 101000 | 101000 | – | 10100x | 1x100x | 1010×0 | 1x10x0 | 101×00 | 101×00 | 1x1x00 | Ø | Ø | Ø | Ø | Ø | 111000 | 111000 | 111000 | 11100x | 11100x | 1110×0 | 1110×0 | Ø | 111×00 | 111×00 | Ø | Ø |
| 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 10×101 | Ø | Ø | x01001 | Ø | Ø | 10100x | x01001 | x01x01 | x01001 | 101001 | Ø | Ø | Ø | Ø | x01101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | 10×001 | Ø | 10100x | 10×001 | 10xx01 | 101001 | 10×101 | 10110x | 101101 | 101001 | 10100x | 101x0x | 10100x | – | 101001 | Ø | Ø | 101101 | 10110x | 10110x | 101101 | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1001 | 1x1x01 | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø |
| 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01001 | Ø | Ø | 10100x | x01001 | x01001 | xx1001 | 101001 | Ø | Ø | Ø | Ø | Ø | 101×01 | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | 11100x | x11001 | x11001 | 111001 | Ø | Ø | Ø | Ø | 1110×1 | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | Ø | 10×001 | Ø | 10100x | 10×001 | 10×001 | 101001 | Ø | Ø | 101×01 | 101001 | 10100x | 10100x | 1x100x | 101001 | – | Ø | Ø | 101×01 | Ø | Ø | 1x1x01 | Ø | Ø | Ø | Ø | 111001 | 11100x | 11100x | 111001 | 111001 | 1110×1 | Ø | 1110×1 | 111×01 | Ø | 111×01 | Ø |
| 101×10 | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | 1010×0 | Ø | Ø | Ø | Ø | x01010 | x01010 | 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | Ø | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | 1011×0 | Ø | 1010×0 | 101010 | 101xx0 | 1010×0 | Ø | Ø | – | 101010 | 1011×0 | 101110 | 1011×0 | Ø | 101110 | Ø | 1×1110 | Ø | Ø | 1×1010 | Ø | Ø | Ø | 1×1010 | 1x1x10 | Ø | Ø | 1×1110 | Ø | 1×1110 |
| 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | 1010×0 | Ø | Ø | Ø | Ø | x01010 | xx1010 | 101010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | 1110×0 | Ø | Ø | Ø | x11010 | x11010 | 111010 | Ø | 11101x | Ø | Ø | Ø | Ø | Ø | Ø | 111×10 | Ø | Ø | Ø | 1010×0 | Ø | Ø | Ø | Ø | Ø | Ø | 1010×0 | 101010 | 1010×0 | 1x10x0 | Ø | Ø | 101010 | – | Ø | 101×10 | Ø | Ø | 1x1x10 | Ø | 111×10 | Ø | 1110×0 | 111010 | 1110×0 | 11101x | Ø | 111010 | 111010 | 11101x | Ø | 111×10 | Ø | 111×10 |
| 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | x01101 | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | x01101 | Ø | 101×01 | Ø | Ø | Ø | Ø | x01101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | 1×1101 | Ø | Ø | Ø | Ø | 10×100 | 101×00 | Ø | 10×101 | 101×01 | 10x10x | 101100 | 101101 | 101x0x | 101×00 | 101100 | 101×00 | 101101 | 101×01 | 1011×0 | Ø | – | 101100 | 101100 | 101101 | 1011×0 | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | 1×1101 | Ø | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø |
| 1011×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | Ø | Ø | Ø | Ø | Ø | 101×10 | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1110 | Ø | Ø | 10×100 | 101×00 | Ø | Ø | Ø | 10×100 | 101100 | 10110x | 101×00 | 101xx0 | 101100 | 101×00 | 10110x | Ø | 101110 | 101×10 | 101100 | – | 101100 | 10110x | 101110 | Ø | 1×1110 | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1110 | Ø | 1×1100 | 1x11x0 | Ø | 1×1110 |
| 1×1100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | 111×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11100 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | Ø | 10×100 | 101×00 | Ø | Ø | Ø | 10×100 | 101100 | 10110x | 101×00 | 101×00 | 101100 | 1x1x00 | 10110x | Ø | 1011×0 | Ø | 101100 | 101100 | – | 1x110x | 1x11x0 | Ø | 1111×0 | Ø | 111×00 | 111×00 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | 111100 | 111100 | 11110x | 1111×0 |
| 1×1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01101 | Ø | 101×01 | Ø | Ø | Ø | Ø | xx1101 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 111×01 | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | 11110x | x11101 | 111101 | Ø | Ø | 1111×1 | Ø | Ø | Ø | Ø | 10×101 | 101×01 | 10×101 | 10110x | 101101 | 101×01 | Ø | 10110x | Ø | 101101 | 1x1x01 | Ø | Ø | 101101 | 10110x | 1x110x | – | Ø | Ø | Ø | 1111×1 | 111×01 | Ø | 11110x | 111×01 | 111101 | Ø | Ø | 1111×1 | 111101 | 11110x | 111101 | 1111×1 |
| 1×1110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 101×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | 111×10 | Ø | Ø | Ø | x11110 | 1111×0 | Ø | Ø | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1011×0 | Ø | Ø | 101×10 | 1011×0 | Ø | Ø | Ø | 101110 | 1x1x10 | 1011×0 | 101110 | 1x11x0 | Ø | – | 11×110 | 111110 | 11111x | Ø | 111×10 | 1111×0 | Ø | Ø | 111×10 | 111110 | 11111x | 1111×0 | 111110 | 11111x | 111110 |
| 11011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x10111 | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | 11×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | – | 110110 | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | 11×110 | 11×111 | Ø | 11×110 | 11×111 | 11x11x |
| 11×110 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 11011x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | 111×10 | Ø | Ø | Ø | x11110 | 1111×0 | Ø | Ø | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | Ø | 1×1110 | 1111×0 | Ø | 111110 | 110110 | – | 11x11x | Ø | 111×10 | 1111×0 | Ø | Ø | 111×10 | 111110 | 11111x | 1111×0 | 111110 | 11111x | 111110 |
| 11×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | x1x111 | 110111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | 111×11 | Ø | Ø | Ø | x11111 | 1111×1 | x11111 | 11111x | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1111×1 | 11111x | 110111 | 11x11x | – | Ø | Ø | Ø | 111×11 | 1111×1 | 111×11 | 11111x | 111111 | 1111×1 | 11111x | 111111 | 111111 |
| 11100x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | x11001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | x11000 | x11000 | 111000 | x11001 | x11001 | 111001 | Ø | Ø | 1110×0 | Ø | 1110×1 | Ø | Ø | 111×00 | Ø | 111×01 | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | Ø | 1×1001 | Ø | Ø | Ø | 1x100x | 1×1000 | 1×1000 | 111000 | 1×1001 | 111001 | Ø | 1110×0 | Ø | Ø | 111×00 | 111×01 | Ø | Ø | Ø | Ø | – | 111000 | 111000 | 111001 | 111001 | 1110xx | 1110×0 | 1110×1 | 111x0x | 111×00 | 111×01 | Ø |
| 1110×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | x110x0 | x11000 | 111000 | Ø | Ø | 11100x | x11010 | x11010 | 111010 | Ø | 11101x | Ø | Ø | 111×00 | Ø | Ø | Ø | 111×10 | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | 1x10x0 | 1×1000 | 111000 | Ø | 11100x | 1×1010 | 111010 | Ø | Ø | 111×00 | Ø | 111×10 | Ø | 111×10 | Ø | 111000 | – | 111000 | 1110xx | 11100x | 111010 | 111010 | 11101x | 111×00 | 111xx0 | Ø | 111×10 |
| 111×00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | x11000 | x11000 | x11x00 | 111000 | Ø | Ø | 11100x | Ø | Ø | 1110×0 | Ø | Ø | x11100 | x11100 | 111100 | Ø | 11110x | Ø | 1111×0 | Ø | Ø | Ø | 1×1000 | Ø | Ø | Ø | Ø | 1×1100 | Ø | 1×1000 | 1×1000 | 1x1x00 | 111000 | Ø | 11100x | Ø | 1110×0 | 1×1100 | 1×1100 | 111100 | 11110x | 1111×0 | Ø | 1111×0 | Ø | 111000 | 111000 | – | 11100x | 111x0x | 1110×0 | 111xx0 | Ø | 111100 | 111100 | 11110x | 1111×0 |
| 1110×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | 1×1001 | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | 11100x | x110x1 | x11001 | 111001 | x11011 | Ø | 11101x | x11011 | 111011 | Ø | Ø | Ø | Ø | 111×01 | Ø | Ø | 111×11 | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | 1×1001 | Ø | Ø | 11100x | 1×1001 | 111001 | Ø | 11101x | Ø | Ø | Ø | 111×01 | Ø | Ø | Ø | 111×11 | 111001 | 1110xx | 11100x | – | 111001 | 111011 | 11101x | 111011 | 111×01 | Ø | 111xx1 | 111×11 |
| 111×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | 1×1001 | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | Ø | x11101 | Ø | Ø | x11001 | Ø | Ø | 11100x | x11001 | x11x01 | 111001 | Ø | Ø | Ø | Ø | 1110×1 | x11101 | Ø | 11110x | x11101 | 111101 | Ø | Ø | 1111×1 | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | 1×1101 | 1×1001 | Ø | Ø | 11100x | 1x1x01 | 111001 | Ø | Ø | 1×1101 | Ø | 11110x | 111101 | Ø | Ø | Ø | 1111×1 | 111001 | 11100x | 111x0x | 111001 | – | 1110×1 | Ø | 111xx1 | 111101 | 11110x | 111101 | 1111×1 |
| 11101x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | 1110×0 | x11011 | Ø | 1110×1 | x1101x | x11010 | 111010 | x11011 | 111011 | Ø | Ø | Ø | Ø | Ø | Ø | 111×10 | 111×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | 1110×0 | Ø | 1110×1 | 1×1010 | 111010 | Ø | Ø | Ø | Ø | 111×10 | Ø | 111×10 | 111×11 | 1110xx | 111010 | 1110×0 | 111011 | 1110×1 | – | 111010 | 111011 | Ø | 111×10 | 111×11 | 111x1x |
| 111×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | 1110×0 | Ø | Ø | Ø | x11010 | x11x10 | 111010 | Ø | 11101x | Ø | x11110 | 1111×0 | Ø | Ø | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1010 | Ø | 1110×0 | Ø | Ø | 1x1x10 | 111010 | Ø | 1×1110 | 1111×0 | Ø | 111110 | 11×110 | 111110 | 11111x | 1110×0 | 111010 | 111xx0 | 11101x | Ø | 111010 | – | 111x1x | 1111×0 | 111110 | 11111x | 111110 |
| 111×11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | 11×111 | Ø | Ø | Ø | Ø | x11011 | Ø | 1110×1 | x11011 | Ø | 11101x | x11x11 | 111011 | Ø | Ø | Ø | x11111 | 1111×1 | x11111 | 11111x | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | Ø | 11101x | Ø | Ø | Ø | 1111×1 | 11111x | 11×111 | 11111x | 111111 | 1110×1 | 11101x | Ø | 111011 | 111xx1 | 111011 | 111x1x | – | 1111×1 | 11111x | 111111 | 111111 |
| 11110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | x11101 | Ø | Ø | Ø | Ø | x11100 | 111×00 | Ø | x11101 | 111×01 | Ø | Ø | Ø | Ø | Ø | x1110x | x11100 | 111100 | x11101 | 111101 | Ø | 1111×0 | 1111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1101 | Ø | Ø | 1×1100 | 111×00 | 1×1101 | 111×01 | Ø | Ø | 1x110x | 1×1100 | 111100 | 111101 | 1111×0 | Ø | 1111×0 | 1111×1 | 111x0x | 111×00 | 111100 | 111×01 | 111101 | Ø | 1111×0 | 1111×1 | – | 111100 | 111101 | 1111xx |
| 1111×0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | 111×00 | Ø | Ø | Ø | Ø | x11110 | 111×10 | Ø | Ø | x11100 | x111x0 | 111100 | Ø | 11110x | x11110 | 111110 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | Ø | 1×1100 | 111×00 | Ø | Ø | 1×1110 | 111×10 | 1×1100 | 1x11x0 | 111100 | 11110x | 111110 | 11×110 | 111110 | 11111x | 111×00 | 111xx0 | 111100 | Ø | 11110x | 111×10 | 111110 | 11111x | 111100 | – | 1111xx | 111110 |
| 1111×1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | x11111 | 11×111 | Ø | Ø | Ø | Ø | Ø | x11101 | 111×01 | Ø | Ø | Ø | x11111 | 111×11 | x11101 | Ø | 11110x | x111x1 | 111101 | x11111 | 11111x | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | 1×1101 | 111×01 | Ø | Ø | 1×1101 | Ø | 11110x | 111101 | 11111x | 11×111 | 11111x | 111111 | 111×01 | Ø | 11110x | 111xx1 | 111101 | 111×11 | 11111x | 111111 | 111101 | 1111xx | – | 111111 |
| 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11111 | 11×111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11110 | 111×10 | x11111 | 111×11 | Ø | x11110 | 1111×0 | x11111 | 1111×1 | x1111x | 111110 | 111111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | Ø | 1×1110 | 1111×0 | 1111×1 | 111110 | 11x11x | 111110 | 111111 | Ø | 111×10 | 1111×0 | 111×11 | 1111×1 | 111x1x | 111110 | 111111 | 1111xx | 111110 | 111111 | – |
Z1=
Ĉ2=C1∪(C1*C1)
C2=>
| 000xx0, 00x0x0, 0x00x0 0x0x00, x00x00, 0xx000 x0x000, 0xx010, 0001xx 0x010x, x0010x, 0x01x1 0xx101, x0x101, 0010xx 0x100x, x0100x, 0x10x0 x010x0, xx1000, 0x10x1 0x1x01, x01x01, xx1001 0x101x, xx1010, xx1101 010x0x, 01x00x, 01x0x0 01xx00, 01xx01, 01x10x 01x1x1, x1x111, 0110xx 011x0x, x1100x, 011xx0 x110x0, x11x00, 011xx1 x110x1, x11x01, 011x1x x1101x, x11x10, x11x11 0111xx, x1110x, x111x0 x111x1, x1111x, 100x0x 10x00x, 10xx00, 10xx01 10x10x, 101x0x, 1x100x 101xx0, 1x10x0, 1x1x00 1x1x01, 1x1x10, 1x110x 1x11x0, 11x11x, 1110xx 111x0x, 111xx0, 111xx1 111x1x, 1111xx |
| 000xx0 | 00x0x0 | 0x00x0 | 0x0x00 | x00x00 | 0xx000 | x0x000 | 0xx010 | 0001xx | 0x010x | x0010x | 0x01x1 | 0xx101 | x0x101 | 0010xx | 0x100x | x0100x | 0x10x0 | x010x0 | xx1000 | 0x10x1 | 0x1x01 | x01x01 | xx1001 | 0x101x | xx1010 | xx1101 | 010x0x | 01x00x | 01x0x0 | 01xx00 | 01xx01 | 01x10x | 01x1x1 | x1x111 | 0110xx | 011x0x | x1100x | 011xx0 | x110x0 | x11x00 | 011xx1 | x110x1 | x11x01 | 011x1x | x1101x | x11x10 | x11x11 | 0111xx | x1110x | x111x0 | x111x1 | x1111x | 100x0x | 10x00x | 10xx00 | 10xx01 | 10x10x | 101x0x | 1x100x | 101xx0 | 1x10x0 | 1x1x00 | 1x1x01 | 1x1x10 | 1x110x | 1x11x0 | 11x11x | 1110xx | 111x0x | 111xx0 | 111xx1 | 111x1x | 1111xx | |
| 000xx0 | – | 0000×0 | 0000×0 | 000×00 | 000×00 | 000000 | 000000 | 000010 | 0001×0 | 000100 | 000100 | 0001xx | 00010x | 00010x | 00x0x0 | 00×000 | 00×000 | 00x0x0 | 00x0x0 | 00×000 | Ø | Ø | Ø | Ø | 00×010 | 00×010 | Ø | 0x0x00 | 0x0000 | 0x00x0 | 0x0x00 | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x00x00 | x00000 | x00x00 | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 00x0x0 | 0000×0 | – | 0000×0 | 000000 | 000000 | 00×000 | 00×000 | 00×010 | 000xx0 | 000×00 | 000×00 | Ø | Ø | Ø | 0010×0 | 001000 | 001000 | 0010×0 | 0010×0 | 001000 | 0010xx | 00100x | 00100x | 00100x | 001010 | 001010 | Ø | 0x0000 | 0xx000 | 0xx0x0 | 0xx000 | Ø | Ø | Ø | Ø | 0x10x0 | 0x1000 | 0x1000 | 0x10x0 | 0x10x0 | 0x1000 | Ø | Ø | Ø | 0x1010 | 0x1010 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x0x000 | x0x000 | Ø | Ø | x01000 | x01000 | x010x0 | x010x0 | x01000 | Ø | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x00x0 | 0000×0 | 0000×0 | – | 0x0000 | 000000 | 0x0000 | 000000 | 0x0010 | 000xx0 | 0x0x00 | 000×00 | Ø | Ø | Ø | 00x0x0 | 0xx000 | 00×000 | 0xx0x0 | 00x0x0 | 0xx000 | Ø | Ø | Ø | Ø | 0xx010 | 0xx010 | Ø | 010000 | 010000 | 0100×0 | 010000 | 01000x | 010×00 | Ø | Ø | 01x0x0 | 01×000 | 01×000 | 01x0x0 | 01x0x0 | 01×000 | Ø | Ø | Ø | 01×010 | 01×010 | 01×010 | Ø | Ø | Ø | Ø | Ø | Ø | x00000 | x00000 | x00000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x0x00 | 000×00 | 000000 | 0x0000 | – | 000×00 | 0x0000 | 000000 | 0x00x0 | 000100 | 0x0100 | 000100 | 0x010x | 0x010x | 00010x | 00×000 | 0xx000 | 00×000 | 0xx000 | 00×000 | 0xx000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 010×00 | 010000 | 010000 | 010×00 | 010x0x | 010100 | 01010x | Ø | 01×000 | 01xx00 | 01×000 | 01xx00 | 01×000 | 01xx00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×100 | 01×100 | 01×100 | Ø | Ø | x00x00 | x00000 | x00x00 | Ø | x00100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x00x00 | 000×00 | 000000 | 000000 | 000×00 | – | 000000 | x00000 | 0000×0 | 000100 | 000100 | x00100 | 00010x | 00010x | x0010x | 00×000 | 00×000 | x0x000 | 00×000 | x0x000 | x0x000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0x00 | 0x0000 | 0x0000 | 0x0x00 | Ø | 0x0100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100×00 | 100000 | 100×00 | 100x0x | 100100 | 10xx00 | 10×000 | 10xx00 | 10×000 | 10xx00 | Ø | Ø | 10×100 | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0xx000 | 000000 | 00×000 | 0x0000 | 0x0000 | 000000 | – | 00×000 | 0xx0x0 | 000×00 | 0x0x00 | 000×00 | Ø | Ø | Ø | 001000 | 0x1000 | 001000 | 0x1000 | 001000 | 0x1000 | 0x100x | 0x100x | 00100x | 0x100x | 0x10x0 | 0x10x0 | Ø | 010000 | 01×000 | 01×000 | 01×000 | 01x00x | 01xx00 | Ø | Ø | 011000 | 011000 | 011000 | 011000 | 011000 | 011000 | 01100x | 01100x | 01100x | 0110×0 | 0110×0 | 0110×0 | Ø | 011×00 | 011×00 | 011×00 | Ø | Ø | x00000 | x0x000 | x0x000 | Ø | Ø | x01000 | xx1000 | x01000 | xx1000 | xx1000 | Ø | Ø | Ø | Ø | Ø | x11000 | x11000 | x11000 | Ø | Ø | Ø |
| x0x000 | 000000 | 00×000 | 000000 | 000000 | x00000 | 00×000 | – | 00x0x0 | 000×00 | 000×00 | x00x00 | Ø | Ø | Ø | 001000 | 001000 | x01000 | 001000 | x01000 | x01000 | 00100x | 00100x | x0100x | x0100x | 0010×0 | x010x0 | Ø | 0x0000 | 0xx000 | 0xx000 | 0xx000 | Ø | Ø | Ø | Ø | 0x1000 | 0x1000 | xx1000 | 0x1000 | xx1000 | xx1000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 100000 | 10×000 | 10×000 | 10x00x | 10xx00 | 101000 | 101000 | 101000 | 101000 | 101000 | 10100x | 1010×0 | 101×00 | 101×00 | Ø | 1×1000 | 1×1000 | 1×1000 | Ø | Ø | Ø |
| 0xx010 | 000010 | 00×010 | 0x0010 | 0x00x0 | 0000×0 | 0xx0x0 | 00x0x0 | – | 000×10 | Ø | Ø | Ø | Ø | Ø | 001010 | 0x10x0 | 0010×0 | 0x1010 | 001010 | 0x10x0 | 0x101x | Ø | Ø | Ø | 0x1010 | 0x1010 | Ø | 0100×0 | 01x0x0 | 01×010 | 01x0x0 | Ø | Ø | Ø | Ø | 011010 | 0110×0 | 0110×0 | 011010 | 011010 | 0110×0 | 01101x | 01101x | Ø | 011010 | 011010 | 011010 | 01101x | 011×10 | Ø | 011×10 | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | xx1010 | Ø | Ø | xx1010 | Ø | Ø | Ø | x11010 | Ø | x11010 | Ø | x11010 | Ø |
| 0001xx | 0001×0 | 000xx0 | 000xx0 | 000100 | 000100 | 000×00 | 000×00 | 000×10 | – | 00010x | 00010x | 0001×1 | 000101 | 000101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 00×101 | Ø | Ø | Ø | 00×101 | 0x010x | Ø | Ø | 0x0100 | 0x0101 | 0x010x | 0x01x1 | 0x0111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x0010x | Ø | x00100 | x00101 | x0010x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x010x | 000100 | 000×00 | 0x0x00 | 0x0100 | 000100 | 0x0x00 | 000×00 | Ø | 00010x | – | 00010x | 0x0101 | 0x0101 | 000101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0xx101 | 00×101 | Ø | Ø | Ø | 0xx101 | 01010x | 010x0x | 010×00 | 010100 | 010101 | 01010x | 010101 | 0101×1 | Ø | 01x10x | Ø | 01×100 | Ø | 01×100 | 01×101 | Ø | 01×101 | Ø | Ø | Ø | Ø | 01x10x | 01x10x | 01×100 | 01×101 | Ø | x0010x | Ø | x00100 | x00101 | x0010x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| x0010x | 000100 | 000×00 | 000×00 | 000100 | x00100 | 000×00 | x00x00 | Ø | 00010x | 00010x | – | 000101 | 000101 | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | x0x101 | Ø | Ø | Ø | x0x101 | 0x010x | Ø | Ø | 0x0100 | 0x0101 | 0x010x | 0x0101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10010x | 100x0x | 100100 | 100101 | 10010x | 10x10x | Ø | 10×100 | Ø | 10×100 | 10×101 | Ø | 10x10x | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x01x1 | 0001xx | Ø | Ø | 0x010x | 00010x | Ø | Ø | Ø | 0001×1 | 0x0101 | 000101 | – | 0x0101 | 000101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0xx101 | 00×101 | Ø | Ø | Ø | 0xx101 | 010101 | 010×01 | Ø | 01010x | 010101 | 010101 | 0101×1 | 010111 | Ø | 01×101 | Ø | Ø | Ø | Ø | 01x1x1 | Ø | 01×101 | 01×111 | Ø | Ø | 01×111 | 01x1x1 | 01×101 | Ø | 01x1x1 | 01×111 | x00101 | Ø | Ø | x00101 | x00101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø |
| 0xx101 | 00010x | Ø | Ø | 0x010x | 00010x | Ø | Ø | Ø | 000101 | 0x0101 | 000101 | 0x0101 | – | 00×101 | 001×01 | 0x1x01 | 001×01 | Ø | Ø | Ø | 0x1x01 | 0x1101 | 001101 | 0x1x01 | Ø | Ø | 0x1101 | 010101 | 01xx01 | Ø | 01x10x | 01×101 | 01×101 | 01×101 | 01x1x1 | 011×01 | 011101 | 011×01 | 01110x | Ø | 01110x | 011101 | 011×01 | 011101 | 0111×1 | Ø | Ø | 0111×1 | 011101 | 011101 | 01110x | 011101 | 0111×1 | x00101 | Ø | Ø | x0x101 | x0x101 | x01101 | Ø | Ø | Ø | Ø | xx1101 | Ø | xx1101 | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø | x11101 |
| x0x101 | 00010x | Ø | Ø | 00010x | x0010x | Ø | Ø | Ø | 000101 | 000101 | x00101 | 000101 | 00×101 | – | 001×01 | 001×01 | x01x01 | Ø | Ø | Ø | 001×01 | 001101 | x01101 | x01x01 | Ø | Ø | x01101 | 0x0101 | Ø | Ø | Ø | 0xx101 | 0xx101 | 0xx101 | Ø | Ø | 0x1101 | Ø | Ø | Ø | Ø | 0x1101 | Ø | xx1101 | Ø | Ø | Ø | Ø | 0x1101 | xx1101 | Ø | xx1101 | Ø | 100101 | 10xx01 | 10x10x | 10×101 | 10×101 | 101101 | 101×01 | 10110x | Ø | 10110x | 101101 | Ø | 101101 | 10110x | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø | 1×1101 |
| 0010xx | 00x0x0 | 0010×0 | 00x0x0 | 00×000 | 00×000 | 001000 | 001000 | 001010 | Ø | Ø | Ø | Ø | 001×01 | 001×01 | – | 00100x | 00100x | 0010×0 | 0010×0 | 001000 | 0010×1 | 001001 | 001001 | 001001 | 00101x | 001010 | 001×01 | Ø | 0x100x | 0x10x0 | 0x1000 | 0x1001 | Ø | Ø | Ø | 0x10xx | 0x100x | 0x100x | 0x10x0 | 0x10x0 | 0x1000 | 0x10x1 | 0x10x1 | 0x1001 | 0x101x | 0x101x | 0x1010 | 0x1011 | Ø | Ø | Ø | Ø | Ø | Ø | x0100x | x01000 | x01001 | Ø | x0100x | x0100x | x010x0 | x010x0 | x01000 | x01001 | x01010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x100x | 00×000 | 001000 | 0xx000 | 0xx000 | 00×000 | 0x1000 | 001000 | 0x10x0 | Ø | Ø | Ø | Ø | 0x1x01 | 001×01 | 00100x | – | 00100x | 0x1000 | 001000 | 0x1000 | 0x1001 | 0x1001 | 001001 | 0x1001 | 0x10xx | 0x10x0 | 0x1x01 | 01x00x | 01100x | 011000 | 011000 | 011001 | 011x0x | 011×01 | Ø | 01100x | 01100x | 01100x | 011000 | 011000 | 011000 | 011001 | 011001 | 011001 | 0110xx | 0110xx | 0110×0 | 0110×1 | 011x0x | 011x0x | 011×00 | 011×01 | Ø | Ø | x0100x | x01000 | x01001 | Ø | x0100x | xx100x | x01000 | xx1000 | xx1000 | xx1001 | Ø | Ø | Ø | Ø | x1100x | x1100x | x11000 | x11001 | Ø | Ø |
| x0100x | 00×000 | 001000 | 00×000 | 00×000 | x0x000 | 001000 | x01000 | 0010×0 | Ø | Ø | Ø | Ø | 001×01 | x01x01 | 00100x | 00100x | – | 001000 | x01000 | x01000 | 001001 | 001001 | x01001 | x01001 | 0010xx | x010x0 | x01x01 | Ø | 0x100x | 0x1000 | 0x1000 | 0x1001 | Ø | Ø | Ø | 0x100x | 0x100x | xx100x | 0x1000 | xx1000 | xx1000 | 0x1001 | xx1001 | xx1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10x00x | 10100x | 101000 | 101001 | 101x0x | 10100x | 10100x | 101000 | 101000 | 101000 | 101001 | 1010×0 | 101x0x | 101×00 | Ø | 1x100x | 1x100x | 1×1000 | 1×1001 | Ø | Ø |
| 0x10x0 | 00x0x0 | 0010×0 | 0xx0x0 | 0xx000 | 00×000 | 0x1000 | 001000 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 0x1000 | 001000 | – | 0010×0 | 0x1000 | 0x10xx | 0x100x | 00100x | 0x100x | 0x1010 | 0x1010 | Ø | 01×000 | 011000 | 0110×0 | 011000 | 01100x | 011×00 | Ø | Ø | 0110×0 | 011000 | 011000 | 0110×0 | 0110×0 | 011000 | 0110xx | 0110xx | 01100x | 011010 | 011010 | 011010 | 01101x | 011xx0 | 011×00 | 011xx0 | Ø | 011×10 | Ø | x01000 | x01000 | Ø | Ø | x01000 | xx1000 | x010x0 | xx10x0 | xx1000 | Ø | xx1010 | Ø | Ø | Ø | x110x0 | x11000 | x110x0 | Ø | x11010 | Ø |
| x010x0 | 00x0x0 | 0010×0 | 00x0x0 | 00×000 | x0x000 | 001000 | x01000 | 001010 | Ø | Ø | Ø | Ø | Ø | Ø | 0010×0 | 001000 | x01000 | 0010×0 | – | x01000 | 0010xx | 00100x | x0100x | x0100x | 001010 | x01010 | Ø | Ø | 0x1000 | 0x10x0 | 0x1000 | Ø | Ø | Ø | Ø | 0x10x0 | 0x1000 | xx1000 | 0x10x0 | xx10x0 | xx1000 | Ø | Ø | Ø | 0x1010 | xx1010 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | 10×000 | 101000 | 101000 | 10100x | 101×00 | 101000 | 101000 | 1010×0 | 1010×0 | 101000 | 10100x | 101010 | 101×00 | 101xx0 | Ø | 1x10x0 | 1×1000 | 1x10x0 | Ø | 1×1010 | Ø |
| xx1000 | 00×000 | 001000 | 0xx000 | 0xx000 | x0x000 | 0x1000 | x01000 | 0x10x0 | Ø | Ø | Ø | Ø | Ø | Ø | 001000 | 0x1000 | x01000 | 0x1000 | x01000 | – | 0x100x | 0x100x | x0100x | xx100x | 0x10x0 | xx10x0 | Ø | 01×000 | 011000 | 011000 | 011000 | 01100x | 011×00 | Ø | Ø | 011000 | 011000 | x11000 | 011000 | x11000 | x11000 | 01100x | x1100x | x1100x | 0110×0 | x110x0 | x110x0 | Ø | 011×00 | x11x00 | x11x00 | Ø | Ø | 10×000 | 101000 | 101000 | 10100x | 101×00 | 101000 | 1×1000 | 101000 | 1×1000 | 1×1000 | 1x100x | 1x10x0 | 1x1x00 | 1x1x00 | Ø | 111000 | 111000 | 111000 | 11100x | 1110×0 | 111×00 |
| 0x10x1 | Ø | 0010xx | Ø | Ø | Ø | 0x100x | 00100x | 0x101x | Ø | Ø | Ø | Ø | 0x1x01 | 001×01 | 0010×1 | 0x1001 | 001001 | 0x10xx | 0010xx | 0x100x | – | 0x1001 | 001001 | 0x1001 | 0x1011 | 0x101x | 0x1x01 | 01×001 | 011001 | 0110xx | 01100x | 011001 | 011×01 | 011xx1 | 011×11 | 0110×1 | 011001 | 011001 | 0110xx | 0110xx | 01100x | 0110×1 | 0110×1 | 011001 | 011011 | 011011 | 01101x | 011011 | 011xx1 | 011×01 | Ø | 011xx1 | 011×11 | Ø | x01001 | Ø | x01001 | Ø | x01001 | xx1001 | Ø | Ø | Ø | xx1001 | Ø | Ø | Ø | Ø | x110x1 | x11001 | Ø | x110x1 | x11011 | Ø |
| 0x1x01 | Ø | 00100x | Ø | Ø | Ø | 0x100x | 00100x | Ø | 00×101 | 0xx101 | 00×101 | 0xx101 | 0x1101 | 001101 | 001001 | 0x1001 | 001001 | 0x100x | 00100x | 0x100x | 0x1001 | – | 001×01 | 0x1001 | 0x10x1 | Ø | 0x1101 | 01xx01 | 011001 | 01100x | 011x0x | 011×01 | 011101 | 011101 | 0111×1 | 011001 | 011×01 | 011001 | 011x0x | 01100x | 011x0x | 011×01 | 011001 | 011×01 | 011xx1 | 0110×1 | Ø | 011xx1 | 011101 | 011101 | 01110x | 011101 | 0111×1 | Ø | x01001 | Ø | x01x01 | x01101 | x01x01 | xx1001 | Ø | Ø | Ø | xx1x01 | Ø | xx1101 | Ø | Ø | x11001 | x11x01 | Ø | x11x01 | Ø | x11101 |
| x01x01 | Ø | 00100x | Ø | Ø | Ø | 00100x | x0100x | Ø | 00×101 | 00×101 | x0x101 | 00×101 | 001101 | x01101 | 001001 | 001001 | x01001 | 00100x | x0100x | x0100x | 001001 | 001×01 | – | x01001 | 0010×1 | Ø | x01101 | Ø | 0x1001 | Ø | Ø | 0x1x01 | 0x1101 | 0x1101 | Ø | 0x1001 | 0x1x01 | xx1001 | Ø | Ø | Ø | 0x1x01 | xx1001 | xx1x01 | Ø | Ø | Ø | Ø | 0x1101 | xx1101 | Ø | xx1101 | Ø | 10xx01 | 101001 | 101x0x | 101×01 | 101101 | 101×01 | 101001 | 101x0x | 10100x | 101x0x | 101×01 | Ø | 101101 | 10110x | Ø | 1×1001 | 1x1x01 | Ø | 1x1x01 | Ø | 1×1101 |
| xx1001 | Ø | 00100x | Ø | Ø | Ø | 0x100x | x0100x | Ø | Ø | Ø | Ø | Ø | 0x1x01 | x01x01 | 001001 | 0x1001 | x01001 | 0x100x | x0100x | xx100x | 0x1001 | 0x1001 | x01001 | – | 0x10x1 | Ø | xx1x01 | 01×001 | 011001 | 01100x | 01100x | 011001 | 011×01 | 011×01 | Ø | 011001 | 011001 | x11001 | 01100x | x1100x | x1100x | 011001 | x11001 | x11001 | 0110×1 | x110x1 | Ø | x110x1 | 011×01 | x11x01 | Ø | x11x01 | Ø | 10×001 | 101001 | 10100x | 101001 | 101×01 | 101001 | 1×1001 | 10100x | 1x100x | 1x100x | 1×1001 | Ø | 1x1x01 | Ø | Ø | 111001 | 111001 | 11100x | 111001 | 1110×1 | 111×01 |
| 0x101x | 00×010 | 001010 | 0xx010 | Ø | Ø | 0x10x0 | 0010×0 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 00101x | 0x10xx | 0010xx | 0x1010 | 001010 | 0x10x0 | 0x1011 | 0x10x1 | 0010×1 | 0x10x1 | – | 0x1010 | Ø | Ø | 0110xx | 011010 | 0110×0 | 0110×1 | Ø | 011×11 | 011×11 | 01101x | 0110xx | 0110xx | 011010 | 011010 | 0110×0 | 011011 | 011011 | 0110×1 | 01101x | 01101x | 011010 | 011011 | 011x1x | Ø | 011×10 | 011×11 | 011x1x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | xx1010 | Ø | Ø | xx1010 | Ø | Ø | Ø | x1101x | Ø | x11010 | x11011 | x1101x | Ø |
| xx1010 | 00×010 | 001010 | 0xx010 | Ø | Ø | 0x10x0 | x010x0 | 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | 001010 | 0x10x0 | x010x0 | 0x1010 | x01010 | xx10x0 | 0x101x | Ø | Ø | Ø | 0x1010 | – | Ø | Ø | 0110×0 | 011010 | 0110×0 | Ø | Ø | Ø | Ø | 011010 | 0110×0 | x110x0 | 011010 | x11010 | x110x0 | 01101x | x1101x | Ø | 011010 | x11010 | x11010 | x1101x | 011×10 | Ø | x11x10 | Ø | x11x10 | Ø | 1010×0 | 1010×0 | Ø | Ø | 1010×0 | 1x10x0 | 101010 | 1×1010 | 1x10x0 | Ø | 1×1010 | Ø | 1x1x10 | 111×10 | 111010 | 1110×0 | 111010 | 11101x | 111010 | 111×10 |
| xx1101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 00×101 | 0xx101 | x0x101 | 0xx101 | 0x1101 | x01101 | 001×01 | 0x1x01 | x01x01 | Ø | Ø | Ø | 0x1x01 | 0x1101 | x01101 | xx1x01 | Ø | Ø | – | 01×101 | 011×01 | Ø | 01110x | 011101 | 011101 | 011101 | x111x1 | 011×01 | 011101 | x11x01 | 01110x | Ø | x1110x | 011101 | x11x01 | x11101 | 0111×1 | Ø | Ø | x111x1 | 011101 | x11101 | x1110x | x11101 | x111x1 | 10×101 | 101×01 | 10110x | 101101 | 101101 | 101101 | 1x1x01 | 10110x | Ø | 1x110x | 1×1101 | Ø | 1×1101 | 1x110x | 1111×1 | 111×01 | 111101 | 11110x | 111101 | 1111×1 | 111101 |
| 010x0x | 0x0x00 | 0x0000 | 010000 | 010×00 | 0x0x00 | 010000 | 0x0000 | 0100×0 | 0x010x | 01010x | 0x010x | 010101 | 010101 | 0x0101 | Ø | 01x00x | Ø | 01×000 | Ø | 01×000 | 01×001 | 01xx01 | Ø | 01×001 | Ø | Ø | 01×101 | – | 01000x | 010000 | 010×00 | 010×01 | 01010x | 010101 | 0101×1 | 01x00x | 01xx0x | 01x00x | 01xx00 | 01×000 | 01xx00 | 01xx01 | 01×001 | 01xx01 | Ø | Ø | Ø | Ø | 01x10x | 01x10x | 01×100 | 01×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 01x00x | 0x0000 | 0xx000 | 010000 | 010000 | 0x0000 | 01×000 | 0xx000 | 01x0x0 | Ø | 010x0x | Ø | 010×01 | 01xx01 | Ø | 0x100x | 01100x | 0x100x | 011000 | 0x1000 | 011000 | 011001 | 011001 | 0x1001 | 011001 | 0110xx | 0110×0 | 011×01 | 01000x | – | 01×000 | 01×000 | 01×001 | 01xx0x | 01xx01 | Ø | 01100x | 01100x | 01100x | 011000 | 011000 | 011000 | 011001 | 011001 | 011001 | 0110xx | 0110xx | 0110×0 | 0110×1 | 011x0x | 011x0x | 011×00 | 011×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | Ø | x11000 | x11000 | x11001 | Ø | Ø | Ø | Ø | x1100x | x1100x | x11000 | x11001 | Ø | Ø |
| 01x0x0 | 0x00x0 | 0xx0x0 | 0100×0 | 010000 | 0x0000 | 01×000 | 0xx000 | 01×010 | Ø | 010×00 | Ø | Ø | Ø | Ø | 0x10x0 | 011000 | 0x1000 | 0110×0 | 0x10x0 | 011000 | 0110xx | 01100x | Ø | 01100x | 011010 | 011010 | Ø | 010000 | 01×000 | – | 01×000 | 01x00x | 01xx00 | Ø | Ø | 0110×0 | 011000 | 011000 | 0110×0 | 0110×0 | 011000 | 0110xx | 0110xx | 01100x | 011010 | 011010 | 011010 | 01101x | 011xx0 | 011×00 | 011xx0 | Ø | 011×10 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x110x0 | x11000 | Ø | x11010 | Ø | Ø | Ø | x110x0 | x11000 | x110x0 | Ø | x11010 | Ø |
| 01xx00 | 0x0x00 | 0xx000 | 010000 | 010×00 | 0x0x00 | 01×000 | 0xx000 | 01x0x0 | 0x0100 | 010100 | 0x0100 | 01010x | 01x10x | Ø | 0x1000 | 011000 | 0x1000 | 011000 | 0x1000 | 011000 | 01100x | 011x0x | Ø | 01100x | 0110×0 | 0110×0 | 01110x | 010×00 | 01×000 | 01×000 | – | 01xx0x | 01×100 | 01x10x | Ø | 011000 | 011×00 | 011000 | 011×00 | 011000 | 011×00 | 011x0x | 01100x | 011x0x | 011xx0 | 0110×0 | 011xx0 | Ø | 011100 | 011100 | 011100 | 01110x | 0111×0 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x11000 | x11x00 | Ø | Ø | x11100 | x11100 | Ø | x11000 | x11x00 | x11x00 | Ø | Ø | x11100 |
| 01xx01 | Ø | Ø | 01000x | 010x0x | Ø | 01x00x | Ø | Ø | 0x0101 | 010101 | 0x0101 | 010101 | 01×101 | 0xx101 | 0x1001 | 011001 | 0x1001 | 01100x | Ø | 01100x | 011001 | 011×01 | 0x1x01 | 011001 | 0110×1 | Ø | 011101 | 010×01 | 01×001 | 01x00x | 01xx0x | – | 01×101 | 01×101 | 01x1x1 | 011001 | 011×01 | 011001 | 011x0x | 01100x | 011x0x | 011×01 | 011001 | 011×01 | 011xx1 | 0110×1 | Ø | 011xx1 | 011101 | 011101 | 01110x | 011101 | 0111×1 | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | x11x01 | Ø | x11101 | Ø | Ø | x11001 | x11x01 | Ø | x11x01 | Ø | x11101 |
| 01x10x | 0x0100 | Ø | 010×00 | 010100 | 0x0100 | 01xx00 | Ø | Ø | 0x010x | 01010x | 0x010x | 010101 | 01×101 | 0xx101 | Ø | 011x0x | Ø | 011×00 | Ø | 011×00 | 011×01 | 011101 | 0x1101 | 011×01 | Ø | Ø | 011101 | 01010x | 01xx0x | 01xx00 | 01×100 | 01×101 | – | 01×101 | 01x1x1 | 011x0x | 01110x | 011x0x | 011100 | 011×00 | 011100 | 011101 | 011×01 | 011101 | 0111xx | Ø | 0111×0 | 0111×1 | 01110x | 01110x | 011100 | 011101 | 0111xx | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11101 | Ø | x1110x | x11100 | Ø | Ø | x1110x | x11100 | x11101 | Ø | x1110x |
| 01x1x1 | Ø | Ø | Ø | 01010x | Ø | Ø | Ø | Ø | 0x01x1 | 010101 | 0x0101 | 0101×1 | 01×101 | 0xx101 | Ø | 011×01 | Ø | Ø | Ø | Ø | 011xx1 | 011101 | 0x1101 | 011×01 | 011×11 | Ø | 011101 | 010101 | 01xx01 | Ø | 01x10x | 01×101 | 01×101 | – | 01×111 | 011xx1 | 011101 | 011×01 | 0111xx | Ø | 01110x | 0111×1 | 011xx1 | 011101 | 011111 | 011×11 | 01111x | 011111 | 0111×1 | 011101 | 0111xx | 0111×1 | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | Ø | x11101 | Ø | x1x111 | Ø | x11101 | Ø | x111x1 | x11111 | x111x1 |
| x1x111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 0x0111 | 0101×1 | Ø | 010111 | 01x1x1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | 011×11 | Ø | x111x1 | 0101×1 | Ø | Ø | Ø | 01x1x1 | 01x1x1 | 01×111 | – | 011×11 | 0111×1 | Ø | 01111x | Ø | Ø | 011111 | x11x11 | x111x1 | 011111 | x11x11 | x1111x | x11111 | 011111 | x111x1 | x1111x | x11111 | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1111×1 | 11111x | 1111×1 | 11111x | 11×111 | 111×11 | 1111×1 | 11111x | 111111 | 111111 | 111111 |
| 0110xx | Ø | 0x10x0 | 01x0x0 | 01×000 | Ø | 011000 | 0x1000 | 011010 | Ø | Ø | Ø | Ø | 011×01 | Ø | 0x10xx | 01100x | 0x100x | 0110×0 | 0x10x0 | 011000 | 0110×1 | 011001 | 0x1001 | 011001 | 01101x | 011010 | 011×01 | 01x00x | 01100x | 0110×0 | 011000 | 011001 | 011x0x | 011xx1 | 011×11 | – | 01100x | 01100x | 0110×0 | 0110×0 | 011000 | 0110×1 | 0110×1 | 011001 | 01101x | 01101x | 011010 | 011011 | 011xxx | 011x0x | 011xx0 | 011xx1 | 011x1x | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | Ø | x110x0 | x11000 | x11001 | x11010 | Ø | Ø | Ø | x110xx | x1100x | x110x0 | x110x1 | x1101x | Ø |
| 011x0x | Ø | 0x1000 | 01×000 | 01xx00 | Ø | 011000 | 0x1000 | 0110×0 | Ø | 01x10x | Ø | 01×101 | 011101 | 0x1101 | 0x100x | 01100x | 0x100x | 011000 | 0x1000 | 011000 | 011001 | 011×01 | 0x1x01 | 011001 | 0110xx | 0110×0 | 011101 | 01xx0x | 01100x | 011000 | 011×00 | 011×01 | 01110x | 011101 | 0111×1 | 01100x | – | 01100x | 011×00 | 011000 | 011×00 | 011×01 | 011001 | 011×01 | 011xxx | 0110xx | 011xx0 | 011xx1 | 01110x | 01110x | 011100 | 011101 | 0111xx | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | Ø | x11000 | x11x00 | x11x01 | Ø | x1110x | x11100 | Ø | x1100x | x11x0x | x11x00 | x11x01 | Ø | x1110x |
| x1100x | Ø | 0x1000 | 01×000 | 01×000 | Ø | 011000 | xx1000 | 0110×0 | Ø | Ø | Ø | Ø | 011×01 | Ø | 0x100x | 01100x | xx100x | 011000 | xx1000 | x11000 | 011001 | 011001 | xx1001 | x11001 | 0110xx | x110x0 | x11x01 | 01x00x | 01100x | 011000 | 011000 | 011001 | 011x0x | 011×01 | Ø | 01100x | 01100x | – | 011000 | x11000 | x11000 | 011001 | x11001 | x11001 | 0110xx | x110xx | x110x0 | x110x1 | 011x0x | x11x0x | x11x00 | x11x01 | Ø | Ø | 1x100x | 1×1000 | 1×1001 | Ø | 1x100x | 11100x | 1×1000 | 111000 | 111000 | 111001 | 1110×0 | 111x0x | 111×00 | Ø | 11100x | 11100x | 111000 | 111001 | 1110xx | 111x0x |
| 011xx0 | Ø | 0x10x0 | 01x0x0 | 01xx00 | Ø | 011000 | 0x1000 | 011010 | Ø | 01×100 | Ø | Ø | 01110x | Ø | 0x10x0 | 011000 | 0x1000 | 0110×0 | 0x10x0 | 011000 | 0110xx | 011x0x | Ø | 01100x | 011010 | 011010 | 01110x | 01xx00 | 011000 | 0110×0 | 011×00 | 011x0x | 011100 | 0111xx | 01111x | 0110×0 | 011×00 | 011000 | – | 0110×0 | 011×00 | 011xxx | 0110xx | 011x0x | 011×10 | 011010 | 011×10 | 011x1x | 0111×0 | 011100 | 0111×0 | 0111xx | 011110 | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | Ø | x110x0 | x11x00 | Ø | x11x10 | x11100 | x111x0 | x11110 | x110x0 | x11x00 | x11xx0 | Ø | x11x10 | x111x0 |
| x110x0 | Ø | 0x10x0 | 01x0x0 | 01×000 | Ø | 011000 | xx1000 | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x10x0 | 011000 | xx1000 | 0110×0 | xx10x0 | x11000 | 0110xx | 01100x | Ø | x1100x | 011010 | x11010 | Ø | 01×000 | 011000 | 0110×0 | 011000 | 01100x | 011×00 | Ø | Ø | 0110×0 | 011000 | x11000 | 0110×0 | – | x11000 | 0110xx | x110xx | x1100x | 011010 | x11010 | x11010 | x1101x | 011xx0 | x11x00 | x11xx0 | Ø | x11x10 | Ø | 1×1000 | 1×1000 | Ø | Ø | 1×1000 | 111000 | 1x10x0 | 1110×0 | 111000 | 11100x | 111010 | 111×00 | 111xx0 | 111×10 | 1110×0 | 111000 | 1110×0 | 1110xx | 111010 | 111xx0 |
| x11x00 | Ø | 0x1000 | 01×000 | 01xx00 | Ø | 011000 | xx1000 | 0110×0 | Ø | 01×100 | Ø | Ø | 01110x | Ø | 0x1000 | 011000 | xx1000 | 011000 | xx1000 | x11000 | 01100x | 011x0x | Ø | x1100x | 0110×0 | x110x0 | x1110x | 01xx00 | 011000 | 011000 | 011×00 | 011x0x | 011100 | 01110x | Ø | 011000 | 011×00 | x11000 | 011×00 | x11000 | – | 011x0x | x1100x | x11x0x | 011xx0 | x110x0 | x11xx0 | Ø | 011100 | x11100 | x11100 | x1110x | x111x0 | Ø | 1×1000 | 1x1x00 | Ø | 1×1100 | 1x1x00 | 111000 | 1x1x00 | 111000 | 111×00 | 111x0x | 111xx0 | 111100 | 111100 | 1111×0 | 111000 | 111×00 | 111×00 | 111x0x | 111xx0 | 111100 |
| 011xx1 | Ø | Ø | Ø | Ø | Ø | 01100x | Ø | 01101x | Ø | 01×101 | Ø | 01x1x1 | 011101 | 0x1101 | 0x10x1 | 011001 | 0x1001 | 0110xx | Ø | 01100x | 0110×1 | 011×01 | 0x1x01 | 011001 | 011011 | 01101x | 011101 | 01xx01 | 011001 | 0110xx | 011x0x | 011×01 | 011101 | 0111×1 | 011111 | 0110×1 | 011×01 | 011001 | 011xxx | 0110xx | 011x0x | – | 0110×1 | 011×01 | 011×11 | 011011 | 011x1x | 011×11 | 0111×1 | 011101 | 0111xx | 0111×1 | 011111 | Ø | Ø | Ø | Ø | Ø | Ø | x11001 | Ø | Ø | Ø | x11x01 | Ø | x11101 | Ø | x11111 | x110x1 | x11x01 | Ø | x11xx1 | x11x11 | x111x1 |
| x110x1 | Ø | Ø | Ø | Ø | Ø | 01100x | Ø | 01101x | Ø | Ø | Ø | Ø | 011×01 | Ø | 0x10x1 | 011001 | xx1001 | 0110xx | Ø | x1100x | 0110×1 | 011001 | xx1001 | x11001 | 011011 | x1101x | x11x01 | 01×001 | 011001 | 0110xx | 01100x | 011001 | 011×01 | 011xx1 | x11x11 | 0110×1 | 011001 | x11001 | 0110xx | x110xx | x1100x | 0110×1 | – | x11001 | 011011 | x11011 | x1101x | x11011 | 011xx1 | x11x01 | Ø | x11xx1 | x11x11 | Ø | 1×1001 | Ø | 1×1001 | Ø | 1×1001 | 111001 | Ø | 1110xx | 11100x | 111001 | 11101x | 111×01 | Ø | 111×11 | 1110×1 | 111001 | 1110xx | 1110×1 | 111011 | 111xx1 |
| x11x01 | Ø | Ø | Ø | Ø | Ø | 01100x | Ø | Ø | Ø | 01×101 | Ø | 01×101 | 011101 | xx1101 | 0x1001 | 011001 | xx1001 | 01100x | Ø | x1100x | 011001 | 011×01 | xx1x01 | x11001 | 0110×1 | Ø | x11101 | 01xx01 | 011001 | 01100x | 011x0x | 011×01 | 011101 | 011101 | x111x1 | 011001 | 011×01 | x11001 | 011x0x | x1100x | x11x0x | 011×01 | x11001 | – | 011xx1 | x110x1 | Ø | x11xx1 | 011101 | x11101 | x1110x | x11101 | x111x1 | Ø | 1×1001 | Ø | 1x1x01 | 1×1101 | 1x1x01 | 111001 | Ø | 11100x | 111x0x | 111×01 | Ø | 111101 | 11110x | 1111×1 | 111001 | 111×01 | 111x0x | 111×01 | 111xx1 | 111101 |
| 011x1x | Ø | 0x1010 | 01×010 | Ø | Ø | 0110×0 | Ø | 011010 | Ø | Ø | Ø | 01×111 | 0111×1 | Ø | 0x101x | 0110xx | Ø | 011010 | 0x1010 | 0110×0 | 011011 | 011xx1 | Ø | 0110×1 | 01101x | 011010 | 0111×1 | Ø | 0110xx | 011010 | 011xx0 | 011xx1 | 0111xx | 011111 | 011111 | 01101x | 011xxx | 0110xx | 011×10 | 011010 | 011xx0 | 011×11 | 011011 | 011xx1 | – | 01101x | 011×10 | 011×11 | 01111x | 0111xx | 011110 | 011111 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | x11x10 | Ø | x11110 | x1111x | x1101x | Ø | x11x10 | x11x11 | x11x1x | x1111x |
| x1101x | Ø | 0x1010 | 01×010 | Ø | Ø | 0110×0 | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x101x | 0110xx | Ø | 011010 | xx1010 | x110x0 | 011011 | 0110×1 | Ø | x110x1 | 01101x | x11010 | Ø | Ø | 0110xx | 011010 | 0110×0 | 0110×1 | Ø | 011×11 | x11x11 | 01101x | 0110xx | x110xx | 011010 | x11010 | x110x0 | 011011 | x11011 | x110x1 | 01101x | – | x11010 | x11011 | 011x1x | Ø | x11x10 | x11x11 | x11x1x | Ø | Ø | Ø | Ø | Ø | Ø | 1110xx | 1×1010 | 111010 | 1110×0 | 1110×1 | 111010 | Ø | 111×10 | 111x1x | 11101x | 1110xx | 111010 | 111011 | 11101x | 111x1x |
| x11x10 | Ø | 0x1010 | 01×010 | Ø | Ø | 0110×0 | Ø | 011010 | Ø | Ø | Ø | Ø | Ø | Ø | 0x1010 | 0110×0 | Ø | 011010 | xx1010 | x110x0 | 01101x | Ø | Ø | Ø | 011010 | x11010 | Ø | Ø | 0110×0 | 011010 | 011xx0 | Ø | 0111×0 | 01111x | x1111x | 011010 | 011xx0 | x110x0 | 011×10 | x11010 | x11xx0 | 011x1x | x1101x | Ø | 011×10 | x11010 | – | x11x1x | 011110 | x111x0 | x11110 | x1111x | x11110 | Ø | Ø | Ø | Ø | Ø | Ø | 1110×0 | 1x1x10 | 111010 | 111xx0 | Ø | 111×10 | 1111×0 | 111110 | 111110 | 111010 | 111xx0 | 111×10 | 111x1x | 111×10 | 111110 |
| x11x11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01101x | Ø | Ø | Ø | 01×111 | 0111×1 | Ø | 0x1011 | 0110×1 | Ø | 01101x | Ø | Ø | 011011 | 011xx1 | Ø | x110x1 | 011011 | x1101x | x111x1 | Ø | 0110×1 | 01101x | Ø | 011xx1 | 0111×1 | 011111 | x11111 | 011011 | 011xx1 | x110x1 | 011x1x | x1101x | Ø | 011×11 | x11011 | x11xx1 | 011×11 | x11011 | x11x1x | – | 011111 | x111x1 | x1111x | x11111 | x11111 | Ø | Ø | Ø | Ø | Ø | Ø | 1110×1 | Ø | 11101x | Ø | 111xx1 | 111x1x | 1111×1 | 11111x | 111111 | 111011 | 111xx1 | 111x1x | 111×11 | 111×11 | 111111 |
| 0111xx | Ø | Ø | Ø | 01×100 | Ø | 011×00 | Ø | 011×10 | Ø | 01x10x | Ø | 01x1x1 | 011101 | 0x1101 | Ø | 011x0x | Ø | 011xx0 | Ø | 011×00 | 011xx1 | 011101 | 0x1101 | 011×01 | 011x1x | 011×10 | 011101 | 01x10x | 011x0x | 011xx0 | 011100 | 011101 | 01110x | 0111×1 | 011111 | 011xxx | 01110x | 011x0x | 0111×0 | 011xx0 | 011100 | 0111×1 | 011xx1 | 011101 | 01111x | 011x1x | 011110 | 011111 | – | 01110x | 0111×0 | 0111×1 | 01111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11100 | x11101 | x11110 | x1110x | x111x0 | x1111x | Ø | x1110x | x111x0 | x111x1 | x1111x | x111xx |
| x1110x | Ø | Ø | Ø | 01×100 | Ø | 011×00 | Ø | Ø | Ø | 01x10x | Ø | 01×101 | 011101 | xx1101 | Ø | 011x0x | Ø | 011×00 | Ø | x11x00 | 011×01 | 011101 | xx1101 | x11x01 | Ø | Ø | x11101 | 01x10x | 011x0x | 011×00 | 011100 | 011101 | 01110x | 011101 | x111x1 | 011x0x | 01110x | x11x0x | 011100 | x11x00 | x11100 | 011101 | x11x01 | x11101 | 0111xx | Ø | x111x0 | x111x1 | 01110x | – | x11100 | x11101 | x111xx | Ø | Ø | 1×1100 | 1×1101 | 1x110x | 1x110x | 111x0x | 1×1100 | 111×00 | 111100 | 111101 | 1111×0 | 11110x | 111100 | 1111xx | 111x0x | 11110x | 111100 | 111101 | 1111xx | 11110x |
| x111x0 | Ø | Ø | Ø | 01×100 | Ø | 011×00 | Ø | 011×10 | Ø | 01×100 | Ø | Ø | 01110x | Ø | Ø | 011×00 | Ø | 011xx0 | Ø | x11x00 | Ø | 01110x | Ø | Ø | 011×10 | x11x10 | x1110x | 01×100 | 011×00 | 011xx0 | 011100 | 01110x | 011100 | 0111xx | x1111x | 011xx0 | 011100 | x11x00 | 0111×0 | x11xx0 | x11100 | 0111xx | Ø | x1110x | 011110 | x11x10 | x11110 | x1111x | 0111×0 | x11100 | – | x111xx | x11110 | Ø | Ø | 1×1100 | Ø | 1×1100 | 1×1100 | 111×00 | 1x11x0 | 111xx0 | 111100 | 11110x | 111110 | 111100 | 1111×0 | 111110 | 111xx0 | 111100 | 1111×0 | 1111xx | 111110 | 1111×0 |
| x111x1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 01×101 | Ø | 01x1x1 | 011101 | xx1101 | Ø | 011×01 | Ø | Ø | Ø | Ø | 011xx1 | 011101 | xx1101 | x11x01 | 011×11 | Ø | x11101 | 01×101 | 011×01 | Ø | 01110x | 011101 | 011101 | 0111×1 | x11111 | 011xx1 | 011101 | x11x01 | 0111xx | Ø | x1110x | 0111×1 | x11xx1 | x11101 | 011111 | x11x11 | x1111x | x11111 | 0111×1 | x11101 | x111xx | – | x11111 | Ø | Ø | Ø | 1×1101 | 1×1101 | 1×1101 | 111×01 | Ø | Ø | 11110x | 111101 | 11111x | 111101 | 1111xx | 111111 | 111xx1 | 111101 | 1111xx | 1111×1 | 111111 | 1111×1 |
| x1111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | Ø | 01×111 | 0111×1 | Ø | Ø | Ø | Ø | 011×10 | Ø | Ø | 011×11 | 0111×1 | Ø | Ø | 011x1x | x11x10 | x111x1 | Ø | Ø | 011×10 | 0111×0 | 0111×1 | 0111xx | 011111 | x11111 | 011x1x | 0111xx | Ø | 011110 | x11x10 | x111x0 | 011111 | x11x11 | x111x1 | 01111x | x11x1x | x11110 | x11111 | 01111x | x111xx | x11110 | x11111 | – | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | 1111×0 | 1111×1 | 111110 | 1111xx | 111110 | 11111x | 111x1x | 1111xx | 111110 | 111111 | 11111x | 11111x |
| 100x0x | x00x00 | x00000 | x00000 | x00x00 | 100×00 | x00000 | 100000 | Ø | x0010x | x0010x | 10010x | x00101 | x00101 | 100101 | Ø | Ø | 10x00x | Ø | 10×000 | 10×000 | Ø | Ø | 10xx01 | 10×001 | Ø | Ø | 10×101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | – | 10000x | 100×00 | 100×01 | 10010x | 10xx0x | 10x00x | 10xx00 | 10×000 | 10xx00 | 10xx01 | Ø | 10x10x | 10×100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 10x00x | x00000 | x0x000 | x00000 | x00000 | 100000 | x0x000 | 10×000 | Ø | Ø | Ø | 100x0x | Ø | Ø | 10xx01 | x0100x | x0100x | 10100x | x01000 | 101000 | 101000 | x01001 | x01001 | 101001 | 101001 | Ø | 1010×0 | 101×01 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1x100x | Ø | 1×1000 | 1×1000 | Ø | 1×1001 | 1×1001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 10000x | – | 10×000 | 10×001 | 10xx0x | 10100x | 10100x | 101000 | 101000 | 101000 | 101001 | 1010×0 | 101x0x | 101×00 | Ø | 1x100x | 1x100x | 1×1000 | 1×1001 | Ø | Ø |
| 10xx00 | x00x00 | x0x000 | x00000 | x00x00 | 100×00 | x0x000 | 10×000 | Ø | x00100 | x00100 | 100100 | Ø | Ø | 10x10x | x01000 | x01000 | 101000 | x01000 | 101000 | 101000 | Ø | Ø | 101x0x | 10100x | Ø | 1010×0 | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | 1×1000 | 1x1x00 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | 1×1100 | Ø | Ø | 100×00 | 10×000 | – | 10xx0x | 10×100 | 101×00 | 101000 | 101×00 | 101000 | 101×00 | 101x0x | 101xx0 | 101100 | 101100 | Ø | 1×1000 | 1x1x00 | 1x1x00 | Ø | Ø | 1×1100 |
| 10xx01 | Ø | Ø | Ø | Ø | 100x0x | Ø | 10x00x | Ø | x00101 | x00101 | 100101 | x00101 | x0x101 | 10×101 | x01001 | x01001 | 101001 | Ø | 10100x | 10100x | x01001 | x01x01 | 101×01 | 101001 | Ø | Ø | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1001 | Ø | Ø | Ø | Ø | 1×1001 | 1x1x01 | Ø | Ø | Ø | Ø | Ø | 1×1101 | Ø | 1×1101 | Ø | 100×01 | 10×001 | 10xx0x | – | 10×101 | 101×01 | 101001 | 101x0x | 10100x | 101x0x | 101×01 | Ø | 101101 | 10110x | Ø | 1×1001 | 1x1x01 | Ø | 1x1x01 | Ø | 1×1101 |
| 10x10x | x00100 | Ø | Ø | x00100 | 100100 | Ø | 10xx00 | Ø | x0010x | x0010x | 10010x | x00101 | x0x101 | 10×101 | Ø | Ø | 101x0x | Ø | 101×00 | 101×00 | Ø | x01101 | 101101 | 101×01 | Ø | Ø | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1100 | Ø | Ø | 1×1101 | Ø | Ø | Ø | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø | 10010x | 10xx0x | 10×100 | 10×101 | – | 10110x | 101x0x | 101100 | 101×00 | 101100 | 101101 | 1011×0 | 10110x | 101100 | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø | 1x110x |
| 101x0x | Ø | x01000 | Ø | Ø | 10xx00 | x01000 | 101000 | Ø | Ø | Ø | 10x10x | Ø | x01101 | 101101 | x0100x | x0100x | 10100x | x01000 | 101000 | 101000 | x01001 | x01x01 | 101×01 | 101001 | Ø | 1010×0 | 101101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1x100x | Ø | 1×1000 | 1x1x00 | Ø | 1×1001 | 1x1x01 | Ø | Ø | Ø | Ø | Ø | 1x110x | 1×1100 | 1×1101 | Ø | 10xx0x | 10100x | 101×00 | 101×01 | 10110x | – | 10100x | 101×00 | 101000 | 101×00 | 101×01 | 101xx0 | 10110x | 101100 | Ø | 1x100x | 1x1x0x | 1x1x00 | 1x1x01 | Ø | 1x110x |
| 1x100x | Ø | x01000 | Ø | Ø | 10×000 | xx1000 | 101000 | Ø | Ø | Ø | Ø | Ø | Ø | 101×01 | x0100x | xx100x | 10100x | xx1000 | 101000 | 1×1000 | xx1001 | xx1001 | 101001 | 1×1001 | Ø | 1x10x0 | 1x1x01 | Ø | x1100x | x11000 | x11000 | x11001 | Ø | Ø | Ø | x1100x | x1100x | 11100x | x11000 | 111000 | 111000 | x11001 | 111001 | 111001 | Ø | 1110xx | 1110×0 | 1110×1 | Ø | 111x0x | 111×00 | 111×01 | Ø | 10x00x | 10100x | 101000 | 101001 | 101x0x | 10100x | – | 101000 | 1×1000 | 1×1000 | 1×1001 | 1x10x0 | 1x1x0x | 1x1x00 | Ø | 11100x | 11100x | 111000 | 111001 | 1110xx | 111x0x |
| 101xx0 | Ø | x010x0 | Ø | Ø | 10xx00 | x01000 | 101000 | x01010 | Ø | Ø | 10×100 | Ø | Ø | 10110x | x010x0 | x01000 | 101000 | x010x0 | 1010×0 | 101000 | Ø | Ø | 101x0x | 10100x | x01010 | 101010 | 10110x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1000 | Ø | 1x10x0 | 1x1x00 | Ø | Ø | Ø | Ø | 1×1010 | 1x1x10 | Ø | Ø | 1×1100 | 1x11x0 | Ø | 1×1110 | 10xx00 | 101000 | 101×00 | 101x0x | 101100 | 101×00 | 101000 | – | 1010×0 | 101×00 | 101x0x | 101×10 | 101100 | 1011×0 | 1×1110 | 1x10x0 | 1x1x00 | 1x1xx0 | Ø | 1x1x10 | 1x11x0 |
| 1x10x0 | Ø | x010x0 | Ø | Ø | 10×000 | xx1000 | 101000 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | x010x0 | xx1000 | 101000 | xx10x0 | 1010×0 | 1×1000 | Ø | Ø | 10100x | 1x100x | xx1010 | 1×1010 | Ø | Ø | x11000 | x110x0 | x11000 | Ø | Ø | Ø | Ø | x110x0 | x11000 | 111000 | x110x0 | 1110×0 | 111000 | Ø | 1110xx | 11100x | x11010 | 111010 | 111010 | 11101x | Ø | 111×00 | 111xx0 | Ø | 111×10 | 10×000 | 101000 | 101000 | 10100x | 101×00 | 101000 | 1×1000 | 1010×0 | – | 1×1000 | 1x100x | 1×1010 | 1x1x00 | 1x1xx0 | 111×10 | 1110×0 | 111000 | 1110×0 | 1110xx | 111010 | 111xx0 |
| 1x1x00 | Ø | x01000 | Ø | Ø | 10xx00 | xx1000 | 101000 | Ø | Ø | Ø | 10×100 | Ø | Ø | 10110x | x01000 | xx1000 | 101000 | xx1000 | 101000 | 1×1000 | Ø | Ø | 101x0x | 1x100x | Ø | 1x10x0 | 1x110x | Ø | x11000 | x11000 | x11x00 | Ø | x11100 | Ø | Ø | x11000 | x11x00 | 111000 | x11x00 | 111000 | 111×00 | Ø | 11100x | 111x0x | Ø | 1110×0 | 111xx0 | Ø | x11100 | 111100 | 111100 | 11110x | 1111×0 | 10xx00 | 101000 | 101×00 | 101x0x | 101100 | 101×00 | 1×1000 | 101×00 | 1×1000 | – | 1x1x0x | 1x1xx0 | 1×1100 | 1×1100 | 1111×0 | 111000 | 111×00 | 111×00 | 111x0x | 111xx0 | 111100 |
| 1x1x01 | Ø | Ø | Ø | Ø | Ø | Ø | 10100x | Ø | Ø | Ø | 10×101 | Ø | xx1101 | 101101 | x01001 | xx1001 | 101001 | Ø | 10100x | 1x100x | xx1001 | xx1x01 | 101×01 | 1×1001 | Ø | Ø | 1×1101 | Ø | x11001 | Ø | Ø | x11x01 | x11101 | x11101 | 1111×1 | x11001 | x11x01 | 111001 | Ø | 11100x | 111x0x | x11x01 | 111001 | 111×01 | Ø | 1110×1 | Ø | 111xx1 | x11101 | 111101 | 11110x | 111101 | 1111×1 | 10xx01 | 101001 | 101x0x | 101×01 | 101101 | 101×01 | 1×1001 | 101x0x | 1x100x | 1x1x0x | – | Ø | 1×1101 | 1x110x | 1111×1 | 111001 | 111×01 | 111x0x | 111×01 | 111xx1 | 111101 |
| 1x1x10 | Ø | x01010 | Ø | Ø | Ø | Ø | 1010×0 | xx1010 | Ø | Ø | Ø | Ø | Ø | Ø | x01010 | Ø | 1010×0 | xx1010 | 101010 | 1x10x0 | Ø | Ø | Ø | Ø | xx1010 | 1×1010 | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | 11111x | x11010 | Ø | 1110×0 | x11x10 | 111010 | 111xx0 | Ø | 11101x | Ø | x11x10 | 111010 | 111×10 | 111x1x | x11110 | 1111×0 | 111110 | 11111x | 111110 | Ø | 1010×0 | 101xx0 | Ø | 1011×0 | 101xx0 | 1x10x0 | 101×10 | 1×1010 | 1x1xx0 | Ø | – | 1x11x0 | 1×1110 | 111110 | 111010 | 111xx0 | 111×10 | 111x1x | 111×10 | 111110 |
| 1x110x | Ø | Ø | Ø | Ø | 10×100 | Ø | 101×00 | Ø | Ø | Ø | 10x10x | Ø | xx1101 | 101101 | Ø | Ø | 101x0x | Ø | 101×00 | 1x1x00 | Ø | xx1101 | 101101 | 1x1x01 | Ø | Ø | 1×1101 | Ø | Ø | Ø | x11100 | x11101 | x1110x | x11101 | 1111×1 | Ø | x1110x | 111x0x | x11100 | 111×00 | 111100 | x11101 | 111×01 | 111101 | Ø | Ø | 1111×0 | 1111×1 | x1110x | 11110x | 111100 | 111101 | 1111xx | 10x10x | 101x0x | 101100 | 101101 | 10110x | 10110x | 1x1x0x | 101100 | 1x1x00 | 1×1100 | 1×1101 | 1x11x0 | – | 1×1100 | 1111xx | 111x0x | 11110x | 111100 | 111101 | 1111xx | 11110x |
| 1x11x0 | Ø | Ø | Ø | Ø | 10×100 | Ø | 101×00 | Ø | Ø | Ø | 10×100 | Ø | Ø | 10110x | Ø | Ø | 101×00 | Ø | 101xx0 | 1x1x00 | Ø | Ø | 10110x | Ø | Ø | 1x1x10 | 1x110x | Ø | Ø | Ø | x11100 | Ø | x11100 | Ø | 11111x | Ø | x11100 | 111×00 | x111x0 | 111xx0 | 111100 | Ø | Ø | 11110x | x11110 | 111×10 | 111110 | 11111x | x111x0 | 111100 | 1111×0 | 1111xx | 111110 | 10×100 | 101×00 | 101100 | 10110x | 101100 | 101100 | 1x1x00 | 1011×0 | 1x1xx0 | 1×1100 | 1x110x | 1×1110 | 1×1100 | – | 111110 | 111xx0 | 111100 | 1111×0 | 1111xx | 111110 | 1111×0 |
| 11x11x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x10111 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 111×10 | 1111×1 | Ø | Ø | Ø | Ø | Ø | Ø | x1x111 | 11×111 | Ø | Ø | Ø | x11110 | 111×10 | 1111×0 | x11111 | 111×11 | 1111×1 | x1111x | 111x1x | 111110 | 111111 | x1111x | 1111xx | 111110 | 111111 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | 1×1110 | 111×10 | 1111×0 | 1111×1 | 111110 | 1111xx | 111110 | – | 111x1x | 1111xx | 111110 | 111111 | 11111x | 11111x |
| 1110xx | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x1100x | 1x100x | x110x0 | 1x10x0 | 111000 | x110x1 | x11001 | 1×1001 | 111001 | x1101x | 111010 | 111×01 | Ø | x1100x | x110x0 | x11000 | x11001 | Ø | Ø | 111×11 | x110xx | x1100x | 11100x | x110x0 | 1110×0 | 111000 | x110x1 | 1110×1 | 111001 | x1101x | 11101x | 111010 | 111011 | Ø | 111x0x | 111xx0 | 111xx1 | 111x1x | Ø | 1x100x | 1×1000 | 1×1001 | Ø | 1x100x | 11100x | 1x10x0 | 1110×0 | 111000 | 111001 | 111010 | 111x0x | 111xx0 | 111x1x | – | 11100x | 1110×0 | 1110×1 | 11101x | 111xxx |
| 111x0x | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | x1100x | 1x100x | x11000 | 1×1000 | 111000 | x11001 | x11x01 | 1x1x01 | 111001 | Ø | 1110×0 | 111101 | Ø | x1100x | x11000 | x11x00 | x11x01 | x1110x | x11101 | 1111×1 | x1100x | x11x0x | 11100x | x11x00 | 111000 | 111×00 | x11x01 | 111001 | 111×01 | Ø | 1110xx | 111xx0 | 111xx1 | x1110x | 11110x | 111100 | 111101 | 1111xx | Ø | 1x100x | 1x1x00 | 1x1x01 | 1x110x | 1x1x0x | 11100x | 1x1x00 | 111000 | 111×00 | 111×01 | 111xx0 | 11110x | 111100 | 1111xx | 11100x | – | 111×00 | 111×01 | 111xxx | 11110x |
| 111xx0 | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11000 | 1×1000 | x110x0 | 1x10x0 | 111000 | Ø | Ø | Ø | 11100x | x11010 | 111010 | 11110x | Ø | x11000 | x110x0 | x11x00 | Ø | x11100 | Ø | 11111x | x110x0 | x11x00 | 111000 | x11xx0 | 1110×0 | 111×00 | Ø | 1110xx | 111x0x | x11x10 | 111010 | 111×10 | 111x1x | x111x0 | 111100 | 1111×0 | 1111xx | 111110 | Ø | 1×1000 | 1x1x00 | Ø | 1×1100 | 1x1x00 | 111000 | 1x1xx0 | 1110×0 | 111×00 | 111x0x | 111×10 | 111100 | 1111×0 | 111110 | 1110×0 | 111×00 | – | 111xxx | 111×10 | 1111×0 |
| 111xx1 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | x11001 | 1×1001 | Ø | Ø | 11100x | x110x1 | x11x01 | 1x1x01 | 111001 | x11011 | 11101x | 111101 | Ø | x11001 | Ø | Ø | x11x01 | x11101 | x111x1 | 111111 | x110x1 | x11x01 | 111001 | Ø | 1110xx | 111x0x | x11xx1 | 1110×1 | 111×01 | x11x11 | 111011 | 111x1x | 111×11 | x111x1 | 111101 | 1111xx | 1111×1 | 111111 | Ø | 1×1001 | Ø | 1x1x01 | 1×1101 | 1x1x01 | 111001 | Ø | 1110xx | 111x0x | 111×01 | 111x1x | 111101 | 1111xx | 111111 | 1110×1 | 111×01 | 111xxx | – | 111×11 | 1111×1 |
| 111x1x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11010 | 1×1010 | 1110×0 | x11011 | Ø | Ø | 1110×1 | x1101x | 111010 | 1111×1 | Ø | Ø | x11010 | Ø | Ø | Ø | x11111 | 111111 | x1101x | Ø | 1110xx | x11x10 | 111010 | 111xx0 | x11x11 | 111011 | 111xx1 | x11x1x | 11101x | 111×10 | 111×11 | x1111x | 1111xx | 111110 | 111111 | 11111x | Ø | Ø | Ø | Ø | Ø | Ø | 1110xx | 1x1x10 | 111010 | 111xx0 | 111xx1 | 111×10 | 1111xx | 111110 | 11111x | 11101x | 111xxx | 111×10 | 111×11 | – | 11111x |
| 1111xx | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | x11101 | 1×1101 | Ø | Ø | Ø | Ø | Ø | 111×00 | Ø | x11101 | 1×1101 | 111×01 | Ø | 111×10 | 111101 | Ø | Ø | Ø | x11100 | x11101 | x1110x | x111x1 | 111111 | Ø | x1110x | 111x0x | x111x0 | 111xx0 | 111100 | x111x1 | 111xx1 | 111101 | x1111x | 111x1x | 111110 | 111111 | x111xx | 11110x | 1111×0 | 1111×1 | 11111x | Ø | Ø | 1×1100 | 1×1101 | 1x110x | 1x110x | 111x0x | 1x11x0 | 111xx0 | 111100 | 111101 | 111110 | 11110x | 1111×0 | 11111x | 111xxx | 11110x | 1111×0 | 1111×1 | 11111x | – |
Z2=
Ĉ3=C2∪(C2*C2)
C3=>
| 0xx0x0, 0x10xx, xx100x xx10x0, xx1x01, 01xx0x 011xxx, x110xx, x11x0x x11xx0, x11xx1, x11x1x x111xx, 10xx0x, 1x1x0x 1x1xx0, 111xxx |
| 0xx0x0 | 0x10xx | xx100x | xx10x0 | xx1x01 | 01xx0x | 011xxx | x110xx | x11x0x | x11xx0 | x11xx1 | x11x1x | x111xx | 10xx0x | 1x1x0x | 1x1xx0 | 111xxx | |
| 0xx0x0 | – | 0x10x0 | 0x1000 | 0x10x0 | 0x100x | 01×000 | 0110×0 | 0110×0 | 011000 | 0110×0 | 0110xx | 011010 | 011xx0 | x0x000 | xx1000 | xx10x0 | x110x0 |
| 0x10xx | 0x10x0 | – | 0x100x | 0x10x0 | 0x1001 | 01100x | 0110xx | 0110xx | 01100x | 0110×0 | 0110×1 | 01101x | 011xxx | x0100x | xx100x | xx10x0 | x110xx |
| xx100x | 0x1000 | 0x100x | – | xx1000 | xx1001 | 01100x | 01100x | x1100x | x1100x | x11000 | x11001 | x110xx | x11x0x | 10100x | 1x100x | 1×1000 | 11100x |
| xx10x0 | 0x10x0 | 0x10x0 | xx1000 | – | xx100x | 011000 | 0110×0 | x110x0 | x11000 | x110x0 | x110xx | x11010 | x11xx0 | 101000 | 1×1000 | 1x10x0 | 1110×0 |
| xx1x01 | 0x100x | 0x1001 | xx1001 | xx100x | – | 011×01 | 011×01 | x11001 | x11x01 | x11x0x | x11x01 | x11xx1 | x11101 | 101×01 | 1x1x01 | 1x1x0x | 111×01 |
| 01xx0x | 01×000 | 01100x | 01100x | 011000 | 011×01 | – | 011x0x | 01100x | 011x0x | 011×00 | 011×01 | 011xxx | 01110x | Ø | x11x0x | x11x00 | x11x0x |
| 011xxx | 0110×0 | 0110xx | 01100x | 0110×0 | 011×01 | 011x0x | – | 0110xx | 011x0x | 011xx0 | 011xx1 | 011x1x | 0111xx | Ø | x11x0x | x11xx0 | x11xxx |
| x110xx | 0110×0 | 0110xx | x1100x | x110x0 | x11001 | 01100x | 0110xx | – | x1100x | x110x0 | x110x1 | x1101x | x11xxx | 1x100x | 11100x | 1110×0 | 1110xx |
| x11x0x | 011000 | 01100x | x1100x | x11000 | x11x01 | 011x0x | 011x0x | x1100x | – | x11x00 | x11x01 | x11xxx | x1110x | 1x1x0x | 111x0x | 111×00 | 111x0x |
| x11xx0 | 0110×0 | 0110×0 | x11000 | x110x0 | x11x0x | 011×00 | 011xx0 | x110x0 | x11x00 | – | x11xxx | x11x10 | x111x0 | 1x1x00 | 111×00 | 111xx0 | 111xx0 |
| x11xx1 | 0110xx | 0110×1 | x11001 | x110xx | x11x01 | 011×01 | 011xx1 | x110x1 | x11x01 | x11xxx | – | x11x11 | x111x1 | 1x1x01 | 111×01 | 111xxx | 111xx1 |
| x11x1x | 011010 | 01101x | x110xx | x11010 | x11xx1 | 011xxx | 011x1x | x1101x | x11xxx | x11x10 | x11x11 | – | x1111x | Ø | 111xxx | 111×10 | 111x1x |
| x111xx | 011xx0 | 011xxx | x11x0x | x11xx0 | x11101 | 01110x | 0111xx | x11xxx | x1110x | x111x0 | x111x1 | x1111x | – | 1x110x | 11110x | 1111×0 | 1111xx |
| 10xx0x | x0x000 | x0100x | 10100x | 101000 | 101×01 | Ø | Ø | 1x100x | 1x1x0x | 1x1x00 | 1x1x01 | Ø | 1x110x | – | 101x0x | 101×00 | 1x1x0x |
| 1x1x0x | xx1000 | xx100x | 1x100x | 1×1000 | 1x1x01 | x11x0x | x11x0x | 11100x | 111x0x | 111×00 | 111×01 | 111xxx | 11110x | 101x0x | – | 1x1x00 | 111x0x |
| 1x1xx0 | xx10x0 | xx10x0 | 1×1000 | 1x10x0 | 1x1x0x | x11x00 | x11xx0 | 1110×0 | 111×00 | 111xx0 | 111xxx | 111×10 | 1111×0 | 101×00 | 1x1x00 | – | 111xx0 |
| 111xxx | x110x0 | x110xx | 11100x | 1110×0 | 111×01 | x11x0x | x11xxx | 1110xx | 111x0x | 111xx0 | 111xx1 | 111x1x | 1111xx | 1x1x0x | 111x0x | 111xx0 | – |
Z3=
Ĉ4=C3∪(C3*C3)
C4=>
| x11xxx | |
| x11xxx | – |
Z4=
Ĉ5=C4∪(C4*C4)
C5=>Ø
Z = Z0∪Z1∪Z2∪Z3∪Z4
Z=>
| 1000×1, 000xx0, 0x0x00 x00x00, x0x000, 0001xx 0x010x, x0010x, 0x01x1 0xx101, x0x101, 01x1x1 x1x111, 11x11x, 0xx0x0 0x10xx, xx100x, xx10x0 xx1x01, 01xx0x, 10xx0x 1x1x0x, 1x1xx0, x11xxx |
Нахождение тупиковых форм.
| 1000×1 | 000xx0 | 0x0x00 | x00x00 | x0x000 | 0001xx | 0x010x | x0010x | 0x01x1 | 0xx101 | x0x101 | 01x1x1 | x1x111 | 11x11x | 0xx0x0 | 0x10xx | xx100x | xx10x0 | xx1x01 | 01xx0x | 10xx0x | 1x1x0x | 1x1xx0 | x11xxx | ||
|
1000×1 |
– |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
1000×1 |
100011 |
100011 |
100011 |
100011 |
v |
|
000xx0 |
000xx0 |
– |
000×10 |
000×10 |
000×10 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
000010 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0x0x00 |
0x0x00 |
010×00 |
– |
010×00 |
010×00 |
010×00 |
010000 |
010000 |
010000 |
010000 |
010000 |
010000 |
010000 |
010000 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x00x00 |
x00x00 |
100×00 |
100×00 |
– |
100100 |
100100 |
100100 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x0x000 |
x0x000 |
x01000 |
x01000 |
x01000 |
– |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
x01000 |
101000 |
101000 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0001xx |
0001xx |
0001×1 |
0001×1 |
0001×1 |
0001×1 |
– |
000111 |
000111 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0x010x |
0x010x |
0x0101 |
0x0101 |
0x0101 |
0x0101 |
010101 |
– |
010101 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x0010x |
x0010x |
x00101 |
x00101 |
x00101 |
x00101 |
100101 |
100101 |
– |
100101 |
100101 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0x01x1 |
0x01x1 |
0x01x1 |
0x01x1 |
0x01x1 |
0x01x1 |
0101×1 |
010111 |
010111 |
– |
010111 |
010111 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
0xx101 |
0xx101 |
0xx101 |
0xx101 |
0xx101 |
0xx101 |
0x1101 |
0x1101 |
0x1101 |
0x1101 |
– |
011101 |
Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x0x101 |
x0x101 |
x0x101 |
x0x101 |
x0x101 |
x0x101 |
x01101 |
x01101 |
x01101 |
x01101 |
101101 |
– |
101101 |
101101 |
101101 |
101101 |
101101 |
101101 |
101101 |
Ø | Ø | Ø | Ø | Ø | Ø | |
|
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01x1x1 |
01×111 |
01×111 |
011111 |
011111 |
011111 |
– | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x1x111 |
x11111 |
x11111 |
x11111 |
111111 |
– | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
|
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11x11x |
11×110 |
– |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
11×110 |
110110 |
110110 |
v |
|
0xx0x0 |
0xx0x0 |
0x10x0 |
0x10x0 |
0x10x0 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
0x1010 |
– |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
010010 |
v |
|
0x10xx |
0x10xx |
0x10xx |
0x10xx |
0x10xx |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
0x10x1 |
– |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
0x1011 |
001011 |
v |
|
xx100x |
xx100x |
xx100x |
xx100x |
xx100x |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
1×1001 |
– |
1×1001 |
Ø | Ø | Ø | Ø | Ø | Ø | |
|
xx10x0 |
xx10x0 |
xx10x0 |
xx10x0 |
xx10x0 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
xx1010 |
1×1010 |
1×1010 |
1×1010 |
– |
1×1010 |
1×1010 |
1×1010 |
1×1010 |
Ø | Ø | |
|
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
xx1001 |
1×1001 |
111101 |
111101 |
– |
111101 |
111101 |
Ø | Ø | Ø | |
|
01xx0x |
01xx0x |
01xx0x |
01xx01 |
01xx01 |
01xx01 |
01xx01 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
01×001 |
010001 |
010001 |
010001 |
010001 |
– |
010001 |
010001 |
010001 |
010001 |
v |
|
10xx0x |
10xx00 |
10xx00 |
10xx00 |
101×00 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
101100 |
– | Ø | Ø | Ø | |
|
1x1x0x |
1x1x0x |
1x1x0x |
1x1x0x |
1x1x0x |
1x1x01 |
1x1x01 |
1x1x01 |
1x1x01 |
1x1x01 |
1x1x01 |
1×1001 |
1×1001 |
1×1001 |
1×1001 |
1×1001 |
1×1001 |
111101 |
111101 |
1×1100 |
1×1100 |
111100 |
– | Ø | Ø | |
|
1x1xx0 |
1x1xx0 |
1x1xx0 |
1x1xx0 |
1x1xx0 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1x1x10 |
1×1010 |
1×1010 |
1×1010 |
1×1010 |
101110 |
101110 |
101110 |
101110 |
101110 |
– |
101110 |
v |
|
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xxx |
x11xx0 |
x11xx0 |
x11xx0 |
x11xx0, x11x10, x1101x |
x11x00, x110x0, 011xx0 |
x11100, 111×00, 1110×0 |
x11100, 111×00, 1110×0 |
x11100 |
x11100 |
x11100 |
111100 |
111100 |
011110 |
011110 |
– | v |
E0:
L1=L0#E0
| 11x11x | 0xx0x0 | 01xx0x | 1x1xx0 | x11xxx | |
|
000000, 000100, 000101 |
000000, 000100, 000101 |
000100, 000101, 000111 |
000100, 000101, 000111 |
000100, 000101, 000111 |
000100 |
L1:

До упорядочивания:
| 000100 | 000101 | 000111 | 001001 | 010111 | 100101 | 101001 | 101101 | |
| 1000×1 | ||||||||
| 000xx0 | + | |||||||
| 0x0x00 | + | |||||||
| x00x00 | + | |||||||
| x0x000 | ||||||||
| 0001xx | + | + | + | |||||
| 0x010x | + | + | ||||||
| x0010x | + | + | + | |||||
| 0x01x1 | + | + | + | |||||
| 0xx101 | + | |||||||
| x0x101 | + | + | + | |||||
| 01x1x1 | + | |||||||
| x1x111 | + | |||||||
| 0x10xx | + | |||||||
| xx100x | + | + | ||||||
| xx10x0 | ||||||||
| xx1x01 | + | + | + | |||||
| 10xx0x | + | + | + | |||||
| 1x1x0x | + | + |
После упорядочивания:
| 000100 | 000101 | 000111 | 001001 | 010111 | 100101 | 101001 | 101101 | |
| 0001xx | + | + | + | |||||
| x0010x | + | + | + | |||||
| 0x01x1 | + | + | + | |||||
| x0x101 | + | + | + | |||||
| xx1x01 | + | + | + | |||||
| 10xx0x | + | + | + |

Z1:
| 0001xx | x0010x | 0x01x1 | x0x101 | xx1x01 | 10xx0x | ||
|
0001xx |
– |
00011x |
000110 |
000110 |
000110 |
000110 |
v |
|
x0010x |
10010x |
– |
10010x |
100100 |
100100 |
Ø | |
|
0x01x1 |
0101×1 |
0101×1 |
– |
0101×1 |
0101×1 |
0101×1 |
v |
|
x0x101 |
x01101 |
x01101 |
x01101 |
– | Ø | Ø | |
|
xx1x01 |
xx1x01 |
xx1x01 |
xx1x01 |
xx1001 |
– |
x11001 |
v |
|
10xx0x |
10xx0x |
10x00x |
10x00x |
10x00x |
10×000 |
– | v |
E1:
L2=L1#E1
| 0x01x1 | xx1x01 | |
|
000100 |
000100 |
000100 |
L2:

До упорядочивания:
| 000100 | 100101 | |
| 0001xx | + | |
| x0010x | + | + |
| x0x101 | + | |
| 10xx0x | + |
После упорядочивания:
| 000100 | 100101 | |
| x0010x | + | + |
| 10xx0x | + |

Z2:
| x0010x | 10xx0x | ||
|
x0010x |
– |
00010x |
v |
|
10xx0x |
10x00x |
– | v |
E2:
L3=L2#E2
| x0010x | |
|
000100 |
Ø |
L3:Ø


Z3:
E:
МДНФ:x1x2x4x5 v x1x4x6 v x1x2x5 v x1x3x6 v x2x3 v x1x3x4x6 v x3x5x6 v x2x3x4x5, цена=26
3. Анализ полученных результатов
Все результаты:
Результат метода Квайна
f1 = x1x3x4x6 v x1x2x4x6 v x1x3x5x6 v x1x2x4x5 v x3x4x5 v x3x4x6 v x1x2x4x5x6 v x1x3x5x6 v x1x2x3x5 v x2x3x4x5 v x1x2x3x5 v x2x3x6, цена=46
Результат метода Карно
f2 = x1x2x3x4x6 v x1x2x4x5 v x1x4x6 v x1x3x4 v x1x2x5 v x1x3x6 v x2x3 v x1x2x3x4 v x1x3x4x6 v x1x2x5 v x3x5x6, цена=37
Результат метода Кубических покрытий
f3 = x1x2x4x5 v x1x4x6 v x1x2x5 v x1x3x6 v x2x3 v x1x3x4x6 v x3x5x6 v x2x3x4x5, цена=26
| Набор | Исходная | После Квайна | После Карно | После Кубических покрытий |
| x1x2x3x4x5x6 | f0 | f1 | f2 | f3 |
| 000000 | 1 | 1 | 1 | 1 |
| 000001 | 0 | 0 | 0 | 0 |
| 000010 | ? | 0 | 1 | 1 |
| 000011 | 0 | 0 | 0 | 0 |
| 000100 | 1 | 1 | 1 | 1 |
| 000101 | 1 | 1 | 1 | 1 |
| 000110 | ? | 0 | 1 | 0 |
| 000111 | 1 | 1 | 1 | 1 |
| 001000 | 1 | 1 | 1 | 1 |
| 001001 | 1 | 1 | 1 | 1 |
| 001010 | 1 | 1 | 1 | 1 |
| 001011 | ? | 0 | 1 | 0 |
| 001100 | 0 | 0 | 0 | 0 |
| 001101 | ? | 0 | 1 | 1 |
| 001110 | 0 | 0 | 0 | 0 |
| 001111 | 0 | 0 | 0 | 0 |
| 010000 | 1 | 1 | 1 | 1 |
| 010001 | 1 | 1 | 1 | 1 |
| 010010 | 1 | 1 | 1 | 1 |
| 010011 | 0 | 0 | 0 | 0 |
| 010100 | 1 | 1 | 1 | 1 |
| 010101 | 1 | 1 | 1 | 1 |
| 010110 | 0 | 0 | 0 | 0 |
| 010111 | 1 | 1 | 1 | 1 |
| 011000 | 1 | 1 | 1 | 1 |
| 011001 | 1 | 1 | 1 | 1 |
| 011010 | 1 | 1 | 1 | 1 |
| 011011 | ? | 0 | 1 | 1 |
| 011100 | 1 | 1 | 1 | 1 |
| 011101 | ? | 0 | 1 | 1 |
| 011110 | 1 | 1 | 1 | 1 |
| 011111 | 1 | 1 | 1 | 1 |
| 100000 | ? | 0 | 1 | 0 |
| 100001 | ? | 0 | 1 | 0 |
| 100010 | 0 | 0 | 0 | 0 |
| 100011 | ? | 0 | 1 | 0 |
| 100100 | ? | 0 | 1 | 1 |
| 100101 | 1 | 1 | 1 | 1 |
| 100110 | 0 | 0 | 0 | 0 |
| 100111 | 0 | 0 | 0 | 0 |
| 101000 | 1 | 1 | 1 | 1 |
| 101001 | 1 | 1 | 1 | 1 |
| 101010 | 1 | 1 | 1 | 1 |
| 101011 | 0 | 0 | 0 | 0 |
| 101100 | ? | 0 | 1 | 1 |
| 101101 | 1 | 1 | 1 | 1 |
| 101110 | 1 | 1 | 1 | 1 |
| 101111 | 0 | 0 | 0 | 0 |
| 110000 | 0 | 0 | 0 | 0 |
| 110001 | 0 | 0 | 0 | 0 |
| 110010 | 0 | 0 | 0 | 0 |
| 110011 | 0 | 0 | 0 | 0 |
| 110100 | 0 | 0 | 0 | 0 |
| 110101 | 0 | 0 | 0 | 0 |
| 110110 | 1 | 1 | 1 | 1 |
| 110111 | 1 | 1 | 1 | 1 |
| 111000 | 1 | 1 | 1 | 1 |
| 111001 | 1 | 1 | 1 | 1 |
| 111010 | 1 | 1 | 1 | 1 |
| 111011 | ? | 0 | 1 | 1 |
| 111100 | 1 | 1 | 1 | 1 |
| 111101 | 1 | 1 | 1 | 1 |
| 111110 | 1 | 1 | 1 | 1 |
| 111111 | 1 | 1 | 1 | 1 |
АНАЛИЗ
По таблице истинности видно, что минимизация функции проведена верно.
В результате минимизации получили минимальные дизъюнктивные нормальные формы:
- Доопределив функцию нулями, методом Квайна получили МДНФ цены 46
- Доопределив функцию единицами, методом карт Карно получили МДНФ цены 37
- Доопределяя функцию по ходу выполнения алгоритма, методом кубических покрытий получили МДНФ цены 26
Метод кубических покрытий приводит к наименьшей МДНФ. Это связано с тем, что минимизируется не полностью определенная функция. В результате минимальная форма принимает на наборах, на которых исходная функция не определена, такие значения, которые соответствуют наиболее оптимальному покрытию. Из всех методов наиболее трудоемким оказывается также метод кубических покрытий, но он удобен для программной реализации минимизации. Наименее трудоемким оказался метод Квайне.
4 Список литературы
- http://www.google.com/search?q=минимизация+переключательных+функций
- file:///C:/Users/Viktor/Desktop/tmp2/minsf/index.html#24