Как найти цену риска - Сайт, где вы сможете решить свои вопросы

Трейдинг21 октября 2020 в 08:0037 819

Формулы для расчёта в Excel

Разновидности риска

Метод VAR

Рис. 1. Список авторизованных вендоров

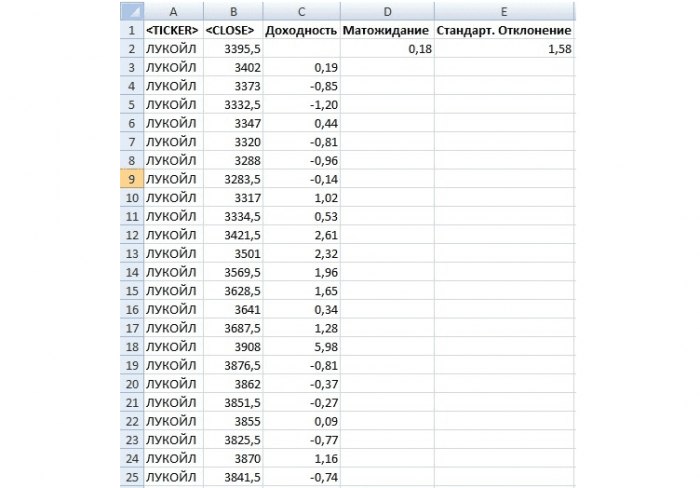
Рис. 2. Вычисление математического ожидания и стандартного отклонения

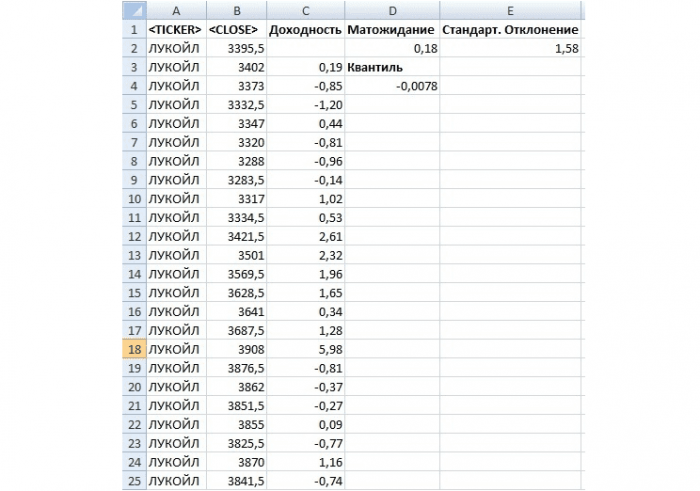
Рис. 3. Определение квантиля

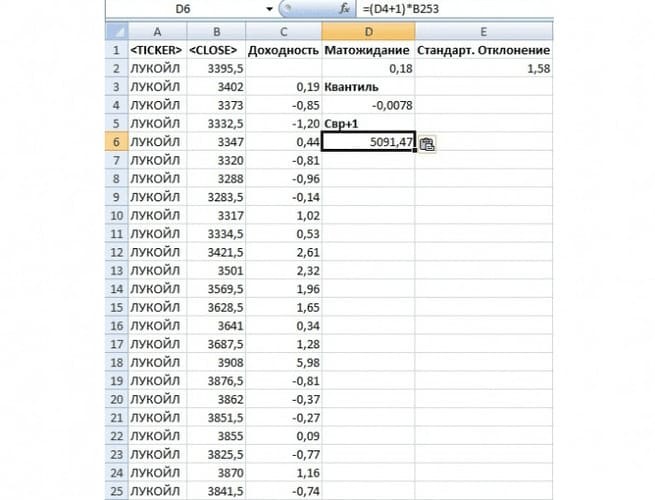
Рис. 4. Определение минимальной стоимости акции с вероятностью 99% на следующий день

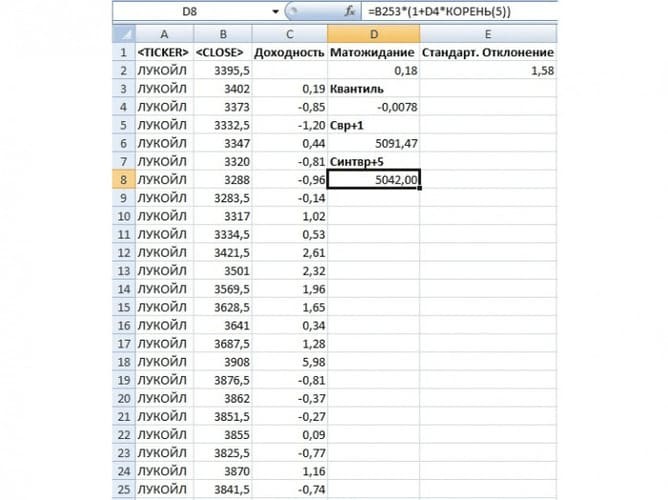
Рис. 5. Определение минимальной стоимости акции с вероятностью 99% через пять дней

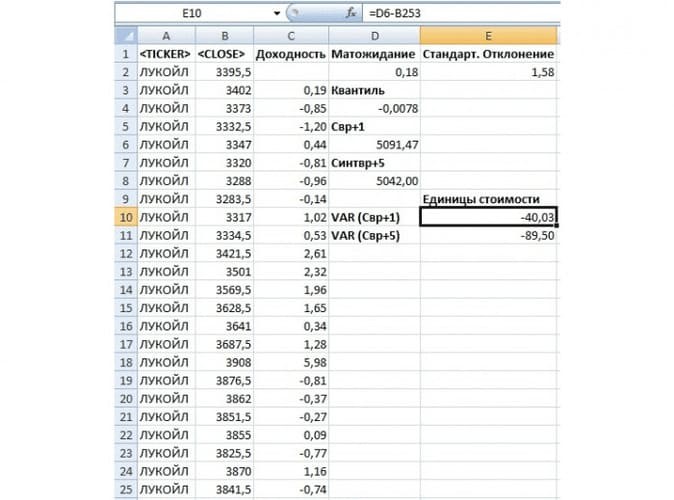
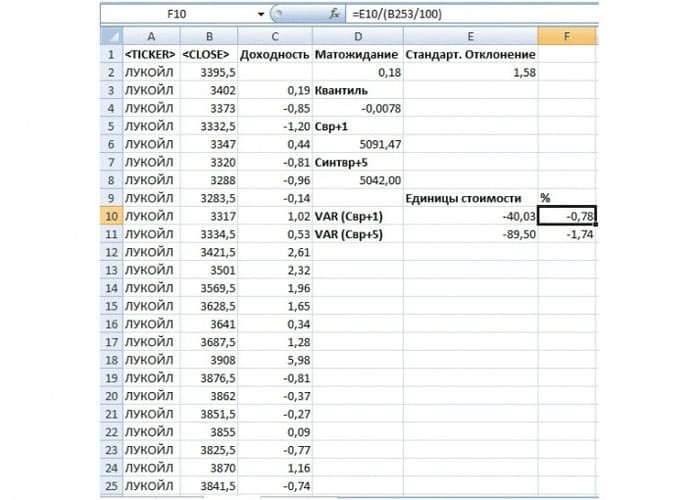
Рис. 6. Определение риска ценового изменения на следующий день и через пять дней

Больше интересных материалов

Источник

Стоимость под риском^[1] (англ. Value at risk, VaR) — стоимостная мера риска. Это выраженная в денежных единицах оценка величины, которую не превысят ожидаемые в течение данного периода времени потери с заданной вероятностью.

VaR характеризуется тремя параметрами:

Временной горизонт, который зависит от рассматриваемой ситуации. По базельским документам — 10 дней, по методике RiskMetrics — 1 день. Чаще распространен расчет с временным горизонтом 1 день. 10 дней используется для расчета величины капитала, покрывающего возможные убытки.
Доверительный уровень (confidence level) — уровень допустимого риска. По базельским документам используется величина 99 %, в системе RiskMetrics — 95 %.
Базовая валюта, в которой измеряется показатель.

VaR — это величина убытков, которая с вероятностью, равной уровню доверия (например, 99 %), не будет превышена. Следовательно, в 1 % случаев убыток составит величину, большую чем VaR.

Проще говоря, вычисление величины VaR проводится с целью заключения утверждения подобного типа: «Есть уверенность на X% (с вероятностью X/100), что потери не превысят Y долларов в течение следующих N дней». В данном предложении неизвестная величина Y является VaR.

Общие свойства[править | править код]

VaR является относительно простой в интерпретации риск-метрикой, характеризующей в целом исследуемое распределение. Ей присущи два основных недостатка^[2]^:21-22:

С помощью VaR невозможно оценить размер убытков вне доверительного уровня. Для этих целей применяется дополнительная метрика: ожидаемые потери (англ. Expected Shortfall).^[⇨]
VaR в общем случае не является когерентной риск-метрикой, поскольку не обладает свойством полуаддитивности. Исключением является случай эллиптического распределения^[en]^[3]^[4].

Методы измерения[править | править код]

Способы оценки VaR:

Исторический (непараметрический): распределение доходностей берётся из уже реализовавшегося временного ряда. То есть предполагается, что распределение доходностей в будущем будут аналогично историческому.^[⇨]
Параметрический: оценка выполняется в предположении, что известен вид распределения доходностей (чаще всего оно предполагается нормальным или логнормальным).^[⇨]
Метод Монте-Карло.^[⇨]

Непараметрические методы[править | править код]

Пример отсечения 5 % худших доходностей

Непараметрические подходы являются наименее ограничительными относительно принимаемых условий.

Исторический метод[править | править код]

Для выполнения исторической оценки достаточно проранжировать исторические значения доходностей от наибольшего к наименьшему. Первое значение, превышающее установленный доверительный уровень, и будет искомым значением VaR.

То есть для доверительного интервала следует выбирать значение доходности с номером ,

где:

Бутстрэппинг[править | править код]

Бутстрэп — относительно простая методика, заключающаяся в перевыборке «с возвратом» из имеющейся популяции^[5]^:85-86.

Непараметрическая оценка плотности распределения[править | править код]

Пример построения непрерывной суррогатной функции плотности распределения методом интерполирования^[5]^:87

Недостаток исторического подхода — дискретность имеющихся наблюдений, что затрудняет оценку VaR для промежуточных значений. Непараметрическая оценка плотности распределения позволяет обойти это ограничение посредством интерполирования между имеющимися историческими значениями.

Одним из наиболее простых решений является интерполяция по медианным значениям между каждыми двумя соседними наблюдениями.

В результате интерполяции выполняется построение непрерывной суррогатной функции плотности распределения^[5]^:86-88.

Взвешенные исторические подходы[править | править код]

Взвешенные исторические подходы используются для обхода эффекта резкого отсечения значений за граничной точкой. Так, при невзвешенном подходе вес отсечённых значений принимается равным 0, а каждого из оставшихся — $n^{{-1}}$ . Соответственно, рассчитываемое значение VaR будет искажено из-за чрезмерного значения весов оставшихся значений. Кроме того, невзвешенные подходы предполагают отсутствие зависимости наблюдений от внешних факторов и между собой, что не соответствует реальному рынку^[6]^[5]^:92-93.

Историческое моделирование, взвешенное по возрасту[править | править код]

Взвешивание по возрасту позволяет назначить более новым наблюдениям больший вес по сравнению с более старыми.

Один из методов — назначение весам параметра затухания ${displaystyle lambda ^{i}in (0;1)}$ со степенью , прямо пропорциональной порядковому номеру наблюдения^[7]. То есть если принять вес наблюдения за предыдущий день, равный $w_{1}$ , то веса наблюдений за предшествующие ему дни будут равны: ${displaystyle w_{2}=lambda w_{1}}$ , ${displaystyle w_{3}=lambda ^{2}w_{1}}$ и т. д. Параметр затухания ${displaystyle lambda ^{i}}$ позволяет задать экспоненциальную скорость затухания весов наблюдений; значения, близкие 1, соответствуют низкой скорости затухания, близкие 0 — высокой. При этом вес наблюдения за предыдущий день принимается равным:

${displaystyle w_{i}={frac {lambda ^{i-1}(1-lambda )}{1-lambda ^{n}}}}$

где — совокупное количество наблюдений.

Соответственно:

${displaystyle sum _{i=1}^{n}w_{i}=1}$

^[5]^:93.

Историческое моделирование, взвешенное по волатильности[править | править код]

Предложенное в 1998 году Халлом^[en] и Уайтом^[en] взвешивание по волатильности позволяет учесть эффект циклов пониженной и повышенной волатильности. Использование стабильных значений волатильности в периоды повышенной рыночной турбулентности приведёт к недооценке VaR. И наоборот, повышенная волатильность в расчётах в периоды стабильного рынка приведёт к завышению оценки VaR.

Корректировка по волатильности выполняется по прогнозным значениям, полученным моделями GARCH или EWMA. Например, если прогноз выполняется для некоего будущего дня , откалиброванное значение доходности получается следующим образом:

${displaystyle r_{t,i}^{*}={frac {sigma _{T,i}}{sigma _{t,i}}}r_{t,i}}$

где:

Историческое моделирование, взвешенное по корреляции[править | править код]

Взвешивание по корреляции позволяет выполнить калибровку на различия между текущими и историческими значениями корреляции между парами активов.

Подход подразумевает применение ковариационных матриц, скорректированных с учётом актуализированных значений волатильностей активов (диагональные элементы ковариационной матрицы)^[9]^[5]^:95-96.

Фильтрованное историческое моделирование[править | править код]

Фильтрованное историческое моделирование является наиболее продвинутым непараметрическим методом. Он сочетает в себе полу-параметрический бутстрэппинг с моделями условной волатильности (типа GARCH).

Метод чувствителен к рыночным показателям и может выдать результат вне диапазона исторических значений. Фильтрованное историческое моделирование относительно быстро отрабатывает даже для больших портфелей и обладает хорошей прогнозирующей способностью^[10].

Недостатком метода является недостаточный учёт экстремальных исторических значений^[11]^[5]^:96-98.

Параметрические методы[править | править код]

Параметрический метод для изолированного актива[править | править код]

В случае, если портфель состоит из одной позиции, значение VaR для нормального распределения принимается равным:

${displaystyle VaR_{i}=V_{i}(-mu _{i}T+z_{alpha }sigma _{i}{sqrt {T}})}$

где:

— размер позиции,
$mu _{i}$ — доходность позиции за единицу времени,
— волатильность позиции в единицу времени,
— оцениваемый горизонт.

Соответственно, для логнормального распределения справедливо следующее соотношение^[5]^:161:

${displaystyle VaR_{i}=V_{i}(1-e^{-mu _{i}T+z_{alpha }sigma _{i}{sqrt {T}}})}$

Параметрический метод для многокомпонентного портфеля (вариационно-ковариационный)[править | править код]

Пусть имеется активов, стоимость которых V_i может случайным образом изменяться. Темпы возможного прироста стоимости активов обозначим $r_{i}$ и назовем их доходностями. Обозначим $r=(r_{1},r_{2},...,r_{n})$ — вектор доходностей (случайных величин) этих активов и $Sigma =[sigma _{{ij}}]$ — ковариационную матрицу (матрица ковариаций $sigma_{ij}$ ) доходностей. Все доходности вычисляются для выбранного периода.

Портфель активов характеризуется вектором структуры $d=(d_{1},d_{2},...,d_{n})$ , где $d_{i}=V_{i}/sum _{{j=1}}^{n}V_{j}=V_{i}/V_{p}$ — доля стоимости -го актива в портфеле.

Тогда доходность портфеля выразится через доходности активов следующим образом:

$r_{p}=d^{T}r=sum _{{i=1}}^{n}d_{i}r_{i}$

Тогда ожидаемая (математическое ожидание) доходность портфеля выражается через ожидаемые доходности активов следующим образом:

$mu _{p}=E(r_{p})=d^{T}E(r)=sum _{{i=1}}^{n}d_{i}E(r_{i})=sum _{{i=1}}^{n}d_{i}mu _{i}$

а дисперсия портфеля будет равна

$sigma _{p}^{2}=V(r_{p})=V(d^{T}r)=d^{T}Sigma d=sum _{{i=1}}^{n}sum _{{j=1}}^{n}sigma _{{ij}}d_{i}d_{j}$

Если предполагается нормальное распределение доходностей, то для заданной вероятности alpha (например, 5 % или 1 %):

${displaystyle P(r_{p}<mu _{p}-z_{alpha }sigma _{p})=alpha }$

где $z_{alpha }$ — односторонняя alpha -квантиль стандартного нормального распределения.

Следовательно, величина VaR оценивается как

${displaystyle VaR=V_{p}(-mu _{p}T+z_{alpha }sigma _{p}{sqrt {T}})}$

На практике истинное значение ковариаций, в том числе дисперсий «доходностей» неизвестны. Они оцениваются по выборочным данным за длительный период по соответствующим формулам. При этом предполагается стационарность «доходностей» активов.

VaR в теории экстремальных значений[править | править код]

Согласно теореме Фишера — Типпетта — Гнеденко^[en] (1928), являющейся ключевой в теории экстремальных значений^[en] (англ. EVT), выборка экстремальных значений $M_{n}$ размером принимает вид обобщённого распределения экстремальных значений^[en] (англ. GEV):

${displaystyle Fleft(X|xi ,mu ,sigma right)={begin{cases}e^{-left(1+xi times {frac {x-mu }{sigma }}right)^{-1/xi ,}}&,xi neq 0\e^{-e^{frac {x-mu }{sigma }}}&,xi =0end{cases}}}$

где:

— «хвостовой» индекс, определяющий форму распределения,
— параметр сдвига,
— масштабирующий параметр.

При этом должно соблюдаться условие:

${displaystyle 1+xi times {frac {x-mu }{sigma }}>0}$

К распределению убытков выше некоторого установленного высокого порога применяется разновидность EVT под названием подхода превышений над порогом (англ. peaks-over-threshold; POT). Распределение для порога со значением , превышение которого не будет большим значения , приобретает вид:

${displaystyle F_{u}(x)=Pleft(X-uleqslant x|X>uright)={frac {F(x+u)-F(u)}{1-F(u)}}}$

VaR и ES для подхода POT выражаются, соответственно, следующим образом:

${displaystyle VaR=u+{frac {beta }{xi }}left({frac {n}{N_{u}}}left(1-alpha right)^{-xi }-1right)}$

${displaystyle ES={frac {VaR+beta -xi u}{1-xi }}}$

где:

Метод Монте-Карло[править | править код]

В случае однофакторной модели изменение цены позиции описывается геометрическим броуновским движением. Соответственно, генерируются значения дрифтов phi (винеровских процессов), определяемых нормальным распределением^[5]^:213-214:

${displaystyle {frac {Delta S}{S}}=mu Delta T+phi sigma {sqrt {Delta T}}}$

В случае же многофакторной модели матрица корреляций значений дрифтов разных позиций предварительно обрабатывается разложением Холецкого или другими, менее ограничительными, но более вычислительно затратными преобразованиями^[5]^:215-217.

Симуляции методом Монте-Карло широко применяются для прайсинга комплексных портфелей и нелинейных деривативов. Одной из основных препятствием в использовании метода являются высокие требования к вычислительным мощностям^[5]^:225.

Ожидаемые потери (Expected Shortfall)[править | править код]

Одним из способов оценки портфельных рисков является оценка ожидаемых потерь (англ. Expected Shortfall, ES) — взвешенное по вероятности математическое ожидание потерь в хвосте распределения за предельным значением VaR^[13].

Если случайную величину возможных потерь обозначить , то определение ES:

${displaystyle ES_{alpha }=E(X|X>VaR_{alpha })}$

Таким образом, если $Xin L^{p}({mathcal {F}})$ (где Lp (пространство)) — это потери портфеля в некотором будущем и , тогда формула определения средних ожидаемых потерь:

${displaystyle ES_{alpha }={frac {1}{alpha }}int _{0}^{alpha }VaR_{gamma }(X)dgamma ={frac {1}{alpha }}int _{-infty }^{-VaR_{alpha }}xp(x)dx}$

где $VaR_{{gamma }}$ — Value at Risk уровня gamma , p(x) — плотность распределения потерь.

В отличие от базового VaR, такая мера позволяет уже не только выделить нетипичный уровень потерь, но и показывает, что, скорее всего, произойдет при их реализации. ES уровня alpha определяет ожидаемый возврат по портфелю в alpha худших случаях. CVaR оценивает значение (или риск) инвестиций консервативным образом, ориентируясь на менее прибыльные результаты. При больших значениях alpha CVaR игнорирует самые прибыльные стратегии, у которых мала вероятность наступления, при малых значениях alpha CVaR строится на самых плохих сценариях. Значение , которое часто используется на практике, составляет .

В случае нормального распределения ES будет равен:

$ES_{{alpha }}={frac {1}{alpha }}phi [Phi ^{{-1}}(alpha )]sigma _{p}$

где phi — плотность, а Phi — интегральная функция стандартного нормального распределения ( $Phi ^{{-1}}(alpha )$ — это квантиль уровня alpha ).

Маппинг VaR[править | править код]

Пример маппинга (декомпозиции) по риск-факторам^[14]^:280

Суть маппинга VaR (англ. VaR mapping) сводится к замене позиций различных инструментов на соответствующие риск-факторы с дальнейшей их агрегацией^[14]^:278.

Риски портфеля могут быть разделены на два типа: диверсифицируемый (англ. specific risk) и общий рыночный риск (англ. general market risk). Первый риск может быть снижен посредством использования более точных и вычислительно затратных моделей.

Если доходность инструментов в портфеле представлена в виде:

${displaystyle r_{i}=alpha +beta _{i}r_{m}+epsilon _{i}}$

то дисперсия портфеля с активов выражается следующим образом:

${displaystyle sigma _{p}^{2}=beta _{p}^{2}sigma _{m}^{2}+sum _{i=1}^{n}omega _{i}^{2}sigma _{epsilon ,i}^{2}}$

где первый член соответствует рыночному риску, второй — диверсифицируемому, связанному со специфическими риск-факторами^[14]^:281-282.

Инструменты с фиксированной доходностью[править | править код]

Следующим этапом после выбора специфических риск-факторов является маппинг VaR на эти факторы.

Для портфелей с фиксированной доходностью применяется один из трёх методов:

маппинг по номинальной стоимости (англ. principal mapping) — самый простой метод: VaR рассчитывается для бескупонной облигации, срок погашения которой совпадает со средним сроком обращения исследуемого портфеля. Использование метода приводит к завышенной оценке VaR ввиду игнорирования пересекающихся купонных платежей^[14]^:284.
маппинг по дюрации (англ. duration mapping) — маппинг на бескупонную облигацию с дюрацией, равной дюрации портфеля.
маппинг по денежным потокам (англ. cash-flow mapping) — самый сложный метод: денежные потоки группируются по корзинам с различными сроками обращения (англ. maturity buckets)^[14]^:283.

В последнем случае каждый поток приводится по дисконтированной стоимости по ставке кривой бескупонной доходности. Если соответствующие бескупонные облигации полностью скоррелированы между собой, то недиверсифицированная VaR представляется в виде:

${displaystyle VaR_{p}=sum _{i=1}^{n}left|x_{i}rightvert VaR_{i}}$

где:

$x_{i}$ — дисконтированные значения потоков,
${displaystyle VaR_{i}}$ — индивидуальные значения VaR потоков (в %).

Если же бескупонные облигации не идеально скоррелированы, возникает эффект диверсификации, и VaR представляется в виде:

${displaystyle VaR_{p}=alpha {sqrt {x'Sigma x}}={sqrt {(xtimes V)'R(xtimes V)}}}$

где:

Форварды[править | править код]

Форварды являются простейшими линейными деривативами, которые могут быть представлены синтетическим портфелем из базовых риск-факторов. Например, длинный годовой контракт на покупку в будущем евро за доллары США аналогичен портфелю из трёх следующих позиций:

Короткая позиция в казначейских векселях,
Длинная позиция в годовых евровекселях,
Длинная позиция в евро.

Для оценки VaR такого валютного форварда следует использовать значения индивидуальных VaR вышеуказанных позиций с последующим применением матрицы корреляций между ними^[14]^:289-292.

FRA[править | править код]

Суть декомпозиции FRA также сводится в представлении контракта в виде синтетического портфеля с дальнейшей оценкой компонентных VaR (англ. component VaR) базовых позиций. Например, длинный 6 x 12 FRA представим в виде портфеля из длинных 6-месячных казначейских облигаций и коротких 12-месячных казначейских облигаций^[14]^:294-295.

Процентные свопы[править | править код]

Процентные свопы могут быть декомпозированы в соответствии с фиксированной и плавающей ногой, соответственно, на облигации с фиксированным и плавающим купоном^[14]^:296.

Опционы[править | править код]

Дельта-нормальный подход, описанный выше, предполагает линейную зависимость дериватива от базового актива. Этот метод может ограниченно применяться и для опционов, которые являются нелинейными инструментами. Так, следуя модели Блэка — Шоулза, внутренняя стоимость европейского колл-опциона определяется соотношением:

${displaystyle c=SN(d_{1})-Xe^{-rT}N(d_{2})}$

где:

${displaystyle d_{1}={frac {ln({frac {S}{X}})+(r+{frac {sigma ^{2}}{2}})T}{sigma {sqrt {T}}}}}$

${displaystyle d_{2}=d_{1}-sigma {sqrt {T}}}$

Соответственно, внутренняя стоимость, продифференцированная по частным производным:

${displaystyle dc=Delta dS+{frac {1}{2}}Gamma dS^{2}+dots }$

где:

${displaystyle Delta =e^{-rT}N(d_{1})}$

Дельта опцинов в целом не является постоянной величиной и монотонно возрастает в зависимости от спот-цены базового актива. Кроме того, для краткосрочных опционов эта зависимость проявляет значительный нелинейный характер. Соответственно, в контексте опционов дельта-нормальный подход применим только для долгосрочных договоров на коротких горизонтах, например, 1 день^[14]^:298-300.

VaR в оценке риска ликвидности[править | править код]

Ликвидность на финансовых рынках подразделяется на (i) экзогенную, определяющуюся бид — аск спредом, и (ii) эндогенную, когда риск ликвидности в сделке определяется самой сделкой (то есть сделка настолько крупная, что двигает цены для всего своего рынка).

В предположении экзогенной ликвидности и постоянного спреда поправка VaR на риск ликвидности определяется соотношением:

${displaystyle LVaR=VaR+LC=Vleft(1-e^{mu -zsigma }+{frac {ask-bid}{ask+bid}}right)}$

где:

— стоимость ликвидности,
— размер позиции,
— цена продажи,
— цена покупки.

В случае же эндогенной ликвидности вводится значение эластичности спроса eta :

${displaystyle eta ={dfrac {Delta P/P}{Delta N/N}}<0;Delta N/N>0}$

где:

— размер рынка,
— рыночная цена.

Соответственно:

${displaystyle LVaR=VaRleft(1-{frac {Delta P}{P}}right)=VaRleft(1-eta {frac {Delta N}{N}}right)}$

Подходы для экзогенной и эндогенной ликвидности могут быть объединены^[5]^:309-315:

${displaystyle {frac {LVaR}{VaR}}{Bigg |}_{combined}={frac {LVaR}{VaR}}{Bigg |}_{exogenous}times {frac {LVaR}{VaR}}{Bigg |}_{endogenous}}$

Ретроспективное тестирование[править | править код]

Ретроспективное тестирование (бэктестинг; англ. Backtesting) заключается в сравнении значений убытков, предсказанных моделью VaR, с реальными данными. Количество реальных убытков не должно превышать значение уровня значимости alpha ; например, для доверительного уровня 90 % количество исключений не должно быть больше 10^[14]^:139-142.

Бэктестинг используется для верификации моделей VaR и проводится по схеме Бернулли:

${displaystyle z={frac {x-pT}{sqrt {p(1-p)T}}}}$

где:

— z-оценка,
— количество исключений,
— уровень значимости,
— временной интервал.

Полученная z-оценка сравнивается с критическим значением , соответствующим выбранному одностороннему доверительному уровню (1-p) нормального распределения. В случае если , следует отвергнуть нулевую гипотезу о несмещённости VaR и провести калибровку модели (количество исключений превышает допустимый уровень)^[14]^:143-144.

Пример бэктестинга по схеме Бернулли

Например, требуется рассчитать максимально допустимое количество исключений для 10-дневной модели 99% VaR на горизонте 10 лет с точностью 95% при условии 250 торговых дней в году.

В таком случае z-оценка определяется квантилем для односторонней критической области нормального распределения с вероятностью 95%. Соответствующий квантиль равен приблизительно 1,96.

Таким образом:

${displaystyle {frac {x-pT}{sqrt {p(1-p)T}}}leqslant z(approx 1,96)Rightarrow }$

${displaystyle {frac {x-0,01*2500}{sqrt {0,01(1-0,01)*2500}}}leqslant 1,96Rightarrow }$

То есть количество исключений для указанных вводных данных не должно превышать 34.

При выборе допустимого количества исключений следует руководствоваться компромиссом между ошибками первого и второго рода — то есть модель должна характеризоваться как низким количеством ошибок первого рода (неверное отвержение верной нулевой гипотезы), так и очень низким количеством ошибок второго рода (неверное принятие неверной нулевой гипотезы)^[14]^:146.

Безусловная валидация[править | править код]

В случае, если не учитывается взаимная зависимость исключений или их временны́е характеристики, такая валидация модели VaR обозначается как безусловная (англ. Unconditional coverage).

Тест отношения правдоподобия (LR) выполняется следующим образом:

${displaystyle LR_{uc}=2lnleft(left(1-{frac {n}{N}}right)^{N-n}left({frac {n}{N}}right)^{n}right)-2lnleft(p^{n}left(1-pright)^{N-n}right)=2lnleft(left({frac {1-n/N,}{1-p}}right)^{N-n}left({frac {n/N,}{p}}right)^{n}right)}$

где:

— количество исключений,
— размер выборки,
— уровень вероятности.

Для уровня достоверности 95 % должно выполняться условие ${displaystyle LR_{uc}<3,841}$ , в противном случае гипотеза о точности модели должна быть отвергнута^[15]^[14]^:146-147.

Условная валидация[править | править код]

Условная валидация дополняет безусловную предположением о переменной временно́й характеристике исследуемых данных и складывается из двух компонент:

${displaystyle LR_{cc}=LR_{uc}+LR_{ind}}$

где ${displaystyle LR_{ind}}$ — LR-тест на последовательную независимость исключительных событий^[5]^:329.

${displaystyle LR_{uc}}$ и ${displaystyle LR_{ind}}$ представлены независимыми распределениями ${displaystyle chi ^{2}(1)}$ , а их сумма, соответственно, распределением ${displaystyle chi ^{2}(2)}$ . Соответственно, при уровне достоверности 95 % модель следует отклонить при значении ${displaystyle LR_{cc}>5,99}$ ^[14]^:152.

Регуляторные требования[править | править код]

Базель I 1996a[править | править код]

В 1996 году Базельский комитет принял поправку к соглашению Базель I от 1988 года. В соответствии с ней в зависимости от количества исключений в однодневной модели VaR 99 % при ретроспективном тестировании по 250 прошедшим торговым дням к регуляторному капиталу следует применять тот или иной повышающий (штрафной) коэффициент — множитель.

Были установлены следующие зоны^[14]^:148:

Зона	Количество исключений	Множитель
Зелёная	0-4	3,00
Жёлтая	5	3,40
6	3,50
7	3,65
8	3,75
9	3,85
Красная	>10	4,00

В жёлтой зоне размер повышающего коэффициента устанавливается по усмотрению контролирующего органа в зависимости от причин исключения. К ним относятся:

недостаточная базовая целостность модели,
недостаточная точность модели,
внутридневная торговля,
невезение.

Первые две категории подразумевают обязательное применение штрафа, для третьей категории оно должно быть принято во внимание, для четвёртой наложение штрафных санкций не предполагается^[16]^[14]^:149^[17]^:358-359.

Согласно той же поправке, VaR для рыночного риска следовало рассчитывать для 10-дневного горизонта на уровне 99 % в соответствии с соотношением:

${displaystyle VaR_{MR}=maxleft(VaR_{t-1},m_{c}times VaR_{avg}right)+SRC}$

где:

Базель II[править | править код]

В июне 1999 года было введено соглашение Базель II. Помимо прочего оно вводило продвинутый подход на основе внутренних рейтингов (англ. Advanced IRB Approach) для расчёта капитала на покрытие кредитного риска. По нему необходимо рассчитывать VaR 99,9 % на горизонте 1 года с применением однофакторной гауссовой копулы^[17]^{:360; 363-364}.

Базель II.5[править | править код]

Поправка к соглашению Базель II, введённая в действие в январе 2012 года, определяла требования к стресс-тестированию модели VaR:

${displaystyle VaR_{ST}=maxleft(VaR_{t-1},m_{c}times VaR_{avg}right)+maxleft(sVaR_{t-1},m_{s}times sVaR_{avg}right)}$

Новое требование привело к увеличению требований к уровню капитала на покрытие рыночного риска как минимум вдвое^[17]^:378-379.

VaR в портфельной оптимизации[править | править код]

При решении задачи построения оптимального портфеля часто используются различные меры рисков, такие как дисперсия, VaR, CVaR, DaR, CDaR. Существуют различные постановки задач оптимизации, где меры рисков используются как при построении целевых функций, так и для определения множества допустимых решений (ограничения)^[18]. Для решения подобных задач на практике используются специализированные пакеты численной оптимизации, например, PSG.

Для оценки компонентов портфелей, состоящих из различных активов, применяется маржинальная VaR (MVaR). Она выражается в чувствительности портфельной VaR к размеру $P_{i}$ i-й компоненты портфеля^[17]^:283:

${displaystyle MVaR_{i}={frac {partial VaR}{partial P_{i}}}}$

В свою очередь, инкрементальная VaR (IVaR) соответствует абсолютному значению изменения портфельной VaR при добавлении в портфель i-й компоненты^[17]^:283:

${displaystyle IVaR_{i}=VaR_{P+i}-VaR_{P}}$

Также используется такое понятие, как компонентная VaR (CVaR) — альтернатива инкрементной VaR, выражающаяся в количестве риска, привносимого каждой отдельной компонентой. Для хорошо диверсифицированного портфеля CVaR выражается через MVaR^[17]^:283-284:

${displaystyle CVaR_{i}={frac {partial VaR}{partial P_{i}}}P_{i}=MVaR_{i}times P_{i}}$

VaR в управлении рисками[править | править код]

Филипп Джорион писал^[19]:

Наибольшая польза VAR заключается в наложении структурированной методологии для критического мышления о риске. Учреждения, которые проходят через процесс вычисления VAR, вынуждены встать перед фактом их подверженности финансовым рискам и создать надлежащие функции управления риском. Таким образом, процесс получения VAR может быть столь же важен, как и само число VAR.

<…> the greatest benefit of VAR lies in the imposition of a structured methodology for critically thinking about risk. Institutions that go through the process of computing their VAR are forced to confront their exposure to financial risks and to set up a proper risk management function. Thus the process of getting to VAR may be as important as the number itself.

Использование некорректной модели VaR стало в конце XX века одной из причин краха крупнейшего хедж-фонда LTCM^[20].

Примечания[править | править код]

↑ Халл, Д. К. Стоимость под риском // Опционы, фьючерсы и другие производные финансовые инструменты. — 6. — Издательский дом Вильямс, 2008. — С. 597. — 1051 с. — ISBN 5845912059.
↑ Gregory, 2015.
↑ McNeil A., Frey R., Embrechts P. Risk Measures for Linear Portfolios // Quantitative Risk Management: Concepts, Techniques and Tools. — Princeton University Press, 2015. — P. 297. — 720 p. — (Princeton Series in Finance). — ISBN 0691166277.
↑ Artzner P. et al. Coherent measures of risk : [англ.] // Mathematical finance. — 1999. — Vol. 3, no. 9. — P. 203—228. — doi:10.1111/1467-9965.00068.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² ¹³ ¹⁴ ¹⁵ ¹⁶ Dowd, 2005.
↑ Shimko D., Humphreys B., Pant V. End-user’s Guide Hysterical Simulation : [англ.] // Risk. — 1998. — Т. 11. — P. 47—50.
↑ Boudoukh J., Richardson M., Whitelaw R. The best of both worlds : [англ.] // Risk. — 1998. — Т. 11, № 5. — P. 64—67.
↑ Hull J. C., White A. Incorporating volatility updating into the historical simulation method for value-at-risk : [англ.] // Journal of risk. — Vol. 1, no. 1. — P. 5—19.
↑ Duffie D., Pan J. An overview of value at risk : [англ.] // Journal of derivatives. — 1997. — Vol. 4, no. 3. — P. 7—49.
↑ Barone‐Adesi G., Giannopoulos K. Non parametric var techniques. myths and realities : [англ.] // Economic Note. — 2001. — Vol. 30, no. 2. — P. 167—181.
↑ Pritsker M. The hidden dangers of historical simulation : [англ.] // Journal of Banking & Finance. — 2006. — Vol. 30, no. 2. — P. 561—582.
↑ Embrechts P. et al.. Extreme value theory as a risk management tool : [англ.] // North American Actuarial Journal. — 1999. — Vol. 3, no. 2. — P. 30—41. — doi:10.1080/10920277.1999.10595797.
↑ Jorion P. Tools for Measuring Risk // Value at Risk: The New Benchmark for Managing Financial Risk. — 3. — McGraw-Hill, 2006. — P. 91. — 596 p. — ISBN 9780071464956.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² ¹³ ¹⁴ ¹⁵ ¹⁶ ¹⁷ Jorion, 2006.
↑ Kupiec P. H. Techniques for Verifying the Accuracy of Risk Measurement Models : [англ.] // The Journal of Derivatives. — 1995. — Vol. 3, no. 2 (January). — P. 73—84. — doi:10.3905/jod.1995.407942.
↑ Supervisory framework for the use of ‘backtesting’ in conjunction with the internal models approach to market risk capital requirements (англ.). Bank for International Settlements. Дата обращения: 12 декабря 2019. Архивировано 4 ноября 2020 года.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ Hull, 2018.
↑ Lim C., Sherali H. D., Uryasev S. Portfolio optimization by minimizing conditional value-at-risk via nondifferentiable optimization : [англ.] // Computational Optimization and Applications. — 2010. — Vol. 46, no. 3. — P. 391—415. — doi:10.1007/s10589-008-9196-3.
↑ Jorion P. In defense of VaR : [англ.] // Derivatives Strategy. — 1997. — Vol. 2, № 4. — P. 20–23.
↑ Crouhy M., Galai D., Mark R. The Essentials of Risk Management. — McGraw-Hill, 2014. — P. 551. — ISBN 0071818510.

Литература[править | править код]

Allen L., Boudoukh J., Saunders A. Understanding Market, Credit, and Operational Risk: The Value at Risk Approach (англ.). — 1. — Wiley-Blackwell, 2004. — 284 p. — ISBN 0631227091.
Dowd K. Measuring Market Risk (англ.). — 2. — John Wiley & Sons Ltd, 2005. — 390 p. — ISBN 9780470013038.
Gregory J. The xVA Challenge: Counterparty Credit Risk, Funding, Collateral and Capital (англ.). — John Wiley & Sons, 2015. — 496 p. — (The Wiley Finance Series). — ISBN 1119109418.
Hull J. C. Risk Management and Financial Institutions (англ.). — Wiley, 2018. — 800 p. — (Wiley Finance). — ISBN 1119448115.
Jorion P. VAR mapping // Value at Risk: The New Benchmark for Managing Financial Risk (англ.). — McGraw-Hill, 2006. — 602 p. — ISBN 9780071464956.

Источник

Размер «плеча» – то есть суммы, которую вы можете использовать взаймы под обеспечение имеющихся у вас ценных бумаг, рассчитывается для каждой ценной бумаги.

Общий принцип маржинального кредитования – стоимость портфеля ценных бумаг клиента должен быть больше, чем начальная и минимальная маржа.

Начальная маржа – это сумма в рублях, которая получена путем умножения стоимости каждой ликвидной ценной бумаги в портфеле клиента на начальную ставку риска по этой бумаге и последующим сложением получившихся результатов.

Минимальная маржа – это сумма в рублях, которая получена путем умножения Начальной маржи на 0.5.

Если стоимость портфеля снизилась ниже начальной маржи, то клиент уже не может открывать новые позиции в займы. Если стоимость портфеля снизилась ниже минимальной маржи, то позиции клиента закрываются брокером (маржин-колл).

При выставлении клиентом заявки на покупку или продажу ценных бумаг, торговая система произведет расчет начального и минимального уровня маржи. Если правила по стоимости портфеля не будут соблюдены, заявка не будет выставлена.

Необходимо помнить, что маржинальная торговля связана с повышенным риском. Клиент, который торгует с «плечом» обязан следить за уровнем маржи и принимать меры по закрытию части позиций, пока не наступил маржин-колл.

Подробные условия совершения Маржинальных и Необеспеченных сделок (часть 9, 10 Регламента) .

Формула расчета начальной и минимальной маржи

Начальная маржа = ∑ (Кол-во ликвидных ЦБ * Цена последней сделки * Начальная ставка риска.)

Минимальная маржа =Начальная маржа * 0.5.

Начальная ставка риска определена для каждой ликвидной ценной бумаги на основании базовых ставок риска Национального клирингового центра и формул, приведенных в в Указании Банка России от №5636-У.

Брокер имеет право устанавливать собственные повышенные ставки риска

Формула расчета стоимости портфеля

Стоимость портфеля = Активы по ЦБ + Активы по ДС – Обязательства по ЦБ – Обязательства по ДС.

При этом учитываются и все нерассчитанные сделки. В стоимости портфеля учитываются только ликвидные ценные бумаги.

Ситуация 1:

Стоимость портфеля > Начальная маржа

Это означает, что клиент может открывать маржинальные позиции.

Ситуация 2:

Начальная маржа > Стоимость портфеля > Минимальная маржа

Это означает, что клиент уже не может открывать новые маржинальные позиции, нужно следить за движением рынка и своевременно закрывать часть позиций во избежание маржин-колла.

Ситуация 3:

Минимальная маржа > Стоимость портфеля

Это означает, что брокер вынужден принудительно закрыть часть позиций клиента (маржин-колл).

Подробнее о расчете маржи и выставлении заявок в QUIK с «плечом» >>>

Пример:

Начальная маржа = ∑(стоимость ЦБ * Начальная ставка риска по ЦБ)

ЦБ	Количество ЦБ с учетом плановой позиции (1)	Цена последней сделки (2)	Стоимость ЦБ по цене последней сделки (3)	Начальная ставка риска¹(4)	Начальная маржа¹
			=(1)*(2)		=(3)*(4)
Лукойл-во-ао	-20	1961,9	39 238,00	0,2	7 847,6
Интер РАО ЕЭС- в3-ао	45000000	0,011308	508 860,00	0,4	203 544
Газпром-ао	3000	147,64	442 920,00	0,2	88 584
Начальная маржа для портфеля:	299 975,6

То есть пока стоимость портфеля выше 299 975,6р., клиент может открывать маржинальные позиции. Как только стоимость портфеля снизилась менее 299 975,6р., необходимо следить за дальнейшей динамикой и минимальной маржой.

Минимальная маржа = Начальная маржа * 0.5.

Минимальная маржа для портфеля:

149 987,8

В данном случае 149 987,8 это критическая сумма. Если портфель снизится ниже этой суммы, часть позиций будут принудительно закрыты брокером (маржин-колл).

Источник

Открыть эту статью в PDF

Что такое премия за риск

Премия за риск (Risk Premium) — увеличение величины ставки дисконтирования в оценке инвестиций или бизнеса, призванное учесть более высокий риск изучаемых доходов по сравнению с некоторым базовым уровнем.

Например, после определения требуемой доходности для акций, торгующихся на фондовом рынке, можно добавить премию за риск, учитывающую, что конкретная компания, которую мы оцениваем, более рискованная инвестиция, чем вложения в фондовый рынок в целом. Другой вариант — после расчета стоимость капитала компании можно добавить в премию за риск в оценке нового проекта этой компании, так как этот новый проект более рискованный, чем устоявшаяся, стабильная деятельность основного бизнеса.

Применение премии за риск основано на важной основополагающей гипотезе инвестиционного анализа: все инвесторы предпочитают избегать риска и готовы принимать более высокий уровень риска только в том случае, если он обещает более высокий уровень дохода. Иначе говоря, зависимость требуемого инвестором дохода от уровня риска выглядит так:

Эта линия называется линией рынка капитала. Хотя предположение о том, что она имеет именно такой наклон (то есть за любой риск инвестор требует премию) в целом верно и отражает суть рынков капитала, в частных случаях это правило нередко нарушается.

Пример: хорошо известен следующий эксперимент. Группе людей предлагают выбрать между двумя вариантами инвестиций. Первый с вероятностью 100% приносит убыток 10%. Второй с вероятностью 50% принесет прибыль 10% и с вероятностью 50% — убыток 30%. В обоих случаях ожидаемая доходность равна10%, но второй вариант связан с большей неопределенностью (то есть риском). Значительная, иногда подавляющая, часть опрошенных выбирает второй вариант, то есть не избегают риска, а наоборот, предпочитают его, хотя за этот риск они не получают рост ожидаемой доходности. Таким образом, на практике повышенные риски не всегда требуют премии за риск.

Премия за риск может иногда выражаться не в процентах, добавляемых к ставке дисконтирования, а в множителе, который применяют к полученной оценке. В таких случаях ее обычно называют скидка за риск.

Полный риск и систематический риск

В инвестиционном анализе под риском подразумевают возможные колебания доходности от инвестиций. Такой риск называют полным риском. Его можно разложить на две составляющие:

Несистематический риск — колебания доходности, определяемые свойствами самой инвестиции, и не связанные с общими изменениями на рынке. Например, компания выводит на рынок новый продукт, и мы пока не знаем, будет ли он успешным.
Систематический риск — риск, связанный с колебаниями всего рынка, определяемый зависимостью успешности компании или проекта от общего состояния экономики и отрасли. Например, продажи и прибыль всех компаний одновременно оказываются подвержены влиянию экономического кризиса.

В инвестиционном анализе часто игнорируют индивидуальный, несистематический риск, так как в большом инвестиционном портфеле эти колебания доходности у разных акций не зависят друг от друга и компенсируют друг друга за счет диверсификации. С другой стороны, систематический риск нельзя диверсифицировать, так как множество компаний под его действием изменяют свою доходность синхронно. На этой концепции основана модель CAPM и вычисление рисковой премии через бету. Тогда премия за риск будет равна:

где ERP — премия фондового рынка (Equity Risk Premium, ее также иногда называют MRP, Market Risk Premium),

β – бета, показатель систематического риска акции

Rm — доходность рынка акций, рассчитанная на основе рыночного индекса.

Обратите внимание, что в этом случае премией за риск мы называем всю дополнительную доходность сверх безрисковой ставки. Но одновременно мы можем вычислить и премию за риск конкретной акции относительно ставки, применяемой для рыночного индекса: Rm × (β-1). Таким образом, премия за риск — относительное понятие, и она может рассчитываться от разной базы.

Риск ликвидности

Премия за риск не всегда добавляется в связи с более высоким уровнем колебаний доходности. Риски инвестора могут не иметь готового измерения в форме потенциальных прибылей и убытков. Один из факторов, которые могут влиять на риск, — ликвидность, то есть возможность быстро продать акции и выйти из инвестиции. Сравните два варианта:

Инвестиция 1 — покупка пакета акций публичной компании. Такие акции могут быть проданы по их текущей рыночной цене в течение одного рабочего дня.
Инвестиция 2 — строительство уникальной производственной установки. Вполне возможно, что ее вообще нельзя будет продать, так как не каждый сможет использовать ее. В результате, вне зависимости от планов инвестора, он будет владеть ею до тех пор, пока она будет зарабатывать ожидаемый доход. На возврат инвестиций потребуются годы.

Очевидно, что если ожидаемые доходы от акций публичной компании будут равны ожидаемым доходам от второго варианта, наиболее удобным решением будет первое. Чтобы отразить эту разницу, в ставку дисконтирования вводят премию за низкую ликвидность.

Математического правила для расчета премии за ликвидность нет, но на практике она может находиться в пределах от 1% до 5%.

Другие методы учета премии за риск

По сути, все модели и методы для расчета ставки дисконтирования, сводятся к тому, как рассчитать разные компоненты премий за риск. Кроме упомянутой модели CAPM встречается, также, применение таких методов:

Модель Фама-Френча добавляет в CAPM два новых фактора в дополнение к доходности рыночного индекса: SMB — Small Minus Big и HML — High Minus Low.

Теория арбитражного ценообразования (Arbitrage Pricing Theory, APT) идет дальше и выдвигает гипотезу, что параметров может быть не один, как в CAPM, и не три, как в модели Фама-Френча, а произвольное количество.

Модель Build-Up использует подход, противоположный тому, что предлагается в моделях Фама-Френча или APT. Вместо того, чтобы сложным образом вычислять ставку дисконтирования на основе регрессии, статистики и сложных математических вычислений, аналитику предлагается вычислить ставку дисконтирования для похожей крупной компании, а потом «надстроить» (отсюда и название метода, build up — надстраивать) к ней дополнительные премии, опираясь на свой опыт.

Подробнее об этих методах рассказано в статье Ставка дисконтирования для акционерного капитала

Такие статьи мы публикуем регулярно. Чтобы получать информацию о новых материалах, а также быть в курсе учебных программ, вы можете подписаться на новостную рассылку.

Если вам необходимо отработать определенные навыки в области инвестиционного или финансового анализа и планирования, посмотрите программы наших семинаров.

Источник

Менеджмент • 15 сентября 2022 • 5 мин чтения

Угроза или возможность: как работать с рисками в проектах

В бизнесе важно не бояться форс-мажоров, а уметь ими управлять. Для этого нужно собрать и проанализировать все риски, а потом выстроить стратегию работы с ними. Рассказываем, как это сделать.

Что такое риски в проекте
Зачем управлять рисками
Основные виды рисков
Оценка рисков проекта
Стратегии управления рисками
Этапы управления рисками
Как составить план по управлению рисками
Совет эксперта

Что такое риски в проекте

Менеджер проектов может написать идеальный план работы, но в 99% случаев что-то пойдёт не так: подведёт подрядчик, смежный отдел провалит сроки или во время переговоров с клиентами во всём районе выключится свет. Риск — это событие с долей неопределённости, которая может сказаться на проекте отрицательно или положительно, привести к возникновению угроз для проекта или появлению возможностей. Риски бывают негативными и позитивными.

❌ Негативный риск
Компания «Бурёнка» производит молочные продукты в Рязани и продаёт их в центральной России. «Бурёнка» заключила контракт с сетью продовольственных магазинов в Новосибирске, но в первую же отгрузку логистическая компания не предоставила машину, запасного варианта не было, и пришлось заплатить штраф 500 000 рублей за невыполнение обязательств по контракту.

✅ Позитивный риск
Локальный бренд одежды запланировал выпустить несколько моделей пуховиков. Когда покупали ткань, оказалось, что фабрика сделает скидку и себестоимость каждого изделия снизится на 10%.

Негативный риск — это не проблема, а только её вероятность. Если компания его учитывает, то сможет скорректировать действия, когда риск приведёт к проблеме.

Риск: «Бурёнка» первый раз работает с логистической компанией, поэтому есть риск, что будут проблемы с доставкой.

Проблема: компания сорвёт сроки поставки, сеть магазинов выставит штрафы и прекратит сотрудничество.

Решение: договориться с другими логистами, которые работают со срочными заказами и могут быстро предоставить машину.

Маршрут построен: что такое дорожная карта проекта и зачем она нужна

Зачем управлять рисками

Рисками учатся управлять для того, чтобы не только снижать их вероятность, но и принимать последствия. Какими бывают цели управления рисками проекта:

● Снизить финансовые потери. В примере с «Бурёнкой» заплатить за машину по двойному тарифу обойдётся дешевле, чем оплачивать штраф.

● Не затягивать сроки проекта. Например, компания планирует выпустить приложение до Нового года. Менеджер проектов знает, что в предновогоднюю пору очень много заказов, команда разработчиков перегружена и, скорее всего, не успеет выполнить свою часть работы, поэтому нанимает проектных работников и делегирует им часть задач, с целью управления рисками.

● Оправдывать доверие клиентов. Если подрядчик постоянно срывает сроки или выходит за рамки бюджета, он создаёт ненужные финансовые риски, и с ним вряд ли продолжат работать.

● Снизить уровень стресса в команде. Сотрудники меньше переживают, когда знают, что риск может наступить, и у них есть чёткие инструкции, как справиться с его последствиями.

● Использовать риски как возможности. Если учитывать не только негативные, но и положительные риски, у компании появится больше возможностей для развития. Например, с июля 2022 года, чтобы попасть на футбольный матч, нужно оформить паспорт болельщика. Для билетных сервисов это событие стало рисковым: отлаженная система продаж могла зависнуть, а болельщики потеряли бы возможность купить билеты на сайте. Те, кто взяли этот риск в работу и перенастроили свою платформу, теперь выгодно выделяются среди конкурентов.

На курсе «Менеджер проектов» студенты учатся применять алгоритмы управления рисками на практических задачах. Наставники курса — действующие менеджеры проектов, которые делятся своим опытом и помогают выбрать правильную стратегию.

Зарабатывайте, управляя проектами

Освойте профессию с нуля за 6 месяцев, научитесь вести переговоры и строить отношения с клиентами. Пройдите бесплатную вводную часть курса «Менеджер проектов», чтобы попробовать себя в новой роли.

Основные виды рисков

По причинам риски бизнес-процессов можно разделить на внутренние и внешние:

● Внутренние риски проекта зависят от компании, сотрудников, процессов или оборудования. Например, компания по производству детской мебели «Деревяшки» закупила новое оборудование, которое дешевле в обслуживании. Руководство выиграло тендер по обустройству детских садов в одном из городов России, и теперь есть риск, что новое оборудование не выдержит такую большую нагрузку и выйдет из строя.

● Внешние риски могут возникнуть по причинам, не зависящим от компании: погода, новые законы, стихийные бедствия. Например, частной школе или вузу стоит учитывать риск, что осенью количество заболевших COVID-19 увеличится. Значит, придётся переходить на онлайн-обучение, обеспечить педагогов ноутбуками и гарнитурами, подготовить аккаунты на платформах для конференций или создать собственную LMS-систему.

По возможным последствиям риски бывают:

● Временные
Последствия этих рисков приведут к нарушению сроков проекта. Например, бренд детской одежды планирует к сентябрю выпустить новую коллекцию школьной формы. Если запланировать основной пошив моделей на лето, есть риск, что произойдёт задержка по срокам из-за того, что многие швеи и закройщики уйдут в отпуск.

● Бюджетные
Такие финансовые риски грозят увеличением проектной сметы. К примеру, компания-застройщик может не вписаться в запланированный бюджет, если курс доллара вырастет и это приведёт к повышению стоимости сырья.

● Риски объёмов работ
Они влияют на трудочасы команды или отдельных сотрудников. Допустим, команда дизайнеров готовит айдентику для ресторана при сыроварне, у которой несколько учредителей, и все хотят участвовать в выборе логотипа. Есть риск, что согласование дизайна может затянуться и замечаний будет больше.

● Риски взаимодействия или зависимости
Возникают, когда один этап проекта зависит от окончания другого. Например, компания «Бурёнка» планирует запустить в продажу новое обезжиренное молоко. Уже подписали договор с торговой сетью. Если дизайнер уйдёт в отпуск, он не успеет подготовить новую этикетку, чтобы её выпустили к дате отгрузки.

По размеру возможных потерь виды рисков проекта делятся на три вида:

● Допустимые
Это значит, что если риск перерастёт в проблему, то потери не превысят размер прибыли. Например, если компания не успеет закупить сырьё по старым ценам, а новые вырастут максимум на 5%, это не сильно отразится на размере выручки.

● Критические
Могут привести к потере выручки или вложенных в проект денег. Например, если курьер не успеет привезти партию праздничных тортов к назначенной дате, товары не примут, продукты испортятся, их придётся утилизировать, и кондитерская понесёт убытки.

● Катастрофические
Могут привести к последствиям, которые обанкротят компанию,будут угрожать жизни и здоровью людей, влиять на экологию. Пример последствий катастрофического риска — авария на Чернобыльской АЭС. Сотрудники станции предполагали, что реактор не справится с нагрузкой, но не предприняли действий, чтобы избежать этого риска.

Оценка рисков проекта

Анализ рисков проекта происходит по двум направлениям: качественному и количественному. В качественном анализе рисков описывают:

● что может произойти;

● когда;

● что это повлечёт за собой;

● какова вероятность такого риска.

Качественный анализ показывает, какому риску стоит уделить внимание в первую очередь, какой с большей вероятностью приведёт к максимальным затратам

Пример таблицы качественного анализа из свода знаний по управлению проектами PMBOK

Методы качественного анализа риска проекта:

● Метод экспертных оценок
Он основан на мнении людей с опытом в данном проекте. Такой анализ можно провести в формате мозгового штурма или используя метод Дельфи, суть которого в опросе группы независимых экспертов. Опрос должен быть анонимным, чтобы на мнения не влияли личные взаимоотношения или должности участников.

● SWOT-анализ
Это анализ сильных сторон (англ. strengths), слабых сторон (англ. weaknesses), возможностей (англ. opportunities) и угроз (англ. threats).

Например, оператор мобильной связи планирует запустить новую услугу — голосового помощника. Команда проводит анализ рисков бизнес-процессов и определяет, что сильные стороны проекта — это алгоритм, который обучит робота отвечать на вопросы клиентов из разных сфер услуг: от салонов красоты до университетов. Слабые стороны в том, что обучать помощника долго и для этого нужны записи разговоров клиентов. Возможности новой услуги — расширение аудитории и привлечение новых клиентов. Угрозы — это стереотипы, что голосовые роботы говорят сухо, по шаблону и раздражают клиентов.

● Спираль рисков
Спираль показывает ранжирование рисков в зависимости от степени их вероятности и влияния на проект. Чем больше цифры, тем выше риск. Например, риск того, что менеджер уйдёт в отпуск, минимальный и не повлечёт серьёзных последствий. А если логистическая компания не успеет найти достаточное количество машин к нужной дате, это уже критический риск.

Каждому риску присваивают оценку в зависимости от вероятности и тяжести последствий

Количественный анализ определяет, сколько денег или времени компания потеряет, если риск наступит. Этот анализ проводят после качественного и учитывают риски с высокой вероятностью и значительными последствиями. Например, если компания-застройщик сдаст квартиру с ремонтом ненадлежащего качества, то покупатели смогут обратиться в суд и потребовать компенсацию от 500 000 рублей. Если в доме 200 квартир, то финансовые потери компании составят более 100 миллионов рублей.

Качественный и количественный анализы помогут разделить риски на три группы:

1. Риски с высокой степенью вероятности и влияния.
От них нужно защититься в первую очередь.

2. Риски с высокой вероятностью и низким влиянием или с низкой вероятностью, но высоким влиянием.
Достаточно держать под контролем.

3. Риски с низкой вероятностью и низким влиянием.
Учитывать, но не тратить время и силы на предотвращение.

Стратегии управления рисками

Управление рисками проекта — это не просто алгоритм действий, а постоянный анализ и принятие решений, поиск баланса между затратами на то, чтобы избежать рисков, и стоимостью их последствий. Разберём четыре основных метода управления негативными рисками проекта:

1. Уклонение — способ избежать риска, изменив ход реализации проекта.

Риск: автомобильный завод закупил новое оборудование, чтобы выпустить большую партию деталей. Технологи ещё не разобрались в новом оборудовании, из-за этого выпуск деталей может задержаться.

Решение: отложить использование нового оборудования и закончить заказ на старом.

2. Принятие подходит, если риск не влечёт за собой тяжёлых последствий, но имеет высокую или среднюю вероятность. Риск учитывают, но ничего не предпринимают для снижения или устранения. Метод принятия используют, когда:

● невозможно исключить все риски из проекта;

● последствия риска некритичны;

● затраты на снижение риска превышают вероятные потери.

Принятие бывает пассивным и активным. В первом случае компания принимает риск и ничего не делает, а во втором для устранения вероятных последствий риска создают резерв ресурсов, например денежных.

Риск: школа иностранных языков хочет запустить новый онлайн-курс по испанскому для взрослых. Методист ещё не закончил предыдущий проект и, скорее всего, не успеет выполнить свою часть работы к поставленным срокам, поэтому их придётся сдвигать.

Решение: у школы нет задачи выпустить курс побыстрее. Важно уложиться в бюджет и не привлекать сторонние ресурсы. Поэтому риск принимают и начинают работу по другим направлениям, чтобы минимизировать задержку.

3. Снижение — это метод управления рисками, направленный на уменьшение их вероятности или негативных последствий.

В отличие от стратегии уклонения, здесь меры по снижению риска принимаются до его наступления, но ход проекта не меняется. После принятия мер вероятность риска или его последствия снижаются

Риск: на швейную фабрику поставили новое оборудование. Руководители цеха боятся, что оно может дать сбой или выйти из строя.

Решение: провести дополнительные испытания, выделить опытную группу специалистов, которые проверят оборудование на практике.

4. Передача рисков подразумевает, что их негативные последствия берёт на себя третья сторона. Например, компания может справляться с финансовыми рисками с помощью страхования, условий договора или гарантийных обязательств.

С помощью внешних источников компания снимает с себя нагрузку, связанную с предотвращением риска и работой с последствиями

Риск: строительная компания на начальном этапе не может точно назвать сроки, объёмы работ и количество материалов. Если нужно будет докупать материалы по новым ценам, можно не вписаться в смету.

Решение: риск повышения стоимости материалов принимает на себя заказчик.

Для позитивных рисков стратегии другие:

● Использование позитивных рисков — это поиск возможностей. Например, если привлечь сильного специалиста, проект будет сдан раньше срока и сотрудники получат премию за перевыполнение KPI. Менеджер проекта принимает решение использовать этот риск и выносит на обсуждение идею о найме дополнительного сотрудника.

● Совместное использование — это объединение компаний, предприятий, создание партнёрств, чтобы они могли вместе реагировать на позитивные риски. Например, книжный магазин приглашает известного писателя провести мастер-класс. Чтобы привлечь больше посетителей, они решают провести совместную акцию с университетом, предоставив студентам скидки.

● Усиление повышает вероятность, что позитивный риск возникнет, и увеличивает его положительное влияние на проект. Например, если сеть производителей молочных продуктов «Кормилица» подпишет контракт с компанией «Бурёнка», то они смогут увеличить объём выпускаемой продукции и снизить затраты на логистику. Чтобы усилить этот риск, менеджер едет на переговоры с руководством сети.

Этапы управления рисками

Нужно вести внутреннюю документацию и фиксировать всю работу над рисками, чтобы другие сотрудники могли посмотреть, с какими проблемами сталкивались команды раньше

Процесс управления рисками проекта можно разделить на шесть этапов:

1. Выявление рисков проекта.
Для выявления рисков проводят мозговой штурм и обсуждают возможные форс-мажоры. Если команда большая, менеджеру лучше разделить участников на группы и провести совещание в формате «мирового кафе» — когда небольшая группа людей обсуждает задачу в непринуждённой обстановке. Чтобы не упустить из виду серьёзный риск и не потратить все силы на снижение несущественного, менеджеру проекта надо применять критическое мышление.

2. Оценка рисков реализации проекта.
Делается с помощью качественного или количественного анализа.

3. Составление плана управления рисками проекта.
Команда подбирает стратегию к каждому риску: уклонению, принятию, снижению или передаче.

4. Реагирование на риски согласно плану.

5. Мониторинг рисков.
Команда отслеживает выполнение плана и возникновение новых рисков, влияние рисков на проект и результаты, которых добились. Бывает, что уклонение от одного риска провоцирует другой. Поэтому менеджер должен постоянно отслеживать работу по проекту и вносить корректировки.

6. Описание возникших рисков.
Помогает в работе со следующими проектами и упрощает работу менеджера.

Как составить план по управлению рисками

План по управлению рисками — это документ, который ещё называют картой риска. Формат плана может быть любой: от таблицы Excel до онлайн-доски для совместной работы, например Confluence. Составлять план начинают после качественного и количественного анализов рисков и заносят туда последовательность действий, которые команда будет предпринимать в зависимости от выбранной стратегии.

В карте риска обязательно должны быть:

● Ответственный
За оценку, контроль и управление конкретным риском. Например, молодой команде разработчиков не хватает опыта, чтобы быстро выполнить объём работы для запуска нового мобильного приложения. Менеджер проекта видит риск не успеть вовремя и назначает ответственного — старшего разработчика, который будет следить за скоростью выполнения задач и отвечать за соблюдение сроков.

● Стратегия
Для каждого риска выбирают и заносят в карту стратегию: уклонение, принятие, снижение или передачу. В примере менеджер проекта понял, что затягивать сроки выпуска нового приложения нельзя, поэтому выбрал метод снижения риска.

● Воздействие на риск
Конкретные методы работы с риском бизнес-процессов или проектов. Методом может быть любое действие, которое снизит вероятность риска или последствий: например, привлечение опытного наставника, дополнительных сотрудников, распределение нагрузки между командами.

● Стоимость воздействия
Эксперты оценивают, во сколько обойдётся снижение рисков. Можно сразу прописывать примерную сумму затрат на работу с рисками, а можно использовать градацию: высокая, средняя или низкая.

Карта помогает увидеть решения по работе с каждым риском и оценить бюджет

● Документы
Они нужны, чтобы регламентировать процессы управления риском. Например, в одной компании над выявлением рисков проектов может работать только один ответственный, а в другой по регламенту должна быть команда из 15 человек.

● Вероятность и последствия
Эксперты оценивают их по специальной шкале. Ими могут быть сотрудники, которые работают над проектом. Например, в образовательном проекте это учителя, кураторы или методисты, а в автомобильной компании — инженеры и технологи.

Для каждого проекта создаётся шкала, которая помогает быстро ранжировать риски. Ответственный определяет значения последствий и вероятности наступления рисков и вносит данные в матрицу.

Например, риски, которые получили коэффициент от 1 до 5, относятся к группе с низкими вероятностью и влиянием. От 5 до 20 — низкая вероятность и высокое влияние или высокая вероятность и низкое влияние. От 20 до 30 — высокие вероятность и влияние. Красным цветом выделены риски, которые могут привести к значительным последствиям, с ними нужно работать в первую очередь. Жёлтым обозначены риски, требующие внимания, но не срочно, а зелёным — те, которые можно принять

● Оценка риска
Чтобы оценить риск, нужно умножить коэффициент вероятности на коэффициент последствия, которые определили эксперты.

Когда карта рисков заполнена, менеджер видит целостную картину и может объективно принимать решение, с какими рисками нужно работать, а какие — принять

Совет эксперта

Роман Голайдо
«Бороться с рисками бессмысленно — ими надо управлять. Для этого можно использовать методику, которая описана в статье, и сочетать разные методы снижения риска. Если не заниматься управлением рисками, это приведёт к срыву проекта и отрицательно скажется на репутации специалиста и компании. Помните, что в управлении рисками важно находить баланс между последствиями и стоимостью работы».

Преподаватель на курсе «Управление командами», performance leader

Agile: что это такое и где используется, принципы методологии

Методологии управления проектами

Источник

Разновидности риска

Метод VAR

Общие свойства[править | править код]

Методы измерения[править | править код]

Непараметрические методы[править | править код]

Исторический метод[править | править код]

Бутстрэппинг[править | править код]

Непараметрическая оценка плотности распределения[править | править код]

Взвешенные исторические подходы[править | править код]

Историческое моделирование, взвешенное по возрасту[править | править код]

Историческое моделирование, взвешенное по волатильности[править | править код]

Историческое моделирование, взвешенное по корреляции[править | править код]

Фильтрованное историческое моделирование[править | править код]

Параметрические методы[править | править код]

Параметрический метод для изолированного актива[править | править код]

Параметрический метод для многокомпонентного портфеля (вариационно-ковариационный)[править | править код]

VaR в теории экстремальных значений[править | править код]

Метод Монте-Карло[править | править код]

Ожидаемые потери (Expected Shortfall)[править | править код]

Маппинг VaR[править | править код]

Инструменты с фиксированной доходностью[править | править код]

Форварды[править | править код]

FRA[править | править код]

Процентные свопы[править | править код]

Опционы[править | править код]

VaR в оценке риска ликвидности[править | править код]

Ретроспективное тестирование[править | править код]

Безусловная валидация[править | править код]

Условная валидация[править | править код]

Регуляторные требования[править | править код]

Базель I 1996a[править | править код]

Базель II[править | править код]

Базель II.5[править | править код]

VaR в портфельной оптимизации[править | править код]

VaR в управлении рисками[править | править код]

Примечания[править | править код]

Литература[править | править код]

Что такое премия за риск

Полный риск и систематический риск

Риск ликвидности

Другие методы учета премии за риск

Угроза или возможность: как работать с рисками в проектах

Что такое риски в проекте

Зачем управлять рисками

Основные виды рисков

Оценка рисков проекта

Стратегии управления рисками

Этапы управления рисками

Как составить план по управлению рисками

Совет эксперта

Вам также может понравиться

Как составить таблицу расчета перевозок

Клубная музыка как найти

Как найти улицу марата

Добавить комментарий Отменить ответ