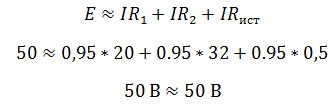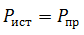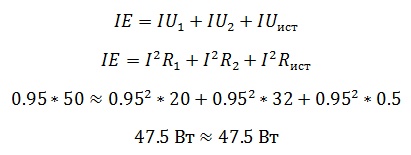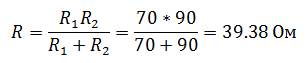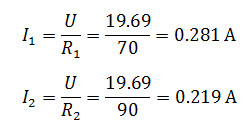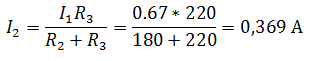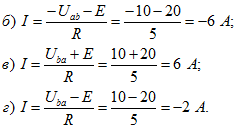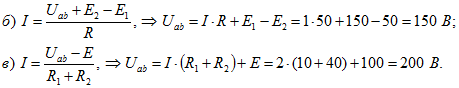Главная
→
Примеры решения задач ТОЭ
→
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Основные положения и соотношения
1. Источники электрической энергии
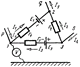
Реальный источник электрической энергии можно изобразить двояко: а) в виде генератора напряжения, который характеризуется э.д.с. Е, численно равной напряжению холостого хода источника, и включенной последовательно с сопротивлением r0 (рис. 1, а), б) в виде генератора тока, который характеризуется током Iк, численно равным току короткого замыкания реального источника, и параллельно соединенной проводимостью g0 (рис. 1, б).
Переход от генератора напряжения к эквивалентному генератору тока осуществляется по формулам
I к = E r 0 , g 0 = 1 r 0 , (1)
а обратный переход от генератора тока к эквивалентному генератору напряжения по следующим формулам
E= I к g 0 , r 0 = 1 g 0 . (2)
У идеального генератора напряжения внутреннее сопротивление равно нулю, тогда как у идеального генератора тока внутренняя проводимость равна нулю.
2. Закон Ома
Закон Ома применяется для ветви или для одноконтурной замкнутой цепи (не имеющей разветвлений).
Для написания закона Ома следует прежде всего выбрать произвольно некоторое положительное направление для тока.
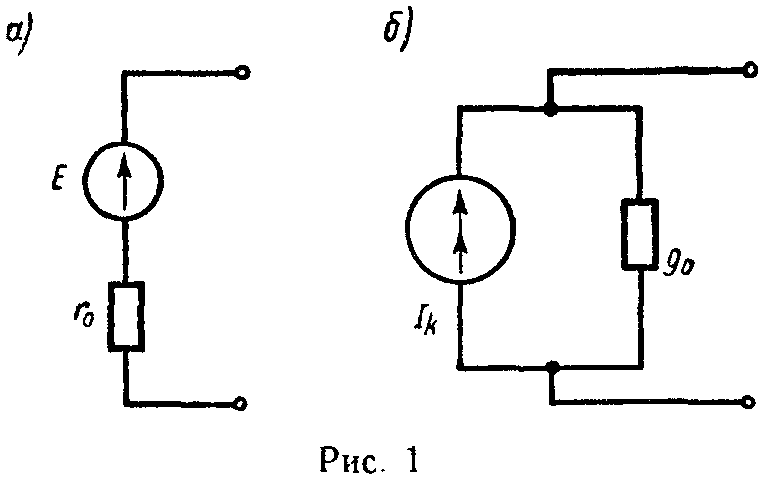
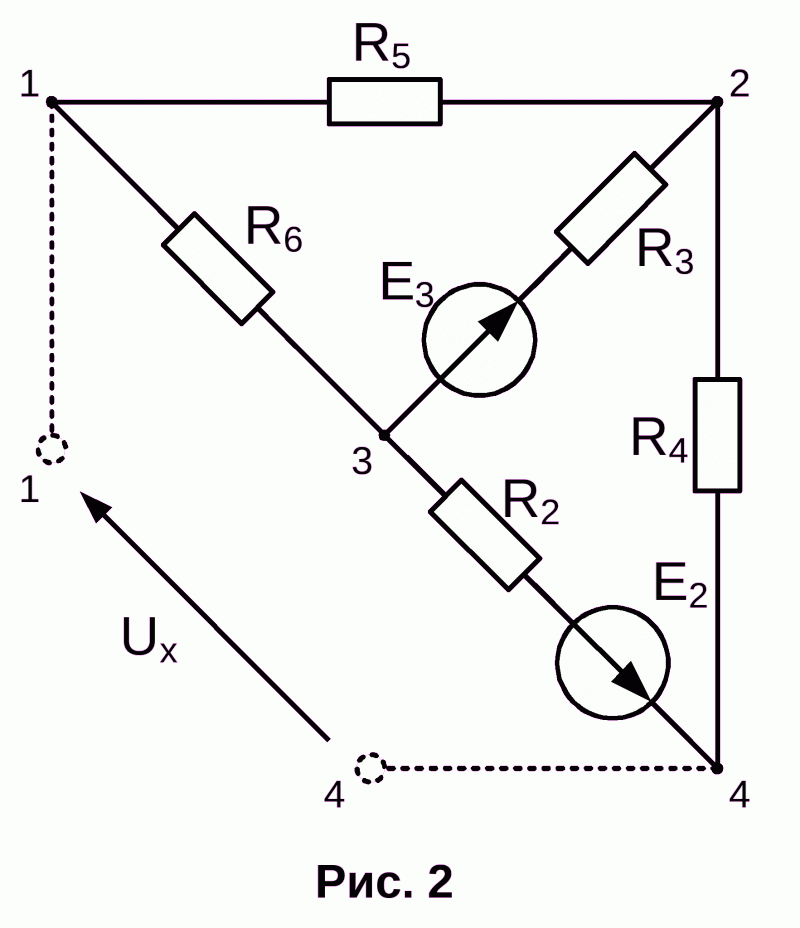
а) Для ветви, состоящей только из сопротивлений и не содержащей э.д.с. (например, для ветви mn на рис. 2), при положительном направлении для тока от точки m к точке n ток равен
I= φ m − φ n r mn = U mn r mn . (3)
Здесь φm и φn — потенциалы точек m и n, Umn = φm — φn — разность потенциалов или напряжение между точками m и n, rmn = r4 + r5 — полное сопротивление ветви между точками m и n.
Пример — в задаче 17.
б) Для замкнутой одноконтурной цепи
I= ΣE Σr , (4)
где Σr — арифметическая сумма всех внешних и внутренних сопротивлений цепи, ΣE — алгебраическая сумма ее электродвижущих сил.
Со знаком плюс берут те э.д.с., направления которых совпадают с выбранным положительным направлением для тока, и со знаком минус — э.д.с. с противоположными направлениями.
Примеры — в задачах 15 и 17.
в) Для ветви, содержащей э.д.с. и сопротивления (например, для ветви acb на рис. 2),
I 1 = φ a − φ b +ΣE Σ r ab = U ab + E 1 − E 2 r 1 + r 2 + r 9 , (5)
где Uab = φa — φb — напряжение на концах ветви acb, отсчитываемое по выбранному положительному направлению тока, ΣE — алгебраическая сумма э.д.с., находящихся в этой ветви, а Σr — арифметическая сумма ее сопротивлений.
Формулу (5) называют обобщенным законом Ома.
Примеры — в задачах 15 и 17.
3. Законы Кирхгофа
Для написания законов Кирхгофа следует прежде всего задаться положительными направлениями для токов в каждой ветви.
Первый закон Кирхгофа
∑ k=1 n I k =0, (6)
Алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю. Токи, притекающие к узлу, условно принимаются положительными, а вытекающие из него — отрицательными (или наоборот).
Второй закон Кирхгофа
∑ k=1 n I k ⋅ r k = ∑ k=1 n E k . (7)
Алгебраическая сумма падений напряжений любого замкнутого контура равна алгебраической сумме э.д.с. в нем.
Направление обхода контура выбирается произвольно. При записи левой части равенства со знаком плюс берутся падения напряжения в тех ветвях, в которых положительное направление тока совпадает с направлением обхода (независимо от направления э.д.с. в этих ветвях), и со знаком минус — падения напряжения в тех ветвях, в которых положительное направление, тока противоположно направлению обхода. При записи правой части равенства э.д.с., направления которых совпадают с выбранным направлением обхода (независимо от направления тока, протекающего через них), принимаются положительными, а э.д.с., направленные против выбранного направления обхода, принимаются отрицательными.
Пример — в задаче 29.
Распределение напряжений при последовательном соединении двух сопротивлений (см. рис. 2)
I 1 = U 1 r 1 = U 2 r 2 = U r 1 + r 2 ,
U 1 =U⋅ r 1 r 1 + r 2 , U 2 =U⋅ r 2 r 1 + r 2 . (8)
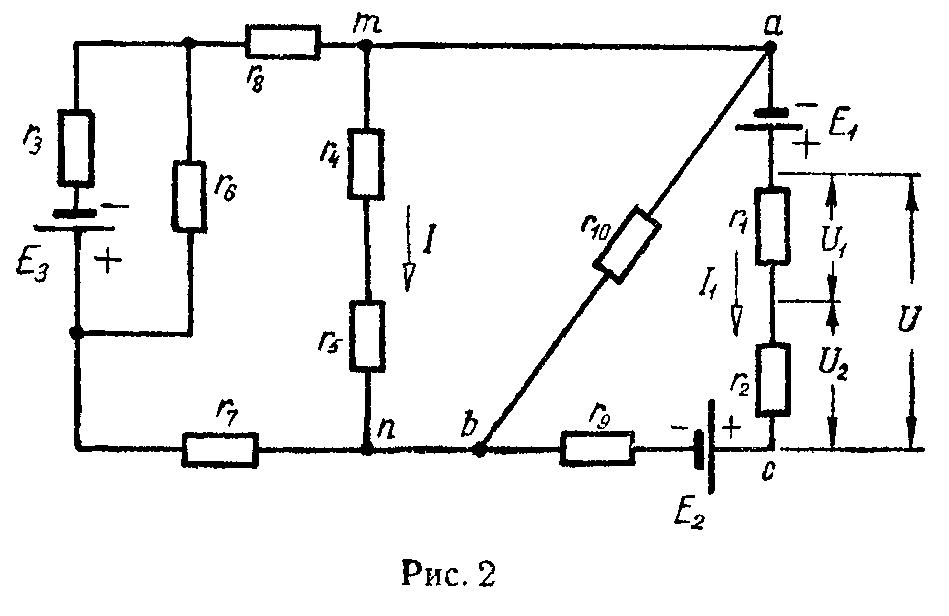
Распределение токов в двух параллельных ветвях — формула разброса токов или формула делителя токов (рис. 3)
U 2 = U 3 = U 2,3 , I 2 ⋅ r 2 = I 3 ⋅ r 3 = I 1 ⋅ r 2,3 = I 1 ⋅ r 2 ⋅ r 3 r 2 + r 3 ,
I 2 = I 1 ⋅ r 3 r 2 + r 3 , I 3 = I 1 ⋅ r 2 r 2 + r 3 . (9)
Распределение напряжений при последовательном соединении n сопротивлений
U k =U⋅ r k ∑ k=1 n r k .
Распределение токов в n параллельных ветвях
I k =I⋅ g k ∑ k=1 n g k .
4. Методы расчета сложных цепей постоянного тока
Пусть электрическая цепь состоит из p ветвей и имеет q узлов.
Применение законов Кирхгофа
Прежде всего, устанавливается число неизвестных токов, которое равно числу ветвей (p). Для каждой ветви задаются положительным направлением для тока.
Число n1 независимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов без единицы
n1 = q – 1.
Число n2 независимых уравнений, составляемых по второму закону Кирхгофа, равно числу ячеек (контуров)
n2 = p — q + 1.
Общее число уравнений n, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов
n = n1 + n2 = p.
Решение этой системы уравнений дает значения искомых токов.
Пример — в задаче 29.
Метод контурных токов (МКТ, Максвелла).
Число n независимых контуров цепи равно числу уравнений по второму закону Кирхгофа
n = n2 = p — q + 1.
Расчет цепи методом контурных токов, состоящей из n независимых контуров, сводится к решению системы из n уравнений, составляемых для контурных токов I11, I22, …, Inn; ток в каждой ветви находится как алгебраическая сумма контурных токов, обтекающих эту ветвь.
Выбор направлений контурных токов произволен. Каждая из ветвей сложной электрической цепи должна войти хотя бы в один контур.
Система уравнений МКТ для n контурных токов имеет вид
{ r 11 ⋅ I 11 + r 12 ⋅ I 22 +…+ r 1n ⋅ I nn = E 11 ; r 21 ⋅ I 11 + r 22 ⋅ I 22 +…+ r 2n ⋅ I nn = E 22 ; ………………………………………………. r n1 ⋅ I 11 + r n2 ⋅ I 22 +…+ r nn ⋅ I nn = E nn . (10)
Здесь rkk — собственное сопротивление контура k (сумма сопротивлений всех ветвей, входящих в контур k), rkl — общее сопротивление контуров k и l, причем rkl = rlk; если направления контурных токов в ветви, общей для контуров k и l, совпадают, то rkl положительно (rkl > 0), в противном случае rkl — отрицательно (rkl < 0); Ekk — алгебраическая сумма э.д.с., включенных в ветви, образующие контур k.
Пример — в задаче 41.
Метод узловых потенциалов (МУП)
Число n независимых узлов цепи равно числу уравнений по первому закону Кирхгофа
n = n1 = q — 1.
Для определения потенциалов всех узлов электрической схемы, имеющей q узлов, следует принять потенциал одного из узлов равным нулю, а для определения потенциалов остальных n = q — 1 узлов составляется следующая система уравнений
{ φ 1 ⋅ g 11 + φ 2 ⋅ g 12 +…+ φ n ⋅ g 1n = ∑ 1 Eg ; φ 1 ⋅ g 21 + φ 2 ⋅ g 22 +…+ φ n ⋅ g 2n = ∑ 2 Eg ; ……………………………………………….. φ 1 ⋅ g n1 + φ 2 ⋅ g n2 +…+ φ n ⋅ g nn = ∑ n Eg . (11)
Здесь gss — сумма проводимостей ветвей, присоединенных к узлу s; gsq — сумма проводимостей, соединяющих узел s с узлом q; – алгебраическая сумма произведений э.д.с. ветвей, примыкающих к узлу s, на их проводимости (т.е. токов короткого замыкания этих ветвей); при этом со знаком плюс берутся те из произведений Eg, в ветвях которых э.д.с. действуют в направлении узла s, и со знаком минус — в направлении от узла.
Определив потенциалы узлов, находят токи в ветвях посредством закона Ома.
Этим методом рекомендуется пользоваться в тех случаях, когда число уравнений здесь будет меньше числа уравнений, составленных по методу контурных токов.
Примеры — в задачах 44 и 45.
Метод наложения
Ток в любой ветви может быть рассчитан как алгебраическая сумма токов, вызываемых в ней каждой э.д.с. в отдельности. При этом надо иметь в виду, что когда ведется расчет для какой-либо одной действующей э.д.с., то вместо остальных источников должны быть включены сопротивления, равные внутренним сопротивлениям этих источников.
Примеры — в задачах 47 и 49.
Метод эквивалентных преобразований
Во всех случаях применения метода эквивалентных преобразований замена одних схем другими, им эквивалентными, не должна привести к изменению токов или напряжений на участках цепи, не подвергшихся преобразованию.
1) Замена последовательных сопротивлений одним эквивалентным. Сопротивления последовательны, если они обтекаются одним и тем же током. Например, на схеме цепи, изображенной на рис. 2, сопротивления r1, r2 и r9 соединены последовательно; так же последовательны сопротивления r7 и r8.
Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных участков, равно сумме этих сопротивлений этих участков
r э = r 1 + r 2 +…+ r n = ∑ k=1 n r k . (12)
2) Замена параллельных сопротивлений одним эквивалентным. Сопротивления параллельны, если все они присоединены к одной паре узлов. Например (рис. 2), сопротивления r45 = r4 + r5 и r10 параллельны.
Эквивалентная проводимость цепи, состоящей из n параллельно соединенных ветвей равна сумме этих проводимостей этих ветвей. Эквивалентное сопротивление такой цепи находится как величина обратная эквивалентной проводимости этой цепи
1 r э = 1 r 1 + 1 r 2 +…+ 1 r n = ∑ k=1 n 1 r k . (13)
В частном случае параллельного соединения двух сопротивлений r1 и r2 эквивалентное сопротивление
r э = r 1 ⋅ r 2 r 1 + r 2 . (14)
3) Замена смешанного соединения сопротивлений одним эквивалентным. Смешанное соединение — это сочетание последовательного и параллельного соединения сопротивлений. Например, сопротивления r1, r2 и r3 (рис. 3) находятся в смешанном соединении. Их эквивалентное сопротивление равно
r э = r 1 + r 2,3 = r 1 + r 2 ⋅ r 3 r 2 + r 3 . (15)
При смешанном соединении сопротивлений токи ветвей цепи (рис. 3):
по закону Ома
I 1 = U r э , (16)
по формуле разброса токов (делителя токов)
I 2 = I 1 ⋅ r 3 r 2 + r 3 , I 3 = I 1 ⋅ r 2 r 2 + r 3 .
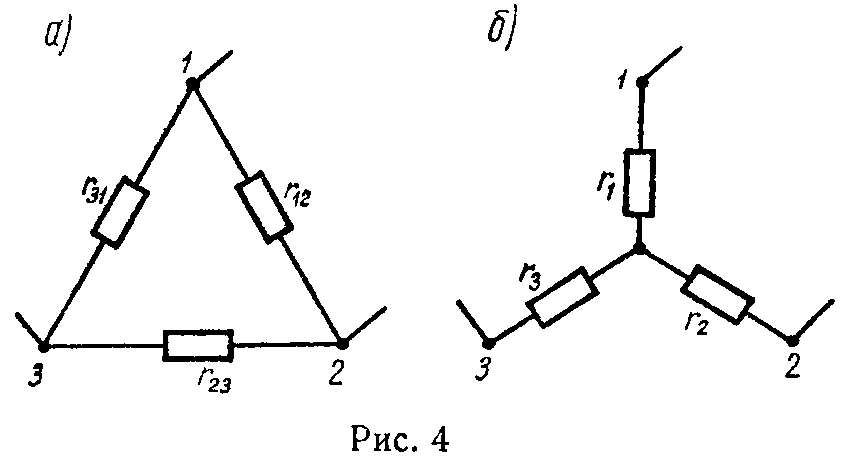
4) Формулы преобразования треугольника сопротивлений (рис. 4, а) в эквивалентную звезду сопротивлений (рис. 4, б) и наоборот имеют вид
{ r 1 = r 12 ⋅ r 31 r 12 + r 23 + r 31 ; r 2 = r 23 ⋅ r 12 r 12 + r 23 + r 31 ; r 3 = r 31 ⋅ r 23 r 12 + r 23 + r 31 , (17)
{ g 12 = g 1 ⋅ g 2 g 1 + g 2 + g 3 ; g 23 = g 2 ⋅ g 3 g 1 + g 2 + g 3 ; g 31 = g 3 ⋅ g 1 g 1 + g 2 + g 3 , (18)
где g — проводимость соответствующей ветви.
Формулы (18) можно записать через сопротивления так
r 12 = r 1 + r 2 + r 1 ⋅ r 2 r 3 ; r 23 = r 2 + r 3 + r 2 ⋅ r 3 r 1 ; r 31 = r 3 + r 1 + r 3 ⋅ r 1 r 2 . (19)
Пример — в задаче 51.
Метод эквивалентного генератора напряжения (метод холостого хода и короткого замыкания или метод активного двухполюсника)
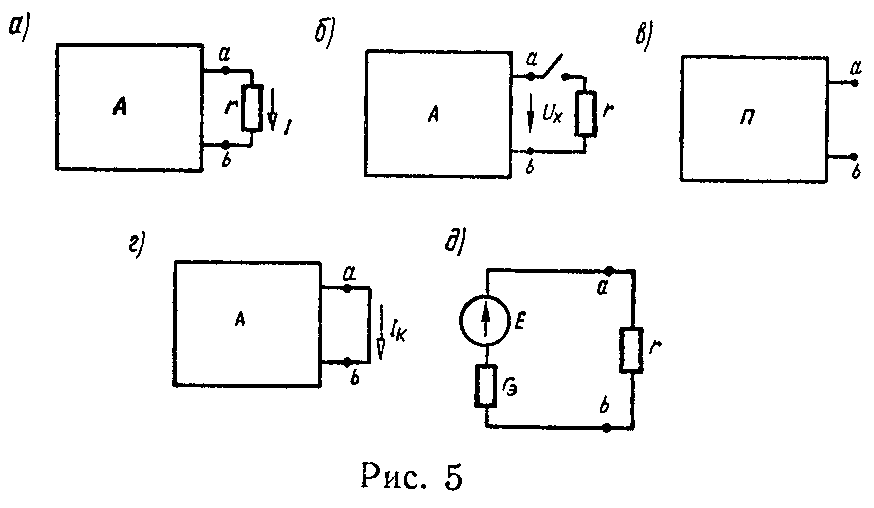
Для нахождения тока I в ветви ab, сопротивление которой r (рис. 5, а, буква А на рисунке обозначает активный двухполюсник), надо разомкнуть эту ветвь и при этом найти (любым способом) разность потенциалов на зажимах разомкнутой ветви — Uх (рис. 5, б). Затем надо вычислить сопротивление короткого замыкания rк, равное эквивалентному сопротивлению всей остальной цепи, вычисленному в предположении, что в ней отсутствуют э.д.с. (при этом внутренние сопротивления источников сохраняются) и что она питается от постороннего источника, присоединенного непосредственно к зажимам a и b (рис. 5, в; буква П на рисунке обозначает пассивный двухполюсник).
Сопротивление rк может быть вычислено либо непосредственно по схеме рис. 5, в, либо из соотношения
r к = U х I к , (20)
где Iк — ток короткого замыкания, протекающий по ветви ab, если ее сопротивление r сделать равным нулю (рис. 5, г).
Заданная схема (рис. 5, а) может быть заменена эквивалентным генератором напряжения с э.д.с. E = Uх и внутренним сопротивлением rэ = rк, присоединенным к зажимам ab сопротивления r (рис. 5, д).
Ток в искомой ветви, имеющей сопротивление r, определяется из формулы закона Ома
I= U х r+ r к . (21)
Примеры — в задачах 55 и 56.
Метод эквивалентного генератора тока
В предыдущем пункте показано, как в любой сложной цепи можно получить эквивалентный генератор напряжения с э.д.с. E и внутренним сопротивлением rк. Этот генератор напряжения (рис. 5, д) на основании формул (1) может быть заменен эквивалентным генератором тока (рис. 1, б) по формулам
I к = U х r к , g 0 = 1 r к . (22)
где Iк — ток эквивалентного генератора тока, равный току короткого замыкания в той ветви, по отношению к которой производится эквивалентное преобразование всей остальной части цепи, g0 — внутренняя проводимость, равная эквивалентной проводимости всей остальной цепи между зажимами ab, к которым присоединен приемник энергии, в предположении, что э.д.с. всех генераторов равны нулю.
Пример — в задаче 65.
Метод замены нескольких параллельных генераторов напряжения одним эквивалентным
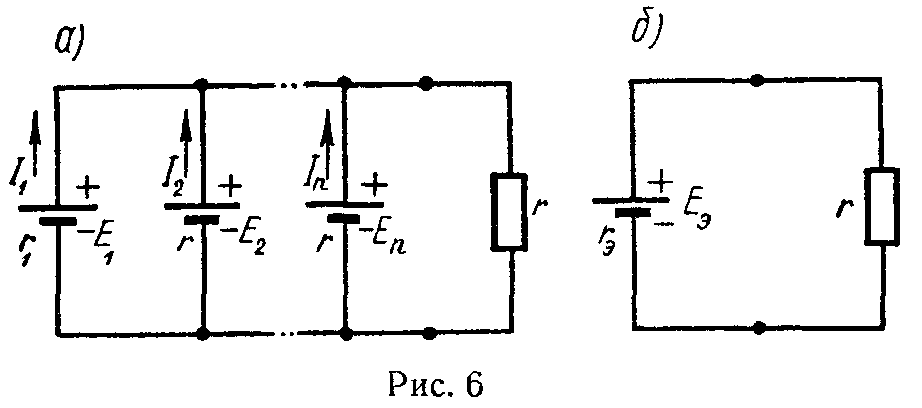
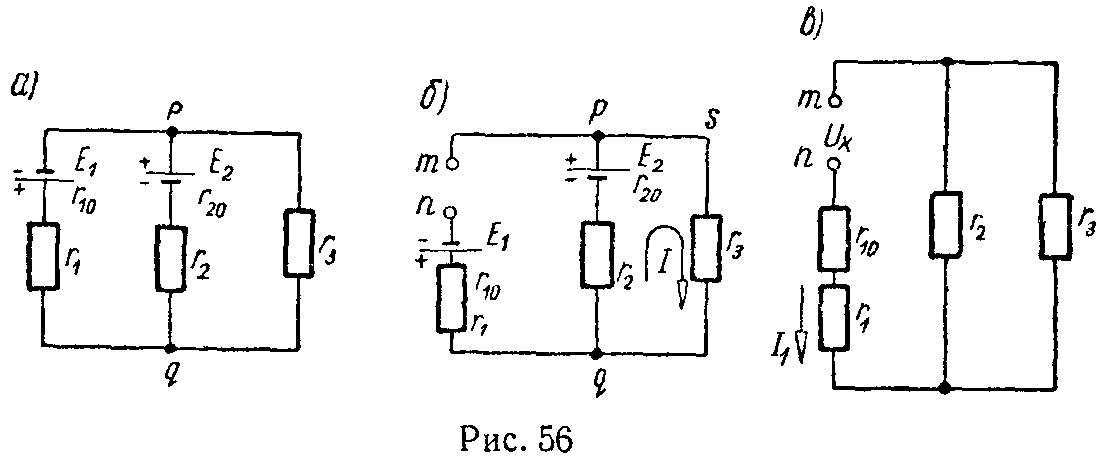
Если имеется несколько генераторов напряжения с э.д.с. E1, E2, …, En и внутренними сопротивлениями r1, r2, …, rn, работающие параллельно на общее сопротивление нагрузки r (рис. 6, а), то они могут быть заменены одним эквивалентным генератором напряжений, э.д.с. которого Eэ, а внутреннее сопротивление rэ (рис. 6, б),
при этом
{ E э = ∑ k=1 n E k g k ∑ k=1 n g k ; 1 r э = 1 r 1 + 1 r 2 +…+ 1 r n ; g k = 1 r k . (23)
Ток в сопротивлении r определится по формуле
I= E э r+ r э . (24)
Ток в каждой из ветвей находится по формуле
I k = E k −U r k , (25)
где U = I·r.
Пример — в задаче 60.
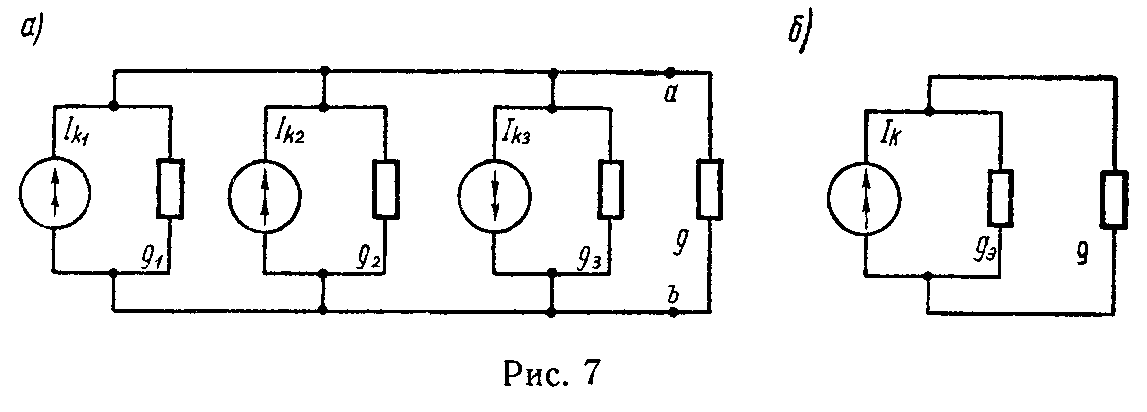
Метод замены параллельно соединенных генераторов тока одним эквивалентным
Если несколько генераторов тока с токами Ik1, Ik2, …, Ikn и внутренними проводимостями g1, g2, …, gn соединены параллельно (рис. 7, а) и работают на общий приемник энергии с проводимостью g то они могут быть заменены одним эквивалентным генератором тока (рис. 7, б), ток которого Ik равен алгебраической сумме токов, а его внутренняя проводимость равна сумме внутренних проводимостей отдельных генераторов
I k = I k1 + I k2 − I k3 +…= ∑ m=1 n I km , (26)
g э = g 1 + g 2 + g 3 +…= ∑ m=1 n g m . (27)
5. Принцип взаимности
Принцип взаимности гласит: если э.д.с. E, находящаяся в ветви ab сколь угодно сложной цепи, вызывает ток в другой ветви cd этой же цепи, то при переносе этой э.д.с. в ветвь cd она вызовет в ветви ab такой же ток I.
6. Принцип компенсации
Принцип компенсации: любое сопротивление в электрической цепи может без изменения распределения токов в ее ветвях быть заменено э.д.с., численно равной падению напряжения в заменяемом сопротивлении и направленной навстречу току.
7. Входное сопротивление цепи относительно ветви
Входное сопротивление цепи относительно ветви k определяется как отношение э.д.с. Ek, действующей в этой ветви, к току Ik в этой же ветви при э.д.с. в остальных ветвях равных нулю
r kk = E k I k . (28)
Входная проводимость ветви k — величина обратная входному сопротивлению этой ветви
g kk = 1 r kk . (29)
Взаимное сопротивление (передаточное сопротивление) ветвей k и l — отношение э.д.с. Ek, действующей в ветви k, к току Il, проходящему по ветви l при э.д.с. в остальных ветвях равных нулю
r kl = E k I l . (30)
Взаимная проводимость ветвей k и l — величина обратная взаимному сопротивлению тех же ветвей
g kl = 1 r kl . (31)
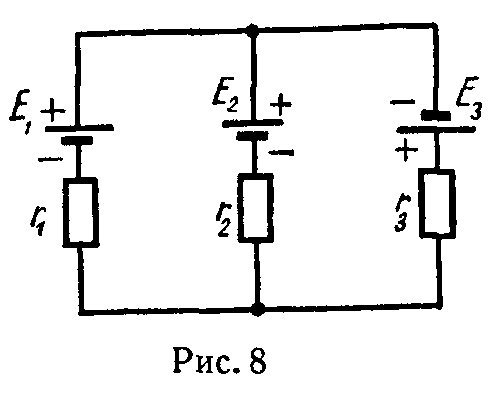
Пример. Для схемы рис. 8 входные сопротивления цепи относительно ветвей 1, 2 и 3 соответственно равны
r 11 = D r 2 + r 3 , r 22 = D r 1 + r 3 , r 33 = D r 1 + r 2 ,
а взаимные сопротивления ветвей 1 и 2, 2 и 3, 3 и 1 соответственно равны
r 12 = r 21 = D r 3 , r 23 = r 32 = D r 1 , r 13 = r 31 = D r 2 ,
где D = r1·r2 + r1·r3 + r2·r3.
8. Баланс мощностей
Для любой замкнутой электрической цепи сумма мощностей, развиваемых источниками электрической энергии, равна сумме мощностей, расходуемых в приемниках энергии
ΣPист = ΣPпотреб, или ΣEI = ΣI2r (32)
где ΣEI — алгебраическая сумма; здесь положительны те из слагаемых, для которых направления действия э.д.с. E и соответствующего тока I совпадают, в противном случае слагаемое отрицательно (при выборе положительных направлений токов в ветвях с э.д.с. выбираем направление тока совпадающим с действием соответствующей э.д.с.); ΣI2r — арифметическая сумма; здесь должны быть учтены как внешние сопротивления, так и сопротивления самих источников энергии.
Упражнения и задачи
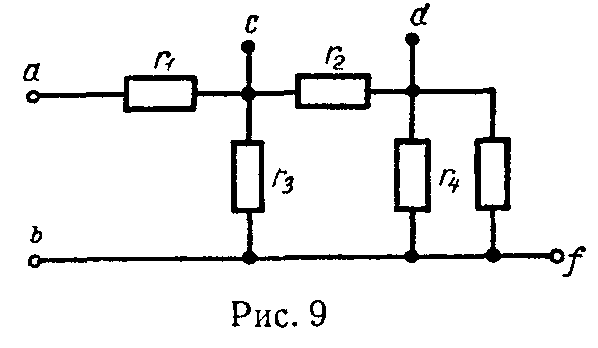
Задача 1. Для цепи (рис. 9) найти эквивалентные сопротивления между зажимами a и b, c и d, d и f, если r1 = 6 Ом, r2 = 5 Ом. r3 = 15 Ом, r4 = 30 Ом, r5 = 6 Ом.
Решение
Расчет сопротивления rab.
Эквивалентное сопротивление соединенных параллельно сопротивлений r4 и r5 найдем по формуле (14)
r 45 = r 4 ⋅ r 5 r 4 + r 5 = 30⋅6 30+6 =5 Ом;
оно соединено последовательно с r2; их общее сопротивление
r’ = r2 + r45 = 5 + 5 = 10 Ом.
Сопротивление цепи состоит из сопротивления r1, последовательно с которым соединены два параллельных сопротивления r’ и r3
r ab = r 1 + r ′ ⋅ r 3 r ′ + r 3 =6+ 10⋅15 10+15 =12 Ом.
Расчет сопротивления rcd.
Сопротивления r4 и r5 теперь соединены параллельно друг другу; сопротивление r3 к ним включено последовательно
r ″ = r 3 + r 4 ⋅ r 5 r 4 + r 5 =15+ 30⋅6 30+6 =20 Ом.
Сопротивление rcd состоит из двух параллельно соединенных сопротивлений r2 и r» и равно
r cd = r 2 ⋅ r ″ r 2 + r ″ = 5⋅20 5+20 =4 Ом.
Расчет сопротивления rdf.
Эквивалентное сопротивление цепи между точками d и f состоит из трех параллельно соединенных сопротивлений: r5, r4 и r2 + r3 и может быть определено по формуле (13)
1 r df = 1 r 5 + 1 r 4 + 1 r 2 + r 3 = 1 6 + 1 30 + 1 20 = 1 4 ,
откуда rdf. = 4 ом.
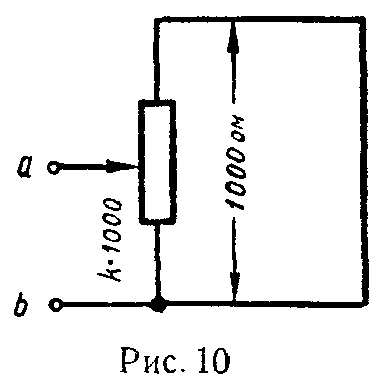
Задача 2. Для цепи (рис. 10) начертить кривую зависимости эквивалентного сопротивления между точками a и b как функцию от k (0 ≤ k ≤ 10).
Ответ: при k = 0 и k = 1 rab = 0; при k = 0,5 rabмакс = 250 Ом.
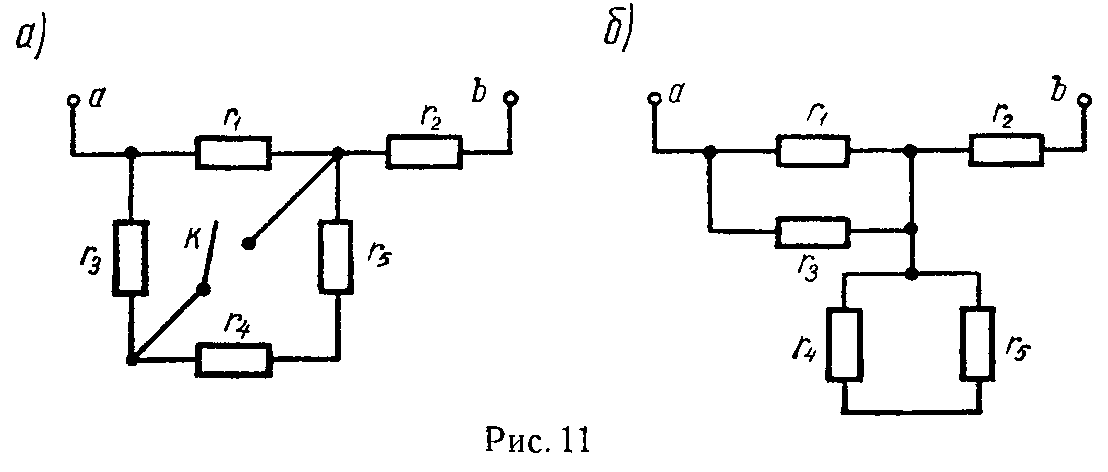
Задача 3. Цепь, схема которой изображена на рис. 11, а, состоит из пяти одинаковых сопротивлений r1 = r2 = r3 = r4 = r5 = 10 кОм.
Чему равно сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К?
Решение
Ключ разомкнут.
Сопротивления r3, r4 и r5 соединены между собой последовательно; заменяющее их эквивалентное сопротивление является параллельным к сопротивлению r1; величина сопротивления, заменяющего r3, r4, r5 и r1, равна
r ′ = r 1 ⋅ ( r 3 + r 4 + r 5 ) r 1 + ( r 3 + r 4 + r 5 ) = 10⋅30 40 =7,5 кОм.
Искомое сопротивление цепи
rab = r’ + r2 = 7,5 + 10 = 17,5 кОм.
Ключ замкнут.
В этом случае сопротивления r1 и r3 соединены параллельно друг другу, а сопротивления r4 и r5 закорочены (рис. 11, б). Искомое сопротивление цепи будет
r ab = r 1 ⋅ r 3 r 1 + r 3 + r 2 = 10⋅10 20 +10=15 кОм.
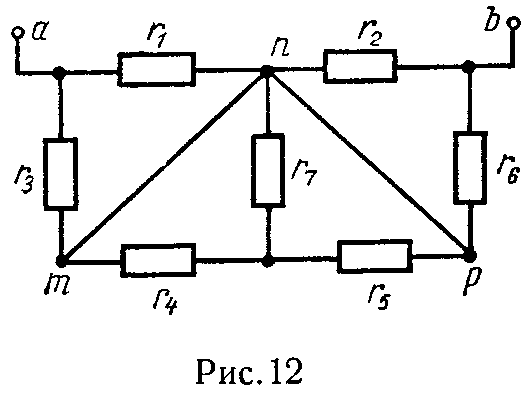
Задача 4. Вычислить эквивалентное сопротивление цепи (рис. 12) между зажимами a и b, если все семь ее сопротивлений одинаковы:
Указание. Обратить внимание на закорачивающие проводники mn и np.
Ответ: 10 Ом.
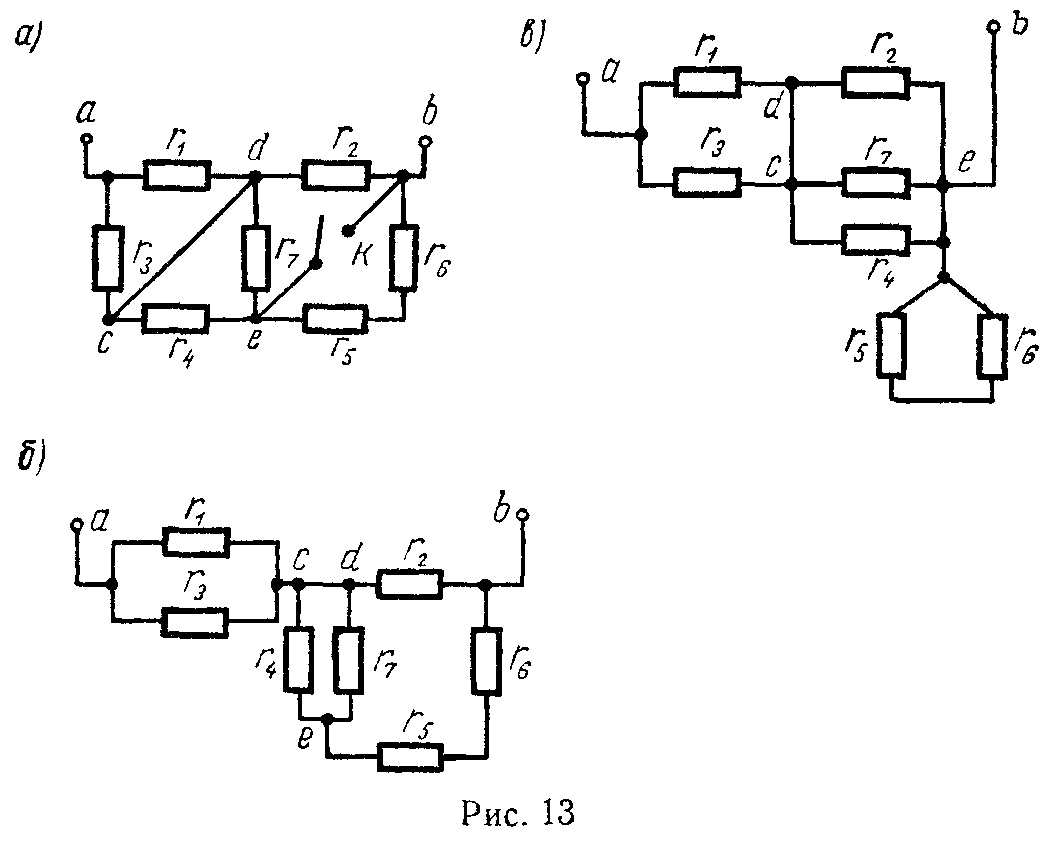
Задача 5. Определить эквивалентное сопротивление цепи между точками a и b при разомкнутом и замкнутом ключе К (рис. 13, а): r1 = r2 = r3 = r4 = r5 = r6 = r7 = 10 Ом.
Решение
При разомкнутом ключе заданная схема может быть изображена согласно рис. 13, б.
Искомое сопротивление
r ab = r 1 ⋅ r 3 r 1 + r 3 = ( r 5 + r 6 + r 4 ⋅ r 7 r 4 + r 7 )⋅ r 2 r 5 + r 6 + r 4 ⋅ r 7 r 4 + r 7 + r 2 =5+ 25⋅10 35 =12,1 Ом.
При замкнутом ключе заданная схема имеет вид, изображенный на рис. 13, в.
Сопротивление цепи равно сумме двух сопротивлений
r ′ = r 1 ⋅ r 3 r 1 + r 3 10⋅10 20 =5 Ом,
и r”, определяемого из формулы
1 r ″ = 1 r 4 + 1 r 7 + 1 r 2 ,
откуда r’ = 3,33 Ом. Таким образом,
r ab = r ′ + r ″ =5+3,33=8,33 Ом.
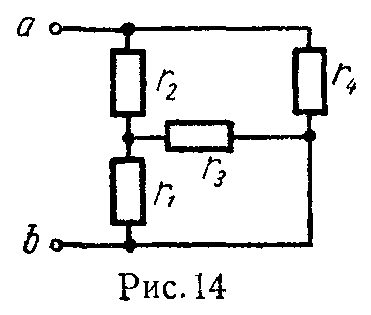
Задача 6. Найти эквивалентное сопротивление между зажимами a и b для схемы рис. 14. Даны: r1 = 600 Ом, r2 = 360 Ом, r3 = 400 Ом, r4 = 300 Ом.
Ответ: 200 Ом.
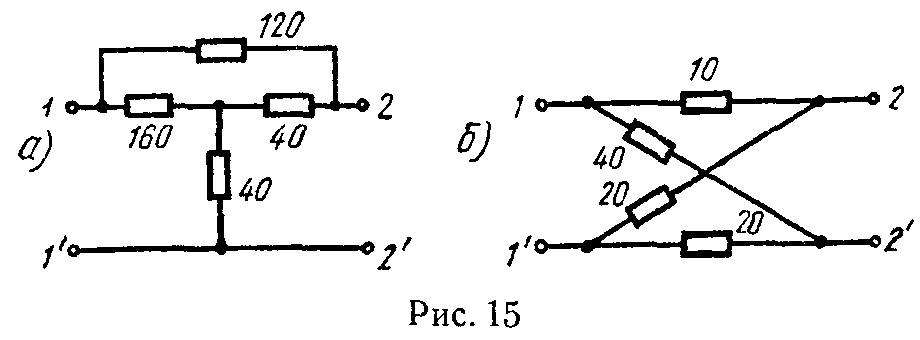
Задача 7. Определить сопротивление каждой из цепей (рис. 15, а и б) между зажимами 1–1′ при холостом ходе (точки 2 и 2′ разомкнуты) и при коротком замыкании (точки 2 и 2′ закорочены). Сопротивления в омах даны на схеме.
Ответ: а) r1х = 120 Ом, r1к = 72 Ом; б) r1х = 20 Ом, r1к = 18 Ом.
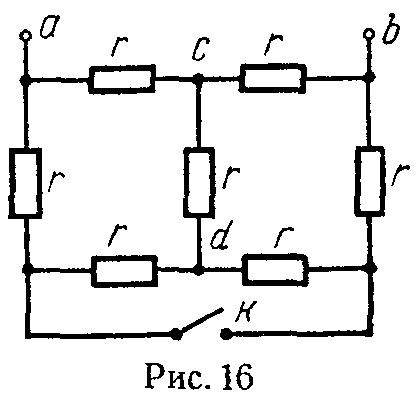
Задача 8. Вычислить сопротивление между зажимами a и b для схемы рис. 16 при разомкнутом и замкнутом ключе К. Все семь сопротивлений одинаковы и каждое равно r = 30 Ом.
Указание. Учесть, что точки c и d равнопотенциальны.
Ответ: При разомкнутом ключе rab = 40 Ом; при замкнутом — rab = 30 Ом.
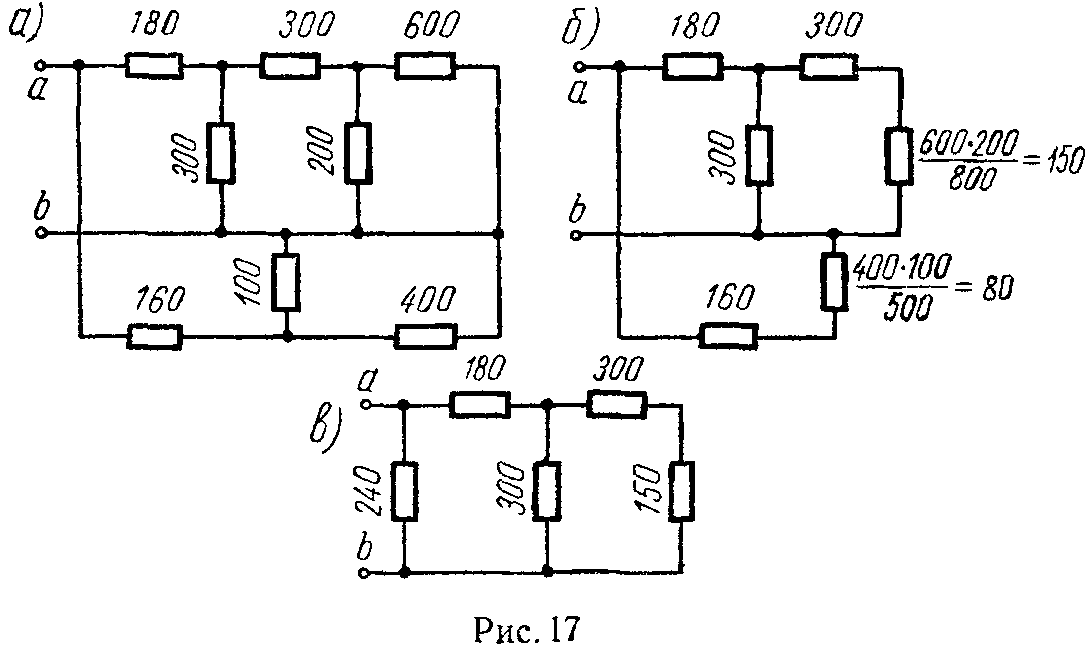
Задача 9. Найти сопротивление между зажимами a и b для схемы рис. 17, а. Значения сопротивлений в омах даны на схеме.
Решение
От данной схемы можно перейти к более простым схемам, изображенным на рис. 17, б и в. Искомое сопротивление
r ab = 240⋅ ( 180+ 300⋅450 750 ) 240+180+ 300⋅450 750 =144 Ом.
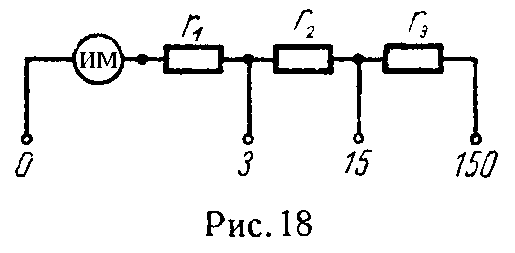
Задача 10. Имеется вольтметр, который может быть включен па три предела измерения: 3; 15 и 150 В (рис. 18). Максимально допустимый ток в измерительном механизме 30 мА.
Найти сопротивления r1, r2 и r3.
Решение
Полагаем внутреннее сопротивление измерительного механизма (ИМ) равным нулю.
На пределе измерения 3 В: ток 30 мА, сопротивление r1 = 3/0,030 = 100 Ом.
На пределе измерения 15 В: ток 30 мА, сопротивление r1 + r2 = 15/0,030 = 500 Ом, а сопротивление r2 = 500 — 100 = 400 Ом.
Аналогично находится r3 = 4500 Ом.
Задача 11. Два вольтметра, пределы измерения которых равны 150 и 100 В и внутренние сопротивления — 15000 и 7500 Ом, соединенные последовательно друг с другом и с добавочным сопротивлением 2500 Ом, подключены к сети 220 В. Чему равно показание каждого вольтметра?
Ответ: 132 и 66 В.
Задача 12. Батарея, э.д.с. которой E = 6,4 В и внутреннее сопротивление r0 = 0,1 Ом, присоединена к сопротивлению r = 3,1 Ом. Найти ток батареи и напряжение на ее зажимах.
Решение
Применяя формулу закона Ома для замкнутой цепи (формула 4), находим ток
I= E r+ r 0 = 6,1 3,1+0,1 =2 А.
Напряжение на зажимах батареи может быть найдено двумя путями: или
U = E — I·r0 = 6,4 — 2·0,1 = 6,2 В,
или
U = I·r = 2·3,1 = 6,2 В.
Задача 13. Напряжение холостого хода батареи равно 16,4 В. Чему равно внутреннее сопротивление батареи, если при токе во внешней цепи, равном 8 А, напряжение на ее зажимах равно 15,2 В?
Ответ: 0,15 Ом.
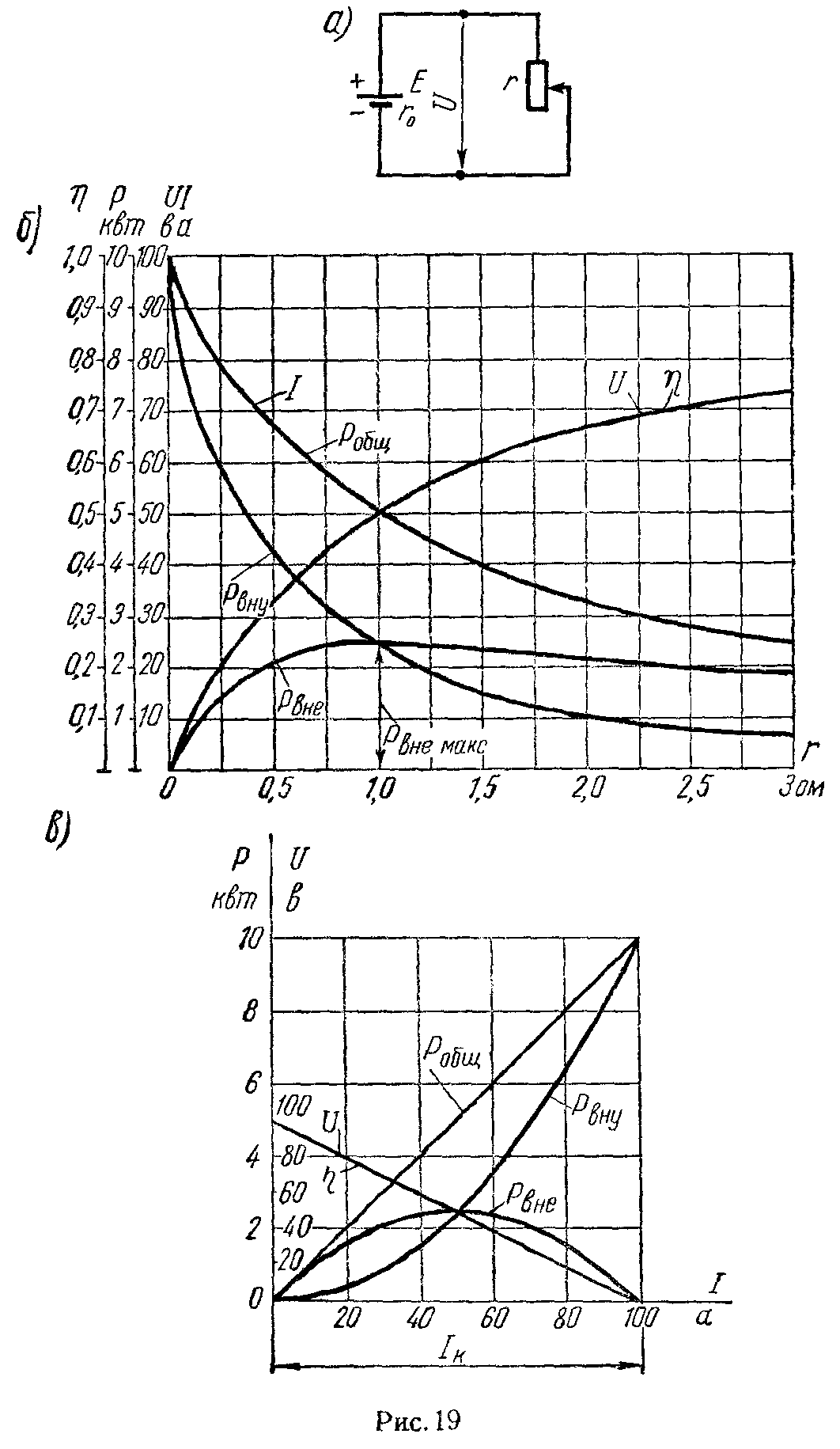
Задача 14. Источник с э.д.с. E = 100 В, внутренним сопротивлением r0 = 1 Ом замкнут на внешнее сопротивление r, которое меняется от нуля до бесконечности (рис. 19, а). Определить в функции этого сопротивления: 1) ток I; 2) напряжение на зажимах источника U; 3) мощность, отдаваемую источником во внешнюю цепь Pвнеш; 4) мощность, затрачиваемую в самом источнике Pвнутр; 5) общую мощность Pобщ; 6) коэффициент полезного действия η. При каком внешнем сопротивлении Pвнеш будет максимальным? Чему оно равно?
Построить кривые I = F1 (r), U = F2 (r), Pвнеш = F3 (r), Pвнутр = F4 (r), Pобщ = F5 (r), η = F6 (r).
Написать уравнения и построить кривые зависимостей U, Pвнеш, Pвнутр, Pобщ и η в функции тока I.
Решение
1)
I= E r+ r 0 = 100 r+1 ;
2)
I=I⋅r= E⋅r r+ r 0 = 100⋅r r+1 ;
3)
P внеш = I 2 ⋅r= E 2 ⋅r ( r+ r 0 ) 2 = 10000⋅r ( r+1 ) 2 ;
4)
P внутр = I 2 ⋅ r 0 = E 2 ⋅ r 0 ( r+ r 0 ) 2 = 10000 ( r+1 ) 2 ;
5)
P общ = I 2 ⋅ ( r+ r 0 )= E 2 ( r+ r 0 ) = 10000 r+1 ;
6)
η= P внеш P общ = r r+ r 0 = r r+1 .
Определим r, при котором Pвнеш будет максимально. Для этого вычислим производную от Pвнеш по r и приравняем ее нулю
d P внеш dr = E 2 d dr r ( r+ r 0 ) 2 = E 2 d dr r⋅ ( r+ r 0 ) 2 −r⋅ d dr ( r+ r 0 ) 2 ( r+ r 0 ) 4 = = E 2 ( r+ r 0 ) 2 −r⋅2 ( r+ r 0 ) ( r+ r 0 ) 4 = E 2 r 0 −r ( r+ r 0 ) 3 =0.
Взяв вторую производную, можно убедиться, что она отрицательна. Это соответствует условию максимума.
Отсюда найдем, что r = r0, т.е. при внешнем сопротивлении равном внутреннему сопротивлению, мощность, поступающая во внешнюю цепь, будет максимальна. При этом, по уравнению (6), коэффициент полезного действия равен 0,5. Величина максимальной мощности, поступающей во внешнюю цепь при r = r0, по уравнению (3) равна
P внеш.макс = [ E 2 ⋅r ( r+ r 0 ) 2 ] r= r 0 = E 2 4r =2500 Вт.
По написанным выше уравнениям на рис. 19, б построены кривые.
Искомые уравнения зависимостей в функции тока имеют вид
U=E−I⋅ r 0 ; P внеш =E⋅I− I 2 ⋅ r 0 ; P внутр = I 2 ⋅ r 0 ; P общ =E⋅I; η=1− I⋅ r 0 E .
По этим уравнениям на рис. 19, в построены кривые.
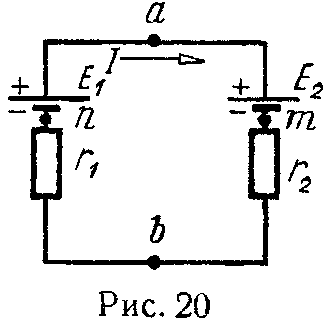
Задача 15. В схеме (рис. 20) э.д.с. E1 = 120 В, E2 = 40 В, а сопротивления r1 = 12 Ом, r2 = 8 Ом. Внутренние сопротивления источников энергии равны нулю. Определить напряжение между точками a и b.
Решение
Задавшись положительным направлением тока по часовой стрелке, на основании закона Ома (формула 4) имеем
I= E 1 − E 2 r 1 + r 2 = 120−40 12+8 =4 А.
Так как результат оказался положительным, то, следовательно, фактическое направление тока совпадает с выбранным. Напряжение между точками a и b можно найти по закону Ома (формула 5), примененному к участку amb
I= U ab − E 2 r 2 ,
откуда
U ab = E 2 +I⋅ r 2 =40+4⋅8=72 В.
Такой же результат можно получить, если применить ту же формулу к участку bna
I= U ba + E 1 r 1 ,
откуда
U ba =I⋅ r 1 − E 1 =4⋅12−120=−72 В,
а, следовательно, Uab = 72 В.
Замечание. Следует запомнить, что если на участке цепи, содержащем э.д.с. и сопротивление, ток и э.д.с. совпадают по направлению, то напряжение на зажимах участка меньше э.д.с. на величину падения напряжения в сопротивлении участка, а если направление тока противоположно направлению э.д.с., то напряжение на зажимах участка больше э.д.с. на величину падения напряжения в рассматриваемом участке.
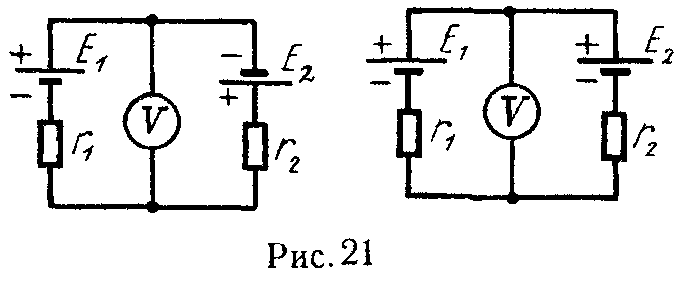
Задача 16. Определить показание вольтметра (рис. 21), сопротивление которого весьма велико по сравнению с r1 и r2.
Для обоих случаев даны: E1 = 40 В, E2 = 10 В, r1 = r2 = 5 Ом. Внутренними сопротивлениями источников энергии пренебречь.
Ответ: а) 15 В, б) 25 В.
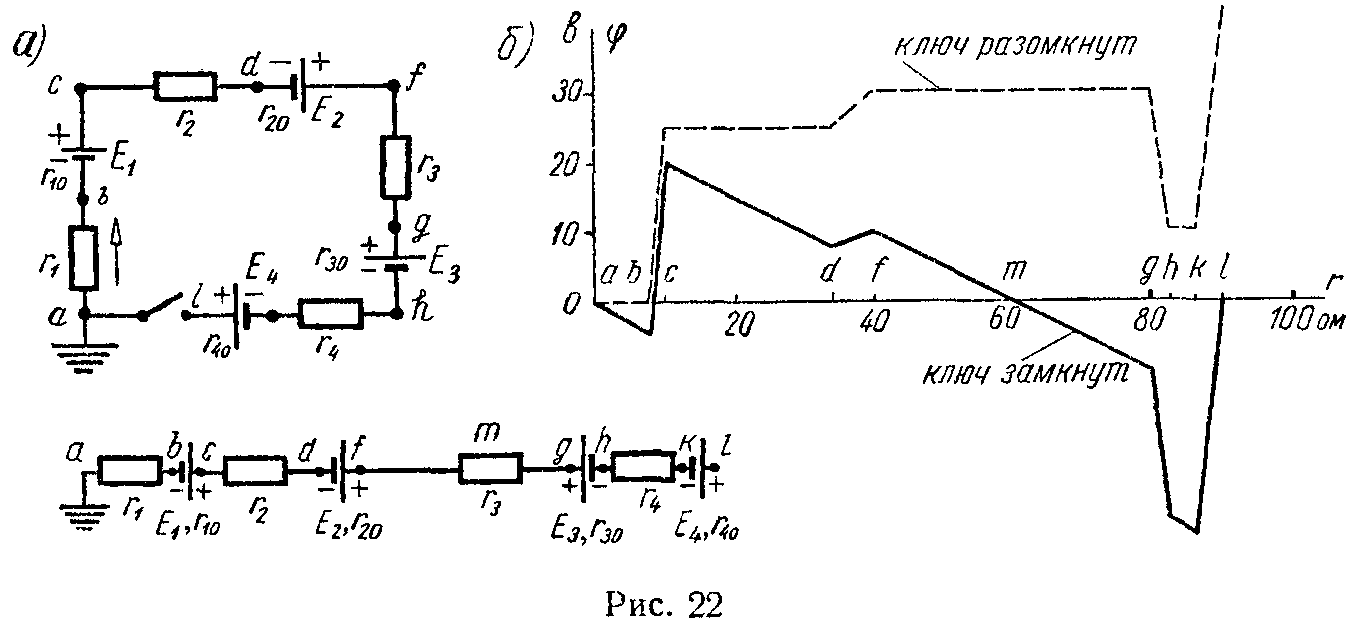
Задача 17. Построить график изменения потенциала вдоль цепи, изображенной на рис. 22, а, при замкнутом ключе и при разомкнутом ключе, предполагая в обоих случаях, что точка a заземлена (φa = 0).
В схеме найти точку, равнопотенцнальную точке a. Определить, потенциал какой точки следует принять равным нулю, чтобы потенциалы всех остальных точек были положительны (при замкнутом ключе).
Электродвижущие силы равны: E1 = 25 В, E2 = 5 В, E3 = 20 В, E4 = 35 В.
Внешние сопротивления имеют следующие значения: r1 = 8 Ом, r2 = 24 Ом, r3 = 40 Ом, r4 = 4 Ом. Внутренние сопротивления источников электрической энергии равны: r10 = 2 Ом, r20 = 6 Ом, r30 = 2 Ом, r40 = 4 Ом.
Решение
Ключ замкнут. Задавшись положительным направлением тока по часовой стрелке, на основании закона Ома (формула 4) найдем ток
I= E 1 + E 2 − E 3 + E 4 r 1 + r 10 + r 2 + r 20 + r 3 + r 30 + r 4 + r 40 = 45 90 =0,5 А.
Пользуясь формулами (3) и (5), вычислим потенциалы всех точек, обходя контур тока по часовой стрелке
φ a =0; φ b = φ a −I⋅ r 1 =0−0,5⋅8=−4 B; φ c = φ b + E 1 −I⋅ r 10 = ( −4 )+25−0,5⋅2=20 B; φ d = φ c −I⋅ r 2 =20−0,5⋅24=8 B; φ f = φ d + E 2 −I⋅ r 20 =8+5−0,5⋅6=10 B; φ g = φ f −I⋅ r 3 =10−0,5⋅40=−10 B; φ h = φ g − E 3 −I⋅ r 30 = ( −10 )−20−0,5⋅2=−31 B; φ k = φ h −I⋅ r 4 = ( −31 )−0,5⋅4=−33 B; φ a = φ k + E 4 −I⋅ r 40 = ( −33 )+35−0,5⋅4=0.
На рис. 22, б начерчен потенциальный график. По оси абсцисс отложены величины сопротивлений отдельных участков цепи, а по оси ординат — значения потенциалов в отдельных точках цепи.
Найдем точку, равнопотенциальную точке a. Из графика видно, что искомая точка m находится на участке сопротивления fg, так как в этой точке прямая падения потенциалов пересекает ось абсцисс, потенциал которой равен φa = 0. Обозначая участок сопротивления между точками f и m через rfm и применяя к участку abcdfm формулу закона Ома (5) и учитывая, что φa = φm, найдем
I= φ a − φ m + E 1 + E 2 r 1 + r 10 + r 2 + r 20 + r fm ,
или
0,5= 30 40+ r fm ,
откуда rfm = 20 Ом, т.е. точка m находится на середине сопротивления r3.
Для нахождения точки, потенциал которой следует принять равным нулю при условии, чтобы потенциалы всех остальных точек были положительны, следует обратиться к потенциальному графику, из которого видно, что такой точкой является точка k.
Ключ разомкнут. Тока в цепи нет, поэтому точки a и b равнопотенциальны, т. е. φa = φb = 0. Потенциал точки c превышает потенциал точки b на величину э.д.с. E1 и φc = E1 = 25 В; рассуждая аналогично, найдем
φ d = φ c =25 B; φ f = φ d + E 2 =25+5=30 B; φ g = φ f =30 B; φ h = φ g − E 3 =30−20=10 B; φ k = φ h =10 B; φ l = φ k + E 4 =10+35=45 B.
На основе полученных результатов на рис. 22, б начерчен график изменения потенциала при разомкнутом ключе.
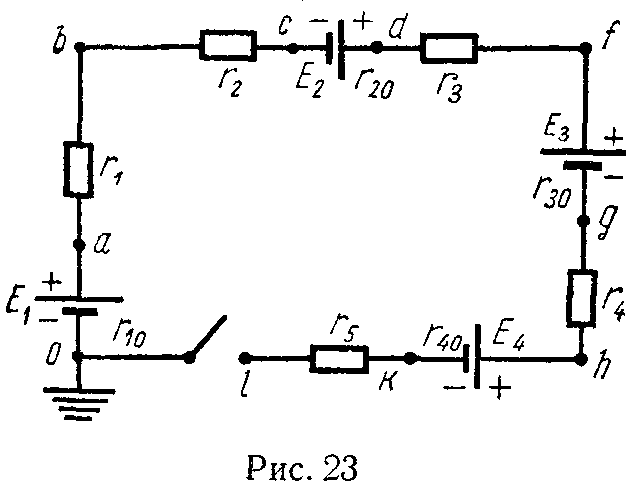
Задача 18. Для схемы рис. 23 построить потенциальные графики 0abcdfghkl при разомкнутом и замкнутом ключе, если E1 = 60 В, E2 = 40 В, E3 = 25 В, E4 = 15 В, r10 = 6 Ом, r20 = 4 Ом, r30 = 3 Ом, r40 = 2 Ом, r1 = 24 Ом, r2 = 16 Ом, r3 = 25 Ом, r4 = 22 Ом, r5 = 18 Ом.
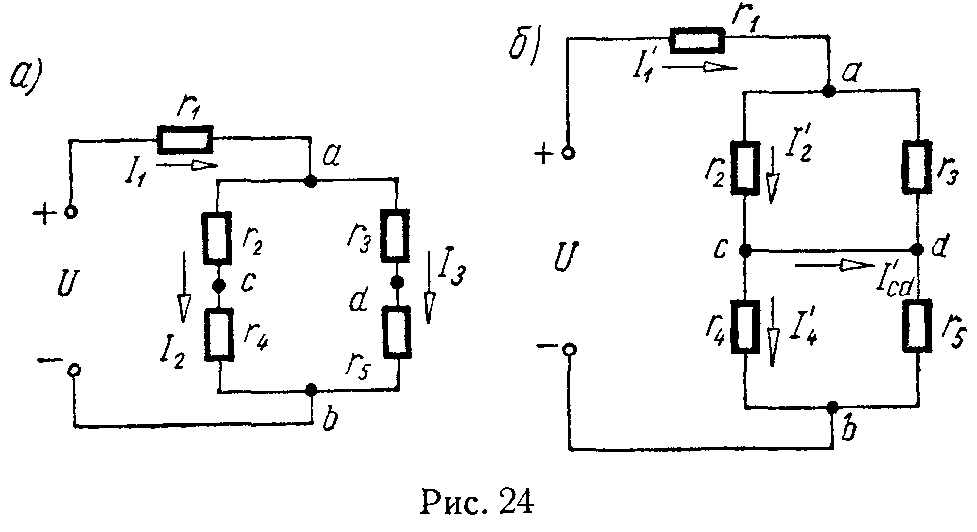
Задача 19. Определить токи в ветвях цепи (рис. 24, а) и напряжение между точками c и d и показание амперметра, включенного между точками c и d. Сопротивление амперметра считать равным нулю. Сопротивления элементов цепи r1 = 10 Ом, r2 = r3 = r5 = 25 Ом, r4 = 50 Ом, а приложенное к ней напряжение U = 120 В.
Решение
Эквивалентное сопротивление всей цепи (рис. 24, а) равно
r= r 1 + ( r 2 + r 4 )⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =10+ 75⋅50 125 =40 Ом.
В неразветвленной части цепи протекает ток
I= U r = 120 40 =30 А.
Токи, протекающие через сопротивления r2 + r4 и r3 + r5, можно найти различными способами.
1) В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формулы 9)
I 2 = I 1 ⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 50 125 =1,2 А, I 3 = I 1 ⋅ ( r 2 + r 4 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 75 125 =1,8 А.
2) Найдем напряжение на зажимах параллельных ветвей
U ab = I 1 ⋅ ( r 2 + r 4 )⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 75⋅50 125 =90 В.
Токи в ветвях с сопротивлениями r2 + r4 и r3 + r5 равны
I 2 = U ab r 2 + r 4 = 90 75 =1,2 А, I 3 = U ab r 3 + r 5 = 90 50 =1,8 А.
Напряжение на зажимах параллельных ветвей может быть найдена как разность между приложенным напряжением и падением напряжения на сопротивлении r1
U ab =U− I 1 ⋅ r 1 =120−3⋅10=90 В.
Найдем напряжение между точками c и d
U cd =− I 2 ⋅ r 2 + I 3 ⋅ r 3 =−1,2⋅25+1,8⋅25=15 В.
Наконец, вычислим ток, проходящий через амперметр, он равен току короткого замыкания I’cd (рис. 24, б). Для его нахождения вычислим токи
I ′ 1 = U r 1 + r 2 ⋅ r 3 r 2 + r 3 + r 4 ⋅ r 5 r 4 + r 5 = 144 47 А, I ′ 2 = I ′ 1 ⋅ r 3 r 2 + r 3 = 144 47 ⋅ 1 2 = 72 47 А, I ′ 4 = I ′ 1 ⋅ r 5 r 4 + r 5 = 144 47 ⋅ 25 75 = 48 47 А.
Искомый ток, проходящий через амперметр, равен
I A = I ′ cd = I ′ 2 − I ′ 4 = 72 47 − 48 47 = 24 47 =0.51 А.
Задача 20. Для измерения тока применены амперметры, пределы измерений которых равны 5 и 2,5 А, и шунт, сопротивление которого неизвестно. Первый амперметр, включенный с шунтом в некоторую цепь, показал 3,6 А, второй — с тем же шунтом показал в той же цепи ток 2 А. Сопротивления амперметров r1 = 0,002 Ом и r2 = 0,004 Ом. Чему равен ток в цепи?
Ответ: 18 А; rш = 0,0005 А.
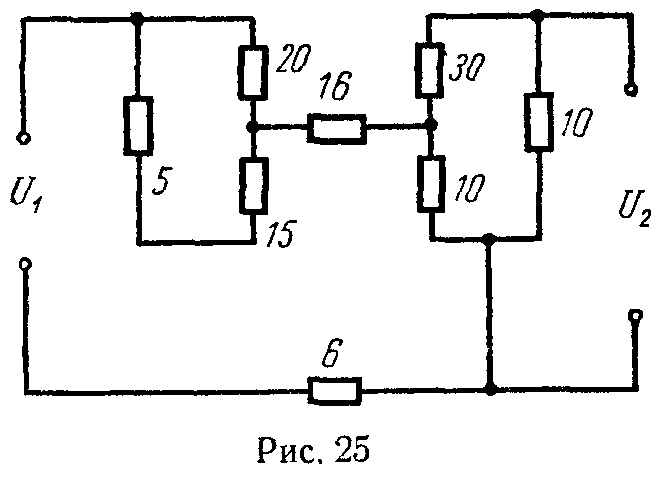
Задача 21. Для цепи рис. 25 определить отношение напряжения на выходе U2 к напряжению на входе цепи U1. Сопротивления отдельных ветвей цепи в омах указаны на схеме.
Ответ: U2: U1 = 0,05.
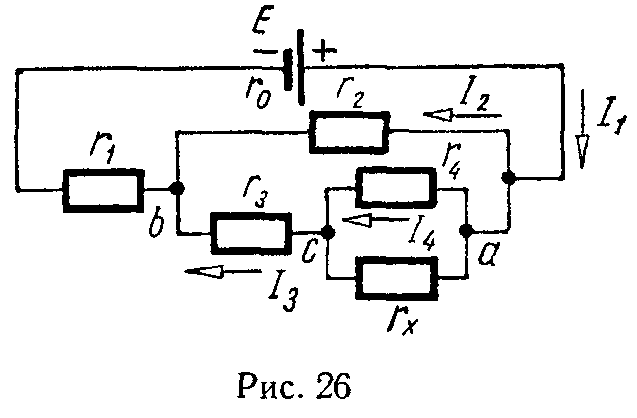
Задача 22. В схеме (рис. 26) найти сопротивление rx, если I1 = 2,6 А, I3 = 0,6 А, r1 = 0,5 Ом, r2 =1,4 Ом, r3 = 3 Ом, r4 = 2,5 Ом. Найти э.д.с. батареи E, если ее внутреннее сопротивление r0 = 0,1 Ом.
Решение
На основании первого закона Кирхгофа найдем
I2 = I1 — I3 = 2,6 — 0,6 = 2 А.
По закону Ома, примененному к участку, содержащему сопротивление r2, найдем
Uab = I2·r2 = 2·1,4 = 2,8 В.
Применяя закон Ома к участку цепи ab, содержащему э.д.с. E и сопротивления r1 и r0, найдем искомую э.д.с.
E = Uab + I1· (r1 + r0) = 2,8 + 2,6·0,6 = 4,36 В.
Теперь найдем напряжение на параллельных ветвях с сопротивлениями r4 и rx и токи в них
Uac = Uab — I3·r3 = 2,8 — 0,6·3 = 1 В;
I4 = Uac/r4 = 1/2,5 = 0,4 А;
Ix = I3 — I4 = 0,6 — 0,4 = 0,2 А.
Искомое сопротивление
rx = Uac/Ix = 1/0,2 = 5 Ом.
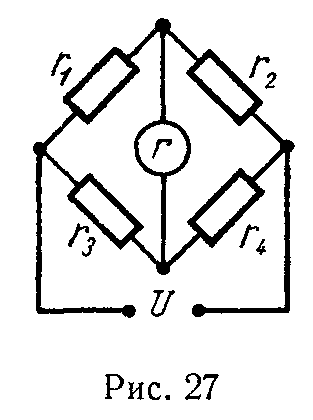
Задача 23. В схеме мостика (рис. 27) известны сопротивления r1 = 1300 Ом, r2 = 800 Ом, r3 = 400 Ом. Сопротивление гальванометра rг = 600 Ом. Через, сопротивление r1 протекает ток I1 = 1 мА. К мостику приложено напряжение U = 2,5 В.
Найти сопротивление r4.
Ответ: 750 Ом.
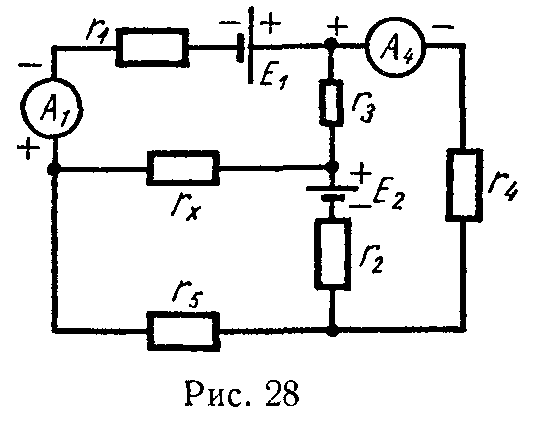
Задача 24. В цепи (рис. 28) найти E1 и rx, если E2 = 3 В, r1 = r2 = 1 кОм, r3 = 4 кОм, r4 = 2 кОм, r5 = 1 кОм. Внутренние сопротивления батарей принять равными нулю.
Амперметр А1 показывает 4 мА, а А4 — 3 мА; полярности приборов показаны на схеме, а их сопротивлениями можно пренебречь.
Ответ: E1 = 12 В, rx = 2 Ом.
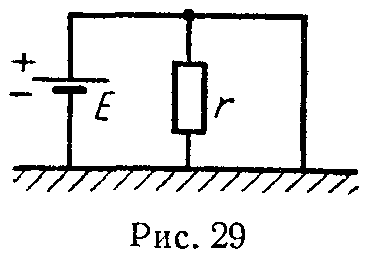
Задача 25. Однопроводная линия с сопротивлением r0 на единицу длины, питаемая батареей с э.д.с., равной E, закорочена на приемном конце (рис. 29).
В каком месте линия должна иметь утечку с сопротивлением r, чтобы ток I на приемном конце был минимальным?
Ответ: по середине линии.
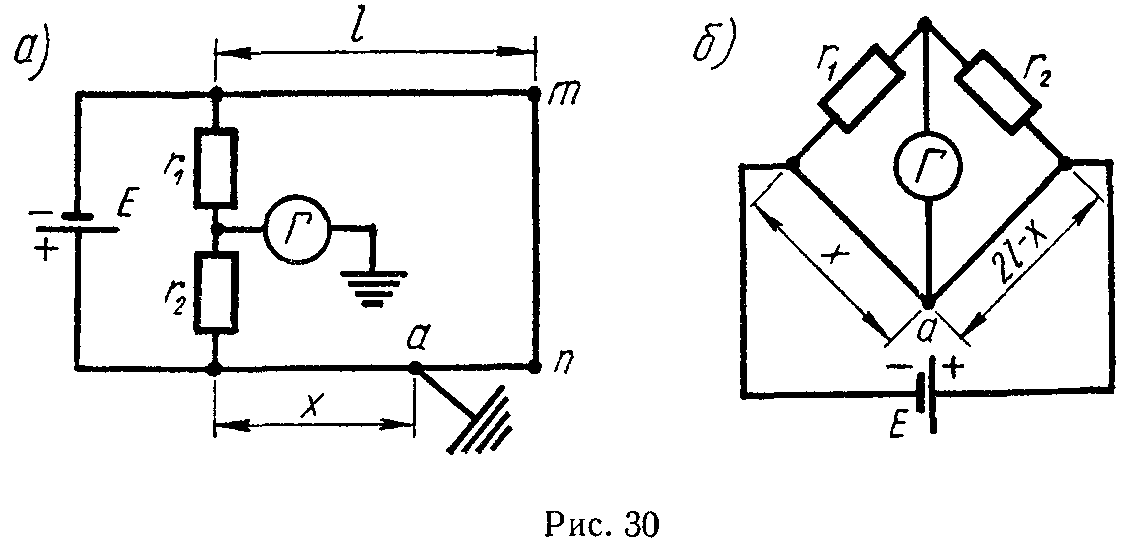
Задача 26. Для определения места повреждения изоляции линии применяется схема, изображенная на рис. 30, а; r1 и r2 — магазины сопротивлений.
Правый зажим гальванометра заземлен. Свободные концы тип линии соединены между собой накоротко. Подбором сопротивлений r1 и r2 добиваются отсутствия тока в гальванометре.
Показать, что если сечения обоих проводов одинаковы, то расстояние от места повреждения изоляции a до начала линии равно
2l⋅ r 2 r 1 + r 2 .
Указание. Заданная схема может быть заменена схемой рис. 30, б.
Задача 27. При проверке постоянной C счетчика оказалось, что при силе тока 10 А и напряжении 120 В якорь его в продолжение 30 сек сделал 37 оборотов. Определить ошибку в показаниях счетчика, если на счетчике указано, что 1 ГВт·ч соответствует 400 оборотам счетчика.
Примечание. Постоянной счетчика называется число ватт-часов, приходящихся на один оборот счетчика.
Ответ: 7,5%.
Задача 28. Каково должно быть сечение медных проводов линии для передачи потребителю мощности P = 16 кВт при условии, что потеря мощности не превысит p = 5%, если длина линии l = 180 м и напряжение в конце линии равно U = 220 В?
Ответ: точное значение 41,8 мм2, по ГОСТ надо взять 50 мм2.
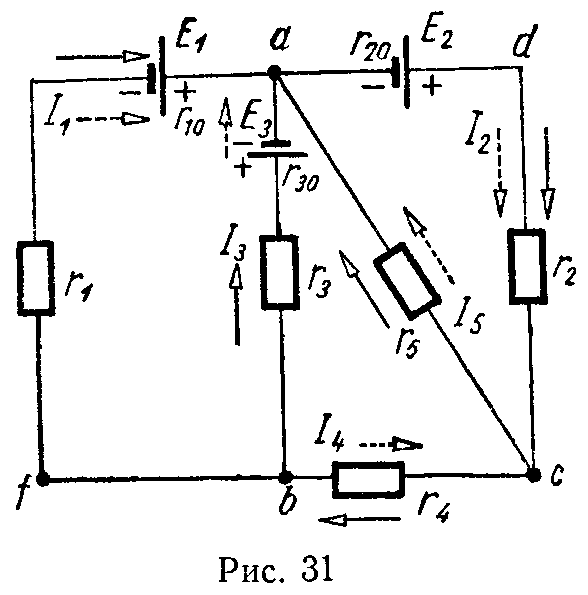
Задача 29. Для схемы (рис. 31), пользуясь законами Кирхгофа, найти токи и проверить баланс мощностей, если E1 = 15 В, E2 = 70 В, E3 = 5 В, r10 = r20 = 1 Ом, r30 = 2 Ом, r1 = 5 Ом, r1 = 5 Ом, r2 = 4 Ом, r3 = 8 Ом, r4 = 2,5 Ом, r5 = 15 Ом.
Решение
Всего узлов в схеме три (a, b, c), следовательно, число независимых уравнений, составляемых по первому закону Кирхгофа, будет на единицу меньше, т.е. два. Число контуров равно трем, следовательно, по второму закону Кирхгофа можно составить три взаимно независимых уравнения. Таким образом, общее число независимых уравнений, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов в пяти ветвях схемы.
Выберем положительные направления для токов, которые обозначены пунктирными стрелками, и составим систему уравнений Кирхгофа:
для узла a
I1 — I2 + I3 + I5 = 0; (1)
для узла b
–I1 — I3 — I4 = 0; (2)
для контура abfa
E1 + E3 = I1· (r1 + r10) — I3· (r3 + r30); (3)
для контура abca
E3 = –I3· (r3 + r30) + I4·r4 + I5·r5; (4)
для контура adca
E2 = I2· (r2 + r20) + I5·r5. (5)
Уравнения (1) — (5) после подстановки в них числовых значений будут иметь следующий вид
I1 — I2 + I3 + I5 = 0,
I1 + I3 + I4 = 0,
6I1 — 10I3 = 20,
–10I3 + 2,5I4 + 15I5 = 5,
5I2 + 15I5 = 70.
Решая эту систему уравнений, получим
I1 = 5 А; I2 = 8 А; I3 = 1 А; I4 = –6 А; I5 = 2 А.
Отрицательный знак для тока I4 означает, что истинное направление этого тока противоположно принятому. При проверке баланса мощностей надо иметь в виду, что в тех ветвях цепи, где истинное направление тока совпадает с направлением э.д.с., соответствующая э.д.с. будет являться источником энергии, а в тех участках, где направления э.д.с. и тока противоположны, э.д.с. будет являться потребителем энергии. Все сопротивления как внешние, так и самих источников, независимо от направления протекающего через них тока, будут являться потребителями энергии.
Баланс мощностей для рассматриваемой схемы будет
E1·I1 + E2·I2 + E3· (–I3) = I12· (r1 + r10) + I22· (r2 + r20) + I32· (r3 + r30) + I42·r4 + I52·r5,
или
15·5 + 70·8 — 5·1 = 52·6 + 82·5 + 12·10 + 62·2,5 + 22·15,
получено тождество 630 Вт = 630 Вт.
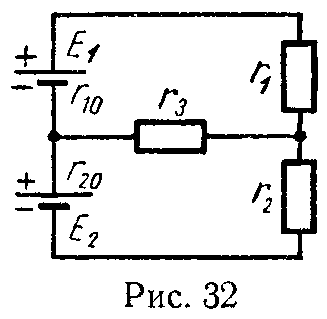
Задача 30. В схеме (рис. 32) найти все токи, если известны: E1 = 20 В, E2 = 1,1 В, r10 = 0,2 Ом, r20 = 0,4 Ом, r1 = r2 = 5 Ом, r3 = 7 Ом.
Ответ: 2,5 А, 1,5 А, 1 А.
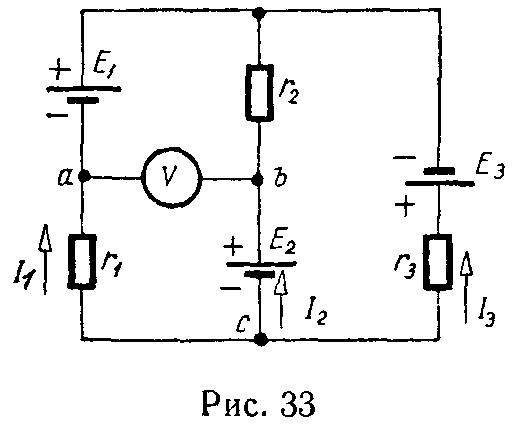
Задача 31. Для цепи, изображенной на рис. 33, рассчитать токи и определить показание вольтметра, если E1 = 40 В, E2 = 5 В, E3 = 25 В, r1 = 5 Ом, r2 = r3 = 10 Ом.
Внутренними сопротивлениями источников энергии и током, протекающим через вольтметр, можно пренебречь.
Ответ: I1 = 5 А, I2 = 1 А, I3 = 4 А, Uba = 30 В.
Задача 32. Аккумуляторная батарея из 20 последовательно соединенных элементов работает параллельно с генератором на сеть, имеющую нагрузку 30 А. Каждый аккумулятор имеет э.д.с. 1,82 В и сопротивление 0,001 Ом. Э.д.с. генератора 36,4 В и его сопротивление 0,04 Ом. Определить нагрузку генератора и батареи (т. е. отдаваемые ими токи) и напряжение на их зажимах.
Какую э.д.с. должен развивать генератор, чтобы нагрузка распределилась поровну между генератором и батареей?
Ответ: 20 А, 10 А, 36 В, 36,7 В.
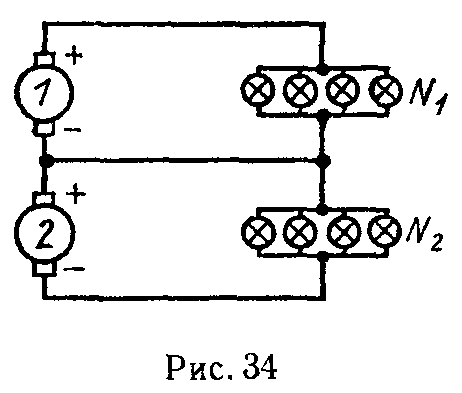
Задача 33. По трехпроводной линии длиной 0,5 км (рис. 34) от двух генераторов 1 и 2 питаются две группы ламп 50 Вт, 110 В.
В первой группе — N1 = 200 ламп, а во второй — N2 = 600 ламп. Сечение крайних проводов q = 35 мм2, а сечение среднего (нулевого) провода q0 = 16 мм2. Каждый генератор имеет внутреннее сопротивление 0,01 Ом и развивает э.д.с. 120 В. Определить токи во всех проводах линии и напряжение на зажимах каждой группы ламп, сопротивления которых считать постоянным. Материал проводов линии — медь.
Ответ: I1 = 98 А, I2 = 144 А, I0 = 46 А, U1 = 102 В, U2 = 71 В.
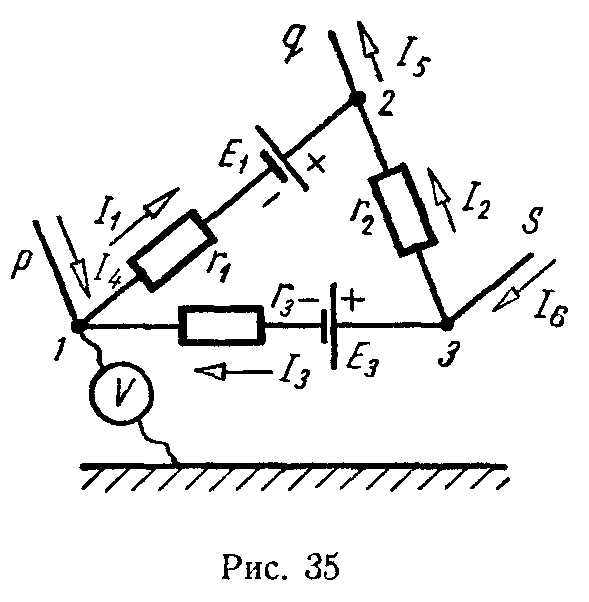
Задача 34. Напряжения, измеренные электростатическим вольтметром, между узловыми точками схемы и землей, равны: U10 = –15 В, U20 = 52 В, U30 = 64 В (рис. 35).
Определить токи в ветвях и отходящих проводах при следующих данных: E1 = 80 В, E3 = 70 В, r1 = 5 Ом, r2 = 10 Ом, r3 = 12 Ом.
Решение
Вычислим напряжения между точками 1 и 2, 2 и 3, 3 и 1
U10 — U20 = U12 = (–15) — 52 = –67 В,
U20 — U30 = U23 = 52 — 64 = –12 В,
U30 — U10 = U31 = 64 — (–15) = 79 В.
Применяя к ветвям 1–2, 2–3, 3–1 закон Ома, найдем токи
I 1 = U 12 + E 1 r 1 = ( −67 )+80 5 =2,6 А, I 2 = U 32 r 2 = 12 10 =1,2 А, I 3 = U 31 − E 3 r 3 = 79−70 12 =0,75 А.
Так как все токи оказались положительными, то они имеют направления в соответствии с только что записанными уравнениями и нанесены на рис. 35.
Токи в ответвлениях от узловых точек 1–p, 2–q, 3–s находим по первому закону Кирхгофа
I4 = I1 — I3 = 1,85 А, I5 = I1 + I2 = 3,8 А, I6 = I2 + I3 = 1,95 А.
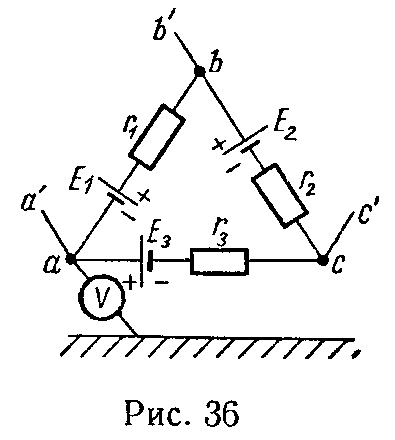
Задача 35. В цепи (рис. 36) известны э.д.с. E1 = 120 В, E2 = 40 В, E3 = 70 В и сопротивления r1 = 20 Ом, r2 = 10 Ом, r3 = 40 Ом.
Потенциалы точек a, b и c относительно земли соответственно равны (определены посредством вольтметра): Ua0 =160 В, Ub0 = 180 В, Uc0 = 50 В. Определить токи в ветвях ab, bc, ca и в проводах aa’, bb’ и cc’, подходящих к точкам a, b и c.
Ответ: I1 = 5 А, I2 = 9 А, I3 = 1 А.
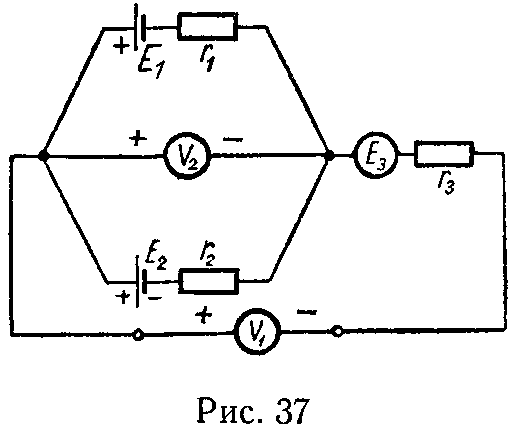
Задача 36. В цепи (рис. 37) известны э.д.с. E1 = 40 В, E2 = 30 В.
Сопротивления элементов схемы r1 = 8 Ом, r2 = 5 Ом, r3 = 10 Ом. Показания вольтметров соответственно равны: U1 = 125 В, U2 = 60 В; полярность зажимов вольтметров показана на схеме. Пренебрегая внутренними сопротивлениями источников электрической энергии и считая потребляемые вольтметрами токи приближенно равными нулю, определить величину и полярность э.д.с. E3. Найти все токи.
Ответ: E3 = 20 В, I1 = 2,5 А, I2 = 6 А, I3 = 8,5 А.
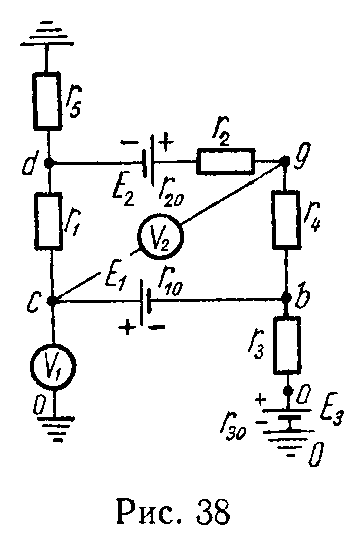
Задача 37. В цепи, изображенной на рис. 38, найти токи и показания вольтметров, включенных между точками 0 и c, c и g, если известно, что E1 = 32 В, E2 = 64 В, E3 = 72 В, r1 = 9 Ом, r10 = 1 Ом, r2 = 5 Ом, r20 = 1 Ом, r3 = 2 Ом, r30 = 1 Ом, r4 = 2 Ом, r5 = 1 Ом. Сопротивления вольтметров весьма велики по сравнению с сопротивлениями элементов цепи.
Ответ: I1 = 5 А, I2 = 9 А, I3 = 1 А.
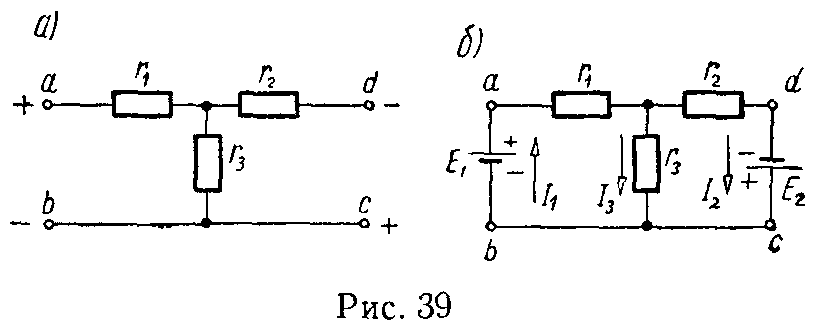
Задача 38. Для схемы (рис. 39, а) найти токи и проверить баланс мощностей, если Uab = 12 В, Ucd = 5,6 В, r1 = 4 Ом, r2 = 5 Ом, r3 = 3 Ом.
Решение
Данная схема может быть заменена эквивалентной, в которой между точками a и b, а также c и d включены э.д.с., численное значение которых E1 = Uab и E2 = Ucd, а их внутренние сопротивления равны нулю (рис. 39, б). Обращаем внимание на то, что при включении э.д.с. следует соблюдать заданные полярности напряжений.
Задавшись направлениями для токов, составим систему уравнений Кирхгофа
I1 — I2 — I3 = 0,
E1 = I1·r1 + I3·r3,
E2 = I2·r2 — I3·r3.
Подставляя сюда числовые значения и решая систему уравнений, найдем:
I1 = 2,4 А, I2 = 1,6 А, I3 = 0,8 А.
Для проверки баланса мощностей составим уравнение
Uab·I1 + Ucd·I2 = I12·r1 + I22·r2 + I32·r3,
12·2,4 + 5,6·1,6 = 2,42·4 + 1,62·5 + 0,82·3;
получено тождество 37,76 = 37,76.
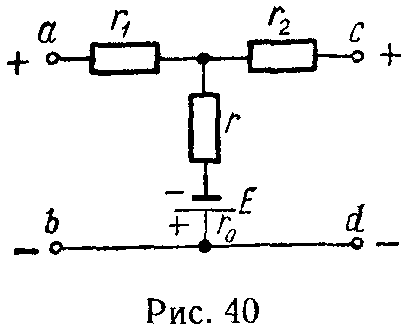
Задача 39. В цепи (рис. 40) найти токи и проверить баланс мощностей, если Uab = 16 В, Ucd = 11,2 В, E = 5 В, r0 = 0, r = 10 Ом, r1 = 5 Ом, r2 = 4 Ом.
Ответ: I1 = 1,2 А, I2 = 0,3 А, I = 1,5 А.
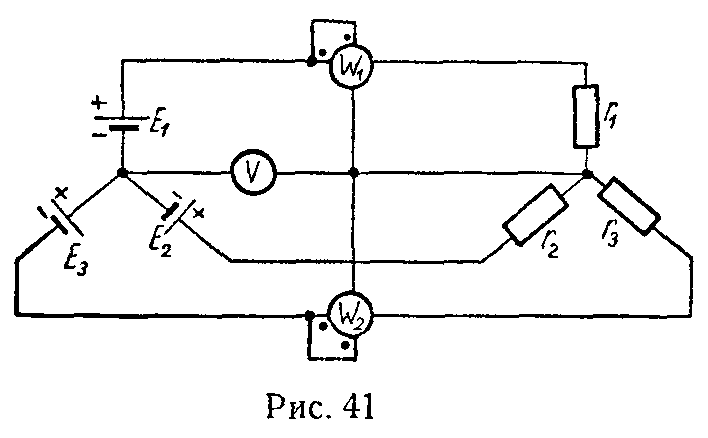
Задача 40. Чему равно показание вольтметра на рис. 41, если током вольтметра можно пренебречь по сравнению с токами в нагрузках? Внутренние сопротивления батарей принять равными нулю.
Определить показания ваттметров и убедиться в том, что их сумма равна сумме мощностей, расходуемых в сопротивлениях r1, r2 и r3. Потерями в катушках ваттметров пренебречь.
Дано: E1 = 30 В, E2 = 21 В, E3 = 5 В, r1 = 5 Ом, r2 = 10 Ом, r3 = 50 Ом.
Ответ: 25 В, P1 = 9 Вт, P2 = 15,6 Вт.
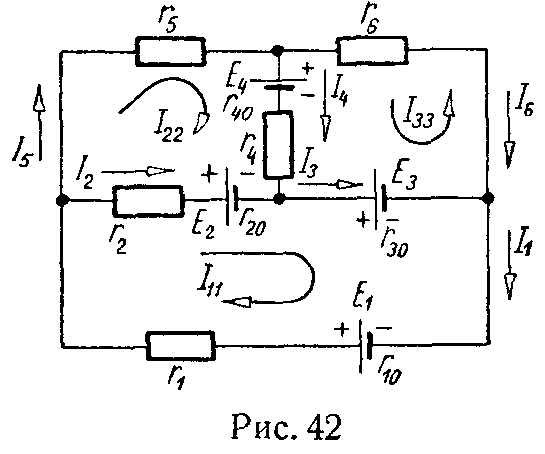
Задача 41. Методом контурных токов найти токи в цепи, схема которой изображена на рис. 42; даны: E1 = 100 В, E2 = 30 В, E3 = 10 В, E4 = 6 В, r1 = 10 Ом, r2 = 10 Ом, r4 = 6 Ом, r5 = 5 Ом, r6 = 15 Ом, r10 = r20 = r30 = 0, r40 = 1 Ом.
Решение
Выберем направления контурных токов, которые обозначим через I11, I22, I33.
Составим систему уравнений для контуров
E1 — E2 — E3 = I11· (r1 + r10 + r2 + r20 + r30) — I22· (r2 + r20) + I33·r30,
E2 — E4 = I22· (r2 + r20 + r5 + r4 + r40) + I33· (r4 + r40) — I11· (r2 + r20),
–E3 — E4 = I33· (r30 + r6 + r4 + r40) + I22· (r4 + r40) + I11·r30.
После подстановки числовых значений будем иметь
60 = 20·I11 — 10·I22 + 0·I33,
24 = –10·I11 + 22·I22 + 7·I33,
–16 = 0·I11 + 7·I22 + 22·I33.
Решив эту систему уравнений, найдем контурные токи
I11 = 5 А, I22 = 4 А, I33 = –2 А.
Теперь найдем истинные токи во всех ветвях.
В ветви, где действует э.д.с. E1, истинный ток I1 имеет направление контурного тока I11 и равен
I1 = I11 = 5 А.
В ветви с сопротивлением r5 истинный ток I5 имеет направление контурного тока I22 и равен
I5 = I22 = 4 А.
В ветви с сопротивлением r6 истинный ток I6 имеет направление, противоположное контурному току I33, и равен
I6 = –I33 = — (–2) = 2 А.
В ветви с сопротивлением r2 истинный ток I2 получится от наложения контурных токов I11 и I22 и будет иметь направление большего контурного тока I11;
I2 = I11 — I22 = 5 — 4 = 1 А.
В ветви с сопротивлением r4 истинный ток I4 получится от наложения контурных токов I22 и I33 и будет иметь направление контурного тока I22;
I4 = I22 + I33 = 4 + (–2) = 2 А.
В ветви, где действует э.д.с. E3, истинный ток I3 получится от наложения контурных токов I11 и I33 и будет иметь направление тока I11;
I3 = I11 + I33 = 5 + (–2) = 3 А.
Эта же задача может быть решена методом определителей. Для этого уравнения для контурных токов следует записать в форме (10), а именно
{ r 11 ⋅ I 11 + r 12 ⋅ I 22 + r 13 ⋅ I 33 = E 11 ; r 21 ⋅ I 11 + r 22 ⋅ I 22 + r 23 ⋅ I 33 = E 22 ; r 31 ⋅ I 11 + r 32 ⋅ I 22 + r 33 ⋅ I 33 = E 33 ,
где контурные сопротивления
r11 = r1 + r10 + r2 + r20 + r30 = 20 Ом;
r22 = r2 + r20 + r5 + r4 + r40 = 22 Ом;
r33 = r30 + r6 + r4 + r40 = 22 Ом,
взаимные сопротивления контуров
r12 = r21 = — (r2 + r20) = –10 Ом;
r13 = r31 = r30 = 0;
r23 = r32 = r4 + r40 = 7 Ом,
контурные э.д.с.
E11 = E1 — E2 — E3 = 60 В;
E22 = E2 — E4 = 24 В;
E33 = –E3 — E4 = –16 В.
Получим численную систему уравнений метода контурных токов
{ 20⋅ I 11 − 10⋅ I 22 + 0⋅ I 33 =60; −10⋅ I 11 +22⋅ I 22 + 7⋅ I 33 =24; 0⋅ I 11 + 7⋅ I 22 +22⋅ I 33 =−16,
или в матричной форме записи
( 20 −10 0 −10 22 7 0 7 22 )⋅ ( I 11 I 22 I 33 )= ( 60 24 −16 ).
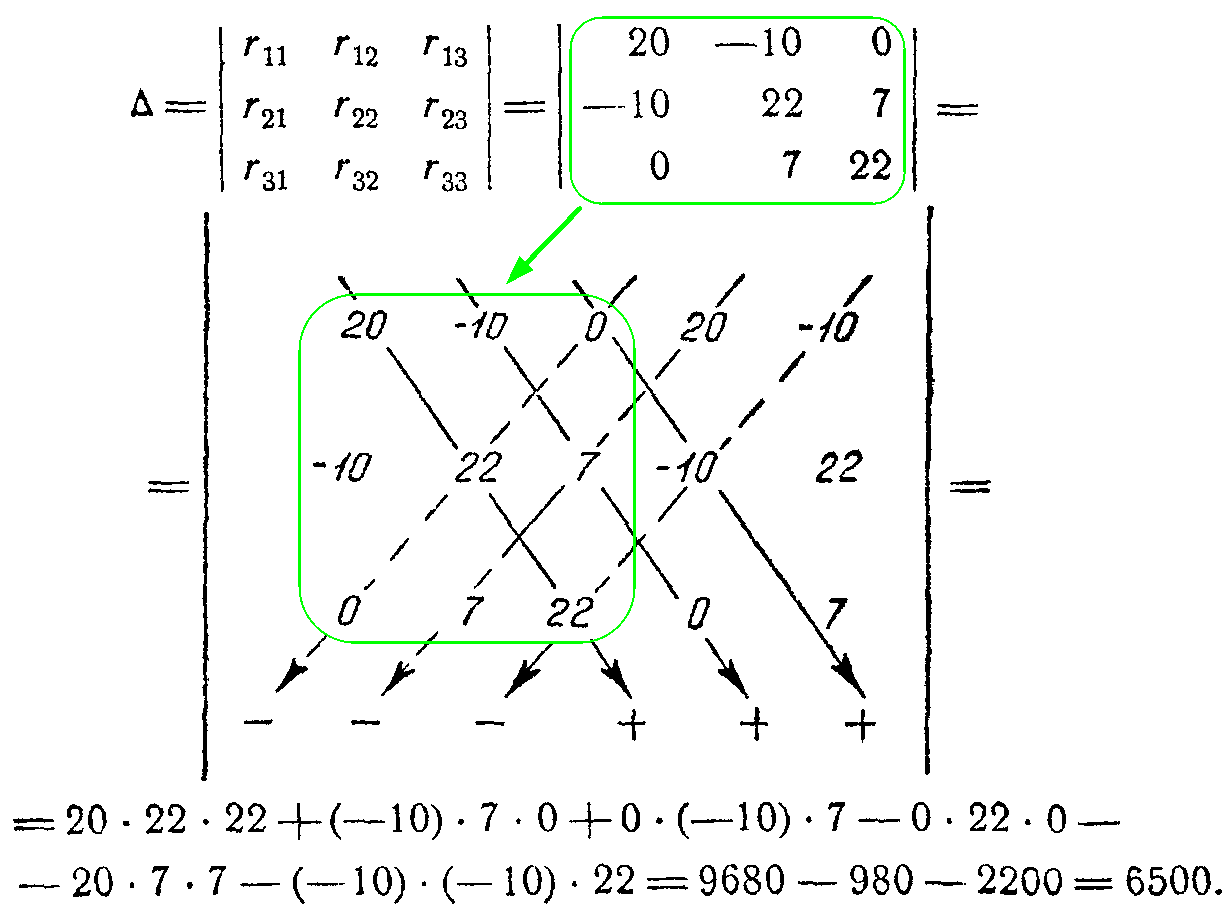
Составим главный определитель системы? и вычислим его значение
Вычислим значения вспомогательных определителей
Δ 11 =| E 11 r 12 r 13 E 22 r 22 r 23 E 33 r 32 r 33 |=| 60 −10 0 24 22 7 −16 7 22 |=32500; Δ 22 =| r 11 E 11 r 13 r 21 E 22 r 23 r 31 E 33 r 33 |=| 20 60 0 −10 24 7 0 −16 22 |=26000; Δ 33 =| r 11 r 12 E 11 r 21 r 22 E 22 r 31 r 32 E 33 |=| 20 −10 60 −10 22 24 0 7 −16 |=−13000.
Искомые контурные токи определяем по формулам
I 11 = Δ 11 Δ = 32500 6500 =5 А; I 22 = Δ 22 Δ = 26000 6500 =4 А; I 33 = Δ 33 Δ = −13000 6500 =−2 А.
Мы получили те же результаты, что и ранее.
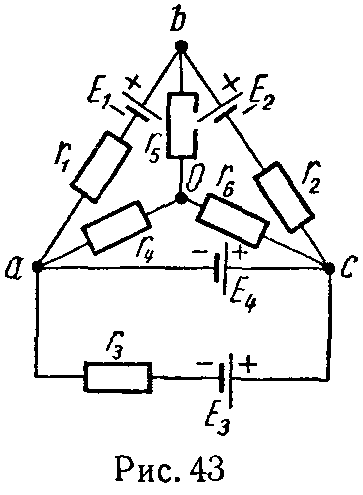
Задача 42. Найти все токи и определить потенциалы точек a, b, c и 0 относительно земли (рис. 43).
Задачу решить методом контурных токов, Внутренние сопротивления источников электрической энергии считать равными нулю: E1 = 85 В, E2 = 84 В, E3 = 5 В, E4 = 12 В, r1 = 8 Ом, r2 = 10 Ом, r3 = 10 Ом, r4 = 10 Ом, r5 = 10 Ом, r6 = 4 Ом.
Ответ: I1 = 2 А, I2 = 2,7 А, I3 = 0,7 А, I4 = 2,2 А, I5 = 4,7 А, I6 = 2,5 А.
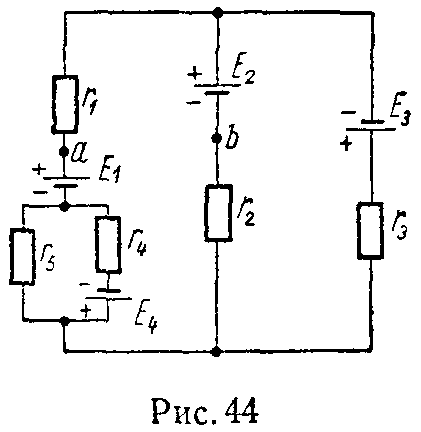
Задача 43. Для схемы (рис. 44) найти токи и Uab, если E1 = 70 В, E2 = 5 В, E3 = 15 В, E4 = 10 В, r1 = 5 Ом, r2 = r3 = 10 Ом, r4 = 5 Ом, r5 = 3 Ом.
Задачу решить методом контурных токов. Внутренние сопротивления источников энергии равны нулю.
Ответ: I1 = 6 А, I2 = 2 А, I3 = 4 А, I4 = 1 А, I5 = 5 А.
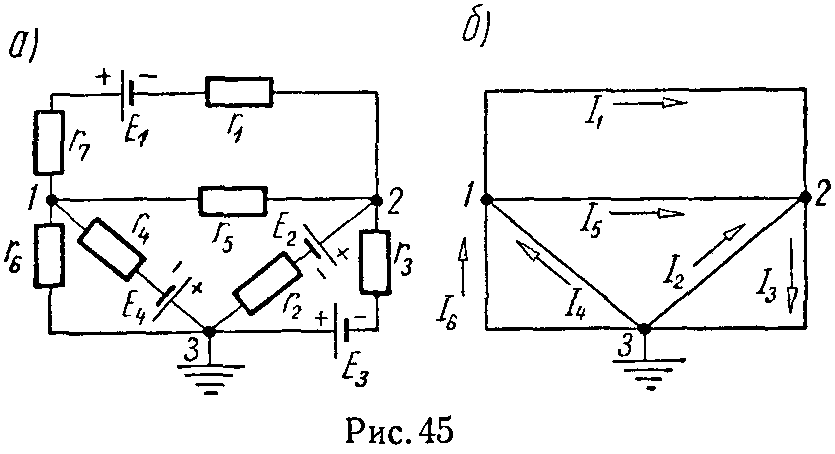
Задача 44. Для схемы, изображенной на рисунке 45, а, пользуясь методом узловых потенциалов, определить все токи. Данные схемы: E1 = 30 В, E2 = 10 В, E3 = 200 В, E4 = 56 В, r1 = 20 Ом, r2 = 30 Ом, r3 = 6 Ом, r4 = 8 Ом, r5 = 15 Ом, r6 = 40 Ом, r7 = 10 Ом. Внутренние сопротивления источников напряжения равны нулю.
Решение
Примем потенциал точки 3 равным нулю. Тогда, на основании формулы (11), запишем систему уравнений для определения потенциалов точек 1 и 2
φ 1 ⋅ g 11 + φ 2 ⋅ g 12 = ∑ 1 E⋅g , (1) φ 1 ⋅ g 21 + φ 2 ⋅ g 22 = ∑ 2 E⋅g . (2)
Подсчитаем g11 — сумму проводимостей, присоединенных к узлу 1
g 11 = 1 r 1 + r 7 + 1 r 5 + 1 r 4 + 1 r 6 = 1 30 + 1 15 + 1 8 + 1 40 =0,25 1 Ом .
Аналогично g22 — сумма проводимостей, присоединенных к узлу 2
g 22 = 1 r 1 + r 7 + 1 r 5 + 1 r 2 + 1 r 3 = 1 30 + 1 15 + 1 30 + 1 6 =0,3 1 Ом .
Взаимные проводимости первого и второго узлов
g 12 = g 21 =− ( 1 r 1 + r 7 + 1 r 5 )=− 1 30 − 1 15 =−0,1 1 Ом .
Подставим в уравнения (1) и (2) числовые значения
0,25⋅ φ 1 + ( −0,1 )⋅ φ 2 =30⋅ 1 30 −56⋅ 1 8 =−6, ( −0,1 )⋅ φ 1 +0,3⋅ φ 2 =−30⋅ 1 30 +10⋅ 1 30 −200⋅ 1 6 =−34.
Решив последние два уравнения, найдем потенциалы точек 1 и 2
φ1 = –80 В; φ2 = –140 В.
Наконец, применяя закон Ома для отдельных ветвей, определим искомые токи
I 1 = φ 1 − φ 2 − E 1 r 1 = ( −80 )− ( −140 )−30 30 =1 А; I 2 = φ 3 − φ 2 + E 2 r 2 = 0− ( −140 )+10 30 =5 А; I 3 = φ 2 − φ 3 + E 3 r 3 = ( −140 )−0+200 6 =5 А; I 4 = φ 3 − φ 1 − E 4 r 4 = 0− ( −80 )−56 8 =3 А; I 5 = φ 1 − φ 2 r 5 = ( −80 )− ( −140 ) 15 =4 А.
Направления найденных токов указаны на скелетной схеме (рис. 45, б).
Рекомендуем читателю решить ту же задачу, приняв за нуль потенциал узловой точки 1.
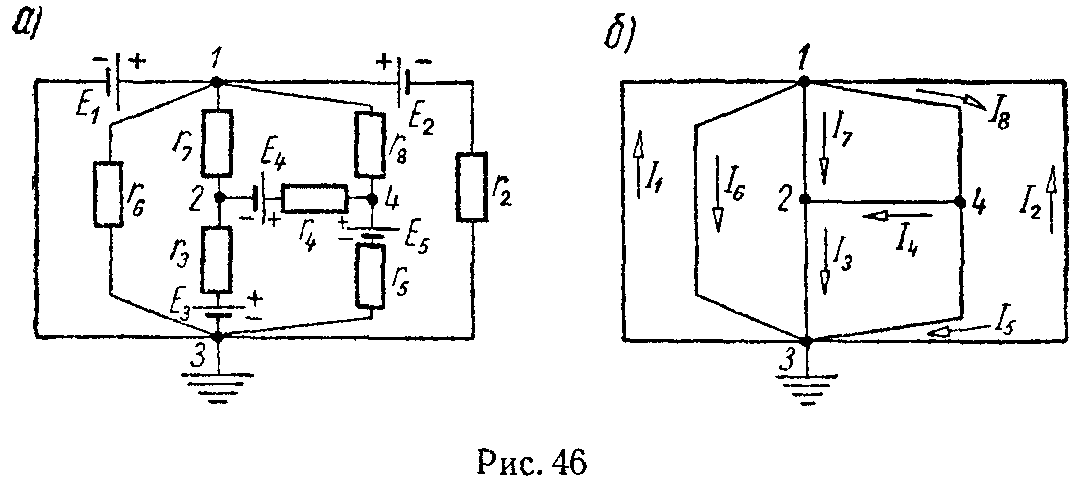
Задача 45. Методом узловых потенциалов определить токи во всех ветвях схемы, изображенной на рис. 46, а; заданы: E1 = 20 В, E2 = 30 В, E3 = 2 В, E4 = 1,2 В, E5 = 5,6 В, r2 = 50 Ом, r3 = 10 Ом, r4 = 20 Ом, r5 = 10 Ом, r6 = 100 Ом, r7 = 50 Ом, r8 = 20 Ом.
Внутренние сопротивления источников напряжения считать равными нулю.
Решение
В тех случаях, когда в цепи имеется ветвь с э.д.с., но не содержащая сопротивления, целесообразно принять равным нулю потенциал одной из узловых точек, к которой подходит указанная ветвь.
В нашем случае примем потенциал узла 3 равным нулю (φ3 = 0). Тогда потенциал точки 1 имеет значение, равное E1, т.е. φ1 = 20 В. Общее число уравнений уменьшается и равняется числу узлов минус два. В нашей задаче достаточно составить всего два уравнения для узлов 2 и 4.
Определим сумму проводимостей, присоединенных к узлу 2
g 22 = 1 r 3 + 1 r 4 + 1 r 7 =0,17 1 Ом ,
и, соответственно, к узлу 4
g 44 = 1 r 4 + 1 r 5 + 1 r 8 =0,2 1 Ом .
Найдем взаимные проводимости узлов 2 и 1, 2 и 4, 4 и 1
g 12 = g 21 =− 1 r 7 =−0,02 1 Ом , g 24 = g 42 =− 1 r 4 =−0,05 1 Ом , g 14 = g 41 =− 1 r 8 =−0,05 1 Ом .
Вычислим суммы произведений э.д,с. на проводимости, присоединенные соответственно к узлам 2 и 4
∑ 2 E⋅g = E 3 ⋅ g 3 − E 4 ⋅ g 4 =0,14 В Ом , ∑ 4 E⋅g = E 4 ⋅ g 4 + E 5 ⋅ g 5 =0,62 В Ом .
Составим систему уравнений на основании формул (11) для узла 2:
φ 1 ⋅ g 21 + φ 2 ⋅ g 22 + φ 4 ⋅ g 24 = ∑ 2 E⋅g ,
для узла 4
φ 1 ⋅ g 41 + φ 2 ⋅ g 42 + φ 4 ⋅ g 44 = ∑ 4 E⋅g .
Подставляя сюда числовые значения, получим
0,17⋅ φ 2 + ( −0,05 )⋅ φ 4 =0,54, ( −0,05 )⋅ φ 2 +0,2⋅ φ 4 =1,62.
Решая эту систему уравнений, найдем
φ2 = 6 В; φ4 = 9,6 В.
Наконец, применяя к отдельным ветвям формулы закона Ома, получим значения всех токов, которые нанесены на скелетной схеме (46, б)
I2 = 0,2 А, I3 = 0,4 А, I4 = 0,12 А, I5 = 0,4 А, I6 = 0,2 А, I7 = 0,28 А, I8 = 0,52 А.
Ток I1 определяется на основании первого закона Кирхгофа
I1 = I3 + I5 + I6 – I2 = 0,8 А.
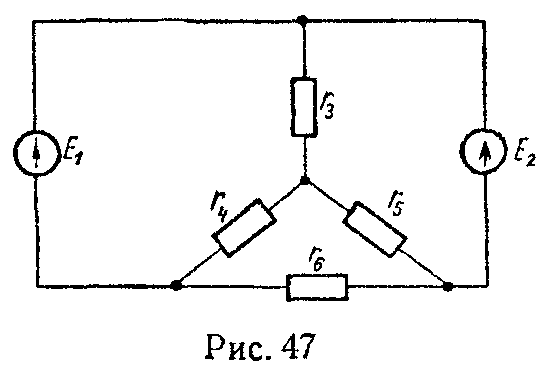
Задача 46. Методом узловых потенциалов рассчитать токи в цепи (рис. 47). Даны: E1 = 160 мВ, E2 = 300 мВ, r3 = r4 = 100 Ом, r5 = 150 Ом, r6 = 40 Ом. Внутренние сопротивления генераторов напряжения равны нулю.
Указание. Для решения задачи достаточно составить всего одно уравнение, так как в схеме имеется две ветви с э.д.с., но не содержащие сопротивления, а узлов в схеме четыре.
Ответ: I1 = 2,25 мА, I2 = 1,4 мА, I3 = 0,85 мА, I4 = 0,75 мА, I5 = 0,1 мА, I6 = 1,5 мА.
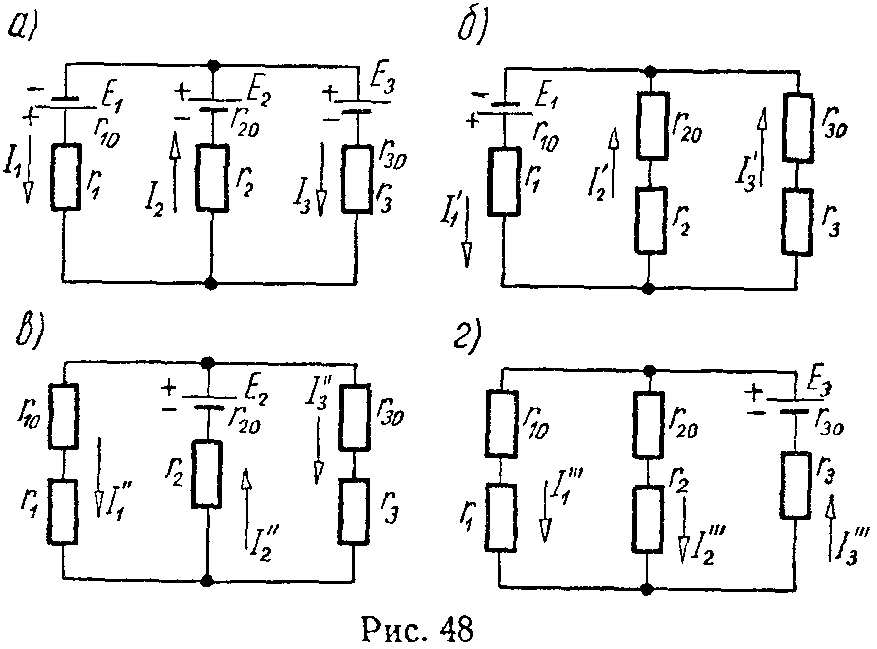
Задача 47. Методом наложения рассчитать токи в схеме (рис. 48. а), если E1 = 10 В, E2 = 40 В, E3 = 5 В, r10 = 5 Ом, r20 = r30 = 2 Ом, r1 = 30 Ом, r2 = 3 Ом, r3 = 8 Ом.
Решение
Сначала предполагаем, что действует только э.д.с. E1, а э.д.с. E2 и E3 считаем недействующими (рис. 48, б), тогда
I ′ 1 = E 1 r 1Э ,
где
r 1Э = r 1 + r 10 + ( r 2 + r 20 )⋅ ( r 3 + r 30 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) =35+ 5⋅10 15 = 115 3 Ом.
Ток
I ′ 1 = E 1 r 1Э = 10 115/3 = 6 23 А.
Токи в параллельных ветвях найдем согласно формуле (9)
I ′ 2 = I ′ 1 ⋅ ( r 3 + r 30 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) = 6 23 ⋅ 10 15 = 4 23 А, I ′ 3 = I ′ 1 ⋅ ( r 2 + r 20 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) = 6 23 ⋅ 5 15 = 2 23 А.
Теперь проведем расчет, предполагая, что действует э.д.с. E2, а э.д.с. E1 и E3 считаем недействующими (рис. 48, в)
I ″ 2 = E 2 r 2Э ; r 2Э = r 2 + r 20 + ( r 1 + r 10 )⋅ ( r 3 + r 30 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 115 9 Ом; I ″ 2 = E 2 r 2Э = 40 115/9 = 72 23 А; I ″ 1 = I ″ 2 ⋅ ( r 3 + r 30 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 72 23 ⋅ 10 45 = 16 23 А; I ″ 3 = I ″ 2 ⋅ ( r 1 + r 10 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 72 23 ⋅ 35 45 = 56 23 А.
Аналогично рассчитываем величины токов при действии только одной э.д.с. E3 (рис. 48, г)
I ? 3 = E 3 r 3Э ; r 3Э = r 3 + r 30 + ( r 1 + r 10 )⋅ ( r 2 + r 20 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 115 8 Ом; I ? 3 = E 3 r 3Э = 5 115/8 = 8 23 А; I ? 1 = I ? 3 ⋅ ( r 2 + r 20 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 8 23 ⋅ 5 40 = 1 23 А; I ? 2 = I ? 3 ⋅ ( r 1 + r 10 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 8 23 ⋅ 35 40 = 7 23 А.
Истинное значение тока в каждой ветви найдется как алгебраическая сумма токов, определяемых каждой э.д.с. в отдельности.
Ток в первой ветви
I 1 = I ′ 1 + I ″ 1 + I ? 1 = 6 23 + 16 23 + 1 23 =1 А.
Ток во второй ветви
I 2 = I ′ 2 + I ″ 2 − I ? 2 = 4 23 + 72 23 − 7 23 =3 А.
Ток в третьей ветви
I 3 =− I ′ 3 + I ″ 3 − I ? 3 =− 2 23 + 56 23 − 8 23 =2 А.
Направления этих токов показаны на рис. 48, а.
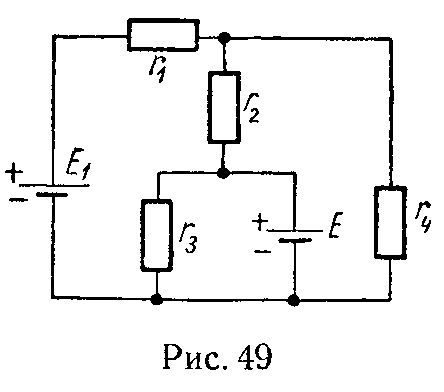
Задача 48. Найти токи в ветвях цепи, изображенной на рис. 49, если известны E1 = 125 мВ, E = 120 мВ, r1 = 40 Ом, r2 = 36 Ом, r3 = r4 = 60 Ом. Внутренними сопротивлениями источников пренебречь. Задачу решить методами наложения и контурных токов.
Ответ: I1 = 0,8 А, I2 = 0,75 А, I3 = 2 А, I4 = 1,55 А, I = 2,75 А.
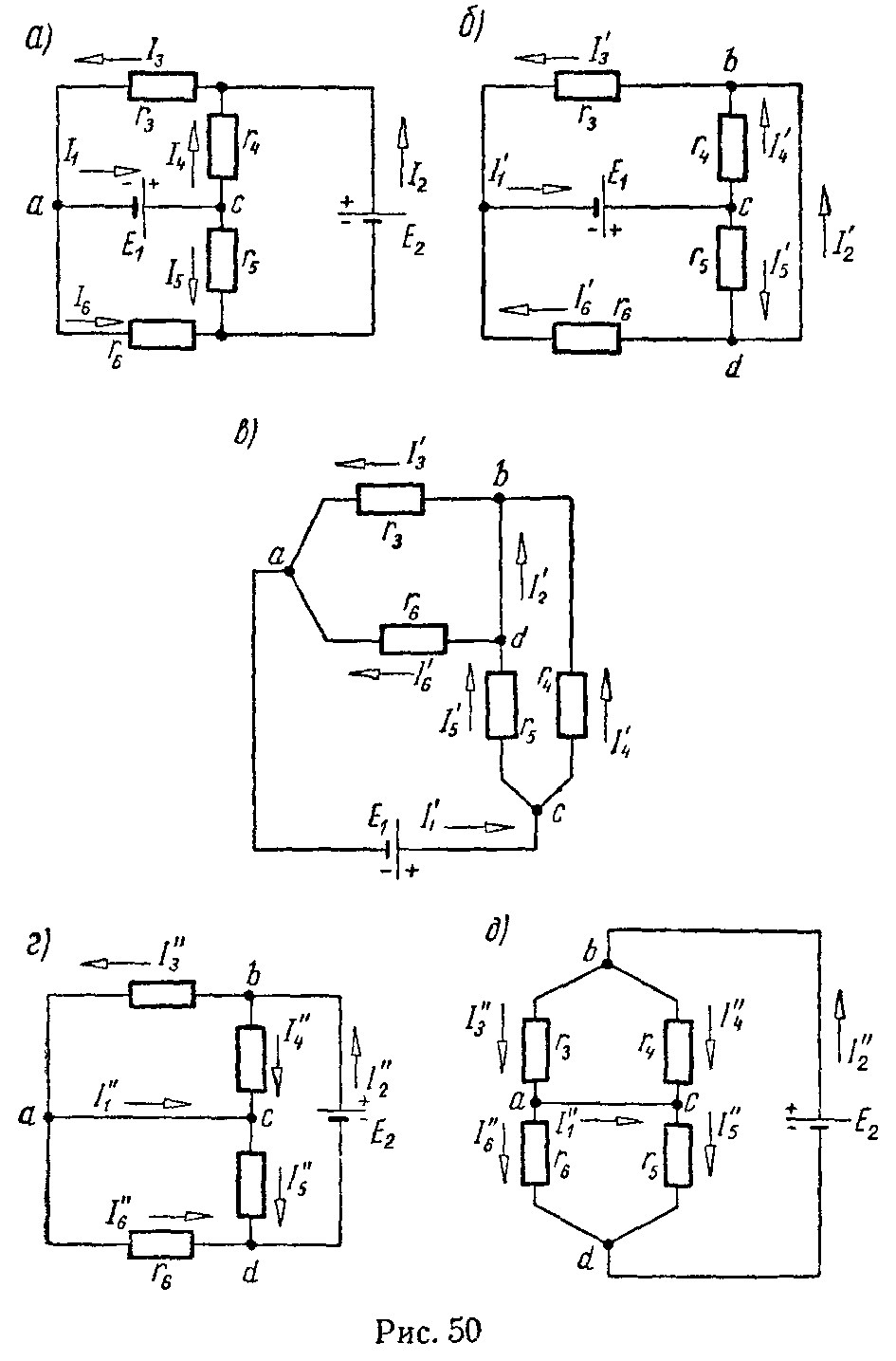
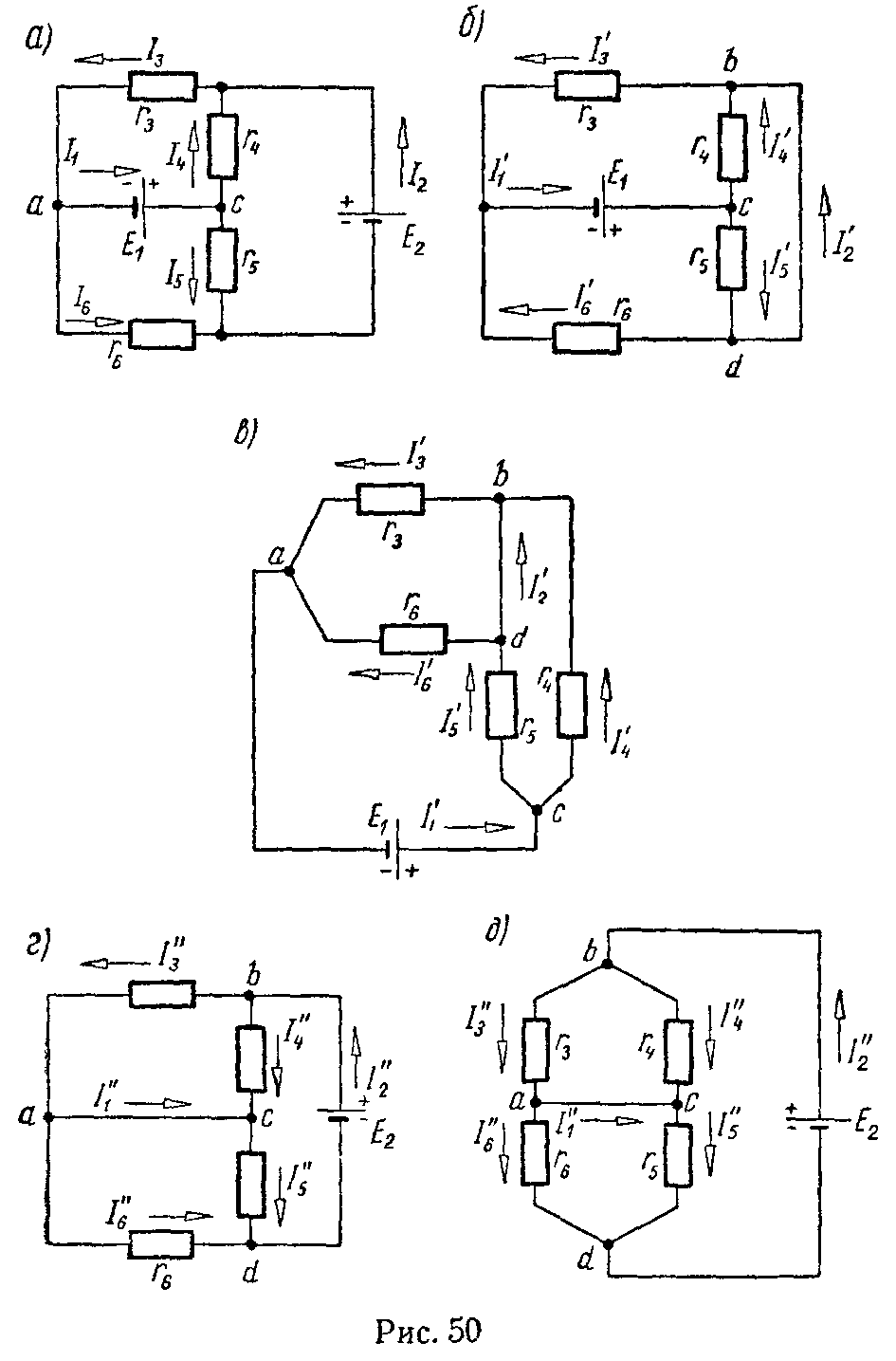
Задача 49. В схеме (рис. 50, а) методом наложения найти все токи. Внутренние сопротивления источников э.д.с. принять равными нулю. Электродвижущие силы и сопротивления элементов цепи имеют следующие значения: E1 = 96 В, E2 = 75 В, r3 = 3 Ом, r4 = 15 Ом, r5 = 10 Ом, r6 = 6 Ом.
Решение
Положим, что действует только э.д.с. E1, а э.д.с. E2 не действует. В этом случае схема примет вид, изображенный на рис. 50, б. Так как внутреннее сопротивление э.д.с. E2 равно нулю, то на его месте между точками b и d показано короткое замыкание. Для большей наглядности схему рис. 50, б можно начертить в виде, показанном на рис. 50, в.
Полное сопротивление этой схемы равно
r 1экв = r 3 ⋅ r 6 r 3 + r 6 + r 4 ⋅ r 5 r 4 + r 5 = 3⋅6 9 + 15⋅10 25 =8 Ом.
Определим все токи
I ′ 1 = E 1 r 1экв = 96 8 =12 А, I ′ 3 = I ′ 1 ⋅ r 6 r 3 + r 6 =12⋅ 6 9 =8 А; I ′ 6 = I ′ 1 − I ′ 3 =4 А; I ′ 4 = I ′ 1 ⋅ r 5 r 4 + r 5 =12⋅ 10 25 =4,8 А; I ′ 5 = I ′ 1 − I ′ 4 =7,2 А; I ′ 2 = I ′ 3 − I ′ 4 =8−4,8=3,2 А или I ′ 2 = I ′ 5 − I ′ 6 =3,2 А .
Теперь положим, что действует только э.д.с. E2, а э.д.с. E1 считаем недействующей (рис. 50, г).
Схему (рис. 50, г) для большей наглядности можно представить в виде, показанном на рис. 50, д. Ее полное сонротивление
r 2экв = r 3 ⋅ r 4 r 3 + r 4 + r 5 ⋅ r 6 r 5 + r 6 = 3⋅15 18 + 6⋅10 16 =6,25 Ом.
Вычислим все токи
I ″ 2 = E 2 r 2экв = 75 6,25 =12 А, I ″ 3 = I ″ 2 ⋅ r 4 r 3 + r 4 =12⋅ 15 18 =10 А; I ″ 4 = I ″ 2 − I ″ 3 =2 А; I ″ 6 = I ″ 2 ⋅ r 5 r 5 + r 6 =12⋅ 10 16 =7,5 А; I ″ 5 = I ″ 2 − I ″ 6 =4,5 А; I ″ 1 = I ″ 3 − I ″ 6 =10−7,5=2,5 А .
Складывая алгебраически токи, полученные от действия каждой э.д.с. в отдельности (рис. 50, б и 50, г), найдем истинные токи в каждой ветви (они нанесены на рис. 50, а)
I 1 = I ′ 1 + I ″ 1 =12+2,5=14,5 А, I 2 = I ′ 2 + I ″ 2 =3,2+12=15,2 А, I 3 = I ′ 3 + I ″ 3 =8+10=18 А, I 4 = I ′ 4 − I ″ 4 =4,8−2=2,8 А, I 5 = I ′ 5 + I ″ 5 =7,2+4,5=11,7 А, I 6 = I ′ 6 − I ″ 6 =7,5−4=3,5 А.
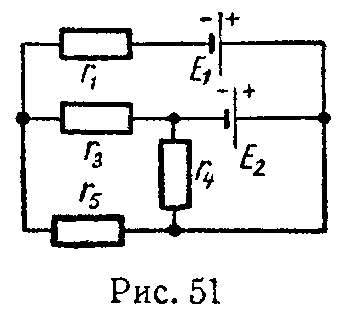
Задача 50. Для схемы (рис. 51) методами наложения, контурных токов и при помощи законов Кирхгофа найти все токи. Внутренние сопротивления источников электрической энергии считать равными нулю.
Дано: E1 = 90 В, E2 = 54 В, r1 = 30 Ом, r3 = 60 Ом, r4 = 24 Ом, r5 = 20 Ом.
Ответ: I1 = 1,7 А, I2 = 2,5 А, I3 = 0,25 А, I4 = 2,25 А, I5 = 1,95 А.
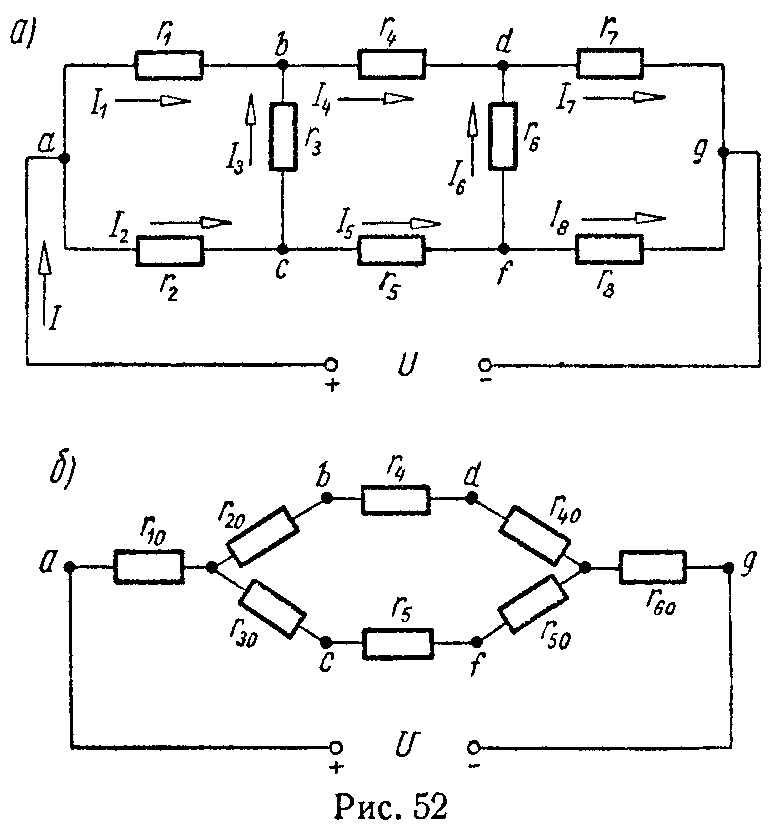
Задача 51. Найти эквивалентное сопротивление цепи (рис. 52, а) и все токи, если U = 114 В, r1 = 30 Ом, r2 = r3 = 10 Ом, r4 = 26 Ом, r5 = 11 Ом, r6 = 10 Ом, r7 = 40 Ом, r8 = 50 Ом. Задачу решить методом преобразования треугольника сопротивлений в эквивалентную звезду.
Решение
Заменим треугольники сопротивлений abc и dfg эквивалентными звездами (рис. 52, б).
Подсчитаем сопротивления лучей звезды r10, r20 и r30, эквивалентной треугольнику abc сопротивлений r1, r2 и r3 (формулы 17)
r 10 = r 1 ⋅ r 2 r 1 + r 2 + r 3 =6 Ом, r 20 = r 1 ⋅ r 3 r 1 + r 2 + r 3 =6 Ом, r 30 = r 2 ⋅ r 3 r 1 + r 2 + r 3 =2 Ом.
Сопротивления лучей звезды r40, r50, r60 эквивалентной треугольнику dfg сопротивлений r6, r7, r8, равны
r 40 = r 6 ⋅ r 7 r 6 + r 7 + r 8 =4 Ом, r 50 = r 6 ⋅ r 8 r 6 + r 7 + r 8 =5 Ом, r 60 = r 7 ⋅ r 8 r 6 + r 7 + r 8 =20 Ом.
Эквивалентное сопротивление всей схемы
r Э = r 10 + r I ⋅ r II r I + r II + r 60 =38 Ом,
где
r I = r 20 + r 4 + r 40 =36 Ом, r II = r 3 + r 5 + r 50 =18 Ом.
Ток в неразветвленной части цепи
I= U r Э = 114 38 =3 А.
Токи в параллельных ветвях I’ (r20r4r40) и I» (r30r5r50)
I ′ =I⋅ r II r I + r II =3⋅ 18 36+18 =1 А; I ″ =I⋅ r I r I + r II =3⋅ 36 36+18 =2 А.
Теперь найдем токи в сопротивлениях заданной цепи. Для этого предварительно из схемы (рис. 52, б) найдем напряжения между точками a и b, a и c, b и c, d и g, f и g, d и f
U ab =I⋅ r 10 + I ′ ⋅ r 20 =3⋅6+1⋅6=24 В; U ac =I⋅ r 10 + I ″ ⋅ r 30 =3⋅6+2⋅2=22 В; U ab − U ac = ( φ a − φ b )− ( φ a − φ c )= φ c − φ b = U cb =24−22=2 В; U dg = I ′ ⋅ r 40 +I⋅ r 60 =1⋅4+3⋅20=64 В; U fg = I ″ ⋅ r 50 +I⋅ r 60 =2⋅5+3⋅20=70 В; U fg − U dg = ( φ f − φ g )− ( φ d − φ g )= φ f − φ d = U fd =70−64=6 В.
искомые токи будут
I 1 = U ab r 1 = 24 30 =0,8 А, I 2 = U ac r 2 = 22 10 =2,2 А, I 3 = U cb r 3 = 2 10 =0,2 А, I 4 = I ′ =1 А, I 5 = I ″ =2 А, I 6 = U fd r 8 = 6 10 =0,6 А, I 7 = U dg r 7 = 64 40 =1,6 А, I 8 = U fg r 8 = 70 50 =1,4 А.
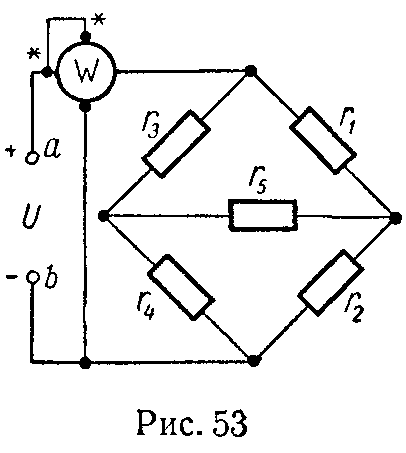
Задача 52. В схеме (рис. 53) найти токи, применив преобразование треугольника в звезду. Определить эквивалентное сопротивление между точками a и b.
Приложенное напряжение U = 30 В; сопротивления: r1 = 60 Ом, r2 = 120 Ом, r3 = 180 Ом, r4 = 80 Ом, r5 = 120 Ом.
Определить показание ваттметра и убедиться в том, что оно равно сумме мощностей, расходуемых во всех сопротивлениях.
Ответ: I = 0,3 А, I1 = 0,2 А, I2 = 0,15 А, I3 = 0,1 А, I4 = 0,15 А, I5 = 0,05 А, rab = 100 Ом, P = 9 Вт.
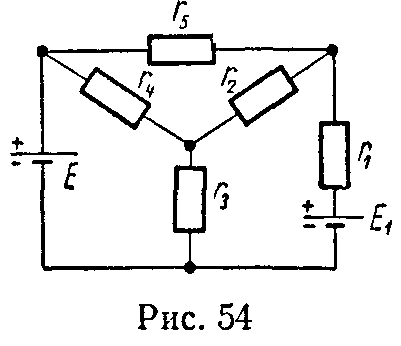
Задача 53. Вычислить токи, проходящие во всех ветвях схемы (рис. 54), если E = 213 В, E1 = 90 В, r1 = 6 Ом, r2 = 40 Ом, r3 = 10 Ом, r4 = 100 Ом, r5 = 60 Ом.
Задачу решить преобразованием треугольника в эквивалентную звезду. Внутренними сопротивлениями источников напряжения пренебречь.
Определить входное сопротивление относительно ветви r1 и взаимное сопротивление ветвей r1 и r2.
Ответ: I = 3,8 А, I1 = 0,5 А, I2 = 1,5 А, I3 = 3,3 А, I4 = 1,8 А, I5 = 2 А, r11 = 33 Ом, r12 = 60 Ом.
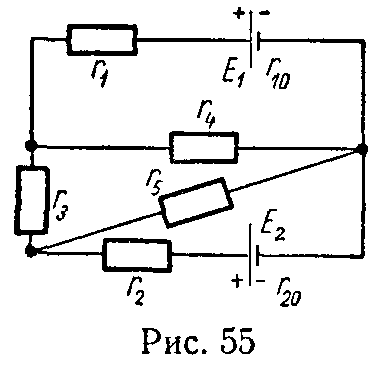
Задача 54. Определить величины токов, проходящих по цепи, схема которой показана на рис. 55.
Данные цепи: E1 = 100 В, E2 = 140 В, r1 = 15 Ом, r2 = 5 Ом, r3 = 10 Ом, r4 = 4 Ом, r5 = 50 Ом, r10 = r20 = 0.
Задачу решить методами контурных токов и узловых потенциалов.
Ответ: I1 = 4 А, I2 = 8 А, I3 = 6 А, I4 = 10 А, I5 = 2 А.
Задача 55. Для схемы (рис. 56, а) найти методом эквивалентного генератора напряжения ток в ветви с сопротивлением r1, если E1 = 18 В, E2 = 21 В, r10 = 1 Ом, r1 = 2 Ом, r20 = 0, r2 = 9 Ом, r3 = 6 Ом.
Решение
Разомкнем цепь, содержащую сопротивление r1, и найдем напряжение между точками m и n (рис. 56, б).
Очевидно, что в разомкнутой ветви тока нет, точки m и p равнопотенциальны (φm = φp), а потенциал точки q превышает потенциал точки n на величину φq — φn = E1.
Имея это в виду, определим Ux = Umn
φm = φp, φn = φq — E1,
φm — φn = φp — φq + E1, Umn = Upq + E1.
Найдем напряжение Upq. Для этого сначала определим ток в контуре psqp
I= E 2 r 2 + r 20 + r 3 = 21 15 =1,4 А.
По закону Ома
Upq = I·r3 = 1,4·6 = 8,4 В.
Окончательно
Ux = Umn = Upq + E1 = 8,4 + 18 = 26,4 В.
Для нахождения тока в ветви r1 сначала определим сопротивление короткого замыкания (рис. 56, в)
r k = r 2 ⋅ r 3 r 2 + r 3 = 9⋅6 15 =3,6 Ом.
Искомый ток
I 1 = U x r 1 + r 10 + r k = 26,4 1+2+3,6 =4 А.
Этот ток течет от точки m к точке n.
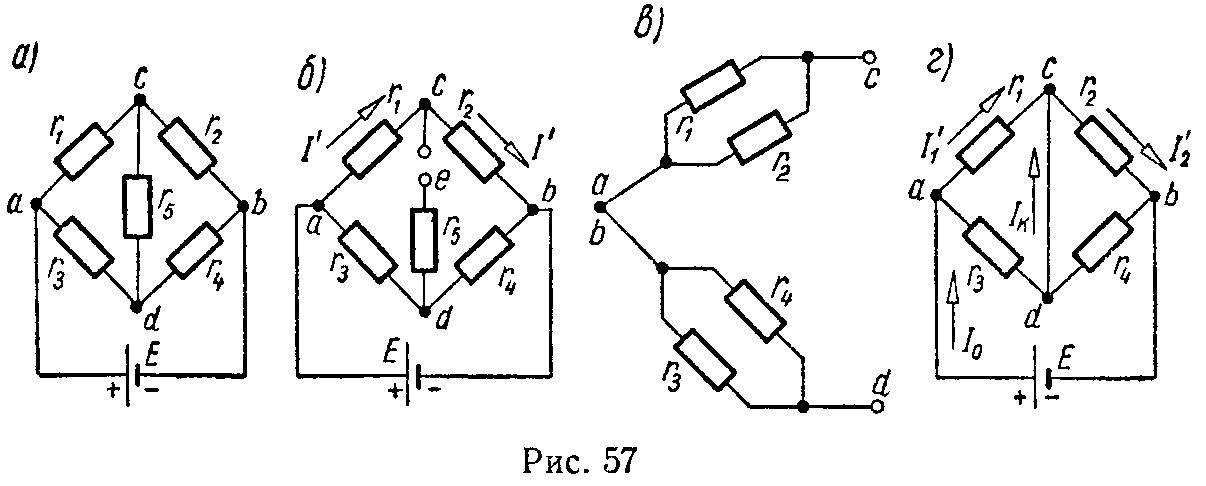
Задача 56. Методом эквивалентного генератора напряжения найти ток (рис. 57, а), проходящий через сопротивление r5, если E = 120 В, r1 = 60 Ом, r2 = 15 Ом, r3 = 90 Ом, r4 = 60 Ом, r5 = 12 Ом. Внутреннее сопротивление источника напряжения равно нулю.
Решение
Разомкнем сопротивление r5 и. найдем напряжение между точками c и e (рис. 57, б).
Через сопротивления r1 и r2 протекает ток I’, а через r3 и r4 ток I»
I ′ = E r 1 + r 2 = 120 75 =1,6 А, I ″ = E r 3 + r 4 = 120 150 =0,8 А, φ a − φ c = U ac = I ′ ⋅ r 1 =1,6⋅60=96 В, φ a − φ d = U ad = I ″ ⋅ r 3 =0,8⋅90=72 В, ( φ a − φ c )− ( φ a − φ d )= φ d − φ c = U dc =24 В.
Но так как φd = φe, то Udc = Uec. Итак, напряжение холостого хода Ux = 24 В.
Теперь найдем сопротивление короткого замыкания. Определим его двумя способами.
1) Путем непосредственного подсчета по схеме.
В этом случае надо э.д.с. выключить, оставив ее внутреннее сопротивление, равное в данном случае нулю (рис. 57, в). Сопротивление короткого замыкания двухполюсника равно сопротивлению цепи между точками c и d
r k = r 1 ⋅ r 2 r 1 + r 2 + r 3 ⋅ r 4 r 3 + r 4 = 60⋅15 75 + 90⋅60 150 =48 Ом.
2) То же сопротивление можно найти и другим путем. Для этого надо замкнуть точки c и d накоротко, вычислить ток Iк, протекающий через короткозамкнутый участок (рис. 57, г), и сопротивление короткого замыкания определить по формуле (20).
Сопротивление схемы равно
r cx = r 1 ⋅ r 3 r 1 + r 3 + r 2 ⋅ r 4 r 2 + r 4 = 60⋅90 150 + 15⋅60 75 =48 Ом.
Найдем токи в ветвях
I 0 = E r cx = 120 48 =2,5 А, I ′ 1 = I 0 ⋅ r 3 r 1 + r 3 =2,5⋅ 90 150 =1,5 А, I ′ 2 = I 0 ⋅ r 4 r 2 + r 4 =2,5⋅ 60 75 =2 А.
Отсюда
I k = I ′ 2 − I ′ 1 =0,5 А.
Сопротивление короткого замыкания (формула 20) равно
r k = U x I k = 24 0,5 =48 Ом.
Искомый ток находим по формуле (21)
I 5 = U x r 5 + r k = 24 12+48 =0,4 А.
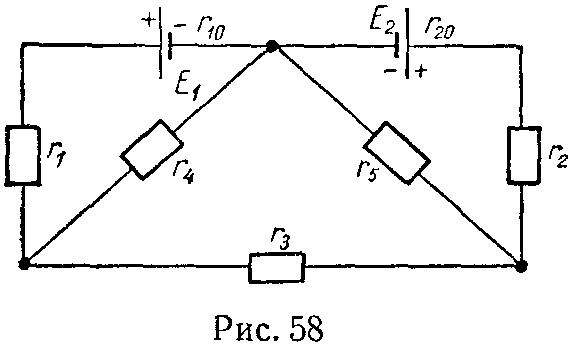
Задача 57. Для схемы (рис. 58) методом эквивалентного генератора напряжений найти ток в ветви с сопротивлением r3, если E1 = 5 В, E2 = 7 В, r1 = 7,5 Ом, r2 = 2,5 Ом, r3 = 5 Ом, r4 = 2 Ом, r5 = 25 Ом, r10 = r20 = 0.
Ответ: I3 = 0,6 А.
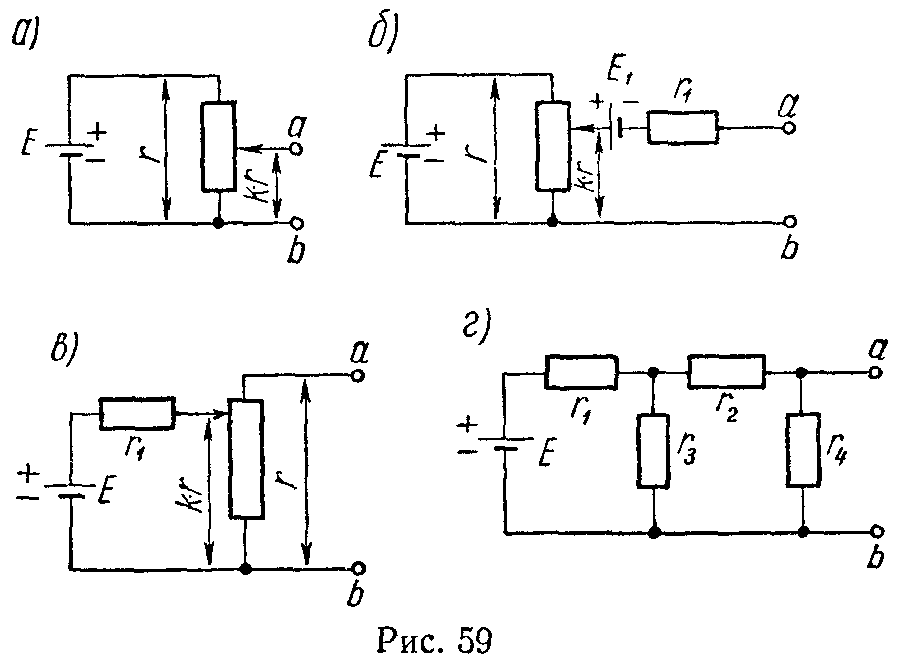
Задача 58. Пользуясь методом эквивалентного генератора напряжений, найти э.д.с. и внутреннее сопротивление источников, эквивалентных каждой из схем (рис. 59 а, б, в и г; 0 < k < 1). Внутренние сопротивления источников энергий равны нулю.
Ответ: 1) U0 = k·E, rk = k· (1 — k)·r; 2) U0 = k·E — E1, rk = r1 + k· (1 — k)·r;
3) U 0 = k⋅E⋅r r 1 +k⋅r , r k = ( 1−k )⋅r+ k⋅r⋅ r 1 k⋅r+ r 1 ;
4) U 0 = E⋅ r 3 r 4 r 1 r 2 + r 1 r 3 + r 1 r 4 + r 2 r 3 + r 3 r 4 , r k = r 4 ⋅ ( r 1 r 2 + r 1 r 3 + r 2 r 3 ) r 1 r 2 + r 1 r 3 + r 1 r 4 + r 2 r 3 + r 3 r 4 .
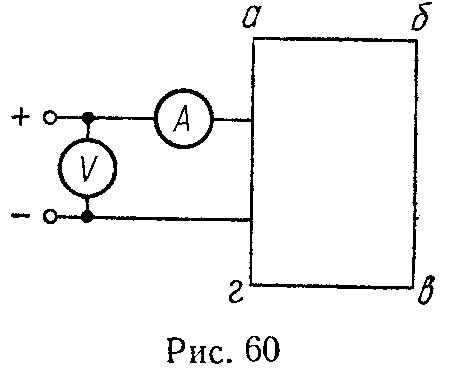
Задача 59. По показаниям приборов, полученным из двух опытов, найти э.д.с. и внутреннее сопротивление источника электрической энергии, эквивалентного схеме (рис. 60), в случаях:
|
1) |
U, B |
I, A |
2) |
U, B |
I, A |
3) |
U, B |
I, A |
|
20 |
2 |
20 |
12 |
20 |
3 |
|||
|
30 |
3 |
30 |
14 |
30 |
5 |
Примечание. В части схемы, обведенной на рис. 60 четырехугольником абвг и называемой двухполюсником, в действительности может быть включено большое количество различных э.д.с. и сопротивлений так, что полный расчет занял бы слишком много времени. Поэтому решено ограничиться экспериментальным исследованием двухполюсника, результаты которого помещены в таблице данных.
Ответ: 1) сопротивление 10 Ом. 2) источник энергии с э.д.с. 40 В и внутренним сопротивлением 5 Ом. 3) источник энергии с э.д.с. 5 В и внутренним сопротивлением 5 Ом.
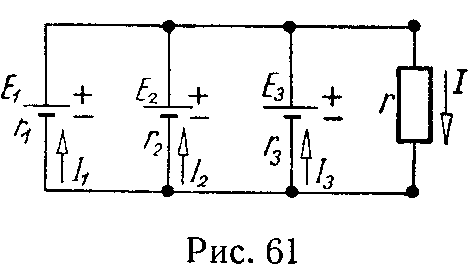
Задача 60. Три генератора напряжений, э.д.с. которых E1 = 48 В, E2 = 45 В, E3 = 45 В, а внутренние сопротивления r1 = 1,2 Ом, r2 = 1 Ом, r3 = 1,5 Ом, работают параллельно на общую нагрузку, сопротивление которой r = 4,2 Ом (рис. 61).
Произвести замену заданных генераторов напряжений одним эквивалентным, определив его э.д.с. и внутреннее сопротивление. Чему равны токи, протекающие через каждый генератор и нагрузку?
Решение
Значения э.д.с. и внутреннего сопротивления эквивалентного генератора напряжения могут быть определены по формулам (23)
E Э = E 1 ⋅ 1 r 1 + E 2 ⋅ 1 r 2 + E 3 ⋅ 1 r 3 1 r 1 + 1 r 2 + 1 r 3 = 115 2,5 =46 В, 1 r Э = 1 r 1 + 1 r 2 + 1 r 3 =2,5 1 Ом , r Э = 1 2,5 =0,4 Ом.
Ток в нагрузке
I= E Э r+ r Э = 46 4,2+0,4 =10 А.
Напряжение на нагрузке
U=I⋅r=10⋅4,2=42 В.
Таково же напряжение на каждой из параллельных ветвей. Ток в каждой из ветвей найдем по формуле (25)
I 1 = E 1 −U r 1 = 48−42 1,2 =5 А, I 2 = E 2 −U r 2 = 45−42 1 =3 А, I 3 = E 3 −U r 3 = 45−42 1,5 =2 А.
Проверка показывает, что ток в нагрузке I равен сумме трех токов: I1, I2 и I3.
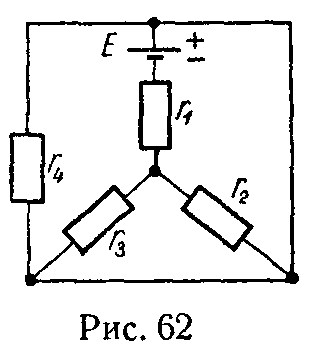
Задача 61. Для цепи, изображенной на рис. 62, проверить принцип взаимности, если э.д.с. E переместить в ветвь с сопротивлением r3.
Даны: E = 80 В, r1 = 8 Ом, r2 = 20 Ом, r3 = 30 Ом, r4 = 12 Ом.
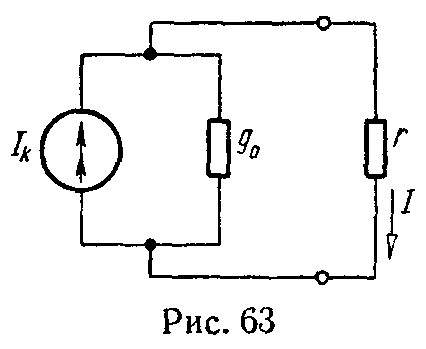
Задача 62. Определить ток, проходящий через сопротивление r = 5 Ом, подключенное к генератору тока (рис. 63), параметры которого имеют следующие величины: ток Ik = 6 мА, внутренняя проводимость g0 = 0,04 1/Ом.
Решение
Внутреннее сопротивление генератора тока
r 0 = 1 g 0 = 1 0,04 =25 Ом.
Ток Ik распределяется по двум параллельным ветвям r и r0 обратно пропорционально их сопротивлениям. Поэтому искомый ток
I= I k ⋅ r 0 r 0 +r =6⋅ 25 25+5 =5 мА.
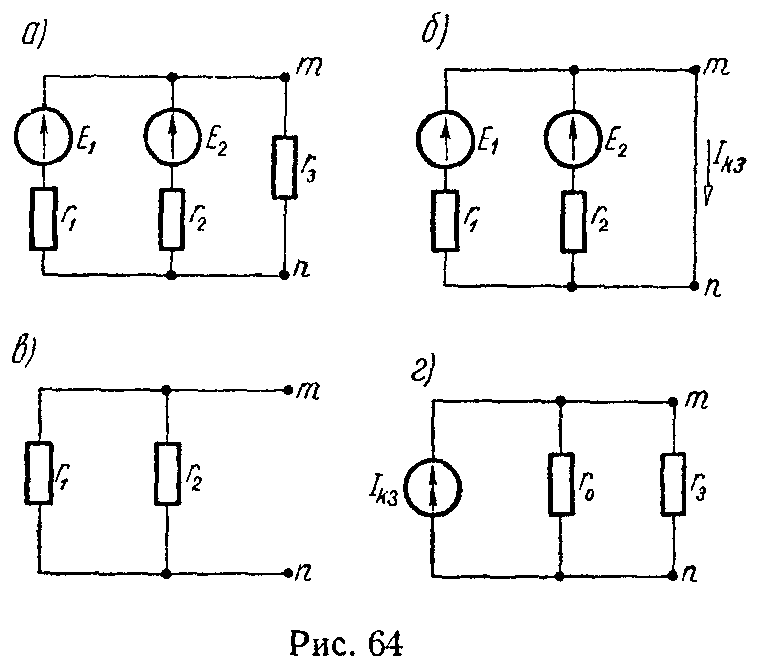
Задача 63. Пользуясь теоремой об эквивалентном генераторе тока, определить ток I3 в ветви r3 = 12 Ом (рис. 64, а). Электродвижущие силы генераторов напряжения равны E1 = 120 В, E2 = 100 В, их внутренние сопротивления r1 = 6 Ом, r2 = 4 Ом.
Решение
Из теории известно, что ток эквивалентного генератора тока равен току короткого замыкания Iкз, проходящему между короткозамкнутыми зажимами m и n, к которым подключена данная ветвь (рис. 64, б)
I кз = E 1 r 1 + E 2 r 2 =45 А,
а внутренняя проводимость генератора тока равна проводимости пассивной цепи между зажимами m и n при разомкнутой ветви r3 (рис. 64, в)
g 0 = 1 r 1 + 1 r 2 = 5 12 1 Ом , r 0 = 1 g 0 =2,4 Ом.
Схема эквивалентного генератора тока представлена на рис. 64 г.
Искомый ток
I 3 = I кз ⋅ r 0 r 0 + r 3 =45⋅ 2,4 2,4+12 =7,5 А.
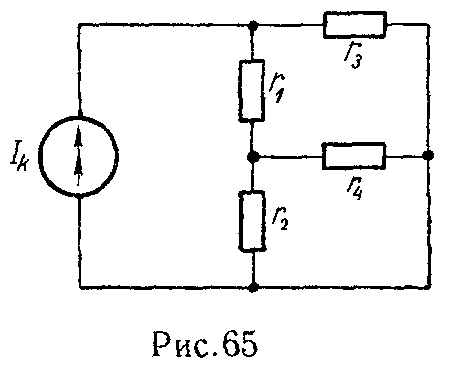
Задача 64. Генератор тока создает в цепи ток Ik = 30 мА (рис. 65). Внутренней проводимостью генератора можно пренебречь.
Чему равны токи в ветвях, сопротивления которых равны r1 =1,8 кОм, r2 = 3 кОм, r3 = 1,5 кОм, r4 = 2 кОм.
Ответ: I1 = 10 мА, I2 = 4 мА, I3 = 20 мА, I4 = 6 мА.
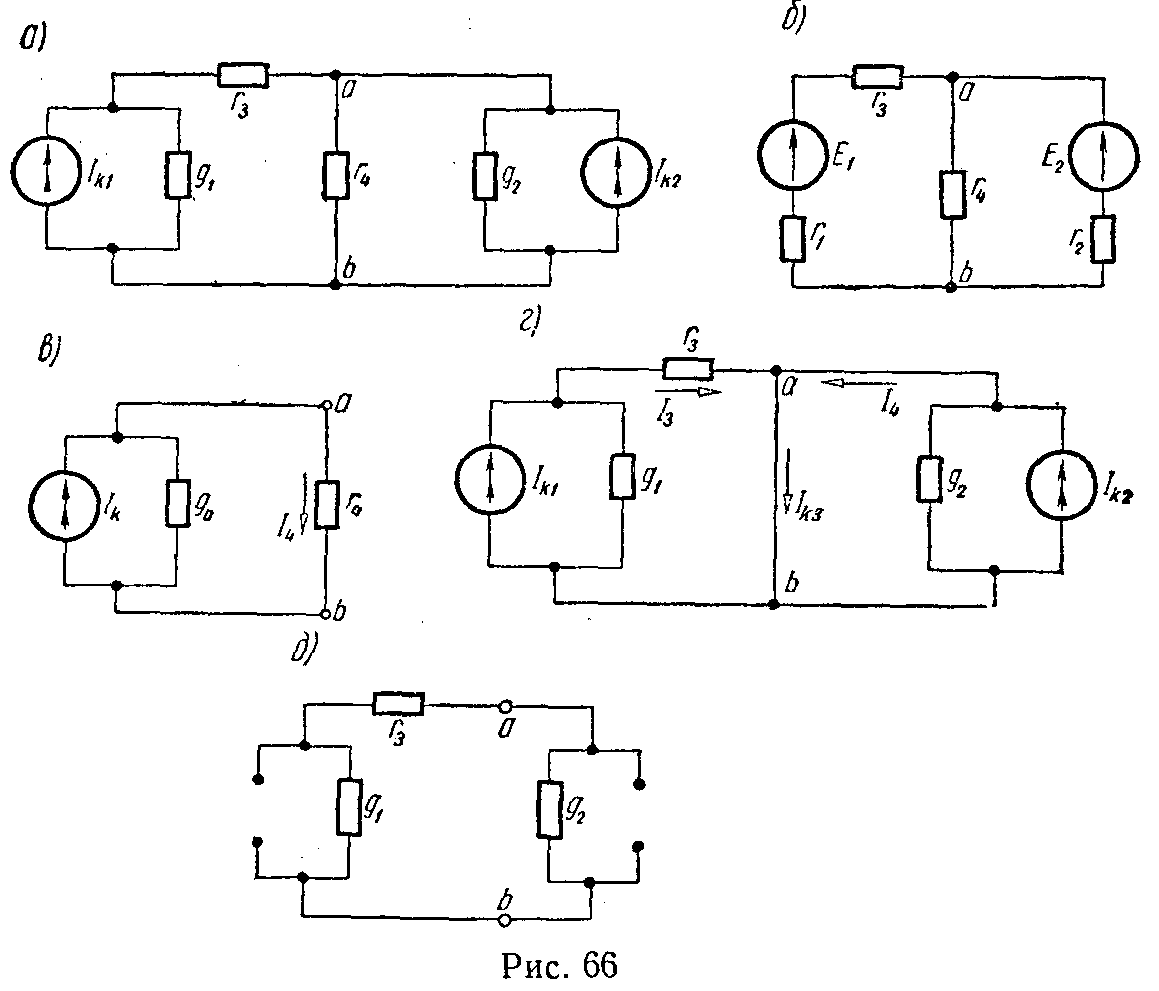
Задача 65. Два генератора тока соединены в цепь, показанную на рис. 66, а. Ток первого генератора Ik1 = 3 мА, его внутренняя проводимость g1 = 0,05 1/Ом, второго — Ik2 = 2 мА, g2 = 0,01 1/Ом. Сопротивления равны: r3 = 5 Ом, r4 = 30 Ом.
Определить ток, проходящий через сопротивление r4.
Решение
1-й способ. Преобразуем генераторы тока в эквивалентные генераторы напряжения, получим схему рис. 66, б. Э.д.с. и внутренние сопротивления генераторов напряжения находим по формулам (2)
E 1 = I k1 g 1 = 3 0,05 =60 мВ, r 1 = 1 g 1 = 1 0,05 =20 Ом, E 2 = I k2 g 2 = 2 0,01 =200 мВ, r 2 = 1 g 2 = 1 0,01 =100 Ом.
Далее, любым способом находим искомый ток. Обозначим
По методу узловых потенциалов находим
U ab = E 1 ⋅ 1 r 1 + r 3 + E 2 ⋅ 1 r 2 1 r 1 + r 3 + 1 r 2 + 1 r 4 = 60⋅ 1 20+5 +200⋅ 1 100 1 20+5 + 1 100 + 1 30 =52,8 мВ.
Искомый ток
I 4 = U ab r 4 = 52,8 30 =1,76 мА.
2-й способ. Решим задачу методом эквивалентного генератора тока. Для этого заменим всю цепь, за исключением ветви с r4 эквивалентным генератором тока (рис. 66, в). Для определения его параметров Ik и g0 сначала исключим ветвь с r4, а точки a и b закоротим (рис. 66, г). Найдем ток короткого замыкания Iкз. Предварительно определим токи I3 и I4
I 3 = I k1 ⋅ 1 g 1 1 g 1 + r 3 =3⋅ 20 25 =2,4 мА, I 4 = I k2 =2 мА .
Следовательно, ток эквивалентного генератора тока
Ik = I3 + I4 = 2,4 + 2 = 4,4 А.
Теперь определим внутреннюю проводимость эквивалентного генератора тока g0 между точками a и b. Для этого исключим генераторы токов и оставим лишь их внутренние сопротивления (рис. 66, д)
g 0 = g ab = 1 1 g 1 + r 3 + g 2 = 1 20+5 +0,01=0,05 См .
Ток в искомой ветви (рис. 66, в) равен
I 4 = I k ⋅ 1 g 0 1 g 0 + r 4 =4,4⋅ 20 20+30 =1,76 мА .
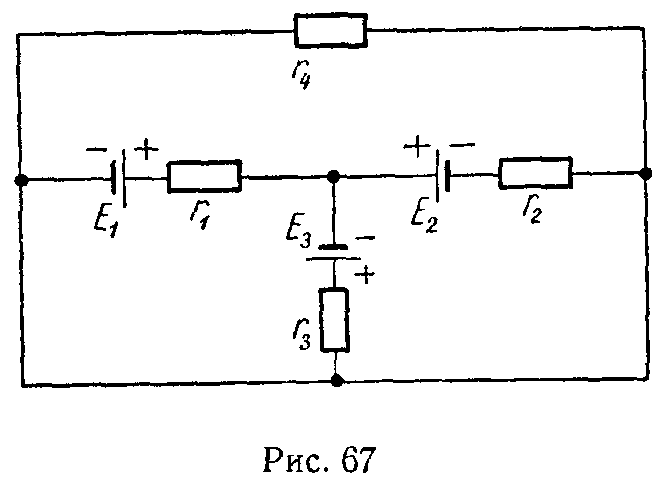
Задача 66. В схеме рис. 67 простейшим способом вычислить токи. Даны: E1 = 100 В, E2 = 80 В, E3 = 40 В, r1 = 10 Ом, r2 = 10 Ом, r3 = 20 Ом, r4 = 30 Ом.
Внутренние сопротивления источников напряжения равны нулю.
Ответ: I1 = 3,6 А, I2 = 1,6 А, I3 = 5,2 А, I4 = 0.
В начало статьи Линейные электрические цепи постоянного тока

Генератор напряжения,
закон Ома,
обобщенный закон Ома,
Законы Кирхгофа,
первый закон Кирхгофа,
второй закон Кирхгофа,
метод контурных токов,
метод узловых потенциалов,
метод наложения,
Метод эквивалентных преобразований,
метод эквивалентного генератора,
метод активного двухполюсника,
принцип взаимности,
принцип компенсации,
входная проводимость,
взаимная проводимость,
баланс мощностей
Расчет простых цепей постоянного тока
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.
Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
А затем напряжение
Зная напряжения, найдем токи, протекающие через резисторы
Как видите, токи получились теми же.
Пример 3
В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
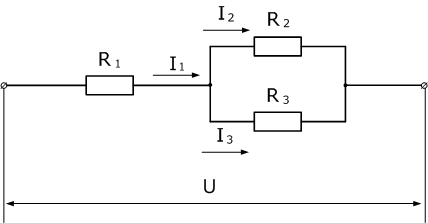
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Эквивалентное сопротивление и ток в цепи

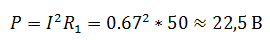
Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2
Таким образом производится расчет простых цепей постоянного тока.
Применение закона Ома к расчету линейных электрических цепей постоянного тока
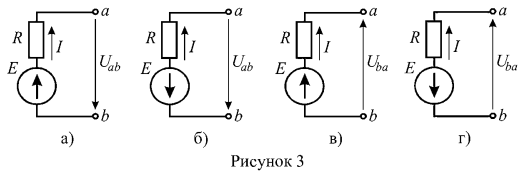
1. Найти ток ветви (рисунок 3), если: U=10 В, Е=20 В, R=5 Ом.
Решение:
Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
Аналогично определяются токи в схемах б, в, г рисунка 3:
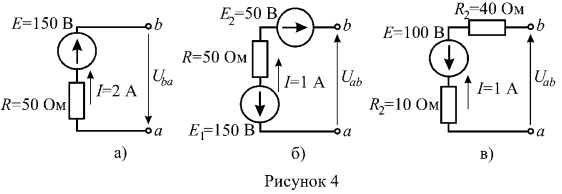
2. Найти напряжение между зажимами нетвей (рисунок 4).
Решение:
Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:
откуда выразим напряжение на зажимах:
Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.
3. Определить неизвестные потенциалы точек участка цени (рисунок 5).
Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:
откуда выразим напряжение на зажимах ветви:
Если представить напряжение как разность потенциалов:
тогда при известных параметрах цепи, токе и потенциале определим потенциал
:
Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС , без учета внутреннего сопротивления источника, по величине равно
и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
и тогда, зная потенциал , определим потенциал точки С:
Потенциал точки d больше потенциала точки С на величину падения напряжения на сопротивлении R:
тогда
Потенциал точки а определяем с учетом направления напряжения на зажимах источника ЭДС
. Напряжение
направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
откуда следует, что
или
Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки С, параметрах элементов и токе, определим потенциалы крайних точек участка цепи . Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
откуда следует
Напряжение на участке с — а, равное по величине Е, направлено от точки с большим потенциалом к точке с меньшим потенциалом:
4. В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: , входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением
. Определить величину сопротивления резистора
.
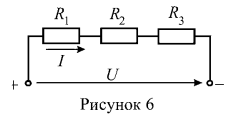
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:
или, согласно закону Ома:
По известному значению мощности на резистивном элементе и величине сопротивления этого элемента определим ток в ветви:
По закону Ома напряжение на зажимах определится:
тогда величина сопротивления резистивного элемента:
5. Определить показания вольтметров цепи (рисунок 7), если .
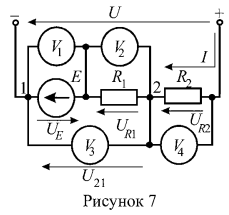
Ток в цепи определим по закону Ома:
Вольтметр показывает напряжение на источнике ЭДС Е:
Вольтметры показывают величину падения напряжения на резистивных элементах
:
Вольтметр , показывает напряжение на участке 2 — 1
, которое определим как алгебраическую сумма напряжений
:
6. Ток симметричной цепи (рисунок 8) , внутреннее сопротивлении источника ЭДС
. Определить ЭДС Е и мощность источника энергии.
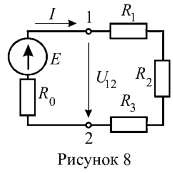
Напряжение на зажимах 1 — 2 определим по закону Ома для пассивной ветви:
Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:
Мощность, развиваемая источником энергии, определится:
Соловьев Валерий Иванович
преподаватель – методист высшей категории
Таврический колледж ФГАОУ ВО «Крымский
федеральный университет имени В. И. Вернадского»
г. Симферополь, Республика Крым
Решение типовых задач по расчету электрических цепей
постоянного и переменного тока
Изучение электротехники предусматривает овладение теоретическими
знаниями и приобретение определенных практических навыков. Особая роль в этом
процессе, наряду с выполнением лабораторных и практических работ, отводится
решению задач, которые позволяют использовать полученные теоретические сведения
по конкретным разделам и темам электротехники.
Настоящее методическое пособие предназначено для закрепления
теоретического материала по разделам:
·
Электрическое и магнитное
поле;
·
Электрические цепи
постоянного тока;
·
Электрические цепи
переменного тока.
Пособие содержит
примеры решения типовых задач по электротехнике.
Раздел 1. Элетрическое и магнитное поле
Задача №1
В
электрическом поле при перемещении заряда q = 2•10‾4
к совершена работа A = 0,4 дж. Определить напряжение между
начальной и конечной точками пути.
Решение:
U = =
= 2000
в = 2 кв.
Ответ:
Напряжение между начальной и конечной точками пути при перемещении заряда q
= 2•10‾4 к равно 2 кв .
Задача №2
Определить напряженность магнитного поля и магнитную
индукцию в точках, расположенных на расстояниях 0,2; 0,4 и 1
см от оси прямолинейного провода. Радиус провода r = 0,4
см; электрический
ток в проводе I = 50А и магнитная проницаемость μ
= 1.
Решение:
Точка, лежащая на расстоянии 0,2
см от оси провода, находится внутри провода:
H =
=
= 1000
;
B = μ
• H
= 4
• 10
•2000 = 25 гс.
Точка, лежащая на расстоянии 0,4
см от оси провода, находится на его поверхности:
H =
=
= 2000
;
B = μ
• H
= 4
= 25 гс.
Точка, лежащая на расстоянии 1
см, лежит за пределами провода:
H =
=
= 800
;
B = μ
• H
= 4
= 10 гс.
Ответ: Напряженность
магнитного поля и магнитная индукция в точках, расположенных на расстояниях 0,2;
0,4 и 1 см от оси прямолинейного провода равна
H = 1000
;
B = 25 гс.
H = 2000
;
B = 25 гс.
H = 800
;
B = 10 гс.
Раздел 2. Электрические цепи постоянного тока
Задача №3
Найти сопротивление между точками А и D,
приведенной на рисунке электрической схемы, если каждое из трех сопротивлений
равно 1 Ом. (Сопротивлением соединительных проводов пренебречь).
Решение:
Так как точки А и С, а также точки В и D
соединены проводниками, сопротивление которых мы не учитываем, то схему представленную
в условии задачи можно заменить эквивалентной схемой.
Из нее видно, что сопротивление между точками А и D можно
вычислить по формуле для параллельного соединения проводников.
=
+
+
=
;
Откуда
R =
=
0,33 Ом.
Ответ: Сопротивление между
точками А и D равно
R
0,33 Ом.
Задача №4
Мощность, потребляемая нагрузочным сопротивлением RH = 9,9 Ом, измеряется с помощью
вольтметра и амперметра. Вольтметр показывает 120В, амперметр 12А.
Считая, что показания приборов не содержат
погрешностей (ошибки исключены с помощью поправок), подсчитать мощность, выделяющуюся
в сопротивлении RH. Найти погрешность измерения
мощности.
Решение:
Мощность, выделяющаяся в сопротивлении Rн , подсчитанная по показаниям приборов,
Риз
= UI = 120 ∙ 12 = 1440 Вт,
Действительное значение этой мощности
Р = I∙ Rн = 122 ∙ 9,9 = 1425,6 Вт.
Абсолютная погрешность измерения
ΔP = Риз – Р = 1440 —
1425,6 = 14,4 Вт.
Относительная
погрешность измерения
δ = ΔP/Р = 14,4/1425,6 = 0,0101 ≈ 1%.
Таким образом,
проведя измерение абсолютно точными приборами, получаем значение мощности, на 1
% отличающееся от действительного.
Такая погрешность, вызванная
самой схемой измерения, называется систематической или методической.
Эта погрешность
может быть найдена и непосредственно по известной формуле
δ = RA / Rн
Внутреннее
сопротивление амперметра
RA =
– Rн =
– 9,9 = 0,1 Ом
Погрешность
δ = RA / Rн = 0,1/9,9 = 0,0101.
Ответ: Погрешность измерения мощности δ
= 0,0101 ≈ 1%.
Задача №5
Для изготовления обмотки нагревательного прибора при напряжении
220 В и токе 2 А применяется нихромовая лента. Определить длину
ленты, приняв допустимую плотность тока δ = 10 :
ρнихрома= 1,1 – удельное сопротивление нихрома.
Решение:
S = =
= 0,2 мм
.
Сопротивление обмотки
r
= =
= 110 ом.
Определяем
длину ленты
l = =
= 20
м.
Ответ: Длина нихромовой
ленты равна 20 м.
Задача №6
Определить сопротивление медного провода линии передачи
сечением
S = 95мм, длиной l = 120
км при
температурах О и 20 °С.
ρмеди= 0,0175 – удельное сопротивление меди.
αмеди = 0,004
– температурный коэффициент меди.
Решение:
r = ρ•
;
так
как ρ задано как раз для температуры 20° С, то, подставляя значения l и S, находим:
r = 0,0175 •
= 21,7 ом.
Сопротивление провода при 0° С
r = r
•
=21,7 + 21,7 • 0,004 (-20
C) = 20 ом.
Ответ: Сопротивление медного провода линии
передачи сечением S = 95мм, длиной l = 120
км при
температурах О и 20°С равно 20 ом.
Задача №7
Определить напряжение на выходе делителя напряжения, который
подключен к источнику питания 10 В в следующих случаях:
а) напряжение снимается со всего делителя напряжения;
б) напряжения снимается с половины витков делителя
напряжения;
в) напряжение снимается с 1/4 витков делителя напряжения.
Решение:
Напряжение на выходе делителя определяется по формуле:
U = I • R
С другой стороны, ток переменного резистора находится из
соотношения
I
=
Следовательно, отношение напряжения на выходе делителя и напряжения
питания пропорционально отношению сопротивлений R и R т.е.
U =
• U
Отсюда находим искомые значения напряжений на выходе делителя
а) U =
= 10 В;
б) U =
= 5 В;
в) U =
= 2,5 В.
Ответ:
а) напряжение снимается со всего делителя напряжения
U = 10 В;
б) напряжения
снимается с половины витков делителя напряжения
U= 5 В;
в) напряжение снимается с 1/4 витков делителя напряжения U = 2,5 В.
Задача №8
Определять токи и напряжения в электрической цепи,
изображенной на рисунке, при следующих ее данных: Е = 2 в; r = 0,5 ом; r
= 3,5 ом; r
= 5 ом; r
= 100 ом; r
=25 ом.
Решение:
Находим проводимость параллельно соединенных ветвей
gАБ
= g2+ g3 +
g4 = +
+
= 0,25
,
откуда следует, что сопротивление этого участка
r=
= 4 ом.
общее
сопротивление всей цепи
r = r + r
+ r
= 0,5 + 3,5 + 4 = 8 ом.
Ток в неразветвленной части цепи
I =
=
= 0,25 А.
Напряжение между точками АБ
U = I
• r
= 0,25 • 4 = 1 В.
Токи в отдельных ветвях
I=
=
= 0,2 А;
I =
=
= 0,01 А;
I =
=
= 0,04 А.
Ответ: токи и напряжения в электрической
цепи равны:
U = 1 В.
I = 0,25 А.
I=
0,2 А;
I =
0,01 А;
I = 0,04 А.
Задача №9
При разомкнутом ключе К показания вольтметра 2,1
В. Когда ключ замкнут, амперметр фиксирует ток 1А. Внешнее
сопротивление цепи R = 2 Ом. Определить ЭДС источника Е, внутреннее
сопротивление источника R и напряжение на зажимах источника U.
Решение:
Когда цепь тока разорвана, вольтметр, подключенный к
зажимам источника, практически фиксирует значение ЭДС.
Следовательно,
E = 2,1 В.
Для определения R необходимо воспользоваться законом Ома
для всей цепи:
I = ,
Откуда
R + R =
=
= 2,1 Ом.
Так как известно, что внешнее сопротивление цепи R=
2 Ом, то внутренне сопротивление источника
R = 2,1 – 2 = 0,1 Ом.
Напряжение на зажимах источника
U = E – RI
или
U = RI
Подставляя значения в приведенные выражения, получим
U = 2,1 – 0,1 • 1 = 2 B;
U = 2 • 1 = 2В;
Применение формулы U = E – RI предпочтительней, так как
подчеркивается тот факт, что напряжение на зажимах источника меньше ЭДС, причем
с увеличением тока это напряжение уменьшается.
Ответ: E = 2,1 В.
R = Ом.
U = 2 B;
Задача №10
Для электрической цепи представленной на рисунке, методом двух
узлов, определить токи во всех ее ветвях. Задачу решить в общем виде, учесть,
что известны следующие параметры электрической цепи: E1, E2, Ri1, Ri2, R1, R2, R3.
Решение:
Решение
данной задачи состоит в расчете сложной цепи переменного тока методом двух
узлов. Для этого надо применительно к представленной на рисунке
электрической схеме:
1)
выбрать направления всех токов одинаковыми
2)
найти проводимости всех ветвей, См,
G1 =
G2 =
G3 =
3)
определить узловое напряжение Uab
Uab =
(E2G2 – со знаком “минус”, так как E2 имеет противоположное I2 направление);
4) определить токи в ветвях;
I1 = (E1 –
UAB)G1
I2 =
(-E2 – UAB)G2
I3 =
(0 – UAB)G3
5)
если в
результате расчетов какой – либо ток будет получен со знаком «минус», значит,
его действительное направление противоположно выбранному на схеме.
Действительное направление необходимо показать пунктиром на схеме.
Задача №11
Генератор постоянного тока с параллельным
возбуждением работает на нагрузку, сопротивление которой Rн = 5 Ом,
сопротивление обмотки якоря Rя = 0,2 Ом, сопротивление обмотки возбуждения RB=230
Ом, напряжение на зажимах генератора U =230 В.
Определить: а) ЭДС генератора; б) электромагнитную
мощность; в) потери мощности в обмотках якоря и возбуждения?
Решение:
Токи
нагрузки
Iн = U/Rн = 230/5 = 46А
возбуждения
Iв = U/Rв = 230/230 = 1А
Якоря
Iя = Iн
+ Iв = 46 + 1 = 47A
ЭДС генератора
Е = U + Iя ∙ Rя = 230+47 ∙ 0,2 = 239,4 В
Электромагнитная
мощность
Pэ = Е ∙ Iя = 239,4 ∙ 47 = 11251,8 Вт.
Потери мощности
в меди обмотки якоря
Рмя
= Iя ∙ Rя = 472 ∙ 0,2 = 441,8 Вт
Потери
мощности в меди обмотки возбуждения
Рмв
= Iв ∙ Rв = 12 ∙ 230 = 230 Вт
Добавочные потери в соответствие ГОСТом составляют
1 % от
полезной мощности генератора
Рдоб = 0,01 UIн = 0,01 ∙ 230 ∙ 46 = 105,8 Вт
Потери в щеточных контактах
Рк = 2ΔUIя = 2 ∙ 0,5 ∙ 47 = 47 Вт
Ответ: ЭДС генератора Е =
239,4 В; электромагнитную мощность
Pэ = 11251,8 Вт; потери мощности в обмотках якоря Рмя
= 441,8 Вт и возбуждения Рмв = 230 Вт.
Задача №12
Чему равны одинаковые электрические токи,
протекающие в двух параллельных проводах, которые расположены на расстоянии, а
= 20 см друг от друга, если на каждый метр провода действует сила F = 100 н/м?
μ= 4
– магнитная постоянная.
Для воздуха μ = 1
Решение:
I =
=
=
10000А.
Ответ: Электрические
токи, протекающие в двух параллельных проводах, которые расположены на
расстоянии, а = 20 см равны 10000А.
Задача №13
Три конденсатора, емкости которых С = 20 мкф, С
= 25 мкф и С
= 30 мкф, соединяются последовательно.
Определить общую емкость.
Решение:
Записываем формулу для определения общей емкости трех последовательно соединенных конденсаторов.
=
+
+
=
+
+
= 0,05
+ 0,04 + 0,033 = 0,123.
C =
= 8,13 мкф.
Ответ: Общая
емкость трех конденсаторов, соединенных последовательно равна 8,13 мкф.
Задача №14
Определите
емкость батареи конденсаторов, если емкость первого конденсатора С = 1 мкФ, второго – С
= 2 мкФ, третьего – С
= 4 мкФ.
Решение:
Конденсаторы С и С
соединены параллельно, поэтому их
общая емкость
C = С
+ С
;
Конденсатор C соединен последовательно с C
. По
формуле последовательного соединения конденсаторов имеем:
=
+
;
C =
=
=
=
= 0,86 мкф.
Ответ: C = 0,86 мкф.
Задача №15
Три одинаковых конденсатора соединены параллельно в батарею.
Определите емкость батареи, если известно, что при подключении аккумулятора (U
= 2 В) на обкладках каждого
конденсатора накапливается заряд, равный 10Кл.
Решение:
При параллельном соединении конденсаторов имеем:
C
= C + C
+ C
= 3 C
U = U=U
=U
Следовательно,
С = 3
C = 3
,
т. к. C =
; С = 3 •
= 1,5 • 10
Ф.
Ответ: Емкость батареи конденсаторов равна С = 1,5
• 10Ф.
Задача №16
Три конденсатора С, С
, С
емкостью
2 мкф каждый соединены параллельно. Определить их общую емкость.
Решение:
Записываем формулу для определения общей емкости трех
параллельно соединенных конденсаторов. Но, так как, емкость всех трех
конденсаторов одинакова то, можно воспользоваться, более простой формулой.
С = 3 • С
= 3 • 2 = 6 мкф.
Ответ: Общая
емкость трех конденсаторов, соединенных параллельно равна 6 мкф.
Задача №17
Пространство между плоскопараллельными металлическими
пластинам заполнено парафинированной бумагой. Определить допустимое и пробивное
напряжения между пластинами при условии, что допустимое напряжение должно быть
меньше пробивного в 2,5 раза. Расстояние между пластинами d = 0,I мм.
εпр = 104
– пробивная напряженность
парафинированной бумаги.
Решение:
Пробивное напряжение:
U пр =
ε пр • d =104 • 0,1 = 1000 в.
Допустимое напряжение
U ==
= 400 в.
Ответ: Пробивное
напряжение между пластинами равно 1000 в.
Допустимое напряжение по условию задачи должно
быть меньше
пробивного в 2,5 раза и равно 400
в.
Раздел 3. Электрические цепи переменного тока
Задача №18
Электротехническое устройство с потребляемой мощностью
50 Вт и напряжением питания 110 В нужно включить в сеть переменного
напряжения 220 В частотой 50 Гц. Найти емкость конденсатора, который
необходимо подключить последовательно данному устройству, чтобы скомпенсировать
избыточное напряжение.
Решение:
Для решения задачи необходимо определить ток и
напряжение компенсирующего конденсатора, что позволит найти его реактивное
сопротивление, а следовательно, и емкость. Поэтому ток в цепи не должен
превышать
I = =
= 0,455
A.
Напряжение на конденсаторе должно быть равно
векторной разности напряжений питания и нагрузки:
U =
=
= 191
В.
Зная напряжение и ток конденсатора, находим его реактивное
сопротивление:
Х =
=
= 420 Ом.
По известной формуле для определения емкостного
сопротивления
X =
;
находим искомую емкость конденсатора
С = =
= 7,6 • 10
Ф
= 7,6 мкФ.
Ответ: Емкость конденсатора, который необходимо
подключить последовательно данному устройству, чтобы скомпенсировать избыточное
напряжение С = 7,6 мкФ.
Задача №19
В электрическую цепь переменного тока напряжением U = 220В, частотой
f = 50Гц включена катушка с индуктивностью L = 0,0127Гн и активным сопротивлением R = 3Ом.
Определить:
1) реактивное сопротивление катушки;
2) ток в катушке;
3) активную мощность катушки;
4) реактивную мощность катушки;
5) энергию, запасаемую в магнитном поле
катушки.
Решение:
X = ωL = 2
fL = 2 • 3,14 • 50 • 0,0127 = 4 Oм;
Z = =
=5 Oм;
I = =
= 44A;
P = U• I = I
• R
= 44
• 3 = 1936 • 3 = 5808 Вт;
Sin φ = =
= 0,8;
Q = UI sinφ = 220 • 44 • 0,8 = 7744 Вар;
W = LI
= 0,0127 • 44
= 24,59 дж.
Ответ:
X = 4 Oм;
Z = 5 Oм;
I
= 44A;
P
= 5808 Вт;
Sin φ = 0,8;
Q = 7744 Вар;
W =
24,59 дж.
Задача №20
К генератору переменного электрического тока с напряжением
U = 240В и частотой f = 50Гц присоединен конденсатор с емкостью
C = 40 мкф.
Определить: 1) реактивное сопротивление емкости X;
2) ток в электрической цепи;
3) реактивную мощность цепи Q;
4) максимальную энергию, запасаемую
в
электрическом поле конденсатора W.
Решение:
X =
=
= 80 Ом.
I = =
= 3
A.
Q = U • I = 240 • 3 = 720 Вар.
W = C•U
= 40 • 10
•240
= 2,7 дж.
Ответ: Реактивное сопротивление емкости X = 80 Ом.
Ток в электрической
цепи I = 3
A;
Реактивная мощность
цепи Q = 720 Вар;
Максимальная
энергия, запасаемая в электрическом поле
конденсатора W = 2,7 дж.
Задача №21
В электрическую цепь переменного тока напряжением U = 220 В, частотой
f
= 50 Гц включена
катушка с индуктивностью L = 25,5 мГн и активным сопротивлением R = 6 Ом.
Определить: X; Z ; U
; U
; cosφ.
Решение:
X = ωL = 2
=
2 • 3,14 • 50 • 0,0255 = 8 Oм;
Z = =
= 10 Oм;
I = =
= 22
A;
U= I R =
22 • 6 = 132 B;
U = U
= I • X
= 22 •
8 = 176 B;
Cos φ = =
= 0,6.
Ответ: X = 8 Oм;
Z = 10 Oм;
I
= 22 A;
U= 132 B;
U = U
= 176
B;
Cos
φ = 0,6.
Задача №22
В электрическую сеть напряжением 220В включено 16
одинаковых электрических ламп мощностью по 100Вт каждая. Определить
необходимое сечение медного провода, соединяющего эти электрические лампочки.
Площадь поперечного сечения Наиболее допустимый
медного провода, мм электрический
ток, А
0,50
10
0,75 13
1,0 15
Решение:
Полная мощность
Р = P ламп • 16 = 100 • 16 = 1600 Вт.
Ток в проводе
I = =
= 7,273 А.
По таблице, приведенной в условии задачи, выбираем сечение
провода;
S = 0,50
мм.
Ответ: Сечение медного провода, необходимое для
подключения 16 одинаковых электрических ламп мощностью по 100Вт каждая
в электрическую сеть напряжением 220В равно 0,50
мм.
Задача №23
Генератор переменного тока, используемый для
получения переменной электродвижущей силы, имеет частоту вращения 2800 об/мин.
Определить частоту, период и угловую частоту электрического
тока, возникающего при подключении генератора к нагрузке, если число пар
полюсов генератора равно 6.
Решение:
Частота
электрического тока генератора
f = pn/60 = 6 ∙ 2800/60 = 280 Гц.
Период
Т= 1
/ f = 1/280 = 0,0036 с
и
угловая частота
ω = 2π/Т = 2 π f = 2 ∙ 3,14 ∙ 280 = 1750 1/с.
Ответ: Частота электрического
тока равна f = 280 Гц,
период
электрического тока равен Т= 0,0036 с,
угловая частота электрического тока равна ω = 1750 1/с.
Задача №24
В электрическую цепь переменного тока напряжением U = 220 В, частотой
f = 50 Гц включена катушка с индуктивностью L = 25,5 мГн и активным сопротивлением R = 6 Ом; I
= 22 A; U= 132 B; Cos
φ = 0,6.
Определить:
1) максимальную мощность в активном сопротивлении
P;
2) активную мощность;
3) реактивную мощность;
4) полную мощность.
Решение:
P = 2 U
I = 2 • 132 • 22 = 5808 Вт.
P = UI
cos φ = 220 • 22 • 0,6 = 2904 Вт.
Q = UI
sin φ =220 • 22 • 0,8 = 3872 Вар.
S = UI = 220 • 22 = 4840 BA.
Ответ: P = 5808 Вт.
P = 2904 Вт.
Q = 3872 Вар.
S = 4840 BA.
Задача №25
Лампа накаливания включена параллельно с линейным резистором
R2 = 30 Ом.
Построить зависимость эквивалентного
сопротивления Rэк цепи от напряжения U на его зажимах.
Методом последовательных приближений
определить напряжение U при токе в неразветвленной части цепи I = 5А.
Вольт-амперная характеристика лампы задана в таблице.
|
U, B |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
|
I, A |
0 |
0,6 |
1,1 |
1,5 |
1,85 |
2,15 |
2,4 |
Решение:
Построим вольт-амперные характеристики элементов цепи.
На рисунке: I(U) —
характеристика лампы и I2(U) — характеристика резистора R2.
Сложив ординаты
этих характеристик при различных значениях напряжения, получим вольт-амперную
характеристику всей цепи, т. е. зависимость тока в неразветвленной части цепи
от приложенного напряжения I(U). Эквивалентное сопротивление схемы найдем
как отношение Rэк = U/I для различных значений приложенного напряжения.
Результаты вычислений приведены на графике представленном
на рисунке.
При расчете электрических цепей в большинстве случаев известны параметры источников ЭДС или напряжения, сопротивления элементов электрической цепи, и задача сводится к определению токов в ветвях цепи. Таким образом, электрическая цепь на рис.
Точка Н определяет номинальный режим, если напряжение и ток соответствуют их номинальным значениям Uном и Iном, приведенным в паспорте источника электрической энергии.
Элемент электрической цепи, параметры которого сопротивление и др.
Электрические цепи (часть 1)
Элементы цепи Электрическая цепь содержит в себе такие составляющие, как источники энергии, потребители, а также соединяющие их провода. По закону Ома токи в каждой ветви: По первому закону Кирхгофа общий ток Смешанное соединение — комбинация первых двух соединений, где параллельное соединение может быть преобразовано к последовательному.
Для их составления необходимо задать условные направления токов в ветвях номер введем в соответствии с порядковым номером сопротивлений.
Метод узловых потенциалов Вторым методом, которым пользуются для решения сложных цепей, является метод узловых потенциалов. Тогда из выражения 1.
Внешняя вольт-амперная характеристика источника электрической энергии Точка X вольт-амперной характеристики источника электрической энергии отвечает режиму холостого хода х.
Подключение цепи к источнику постоянной ЭДС 5. Существуют дополнительные приборы цепи, например, выключатели, измерители тока и защитные аппараты.
КОНДЕНСАТОР В ЦЕПИ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА [РадиолюбительTV 89]
Электрическая цепь постоянного тока
Алгебраическая сумма падений напряжений на резистивных элементах в любом замкнутом контуре равно алгебраической сумме ЭДС. Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке.
Источник электрической энергии характеризуется понятием ЭДС Е , под которой понимают величину, численно равную энергии, получаемой внутри источника единицей электрического заряда.
При расчете в схеме электрической цепи выделяют несколько основных элементов. Этот метод основан на составлении уравнений по первому закону Кирхгофа: Схема сложной электрической цепи с двумя узлами.
Для разных электротехнических устройств указывают свои номинальные параметры.
Электрическая цепь в режиме короткого замыкания имеет сопротивление, которое равно нулю. В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают.
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников.
В случае последовательного соединения сопротивлений в ветви В общем виде уравнения узловых потенциалов имеют вид: Если в схеме имеются источники тока, то слагаемое в правой части будет равно сумме источников тока: Метод узловых потенциалов имеет преимущество, если число независимых узлов меньше числа контуров. Желательно во всех контурах положительные направления обхода выбирать одинаковыми, например, по часовой стрелке, как показано на рис.
Устройство и принцип работы двигателя постоянного тока. Схема двигателя постоянного тока.
Похожие статьи
Такая система известна, как электрическая цепь. Схема электрической цепи.
Ознакомившись с основными характеристиками и видами такой системы, как электрическая цепь, становится возможным понять принцип функционирования любого электрооборудования.
Отключение цепи от источника постоянной ЭДС 5. В противном случае это слагаемое отрицательно. При анализе электрической цепи рассматривают следующие режимы работы: холостого хода, номинальный, короткого замыкания и согласованный.
Электрическая цепь и электрический ток, протекающий по ней, характеризуют электромагнитные процессы при помощи напряжения и силы тока. Для электрической цепи на рис.
Для контура. Это произойдет, если к зажимам аb двухполюсника присоединена внешняя цепь с источниками питания. Точка К характеризует режим короткого замыкания к. Первый закон Кирхгофа: сумма токов в узле равна нулю 1.
Elektrotechnik fuer Grundlagen der Elektronik
Эта вольт-амперная характеристика строится по двум точкам 1 и 2 рис. Активный двухполюсник содержит источники электрической энергии, а пассивный двухполюсник их не содержит.
Мощность цепи несинусоидального тока 4. Для расчета цепей с двухполюсниками реальные активные и пассивные элементы цепи представляются схемами замещения. По этой причине для расчета сложных электрических цепей разработаны более рациональные методы расчета, основные из них рассмотрены ниже. За направление электрического тока в электротехнике принято направление, противоположное направлению движения электронов. Сложной электрической цепью называется цепь, содержащая несколько источников и которую нельзя свернуть до простой цепи последовательного или параллельного соединения.
Зная токи, можно найти напряжения на элементах цепи, мощность отдельных элементов и электрической цепи в целом, мощность источников и др. Контур — любой замкнутый путь, проходящий по нескольким ветвям.
как решать задачи со сложными схемами
Элементы цепи
При сравнении внешних характеристик источника ЭДС рис. Мощность трёхфазной цепи 3.
Классический метод расчёта переходных процессов 5. В зависимости от электропроводности все вещества подразделяют на: 1.
Последовательное соединение в цепи Большое количество электрических цепей состоят из нескольких приемников тока.
Согласованный режим Согласованный режим электрической цепи обеспечивает максимальную передачу активной мощности от источника питания к потребителю. На схеме этот элемент выглядит следующим образом. В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают.
Метод узловых потенциалов
Идеальному источнику тока приписывают внутреннее сопротивление, стремящееся к бесконечно большому значению, и неизменный ток Iк не зависящий от напряжения на его зажимах, равный току коротного замыкания, вследствие чего неограниченное увеличение присоединенной к источнику нагрузки сопровождается теоретически неограниченным возрастанием напряжения и мощности. Электрическая цепь и электрический ток, протекающий по ней, характеризуют электромагнитные процессы при помощи напряжения и силы тока.
Различают два рода тока: 1. Ветвь электрической цепи схемы — участок цепи с одним и тем же током. Последовательное включение источников питания источников ЭДС применяется тогда, когда требуется создать напряжение требуемой величины, а рабочий ток в цепи меньше или равен номинальному току одного источника ЭДС рис. Между узлами 1 и 3 имеются две параллельные ветви с источниками ЭДС Е1 и Е2 , между узлами 2 и 3 также имеются две параллельные ветви с резисторами R1 и R2. Данное устройство работы системы применяется к любому электрическому бытовому прибору.
По этой причине для расчета сложных электрических цепей разработаны более рациональные методы расчета, основные из них рассмотрены ниже. Сопротивление в этой электрической цепи приравнивается к сумме сопротивлений всех проводников системы. При сравнении внешних характеристик источника ЭДС рис. В случае когда у одного приемника энергии сопротивление меньше, через него может пройти больше тока, чем через другие элементы системы.
Классический метод расчёта переходных процессов 5. Стрелка в кружке указывает направление возрастания потенциала внутри источника ЭДС. Электрический ток в такой электрической системе имеет несколько вариантов пути прохождения. Это уравнение является линейным. В состав цепи входят: 1.
Законы Кирхгофа — Теория и задача