Как найти цепное отклонение

Не совсем так.
Базисные Т. роста отражают интенсивность роста показателя за весь отрезок времени; цепные Т. р. показывают интенсивность его по годам, соответственно темпы прироста — увеличение (в процентах) по сравнению с базисным и каждым предыдущим годом.

Темп прироста=(а2009-а2008)/а2008*100 – т. е. на сколько процентов увеличился/снизился показатель. Когда считаем цепные берется показатель предыдущего года, а когда базисные – берем за базис 2008 год.
Год Параметр Темп прироста (цепной) , %Темп прироста (базисный) , %
200831 727 – –
200936 25914,2843634814,28436348
20104362920,3259880337,51378952

Обобщённую характеристику интенсивности экономического развития, за несколько лет дают среднегодовые Т. р. (и прироста) , которые исчисляются как средняя геометрическая из годовых темпов. Или по формуле: Корень У2010-У2008 из т-1, где У — абсолютные уровни ряда динамики, а т-1 — число лет (уровней ряда динамики) в изучаемом отрезке времени (без базисного) , т. е. 2 в вашем случае.

Среднегодовой Т. р. за три года (2008—2010) составит = 1,172662737 (или 117,3%), а среднегодовой темп прироста равен 17,3%.

Способ
абсолютных разниц является одной из
модификаций элиминирования. Как и способ
цепной подстановки, он применяется для
расчета влияния факторов на прирост
результативного показателя в
детерминированном анализе, но только
в мультипликативных и мультипликативноаддитивных
моделях: Y = (а – b)с и У = a(b – с). И хотя его
использование ограничено, но благодаря
своей простоте он получил широкое
применение в АХД. Особенно эффективно
применяется этот способ в том случае,
если исходные данные уже содержат
абсолютные отклонения по факторным
показателям.

Этот
способ является техническим упрощением
метода цепных подстановок.

Его
суть состоит в том, что находится
абсолютное отклонение по каждому
фактору, затем определяется влияние
этого отклонения на изменение обобщающего
показателя.

Сначала
находятся абсолютные отклонения по
каждому фактору:

A
= A1 – A0

B
= B1 – B0

C
= C1 – C0

D
= D1 – D0.

Полученные
абсолютные отклонения подставляются
в общую фор-мулу, и определяются изменения
обобщающего показателя за счет каждого
фактора:

Ya
= A*B0* C0* D0

Yb
= A1*B* C0* D0

Yc
= A1*B1* C* D0

Yd
= A1*B1* C1* D.

Баланс
отклонений: Y1
– Y0
=Y
=Ya
+Yb
+Yc
+Yd.

14. Текущий экономический анализ

Текущий
анализ является ретроспективным анализом
уже осуществленной хоз. деятельности.

Главная
задача – объективная оценка результатов
коммерческой деятельности, комплексное
выявление неиспользованных резервов,
мобилизация их, выявление недочетов в
работе и их виновников, достижение
полного соответствия материального и
морального стимулирования по результатам
труда и качеству работы.

Его
недостатки – выявленные резервы означают
навсегда потерянные возможности роста
эффективности производства, поскольку
относятся к прошлому периоду.

Результаты
текущего анализа используются для
решения проблем стратегического
управления, в том числе технико-экономического
планирования, так как научно обоснованное
планирование предусматривает глубокий
анализ хозяйственного положения к
моменту начала планового периода.

Этот
вид анализа предусматривает регистрацию
хоз. ситуации, и результатов с целью
учёта в будущей работе. В связи с тем,
что текущий анализ является ретроспективным,
для повышения его действенности 1 из
главных задач анализа является ускорение
представления отчетности и ее аналитической
обработки.

Текущий
анализ проводится всеми экономическими
и техническими службами, всеми структурными
подразделениями по всем разделам и
нормам анализа. Результаты текущего
анализа являются основанием для
составления пояснительной записки к
годовому отчету предприятия.

Особенность
методики текущего анализа состоит в
том, что фактические результаты
деятельности оцениваются в сравнении
с предшествующим периодом.

Отклонения
от базы сравнения расшифровываются по
технико-экономическим факторам,
определяющим эти отклонения, устанавливаются
т.ж. ответственные лица, службы, намечаются
меры по ликвидации недочетов в работе.

Если
же отклонения имеют положительный
характер, выясняются условия, определившие
такое положительное влияние. Одной из
основных отличительных черт текущего
анализа – наиболее полный и глубокий
анализ хозяйственной деятельности; он
опирается на результаты оперативного
анализа и одновременно служит базой
перспективного (прогнозного) анализа.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Формулы

1. Определение характеристик составляющих звеньев размерной цепи
1.1.
Допуск i-го звена размерной цепи определим по формуле:

T(A i ) = Es(A i ) – Ei(A i )

(1)

где
Es(A _i ) – верхнее отклонение звена;
Ei(A _i ) – нижнее отклонение звена;
i – индекс звена;

1.2.
Середину поля допуска i-го звена определим по формуле:

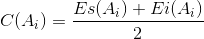(2)

2. Определение характеристик замыкающего звена
2.1.
Номинальное значение замыкающего звена AΔ определим по формуле:

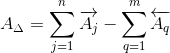(3)

где
A _j – номинальный размер любого увеличивающего звена;
A _q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;

2.2.
Допуск замыкающего звена AΔ определим по формуле:

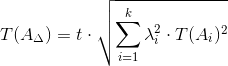(4)

где
Т(А _i ) – допуск любого составляющего звена;
k – число звеньев размерной цепи;
λ – коэффициент относительного рассеяния.
Зависит от принятого закона распределения размера:
— для нормального распределения(Гаусса) λ ² = 1/9,
— для закона треугольника(Симпсона) λ ² = 1/6,
— для закона равной вероятности λ ² = 1/3.
t – коэффициент риска, определяющий количество бракованных деталей;

2.3.
Координата середины поля допуска замыкающего звена определяется по формуле:

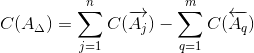(5)

где
C(A _j ) – координата середины поля допуска любого увеличивающего звена;
C(A _q ) – координата середины поля допуска любого уменьшающего звена;

2.4. Предельные отклонения замыкающего звена.
2.4.1
Верхнее отклонение замыкающего звена Es(A_Δ) определим по формуле:

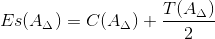(6)

где
C(A _Δ) – координата середины поля допуска замыкающего звена
T(A _Δ) – допуск замыкающего звена;

2.4.2.
Нижнее отклонение замыкающего звена Ei(A_Δ) определим по формуле:

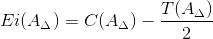(7)

Пример
Задание:
Требуется проверить наличие и величину зазора AΔ.
Определить допуск и предельные отклонения размера замыкающего звена (см. рис. 1) по теоретико-вероятностному методу, приняв t=3, λ² = 1/9,

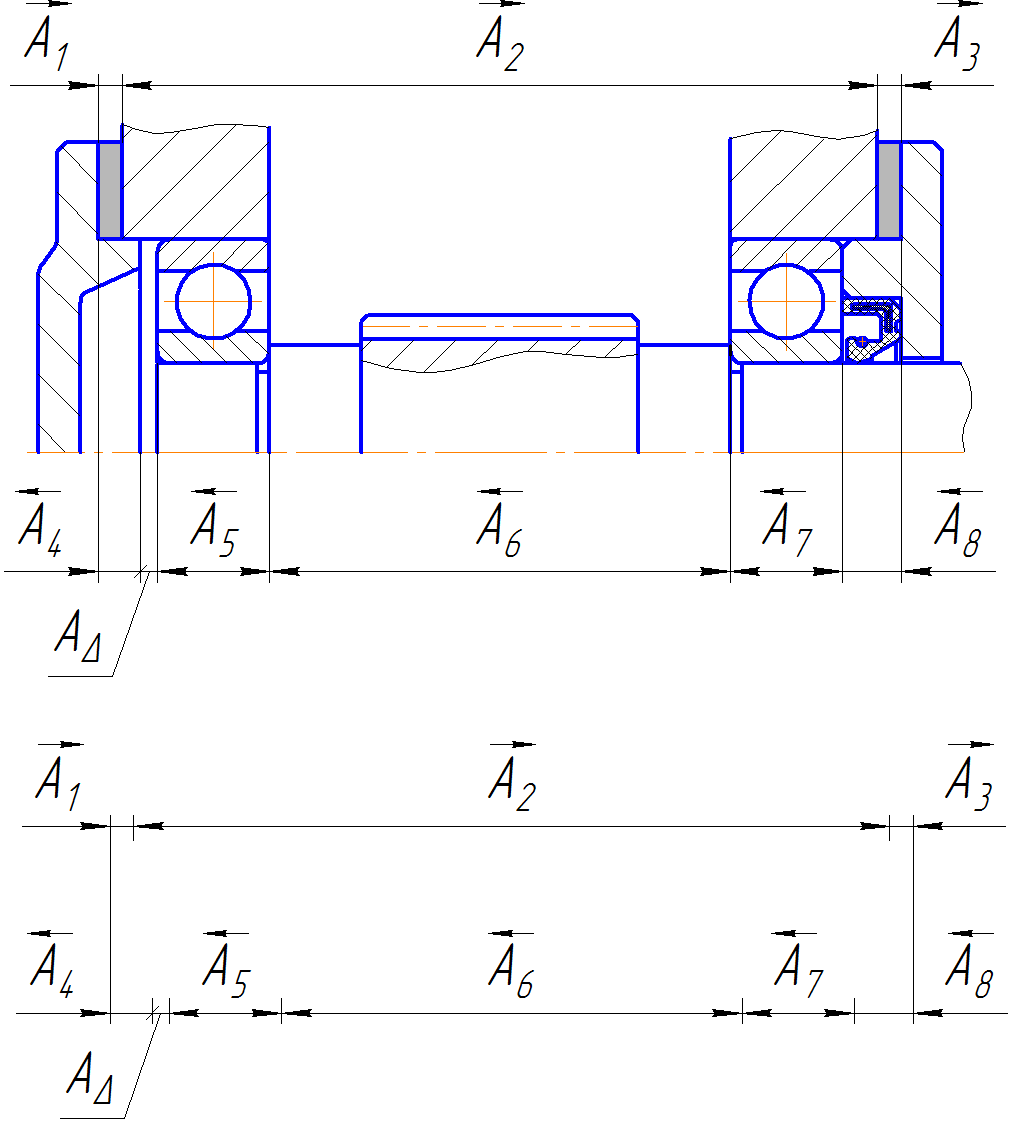
Рисунок 1 – Сборочная размерная цепь.

Исходные данные:
Звенья размерной цепи:
Допуски и координаты середины поля допуска составляющих звеньев определены по формулам
(1) и (2).

A1 = 1-0,015 (мм);	Т(A1)=0,015 (мм);	C(A1) = -0,0075 (мм);
A2 = 206 +0,35 (мм); -0,05	Т(A2)=0,4 (мм);	C(A2) = 0,15(мм);
A3 = 1-0,015 (мм);	Т(A3)=0,015 (мм);	C(A3) = -0,0075 (мм);
A4 = 10-0,06 (мм);	Т(A4)=0,06 (мм);	C(A4) = -0,03 (мм);
A5 = 19-0,12 (мм);	Т(A5)=0,12 (мм);	C(A5) = -0,06 (мм);
A6 = 150 -0,08 (мм); -0,24	Т(A6)=0,16 (мм);	C(A6) = -0,16 (мм);
A7 = 19-0,12 (мм);	Т(A7)=0,12 (мм);	C(A7)= -0,06 (мм);
A8 = 10-0,06 (мм);	Т(A8)=0,06 (мм);	C(A8)= -0,03 (мм);

Увеличивающие звенья: A₁, A₂, A₃;
Уменьшающие звенья: A₄, A₅, A₆, A₇, A₈;
Замыкающее звено: A_Δ

Решение:
1. Номинальный размер замыкающего звена
Номинальный размер замыкающего звена AΔ определим по формуле

.
Для заданной размерной цепи формула (3) принимает вид:
A_Δ = A₁ + A₂ + A₃ – (A₄ + A₅ + A₆ + A₇ + A₈)
A_Δ = 1 + 206 + 1 – (10 + 19 + 150 + 19 + 10) = 0(мм)

2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле

.
Для заданной размерной цепи формула (4) принимает вид:

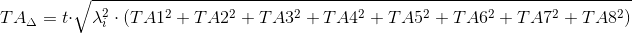
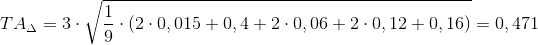
3. Координаты середины поля допуска замыкающего звена
Координату середины поля допуска замыкающего звена определим по формуле

:
Для заданной размерной цепи формула (5) принимает вид:
С(A_Δ) = С(A₁) + С(A₂) + С(A₃) – (С(A₄) + С(A₅) + С(A₆) + С(A₇) + С(A₈))
С(A_Δ) = (-0,0075) + 0,15 + (-0,0075) – ((-0,03) + (-0,06) + (-0,16) + (-0,06) + (-0,03)) = 0,475 (мм)

4. Предельные отклонения замыкающего звена
4.1. Верхнее отклонение замыкающего звена EsAΔ определим по формуле
EsAΔ = 0,475 + 0,5·0,471 = 0,71(мм)

4.2. Нижнее отклонение замыкающего звена EiAΔ определим по формуле
EiAΔ = 0,475 – 0,5·0,471 = 0,24(мм)

Расчет размерных цепей онлайн. Обратная задача.

Замыкающее звено:

Сущность метода цепных подстановок

Метод расчета по цепным подстановкам является важным элементом методики экономического анализа, заключающийся в последовательной замене плановых величин одного из алгебраического слагаемого (сомножителя) фактической его величиной с сохранением в неизменном состоянии остальных показателей.

Этот метод экономического анализа используется в тех случаях, когда необходимо определить зависимость между изучаемыми явлениями, имеющую строго функциональный характер. Данная зависимость представляет собой прямую или обратно пропорциональную зависимость. В таком случае анализируемый совокупный показатель в качестве функции нескольких переменных изображается в форме алгебраической суммы, произведения или отношения (деление) одних показателей к другим.

Степень влияния соответствующего показателя можно выявить последовательным вычитанием, когда из второго расчета вычитают первый, из третьего вычитают второй и т.д. Первый расчет содержит все плановые величины, а последний фактические величины.

В процессе определения взаимодействия двух факторов (показателей) производят три расчета; трех факторов – делают четыре расчета; четырех факторов – осуществляют пять расчетов.

«Цепные подстановки в экономическом анализе» 👇

Так как первый расчет состоит только из плановых величин, его результаты берут в готовом виде из планов предприятия (организации, объединений). Результат последнего расчета со всеми фактическими показателями берут из квартального или годового отчета. По этой причине на практике количество расчетов оказывается не на единицу больше, а на единицу меньше, то есть осуществляют только промежуточный расчет.

Алгоритм метода

Алгоритм метода цепных подстановок демонстрируется примером вычисления влияния изменения величины частных показателей на величину показателя, который представлен в виде следующей рассчитываемой формулы:

$F = a • b • c$

Данная формула представляет собой мультипликативную модель.

В этом расчете показатели с нулем соответствуют базисному периоду, поскольку он является индексом базисного показателя.
Единица соответствует отчётному периоду и является индексом показателя отчётного периода.

При этом базисное значение $F$ равняется следующему равенству:

$F_0 = a_0 • b_0 • c_0$

Фактическое значение будет выглядеть следующим образом:

$F_1 = a_1 • b_1 • c_1$

При этом общее отклонение фактического показателя от базисного показателя выражается специальной формулой.

Очевидно, что данное равенство равняется сумме отклонений, которые получены под воздействием изменения частных показателей.

Проверить расчеты можно, сопоставив баланса отклонений, при этом общее отклонение фактических показателей от базисных должно приравниваться к сумме отклонений под воздействием изменения частных показателей.

В этой статье мы разберем факторный анализ и метод цепных подстановок. Рассмотрим все особенности применения данного метода в решении экономических задач.

Метод цепных подстановок в экономическом анализе

Любой бухгалтер, составив аналитическую таблицу за какой-то период, будь то отчёт о прибылях и убытках, или любая другая экономическая отчётность, делает:

— горизонтальный анализ, то есть сравнивает текущие показатели с какими-то прошлыми показателями;

— вертикальный анализ, то есть анализирует структуру доходной части или затратной части — какая из статей затрат занимает определённую долю отчётности.

Но помимо этих двух анализов есть еще один не менее важный — это факторный анализ. Он более сложный. Факторный анализ полученных показателей указывает на то, какие факторы повлияли на прибыль в худшую или лучшую сторону.

Факторный анализ бывает нескольких видов. Сегодня мы поговорим непосредственно о методе цепных подстановок.

Способ цепной подстановки в детерминированным факторным анализе используется для того, чтобы выявить, какие факторы влияли на анализируемый показатель, определить, какой из всех действующих факторов имел решающие влияние на изменение показателя.

МЦП широко применяется в анализе. Его можно использовать для различных формул:

— для кратных моделей, когда они представлены в виде дроби: допустим, отношение товарной продукции к основным средствам является фондоотдачей (ФО = ТП/ОС)

— его можно использовать для аддитивных моделей. Допустим, затраты равны сумме материальных затрат, амортизации, оплаты труда и прочего (З = МЗ+А+ОТ+ПР)

— его можно использовать для мультипликативных моделей. Например, товарная продукция равняется произведению основных средств на фондоотдачу (ТП = ОС*ФО)

В этом заключается универсальность данного метода.

Особенность расчёта метода цепной подстановки основана на том, что меняется постепенно нулевое значение показателя на единичное. Что это означает: нулевой показатель — это то же самое изменение планового значения на фактическое. Степень влияния каждого признака фактора определяется последовательным вычитанием из старого расчёта первого, из третьего — второго и так далее.

Перед расчётом необходимо:

• Выявить чёткую зависимость между показателями (она должна быть функциональной или детерминированной).
• Определить, какой показатель количественный, а какой показатель качественный.
• Необходимо определить последовательность подстановки показателей. Вначале пишут количественные, а затем качественные показатели.

Существуют различные модификации данного способа анализа, например, метод абсолютных разниц.

Разберём условные обозначения, которые будут использоваться в формулах для проведения факторного анализа в данной статье.

РП — это результативный показатель, то есть анализируемый показатель

Ф1, Ф2, Ф3 — это факторы под соответствующим номерами (первый фактор, второй и так далее)

Влияние этих факторов мы будем изучать именно на результативный показатель.

Индексы, которые будут фигурировать в формуле:

Индекс 1 показывает, что сравниваемое значение мы берём как фактическое, то есть за конкретный период времени, сейчас.

Нулевой индекс (0) представляет собой базисное значение. То есть это база сравнения, за которую могут приниматься плановые значения, показатели предыдущего периода либо нормативное значение.

Формула факторного анализа методом цепной подстановки на примере двухфакторной мультипликативной модели:

РП = Ф1*Ф2

Расчёты будут состоять из двух этапов.

На первом этапе в расчётах последовательно базисные, то есть нулевые значения факторов будут заменяться на фактически значения. При этом мы будем получать не реальные, а условные или относительные расчёты, так как не все факторы будут на уровне одного и того же периода, а будут соединены данные двух периодов — сравниваемого и фактического.

Следует иметь в виду, что количество условных расчётов будет на один меньше, чем самих факторов. А количество расчётов всего, наоборот, на один больше.

РП = Ф1 * Ф2 * Ф3

РП_усл1 = Ф1₁ * Ф2 * Ф3 ⤣

РП_усл2 = Ф1₁ * Ф2₁ * Ф3 ⤣

РП₁ = Ф1₁ * Ф2₁ * Ф3₁ ⤣

На втором этапе (влияние факторов) нужно из каждого последующего расчёта вычесть предыдущий. Вычитание на втором этапе будет происходить последовательно, то есть по цепочке. Поэтому этот способ так и называется — ведь мы используем цепные подстановки.

Δ РП_ф1 = РП_усл1 — РП

Δ РП_ф2 = РП_усл2 — РП_усл1

Δ РП_ф3 = РП₁ — РП_усл2

Преимущества и недостатки

Чем этот метод хорош? Тем, что этот метод универсальный для всех детерминированных факторных моделей. Другие методы подходят не для всех или же вообще используются только для конкретных моделей.

Как у любого другого, у метода цепных подстановок есть свой недостаток. Недостатком является то, что в результате расчёта возникает неразложимый остаток (или погрешность), которая автоматически прибавляется к последнему элементу факторной модели.

Факторный анализ методом цепных подстановок: пример

Рассмотрим пример использования метода цепной подстановки на основе мультипликативной модели.

У нас есть исходная формула

ТП = ОС*ФО

Товарная продукция равняется основные средства умножить на фондоотдачу.

Например,

1. Вот данные об объеме товарной продукции в рублях за предыдущий период (2021 год):

• ТП = 12 млн руб., основные средства = 4 млн. руб, фондоотдача = 3 млн. руб.

1. Данные об объеме товарной продукции в рублях за текущий период (2022 год):

• ТП = 14 млн руб., основные средства = 5 млн. руб, фондоотдача = 2.8 млн. руб.

Рассмотрим по схеме, описанной выше:

1. В данном случае связь у нас будет функциональная и детерминированная, потому что существует чёткая формула определения степени влияния факторов на показатели товарной продукции.

2. Теперь определяем, какой показатель качественный, а какой количественный. Величина основных средств (баланс) — это количественные показатели, а фондоотдача — это, соответственно, качественные показатели. Поэтому в начале пишем количественные показатели (что, собственно, у нас и сделано в самой формуле), а затем качественные показатели.

Начинаем расчёт. Так как у нас здесь два показателя (основные средства и фондоотдача), то расчёта будет три.

Первый расчёт. Здесь мы определяем факторы в плановом или нулевом периоде.

ТП = ОС*ФО

Второй расчёт. ТП (ОС) = ОС₁*ФО

Третий расчет. ТП (ФО) = ОС₁*ФО₁

Итак, мы сделали определённые расчёты. Далее нам нужно определить степень влияния факторов на результат.

Степень влияния фактора ОС на товарную продукцию:

Δ ТП (ОС) = Второй расчет — первый = ОС₁*ФО — ОС*ФО = 5*3 — 4*3 = 15-12 = 3

Если в расчёте получится результат со знаком плюс, то, значит, фактор влияет положительно, если получается результат со знаком минус, то это отрицательное влияние фактора.

Теперь рассмотрим степень влияния фондоотдачи на товарную продукцию:

Δ ТП (ФО) = третий расчет — второй = ОС₁*ФО₁ — ОС₁*ФО = 5*2.8 — 5*3 = 14-15 = −1

После всех этих расчётов необходимо сделать проверку, чтобы проверить правильность своих расчётов. Проверка состоит в том, что сумма отклонений факторов должна равняться отклонению общему.

Δ ТП (ОС) + Δ ТП (ФО) = Δ ТП общее

Общее отклонение = ТП₁ — ТП = 14-12 = 2

3 + (-1) = 2

Расчеты мы провели верно.

Чем занимается Планово-экономический отдел