помощь очень нужна. как найти цепной индекс цен??
Ученик
(183),
закрыт
11 лет назад
Дополнен 11 лет назад
а тогда базисный как???
Александра Харченко
Гений
(66117)
11 лет назад
Если Вам даны только два периода, то цепной индекс цен и базисный индекс цен – это одно и то же.
Если периодов несколько, то цепной индекс цен – отношение следующего периода к предыдущему (февраль / январь, март / февраль…. декабрь/январь) , а базисный – отношение последнего периода к самому первому (декабрь/январь)
T-Cat
Оракул
(53751)
11 лет назад
Цепные индексы – это когда значение текущего периода делится на значение предыдущего.
Например, цепной индекс = Цена Ноябрь/Цена Октябрь
Если
известные данные за несколько периодов
(больше двух), по ним может быть построен
ряд (система) индексов: либо с постоянной
для всех базой сравнения, либо с
переменной.
Выбор
базы сравнения
и весов
индексов –
это два важнейших методологических
вопроса построения систем
индексов.
Системы используются при изучении
динамики социально-экономических
явлений и характеризуют изменения,
происходящие в изучаемом явлении в
течение исследуемого периода времени.
Системой
индексов
называется ряд последовательно
построенных индексов
Система
базисных индексов
– это ряд последовательно вычисленных
индексов одного и того же явления с
постоянной
базой сравнения,
т.е. в знаменателе всех индексов находится
индексируемая величина базисного
периода.
Система
цепных индексов
– это ряд индексов одного и того же
явления, вычисленный с меняющейся
от индекса к индексу
базой сравнения.
Выбор
проводится в зависимости от цели
анализа: базисные
индексы дают
более наглядную характеристику общей
тенденции развития
исследуемого явления, а цепные
– четче отражают последовательность
изменения уровней во времени.
9.1. Цепные и базисные индивидуальные индексы
Системы
цепных и базисных индексов могут быть
построены для индивидуальных
и общих
индексов. Пример системы индивидуальных
индексов дан в табл. 5.
Таблица
5
|
Название |
Система |
|
|
базисных |
цепных |
|
|
Индекс |
|
|
|
Индекс |
|
|
|
Индекс |
|
|
Между
цепными и базисными индексами существует
определенная взаимосвязь,
что позволяет переходить от одних
индексов к другим.
а)
переход от цепных
к базисным
осуществляется перемножением
последовательно цепные
индексы, например:
![]()
![]() =
=
![]() ;
;![]()
![]()
![]() =
=![]() и т.д.
и т.д.
а)
переход от базисных
к цепным
осуществляется через отношение двух
последовательных базисных
индексов, например:
![]() :
:
![]() =
=![]() и т.д.
и т.д.
9.2. Цепные и базисные общие (сводные) индексы
Если,
например, известны данные по предприятию
о выпуске q
нескольких видов продукции (А,
Б,
В
и т.д.) и о ценах р
на нее за четыре периода, то при вычислении
цепных и базисных общих
индексов физического объема и цен можно
по-разному решать вопрос о весах
(соизмерителях).
Системой
индексов с постоянными весами
называется система общих (сводных)
индексов одного и того же явления,
вычисленных с весами, не
меняющимися
при переходе от одного индекса к другому.
Постоянные веса позволяют исключить
влияние изменения структуры на величину
индекса.
Примеры.
-
Цепные
индексы физического объема
по агрегатной
формуле
(продукцию всех
периодов можно
оценить в одних и тех же ценах, предположим
в ценах первого периода
 ,
,
т.е.соизмерителем
(весом)
будет служить постоянная величина
 ):
):
![]() =
=
![]() ;
;![]() =
=![]() ;
;![]() =
=![]() .
.
-
Цепные
индексы цен
(предположим, в качестве соизмерителя
(веса)
примем
 ):
):
![]() =
=
![]() ;
;![]() =
=![]() ;
;![]() =
=![]() .
.
Система
индексов с переменными весами
представляет собой систему общих
(сводных) индексов одного и того же
явления, вычисленных с весами,
последовательно меняющимися от одного
индекса к другому. Переменные веса это
веса отчетного периода.
Примеры.
-
Вычисляя
цепные
индексы физического объема,
можно было поступить так: для каждого
периода строить индекс объема, принимая
в качестве весов цены предыдущего
периода:
![]() =
=
![]() ;
;![]() =
=![]() ;
;![]() =
=![]() .
.
-
Цепные
индексы цен
(т.е. применяются веса
текущего периода):
![]() =
=
![]() ;
;![]() =
=![]() ;
;![]() =
=![]() .
.
Замечания.
1)
Для общих (агрегатных) индексов переход
от цепных индексов к базисным строго
математически
возможен лишь для индексов с постоянными
весами (например,
на основе записанных выше цепных
индексов физического
объема с постоянными
весами путем
перемножения их легко получить
соответствующий базисный
индекс
физического объема, в частности:


![]() =
=![]() ).
).
2)
При применении такого перехода (т.е. от
цепных индексов к базисным) к индексам
с переменными
весами
необходимо
оговорить
условность
такого перехода и отметить,
что структура (состав) «агрегата» (для
которого вычисляется индекс) мало
подвержена изменениям (отметим, это
условие только предполагается).
По данным Федеральной службы государственной статистики о средних ценах на уголь и объемах его производства в РФ за три года:
| Год | Цена за 1 т, руб. | Произведено, тыс. т. |
|---|---|---|
| 2011 | 1005 | 336 293 |
| 2012 | 955 | 356 781 |
| 2013 | 962 | 351 232 |
при условии 100 %-й реализации угля в каждом году, определите цепные и базисные индивидуальные индексы цен, физического объема реализации и товарооборота. Проверьте взаимосвязь цепных и базисных индексов.
Решение:
1. а) Цепные индивидуальные индексы цен на уголь вычисляются с меняющейся от индекса к индексу базой сравнения:
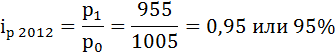
где
р1 – цена угля в 2012 году (текущем),
р0 – цена угля в 2011 году (базисном).
В 2012 году в Российской Федерации наблюдается снижение цен на уголь по сравнению с 2011 годом на 5%.
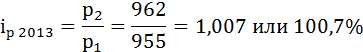
где
р2 – цена угля в 2013 году (текущем),
р1 – цена угля в 2012 году (базисном).
В 2013 году в РФ цены на уголь по сравнению с 2012 годом возросли на 0,7%.
б) Базисные индивидуальные индексы цен на уголь вычисляются с постоянной базой сравнения, то есть в знаменателе всех индексов находится индексируемая величина базисного периода:
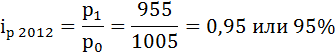
где
р1 – цена угля в 2012 году (текущем),
р0 – цена угля в 2011 году (базисном).
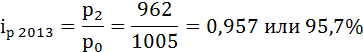
где
р2 – цена угля в 2013 году (текущем),
р0 – цена угля в 2011 году (базисном).
Проверим взаимосвязь цепных индексов.
Если последовательно перемножить цепные индексы, можно получить конечный базисный индекс:
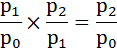
И действительно:
0,95 × 1,007 = 0,957
Проверим взаимосвязь базисных индексов:
Зная последовательные значения базисных индексов, легко рассчитать на их основе конечный цепной индекс:
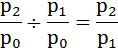
0,957 / 0,95 = 1,007
2. а) Цепные индивидуальные индексы физического объема реализации угля вычисляются, аналогично. То есть с меняющейся от индекса к индексу базой сравнения:
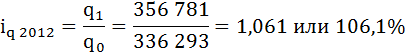
где
q1 – физический объем реализации угля в 2012 году (текущем),
q0 – физический объем реализации угля в 2011 году (базисном).
В 2012 году в РФ наблюдается рост физического объема реализации угля по сравнению с 2011 годом на 6,1%.
В 2013 году в РФ физический объем реализации угля по сравнению с 2012 годом снизился на 1,6%:
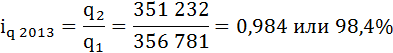
где
q2 – физический объем реализации угля в 2013 году (текущем),
q1 – физический объем реализации угля в 2012 году (базисном).
б) Базисные индивидуальные индексы физического объёма на уголь вычисляются с постоянной базой сравнения, то есть в знаменателе всех индексов находится индексируемая величина базисного периода.
Базисный индекс 2012 года совпадает с величиной цепного индекса 2012 года:
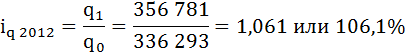
где
q1 – физический объем реализации угля в 2012 году (текущем),
q0 – физический объем реализации угля в 2011 году (базисном).
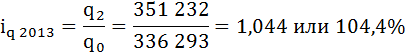
где
q2 – физический объем реализации угля в 2013 году (текущем),
q0 – физический объем реализации угля в 2011 году (базисном).
Физический объем реализации угля в 2013 году вырос на 4,4% по сравнению с 2011 годом.
Проверим взаимосвязь цепных индексов.
Если последовательно перемножить цепные индексы, можно получить конечный базисный индекс:
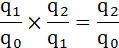
1,061 × 0,984 = 1,044
Проверим взаимосвязь базисных индексов:
Зная последовательные значения базисных индексов, легко рассчитать на их основе конечный цепной индекс:
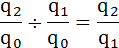
1,044 / 1,061 = 0,984
3. а) Рассчитаем цепные индивидуальные индексы товарооборота:
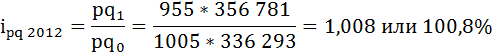
где
рq1 – товарооборот угля в 2012 году (текущем),
рq0 – товарооборот угля в 2011 году (базисном).
В 2012 году в РФ наблюдается рост товарооборота угля по сравнению с 2011 годом на 0,8%.
В 2013 году в РФ товарооборот угля по сравнению с 2012 годом упал на 0,8%:
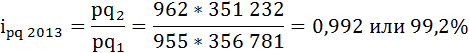
где
рq2 – товарооборот угля в 2013 году (текущем),
рq1 – товарооборот угля в 2012 году (базисном).
б) Базисные индивидуальные индексы товарооборота угля вычисляются с постоянной базой сравнения, то есть в знаменателе всех индексов находится индексируемая величина базисного периода.
Базисный индекс товарооборота 2012 года совпадает с величиной цепного индекса товарооборота 2012 года:
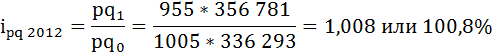
где
рq1 – товарооборот угля в 2012 году (текущем),
рq0 – товарооборот угля в 2011 году (базисном).
Базисный индекс товарооборота в 2013 году будет равен:
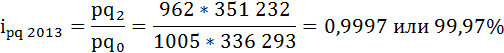
где
рq2 – товарооборот угля в 2013 году (текущем),
рq0 – товарооборот угля в 2011 году (базисном).
Товарооборот угля в 2013 году по сравнению с 2011 годом снизился на 0,03%.
Проверим взаимосвязь цепных индексов товарооборота.
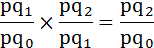
Взаимосвязь наблюдается:
1,008 × 0,992 = 0,9997
Проверим взаимосвязь базисных индексов товарооборота:
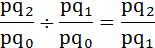
0,9997/ 1,008 = 0,992.
Базисные и цепные индексы
При вычислении индексов, как мы уже установили, необходимо иметь данные за 2 периода, или 2 сравниваемых уровня.
Если же имеются данные за несколько периодов или уровней, то в качестве базы для сравнения может быть принят или один и тот же начальный уровень (для всех остальных), или для каждого последующего уровня – предшествующий ему.
В первом случае мы получим индексы с постоянной базой – базисные, во втором – индексы с переменной базой – цепные. И базисные, и цепные индексы имеют определенное значение в экономическом анализе.
Базисные индексы характеризуют изменения явлений за длительный период времени по отношению к какой-либо одной отправной точке (периоду или моменту времени).
Цепные индексы позволяют следить за текущими изменениями явлений. Поэтому вопрос о том каким индексом воспользоваться в каждом конкретном случае, решают исходя из задач исследования.
Если базисные и цепные индексы охватывают один и тот же период времени, между ними существует взаимосвязь:
1) произведение цепных индексов равно конечному базисному;
2) отношение последующего базисного индекса к предыдущему, равно соответствующему цепному индексу.
Существующая взаимосвязь дает возможность исчислять базисные индексы по данным о цепных и наоборот.
НАПРИМЕР: производство продукции шоколадной фабрики характеризуется следующими данными:
| 1996 г. | 1997 г. | 1998 г. | 1999 г. | 2000 г. | |
| Продукция, млн. грн. | 5 (q0) | 7 (q1) | 12 (q2) | 22 (q3) | 30 (q4) |
| Базисные индексы | 1,00 | 1,4 | 2,4 | 4,4 | 6,0 |
| Цепные индексы | 1,00 | 1,4 | 1,7 | 1,8 | 1,4 |
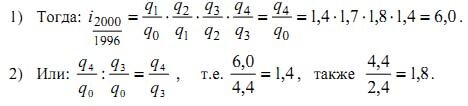
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
Открыть эту статью в PDF
Индекс инфляции в моделях
Долгосрочные финансовые прогнозы охватывают много лет деятельности бизнеса и на протяжении срока планирования цены, использованные в них, будут меняться. Как правило, моделирование основано на текущем значении цен и их ожидаемых изменениях под действием инфляции.
Если планирование основано на номинальных ценах, то все суммы доходов и затрат по статьям, подверженным инфляции, должны меняться от периода к периоду. Если планирование ведется в реальных ценах, то никакие цены не меняются, но прогноз инфляции все равно должен быть представлен в модели, так как эту инфляцию надо будет вычитать из ставки дисконтирования и других аналогичных ставок. Подробнее о номинальных и реальных ценах можно узнать здесь.
Для применения инфляции в модель обычно включают раздел прогноза макроэкономических показателей, который может выглядеть таким образом:

Здесь для применения инфляции к будущим ценам подготовлено два индекса.
Цепной индекс инфляции рассчитывается по отношению к предыдущему периоду. Он как бы по цепочке, от периода к периоду, передает влияние инфляции. Такой индекс удобно использовать по отношению к параметрам, для которых в модели отдельно задана цена и физические объемы.
Базисный индекс инфляции показывает влияние инфляции нарастающим итогом от начала проекта. Он удобен в работе со статьями доходов и затрат, задаваемых денежными суммами, без деления на объемы и цены.
Формула индекса инфляции
Формула расчета индекса инфляции зависит от допущений, принимаемых при построении модели. В приведенном выше примере сделано допущение, что цены в модели были определены в 2021 году, а средние цены 2022 года будут отличаться от них на величину годовой инфляции. Тогда индекс 2022 года равен 1+I22, где I22 — инфляция 2022 года.
Другое возможное допущение — цены были определены в начале 2022 года, равномерно росли с инфляцией в течение года, и среднегодовые цены первого года примерно соответствуют ценам 1 июля — то есть надо считать с влиянием полугодовой инфляции.
Формула первого периода несколько изменится, теперь это:
и вся таблица немного изменит свои значения:

Наконец, мы можем предположить, что цена определена на начало 2022 года, а в модели мы допускаем, что все денежные потоки и цены приходятся на первый день любого расчетного периода. Тогда для первого года никакого влияния инфляции не будет, и таблица примет вид:

Во всех приведенных примерах предполагалось, что шаг планирования финансовой модели — год. Если планирование ведется не по годам, а по кварталам или месяцам, то формула индекса инфляции меняется. Наиболее удобный и универсальный вариант формулы для цепного индекса выглядит так:
где I — годовая инфляция
m — число месяцев в расчетном периоде
Пример реализации индекса инфляции
Подробную инструкцию по включению инфляции в финансовые модели можно посмотреть в этом видео:
Такие статьи мы публикуем регулярно. Чтобы получать информацию о новых материалах, а также быть в курсе учебных программ, вы можете подписаться на новостную рассылку.
Если вам необходимо отработать определенные навыки в области инвестиционного или финансового анализа и планирования, посмотрите программы наших семинаров.


