Разряды и классы чисел
- Классы чисел
- Разряды чисел
Классы чисел
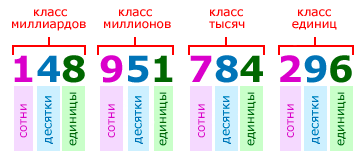
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса:
Названия классов многозначных чисел справа налево:
- первый — класс единиц,
- второй — класс тысяч,
- третий — класс миллионов,
- четвёртый — класс миллиардов,
- пятый — класс триллионов,
- шестой — класс квадриллионов,
- седьмой — класс квинтиллионов,
- восьмой — класс секстиллионов.
Для удобства чтения записи многозначного числа, между классами оставляется небольшой пробел. Например, чтобы прочитать число 148951784296, выделим в нём классы:
148 951 784 296
и прочитаем число единиц каждого класса слева направо:
148 миллиардов 951 миллион 784 тысячи 296.
При чтении класса единиц в конце обычно не добавляют слово единиц
.
Разряды чисел
Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
Разряд числа — это позиция (место) цифры в записи числа.
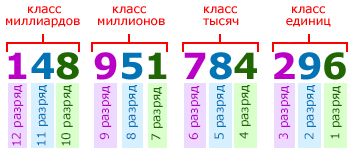
Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
- Единицы называют единицами первого разряда (или простыми единицами) и пишутся на первом месте справа.
- Десятки — единицами второго разряда и пишутся в числе на втором месте справа.
- Сотни — единицами третьего разряда и пишутся на третьем месте справа.
- Единицы тысяч — единицами четвёртого разряда и пишутся на четвёртом месте справа.
- Десятки тысяч — единицами пятого разряда и пишутся на пятом месте справа.
- Сотни тысяч — единицами шестого разряда и пишутся в числе на шестом месте справа и так далее.
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Пример. Запишите цифрами число, которое содержит:
1) 37 единиц второго класса и 565 единиц первого класса;
2) 450 единиц второго класса и 9 единиц первого класса;
3) 8 единиц второго класса и 50 единиц первого класса.
Решение:
1) 37 565;
2) 450 009;
3) 8 050.
Все разрядные единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда:
| 10 единиц | = | 1 десяток; |
| 10 десятков | = | 1 сотня; |
| 10 сотен | = | 1 тысяча; |
| 10 тысяч | = | 1 десяток тысяч; |
| 10 десятков тысяч | = | 1 сотня тысяч; |
| 10 сотен тысяч | = | 1 тысяча тысяч (1 миллион); |
и так далее.
Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.
Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.
Цифра 0 в каком-нибудь разряде означает отсутствие единиц в данном разряде.
Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
24 527 — двадцать четыре тысячи пятьсот двадцать семь.
20 507 — двадцать тысяч пятьсот семь.
Видеоурок по этой теме можно посмотреть по ссылке: Разряды и классы. Десятичная система счисления.
Пройти тест по теме «Натуральные числа и действия над ними» можно по ссылке. Проверьте свои знания!
Мы выяснили, что в записи натурального числа значение, роль любой цифры зависит от места ее расположения в числе.
Определение
Разряд – это позиция, место расположения цифры в записи числа, начиная справа.
То есть, таблицу 2. в разделе чтение и запись натуральных чисел можно переписать следующим образом:
Таблица 1. Значение разрядов натуральных чисел.
Кроме единиц 1-го разряда, которые носят имя простые, все остальные именуются составные.
Любая составная единица, которая находится на позиции большего разряда, чем другая, называется единицей высшего разряда. Другая, соответственно, носит название единица низшего разряда.
Например, единицы 6-го разряда – это высший разряд по отношению к единицам 3-го разряда, и низшим разрядом по сравнению с единицами 9-го разряда.
Самый младший разряд, как видно из таблицы, это разряд единиц. Цифра этого разряда всегда находится в конце любого натурального числа, то есть, это самая правая цифра.
Например, в числе 7777 четыре цифры 7, стоящих в разных разрядах, первом, втором, третьем и четвертом.
Цифра 7, которая стоит здесь на первом месте справа, означает 7 единиц (простых), на втором месте справа – 7 десятков, на третьем месте справа – 7 сотен, на четвертом месте справа – 7 единиц тысяч (говорят просто: семь тысяч).
Запомните
Если в натуральном числе нет ни одной единицы какого-либо разряда, тогда в этом разряде пишется цифра 0 (нуль).
В начале числа (слева) нули не ставятся.
Примеры:
Записывать число 503 как 0503, 00503, 000503 и т.д. – неправильно.
Число 503 содержит 5 сотен, 0 десятков, 3 единицы.
Подобная запись числа по наименованию разрядов, входящих в его состав, называется разрядный состав числа. Подробнее об этом читайте в разделе «Разрядные слагаемые».
Любые 10 единиц какого-нибудь разряда создают 1 единицу следующего за ним большего разряда. К примеру, 10 простых единиц создают 1 десяток, 10 сотен создают 1 тысячу.
И наоборот, любая единица высшего разряда включает в себя 10 единиц следующего за ней низшего разряда.
Из таблицы 1 можно заметить, что определенные части в наименовании значений, а именно: единицы, десятки, сотни, повторяются с различными дополнениями, такими как тысячи, миллионы, миллиарды. Например, единицы сотен и единицы миллиардов, сотни миллионов и сотни тысяч и пр.
Поэтому можно сгруппировать разряды единиц по три в каждом, начиная с самого маленького, то есть, справа.
Определение
Класс – это группа разрядов, содержащая в себе три разряда: единицы, десятки и сотни.
Классы, как и разряды, считают справа налево.
При записи многозначного числа можно оставлять небольшой пробел между разными классами, либо разделять их точками. Делается это для удобства чтения натуральных чисел.
Сколько содержится в числе единиц какого-нибудь разряда
Рассмотрим на примере. Допустим, необходимо определить, сколько всего десятков содержит в себе число 28924, то есть, сколько их содержится в десятках тысяч, в тысячах, в сотнях и в десятках данного числа вместе.
Простые десятки стоят на втором справа месте в числе. В нашем примере на этом месте находится цифра 2, это означает, что в данном числе два простых десятка. Следующая влево цифра – это 9, она показывает количество сотен. Но каждая простая сотня содержит в себе 10 десятков, поэтому в 9 сотнях их заключено 90. Слева от девятки, на четвертой позиции, стоит цифра 8, которая означает количество тысяч. Зная, что каждая тысяча содержит в себе 10 сотен, а, следовательно, 100 десятков, легко понять, что 8 тысяч заключают в себе 800 десятков. Следом за цифрой 8 влево идет цифра 2, она означает десятки тысяч. Но каждый десяток тысяч содержит в себе 10 тысяч, то есть, 100 сотен, и, следовательно, 1000 десятков, поэтому в 20 тысячах заключено 2000 десятков.
Итак, всего число в нашем примере содержит 2000 десятков, да еще 800 десятков, да еще 90 десятков, и еще 2 десятка, то есть, 2892 десятка.
Аналогичным образом можно узнать, что в числе из нашего примера содержится 289 сотен.
Запомните
Для того, чтобы узнать, сколько всего единиц какого-нибудь разряда содержится в любом числе, необходимо мысленно убрать из него все единицы более низких разрядов, после чего прочитать то число, которое получилось.
Еще один пример: число 54.128.312 содержит: 5.412.831 десятков, 541.283 сотен, 54.128 тысяч, 5.412 десятков тысяч, 541 сотен тысяч, 54 миллиона, 5 десятков миллионов.
В математике разряды чисел — это позиции цифр в числе (место, где располагается цифра). Их нужно читать справа налево.
Рассмотрим число 345, которое состоит из трех цифр:
➤ первая позиция — цифра 5 — разряд единиц
➤ вторая позиция — цифра 4 —разряд десятков
➤ третья позиция — цифра 3 —разряд сотен
Разряды также сообщают нам информацию о количестве единиц, десятков и сотен.
➤ первая позиция — цифра 5 — разряд единиц содержит 5 единиц (1+1+1+1+1)
➤ вторая позиция — цифра 4 —разряд десятков содержит четыре десятка (10+10+10+10)
➤ третья позиция — цифра 3 —разряд сотен содержит три сотни (100+100+100)
Если сложить число единиц, число десятков и число сотен, то получим наше изначальное число 345:
(1+1+1+1+1)+(10+10+10+10)+(100+100+100)
Слова единицы, десятки, сотни, заменяют собой множители 1, 10 и 100.
Например, рассмотрим наше число 345:
➤ в разряде единиц — множитель 1 содержится в разряде единиц 5 раз: 1 × 5 = 5
➤ в разряде десятков — множитель 10 содержится в разряде десятков 4 раза: 10 × 4 = 40
➤ в разряде сотен — множитель 100 содержится в разряде сотен 3 раза: 100 × 3 = 300
Если сложить полученные результаты 5 + 40 + 300, то получим число 345.
Другие группировки
➤ То же самое будет происходить если мы скажем, что число 345 содержит 34 десятка и 3 единицы. Другими словами,
— десятки будут сгруппированы 34 раза: 10 × 34 = 340
— единицы будут сгруппированы 5 раз: 1 × 5 = 5
Если сложить полученные результаты 340 и 5, снова получим число 345.
➤ Также возможно группировка, при которой не будет распределения на десятки и сотни. В таком случае число 345 будет читаться как «триста сорок пять единиц»: 1 × 345 = 345.
Старшие разряды
Далее рассмотрим более старшие разряды: тысяч, десятков тысяч, сотен тысяч, миллионов и т.д.
Рассмотрим число: 1 234 567
разряд единиц — 7 единицы,
разряд десятков — 6 десятков,
разряд сотен — 5 сотен,
разряд тысяч — 4 тысячи,
разряд десятков тысяч — 3 десятка тысяч,
разряд сотен тысяч — 2 сотни тысяч,
разряд миллионов — 1 миллион.
Применение разрядов
Применение разрядов при решение примеров облегчают некоторые вычисления. Например, когда нужно сложить два трехзначных числа, то можно сложить все разряды по отдельности: единицы, десятки и сотни. Начинать нужно с разряда единиц и т.д.
Рассмотрим пример: 123 + 456 =
В первую очередь после знака равно (=) мысленно поставим три точки. Вместо этих точек будет располагаться новое число (наш ответ): 123 + 456 = . . .
Начинаем складывать:
1) из разряда единиц берем числа 3 и 6, получаем 9 ➜ 123 + 456 = . . 9
2) из разряда десятков берем числа 2 и 5, получаем 7 ➜ 123 + 456 = . 7 9
3) из разряда сотен берем числа 1 и 4, получаем 5 ➜ 123 + 456 = 5 7 9
Таким образом, если к числу 123 прибавить 456 , получается 579.
Этот принцип действует, если решать примеры в столбик:
? Важно! Каждый разряд записывается друг под другом: единицы под единицами, десятки под десятками, сотни под сотнями и т.д. При неправильном размещении разрядов пример будет решен не правильно!
? Чтобы потренироваться решать примеры в столбик на сложение, можно скачать программу «Сложение и вычитание в столбик«.
Переполнение разряда
Разряд характеризуется одной цифрой от 0 до 9. Но иногда при вычислении числового выражения может произойти переполнение разряда.
Рассмотрим пример: 56+89.
При сложении единиц этих чисел получаем 15 (6+9), а при сложении десятков получаем 13 (5+8).
1) При сложении 9 и 6 единиц у нас получилось 15 единиц — это 1 десяток и 5 единиц.
Поэтому в разряд десятков записываем 5, а 1 десяток мы будем прибавлять к десяткам при их сложении.
2) При сложении десятков получаем 13 (5+8) — это 1 сотня и 3 десятка.
Поэтому в разряд десятков мы запишем 4 (3 десятка + 1 десяток, полученный при сложении единиц). Так как в примере разряд сотней не складывается, то мы просто впереди приписываем единицу.
| 1 5 6 + 8 9 = . . ➜ 5 6 + 8 9 = . 5 ➜ 5 6 + 8 9 = 1 4 5 |
Этот принцип действует также при решении примеров в столбик:
|
+ |
1 |
|
1 1 |
|
| 1 4 5 | 6 2 7 |
Примеры на вычитание
Теперь рассмотрим примеры на вычитание. Вычитать также нужно по разрядам.
Пример: 68–45.
Начинаем с разряда единиц. При вычитании единиц этих чисел получаем 3 (8-5).
Затем вычитаем десятки. При вычитании десятков получаем 2(6-4).
6 8 – 4 5 = . . ➜ 6 8 – 4 5 = . 3 ➜ 6 8 – 4 5 = 2 3
Пример: 42-15.
1) В разряде единиц числа 42 содержится две единицы, а в разряде единиц числа 15 — пять единиц. От двух единиц нельзя вычесть пять единиц, поскольку две единицы меньше, чем пять единиц.
Чтобы выполнить вычитание, две единицы должны взять несколько единиц у соседней группы (разряда десятков) ➜ Поэтому берем один десяток.
Получаем, что мы число 42 разделили на 3 десятка и 12 единиц. Из 12 вычитаем 5 и получаем 7. Записываем цифру 7 в разряде единиц нового числа.
2) Теперь вычитаем десятки. Поскольку разряд десятков отдал единицам один десяток, сейчас он имеет не четыре, а три десятка. Поэтому вычитаем из 3 десятков один десяток. Останется 2 десятка. Записываем цифру 2 в разряде десятков нового числа.
Чтобы не забывать, что в каком-то разряде был взят один десяток (либо сотня либо тысяча), над этим разрядом принято ставить точку.
| • • 4 2 – 1 5 = 4 2 – 1 5 = . 7 ➜ 4 2 – 1 5 = 2 7 |
Этот принцип действует также при решении примеров в столбик:
|
– |
• |
|
• • |
|
| 2 7 | 2 4 4 |
Во втором примере:
1) Вычитаем единицы. разряде единиц числа 823 содержится 3 единицы, а в разряде единиц числа 579 — 9 единиц. От 3 единиц не вычесть 9 единиц, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток. Взятый один десяток и три единицы вместе образуют 13 единиц. От 13 единиц вычитаем 9 единиц, получится 4 единицы. Записываем цифру 4 в разряде единиц нового числа.
2) Вычитаем десятки. Раньше разряд десятков числа 823 содержал 2десятка, но мы взяли с него один десяток, и теперь в разряде десятков содержатся 1 десяток. Из 1 десятка нужно вычесть 7 десятков, поэтому берем одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню. Взятая 1 сотня и 1 десяток вместе образуют 11 десятков. От 11 десятков вычитаем 7 десятков, получаем 4 десятка. Записываем цифру 4 в разряде десятков нового числа.
3) Вычитаем сотни. Раньше разряд сотен числа 823 содержал 8 сотен, но мы взяли с него 1сотню, и теперь в разряде сотен содержатся 7 сотен. Из 7 сотен можно вычесть 5 сотен, получается 2 сотни. Записываем цифру 2 в разряде сотен нового числа.
? Чтобы потренироваться решать примеры в столбик на вычитание, можно скачать программу «Сложение и вычитание в столбик«.
Вычитание из круглых чисел
Намного сложнее вычитать из чисел вида 100, 200, 300, 1000, 10000. То есть числа, у которых на конце нули. Чтобы выполнить вычитание, каждому разряду приходится занимать десятки/сотни/ тысячи у следующего разряда.
Выполнять вычитание таким традиционным методом сложно, поэтому можно воспользоваться нестандартным способом. Для этого уменьшить вычитаемое число на одну единицу. Далее из полученного результата вычесть вычитаемое и к полученной разности прибавить единицу.
Пример: 1000–123
1) уменьшим уменьшаемое на 1: 1000–1=999
2) из числа 999 вычтем 123: 999-123=876
3) к этому ответу прибавляем 1: 876+1=877.
Получили: 1000+123=877.
Home » 5 класс » Многозначные числа. Единицы разрядов и классов. Сумма разрядных слагаемых.
Многозначные числа.
Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.
Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.
Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.
Трехзначные числа состоят из трех цифр, например: 354, 444, 780.
Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.
Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.
Разряды чисел.
Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.
Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.
Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда. Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.
Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.
Такой разбор числа называется разрядным составом числа.
Классы.
Многозначные числа разбивают на группы по три цифры справа налево. Такие группы цифр называют классам. Первый класс справа называется классом единиц, второй называется классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов, пятый – классом триллионов, шестой – классом квадриллионов, седьмой – классом квинтиллионов, восьмой – классом секстиллионов.
Класс единиц – первый класс справа с конца три цифры состоит из разряда единиц, разряда десятков и разряда сотен.
Класс тысяч – второй класс состоит из разряда: единиц тысяч, десятков тысяч и сотен тысяч.
Класс миллионов – третий класс состоит из разряда: единиц миллионов, десятков миллионов и сотен миллионов.
Разберем пример:
У нас есть число 13 562 006 891.
Это число имеет 891 единиц в классе единиц, 6 единиц в классе тысяч, 562 единиц в классе миллионов и 13 единиц в классе миллиардов.
Таблица разрядов и классов.
Чтобы прочитать натуральное число 13562006891 нужно справа отметить по три цифры класса 13 562 006 891 и прочитать число единиц каждого класса слева направо:

Сумма разрядных слагаемых.
Любое натурально число имеющее различные разряды можно разложить на сумму разрядных слагаемых. Рассмотрим пример:
Число 4062 распишем на разряды.
4 тысяч 0 сотен 6 десятков 2 единиц или по-другому можно записать
4062=4 ⋅1000+0 ⋅100+6 ⋅10+2
Следующий пример:
26490=2 ⋅10000+6 ⋅1000+4 ⋅100+9 ⋅10+0
Вопросы по теме:
Назовите первые четыре класса в записи натуральных чисел?
Ответ: класс единиц, класс тысяч, класс миллионов, класс миллиардов.
Как читают многозначные числа?
Ответ: многозначные числа читают слева направо. Разбивают число по 3 цифры с конца на классы, называют все цифры, кроме нуля. Цифра 0 в записи числа означают отсутствие разряда.
Какие цифры могут стоять в любом разряде числа, кроме высшего?
Ответ: 0, 1, 2, 3, 4. 5, 6, 7, 8, 9.
Какие цифры могут стоять в высшем разряде числа?
Ответ: 1, 2, 3, 4. 5, 6, 7, 8, 9.
Что такое сумма разрядных слагаемых?
Ответ: Это разложение натурального числа на разряды и суммирование их.
Сколько десятков в сотне?
Ответ: в сотне 10 десятков.(10+10+10+10+10+10+10+10+10+10=100)
Сколько сотен в тысячи?
Ответ: в тысячи 10 сотен. (100+100+100+100+100+100+100+100+100+100=1000)
Сколько десятков в тысячи?
Ответ: в тысячи 100 десятков.
Сколько тысяч в миллионе?
Ответ: в миллионе 1000 тысяч.
Примеры на задачи.
Пример №1:
Запишите и прочитайте число: а) пятизначное б) шестизначное.
Ответ: а) 35 100 (тридцать пять тысяч сто) б) 803 273 (восемьсот три тысячи двести семьдесят три)
Пример №2:
Сколько натуральных чисел: а) однозначных б) двузначных?
Ответ: а) однозначных натуральных чисел 10 (0, 1, 2, 3, 4. 5, 6, 7, 8, 9), б) двузначных натуральных чисел 90 (10, 11, 12, …,99)
Пример №3:
В записи числа 10398 назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, …
Ответ: 8 – разряд единиц, 9 – разряд десятков, 3 – разряд сотен, 0 – разряд тысяч, 1 – разряд десятков тысяч.
Пример №4:
Напишите наименьшее трехзначное число и наибольшее пятизначное число.
Ответ: 100 и 99999.
Пример №5:
Запишите число 56976 в виде суммы разрядных слагаемых:
Ответ: 56976=50000+6000+900+70+6=5⋅10000+6⋅1000+9⋅100+7⋅10+6