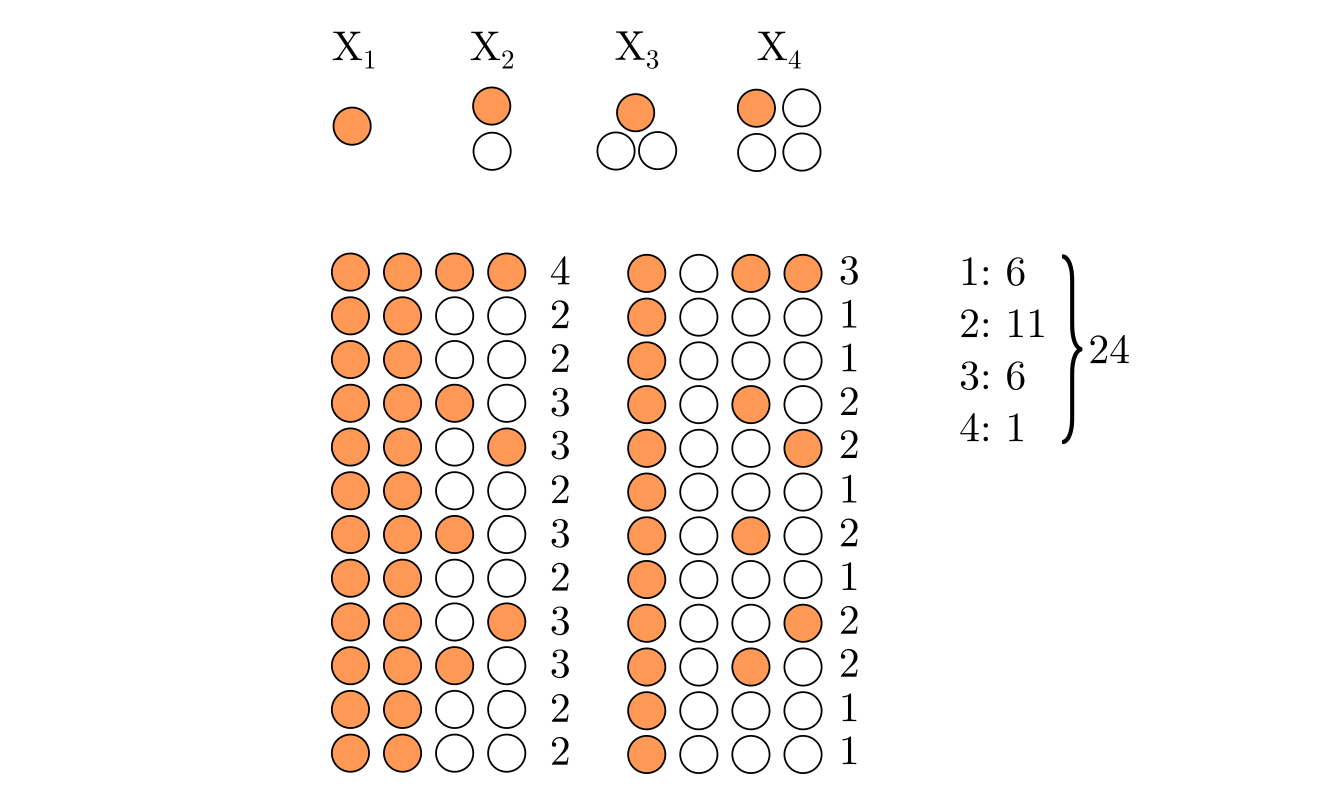Как найти цикл перестановки

Действие перестановки на набор элементов

Определение:

Пусть — перестановка из элементов, и — множество некоторых объектов, занумерованных числами от до . Тогда результатом действия перестановки на этот набор объектов назовём множество объектов , занумерованных числами от одного до , причём .

Обозначим за множество (не пронумерованных) объектов . Поскольку перестановку можно рассматривать как отображение , а нумерацию как отображение , то действие перестановки можно определить как композицию отображений .

Например, рассмотрим множество и перестановку . Тогда результат действия на — упорядоченное множество . Если рассмотреть граф перестановки (описано ниже), то действие перестановки можно представить таким образом: каждый элемент устанавливается в вершину графа, соответствующую номеру этого элемента, после чего каждый элемент передвигается по исходящему из этой вершины ребру.

Также, композицию перестановок можно выразить как действие одной перестановки на другую.
Стоит отметить, что действие перестановки соответствует переходу по графу раз.

Действие обратной перестановки над множеством соответствует переходу элементов по развёрнутым рёбрам и даёт упорядоченное множество , для которого верно .

Утверждение:

Если , то ;

Поскольку можно представить как , то

Циклы

Определение:

Циклом длины называется такая перестановка которая тождественна на всём множестве кроме подмножества и , . Обозначается .

Перестановку можно записать в виде произведения непересекающихся циклов, причём единственным образом с точностью до порядка следования циклов в произведении. Например: .

Цикл может быть записан по разному, например, в приведенном выше примере цикл может быть записан как , , но не может быть записан как .

Перестановку можно представить в виде графа. Граф содержит ребро от вершины к вершине если . Тогда циклы перестановки соответствуют циклическим путям в графе.

С циклами связаны некоторые интересные свойства перестановок.

Определение:

Степенью перестановки называется минимальное число такое, что

Утверждение:

Степень перестановки равна наименьшему общему кратному длин всех циклов

Пусть — степень перестановки. Граф перестановки разбит на циклы, и для того, чтобы какой-то элемент прошёл по своему циклу один раз, нужно возвести перестановку в степень , где — длина цикла. Если элемент проходит цикл несколько раз и возвращается на своё место, то можно сделать вывод о том, что перестановка возводится в степень кратную . Тогда только в том случае, когда делится на длины всех циклов, все элементы вернутся на свои места, а наименьшее такое — это НОК длин всех циклов.

Утверждение:

Если длины всех циклов не превышают , то перестановка является инволюцией.

Действительно, в таком случае по вышеупомянутому . Домножив на получим .

Поиск всех циклов в перестановке

Задача:

Дана перестановка из элементов, требуется найти все циклы в ней.

Рассмотрим элемент перестановки . Добавим его к циклу, отметим позицию посещенной и перейдем к . Если мы перешли в позицию , которую уже посещали, значит мы нашли очередной цикл перестановки. Перейдем к первой непосещенной позиции и продолжим поиск.

Рассмотрим в качестве примера поиск циклов в перестановке :

1. В позиции находится число . Добавим его к новому циклу и перейдем в позицию . Аналогично добавим к циклу числа и . Перейдем в позицию , которую мы уже посещали — нашли первый цикл .
2. Аналогично найдем второй цикл .
3. Таким образом,

Псевдокод алгоритма

 function findCycles(int p[]):
   vector<bool> used(n)             // массив, где отмечены посещенные позиции
 
   for i = 1 to n
     if not used[i]
       j = i
       vector<int> cycle
       while not used[j]
         cycle.push_back(p[j])
         used[j] = true
         j = p[j]
       print cycle                  // выведем на экран очередной цикл перестановки

См. также

• Теорема Кэли

Источники

• Википедия — Перестановка
• Wikipedia — Permutation

В теории групп циклическая перестановка — это перестановка элементов некоторого множества X, которая переставляет элементы некоторого подмножества S множества X циклическим образом, сохраняя на месте остальные элементы X (т.е. отображая их в себя). Например, перестановка {1, 2, 3, 4}, переводящая 1 в 3, 3 в 2, 2 в 4 и 4 в 1 является циклической, в то время как перестановка, переводящая 1 в 3, 3 в 1, 2 в 4 и 4 в 2 циклической не является.

Цикл в перестановке — это подмножество элементов, которые переставляются циклическим образом. Множество S называется орбитой цикла. Каждую перестановку конечного множества элементов можно разложить в объединение циклов с непересекающимися орбитами. В некоторых контекстах циклическая перестановка сама по себе называется циклом.

Определение[править | править код]

Перестановка называется циклической тогда и только тогда, когда она состоит из единственного нетривиального цикла (т.е. цикла длиной больше 1)^[1].

Пример:

Некоторые авторы ограничивают определение только теми перестановками, которые имеют в точности один цикл (то есть, не разрешаются перестановки, имеющие фиксированные точки^[2].

Пример:

Более формально, перестановка множества X, которая является биективной функцией , называется циклической, если действие на X подгруппы с генератором имеет максимум одну орбиту из более чем одного элемента^[3]. Это понятие чаще всего используется, когда X является конечным множеством. Тогда, конечно, наибольшая орбита S также конечна. Пусть  — любой элемент S, положим для любого . Если множество S конечно, имеется минимальное число , для которого . Тогда и является перестановкой, определённой формулой

для

и для любого элемента . Элементы, не фиксируемые отображением , можно представить как

.

Цикл можно записать с использованием компактной циклической записи (запятая между элементами в такой записи не ставится, чтобы избежать путаницы с кортежами). Длина цикла — это число элементов его наибольшей орбиты. В циклической записи циклы длины 1 часто опускаются, если это не вызывает путаницы^[4].

Основные свойства[править | править код]

По одному из основных свойств симметрических групп, любую перестановку можно представить как произведение непересекающихся циклов (более точно — циклов с непересекающимися орбитами). Такие циклы можно переставлять друг с другом, и выражение перестановки единственно с точностью до порядка циклов (заметим, что циклическая запись не единственна — любой k-цикл сам по себе может быть записан k различными способами в зависимости от выбора в его орбите). Мультимножество длин циклов (цикловый тип) однозначно определяется перестановкой.

Число различных циклов длины k в симметрической группе S_n задаётся для следующей формулой

Цикл длины k имеет чётность (−1)^k − 1.

Транспозиции[править | править код]

Цикл, состоящий из двух элементов, называется транспозицией. Например, перестановка {1, 4, 3, 2}, переводящая 1 в 1, 2 в 4, 3 в 3 и 4 в 2 является транспозицией (а именно, транспозицией, переставляющей 2 и 4).

Любую перестановку можно представить как композицию (произведение) транспозиций — формально, они являются генераторами группы^[5]. Более того, любую перестановку упорядоченного множества X = {1, 2, …, n} можно выразить как произведение смежных транспозиций, то есть транспозиций вида Действительно, любую транспозицию можно представить в виде произведения смежных транспозиций.

Разложение перестановки в произведение транспозиций можно получить, например, путём выписывания перестановки как произведения различных циклов, а затем итеративного разложения циклов длины 3 и более в произведение транспозиции и цикла на единицу короче:

Симметрическая группа является группой Коксетера, в том смысле, что она порождается элементами порядка 2 (смежными транспозициями) и все соотношения имеют определённый вид.

Один из главных результатов элементарной теории симметрических групп утверждает, что либо все разложения данной перестановки на транспозиции имеют чётное число транспозиций, либо все разложения имеют нечётное число транспозиций^[6]. Это позволяет чётности перестановки быть хорошо определённой функцией.

См. также[править | править код]

• Циклическая сортировка^[en] — алгоритм сортировки, основанный на идее, что массив можно разложить на циклы, которые можно индивидуально прокрутить, чтобы получить сортированный массив
• Циклы и фиксированные точки^[en]
• Циклические перестановки целых чисел^[en]
• Циклические перестановки в протеинах^[en]

Примечание[править | править код]

Литература[править | править код]

• Anderson M., Feil T. . A First Course in Abstract Algebra. 2nd edition. — Boca Raton: Chapman & Hall/CRC, 2005. — 696 p. — ISBN 1-58488-515-7.
• Fraleigh J. . A First Course in Abstract Algebra. 5th edition. — Reading: Addison-Wesley, 1993. — 576 p. — ISBN 978-0-201-53467-2.
• Rotman J. J. . A First Course in Abstract Algebra with Applications. 3rd edition. — Upper Saddle River: Prentice Hall, 2006. — 581 p. — ISBN 978-0-13-186267-8.
• Sagan B. E. . The Symmetric Group: Representations, Combinatorial Algorithms & Symmetric Functions. — Belmont: Wadsworth, 1991. — 197 p. — ISBN 978-0-534-15540-7.
• Bogart K. P. . Introductory Combinatorics. 2nd edition. — San Diego: Harcourt, Brace, Jovanovich, 1990. — 622 p. — ISBN 0-15-541576-X.
• Gross J. L. . Combinatorial Methods with Computer Applications. — Boca Raton: Chapman & Hall/CRC, 2008. — xvii + 644 p. — ISBN 978-1-58488-743-0.

Ссылки[править | править код]

• Permutations as a Product of Transpositions

Разложение перестановок, циклы, транспозиции

Выясним,
как “ведет себя” перестановка в области
определения. Рассмотрим произвольную
перестановку

.

Эта перестановка
переводит единицу в четверку, четверку
в единицу, двойка переходит в тройку, а
тройка в двойку.

Если все перечисленные
замены записать в той последовательности,
в которой мы их производили, то
рассматриваемая перестановка примет
вид:

.

Нетрудно
заметить, что перестановка 
оказалась, по существу, разложенной на
две части.

.

Это
означает, что наша перестановка состоит
из двух независимых частей, каждая из
которых перемещает элементы, принадлежащие
её собственной области определения
(рис. 1).

Рис.
1 –
Разложение перестановки
.

Именно
потому, что обе части перестановки 
независимы, совершенно безразлично,
какую из перестановок

выполнять первой,
а какую второй. Если перестановки

выполнять
последовательно одну за другой, то такие
действия можно рассматривать, как
умножение перестановок. Однако до сих
пор мы говорили об умножении перестановок
в тех случаях, когда области определения
перестановок совпадали. Здесь же области
определения перестановок различны.

Преодолеть возникшую
проблему не составляет труда: условимся
считать, что наши перестановки переводят
каждый “недостающий” элемент в самого
себя.

Таким
образом, перестановка 
допускает следующее разложение в
произведение двух независимых
перестановок:

.

Легко заметить,
что в данном разложении нижние строки
совершенно излишни. Действительно,
верхние строки состоят из тех же
элементов, что и нижние, причем каждый
элемент под действием перестановки
переходит в следующий. Это позволяет
представить нашу перестановку в виде

.

Перестановки,
стоящие в правой части, называются
независимыми циклами, а представление
перестановки

в виде

называется
разложением перестановки
в произведение независимых циклов.

Определение. Длиной
цикла
называется количество входящих в него
элементов (в данном случае циклы имеют
длину, равную двум).

Перестановка

допускает разложение
только в один цикл

длиной 4.

Разложение
перестановки 
в произведение независимых циклов
эквивалентно разбиению множества 
на непересекающиеся классы

,
где
,.

Известно, что
разбиение множества на непересекающиеся
классы эквивалентно введению некоторого
отношения эквивалентности. Элементы,
входящие в один из циклов, являются
эквивалентными между собой, а сами циклы
представляют собой классы эквивалентности.

Если
некоторая перестановка, определенная
на множестве,
которую можно представить в виде
произведения независимых циклов

,

то
элементы множества 
можно представить в виде объединения
р попарно непересекающихся подмножеств

.

Таких, что

.

Множества
называются-орбитами.
Название это вполне обоснованно. Каждая
точка
принадлежит в точности одному классу
эквивалентности, напримерили– орбите.

Если
,
тосостоит из образов точки i при действии
степеней элемента

,

где
– длина k-го цикла орбиты.
Очевидно, что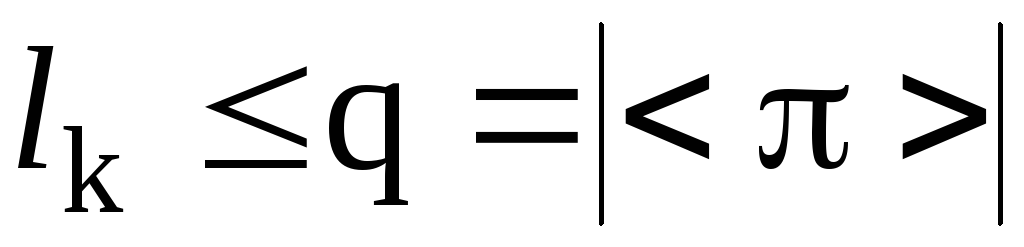и,
причем– наименьшее число, обладающее этим
свойством.

Цикл
можно представить в виде:

. (4)

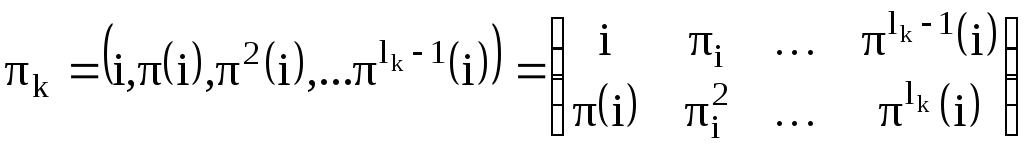
Цикл _k
оставляет на месте все точки из множества
,
а для любой точки

(5)

Это
свойство дает нам основание называть
циклы
независимыми или непересекающимися
циклами.

Теорема. Каждая
перестановка
может быть представлена в виде произведениянезависимых циклов длины.
Это разложение определено однозначно
с точностью до порядка следования
циклов.

. (6)

Замечание. Длина
каждого k-го цикла –
,больше
или равна двум. Если циклимеет длину равную единице, то он
действует как единичная перестановка
и его в произведении (5) естественно
опускать.

Например, перестановку

можно представить
в виде

.

Запись
перестановки 
в виде произведения независимых циклов
(5) позволяет легко найти порядок
перестановки

.

Следствие 1. Порядок
перестановки(порядок циклической подгруппы)
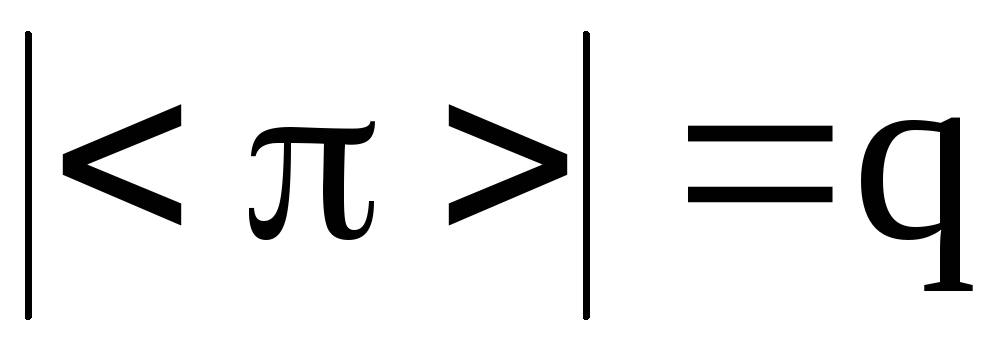
равен наименьшему общему кратному (НОК)
длин независимых циклов, входящих в
разложение.

Доказательство. Представим
перестановку
в виде произведения независимых циклов

. (7)

Тогда

Так как
циклы
независимы (они действуют на различных
множествах),
и если q – порядок циклической подгруппы,

,

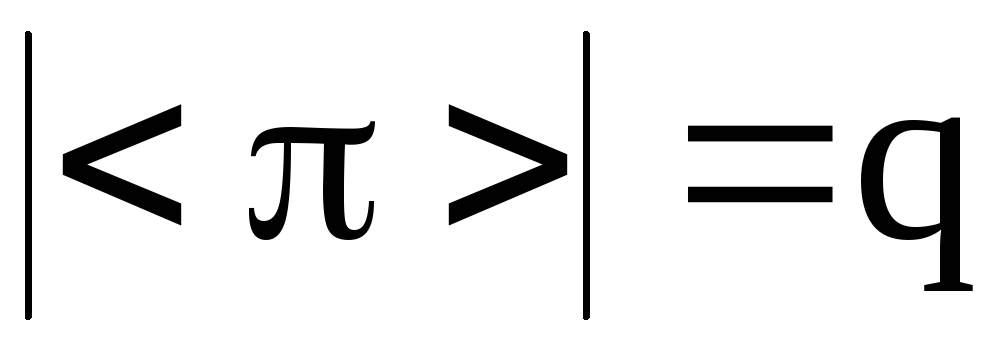
то

,

где
.

Следовательно,
q – общее кратное порядков циклов _k,
которые совпадают с их длинами
.

Если q – наименьшее
положительное число, для которого

,то

и

. (8)

Замечание. Два
любых целых числа m и n можно записать в
виде произведений одних и тех же простых
чисел

.

Например

,

тогда

,

где

Множество простых
чисел

.

Пример. Определить
порядок перестановки
вида

.

Решение. Представим
перестановку 
в виде произведения независимых циклов,
т.е.

.

Длины
независимых цикловравны

Следовательно,
порядок рассматриваемой перестановки
равен 28.

Определение. Цикл
длиной два называется транспозицией.
Любая транспозиция имеет вид
и оставляет на местах все символы за
исключением.

Теорема. Каждая
перестановка
может быть представлена в виде произведения
транспозиции.

Доказательство. Теорема
будет доказана, если мы сможем представить
в виде произведений транспозиций каждый
из циклов _k,
входящих в разложения перестановки:
.

Рассмотрим
произвольный цикл
,
напримери произведем его разложение в произведение
транспозиций.

Алгоритм
разложения цикла
в произведение транспозиций представлен
на рисунке 2.

Цикл
транспозиции

Рис
2.
– Разложение цикла
в произведение транспозиций.

После
завершения всех операций на месте
каждого элемента цикла
оказался следующий за ним элемент, а
первый элемент перешел на последнее
место. Таким образом, циклоказался разложенным в произведение
транспозиций:

Естественно, это
разложение не единственно. Например

.

Важно
другое – и в первом и во втором его
разложении имеется равное количество
транспозиций – четыре. Если
,
то количество транспозиций равно.
Раскладывая аналогичным образом каждый
циклперестановкив произведение транспозиции, мы получим
разложение всей перестановкив произведение транспозиций.

Замечание. Количество
транспозиций в цикле
может быть и больше четырех! Возьмем
произвольную транспозицию из разложения
этого цикла, например,.
Тогда произведениесовпадает с тождественной перестановкой
и циклможно представить в виде

или

,

или

.

Легко
заметить, что во всех этих случаях число
транспозиций четно и равно 4,6,8. Ясно,
что способ, «удлиняющий» разложение,
не изменяет четности исходного разложения.

Теорема. Пусть

– перестановка из
,
а

. (9)

какое-либо
разложение 
в произведении транспозиций. Тогда
число

(10)

называется
четностью (сигнатурой или знаком)
перестановки 
и полностью определяется ,
т.е. не зависит от способа разложения
перестановки 
в произведение транспозиций. Кроме
того, если
,
то

. (11)

Данную теорему
приводим без доказательства. Доказательство
теоремы приведено в [1].

Определение. Перестановка
называется четной, если,
и нечетной, если.

Из
определения четности перестановки
вытекает, что все транспозиции – нечетные
перестановки. Действительно, если
– транспозиция, то,
тогда

Следствие 1. Все
четные перестановки степени n образуют
подгруппу
порядка(она называется знакопеременной группой
степени n).

Следствие 2. Пусть
перестановка
разложена в произведение независимых
цикловдлин,
где,,
…,,
…,– длины независимых циклов.

Тогда

. (12)

Доказательство. Действительно,
по предыдущей теореме имеем

.

Кроме
того,
поскольку каждыйцикл записывается в виде произведениятранспозиций, то

.

Соседние файлы в папке SAVE

• #
• #
• #
• #

From Wikipedia, the free encyclopedia

In mathematics, and in particular in group theory, a cyclic permutation (or cycle) is a permutation of the elements of some set X which maps the elements of some subset S of X to each other in a cyclic fashion, while fixing (that is, mapping to themselves) all other elements of X. If S has k elements, the cycle is called a k-cycle. Cycles are often denoted by the list of their elements enclosed with parentheses, in the order to which they are permuted.

For example, given X = {1, 2, 3, 4}, the permutation (1, 3, 2, 4) that sends 1 to 3, 3 to 2, 2 to 4 and 4 to 1 (so S = X) is a 4-cycle, and the permutation (1, 3, 2) that sends 1 to 3, 3 to 2, 2 to 1 and 4 to 4 (so S = {1, 2, 3} and 4 is a fixed element) is a 3-cycle. On the other hand, the permutation that sends 1 to 3, 3 to 1, 2 to 4 and 4 to 2 is not a cyclic permutation because it separately permutes the pairs {1, 3} and {2, 4}.

The set S is called the orbit of the cycle. Every permutation on finitely many elements can be decomposed into cycles on disjoint orbits.

The individual cyclic parts of a permutation are also called cycles, thus the second example is composed of a 3-cycle and a 1-cycle (or fixed point) and the third is composed of two 2-cycles, and denoted (1, 3) (2, 4).

Definition[edit]

A permutation is called a cyclic permutation if and only if it has a single nontrivial cycle (a cycle of length > 1).^[1]

For example, the permutation, written in two-line notation (in two ways) and also cycle notation,

is a six-cycle; its cycle diagram is shown at right.

Some authors restrict the definition to only those permutations which consist of one nontrivial cycle (that is, no fixed points allowed).^[2]

For example, the permutation

is a cyclic permutation under this more restrictive definition, while the preceding example is not.

More formally, a permutation of a set X, viewed as a bijective function , is called a cycle if the action on X of the subgroup generated by has at most one orbit with more than a single element.^[3] This notion is most commonly used when X is a finite set; then of course the largest orbit, S, is also finite. Let be any element of S, and put for any . If S is finite, there is a minimal number for which . Then , and is the permutation defined by

for 0 ≤ i < k

and for any element of . The elements not fixed by can be pictured as

.

A cycle can be written using the compact cycle notation (there are no commas between elements in this notation, to avoid confusion with a k-tuple). The length of a cycle is the number of elements of its largest orbit. A cycle of length k is also called a k-cycle.

The orbit of a 1-cycle is called a fixed point of the permutation, but as a permutation every 1-cycle is the identity permutation.^[4] When cycle notation is used, the 1-cycles are often suppressed when no confusion will result.^[5]

Basic properties[edit]

One of the basic results on symmetric groups is that any permutation can be expressed as the product of disjoint cycles (more precisely: cycles with disjoint orbits); such cycles commute with each other, and the expression of the permutation is unique up to the order of the cycles.^[a] The multiset of lengths of the cycles in this expression (the cycle type) is therefore uniquely determined by the permutation, and both the signature and the conjugacy class of the permutation in the symmetric group are determined by it.^[6]

The number of k-cycles in the symmetric group S_n is given, for , by the following equivalent formulas:

A k-cycle has signature (−1)^k − 1.

The inverse of a cycle is given by reversing the order of the entries: . In particular, since , every two-cycle is its own inverse. Since disjoint cycles commute, the inverse of a product of disjoint cycles is the result of reversing each of the cycles separately.

Transpositions[edit]

“Transposition (mathematics)” redirects here. For matrix transposition, see Transpose.

A cycle with only two elements is called a transposition. For example, the permutation that swaps 2 and 4. Since it is a 2-cycle, it can be written as .

Properties[edit]

Any permutation can be expressed as the composition (product) of transpositions—formally, they are generators for the group.^[7] In fact, when the set being permuted is {1, 2, …, n} for some integer n, then any permutation can be expressed as a product of adjacent transpositions and so on. This follows because an arbitrary transposition can be expressed as the product of adjacent transpositions. Concretely, one can express the transposition where by moving k to l one step at a time, then moving l back to where k was, which interchanges these two and makes no other changes:

The decomposition of a permutation into a product of transpositions is obtained for example by writing the permutation as a product of disjoint cycles, and then splitting iteratively each of the cycles of length 3 and longer into a product of a transposition and a cycle of length one less:

This means the initial request is to move to to to and finally to Instead one may roll the elements keeping where it is by executing the right factor first (as usual in operator notation, and following the convention in the article Permutation). This has moved to the position of so after the first permutation, the elements and are not yet at their final positions. The transposition executed thereafter, then addresses by the index of to swap what initially were and

In fact, the symmetric group is a Coxeter group, meaning that it is generated by elements of order 2 (the adjacent transpositions), and all relations are of a certain form.

One of the main results on symmetric groups states that either all of the decompositions of a given permutation into transpositions have an even number of transpositions, or they all have an odd number of transpositions.^[8] This permits the parity of a permutation to be a well-defined concept.

See also[edit]

• Cycle sort – a sorting algorithm that is based on the idea that the permutation to be sorted can be factored into cycles, which can individually be rotated to give a sorted result
• Cycles and fixed points
• Cyclic permutation of integer
• Cycle notation
• Circular permutation in proteins
• Fisher–Yates shuffle

Notes[edit]

References[edit]

Sources[edit]

• Anderson, Marlow and Feil, Todd (2005), A First Course in Abstract Algebra, Chapman & Hall/CRC; 2nd edition. ISBN 1-58488-515-7.
• Fraleigh, John (1993), A first course in abstract algebra (5th ed.), Addison Wesley, ISBN 978-0-201-53467-2
• Rotman, Joseph J. (2006), A First Course in Abstract Algebra with Applications (3rd ed.), Prentice-Hall, ISBN 978-0-13-186267-8
• Sagan, Bruce E. (1991), The Symmetric Group / Representations, Combinatorial Algorithms & Symmetric Functions, Wadsworth & Brooks/Cole, ISBN 978-0-534-15540-7

External links[edit]

This article incorporates material from cycle on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Распределение для рекордов, циклических перестановок и количества дел, которые вы успеете сделать за свою жизнь

Сегодня я хочу рассказать о трёх задачах, практически не связанных друг с другом, и объединённых лишь тем, что все они приводят к распределению случайных дискретных величин, с функцией вероятности, выражающейся через числа Стирлинга первого рода. Это распределение не относится к числу популярных и широко известных, у него даже имени устоявшегося нет. Так что пусть в русскоязычной сети появится статья, в которой будут описаны и контекст, в котором это распределение появляется, и его основные свойства. На нашем пути встретятся перестановки, стохастические цепочки, свёртка распределений, немного алгебры и даже Ага!-момент в конце статьи.

Приглашаю к чтению тех, кто хочет расширить свой кругозор, или просто любит всякую комбинаторику с вероятностями.

Сюжет первый. Рекорды

В одном околоматематическом паблике появилась любопытная задачка.

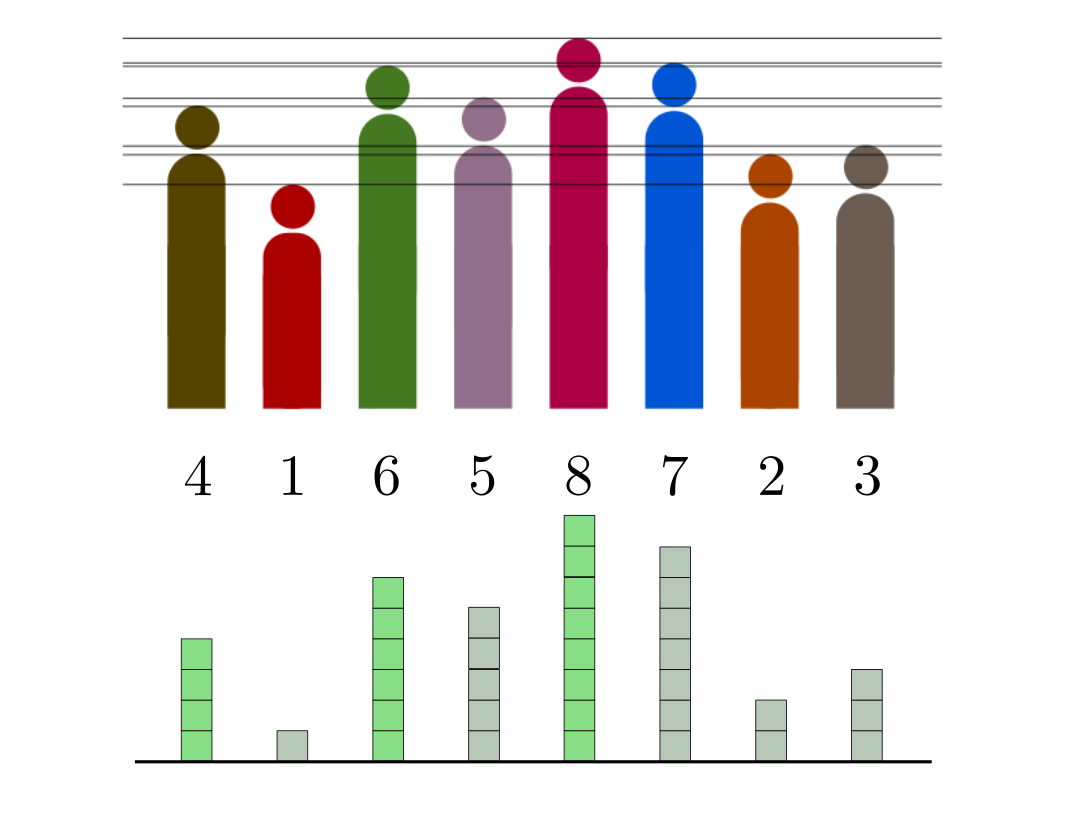
В затылок друг другу выстроились восемь человек. Более высокие загораживают более низких так, что тех не видно. Чему равно математическое ожидание числа людей, которых видно?

Можете, если хотите, переформулировать задачу для видимых домов в микрорайоне с многоэтажной застройкой.

Попытки во время прогулки оценить возможный ход решения в уме, привели к соображению, что нужно знать распределение людей по высоте, ведь, если оно будет равномерным, то получится один ответ, а если, например, вырожденным (все люди в очереди одинакового роста), то другой, а именно, единица. Нужно пробовать и экспериментировать.

Так субботняя прогулка привела меня к компьютеру, и через часик была готова нехитрая программка, моделирующая людей в очереди, набором чисел. Она честно перебирает все возможные варианты, коих в очереди из человек будет , если люди имеют  различных значений роста, вычисляет количество видимого народа, и даже учитывает распределение людей по росту и ведёт статистику. С её помощью быстро удалось просчитать разные варианты, и они говорили о том, что, всё-таки, для ответа нам нужно знать то, каким именно будет распределение вероятности для высоты людей. То есть, ответ зависит от этого распределения и одним числом его не выразить.

Увлёкшись, я даже воспользовался статистикой по длине нынешнего народонаселения из одной статьи на Хабре, и подставил её в программу. И вот тут я с удивлением обнаружил, что от конкретного выбора распределения ответ меняется, но как-то… неубедительно. Гораздо больше на него влияет количество разнообразных вариантов роста, или, выражаясь более формально, мощность носителя распределения. Более того, по мере увеличения числа этих вариантов, среднее число видимых людей неспешно сходится к некоторому значению, фиксированному для длины очереди.

Размышления о распределении для роста завели меня не туда. А тем временем, один из комментаторов уже выдал ответ, причём, для меня несколько неожиданный. Среднее количество видимых людей в очереди, по его версии, оказалось равно гармоническому числу (частичной сумме гармонического ряда): 

Как выяснилось, приведённый результат был тоже получен с помощью численного эксперимента на компьютере. Сравнение этого ответа с моим показало, что оно верно описывает то самое предельное значение, которое получается в случае непрерывной функции распределения роста людей.

Гармонические числа не так уж часто встречаются в теории вероятностей и в комбинаторике, и я, по-киношному прищурившись, произнёс: “Мне кажется я знаю этого парня…” Похоже, мы имеем дело с распределением, которое можно считать довольно редким и далёким от популярности, в отличие от нормального, экспоненциального, гамма-распределения и прочих устойчивых и высокоэнтропийных звёзд теории вероятностей и статистики. Это распределение рекордных случайных величин.

Если мы заменим настоящий рост людей на их порядковый номер в ранжировании по росту, то ответ на вопрос: “Кто кого загораживает?” или, что то же самое: “Кто является рекордсменом?” не изменится. Таким образом, мы можем смело забыть о конкретном распределении, лишь бы оно было непрерывным, и свести задачу от перебора вариантов, к перебору перестановок из  различимых элементов, которых, как известно, штук. Итак, задача наша формализуется следующим образом:

Найти распределение для числа рекордов в перестановках длины n.

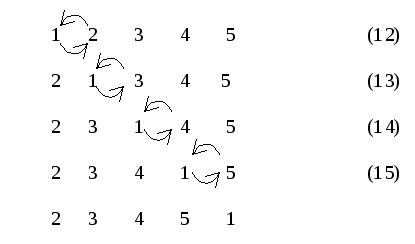
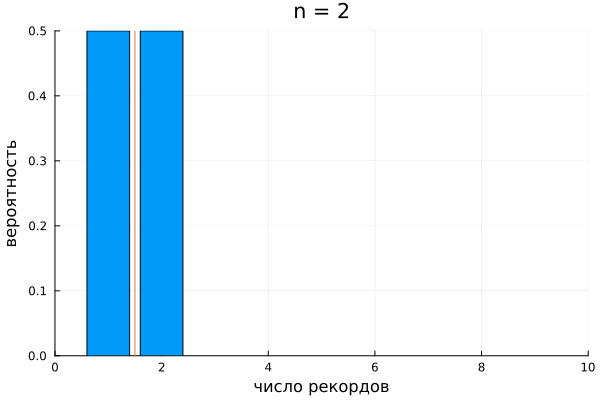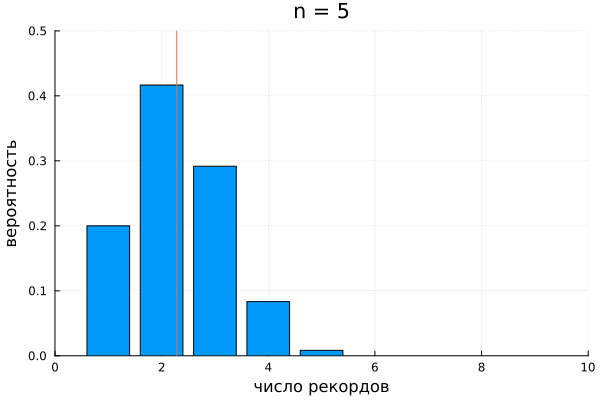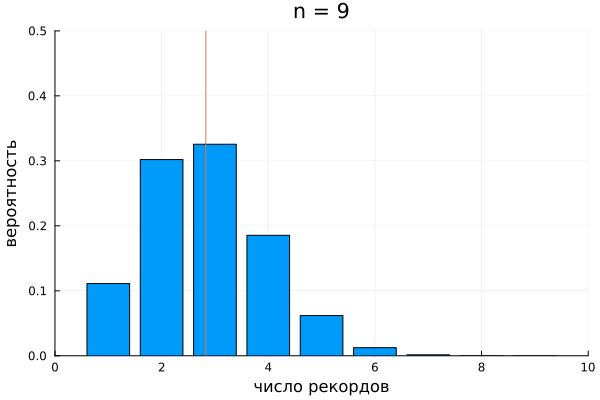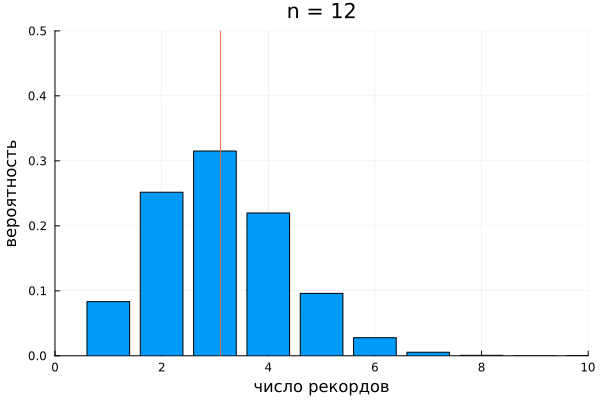
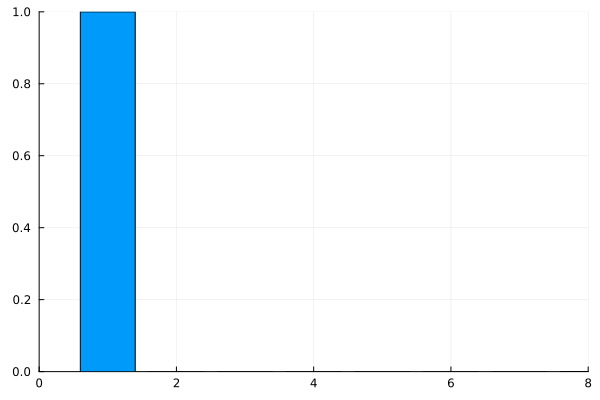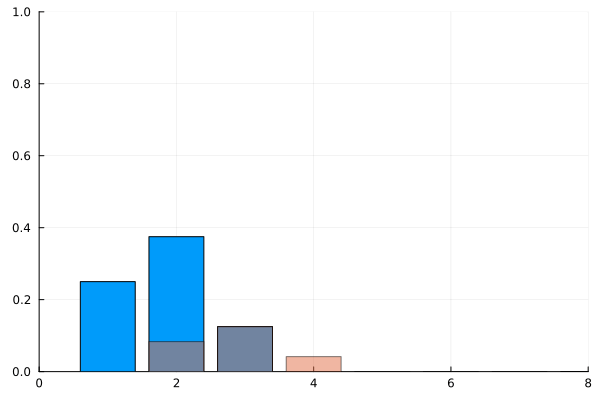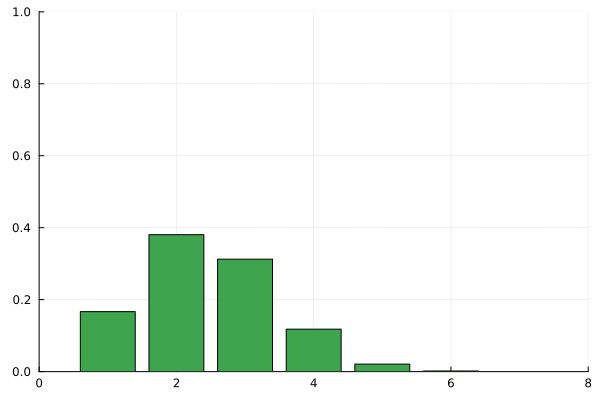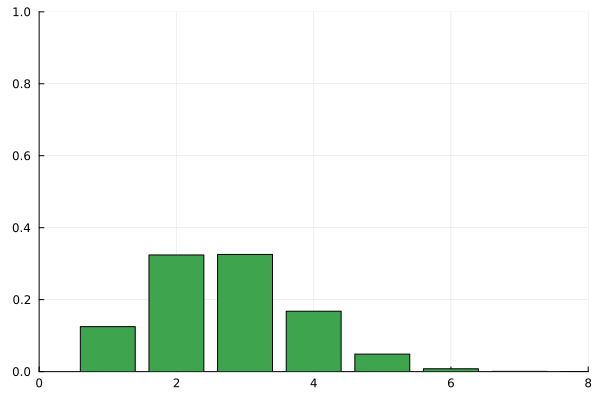
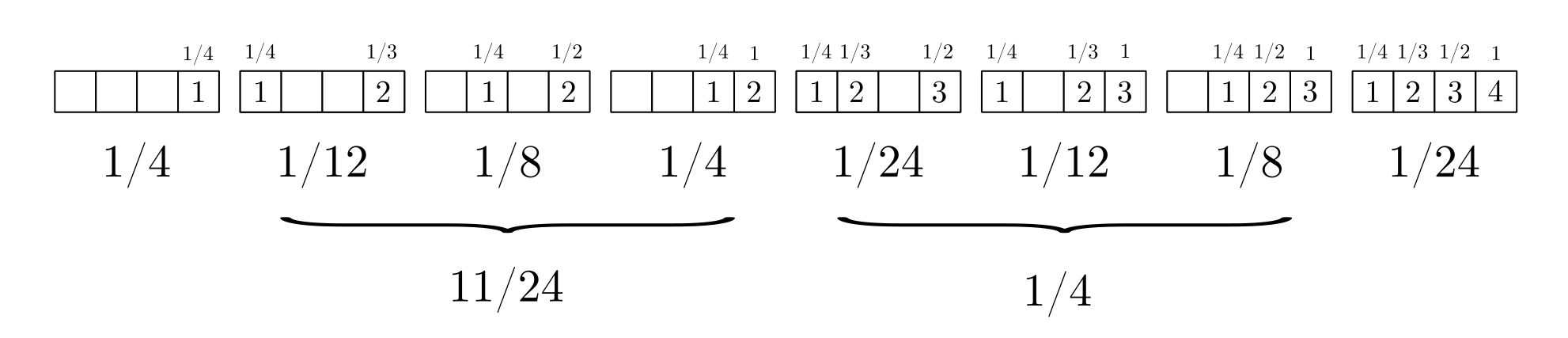
В комбинаторике полезно поиграть с исследуемой системой на малых числах. Посмотрим на то, как рекорды распределяются в перестановках длины 2, 3 и 4:

Пусть это количество перестановок длины  таких, чтобы количество рекордов в них было равно Выясним, чему будет равно то есть, сколько будет способов получить  рекордов, если мы добавим в перестановку ещё один элемент. Если его величина превышает все уже задействованные числа, то мы можем поставить его в конце последовательности и количество способов получить  рекордов будет равно -тым рекордом будет этот последний элемент. Если же его величина оказывается где-то посередине, то существует ровно  способов его поставить так, чтобы в любом из уже рассмотренных вариантов он оказался загорожен каким-нибудь рекордом и не нарушил числа . Таким образом, получается, что

Если в последовательности всего один элемент, то Кроме того, есть пара тривиальных граничных значений для отсутствия рекордов и отсутствия людей в очереди:

Итак, мы получили ответ в форме рекуррентного соотношения. Оно в точности совпадает с определением беззнаковых чисел Стирлинга первого рода. Для них принято обозначение, похожее на число сочетаний, только в квадратных скобках. Определяются они так:

Всех перестановок, как мы помним, штук, так что можно от количества перестановок с указанным числом рекордов, перейти к вероятностям.

Я позволю себе называть это распределение именем Стирлинга и обозначу . Было бы разумным называть гармоническим распределением, но это имя уже занято. Перечислим основные характеристики распределения Стирлинга.

Носитель распределения:

Функция вероятности:

Среднее:

Дисперсия:

Функция распределения в конечной форме не выражается, но имея функцию вероятности, несложно вычислить её прямым суммированием.

Сразу замечу, что то, что среднее для этого распределения выражается гармоническими числами, является его ключевым свойством, о котором мы подробно поговорим ниже. То, что это так, несложно доказать индукцией по Однако, есть и другие способы доказательства, один из них хорошо и подробно изложен в статье Артура Бенджамина с соавторами A Stirling Encounter with Harmonic Numbers, которую я рекомендую тем, кто хочет познакомиться с числами Стирлинга первого рода в контексте комбинаторики.

Сюжет второй. Стохастические цепочки

С героем нашего рассказа я впервые встретился несколько лет назад, когда решал совсем другую задачу, работая над научно-популярной книгой посвящённой законам подлости. Тогда я выяснял, каким будет распределение для длины цепочки последовательных дел, которые можно успеть выполнить до наступления некоторого предельного срока, дедлайна.

Постановка задачи была такой. Пусть в нашем распоряжении имеется дней. В этот срок необходимо выполнить некоторую работу, состоящую из цепочки последовательных этапов. Говоря “последовательных” я имею в виду, что -тый этап можно выполнить только по завершении этапа, никакого распараллеливания процессов не предполагается, так что два дела в один день выполнить не удастся. При этом исполнитель придерживается безалаберной, но вполне реалистичной житейской стратегии: в какой-то, произвольно выбранный день, выполняется первый этап работы; второй этап выполняется в один из оставшихся дней, третий — в какой-либо день после второго, и так далее, до тех пор, пока не наступит дедлайн. Я хотел найти вероятность для того, что цепочка будет иметь максимальную длину . Под максимальной длиной подразумевается, что этап выполнить уже не удастся, или, что то же самое, что выполнение -ого этапа приходится на последний -ный день.

Мы будем рассуждать, рассматривая размещение точек в обратном порядке. Любая цепочка завершается выполнением последнего этапа в последний день. Вероятность того, что первый и последний этап придётся именно на день с номером , будет равна , ведь для нашего безалаберного исполнителя все дни одинаковы. Дальше можно действовать индуктивно. Для произвольного последний этап обязательно должен случиться в последний день, это, как мы знаем, может случиться с вероятностью . Потом мы можем выполнить предпоследний этап в любой из предыдущих дней, скажем в день с номером m, сведя при этом задачу к случаю этапов и дней. Выбор ограничен сверху числом , поскольку два этапа — последний и предпоследний — уже на местах. Сложив вероятности всех таких вариантов, мы получим вероятность Таким образом, у нас уже есть способ получить точное решение искомой задачи, но для этого нужно знать решения всех входящих в неё подзадач:

Полученную рекуррентную формулу мне, не без труда, удалось упростить, приведя к форме:

которая соответствует распределению Стирлинга.

То, что ожидаемое число последовательных дел, которые можно успеть выполнить, имея ограниченное время, выражается гармоническим числом, наводит на философские мысли. Гармонические числа растут неограниченно,но чрезвычайно медленно, и имея серьёзные планы на пять, десять или на пятьдесят лет, нужно иметь в виду, что если выполнять их не регулярно, а придерживаясь стратегии “когда-нибудь обязательно сделаю”, то и за всю жизнь можно успеть сделать не так уж много.

Сюжет третий. Циклы в перестановках

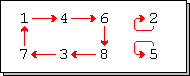
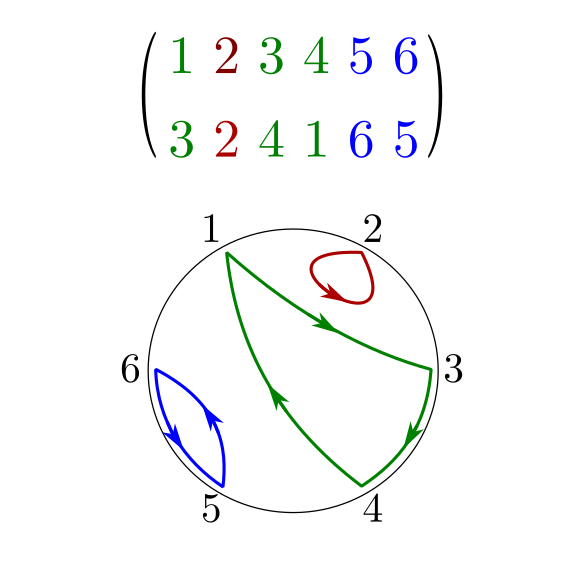
В любой справочной или вводной статье, посвящённой числам Стирлинга первого рода, говорится, что они фигурируют в комбинаторике, а именно, отражают количество перестановок, имеющих ровно циклов. Напомню, что любую перестановку можно однозначно представить в виде произведения непересекающихся циклов. Например, перестановка содержит в себе такие циклы: и и одну неподвижную точку 2, которую можно считать тривиальным циклом. На иллюстрации она показана в форме подстановки, для наглядности.

То что количество циклов связано с числами Стирлинга, доказывается точно такими же, рассуждениями, какими мы вывели рекуррентное соотношение для числа рекордов в последовательности различающихся величин.

Пусть — это число циклов длины в перестановке длины . Увеличим длину перестановки на единицу, и вычислим . При этом возможны два случая:

1. Дополнительный элемент может оказаться неподвижной точкой, и для того, чтобы число осталось неизменным, мы должны прибавить этот тривиальный цикл только к тем перестановкам длины , в которых число циклов равно . Количество таких перестановок .

2. Новый элемент может войти в перестановку, имеющую циклов, став частью одного из них. Это можно сделать вставив новый элемент между любыми двумя элементами перестановки длины , в том числе, между последним и первым элементами, которые могут входить в один цикл. Таким образом, получается различных вариантов добавления элемента, не нарушающих числа циклов, в каждую из перестановок с циклами. Так мы получаем ещё перестановок.

Складывая эти два результата, мы вновь получим рекуррентное соотношение для беззнаковых чисел Стирлинга первого рода:

Осталось заметить, что перестановка с единственным элементом имеет единственный цикл , и что не существует перестановок без циклов, а также циклов без элементов в перестановке:

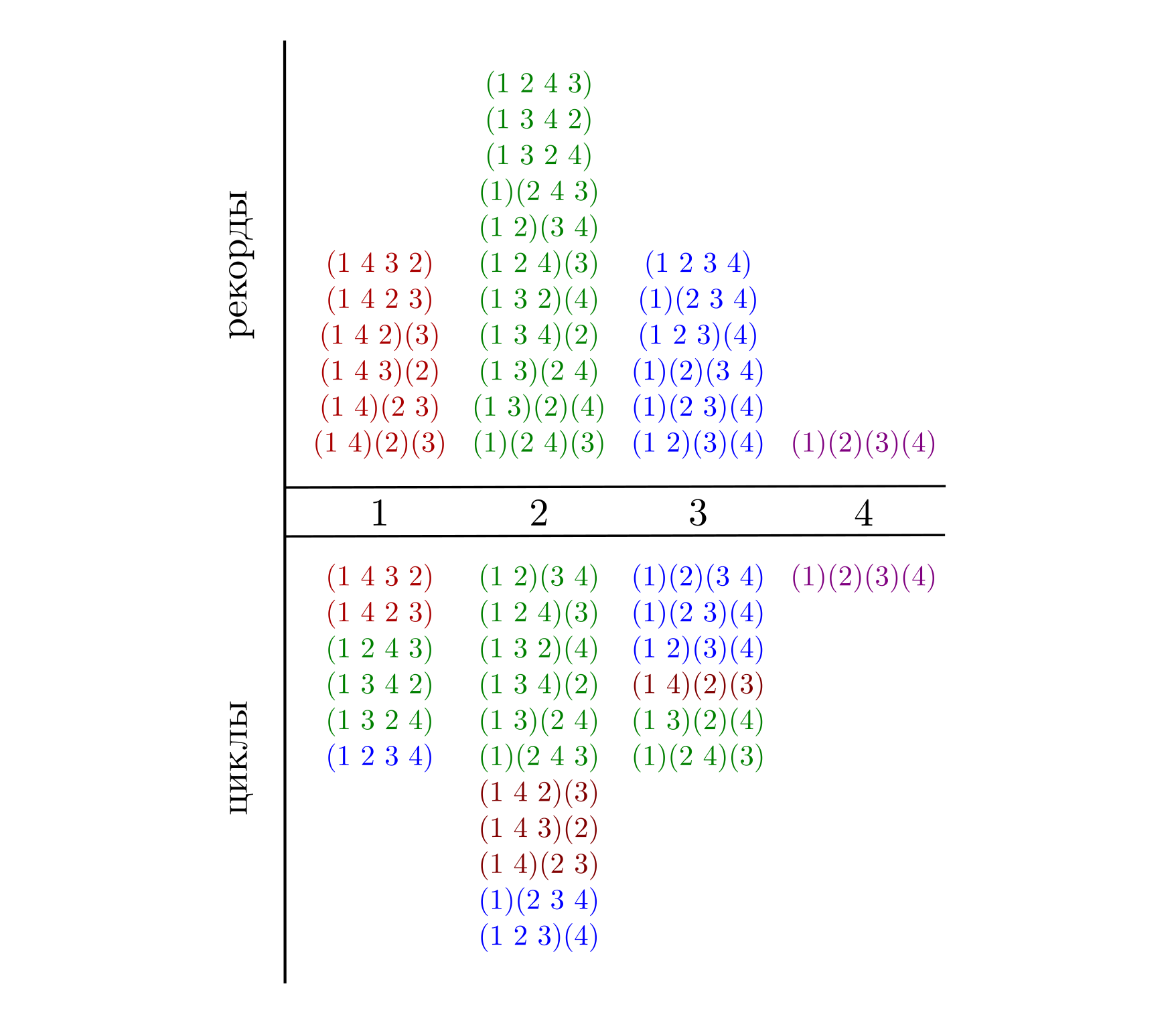
Совпадение формул,и даже приводящих к ним рассуждений, может создать ощущение, что число циклов и число рекордов должны быть как-то связаны. Но если мы посмотрим на то, как по количеству рекордов и циклов перестановки делятся на классы, то увидим, что эти классы имеют одинаковую мощность, однако между ними есть “беглые” элементы.

Что же объединяет эти сюжеты?

Рассмотренные нами три задачи не сводятся друг к другу. В каждой из них к числам Стирлинга приводит свой путь. И хотя в случае подсчёта рекордов и циклов в перестановках, рассуждения были одинаковыми, различия в получающихся классах эквивалентности говорят о том, что эти задачи можно считать независимыми. Как же связаны рекорды, стохастические цепочки и циклы в перестановках? Оказывается, объединяет их алгебра многочленов.

Сравните коэффициенты в этих многочленах с гистограммами, полученными нами для перестановок. В том, что это, действительно, числа Стирлинга первого рода, легко убедиться, раскрыв скобки в выражении, определяющем :

Если вычислить коэффициент при в обозначив его, как , то получится знакомое выражение:

Поделив восходящий факториал на , получим многочлен в котором коэффициенты при равны вероятностям для числа в распределении Стирлинга:

Такие многочлены называются производящими функциями вероятности для дискретного распределения.

Но при чём тут рассмотренные нами задачи? Давайте присмотримся к тому факту, что математическое ожидание для случайной величины, подчиняющейся распределению Стирлинга, равно гармоническому числу, то есть, сумме дробей:

Математическое ожидание линейно, это значит, что матожидание для суммы случайных величин равно сумме матожиданий для каждой из них. Это наводит на мысль: не является ли распределение Стирлинга распределением для суммы случайных величин, каждая из которых имеет математическое ожидание, равное ?

Распределение для суммы случайных величин вычисляется, как свёртка их распределений. Свёртка — не самая интуитивно понятная операция, но в случае дискретных распределений мы можем воспользоваться тем, что коэффициенты произведения многочленов представляют свёртку последовательностей коэффициентов этих многочленов. Значит, произведение производящих функций вероятности для двух распределений будет производящей функцией для их свёртки.

Например, многочлен с коэффициентами, соответствующими распределению Бернулли с вероятностью , имеет вид . Свёрткой бернуллиевых величин будет произведение этих многочленов, или, согласно биномиальной формуле:

В коэффициентах этого многочлена мы без труда разглядим биномиальное распределение.

Вооружившись этим знанием, давайте перепишем выражение для производящей функции для распределения Стирлинга таким образом:

Теперь видно, что каждый множитель здесь — это производящая функция вероятности для распределения Бернулли с параметрами . Таким образом, мы можем сделать важный вывод:

Сумма случайных величин, подчиняющихся распределениям Бернулли с гармонично убывающими вероятностями, подчиняется распределению Стирлинга:

Методом “пристального всматривания”, можно разглядеть это свойство в рекуррентной формуле для вероятности длины стохастической цепочки с дедлайном, в индуктивной форме:

где кружком обозначен оператор свёртки. Именно этот итерационный процесс показан на анимации.

Эта связь с распределением Бернулли и есть основное свойство распределения Стирлинга, которое кроется во всех трёх задачах и “уши” которого “торчат” в выражении для среднего значения. Похоже, что в каждой из них мы имеем дело с суммами случайных величин, подчиняющиеся распределению Бернулли с параметром . Давайте выясним, что это за величины для каждого из трёх сюжетов.

Циклы

Применительно к циклам в перестановках, нетрудно показать, что вероятность в случайной перестановке длины встретить цикл длины равна .

Действительно, среди всех возможных перестановок, содержат некоторый конкретный цикл длины . При этом существует способов наполнить этот цикл элементами и способов переставить в нём элементы, получая уникальные циклы (деление на исключает одинаковые циклы, отличающиеся друг от друга лишь циклической перестановкой). Итого, вероятность обнаружить цикл длины равна:

Рекорды

Вероятность того, что в перестановке длины рекордом будет конкретное число , равна Убедиться в этом можно пересчитав сколько раз рекордными оказывались числа 1, 2, 3 и 4 в примерах, приведённых на иллюстрации, показывающей гистограммы для числа рекордов в перестановках .

Число может стать рекордом, только если все числа превышающие его, оказываются по правую сторону от его позиции в перестановке, при этом, нас не интересует расположение чисел не превышающих . Перестановку, в которой число является рекордом, можно схематично показать так: . Здесь буквами условно обозначены числа превышающие , количество которых равно .

Множество всех перестановок такого вида можно факторизовать, считая эквивалентными те перестановки, в которых последовательность одинакова, не зависимо от их конкретного положения. Все классы эквивалентности будут содержать одинаковое количество элементов, равное

а всего таких классов будет Перемножив эти два выражения, мы получим общее количество перестановок, в которых число является рекордом:

Поделив его на , получаем искомую вероятность

Например, в перестановке длиной 4, вероятность того, что число 4 будет рекордом равна 1, для 3 она равна , для 2 — , и для 1 — .

Стохастические цепочки

В результате описанной нами безалаберной стратегии выполнения дел до наступления дедлайна, получаются строго возрастающие последовательности индексов от до , соответствующих этапам работы. В качестве примера, перечислим все возможные последовательности этапов для четырёх дней:

Если бы расположение этапов по дням было независимым друг от друга, то все эти восемь вариантов были бы равновероятны, и мы получили бы биномиальное распределение для длин цепочек. Однако, время выполнения этапов в цепочках зависит от времени предыдущих этапов. При этом, по мере уменьшения числа оставшихся дней, вероятность выбора конкретного дня для очередного этапа увеличивается:

Для каждой цепочки эти вероятности перемножаются, в свою очередь, вероятности для цепочек с одинаковым числом этапов, складываются. Так получается распределение вероятности для длин цепочек в случае четырёх дней. Умножив эти вероятности на мы получим последовательность чисел Стирлинга для : 6, 11, 6 и 1.

Если с помощью диаграммы аккуратно вычислить вероятность того, что этап работы придётся на день то получим следующее распределение по дням:

---

Переводя все наши задачи на классический язык теории вероятностей, можно все их свести к такой канонической форме:

В урне находится шаров, пронумерованных числами от 1 до . Доставая из урны по одному шару, составляем из них убывающую последовательность натуральных чисел, игнорируя шары с номерами, превышающими номер, который является текущим минимумом.

Вероятность того, что конкретный номер окажется в полученной последовательности равна , в силу линейности среднего, ожидаемая длина последовательности выражается гармоническим числом , а длина последовательности подчиняется распределению Стирлинга.