Формула циклической частоты колебаний в физике
Формула циклической частоты колебаний
Определение и формула циклической частоты колебаний
Определение
Циклическая частота – это параметр, характеризующий колебательные движения. Обозначают эту скалярную
величину как $omega $, иногда ${omega }_0$.
Напомним, что уравнение гармонических колебаний параметра $xi $ можно записать как:
[xi left(tright)=A{cos left({omega }_0t+{varphi }_0right) }left(1right),]
где $A={xi }_{max}$ – амплитуда колебаний величины $xi $; $left({omega }_0t+{varphi }_0right)$=$varphi $ – фаза колебаний; ${varphi }_0$ – начальная фаза колебаний.
Циклическую частоту при гармонических колебаниях определяют как частную производную от фазы колебаний ($varphi $) по времени ($t$):
[{omega }_0=frac{?varphi }{partial t}=dot{varphi }left(2right).]
Циклическая частота колебаний связана с периодом ($T$) колебаний формулой:
[{omega }_0=frac{2pi }{T}left(3right).]
Циклическую частоту с частотой $?$$?$ связывает выражение:
[{omega }_0=2pi nu left(4right).]
Формулы для частных случаев нахождения циклической частоты
Пружинный маятник совершает гармонические колебания с циклической частотой равной:
[{omega }_0=sqrt{frac{k}{m}}left(5right),]
$k$ – коэффициент упругости пружины; $m$ – масса груза на пружине.
Гармонические колебания физического маятника происходят с циклической частотой равной:
[{omega }_0=sqrt{frac{mga}{J}}left(6right),]
где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние между центром масс маятника и точкой подвеса; $m$ – масса маятника.
Частным случаем физического маятника является математический маятник (физический маятник, масса которого сосредоточена в точке), циклическая частота его колебаний может быть найдена как:
[{omega }_0=sqrt{frac{g}{l}}left(7right),]
где $l$ – длина подвеса, на которой находится материальная точка.
Частота колебаний в электрическом контуре равна:
[{omega }_0=frac{1}{sqrt{LC}}left(8right),]
где $C$ – емкость конденсатора, который входит в контур; $L$ – индуктивность катушки контура.
Если колебаний являются затухающими, то их частоту находят как:
[omega =sqrt{{omega }^2_0-{delta }^2}left(9right),]
где $delta $ – коэффициент затухания; в случае с затуханием колебаний, ${omega }_0$ называют собственной угловой частотой колебаний.
Примеры задач с решением
Пример 1
Задание. В электрический колебательный контур (рис.1) входит соленоид, длина которого $l$, площадь поперечного сечения $S_1$, число витков $N $и плоский конденсатор с расстоянием между пластинами $d$, площадью пластин $S_2$. Какова частота собственных колебаний контура (${omega }_0$)?
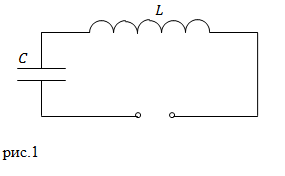
Решение. Основой для решения задачи служить формула для частоты колебаний в электрическом контуре:
[{omega }_0=frac{1}{sqrt{LC}}left(1.1right).]
Элементом, обладающим индукцией в нашем контуре является соленоид. Индуктивность соленоида равна:
[L=mu {mu }_0frac{N^2S_1}{l}left(1.2right),]
где $mu =1$, ${mu }_0$ – магнитная постоянная.
Емкость плоского конденсатора вычислим по формуле:
[C=frac{varepsilon {varepsilon }_{0 }S_2}{d}left(1.3right),]
где $varepsilon =1$, ${varepsilon }_{0 }$ – электрическая постоянная.
Правые части выражений (1.2) и (1.3) подставим в (1.1) вместо соответствующих величин:
[{omega }_0=frac{1}{sqrt{LC}}=sqrt{frac{ld}{{{mu }_0{varepsilon }_{0 }N}^2S_1S_2}}left(1.4right).]
Ответ. ${omega }_0=sqrt{frac{ld}{{{mu }_0{varepsilon }_{0 }N}^2S_1S_2}}$
Пример 2
Задание. Чему равна циклическая частота гармонических колебаний материальной точки, если амплитуда скорости точки равна ${dot{x}}_{max}=v_0$, амплитуда ее ускорения: ${ddot{x}}_{max}=a_0$? Начальная фаза колебаний равна нулю.
Решение. Из контекста условий задачи понятно, что колебания совершает координата $x$, поэтому уравнение колебаний (в общем виде) запишем как:
[xleft(tright)=A{cos left({omega }_0t+{varphi }_0right)= }A{cos left({omega }_0tright) }left(2.1right),]
По условию задачи ${varphi }_0$=0. Тогда уравнение для скорости изменения параметра $xleft(tright)$ имеет вид:
[dot{x}left(tright)=vleft(tright)=-A{omega }_0{sin left({omega }_0tright)left(2.2right). }]
Из выражения (2.2) следует, что:
[{dot{x}}_{max}=v_0=A{omega }_0left(2.3right).]
Уравнение для ускорения материальной точки, используя (2.2) запишем как:
[ddot{x}left(tright)=aleft(tright)=-A{{omega }_0}^2{cos left({omega }_0tright)left(2.4right). }]
Получаем, что:
[{ddot{x}}_{max}=A{{omega }_0}^2=a_0 left(2.5right).]
Мы получили следующую систему из двух уравнений с двумя неизвестными:
[left{ begin{array}{c}
v_0=A{omega }_0 \
a_0=A{{omega }_0}^2 end{array}
right.left(2.6right).]
Найдем отношение $frac{a_0}{v_0}$, получим:
[frac{a_0}{v_0}={omega }_0.]
Ответ. ${omega }_0=frac{a_0}{v_0}$
Читать дальше: формула частоты колебаний пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Электромагнитные колебания и волны

Содержание
- Свободные электромагнитные колебания. Колебательный контур
- Вынужденные электромагнитные колебания. Резонанс
- Гармонические электромагнитные колебания
- Переменный ток. Производство, передача и потребление электрической энергии
- Емкостное сопротивление
- Электромагнитное поле
- Свойства электромагнитных волн
- Различные виды электромагнитных излучений и их применение
- Основные формулы раздела «Электромагнитные колебания и волны»
Свободные электромагнитные колебания. Колебательный контур
Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
Колебательный контур — это замкнутый контур, образованный последовательно соединенными конденсатором и катушкой.
Сопротивление катушки ( R ) равно нулю.
Если зарядить конденсатор до напряжения ( U_m ), то в начальный момент времени ( t_1=0 ), напряжение на конденсаторе будет равно ( U_m ). Заряд конденсатора в этот момент времени будет равен ( q_m=CU_m ). Сила тока равна нулю.
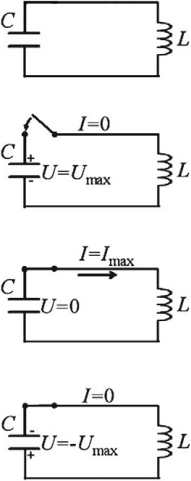
Полная энергия системы будет равна энергии электрического поля:
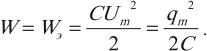
Конденсатор начинает разряжаться, по катушке начинает течь ток. Вследствие самоиндукции в катушке конденсатор разряжается постепенно.
Ток достигает своего максимального значения ( I_m ) в момент времени ( t_2=T/4 ). Заряд конденсатора в этот момент равен нулю, напряжение на конденсаторе равно нулю.
Полная энергия системы в этот момент времени равна энергии магнитного поля:
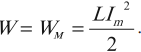
В следующий момент времени ток течет в том же направлении, постепенно (вследствие явления самоиндукции) уменьшаясь до нуля. Конденсатор перезаряжается. Заряды обкладок имеют заряды, по знаку противоположные первоначальным.
В момент времени ( t_3=T/2 ) заряд конденсатора равен ( q_m ), напряжение равно ( U_m ), сила тока равна нулю.
Полная энергия системы равна энергии электрического поля конденсатора.
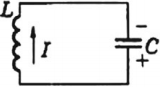
Затем конденсатор снова разряжается, но ток через катушку течет в обратном направлении.
В момент времени ( t_4=3T/4 ) сила тока в катушке достигает максимального значения, напряжение на конденсаторе и его заряд равны нулю. С этого момента ток в катушке начинает убывать, но не сразу (явление самоиндукции). Энергия магнитного поля переходит в энергию электрического поля. Конденсатор начинает заряжаться, и через некоторое время его заряд равен первоначальному, а сила тока станет равной нулю.
Через время, равное периоду ( T ), система возвращается в начальное состояние. Совершилось одно полное колебание, дальше процесс повторяется.
Важно!
Колебания, происходящие в колебательном контуре, – свободные. Они совершаются без какого-либо внешнего воздействия — только за счет энергии, запасенной в контуре.
В контуре происходят превращения энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. В любой произвольный момент времени полная энергия в контуре равна:
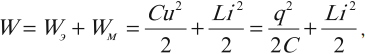
где ( i, u, q ) – мгновенные значения силы тока, напряжения, заряда в любой момент времени.
Эти колебания являются затухающими. Амплитуда колебаний постепенно уменьшается из-за электрического сопротивления проводников.
Вынужденные электромагнитные колебания. Резонанс
Вынужденными электромагнитными колебаниями называют периодические изменения заряда, силы тока и напряжения в колебательном контуре, происходящие под действием периодически изменяющейся синусоидальной (переменной) ЭДС от внешнего источника:
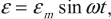
где ( varepsilon ) – мгновенное значение ЭДС, ( varepsilon_m ) – амплитудное значение ЭДС.
При этом к контуру подводится энергия, необходимая для компенсации потерь энергии в контуре из-за наличия сопротивления.
Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением при совпадении частоты вынужденных колебаний внешней ЭДС с частотой собственных колебаний в контуре.
Емкостное и индуктивное сопротивления по-разному изменяются в зависимости от частоты. С увеличением частоты растет индуктивное сопротивление, а емкостное уменьшается. С уменьшением частоты растет емкостное сопротивление и уменьшается индуктивное сопротивление. Кроме того, колебания напряжения на конденсаторе и катушке имеют разный сдвиг фаз по отношению к колебаниям силы тока: для катушки колебания напряжения и силы тока имеют сдвиг фаз ( varphi_L=-pi/2 ), а на конденсаторе ( varphi_C=pi/2 ). Это означает, что когда растет энергия магнитного поля катушки, то энергия электрического поля конденсатора убывает, и наоборот. При резонансной частоте индуктивное и емкостное сопротивления компенсируют друг друга и цепь обладает только активным сопротивлением. При резонансе выполняется условие:
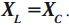
Резонансная частота вычисляется по формуле:
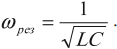
Важно!
Резонансная частота не зависит от активного сопротивления ( R ). Но чем меньше активное сопротивление цепи, тем ярче выражен резонанс.
Чем меньше потери энергии в цепи, тем сильнее выражен резонанс. Если активное сопротивление очень мало ( (Rto0) ), то резонансное значение силы тока неограниченно возрастает. С увеличением сопротивления максимальное значение силы тока уменьшается, и при больших значениях сопротивления резонанс не наблюдается.
График зависимости амплитуды силы тока от частоты называется резонансной кривой. Резонансная кривая имеет больший максимум в цепи с меньшим активным сопротивлением.
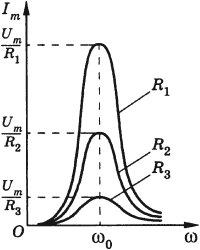
Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке. Эти напряжения становятся одинаковыми и во много раз больше внешнего напряжения. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. При резонансе амплитуды этих напряжений одинаковы и они компенсируют друг друга. Падение напряжения происходит только на активном сопротивлении.
При резонансе возникают наилучшие условия для поступления энергии от источника напряжения в цепь: при резонансе колебания напряжения в цепи совпадают по фазе с колебаниями силы тока. Установление колебаний происходит постепенно. Чем меньше сопротивление, тем больше времени требуется для достижения максимального значения силы тока за счет энергии, поступающей от источника.
Явление резонанса используется в радиосвязи. Каждая передающая станция работает на определенной частоте. С приемной антенной индуктивно связан колебательный контур. При приеме сигнала в катушке возникают переменные ЭДС. С помощью конденсатора переменной емкости добиваются совпадения частоты контура с частотой принимаемых колебаний. Из колебаний всевозможных частот, возбужденных в антенне, контур выделяет колебания, равные его собственной частоте.
Резонанс может привести к перегреву проводов и аварии, если цепь не рассчитана на работу в условиях резонанса.
Гармонические электромагнитные колебания
Гармоническими электромагнитными колебаниями называются периодические изменения заряда, силы тока и напряжения, происходящие по гармоническому – синусоидальному или косинусоидальному – закону.
В электрических цепях это могут быть колебания:
- силы тока – ( i=I_mcos(omega t+varphi+frac{pi}{2}); )
- напряжения – ( u=U_mcos(omega t+varphi); )
- заряда – ( q=q_mcos(omega t+varphi); )
- ЭДС – ( varepsilon=varepsilon_msinomega t. )
В этих уравнениях ( omega ) –циклическая частота, ( varphi ) – начальная фаза колебаний, амплитудные значения: силы тока – ( I_m ), напряжения – ( U_m ) и заряда – ( q_m ).
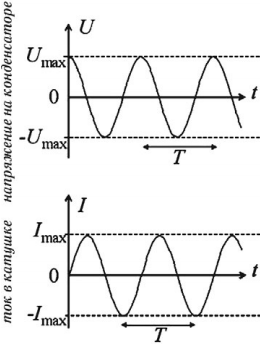
Важно!
Если в начальный момент времени заряд имеет максимальное значение, а сила тока равна нулю, то колебания заряда совершаются по закону косинуса с начальной фазой, равной нулю. Если в начальный момент времени заряд равен нулю, а сила тока максимальна, то колебания заряда совершаются по закону синуса.
Сила тока равна первой производной заряда от времени:
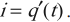
Амплитуда колебаний силы тока равна:
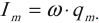
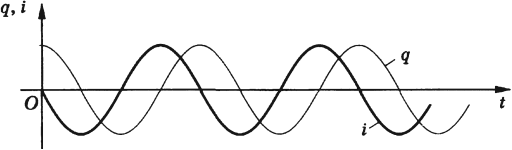
Колебания заряда и напряжения в колебательном контуре происходят в одинаковых фазах. Амплитуда напряжения равна:
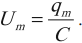
Колебания силы тока смещены по фазе относительно колебаний заряда на ( pi/2 ).
Период свободных электромагнитных колебаний
Период свободных электромагнитных колебаний находится по формуле Томсона:
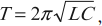
где ( L ) – индуктивность катушки, ( C ) – электроемкость конденсатора.
Циклическая частота: ( omega=frac{2pi}{T}=frac{1}{sqrt{LC}} )
Важно!
Период и циклическая частота не зависят от начальных условий, а определяются только индуктивностью катушки и электроемкостью конденсатора. Амплитуда колебаний заряда и силы тока определяются начальным запасом энергии в контуре.
При свободных гармонических колебаниях происходит периодическое преобразование энергии. Период колебаний энергии в два раза меньше, чем период колебаний заряда, силы тока и напряжения. Частота колебаний энергии в два раза больше частоты колебаний заряда, силы тока и напряжения.
Переменный ток. Производство, передача и потребление электрической энергии
Переменным называется ток, изменяющийся по величине и направлению по гармоническому закону.
Переменный ток представляет пример вынужденных электромагнитных колебаний. Для описания переменного электрического тока используют следующие величины:
• мгновенное значение силы тока – i;
• мгновенное значение напряжения – u;
• амплитудное значение силы тока – Im;
• амплитудное значение напряжения –Um.
Цепь переменного тока представляет собой колебательный контур, к которому приложена внешняя синусоидальная ЭДС. В цепь переменного тока могут включаться различные нагрузки: резистор, катушка, конденсатор.
Активное сопротивление
Проводник, преобразующий всю энергию электрического тока во внутреннюю, называется активным сопротивлением ( R ). (Эту величину мы раньше называли сопротивлением.) Активное сопротивление зависит от материала проводника, его длины и площади поперечного сечения и не зависит от частоты переменного тока.
В проводнике с активным сопротивлением колебания силы тока и напряжения совпадают по фазе:
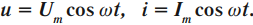
Мгновенное значение мощности: ( p=i^2R, )
среднее значение мощности за период: ( overline{p}=frac{I_m^2R}{2}. )
Действующим значением силы переменного тока ( I_Д ) называют значение силы постоянного тока, который в том же проводнике выделяет то же количество теплоты , что и переменный ток за то же время:
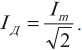
Действующим значением напряжения переменного тока ( U_Д ) называют значение напряжения постоянного тока, который в том же проводнике выделяет то же количество теплоты, что и переменный ток за то же время:
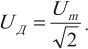
Для цепи с активным сопротивлением выполняется закон Ома для мгновенных, амплитудных и действующих значений.
Индуктивное сопротивление
Катушка в цепи переменного тока имеет большее сопротивление, чем в цепи постоянного тока. В такой цепи колебания напряжения опережают колебания силы тока по фазе на ( pi/2 ). Колебания силы тока и напряжения происходят по закону:
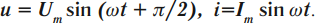
Амплитуда силы тока в катушке:
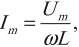
где ( L ) – индуктивность катушки.
Индуктивным сопротивлением ( X_L ) называют физическую величину, равную произведению циклической частоты на индуктивность катушки:
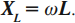
Индуктивное сопротивление прямо пропорционально частоте. Физический смысл индуктивного сопротивления: ЭДС самоиндукции препятствует изменению в ней силы тока. Это приводит к существованию индуктивного сопротивления, уменьшающего силу тока.
Для цепи с индуктивным сопротивлением выполняется закон Ома.
Емкостное сопротивление
В цепи постоянного тока через конденсатор ток не идет. Для переменного тока конденсатор обладает конечным сопротивлением, обратно пропорциональным его емкости. В цепи переменного тока сопротивление конденсатора меньше, чем в цепи постоянного тока.
В такой цепи колебания напряжения отстают от колебаний силы тока по фазе на ( pi/2 ). Колебания силы тока и напряжения происходят по закону:
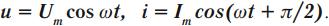
Амплитуда силы тока в катушке: ( I_m=Comega U_m. ).
Если ввести обозначение ( X_C=frac{1}{omega C} ), то получим соотношение между амплитудными значениями силы тока и напряжения, аналогичное закону Ома: ( I_m=frac{U_m}{X_C}. )
Емкостным сопротивлением ( X_C ) называют величину, обратную произведению циклической частоты на электроемкость конденсатора. Емкостное сопротивление обратно пропорционально частоте.
Физический смысл емкостного сопротивления: изменению переменного тока в любой момент времени противодействует электрическое поле между обкладками конденсатора.
В цепи переменного тока колебания силы тока и ЭДС происходят по синусоидальному закону с одинаковой циклической частотой ( omega ) и разностью фаз ( varphi ):
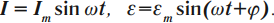
Соотношения амплитудных значений силы тока ( I_m ) и ЭДС ( varepsilon_m ) в цепи переменного тока связаны между собой законом Ома для цепи переменного тока:
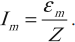
Он гласит: амплитуда силы переменного тока прямо пропорциональна амплитуде ЭДС и обратно пропорциональна полному сопротивлению цепи:
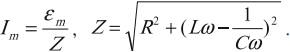
Величина ( Z ) называется полным сопротивлением цепи переменного тока.
Электрическая энергия имеет перед другими видами энергии следующие преимущества:
- можно передавать на большие расстояния с малыми потерями;
- удобно распределять между потребителями;
- легко превращать в другие виды энергии.
В настоящее время производится и используется энергия переменного тока. Это связано с возможностью преобразовывать его напряжение и силу тока с малыми потерями энергии, что особенно важно при передаче электроэнергии на большие расстояния.
Различают следующие типы электростанций:
- тепловые;
- гидроэлектростанции;
- атомные.
Получение переменного тока
Переменный ток получают с помощью генератора переменного тока.
Генератор переменного тока (электромеханический генератор переменного тока) – это устройство, преобразующее механическую энергию в электрическую. В основе работы генератора переменного тока лежит явление электромагнитной индукции.
Процесс получения переменного тока можно рассмотреть на примере вращения витка провода в однородном магнитном поле. Магнитный поток через площадь витка равен:
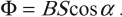
Если период вращения витка ( T ), то угол ( alpha=frac{2pi t}{T}=omega t ).
Тогда ( Phi=BScosomega t. )
ЭДС индукции изменяется по закону ( e=-Phi’=BSomegasinomega t=varepsilon_msinomega t. )
Амплитуда ЭДС ( varepsilon_m=BSomega. )
Если рамка содержит ( N ) витков, то ( varepsilon_m=NBSomega. )
Основные части генератора переменного тока:
- обмотка статора с большим числом витков, в ней индуцируется ЭДС. Статор состоит из отдельных пластин из электротехнической стали для уменьшения нагрева от вихревых токов;
- ротор (вращающаяся часть генератора) создает магнитное поле. Для получения нужной частоты переменного тока может иметь несколько пар полюсов. На гидроэлектростанциях в генераторе число пар полюсов равно 40–50, на тепловых электростанциях – 10-16;
- клеммы для снятия напряжения.
Промышленные генераторы вырабатывают напряжение порядка 104 В. Промышленная частота переменного тока в нашей стране 50 Гц.
Передача электроэнергии
Электроэнергия производится в основном вдалеке от основных потребителей энергии, там, где есть топливные ресурсы.
С электростанции переменный ток по проводам линии электропередач (ЛЭП) поступает к различным потребителям электрической энергии. Для уменьшения потерь при передаче переменного тока необходимо использовать высокое напряжение. Чем длиннее линия, тем выше должно быть напряжение. В высоковольтных ЛЭП оно может достигать 500 кВ. Генераторы на электростанциях вырабатывают напряжение 16–20 кВ. Потребителям не нужно высокое напряжение. Возникает необходимость преобразования напряжения. С электростанции электрический ток поступает на повышающую подстанцию, затем передается по линии электропередач на понижающую подстанцию, где напряжение понижается до 6–10 кВ, а затем до 220–380 В. Для преобразования напряжения используют трансформатор.
Трансформатор – устройство, преобразующее переменное напряжение без изменения его частоты.
На схемах трансформатор обозначается:
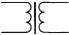
Основные части трансформатора:
- замкнутый сердечник из электротехнической стали;
- две катушки-обмотки.
Катушка, подключаемая к источнику переменного напряжения, называется первичной обмоткой; катушка, к которой подключается нагрузка, – вторичной обмоткой.
Сердечник набирается из отдельных пластин для уменьшения потерь на нагревание вихревыми токами.
Принцип действия основан на явлении электромагнитной индукции. При подключении первичной обмотки к полюсам источника напряжения в ней возникает переменный ток. Напряжение изменяется с течением времени по гармоническому закону. С такой же частотой будут изменяться сила тока в катушке и магнитный поток, создаваемый этим током.
При изменении магнитного потока в каждом витке провода первичной обмотки возникает переменная ЭДС самоиндукции. Этот магнитный поток будет пронизывать и вторую катушку. В каждом ее витке возникает ЭДС индукции, изменяющаяся по гармоническому закону с той же частотой. Число витков в обмотках различно. Отношение ЭДС самоиндукции ( varepsilon_1 ) в первичной обмотке к ЭДС индукции во вторичной обмотке ( varepsilon_2 ) равно отношению числа витков в первичной обмотке ( N_1 ) к числу витков во вторичной обмотке ( N_2 ):
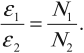
Режим работы
- Режим холостого хода – разомкнута цепь вторичной обмотки. Напряжение ( U_2 ) на ее концах в любой момент времени равно ЭДС индукции ( varepsilon_2 ), взятой с противоположным знаком. Поэтому можно записать:
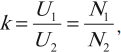
где ( k ) – коэффициент трансформации.
Если ( k>1 ), то трансформатор понижающий, если ( k<1 ), то повышающий.
- Режим нагрузки. При подключении нагрузки к концам вторичной обмотки в ней возникает переменный ток. Напряжение ( U_2 ) на ее концах в любой момент времени отличается от ЭДС индукции ( varepsilon_2 ) на величину падения напряжения на внутреннем сопротивлении вторичной обмотки ( r ): ( U_2=varepsilon_2-I_2r ) или ( U_2=I_2R ).
Мощность тока в обмотках одинакова. Поэтому увеличение напряжения на входе повышающего трансформатора в ( k ) раз сопровождается уменьшением силы тока во вторичной катушке во столько же раз.
В трансформаторе нет потерь на трение, так как нет вращающихся частей. Потери в сердечнике состоят из потерь на нагревание и на перемагничивание.
Отношение мощности ( P_2 ), потребляемой нагрузкой, к мощности ( P_1 ), потребляемой первичной обмоткой трансформатора, называется коэффициентом полезного действия трансформатора:
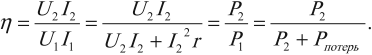
КПД трансформатора – 98%.
Потребление электрической энергии: промышленность – около 70%; сельское хозяйство; транспорт; строительство; средства связи; в быту.
Электромагнитное поле
Электромагнитное поле – это особый вид материи, с помощью которого осуществляется электромагнитное взаимодействие заряженных тел или частиц.
Это понятие было введено Д. Максвеллом, развившим идеи Фарадея о том, что переменное магнитное поле порождает вихревое электрическое поле.
Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Вихревое электрическое поле порождает появление вихревого магнитного поля и так далее. Эти переменные электрическое и магнитное поля, существующие одновременно, и образуют единое электромагнитное поле.
Характеристиками этого поля являются вектор напряженности и вектор магнитной индукции.
Если электрический заряд покоится, то вокруг него существует только электрическое поле.
Если напряженность электрического поля равна нулю, а магнитная индукция отлична от нуля, то обнаруживается только магнитное поле.
Если электрический заряд двигается с постоянной скоростью, то вокруг него существует электромагнитное поле.
Максвелл предположил, что при ускоренном движении зарядов в пространстве будет возникать возмущение, которое будет распространяться в вакууме с конечной скоростью. Когда это возмущение достигнет второго заряда, то изменится сила, с которой электромагнитное поле действует на этот заряд.
При ускоренном движении заряда происходит излучение электромагнитной волны. Электромагнитное поле материально. Оно распространяется в пространстве в виде электромагнитной волны.
Свойства электромагнитных волн
Электромагнитная волна – это изменяющееся во времени и распространяющееся в пространстве электромагнитное поле.
Существование электромагнитных волн было теоретически предсказано английским физиком Дж. Максвеллом в 1864 году. Электромагнитные волны были открыты Г. Герцем.
Источник электромагнитной волны – ускоренно движущаяся заряженная частица – колеблющийся заряд.
Важно!
Наличие ускорения – главное условие излучения электромагнитной волны. Интенсивность излученной волны тем больше, чем больше ускорение, с которым движется заряд.
Источниками электромагнитных волн служат антенны различных конструкций, в которых возбуждаются высокочастотные колебания.
Электромагнитная волна называется монохроматической, если векторы ( vec{E} ) и ( vec{B} ) совершают гармонические колебания с одинаковой частотой (частотой волны).
Длина электромагнитной волны: ( lambda=cT=frac{c}{nu}, )
где ( c ) – скорость электромагнитной волны, ( T ) – период, ( nu ) – частота электромагнитной волны.
Свойства электромагнитных волн
- В вакууме электромагнитная волна распространяется с конечной скоростью, равной скорости света 3·108 м/с.
- Электромагнитная волна поперечная. Колебания векторов напряженности переменного электрического поля и магнитной индукции переменного магнитного поля взаимно перпендикулярны и лежат в плоскости, перпендикулярной к вектору скорости волны.
- Электромагнитная волна переносит энергию в направлении распространения волны.
Важно!
Электромагнитная волна в отличие от механической волны может распространяться в вакууме.
Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени.
Обозначение – ( I ), единица измерения в СИ – ватт на квадратный метр (Вт/м2).
Важно!
Плотность потока излучения электромагнитной волны от точечного источника убывает обратно пропорционально квадрату расстояния от источника и пропорциональна четвертой степени частоты.
Электромагнитная волна обладает общими для любых волн свойствами, это:
- отражение,
- преломление,
- интерференция,
- дифракция,
- поляризация.
Электромагнитная волна производит давление на вещество. Это означает, что у электромагнитной волны есть импульс.
Различные виды электромагнитных излучений и их применение
Электромагнитные излучения имеют длины волн от 10-12 до 104 м или частоты от 3·104 до 3·1020.
Различают следующие виды электромагнитных излучений:
- радиоволны;
- инфракрасное излучение;
- видимое излучение (свет);
- ультрафиолетовое излучение;
- рентгеновское излучение;
- гамма-излучение.
Границы между диапазонами условны, но излучения имеют качественные различия в свойствах. При переходе от излучений с малой частотой к излучениям с большей частотой волновые свойства проявляются слабее, а корпускулярные (квантовые) – сильнее.
Радиоволны
( lambda ) = 103–10-3 м, ( nu ) = 105–1011 Гц. Источники радиоволн – колебательный контур, вибратор.
Радиоволны делятся на:
- длинные (длина больше 1 км);
- средние (от 100 м до 1 км);
- короткие (от 10 до 100 м);
- ультракороткие (меньше 10 м).
Свойства: отражение, поглощение, интерференция, дифракция. Применение: радиосвязь, телевидение, радиолокация.
Радиосвязью называется передача информации с помощью радиоволн. Радиосвязь осуществляется с помощью модулированных радиоволн. Модуляцией радиоволны называется изменение ее параметров (амплитуды, частоты, начальной фазы) с частотой, меньшей частоты передаваемой волны.
Схема радиосвязи показана на рисунке:
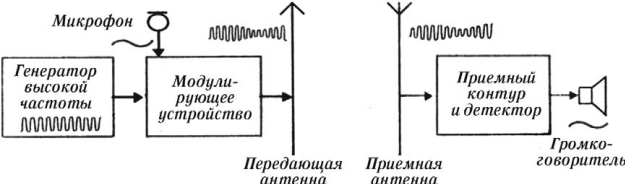
Передача радиоволн. Генератор высокой частоты вырабатывает высокочастотные колебания несущей частоты. Звуковые колебания поступают в микрофон, где преобразуются в электромагнитные колебания. В модуляторе эти колебания преобразуются в модулированные колебания. После усиления модулированные колебания поступают в передающую антенну, которая излучает электромагнитные волны. На рисунке показан звуковой сигнал низкой частоты и модулированный высокочастотный сигнал.
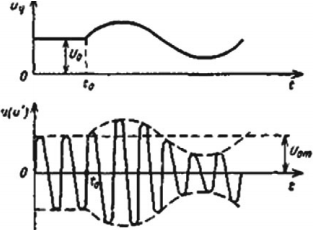
Прием радиоволн. Электромагнитные колебания поступают в приемную антенну и вызывают электромагнитные колебания в приемном контуре. Эти колебания поступают в усилитель, а затем в детектор. В качестве детектора используют устройство с односторонней проводимостью. Это может быть полупроводниковый диод. В детекторе сигнал демодулируют (детектируют). Процесс детектирования заключается в выделении из высокочастотных модулированных колебаний колебаний низкой (звуковой) частоты. После сглаживания и усиления сигнал поступает в динамик. На рисунке показаны процессы детектирования (демодуляции) и сглаживания.
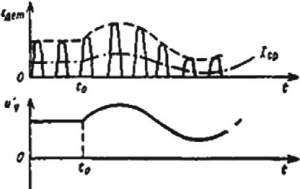
Радиолокацией называют обнаружение и определение местоположения объектов с помощью радиоволн. Излучение осуществляется короткими импульсами. В интервале времени между излучением двух последовательных импульсов осуществляется прием отраженного от объекта сигнала. Для радиолокации используют ультракороткие радиоволны.
Инфракрасное (тепловое) излучение
( lambda ) = 10-3 – 10-7 м, ( nu ) = 1011 – 1014 Гц. Источники – атомы и молекулы вещества.
Это излучение испускают все тела при температуре, отличной от 0 К. Свойства: нагревает вещество при поглощении; интерференция; дифракция; проходит через дождь, снег, дымку; невидимо; преломление, отражение. Применение: в приборах ночного видения, в физиотерапии, промышленности (для сушки). Регистрируют с помощью термопары, болометра, фотографическим методом.
Видимое излучение
( lambda ) = 8·10-7 – 4·10-7 м, ( nu ) = 4·1011 – 8·1014 Гц.
Это излучение воспринимается глазом. Свойства: отражение, преломление, поглощение, интерференция, дифракция.
Ультрафиолетовое излучение
( lambda ) = 10-8 – 4·10-7 м, ( nu ) = 8·1014 – 3·1015 Гц. Источники – кварцевые лампы.
Ультрафиолетовое излучение дают светящиеся пары ртути и твердые тела, у которых температура выше 1000°С. Свойства: химическое действие; большая проникающая способность; биологическое действие; невидимо. Применение: в медицине, промышленности. Регистрируют фотографическими методами.
Рентгеновское излучение
( lambda ) = 10-8 – 10-11 м, ( nu ) = 3·1016 – 3·1019 Гц. Источник – рентгеновские трубки.
Возникает при торможении быстрых электронов. Свойства: высокая химическая активность; биологическое действие; интерференция; дифракция на кристаллической решетке; высокая проникающая способность. Применение: в медицине, промышленности, науке.
Гамма-излучение
Длина волны меньше 10-11 м, частота от 1020 Гц и выше. Источник – ядерные реакции.
Свойства: высокая проникающая способность, сильное биологическое действие. Применение: в медицине, промышленности (дефектоскопия), науке.
Шкала электромагнитных излучений позволяет сделать вывод: все электромагнитные излучения обладают одновременно волновыми и квантовыми свойствами, которые дополняют друг друга.
Важно!
Волновые свойства сильнее выражены при малых частотах и больших длинах волн, а квантовые – при больших частотах и малых длинах волн.
Решение задач по теме «Электромагнитные колебания и волны»
По этой теме можно выделить четыре группы задач:
- на определение параметров колебательного контура;
- на уравнения гармонических электромагнитных колебаний;
- на применение закона Ома;
- на расчет мощности и КПД трансформатора.
Решение первой группы задач на определение параметров колебательного контура основано на использовании формулы Томсона (формулы периода свободных электромагнитных колебаний) и закона сохранения и превращения энергии в колебательном контуре. Поэтому необходимо записать уравнения для мгновенных значений заряда и напряжения на конденсаторе и силы тока в катушке; записать уравнение для полной энергии колебательного контура в произвольный момент времени. В качестве дополнительных формул могут понадобиться формулы электроемкости плоского конденсатора, индуктивности катушки и длины электромагнитной волны. Помните, что скорость распространения электромагнитной волны в вакууме равна скорости света – 3·108 м/с. В среде с показателем преломления ( n ) скорость света можно рассчитать по формуле: ( v=frac{c}{n}. )
Важно!
Амплитудное значение напряжения – ( U_m=frac{q_m}{C} ), амплитудное значение силы тока – ( I_m=q_momega ).
При решении второй группы задач на уравнения гармонических электромагнитных колебаний рекомендуется записать заданное в задаче уравнение и уравнение гармонических колебаний в общем виде. Сравнить эти уравнения и определить основные характеристики: амплитуду, частоту, фазу.
При решении задач на закон Ома нужно помнить, что электроизмерительные приборы показывают действующие значения напряжения и силы тока. Действующие значения величин пропорциональны амплитудным значениям. Важно помнить, что резонанс возникает при равенстве индуктивного и емкостного сопротивлений.
Решение четвертой группы задач на расчет мощности и КПД трансформатора опирается на знание формул КПД и мощности в цепи.
Основные формулы раздела «Электромагнитные колебания и волны»



Электромагнитные колебания и волны
3.2 (64.07%) 54 votes
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.

Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):

Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):

Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.

Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Определение
Переменный ток — вынужденные электромагнитные колебания.
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Определение
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
Внимание!
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙108 м/с).
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
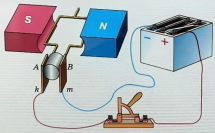
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
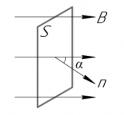
Численно магнитный поток определяется формулой:
Φ=BScosα
При равномерном вращении рамки угол α увеличивается пропорционально времени:
α=2πnt
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Φ=BScos2πnt
Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:
ω=2πn
Следовательно:
Φ=BScosωt
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
e=−Φ´=−BS(cosωt)´=BSωsinωt=εmaxsinωt
εmax — амплитуда ЭДС индукции, равная:
εmax=BSω
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
u=Umaxsinωt
u=Umaxcosωt
где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).
Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:
i=Imaxsin(ωt+φс)
где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
u=Umaxcosωt=12cos300,25π=12√22≈8,5 (В).
Активное сопротивление в цепи переменного тока
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
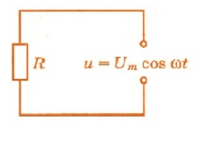
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
u=Umaxcosωt
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
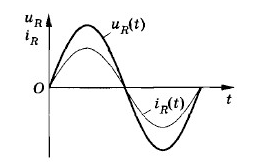
i=uR=UmaxcosωtR=Imaxcosωt
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Imax=UmaxR
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Определение
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
P=I2R
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
p=i2R
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p=(Imaxcosωt)2R
Вспомним из курса математики:
cos2α=1+cos2α2
Отсюда:
p=I2max2R(1+cos2ωt)=I2maxR2+I2maxR2cos2ωt
График зависимости мгновенной мощности от времени:
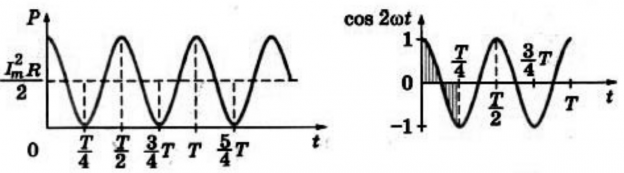
На протяжении первой четверти периода, когда cos2ωt>0, мощность в любой момент времени больше величины I2maxR2. На протяжении второй четверти периода, когда cos2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos2ωt=0, следовательно, средняя за период мощность равна I2maxR2.
Средняя мощность −p равна:
−p=I2maxR2=−i2R
Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcosωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p=(Imaxcosωt)2R=10(1·cos(100π·1)2=10 (Дж)
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
−i2=I2max2
Определение
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I=√−i2=Imax√2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U=√−u2=Umax√2
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
P=I2R=UI
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P=I2R
I=Imax√2
P=(Imax√2)2R=I2max2R=222·5=10 ⎛⎝Дж⎞⎠
Задание EF22720
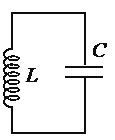 В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону UC = U0cos ωt, где U0 = 5 В, ω = 1000π с–1. Определите период колебаний напряжения на конденсаторе.
В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону UC = U0cos ωt, где U0 = 5 В, ω = 1000π с–1. Определите период колебаний напряжения на конденсаторе.
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу Томсона.
3.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.
• Амплитуда напряжения: U0=5 В.
• Циклическая частота колебаний: ω = 1000π с–1.
Запишем формулу Томсона:
T=2πω=2π1000π=21000=0,002 (с)
Ответ: 0,002
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18735
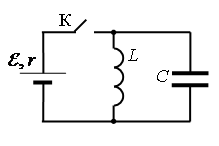 В электрической цепи, показанной на рисунке, ключ К длительное время замкнут, E=6 В, r = 2 Ом, L = 1 мГн. В момент t = 0 ключ К размыкают. Амплитуда напряжения на конденсаторе в ходе возникших в контуре электромагнитных колебаний равна ЭДС источника. В какой момент времени напряжение на конденсаторе в первый раз достигнет значения E? Сопротивлением проводов и активным сопротивлением катушки индуктивности пренебречь. Ответ запишите в мкс.
В электрической цепи, показанной на рисунке, ключ К длительное время замкнут, E=6 В, r = 2 Ом, L = 1 мГн. В момент t = 0 ключ К размыкают. Амплитуда напряжения на конденсаторе в ходе возникших в контуре электромагнитных колебаний равна ЭДС источника. В какой момент времени напряжение на конденсаторе в первый раз достигнет значения E? Сопротивлением проводов и активным сопротивлением катушки индуктивности пренебречь. Ответ запишите в мкс.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Описать, что происходит в момент замыкания и размыкания цепи.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε=5 В.
• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.
• Сопротивление ЭДС источника тока: r = 2 Ом.
• Индуктивность катушки: L = 1 мГн.
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18116
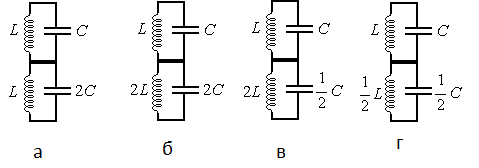
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?
Алгоритм решения
- Выделить цель эксперимента.
- Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
- Выбрать верную пару контуров
Решение
Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18656
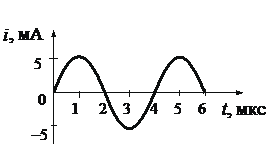 На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.
На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.
Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.6k
Циклическая частота колебаний
Мерой колебательного движения служит циклическая (или угловая, или круговая) частотой колебаний.
Это скалярная физическая величина.
Циклическая частота при гармонических колебаниях
Пусть колебания совершает материальная точка. При этом материальная точка через равные промежутки времени проходит через одно и то же положение.
Самыми простыми колебаниями являются гармонические колебания. Рассмотрим следующую кинематическую модель. Точка M с постоянной по модулю скоростью ($v$) движется по окружности радиуса A. В этом случае ее угловую скорость обозначим $<omega >_0$, эта скорость постоянна (рис.1).
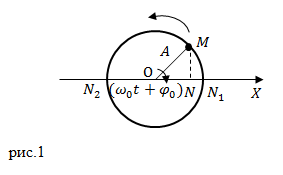
Проекция точки $M$ на диаметр окружности (точка $N$), на ось X, выполняет колебания от $N_1$ до $N_2 $и обратно. Такое колебание N ,будет гармоническим. Для описания колебания точки N необходимо записать координату точки N, как функцию от времени ($t$). Пусть при $t=0$ радиус OM образует с осью X угол $<varphi >_0$. Через некоторый промежуток времени этот угол изменится на величину $<omega >_0t$ и будет равен $<omega >_0t+<varphi >_0$, тогда:
Выражение (1) является аналитической формой записи гармонического колебания точки N по диаметру $N_1N_2$.
Обратимся к выражению (1). Величина $A$ – это максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О – центра окружности), называется амплитудой колебаний.
Параметр $<omega >_0$ – циклическая частота колебаний. $varphi =(<omega >_0t+<varphi >_0$) – фаза колебаний; $<varphi >_0$ – начальная фаза колебаний.
Циклическую частоту гармонических колебаний можно определить как частную производную от фазы колебаний по времени:
При $<varphi >_0=0$, уравнение колебаний (1) преобразуется к виду:
Если начальная фаза колебаний равна $<varphi >_0=frac<pi ><2>$ , то получим уравнение колебаний в виде:
Выражения (3) и (4) показывают, что при гармонических колебаниях абсцисса $x$ – это функция синус или косинус от времени. При графическом изображении гармонических колебаний получается косинусоида или синусоида. Форма кривой определена амплитудой колебаний и величиной циклической частоты. Положение кривой зависит от начальной фазы.
Циклическую частоту колебаний можно выразить через период (T) колебаний:
Циклическую частоту с частотой $?$$?$ свяжем выражением:
Единицей измерения циклической частоты в Международной системе единиц (СИ) является радиан, деленный на секунду:
Размерность циклической частоты:
Частные случаи формул для вычисления циклической частоты
Груз на пружине (пружинный маятник – идеальная модель) совершает гармонические колебания с круговой частотой равной:
$k$ – коэффициент упругости пружины; $m$ – масса груза на пружине.
Малые колебания физического маятника будут приблизительно гармоническими колебаниями с циклической частотой равной:
где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние между центром масс маятника и точкой подвеса; $m$ – масса маятника.
Примером физического маятника является математический маятник. Круговая частота его колебаний равна:
где $l$ – длина подвеса.
Угловая частота затухающих колебаний находится как:
где $delta $ – коэффициент затухания; в случае с затуханием колебаний $<omega >_0$ называют собственной угловой частотой колебаний.
Примеры задач с решением
Задание: Чему равна циклическая частота гармонических колебаний, если максимальная скорость материальной точки равна $<dot>_=10 frac<см><с>$, а ее максимальное ускорение $<ddot>_=100 frac<см><с^2>$?
Решение: Основой решения задачи станет уравнение гармонических колебаний точки, так как из условий, очевидно, что они происходят по оси X:
Скорость колебаний найдем, используя уравнение (1.1) и кинематическую связь координаты $x$ и соответствующей компоненты скорости:
Максимальное значение скорости (амплитуда скорости) равна:
Ускорение точки вычислим как:
Из формулы (1.3) выразим амплитуду, подставим ее в (1.5), получим циклическую частоту:
Вычислим циклическую частоту:
Задание: На длинном невесомом стержне закреплены два груза одинаковой массы. Один груз находится на середине стержня, другой на его конце (рис.2). Система совершает колебания около горизонтальной оси, проходящей через свободный конец стрежня. Какова циклическая частота колебаний? Длина стержня равна $l$.
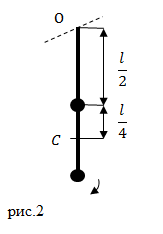
Решение: Основой для решения задачи является формула нахождения частоты колебаний физического маятника:
где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние между центром масс маятника и точкой подвеса; $m$ – масса маятника. Масса маятника по условию задачи состоит из масс двух одинаковых шариков (масса одного шарика $frac<2>$). В нашем случае расстояние $a$ равно расстоянию между точками O и C (см. рис.2):
Найдем момент инерции системы из двух точечных масс. Относительно центра масс (если ось вращения провести через точку C), момент инерции системы ($J_0$) равен:
Момент инерции нашей системы относительно оси, проходящей через точку О найдем по теореме Штейнера:
Подставим правые части выражение (2.2) и (2.4) в (2.1) вместо соответствующих величин:
Циклическая частота колебаний – формула
Любые колебательные процессы в Природе (в том числе и непериодические) могут быть представлены в виде бесконечной суммы простых гармонических колебаний. Поэтому в первую очередь изучаются гармонические колебания. Рассмотрим такую характеристику этих колебаний, как циклическая частота.

Период и частота гармонических колебаний
Впервые гармоническими колебаниями заинтересовались еще античные философы, изучая вопросы музыкальной гармонии. Поэтому простейшие колебания, происходящие по закону круговых функций (синуса или косинуса), называются гармоническими.
Формула гармонических колебаний:

Рис. 1. График гармонических колебаний.
Как можно видеть из графика колебаний (а также из изучения круговых функций в математическом анализе), функции эти регулярно повторяют свои значения. Более того, регулярно повторяется форма графика колебаний. Это свойство функции называется периодичностью. То есть, функция, обладающая периодичностью, имеет равные значения на промежутках, равных своему периоду.
Период обозначается латинской буквой $T$. Однако, физический и математический подход к измерению периода немного различен.
В математике в качестве аргумента круговой функции рассматривается угол поворота вектора, образующего ее, и этот угол удобно измерять в радианах (каждый радиан равен дуге, имеющей длину радиуса). В радианах измеряется и период круговой функции. Для простого синуса или косинуса $T = 2pi$.

Рис. 2. Период синуса и косинуса.
В физике угол поворота менее важен, нередко такой угол даже невозможно указать (например, для колебаний пружинного маятника). Поэтому в физике период измеряется в единицах времени – секундах. Дополнительно это дает возможность ввести специальную характеристику, позволяющую определить «скорость» колебаний – частоту (обозначается греческой буквой $nu$ («ню»).
Если период показывает, за сколько времени совершается одно колебание, то частота показывает, сколько колебаний совершается за одну секунду:
Частота измеряется в колебаниях в секунду или Герцах (Гц). Один герц – это одно колебание в секунду.
Круговая частота
Как видим, физический и математический подход к описанию периода функций несколько отличаются, и возникает вопрос их связи.
Из приведенной выше формулы гармонических колебаний можно видеть, что она имеет период:
В эту формулу входит параметр $omega$, который обратно пропорционален периоду. При сравнении этой формулы с формулой частоты можно получить:
Или, после упрощений:
Таким образом, параметр $omega$ в $2pi$ раз больше частоты колебаний. Поскольку в одном круге $2pi$ радиан, то параметр $omega$ называется «круговой» или «циклической» частотой.
Физический смысл частоты – это количество колебаний, происходящих в системе за единицу времени, а физический смысл круговой частоты – это количество радиан, проходящих функцией, описывающей систему, за единицу времени.

Рис. 3. Круговая (циклическая) частота.
Таким образом, удобный и наглядный параметр частоты может быть легко преобразован для вида, удобного в математических преобразованиях.
Что мы узнали?
Круговая (циклическая) частота – это важный параметр гармонического колебания, удобный в математической обработке функций. Круговая частота обозначает количество радиан, прошедших гармонической функцией за единицу времени. Она прямо пропорциональна обычной частоте.
Характеристики колебаний
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.

Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_ <0>) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):

Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac<1> right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^ <-1>right) ), потому, что по свойствам степени ( large displaystyle frac<1> = c^ <-1>).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac<text<рад>> right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac<1> ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_ <0>).
(large varphi_ <0>left(text <рад>right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина (large varphi_ <0>) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_ <0>) принимаем равной нулю.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_ <0>) будет отличаться от нулевого значения.
Определим угол (large varphi_ <0>) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_ <0>) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_ <0>).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text <сек>right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac<Delta t >):
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
(large displaystyle frac<1> <4>cdot 2pi = frac<pi > <2>=varphi_ <0>)
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac<pi > <2>) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac<pi > <2>) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_ <0>= 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_ <0>) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_<0>) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_<0>) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_<0>) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
( large varphi_<01>) – для первого процесса и,
( large varphi_<02>) – для второго процесса.

Определим разность фаз между первым и вторым колебательными процессами:
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text <шт>right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
(large nu left( text <Гц>right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
- Связь между частотой и циклической частотой колебаний:
(large displaystyle omega left( frac<text<рад>> right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
(large varphi_ <0>left( text <рад>right) ) — начальная фаза;
(large varphi left( text <рад>right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
[spoiler title=”источники:”]
http://kupuk.net/uroki/fizika/ciklicheskaia-chastota-kolebanii-formyla/
[/spoiler]
