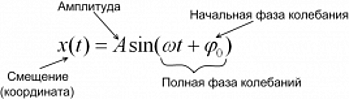Формула циклической частоты колебаний в физике
Формула циклической частоты колебаний
Определение и формула циклической частоты колебаний
Определение
Циклическая частота – это параметр, характеризующий колебательные движения. Обозначают эту скалярную
величину как $omega $, иногда ${omega }_0$.
Напомним, что уравнение гармонических колебаний параметра $xi $ можно записать как:
[xi left(tright)=A{cos left({omega }_0t+{varphi }_0right) }left(1right),]
где $A={xi }_{max}$ – амплитуда колебаний величины $xi $; $left({omega }_0t+{varphi }_0right)$=$varphi $ – фаза колебаний; ${varphi }_0$ – начальная фаза колебаний.
Циклическую частоту при гармонических колебаниях определяют как частную производную от фазы колебаний ($varphi $) по времени ($t$):
[{omega }_0=frac{?varphi }{partial t}=dot{varphi }left(2right).]
Циклическая частота колебаний связана с периодом ($T$) колебаний формулой:
[{omega }_0=frac{2pi }{T}left(3right).]
Циклическую частоту с частотой $?$$?$ связывает выражение:
[{omega }_0=2pi nu left(4right).]
Формулы для частных случаев нахождения циклической частоты
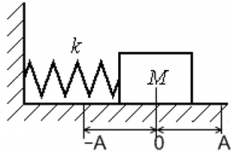
Пружинный маятник совершает гармонические колебания с циклической частотой равной:
[{omega }_0=sqrt{frac{k}{m}}left(5right),]
$k$ – коэффициент упругости пружины; $m$ – масса груза на пружине.
Гармонические колебания физического маятника происходят с циклической частотой равной:
[{omega }_0=sqrt{frac{mga}{J}}left(6right),]
где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние между центром масс маятника и точкой подвеса; $m$ – масса маятника.
Частным случаем физического маятника является математический маятник (физический маятник, масса которого сосредоточена в точке), циклическая частота его колебаний может быть найдена как:
[{omega }_0=sqrt{frac{g}{l}}left(7right),]
где $l$ – длина подвеса, на которой находится материальная точка.
Частота колебаний в электрическом контуре равна:
[{omega }_0=frac{1}{sqrt{LC}}left(8right),]
где $C$ – емкость конденсатора, который входит в контур; $L$ – индуктивность катушки контура.
Если колебаний являются затухающими, то их частоту находят как:
[omega =sqrt{{omega }^2_0-{delta }^2}left(9right),]
где $delta $ – коэффициент затухания; в случае с затуханием колебаний, ${omega }_0$ называют собственной угловой частотой колебаний.
Примеры задач с решением
Пример 1
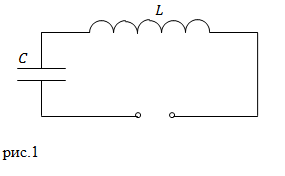
Задание. В электрический колебательный контур (рис.1) входит соленоид, длина которого $l$, площадь поперечного сечения $S_1$, число витков $N $и плоский конденсатор с расстоянием между пластинами $d$, площадью пластин $S_2$. Какова частота собственных колебаний контура (${omega }_0$)?
Решение. Основой для решения задачи служить формула для частоты колебаний в электрическом контуре:
[{omega }_0=frac{1}{sqrt{LC}}left(1.1right).]
Элементом, обладающим индукцией в нашем контуре является соленоид. Индуктивность соленоида равна:
[L=mu {mu }_0frac{N^2S_1}{l}left(1.2right),]
где $mu =1$, ${mu }_0$ – магнитная постоянная.
Емкость плоского конденсатора вычислим по формуле:
[C=frac{varepsilon {varepsilon }_{0 }S_2}{d}left(1.3right),]
где $varepsilon =1$, ${varepsilon }_{0 }$ – электрическая постоянная.
Правые части выражений (1.2) и (1.3) подставим в (1.1) вместо соответствующих величин:
[{omega }_0=frac{1}{sqrt{LC}}=sqrt{frac{ld}{{{mu }_0{varepsilon }_{0 }N}^2S_1S_2}}left(1.4right).]
Ответ. ${omega }_0=sqrt{frac{ld}{{{mu }_0{varepsilon }_{0 }N}^2S_1S_2}}$
Пример 2
Задание. Чему равна циклическая частота гармонических колебаний материальной точки, если амплитуда скорости точки равна ${dot{x}}_{max}=v_0$, амплитуда ее ускорения: ${ddot{x}}_{max}=a_0$? Начальная фаза колебаний равна нулю.
Решение. Из контекста условий задачи понятно, что колебания совершает координата $x$, поэтому уравнение колебаний (в общем виде) запишем как:
[xleft(tright)=A{cos left({omega }_0t+{varphi }_0right)= }A{cos left({omega }_0tright) }left(2.1right),]
По условию задачи ${varphi }_0$=0. Тогда уравнение для скорости изменения параметра $xleft(tright)$ имеет вид:
[dot{x}left(tright)=vleft(tright)=-A{omega }_0{sin left({omega }_0tright)left(2.2right). }]
Из выражения (2.2) следует, что:
[{dot{x}}_{max}=v_0=A{omega }_0left(2.3right).]
Уравнение для ускорения материальной точки, используя (2.2) запишем как:
[ddot{x}left(tright)=aleft(tright)=-A{{omega }_0}^2{cos left({omega }_0tright)left(2.4right). }]
Получаем, что:
[{ddot{x}}_{max}=A{{omega }_0}^2=a_0 left(2.5right).]
Мы получили следующую систему из двух уравнений с двумя неизвестными:
[left{ begin{array}{c}
v_0=A{omega }_0 \
a_0=A{{omega }_0}^2 end{array}
right.left(2.6right).]
Найдем отношение $frac{a_0}{v_0}$, получим:
[frac{a_0}{v_0}={omega }_0.]
Ответ. ${omega }_0=frac{a_0}{v_0}$
Читать дальше: формула частоты колебаний пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
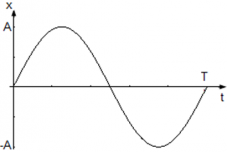
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
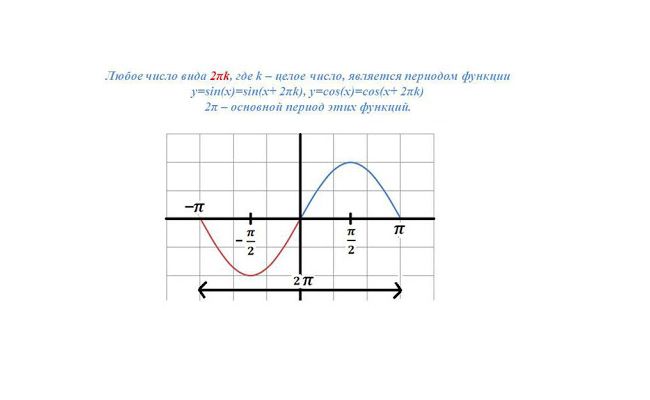
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Циклическая частота колебаний
Мерой колебательного движения служит циклическая (или угловая, или круговая) частотой колебаний.
Это скалярная физическая величина.
Циклическая частота при гармонических колебаниях
Пусть колебания совершает материальная точка. При этом материальная точка через равные промежутки времени проходит через одно и то же положение.
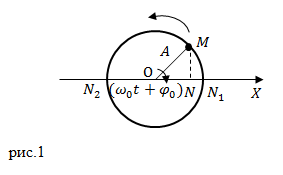
Самыми простыми колебаниями являются гармонические колебания. Рассмотрим следующую кинематическую модель. Точка M с постоянной по модулю скоростью ($v$) движется по окружности радиуса A. В этом случае ее угловую скорость обозначим $<omega >_0$, эта скорость постоянна (рис.1).
Проекция точки $M$ на диаметр окружности (точка $N$), на ось X, выполняет колебания от $N_1$ до $N_2 $и обратно. Такое колебание N ,будет гармоническим. Для описания колебания точки N необходимо записать координату точки N, как функцию от времени ($t$). Пусть при $t=0$ радиус OM образует с осью X угол $<varphi >_0$. Через некоторый промежуток времени этот угол изменится на величину $<omega >_0t$ и будет равен $<omega >_0t+<varphi >_0$, тогда:
Выражение (1) является аналитической формой записи гармонического колебания точки N по диаметру $N_1N_2$.
Обратимся к выражению (1). Величина $A$ – это максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О – центра окружности), называется амплитудой колебаний.
Параметр $<omega >_0$ – циклическая частота колебаний. $varphi =(<omega >_0t+<varphi >_0$) – фаза колебаний; $<varphi >_0$ – начальная фаза колебаний.
Циклическую частоту гармонических колебаний можно определить как частную производную от фазы колебаний по времени:
При $<varphi >_0=0$, уравнение колебаний (1) преобразуется к виду:
Если начальная фаза колебаний равна $<varphi >_0=frac<pi ><2>$ , то получим уравнение колебаний в виде:
Выражения (3) и (4) показывают, что при гармонических колебаниях абсцисса $x$ – это функция синус или косинус от времени. При графическом изображении гармонических колебаний получается косинусоида или синусоида. Форма кривой определена амплитудой колебаний и величиной циклической частоты. Положение кривой зависит от начальной фазы.
Циклическую частоту колебаний можно выразить через период (T) колебаний:
Циклическую частоту с частотой $?$$?$ свяжем выражением:
Единицей измерения циклической частоты в Международной системе единиц (СИ) является радиан, деленный на секунду:
Размерность циклической частоты:
Частные случаи формул для вычисления циклической частоты
Груз на пружине (пружинный маятник – идеальная модель) совершает гармонические колебания с круговой частотой равной:
$k$ – коэффициент упругости пружины; $m$ – масса груза на пружине.
Малые колебания физического маятника будут приблизительно гармоническими колебаниями с циклической частотой равной:
где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние между центром масс маятника и точкой подвеса; $m$ – масса маятника.
Примером физического маятника является математический маятник. Круговая частота его колебаний равна:
где $l$ – длина подвеса.
Угловая частота затухающих колебаний находится как:
где $delta $ – коэффициент затухания; в случае с затуханием колебаний $<omega >_0$ называют собственной угловой частотой колебаний.
Примеры задач с решением
Задание: Чему равна циклическая частота гармонических колебаний, если максимальная скорость материальной точки равна $<dot>_=10 frac<см><с>$, а ее максимальное ускорение $<ddot>_=100 frac<см><с^2>$?
Решение: Основой решения задачи станет уравнение гармонических колебаний точки, так как из условий, очевидно, что они происходят по оси X:
Скорость колебаний найдем, используя уравнение (1.1) и кинематическую связь координаты $x$ и соответствующей компоненты скорости:
Максимальное значение скорости (амплитуда скорости) равна:
Ускорение точки вычислим как:
Из формулы (1.3) выразим амплитуду, подставим ее в (1.5), получим циклическую частоту:
Вычислим циклическую частоту:
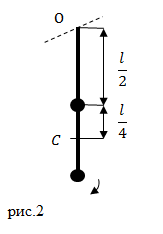
Задание: На длинном невесомом стержне закреплены два груза одинаковой массы. Один груз находится на середине стержня, другой на его конце (рис.2). Система совершает колебания около горизонтальной оси, проходящей через свободный конец стрежня. Какова циклическая частота колебаний? Длина стержня равна $l$.
Решение: Основой для решения задачи является формула нахождения частоты колебаний физического маятника:
где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние между центром масс маятника и точкой подвеса; $m$ – масса маятника. Масса маятника по условию задачи состоит из масс двух одинаковых шариков (масса одного шарика $frac<2>$). В нашем случае расстояние $a$ равно расстоянию между точками O и C (см. рис.2):
Найдем момент инерции системы из двух точечных масс. Относительно центра масс (если ось вращения провести через точку C), момент инерции системы ($J_0$) равен:
Момент инерции нашей системы относительно оси, проходящей через точку О найдем по теореме Штейнера:
Подставим правые части выражение (2.2) и (2.4) в (2.1) вместо соответствующих величин:
17. Механика Читать 0 мин.
17.547. Механические колебания
Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.
Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.
Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $frac<1>$ , где
Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $frac$ , где
N ― количество колебаний;
Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $frac<2pi>$ , где
ω ― циклическая частота [рад/с];
Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:
ω ― циклическая частота [рад/с];
φ0 ― начальная фаза колебаний, [рад];
Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.
Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.
Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.
Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где
φ ― полная фаза колебаний [рад];
φ0 ― начальная фаза колебаний, [рад];
ω ― циклическая частота [рад/с];
Пример анализа гармонических колебаний точки
Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где
ω ― циклическая частота [рад/с].
Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна φ = $frac<pi> <2>+2pi n$ когда x = –A фаза колебаний принимает значения φ = $frac<3pi> <2>+2pi n$ , где n = 0, 1 , 2, … N.
График колебания координаты точки имеет вид:
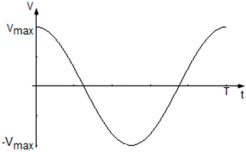
Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где
v ― скорость движения точки [м/с];
Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).
Уравнение скорости точки равно v(t) = Acos(ωt), где
v ― скорость движения точки [м/с];
ω ― циклическая частота [рад/с];
Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.
График колебания скорости точки имеет вид:
Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.
Ускорение ― это производная скорости по времени: a = vt‘, где
a ― ускорение движения точки [м/с2];
v ― скорость движения точки [м/с];
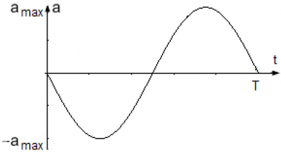
Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).
Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где
a ― ускорение движения точки [м/с2];
ω ― циклическая частота [рад/с];
Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.
График колебания ускорения точки имеет вид:
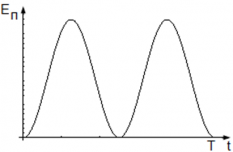
Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где
E ― полная механическая энергия системы, E = const, [Дж];
EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];
EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].
Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).
Потенциальная энергия деформированной пружины равна EП = $frac<2>$ , где
EП ― потенциальная энергия деформированной пружины, [Дж];
k ― коэффициент упругости пружины [Н/м];
x ― деформация пружины (величина ее удлинения или сжатия) [м].
У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $frac<2>$ = $frac<2>$ = $frac <2>cdot A^2 sin^2 (omega t)$ .
Уравнение потенциальной энергии пружинного маятника EП = $frac <2>cdot A^2 sin^2 (omega t)$ , где
EП ― потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
ω ― циклическая частота [рад/с];
Амплитуда потенциальной энергии пружинного маятника равна EПmax = $frac<2>A^2$ , где
EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.
График колебаний потенциальной энергии пружинного маятника:
Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $frac<2>$ , где
Eк ― кинетическая энергия тела, [Дж];
v ― скорость движения тела, [м/с].
У тела, которое совершает колебательные движения, скорость ― переменная величина.
Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $frac<2>$ = $frac <2>cdot (Aomegacos(omega t))^2$ = $frac <2>cdot A^2 omega^2 cos^2 (omega t)$ .
Уравнение кинетической энергии маятника Eк = $frac <2>cdot A^2 omega^2 cos^2 (omega t)$ , где
Eк ― кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с];
Амплитуда кинетической энергии маятника равна EКmax = $frac <2>cdot A^2 omega^2$ , где
EКmax ― максимальная кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с].
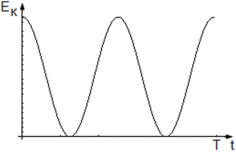
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.
График колебаний кинетической энергии маятника:
Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.
Период колебаний математического маятника равен T = $2pi sqrt<frac>$ , где
l ― длина нити математического маятника [м];
g ― ускорение свободного падения [м/с2].
Период колебаний пружинного маятника равен T = $2pi sqrt<frac>$ , где
Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.
На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.
Механические колебания.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания – это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания – это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия – это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела – это величина его наибольшего отклонения от положения равновесия.
Период колебаний – это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний – это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них – синус и косинус – являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания – это колебания, при которых координата зависит от времени по гармоническому закону:
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому – амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .
Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1) :
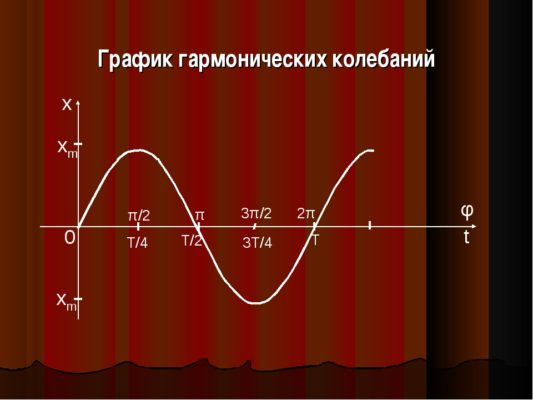
График функции (1) , выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1 .
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:
График гармонических колебаний в этом случае представлен на рис. 2 .
 |
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:
График колебаний представлен на рис. 3 .
 |
| Рис. 3. Закон синуса |
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1) . Дифференцируем это равенство:
Теперь дифференцируем полученное равенство (4) :
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6) , (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий – по начальным значениям координаты и скорости.
Пружинный маятник.
Пружинный маятник – это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4 ). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:
Если 0′ alt=’x>0′ /> (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то 0′ alt=’F_>0′ /> . Знаки и всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
Мы получили уравнение гармонических колебаний вида (6) , в котором
Циклическая частота колебаний пружинного маятника, таким образом, равна:
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10) .
Математический маятник.
Математический маятник – это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5 ). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
 |
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
и спроектируем его на ось :
Если маятник занимает положение как на рисунке (т. е. 0′ alt=’x>0′ /> ), то:
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
Итак, при любом положении маятника имеем:
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11) :
Это – уравнение гармонических колебаний вида (6) , в котором
Следовательно, циклическая частота колебаний математического маятника равна:
Отсюда период колебаний математического маятника:
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6 ).
 |
| Рис. 6. Затухающие колебания |
Вынужденные колебания – это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7 .
 |
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс – явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .
[spoiler title=”источники:”]
http://reshutest.ru/theory/13?theory_id=334
http://ege-study.ru/ru/ege/materialy/fizika/mexanicheskie-kolebaniya/
[/spoiler]
Циклическая частота колебаний

4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
Любые колебательные процессы в Природе (в том числе и непериодические) могут быть представлены в виде бесконечной суммы простых гармонических колебаний. Поэтому в первую очередь изучаются гармонические колебания. Рассмотрим такую характеристику этих колебаний, как циклическая частота.
Период и частота гармонических колебаний
Впервые гармоническими колебаниями заинтересовались еще античные философы, изучая вопросы музыкальной гармонии. Поэтому простейшие колебания, происходящие по закону круговых функций (синуса или косинуса), называются гармоническими.
Формула гармонических колебаний:
$$x=Asin(omega t+varphi)$$
Как можно видеть из графика колебаний (а также из изучения круговых функций в математическом анализе), функции эти регулярно повторяют свои значения. Более того, регулярно повторяется форма графика колебаний. Это свойство функции называется периодичностью. То есть, функция, обладающая периодичностью, имеет равные значения на промежутках, равных своему периоду.
Период обозначается латинской буквой $T$. Однако, физический и математический подход к измерению периода немного различен.
В математике в качестве аргумента круговой функции рассматривается угол поворота вектора, образующего ее, и этот угол удобно измерять в радианах (каждый радиан равен дуге, имеющей длину радиуса). В радианах измеряется и период круговой функции. Для простого синуса или косинуса $T = 2pi$.
В физике угол поворота менее важен, нередко такой угол даже невозможно указать (например, для колебаний пружинного маятника). Поэтому в физике период измеряется в единицах времени – секундах. Дополнительно это дает возможность ввести специальную характеристику, позволяющую определить «скорость» колебаний – частоту (обозначается греческой буквой $nu$ («ню»).
Если период показывает, за сколько времени совершается одно колебание, то частота показывает, сколько колебаний совершается за одну секунду:
$$nu= {1over T}$$
Частота измеряется в колебаниях в секунду или Герцах (Гц). Один герц – это одно колебание в секунду.
Круговая частота
Как видим, физический и математический подход к описанию периода функций несколько отличаются, и возникает вопрос их связи.
Из приведенной выше формулы гармонических колебаний можно видеть, что она имеет период:
$$T = {2pi over omega}$$
В эту формулу входит параметр $omega$, который обратно пропорционален периоду. При сравнении этой формулы с формулой частоты можно получить:
$$T = {2pi over omega}={1over nu}$$
Или, после упрощений:
$$omega = 2pi nu$$
Таким образом, параметр $omega$ в $2pi$ раз больше частоты колебаний. Поскольку в одном круге $2pi$ радиан, то параметр $omega$ называется «круговой» или «циклической» частотой.
Физический смысл частоты – это количество колебаний, происходящих в системе за единицу времени, а физический смысл круговой частоты – это количество радиан, проходящих функцией, описывающей систему, за единицу времени.
Таким образом, удобный и наглядный параметр частоты может быть легко преобразован для вида, удобного в математических преобразованиях.
Что мы узнали?
Круговая (циклическая) частота – это важный параметр гармонического колебания, удобный в математической обработке функций. Круговая частота обозначает количество радиан, прошедших гармонической функцией за единицу времени. Она прямо пропорциональна обычной частоте.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
А какая ваша оценка?
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Механика.pdf
Скачиваний:
63
Добавлен:
12.02.2015
Размер:
1.35 Mб
Скачать
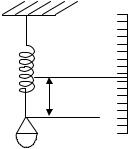
Цель работы: опытная проверка расчета частоты колебания тела на пружине.
Принадлежности: штатив с масштабной линейкой, пружина, чашечка, разновески, секундомер.
Вопросы, знание которых обязательно для допуска к выполнению работы
1.Какие колебания называются гармоническими? Напишите уравнение гармонических колебаний.
2.Что называется амплитудой, частотой, периодом, фазой гармонического колебания?
3.Как связаны между собой период, частота, циклическая частота?
4.Две колеблющиеся материальные точки имеют одинаковые (разные) фазы. Что это означает?
5.Как выражаются скорость и ускорение при гармоническом колебании?
6.Что называется квазиупругой силой? Приведите примеры.
7.Что называется коэффициентом жесткости пружины?
8.От каких параметров пружины зависит коэффициент жесткости?
9.От чего и как зависит частота колебания тела на пружине?
10.Расскажите порядок выполнения работы.
ВВЕДЕНИЕ
Тело, подвешенное на пружине и выведенное из положения равновесия, совершает гармонические колебания. Гармоническими называются колебания, при которых колеблющаяся величина изменяется со временем по закону синуса и косинуса. Для механических колебаний это означает, что смещение те-
|
ла х от положения равновесия происходит по закону: |
|
|
х = х0 sin (ω t + ϕ), |
(1) |
|
41 |
где х0 – амплитуда (максимальное отклонение от положения рав-
новесия), ω = 2 π ν= 2Tπ – циклическая частота (ν– частота коле-
бания; Т- период); t – время, в течение которого совершается колебательный процесс; ϕ – начальная фаза; (ω t + ϕ) – фаза колебания, определяющая состояние системы в момент времени t.
Рассмотрим пружинный маятник (рис. 1), состоящий из легкой пружины, имеющей достаточно большое число витков, и тела массой m. Если оттянуть тело
|
маятника строго вертикально вниз на |
||
|
небольшое расстояние и отпустить, |
||
|
то маятник начнет совершать колеба- |
||
|
X=0 |
ния только вдоль вертикальной линии |
|
|
(колебания с одной степенью свобо- |
||
|
X |
||
|
ды). Колебание тела на пружине в |
||
|
вертикальном направлении происхо- |
||
|
дит под действием двух сил: силы |
||
|
Рис. 1 |
тяжести и упругой силы пружины. |
|
|
При отклонении маятника из положе- |
ния равновесия будет возникать внутренняя возвращающая сила упругости, направленная к точке равновесия. Если величина отклонения маятника мала (много меньше первоначальной длины маятника), можно воспользоваться законом Гука:
где k – коэффициент жесткости пружины, зависящий от ее геометрических размеров и материала, из которого она изготовлена. По второму закону Ньютона:
|
dv |
d2x |
k |
x . |
|||||||
|
F = m a = – k x; |
a = |
= |
= − |
|||||||
|
dt |
dt2 |
|||||||||
|
m |
||||||||||
|
Тогда уравнение гармонических колебаний получим в ви- |
||||||||||
|
де: |
||||||||||
|
m |
d 2 x |
+ k x = 0 . |
(3) |
|||||||
|
dt 2 |
||||||||||
Общее решение этого уравнения имеет вид:
42
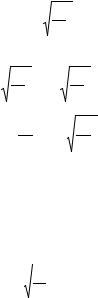
|
x = x |
k |
(4) |
|||
|
0 |
sin |
t +ϕ . |
|||
|
m |
|||||
|
Действительно: |
|||||||||
|
dx |
k |
k |
|||||||
|
= x0 |
, |
(5) |
|||||||
|
dt |
m |
cos |
m |
t +ϕ |
|||||
|
d2 x |
k |
k |
|||||||
|
= −x |
0 |
sin |
t +ϕ . |
(6) |
|||||
|
2 |
|||||||||
|
dt |
m |
m |
|||||||
Подставляя в левую часть уравнения (3) выражение (6), а в правую – значение х из (4), приходим к тождеству, что означает правильность выбора решения в виде уравнения (4).
Из уравнений (4) и (1) следует, что циклическая частота колебаний зависит от коэффициента жесткости пружины и массы колеблющегося тела:
|
ω = |
k . |
(7) |
|
|
m |
Значение начальной фазы определяется в каждом конкретном случае из начальных условий.
Обобщая вывод, сделанный выше, можно утверждать, что гармонические колебания будут совершаться и при действии на тело силы любой природы, лишь бы она подчинялась уравнению
(2). Силы или результирующие силы, хотя и неупругие, но подчиняющиеся уравнению (2), называются квазиупругими. Примером такой силы является результирующая двух сил (силы тяжести и силы натяжения нити), возникающая при отклонении пружинного маятника из положения равновесия.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для расчета частоты колебаний груза на пружине необходимо определить массу этого груза m и коэффициент жесткости пружины k. Кроме того, нужно быть уверенным, что коэффициент k будет постоянным в достаточно широком диапазоне нагрузок и деформации пружины.
1. Определение коэффициента k.
43
Определим k через приращение силы δF и приращение смещения δx:
k =δF/δx.
Для этого на чашечку, подвешенную к пружине, следует класть гирьки так, чтобы нагрузка увеличивалась каждый раз на 20 г, и, соответственно, производить отсчет xi положений чашечки и пружины.
Растяжение пружины отмечают с помощью указателя (горизонтального кусочка проволоки, укрепленного в нижней части пружины). Для избежания ошибок из-за параллакса используют зеркальную шкалу. Для правильного отсчета показаний глаз следует расположить на такой высоте, чтобы указатель совпал со своим изображением в зеркале, укрепленном рядом со шкалой. Затем, не изменяя положения головы, производят отсчет по шкале.
По разности xi до и после нагрузки определяют δx для соответствующей нагрузки: δF = δmg.
Чтобы убедиться, что не произошло неупругих деформаций пружины, необходимо произвести отсчеты и при уменьшающейся нагрузке. Если при разных нагрузках значения коэффициента k в пределах погрешности получаются одинаковыми, то закон Гука выполняется во всем диапазоне нагрузок. В этом случае можно определить среднее значение k.
2. Измерение массы груза.
Масса груза выбирается произвольно. Обычно это чашечка со свинцовой отливкой, к которой можно добавить произвольное число гирек. При подборе массы груза, для которого будет производиться расчет частоты колебаний (причем частота будет проверяться экспериментально), следует учесть, что чем больше масса груза, тем меньше частота. Но при большом количестве гирек при колебаниях они могут выпасть из чашечки.
3.По формуле (7) рассчитать циклическую частоту (при расчете обратите внимание на систему единиц).
4.Результаты измерений занесите в таблицу, определите
относительную и абсолютную погрешности ω.
44

|
Таблица |
||||||
|
№ |
m, кг |
xi, м |
δxi, м |
k, H/м |
ω, 1/c |
ω′, 1/c |
|
п/п |
||||||
|
1 |
0 |
|||||
|
2 |
0.02 |
|||||
|
3 |
0.04 |
|||||
|
4 |
0.06 |
|||||
|
5 |
0.08 |
|||||
|
6 |
0.10 |
|||||
|
7 |
0.12 |
|||||
|
8 |
0.10 |
|||||
|
9 |
0.08 |
|||||
|
10 |
0.06 |
|||||
|
11 |
0.04 |
|||||
|
12 |
0.02 |
|||||
|
13 |
0 |
|||||
|
Среднее |
||||||
|
значение |
5. Необходимо экспериментально проверить рассчитанную циклическую частоту ω′. Для этого с помощью секундомера определяют время t числа N полных колебаний, откуда
ω’= 2Tπ = 2πtN
Опыт выполняется следующим образом. На чашечке устанавливают тот же груз, для которого по формуле (7) был произведен расчет ω. Слегка оттянув чашечку (строго вертикально вниз), приводят груз в колебание. Измерение времени не рекомендуется начинать с момента запуска. После нескольких качаний, усвоив темп счета, запускают секундомер в момент, когда груз занимает крайнее нижнее положение (либо крайнее верхнее). В момент запуска секундомера начинают счет колебаний с цифры “ноль” (а не “раз”). Для одного и того же числа полных колебаний N (N ≥ 20) определяют время колебаний t не менее трех раз. При этом не обязательно каждый раз останавливать чашечку с грузом, а затем снова ее запускать. Расхождение в измеренных промежутках времени не должно сильно превышать
45
погрешность секундомера (∆t = 0.2 с). Кроме того, если обнаружится расхождение во времени t больше, чем t /N , это означает, что при подсчете числа колебаний допущен просчет.
По измеренным t найти tср. Используя tсp и число полных колебаний N, определите Т и ω′.
6.Сравните результаты для ω и ω‘ с учетом их абсолютных погрешностей.
7.Рассчитайте массу чашечки. Поясните, как вы это сде-
лали.
Рекомендуемая литература
1.Савельев И.В. Курс общей физики. T. I. – Киев: Наука, 1977. § 14, 49, 50, 53, 54.
2.Архангельский М.В. Курс физики: механика. – М.: Просвеще-
ние, 1975. С. 62-72, 224-237, 297-305.
|
3. Грабовский Р.И. Курс физики. – М.: Высшая школа, 1970. |
§ |
|
10, 27, 29. |
4.Ландсберг Г.С. Элементарный учебник физики. T. I. – М.:
Наука, 1967. § 58, 59, 60, 61. С. 277-287.
5.Мэрион Дж.Б. Общая физика с биологическими примерами. – М.: Высшая школа, 1986.
6.Кац Ц.Б. Биофизика на уроках физики. – М.: Просвещение, 1988.
Для получения зачета необходимо
1.Продемонстрировать умение экспериментально определять частоту колебаний тела на пружине.
2.Представить отчет по установленной форме.
3.Уметь отвечать на вопросы типа:
а) К пружине с жесткостью k подвешено тело массой m. Затем пружина перерезается пополам и к одной из ее половин снова подвешивается то же тело. Будет ли частота колебаний пружины одинакова в первом и во втором случаях? Если нет, то как будут относиться друг к другу обе частоты? Рассмотрите три
случая: mпр >> m , mпр << m, mпр m.
б) Поясните, как можно сравнить между собой массы тел,
46
измеряячастотыколебаний этих масс, подвешенныхкпружине. в) Поясните качественно, как изменится период колебаний
пружины, если учесть ее массу m?
г) Железная и медная проволоки одинаковых размеров висят в вертикальной плоскости. Нижние концы проволок прикреплены к горизонтальному стержню. Сохранится ли горизонтальность стержня, если к его середине прикрепить груз?
Дополнительные задания и вопросы
Для студентов факультета технологии
ипредпринимательства
1.Что такое колебание? Какие колебательные движения вы знаете?
2.При каких условиях возникают гармонические колеба-
ния?
3.Что можно оказать о напряжении в металлическом брус-
ке:
а) движущемся равномерно, а потом ускоренно в горизонтальном направлении?
б) вращающемся вокруг вертикальной оси? в) свободно падающем?
4.Во сколько раз изменится частота колебаний автомобиля на рессорах после принятия груза, равного массе порожнего автомобиля?
5.Особенность кривошипно-шатунного механизма состоит в том, что он превращает гармонические колебания поршня в равномерное вращение коленчатого вала. Где используется это явление для преобразования неравномерного движения в равномерное?
6.В ряде измерительных приборов имеются успокоители – демпферы, которые служат для ускорения затухания колебаний подвижной части прибора, например стрелки.
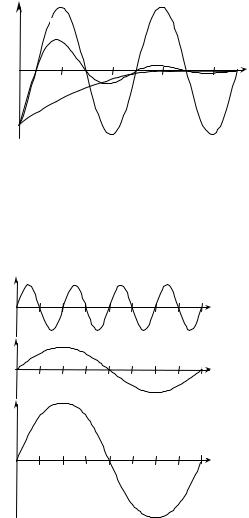
На рис. 2 приведены кривые зависимости измерения амплитуды от времени движения стрелки измерительного прибора.
Укажите:
а) кривую, соответствующую периодическомуколебанию стрелкибезуспокоителя;
47
|
X |
2 |
1 |
|
|
б) кривую, характе- |
|||
|
ризующую затухаю- |
|||
|
t |
щие колебания; |
||
|
3 |
в) кривую апериоди- |
||
|
ческого движения при |
|||
|
сильном успокоении. |
|||
|
Рис. 2 |
Для студентов есте- |
||
|
ственнонаучных фа- |
культетов
1.Что такое звук?
2.Дайте характеристику инфразвука и ультразвука; Рассчитайте длину волны самого низкого (высокого) для человече-
|
X |
t |
ского уха звукового колеба- |
|||
|
ния. |
|||||
|
3. Чем отличаются колеба- |
|||||
|
X |
тельные |
движения, |
графики |
||
|
t |
которых |
представлены |
на |
||
|
рис. 3? Рассчитайте пара- |
|||||
|
метры |
колебательного |
про- |
|||
|
X |
цесса |
(задания возьмите у |
|||
|
преподавателя). |
|||||
|
t |
4. Опишите работу сердца |
||||
|
как колебательной системы. |
|||||
|
5. С чем связана способ- |
|||||
|
ность к ориентации в абсо- |
|||||
|
лютной |
темноте у |
летучих |
|||
|
мышей? |
|||||
|
Рис. 3 |
6. Каким образом |
медузы |
|||
|
узнаютсприближении |
|||||
шторма?
48
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #