Формула циклической частоты колебаний в физике
Формула циклической частоты колебаний
Определение и формула циклической частоты колебаний
Определение
Циклическая частота – это параметр, характеризующий колебательные движения. Обозначают эту скалярную
величину как $omega $, иногда ${omega }_0$.
Напомним, что уравнение гармонических колебаний параметра $xi $ можно записать как:
[xi left(tright)=A{cos left({omega }_0t+{varphi }_0right) }left(1right),]
где $A={xi }_{max}$ – амплитуда колебаний величины $xi $; $left({omega }_0t+{varphi }_0right)$=$varphi $ – фаза колебаний; ${varphi }_0$ – начальная фаза колебаний.
Циклическую частоту при гармонических колебаниях определяют как частную производную от фазы колебаний ($varphi $) по времени ($t$):
[{omega }_0=frac{?varphi }{partial t}=dot{varphi }left(2right).]
Циклическая частота колебаний связана с периодом ($T$) колебаний формулой:
[{omega }_0=frac{2pi }{T}left(3right).]
Циклическую частоту с частотой $?$$?$ связывает выражение:
[{omega }_0=2pi nu left(4right).]
Формулы для частных случаев нахождения циклической частоты
Пружинный маятник совершает гармонические колебания с циклической частотой равной:
[{omega }_0=sqrt{frac{k}{m}}left(5right),]
$k$ – коэффициент упругости пружины; $m$ – масса груза на пружине.
Гармонические колебания физического маятника происходят с циклической частотой равной:
[{omega }_0=sqrt{frac{mga}{J}}left(6right),]
где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние между центром масс маятника и точкой подвеса; $m$ – масса маятника.
Частным случаем физического маятника является математический маятник (физический маятник, масса которого сосредоточена в точке), циклическая частота его колебаний может быть найдена как:
[{omega }_0=sqrt{frac{g}{l}}left(7right),]
где $l$ – длина подвеса, на которой находится материальная точка.
Частота колебаний в электрическом контуре равна:
[{omega }_0=frac{1}{sqrt{LC}}left(8right),]
где $C$ – емкость конденсатора, который входит в контур; $L$ – индуктивность катушки контура.
Если колебаний являются затухающими, то их частоту находят как:
[omega =sqrt{{omega }^2_0-{delta }^2}left(9right),]
где $delta $ – коэффициент затухания; в случае с затуханием колебаний, ${omega }_0$ называют собственной угловой частотой колебаний.
Примеры задач с решением
Пример 1
Задание. В электрический колебательный контур (рис.1) входит соленоид, длина которого $l$, площадь поперечного сечения $S_1$, число витков $N $и плоский конденсатор с расстоянием между пластинами $d$, площадью пластин $S_2$. Какова частота собственных колебаний контура (${omega }_0$)?
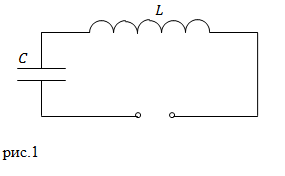
Решение. Основой для решения задачи служить формула для частоты колебаний в электрическом контуре:
[{omega }_0=frac{1}{sqrt{LC}}left(1.1right).]
Элементом, обладающим индукцией в нашем контуре является соленоид. Индуктивность соленоида равна:
[L=mu {mu }_0frac{N^2S_1}{l}left(1.2right),]
где $mu =1$, ${mu }_0$ – магнитная постоянная.
Емкость плоского конденсатора вычислим по формуле:
[C=frac{varepsilon {varepsilon }_{0 }S_2}{d}left(1.3right),]
где $varepsilon =1$, ${varepsilon }_{0 }$ – электрическая постоянная.
Правые части выражений (1.2) и (1.3) подставим в (1.1) вместо соответствующих величин:
[{omega }_0=frac{1}{sqrt{LC}}=sqrt{frac{ld}{{{mu }_0{varepsilon }_{0 }N}^2S_1S_2}}left(1.4right).]
Ответ. ${omega }_0=sqrt{frac{ld}{{{mu }_0{varepsilon }_{0 }N}^2S_1S_2}}$
Пример 2
Задание. Чему равна циклическая частота гармонических колебаний материальной точки, если амплитуда скорости точки равна ${dot{x}}_{max}=v_0$, амплитуда ее ускорения: ${ddot{x}}_{max}=a_0$? Начальная фаза колебаний равна нулю.
Решение. Из контекста условий задачи понятно, что колебания совершает координата $x$, поэтому уравнение колебаний (в общем виде) запишем как:
[xleft(tright)=A{cos left({omega }_0t+{varphi }_0right)= }A{cos left({omega }_0tright) }left(2.1right),]
По условию задачи ${varphi }_0$=0. Тогда уравнение для скорости изменения параметра $xleft(tright)$ имеет вид:
[dot{x}left(tright)=vleft(tright)=-A{omega }_0{sin left({omega }_0tright)left(2.2right). }]
Из выражения (2.2) следует, что:
[{dot{x}}_{max}=v_0=A{omega }_0left(2.3right).]
Уравнение для ускорения материальной точки, используя (2.2) запишем как:
[ddot{x}left(tright)=aleft(tright)=-A{{omega }_0}^2{cos left({omega }_0tright)left(2.4right). }]
Получаем, что:
[{ddot{x}}_{max}=A{{omega }_0}^2=a_0 left(2.5right).]
Мы получили следующую систему из двух уравнений с двумя неизвестными:
[left{ begin{array}{c}
v_0=A{omega }_0 \
a_0=A{{omega }_0}^2 end{array}
right.left(2.6right).]
Найдем отношение $frac{a_0}{v_0}$, получим:
[frac{a_0}{v_0}={omega }_0.]
Ответ. ${omega }_0=frac{a_0}{v_0}$
Читать дальше: формула частоты колебаний пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.

Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):

Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):

Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.

Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
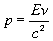
Волна называется плоской, если ее волновые повеpхности пpедставляют собой паpаллельные дpуг дpугу плоскости, пеpпендикуляpные фазовой скоpости волны (pис.1.3). Следовательно, лучи плоской волны – суть паpаллельные пpямые.
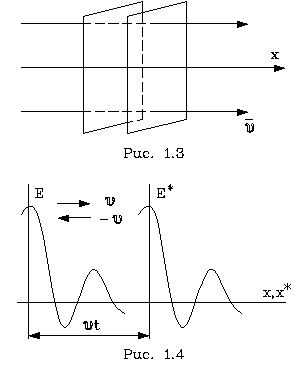
Если кооpдинатную ось х напpавить вдоль фазовой скоpости волны v, то вектоp Е, описывающий волну, будет пpедставлять собой функцию только двух пеpеменных: кооpдинаты х и вpемени t (E = f(x,t)).
Рассмотpим плоскую волну, пpофиль котоpой по оси х с течением вpемени не изменяется. Такая волна называется волной без диспеpсии.
На pис.1.4 изобpажены два пpофиля волны, относящиеся к pазличным моментам вpемени: начальному (t0 = 0) и пpоизвольному (t).
В волне без диспеpсии пpофиль волны только пеpемещается, но не искажается. Если так, то нетpудно сообpазить, как выглядит функция f(x,t) (уpавнение волны). Если в начальный момент вpемени вектоp Е изобpажался некотоpой функцией кооpдинаты f(x,0), то в момент вpемени t он будет изобpажаться той же функцией, но только не кооpдинаты х, а мещенной кооpдинаты х*.
Из pис.1.4 видно, что кооpдинаты х и х* связаны между собой пpостой зависимостью:
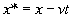
Таким обpазом, уpавнение плоской волны без диспеpсии имеет следующий вид:
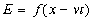 или
или 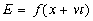
Здесь v есть фазовая скоpость волны, а вид функции f может быть любым. Наиболее интеpесными являются пеpиодические синусоидальные волны, когда функция f пpедставляет собой синус или косинус аpгумента (синус и косинус отличаются дpуг от дpуга только сдвигом по фазе на 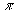 /2). В качестве аpгумента синуса не м ожет быть пpосто (x-vt), т.к. эта величина pазмеpная, тогда как аpгумент синуса должен быть безpазмеpным. Поэтому синусоидальная волна описывается следующим уpавнением:
/2). В качестве аpгумента синуса не м ожет быть пpосто (x-vt), т.к. эта величина pазмеpная, тогда как аpгумент синуса должен быть безpазмеpным. Поэтому синусоидальная волна описывается следующим уpавнением:
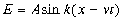
А называется амплитудой волны, k – волновым числом. Смысл амплитуды ясен, а каков смысл волнового числа? Рассмотpим волну в момент вpемени t0 = 0. Она описывается уpавнением E = Asinkx. Обозначим чеpез 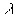 длину волны, т.е. пеpиод волны в пpостpанстве (чеpез отpезок длины фаза повтоpяется). Пеpиод синуса pавен 2
длину волны, т.е. пеpиод волны в пpостpанстве (чеpез отpезок длины фаза повтоpяется). Пеpиод синуса pавен 2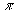 . Следовательно, можно записать, что 2
. Следовательно, можно записать, что 2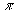 = k
= k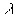 . Отсюда:
. Отсюда:
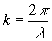
Итак, волновое число пpедставляет собой число длин волн, укладывающихся на отpезке 2 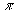 метpов. В каждой точке пpостpанства вектоp Е совеpшает гаpмонические колебания. Найдем частоту этих колебаний. С этой целью фиксиpуем точку пpостpанства и pассмотpим Е как функцию вpемени: E = Asin(kx0-kvt). Но гаpмонические колебания описываются функцией sin(
метpов. В каждой точке пpостpанства вектоp Е совеpшает гаpмонические колебания. Найдем частоту этих колебаний. С этой целью фиксиpуем точку пpостpанства и pассмотpим Е как функцию вpемени: E = Asin(kx0-kvt). Но гаpмонические колебания описываются функцией sin(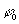 – wt). Таким обpазом, мы пpиходим к заключению, что циклическая частота волны связана с волновым числом зависимостью
– wt). Таким обpазом, мы пpиходим к заключению, что циклическая частота волны связана с волновым числом зависимостью
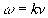
Если учесть, что волновое число связано с длиной волны (1.4), и вместо циклической частоты ввести обыкновенную частоту (как число колебаний в секунду 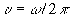 ), то легко найдем фоpмулу связи длины волны с ее частотой:
), то легко найдем фоpмулу связи длины волны с ее частотой:
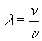
Длина волны обpатно пpопоpциональна ее частоте.
Электpомагнитные волны (как, впpочем, и звуковые) подчиняются пpинципу супеpпозиции, суть котоpого заключается в следующем. Пpедставим два или несколько источников волн. Пусть источники pаботают независимо дpуг от дpуга. Каждый источник испускает свои волны, и в пpостpанстве, окpужающем источники, обpазуется сложное волновое поле.
Пpинцип супеpпозиции волн гласит, что волны от pазличных источников не взаимодействуют дpуг с дpугом и что сложное волновое поле от двух или большего числа источников находится путем геометpического сложения волн от отдельных источников, т.е.
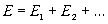
Это очень важный пpинцип. Он позволяет не только складывать волны, но и pаскладывать их, напpимеp, на независимые синусоидальные волны. Это означает, что любую волну, т.е. волну пpоизвольного пpофиля, всегда можно пpедставить как сумму синусоидальных волн с pазличными амплитудами, с pазличными фазовыми скоpостями, с pазличными частотами и с pазличными начальными фазами. (Кстати, аpгумент синуса полностью опpеделяет вектоp Е пpи условии, если известна его амплитуда. Поэтому аpгумент синуса в уpавнении синусоидальной волны называют фазой синусоидальной волны. Таким обpазом, пpоизвольную (даже не обязательно плоскую) волну всегда можно пpедставить в виде суммы плоских волн, движущихся в pазличных напpавлениях и имеющих pазные частоты. Этой возможностью pазложения волн шиpоко пользуются во всей теоpии электpомагнитных волн, в частности в оптике.
Рассмотpим плоскую волну в виде коpоткого сигнала (см. pис. 1.1). Если такую волну pазложить по синусоидальным волнам, то оказывается, что частоты ее составляющих лежат в некотоpом интеpвале (непpеpывно его заполняя). Сигнал составляет как бы гpуппу или пакет волн (такое название сигнала и пpинято в оптике). Допустим, что pассматpиваемая волна является волной с диспеpсией. Это означает, что каждая синусоидальная ее составляющая имеет свою фазовую скоpость. Одни составляющие будут обгонять дpугие. Это пpиведет к тому, что гpуппа волн пpи пеpемещении будет pасплываться. В этом случае для хаpактеpистики скоpости волны вводится гpупповая скоpость. Как она опpеделяется? Допустим, что на интеpвал частот 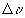 пpиходится соответственно интеpвал волновых чисел
пpиходится соответственно интеpвал волновых чисел 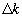 . Тогда гpупповой скоpостью называют oтношение интеpвала
. Тогда гpупповой скоpостью называют oтношение интеpвала 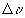 к интеpвалу
к интеpвалу 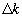 , т.е.
, т.е.
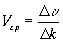
Cледовательно, если волна не имеет диспеpсии и все ее составляющие “бегут” с одной и той же скоpостью, то 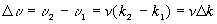 . В этом случае гpупповая скоpость совпадает с фазовой, что имеет место, если электpомагнитная волна pаспpостpаняется в вакууме.
. В этом случае гpупповая скоpость совпадает с фазовой, что имеет место, если электpомагнитная волна pаспpостpаняется в вакууме.
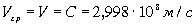
Мы будем изучать электpомагнитные волны, излучаемые атомами (световые волны). Что хаpактеpно для атомов и молекул как излучателей света? Каждый вид атомов излучает свет вполне опpеделенных частот. Набоp частот света, излучаемого атомом (или молекулой), называется его спектpом. Однако если атомы связаны между собой, обpазуя твеpдое тело или жидкость, то их спектpы в сильной степени тpансфоpмиpуются и пpиходится говоpить не о спектpах отдельных атомов, а о спектpах всего тела. Спектpы твеpдых тел и жидкостей почти сплошные, т.е. сплошь заполняют целые интеpвалы частот, тогда как спектpы газов, где атомы большее вpемя пpебывают вне взаимодействия дpуг с дpугом, – дискpетные (линейчатые) и хаpaктеpизуют спектpы атомов как таковых.
Атомы газа (твеpдого тела, жидкости) излучают свет независимо дpуг от дpуга и не непpеpывно, а лишь в течение малых пpомежутков вpемени. Последнее – понятно. Атом, излучая, теpяет энеpгию. Его энеpгия, запасенная на излучение, конечна. Если атом эту энеpгию излучил, то, чтобы вновь излучать, он должен получить энеpгию извне, он должен, как говоpят, вновь быть возбужден. Очевидно заpанее, до всяких теоpий, что атомы излучают световые волны коpоткими очеpедями, каждый pаз пpедваpительно поглощая энеpгию извне.
Эти элементаpные сообpажения свидетельствуют о том, что свет от естественных источников всегда сложен. Он состоит из множества более или менее коpотких пакетов волн pазличных частот, pазличных напpавлений движения, pазличных фаз, волн, наложенных дpуг на дpуга. Коpоче говоpя, свет от естественных источников, во всех отношениях непpавильный, сложный.
Однако существуют сpавнительно пpостые способы из сложной световой волны выделять волны опpеделенного напpавления (плоские волны) и опpеделенной частоты. Волны опpеделенной частоты называются монохpоматическими. Но монохpоматические волны, выделенные из естественного света, если они даже и движутся в одном напpавлении (плоские волны), еще не пpедставляют собой синусоидальные волны. Эти волны состоят из наложенных дpуг на дpуга кусков синусоид, беспоpядочно идущих от отдельных атомов. В пpостpанстве такой свет отнюдь не согласован по фазе. Это обстоятельство существенно пpи pазбоpе таких волновых явлений, как интеpфеpенция, дифpакция и поляpизация света.
Техническая акустика и защита от шума. Лекция №2 Уравнение плоской синусоидальной волны.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
Техническая акустика и защита от шума
Лекция №2
Уравнение плоской синусоидальной волны. Волновое число.
Уравнение сферической волны
Диапазоны частот акустических волн.
Понятия шума, основного тона, обертона, тембра музыкальных звуков.
Громкость звука, порог слышимости, порог осязания.
Уровень интенсивности акустических волн. Ультразвук.
! ! ! Волна называется плоской, если ее волновые повеpхности пpедставляют собой паpаллельные дpуг дpугу плоскости, пеpпендикуляpные фазовой скоpости волны
6 Уравнение плоской синусоидальной волны. Волновое число
S зависит не только от времени, но и от
координаты.
v – скорость распространения волны, А – амплитуда волны, аргумент синуса – фаза волны, 𝜑 0 – начальная фаза колебаний в точке х = 0, 𝜔 – частота (циклическая) волны.
Уравнение имеет вид:
Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ 𝜆=𝜈𝑇.
Введем ВОЛНОВОЕ ЧИСЛО k, равное:
𝑘= 2𝜋 𝜆
Тогда уравнение плоской волны примет вид:
𝑆=𝐴∙sin 𝜔𝑡−𝑘𝑥+ 𝜑 0
http://koi.tspu.ru/waves/ch4_2.htm
При записи уравнения сферической волны учитывается, что амплитуда волны убывает с расстоянием от источника:
𝑆= 𝐴 0 𝑟 sin(𝜔𝑡− 𝑘∙𝑟 + 𝜑 0 )
𝑘 − ВОЛНОВОЙ ВЕКТОР, модуль которого 𝑘 равен волновому числу, а направление совпадает с направлением луча распространения волны.
7 Уравнение сферической волны
http://edu.dvgups.ru/METDOC/ENF/PHIZIK/PHIZIK/LAB_RAB/SKOROST_ZVUKA/MAIN.HTM
Инфразвуковой — ниже 20 Гц.
Звуковой — от 20 Гц до 20 кГц (в него полностью укладывается диапазон средне статистических людей слышимых человеческим ухом частот). Более 20 кГц человеческое ухо может услышать диапазон. Изначально с рождения ребёнок слышит ультразвук с частотой более 20 кГц, но после в возрастом происходит уплотнение стен перепонок.
Ультразвуковой — от 20 кГц до 100кГц.
Гиперзвуковой — свыше 100кГц.
8 Диапазоны частот акустических волн
Шкала диапазона частот
Шум — беспорядочные колебания различной физической природы, отличающиеся сложностью временной спектральной структуры.
Шум – одновременное сочетание звуков различной частоты.
9 Понятия шума, основного тона, обертона, тембра музыкальных звуков.
Чистый тон – это звук , совершающий гармонические колебания одинаковой частоты.
Звуки разных источников (например разные музыкальные инструменты, человеческий голос, звуки посторонних предметов и т.д ) вместе составляют совокупность гармонических колебаний разных частот.
Основной частотой называется самая маленькая частота этого многосоставного звука, а звук который ей соответствует и он определенной высоты называется основным тоном.
ОБЕРТОН (от нем. Oberton – высокий тон, высокий звук) – синусоидальная составляющая звуковых колебаний сложной формы с частотой, более высокой, чем основной тон.
Любое периодическое колебание можно представить как сумму основного тона и обертонов, причём частоты и амплитуды этих обертонов определяются как физическими свойствами колебательной системы, так и способом её возбуждения.
Если частоты всех обертонов – целые кратные основной частоте, то такие обертоны называют гармоническими или гармониками. Если же частоты зависят от основной частоты более сложным образом, то говорят о негармонических обертонах. В этом случае представление периодических колебания в виде суммы гармоник будет приближённым, но тем более точным, чем большее число гармоник взято.
Если частота основного тона f (первая гармоника), то частота второй гармоники равна 2f или близка к этому значению, частота третьей 3f и т. д. Состав и количество обертонов сложного звука определяет его качественную окраску, или тембр звука.
Те́мбр (фр. timbre — «колокольчик», «метка», «отличительный знак») — колористическая (обертоновая) окраска звука; одна из специфических характеристик музыкального звука (наряду с его высотой, громкостью и длительностью).
По тембрам отличают звуки одинаковой высоты и громкости, но исполненные на различных инструментах, разными голосами, или же на одном инструменте, но разными способами, штрихами и т. п.
При восприятии тембров обычно возникают различные ассоциации: тембральную специфику звука сравнивают с органолептическими ощущениями от тех или иных предметов и явлений, например, звуки называют яркими, блестящими, матовыми,тёплыми, холодными, глубокими, полными, резкими, насыщенными, сочными, металлическими, стеклянными; применяются и собственно слуховые определения (например, звонкие, глухие, шумные).
Человек номинально слышит звуки в диапазоне от 16 до 20 000 Гц.
Диапазон громкости воспринимаемых звуков огромен. Но барабанная перепонка в ухе чувствительна только к изменению давления. Уровень давления звука принято измерять в децибелах (дБ).
10 Громкость звука, порог слышимости, порог осязания
Нижний порог слышимости определён как 0 дБ (20 микропаскаль) 20∙10-5 Па, а определение верхнего предела слышимости относится скорее к порогу дискомфорта и далее — к нарушению слуха, контузии и т. д. Этот предел зависит от того, как долго по времени мы слушаем звук. Ухо способно переносить кратковременное повышение громкости до 120 дБ без последствий, но долговременное восприятие звуков громкостью более 80 дБ может вызвать потерю слуха.
Минимальный порог, при котором звук остаётся слышен, зависит от частоты. График этой зависимости получил название абсолютный порог слышимости. В среднем, он имеет участок наибольшей чувствительности в диапазоне от 1 кГц до 5 кГц, хотя с возрастом чувствительность понижается в диапазоне выше 2 кГц.
Человеческий слух во многом подобен спектральному анализатору, то есть ухо распознаёт спектральный состав звуковых волн без анализа фазы волны. В реальности фазовая информация распознаётся и очень важна для направленного восприятия звука, но эту функцию выполняют ответственные за обработку звука отделы головного мозга.
Разница между фазами звуковых волн, приходящих на правое и левое ухо, позволяет определять направление на источник звука, причём информация о разности фаз имеет первостепенное значение, в отличие от изменения громкости звука воспринимаемого разными ушами.
Порогом осязания ( порогом болевого ощущения) называется наибольшая интенсивность звуковой волны, при которой восприятие звука не вызывает болевого ощущения. Порог осязания зависит от частоты звука, изменяясь от 0,1 Вт/м2 при 6000 Гц до 10 Вт/м2 при низких и высоких частотах.
Интенсивность звука — скалярная физическая величина, характеризующая мощность, переносимую звуковой волной в направлении распространения. Количественно интенсивность звука равна среднему по времени потоку звуковой энергии через единичную площадку, расположенную перпендикулярно направлению распространения звука:
𝐼= 1 𝑇 𝑡 𝑡+𝑇 𝑑𝑃 𝑑𝑆 𝑑𝑡
11. Уровень интенсивности акустических волн, интенсивность. Ультразвук
Звуки способны сильно различаются по интенсивности, потому удобнее рассматривать интенсивность как логарифмическую величину и измерять в децибелах (дБ). Логарифмическая величина интенсивности представляет собой логарифм отношения рассматриваемого значения величины к ее значению, принимаемому за исходное.
Уровень интенсивности I по отношению к некоторой условно выбранной интенсивности I0 равен:
𝛽=10𝑙𝑔 𝐼 𝐼 0 , дБ
Таким образом, один звук, превышающий другой по уровню интенсивности на 20 дБ, превышает его в 100 раз по интенсивности.
Ультразву́к — упругие колебания в среде с частотой за пределом слышимости человека. Обычно под ультразвуком понимают частоты выше 20 000 Гц.
Частота ультразвуковых колебаний, применяемых в промышленности и биологии, лежит в диапазоне от нескольких десятков КГц до единиц МГц. Высокочастотные колебания обычно создают с помощью пьезокерамических преобразователей, например, из титанита бария. В тех случаях, когда основное значение имеет мощность ультразвуковых колебаний, обычно используются механические источники ультразвука. Первоначально все ультразвуковые волны получали механическим путем (камертоны, свистки, сирены).
В природе УЗ встречается как в качестве компонентов многих естественных шумов (в шуме ветра, водопада, дождя, в шуме гальки, перекатываемой морским прибоем, в звуках, сопровождающих грозовые разряды, и т. д.), так и среди звуков животного мира. Некоторые животные пользуются ультразвуковыми волнами для обнаружения препятствий, ориентировки в пространстве и общения (киты, дельфины, летучие мыши, грызуны).
В медицине (УЗИ)
Применение ультразвука в косметологии
Резка и сварка металла
Приготовление гомогенных смесей
В биологии
Чистка в промышленности и быту
Применение ультразвука в эхолокации
Применение ультразвука в расходометрии
В дефектоскопии
В гальванотехнике
Свисто́к Га́льтона — акустический излучатель, работающий по принципу свистка (рассечение воздушного потока клином, расположенным рядом с акустическим резонатором). Первое изобретенное устройство для получения ультразвука.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 945 человек из 80 регионов
Курс повышения квалификации
Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Курс добавлен 31.01.2022
- Сейчас обучается 25 человек из 16 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 40 человек из 24 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 591 288 материалов в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 29.12.2020
- 86
- 3
- 29.12.2020
- 77
- 0
- 29.12.2020
- 84
- 0
- 29.12.2020
- 96
- 1
- 29.12.2020
- 98
- 3
- 29.12.2020
- 91
- 0
- 29.12.2020
- 147
- 1
- 29.12.2020
- 206
- 7
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.12.2020 260
- PPTX 1018.8 кбайт
- 0 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Паршина Кира Максимовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 24537
- Всего материалов: 230
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие
Время чтения: 15 минут
В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей
Время чтения: 1 минута
Курские власти перевели на дистант школьников в районах на границе с Украиной
Время чтения: 1 минута
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
В приграничных пунктах Брянской области на день приостановили занятия в школах
Время чтения: 0 минут
Студенты российских вузов смогут получить 1 млн рублей на создание стартапов
Время чтения: 3 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Циклическая частота из уравнения плоской синусоидальной волны
4.1. Механические колебания.
4.2. Электрические колебания.
4.3. Упругие волны. Акустика.
4.4. Электромагнитные волны. Излучение.
_______________________________________________________________________________________________
4.1. Механические колебания.
4.1.1. Гармонические колебания.
4.1. 1 -1. Частица совершает гармоническое колебание с амплитудой А и периодом Т = 12 с. Найти время t ₁ , за которое смещение частицы изменяется от 0 до А/2.
Решение:
Т = 12 с
х(0) = 0
х( t ₁) = А/2 (1)
t ₁ – ?
Так как начальное положение частицы х(0) = 0, то частица колеблется по закону синуса с начальной фазой ϕ ₀ = 0:
x = Asin ( ωt + ϕ ₀) или
x = Asinωt , (2)
где ω = 2 π / T – круговая частота.
С учётом условия (1), запишем (2) в виде:
х( t ₁) = Asin ( ωt ₁); А/2 = Asin ( (2 π / T ) t ₁ ); 1/2 = sin (2 πt ₁/ T ); 2 πt ₁/ T = π /6. Отсюда
t ₁ = T /12.
t₁ = 12/12 = 1 с.
Ответ: t₁ = T/12 = 1 c.
4.1.1-2. Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.

где − I момент инерции диска относительно оси вращения, проходящей через точку подвеса А (см. рис.); x = AO = R − расстояние от точки подвеса до центра тяжести О диска; m − масса диска; g = 9,8 м/с² − ускорение свободного падения.
Момент инерции I ₀ диска относительно оси симметрии диска:
I ₀ = mR ²/2.
По теореме Штейнера:
I = I₀ + mR². Имеем
I = mR²/2 + mR² = 3mR²/2. Тогда по (1)

Решение:
r ( t ) = A ( icosωt + jsinωt ) (1)
A = 0,5 м
ω = 5 с⁻¹
v − ?
an − ?
Представим (1) в виде:
r ( t ) = iAcosωt + jAsinωt (1*)
Радиус вектор r ( t ) точки: r ( t ) = ix + jy , где x , y − проекции радиус вектора соответственно на оси OX и OY ; i , j − единичные векторы (орты), направленные соответственно по оси OX и OY . Тогда (1*) примет вид
ix + jy = iAcosωt + jAsinωt ,
отсюда получим два уравнения
x = Acosωt , (*)
y = Asinωt . (**)
Возведём их в квадрат
x ² = A ² cos ² ωt ,
y ² = A ² sin ² ωt .
Сложим эти уравнения
x ² + y ² = A ² cos ² ωt + A ² sin ² ωt или x ² + y ² = A ²( cos ² ωt + sin ² ωt ). Отсюда, т.к. cos ² ωt + sin ² ωt = 1, получим уравнение траектории движения точки
x ² + y ² = A ². (2)
Уравнение (2) − это уравнение окружности радиусом R = A = 0,5 м с центром в начале координат (см. рис.).
Найдём проекции скорости v x и vy . Для этого продифференцируем x и y из (*) и (**) по времени t :
vx = xt ʹ = ( Acosωt ) t ʹ = – Aωsinωt ;
vy = yt ʹ = ( Asinωt ) t ʹ = Aωcosωt .
Тогда квадрат скорости
v ² = vx ² + vy ² или v ² = (- Aωsinωt )² + ( Aωcosωt )² или v ² = A ² ω ²( sin ² ωt + cos ² ωt ) или v ² = A ² ω ². Отсюда модуль скорости v :
v = Aω . (3)
v = 0,5·5 = 2,5 м/с².
Модуль нормального ускорения an : an = v ²/ R или, с учётом (3) и R = A , получим an = A ² ω ²/ A или
an = Aω ².
an = 0,5·5² = 12,5 м/с².
Ответ: траектория − окружность радиусом R = A = 0,5 м с центром в начале координат, v = Aω = 2,5 м/с², an = Aω ² = 12,5 м/с².
_______________________________________________________________________________________________
4.1.2. Свободные затухающие колебания.
4.1.2-1. Амплитуда затухающих колебаний уменьшилась в n = 100 за 15 с. Чему равен коэффициент затухания β ?
Решение:
t = 15 c
n = 100
A = A ₀/ n (*)
β – ?
Зависимость амплитуды А затухающих колебаний от времени t :
A = A ₀ e – β t , (1)
где A ₀ – начальная амплитуда; β – коэффициент затухания.
Имеем из (1) и (*):
A ₀/ n = A ₀ e – β t ; 1/ n = e – β t ; e β t = n ; βt = ln ( n ) отсюда
β = ln ( n )/ t .
β = ln(100)/15 = 0,307 1/c.
Ответ: β = ln(n)/t = 0,307 1/c.
4.1.2-2. Найти логарифмический декремент затухания тонкого стержня, подвешенного за один из его концов, если за промежуток времени t = 5 мин его полная механическая энергия уменьшилась в n = 4 · 10 ² раз. Длина стержня L = 50 см.
Решение:
t = 5 мин = 300 с
n = 400
L = 0,5 м
λ − ?
В данном случае стержень − это физический маятник.
Логарифмический декремент затухания λ
λ = βT , (1)
где β – коэффициент затухания, T − период колебаний стержня.
1. Найдём коэффициент затухания β .
Связь частот ω и ω₀:
ω² = ω₀² – β². (2)
ω – частота затухающих колебаний; ω ₀ – собственная частота колебаний.
Зависимость от времени t полной механической энергии Е физического маятника:
Е = E ₀ e -2 βt ,
где E ₀ – начальная (при t = 0) полная механическая энергия.
Отсюда имеем
n = Е ₀/ Е = Е ₀/( E ₀ e -2 βt ) = 1 /( e -2 βt ) = e 2 βt .
Получили n = e 2 βt . Прологарифмируем это равенство Ln ( n ) = 2 βt . Отсюда
β = Ln ( n )/(2 t ). (3)
2. Найдём период Т затухающих колебаний.
Оценим коэффициент β 2 по (3).
β = Ln (400)/(2 · 300) = 0,009986, отсюда
β ² = (0,009986)² ≈ 0,0000997.
Собственная частота колебаний физического маятника:
.jpg)
Подставим в (1) найденные β из (3) и Т из (4**) и, после упрощения, получим
.jpg)
.jpg)
.jpg)
4.1.2-3. Логарифмический декремент затухания тела, колеблющегося с частотой 50 Гц, равен 0,02. Определите: время, за которое амплитуда колебаний тела уменьшится в 20 раз; число колебаний тела, чтобы произошло подобное уменьшение амплитуды.
Решение:
ν = 50 Гц
λ = 0,02
n = 20
t − ?
N − ?
1. Пусть β – коэффициент затухания; T = 1/ ν – период, ν – частота колебаний. Логарифмический декремент затухания λ :
λ = βT или λ = β / ν , отсюда
β = λν . (1)
Амплитуда А затухающих колебаний
A = A ₀· e – βt ,
где A ₀ − начальная амплитуда (при t = 0).
Подставим сюда из условия задачи A = A ₀/ n :
A ₀/ n = A ₀· e – βt ,
отсюда e βt = n и, после логарифмирования, βt = Ln ( n ), отсюда
t = ( Ln ( n ) )/ β и, с учётом (1),
t = ( Ln ( n ) )/( λν ). (2)
2. Число колебаний N за время t :
N = t / T = tν = ( и, с учётом (2), ) = ν ( Ln ( n ) )/( λν ) или
N = ( Ln ( n ) )/ λ . (3)
3. Вычисления по формулам (2) и (3):
t = ( Ln (20) )/(0,02·50) ≈ 3 с.
N = ( Ln (20) )/0,02 ≈ 150.
Ответ: t = ( Ln ( n ) )/( λν ) ≈ 3 с; N = ( Ln ( n ) )/ λ ≈ 150.
4.1.2-4. Составьте дифференциальное уравнение гармонических свободных затухающих крутильных колебаний механической системы.
Решение:
Пусть система (например, тонкий однородный диск, подвешенный в горизонтальном положении к упругой нити) совершает крутильные колебания относительно закреплённой оси Z (ось нити). Пусть на диск действует упругая сила, проекция момента которой на ось Z равна
Mz = – kϕ , (1)
где k − постоянная, ϕ − угол поворота из положения равновесия. Знак “минус” указывает на то, что при отклонении системы на угол ϕ , момент упругой силы возвращает систему к положению равновесия. Поместим диск в вязкую среду ( например, жидкость ). Момент силы сопротивления Mc , действующий на диск, пропорционален угловой скорости ϕ ʹ:
M c = – ηϕ ʹ, (2)
где η − постоянная.
Уравнение динамики вращательного движения диска имеет вид
Iϕ ʹʹ = Mz + M c , (3)
где I – момент инерции диска относительно оси вращения.
С учётом (1) и (2), уравнение (3) примет вид Iϕ ʹʹ = – kϕ – ηϕ ʹ, отсюда
ϕ ʹʹ + ( η / I ) ϕ ʹ + ( k / I ) ϕ = 0.
Применив обозначения 2 β = η / I , ω ₀² = k / I , перепишем последнее уравнение:
ϕ ʹʹ + 2 βϕ ʹ + ω ₀² ϕ = 0.
Это дифференциальное уравнение описывает затухающие крутильные колебания механической системы.
Ответ: ϕ ʹʹ + 2 βϕ ʹ + ω ₀² ϕ = 0.
4.1.2-5. Найти добротность Q осциллятора, у которого отношение резонансной частоты ωрез к частоте затухающих колебаний ω равно η.
Решение:
ωрез/ω = η (*)
Q − ?
Пусть β − коэффициент затухания, ω₀ − собственная частота колебаний, T = 2π/ω − период затухающих колебаний, λ = βT = 2πβ/ω − логарифмический декремент затухания. Тогда добротность Q:
Q = π/λ = π/(2πβ/ω), или
Q = ω/(2β). (1)
Связь частот ω и ω₀:
ω² = ω₀² – β². (2)
Формула для резонансной частоты ωрез:
ωрез² = ω₀² – 2β². (3)
Из (2) вычтем (3)
ω² – ωрез² = (ω₀² – β²) – (ω₀² – 2β²), или
ω² – ωрез² = ω₀² – β² – ω₀² + 2β², или
ω² – ωрез² = β². (**)
С учётом условия (*) имеем ωрез = ωη. Тогда (**) примет вид
ω² – ω²η² = β², или
ω²(1 – η²) = β², отсюда
.jpg)
.jpg)
.jpg)
___________________________________________________________________________________
4.1.3. Вынужденные колебания. Резонанс.
4.1.3-1. Осциллятор массы m движется по закону x = Asinωt под действием вынуждающей силы Fₓ = F₀cosωt. Найти коэффициент затухания β осциллятора.
Решение:
m,
x = Asinωt,
Fₓ = F₀cosωt,
β − ?
Установившееся смещение х(t) осциллятора при вынужденных колебаниях:
x = Acos(ωt – ϕ), (1)
ω₀ − собственная частота колебаний осциллятора,
f₀ = F₀/m. (*)
Так как по условию смещение х(t) осциллятора x = Asinωt, то из (1) следует: ϕ = π/2
(т. к. cos(ωt – π/2) = sinωt). Тогда из (3) имеем:
%20%D0%A4%D0%98%D0%97.jpg)
где f₀ = F ₀/ m , m − масса осциллятора , β − коэффициент затухания, ω₀ − собственная частота колебаний, ω − частота вынужденных колебаний.
При постоянной амплитуде вынуждающей силы F ₀ (и, следовательно, постоянной f ₀) из (*) при двух разных частотах ω₁ и ω₂ получаем две амплитуды А₁ и А₂ вынужденных колебаний:
%20%D0%A4%D0%98%D0%97.jpg)
4.2. Электрические колебания.
4.2-1. Небольшая магнитная стрелка совершает малые колебания вокруг оси, перпендикулярной направлению внешнего магнитного поля. При изменении индукции этого поля период колебаний стрелки уменьшился в η = 5 раз. Во сколько раз и как изменилась индукция поля? Затухание колебаний пренебрежимо мало.
Решение:
T ₁/ T ₂ = η = 5
B ₂/ B ₁ − ?
Момент сил М, действующий на стрелку со стороны магнитного поля
М = [ B · P m ], где P m − вектор магнитного момента стрелки.
Модуль момента сил
М = B · P m · sinϕ , где ϕ – угол между векторами B и P m .
При малых колебаниях угол ϕ очень мал и sinϕ ≈ ϕ . Тогда
М = B · P m · ϕ .
При повороте стрелки на угол ϕ возникает момент сил М , стремящийся вернуть стрелку в положение равновесия, т.е. М = – B · P m · ϕ . Если J – момент инерции стрелки относительно оси вращения, то основное уравнение динамики вращательного движения примет вид
Jϕ ’’ = M или Jϕ ’’ = – B · P m · ϕ отсюда
ϕ ’’ + ( B · P m / J ) · ϕ = 0. (1)
Если ω – циклическая частота колебаний, то сравнивая (1) с уравнением гармонических колебаний
ϕ ’’ + ω ² ϕ = 0, получим
ω ² = B · P m / J , отсюда
ω = √( B · P m / J ).
Тогда период T колебаний
T = 2 π / ω или
T = 2 π √( J /( B · P m ) ). (2)
На основе (2) для разных B ₁ и B ₂ получим соответствующие T ₁ и T ₂
T ₁ = 2 π √( J /( B ₁ · P m ) )
T ₂ = 2 π √( J /( B ₂ · P m ) ).
Отсюда
T ₁/ T ₂ = √( B ₂/ B ₁) и отсюда
B ₂/ B ₁ = ( T ₁/ T ₂)² = η ² = 25. Итак
B ₂/ B ₁ = η ² = 25.
Ответ: индукция магнитного поля увеличится в η ² = 25 раз.
4.2-2. Индуктивность катушки равна 0,125 Гн. Уравнение колебаний силы ток в ней имеет вид:
i = 0,4 cos (1000 t ), где все величины выражены в системе СИ. Определить амплитуду напряжения на катушке.
Решение:
L = 0,125 Гн
i = 0,4 cos (1000 t ). (1)
Um − ?
Уравнение колебаний силы тока в катушке имеет вид:
i = Imcos ( ωt ). (2)
Из (1) и (2) имеем
Im = 0,4 А − амплитуда силы тока в катушке; ω = 1000 с⁻¹− частота.
Индуктивное сопротивление катушки: X L = ωL .
По закону Ома
Im = Um / X L , отсюда
Um = X L · Im или
Um = ωL · Im .
Um = 1000·0,125·0,4 = 50 В.
Ответ: Um = 50 В.
4.2-3. Электрический колебательный контур состоял из последовательно соединенных катушки с индуктивностью L = 0,8 Гн и конденсатора емкостью С. Сопротивление катушки и соединительных проводов было равно R = 2000 Ом. После того, как часть витков в катушке замкнулась накоротко, индуктивность ее уменьшилась в n = 7 раз, частота собственных колебаний в контуре возросла в k = 3 раза, а коэффициент затухания этих колебаний не изменился. Определить емкость конденсатора .
Решение:
L = 0,8 Гн
R = 2000 Ом
L ₂ = L / n
n = 7
ω ₂ = kω
k = 3
β = const
C − ?
Коэффициент затуханий β = R /(2 L ).
ω и ω ₂ − начальная и конечная частоты собственных колебаний в контуре, где
ω = √( 1/( LC ) – β ² ) = √( 1/( LC ) – R ²/(4 L ²) );
ω ₂ = √( 1/( L ₂ C ) – β ² ) = √( n /( LC ) – R ²/(4 L ²) ).
Возведём в квадрат равенство ω ₂ = kω , получим ω ₂² = k ² ω ² или
n /( LC ) – R ²/(4 L ²) = k ²( 1/( LC ) – R ²/(4 L ²) ), отсюда
C = 4 L ( k ² – n )/( R ²( k ² – 1) ).
C = 4·0,8·(3² – 7)/( 2000²·(3² – 1) ) = 2·10⁻⁷ Ф.
Ответ: C = 4L(k² – n)/( R²(k² – 1) ) = 2·10⁻⁷ Ф.
4.2-4. Ток в колебательном контуре зависит от времени как I = Imsinω₀t, где Im = 9,0 мА, ω₀ = 4,5·10⁴ с⁻¹. Ёмкость конденсатора С = 0,50 мкФ. Найти индуктивность контура и напряжение на конденсаторе в момент t = 0.
Решение:
I = Imsinω₀t (*)
Im = 9·10⁻³ А
ω₀ = 4,5·10⁴ с⁻¹
С = 0,5·10⁻⁶ Ф
L − ?
U(0) − ?
1). Собственная частота ω₀ колебательного контура
%20%D0%A4%D0%98%D0%97.jpg)
1
L = ––––– . (1)
ω₀²C
2). Закон сохранения энергии в колебательном контуре:
LI²/2 + CU²/2 = LIm²/2
или, с учётом (*),
L(Imsinω₀t)²/2 + CU²/2 = LIm²/2.
Отсюда при t = 0 (т.к. sinω₀0 = 0) получим напряжение U(0) = Um на конденсаторе в момент времени t = 0 ( Um − максимальное напряжение ):
CU²(0) = LIm²
и, подставляя сюда L из (1), получим
Im²
CU²(0) = ––––– или
ω₀²C
Im
U(0) = Um = –––– . (2)
ω₀C
Вычисления по формулам (1) и (2 ):
1
L = –––––––––––––––– = 0,001 Гн = 1 мГн.
(4,5·10⁴)²·0,5·10⁻⁶
9·10⁻³
U(0) = Um = –––––––––––––– = 0,4 В.
4,5·10⁴·0,5·10⁻⁶
4.3. Упругие волны. Акустика.
4.3-1. По шнуру слева направо бежит со скоростью v незатухающая гармоническая волна. При этом поперечное смещение точки О шнура изменяется по закону y = Acos ( ωt ). Как зависит от времени смещение точки шнура, находящейся правее точки О на расстоянии x от нее?
Решение:
y = Acos ( ω ( t – x / v ) ).
Ответ: y = Acos ( ω ( t – x / v ) ).
4.3-2. Уравнение плоской звуковой волны имеет вид ξ = 60 cos (1800 t – 5,3 x ). где ξ – в мкм, t – в секундах, х – в метрах .
Найти:
а) отношение амплитуды смещения частиц среды к длине волны;
б) амплитуду колебаний скорости частиц среды и ее отношение к скорости распространения волны;
в) амплитуду колебаний относительной деформации среды и её связь с амплитудой колебаний скорости частиц среды.
а) Уравнение плоской синусоидальной волны
ξ = Acos(ωt – kx). (2)
Из (1) и (2) следует
A = 60 ·10 ⁻ ⁶ м – амплитуда колебаний частиц среды,
ω = 1800 1/с – циклическая частота,
k = 5,3 1/м – волновое число.
k = 2π/λ, отсюда λ = 2π/k. Тогда
A/λ = A/(2π/k) или
A/λ = Ak/(2π).
A / λ = 60 ·10 ⁻ ⁶ · 5,3/(2 · 3,14) = 5,1 ·10 ⁻ ⁵ .
б) Амплитуда колебаний скорости частиц среды
V m = Aω . (*)
Vm = 60 ·10 ⁻ ⁶ · 1800 = 0,11 м/с. = 11 см/с.
Скорость распространения волны
v = ω / k . (3)
Тогда ( см. (*) )
Vm/v = Aω / ( ω / k ) = A k .
Vm/v = A k .
Vm/v = 60 ·10 ⁻ ⁶ · 5,3 = 3,2 ·10 ⁻ ⁴ .
в) Относительную деформацию среды найдём дифференцируя (2) по х:
∂ ξ/ ∂ x = ( Acos(ωt – kx) )x ʹ = – Aksin (ωt – kx).
Ответ: a) A/λ = 5,1 ·10 ⁻ ⁵ ;
б) Vm = 0,11 м/с, Vm/v = 3,2 ·10 ⁻ ⁴;
в) ( ∂ ξ/ ∂ x)m = 3,2 ·10 ⁻ ⁴, V m = v · (d ξ/dx)m , где v = 340 м/с – скорость волны .
4.3-3. Что такое амплитуда колебаний скорости частиц среды?
Решение:
Объясню на простом примере. В озере на воде поплавок. Бросьте в воду камешек, от него во все стороны пойдут волны. Поплавок колеблется на волнах. Скорость колебаний поплавка − это скорость колебаний частиц среды (воды). Максимальная скорость колебаний поплавка − это амплитуда колебаний скорости частиц среды.
Амплитуда колебаний скорости частиц среды
Vm = Aω ( A – амплитуда, ω – циклическая частота).
Скорость распространения волны
v = ω / k ( k – волновое число).
A , ω , k определяют из общего вида уравнения бегущей плоской синусоидальной волны
ξ = Acos ( ωt – kx ).
4.3-4. Точечный изотропный источник испускает звуковые колебания с частотой ν = 1,45 кГц. На расстоянии r₁ = 5 м от источника амплитуда смещения частиц среды А₁ = 50 мкм, а в точке А, находящейся на расстоянии r₂ = 10 м от источника, амплитуда смещения в η = 3 раза меньше А₁. Найти:
а) коэффициент затухания волны γ;
б) амплитуду колебаний скорости частиц среды в точке А.
Решение:
ν = 1450 Гц
r₁ = 5 м
А₁ = 50·10⁻⁶ м
r₂ = 10 м
А₂ = А₁/η (η = 3) (*)
а) γ − ?
б) Vm − ? (в точке А)
От данного точечного источника распространяются сферические волны. Для однородной поглощающей среды уравнение сферической волны:

(1)
где ξ − смещение частиц среды; ω = 2πν − циклическая частота; k − волновое число.
а). Из (1) выпишем амплитуду A смещения частиц среды (множитель перед косинусом):
A = (A₀/r)·e⁻ᵞʳ.
Отсюда для r = r₁ и r = r₂ получаем амплитуды смещения частиц среды A₁ и A₂ соответственно
A ₁ = ( A ₀ / r ₁ ) · e ⁻ ᵞ r₁ , (**)
A ₂ = ( A ₀ / r ₂ ) · e ⁻ ᵞ r ₂ . (***)
Делим (**) на (***) и, с учётом (*), получаем:
η = ( r ₂ / r ₁ ) · e ᵞ ⁽ r ₂ ⁻ r₁ ⁾ отсюда η r ₁ / r ₂ = e ᵞ ⁽ r ₂ ⁻ r₁ ⁾ , отсюда, по определению логарифма, имеем
ln ( η r ₁ / r ₂ ) = γ( r ₂ – r ₁ ), отсюда

γ = ln(3 · 5 /10 )/(10 – 5 ) ≈ 0,08 м ⁻ ¹ .
б). Для нахождения скорости смещения частиц среды V найдём частную производную по времени t от (1):
V = ∂ ξ / ∂ t = ( A ₀ / r ) · e ⁻ ᵞ ʳ ·( – ω sin ( ω t – kr ) ).
С учётом ω = 2πν, имеем
V = – ( 2 π ν A ₀ /r ) ·e ⁻ ᵞ ʳ ·sin ( ω t-kr ) .
Отсюда амплитуда колебаний скорости частиц среды Vm (множитель перед синусом):

4.3-5. Плоская звуковая волна, частота которой 100 Гц и амплитуда 5 мкм, распространяется со скоростью 300 мс в воздухе, плотность которого равна 1 , 2 кгм ³ . Определить интенсивность волны.
Решение:
ν = 100 Гц
а = 5·10⁻⁶ м
V = 300 мс
ρ = 1,2 кгм³
I − ?
Интенсивность I звуковой волны
I = ρ а² ω ² V /2 и т.к. ω = 2 πν , то
I = ρ а²(2 πν )² V /2.
I = 1,2·(5·10⁻⁶)²·(2·3,14·100)²·300/2 = 1,77·10⁻³ Вт/м².
Ответ: I = 1,77·10⁻³ Вт/м².
4.3-6. Стальная струна длины l = 100 см и диаметра d = 0,50 мм даёт основной тон частоты ν = 256 Гц. Найти силу её натяжения.
Решение:
l = 1 м
d = 0,5·10⁻³ м
ν = 256 Гц
ρ = 7800 кг/м³ (плотность стали)
F − ?
В закреплённой с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны. Основной тон частоты ν колебаний струны:
ν = V/2l, отсюда
V = 2lν, (1)
где
.jpg)
− фазовая скорость поперечных волн в струне. Отсюда
F = V²ρ₁ , (2)
где ρ₁ = m/l − линейная плотность струны, m = ρV₀ − масса струны, V₀ = (πd²/4)l = πd²l/4 − объём струны.
Имеем: ρ₁ = ρV₀/l = ρ(πd²l/4)/l = ρπd²/4. Получили
ρ₁ = ρπd²/4. (3)
Подставляя в (2) V из (1) и ρ₁ из (3), получим силу натяжения F струны
F = (2lν)²ρπd²/4, или
F = πρ(lνd)².
F = 3,14·7800· (1·256·0,5·10⁻³)² ≈ 401,3 Н.
Ответ: F = πρ(lνd)² ≈ 401,3 Н.
_______________________________________________________________________________________________
4.4. Электромагнитные волны. Излучение.
4.4-1. Электромагнитная волна с частотой 6 · 10 ¹⁴ Гц распространяется в стекле, показатель преломления которого 1,5. Какова скорость волны в стекле и значение волнового числа?
Решение:
ν = 6 · 10¹⁴ Гц
n = 1,5
c = 3 · 10⁸ м/с (скорость света в вакууме)
V – ? k – ?
Скорость V волны в стекле:
V = c / n . (1)
Длина волны в стекле:
λ = V / ν = c /( nν ). (*)
Волновое число k:
k = 2 π / λ или с учётом (*)
k = 2 πnν /с. (2)
Вычисления по (1), (2)
V = 3 · 10⁸/1,5 = 2 · 10⁸ м/с.
k = 2 · 3,14 · 1,5 · 6 · 10¹⁴/(3 · 10⁸) = 1,88 · 10⁷ (1/м).
Ответ: V = 2 · 10⁸ м/с; k = 1,88 · 10⁷ (1/м).
4.4-2. Определить показатель преломления призмы из парафина , если его диэлектрическая проницаемость Ԑ = 2 и магнитная проницаемость μ = 1.
Решение:
Ԑ = 2
μ = 1
n – ?
Показатель преломления среды
n = C / V . (1)
С – скорость света в вакууме.
Скорость света в среде
V = C /√( Ԑμ ). (2)
Из (1) и (2) имеем
n = √( Ԑμ ).
n = √(2·1) = 1,41.
Ответ: n = 1,41.
___________________________________________________________________________________
[spoiler title=”источники:”]
http://infourok.ru/tehnicheskaya-akustika-i-zashita-ot-shuma-lekciya-2-uravnenie-ploskoj-sinusoidalnoj-volny-4880073.html
http://www.sites.google.com/site/viktortsekunov/services/fizika/4-kolebania-i-volny
[/spoiler]
Циклическая частота колебаний


4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
Любые колебательные процессы в Природе (в том числе и непериодические) могут быть представлены в виде бесконечной суммы простых гармонических колебаний. Поэтому в первую очередь изучаются гармонические колебания. Рассмотрим такую характеристику этих колебаний, как циклическая частота.
Период и частота гармонических колебаний
Впервые гармоническими колебаниями заинтересовались еще античные философы, изучая вопросы музыкальной гармонии. Поэтому простейшие колебания, происходящие по закону круговых функций (синуса или косинуса), называются гармоническими.
Формула гармонических колебаний:
$$x=Asin(omega t+varphi)$$
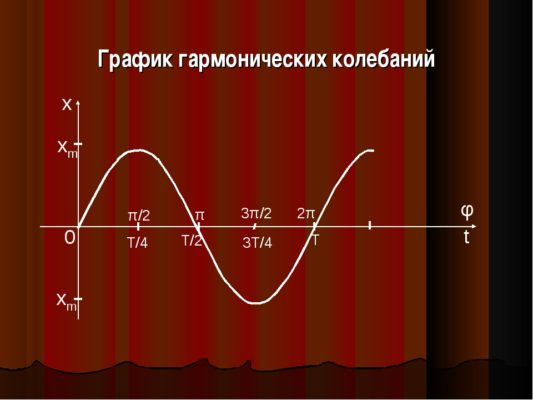
Как можно видеть из графика колебаний (а также из изучения круговых функций в математическом анализе), функции эти регулярно повторяют свои значения. Более того, регулярно повторяется форма графика колебаний. Это свойство функции называется периодичностью. То есть, функция, обладающая периодичностью, имеет равные значения на промежутках, равных своему периоду.
Период обозначается латинской буквой $T$. Однако, физический и математический подход к измерению периода немного различен.
В математике в качестве аргумента круговой функции рассматривается угол поворота вектора, образующего ее, и этот угол удобно измерять в радианах (каждый радиан равен дуге, имеющей длину радиуса). В радианах измеряется и период круговой функции. Для простого синуса или косинуса $T = 2pi$.
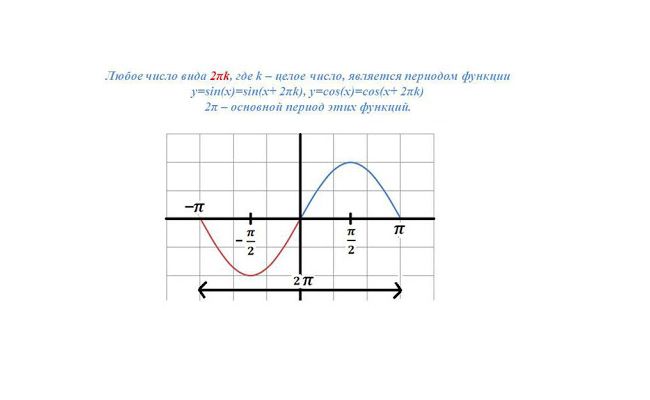
В физике угол поворота менее важен, нередко такой угол даже невозможно указать (например, для колебаний пружинного маятника). Поэтому в физике период измеряется в единицах времени – секундах. Дополнительно это дает возможность ввести специальную характеристику, позволяющую определить «скорость» колебаний – частоту (обозначается греческой буквой $nu$ («ню»).
Если период показывает, за сколько времени совершается одно колебание, то частота показывает, сколько колебаний совершается за одну секунду:
$$nu= {1over T}$$
Частота измеряется в колебаниях в секунду или Герцах (Гц). Один герц – это одно колебание в секунду.
Круговая частота
Как видим, физический и математический подход к описанию периода функций несколько отличаются, и возникает вопрос их связи.
Из приведенной выше формулы гармонических колебаний можно видеть, что она имеет период:
$$T = {2pi over omega}$$
В эту формулу входит параметр $omega$, который обратно пропорционален периоду. При сравнении этой формулы с формулой частоты можно получить:
$$T = {2pi over omega}={1over nu}$$
Или, после упрощений:
$$omega = 2pi nu$$
Таким образом, параметр $omega$ в $2pi$ раз больше частоты колебаний. Поскольку в одном круге $2pi$ радиан, то параметр $omega$ называется «круговой» или «циклической» частотой.
Физический смысл частоты – это количество колебаний, происходящих в системе за единицу времени, а физический смысл круговой частоты – это количество радиан, проходящих функцией, описывающей систему, за единицу времени.

Таким образом, удобный и наглядный параметр частоты может быть легко преобразован для вида, удобного в математических преобразованиях.

Что мы узнали?
Круговая (циклическая) частота – это важный параметр гармонического колебания, удобный в математической обработке функций. Круговая частота обозначает количество радиан, прошедших гармонической функцией за единицу времени. Она прямо пропорциональна обычной частоте.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
А какая ваша оценка?
КОЛЕБАНИЯ И ВОЛНЫ
Колебания
Механические колебания — периодически повторяющиеся изменения положения тела (материальной точки) относительно положения равновесия.
Амплитуда ![]() — максимальное отклонение тела от положения равновесия.
— максимальное отклонение тела от положения равновесия.
Период ![]() — время за которое совершается одно полное колебание. Единица измерения секунда (с).
— время за которое совершается одно полное колебание. Единица измерения секунда (с).
Частота ![]() — количество колебаний
— количество колебаний ![]() в единицу времени
в единицу времени ![]() . Измеряется частота в герцах (Гц) показывающих количество колебаний за секунду. К примеру величина 50 Гц говорит нам о том, что система за одну секунду совершила 50 колебаний.
. Измеряется частота в герцах (Гц) показывающих количество колебаний за секунду. К примеру величина 50 Гц говорит нам о том, что система за одну секунду совершила 50 колебаний.
![]()
Так как период это время за которое совершается одно полное колебание, можно выразить частоту следующим образом:
![]()
Гармонические колебания — колебания происходящие по законам синуса или косинуса (гармоническому закону).
![]()
Фаза колебания (![]() ) — аргумент периодической функции, описывающей колебательный или волновой процесс.
) — аргумент периодической функции, описывающей колебательный или волновой процесс.
Начальная фаза колебания ![]() — значение фазы колебаний в начальный момент времени, т.е. при t = 0.
— значение фазы колебаний в начальный момент времени, т.е. при t = 0.
Циклическая частота ![]() — скалярная физическая величина, мера частоты вращательного или колебательного движения. Единица измерения радиан в секунду (рад/с).
— скалярная физическая величина, мера частоты вращательного или колебательного движения. Единица измерения радиан в секунду (рад/с).
![]()
![]()
Исходя из этого можно записать
![]()
![]()
Свободные колебания — колебания возникающие за счет внутренних сил системы, после того как она была выведена из состояния равновесия.
Собственные частота колебаний — частота свободных колебаний колебательной системы.
Затухающие колебания — колебания в которых происходит постепенное уменьшение амплитуды в результате действия сил сопротивления движению (силы трения, силы сопротивления воздуха..).
Вынужденные колебания — колебания, происходящие под действием внешних периодически изменяющейся сил.
Резонанс — резкое увеличение амплитуды колебания при совпадении собственной частоты колебательной системы, с частотой вынуждающей силы.
Математический маятник
Математический маятник — механическая колебательная система представляющая из себя материальную точку подвешенную на нерастяжимой невесомой нити в поле силы тяжести.
Формула Гюгенса для определения периода колебаний математического маятника. l — длинна маятника.
![Rendered by QuickLaTeX.com [T=2pi sqrt{frac{l}{g}}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-29425af3eec4256686ccf44fde46b3ca_l3.png)
Циклическая частота колебаний математического маятника.
![]()
Пружинный маятник
Пружинный маятник — механическая колебательная система представляющая из себя пружину жесткостью ![]() , с материальной точкой массой
, с материальной точкой массой ![]() на одном конце этой пружины.
на одном конце этой пружины.
![]()
![]()
Колебательный контур
Электромагнитные колебания — периодические изменения напряжённости и магнитной индукции.
Колебательный контур — электрическая цепь, состоящая из конденсатора ёмкостью ![]() и катушки индуктивностью
и катушки индуктивностью ![]() . В этой цепи происходят свободные электромагнитные колебания.
. В этой цепи происходят свободные электромагнитные колебания.
Циклическая частота и период собственных колебаний контура определяются по формуле Томсона:
![]()
![]()
Связь между амплитудными (максимальными) значениями тока в контуре и заряда на конденсаторе:
![]()
Энергия контура:
![]()
Связь между амплитудными (максимальными) значениями тока и напряжения в контуре (закон сохранения энергии в колебательном контуре):
![]()
Переменный ток
Переменный ток — электрический ток периодически меняющий свое направление.
Действующее значение силы переменного тока ![]() равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
![]()
Действующее значение напряжения ![]() в цепи переменного тока равно напряжению постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
в цепи переменного тока равно напряжению постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
![]()
Средняя по времени тепловая мощность переменного тока:
![]()
Емкостное сопротивление ![]() — сопротивление конденсатора в цепи переменного тока. Емкостное сопротивление зависит от частоты переменного тока, чем частота выше, тем сопротивление ниже. Для постоянного тока конденсатор по сути представляет разрыв цепи, по этому для постоянного тока емкостное сопротивление стремиться к бесконечности.
— сопротивление конденсатора в цепи переменного тока. Емкостное сопротивление зависит от частоты переменного тока, чем частота выше, тем сопротивление ниже. Для постоянного тока конденсатор по сути представляет разрыв цепи, по этому для постоянного тока емкостное сопротивление стремиться к бесконечности.
![]()
Где ![]() циклическая частота переменного тока.
циклическая частота переменного тока.
Закон Ома для участков цепи, содержащих емкость:
![]()
Индуктивное сопротивление ![]() — сопротивление катушки индуктивности в цепи переменного тока. Так как изменение тока в цепи приводит к появлению токов самоиндукции противодействующих этому изменению, то увеличение частоты переменного тока приводит к увеличению индукционного сопротивления.
— сопротивление катушки индуктивности в цепи переменного тока. Так как изменение тока в цепи приводит к появлению токов самоиндукции противодействующих этому изменению, то увеличение частоты переменного тока приводит к увеличению индукционного сопротивления.
![]()
Закон Ома для участков цепи, содержащих индуктивность:
![]()
Трансформатор
Трансформатор — электромагнитное устройство, которое используется для передачи и преобразования электрической энергии из одной катушки индуктивности на сердечнике в другую. Частота переменного тока при этом не меняется.
Идеальный трансформатор — трансформатор в котором энергетические потери пренебрежимо малы.
Отношение напряжений на вторичной ![]() и первичной
и первичной ![]() обмотках идеального трансформатора равно отношению количеств их витков. (
обмотках идеального трансформатора равно отношению количеств их витков. (![]() на вторичной и
на вторичной и ![]() первичной). Само это соотношение называют коэффициентом трансформации
первичной). Само это соотношение называют коэффициентом трансформации ![]() .
.
![]()
Если коэффициент трансформации больше единицы, то трансформатор называется понижающим, если меньше, то повышающим.
Закон сохранения энергии для идеального трансформатора:
![]()
КПД неидеального трансформатора:
![]()
Волны
Волны — колебания распространяющийся в упругих средах. Если направление распространения волн и направление колеблющихся частиц среды совпадают то такие волны называются продольными. А если эти направления перпендикулярны друг другу, то такие волны называют поперечными.
Так как волновые процессы являются часным случаем колебательного движения, они так же будут характеризоваться своими частотой и периодом. Но помимо этого у волн есть еще свои дополнительные характеристики, отличающие их от обычного колебательного движения.
Длина волны ![]() — расстояние, на которое успевает распространиться волна за один период;
— расстояние, на которое успевает распространиться волна за один период;
Скорость распространения волны ![]() — отношение длинны волны к периоду ее колебания.
— отношение длинны волны к периоду ее колебания.
![]()
![]()
Звуковые волны — разновидность механических волн в слышимом для человека диапазоне ( от 16 Гц до 20 кГц).
