Для
нахождения цикломатического числа
нужно прежде всего определить число
компонент связности графа (см. 3.3.1.6) Это
необходимо для вычисления цикломатического
числа по формуле:
(G)=m-n+k(G)
Затем
следует составить матрицу циклов и
выбрать наиболее оптимальное сочетание
удаляемых ребер для устранения всех
циклов в графе.
Пример:
на рис. 3.17 дан граф. Составить матрицу
циклов и найти цикломатическое число.
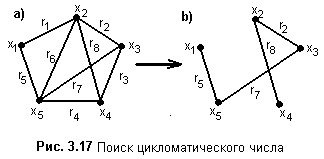
Ниже представлена
матирица циклов.
-
c
r1
r2
r3
r4
r5
r6
r7
r8
c1
1
0
0
0
1
1
0
0
c2
1
1
0
0
1
0
1
0
c3
1
0
0
1
1
0
0
1
c4
1
1
1
1
1
0
0
0
c5
0
0
0
1
0
1
0
1
c6
0
1
1
1
0
1
0
0
c7
0
1
0
0
0
1
1
0
c8
0
1
1
0
0
0
0
1
c9
0
0
1
1
0
0
1
0
c10
0
0
0
1
0
1
0
1
Интересно
отметить, что операция (сiсj)
формирует
вектор-строку другого цикла.
с1=10001100 с1=10001100
с6=
01110100
с2=11001010 с4=11111000 с8=
01100001
с7=01000110 с6
=01110100 с10=00010101
и т.д.
В
данном графе четыре базовых цикла: {r1,
r5, r6},
{r4, r6,
r8}, {r2,
r3, r8},
{r3, r4,
r7}. Если удалить
четыре ребра в каждом базовом цикле, то
будут устранены в графе все циклы.
Например, {r1, r3, r4, r6}.
Если
k(G)=1, то (G)=m-n+k(G)=4.
3.4.1.9. Поиск хроматического числа графа
Прежде,
чем определять число красок для
раскрашивания вершин по числу ребер в
циклах, следует найти клику графа,
содержащую наибольшее число вершин
полного подграфа.
Если
клика содержит n3,
то хроматическое число должно быть
равным (G)=n.
В противном случае можно оценивать (G)
числу ребер в цикле.
Если
число ребер в цикле есть четное число,
то (G)=2,
если нечетное – (G)=3.
Пример:
На рис. 3.17а) дан граф. Определить его
хроматическое число.
Проверим
число красок по трем основаниям:
1)
граф содержит циклы четной и нечетной
длины, т. е. число красок должно быть
(G)3;
2)
наибольшая степень вершин x2 и x5 равна
4, т. е. Число красок должно быть (G)5;
3)
плотность графа (G)=4
(см. таблицу ниже), т. е. полный
подграф содержит четыре вершины.
Следовательно, число красок должно быть
(G)4.
|
r |
x |
x2 |
x3 |
x4 |
x5 |
q |
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
x1 |
0 |
1 |
0 |
0 |
1 |
x1 |
1 |
1 |
0 |
0 |
1 |
|
|
x2 |
1 |
0 |
1 |
1 |
1 |
x2 |
1 |
1 |
1 |
1 |
1 |
|
|
x3 |
0 |
1 |
0 |
1 |
1 |
x3 |
0 |
1 |
1 |
1 |
1 |
|
|
x4 |
0 |
1 |
1 |
0 |
1 |
x4 |
0 |
1 |
1 |
1 |
1 |
|
|
x5 |
1 |
1 |
1 |
1 |
0 |
x5 |
1 |
1 |
1 |
1 |
1 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Привет, Вы узнаете про цикломатическая сложность, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
цикломатическая сложность, цикломатическое число
, настоятельно рекомендую прочитать все из категории Качество и тестирование программного обеспечения. Quality Assurance..
цикломатическая сложность программы (англ. cyclomatic complexity of a program) — структурная (или топологическая) мера сложности компьютерной программы. Мера была разработана Томасом Дж. Маккейбом в 1976 году.
При вычислении цикломатической сложности используется граф потока управления программы. Узлы графа соответствуют неделимым группам команд программы, они соединены ориентированными ребрами, если группа команд, соответствующая второму узлу, может быть выполнена непосредственно после группы команд первого узла. Цикломатическая сложность может быть также вычислена для отдельных функций, модулей, методов или классов в пределах программы.
Маккейб применял вычисление цикломатической сложности при тестировании. Предложенный им метод заключался в тестировании каждого линейно независимого маршрута через программу, в этом случае число необходимых тестов равно цикломатической сложности программы.
Описание
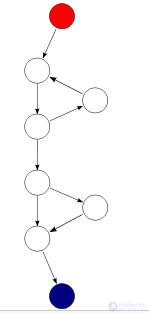
Граф управления потоком простой программы. Программа начинает выполняться с красного узла, затем идут циклы (после красного узла идут две группы по три узла). Выход из цикла осуществляется через условный оператор (нижняя группа узлов) и конечный выход из программы в синем узле. Для этого графа E = 9, N = 8 и P = 1, цикломатическая сложность программы равна 9 − 8 + 2 × 1 = 3 (рассчитано по первому варианту)
Цикломатическая сложность части программного кода — количество линейно независимых маршрутов через программный код. Например, если исходный код не содержит никаких точек ветвления или циклов, то сложность равна единице, поскольку есть только единственный маршрут через код. Если код имеет единственный оператор IF, содержащий простое условие, то существует два пути через код: один если условие оператора IF имеет значение TRUE и один — если FALSE.
Математически цикломатическая сложность структурированной программы определяется с помощью ориентированного графа, узлами которого являются блоки программы, соединенные ребрами, если управление может переходить с одного блока на другой. Тогда сложность определяется как: :
M = E − N + 2P,
где:
M = цикломатическая сложность,
E = количество ребер в графе,
N = количество узлов в графе,
P = количество компонент связности.
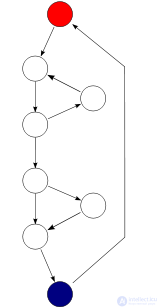
Сильносвязный граф управления потоком той же функции . Об этом говорит сайт https://intellect.icu . Для этого графа E = 10, N = 8 и P = 1, следовательно, цикломатическая сложность программы, рассчитанная по второму варианту, также равна 10 − 8 + 1 =3
В другой формулировке используется граф, в котором каждая точка выхода соединена с точкой входа. В этом случае граф является сильносвязным, и цикломатическая сложность программы равна цикломатическому числу этого графа (также известному как первое число Бетти), которое определяется как
M = E − N + P.
Это определение может рассматриваться как вычисление числа линейно независимых циклов, которые существуют в графе, то есть тех циклов, которые не содержат в себе других циклов. Так как каждая точка выхода соединена с точкой входа, то существует по крайней мере один цикл для каждой точки выхода.
Для простой программы, или подпрограммы, или метода P всегда равно 1. Однако цикломатическая сложность может применяться к нескольким таким программам или подпрограммам (например, ко всем методам в классе), в таком случае P равно числу подпрограмм, о которых идет речь, так как каждая подпрограмма может быть представлена как независимая часть графа.
Может быть показано, что цикломатическая сложность любой структурированной программы с только одной точкой входа и одной точкой выхода эквивалентна числу точек ветвления (то есть, операторов if или условных циклов), содержащихся в этой программе, плюс один.
Цикломатическая сложность может быть распространена на программу с многочисленными точками выхода; в этом случае она равна
π − s + 2,
где:
π — число точек ветвления в программе,
s — число точек выхода.
Формальное определение
Формально, цикломатическая сложность может быть определена как относительное число Бетти:
то есть «первая гомология графа G относительно терминальных узлов t. Это другой способ сказать «число линейно независимых маршрутов через граф от входа к выходу».
Кроме того, цикломатическую сложность можно вычислить через абсолютное число Бетти (с помощью абсолютной гомологии, а не относительной), объединив все терминальные узлы данного компонента (что эквивалентно соединению точек выхода с точкой входа), в этом случае для нового, расширенного, графа
цикломатическое число графа
Цикломатическим числом графа называется число, равное увеличенной на единицу разности между числом ребер и числом вершин графа:
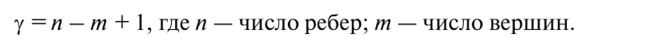
Цикломатическое число графа показывает, сколько ребер надо удалить из графа, чтобы в нем не осталось ни одного цикла.
Задача 1. Дан граф, у которого т = 6, п = 9 (рис. 8.18, а). Определить, сколько ребер на графе нужно удалить, чтобы в нем не осталось ни одого цикла.
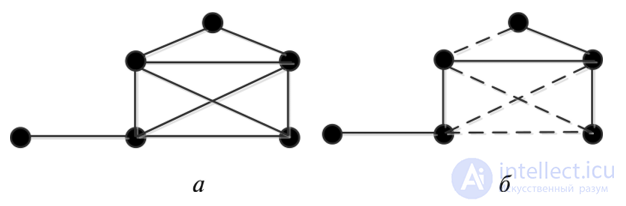
Рис. 8.18. Исходный граф (о) и остовный подграф (б)
(——-) удаленные ребра
Для заданного графа цикломатическое число у = 9 — 6 + 1 = 4. Это означает, что если на графе удалить 4 ребра, то в нем не останется ни одного цикла. Тогда остовный подграф будет иметь вид, показанный на рис. 8.18, б.
Задача 2. Какое минимальное число дверей нужно предусмотреть в замке (рис. 8.19), чтобы попасть во все комнаты (дверь — одно ребро).
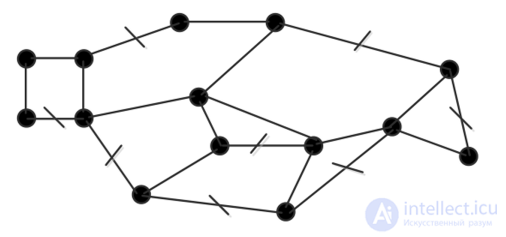
Рис. 8.19. Схема замка (вид сверху)
Решение. Число вершин т = 14, число ребер п = 21. Цикломатическое число у = 21 — 14+1 = 8. Следовательно, в замке нужно предусмотреть 8 дверей. Наряду с цикломатическим числом в теории графов вводится понятие коцикломатического числа. Пусть в графе т — число ребер, п — число вершин, р — число компонент связности. Величина г = п—р называется коцикломатическим числом (число ребер в остовах всехр связных компонент графа).
Применение
Ограничение сложности при разработке
Одно из первоначально предложенных Маккейбом применений состоит в том, что необходимо ограничивать сложность программ во время их разработки. Он рекомендует, чтобы программистов обязывали вычислять сложность разрабатываемых ими модулей и разделять модули на более мелкие всякий раз, когда цикломатическая сложность этих модулей превысит десять. Эта практика была включена НИСТ-ом в методику структурного тестирования с замечанием, что со времени исходной публикации Маккейба выбор значения 10 получил весомые подтверждения, однако в некоторых случаях может быть целесообразно ослабить ограничение и разрешить модули со сложностью до 15. В данной методике признается, что иногда могут существовать причины для выхода за рамки согласованного лимита. Это сформулировано как рекомендация: «Для каждого модуля следует либо ограничивать цикломатическую сложность до согласованных пределов, либо предоставить письменное объяснение того, почему лимит был превышен».
Применение при тестировании программного обеспечения
Другое применение цикломатической сложности — определение количества тестов, необходимых для полного покрытия кода.
Он полезен, поскольку цикломатическая сложность M имеет два свойства, для конкретного модуля:
- M — оценка сверху для количества тестов, обеспечивающих покрытие условий (точек ветвления);
- M — оценка снизу для количества маршрутов через граф потока управления и, таким образом, количества тестов для полного покрытия путей.
В составе других метрик
Цикломатическая сложность используется в качестве одного из параметров в индексе удобства сопровождения (англ. maintainability index) .
См. также
- Качество программного обеспечения
- Аварии по причине сбоя ЭВМ
- Антипаттерны
- Формальные методы
- Качество программного обеспечения
- Вязкость ( программирование )
- Долгосрочная поддержка программного обеспечения
- Когнитивные измерения
- Кризис программного обеспечения
- Обеспечение качества программного обеспечения
- Обходной прием
- Статистическая модель Миллса
- Тупиковая запись
- Цикломатическая сложность
- Эффект второй системы
- Capability Maturity Model
- FURPS
- технический долг
В общем, мой друг ты одолел чтение этой статьи об цикломатическая сложность. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое цикломатическая сложность, цикломатическое число
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Качество и тестирование программного обеспечения. Quality Assurance.

Этот граф имеет контурный ранг r = 2, поскольку его можно превратить в дерево удалением двух рёбер, например, рёбер 1–2 и 2–3, но удаление лишь одного ребра оставляет цикл в графе.
В теории графов контурный ранг [1] неориентированного графа — это минимальное число рёбер, удаление которых разрушает все циклы графа, превращая его в дерево или лес. Контурный ранг можно понимать также как число независимых циклов в графе. В отличие от соответствующей задачи нахождения разрезающего циклы набора дуг[en] для ориентированных графов, контурный ранг r легко вычисляется по формуле
,
где m — число рёбер заданного графа, n — число вершин, а c — число компонент связности
[2]. Можно также эффективно построить множество рёбер минимального размера, разбивающих циклы, используя либо жадный алгоритм, либо дополнение остовного дерева.
Контурный ранг известен также как цикломатическое число графа. Его можно объяснить в терминах алгебраической теории графов как размерность циклического пространства графа, в терминах матроидов с использованием понятия коранга графовых матроидов[en] [3] и в терминах топологии как одно из чисел Бетти топологического пространства, производного от графа. Контурный ранг подсчитывает число ушей в ушной декомпозиции графа, что даёт базис для понятия параметризованной сложности[en] на почти деревьях и применяется в метриках программного обеспечения как часть определения цикломатической сложности фрагмента кода. Под названием цикломатическая сложность понятие было введено Густавом Кирхгофом[4][5].
Ранг матроида и построение минимального разрезающего циклы множества[править | править код]
Контурный ранг графа G можно описать с помощью теории матроидов как коранг графового матроида[en] для G [6]. Если учесть свойство жадности матроидов, это означает, что можно найти минимальный набор рёбер, разрушающий все циклы, используя жадный алгоритм, выбирающий на каждом шаге ребро, принадлежащее по меньшей мере одному циклу оставшегося графа.
С другой стороны, минимальный набор множеств, разрушающий все циклы, можно найти путём построения остовного леса графа G и выбора дополняющего множества рёбер, не принадлежащих остовному лесу.
Число независимых циклов[править | править код]
В алгебраической теории графов, контурный ранг — это размерность пространства циклов графа 
Этот подсчёт независимых циклов может быть объяснён с помощью теории гомологий, ветви топологии. Любой граф G можно рассматривать как пример 1-мерного симплициального комплекса, одного из видов топологического пространства, образованного представлением каждого ребра графа отрезком и склеиванием этих отрезков на концах.
Цикломатическое число является рангом первой (целой) группы гомологий этого комплекса [7],
В связи с такой топологической связью цикломатическое число графа G называется также первым числом Бетти графа G [8]. В более общем случае первое число Бетти любого топологического пространства подсчитывает число независимых циклов в пространстве.
Контурный ранг графа связан с рангом его матрицы инцидентности 

Приложения[править | править код]
Коэффициент сетчатости[править | править код]
Вариант контурного ранга планарного графа, нормализованный путём деления на максимально возможный контурный ранг любого планарного графа с тем же набором вершин, называется коэффициентом сетчатости. Для связных планарных графов с m рёбрами и n вершинами коэффициент сетчатости можно вычислить по формуле[9]
В этой формуле числитель 

Ушная декомпозиция[править | править код]
Контурный ранг отражает число ушей в ушной декомпозиции графа, разложении рёбер графа на пути и циклы, что часто оказывается полезным в алгоритмах на графах. В частности, граф вершинно 2-связен тогда и только тогда, когда он имеет открытую ушную декомпозицию, последовательность подграфов, в котором первый подграф является простым циклом, а оставшиеся подграфы являются простыми путями и каждый путь начинается и кончается в вершинах, принадлежащих предыдущим подграфам, и каждая внутренняя вершина пути появляется первый раз в этом пути. В любом двусвязном графе с контурным рангом 

Почти деревья[править | править код]
Граф с цикломатическим числом 
Некоторые авторы изучали параметризованную сложность[en] алгоритмах на почти r-деревьях с параметризацией по 
Обобщение для ориентированных графов[править | править код]
Циклический ранг — это инвариант ориентированных графов, измеряющий уровень вложенности циклов в графе. Этот инвариант имеет более сложное определение, чем цикломатический ранг (тесно связанный с определением глубины дерева для неориентированных графов) и вычисление его существенно сложнее. Другая задача для ориентированных графов, связанная с цикломатическим рангом — определение минимального разрезающего циклы набора дуг[en], то есть минимального набора дуг, удаление которых разрушает все ориентированные циклы. Обе задачи, вычисление циклического ранга и определение минимального рарезающиего циклы набора дуг, являются NP-трудными.
Также можно вычислить более простой инвариант ориентированных графов, если игнорировать направления рёбер и вычислить циклический ранг неориентированного графа. Этот принцип образует базис для определения цикломатической сложности, меры сложности компьютерной программы для оценки сложности фрагмента компьютерного кода.
Связанные понятия[править | править код]
Другие числа, определяемые в терминах удаления рёбер из неориентированного графа, включают рёберной связности, минимальное число рёбер, удаление которых приводит к потере связности, и число предотвращения паросочетаний[en], минимальное число рёбер, удаление которых приводит к потере существования совершенного паросочетания.
Примечания[править | править код]
- ↑ В русскоязычной литературе и cycle rank, и circuit rank часто переводятся одинаково — циклический ранг. В англоязычной литературе первый термин относится к ориентированным графам, второй — к неориентированным. В данной статье для ориентированных графов используется термин «циклический ранг», для неориентированных графов — «контурный ранг»
- ↑ 1 2 Berge, 2001, с. 27–30.
- ↑ В русскоязычной литературе употребляется также термин графический матроид, что является калькой английского graphic matroid и не совсем соответствует сущности понятия.
- ↑ Kotiuga, 2010, с. 20.
- ↑ Hage, 1996, с. 48.
- ↑ Berge, 1976, с. 477.
- ↑ Serre, 2003, с. 23.
- ↑ Berkolaiko, Kuchment, 2013, с. 4.
- ↑ Buhl, Gautrais, Sole и др., 2004, с. 123–129.
- ↑ Whitney, 1932, с. 339–362.
- ↑ Brualdi, 2006, с. 349.
- ↑ Coppersmith, Vishkin, 1985, с. 27–45.
- ↑ Fiala, Kloks, Kratochvíl, 2001, с. 59–72.
Литература[править | править код]
- Claude Berge. The Theory of Graphs. — Courier Dover Publications, 2001. — ISBN 9780486419756.
- Claude Berge. Graphs and Hypergraphs. — Elsevier, 1976. — Т. 6. — (North-Holland Mathematical Library). — ISBN 9780720424539.
- К. Берж. Теория графов и её применение.
- J. Buhl, J. Gautrais, R.V. Sole, P. Kuntz, S. Valverde, J.L. Deneubourg, G. Theraulaz. Efficiency and robustness in ant networks of galleries // The European Physical Journal B-Condensed Matter and Complex Systems. — Springer-Verlag, 2004. — Т. 42, вып. 1. — С. 123–129. — doi:10.1140/epjb/e2004-00364-9.
- H. Whitney. Non-separable and planar graphs // Transactions of the American Mathematical Society. — 1932. — Т. 34. — С. 339–362. — doi:10.2307/1989545. См. Теоремы 18 (связь ушной декомпозиции с циклическим рангом) и 19 (о существовании ушной декомпозиции)
- Richard A. Brualdi. Combinatorial matrix classes. — Cambridge: Cambridge University Press, 2006. — Т. 108. — С. 349. — (Encyclopedia of Mathematics and Its Applications). — ISBN 0-521-86565-4.
- Don Coppersmith, Uzi Vishkin. Solving NP-hard problems in ‘almost trees’: Vertex cover // Discrete Applied Mathematics. — 1985. — Т. 10, вып. 1. — С. 27–45. — doi:10.1016/0166-218X(85)90057-5.
- Jiří Fiala, Ton Kloks, Jan Kratochvíl. Fixed-parameter complexity of λ-labelings // Discrete Applied Mathematics. — 2001. — Т. 113, вып. 1. — С. 59–72. — doi:10.1016/S0166-218X(00)00387-5.
- Peter Robert Kotiuga. A Celebration of the Mathematical Legacy of Raoul Bott. — American Mathematical Soc., 2010. — С. 20. — ISBN 978-0-8218-8381-5.
- Per Hage. Island Networks: Communication, Kinship, and Classification Structures in Oceania. — Cambridge University Press, 1996. — С. 48. — ISBN 978-0-521-55232-5.
- Jean-Pierre Serre. Trees. — Springer, 2003. — С. 23. — (Springer Monographs in Mathematics).
- Gregory Berkolaiko, Peter Kuchment. Introduction to Quantum Graphs. — American Mathematical Soc., 2013. — С. 4. — ISBN 978-0-8218-9211-4.
Аннотация: Рассматриваются некоторые характеристические числа графа, позволяющие в ряде случаев упростить решение задач исследования топологических свойств графа.
Изложить основные понятия теории графов, знание которых является обязательным при современном конструкторском проектировании РЭС.
Рассмотрим некоторые характеристические числа графа, позволяющие в ряде случаев упростить решение задач исследования топологических свойств графа.
К таким числам, не зависящим от изоморфных преобразований, относятся: цикломатическое 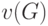 и хроматическое
и хроматическое 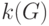 числа, числа внутренней
числа, числа внутренней  и внешней
и внешней 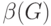 устойчивости графа.
устойчивости графа.
18. 1. Цикломатическое число
При рассмотрении произвольного неориентированного графа 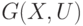 без петель с
без петель с  и
и  , состоящего из ”
, состоящего из ”  ” компонент связности, величину
” компонент связности, величину
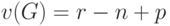 |
( 18.1) |
называют цикломатическим числом графа.
Иногда вводят понятие ранга графа
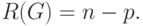 |
( 18.2) |
В этом случае цикломатическое число
 |
( 18.3) |
Цикломатическое число графа указывает то наименьшее число рёбер, которое нужно удалить из данного графа, чтобы получить дерево (для связного графа) или лес (для несвязного графа), т.е. добиться отсутствия у графа циклов.
Цикломатическое число всегда неотрицательно.
Основное свойство цикломатического числа формулируется в виде теоремы:
Цикломатическое число мультиграфа равно максимальному числу независимых циклов.
Знание цикломатического числа оказывается полезным при анализе топологии электронных схем, а также для решения целого класса задач конструкторского проектирования РЭС.
Пример. Если рассматривать конструкцию печатной платы, то схему электрических соединений можно интерпретировать графом  , где
, где  – множество областей контактных площадок, внутри которых проведение проводников запрещено, a
– множество областей контактных площадок, внутри которых проведение проводников запрещено, a  – множество трасс.
– множество трасс.
При этом всё коммутационное пространство разбивается проведёнными соединениями на отдельные, локально замкнутые области
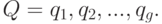 |
( 18.4) |
Любые две вершины 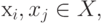 находящиеся в различных областях
находящиеся в различных областях  , не могут быть соединены ребром
, не могут быть соединены ребром 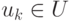 без пересечения рёбер (соединений), ограничивающих области
без пересечения рёбер (соединений), ограничивающих области 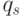 и
и 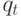 .
.
В связи с этим возникает необходимость контроля непопадания смежных вершин в различные изолированные области.
Цикломатическое число 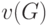 позволяет определить число таких локально замкнутых областей и перейти к решению задачи рационального перераспределения рёбер графа
позволяет определить число таких локально замкнутых областей и перейти к решению задачи рационального перераспределения рёбер графа  .
.
18. 2. Хроматическое число
Пусть, задан граф  без петель. Разобьём множество его вершин на k непересекающихся подмножеств
без петель. Разобьём множество его вершин на k непересекающихся подмножеств
![X_{1}, X_{2}, … , X_{k}, X =bigcuplimits_{i=1}^k{X_i}, forall X_{i}, X_{j} subset X; [X_{i}cap X_{j}=varnothing]](https://intuit.ru/sites/default/files/tex_cache/23e06f585e860f2b2ed711a704b97972.png) |
( 18.5) |
так, чтобы любые две смежные вершины  принадлежали разным подмножествам, т.е. чтобы рёбра графа
принадлежали разным подмножествам, т.е. чтобы рёбра графа  соединяли вершины из разных подмножеств
соединяли вершины из разных подмножеств
![forall X_s in X[X_sin X_i Leftarrow ГX_s notsubset X_i]](https://intuit.ru/sites/default/files/tex_cache/3cbee1db53257456d43fe4a6724d7b9f.png) |
( 18.6) |
Отметим все вершины  индексами
индексами  (т.е. раскрасим вершины
(т.е. раскрасим вершины  цветами), причём вершины внутри каждого подмножества
цветами), причём вершины внутри каждого подмножества 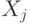 помечают одним индексом (раскрашивают одним цветом). Подмножества формируют таким образом, чтобы концы любого ребра графа имели различные индексы.
помечают одним индексом (раскрашивают одним цветом). Подмножества формируют таким образом, чтобы концы любого ребра графа имели различные индексы.
Наименьшее возможное число подмножеств, получаемое в результате такого разбиения вершин графа  , называют хроматическим числом графа
, называют хроматическим числом графа 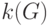 , граф
, граф  называют
называют  – хроматическим,а выражения (18.5) и (18.6)- хроматическим разложением
– хроматическим,а выражения (18.5) и (18.6)- хроматическим разложением  .
.
Особое значение имеет частный вид  – хроматического графа – бихроматический или двудольный граф, для которого множество вершин
– хроматического графа – бихроматический или двудольный граф, для которого множество вершин  можно разбить на два непересекающихся подмножества
можно разбить на два непересекающихся подмножества 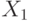 и
и 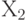 так, чтобы никакое ребро не соединяло бы вершины одного и того же подмножества, т.е.
так, чтобы никакое ребро не соединяло бы вершины одного и того же подмножества, т.е.
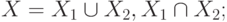 |
( 18.7) |
![forall x_{i} , x_{j}in X [(x_{i} , x_{j}) = u_{f }in U Leftarrow (x_{i}in X_{1 }& x_{j}in X_{2})cup (x_{i}in X_{2} & x_{j}in X_{1})].](https://intuit.ru/sites/default/files/tex_cache/b5d437360d99f3975561cc540627f9d7.png)
Такие графы называют графами Кёнига и обозначают 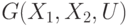 .
.
Критерий бихроматичности произвольного графа формулируется теоремой Кёнига, согласно которой обыкновенный граф  является бихроматическим тогда и только тогда, когда он не содержит циклов нечётной длины.
является бихроматическим тогда и только тогда, когда он не содержит циклов нечётной длины.
Если граф  – дерево, т.е. в нём полностью отсутствуют циклы (существуют лишь циклы нулевой длины), то он является бихроматическим графом и может быть представлен в виде двудольного графа (рис. 18.1).
– дерево, т.е. в нём полностью отсутствуют циклы (существуют лишь циклы нулевой длины), то он является бихроматическим графом и может быть представлен в виде двудольного графа (рис. 18.1).
Граф Кёнига 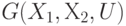 называют полным, если каждая вершина
называют полным, если каждая вершина 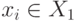 смежна с каждой вершиной
смежна с каждой вершиной 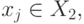 и наоборот.
и наоборот.
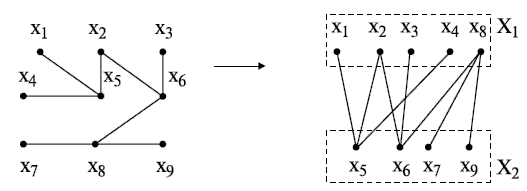
Рис.
18.1.
Пример двудольного графа
Пример. Рассмотрим пример бихроматического графа 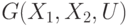 , у которого
, у которого
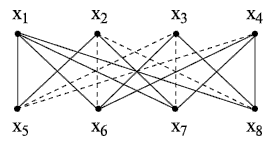
Рис.
18.2.
Бихроматический граф
При добавлении к этому графу рёбер 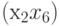 ,
, 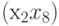 ,
, 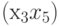 ,
, 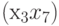 и
и  получим полный бихроматический граф. Очевидно, что подмножество
получим полный бихроматический граф. Очевидно, что подмножество 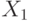 множества вершин
множества вершин  можно раскрасить в один цвет, а
можно раскрасить в один цвет, а  – в другой.
– в другой.
Число рёбер полного бихроматического графа 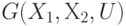
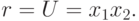
При составлении целого ряда алгоритмов проектирования РЭС используют операцию удаления некоторых вершин и рёбер графа. При этом особое значение приобретает понятие критического графа.
Граф  называют критическим, если удаление любой вершины
называют критическим, если удаление любой вершины  с инцидентными ей рёбрами уменьшает хроматическое число графа.
с инцидентными ей рёбрами уменьшает хроматическое число графа.
Критическим  – хроматическим графом является одна вершина; критическим 2 – хроматическим – две вершины, соединённые ребром; критическим
– хроматическим графом является одна вершина; критическим 2 – хроматическим – две вершины, соединённые ребром; критическим  – хроматическим – простой цикл нечётной длины, так как при удалении из него любой вершины с инцидентными ей рёбрами получим двудольный граф. Очевидно, что полный граф всегда является критическим, причём его хроматическое число равно
– хроматическим – простой цикл нечётной длины, так как при удалении из него любой вершины с инцидентными ей рёбрами получим двудольный граф. Очевидно, что полный граф всегда является критическим, причём его хроматическое число равно
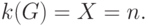
В отличие от цикломатического числа определение хроматического числа осуществляется с помощью сравнительно сложных алгоритмов, в основу большинства которых положены методы целочисленного линейного программирования.
Оценка хроматического числа через число вершин графа  имеет вид:
имеет вид:
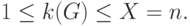
В этом выражении нижняя граница соответствует пустым, а верхняя – полным графам.
На практике для простых связных графов оценить величину  можно следующим образом.
можно следующим образом.
Сначала выбираем вершину с минимальной локальной степенью и пометим (раскрасим) её, затем произведём хроматическую раскраску вершин, смежных с данной, и так далее.
Например, для графа на рис. 18.2, б сначала выбираем вершину 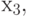 для которой
для которой  , и раскрасим её в красный цвет. Тогда вершину
, и раскрасим её в красный цвет. Тогда вершину 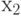 можно раскрасить в синий цвет, а вершины
можно раскрасить в синий цвет, а вершины 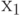 и
и 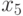 – в красный (они не смежны с
– в красный (они не смежны с 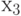 ). Вершины
). Вершины 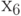 и
и 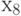 можно раскрасить в синий цвет, а оставшиеся вершины
можно раскрасить в синий цвет, а оставшиеся вершины 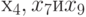 – в жёлтый. На раскраску вершин графа пошло три краски
– в жёлтый. На раскраску вершин графа пошло три краски 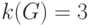 .
.
Знание хроматического числа графа позволяет в ряде случаев упростить алгоритмы, используемые на этапе конструкторского проектирования РЭС.
Пример. Рассмотрим задачу оценки числа слоёв многослойной печатной платы. Пусть, граф  интерпретирует фрагмент коммутационного поля платы, где х – множество областей контактных площадок конструктивных элементов, внутри которых проведение проводников запрещено, a
интерпретирует фрагмент коммутационного поля платы, где х – множество областей контактных площадок конструктивных элементов, внутри которых проведение проводников запрещено, a  – множество трасс платы.
– множество трасс платы.
Построим граф пересечений 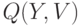 , в котором вершинами являются отдельные компоненты связности (электрические цепи) графа
, в котором вершинами являются отдельные компоненты связности (электрические цепи) графа  , причём
, причём 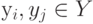 смежны, если соответствующие им компоненты связности
смежны, если соответствующие им компоненты связности  и
и 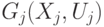 перекрывают друг друга.
перекрывают друг друга.
При этом хроматическое число 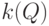 графа
графа 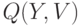 определит верхнюю границу числа коммутационных слоев рассматриваемого фрагмента платы (в нашем примере
определит верхнюю границу числа коммутационных слоев рассматриваемого фрагмента платы (в нашем примере  ). В этом случае цепи, соответствующие вершинам одного цвета графа
). В этом случае цепи, соответствующие вершинам одного цвета графа 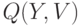 , можно располагать в одном слое печатной платы.
, можно располагать в одном слое печатной платы.
![{displaystyle r=operatorname {rank} left[H_{1}(G,mathbb {Z} )right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33317573927c3cd825b3db1110427c8a94dc8641)

