Given the root of a Directed graph, The task is to check whether the graph contains a cycle or not.
Examples:
Input: N = 4, E = 6
Example of graph
Output: Yes
Explanation: The diagram clearly shows a cycle 0 -> 2 -> 0Input: N = 4, E = 4
Output: No
Explanation: The diagram clearly shows no cycle
Approach:
The problem can be solved based on the following idea:
To find cycle in a directed graph we can use the Depth First Traversal (DFS) technique. It is based on the idea that there is a cycle in a graph only if there is a back edge [i.e., a node points to one of its ancestors] present in the graph.
To detect a back edge, we need to keep track of the nodes visited till now and the nodes that are in the current recursion stack [i.e., the current path that we are visiting]. If during recursion, we reach a node that is already in the recursion stack, there is a cycle present in the graph.
Note: If the graph is disconnected then get the DFS forest and check for a cycle in individual trees by checking back edges.
Follow the below steps to Implement the idea:
- Create a recursive dfs function that has the following parameters – current vertex, visited array, and recursion stack.
- Mark the current node as visited and also mark the index in the recursion stack.
- Iterate a loop for all the vertices and for each vertex, call the recursive function if it is not yet visited (This step is done to make sure that if there is a forest of graphs, we are checking each forest):
- In each recursion call, Find all the adjacent vertices of the current vertex which are not visited:
- If an adjacent vertex is already marked in the recursion stack then return true.
- Otherwise, call the recursive function for that adjacent vertex.
- While returning from the recursion call, unmark the current node from the recursion stack, to represent that the current node is no longer a part of the path being traced.
- In each recursion call, Find all the adjacent vertices of the current vertex which are not visited:
- If any of the functions returns true, stop the future function calls and return true as the answer.
Illustration:
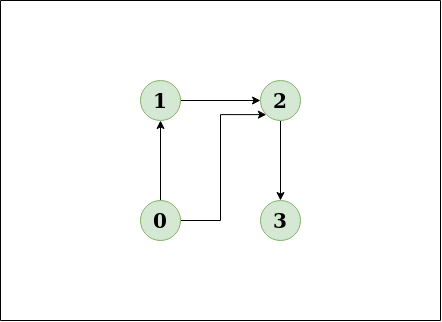
Consider the following graph:
Example of a Directed Graph
Consider we start the iteration from vertex 0.
- Initially, 0 will be marked in both the visited[] and recStack[] array as it is a part of the current path.
Vertex 0 is visited
- Now 0 has two adjacent vertices 1 and 2. Let us consider traversal to the vertex 1. So 1 will be marked in both visited[] and recStack[].
Vertex 1 is visited
- Vertex 1 has only one adjacent vertex. Call the recursive function for 2 and mark it in visited[] and recStack[].
Vertex 2 is visited
- Vertex 2 also has two adjacent vertices.
- Vertex 0 is visited and already marked in the recStack[]. So if 0 is checked first, we will get the answer that there is a cycle present.
- On the other hand, if vertex 3 is checked first, then 3 will be marked in visited[] and recStack[].
Vertex 3 is visited
- While returning from the recursion call for 3, it will be unmarked from recStack[] as it is now not a part of the path currently being traced.
Vertex 3 is unmarked from recStack[]
- Now we have only one option to check, vertex 0, which is already marked in recStack[].
So, we can conclude that a cycle exists. We can also find the cycle if we have traversed to vertex 2 from 0 itself in this same way.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class Graph {
int V;
list<int>* adj;
bool isCyclicUtil(int v, bool visited[], bool* rs);
public:
Graph(int V);
void addEdge(int v, int w);
bool isCyclic();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
}
bool Graph::isCyclicUtil(int v, bool visited[],
bool* recStack)
{
if (visited[v] == false) {
visited[v] = true;
recStack[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i) {
if (!visited[*i]
&& isCyclicUtil(*i, visited, recStack))
return true;
else if (recStack[*i])
return true;
}
}
recStack[v] = false;
return false;
}
bool Graph::isCyclic()
{
bool* visited = new bool[V];
bool* recStack = new bool[V];
for (int i = 0; i < V; i++) {
visited[i] = false;
recStack[i] = false;
}
for (int i = 0; i < V; i++)
if (!visited[i]
&& isCyclicUtil(i, visited, recStack))
return true;
return false;
}
int main()
{
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
if (g.isCyclic())
cout << "Graph contains cycle";
else
cout << "Graph doesn't contain cycle";
return 0;
}
Java
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
class Graph {
private final int V;
private final List<List<Integer>> adj;
public Graph(int V)
{
this.V = V;
adj = new ArrayList<>(V);
for (int i = 0; i < V; i++)
adj.add(new LinkedList<>());
}
private boolean isCyclicUtil(int i, boolean[] visited,
boolean[] recStack)
{
if (recStack[i])
return true;
if (visited[i])
return false;
visited[i] = true;
recStack[i] = true;
List<Integer> children = adj.get(i);
for (Integer c: children)
if (isCyclicUtil(c, visited, recStack))
return true;
recStack[i] = false;
return false;
}
private void addEdge(int source, int dest) {
adj.get(source).add(dest);
}
private boolean isCyclic()
{
boolean[] visited = new boolean[V];
boolean[] recStack = new boolean[V];
for (int i = 0; i < V; i++)
if (isCyclicUtil(i, visited, recStack))
return true;
return false;
}
public static void main(String[] args)
{
Graph graph = new Graph(4);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(2, 0);
graph.addEdge(2, 3);
graph.addEdge(3, 3);
if(graph.isCyclic())
System.out.println("Graph contains cycle");
else
System.out.println("Graph doesn't "
+ "contain cycle");
}
}
Python3
from collections import defaultdict
class Graph():
def __init__(self, vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self, u, v):
self.graph[u].append(v)
def isCyclicUtil(self, v, visited, recStack):
visited[v] = True
recStack[v] = True
for neighbour in self.graph[v]:
if visited[neighbour] == False:
if self.isCyclicUtil(neighbour, visited, recStack) == True:
return True
elif recStack[neighbour] == True:
return True
recStack[v] = False
return False
def isCyclic(self):
visited = [False] * (self.V + 1)
recStack = [False] * (self.V + 1)
for node in range(self.V):
if visited[node] == False:
if self.isCyclicUtil(node, visited, recStack) == True:
return True
return False
if __name__ == '__main__':
g = Graph(4)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
if g.isCyclic() == 1:
print("Graph contains cycle")
else:
print("Graph doesn't contain cycle")
C#
using System;
using System.Collections.Generic;
public class Graph {
private readonly int V;
private readonly List<List<int> > adj;
public Graph(int V)
{
this.V = V;
adj = new List<List<int> >(V);
for (int i = 0; i < V; i++)
adj.Add(new List<int>());
}
private bool isCyclicUtil(int i, bool[] visited,
bool[] recStack)
{
if (recStack[i])
return true;
if (visited[i])
return false;
visited[i] = true;
recStack[i] = true;
List<int> children = adj[i];
foreach(int c in children) if (
isCyclicUtil(c, visited, recStack)) return true;
recStack[i] = false;
return false;
}
private void addEdge(int sou, int dest)
{
adj[sou].Add(dest);
}
private bool isCyclic()
{
bool[] visited = new bool[V];
bool[] recStack = new bool[V];
for (int i = 0; i < V; i++)
if (isCyclicUtil(i, visited, recStack))
return true;
return false;
}
public static void Main(String[] args)
{
Graph graph = new Graph(4);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(2, 0);
graph.addEdge(2, 3);
graph.addEdge(3, 3);
if (graph.isCyclic())
Console.WriteLine("Graph contains cycle");
else
Console.WriteLine("Graph doesn't "
+ "contain cycle");
}
}
Javascript
let V;
let adj=[];
function Graph(v)
{
V=v;
for (let i = 0; i < V; i++)
adj.push([]);
}
function isCyclicUtil(i,visited,recStack)
{
if (recStack[i])
return true;
if (visited[i])
return false;
visited[i] = true;
recStack[i] = true;
let children = adj[i];
for (let c=0;c< children.length;c++)
if (isCyclicUtil(children, visited, recStack))
return true;
recStack[i] = false;
return false;
}
function addEdge(source,dest)
{
adj .push(dest);
}
function isCyclic()
{
let visited = new Array(V);
let recStack = new Array(V);
for(let i=0;i<V;i++)
{
visited[i]=false;
recStack[i]=false;
}
for (let i = 0; i < V; i++)
if (isCyclicUtil(i, visited, recStack))
return true;
return false;
}
Graph(4);
addEdge(0, 1);
addEdge(0, 2);
addEdge(1, 2);
addEdge(2, 0);
addEdge(2, 3);
addEdge(3, 3);
if(isCyclic())
console.log("Graph contains cycle");
else
console.log("Graph doesn't "
+ "contain cycle");
Output
Graph contains cycle
Time Complexity: O(V + E), the Time Complexity of this method is the same as the time complexity of DFS traversal which is O(V+E).
Auxiliary Space: O(V). To store the visited and recursion stack O(V) space is needed.
In the below article, another O(V + E) method is discussed :
Detect Cycle in a direct graph using colors
Another Approcah:
Using Kahn’s Algorithm:
For arranging the vertices of a directed acyclic graph (DAG) such that for every directed edge from vertex A to vertex B, A occurs before B in the ordering, Kahn’s algorithm is a well-known approach for topological sorting.
The first step of Kahn’s technique is to identify all the vertices that have no dependencies and have zero incoming edges. These vertices are then taken out of the graph and added to the output list. The remaining vertices are subjected to the same procedure, with each iteration eliminating the vertices with no incoming edges until all vertices have been handled.
The algorithm operates on the premise that a vertex can be visited securely and added to the output list if it doesn’t have any incoming edges. The problem is transformed into a smaller DAG by eliminating this vertex, which also eliminates all of its outgoing edges. Each vertex’s incoming edges are tracked by the algorithm, which updates them when vertices are dropped.
The algorithm is explained in detail below:
- Calculate the in-degree (number of incoming edges) for each vertex in the DAG and set the starting value of the visited nodes count to 0.
- Select all of the vertices with in-degree values of 0, then enqueue them all.
- Add one more visited node to the count after removing a vertex from the queue (Dequeue operation).
- For each of its neighbouring nodes or vertices, reduce in-degree by 1.
- Add a node or vertex to the queue if the in-degree of any nearby nodes or vertices is lowered to zero.
- Up until the queue is empty, repeat step 3.
- The topological sort is not possible for the provided graph if the number of visited nodes is not equal to the number of graph vertices.
Explanation:
The Graph class has been implemented in below code, and the graph is represented as an adjacency list. Additionally, a method called isCyclic that runs a BFS traversal of the graph in order to find cycles has been defined. Prior to enqueuing vertices with a 0 in-degree, the isCyclic function determines the in-degree of each vertex. Then it eliminates vertices with 0 in-degree and lowers the in-degree of the vertices next to them. Any adjacent vertex that has an in-degree of 0 is enqueued. If not all vertices are visited, indicating a cycle, the method returns true and keeps track of the number of visited vertices.
C++
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
class Graph {
private:
int V;
vector<vector<int>> adj;
public:
Graph(int V) {
this->V = V;
adj.resize(V);
}
void addEdge(int v, int w) {
adj[v].push_back(w);
}
bool isCyclic() {
vector<int> inDegree(V, 0);
queue<int> q;
int visited = 0;
for (int u = 0; u < V; u++) {
for (auto v : adj[u]) {
inDegree[v]++;
}
}
for (int u = 0; u < V; u++) {
if (inDegree[u] == 0) {
q.push(u);
}
}
while (!q.empty()) {
int u = q.front();
q.pop();
visited++;
for (auto v : adj[u]) {
inDegree[v]--;
if (inDegree[v] == 0) {
q.push(v);
}
}
}
return visited != V;
}
};
int main() {
Graph g(6);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 3);
g.addEdge(4, 1);
g.addEdge(4, 5);
g.addEdge(5, 3);
if (g.isCyclic()) {
cout << "Graph contains cycle." << endl;
} else {
cout << "Graph does not contain cycle." << endl;
}
return 0;
}
Output
Graph does not contain cycle.
Time Complexity: O(V + E), the Time Complexity of this method is the same as the time complexity of DFS traversal which is O(V+E).
Auxiliary Space: O(V). To store the visited and recursion stack O(V) space is needed.
Last Updated :
08 May, 2023
Like Article
Save Article
| Задача: |
| Дан граф, требуется проверить наличие цикла в этом графе. |
Содержание
- 1 Алгоритм
- 2 Доказательство
- 3 Реализация для случая ориентированного графа
- 4 См. также
- 5 Источники информации
Алгоритм
Будем решать задачу с помощью поиска в глубину.
В случае ориентированного графа произведём серию обходов. То есть из каждой вершины, в которую мы ещё ни разу не приходили, запустим поиск в глубину, который при входе в вершину будет красить её в серый цвет, а при выходе из нее — в чёрный. И, если алгоритм пытается пойти в серую вершину, то это означает, что цикл найден.
В случае неориентированного графа, одно ребро не должно встречаться в цикле дважды по определению. Поэтому необходимо дополнительно проверять, что текущее рассматриваемое из вершины ребро не является тем ребром, по которому мы пришли в эту вершину.
Заметим, что, если в графе есть вершины с петлями, то алгоритм будет работать корректно, так как при запуске поиска в глубину из такой вершины, найдется ребро, ведущее в нее же, а значит эта петля и будет являться циклом.
Для восстановления самого цикла достаточно при запуске поиска в глубину из очередной вершины добавлять эту вершину в стек. Когда поиск в глубину нашел вершину, которая лежит на цикле, будем последовательно вынимать вершины из стека, пока не встретим найденную еще раз. Все вынутые вершины будут лежать на искомом цикле.
Асимптотика поиска цикла совпадает с асимптотикой поиска в глубину — .
Момент нахождения цикла: синие ребра — уже пройденные, красное ребро ведет в серую, уже пройденную, вершину.
Доказательство
Пусть дан граф . Запустим . Рассмотрим выполнение процедуры поиска в глубину от некоторой вершины . Так как все серые вершины лежат в стеке рекурсии, то для них вершина достижима, так как между соседними вершинами в стеке есть ребро. Тогда, если из рассматриваемой вершины существует ребро в серую вершину , то это значит, что из вершины существует путь в и из вершины существует путь в состоящий из одного ребра. И так как оба эти пути не пересекаются, то цикл существует.
Докажем, что если в графе существует цикл, то его всегда найдет. Пусть — первая вершина принадлежащая циклу, рассмотренная поиском в глубину. Тогда существует вершина , принадлежащая циклу и имеющая ребро в вершину . Так как из вершины в вершину существует белый путь (они лежат на одном цикле), то по лемме о белых путях во время выполнения процедуры поиска в глубину от вершины , вершина будет серой. Так как из есть ребро в , то это ребро в серую вершину. Следовательно нашел цикл.
Реализация для случая ориентированного графа
// color — массив цветов, изначально все вершины белые func dfs(v: vertex): // v — вершина, в которой мы сейчас находимся color[v] = grey for (u: vu E) if (color[u] == white) dfs(u) if (color[u] == grey) print() // вывод ответа color[v] = black
См. также
- Использование обхода в глубину для проверки связности
- Использование обхода в глубину для топологической сортировки
- Использование обхода в глубину для поиска компонент сильной связности
- Использование обхода в глубину для поиска точек сочленения
- Использование обхода в глубину для поиска мостов
Источники информации
- MAXimal :: algo — «Проверка графа на ацикличность и нахождение цикла»
- Прикладные задачи алгоритма DFS
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ.[1] — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 1296.
Напомним, что циклом в графе $G$ называется ненулевой путь, ведущий из вершины $v$ в саму себя. Граф называют ацикличным, если в нем нет циклов.
Для нахождения цикла, рассмотрим такой альтернативные способ делать обход в глубину:
void dfs(int v, int p = -1) {
for (int u : g[v])
if (u != p)
dfs(u, v);
}
Здесь мы вместо массива used передаем в рекурсию параметр $p$, равный номеру вершины, откуда мы пришли, или $-1$, если мы начали обход в этой вершине.
Этот способ корректен только для деревьев — проверка u != p гарантирует, что мы не пойдем обратно по ребру, однако если в графе есть цикл, то мы в какой то момент вызовем dfs второй раз с одними и теми же параметрами и попадем в бесконечный цикл.
Если мы можем определять, попали ли мы в бесконечный цикл, то это ровно то, что нам нужно. Модифицируем dfs так, чтобы мы могли определять момент, когда мы входим в цикл. Для этого просто вернем массив used обратно, но будем использовать его для проверки, были ли мы когда-то в вершине, которую мы собираемся посетить — это будет означать, что цикл существует.
const int maxn = 1e5;
bool used[maxn];
void dfs(int v, int p = -1) {
if (used[v]) {
cout << "Graph has a cycle" << endl;
exit(0);
}
used[v] = true;
for (int u : g[v])
if (u != p)
dfs(u, v);
}
Если нужно восстанавливать сам цикл, то можно вместо завершения программы возвращаться из рекурсии несколько раз и выписывать вершины, пока не дойдем до той, в которой нашелся цикл.
// возвращает -1, если цикл не нашелся, и вершину начала цикла в противном случае
int dfs(int v, int p = -1) {
if (used[v]) {
cout << "Graph has a cycle, namely:" << endl;
return v;
}
used[v] = true;
for (int u : g[v]) {
if (u != p) {
int k = dfs(u, v);
if (k != -1) {
cout << v << endl;
if (k == v)
exit(0);
return k;
}
}
}
return -1;
}
Как и со всеми обходами, если в графе больше одной компоненты связности, или если граф ориентированный, то dfs нужно запускать несколько раз от вершин разных компонент.
for (int v = 0; v < n; v++)
if (!used[v])
dfs(v);
Как я простые циклы искал
Время на прочтение
13 мин
Количество просмотров 13K

Увидел я не много… хотя было всего лишь 4 часа утра. Пару ссылок на алгоритмы ссылка1, ссылка2, и много намеком на то, что пора спать циклов в графе может быть много, и в общем случае задача не решаемая. И еще вопрос на хабре на эту тему, ответ на который меня тоже не спас — про поиск в глубину я и так знал.
Но раз я решил, то даже NP сложную задачу решу за P тем более я пью воду, а не кофе — а она не может резко закончиться. И я знал, что в рамках моей задачи найти все циклы должно быть возможным за маленькое время, без суперкомпьютеров — не тот порядок величин у меня.
Немного отвлечемся от детектива, и поймем зачем мне это нужно.
Что за библиотека?
Библиотека называется DITranquillity написана на языке Swift, и её задача — внедрять зависимости. С задачей внедрения зависимостей библиотека справляется на ура, имеет возможности которые не умеют другие библиотеки на Swift, и делает это с хорошей скоростью.
Но зачем мне взбрело проверять циклы в графе зависимостей?
Ради киллерфичи — если библиотека делает основной функционал на ура, то ищешь способы её улучшить и сделать лучше. А киллефича — это проверка графа зависимостей на правильность — это набор разных проверок, которые позволяют избежать проблем во время исполнения, что экономит время разработки. И проверка на циклы выделяется отдельно среди всех проверок, так как эта операция занимает гораздо больше времени. И до недавнего времени некультурно больше времени.
О проблеме я знал давно, но понимал, что в том виде, в каком сейчас хранится граф сделать быструю проверку сложно. Да и раз уж библиотека умеет проверять граф зависимостей, то сделать “Graph API” само напрашивается. “Graph API” — позволяет отдавать граф зависимостей для внешнего пользования, чтобы:
- Его проанализировать как-то на свой лад. Например, в своё время, для работы собрал автоматически все зависимости между нашими модулями, что помогло убрать лишние зависимости и ускорить сборку.
- Пока нет, но когда-нибудь будет — визуализация этого графа с помощью graphvis.
- Проверка графа на корректность.
Особенно ради второго — кто как, а мне нравится смотреть на эти ужасные картинки и понимать как же все плохо…
Исходные данные
Давайте посмотрим, с чем предстоит работать:
- MacBook pro 2019, 2,6 GHz 6-Core i7, 32 Gb, Xcode 11.4, Swift 5.2
- Проект на языке Swift с 300к+ строчек кода (пустые строки и комментарии не в счёт)
- Более 900 вершин
- Более 2000 ребер
- Максимальная глубина зависимостей достигает 40
- Почти 7000 циклов
Все замеры делаются в debug режиме, не в release, так как использовать проверку графа будут только в debug.
До этой ночи, время проверки составляло 95 минут.
Для не терпеливых
После оптимизации время проверки уменьшилось до 3 секунд, то есть ускорение составило три порядка.
Этап 1. Представление графа
Возвращаемся к нашему детективу. Мой графне Монте Кристо, он ориентированный.
Каждая вершина графа это компонент, ну или проще информация о классе. До появления Graph API все компоненты хранились в словаре, и каждый раз приходилось в него лазить, еще и ключ создавать. Что не очень быстро. Поэтому, будучи в здравом уме, я понимал, что граф надо представить в удобном виде.
Как человек, недалекий от теории графов, я помнил только одно представление графа — Матрица смежности. Правда моё создание подсказывало, что есть и другие, и немного поднапряг память, я вспомнил три варианта представления графа:
- Список вершин и список ребер — отдельно храним вершины, отдельно храним ребра.
- Матрица смежности — для каждой вершины храним информацию, есть ли переход в другую вершину
- Список смежности — для каждой вершины храним список переходов
Но прежде чем напрягать мозги, пальцы уже сделали своё дело, и пока я думал какой сейчас час, на экране уже успел появиться код для создания графа в виде матрицы смежности. Жалко конечно, но код пришлось переписать — для моей задачи важнее как можно быстрее находить исходящие ребра, а вот входящие меня мало интересуют. Да и память в наше время безгранична — почему бы её не сэкономить?
Переписав код, получилось что-то на подобии такого:
Graph:
vertices: [Vertex]
adjacencyList: [[Edge]]
Vertex:
more information about vertex
Edge:
toIndices: [Int]
information about edgeГде Vertex информация о вершине, а Edge информация о переходе, в том числе и индексы, куда по этому ребру можно перейти.
Обращаю внимание что ребро хранит переход не один в один, а один в много. Это сделано специально, чтобы обеспечить уникальность рёбер, что в случае зависимостей очень важно, так как два перехода на две вершины, и один переход на две вершины означает разное.
Этап 2. Наивный поиск в глубину
Из начала статьи все же помнят, что к этому моменту было уже 4 часа утра, а значит, единственная идея, как реализовать поиск всех простых циклов была та, что я нашел в гугле, да и мой учитель всегда говорил — “прежде чем оптимизировать, убедись, что это необходимо”. Поэтому первым делом я написал обычный поиск в глубину:
Код
func findAllCycles() -> [Cycle] {
result: [Cycle] = []
for index in vertices {
result += findCycles(from: index)
}
return result
}
func findCycles(from index: Int) -> [Cycle] {
result: [Cycle] = []
dfs(startIndex: index, currentIndex: index, visitedIndices: [], result: &result)
return result
}
func dfs(startIndex: Int,
currentIndex: Int,
// visitedIndices каждый раз копируется
visitedIndices: Set<Int>,
// result всегда один - это ссылка
result: ref [Cycle]) {
if currentIndex == startIndex && !visitedIndices.isEmpty {
result.append(cycle)
return
}
if visitedIndices.contains(currentIndex) {
return
}
visitedIndices += [currentIndex]
for toIndex in adjacencyList[currentIndex] {
dfs(startIndex: startIndex, currentIndex: toIndex, visitedIndices: visitedIndices, result: &result)
}
}Запустил этот алгоритм, подождал 10 минут… И, конечно же, ушел спать — А то уже солнце появилось из-за верхушек зданий…
Пока спал, думал — а почему так долго? Про размер графа я уже писал, но в чем проблема данного алгоритма? Судорожно вспоминая дебажные логи вспомнил, что для многих вершин количество вызовов функции dfs составляет миллион, а для некоторых по 30 миллионов раз. То есть в среднем 900 вершин * 1000000 = 900.000.000 вызовов функции dfs…
Откуда такие бешеные цифры? Будь бы это обычный лес, то все бы работало быстро, но у нас же граф с циклами… ZZzzz…
Этап 3. Наивная оптимизация
Проснулся я снова не по завету после обеда, и первым делом было не пойти в туалет, и уж точно не поесть, а посмотреть, сколько же выполнялся мой алгоритм, а ну да всего-то полтора часа… Ну, ладно, я за ночь придумал, как оптимизировать!
В первой реализации ищутся циклы, проходящие только через указанную вершину, а все подциклы, найденные при поиске основных циклов, просто игнорируются. Возникает желание перестать их игнорировать — тогда получается, что можно выкидывать из рассмотрения все вершины, через которые мы уже прошли. Сделать это не так сложно, правда, когда пальцы не попадают по клавиатуре чуть сложнее, но каких-то полчаса и готово:
Код
func findAllCycles() -> [Cycle] {
globalVisitedIndices: Set<Int> = []
result: [Cycle] = []
for index in vertices {
if globalVisitedIndices.containts(index) {
continue
}
result += findCycles(from: index, globalVisitedIndices: &globalVisitedIndices)
}
return result
}
func findCycles(from index: Int, globalVisitedIndices: ref Set<Int>) -> [Cycle] {
result: [Cycle] = []
dfs(currentIndex: index, visitedIndices: [], globalVisitedIndices, &globalVisitedIndices, result: &result)
return result
}
func dfs(currentIndex: Int,
// visitedIndices каждый раз копируется
visitedIndices: Set<Int>,
// globalVisitedIndices всегда один - это ссылка
globalVisitedIndices: ref Set<Int>,
// result всегда один - это ссылка
result: ref [Cycle]) {
if visitedIndices.contains(currentIndex) {
// если visitedIndices упорядочен, то вырезав кусок, можно получить информацию о цикле
result.append(cycle)
return
}
visitedIndices += [currentIndex]
for toIndex in adjacencyList[currentIndex] {
dfs(currentIndex: toIndex, visitedIndices: visitedIndices, globalVisitedIndices: &globalVisitedIndices, result: &result)
}
}Дальше по заповедям программиста “Программист ест, билд идёт” я ушел есть… Ем я быстро. Вернувшись через 10 минут и увидев, что все еще нет результата, я огорчился, и решил подумать, в чем же проблема:
- Если у меня несколько больших раздельных циклов, то на каждый такой цикл тратится уйму времени, благо, всего один раз.
- Многие циклы “дублируются” — нужно проверять уникальность при добавлении, а это время на сравнение.
Интуиция мне подсказывала, что первый вариант был лучше. На самом деле он понятней для анализа, так как мы запоминаем циклы для конкретной вершины, а не для всего подряд.
Этап 4. А что если отсекать листья из поиска
Проснуться я уже успел, а значит самое время для листочка и карандаша. Посмотрев на цифры, нарисовав картинки на листочке, стало понятно, что листья обходить не имеет смысла, и даже не листья, а целые ветки, которые не имеют циклов. Смысл в них заходить, если мы ищем циклы? Вот их и будем отсекать. Пока это думал, руки уже все сделали, и даже нажали run… Ого, вот это оптимизация — глазом моргнуть не успел, а уже все нашло… Ой, а чего циклов так мало то нашлось… Эх… А всё ясно проблема в том, что я не налил себе стакан воды. На самом деле проблема вот в этой строчке:
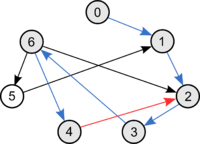
if visitedIndices.contains(currentIndex) {Я решил, что в этом случае мы тоже наткнулись на лист, но это неверно. Давайте рассмотрим вот такой граф:
В этом графе есть под цикл B->E->C значит, этот if выполнится. Теперь предположим, что вначале мы идем так:
A->B->E->C->B!.. При таком проходе C, Е помечается как лист. После находим цикл A->B->D->A.
Но Цикл A->C->B->D->A будет упущен, так как вершина C помечена как лист.
Если это исправить и отбрасывать только листовые под ветки, то количество вызовов dfs снижается, но не значительно.
Этап 5. Делаем подготовку к поиску
Ладно, еще целых полдня впереди. Посмотрев картинки и различные дебажные логи, стало понятно, что есть ситуации, где функция dfs вызывается 30 миллионов раз, но находится всего 1-2 цикла. Такое возможно в случаях на подобии:
Где “Big” это какой-то большой граф с кучей циклов, но не имеющий цикла на A.
И тут возникает идея! Для всех вершин из Big и C, можно заранее узнать, что они не имеют переходов на A или B, а значит, при переходе на C понятно, что эту вершину не нужно рассматривать, так как из нее нельзя попасть в A.
Как это узнать? Заранее, для каждой вершины запустить или поиск в глубину, или в ширину, и не посещать одну вершину дважды. После сохранить посещенные вершины. Такой поиск в худшем случае на полном графе займет O(N^2) времени, а на реальных данных намного меньше.
Текст для статьи я писал гораздо дольше, чем код для реализации:
Код
func findAllCycles() -> [Cycle] {
reachableIndices: [Set<Int>] = findAllReachableIndices()
result: [Cycle] = []
for index in vertices {
result += findCycles(from: index, reachableIndices: &reachableIndices)
}
return result
}
func findAllReachableIndices() -> [Set<Int>] {
reachableIndices: [Set<Int>] = []
for index in vertices {
reachableIndices[index] = findAllReachableIndices(for: index)
}
return reachableIndices
}
func findAllReachableIndices(for startIndex: Int) -> Set<Int> {
visited: Set<Int> = []
stack: [Int] = [startIndex]
while fromIndex = stack.popFirst() {
visited.insert(fromIndex)
for toIndex in adjacencyList[fromIndex] {
if !visited.contains(toIndex) {
stack.append(toIndex)
}
}
}
return visited
}
func findCycles(from index: Int, reachableIndices: ref [Set<Int>]) -> [Cycle] {
result: [Cycle] = []
dfs(startIndex: index, currentIndex: index, visitedIndices: [], reachableIndices: &reachableIndices, result: &result)
return result
}
func dfs(startIndex: Int,
currentIndex: Int,
visitedIndices: Set<Int>,
reachableIndices: ref [Set<Int>],
result: ref [Cycle]) {
if currentIndex == startIndex && !visitedIndices.isEmpty {
result.append(cycle)
return
}
if visitedIndices.contains(currentIndex) {
return
}
if !reachableIndices[currentIndex].contains(startIndex) {
return
}
visitedIndices += [currentIndex]
for toIndex in adjacencyList[currentIndex] {
dfs(startIndex: startIndex, currentIndex: toIndex, visitedIndices: visitedIndices, result: &result)
}
}Готовясь к худшему, я запустил новую реализацию, и пошел смотреть в окно на ближайшее дерево, в 5 метрах — вдаль смотреть говорят полезно. И вот счастье — код полностью исполнился за 15 минут, что в 6-7 раз быстрее прошлого варианта. Порадовавшись мини победе, и порефачив код, я начал думать, что же делать — такой результат меня не устраивал.
Этап 6. Можно ли использовать прошлые результаты?
Все время пока я писал код, и пока спал, меня мучил вопрос — а можно ли как-то использовать результат прошлых вычислений. Ведь уже найдены все циклы через некоторую вершину, наверное, что-то это да значит для других циклов.
Чтобы понять, что это значит, мне понадобилось сделать три итерации, каждая из которых была оптимальней предыдущей.
Все началось с вопроса — “Зачем начинать поиск с новой вершины, если все исходящие ребра ведут в вершины, которые или не содержат цикла, или это вершина через которую уже были построены все циклы?”. Потом поток мыслей дошел до того что проверку можно делать рекурсивно. Это позволило уменьшить время до 5 минут.
И только выпив залпом весь стакан с водой, а он 250мл, я осознал, что эту проверку можно вставить, прям внутри поиска в глубину:
Код
func findAllCycles() -> [Cycle] {
reachableIndices: [Set<Int>] = findAllReachableIndices()
result: [Cycle] = []
for index in vertices {
result += findCycles(from: index, reachableIndices: &reachableIndices)
}
return result
}
func findAllReachableIndices() -> [Set<Int>] {
reachableIndices: [Set<Int>] = []
for index in vertices {
reachableIndices[index] = findAllReachableIndices(for: index)
}
return reachableIndices
}
func findAllReachableIndices(for startIndex: Int) -> Set<Int> {
visited: Set<Int> = []
stack: [Int] = [startIndex]
while fromIndex = stack.popFirst() {
visited.insert(fromIndex)
for toIndex in adjacencyList[fromIndex] {
if !visited.contains(toIndex) {
stack.append(toIndex)
}
}
}
return visited
}
func findCycles(from index: Int, reachableIndices: ref [Set<Int>]) -> [Cycle] {
result: [Cycle] = []
dfs(startIndex: index, currentIndex: index, visitedIndices: [], reachableIndices: &reachableIndices, result: &result)
return result
}
func dfs(startIndex: Int,
currentIndex: Int,
visitedIndices: Set<Int>,
reachableIndices: ref [Set<Int>],
result: ref [Cycle]) {
if currentIndex == startIndex && !visitedIndices.isEmpty {
result.append(cycle)
return
}
if visitedIndices.contains(currentIndex) {
return
}
if currentIndex < startIndex || !reachableIndices[currentIndex].contains(startIndex) {
return
}
visitedIndices += [currentIndex]
for toIndex in adjacencyList[currentIndex] {
dfs(startIndex: startIndex, currentIndex: toIndex, visitedIndices: visitedIndices, result: &result)
}
}Изменения только тут: if currentIndex < startIndex.
Посмотрев на это простое решение, я нажал run, и был уже готов снова отойти от компьютера, как вдруг — все проверки прошли… 6 секунд? Не, не может быть… Но по дебажным логам все циклы были найдены.
Конечно, я подсознательно понимал, почему оно работает, и что я сделал. Постараюсь эту идею сформировать в тексте — Если уже найдены все циклы, проходящие через вершину A, то при поиске циклов проходящих через любые другие вершины, рассматривать вершину A не имеет смысла. Так как уже найдены все циклы через A, значит нельзя найти новых циклов через неё.
Такая проверка не только сильно ускоряет работу, но и полностью устраняет появление дублей, без необходимости их обрезать/сравнивать.
Что позволяет сэкономить время на способе хранения циклов — можно или вообще не хранить их или хранить в обычном массиве, а не множестве. Это экономит еще 5-10% времени исполнения.
Этап 6. Профайл
Результат в 5-6 секунд меня уже устраивал, но хотелось еще быстрее, на улице еще солнце даже светит! Поэтому я открыл профайл. Я понимал, что на языке Swift низкоуровневая оптимизация почти невозможна, но иногда находишь проблемы в неожиданных местах.
И какое было моё удивление, когда я обнаружил, что половину времени из 6 секунд занимают логи библиотеки… Особенно с учетом, что я их выключил. Как говорится — “ты видишь суслика? А он есть…”. У меня суслик оказался большим — на пол поля. Проблема была типичная — некоторое строковое выражение считалось всегда, независимо от необходимости писать его в логи.
Запустив приложение и увидев 3 секунды, я уже хотел было остановиться, но меня мучило одно предчувствие в обходе в ширину. Я давно знал, что массивы у Apple сделаны так, что вставка в начало и в конец массива занимает константное время в силу кольцевой реализации внутри (извиняюсь, я не помню, как правильно это называется). И на языке Swift у массива есть интересная функция popLast(), но нет аналога для первого элемента. Но проще показать.
было (язык Swift)
var visited: Set<Int> = []
var stack: [Int] = [startVertexIndex]
while let fromIndex = stack.first {
stack.removeFirst()
visited.insert(fromIndex)
for toIndex in graph.adjacencyList[fromIndex].flatMap({ $0.toIndices }) {
if !visited.contains(toIndex) {
stack.append(toIndex)
}
}
}
return visitedcтало (язык Swift)
var visited: Set<Int> = []
var stack: [Int] = [startVertexIndex]
while let fromIndex = stack.popLast() {
visited.insert(fromIndex)
for toIndex in graph.adjacencyList[fromIndex].flatMap({ $0.toIndices }) {
if !visited.contains(toIndex) {
stack.insert(toIndex, at: 0)
}
}
}
return visitedВроде изменения не значительные и, кажется, что второй код должен работать медленнее — и на многих языках второй код будет работать медленнее, но на Swift он быстрее на 5-10%.
Итоги
А какие могут быть итоги? Цифры говорят сами за себя — было 95 минут, стало 2.5-3 секунды, да еще и добавилось новых проверок.
Три секунды тоже выглядит не шустро, но не стоит забывать, что это на большом и не красивом графе зависимостей — такие днем с огнем не сыщешь в мобильной разработке.
Да и на другом проекте, который больше похож на средний мобильный проект, время с 15 минут уменьшилось до менее секунды, при этом на более слабом железе.
Ну а появлению статьи благодарим гугл — который не захотел мне помогать, и я придумывал все из головы, хоть и понимаю, что Америку я не открыл.
Весь код на языке Swift можно найти в папке.
Немного рекламы и Планы
Кому понравилась статья, или не понравилась, пожалуйста, зайдите на страницу библиотеки и поставьте ей звёздочку.
Я каждый раз озвучиваю планы по развитию, каждый раз говорю “скоро” и всегда скоро оказывается когда-нибудь. Поэтому сроков называть не буду, но когда-нибудь это появится:
- Конвертация графа зависимостей в формат для graphvis — а он в свою очередь позволит просматривать графы визуально.
- Оптимизация основного функционала библиотеки — С появлением большого количества новых возможностей, моя библиотека хоть и осталось быстрой, но теперь она не сверх быстрая, а на уровне других библиотек.
- Переход на проверку графа и поиск проблем во время компиляции, а не при запуске приложения.
P.S. Если отключить 5 этап полностью, это который добавление доп. действия перед началом поиска, то скорость работы понизится в 1.5 раза — до 4.5 секунд. То есть в этой операции даже после всех других оптимизаций есть толк.
P.P.S. Некоторые факты из статьи выдуманные, для придания красоты картины. Но, я на самом деле пью только чистую воду, и не пью чай/кофе/алкоголь.
UPD: По просьбе добавляю ссылку на сам граф. Он описан в dot формате, имена вершин просто нумерацией. Ссылка
Посмотреть на то как это выглядит визуально можно по этой ссылке.
UPD: banshchikov нашёл другой алгоритм Donald B. Johnson. Более того есть его реализация на swift.
Я решил сравнить свой алгоритм, и этот алгоритм на имеющемся графе.
Вот что получилось:
Время измерялось только на поиск циклов. Сторонняя библиотека конвертирует входные данные в удобные ей, но подобная конвертация должна занимать не более 0.1 секунды. А как видно время отличается на порядок (а в релизе на два). И списать такую большую разницу на неоптимальную реализацию нельзя.
- Как я писал, в моей в библиотеки ребра это не просто переход из одной вершины в другую. В стороннюю реализацию подобную информацию передать нельзя, поэтому количество найденных циклов не совпадает. Из-за этого в результатах ищутся все уникальные циклы по вершинам, без учета рёбер, дабы убедиться в совпадении результата.
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
Поиск циклов и матрица смежности
—
Алгоритмы на графах
В этом и других курсах вы могли сталкиваться с различными учебными проектами. Обычно они достаточно реалистичные, но одно различие все таки есть — все учебные проекты небольшие.
Реальные проекты намного больше учебных. Чтобы разработчики не путались в коде, обычно большие проекты состоят из отдельных пакетов. При этом появляются зависимости.
Например, если пакет А импортирует или использует пакет Б, мы говорим: «А зависит от Б». На схеме эту зависимость можно обозначить так:

Чтобы собрать проект, нам нужно загружать или компилировать пакеты в правильном порядке. Если А зависит от Б, то сначала надо загрузить пакет Б, и только потом перейти к пакету А.
Когда пакетов в проекте много, количество зависимостей тоже растет. Вместе они образуют сложный граф зависимостей:

Пакеты из этого графа можно загружать или компилировать в правильном порядке. Судя по графу, возможно три варианта:
-
Д, Б, В, Г, А
-
Д, Г, В, Б, А
-
Д, В, Г, Б, А
У нас есть выбор, потому что ветки Г и Б + В не зависят друг от друга. В любом случае первым пакетом следует Д, потому что он ни от кого не зависит. Последним идет пакет А, потому что от него никто не зависит.
Подобная структура зависимостей часто встречается в программировании. Например, таким образом мы описываем связи между классами, которые задействованы в коде. Это называется внедрение зависимостей (Dependency Injection).
Но есть проблема — часто программисты не описывают граф целиком, а только указывают, от каких узлов зависит очередной узел.
Это приводит к тому, что в графе может появиться циклическая зависимость:

В циклическом графе невозможно определить правильный порядок компиляции пакетов или создания объектов. Справиться с этой сложностью помогают системы сборки и библиотеки внедрения зависимостей. Именно благодаря им программисты находят циклы в описанных графах.
В этом уроке мы научимся искать циклы в ориентированных графах. Задача для неориентированных графов на практике встречается гораздо реже, поэтому мы не станем обсуждать ее подробно. Она решается похожим образом, так что алгоритм можно без труда адаптировать.
Матрица смежности
В прошлых уроках мы познакомились с двумя способами представления графов:
-
Со списками смежности
-
С неявным представлением
Сегодня изучим матрицу смежности — еще одну структуру данных, которую часто применяют при работе с графами.
Все вершины графа мы храним в массиве, так что у каждой вершины появляется уникальный порядковый номер. В большинстве современных языков программирования нумерация элементов начинается с ноля. Поэтому у нас будут вершина
, вершина
, вершина
и так далее:

Важно, что номера вершин идут подряд без пропусков.
Вместе с массивом мы храним матрицу — двумерный массив. Ее ширина и высота равны количеству вершин. Есть речь идет об обычном невзвешенном графе, элементами массива будут:
-
Либо булевы значения —
и
-
Либо числа
и
Вернемся к рисунку выше. На нем мы видим, какие вершины связаны между собой. Эту информацию мы можем записать в матрицу смежности. Помните, что нумерация вершин начинается с 0, поэтому нумерация столбцов и строк сдвигается на единицу.
-
На графе вершина
связана с вершиной
— записываем
в строку
и столбец
:
-
На графе вершина
не связана с вершиной
— записываем
в строку
и столбец
:
Перебирая элементы строки, мы можем найти все связанные вершины.
Во взвешенном графе вместо булевых значений мы можем хранить числа:
-
Если вершины не связаны —
-
Если вершины связаны — число, обозначающее вес ребра
Матрица смежности подходит для хранения ориентированных графов. Для хранения неориентированных графов программисты используют небольшой трюк, делая матрицу симметричной. Для примера представим, что мы хотим связать вершины
и
. В этом случае мы записываем
два раза:
-
В столбец
и строку
-
В столбец
и строку
Так мы получаем двустороннюю связь.
Поиск цикла
Обычно нам надо убедиться, что в графе нет циклов. Поэтому мы пытаемся найти хотя бы один любой цикл. Если нам это удается, то мы подсказываем пользователю, из каких вершин он состоит.
Оказывается, для поиска циклов не надо изобретать нового алгоритма — можно адаптировать обход графа в глубину. При обходе мы будем помечать посещенные вершины. В реальной программе каждой вершине будет приписан числовой код, но при объяснении алгоритма принято говорить о «перекрашивании» вершин.
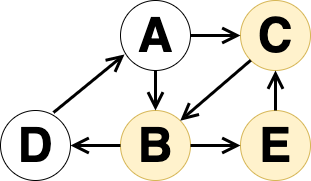
Попробуем найти цикл в таком небольшом графе:

В начале все вершины в графе белые. Такому графу соответствует матрица смежности, изображенная ниже:
Начинать можно с любой вершины. Мы начнем с вершины
, которой соответствует верхняя строка в матрице.
Перекрашиваем вершину в серый цвет. Это означает, что мы начали с ней работать:

Ищем в первой строке связанные вершины. Они помечены значением
.
Видим, что вершина
связана со вторым элементом строки — вершиной
. Начинаем работать с ней и также перекрашиваем ее в серый цвет:

Чтобы обнаружить связанные вершины, рассмотрим вторую строку сверху. Она соответствует вершине
. Похожим образом продолжаем перекрашивать вершины. Следующие на очереди —
и
:

Из вершины
двигаться некуда. Мы завершаем ее обработку, перекрашиваем в черный цвет и возвращаемся в вершину
.
У второй вершины есть еще одна необработанная вершина —
. Перекрашиваем ее в серый цвет:

У вершины
также нет связанный вершин. Завершаем ее обработку, перекрашиваем в черный цвет, снова возвращаемся в вершину 2.
Теперь и у вершины
обработаны все соседи — значит, ее обработка также завершена. Перекрашиваем ее в черный цвет и возвращаемся в вершину
:

У вершины
есть следующая необработанная вершина — это
.
В свою очередь у вершины
есть необработанная вершина
:

Вершина
связана с вершиной
, которая окрашена в серый цвет. Это значит, что мы обнаружили цикл.
Далее нужно разобраться, какие вершины входят в цикл. Для этого мы возвращаемся назад, пока не встретим вершину
. Так мы выясним, что в нашем примере в цикл попадают вершины
,
,
и
.
Если мы встречаем черную вершину, это означает, что цикл в нашем графе есть, но он не опасен. Двигаясь по стрелкам, мы не попадаем в замкнутый круг:

Двигаясь по стрелкам, ромб слева можно обойти без зацикливания, а ромб справа — нет. Другими словами, встречая черную вершину, мы должны ее пропускать. Черная вершина означает, что мы встретили уже обработанную область графа без циклов.
Реализация
Теперь посмотрим, как такой алгоритм реализуется в коде:
class Graph {
vertices;
size;
edges;
constructor(vertices) {
this.vertices = vertices;
this.size = vertices.length;
this.edges = Array.from({length: this.size}, () => {
return Array(this.size).fill(false);
});
}
addEdge(value1, value2) {
const row = this.vertices.indexOf(value1);
const column = this.vertices.indexOf(value2);
this.edges[row][column] = true;
}
findCycle() {
const WHITE = 0;
const GRAY = 1;
const BLACK = 2;
let colors = Array(this.size).fill(WHITE);
const visit = i => {
if (colors[i] === BLACK) {
return null;
} else if (colors[i] === GRAY) {
return [];
}
colors[i] = GRAY;
for (let j = 0; j < this.size; j++) {
if (this.edges[i][j]) {
const result = visit(j);
if (Array.isArray(result)) {
return [...result, this.vertices[i]];
}
}
}
colors[i] = BLACK;
return null;
};
return visit(0);
}
}Как и в прошлых уроках, для работы с графом сделаем класс Graph. В конструкторе мы будем получать массив значений в вершинах графа. Размер массива сохраним в поле size для последующего использования. Также сразу создадим квадратную матрицу смежности, заполним ее значением false:
constructor(vertices) {
this.vertices = vertices;
this.size = vertices.length;
this.edges = Array.from({length: this.size}, () => {
return Array(this.size).fill(false);
});
}Далее мы создаем связь. По сути, это нахождение элемента в матрице и присвоение ему значения true:
addEdge(value1, value2) {
const row = this.vertices.indexOf(value1);
const column = this.vertices.indexOf(value2);
this.edges[row][column] = true;
}Для поиска циклов нам потребуются константы, чтобы обозначать белый, серый и черный цвет вершин, а также массив цветов всех вершин. В начале работы алгоритма все вершины белые:
const WHITE = 0;
const GRAY = 1;
const BLACK = 2;
let colors = Array(this.size).fill(WHITE);Функция возвращает массив вершин, образующих либо цикл, либо значение null при отсутствии циклов.
Основная работа делается во внутренней рекурсивной функции visit(). В качестве параметра она получает порядковый номер вершины. Так как нумерация начинается с нуля, первой вершине соответствует номер 0.
В массиве colors функция выясняет цвет вершины. Если вершина черная, функция сразу прекращает свою работу. Если вершина серая, функция также прекращает работу, но в качестве результата возвращает пустой массив:
if (colors[i] === BLACK) {
return null;
} else if (colors[i] === GRAY) {
return [];
}В середине мы обрабатываем текущую вершину. Перекрашиваем ее в серый цвет, а после обработки всех связанных вершин — в черный:
colors[i] = GRAY;
for (let j = 0; j < this.size; j++) {
if (this.edges[i][j]) {
const result = visit(j);
if (Array.isArray(result)) {
return [...result, this.vertices[i]];
}
}
}
colors[i] = BLACK;
return null;Обработка связанных вершин заключается в поочередном рекурсивном вызове функции visit(). Если во время очередного вызова функция возвращает массив, это значит, что мы нашли цикл. Добавляем в массив текущую вершину и возвращаем новое значение.
Когда рекурсия развернется, в массиве окажутся все вершины из цикла. Именно этот массив и получит программист, вызвавший функцию.
Чтобы проверить наш код, создадим граф из примера выше и попытаемся найти в нем цикл:
let graph = new Graph(['0', '1', '2', '3', '4', '5', '6']);
graph.addEdge('0', '1');
graph.addEdge('1', '2');
graph.addEdge('1', '5');
graph.addEdge('2', '3');
graph.addEdge('2', '4');
graph.addEdge('5', '6');
graph.addEdge('6', '0');
let cycle = graph.findCycle(); // [ '6', '5', '1', '0' ]





![Vertex 3 is unmarked from recStack[]](https://media.geeksforgeeks.org/wp-content/uploads/20230322115353/img5drawio.webp)