Как найти циркуляцию магнитной индукции по контуру - Сайт, где вы сможете решить свои вопросы

Французские ученые Ж. Био и Ф. Савар в 1820-м году проводили эксперименты над магнитным полем постоянных токов. Физики доказали, что индукция магнитного поля проходящих по проводнику токов зависит от совместного действия всех участков данного проводника. Работа магнитного поля основана на принципе суперпозиции.

Определение 1

Принцип суперпозиции: если магнитное поле работает за счет нескольких проводников с током, тогда индукция результативного поля – это совокупность индукций полей, которые создаются каждым проводником по отдельности.

Индукция B→ проводника с током представлена, как векторная сумма элементарных индукций ∆B→ вырабатываемых отдельными участками проводника. На практике нельзя отделить один участок проводника с током, поскольку постоянные токи всегда замкнутые. Возможно лишь измерить совокупную индукцию магнитного поля, которое создают все элементы тока. Как найти индукцию магнитного поля?

Закон Био–Савара

Определение 2

Закон Био-Савара определил вклад ∆B→ в магнитную индукцию B→ результативного магнитного поля, образуемый маленьким участком Δl проводника с током I.

∆B=μ0·I·∆l·sin α4πr2.

В формуле r – это расстояние от заданного участка Δl до точки наблюдения, α – это угол между направлением на точку наблюдения и направлением тока на заданном участке, μ0 – это магнитная постоянная.

Используя правило буравчика, определим направление вектора ∆B→: оно указывает на ту сторону, в которую вращается рукоятка буравчика при его поступательном движении вдоль тока. Рисунок 1.17.1 наглядно показывает закон Био-Савара с применением магнитного поля прямолинейного проводника с током. Если сложить (интегрировать) вклады в магнитное поле всех участков проводника с током, тогда получим формулу для магнитной индукции поля прямого тока:

B=μ0I2πR.

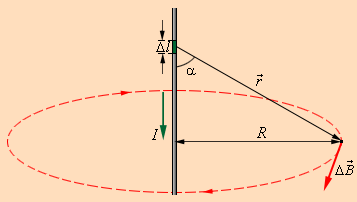
Рисунок 1.17.1. Иллюстрация закона Био–Савара.

С помощью этого закона можно определять магнитные поля токов с различными конфигурациями. Запросто рассчитать магнитное поле в центре кругового витка с током. Вычисления приводят к соотношению:

B=μ0I2πR,

где R – это радиус кругового проводника.

Чтобы определить направление вектора B→ тоже используется правило буравчика, только в этом случае рукоятка вращается по направлению кругового тока, а поступательное движение буравчика указывает, куда направлен вектор магнитной индукции.

Теорема о циркуляции вектора магнитной индукции

Определение 3

Вычисления магнитного поля зачастую упрощаются с учетом симметрии в конфигурации токов. В этом помогает теорема о циркуляции вектора магнитной индукции.

Объясним, что означает циркуляция вектора B→. Допустим, в пространстве с магнитным полем существует какой-то условный замкнутый контур, а также положительное направление его обхода. Тогда, на каждом отдельном маленьком участке Δl данного контура определяется касательная составляющая Bl вектора B→ в этом месте, то есть определяется проекция вектора B→ на направление касательной к заданному участку контура. Рисунок 1.17.2 наглядно демонстрирует это.

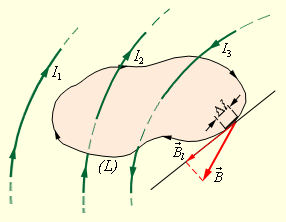
Рисунок 1.17.2. Замкнутый контур (L) с заданным направлением обхода. Изображение токов I1, I2 и
I3, создающих магнитное поле.

Определение 4

Циркуляция вектора B→ – это сумма произведений Bl∆l, взятая по целому контуру L: B→=∑(L)Bl∆l.

Некоторые токи, при которых магнитное поле создается, пропускают выбранный контур L тем временем, как остальные токи находятся в стороне от контура.

Теорема 1

Согласно теореме о циркуляции, циркуляция вектора B→ магнитного поля постоянных токов по любому из контуров L все время определяется, как произведение магнитной постоянной μ0 на сумму всех токов:

∑(L)Bl∆l=μ0∑li.

Пример 1

На рисунке 1.17.2 продемонстрирован пример с несколькими проводниками с токами, образующими магнитное поле. Ток I2 и ток I3 пронзают контур L в противоположных направлениях, им приписываются различные знаки. Положительным является ток, который связан с заданным направлением обхода контура по правилу буравчика.

Значит, I3>0, а I2<0. Ток I1 не пронзает контур L.

Теорема о циркуляции в этом примере математически выражается следующей формулой:

∑(L)Bl∆l=μ0(I3-I2).

Общий вид теоремы о циркуляции можно вывести из принципа суперпозиции и закона Био-Савара.

Пример 2

Самый простой пример использования теоремы о циркуляции – это вывод формулы магнитного поля прямолинейного проводника с током. С учетом симметрии в этой задаче контуром L лучше выбрать окружность какого-то радиуса R, лежащую в перпендикулярной проводнику плоскости. Центр окружности задан в какой-то точке проводника. Из-за симметрии вектор B→ направляется по касательной (Bl=B), а его модуль имеет одинаковое значение по всей окружности. Использование теоремы о циркуляции приводит к выражению:

∑(L)Bl∆l=2πRB=μ0I,

отсюда можно вывести формулу для модуля магнитной индукции поля прямолинейного проводника с током, приведенную раньше.

Из данного примера видно, что теорема о циркуляции вектора магнитной индукции B→ можно использовать для вычисления магнитных полей, которые создаются симметричным распределением токов, когда можно наугад определить общую структуру поля.

Существует много примеров определения магнитных полей при помощи теоремы о циркуляции.

Пример 3

Рассмотрим одну из них – это задачу расчета поля тороидальной катушки (рисунок 1.17.3).

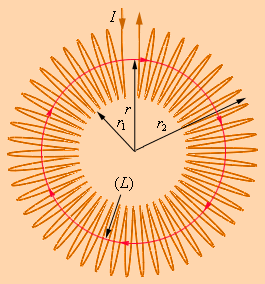
Рисунок 1.17.3. Использование теоремы о циркуляции к тороидальной катушке.

Предположим, что катушка намотана виток к витку на ненамагниченный тороидальный сердечник. В ней линии магнитной индукции сходятся внутри катушки и выступают концентрическими окружностями. Они имеет такое направление, что, смотря вдоль них, наблюдатель увидел бы ток в витках, циркулирующих по часовой стрелке.

Одна линия индукции какого-то радиуса r1≤r<r2 представлена на рисунке 1.17.3. Используем теорему о циркуляции для контура L в виде окружности, которая совпадает с линией индукции магнитного поля, изображенной на рисунке 1.17.3. Опираясь на соображения о симметрии, делаем вывод, что модуль вектора B→ имеет одинаковое значение по всей линии. Исходя из теоремы о циркуляции, запишем:

B·2πr=μ0IN,

где N – это полное количество витков, а I – это ток, протекающий по виткам катушки. Значит, B=μ0IN2πr.

Так, модуль вектора магнитной индукции в тороидальной катушке находится в зависимости от радиуса r. При условии, что сердечник катушки тонкий, то есть r2–r1≪r, тогда магнитное поле внутри катушки почти однородное.

Величина n=N 2πr – это количество витков на единицу длины катушки. Следовательно, B=μ0In.

Сюда не относится радиус тора, потому оно действует и в предельном случае r→∞.

Определение 5

Однако в пределе каждая часть тороидальной катушки при необходимости рассматривается в качестве длинной прямолинейной катушки, которая называется соленоид. Вдали торцов такой катушки модуль магнитной индукции определяется, как соотношение в случае с тороидальной катушкой.

На рисунке 1.17.4 представлено магнитное поле катушки конечной длины. Обращаем внимание, что в центре катушки магнитное поле почти однородное и намного сильнее, чем снаружи. Это объясняется густотой линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле полностью находится внутри него.

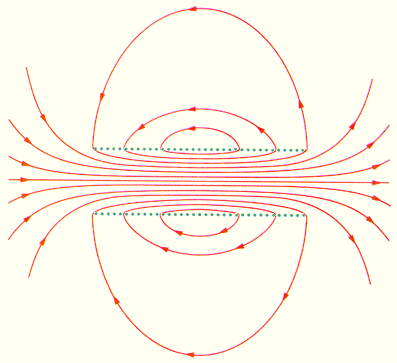
Рисунок 1.17.4. Магнитное поле катушки конечной длины. В центральной части соленоида магнитное поле почти однородное и существенно больше по модулю поля вне катушки.

В случае с бесконечно длинным соленоидом соотношение для модуля магнитной индукции получаем прямо из теоремы о циркуляции, применяя ее к прямоугольному контуру, изображенному на рисунке 1.17.5.

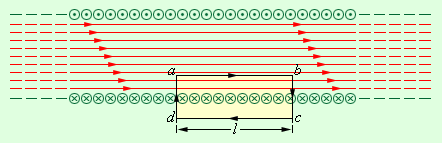
Рисунок 1.17.5. Теорема о циркуляции при расчете магнитного поля бесконечно длинного соленоида.

Проекция вектора магнитной индукции на направление обхода контура abcd только на стороне ab отлична от 0. Значит, циркуляция вектора B→ по контуру равняется Bl, где l – это длина стороны ab. Количество витков соленоида, пронзающих контур abcd, равняется n·l, где n – это количество витков на единицу длины соленоида, а полный ток, пронзающий контур, равняется Inl. Из теоремы о циркуляции, Bl=μ0Inl.

Отсюда B=μ0In.

Данное вычисление совпадает с формулой для магнитного поля тонкой тороидальной катушки.

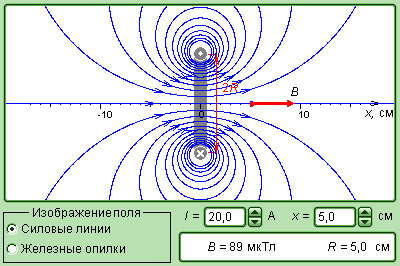
Рисунок 1.17.6. Модель магнитного поля кругового витка с током.

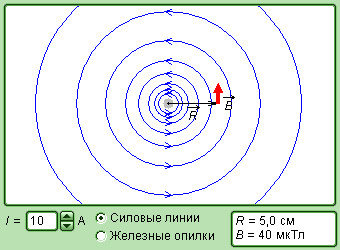
Рисунок 1.17.7. Модель магнитного поля прямого тока.

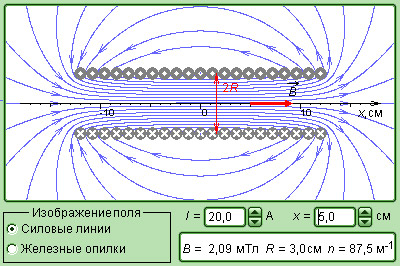
Рисунок 1.17.8. Модель магнитного поля соленоида.

Источник

Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером^{[источник не указан 752 дня]} в 1826 году^{[источник не указан 752 дня]}. В 1861 году Джеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой, и обобщил её (см. ниже). Уравнение, представляющее собой содержание теоремы в этом обобщённом виде, входит в число уравнений Максвелла. (Для случая постоянных электрических полей — то есть в принципе в магнитостатике — верна теорема в первоначальном виде, сформулированном Ампером и приведённом в статье первым; для общего случая правая часть должна быть дополнена членом с производной напряжённости электрического поля по времени — см. ниже). Теорема гласит^[1]:

Эта теорема, особенно в иностранной или переводной литературе, называется также теоремой Ампера или законом Ампера о циркуляции (англ. Ampère’s circuital law). Последнее название подразумевает рассмотрение закона Ампера в качестве более фундаментального утверждения, чем закон Био — Савара — Лапласа, который в свою очередь рассматривается уже в качестве следствия (что, в целом, соответствует современному варианту построения электродинамики).

Для общего случая (классической) электродинамики формула должна быть дополнена в правой части членом, содержащим производную по времени от электрического поля (см. уравнения Максвелла, а также параграф «Обобщение» ниже). В таком дополненном виде она представляет собой четвёртое уравнение Максвелла в интегральной форме.

Математическая формулировка[править | править код]

В математической формулировке для магнитостатики теорема имеет^[2] следующий вид^[1]^[3]:

$oint {vec B}cdot {vec {dl}}={frac {4pi }{c}}int {vec j}cdot {vec {ds}}$

Здесь — вектор магнитной индукции, vec j — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме^[4]:

${mathrm {rot}} {vec B}={frac {4pi }{c}}{vec j}$

Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса^[5].

Приведённая выше форма справедлива для вакуума. В случае применения её в среде (веществе), она будет корректна только в случае, если под j понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие в веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы (см. диамагнетики) и магнитные моменты микрочастиц (см.например ферромагнетики).

Поэтому в веществе, если не пренебрегать его магнитными свойствами, часто удобно из полного тока выделить ток намагничения (см. связанные токи), выразив его через величину намагниченности и введя вектор напряжённости магнитного поля

Тогда теорема о циркуляции запишется в форме^[6]

$oint {vec H}cdot {vec {dl}}={frac {4pi }{c}}int {vec j}_{f}cdot {vec {ds}}$

${mathrm {rot}} {vec H}={frac {4pi }{c}}{vec j}_{f},$

где под ${vec j}_{f}$ (в отличие от vec j в формуле выше) имеются в виду т. н. свободные токи, в которых ток намагничения исключён (что бывает удобно практически, поскольку ${vec j}_{f}$ — это обычно уже в сущности макроскопические токи, которые не связаны с намагничением вещества и которые в принципе нетрудно непосредственно измерить)^[7].

В динамическом случае — то есть в общем случае классической электродинамики — когда поля меняются во времени (а в средах при этом меняется и их поляризация) — и речь тогда идёт об обобщённой теореме, включающей , — всё сказанное выше относится и к микроскопическим токам, связанным с изменениями поляризации диэлектрика. Эта часть токов тогда учитывается в члене .

Обобщение[править | править код]

Основным фундаментальным обобщением^[8] теоремы является четвёртое уравнение Максвелла. В интегральной форме оно является прямым обобщением на динамический случай магнитостатической формулы, приведённой выше. Для вакуума^[9]:

$oint {vec B}cdot {vec {dl}}={frac {1}{c}}int (4pi {vec j}+{frac {partial {vec E}}{partial t}})cdot {vec {ds}}$

для среды^[10]:

$oint {vec {H}}cdot {vec {dl}}={frac {4pi }{c}}int {vec j}cdot {vec {ds}}+{frac {1}{c}}{frac {partial }{partial t}}int {vec {D}}cdot {vec {ds}}.$

(Как видим, формулы отличаются от приведённых выше только одним добавочным членом со скоростью изменения электрического поля в правой части).

Дифференциальная форма этого уравнения:

${mathbf {rot}}{vec {B}}={frac {4pi }{c}}{vec j}+{frac {1}{c}}{frac {partial }{partial t}}{vec {E}},$

${mathbf {rot}}{vec {H}}={frac {4pi }{c}}{vec j}+{frac {1}{c}}{frac {partial }{partial t}}{vec {D}}$

(в гауссовой системе, для вакуума и среды соответственно) — также можно при желании считать вариантом обобщения теоремы о циркуляции магнитного поля, поскольку она, конечно, тесно связана с интегральной.

Практическое значение[править | править код]

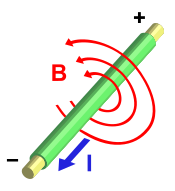
Магнитное поле прямолинейного проводника с током.

Теорема о циркуляции играет в магнитостатике приблизительно ту же роль, что и теорема Гаусса в электростатике. В частности, при наличии определённой симметрии задачи, она позволяет просто находить величину магнитного поля во всём пространстве по заданным токам^[1]. Например, для вычисления магнитного поля от бесконечного прямолинейного проводника с током по закону Био — Савара — Лапласа потребуется вычислить неочевидный интеграл, в то время как теорема о циркуляции (с учётом осевой симметрии задачи) позволяет дать мгновенный ответ:

$B(r)cdot 2pi r={frac {4pi }{c}}Ito B(r)={frac {2I}{cr}}$

Доказательство теоремы о циркуляции[править | править код]

Циркуляция магнитного поля

Если теорема о циркуляции магнитного поля не принимается в качестве аксиомы, то она может быть доказана с помощью закона Био — Савара — Лапласа. Рассмотрим магнитное поле, создаваемое в точке ${displaystyle {vec {p}}=(x_{0};y_{0};z_{0})}$ бесконечным проводом с током, заданным в пространстве кривой C. По закону Био — Савара — Лапласа токовый элемент провода, заданный радиус-вектором , создаёт в точке {vec p} элементарное поле ${displaystyle mathrm {d} {vec {B}}({vec {p}})={mu _{0} over 4pi }{frac {I[mathrm {d} {vec {r}}times ({vec {p}}-{vec {r}})]}{|{vec {p}}-{vec {r}}|^{3}}}}$ .

Полная индукция магнитного поля в точке {vec p} получается интегрированием элементарного поля по всей кривой C в направлении течения тока:

${displaystyle {vec {B}}({vec {p}})={mu _{0} over 4pi }int limits _{mathbb {C} }{frac {I[mathrm {d} {vec {r}}times ({vec {p}}-{vec {r}})]}{|{vec {p}}-{vec {r}}|^{3}}}}$

Нужно сразу отметить, что полученный интеграл не относится ни к одному из двух родов криволинейных интегралов. Как можно заметить, он определяет собой векторную величину, тогда как любой криволинейный интеграл является скалярной величиной. Но допустим, что его всё-таки можно вычислить каким-нибудь способом (например, интегрированием отдельно каждой компоненты вектора). Тогда найдём циркуляцию полученного вектора индукции по некоторому замкнутому контуру Г, обхватывающему провод с током.

По определению циркуляция векторной функции — это криволинейный интеграл второго рода от этой функции по замкнутому контуру в положительном направлении обхода этой кривой. Будем считать положительным направлением нормали к поверхности, натянутой на контур, такое направление, которое образует острый угол с осью z. Тогда положительное направление обхода контура определяется правилом буравчика (правого винта) по отношению к положительной нормали. Будем также считать положительным тот ток, который течёт в направлении положительной нормали контура, охватывающего ток.

Циркуляция будет иметь вид:

${displaystyle Gamma =oint _{Gamma }{vec {B}}cdot mathrm {d} {vec {p}}=oint _{Gamma }{mu _{0}I over 4pi }int limits _{mathbb {C} }{frac {[mathrm {d} {vec {r}}times ({vec {p}}-{vec {r}})]}{|{vec {p}}-{vec {r}}|^{3}}}cdot mathrm {d} {vec {p}}}$

Можно заметить, что под знаками интегралов появилось смешанное произведение векторов , которое по свойству кососимметрии может быть записано следующим образом:

Тогда циркуляция примет вид:

${displaystyle Gamma ={mu _{0}I over 4pi }oint _{Gamma }int limits _{mathbb {C} }({vec {p}}-{vec {r}})cdot {frac {[mathrm {d} {vec {p}}times mathrm {d} {vec {r}}]}{|{vec {p}}-{vec {r}}|^{3}}}}$

Нужно обратить внимание на то, чем является векторное произведение : его величина равна площади параллелограмма, построенного на этих векторах, а направление перпендикулярно этому параллелограмму. Тогда данное векторное произведение можно считать элементарной векторной площадкой поверхности, которую заметает вектор при двойном криволинейном интегрировании, причём угол между и , как можно заметить, является острым. Данная поверхность является цилиндрической поверхностью, охватывающей провод с током, а её сечением является контур циркуляции Г. Тогда двойной криволинейный интеграл можно заменить поверхностным интегралом второго рода по данной поверхности.

Тогда циркуляция примет вид:

${displaystyle Gamma ={mu _{0}I over 4pi }int !!!int _{S}({vec {p}}-{vec {r}})cdot {frac {mathrm {d} {vec {S}}}{|{vec {p}}-{vec {r}}|^{3}}}}$

Если считать поверхность интегрирования стягивающей поверхностью, легко видеть, что поверхностный интеграл представляет собой телесный угол для данной поверхности. Поверхность интегрирования условно можно считать замкнутой на бесконечности. И тогда, поскольку вектор при интегрировании всегда находится внутри поверхности, телесный угол является полным, то есть равным 4pi стерадиан. И тогда циркуляция равна ${displaystyle Gamma ={mu _{0}I over 4pi }4pi =mu _{0}I}$ .

Если бы контур Г не охватывал провод, тогда вектор при интегрировании никогда не находился бы полностью внутри поверхности интегрирования. В этом случае телесный угол был бы равен нулю, как и циркуляция поля: .

Последние два утверждения о телесном угле являются по сути содержанием теоремы Гаусса о потоке вектора напряжённости заряда через произвольную замкнутую поверхность и могут быть доказаны независимо.

Если бы ток тёк в противоположном направлении, угол между векторами и был бы уже тупым (нормаль была бы направлена внутрь поверхности), и циркуляция поменяла бы свой знак на противоположный, что эквивалентно течению тока в прежнем направлении, но с отрицательной силой.

В случае поля, создаваемого несколькими проводниками с током, нужно помнить о свойстве суперпозиции магнитного поля и свойстве аддитивности криволинейного интеграла: циркуляция суперпозиции векторов равна скалярной сумме циркуляций этих векторов.

Примечания[править | править код]

↑ ¹ ² ³ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 235. — 688 с.
↑ Приведено здесь в гауссовой системе единиц; в системе СИ константа в правой части вместо ${frac {4pi }{c}}$ записывается как $mu _{0}$ .
↑ здесь и ниже использована система СГС, в системе СИ коэффициенты отсутствуют
↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 239. — 688 с.
↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 241. — 688 с.
↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 253. — 688 с.
↑ На практике при написании уравнений для среды индекс f у токов как правило опускается, пишется просто . Также часто не делается оговорок о том, что это именно «свободные» токи. В такой феноменологической теории никаких других токов явно не рассматривается, хотя на самом деле (физически) связанные токи, конечно, есть, просто «спрятаны» в другие величины — итп и формально исключены из рассмотрения.
↑ Поскольку это обобщение основывается на верности магнитостатического варианта теоремы Ампера о циркуляции магнитного поля и сохранении заряда (которое может быть принято как постулат) и может быть показано достаточно строго соответствие обобщённого уравнения этим двум посылкам, а при наложении определённых дополнительных условий — и единственность такого обобщения, оно в принципе может быть также сформулировано в виде теоремы.
↑ В гауссовой системе единиц.
↑ В основном тексте — в гауссовой системе единиц. В СИ — так:

$oint {vec {H}}cdot {vec {dl}}=int {vec j}cdot {vec {ds}}+{frac {partial }{partial t}}int {vec {D}}cdot {vec {ds}}.$

Источник

Аналогично циркуляции вектора
напряженности электрического поля
введем циркуляцию вектора магнитной
индукции.

Циркуляцией вектора
по заданному замкнутому контуру
называется интеграл

– вектор элементарной длины, направленный
вдоль обхода контура,– составляющая векторав направлении касательной к контуру,– угол между векторами.

Закон полного тока для магнитного поля
(теорема о циркуляции вектора
):

Циркуляция вектора
по произвольному замкнутому контуру
равна произведениюна алгебраическую сумму токов, охватываемых
этим контуром.

⁼,

– число проводников с током, охватываемых
контуромпроизвольной
формы.

Каждый
ток учитывается столько раз, сколько
он охватывается контуром. Положительным
считается ток, направление которого
связано с направлением обхода по
контуру правилом правого винта.
Например, для рисунка 3,

Рис.3.

7. Магнитное поле соленоида.

Сравнивая циркуляции
ивидим принципиальное различие. Циркуляция
электрического поля равна нулю, то есть
электростатическое поле потенциально.
Работа по замкнутому пути в потенциальном
поле равна нулю.

Циркуляция
не равна нулю. Такое поле является
вихревым. Теорема о циркуляции вектораимеет такое же значение, как теорема
Гаусса в электростатике для потока
через замкнутую поверхность. Эта теорема
позволяет рассчитать индукцию поля без
применения закона Био – Савара- Лапласа

Пусть
длина соленоида
больше диаметра витка,.
Рассчитаем поток векторасквозь соленоид. (см. рис.40. Проведем
замкнутый контурсквозь витки соленоида. Внутри соленоида
()
поле однородно, вне ()
– неоднородно и очень слабо и им можно
пренебречь. Тогда циркуляция векторасквозь замкнутый контурравна

Рис.4.

где
–
угол междуи,
внутри соленоида равный нулю,– магнитная проницаемость сердечника
внутри соленоида,число витков соленоида,– длина соленоида. Тогда

Магнитный поток сквозь один виток
соленоида площадью
равен

А полный поток, сцепленный со всеми
витками соленоида и называемый
потокосцеплением равен

где
– индуктивность соленоида.

Отсюда

Лекция 11 Магнитное поле в веществе.

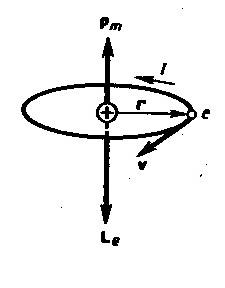
1. Магнитные моменты атомов.

Для объяснения магнитных явлений в
веществе рассматривают движение
электронов в атоме согласно классической
механике. Электрон вращается вокруг
ядра по круговой орбите.

Электрон,
движущийся по орбите эквивалентен
круговому току и обладает поэтому
орбитальным магнитным моментом

и модулем,
так как– сила тока.

– частота вращения электрона,– площадь орбиты. Теперь

Рис.1.

Направление
определяют по правилу буравчика.

Кроме орбитального магнитного момента
электрон обладает собственным магнитным
моментом – спином
.
Спин имеет квантовую природу и не имеет
аналогов в классике. Общий магнитный
момент атома или молекулыравен векторной сумме магнитных моментов
(орбитальных и спиновых) входящих в атом
электронов

Магнитный момент ядра атома в 1000 раз
меньше магнитных моментов электронов
и они не учитываются.

При попадании вещества в магнитное поле
оно намагничивается. Для количественного
описания намагничивания вводят векторную
величину
– намагниченность.

Вектором намагничивания данного вещества
называется физическая величина, численно
равная магнитному моменту единицы
объема

– магнитный момент магнетика, равный
векторной сумме магнитных моментов
отдельных молекул.– измеряется в А/м,– объем магнетика..

Магнитное поле в веществе складывается
из двух полей: внешнего поля, создаваемого
током, и поля создаваемого намагниченным
веществом. Вектор магнитной индукции
результирующего поля в магнетике равен
векторной сумме магнитных индукций
внешнего поля
,
поля образованного намагничивающим
током в вакууме и поля микротоков,

(1)

Магнитное поле макротока описывается
вектором напряженности
.

Опыт показывает, что при небольших
величина вектора намагничивания в
изотропных средах пропорциональна
напряженности поля,
вызывающего намагничение

–
магнитная восприимчивость вещества
(безразмерная величина).

– безразмерная величина представляет
собой магнитную проницаемость вещества.

В зависимости от знака и величины
восприимчивости все магнетики делятся
на три группы:

– диамагнетики
,

– парамагнетики
,

– ферромагнетики
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Продолжаем разбираться с задачами по физике. На этот раз рассмотрим примеры решения задач на тему «Циркуляция магнитного поля».

Заходите в наш телеграм – там найдутся интересные новости и лайфхаки для каждого студента. А еще, у нас есть канал со скидками и акциями, не упустите выгоду!

Теорема о циркуляции магнитного поля, задачи

Прежде, чем мы начнем разбирать примеры решений, напомним про полезные формулы и универсальную памятку по физическим задачам. И обязательно почитайте теорию по теме!

Задача №1 на циркуляцию магнитного поля

Условие

Соленоид длиной l=0,5 м содержит N= 1000 витков. Определить магнитную индукцию В поля внутри соленоида, если сопротевление его обмоток =120 Ом , а напряжение на ее концах U= 60В.

Решение

Согласно теореме о циркуляции магнитного поля:

∮Bdl=μ0∑iIiBl=μ0IN

По закону Ома:

I=UR

Отсюда запишем соотношение для магнитной индукции:

B=μ0UNRl=1,25·10-6·60·1000120·0,5=1,25·10-6Тл

Ответ: 1,25 мкТл.

Задача №2 на циркуляцию магнитного поля

Условие

Определите, пользуясь теоремой о циркуляции вектора магнитной индукции, индукцию и напряженность магнитного поля на оси тороида без сердечника. Тороид содержит N=200 витков, а по его обмотке протекает ток 2 А. Внешний диаметр тороида равен 60 см, внутренний – 40 см.

Решение

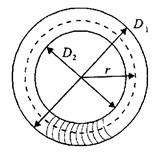
Тороид – это катушка, которая имеет замкнутый сердечник в форме кольца или тора.

Вычислим циркуляцию вектора B по осевой линии:

∮Bdl=μ0∑IiB·2πr=μ0NI

Здесь r – разность между внешним и внутренним диаметром катушки. Из формулы выше можно выразить индукцию:

B=μ0NI2πD1-D2

Чтобы найти напряженность, нужно разделить магнитную индукцию на магнитную постоянную:

H=Bμ0

Подставим значения и рассчитаем:

B=1,25·10-6·200·22π·0,6-0,4=0,39мТл

H=0,39·10-31,25·10-6=312 Ам

Ответ: 0,39 мТл, 312 А/м

Задача №3 на циркуляцию магнитного поля

Условие

По прямому бесконечно длинному проводнику течет ток I=10 А. Пользуясь теоремой о циркуляции вектора магнитной индукции, определите В в точке, расположенной на расстоянии r=10 см от проводника.

Решение

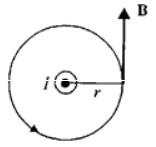
Запишем теорему о циркуляции вектора магнитной индукции:

∮Bdl=μ0∑iI

В данном случае контуром можно выбрать окружность радиуса r, которая лежит в плоскости, перперникулярной проводнику. Проводник находится в центре окружности. Вектор B направлен по касательной, а его модуль одинаков по всей окружности. Теорема о циркуляции примет вид:

B·2πr=μ0IB=μ0I2πr=1,25·10-6·102·3,14·0,1=19,9 мкТл

Ответ: 19,9 мкТл.

Задача №4 на циркуляцию магнитного поля

Условие

Определите циркуляцию вектора магнитной индукции по окружности, через центр которой перпендикулярно ее плоскости проходит бесконечно длинный прямолинейный провод, по которому течет ток I = 5 А.

Решение

Согласно теореме о циркуляции магнитной индукции, циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную:

∮Bdl=μ0∑iI∮Bdl=μ0I=1,25·10-6·5=6,25 мкТл·м

Ответ: 6,25 мкТл*м.

Задача №5 на циркуляцию магнитного поля

Условие

Какова циркуляция вектора напряженности магнитного поля для замкнутого контура L, если I1=4 A, I2=1 A, I3=9 A, I4=1 A?

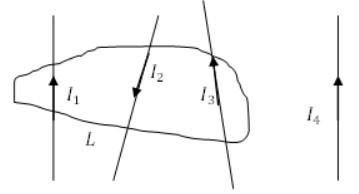
Решение

Согласно теореме, циркуляция вектора магнитной индукции по замкнутому контуру равна сумме токов, пронизывающих контур.

∮Bdl=∑iI

Из рисунка видно, что четвертый ток не влияет на циркуляцию. С учетом направлений токов, запишем:

∮Bdl=I1-I2+I3=4-1+9=12 А

Ответ: 12 А

Вопросы на тему «Теорема о циркуляции вектора магнитной индукции»

Вопрос 1. Что такое циркуляция векторного поля?

Ответ. В общем случае, циркуляция векторного поля по какому-то контуру – это скалярная величина, равная криволинейному интегралу второго рода по данному контуру.

Вопрос 2. Как звучит терема о циркуляции магнитной индукции?

Ответ.

Циркуляция вектора магнитной индукции магнитного поля равна магнитной постоянной, умноженной на алгебраическую сумму токов проводимости, которые охвачены замкнутым контуром, по которому рассматривается циркуляция.

Теорема о циркуляции магнитного поля доказывается с помощью закона Био-Савара-Лапласа.

Вопрос 3. Что такое магнитная индукция?

Ответ. Магнитная индукция – векторная физическая величина, силовая характеритика магнитного поля. Магнитная индукция определяет, с какой силой поле действует на заряд, движущийся в нем с определенной скоростью. Измеряется в Теслах.

Вопрос 4. Что такое напряженность магнитного поля?

Ответ. Напряженность магнитного поля – векторная физическая величина, численно равная:

H=Bμ0

Напряженность равна разности векторов магнитной индукции и намагниченности среды.

Напряженность в вакууме совпадает с магнитной индукцией.

Вопрос 5. Справедлива ли теорема о циркуляции для напряженности поля?

Ответ. Да, справедлива.

Циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов проводимости, которые охвачены замкнутым контуром.

Если у вас не получается быстро решать задачи, не отчаивайтесь! Профессиональный сервис для учащихся поможет ускорить процесс выполнения любого задания: от контрольной до диплома.

Источник

Циркуляция вектора индукции магнитного поля

Содержание:

Теорема о циркуляции вектора индукции магнитного поля
Чему равна циркуляция, закон Био–Савара
Дифференциальная форма теоремы о циркуляции

Теорема о циркуляции вектора индукции магнитного поля

Циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи, прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур.

В виде формулы теорема записывается следующим образом:

(ointlimits_L;overrightarrow Bdoverrightarrow l;=;M_0sum_{k=1}^n;=;M_0I)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В данном случае I будет означать полный ток.

Теорема используется для того, чтобы облегчить вычисление индукции магнитного поля, созданного совокупностью токов, текущих по проводам. Упрощение достигается с учетом симметрии и конфигурации токов. К примеру, с применением этой теоремы возможен расчет магнитной индукции для проводников с высокой степенью симметрии.

Взглянем на циркуляцию вектора (overrightarrow B). Предположим, что условный замкнутый контур находится в пространстве с магнитным полем, а также предположим направление его обхода. В таком случае, касательная составляющая (B_l) вектора (overrightarrow B) определяется на каждом отдельно взятом маленьком участке (triangle l ) этого контура. Иными словами определяется проекция вектора (overrightarrow B) на направление касательной к определенному участку контура.

Циркуляцией вектора (overrightarrow B) является сумма произведений (B_l) и (triangle l), которая взята по целому контуру L: (overrightarrow B = textstylesum_{(L)} B_l triangle l.)

Исходя из этого, можно сформулировать следующее: принимая во внимание теорему о циркуляции, циркуляция вектора (overrightarrow B) магнитного поля постоянных токов по каждому из контуров L в любой момент времени рассчитывается как произведение магнитной постоянной (mu_0) на сумму всех токов:

({textstylesum_{(L)}};B_l;triangle l;=;mu_0;{textstylesum_{}};l_i)

Вывод из теоремы: так как циркуляция индукции магнитного поля не равняется нулю, магнитное поле прямолинейного тока не будет являться потенциальным.

(ointlimits_L;(overrightarrow Bdoverrightarrow l);neq0) , где (overrightarrow B) обозначает вектор магнитной индукции, а dl является элементом произвольного контура L.

Чему равна циркуляция, закон Био–Савара

Циркуляция вектора ( overrightarrow B) прямолинейного тока вдоль замкнутого контура, который не охватывает этот проводник, равняется нулю. В случае, когда несколько токов оказываются охваченными контуром, циркуляция вектора (overrightarrow B) равняется их алгебраической сумме:

(ointlimits_l;(overrightarrow Bdoverrightarrow l);=;mu_0sum_i;l_i)

Закон Био-Савара определяет вклад (triangleoverrightarrow B) в магнитную индукцию (overrightarrow B) результативного магнитного поля, образуемого маленьким участком (triangle l ) проводника с током I.

(triangle B;=;frac{mu_0;I;triangle l;sinleft(alpharight)}{4pi r^2})

В данном случае r является расстоянием от заданного участка (triangle l) до точки наблюдения, (alpha) обозначает угол между направлением на точку наблюдение и направлением тока на определенном участке, а (mu_0) является магнитной постоянной.

Благодаря закону Био-Савара можно определить магнитные поля током с различными конфигурациями и вычислить магнитное поле в центре кругового витка с током.

Дифференциальная форма теоремы о циркуляции

Предположим, что S — это поверхность, охватываемая контуром L. Правило правого винта будет связывать проложенную к поверхности нормаль и направление обхода контура L. В таком случае определить силу тока, текущего через поверхность S, можно с помощью следующей формулы:

(I;=;intlimits_S;overrightarrow jdoverrightarrow S)

В этой формуле (overrightarrow j) будет обозначать объемную плотность тока.

Исходя из этого, используем следующее написание формулы:

(ointlimits_L;overrightarrow Bdoverrightarrow l;=;mu_0intlimits_S;overrightarrow jdoverrightarrow S)

Теперь образуем ротор вектора (rotoverrightarrow B), основываясь на теореме Стокса, уточним, что:

(rotoverrightarrow B;=;begin{vmatrix}i&j&k\fracpartial{partial x}&fracpartial{partial y}&fracpartial{partial z}\B_x&B_y&B_zend{vmatrix} = 0)

Тогда формула примет вид:

(ointlimits_L;overrightarrow Bdoverrightarrow l;=;intlimits_Srotoverrightarrow Bdoverrightarrow S)

Теперь можно записать теорему о циркуляции в дифференциальной форме:

(rotoverrightarrow B;=;frac{4pi}coverrightarrow j)

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Закон Био–Савара

Теорема о циркуляции вектора магнитной индукции

Математическая формулировка[править | править код]

Обобщение[править | править код]

Практическое значение[править | править код]

Доказательство теоремы о циркуляции[править | править код]

Примечания[править | править код]

7. Магнитное поле соленоида.

Лекция 11 Магнитное поле в веществе.

1. Магнитные моменты атомов.

Теорема о циркуляции магнитного поля, задачи

Задача №1 на циркуляцию магнитного поля

Задача №2 на циркуляцию магнитного поля

Задача №3 на циркуляцию магнитного поля

Задача №4 на циркуляцию магнитного поля

Задача №5 на циркуляцию магнитного поля

Вопросы на тему «Теорема о циркуляции вектора магнитной индукции»

Циркуляция вектора индукции магнитного поля

Теорема о циркуляции вектора индукции магнитного поля

Чему равна циркуляция, закон Био–Савара

Дифференциальная форма теоремы о циркуляции

Текст с ошибкой:

Поиск по содержимому

Вам также может понравиться

Как исправить провалы ламинате

Как найти значение биномиальных коэффициентов

Как найти один угол если два известны

Добавить комментарий Отменить ответ