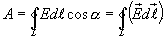Было выявлено, что на заряд q, находящийся в электростатическом поле, действуют консервативные силы, причем работа А на замкнутом пути L равняется нулю:
A=∮LF¯dr¯=q∮LE¯ dr¯=0, где r – это вектор перемещения. Данный интеграл представляет собой циркуляцию вектора напряженности электростатического поля.
Если единичный заряд положительный, то запись приобретает совсем другой вид. Интеграл левой части уравнения и является циркуляцией вектора напряженности по контуру L.
Теорема о циркуляции
Электростатическое поле характеризуется циркуляцией его вектора напряженности по замкнутому полю и равняется нулю. Утверждение называют теоремой о циркуляции вектора напряженности электростатического поля.
Для ее доказательства основываются на работе поля по перемещению заряда, не зависящую от ее траектории. L1 и L2 обозначают в качестве различных путей между точками А и В. При замене их местами получим L=L1+L2. Теорема доказана
Следствие теоремы о циркуляции. Теорема Стокса
Так как линии на напряженности электростатического поля незамкнуты, то это применяют в качестве следствия. Их начало идет с положительных зарядов, а заканчивается отрицательными или их уходом в бесконечность. Теорема верна для статичных зарядов.
Еще одним следствием является непрерывность тангенциальных составляющих напряженности. Это говорит о том, что ее компоненты, являющиеся касательными к выбранной любой поверхности во всякой точке, на обеих сторонах содержат одинаковые значения.
Необходимо выделить произвольную часть поверхности S, которая опирается на контур L.
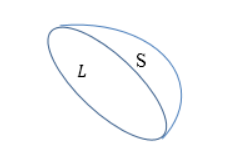
Рисунок 1
По формуле Стокса интеграл от ротора вектора напряженности rot E→, взятый по поверхности
S, равняется циркуляции вектора напряженности вдоль контура, на который опирается данная поверхность.
Значение dS→=dS·n→, n→ является единичным вектором, перпендикулярным участку dS . Интенсивность «завихрения» вектора характеризуется ротором rot E→. Это рассматривают на примере наличия крыльчатки, помещенной в жидкости, изображаемой на рисунке 2. Если ротор не равняется нулю, то крыльчатка будет продолжать вращение, причем с ростом скорости вращения увеличится модуль проекция ротора на ось крыльчатки.
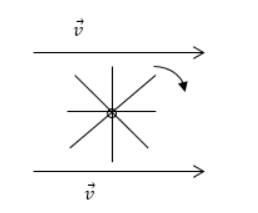
Рисунок 2
Для вычисления ротора применяют формулы:
Если использовать уравнение (6), то циркуляция вектора напряженности будет равной нулю.
При выполнении условия (8) для любой поверхности S, упирающейся на контур L, возможно с подынтегральным выражением, причем для каждой точки поля.
Действие производится аналогично крыльчатке из рисунка 2. На ее концах имеются одинаковые заряды, равные q. Вся система находится в однородном поле с напряженностью E. Если rot E→≠0, то предусмотрено вращение с ускорением, зависящим от проекции ротора на ось крыльчатки. Если поле электростатическое, тогда движение по окружности не происходило бы ни при каком расположении оси. Основная отличительная особенность электростатического поля в том, что оно является безвихревым.
Представление теоремы о циркуляции в дифференциальном виде:
rot E¯=0
Дан рисунок 3 с изображением электростатического поля. Что можно сказать о его характеристиках?
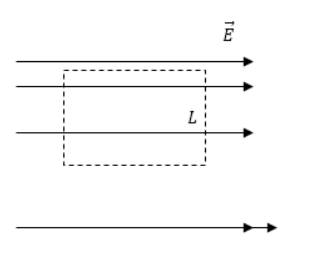
Рисунок 3
Решение
По рисунку видно, что существование электростатического поля невозможно. Для выделенного пунктиром контура циркуляции вектора напряженности применяется формула:
∮LE→ds→≠0.
Это невозможно, так как существует противоречие теоремы о циркуляции. Определение напряженности поля (измеряется в вольтах на метр Вм или в ньютонах на кулон НК) идет с помощью густоты силовых линий, причем с различными значениями. Работа по замкнутому кругу не равна нулю, значит, циркуляция вектора напряженности также нулю не равняется.
Показать, что тангенциальные составляющие вектора напряженности электростатического поля не изменяются при переходе через границу раздела диэлектриков, основываясь на теореме о циркуляции.
Решение
Если рассмотреть границу между двумя диэлектриками с диэлектрическими проницаемостями ε2 и ε1, изображенных на рисунке 4, то видно, что ось Х проходит через середины сторон b. На границе выбирается прямоугольный контур с параметрами длины (а) и ширины (b).
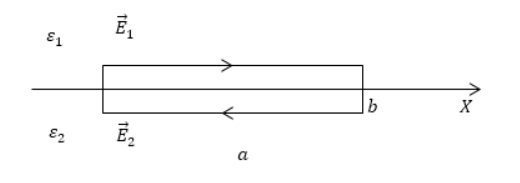
Рисунок 4
Выполнение теоремы о циркуляции обусловлено наличием электростатического поля. Его находят из формулы:
∮LE→ds→=0.
Если контур имеет небольшие размеры, тогда циркуляция вектора напряженности, согласно формуле ∮LE→ds→=0, представляется в виде:
∮LE→ds→=E1xa-E2xa+Eb2b=0.
Eb – это среднее значение E→ на участках, перпендикулярных к границе раздела.
Из формулы ∮LE→ds→=E1xa-E2xa+Eb2b=0 следует:
E2x-E1xa=Eb2b.
Когда b→0, тогда
E2x=E1x.
Выполнение выражения E2x=E1x возможно при произвольном выборе оси Х, которая располагается на границе раздела диэлектриков. Можно представить вектор напряженности в виде двух: тангенциальной Eτ и нормальной En:
E1→=E1n→+E1τ→, E2→=E2n→+E2τ→.
Отсюда следует, что
Eτ1=Eτ2, где Eτi является проекцией вектора напряженности на орт τ, который направлен вдоль границы раздела диэлектриков.
Теорема о циркуляции вектора напряженности
Теорема о циркуляции вектора напряженности
Теорема о циркуляции вектора напряженности электрического поля
Взаимодействие неподвижных зарядов реализуется посредством электростатического поля. Описывают электростатическое поле при помощи вектора напряженности ($overline{E}$), который определен как сила ($overline{F}$), действующая на единичный положительный заряд, размещенный в рассматриваемой точке поля:
[overline{E}=frac{overline{F}}{q}left(1right).]
Электростатические силы являются консервативными, это значит, что их работа по замкнутой траектории ($L$) равна нулю:
[A=ointnolimits_L{overline{F}doverline{r}=}qointnolimits_L{overline{E}doverline{r}=}0 left(2right),]
где $overline{r}$ – перемещение.
Интеграл в формуле (2) называется циркуляцией вектора напряженности электростатического поля. Циркуляция вектора $overline{E}$- это работа, которую могут совершить силы Кулона, перемещая положительный заряд равный единице по контуру.
Учитывая, что $qne 0$, получим:
[ointnolimits_L{overline{E}doverline{r}=}0 left(3right).]
Теорема о циркуляции вектора напряжённости электростатического поля говорит о том, циркуляция $overline{E}$ по замкнутому контуру равна нулю.
В дифференциальной форме теорему о циркуляции записывают как:
[rot overline{E}=0 left(4right).]
Такой вид записи как (4) удобно использовать для проверки потенциальности векторного поля. Потенциальное поле является безвихревым.
Как следствие из теоремы о циркуляции $overline{E}$: работа при перемещении заряда из одной точки поля в другую не зависит от формы траектории движения.
Из теоремы о циркуляции следует, что линии электростатического поля не бывают замкнутыми, они начинаются на положительных, а заканчиваются на отрицательных зарядах.
Теорема о циркуляции вектора напряженности магнитного поля
Физическая величина ($overline{H}$), являющаяся характеристикой магнитного поля, равная:
[overline{H}=frac{overline{B}}{{mu }_0}-{overline{P}}_m(5)]
называется напряженностью магнитного поля. $overline{B}$ – вектор магнитной индукции поля; ${mu }_0$ – магнитная постоянная; ${overline{P}}_m$- вектор намагниченности.
Циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов проводимости, которые охвачены замкнутым контуром, по которому рассматривается циркуляция:
[ointlimits_L{overline{H}doverline{r}=sum{I_m}left(6right).}]
Если направление обхода контура связывается с направлением тока правилом правого винта, то ток в сумме (5) стоит со знаком плюс.
Циркуляция вектора напряженности в общем случае отлична от нуля, это означает, что магнитное поле – это вихревое поле, оно не является потенциальным.
Теорему о циркуляции вектора напряженности магнитного поля доказывают, опираясь на закон Био-Савара-Лапласа и принцип суперпозиции.
Теорема о циркуляции вектора $overline{H}$ исполняет роль, похожую на роль теоремы Гаусса для вектора напряженности электрического поля. Если имеется симметрия при распределении токов, то используя теорему о циркуляции $overline{H},$ находят саму напряженность магнитного поля.
Примеры задач с решением
Пример 1
Задание. Определите, является ли потенциальным электрическое поле, которое задано уравнением: $overline{E}left(x,yright)=Aleft(2xy overline{i}+left(x^2-y^2right)overline{j}right).$
Решение. Из теоремы о циркуляции, которая записана в дифференциальном виде:
[rot overline{E}=0 left(1.1right).]
следует, что если вихрь поля равен нулю, то поле потенциально. Используя определение ротора:
[rot overline{E}=left| begin{array}{ccc}
overline{i} & overline{j} & overline{k} \
frac{partial}{partial x} & frac{partial }{partial y} & frac{partial}{partial z} \
E_x & E_y & E_z end{array}
right|(1.2)]
найдем:
[rot overline{E}=rot left[Aleft(2xy overline{i}+left(x^2-y^2right)overline{j}right)right]=frac{partial E_y}{partial x}overline{k}-frac{partial E_x}{partial y}overline{k}left(1.3right).]
Частные производные от $overline{E}$ равны:
[frac{partial E_y}{partial x}=Acdot 2x;; frac{partial E_x}{partial y}=Acdot 2x left(1.4right).]
Подставляя (1.4) в (1.3), получаем, что
[rot overline{E}=rot left[Aleft(2xy overline{i}+left(x^2-y^2right)overline{j}right)right]=0.]
Ответ. Поле является потенциальным.
Пример 2
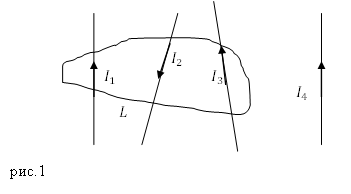
Задание. Какова циркуляция вектора напряженности магнитного поля для замкнутого контура $L$ (рис.1), если $I_1=5 A;; I_2=2 A;; I_3=10 A;; I_4=1 A?$
Решение. Основой для решения задачи служит теорема о циркуляции вектора напряжённости магнитного поля:
[ointlimits_L{overline{H}doverline{r}=sum{I_m}left(2.1right).}]
Контур $L$ охватывает три тока, следовательно:
[ointlimits_L{overline{H}doverline{r}=I_1-I_2+I_3.}]
Вычислим циркуляцию:
[ointlimits_L{overline{H}doverline{r}=5-2+10=13 (А).}]
Ответ. $ointlimits_L{overline{H}doverline{r}=13А .}$
Читать дальше: типы ядерных реакций.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Циркуляцией
вектора напряженности называется
работа, которую совершают электрические
силы при перемещении единичного
положительного заряда по замкнутому
пути L
|
|
Так
как работа сил электростатического
поля по замкнутому контуру равна нулю
(работа сил потенциального поля),
следовательно циркуляция напряженности
электростатического поля по замкнутому
контуру равна нулю.
![]()
Теорема
о циркуляции:
|
Циркуляция магнитного |
Практическое
значение
Теорема о циркуляции играет
в магнитостатике приблизительно
ту же роль, что и теорема
Гаусса электростатике.
В частности, при наличии определённой
симметрии задачи, она позволяет просто
находить величину магнитного поля во
всём пространстве по заданным токам.
Например, для вычисления магнитного
поля от бесконечного прямолинейного
проводника с током по закону
Био — Савара — Лапласа потребуется
вычислить неочевидный интеграл, в то
время как теорема о циркуляции (с учётом
осевой симметрии задачи) позволяет дать
мгновенный ответ:
![]() .
.
26. Диполь. Поле диполя.
Электрический
дипольный момент — векторная физическая
величина, характеризующая, наряду с
суммарным зарядом (и реже используемыми
высшими мультипольными моментами),
электрические свойства системы заряженных
частиц (распределения зарядов) в
смысле создаваемого ею поля и действия
на нее внешних полей. Главная после
суммарного заряда и положения системы
в целом (ее радиус-вектора) характеристика
конфигурации зарядов системы при
наблюдении ее издали.
Его
поле. Для фиксированных угловых координат
(то есть на луче, идущем из центра
электрического диполя на бесконечность)
напряжённость статического электрического
поля диполя или в целом нейтральной
системы зарядов, имеющей ненулевой
дипольный момент, на больших
расстояниях rасимптотически
приближается к виду r−3, электрический
потенциал — к r−2. Таким образом,
статическое поле диполя убывает на
больших расстояниях быстрее, чем поле
простого заряда (но медленнее, чем поле
любого более старшего мультиполя).
Напряжённость
электрического поля и электрический
потенциал неподвижного или медленно
движущегося диполя (или в целом нейтральной
системы зарядов, имеющей ненулевой
дипольный момент) с электрическим
дипольным моментом ![]() на
на
больших расстояниях в главном приближении
выражается как:
![]()
где ![]() —
—
единичный вектор из центра диполя в
направлении точки измерения, а точкой
обозначено скалярное произведение.
Достаточно
просты выражения (в том же приближении,
тождественно совпадающие с формулами,
приведенными выше) для продольной (вдоль
радус-вектора, проведенного от диполя
в данную точку) и поперечной компонент
напряженности электрического поля:
![]()
![]()
где ![]() —
—
угол между направлением вектора
дипольного момента и радиус-вектором
в точку Третья компонента напряженности
электрического поля — ортогональная
плоскости, в которой лежат вектор
дипольного момента и радиус-вектор, —
всегда равна нулю.
27.
Строение диэлектрика.
Диэлектрик во внешнем эл. поле.
Механизмы
поляризации диэлектриков
Строение
диэлектрика.
Вещество,
внесенное в электрическое поле, может
существенно изменить его. Это связано
с тем, что вещество состоит из заряженных
частиц. В отсутствие внешнего поля
частицы распределяются внутри вещества
так, что создаваемое ими электрическое
поле в среднем по объемам, включающим
большое число атомов или молекул, равно
нулю. При наличии внешнего поля происходит
перераспределение заряженных частиц,
и в веществе возникает собственное
электрическое поле. Полное электрическое
поле ![]() складывается
складывается
в соответствии с принципом суперпозиции
из внешнего поля ![]() и
и
внутреннего поля ![]() создаваемого
создаваемого
заряженными частицами вещества.
В
отличие от проводников, в диэлектриках
(изоляторах) нет свободных электрических
зарядов. Они состоят из нейтральных
атомов или молекул. Заряженные частицы
в нейтральном атоме связаны друг с
другом и не могут перемещаться под
действием электрического поля по всему
объему диэлектрика.
Диэлектрик во внешнем эл.
поле.
При
внесении диэлектрика во внешнее
электрическое поле ![]() в
в
нем возникает некоторое перераспределение
зарядов, входящих в состав атомов или
молекул. В результате такого
перераспределения на поверхности
диэлектрического образца появляются
избыточные нескомпенсированные связанные заряды.
Все заряженные частицы, образующие
макроскопические связанные заряды,
по-прежнему входят в состав своих атомов.
Связанные
заряды создают электрическое поле ![]() которое
которое
внутри диэлектрика направлено
противоположно вектору напряженности ![]() внешнего
внешнего
поля. Этот процесс называется поляризацией
диэлектрика.
В результате полное электрическое
поле ![]() внутри
внутри
диэлектрика оказывается по модулю
меньше внешнего поля ![]()
Физическая
величина, равная отношению модуля
напряженности ![]() внешнего
внешнего
электрического поля в вакууме к модулю
напряженности![]() полного
полного
поля в однородном диэлектрике,
называетсядиэлектрической
проницаемостью вещества.
|
Механизмы
поляризации диэлектриков
Существует
несколько механизмов поляризации
диэлектриков. Основными из них
являются ориентационная и электронная поляризации.
Эти механизмы проявляются главным
образом при поляризации газообразных
и жидких диэлектриков.
Ориентационная
или дипольная поляризация возникает
в случае полярных
диэлектриков,
состоящих из молекул, у которых центры
распределения положительных и
отрицательных зарядов не совпадают.
Такие молекулы представляют собой
микроскопические электрические
диполи –
нейтральную совокупность двух зарядов,
равных по модулю и противоположных по
знаку, расположенных на некотором
расстоянии друг от друга. Дипольным
моментом обладает, например, молекула
воды, а также молекулы ряда других
диэлектриков (H2S,
NO2 и
т. д.).
При отсутствии внешнего
электрического поля оси молекулярных
диполей из-за теплового движения
ориентированы хаотично, так что на
поверхности диэлектрика и в любом
элементе объема электрический заряд в
среднем равен нулю.
При внесении
диэлектрика во внешнее поле ![]() возникает
возникает
частичная ориентация молекулярных
диполей. В результате на поверхности
диэлектрика появляются нескомпенсированные
макроскопические связанные заряды,
создающие поле![]() направленное
направленное
навстречу внешнему полю![]() (рис. 1.5.3).
(рис. 1.5.3).
|
|
|
Рисунок Ориентационный |
Поляризация полярных
диэлектриков сильно зависит от
температуры, так как тепловое движение
молекул играет роль дезориентирующего
фактора.
Электронный
или упругий механизм проявляется
при поляризации неполярных диэлектриков,
молекулы которых не обладают в отсутствие
внешнего поля дипольным моментом. Под
действием электрического поля молекулы
неполярных диэлектриков деформируются
– положительные заряды смещаются в
направлении вектора ![]() а
а
отрицательные – в противоположном
направлении. В результате каждая молекула
превращается в электрический диполь,
ось которого направлена вдоль внешнего
поля. На поверхности диэлектрика
появляются нескомпенсированные связанные
заряды, создающие свое поле![]() направленное
направленное
навстречу внешнему полю![]() Так
Так
происходит поляризация неполярного
диэлектрика (рис. 1.5.4).
Деформация
неполярных молекул под действием
внешнего электрического поля не зависит
от их теплового движения, поэтому
поляризация неполярного диэлектрика
не зависит от температуры. Примером
неполярной молекулы может служить
молекула метана CH4.
У этой молекулы четырехкратно
ионизированный ион углерода
C4– располагается
в центре правильной пирамиды, в вершинах
которой находятся ионы водорода H+.
При наложении внешнего электрического
поля ион углерода смещается из центра
пирамиды, и у молекулы возникает дипольный
момент, пропорциональный внешнему полю.
|
|
|
Рисунок Поляризация |
Электрическое
поле ![]() связанных
связанных
зарядов, возникающее при поляризации
полярных и неполярных диэлектриков,
изменяется по модулю прямо пропорционально
модулю внешнего поля![]() В
В
очень сильных электрических полях эта
закономерность может нарушаться, и
тогда проявляются различныенелинейные
эффекты.
В случае полярных диэлектриков в сильных
полях может наблюдаться эффект
насыщения,
когда все молекулярные диполи выстраиваются
вдоль силовых линий. В случае неполярных
диэлектриков сильное внешнее поле,
сравнимое по модулю с внутриатомным
полем, может существенно деформировать
атомы или молекулы вещества и изменить
их электрические свойства. Однако, эти
явления практически никогда не
наблюдаются, так как для этого нужны
поля с напряженностью порядка 1010–1012 В/м.
Между тем, гораздо раньше наступает
электрический пробой диэлектрика.
У многих
неполярных молекул при поляризации
деформируются электронные оболочки,
поэтому этот механизм получил
название электронной
поляризации.
Этот механизм является универсальным,
поскольку деформация электронных
оболочек под действием внешнего поля
происходит в атомах, молекулах и ионах
любого диэлектрика.
В случае
твердых кристаллических диэлектриков
наблюдается так называемая ионная
поляризация,
при которой ионы разных знаков,
составляющие кристаллическую решетку,
при наложении внешнего поля смещаются
в противоположных направлениях,
вследствие чего на гранях кристалла
появляются связанные (нескомпенсированные)
заряды. Примером такого механизма может
служить поляризация кристалла NaCl, в
котором ионы Na+ и
Cl– составляют
две подрешетки, вложенные друг в друга.
В отсутствие внешнего поля каждая элементарная
ячейка кристалла
NaCl (см. Часть I § 3.6 )
электронейтральна и не обладает дипольным
моментом. Во внешнем электрическом поле
обе подрешетки смещаются в противоположных
направлениях, т. е. кристалл поляризуется.
При
поляризации неоднородного
диэлектрика связанные
заряды могут возникать не только на
поверхностях, но и в объеме диэлектрика.
В этом случае электрическое поле ![]() связанных
связанных
зарядов и полное поле![]() могут
могут
иметь сложную структуру, зависящую от
геометрии диэлектрика. Утверждение о
том, что электрическое поле![]() в
в
диэлектрике в ε раз меньше по модулю по
сравнению с внешним полем![]() строго
строго
справедливо только в случаеоднородного
диэлектрика,
заполняющего все пространство, в котором
создано внешнее поле. В частности:
Если в
однородном диэлектрике с диэлектрической
проницаемостью ε находится точечный
заряд Q,
то напряженность поля ![]() создаваемого
создаваемого
этим зарядом в некоторой точке, и
потенциал φ в ε раз меньше, чем в вакууме:
|
28.
Проводники. Эл. поле в проводниках.
Электроемкость.
Конденсатор.
Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Теорема о циркуляции
Ранее мы выяснили, что на заряд (q), который находится в электростатическом поле, действуют консервативные силы, работа ($A$) которых на любом замкнутом пути (L) равна нулю:
где $overrightarrow{s}$- вектор перемещения (не путать с площадью), $overrightarrow{E}$ — вектор напряженности поля.
Для единичного положительного заряда можем записать:
Интеграл в левой части уравнения (2) есть циркуляция вектора напряженности по контуру L. Характерным свойством электростатического поля является то, что циркуляция его вектора напряжённости по любому замкнутому контуру равна нулю. Такое утверждение называется теоремой о циркуляции вектора напряженности электростатического поля.
Докажем теорему о циркуляции на том основании, что работа поля по перемещению заряда не зависит от траектории перемещения заряда в электростатическом поле, что выражается равенством:
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
где $L_1 и L_2$ различные пути между точками А и В. Учтем, что при замене местами пределов интегрирования получим:
Выражение (4) представим как:
где $L=L_1+L_2$. Так теорема доказана.
Следствие теоремы о циркуляции
Следствием теоремы о циркуляции является то, что линии напряженности электростатического поля незамкнуты. Они начинаются на положительных зарядах, а заканчиваются на отрицательных или уходят в бесконечность. Теорема верна именно для статичных зарядов. Другое следствие теоремы: непрерывность тангенциальных составляющих напряженности (в отличие от нормальных составляющих). Это значит, что компоненты напряженности, которые являются касательными к выбранной любой поверхности во всякой ее точке, имеют по обе стороны поверхности равные значения.
Выделим произвольную поверхность S, которая опирается на контур L (рис.1).
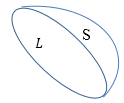
«Циркуляция вектора напряженности электростатического поля» 👇
Рис. 1
В соответствии с формулой Стокса (теоремой Стокса) интеграл от ротора вектора напряженности ($rotoverrightarrow{E}$), взятый по поверхности S равен циркуляции вектора напряженности вдоль контура, на который опирается данная поверхность:
где $doverrightarrow{S}=dScdot overrightarrow{n}$, $overrightarrow{n}$ — единичный вектор перпендикулярный участку dS. Ротор ($rotoverrightarrow{E}$) характеризует интенсивность «завихрения» вектора. Наглядное представление о роторе вектора можно получить, если маленькую легкую крыльчатку (рис.2) поместить в поток жидкости. В тех местах, где ротор не равен нулю, крыльчатка будет вращаться, причем скорость ее вращения будет тем больше, чем больше проекция модуль проекции ротора на ось крыльчатки.
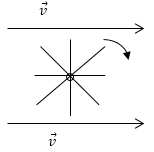
Рис. 2
При практическом вычислении ротора чаще других используют формулы:
Так как в соответствии с уравнением (6) циркуляция вектора напряжённости равна нулю, то мы получаем:
Условие (8) должно выполняться для любой поверхности S, которая опирается на контур L. Это возможно только в том случае, если подынтегральное выражение:
причем для каждой точки поля.
По аналогии с крыльчаткой на рис. 2 представим себе электрическую «крыльчатку». На концах такой «крыльчатки» расположены одинаковые по величине заряды q. Система помещена в однородное поле с напряженностью E. В тех местах, где $rotoverrightarrow{E}ne 0$ такое «устройство» будет вращаться с ускорением, которое зависит от проекции ротора на ось крыльчатки. В случае, электростатического поля такое «устройство» не стало бы вращаться ни при какой ориентации оси. Так как отличительной особенностью электростатического поля является то, что оно безвихревое. Уравнение (9) представляет теорему о циркуляции в дифференциальной форме.
Пример 1
Задание: На рис. 3 изображено электростатическое поле. Что можно сказать о характеристиках данного поля из рисунка?
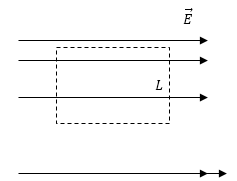
Рис. 3
Решение:
О данном поле можно сказать, что существование такого электростатического поля невозможно. Если выделить контур (он изображен пунктиром). Для такого контура циркуляция вектора напряженности:
[ointlimits_L{overrightarrow{E}doverrightarrow{s}ne 0}left(1.1right),]
что противоречит теореме о циркуляции для электростатического поля. Напряженность поля определяется густотой силовых линий, она в разных частях поля не одинакова, в результате работа по замкнутому контуру будет отличаться от нуля, следовательно, циркуляция вектора напряженности не равна нулю.
Пример 2
Задание: Исходя из теоремы о циркуляции, покажите, что тангенциальные составляющие вектора напряженности электростатического поля не изменяются при переходе через границу раздела диэлектриков.
Решение:
Рассмотрим границу между двумя диэлектриками с диэлектрическими проницаемостями ${varepsilon }_2 и {varepsilon }_1$ (рис.4). Выберем на этой границе небольшой прямоугольный контур с параметрами a – длина, b – ширина. Ось Х проходит через середины сторон b.
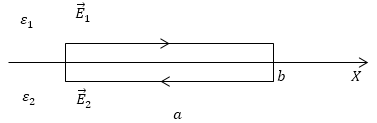
Рис. 4
Для электростатического поля выполняется теорема о циркуляции, которая выражается уравнением:
[ointlimits_L{overrightarrow{E}doverrightarrow{s}=0 left(2.1right).}]
При небольших размерах контура циркуляция вектора напряженности и в соответствии с указанным направлением обхода контура интеграл в формуле (2.1) можно представить как:
[ointlimits_L{overrightarrow{E}doverrightarrow{s}=E_{1x}a-E_{2x}a+leftlangle E_brightrangle 2b=0 left(2.2right),}]
где $leftlangle E_brightrangle $- среднее значение $overrightarrow{E}$ на участках перпендикулярных к границе раздела.
Из (2.2) следует, что:
[{(E}_{2x}-E_{1x})a=leftlangle E_brightrangle 2b (2.3).]
Если $bto 0$, то получаем, что:
[E_{2x}=E_{1x} left(2.4right).]
Выражение (2.4) выполняется при произвольном выборе оси X, которая лежит на границе раздела диэлектриков. Если представить вектор напряженности в виде двух составляющих (тангенциальной $E_{tau } $ и нормальной $E_n$):
[overrightarrow{E_1}=overrightarrow{E_{1n}}+overrightarrow{E_{1tau }},overrightarrow{E_2}=overrightarrow{E_{2n}}+overrightarrow{E_{2tau }} left(2.5right).]
В таком случае из (2.4) запишем:
[E_{tau 1}=E_{tau 2} left(2.6right),]
где $E_{tau i}$- проекция вектора напряженности на орт $tau $, направленный вдоль границы раздела диэлектриков.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Циркуляция вектора напряженности электростатического поля
Было выявлено, что на заряд q , находящийся в электростатическом поле, действуют консервативные силы, причем работа А на замкнутом пути L равняется нулю:
A = ∮ L F ¯ d r ¯ = q ∮ L E ¯ d r ¯ = 0 , где r – это вектор перемещения. Данный интеграл представляет собой циркуляцию вектора напряженности электростатического поля.
Если единичный заряд положительный, то запись приобретает совсем другой вид. Интеграл левой части уравнения и является циркуляцией вектора напряженности по контуру L .
Теорема о циркуляции
Электростатическое поле характеризуется циркуляцией его вектора напряженности по замкнутому полю и равняется нулю. Утверждение называют теоремой о циркуляции вектора напряженности электростатического поля.
Для ее доказательства основываются на работе поля по перемещению заряда, не зависящую от ее траектории. L 1 и L 2 обозначают в качестве различных путей между точками А и В . При замене их местами получим L = L 1 + L 2 . Теорема доказана
Следствие теоремы о циркуляции. Теорема Стокса
Так как линии на напряженности электростатического поля незамкнуты, то это применяют в качестве следствия. Их начало идет с положительных зарядов, а заканчивается отрицательными или их уходом в бесконечность. Теорема верна для статичных зарядов.
Еще одним следствием является непрерывность тангенциальных составляющих напряженности. Это говорит о том, что ее компоненты, являющиеся касательными к выбранной любой поверхности во всякой точке, на обеих сторонах содержат одинаковые значения.
Необходимо выделить произвольную часть поверхности S , которая опирается на контур L .

По формуле Стокса интеграл от ротора вектора напряженности r o t E → , взятый по поверхности
S , равняется циркуляции вектора напряженности вдоль контура, на который опирается данная поверхность.
Значение d S → = d S · n → , n → является единичным вектором, перпендикулярным участку d S . Интенсивность «завихрения» вектора характеризуется ротором r o t E → . Это рассматривают на примере наличия крыльчатки, помещенной в жидкости, изображаемой на рисунке 2 . Если ротор не равняется нулю, то крыльчатка будет продолжать вращение, причем с ростом скорости вращения увеличится модуль проекция ротора на ось крыльчатки.

Для вычисления ротора применяют формулы:
Если использовать уравнение ( 6 ) , то циркуляция вектора напряженности будет равной нулю.
При выполнении условия ( 8 ) для любой поверхности S , упирающейся на контур L , возможно с подынтегральным выражением, причем для каждой точки поля.
Действие производится аналогично крыльчатке из рисунка 2 . На ее концах имеются одинаковые заряды, равные q . Вся система находится в однородном поле с напряженностью E . Если r o t E → ≠ 0 , то предусмотрено вращение с ускорением, зависящим от проекции ротора на ось крыльчатки. Если поле электростатическое, тогда движение по окружности не происходило бы ни при каком расположении оси. Основная отличительная особенность электростатического поля в том, что оно является безвихревым.
Представление теоремы о циркуляции в дифференциальном виде:
Дан рисунок 3 с изображением электростатического поля. Что можно сказать о его характеристиках?

Решение
По рисунку видно, что существование электростатического поля невозможно. Для выделенного пунктиром контура циркуляции вектора напряженности применяется формула:
Это невозможно, так как существует противоречие теоремы о циркуляции. Определение напряженности поля (измеряется в вольтах на метр В м или в ньютонах на кулон Н К ) идет с помощью густоты силовых линий, причем с различными значениями. Работа по замкнутому кругу не равна нулю, значит, циркуляция вектора напряженности также нулю не равняется.
Показать, что тангенциальные составляющие вектора напряженности электростатического поля не изменяются при переходе через границу раздела диэлектриков, основываясь на теореме о циркуляции.
Решение
Если рассмотреть границу между двумя диэлектриками с диэлектрическими проницаемостями ε 2 и ε 1 , изображенных на рисунке 4 , то видно, что ось Х проходит через середины сторон b . На границе выбирается прямоугольный контур с параметрами длины ( а ) и ширины ( b ) .

Выполнение теоремы о циркуляции обусловлено наличием электростатического поля. Его находят из формулы:
Если контур имеет небольшие размеры, тогда циркуляция вектора напряженности, согласно формуле ∮ L E → d s → = 0 , представляется в виде:
∮ L E → d s → = E 1 x a – E 2 x a + ” open=” E b 2 b = 0 .
” open=” E b – это среднее значение E → на участках, перпендикулярных к границе раздела.
Из формулы ∮ L E → d s → = E 1 x a – E 2 x a + ” open=” E b 2 b = 0 следует:
E 2 x – E 1 x a = ” open=” E b 2 b .
Когда b → 0 , тогда
Выполнение выражения E 2 x = E 1 x возможно при произвольном выборе оси Х , которая располагается на границе раздела диэлектриков. Можно представить вектор напряженности в виде двух: тангенциальной E τ и нормальной E n :
E 1 → = E 1 n → + E 1 τ → , E 2 → = E 2 n → + E 2 τ → .
Отсюда следует, что
E τ 1 = E τ 2 , где E τ i является проекцией вектора напряженности на орт τ , который направлен вдоль границы раздела диэлектриков.
Циркуляция вектора напряженности.
При перемещении заряда по произвольному замкнутому пути L работа сил электростатического поля равна нулю. Поскольку, конечное положение заряда равно начальному r1=r2, то и (кружок у знака интеграла указывает на то, что интегрирование производится по замкнутому пути). Так как и , то . Отсюда получаем . Сократив обе части равенства на q0, получим или , где El=Ecosa – проекция вектора Е на направление элементарного перемещения . Интеграл называется циркуляцией вектора напряженности. Таким образом, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Это заключение есть условие потенциальности поля.
Потенциальная энергия заряда.
В потенциальном поле тела обладают потенциальной энергией и работа консервативных сил совершается за счет убыли потенциальной энергии.
Поэтому работу A12 можно представить, как разность потенциальных энергий заряда q0 в начальной и конечной точках поля заряда q :
Потенциальная энергия заряда q0 , находящегося в поле заряда q на расстоянии r от него равна
Считая, что при удалении заряда на бесконечность, потенциальная энергия обращается в нуль, получаем: const = 0 .
Для одноименных зарядов потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов потенциальная энергия из взаимодействия (притяжения) отрицательна.
Если поле создается системой n точечных зарядов, то потенциальная энергия заряда q0 , находящегося в этом поле, равна сумме его потенциальных энергий, создаваемых каждым из зарядов в отдельности:
Потенциал электростатического поля.
Отношение не зависит от пробного заряда q0 и является, энергетической характеристикой поля, называемой потенциалом:
Потенциал ϕ в какой-либо точке электростатического поля есть скалярная физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.
1.7 Связь между напряженностью и потенциалом.
Связь между потенциалом и напряженностью электростатического поля. Эквипотенциальные поверхности.
Как ранее показано, работа сил электростатического поля при перемещении заряда q0 может быть записана с одной стороны, как , с другой же – как убыль потенциальной энергии, т.е. . Здесь dr – есть проекция элементарного перемещения dl заряда на направление силовой линии , – есть малая разность потенциалов двух близко расположенных точек поля. Приравняем правые части равенств и сократим на q0 . Получаем соотношения , . Отсюда .
Рис.1.13. Эквипотенциальные поверхности (сплошные) и силовые линии (пунктирные) поля точечного положительного заряда.
Последнее соотношение представляет связь основных характеристик электростатического поля Е и j. Здесь – быстрота изменения потенциала в направлении силовой линии. Знак минус указывает на то, что вектор направлен в сторону убывания потенциала. Поскольку , можно записать проекции вектора на координатные оси: . Отсюда следует, что . Выражение, стоящее в скобках, называется градиентом скаляра j и обозначается как gradj.
Напряженность электростатического поля равна градиенту потенциала, взятому с обратным знаком .
Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхностями, потенциал всех точек которых одинаков. Потенциал поля одиночного точечного заряда . Эквипотенциальные поверхности в данном случае есть концентрические сферы с центром в точке расположения заряда q (рис.1.13). Эквипотенциальных поверхностей можно провести бесконечное множество, однако принято чертить их с густотой, пропорциональной величине Е.
1.8 Электроемкость, плоский конденсатор.
Электроемкость.
Рассмотрим уединенный проводник — проводник, удаленный от других тел и зарядов . Из опыта следует, что разные проводники, будучи одинаково заряженными, имеют разные потенциалы.
Физическая величина C , равная отношению заряда проводника q к его потенциалу ϕ, называется электрической емкостью этого проводника.
Электроемкость уединенного проводника численно равна заряду, который нужно сообщить этому проводнику для того, чтобы изменить его потенциал на единицу.
Она зависит от формы и размеров проводника и от диэлектрических свойств окружающей среды. Емкости геометрически подобных проводников пропорциональны их линейным размерам.
Пример: Рассмотрим уединенный шар радиуса R, находящийся в однородной среде с диэлектрической проницаемостью e. Ранее было получено, что потенциал шара равен . Тогда емкость шара , т.е. зависит только от его радиуса.
Единица электроемкости —фарад(Ф):1Ф—емкость такогоуединенного проводника, потенциал которого изменяется на 1В при сообщении ему заряда 1Кл. Емкостью 1Ф обладает шар с радиусом R = 9 ⋅10 6 км. Емкость Земли 0,7мФ.


ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.

ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот.

Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Теорема о циркуляции вектора напряженности
Теорема о циркуляции вектора напряженности электрического поля
Взаимодействие неподвижных зарядов реализуется посредством электростатического поля. Описывают электростатическое поле при помощи вектора напряженности ($overline$), который определен как сила ($overline$), действующая на единичный положительный заряд, размещенный в рассматриваемой точке поля:
Электростатические силы являются консервативными, это значит, что их работа по замкнутой траектории ($L$) равна нулю:
где $overline$ – перемещение.
Интеграл в формуле (2) называется циркуляцией вектора напряженности электростатического поля. Циркуляция вектора $overline$- это работа, которую могут совершить силы Кулона, перемещая положительный заряд равный единице по контуру.
Учитывая, что $qne 0$, получим:
Теорема о циркуляции вектора напряжённости электростатического поля говорит о том, циркуляция $overline$ по замкнутому контуру равна нулю.
В дифференциальной форме теорему о циркуляции записывают как:
[rot overline=0 left(4right).]
Такой вид записи как (4) удобно использовать для проверки потенциальности векторного поля. Потенциальное поле является безвихревым.
Как следствие из теоремы о циркуляции $overline$: работа при перемещении заряда из одной точки поля в другую не зависит от формы траектории движения.
Из теоремы о циркуляции следует, что линии электростатического поля не бывают замкнутыми, они начинаются на положительных, а заканчиваются на отрицательных зарядах.
Теорема о циркуляции вектора напряженности магнитного поля
Физическая величина ($overline$), являющаяся характеристикой магнитного поля, равная:
называется напряженностью магнитного поля. $overline$ – вектор магнитной индукции поля; $<mu >_0$ – магнитная постоянная; $<overline
>_m$- вектор намагниченности.
Циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов проводимости, которые охвачены замкнутым контуром, по которому рассматривается циркуляция:
Если направление обхода контура связывается с направлением тока правилом правого винта, то ток в сумме (5) стоит со знаком плюс.
Циркуляция вектора напряженности в общем случае отлична от нуля, это означает, что магнитное поле – это вихревое поле, оно не является потенциальным.
Теорему о циркуляции вектора напряженности магнитного поля доказывают, опираясь на закон Био-Савара-Лапласа и принцип суперпозиции.
Теорема о циркуляции вектора $overline$ исполняет роль, похожую на роль теоремы Гаусса для вектора напряженности электрического поля. Если имеется симметрия при распределении токов, то используя теорему о циркуляции $overline,$ находят саму напряженность магнитного поля.
Примеры задач с решением
Задание. Определите, является ли потенциальным электрическое поле, которое задано уравнением: $overlineleft(x,yright)=Aleft(2xy overline+left(x^2-y^2right)overlineright).$
Решение. Из теоремы о циркуляции, которая записана в дифференциальном виде:
[rot overline=0 left(1.1right).]
следует, что если вихрь поля равен нулю, то поле потенциально. Используя определение ротора:
Частные производные от $overline$ равны:
Подставляя (1.4) в (1.3), получаем, что
[rot overline=rot left[Aleft(2xy overline+left(x^2-y^2right)overlineright)right]=0.]
Ответ. Поле является потенциальным.
Задание. Какова циркуляция вектора напряженности магнитного поля для замкнутого контура $L$ (рис.1), если $I_1=5 A;; I_2=2 A;; I_3=10 A;; I_4=1 A?$
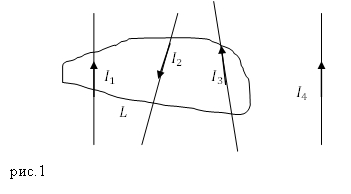
Решение. Основой для решения задачи служит теорема о циркуляции вектора напряжённости магнитного поля:
Контур $L$ охватывает три тока, следовательно:
Ответ. $ointlimits_L<overlinedoverline=13А .>$
[spoiler title=”источники:”]
http://zdamsam.ru/a5859.html
http://www.webmath.ru/poleznoe/fizika/fizika_179_teorema_o_cirkuljacii_vektora_naprjazhennosti.php
[/spoiler]