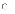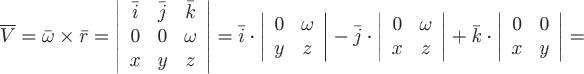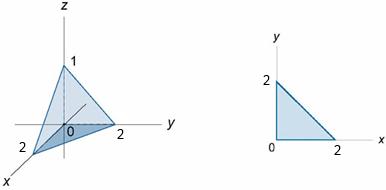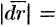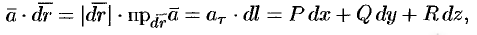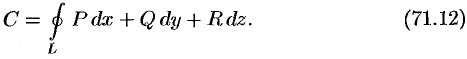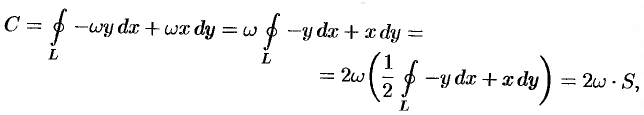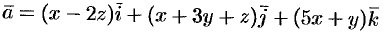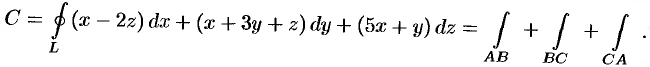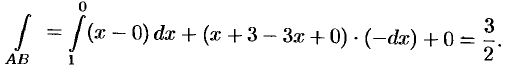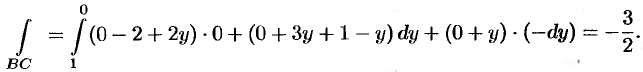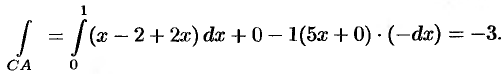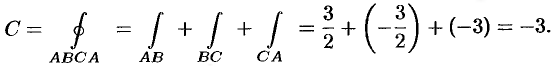Циркуля́цией ве́кторного по́ля по данному замкнутому контуру Γ называется криволинейный интеграл второго рода, взятый по Γ. По определению
где 


Свойства циркуляции[править | править код]
Аддитивность[править | править код]
Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности, то есть
Формула Стокса[править | править код]
Циркуляция вектора F по произвольному контуру Г равна потоку вектора 
где ![operatorname {rot}{mathbf {F}}=[nabla ,{mathbf {F}}]=left|{begin{matrix}{mathbf {e}}_{{x}}&{mathbf {e}}_{{y}}&{mathbf {e}}_{{z}}\{frac {partial }{partial x}}&{frac {partial }{partial y}}&{frac {partial }{partial z}}\F_{{x}}&F_{{y}}&F_{{z}}\end{matrix}}right|](https://wikimedia.org/api/rest_v1/media/math/render/svg/f745cda352a86694bb1892a3d28c069f20b28e26)
В случае, если контур плоский, например лежит в плоскости OXY, справедлива теорема Грина
где 

Физическая интерпретация[править | править код]
Физическая интерпретация циркуляции: Работа поля по замкнутому контуру
Если F — некоторое силовое поле, тогда циркуляция этого поля по некоторому произвольному контуру Γ есть работа этого поля при перемещении точки вдоль контура Г. Отсюда непосредственно следует критерий потенциальности поля: поле является потенциальным когда циркуляция его по произвольному замкнутому контуру есть нуль. Или же, как следует из формулы Стокса, в любой точке области D ротор этого поля есть нуль.
Историческая справка[править | править код]
Термин «циркуляция» был первоначально введен в гидродинамике для расчета движения жидкости по замкнутому каналу.
Рассмотрим течение идеальной несжимаемой жидкости. Выберем произвольный контур Γ. Мысленно представим, что мы (мгновенно) заморозили всю жидкость в объеме, за исключением тонкого канала постоянного сечения, включающего в себя контур Γ. Тогда, в зависимости от первоначального характера течения жидкости, она будет либо неподвижной в канале, либо двигаться вдоль контура (циркулировать). В качестве характеристики такого движения берут величину, равную произведению средней скорости движения жидкости по каналу 
поскольку именно скорость 
Так как при затвердевании стенок канала нормальная к контуру компонента скорости будет погашена (вообразим, что это происходит перед тем, как тангенциальная скорость в канале всюду становится одинаковой вследствие несжимаемости жидкости), жидкость по каналу будет сразу после затвердевания двигаться с тангенциальной составляющей исходной скорости 
где dl — элемент длины контура.
Позже понятие «циркуляция» было распространено на любые векторные поля, даже такие, в которых «циркулировать» в буквальном смысле нечему.
Литература[править | править код]
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т.3. М.: «Наука», 1960.
- Савельев И. В. Курс общей физики. Т2. М.: Астрель • АСТ, 2004.
Циркуляция векторного поля
Пусть
в области
задано
непрерывное векторное полеи
ориентированная гладкая кривая(с
заданным направлением обхода). Обозначим
единичный вектор касательной к линиичерез
,
направление которого совпадает с
выбранным направлением на линии.Определение.
Линейным
интегралом
векторного поля
вдоль
линииназывается
криволинейный интеграл 1 рода от
скалярного произведения векторови
:
,
где
–
дифференциал длины дуги кривой.
Если
ввести в рассмотрение вектор(здесь
–
радиус вектор точки, описывающий линию)
и обозначить его проекции на координатные
оси через,
то предыдущую формулу можно записать
в виде
,
где
вектор
направлен
по касательной к.
Правая часть последнего равенства
является криволинейным интегралом 2
рода.
Если–
силовое поле, то линейный интеграл равен
работе, которую поле совершает по
перемещению материальной точки вдоль
ориентированной линии.Определение.
Линейный
интеграл называется циркуляцией
векторного
поля
,
если–
замкнутая линия.
Если
–
замкнутая пространственная кривая, то
ее направление обхода специально
оговаривается.Пример.
Вычислить циркуляцию векторного поля
по
замкнутой линии,
состоящей из одного витка винтовой
линииот
точкидо
точкии
прямолинейного отрезка.Решение.
Виток
соответствует
изменению параметрав
уравнениях кривой отдо
.
Прямаяимеет
направляющий вектор,
поэтому ее параметрические уравнения
будут,
гдеизменяется
отдо
.
Вычислим циркуляцию как сумму криволинейных
интегралов по дуге винтовой линии и по
прямолинейному отрезку:.Ответ:
.Вопрос.
Циркуляция векторного поля
по
замкнутому контуру,
где,
может быть вычислена по формуле:
Ротор
Определение.
Если векторное поле
имеет
дифференцируемые в точкесоставляющие
,
торотором
(или
вихрем) векторного поля
в
точкеназывается
вектор
,
где
частные производные вычислены в этой
точке.
В символической форме
имеет
вид:

Поясним
физический
смысл ротора
векторного поля. Рассмотрим векторное
поле
как
поле скоростей движущейся жидкости.
Поместим в таком потоке, в определенной
его точке, бесконечно малое колесико с
лопастями, расположенные по окружности
этого колесика. Под воздействием потока
жидкости такое колесико будет вращаться
с некоторой скоростью, зависящей от
направления оси колесика.
Выберем
систему координат так, чтобы его ось
колесика совпадала бы с осью
.
Найдем ротор поля линейных скоростейтвердого
тела, вращающегося вокруг осис
постоянной угловой скоростью,
причем.
Тогда
линейная скорость вращения тела будет
равна:
,
где–
радиус вектор точки.
Тогда
по определению ротора получим (здесь
определитель раскрываем по первой
строке):.
С
точностью до постоянного множителя
ротор поля скоростейпредставляет
собой угловую скорость вращения твердого
тела, т.е. он характеризует “вращательную
компоненту” поля скоростей. С этим
связано само название «ротор» (от
латинского «вращатель»).
Направление
ротора совпадает с направлением
наибольшей плотности циркуляции.Вопрос.
Вторая координата ротора векторного
поля
равна
(введите
с клавиатуры только число)
Ваш
ответ
0
Формула Стокса
Если
функции
дифференцируемы
в областии
в этой области расположен некоторый
замкнутый контур,
то для любой незамкнутой поверхности,
имеющей границу,
имеет местоформула
Стокса:

где
на
берется
та сторона, в точках которой вектор
нормалинаправлен
так, чтобы видимый с его конца обход
контурасовершался
бы против часовой стрелки (ориентация
поверхности согласована с обходом
контура).
Формула Стокса позволяет
свести вычисление циркуляции векторного
поляпо
контурук
вычислению потока полячерез
незамкнутую поверхность,
опирающуюся на контур(здесь
–
граница незамкнутой поверхности).
Заметим, что–
любая поверхность, имеющая границей
контур,
поэтому возможен наиболее простой ее
выбор.
Если через контурпровести
две поверхностии
,
то
.
Учитывая,
что
и
ограничивают
некоторую пространственное телои,
меняя направление нормали на поверхностина
противоположное, т.е. на внешнее по
отношению к,
получим
,
т.
е. поток вихря через замкнутую поверхность
равен . Это означает, что поле вихря
является соленоидальным.
Пример.
Найти
по формуле Стокса циркуляцию векторного
поля
по
линиипересечения
с координатными плоскостями той части
поверхности,
которая лежит в 1 октанте, т.е..
Решение.
Находим
ротор заданного векторного поля:
Пусть
поверхностью с границейявляется
поверхность.
Она является эллиптическим параболоидом
и расположена в первом октанте.
Вычислим
циркуляцию:.
Нормаль
к поверхностиравна
.
Тогда единичная нормаль имеет координаты:
Откуда.
В данном случае,
т.к.в
первом октанте. При этом скалярное
произведение векторови
равно:
.
Отсюда
по формулеполучим:

.Вопрос.
Используя формулу Стокса, циркуляцию
векторного поля
по
линии пересечения параболоидас
координатной плоскостьюможно
свести к вычислению интеграла:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача 1. Найдите циркуляцию векторного поля вдоль контура Г:
,
, лежащего в плоскости
, в положительном направлении относительно орта K.
Решение. Способ 1. Контуром интегрирования Г является АВА: половина окружности радиуса 1 с центром в начале координат и отрезок прямой .
По формуле Стокса имеем
За поверхность S, ограниченную контуром Г, примем полукруг образованный сечением кругового цилиндра
плоскостью
.
Следовательно,
Ответ: .
Способ 2. Можно было решать по определению.
Циркуляция векторного поля вдоль контура Г определяется формулой линейного интеграла вдоль замкнутой линии Г:
Дуга АВ является частью окружности
Вычисляем
Получаем:
Окончательно,
Ответ: .
Задача 2. Найдите поток векторного поля через замкнутую поверхность
,
,
в направлении внешней нормали.
Решение. Поверхностью является пирамида V, образованная плоскостью
и координатными плоскостями.
Проекция поверхности на плоскость XOY есть треугольник D, ограниченный прямыми ,
,
Так как поверхность замкнутая, то можем воспользоваться формулой Остроградского-Гаусса:
Ответ: .
| < Предыдущая | Следующая > |
|---|
Примеры решений задач по теории поля
В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):
Лучшее спасибо – порекомендовать эту страницу
Примеры: базовые понятия теории поля
Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.
Задача 2. Найти дивергенцию и ротор векторного поля $overline{a}=(3x-y) overline{i}+(6z+5x) overline{k}$
Задача 3. Дано скалярное поле $u(x,y,z)$ и векторное поле $overline{a}(x,y,z)$. Найти $grad u$, $div overline{a}$, $rot overline{a}$ в точке $M(1;5;-2)$.
$$u=frac{sqrt{x}}{y}-frac{yz}{x+sqrt{y}}, quad
overline{a}=yzoverline{i} +xzoverline{j} +xyoverline{k}$$
Задача 4. Вычислить потенциальную функцию векторного поля
$$overline{a}=left( frac{x}{y}+ycos x right)overline{i} +left(-frac{x^2}{2y^2}+sin xright)overline{j}.$$
Поток поля через поверхность
Задача 5. Найти поток векторного поля $overline{a}=2x overline{i}+y overline{j}-2z overline{k}$ через часть плоскости $P: 2x+y/2+z=1$, расположенную в первом октанте (нормаль образует острый угол с осью $Oz$).
Задача 6. Найти поток векторного поля $overline{a}$ через часть поверхности $S$, вырезаемую плоскостями $P_1, P_2$ (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
$$ overline{a}=(x^3+xy^2)overline{i}+(y^3+x^2y)overline{j}+z^2overline{k},\
S: x^2+y^2=1, P_1^ z=0; P_2: z=3$$
Задача 7. Найти поток векторного поля $overline{a}$ через замкнутую поверхность $S$ (нормаль внешняя).
$$ overline{a}=xoverline{i}+zoverline{j}-yoverline{k},\
S: z=4-2(x^2+y^2), z=2(x^2+y^2).$$
Задача 8. Найти поток векторного поля $overline{a}=x^3overline{i}+y^3overline{j}+z^3overline{k}$ через замкнутую поверхность $S: x^2+y^2+z^2=1$ (нормаль внешняя).
Задача 9. Найти поток векторного поля $overline{a}$ через часть плоскости $S$, вырезанную плоскостью $P: z=1$ непосредственно и с помощью формулы Гаусса-Остроградского (нормаль внешняя к замкнутой поверхности).
$$overline{a}=(x+xy^2) overline{i} + (y-yx^2)overline{j}+(z-3)overline{k}, quad S: x^2+y^2=z^2 (z geq 0).$$
Циркуляция векторного поля
Задача 10. Найти модуль циркуляции векторного поля $overline{a}=xyoverline{i}+yzoverline{j}+zxoverline{k}$ вдоль контура
$$x^2+y^2=9, x+y+z=1.$$
Задача 11. Найдите циркуляцию вектора $overline{a}=(x^2-y) overline{i}+ xoverline{j}+ overline{k}$ по контуру
$$x^2+y^2=1;\
z=1$$
с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).
Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$.
$$ overline{F} = (3x-1) overline{i}+ (y-x+z)overline{j}+4z overline{k}, $$
$L$ – контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.
Работа векторного поля
Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.
Задача 14. Вычислить работу векторного поля силы $overline{F} = xz overline{i} -overline{j}+y overline{k}$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.
Типовой расчет по теории поля
Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.
$$ overline{F} = z overline{i}+ (x+y)overline{j}+y overline{k}, quad (p): 2x+y+2z=2. $$
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей, оформление производится в Word, срок от 1 дня.
Проконсультируем по задачам теории поля
Полезные ссылки
- Учебник с примерами онлайн по теории поля
- Функции нескольких переменных – задачи с решениями
Циркуляция векторного поля
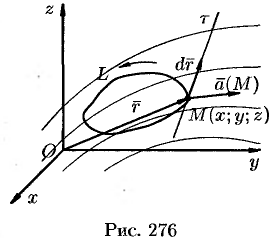
Пусть векторное поле образовано вектором (71.1). Возьмем в этом поле некоторую замкнутую кривую 
Пусть 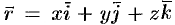


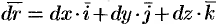
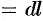
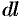
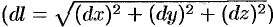
Криволинейный интеграл по замкнутому контуру 

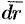

называется циркуляцией вектора а вдоль 
Рассмотрим различные формы записи циркуляции. Так как
где 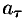

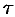

или
Циркуляция 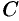

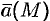

Отметим, что вдоль замкнутых векторных линий циркуляция отлична от нуля, потому что в каждой точке векторной линии скалярное произведение 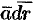

Пример №71.5.
Найти циркуляцию вектора ноля линейных скоростей вращающегося тела (см. пример 69.2) 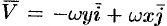

Решение:
Будем считать, что направление нормали к плоскости 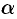
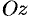
где 

Заметим, что если нормаль к поверхности 
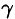
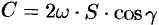
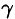
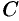
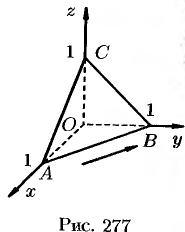
Пример №71.6.
Вычислить циркуляцию векторного поля
вдоль периметра треугольника с вершинами 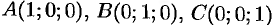
Решение:
Согласно формуле (71.12), имеем:
На отрезке 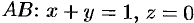
На отрезке 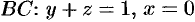
На отрезке 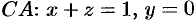
Следовательно,
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны: