|
Решение отправила в личку 🙂 Пусть не так красиво, как Михаил Александрович, зато быстро, как и просили 😉 |
Производные и дифференциалы высших порядков.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Частными производными 2-го порядка функции $u=f(x_1, x_2, …, x_n)$ называются частные производные от ее частных производных первого порядка. Производные второго порядка обозначаются следующим образом: $$frac{partial}{partial x_k}left(frac{partial u}{partial x_k}right)=frac{partial^2u}{partial x^2_k}=f”_{x_kx_k}(x_1, x_2, …, x_k, …, x_n).$$ $$frac{partial}{partial x_l}left(frac{partial u}{partial x_k}right)=frac{partial^2u}{partial x_kpartial x_l}=f”_{x_kx_l}(x_1, x_2, …, x_k, …, x_l, …, x_n).$$ и т. д.
Аналогично определяются и обозначаются частные производные порядка выше второго.
Дифференциалом 2-го порядка $d^2f$ функции $u=f(x_1, x_2,…, x_n)$ называется дифференциал от ее дифференциала 1-го порядка, рассматриваемого ка функция переменных $x_1, x_2, .., x_n$ при фиксированных значениях $dx_1, dx_2, …, dx_n:$ $$d^2u=d(du).$$
Аналогично определяется дифференциал 3-го порядка:$$d^3u=d(d^2u).$$
Вообще, $$d^mu=d(d^{m-1}u).$$
Дифференциал $m$-го порядка функции $u=f(x_1, x_2,…, x_n),$ где $x_1, x_2, .., x_n -$ независимые переменные, выражается символической формулой $$d^mu=left(frac{partial}{partial x_1}dx_1+frac{partial}{partial x_2}dx_2+…+frac{partial}{partial x_n}dx_nright)^mu,$$ которая формально раскрывается по биномиальному закону.
Например, в случае функции $z=f(x, y)$ двух независимых переменных и для дифференциалов 2-го и 3-го порядков справедливы формулы $$d^2z=frac{partial^2 z}{partial x^2}dx^2+2frac{partial^2 z}{partial xpartial y}dxdy+frac{partial^2 z}{partial y^2}dy^2,$$
$$d^3z=frac{partial^3 z}{partial x^3}dx^3+3frac{partial^3 z}{partial x^2partial y}dx^2dy++3frac{partial^3 z}{partial xpartial y^2}dxdy^2+frac{partial^3 z}{partial y^3}dy^3.$$
Примеры.
Найти дифференциалы 1-го и 2-го порядков следующих функций: ($x, y, z -$ независимые переменные):
7.101. $z=x^3+3x^2y-y^3.$
Решение.
$$dz=z’_xdx+z’_ydy.$$
$$z’_x=(x^3+3x^2y-y^3)’_x=3x^2+6xy;$$
$$z’_y=(x^3+3x^2y-y^3)’_y=3x^2-3y^2.$$
Таким образом
$$dz=(3x^2+6xy)dx+(3x^2-3y^2)dy.$$
Дифференцируем вторично, учитывая, что $dx$ и $dy$ не зависят от $x$ и $y$ (т.е. считая $dx$ и $dy$ постоянными): $$d^2z=d((3x^2+6xy)dx+(3x^2-3y^2)dy)=d(3x^2+6xy)dx+d(3x^2-3y^2)dy=$$ $$=(6xdx+6xdy+6ydx)dx+(6xdx-6ydy)dy=6((x+y)dx^2+2xdxdy-ydy^2).$$Ответ: $dz=(3x^2+6xy)dx+(3x^2-3y^2)dy;$ $d^2 z=6((x+y)dx^2+2xdxdy-ydy^2).$
7.108.$u=xy+yz+zx.$
Решение.
$$du=d(xy+yz+zx)=xdy+ydx+ydz+zdy+zdx+xdz=$$ $$=(y+z)dx+(x+z)dy+(x+y)dz.$$
Дифференцируем вторично, учитывая, что $dx,,, dy$ и $dz$ не зависят от $x,,, y$ и $z$ (т.е. считая $dx,, dy$ и $dz$ постоянными): $$d^2u=d((y+z)dx+(x+z)dy+(x+y)dz)=$$ $$=(dy+dz)dx+(dx+dz)dy+(dx+dy)dz=2(dxdy+dxdz+dydz).$$Ответ: $du=(y+z)dx+(x+z)dy+(x+y)dz;$ $d^2 u=2(dxdy+dxdz+dydz).$
7.110.Найти $d^3z,$ если $z=e^ysin x.$
Решение.
$$dz=d(e^ysin x)=e^ycos xdx+sin xe^y dy.$$ Дифференцируем вторично, учитывая, что $dx$ и $dy$ не зависят от $x$ и $y$ (т.е. считая $dx$ и $dy$ постоянными): $$d^2z=d(e^ycos xdx+sin xe^y dy)=$$ $$=-sin x e^ydxdx+cos x e^y dydx+e^ycos xdxdy+sin xe^ydydy=$$ $$=-sin x e^y dx^2+2e^ycos xdxdy+sin xe^y dy^2.$$
$$d^3z=d(-sin x e^y dx^2+2e^ycos xdxdy+sin xe^y dy^2)=$$ $$=(-cos xe^ydx^2-2e^ysin xdxdy+cos xe^ydy^2)dx+$$ $$+(-sin xe^ydx^2+2e^ycos xdxdy+sin xe^ydy^2)dy=$$ $$=-cos xe^ydx^3+-3e^ysin xdx^2dy+3cos xy^ydxdy^2+sin xe^ydy^3.$$
Ответ: $d^3z=-cos xe^ydx^3+-3e^ysin xdx^2dy+3cos xy^ydxdy^2+sin xe^ydy^3.$
7.112. Найти $d^6u,$ если $u=ln(x+y+z).$
Решение.
Будем пользоваться формулой
$$d^mu=left(frac{partial}{partial x_1}dx_1+frac{partial}{partial x_2}dx_2+…+frac{partial}{partial x_n}dx_nright)^mu,$$
$$frac{partial u}{partial x}=frac{partial u}{partial y}=frac{partial u}{partial z}=frac{1}{x+y+z};$$
$$frac{partial^2 u}{partial x^2}=frac{partial^2 u}{partial y^2}=frac{partial^2 u}{partial z^2}=frac{partial^2u}{partial xpartial y}=frac{partial^2u}{partial ypartial x}=frac{partial^2u}{partial xpartial z}=frac{partial^2u}{partial zpartial x}=frac{partial^2u}{partial ypartial z}=frac{partial^2u}{partial zpartial y}=$$ $$=-frac{1}{(x+y+z)^2};$$
…
$$frac{partial^6 u}{partial x^6}=frac{partial^6 u}{partial y^6}=frac{partial^6 u}{partial z^6}=frac{partial^6u}{partial x^5partial y}=frac{partial^6u}{partial x^4partial y^2}=…frac{partial^6u}{partial xpartial y^5}=frac{partial^6u}{partial x^5partial z}=…=$$ $$=frac{partial^6u}{partial xpartial z^5}=frac{partial^6u}{partial y^5partial z}=…=frac{partial^6 u}{partial ypartial z^5}=(-1)^55!frac{1}{(x+y+z)^6}=frac{5!}{(x+y+z)^6}.$$
Отсюда получаем $$d^6(ln(x+y+z))=left(frac{partial}{partial x}dx+frac{partial}{partial y}dy+frac{partial}{partial z}dzright)^6(ln(x+y+z))=$$ $$=-frac{5!}{(x+y+z)^6}(dx+dy+dz)^6.$$
Ответ: $d^6u=-frac{5!}{(x+y+z)^6}(dx+dy+dz)^6.$
Домашнее задание.
Найти дифференциалы 1-го и 2-го порядков следующих функций: ($x, y, z -$ независимые переменные):
7.102. $z=frac{y}{x}-frac{x}{y}.$
7.103. $z=sqrt{x^2+2xy}.$
7.105. $z=(x+y)e^{xy}.$
7.106. $z=xlnfrac{y}{x}.$
7.111. Найти $d^3u,$ если $u=x^3+y^3+z^3-3xyz..$
7.113. Найти $d^mu,$ если $u=e^{ax+by+cz}.$
[АссолЬ]
Знаток
(321),
закрыт
5 лет назад
объясните чайнику. ничего не понимаю.
или это производная от dz/dy, в которой х – число, а у – переменная????
Трудное детство
Оракул
(70151)
10 лет назад
z – это сложная функция зависящая от двух переменных х и у, она описывает некоторую поверхность. смешанная производная z“(x,y) находится так. сначала берем производную по х, считая у постоянной, потом – по у считая х постоянной. например z=x^2+5xy^2-6y^3, z`(x)=2x+5y^2, z“(x,y)=10y. при этом, если мы сначала возмем производную по у, а потом по х, результат не изменится. на самом деле z`(y)=10xy-18y^2, z“(y,x)=10y.
Частной
производной функции двух переменных-
по одной из этих переменных называется
предел отношения соответствующего
частного приращения функции к приращению
данной переменной, когда последнее
стремится к нулю (если этот предел
существует). Обозначсается частная
производная так: zx’,zy’
или f’x(x,y),
f’y(x,y).
Полным
дифференциаломффункции z=f(x,y)
называется сумма произведений частных
производных этой функции на приращения
соответствующих независимых переменных,т.е.
dz=z’xx+z’yy.
При нефиксированных х,у,: dx=x,
dy=y,а
формулу полного дифференциала можно
записать в виде: dz=z’xdx+z’ydy
или dz=(dz/dx)*dx+(dz/dy)*dy
Частными
производными второго порядка функции
z=f(x,y)
называются частные производные от
частных производных первого порядка.
Частные производные второго порядка
четыре. Они обозначаются следующим
образом:
1)Z’’xx=(zx’)’x
или d2z/dx2=d/dx*(dz/dx)
2)z’’xy=(zx’)’y
или
d2z/dydx=d/dy8(dz/dx)
3)z’’yx=(z’y)’x
или
d2z/dxdy=d/dx*(dz/dy)
4)z’’yy=(z’y)’y
или
d2z/dy2=d/dy(dz/dy)
Аналогично
определяются частные производные 3-го
, 4-го и более высоких порядков. Частные
производные второго или более высокого
порядка,взятые по различным переменным,
называются смешанными частными
производными.
15.Экстремумы функции двух независимых переменных. Необходимые и достаточные условия существования экстремума.
Точка
М0(х0,у0)
называется точкой минимума (максимума)
функции z=f(x,y)
если существует такая окрестность точки
М0,
что для всех точек М(х,у) из этой окрестности
выполняется неравенство
f(x0,у0)<f(x,y),(f(x0,у0)>f(x,y).
Точки минимума и максимума функции
z=f(x,y)
называются точками экстремума,а значения
функции в точке М0
сравнивается с её значениями в точках,
достаточно близких к М0.
1)Необходимые
условия экстремума-если М0(х0,у0)-
точка экстремума дифференцируемой
функции z=f(x,y),
то уё частные производные zx’
и zy’
в этой точке равны нулю: zx’(x0,у0)=0
zy’(x0,у0)=0
Точки в которых частные производные
первого порядка равны нулю, наз-ся
критическими или стационарными. В
критических точках функция z=f(x,y)
может иметь экстремум а может и не иметь
его.
2)Достаточное
условие экстремума- пусть функция
z=f(x,y)
: а)определена в некоторой окрестности
критической точки М0(х0,у0),
в которой zx’(x0,у0)=0
и zy’(x0,
y0)=0
б)имеет непрерывные частные производные
второго порядка zxx’’(x0,
y0)=A;
zxy’’(x0,
y0)=B;
zyy’’(x0,
y0)=C.
Тогда если дельта= АС-В2>0
,то функция z=f(x,y)
в точке М0(х0,у0)
экстремума не имеет. В случае дельта=АС-В2=0
вопрос о наличии экстремума остаётся
открытым.
16Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов.
Функция
F(x)
называется первообразной для функции
f(x)
на интервале (a,b)
и для любого x
принадлежащего (a,b)
выполняется равенство F’(x)=f(x)
Если
функция F(x)
является первообразной для функции
f(x)
на интервале (a,b),
то множество всех первообразных для
f(x)
задаётся формулой F(x)+C,
где С-произвольная постоянная.
Множество
всех первообразных функций F(x)+C
для функции f(x)
на интервале (a,b)
называется неопределённым интегралом
от функции f(x)
на этом интервале и обозначается символом
S
f(x)dx,
где S-знак
интеграла; f(x)-подынтегральная
функция; f(x)dx-
подынтегральное выражение; х-переменная
интегральная. Таким образом S
f(x)dx=F(x)+C,где
F(x)-некоторая
первообразная для f(x)
на интервале (a,b).
С-произвольная постоянная.
СВОЙСТВА:
1)производная от неопределённого
интеграла равна подынтегральной функции;
дифференциал от неопределённого
интеграла равен подынтегральному
выражению: (S
f(x)dx)’=f(x);
d(S
f(x)dx)=f(x)dx.
2)неопределённый интеграл от дифференциала
некоторой функции равен сумме этой
функции и произвольной постоянной: S
dF(x)=F(x)+C.
3)постоянный множитель можно выносить
за знак неопределённого интеграла: S
cf(x)dx=с
S
f(x)dx,
c-const.
неопределённых интегралов: S
(f(x)+-g(x)dx=
S
f(x)dx+-S
g(x)dx.
5)если S
f(x)dx=F(x)+C,
а u=f(x)-
произвольная функция, имеющая непрерывную
производную , то S
f(u)du=F(u)+c.
ТАБЛИЦА
ОСНОВНЫХ НЕОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ:
1)S0*dx=C;
2)S18dx=Sdx=x+C;3)Sxadx=xa+1/a+1
+C; 4)S dx/x=ln|x|+C; 5)S axdx=ax/lna
+C; 6)Sexdx=
ex+C;
7)S sinxdx=-cosx+Сж8)S
cos xdx= sinx+С
9) S dx/cos2x=tg+C;
10)S dx/sin2x=-сtgx+C;
11)S dx/корень
1-x2=
arcsinx+C; 12)Sdx/корень
a2-x2=arcsinx/a+C;
13)S dx/корень
x2+-a2=ln|x+корень
x2+-a2|+c;
14) S dx/1+x2=arctgx+C;
15) S dx/a2+x2=1/a
arctgx/a+C; 16)S dx/x2-a2=1/2a
ln |x-a/x+a|+C.
Соседние файлы в папке Шпоры ИУП_1сессия
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Примеры нахождения частных производных
Задача 2. Найти частные производные ![]() ,
, ![]() и
и ![]() , если переменные x, y, и z связаны равенством 4x2 y ez – cos(x3 – z) + 2y2 + 3x = 0.
, если переменные x, y, и z связаны равенством 4x2 y ez – cos(x3 – z) + 2y2 + 3x = 0.
Решение находим с помощью калькулятора.
Для F(x, y, z) = 4x2 y ez – cos(x3 – z) + 2y2 + 3x получаем:
F’x= (4x2 yez – cos(x3 – z) + 2y2 + 3x)’x = [считаем y и z постоянными] =
= 8x y ez + sin( x3 – z)3x2 + 3 = 8x y ez + 3x2 sin( x3 – z) + 3;
F’y= (4x2 y ez – cos(x3 – z) + 2y2 + 3x)’y = [считаем x и z постоянными] =
= 4x2 ez + 4y;
F’z = (4x2 y ez – cos(x3 – z) + 2y2 + 3x)’z = [считаем x и y постоянными] =
= 4x2 y ez – sin (x3 – z).
По формулам находим частные производные:
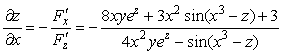 ;
; 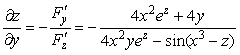
и по формуле (3) получаем: 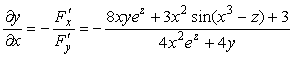 .
.
Ответы:  ;
; 
 .
.
Задание. Найти частные производные функции z в точке A(-1;0).
z = ln(x2+y2)+y/x
Решение.
Находим частные производные:
![]()
![]()
Задание №2. Найти частные производные 1-го и 2-го порядка.
z = x3 + 3x2y – sin(xy)
Скачать решение
Задача 1. Дана функция z = f(x,y). Требуется:
1) найти частные производные dz/dx и dz/dy;
2) найти полный дифференциал dz;
3) показать, что для данной функции справедливо равенство: d2z/dxdy = d2z/dydx.
Пример 1. Показать, что функция ![]() удовлетворяет уравнению
удовлетворяет уравнению ![]() .
.
Решение.
Найдем частные производные ![]() и
и ![]() .
.
 ,
,
 .
.
Подставим их в уравнение

Получим тождество. Следовательно, функция z удовлетворяет данному уравнению.
Пример 2. Дана функция ![]() и две точки A(4;2 )и B(4.03;1.96). Требуется: 1) вычислить значение функции в точке В;
и две точки A(4;2 )и B(4.03;1.96). Требуется: 1) вычислить значение функции в точке В;
2) вычислить приближенное значение функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом;
3) оценить в процентах относительную погрешность, возникшую при замене приращения функции ее дифференциалом.
Решение.
1. ![]()
2.![]()
Итак, z0=5, z≈z0+df(A);  .
.
Найдем ![]() .
.  ,
, ![]() ;
;
 ,
,  ;
;
f(4.03;1.96)=≈5+0.8·0.03+1.2·(-0.04)=5.072.
 ;
;![]() .
.
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
