
С башни высотой h = 25 м бросили камень со скоростью v0
= 15 м/с под углом α = 300 к горизонту. Определите: время полета камня; дальность
полета камня в горизонтальном направлении; скорость полета камня в момент
падения на землю; угол β,
который составит траектория движения камня с горизонтом в точке его падения на
землю. Сопротивление воздуха не учитывать.
Решение.
Сделав чертеж,
выберем систему координат так, чтобы ее начало совпадало с точкой бросания, а
оси были направлены следующим образом: OX – вдоль
поверхности
земли; OY – по нормали в ней в сторону
начального смещения камня. Сложное движения камня по параболе в данном случае
можно представить как результат сложения двух прямолинейных движений:
прямолинейного движения вдоль оси OX и движения тела,
брошенного вертикально вниз, вдоль оси OY.
Составим систему уравнения скорости и
перемещения для их проекций по каждому направлению:
vx = v0 cos α, x = v0 cos α•t;
vy = v0 sin α – gt, y = v0 sin α•t – gt.
В момент времени t, когда камень упадет на землю, его координаты x = s, y = –h. Тогда для определения t получаем уравнение
–h = v0 sin α•t – (gt•t)/2.
Откуда находим время
 .
.
Дальность полета камня s определим из уравнения
 .
.
Скорость камня в момент падения на
землю можно выразить формулой
 ,
,
где
![]() .
.
Подставим вместо vx и vy их выражения, получим скорость полета камня в момент падения на землю
 .
.
Ответ: t = 3,2 c, s = 41 м, v = 27 м/с.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Что такое движение тела брошенного под углом к горизонту
Определение
Движением тела под углом к горизонту в физике называют сложное криволинейное перемещение, которое состоит из двух независимых движений, включая равномерное прямолинейное движение в горизонтальном направлении и свободное падение по вертикали.
В процессе подбрасывания объекта вверх под углом к горизонту вначале наблюдают его равнозамедленный подъем, а затем равноускоренное падение. Скорость перемещения тела, относительно поверхности земли, остается постоянной.
На графике изображено схематичное движение тела, которое подбросили под углом к горизонту. В этом случае α является углом, под которым объект начал свое перемещение. Характеристики такого процесса будут следующими:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Направление вектора скорости тела, которое подбросили под определенным углом к горизонту, будет совпадать с касательной к траектории его перемещения.
- Начальная скорость отличается от направления горизонтальной линии, а обе ее проекции не равны нулю.
- Проекция скорости в начале движения на ось ОХ составляет (V_{ox}=V_{0}cos alpha).
- Проекция начальной скорости на ось ОУ равна (V_{oy}=V_{0}sin alpha).
- Проекция мгновенной скорости на ось ОХ следующая: (V_{x}=V_{0}cos alpha).
- Проекция мгновенной скорости на ось ОУ обладает нулевым значением и рассчитывается следующим образом: (V_{x}=V_{0}sin alpha-gt).
- Ускорение свободного падения на ось ОХ обладает нулевой проекцией, или (g_{x}=0).
- Проекция ускорения свободного падения на ось ОУ равна (–g), или (g_{y}=-g).
К числу кинематических характеристик движения тела, которое подбросили под углом к горизонту, относят модуль мгновенной скорости в определенное время t. Данный показатель можно рассчитать с помощью теоремы Пифагора:
(V=sqrt{V^{2}_{x}+V^{2}_{y}})
Минимальная скорость тела будет замечена в самой верхней точке траектории, а максимальная величина данной характеристики будет достигнута, когда объект только начинает перемещаться, а также в точке падения на поверхность земли. Время подъема представляет собой время, необходимое для достижения телом верхней точки траектории. За полное время объект совершает полет, то есть перемещается от начальной точки к точке приземления.
Дальность полета является перемещением объекта по отношению к оси ОХ. Такую кинематическую характеристику обозначают буквой l. По отношению к оси ОХ тело перемещается, сохраняя постоянство скорости.
Определение
Горизонтальным смещением тела называют смещение данного объекта, относительно оси ОХ.
Расчет горизонтального смещения тела в какой-либо момент времени t выполняют с помощью уравнения координаты х:
(x=x_{0}+V_{0x}t+frac{gxt^{2}}{2})
Зная следующие условия:
- (x_{0}=0);
- проекция ускорения свободного падения, относительно оси ОХ, также имеет нулевое значение;
- проекция начальной скорости на ось ОХ составляет (V_{0}cos alpha).
Записанная формула приобретает следующий вид:
(x=V_{0}cos alpha t)
Мгновенной высотой принято считать высоту, на которой находится объект в определенный момент времени t. Наибольшей высотой подъема является расстояние от поверхности земли до верхней точки траектории движения тела под углом к горизонту.
Вывод формулы, как найти угол и дальность полета
Перемещение объекта, который был брошен под углом к горизонту, необходимо изобразить с помощью суперпозиций, характерных для двух типов движений:
- равномерное горизонтальное движение;
- равноускоренное перемещение в вертикальном направлении с ускорением свободного падения.
Скорость тела будет рассчитываться таким образом:
(v_{0x}=v_{x}=v_{0} cos alpha =const)
(v_{0y}=v_{0}sin alpha)
(v_{y}=v_{0}sin alpha-gt)
Уравнение координаты записывают в следующем виде:
(x=v_{0}cos alpha times t)
(y=v_{0}sin alpha times t-frac{gt^{2}}{2})
В любое время значения скорости тела будут равны:
(v=sqrt{v_{x}^{2}+v_{y}^{2}})
Определить угол между вектором скорости и осью ОХ можно таким образом:
(tan beta =frac{v_{y}}{v_{x}}=frac{v_{0}sin alpha -gt}{v_{0}cos alpha })
Время подъема на максимальную высоту составляет:
(t=frac{v_{0}sin alpha }{g})
Максимальная высота подъема будет рассчитана следующим образом:
(h_{max}=frac{v_{0}^{2}sin ^{2}alpha}{2g})
Полет тела будет длиться определенное время, которое можно рассчитать с помощью формулы:
(t=frac{2v_{0}sin alpha }{g})
Максимальная дальность полета составит:
(L_{max}=frac{v_{0}^{2}sin 2alpha }{g})
Примеры решения задач
В примерах, описывающих движение тела, на которое действует сила тяжести, следует учитывать, что а=g=9,8 м/с2.
Задача 1
Небольшой камень был брошен с ровной горизонтальной поверхности под углом к горизонту. Необходимо определить, какова максимальная высота подъема камня при условии, что, спустя 1 секунду после его начала движения, скорость тела обладала горизонтальным направлением.
Решение
Направление скорости будет горизонтальным в верхней точке перемещения камня. Таким образом, время, за которое он поднимется, составляет 1 секунду. С помощью уравнения времени подъема можно представить формулу произведения скорости в начале полета на синус угла, под которым бросили камень:
(V_{0}sin alpha =gt)
Данное равенство следует подставить в уравнение для расчета максимальной высоты, на которую поднимется камень, и выполнить вычисления:
(h=frac{V_{0}sin ^{2}alpha }{2g}=frac{(gt)^{2}}{2g}=frac{gt^{2}}{2}=frac{10times 1}{2}=5)
Ответ: максимальная высота подъема камня, который бросили под углом к горизонту, составляет 5 метров.
Задача 2
Из орудия выпустили снаряд, начальная скорость которого составляет 490 м/с, под углом 30 градусов к горизонту. Нужно рассчитать, какова высота, дальность и время полета снаряда без учета его вращения и сопротивления воздуха.
Решение
Систему координат и движение тела можно представить схематично:
Составляющие скорости, относительно осей ОХ и ОУ, будут совпадать во время начала движения снаряда:
(V_{0x}=V_{0} cos alpha) сохраняет стабильность значения в любой промежуток времени во время всего перемещения тела.
(V_{0y}=V_{0}sin alpha) будет меняться, согласно формуле равнопеременного движения (V_{y}=V_{0}sin alpha-gt).
В максимальной точке, на которую поднимется снаряд:
(V_{y}=V_{0}sin alpha-gt_{1}=0)
Из этого равенства следует:
(t=frac{V_{0sin alpha }}{g})
Полное время полета тела будет рассчитано по формуле:
(t=2t_{1}=frac{2V_{0}sin alpha }{g}=50)
Высота, на которую поднимется снаряд, определяется с помощью уравнения равнозамедленного перемещения тела:
(h=V_{0y}t_{1}-frac{gt_{1}^{2}}{2}=frac{V_{0}^{2}sin ^{2}alpha }{2g}=3060)
Дальность полета снаряда будет рассчитана таким образом:
(S=V_{0x}t=frac{V_{0}^{2}sin 2alpha }{g}=21000)
Ответ: высота составляет 3060 метров, дальность полета равна 21000 метров, время движения составит 50 секунд.
Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.
Кинематические характеристики движения
Важные факты!
Графически движение горизонтально брошенного тела описывается следующим образом:
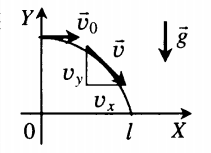
- Вектор скорости горизонтально брошенного тела направлен по касательной к траектории его движения.
- Проекция начальной скорости на ось ОХ равна v0: vox = v0. Ее проекция на ось ОУ равна нулю: voy = 0.
- Проекция мгновенной скорости на ось ОХ равна v0: vx = v0. Ее проекция на ось ОУ равна нулю: vy = –gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
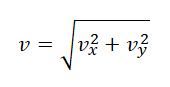
Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:
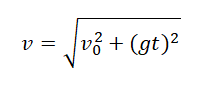
Минимальная скорость в течение всего времени движения равна начальной скорости: vmin = v0.
Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: vmax = v.
Время падения — время, в течение которого перемещалось тело до момента приземления. Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:
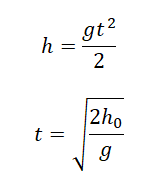
h0 — высота, с которой тело бросили в горизонтальном направлении.
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0tпад
Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий вид:
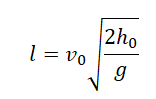
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
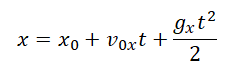
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:
x = v0t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
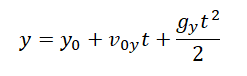
Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?
Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:
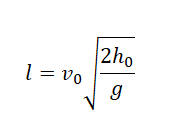
Выразим начальную скорость и вычислим ее:
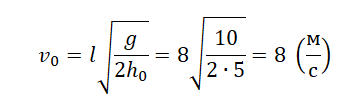
Горизонтальный бросок тела с горы
Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.
График горизонтального броска тела с горы
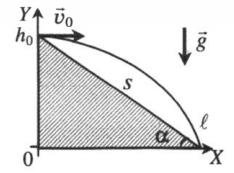
α — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения
Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения. Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:
l = s • cosα
Начальная высота — высота, с которой было брошено тело. Обозначается h0. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:
h0 = s sinα
Пример №2. На горе с углом наклона 30о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?
Выразим это расстояние через дальность полета:
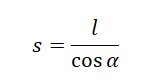
Дальность полета выражается по формуле:
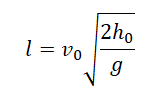
Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:
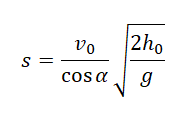
Выразим с учетом формулы начальной высоты:
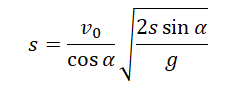
Преобразуем:
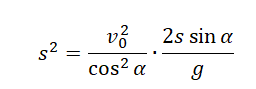
Поделим обе части выражения на общий множитель s:
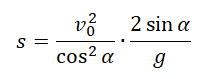
Подставим известные значения:
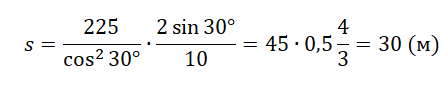
Задание EF18083
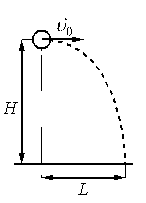
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
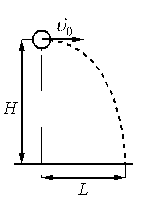
В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2υ0.
Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости и массы.
- Определить характер изменения физической величины при увеличении начальной скорости и массы шарика.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
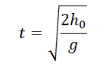
Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
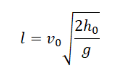
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 313.
Ответ: 313
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18048
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости.
- Определить характер изменения физической величины при уменьшении начальной скорости.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
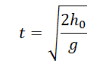
Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
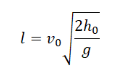
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 323.
Ответ: 323
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 18.2k
Движение тела, брошенного горизонтально
теория по физике 🧲 кинематика
Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.
Кинематические характеристики движения
Графически движение горизонтально брошенного тела описывается следующим образом:

- Вектор скорости горизонтально брошенного тела направлен по касательной к траектории его движения.
- Проекция начальной скорости на ось ОХ равна v0: vox = v0. Ее проекция на ось ОУ равна нулю: voy = 0.
- Проекция мгновенной скорости на ось ОХ равна v0: vx = v0. Ее проекция на ось ОУ равна нулю: vy = –gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
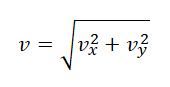
Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:
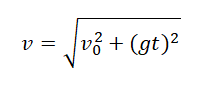
Минимальная скорость в течение всего времени движения равна начальной скорости: vmin = v0.
Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: vmax = v.
Время падения — время, в течение которого перемещалось тело до момента приземления. Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:
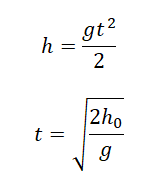
h0 — высота, с которой тело бросили в горизонтальном направлении.
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий вид:
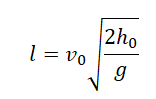
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
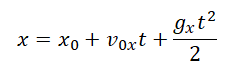
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
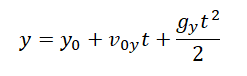
Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?
Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:
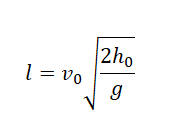
Выразим начальную скорость и вычислим ее:
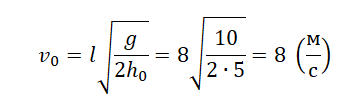
Горизонтальный бросок тела с горы
Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.
График горизонтального броска тела с горы

α — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения
Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения. Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:
Начальная высота — высота, с которой было брошено тело. Обозначается h0. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:
Пример №2. На горе с углом наклона 30 о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?
Выразим это расстояние через дальность полета:
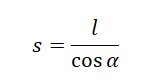
Дальность полета выражается по формуле:
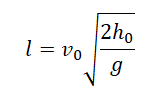
Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:
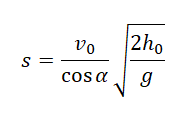
Выразим с учетом формулы начальной высоты:
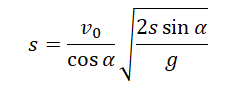
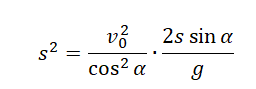
Поделим обе части выражения на общий множитель s:
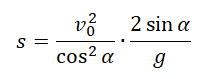
Подставим известные значения:
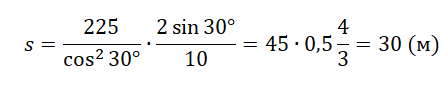
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ 0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).

В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2 υ 0.
Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости и массы.
- Определить характер изменения физической величины при увеличении начальной скорости и массы шарика.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
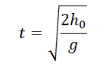
Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
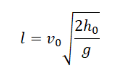
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 313.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ 0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).

Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости.
- Определить характер изменения физической величины при уменьшении начальной скорости.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
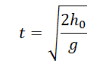
Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
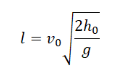
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 323.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Камень брошенный горизонтально летит по окружности
2017-01-12
Озорник бросает камень в горизонтально летящую авиамодель, причем в момент броска направление скорости камня, характеризуемое углом $alpha$ к горизонту, было как раз на модель. Скорость полета авиамодели $u$. Начальная скорость камня $v$. На какой высоте $h$ летела авиамодель, если камень попал в нее? Где это произошло, на восходящем или нисходящем участке траектории камня?
Выберем начало координат в точке, откуда брошен камень (рис.), и приравняем координаты авиамодели и камня в некоторый момент времени $t$:
$h ctg alpha + ut = v cos alpha cdot t$, (1)
$h = v sin alpha cdot t – frac><2>$. (2)
Подставим $h$ из (2) в (1) и выразим $t$ из получившегося уравнения:
Теперь найдем высоту $h$ из (1) и (3):
$h = frac<2u>(v cos alpha – u) tg^ <2>alpha$. (4)
Для ответа на второй вопрос задачи выразим $t$ из уравнения (2)
и приравняем его выражению (3)
$v sin alpha pm sqrt < v^<2>sin^ <2>alpha – 2gh> = 2u tg alpha$. (6)
Знак “+” соответствует нисходящей ветви траектории. В этом случае $v 2u/ cos alpha)$. При $u = (v/2) cos alpha$ камень попадет в авиамодель в верхней точке своей траектории. 1.89. Ускорение пропорционально квадрату скорости.
Ответ: $h = frac<2u> (v cos alpha – u) tg^ <2>alpha$. Камень попадает в авиамодель на нисходящем участке траектории, если $v < 2u/ cos alpha$, и на восходящем, если выполнено обратное неравенство.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ ПО ФИЗИКЕ.
Задачи по теме “тело брошено под углом к горизонту” и движение по окружности.
На этой странице представлены условия типовых задач по физике из сборника задач Бендрикова Г.А. для школьников 9-11 классов и студентов.
Решения этих задач даны на плейлисте видео – СМОТРИ ЗДЕСЬ –
Номера задач здесь и на плейлисте совпадают.
Счастливого разбора «полетов»!
Задачи: тело брошено под углом к горизонту
44. Тело брошено с высоты h горизонтально с начальной скоростью v0. Как зависят от времени координаты тела и его полная скорость? Вывести уравнение траектории.
45. С башни, имеющей высоту h = 25 м, горизонтально брошен камень с начальной скоростью v0 = 10 м/с. На каком расстоянии s от основания башни он упадет на землю?
46. Камень, брошенный с башни горизонтально с начальной скоростью v0 = 10 м/с, упал на расстоянии s = 10 м от башни. С какой высоты h был брошен камень?
47. Тело брошено со стола горизонтально. При падении на пол его скорость v= 7,8 м/с. Высота стола h = 1,5 м. Найти начальную скорость тела v0.
48. Камень брошен с горы горизонтально с начальной скоростью v0 = 15 м/с. Через какое время t его скорость будет направлена под углом а = 45° к горизонту?
49. Камень, брошенный с крыши дома горизонтально с начальной скоростью vq = 15 м/с, упал на землю под углом а = 60° к горизонту. Какова высота h дома?
50. Тело брошено с высоты h= 2 м горизонтально так, что к поверхности земли оно подлетает под углом а = 45° к горизонту. Какое расстояние по горизонтали пролетает тело?
51. Тело брошено горизонтально. Через время t = 5 с после броска направления полной скорости v и полного ускорения а составили угол Р = 45°. Найти полную скорость v тела в этот момент. Считать ускорение свободного падения g = 10 м/с2.
52. Камень брошен с высоты h вверх под углом а к горизонту с начальной скоростью v0. Под каким углом Р к горизонту и с какой скоростью v камень упадет на землю?
53. Тело брошено горизонтально с начальной скоростью v0 = 15 м/с. Найти нормальное ускорение а„ и касательное аг ускорения через время t = 1с после начала движения тела.
54. Тело брошено с земли под углом а к горизонту с начальной скоростью v0. Как зависят от времени скорость v тела и угол Р ее наклона к горизонту?
55. Тело брошено с земли под углом а к горизонту с начальной скоростью un. Найти законы движения для координат тела и получить уравнение траектории.
56. Тело брошено с земли под углом а к горизонту с начальной скоростью и. На какую высоту h поднимется тело? В течение какого времени t будет продолжаться подъем тела?
57. Тело брошено с земли под углом а к горизонту с начальной скоростью v. Какое время t тело будет находиться в полете? Какое расстояние s по горизонтали от места бросания пролетит тело?
58. Тело брошено с земли под углом а к горизонту с начальной скоростью v0. Построить графики зависимости вертикальной проекции скорости vy от времени t; координаты у (высоты); координаты х (расстояния по горизонтали от места бросания).
59. Камень брошен под углом а = 30° к горизонту с начальной скоростью v0 = 10 м/с. Через какое время t камень будет на высоте h = 1 м?
60. Камень, брошенный под углом а = 30° к горизонту, дважды был на одной высоте h: спустя время t1 = 3 с и время t2 = 5 с после начала движения. Найти начальную скорость v0 и высоту h.
61. Тело, брошенное под углом а = 60° к горизонту, через время t – 4 с после начала движения имело вертикальную проекцию скорости vy = 9,8 м/с. Найти расстояние s между местом бросания и местом падения.
62. Камень брошен с башни, имеющей высоту h, с начальной скоростью vQ, направленной под углом а к горизонту. На каком расстоянии s от основания башни упадет камень?
63. Два тела брошены под углами a1 и а2 к горизонту из одной точки. Каково отношение сообщенных им начальных скоростей, если они упали на землю в одном и том же месте?
64. Тело брошено под углом к горизонту с начальной скоростью v0 = 10 м/с. Найти скорость v тела в момент, когда оно оказалось на высоте h = 3 м.
65. Камень брошен с высоты h под углом к горизонту с начальной скоростью v0. С какой скоростью v камень упадет на землю?
66. Тело брошено под углом а к горизонту с начальной скоростью y0. Через какие промежутки времени после бросания скорость тела будет составлять с горизонтом углы р1 = 45° и р2 = 315° ?
67. Какую начальную скорость v0 имел снаряд, вылетевший из пушки под углом a = 30° к горизонту, если он пролетел расстояние s= 17 300 м? Известно, что сопротивление воздуха уменьшило дальность полета в четыре раза.
68. Мотоциклист въезжает на высокий берег рва, параметры которого указаны на рис. Какую минимальную скорость v должен иметь мотоциклист в момент отрыва от берега, чтобы перескочить через ро
69. Камень брошен с башни под углом a = 30° к горизонту с начальной скоростью v0 = 10 м/с. Каково кратчайшее расстояние l между местом бросания и местом нахождения камня спустя время t = 4 с после бросания?
70. Сверхзвуковой самолет летит горизонтально со скоростью v = 1440 км/ч на высоте h = 20 км. Когда самолет пролетает над зенитной установкой, из орудия производится выстрел. Какова должна быть минимальная начальная скорость v0 снаряда и угол а ее с горизонтом, чтобы снаряд попал в самолет?
71. Два тела брошены одновременно из одной точки – одно вверх, другое вниз, оба с начальной скоростью v0 = 30 м/с под углом а = 60° к вертикали. Найти разность уровней, на которых будут находиться тела спустя время f = 2 с.
72. С самолета, летящего горизонтально со скоростью v0, на высоте h0 сброшен груз. На какой высоте h скорость груза будет направлена под углом а к горизонту? Сопротивлением воздуха пренебреч
73. Самолет, оторвавшись от взлетной дорожки, летит по прямой линии, составляющей с горизонтом угол а = 30°, с начальной скоростью v0 = 50 м/с и ускорением а = 3 м/с2. Из самолета спустя время t0 = 5 с после отрыва его от земли выброшен по вертикали вниз ключ с начальной скоростью v0 = 3 м/с относительно самолета. На каком расстоянии от места взлета упадет ключ?
74. С высоты h= 2 м вниз под углом а = 60° к горизонту брошен мяч с начальной скоростью v = 8,7 м/с. Найти расстояние s между двумя последовательными ударами мяча о землю. Удары считать абсолютно упругими.
75. Шарик свободно падает по вертикали на наклонную плоскость. Пролетев расстояние h = 1 м, он упруго отражается и второй раз падает на ту же плоскость. Найти расстояние s между первым и вторым ударами шарика о плоскость, если последняя составляет с горизонтом угол а = 30°.
Задачи на движение по окружности
76. Линейная скорость точек обода вращающегося диска v1=6 м/с, а точек, находящихся на расстоянии r = 10 см ближе к оси вращения, v2 = 2 м/с. Найти частоту вращения диска.
77. Велосипедист Найти радиус R маховика, если при вращении линейная скорость точек на его ободе = 6 м/с, а точек, находящихся на расстоянии г = 15 см ближе к оси вращения, и2 = 5,5 м/с.
78. Велосипедист едет с постоянной скоростью v по прямолинейному участку дороги. Найти мгновенные линейные скорости точек А, В, С, D, Е, лежащих на ободе колеса, относительно земли.
79. Материальная точка движется по окружности радиуса R = 20 см равноускоренно с касательным ускорением ах = 5 см/с2. Через какое время t после начала движения центростремительное ускорение а будет больше ах в 2 раза?
80. Материальная точка, двигаясь равноускоренно по окружности радиуса R = 1 м, прошла за время t 1= 10 с путь s = 50 м. С каким центростремительным ускорением а„ двигалась точка спустя время t2 = 5 с после начала движения?
81. Ось вращающегося диска движется поступательно в горизонтальном направлении со скоростью v. Ось горизонтальна, направление ее движения перпендикулярно к ней самой. Найти мгновенную скорость v1 верхней точки диска, если мгновенная скорость нижней точки диска равна v2.
82. При равноускоренном движении тела по окружности полное ускорение а и линейная скорость v тела образуют угол а = 30°. Найти отношение центростремительного и касательного ускорений.
83. Найти линейную скорость у и центростремительное ускорение а„ точек на экваторе и на широте 60°. Считать радиус Земли R = 6400 км.
84. Маховое колесо, вращающееся с частотой = 240 об/мин, останавливается в течение промежутка времени t = 0,5 мин. Найти число оборотов N, сделанных колесом до полной остановки.
85. Поезд въезжает на закругленный участок пути с начальной скоростью у0 = 54 км/ч и проходит равноускоренно расстояние s = 600 м за время t = 30 с. Радиус закругления R = 1 км. Найти скорость у и полное ускорение а поезда в конце этого участка пути.
86. С колеса автомобиля, движущегося с постоянной скоростью у, слетают комки грязи. Радиус колеса равен R. На какую высоту h над дорогой будет отбрасываться грязь, оторвавшаяся от точки А колеса, указанной на рис. 12? Изменится ли высота h, если колесо будет катиться с пробуксовкой?
87. В винтовой желоб положен тяжелый шарик. С каким ускорением а нужно тянуть нить, намотанную на цилиндр с желобом, чтобы шарик падал свободно, если диаметр цилиндра равен D, а шаг винтового желоба равен r?
РЕШЕНИЯ ЭТИХ ЗАДАЧ даны на плейлисте видео – СМОТРИ ЗДЕСЬ –
Номера задач здесь и на плейлисте совпадают.
Голосование за лучший ответ
Sharky Lions
Мастер
(2137)
4 года назад
в задаче недостаточно данных, нет массы камня, нет приложенной силы, задача не имеет решения…
например исходя из концепции:
к камню массой N
приложена такая сила Р, которая придаст ему скорость 10м/с на расстоянии L= 1/(бесконечность)
таким образом камень сместится на 0… а угол здесь вообще роли не играет, т. к. его влияние также будет стремиться к 0 🙂
следовательно задача не имеет решения из-за недостатка данных, ответ: “неопределённость”
основы баллистики: от массы заряда, зависит дальность полёта снаряда… (т. е. от приложенной силы)
Собака СтрашнаяОракул (50171)
4 года назад
в задаче достаточно данных, если учесть, что подобные задачи подразумевают условия на Земле с постоянным же, принимаемого как правило за десять
Андрей СтепановПросветленный (22756)
4 года назад
Полный бред. В задаче не указаны данные по силе трения, так что задача решается без ее учета. Соответственно масса камня не имеет значения. Так же как и сила, т. к. указана начальная скорость. Так что задача имеет решение и оно указано выше в посте Рустама Искендерова
Рустам Искендеров
Искусственный Интеллект
(133392)
4 года назад
1) Исходя из вертикальной составляющей скорости определяется время подъёма камня по известной ф-ле равнозамедляющегося движения;
2) Умножением двукратного значения времени на горизонтальную составляющую скорости определяется дальность полёта камня. ОТВЕТ: 5 м.
Здесь уск. свободного падения принято равным 10 м/с2. Сопротивлением воздуха, разумеется, пренебрежено.
