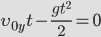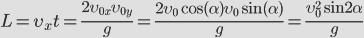Когда объект запускается, он следует параболическому пути и движению, известному как движение снаряда. В этом посте мы рассмотрим параметры и способы их расчета. движение снаряда в подробном анализе.
Когда объект запускается и движется по симметричной параболической траектории, движение называется движением снаряда, а параболический путь объекта называется его траекторией. В этом случае объект перемещается одновременно по вертикали и горизонтали. В результате движение снаряда становится двумерным. При движении снаряда вам нужно только приложить силу в начале траектории; после этого на объект действует только сила тяжести.
Теперь давайте посмотрим, как рассчитать движение снаряда:
Предположим, вы стреляете пушечным ядром. Он начинает двигаться вверх и вперед, пока не достигнет максимальной высоты. С этого момента он будет продолжать двигаться вперед, но в нисходящем направлении. Он отслеживает этот изогнутый маршрут, известный как траектория, имеющая форму параболы. Любой объект, движущийся таким образом, называется движущимся снарядом. Поскольку траектория движения снаряда всегда параболическая, она представляется как:
у = ах + bx2
Прежде чем достичь Земли, пушечное ядро во время своего путешествия пойдет по параболическому маршруту. Компания скорость по оси X остается постоянной на протяжении всего движения, тогда как скорость по оси Y изменяется в зависимости от его положения. Только ускорение свободного падения 9.8 м / с2, управляет этим типом движения. Ускорение, направленное вниз, остается постоянным во время полета ядер.
Кинематические уравнения движения снаряда:
Формула начальной скорости:
Предположим, что начальная скорость равна u, а угол полета снаряда равен. У начальной скорости есть две составляющие: горизонтальная и вертикальная.
Горизонтальная составляющая начальной скорости ux и предоставлено:
ux = ты ᐧ потому что𝛳
Вертикальная составляющая начальной скорости равна uy и определяется выражением:
uy = и ᐧ грех

Время полета снаряда:
Время полета снаряда – это промежуток времени между запускаемым объектом и достижением земли. Величина стартовой скорости и угол полета снаряда определяют время полета, которое обозначается T.
Формула ускорения:
В горизонтальном направлении ускорение отсутствует, поскольку горизонтальная составляющая ускорения остается постоянной на протяжении всего движения. Единственное ускорение в вертикальном направлении происходит за счет силы тяжести.
ax = 0 и
ay = -г
Отрицательный знак означает ускорение вниз.
Формула скорости в момент времени t:
На протяжении всего движения горизонтальная составляющая скорости остается постоянной. Однако, поскольку вертикальное ускорение постоянно, вертикальная составляющая скорости изменяется линейно.
В результате скорость может быть рассчитана в любой момент времени t по следующей формуле:
vx = тыx = ты ᐧ потому что𝛳
vy = u ᐧ sin𝛳 – g ᐧ t
Используя теорему Пифагора, можно найти величину скорости.
Формула смещения в момент времени t:
В момент времени t смещение может быть определено как:
х = (и ᐧ cos𝛳) ᐧ т
y = (u ᐧ sin𝛳) ᐧ t – ½ (gt2)
Формула параболической траектории:
Мы можем использовать уравнения смещения в направлениях x и y, чтобы вывести уравнение для параболической формы движения снаряда:
Формула дальности снаряда:
Общее горизонтальное расстояние, пройденное объектом за время полета, определяется как его дальность. Если объект запускается с земли (начальная высота = 0), формула выглядит следующим образом:
Согласно приведенному выше уравнению, максимальная дальность полета по горизонтали может быть получена при угле полета снаряда 𝛳 = 45 °. Rm представляет собой максимальный диапазон.
Формула максимальной высоты:
Когда вертикаль составляющая скорости равна нулю, vy = 0, максимальная высота может быть достигнута. Поскольку время полета – это полное время снаряда, для достижения максимальной высоты потребуется половина этого времени. Таким образом, время для достижения максимальной высоты составляет:
Таким образом, из уравнения перемещения максимальная высота может быть определена как:
Формула движения снаряда по горизонтали:
Горизонтальный снаряд Движение – это тип движения снаряда, при котором объект запускается горизонтально с возвышенной плоскости, а не с земли.

Угол запуска указывать не нужно, поскольку он параллелен земле (т. Е. Угол равен 0 °). В результате у нас есть только одна начальная составляющая скорости: Vx = V, тогда как Vy = 0.
В этом случае уравнения движения следующие:
Скорость горизонтального движения снаряда:
Горизонтальная скорость: vx = V
И вертикальная скорость: vx = -g ᐧ т
Расстояние, пройденное объектом при горизонтальном движении снаряда:
В этом случае горизонтальное расстояние рассчитывается следующим образом:
х = v ᐧ т
А расстояние по вертикали можно определить как:
y = – (g ᐧ t2) / 2
Ускорение при горизонтальном движении снаряда:
Горизонтальное ускорение ax = 0, так как горизонтальная скорость постоянна..
Вертикальное ускорение аy = -г
Уравнение траектории горизонтального движения снаряда:
Уравнение траектории в этом случае может быть задано следующим образом:
Время полета при горизонтальном движении снаряда:
Время полета в этом случае может быть определено как:
Дальность полета снаряда при горизонтальном движении снаряда:
Дальность полета снаряда при горизонтальном движении снаряда составляет:
Поскольку мы запускаем объект с максимальной высоты, нам не нужно рассчитывать максимальную высоту в этом сценарии.
Давайте посмотрим на некоторые проблемы движения снаряда.
Проблема 1: Каким будет θmax, при котором расстояние от частицы до метателя всегда увеличивается до конца пути снова у земли?
Решение: Горизонтальное расстояние, пройденное объектом, называется его горизонтальным диапазоном и определяется по формуле:
Максимальная дальность полета может быть достигнута при угле выстрела 45 °.
Таким образом, для максимального угла Rm θmax = 45 °.
Задача 2: Если мяч брошен вертикально вверх со скоростью u, расстояние, пройденное за последние t секунд его всплытия, будет:
Решение: Поскольку мяч брошен вертикально, угол полета снаряда 𝛳 = 90 °.
Поскольку 𝛳 = 90 °
Где Tm – время, необходимое объекту для достижения максимальной высоты.
Предположим, что h представляет собой расстояние, пройденное объектом за последние t секунд его подъема. Затем скорость в этот момент рассчитывается следующим образом:
V = u – g ᐧ (T – t)
= u – g ᐧ (u / g – t)
= гт
Таким образом, расстояние, пройденное за последнюю t секунду, составляет:
h = vt – ½ gt2
= гт2 – ½ гт2
= ½ гт2
3 задачи: Частица проецируется под углом 60 ° над горизонтом со скоростью 10 м / с. Через некоторое время скорость составит угол 30 ° от горизонтали. Скорость частицы в этот момент составляет?
Решение: Горизонтальная составляющая скорости определяется как:
vx = ты ᐧ потому что𝛳
Здесь в первом случае угол проекции составляет 60 °, а начальная скорость u = 10 м / с. Таким образом,
vx = ты ᐧ cos60
= 10 x 0.5
= 5 м / с.
Теперь вертикальная составляющая скорости vy изменяется во время движения, но vx остается постоянным. Таким образом,
vx = v ᐧ cos𝛳2
Где 𝛳2 = 30 °, а v – скорость, когда объект составляет угол 𝛳 = 30 ° с горизонтом.
Наш калькулятор движения тела — это инструмент, который поможет вам проанализировать параболическое движение тела. Он может определить время полета, а также компоненты скорости, дальность полета и максимальную высоту полета. Продолжайте читать, если вы хотите понять, что такое движение тела, познакомьтесь с определением движения и определите вышеупомянутые значения с помощью уравнений движения тела.
Что такое движение тела (снаряда)? Определение движения снаряда
Представьте себе лучника, посылающего в воздух стрелу. Она начинает двигаться вверх и вперед при некотором наклоне к земле. Чем дальше она летит, тем медленнее она поднимается — и, наконец, она начинает снижаться, двигаясь теперь вниз и вперед и, наконец, снова ударяясь о землю. Если бы вы могли проследить ее путь, это была бы кривая, называемая траекторией в форме параболы. Любой объект, движущийся таким образом, движется как снаряд.
На снаряд действует только одна сила — сила тяжести. Сопротивление воздуха всегда не учитывается. Если вы начертите диаграмму свободного тела такого объекта, вам нужно будет нарисовать только один направленный вниз вектор и обозначить его «гравитация». Если бы на тело действовали какие-либо другие силы, то — по определению движения снаряда — это не был бы снаряд.
Калькулятор движения снаряда
Анализ движения снаряда
Движение снаряда довольно логично. Предположим, вы знаете начальную скорость объекта V, угол запуска α и начальную высоту h. Наш калькулятор движения снаряда выполняет следующие действия, чтобы найти все оставшиеся параметры:
1. Вычислите составляющие скорости.
- Скорость и ее горизонтальная и вертикальная составляющие
Горизонтальная составляющая скорости Vx равна V * cos (α).
Вертикальная составляющая скорости Vy равна V * sin (α).
Три вектора — V, Vx и Vy — образуют прямоугольный треугольник.
Если вертикальная составляющая скорости равна 0, то это случай горизонтального движения снаряда. Если дополнительно α = 90 °, то это случай свободного падения.
2. Запишите уравнения движения.
Расстояние
- Пройденное расстояние по горизонтали можно выразить как x = Vx * t, где t — время.
Вертикальное расстояние от земли описывается формулой y = h + Vy * t — g * t² / 2, где g — ускорение свободного падения.
Скорость
- Горизонтальная скорость равна Vx.
Вертикальную скорость можно выразить как Vy — g * t.
Ускорение
- Горизонтальное ускорение равно 0.
Вертикальное ускорение равно -g (потому что на снаряд действует только сила тяжести).
3.Рассчитайте время полета.
График движения снаряда: время полета
Полет заканчивается, когда снаряд попадает в землю. Можно сказать, что это происходит, когда вертикальное расстояние от земли равно 0. В случае, когда начальная высота равна 0, формулу можно записать как: Vy * t — g * t² / 2 = 0. Тогда из это уравнение, мы находим, что время полета
t = 2 * Vy / g = 2 * V * sin (α) / g.
Однако, если мы бросаем объект с некоторой возвышенности, тогда формула не так хорошо сокращается, как раньше, и мы получаем квадратное уравнение для решения: h + Vy * t — g * t² / 2 = 0. После решения этой задачи уравнение, получаем:
t = [V * sin (α) + √ ((V * sin (α)) ² + 2 * g * h)] / g
4. Рассчитайте дальность полета снаряда.
График движения снаряда: дальность
Дальность полета снаряда — это общее горизонтальное расстояние, пройденное за время полета. Опять же, если мы запускаем объект с земли (начальная высота = 0), то мы можем записать формулу как R = Vx * t = Vx * 2 * Vy / g. Его также можно преобразовать в форму: R = V² * sin (2α) / g
Ситуация усложняется для начального значения высоты, отличного от 0. Затем нам нужно заменить длинную формулу из предыдущего шага на t:
R = Vx * t = V * cos (α) * [V * sin (α) + √ (V * sin (α)) ² + 2 * g * h)] / g
5. Рассчитайте максимальную высоту.
График движения снаряда: максимальная высота
Когда снаряд достигает максимальной высоты, он перестает двигаться вверх и начинает падать. Это означает, что его вертикальная составляющая скорости изменяется с положительной на отрицательную, другими словами, она равна 0 на короткий момент времени t (Vy = 0).
Если Vy — g * t (Vy = 0) = 0, то мы можем переформулировать это уравнение к t (Vy = 0) = Vy / g.
Теперь мы просто находим расстояние по вертикали от земли в это время: hmax = Vy * t (vy = 0) — g * (t (Vy = 0)) ² / 2 = Vy² / (2 * g) = V² * sin (α) ² / (2 * г)
К счастью, в случае запуска снаряда с некоторой начальной высоты h нам нужно просто добавить это значение в окончательную формулу: hmax = h + V² * sin (α) ² / (2 * g)
Уравнения движения снаряда
Уфф, это было много вычислений! Подведем итог, чтобы сформировать наиболее важные уравнения движения снаряда:
Запуск объекта с земли (начальная высота h = 0)
- Составляющая горизонтальной скорости: Vx = V * cos (α)
Вертикальная составляющая скорости: Vy = V * sin (α)
Время полета: t = 2 * Vy / г
Дальность полета снаряда: R = 2 * Vx * Vy / g
Максимальная высота: hmax = Vy² / (2 * g)
Запуск объекта с некоторой высоты (начальная высота h> 0)
- Составляющая горизонтальной скорости: Vx = V * cos (α)
Вертикальная составляющая скорости: Vy = V * sin (α)
Время полета: t = [Vy + √ (Vy² + 2 * g * h)] / g
Дальность полета снаряда: R = Vx * [Vy + √ (Vy² + 2 * g * h)] / g
Максимальная высота: hmax = h + Vy² / (2 * g)
Использование нашего калькулятора движения снаряда наверняка сэкономит вам много времени. Он также может работать «наоборот». Например, введите время полета, расстояние и начальную высоту и смотрите, как он выполняет все вычисления за вас!
Часто задаваемые вопросы
Должен ли снаряд перемещаться горизонтально?
Нет, движение снаряда и его уравнения охватывают все движущиеся объекты, где единственной силой, действующей на них, является гравитация. Сюда входят объекты, которые подбрасываются прямо вверх, те, которые выбрасываются горизонтально, те, которые имеют горизонтальный и вертикальный компонент, и те, которые просто отбрасываются.
Как может снаряд упасть вокруг Земли?
На снаряд действует только одна сила — сила тяжести. Это означает, что объект в конечном итоге упадет на Землю. Но что делать, если объект движется по горизонтали так быстро, что к тому времени, как он достигает земли, земли уже нет? Это принцип, по которому работают спутники.
Как найти ускорение при движении снаряда?
На объект в метательном движении действует только одна сила — гравитация. Это означает, что любое изменение вертикальной скорости происходит из-за ускорения свободного падения, которое на Земле составляет 9,81 м / с2. В горизонтальном направлении скорость не изменяется, так как сопротивление воздуха считается незначительным, поэтому ускорение равно 0.
Какие факторы влияют на движение снаряда, выпущенного горизонтально?
Начальная скорость, начальная высота, с которой запускается снаряд, и сила тяжести будут влиять на снаряд, запущенный горизонтально. Сопротивление воздуха также будет иметь влияние в реальной жизни, но для большинства теоретических расчетов оно незначительно и поэтому игнорируется. Если у снаряда есть крылья, это также повлияет на его движение, так как он будет скользить.
Что такое снаряд?
Снаряд — это объект, который движется в воздухе и не имеет силы, действующей на него, кроме ускорения свободного падения (это означает, что он не может быть самоходным). Вы, наверное, можете вспомнить множество примеров: брошенный мяч или камень, стрела из лука. Даже Луна — это снаряд по отношению к Земле!
Каковы характеристики движения снаряда?
Свойства движения снаряда заключаются в том, что горизонтальная скорость объекта не изменяется, что его вертикальная скорость постоянно изменяется из-за силы тяжести, что форма его траектории будет параболой и что на объект не влияет сопротивление воздуха.
Кто первым и когда точно описал движение снаряда?
Галилей был первым человеком, который точно описал движение снаряда, разбив движение на горизонтальную и вертикальную составляющие и осознав, что график движения любого объекта всегда будет параболой. Он описал это в своей книге «О движении», опубликованной примерно в 1590-х годах.
Почему снаряд летит по кривой?
Объект следует параболе из-за того, что гравитация влияет на две его составляющие движения — горизонтальную и вертикальную. Горизонтальная составляющая вообще не подвержена влиянию силы тяжести, поэтому изменяется линейно. Однако вертикальная часть постоянно находится под действием силы тяжести, поэтому она будет увеличиваться в высоте, а затем уменьшаться, ускоряясь под действием силы тяжести.
Почему 45 градусов — оптимальный угол для снарядов?
Уравнение для расстояния, пройденного снарядом под действием силы тяжести, имеет вид sin (2θ) v2 / g, где θ — угол, v — начальная скорость, а g — ускорение свободного падения. Предполагая, что v2 / g постоянна, наибольшее расстояние будет, когда sin (2θ) будет максимальным, то есть когда 2θ = 90 градусов. Это означает θ = 45 градусов.
Движение тела, брошенного горизонтально или под углом к горизонту.
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли ( g ) – вдоль вертикальной оси ( y ), вдоль оси х движение равномерное и прямолинейное.
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
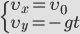
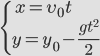
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
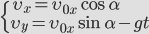
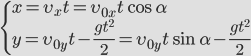
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
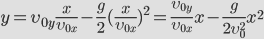 .
.
Мы получили квадратичную зависимость между координатами. Значит траектория – парабола.
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.

Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело .
Время, за которое тело долетит до середины, равно: 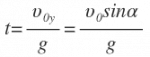
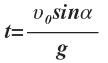
Тогда: 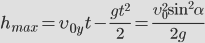
Максимальная высота:
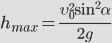
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна 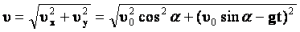
Угол, под которым направлен вектор скорости в любой момент времени:
Баллистическое движение — характеристика, основные формулы и уравнения
Как упадет брошенный предмет, по какой траектории полетит пуля и как рассчитать правильное направление для попадания в цель – всё это объясняется таким понятием как баллистическое движение и изучается соответствующей наукой.

Наверное каждый при просмотре фильмов о работе экспертов-криминалистов слышал выражение «аэробаллистическая экспертиза», и удивлялся тому, как лихо они определяют местоположение стрелка, и тип, а иногда и модель оружия, из которого был произведен, зачастую, фатальный выстрел.
Понятие баллистики
Определение баллистики звучит следующим образом – наука о движении тел, двигающихся в пространстве. Она изучает в первую очередь принципы движения всевозможных объектов, в частности пуль и снарядов, а также законы природы, влияющие на это движение и способность тела преодолевать возникшие на его пути преграды.

Физика и математика — вот основы, на которых базируется эта наука, они позволяют при должных знаниях рассчитывать траекторию полёта пули, исходя из воздействия на неё внешних сил, и её проникающую способность.
Сама же наука о законах полета снарядов делится на 4 направления:
Исследование движения пули или снаряда в канале ствола орудия изучает направление, которое называется внутренняя баллистика.
Поведение снаряда на выходе из канала ствола и в районе дульного среза исследуется промежуточной баллистикой и используется в разработке пламегасящих устройств и глушителей.
Вопросы движения снаряда в атмосфере и при воздействии внешних факторов изучаются внешней баллистикой. Основная область её применения – установление поправок на упреждение и влияние скорости ветра на траекторию.
Изучение проникающей способности снаряда – цель исследований баллистики под названием преградная (терминальная), которую изучают специалисты по вопросам бронезащиты.
История возникновения баллистики
Испокон веков основным занятием человека являлось уничтожение себе подобных. Сперва для этого использовались булыжники и палки, после чего человечество пришло к тому, что дистанционное оружие дает целый ряд преимуществ его владельцу.

Так или иначе баллистика изучалась по мере развития человечества, параллельно с развитием механизмов для поражения противника на расстоянии.
Метательные камни, ножи и дротики, ручные пращи, луки, арбалеты, а впоследствии – баллисты, катапульты, требушеты, толлеоны и, в конце концов, огнестрельное оружие и артиллерийские орудия — все эти средства толкали науку баллистики на протяжении всей своей истории.
Начало изучения траектории полета снаряда, как науки, было положено Николло Тарталья в 1537 году, начавшим исследование кривой движения этого тела. Продолжил изучение Галилей, сформулировав параболическую теорию.

Развивал данную тему и Ньютон, благодаря изучению законов воздушного сопротивления которого стало возможным доказать невозможность параболической кривой полета снаряда. Его дело продолжил Бенджамин Робинс, основное исследование которого — расчет начальной скорости ядра.
Он даже изобрел актуальный по сей день баллистический маятник. Прибор, с помощью которого определяют эффективность взрывчатых веществ, фиксируя при их подрыве угол отклонения маятника.

Далее баллистика развивалась семимильными шагами. Вошедшее в обиход в начале XIX века нарезное оружие, а также использование адаптированных под него снарядов и нового образца патрона, с пулей продолговатой формы, а точнее – необходимость изучения их эффективности и дальнейшей оптимизации, стали серьезным толчком в изучении данной науки, поскольку характеристики нового оружия были весьма высоки, что обуславливало широкую его популярность, и как следствие – высокий спрос.
Одним из ключевых витков истории баллистики стала разработка численного метода интегрирования дифференциальных уравнений, созданного Карлом Рунге и Мартином Кутта. Определенные элементы их метода позволяли с максимальной точностью вести расчеты траектории тел в пространстве.
Появлялись всё новые виды вооружения, конструкторы отчаянно экспериментировали с длиной ствола, внутренними нарезами и наполнением патрона, двигая науку вперед.
Баллистическая траектория
Итак, что же в итоге представляет собой баллистическая траектория? Современная энциклопедия гласит: «Это траектория движения свободно брошенного тела под действием только силы тяжести».

Например, межконтинентальные баллистические ракеты считаются таковыми, поскольку продолжают своё движение к цели после выключения двигателей, как раз-таки по траектории, которую называют баллистической.
Здесь же – расчет ведения огня по настильной траектории, проще говоря – плавно опускающейся линии по ходу полета снаряда, и расчет возможности преодолевать возвышения по пути к конечной точке.
Фактически, таковым является движение любого тела в пространстве, при отсутствии какой-либо дополнительной тяги.
Основные формулы баллистического движения
При расчетах и изучении баллистического движения любого тела, стоит обратить внимание на огромное количество факторов – массу, скорость и обтекаемость тела, атмосферные условия и многое-многое другое. Но даже при учете этого, в баллистике есть свои основные формулы, применяемые в исследованиях.

На брошенное под углом к горизонту тело в полете действует по меньшей мере – сила тяжести и сопротивление воздуха. Если исключить из этого силу сопротивления, то, согласно 2-го закону Ньютона, тело движется с ускорением, равным ускорению свободного падения; проекции ускорения на координатные оси равны ах = 0, ау = -g.
Проекции скорости тела, следовательно, изменяются со временем следующим образом:
Vx = Vx0 = V0 * cos α;
Vy = Vy0 – g * t = V0
* sin α – g * t,
где V0 — начальная скорость, α – угол бросания.
Координаты тела, следовательно, изменяются так:
x = x0 + V0 * t * cos α;
y = y0 + V0 * t * sin α – 0,5 * g * t 2 .
Если за точку отсчета берутся координаты х = у = 0, то:
x = V0 * t * cos α;
y = V0 * t * sin α – 0,5 * g * t 2 .
Дальнейшие расчеты производятся при введении таких переменных как дальность полета и время, в итоге же получается финальное уравнение траектории движения. Выглядит оно следующим образом:
y = x * tg α – g * x 2 / 2 * V0 2 * cos 2 α.
Вычисляем баллистические траектории в играх

При разработке видеоигр часто встречается задача вычисления угла выстрела для попадания в цель. Она настолько распространена, что я писал код для её решения в буквальном смысле для каждой игры, над которой работал.
Когда возникала эта проблема, я обычно брал ручку с блокнотом и решал её с нуля. Мне это надоело. Чтобы сэкономить себе из будущего немного времени, я выложу это решение в Интернет. Кроме того, я расскажу о необычной «фишке», которую предпочитаю использовать из соображений эстетики.
Уравнения движения
Задача всегда начинается одинаково. У нас есть стреляющий и цель: под каким углом нужно стрелять снарядом, чтобы он поразил цель?
Существует четыре основных уравнения движения. В статье мы воспользуемся только одним.
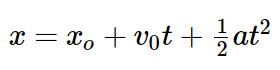
Если объяснять на словах, то конечная позиция РАВНА исходной позиции ПЛЮС скорость, умноженная на время ПЛЮС половина ускорения, умноженная на время в квадрате. Это простое уравнение, для его решения необходимо немного алгебры и несколько тригонометрических тождеств.
Освежим знания
Прежде чем начать, давайте вкратце освежим память.
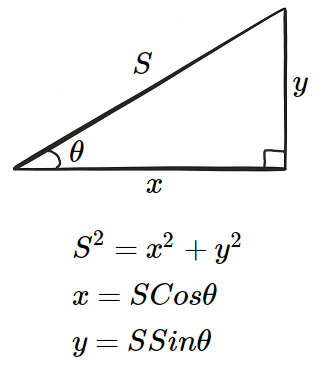
Если дан снаряд с постоянной скоростью S и углом выстрела θ (theta), то мы можем вычислить компоненты скорости x и y. Или если есть S и мы каким-то образом найдём y, то можем вычислить θ и x.
Мы используем алгебру.
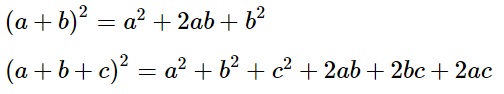
Мы часто будем пользоваться формулой корней квадратного уравнения.
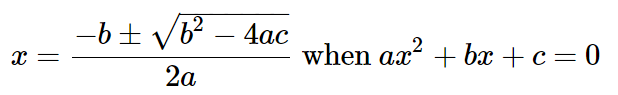
Дальность
При разработке видеоигр нам, вероятно, нужно будет знать максимальную дальность полёта снаряда. Искусственный интеллект должен понимать, насколько близко нужно подойти, а игрокам нужны чёткие наглядные индикаторы опасных зон.
Существует очень простое уравнение максимальной дальности на плоской поверхности. Мы сразу же ринемся в омут с головой и начнём с обобщённого вида.
Если дан снаряд с постоянной скоростью (S) и гравитацией (G), то какой будет его максимальная дальность полёта?
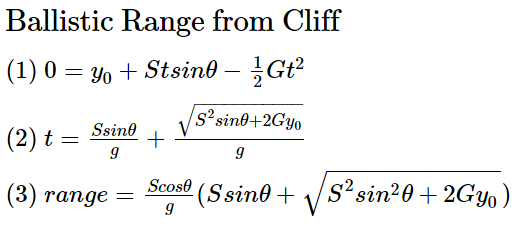
Для тестирования и визуализации я создал демо на Unity. В нём используются чайники, стреляющие чайниками. Пиф-паф!
В демо есть несколько ползунков. В видео показан индикатор дальности стрельбы нашего чайника-турели. При увеличении скорости увеличивается дальность. При снижении гравитации дальность тоже растёт. Всё довольно просто.
Угол стрельбы для попадания по неподвижной мишени
Теперь начинается интересное.
Если снаряд имеет постоянную скорость (S), а гравитация равна (G), то под каким углом его нужно выстреливать, чтобы попасть в неподвижную мишень?
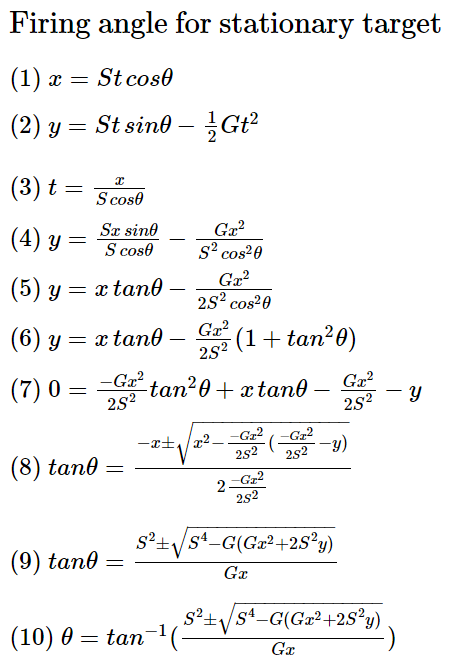
Бах. Теперь у нас есть два уравнения и два неизвестных. Давайте их проанализируем.
- Первое уравнение, два неизвестных (t, θ)
- Второе уравнение, два неизвестных (t, θ)
- Вычислить t из (1)
- Подставить (3) в (2)
- Тригонометрическая подстановка: sin θ/cosθ = tanθ
- Тригонометрическая подстановка: 1/(cos θ)^2 = 1 + (tan θ)^2
- Развернём и преобразуем
- Формула корней квадратного уравнения
- Умножим верхнюю/нижнюю часть на -S^2/x. Перенесём S^4/x^2 под корень
- Применим к каждой части арктангенс
Та-да! В результате мы получили два угла. Один высокий и один низкий. Вот как это выглядит на практике.
Визуальное несовершенство
Взгляните на показанный выше gif. Когда чайник начинает стрелять, всё выглядит довольно неплохо. Высокая дуга красива и радует глаз. Низкая дуга кажется чёткой и эффективной.
Однако при увеличении дальности всё становится не таким красивым. Низкая дуга почти плоская. Высокая дуга чрезмерно высока. В этом и заключается проблема снаряда с постоянной скоростью. Он выглядит красиво, только когда цель находится на границах его радиуса дальности.
Существует ли способ получше?
Скорость горизонтального перемещения
Я часто предпочитаю задавать горизонтальную скорость снаряда, только в плоскости земли. Тогда я могу явным образом задать высоту дуги. То есть переменной становится скорость и гравитация.
Такой подход имеет множество преимуществ. Во-первых, он всегда выглядит красиво!
Во-вторых, его дизайн более интуитивен. Дизайнеров не волнует абсолютная скорость. Им важно, что турель имеет дальность 20 метров и что для перемещения на это расстояние снарядам требуется 1 секунда. Они не обязаны пользоваться строящим графики калькулятором, чтобы менять значения баланса. А художественные изменения не должны влиять на геймплейные механики.
В-третьих, так проще попадать по движущейся мишени. Чуть позже я раскрою это подробнее.
Вот как это выглядит:
Вычисление скорости горизонтального перемещения
Если дан снаряд с горизонтальной скоростью (S) и пиковой высотой (y_peak), то какими должны быть скорость и гравитация для поражения неподвижной мишени?

- Основное уравнение движения
- Решаем (1), подставив 2
- Зададим, что y_peak (пользовательская константа) снаряд достигает во время (1/2)t
- Зададим, что y_end (высота цели) снаряд достигает во время t
- Магия!
- Ещё магия!
- Вектор стрельбы равен (S, v.y) с гравитационным ускорением g
Вуаля! Хотя постойте-ка. Магия? Это жульничество! Да, но вполне оправданное.
Пункты (3) и (4) — это ещё два уравнения с двумя неизвестными. Я ленивый и не хочу их записывать. Плюс я запутаюсь и перепутаю знак, поэтому позволю компьютеру решить их за меня.
Точнее, я воспользовался Wolfram Alpha. Рекомендую каждому иметь Wolfram в своём инструментарии, он довольно полезен.

Если a+c == 2b , то y0 , y_peak и y_end лежат на одной прямой. То есть мы стреляем по прямой.
Скорость горизонтального перемещения при подвижной мишени
Итак, у нас есть два разных вычисления траектории. Однако враги обычно не стоят на месте, они перемещаются. Нам нужно вычислять траекторию, чтобы поражать подвижную мишень.
Именно здесь проявляются все достоинства скорости горизонтального перемещения. Задав скорость в плоскости земли, очень просто выполнить вычисления для подвижной мишени.

- Где X — позиция мишени, а V — её скорость
- Возводим обе части в квадрат.
- Преобразуем в квадратное уравнение
- Применяем формулу корней квадратного уравнения
Пункты с 5 по 9 см. в предыдущем разделе.
Меня это очень радует. Пиу-пиу-пиу!
Постоянная скорость с подвижной мишенью
А что если нам нужно поразить подвижную мишень снарядом с постоянной скоростью? Ой-ёй. Это очень запутанная задача! Даже не знаю, как к ней подступиться.
За всю мою карьеру мне не доводилось её решать. Обычно в играх не нужна точная артиллерия. Это просто неинтересно! Вместо этого мы приблизительно вычисляем будущую позицию и целимся в случайную точку рядом с ней. Игроки воспринимают артиллерийский огонь как дождь из глупых снарядов, а не как гарантированную смерть с лазерным наведением.
В процессе написания этого поста я нашёл решение задачи снаряда с постоянной скоростью и движущейся мишени, которого не было в Интернете в готовом виде. Стоит заметить, что вам, вероятно, не понадобится реализовывать его в своей игре. Но я потратил на него много времени, поэтому не хочу, чтобы оно было потеряно впустую!
Уравнения четвёртой степени
Скорее всего, вы не захотите использовать его в своей игре именно из-за уравнений четвёртой степени. По сути, для решения требуется одно из таких уравнений.
Квадратные уравнения имеют простое и изящное решение в виде формулы корней квадратного уравнения. Кубические уравнения решаемы несколькими разными способами. Однако уравнения четвёртой степени — это настоящая головная боль.
Решение таких уравнений находится далеко за рамками этой статьи. Честно говоря, и за пределами моих математических способностей. К счастью для нас, в книге 1990 года Graphics Gems I есть код для решения уравнений четвёртого порядка. Я использовал этот код для своего демо. Не могу гарантировать его точности и численной устойчивости, используйте его крайне осмотрительно.
Способ первый
Итак, давайте его решим. Каким должен быть угол выстрела снарядом с постоянной скоростью по движущейся мишени? Этот способ взят из поста 2007 года Джеймса Макнейлла и дополнен информацией Райана Джакетта.
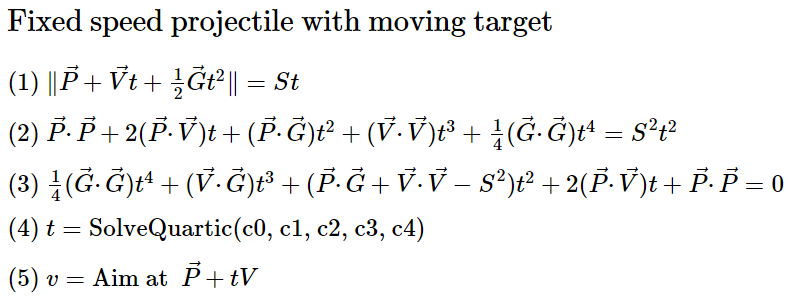
- Где P — позиция мишени, а V — скорость мишени
- Возводим обе части в квадрат
- Преобразуем
- Вычисляем коэффициенты уравнения четвёртого порядка и вставляем в SolveQuartic
- Используем t для вычисления позиции мишени при вычислении траектории до неподвижной точки.
Способ работает. Все сложные задачи выполняет SolveQuartic. Затем мы используем решение для неподвижной мишени, изложенное выше.
Способ второй
Прежде чем я нашёл первый способ, я вывел решение другим способом. Оно состоит из гораздо большего количества шагов. Однако я нахожу конечный результат более изящным. Плюс я потратил примерно восемь листов бумаги и не хочу, чтобы эти деревья пожертвовали собой зазря.
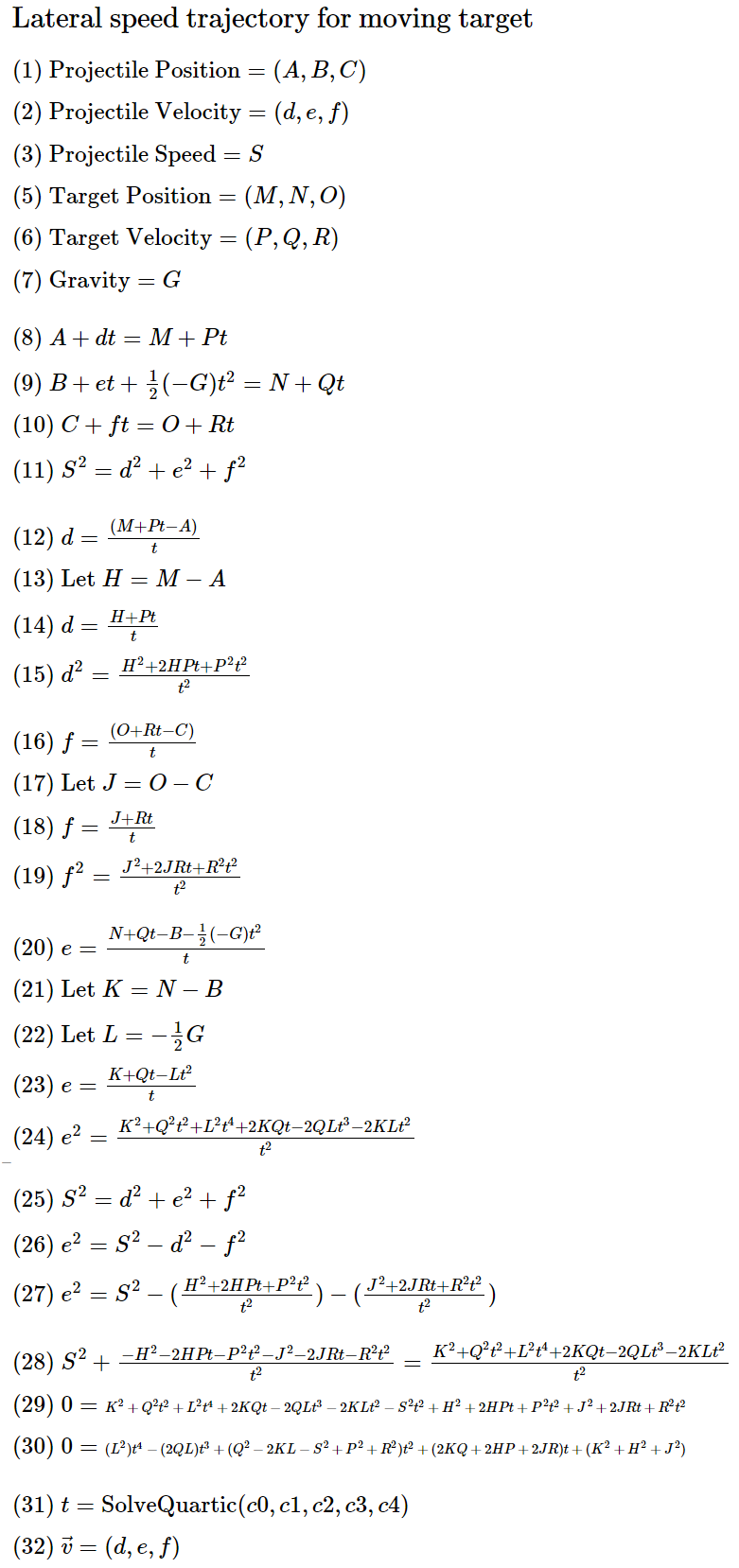
Чёрт возьми. 32 шага!? Это хуже, чем кажется.
1–7 — объявляем переменные.
8–11 — объявляем систему уравнений. Четыре уравнения, четыре неизвестных — d, e, f, t.
12–15 — вычисляем по (8) величину d. Перемножаем d^2 на будущее.
16–19 — вычисляем по (10) величину f. Перемножаем f^2 на будущее.
20–24 — вычисляем по (9) величину e. Перемножаем e^2 на будущее.
25–27 — вычисляем по (11) величину e^2. Подставляем d^2 и f^2.
28–30 — приравниваем (27) к (24). Умножаем на t^2 и преобразуем в уравнение четвёртой степени.
31 — подставляем коэффициенты в SolveQuartic.
32 — подставляем положительные вещественные корни в (14), (18), (23) для d, e, f.
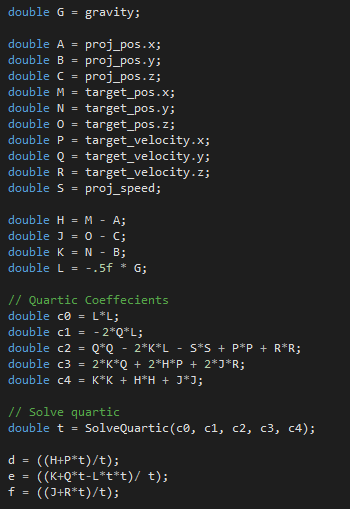
Код довольно короткий. Объявлению переменных отведено больше строк, чем самим вычислениям! Разумеется, кроме SolveQuartic.
Предупреждение
Код, написанный для этого теста, не проверен в бою, а пост никем не рецензировался. Вероятно, в нём есть несколько опечаток, ошибок и неучтённых пограничных случаев. Если найдёте подобные ошибки, пожалуйста, сообщите мне. Втайне, чтобы никто не узнал о моём позоре.
Рассматривайте этот код не как готовое решение, а как опорную точку.
Инструменты
При создании этого поста я использовал несколько инструментов. Многие из них были для меня новыми.
- Unity для создания демо.
- Paper, Affinity Designer и MSPaint для создания изображений.
- Arachnid Latex + MathJax для формул LaTeX.
- FFmpeg для преобразования последовательности скриншотов в анимацию.
- Gfycat для встраивания анимаций.
- Чайник из Юты. Пиу-пиу!
Синтаксис LaTeX ужасен, его сложно учить. Все формулы LaTeX можно найти здесь. Вот пример:

Заключение
Вот и всё. Я потратил на этот пост гораздо больше времени, чем ожидал. Я решил задачу, которую никогда не решал прежде и изучил несколько новых инструментов. И это того стоило.
В этом посте нет ничего нового или оригинального. Я пытался объяснять подробно, но чтобы не быть при этом слишком многословным. Мне очень нравится, что теперь полные описания можно найти в одном месте. Надеюсь, они окажутся полезными для людей.
[spoiler title=”источники:”]
http://sprint-olympic.ru/uroki/fizika/97147-ballisticheskoe-dvijenie-harakteristika-osnovnye-formyly-i-yravneniia.html
http://habr.com/ru/post/538952/
[/spoiler]
| Движение тела, брошенного горизонтально или под углом к горизонту. | |
|
|
 |
|
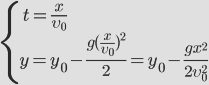 |
– между координатами квадратичная зависимость, траектория – парабола! |
 |
|
| Следовательно, для решения этой задачи необходимо решить уравнение
|
|
| Оно будет иметь решение при t=0 (начало движения) и |  |
|
Зная время полета, найдем максимальное расстояние, которое пролетит тело: Дальность полета: Из этой формулы следует, что: – максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45 0 ; – на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории. |
 |
Вычисляем баллистические траектории в играх
Время на прочтение
7 мин
Количество просмотров 23K

При разработке видеоигр часто встречается задача вычисления угла выстрела для попадания в цель. Она настолько распространена, что я писал код для её решения в буквальном смысле для каждой игры, над которой работал.
Когда возникала эта проблема, я обычно брал ручку с блокнотом и решал её с нуля. Мне это надоело. Чтобы сэкономить себе из будущего немного времени, я выложу это решение в Интернет. Кроме того, я расскажу о необычной «фишке», которую предпочитаю использовать из соображений эстетики.
Уравнения движения
Задача всегда начинается одинаково. У нас есть стреляющий и цель: под каким углом нужно стрелять снарядом, чтобы он поразил цель?
Существует четыре основных уравнения движения. В статье мы воспользуемся только одним.
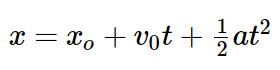
Если объяснять на словах, то конечная позиция РАВНА исходной позиции ПЛЮС скорость, умноженная на время ПЛЮС половина ускорения, умноженная на время в квадрате. Это простое уравнение, для его решения необходимо немного алгебры и несколько тригонометрических тождеств.
Освежим знания
Прежде чем начать, давайте вкратце освежим память.
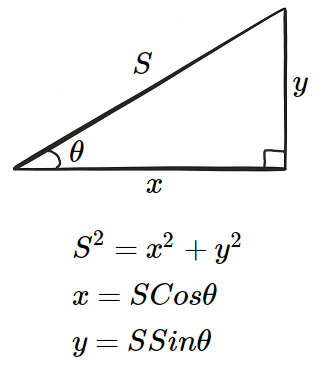
Если дан снаряд с постоянной скоростью S и углом выстрела θ (theta), то мы можем вычислить компоненты скорости x и y. Или если есть S и мы каким-то образом найдём y, то можем вычислить θ и x.
Мы используем алгебру.
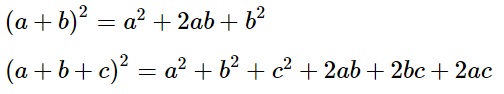
Мы часто будем пользоваться формулой корней квадратного уравнения.
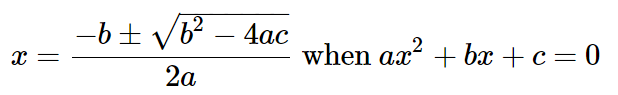
Дальность
При разработке видеоигр нам, вероятно, нужно будет знать максимальную дальность полёта снаряда. Искусственный интеллект должен понимать, насколько близко нужно подойти, а игрокам нужны чёткие наглядные индикаторы опасных зон.
Существует очень простое уравнение максимальной дальности на плоской поверхности. Мы сразу же ринемся в омут с головой и начнём с обобщённого вида.
Если дан снаряд с постоянной скоростью (S) и гравитацией (G), то какой будет его максимальная дальность полёта?

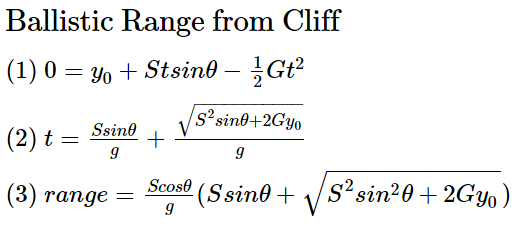
- Подставим известные нам переменные (y0, S, G) в основное уравнение движения.
- Применим формулу корней квадратного уравнения. Отбросим меньшее значение.
- Подставим t в x = S*cos θ*t и упростим.
Демо
Для тестирования и визуализации я создал демо на Unity. В нём используются чайники, стреляющие чайниками. Пиф-паф!
Демо: Unity-демо в WebGL
В демо есть несколько ползунков. В видео показан индикатор дальности стрельбы нашего чайника-турели. При увеличении скорости увеличивается дальность. При снижении гравитации дальность тоже растёт. Всё довольно просто.
Угол стрельбы для попадания по неподвижной мишени
Теперь начинается интересное.
Если снаряд имеет постоянную скорость (S), а гравитация равна (G), то под каким углом его нужно выстреливать, чтобы попасть в неподвижную мишень?
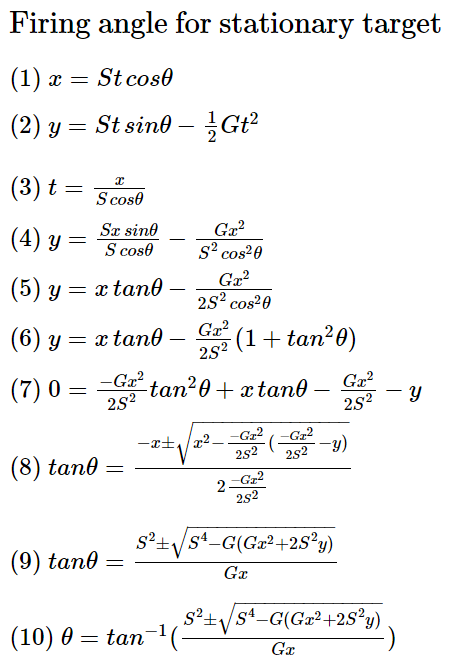
Бах. Теперь у нас есть два уравнения и два неизвестных. Давайте их проанализируем.
- Первое уравнение, два неизвестных (t, θ)
- Второе уравнение, два неизвестных (t, θ)
- Вычислить t из (1)
- Подставить (3) в (2)
- Тригонометрическая подстановка: sin θ/cosθ = tanθ
- Тригонометрическая подстановка: 1/(cos θ)^2 = 1 + (tan θ)^2
- Развернём и преобразуем
- Формула корней квадратного уравнения
- Умножим верхнюю/нижнюю часть на -S^2/x. Перенесём S^4/x^2 под корень
- Применим к каждой части арктангенс
Та-да! В результате мы получили два угла. Один высокий и один низкий. Вот как это выглядит на практике.
Визуальное несовершенство
Взгляните на показанный выше gif. Когда чайник начинает стрелять, всё выглядит довольно неплохо. Высокая дуга красива и радует глаз. Низкая дуга кажется чёткой и эффективной.
Однако при увеличении дальности всё становится не таким красивым. Низкая дуга почти плоская. Высокая дуга чрезмерно высока. В этом и заключается проблема снаряда с постоянной скоростью. Он выглядит красиво, только когда цель находится на границах его радиуса дальности.
Существует ли способ получше?
Скорость горизонтального перемещения
Я часто предпочитаю задавать горизонтальную скорость снаряда, только в плоскости земли. Тогда я могу явным образом задать высоту дуги. То есть переменной становится скорость и гравитация.
Такой подход имеет множество преимуществ. Во-первых, он всегда выглядит красиво!
Во-вторых, его дизайн более интуитивен. Дизайнеров не волнует абсолютная скорость. Им важно, что турель имеет дальность 20 метров и что для перемещения на это расстояние снарядам требуется 1 секунда. Они не обязаны пользоваться строящим графики калькулятором, чтобы менять значения баланса. А художественные изменения не должны влиять на геймплейные механики.
В-третьих, так проще попадать по движущейся мишени. Чуть позже я раскрою это подробнее.
Вот как это выглядит:
Вычисление скорости горизонтального перемещения
Если дан снаряд с горизонтальной скоростью (S) и пиковой высотой (y_peak), то какими должны быть скорость и гравитация для поражения неподвижной мишени?

- Основное уравнение движения
- Решаем (1), подставив 2
- Зададим, что y_peak (пользовательская константа) снаряд достигает во время (1/2)t
- Зададим, что y_end (высота цели) снаряд достигает во время t
- Магия!
- Ещё магия!
- Вектор стрельбы равен (S, v.y) с гравитационным ускорением g
Вуаля! Хотя постойте-ка. Магия? Это жульничество! Да, но вполне оправданное.
Пункты (3) и (4) — это ещё два уравнения с двумя неизвестными. Я ленивый и не хочу их записывать. Плюс я запутаюсь и перепутаю знак, поэтому позволю компьютеру решить их за меня.
Точнее, я воспользовался Wolfram Alpha. Рекомендую каждому иметь Wolfram в своём инструментарии, он довольно полезен.

Если a+c == 2b, то y0, y_peak и y_end лежат на одной прямой. То есть мы стреляем по прямой.
Скорость горизонтального перемещения при подвижной мишени
Итак, у нас есть два разных вычисления траектории. Однако враги обычно не стоят на месте, они перемещаются. Нам нужно вычислять траекторию, чтобы поражать подвижную мишень.
Именно здесь проявляются все достоинства скорости горизонтального перемещения. Задав скорость в плоскости земли, очень просто выполнить вычисления для подвижной мишени.

- Где X — позиция мишени, а V — её скорость
- Возводим обе части в квадрат.
- Преобразуем в квадратное уравнение
- Применяем формулу корней квадратного уравнения
Пункты с 5 по 9 см. в предыдущем разделе.
Меня это очень радует. Пиу-пиу-пиу!
Постоянная скорость с подвижной мишенью
А что если нам нужно поразить подвижную мишень снарядом с постоянной скоростью? Ой-ёй. Это очень запутанная задача! Даже не знаю, как к ней подступиться.
За всю мою карьеру мне не доводилось её решать. Обычно в играх не нужна точная артиллерия. Это просто неинтересно! Вместо этого мы приблизительно вычисляем будущую позицию и целимся в случайную точку рядом с ней. Игроки воспринимают артиллерийский огонь как дождь из глупых снарядов, а не как гарантированную смерть с лазерным наведением.
В процессе написания этого поста я нашёл решение задачи снаряда с постоянной скоростью и движущейся мишени, которого не было в Интернете в готовом виде. Стоит заметить, что вам, вероятно, не понадобится реализовывать его в своей игре. Но я потратил на него много времени, поэтому не хочу, чтобы оно было потеряно впустую!
Уравнения четвёртой степени
Скорее всего, вы не захотите использовать его в своей игре именно из-за уравнений четвёртой степени. По сути, для решения требуется одно из таких уравнений.
Квадратные уравнения имеют простое и изящное решение в виде формулы корней квадратного уравнения. Кубические уравнения решаемы несколькими разными способами. Однако уравнения четвёртой степени — это настоящая головная боль.
Решение таких уравнений находится далеко за рамками этой статьи. Честно говоря, и за пределами моих математических способностей. К счастью для нас, в книге 1990 года Graphics Gems I есть код для решения уравнений четвёртого порядка. Я использовал этот код для своего демо. Не могу гарантировать его точности и численной устойчивости, используйте его крайне осмотрительно.
Способ первый
Итак, давайте его решим. Каким должен быть угол выстрела снарядом с постоянной скоростью по движущейся мишени? Этот способ взят из поста 2007 года Джеймса Макнейлла и дополнен информацией Райана Джакетта.
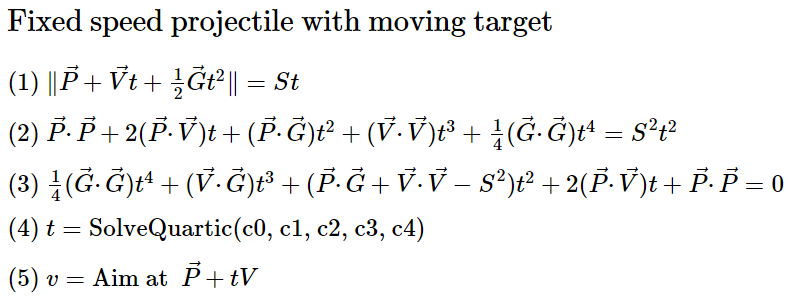
- Где P — позиция мишени, а V — скорость мишени
- Возводим обе части в квадрат
- Преобразуем
- Вычисляем коэффициенты уравнения четвёртого порядка и вставляем в SolveQuartic
- Используем t для вычисления позиции мишени при вычислении траектории до неподвижной точки.
Способ работает. Все сложные задачи выполняет SolveQuartic. Затем мы используем решение для неподвижной мишени, изложенное выше.
Способ второй
Прежде чем я нашёл первый способ, я вывел решение другим способом. Оно состоит из гораздо большего количества шагов. Однако я нахожу конечный результат более изящным. Плюс я потратил примерно восемь листов бумаги и не хочу, чтобы эти деревья пожертвовали собой зазря.
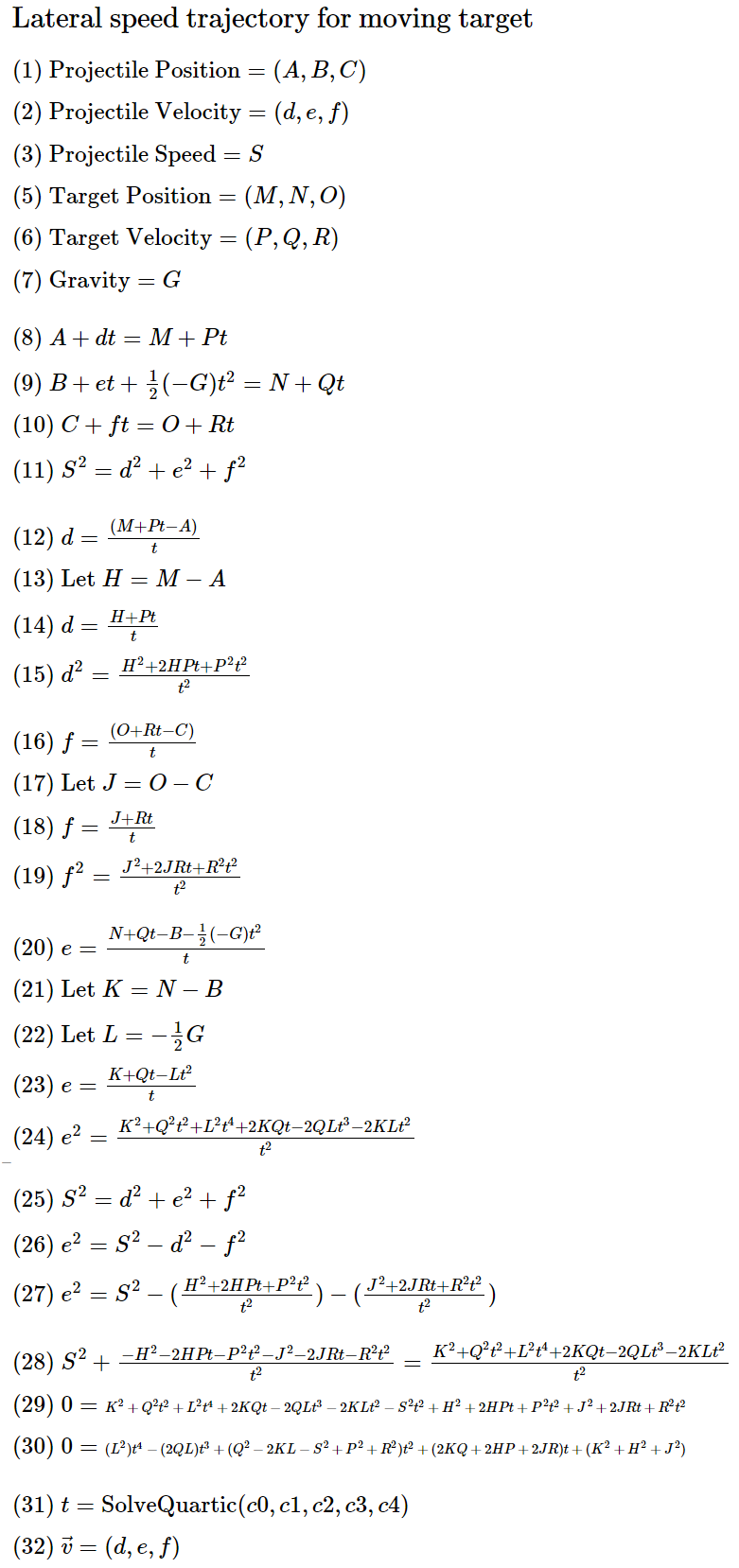
Чёрт возьми. 32 шага!? Это хуже, чем кажется.
1–7 — объявляем переменные.
8–11 — объявляем систему уравнений. Четыре уравнения, четыре неизвестных — d, e, f, t.
12–15 — вычисляем по (8) величину d. Перемножаем d^2 на будущее.
16–19 — вычисляем по (10) величину f. Перемножаем f^2 на будущее.
20–24 — вычисляем по (9) величину e. Перемножаем e^2 на будущее.
25–27 — вычисляем по (11) величину e^2. Подставляем d^2 и f^2.
28–30 — приравниваем (27) к (24). Умножаем на t^2 и преобразуем в уравнение четвёртой степени.
31 — подставляем коэффициенты в SolveQuartic.
32 — подставляем положительные вещественные корни в (14), (18), (23) для d, e, f.
Код довольно короткий. Объявлению переменных отведено больше строк, чем самим вычислениям! Разумеется, кроме SolveQuartic.

Предупреждение
Код, написанный для этого теста, не проверен в бою, а пост никем не рецензировался. Вероятно, в нём есть несколько опечаток, ошибок и неучтённых пограничных случаев. Если найдёте подобные ошибки, пожалуйста, сообщите мне. Втайне, чтобы никто не узнал о моём позоре.
Рассматривайте этот код не как готовое решение, а как опорную точку.
Инструменты
При создании этого поста я использовал несколько инструментов. Многие из них были для меня новыми.
- Unity для создания демо.
- Paper, Affinity Designer и MSPaint для создания изображений.
- Arachnid Latex + MathJax для формул LaTeX.
- FFmpeg для преобразования последовательности скриншотов в анимацию.
- Gfycat для встраивания анимаций.
- Чайник из Юты. Пиу-пиу!
Синтаксис LaTeX ужасен, его сложно учить. Все формулы LaTeX можно найти здесь. Вот пример:

Заключение
Вот и всё. Я потратил на этот пост гораздо больше времени, чем ожидал. Я решил задачу, которую никогда не решал прежде и изучил несколько новых инструментов. И это того стоило.
В этом посте нет ничего нового или оригинального. Я пытался объяснять подробно, но чтобы не быть при этом слишком многословным. Мне очень нравится, что теперь полные описания можно найти в одном месте. Надеюсь, они окажутся полезными для людей.
Исходный код
Проект Unity
Unity-демо в WebGL
Библиографическое описание:
Чичин, Р. А. Исследование зависимости дальности полета снарядов артиллерийских орудий, направленных под углом к горизонту / Р. А. Чичин, Н. Л. Глазкова. — Текст : непосредственный // Юный ученый. — 2016. — № 1 (4). — С. 32-37. — URL: https://moluch.ru/young/archive/4/228/ (дата обращения: 24.05.2023).
В 2015 г. народ России праздновал 70 лет со Дня Победы над фашистской Германией, и 97 лет со дня окончания Первой мировой войны. Множество героических подвигов, сражений вспоминаем мы в преддверие этих дат, но ни одна битва не проходила без артиллерийского орудия.
В военных действиях применялись артиллерийские системы призваны выполнить самые разнообразные задачи: уничтожение живой силы и огневых средств противника в наступлении и обороне, подготовка наступления и сопровождение наступающих подразделений, разрушение прочных оборонительных сооружений, уничтожение танков и иных бронированных подвижных целей на поле боя, борьба с артиллерией и авиацией противника и другие.
Многое зависело от типа артиллерийского орудия, его дислокации и расположения целей поражения или объектов противника, наводка орудий проводилась путем изменения положения дула относительно горизонта. Возникает вопрос: «Как влияет угол запуска на дальность полета снарядов артиллерийских орудий?»
Объект — движение тела, брошенного под углом к горизонту.
Предмет — дальности полета, угол запуска снаряда.
Гипотеза: между углом запуска снаряда и дальностью полета существует обратная зависимость (чем больше угол запуска, тем меньше дальность полета).
Цель: установить зависимость дальности полета снаряда от угла запуска.
Исходя из поставленной цели, были определены следующие задачи:
изучить теоретические вопросы движения тела, брошенного под углом к горизонту;
рассмотреть классификацию типов артиллерийских орудий;
экспериментально исследовать зависимость дальности полета «снаряда» (тела) от угла бросания;
В процессе исследования были использованы следующие методы:
теоретические (обзор литературы по указанной теме, анализ полученной информации);
практические;
экспериментальные.
Экспериментальное исследование зависимости дальности полета тела от угла бросания предполагало установление зависимости дальности полета «снаряда» от угла бросания относительно горизонта.
Эксперимент состоял из трех этапов: организационный, экспериментальный, аналитический.
а) Организационный этап
На данном этапе подготавливаем оборудование (штатив, баллистический пистолет, «снаряд» — металлический шарик, копировальная бумага, лист бумаги, сантиметровая лента), определяем формулу.
б) Экспериментальный этап
Для проведения данного этапа устанавливаем штатив (на полу около стола), на штативе закрепляем баллистический пистолет, на стол кладем лист бумаги, сверху — копировальную бумагу. Результаты представлены в Таблице 1.
Таблица 1
Спецификация измерительных приборов
|
Наименование прибора |
Предел измерения |
Цена деления |
Приборная погрешность |
|
Сантиметровая лента |
1,5 |
0,001 |
0,0005 |
Устанавливаем баллистический пистолет под выбранным углом к горизонту (рис. 1), заряжаем пистолет и производим выстрел, после чего измеряем расстояние от пистолета до места падения «снаряда» и заносим значение прямого измерения в таблицу. Результаты представлены в Таблице 2.


Рис. 1. Экспериментальная установка
Изменяя угол наклона баллистического пистолета, проводим выстрелы и измерения дальности полета «снаряда» (для каждого значения угла проводим пять выстрелов и соответственно пять измерений дальности полета). При выполнении эксперимента необходимо выполнять правила безопасности — не стоять на линии полета «снаряда».
Таблица 2
Результаты измерения дальности полета «снаряда» сантиметровой лентой

где ![]() — угол запуска «снаряда», l– дальность полета «снаряда», lср — среднее арифметическое значение дальности полета «снаряда»
— угол запуска «снаряда», l– дальность полета «снаряда», lср — среднее арифметическое значение дальности полета «снаряда»
Для вычисления среднего значения дальности полета при указанном значении угла запуска «снаряда» используем формулу (1), полученные косвенные измерения записываем в соответствующие стоки таблиц (2,3).
![]() , (1)
, (1)
Проведем вычисления полной погрешности прямых измерений для каждого значения дальности при конкретном угле по формуле (2):
![]() пр+
пр+ ![]() сл, (2)
сл, (2)
где ![]() пр — приборная (инструментальная) погрешность (из табл.1)
пр — приборная (инструментальная) погрешность (из табл.1)
![]() сл- случайная погрешность, рассчитывается по формуле (3).
сл- случайная погрешность, рассчитывается по формуле (3).
 (3)
(3)
Значение результата прямых измерений запишем в соответствие с формулой (4):
х = хср![]() , (4)
, (4)
где ![]() 10 = 0,0043 м,
10 = 0,0043 м, ![]() 20= 0,0059 м,
20= 0,0059 м, ![]() 30= 0,008 м,
30= 0,008 м, ![]() 40 = 0,0163 м,
40 = 0,0163 м, ![]() 45 = 0,0117 м,
45 = 0,0117 м, ![]() 50= 0,0126 м,
50= 0,0126 м, ![]() 60 = 0,0054 м,
60 = 0,0054 м, ![]() 70 = 0,0056 м,
70 = 0,0056 м, ![]() 80 = 0,0034 м.
80 = 0,0034 м.
Запишем результаты прямых в Таблицу 3, где выделим столбцы, содержащие приблизительно равные значения дальности полета «снаряда» (для проведения анализа полученных результатов прямых измерений дальности полета «снаряда»).
Таблица 3
Результаты прямых измерений дальности полета «снаряда», брошенного под углом к горизонту
|
α,° |
10 |
20 |
30 |
40 |
45 |
50 |
60 |
70 |
80 |
|
l ср, м |
0,4522 |
0,7782 |
1,0134 |
1,1488 |
1,223 |
1,1714 |
1,0064 |
0,7614 |
0,4524 |
|
|
х = хср |
х = хср |
|
|
10 |
0,4522 |
0,4524 |
80 |
|
20 |
0,778 |
0,7614 |
70 |
|
30 |
1,0134 |
1,0064 |
60 |
|
40 |
1,1488 |
1,1714 |
50 |
|
45 |
1,223 |
в) Аналитический этап
Анализируя результаты прямых измерений дальности полета «снаряда», брошенного под углом к горизонту формулируем вывод эксперимента.
Между углом запуска «снаряда» и дальностью полета существует зависимость, экспериментально обнаружено:
а) в диапазоне значения углов от 100 до 450 зависимость l(![]() ) прямая — при увеличении значения угла запуска снаряда его дальность полета увеличивается (рис. 2);
) прямая — при увеличении значения угла запуска снаряда его дальность полета увеличивается (рис. 2);

Рис. 2.

б) в диапазоне значения углов от 50 до800зависимость l(![]() ) обратная — при увеличении значения угла запуска снаряда его дальность полета уменьшается (рис. 3).
) обратная — при увеличении значения угла запуска снаряда его дальность полета уменьшается (рис. 3).

Рис. 3.

Поясним результаты Таблицы 3: формула (9) отражает зависимость дальности полета от начальной скорости тела и угла запуска, обратим внимание, что в числителе формулы — функция sin2![]() . Используя формулу приведения (5), докажем, что совпадение значения дальности при выделенных углах не случайно (таблица 4).
. Используя формулу приведения (5), докажем, что совпадение значения дальности при выделенных углах не случайно (таблица 4).
![]() (5)
(5)
Таблица 4
Сравнение значений Sin(2![]()
|
|
Sin(2 |
Sin(2 |
|
|
800 |
Sin( |
Sin(2*100) = Sin (200) |
100 |
|
700 |
Sin( |
Sin(2*200) = Sin (400) |
200 |
|
600 |
Sin( |
Sin(2*300) = Sin (600) |
300 |
|
500 |
Sin( |
Sin(2*400) = Sin (400) |
400 |
Значение Sin(2![]() (рис.4)
(рис.4)

Рис. 4. Знак синуса
Таким образом, на основании полученных результатов можно свидетельствовать, чтогипотеза частично подтверждена, то есть между углом запуска снаряда и дальностью полетаl(![]() ) существует обратная зависимость, но только в диапазоне значений угла от 500 до 800, а в диапазоне значений угла от 100 до 450 обнаружили прямую зависимость l(
) существует обратная зависимость, но только в диапазоне значений угла от 500 до 800, а в диапазоне значений угла от 100 до 450 обнаружили прямую зависимость l(![]() ).
).
Данные зависимости l(![]() ) были использованы на полях сражения при артиллерийских атаках неоднократно с учетом дислокации орудия и расположения цели.
) были использованы на полях сражения при артиллерийских атаках неоднократно с учетом дислокации орудия и расположения цели.
Мы не утверждаем, что артиллеристы знали выражение зависимости l(![]() ) математической формулой, но эти знания приобретались на практике и активно применялись в бою.
) математической формулой, но эти знания приобретались на практике и активно применялись в бою.
Литература:
- «Движение тела, брошенного горизонтально или под углом к горизонту». — Режим доступа: http://www.eduspb.com/node/1669, дата доступа 15.01.2015 г.
- «Изучение движения тела, брошенного под углом к горизонту». — Режим доступа: http://ido.tsu.ru/schools/physmat/data/res/virtlab/text/m2_1.html, дата доступа 15.01.2015 г.
- «Орудие для навесной стрельбы». — Режим доступа: http://universal_ru_en.academic.ru/, дата доступа 24.11.2014 г.
- М. Е. Свирин Классификация артиллерийских систем КА для заинтересованных. — Режим доступа: http://temezhnikov.narod.ru/
- vifrg/20750.htm, дата доступа 24.11.2014 г.
Основные термины (генерируются автоматически): дальность полета, баллистический пистолет, угол запуска, сантиметровая лента, угол бросания, угол запуска снаряда, таблица, артиллерийское орудие, копировальная бумага, обратная зависимость.