Как найти давление через константу равновесия - Сайт, где вы сможете решить свои вопросы

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Понятие химического равновесия

Признаки химического равновесия

Принцип Ле Шателье

Влияние температуры на химическое равновесие

Влияние давления на химическое равновесие

Влияние концентрации на химическое равновесие

Константа химического равновесия

Примеры решения задач

Задачи для самостоятельного решения

Понятие химического равновесия

Равновесным считается состояние системы, которое остается неизменным, причем это состояние не обусловлено действием каких-либо внешних сил. Состояние системы реагирующих веществ, при котором скорость прямой реакции становится равной скорости обратной реакции, называется химическим равновесием. Такое равновесие называется еще подвижным или динамическим равновесием.

Признаки химического равновесия

Состояние системы остается неизменным во времени при сохранении внешних условий.
Равновесие является динамическим, то есть обусловлено протеканием прямой и обратной реакции с одинаковыми скоростями.
Любое внешнее воздействие вызывает изменение в равновесии системы; если внешнее воздействие снимается, то система снова возвращается в исходное состояние.
К состоянию равновесия можно подойти с двух сторон – как со стороны исходных веществ, так и со стороны продуктов реакции.
В состоянии равновесия энергия Гиббса достигает своего минимального значения.

Принцип Ле Шателье

Влияние изменения внешних условий на положение равновесия определяется принципом Ле Шателье (принципом подвижного равновесия):

Если на систему, находящуюся в состоянии равновесия, производить какое–либо внешнее воздействие, то в системе усилится то из направлений процесса, которое ослабляет эффект этого воздействия, и положение равновесия сместится в том же направлении.

Принцип Ле Шателье применим не только к химическим процессам, но и к физическим, таким как кипение, кристаллизация, растворение и т. д.

Рассмотрим влияние различных факторов на химическое равновесие на примере реакции окисления NO:

2NO_(г) + O_2(г) → 2NO_2(г); ΔH^о₂₉₈ = — 113,4 кДж/моль.

Влияние температуры на химическое равновесие

При повышении температуры равновесие сдвигается в сторону эндотермической реакции, при понижении температуры – в сторону экзотермической реакции.

Степень смещения равновесия определяется абсолютной величиной теплового эффекта: чем больше по абсолютной величине энтальпия реакции ΔH, тем значительнее влияние температуры на состояние равновесия.

В рассматриваемой реакции синтеза оксида азота (IV) повышение температуры сместит равновесие в сторону исходных веществ.

Влияние давления на химическое равновесие

Сжатие смещает равновесие в направлении процесса, который сопровождается уменьшением объема газообразных веществ, а понижение давления сдвигает равновесие в противоположную сторону.

В рассматриваемом примере в левой части уравнения находится три объема, а в правой – два. Так как увеличение давления благоприятствует процессу, протекающему с уменьшением объема, то при повышении давления равновесие сместится вправо, т.е. в сторону продукта реакции – NO₂. Уменьшение давления сместит равновесие в обратную сторону. Следует обратить внимание на то, что, если в уравнении обратимой реакции число молекул газообразных веществ в правой и левой частях равны, то изменение давления не оказывает влияния на положение равновесия.

Влияние концентрации на химическое равновесие

Для рассматриваемой реакции введение в равновесную систему дополнительных количеств NO или O₂ вызывает смещение равновесия в том направлении, при котором концентрация этих веществ уменьшается, следовательно, происходит сдвиг равновесия в сторону образования NO₂. Увеличение концентрации NO₂ смещает равновесие в сторону исходных веществ.

Катализатор одинаково ускоряет как прямую, так и обратную реакции и поэтому не влияет на смещение химического равновесия.

При введении в равновесную систему (при Р = const) инертного газа концентрации реагентов (парциальные давления) уменьшаются. Поскольку рассматриваемый процесс окисления NO идет с уменьшением объема, то при добавлении инертного газа равновесие сместится в сторону исходных веществ.

Константа химического равновесия

Для химической реакции:

2NO_(г) + O_2(г) → 2NO_2(г)

константа химической реакции К_с есть отношение:

К_с = [NO₂]²/([NO]² · [O₂]) (1)

В этом уравнении в квадратных скобках – концентрации реагирующих веществ, которые устанавливаются при химическом равновесии, т.е. равновесные концентрации веществ.

Константа химического равновесия связана с изменением энергии Гиббса уравнением:

ΔG_T^о = – RTlnK (2)

Примеры решения задач

Задача 1. При некоторой температуре равновесные концентрации в системе 2CO_(г) + O_{2 (г)}→2CO_{2 (г)}составляли: [CO] = 0,2 моль/л, [O₂] = 0,32 моль/л, [CO₂] = 0,16 моль/л. Определите константу равновесия при этой температуре и исходные концентрации CO и O₂, если исходная смесь не содержала СО₂.

Решение.

2CO_(г) + O_2(г) →2CO_2(г)

Вещество	CO	O₂	CO₂
С_исходн, моль/л	0,36	0,40	0
С_{прореагир,}моль/л	0,16	0,08	0,16
С_равн, моль/л	0,2	0,32	0,16

Во второй строке под С_{прореагир}понимается концентрация прореагировавших исходных веществ и концентрация образующегося CO₂, причем, С_исходн= С_{прореагир}+ С_равн.

Задача 2. Используя справочные данные, рассчитайте константу равновесия процесса

3 H_{2 (г)} + N_{2 (г)} →2 NH_{3 (г)} при 298 К.

Решение.

ΔG₂₉₈^о = 2·(- 16,71) кДж = -33,42·10³ Дж.

ΔG_T^о = — RTlnK.

lnK = 33,42·10³/(8,314× 298) = 13,489. K = 7,21× 10⁵.

Задача 3. Определите равновесную концентрацию HI в системе

H_2(г) + I_2(г) →2HI_(г),

если при некоторой температуре константа равновесия равна 4, а исходные концентрации H₂, I₂ и HI равны, соответственно, 1, 2 и 0 моль/л.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л H_2.

Вещество	H₂	I₂	HI
с_{исходн.}, моль/л	1	2	0
с_{прореагир.}, моль/л	x	x	2x
c_равн., моль/л	1-x	2-x	2x

Тогда, К = (2х)²/((1-х)(2-х))

Решая это уравнение, получаем x = 0,67.

Значит, равновесная концентрация HI равна 2× 0,67 = 1,34 моль/л.

Задача 4. Используя справочные данные, определите температуру, при которой константа равновесия процесса: H_2(г) + HCOH_(г) →CH₃OH_(г) становится равной 1. Принять, что ΔН^о_Т » ΔН^о₂₉₈, а ΔS^о_T » ΔS^о₂₉₈.

Решение.

Если К = 1, то ΔG^о_T = — RTlnK = 0;

ΔG^о_T = ΔН^о₂₉₈ — ТΔ S^о₂₉₈ .

ΔН^о₂₉₈ = -202 – (- 115,9) = -86,1 кДж = — 86,1× 10³ Дж;

ΔS^о₂₉₈ = 239,7 – 218,7 – 130,52 = -109,52 Дж/К;

0 = — 86100 — Т·(-109,52)

Т = 786,15К

Задача 5. Для реакции SO_2(Г) + Cl_2(Г) →SO₂Cl_2(Г) при некоторой температуре константа равновесия равна 4. Определите равновесную концентрацию SO₂Cl₂, если исходные концентрации SO₂, Cl₂ и SO₂Cl₂ равны 2, 2 и 1 моль/л соответственно.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л SO_2.

SO_2(г) + Cl_2(г) →SO₂Cl_2(г)

Вещество	SO₂	Cl₂	SO₂Cl₂
c_{исходн.}, моль/л	2	2	1
c_{прореагир.}, моль/л	x	x	х
c_равн., моль/л	2-x	2-x	x + 1

Тогда получаем:

(х + 1)/(2 — х)² = 4

Решая это уравнение, находим: x₁ = 3 и x₂ = 1,25. Но x₁ = 3 не удовлетворяет условию задачи.

Следовательно, [SO₂Cl₂] = 1,25 + 1 = 2,25 моль/л.

Задачи для самостоятельного решения

1. В какой из приведенных реакций повышение давления сместит равновесие вправо? Ответ обоснуйте.

1) 2 NH_{3 (г)} → 3H_{2 (г)} + N_{2 (г)}

2) ZnCO_{3 (к)} → ZnO_(к) + CO_{2 (г)}

3) 2HBr_(г) → H_{2 (г)} + Br_{2 (ж)}

4) CO_2 (г) + C_{(графит)} →2CO_(г)

Так как увеличение давления благоприятствует процессу, протекающему с уменьшением количества
газообразных веществ, то равновесие сместится вправо в реакции 3.

2. При некоторой температуре равновесные концентрации в системе:

2HBr_(г) →H_{2 (г)} + Br_{2 (г)}

составляли: [HBr] = 0,3 моль/л, [H₂] = 0,6 моль/л, [Br₂] = 0,6 моль/л. Определите константу равновесия и исходную концентрацию HBr.

3. Для реакции H_2(г) + S_(г) →H₂S_(г) при некоторой температуре константа равновесия равна 2. Определите равновесные концентрации H₂ и S, если исходные концентрации H₂, S и H₂S равны, соответственно, 2, 3 и 0 моль/л.

4. Используя справочные данные, вычислите температуру, при которой константа равновесия процесса

CO_2(г) + C_{(графит)} →2CO_(г)

становится равной 1. Примите, что ΔН^о_Т≈ΔН^о₂₉₈, а ΔS^о_T≈ΔS^о₂₉₈

5. Используя справочные данные, рассчитайте константу равновесия процесса:

С₂Н_4(г) →С₂Н_2(г) + Н_2(г) при 298 К

6. Для реакции 2С₃Н_8(г) → н-С₅Н_12(г)+СН_4(г) при температуре 1000 К константа равновесия равна 4. Определите равновесную концентрацию н-пентана, если исходная концентрация пропана равна 5 моль/л.

7. При температуре 500 К константа равновесия процесса:

СО_2(г) + 3Н_2(г) → СН₃ОН_(г) + Н₂О_(г)

равна 3,4·10^-5. Вычислите Δ G^о₅₀₀.

8. При температуре 800 К константа равновесия процесса н-С₆Н_14(г)+ 2С₃Н_6(г)+Н_2(г) равна 8,71. Определите ΔG^о_f,800(С₃Н_6(г)), если ΔG^о_f,800(н-С₆Н_14(г)) = 305,77 кДж/моль.

9. Для реакции СО_(г) + Cl_2(г) →СO₂Cl_2(г) при некоторой температуре равновесная концентрация СO₂Cl_2(г) равна 1,2 моль/л. Определите константу равновесия данного процесса, если исходные концентрации СО_(г) и Cl_2(г) равны соответственно 2,0 и 1,8 моль/л.

10. При некоторой температуре равновесные концентрации в системе 2SО_2(г) + О_2(г) →2SO_3(г) составляли: [SО₂ ]=0,10 моль/л, [О₂]=0,16 моль/л, [SО₃]=0,08 моль/л. Вычислите константу равновесия и исходные концентрации SО₂ и О₂.

К=4,0; исходная концентрация SО₂ составляет 0,18 моль/л;
исходная концентрация О₂ составляет 0,20 моль/л.

Источник

Способы выражения константы равновесия

Для реакции в
смеси идеальных
газов константа
равновесия может быть выражена через
равновесные парциальные
давления компонентов p_i по
формуле^[1]:

где ν_i — стехиометрический
коэффициент (для
исходных веществ принимается отрицательным,
для продуктов — положительным). K_p не
зависит от общего давления, от исходных
количеств веществ или от того, какие
участники реакции были взяты в качестве
исходных, но зависит от температуры ^[2].

Например, для реакции
окисления монооксида
углерода:

2CO
+ O₂ =
2CO₂

константа
равновесия может быть рассчитана по
уравнению:

Если реакция протекает
в идеальном
растворе и
концентрация компонентов выражена
через молярность c_i,
константа равновесия принимает вид:

Для реакций в
смеси реальных
газов или
в реальном растворе вместо парциального
давления и концентрации используют
соответственно фугитивность f_i и
активность a_i:

В некоторых случаях
(в зависимости от способа выражения)
константа равновесия может являться
функцией не только температуры, но и
давления. Так, для реакции в смеси
идеальных газов парциальное давление
компонента может быть выражено по закону
Дальтона через
суммарное давление и мольную долю
компонента (),
тогда легко показать^[2],
что:

где Δn —
изменение числа молей веществ в ходе
реакции. Видно, что K_x зависит
от давления. Если число молей продуктов
реакции равно числу молей исходных
веществ (Δn =
0),
то K_p = K_x.

Стандартная константа равновесия

Стандартная константа
равновесия реакции в смеси идеальных
газов (когда начальные парциальные
давления участников реакции равны их
значениям в стандартном состоянии =
0,1013 МПА или 1 атм) может быть рассчитана
по выражению:

где —
относительные парциальные давления
компонентов, .

Стандартная константа
равновесия — безразмерная величина.
Она связана с K_p соотношением:

Видно, что если выражены
в атмосферах, то и .

Для реакции в смеси
реальных газов в стандартном начальном
состоянии парциальные фугитивности
газов принимаются равными их парциальным
давлениям =
0,1013 МПА или 1 атм. K_f связана
с K⁰ соотношением:

где γ_i —
коэффициент фугитивности i-го реального
газа в смеси.

Константа равновесия реакций в гетерогенных системах

Для гетерогенной химической
реакции, например, между компонентами
реального газа и реального раствора,
константа равновесия в общем случае
может быть выражена уравнением:

где f_i —
фугитивность компонентов газовой фазы,
а a_k —
активность компонентов конденсированной
фазы.

Если конденсированные
фазы (твёрдые или жидкие) представляют
собой практически чистые вещества, их
активности постоянны и могут быть
включены в константу равновесия (то
есть в левую часть выражения выше).
Условно можно принять их равными единице
и, таким образом, исключить из выражения.

Например, для реакции
твёрдофазного восстановления оксида
железа:

FeO_т +
CO_г =
Fe_т +
CO_2г

константа равновесия
(при условии, что газовая фаза идеальна)
имеет вид:

Константа равновесия и изменение энергии Гиббса

Для реакции, протекающей
в изобарно-изотермических условиях,
в некотором неравновесном исходном
состоянии энергии
Гиббса или химические
потенциалы реагирующих
веществ и продуктов реакции в общем
случае не одинаковы, их разность (ΔG_T)
может быть рассчитана по уравнению:

где —
отношение парциальных давлений участников
реакции в исходном состоянии в степенях,
равных их стехиометрическим коэффициентам;
R —универсальная
газовая постоянная.

Это уравнение называют
уравнением изотермы химической реакции.
Оно позволяет рассчитать изменение
энергии Гиббса при протекании процесса
и определить направление протекания
реакции:

при π
< K_p ΔG <
0 — реакция
идёт в прямом направлении, слева направо;

при π
= K_p ΔG =
0 — реакция
достигла равновесного состояния;

при π
> K_p ΔG >
0 — реакция
идёт в обратном направлении.

Стандартная константа
равновесия связана со стандартной
энергией Гиббса реакции
соотношением:

Стандартная энергия
Гиббса реакции в газовой смеси —
энергия Гиббса реакции при стандартных
парциальных давлениях всех компонентов,
равных 0,1013 МПа (1 атм).

Стандартная энергия
Гиббса реакции в растворе — энергия
Гиббса при стандартном
состоянии раствора,
за которое принимают гипотетический раствор
со свойствамипредельно
разбавленного раствора,
но с концентрацией всех реагентов,
равной единице. Величина стандартной
энергии Гиббса реакции может быть
использована для приближенной оценки
термодинамической возможности протекания
реакции в данном направлении, если
начальные условия не сильно отличаются
от стандартных. Кроме того, сравнивая
величины стандартной энергии Гиббса
нескольких реакций, можно выбрать
наиболее предпочтительные, для
которых имеет
наибольшую по модулюотрицательную величину.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
27.03.2015104.12 Кб44WW.doc
#

Источник

У этого термина существуют и другие значения, см. Константа.

Конста́нта равнове́сия — величина, определяющая для данной химической реакции соотношение между термодинамическими активностями (либо, в зависимости от условий протекания реакции, парциальными давлениями, концентрациями или фугитивностями) исходных веществ и продуктов в состоянии химического равновесия (в соответствии с законом действующих масс). Зная константу равновесия реакции, можно рассчитать равновесный состав реагирующей смеси, предельный выход продуктов, определить направление протекания реакции.

Способы выражения константы равновесия[править | править код]

Для реакции в смеси идеальных газов константа равновесия может быть выражена через равновесные парциальные давления компонентов $p_{i}$ по формуле^[1]:

${displaystyle K_{p}=prod p_{i}^{{nu }_{i}},}$

где $nu _{i}$ — стехиометрический коэффициент (для исходных веществ принимается отрицательным, для продуктов — положительным). ${displaystyle K_{p}}$ не зависит от общего давления, от исходных количеств веществ или от того, какие участники реакции были взяты в качестве исходных, но зависит от температуры^[2].

Например, для реакции окисления монооксида углерода:

${displaystyle mathrm {2CO} +mathrm {O} _{2}=mathrm {2CO} _{2}}$

константа равновесия может быть рассчитана по уравнению:

${displaystyle K_{p}={frac {p_{mathrm {CO} _{2}}^{2}}{p_{mathrm {CO} }^{2}cdot p_{mathrm {O} _{2}}}}}$

Если реакция протекает в идеальном растворе и концентрация компонентов выражена через молярность $c_{i}$ , константа равновесия принимает вид:

${displaystyle K_{c}=prod c_{i}^{{nu }_{i}}.}$

Для реакций в смеси реальных газов или в реальном растворе вместо парциального давления и концентрации используют соответственно фугитивность $f_{i}$ и активность $a_{i}$ :

${displaystyle K_{f}=prod f_{i}^{{nu }_{i}}}$

${displaystyle K_{a}=prod a_{i}^{{nu }_{i}}}$

В некоторых случаях (в зависимости от способа выражения) константа равновесия может являться функцией не только температуры, но и давления. Так, для реакции в смеси идеальных газов парциальное давление компонента может быть выражено по закону Дальтона через суммарное давление и мольную долю компонента ( $p_{i}=Pcdot x_{i}$ ), тогда легко показать^[2], что:

${displaystyle K_{p}=K_{x}P^{Delta n},}$

где — изменение числа молей веществ в ходе реакции. Видно, что ${displaystyle K_{x}}$ зависит от давления. Если число молей продуктов реакции равно числу молей исходных веществ (), то $K_{p}=K_{x}$ .

Часто вместо самой константы равновесия ${displaystyle K_{p}}$ используют показатель константы равновесия ${displaystyle mathrm {p} K_{mathrm {p} }}$ , который определяется как отрицательный десятичный логарифм константы ${displaystyle K_{p}}$ :

${displaystyle mathrm {p} K_{mathrm {p} }=-lg left(K_{mathrm {p} }right).}$

Стандартная константа равновесия[править | править код]

Стандартная константа равновесия реакции в смеси идеальных газов (когда начальные парциальные давления участников реакции равны их значениям в стандартном состоянии ${displaystyle p_{i}^{0}=0{,}1013}$ МПа или 1 атм) может быть рассчитана по выражению:

${displaystyle K^{0}=prod ({tilde {p_{i}}})^{v_{i}},}$

где ${tilde {p_{i}}}$ — относительные парциальные давления компонентов, ${tilde {p_{i}}}=p_{i}/p_{i}^{0}$ .

Стандартная константа равновесия — безразмерная величина. Она связана с ${displaystyle K_{p}}$ соотношением:

${displaystyle K_{p}=K^{0}(p_{i}^{0})^{Delta n}.}$

Видно, что если $p_{i}^{0}$ выражены в атмосферах, то $(p_{i}^{0})^{{Delta n}}=1$ и ${displaystyle K_{p}=K^{0}}$ .

Для реакции в смеси реальных газов в стандартном начальном состоянии парциальные фугитивности газов принимаются равными их парциальным давлениям ${displaystyle f_{i}^{0}=p_{i}^{0}=0{,}1013}$ МПа или 1 атм. K_f связана с $K_{0}$ соотношением:

${displaystyle K_{f}=K^{0}(gamma _{i}p_{i}^{0})^{Delta n},}$

где ${displaystyle gamma _{i}}$ — коэффициент фугитивности -го реального газа в смеси.

Константа равновесия реакций в гетерогенных системах[править | править код]

Для гетерогенной химической реакции, например, между компонентами реального газа и реального раствора, константа равновесия в общем случае может быть выражена уравнением:

${displaystyle K_{fa}=~prod (f_{i}^{nu _{i}}a_{k}^{nu _{k}}),}$

где $f_{i}$ — фугитивность компонентов газовой фазы, а $a_{k}$ — активность компонентов конденсированной фазы.

Если конденсированные фазы (твёрдые или жидкие) представляют собой практически чистые вещества, их активности постоянны и могут быть включены в константу равновесия (то есть в левую часть выражения выше). Условно можно принять их равными единице и, таким образом, исключить из выражения.

Например, для реакции твёрдофазного восстановления оксида железа:

${displaystyle mathrm {FeO} mathrm {(sol)} +mathrm {CO} mathrm {(gas)} =mathrm {Fe} mathrm {(sol)} +mathrm {CO} _{2}mathrm {(gas)} }$

константа равновесия (при условии, что газовая фаза идеальна) имеет вид:

${displaystyle K_{p}={frac {p_{mathrm {CO} _{2}}}{p_{mathrm {CO} }}}}$

Термодинамическое описание равновесия[править | править код]

Наряду с обозначением для соотношения активностей веществ в произвольный момент реакции («коэффициент реакции»)

${displaystyle Q_{r}={frac {left{C_{t}right}^{sigma }left{D_{t}right}^{tau }}{left{A_{t}right}^{alpha }left{B_{t}right}^{beta }}}={frac {prod a_{j(t)}^{nu _{j}}}{prod a_{i(t)}^{nu _{i}}}}=prod a_{n(t)}^{nu _{n}}}$

(обозначения для приведённой ниже реакции; последнее равенство написано в обозначении, что стехиометрические коэффициент берутся со знаком «+» для продуктов и со знаком «−» для исходных веществ)

в химической термодинамике используется обозначение ${displaystyle K_{mathrm {eq} }}$ для такого же по форме соотношения между равновесными активностями веществ

${displaystyle K_{mathrm {eq} }={frac {[C]^{sigma }[D]^{tau }}{[A]^{alpha }[B]^{beta }}}={frac {prod a_{j(t=infty )}^{nu _{j}}}{prod a_{i(t=infty )}^{nu _{i}}}}=prod a_{n(t=infty )}^{nu _{n}}}$

(то есть соотношения активностей в момент t=infty

, в момент равновесия). Далее приведено термодинамическое описание химического равновесия и описана связь ${displaystyle K_{mathrm {eq} }}$

со стандартной энергией Гиббса процесса.

В системе, где протекает химическая реакция

{displaystyle alpha A+beta Brightleftharpoons sigma C+tau D}

равновесие может быть описано условием

${displaystyle left({frac {dG}{dxi }}right)_{T,p}=0,}$

где есть химическая переменная

или, то же самое условие равновесия может быть записано с использованием химических потенциалов как

${displaystyle alpha mu _{A}+beta mu _{B}=sigma mu _{C}+tau mu _{D},}$

где химические потенциалы

${displaystyle mu _{A}=mu _{A}^{ominus }+RTln{A},}$

здесь {A} — строго говоря, активность реагента A; при допущениях об идеальных газах можно заменить их на давления, для реальных газов можно заменить на фугитивности, при допущении о том, что раствор подчиняется закону Генри, можно заменить на мольные доли, и при допущении, что раствор подчиняется закону Рауля — на парциальные давления; для системы в равновесии может быть заменена на равновесную молярную концентрацию или на равновесную активность.

Выражение для энергии Гиббса принимает вид

${displaystyle dG=Vdp-SdT+sum _{i=1}^{k}mu _{i}dN_{i},}$

а так как ${displaystyle dN_{i}=nu _{i}dxi }$ , можно записать выражение для производной изобарного потенциала по химической переменной в виде

${displaystyle left({frac {dG}{dxi }}right)_{T,p}=sum _{i=1}^{k}mu _{i}nu _{i}=Delta _{r}G_{T,p}=sigma mu _{C}+tau mu _{D}-alpha mu _{A}-beta mu _{B}=(sigma mu _{C}^{0}+tau mu _{D}^{0})-(alpha mu _{A}^{0}+beta mu _{B}^{0})+(sigma RTln{C}+tau RTln{D})-(alpha RTln{A}+beta RTln{B})=}$

${displaystyle =sum _{i=1}^{k}mu _{i}^{0}nu _{i}+RTln {frac {{C}^{sigma }{D}^{tau }}{{A}^{alpha }{B}^{beta }}}=Delta _{r}G^{0}+RTln Q_{r}.}$

При равновесии (иначе говоря, при условии что время )

${displaystyle Q_{r}=K_{mathrm {eq} }.}$

Записав теперь условие равновесия ${displaystyle Delta _{r}G=0=Delta _{r}G^{0}+RTln K_{mathrm {eq} }}$ найдём связь ${displaystyle K_{mathrm {eq} }}$ со стандартной энергией Гиббса^[3]:

${displaystyle Delta _{r}G^{0}=-RTln K_{mathrm {eq} }.}$

Равновесный состав смеси и направление реакции[править | править код]

Упомянутый выше «коэффициент реакции» (другие обозначения, встречающиеся в литературе — Omega или — «произведение реакции»)

$Q_{r}=prod a_{{n(t)}}^{{nu _{n}}}$

отражает соотношение текущих активностей всех участников реакции и может быть использован для определения направления реакции в момент, для которого известен ^[4]

Если в момент

коэффициент Q>K

, то текущие активности продуктов больше равновесных, и значит они должны уменьшиться к тому моменту, когда установится равновесие, то есть в данный момент протекает обратная реакция;

Если

, то равновесное состояние достигнуто и скорости прямой и обратной реакций равны;

Если

, то $v_{{1}}>v_{{-1}}$

С использованием величины $Q_{r}$ записывается уравнение изотермы химической реакции^[1] (изотермы Вант-Гоффа)

${displaystyle Delta G_{p,T}=RTln Q_{r}-RTln K_{mathrm {eq} }=RTln {frac {Q_{r}}{K_{mathrm {eq} }}}=sum nu _{i}mu _{i},}$

где — стехиометрические коэффициенты (для продуктов — со знаком «+», для исходных веществ — со знаком «−»; так же, как и в выражениях для и ), а — химические потенциалы,

а стандартная энергия Гиббса и стандартная константа суть

${displaystyle Delta G_{p,,T}^{0}=-RTln K_{mathrm {eq} }^{0}=sum nu _{i}mu _{i}^{0},}$

где ${displaystyle mu ^{0}}$ — стандартные химические потенциалы

Уравнение изотермы показывает, как величина связана с изменением свободной энергии реакции:

при

для прямой реакции

, то есть $sum nu _{{j}}mu _{{j}}$

для продуктов прямой реакции больше, чем для исходных веществ — это означает, что прямая реакция запрещена (значит, не запрещена обратная);

при

для прямой реакции

, то есть реакция достигла равновесного состояния;

при

для прямой реакции

, то есть эта самопроизвольное протекание этой реакции разрешено

Величина ${displaystyle K_{mathrm {eq} }}$ по определению имеет смысл только для состояния равновесия, то есть для состояния с ${frac {v_{{1}}}{v_{{-1}}}}=1$ и $Delta G_{r}=0$ . Величина ${displaystyle K_{mathrm {eq} }}$ ничего не говорит о скоростях реакций, но она описывает состав системы в состоянии равновесия.

Если

, то в системе преобладают продукты (прямой) реакции.

Если

, то в системе преобладают исходные вещества (продукты обратной реакции)^[5].

Стандартные состояния[править | править код]

Стандартная энергия Гиббса реакции в газовой смеси — энергия Гиббса реакции при стандартных парциальных давлениях всех компонентов, равных 0,1013 МПа (1 атм).

Для чистого вещества и жидкости стандартная энергия Гиббса совпадает с энергией Гиббса образования этих веществ.

Величина стандартной энергии Гиббса реакции может быть использована для приближенной оценки термодинамической возможности протекания реакции в данном направлении, если начальные условия не сильно отличаются от стандартных. Кроме того, сравнивая величины стандартной энергии Гиббса нескольких реакций, можно выбрать наиболее предпочтительные, для которых $Delta G_{T}^{0}$ имеет наибольшую по модулю отрицательную величину.

Кинетическое описание[править | править код]

Для обратимой химической реакции константа равновесия ${displaystyle K_{mathrm {eq} }}$ может быть выражена через константы скорости прямых и обратных реакций.
Рассмотрим элементарную обратимую химическую реакцию первого порядка

{displaystyle mathrm {A} rightleftarrows mathrm {B} }

По определению, равновесие задаётся условием $v_{{1}}=v_{{-1}}$ , то есть равенством скоростей прямой и обратной реакций.

В соответствии с законом действующих масс

${displaystyle v=k{prod }{a_{j}}^{n_{j}},}$

где — константа скорости соответствующей реакции, а ${a_{j}}^{{n_{j}}}$ — равновесные активности реагентов этой реакции, возведённые в степени, равные их стехиометрическим коэффициентам

можно записать условие равновесия в виде

${displaystyle 1={frac {v_{1}}{v_{-1}}}={frac {k_{1}{prod }{a_{A}}^{n_{A}}}{k_{-1}{prod }{a_{B}}^{n_{B}}}}.}$

То есть

${displaystyle 1={frac {k_{1}}{k_{-1}}}cdot {frac {prod {a_{A}}^{n_{A}}}{prod {a_{B}}^{n_{B}}}}={frac {k_{1}}{k_{-1}}}cdot left(K_{mathrm {eq} }right)^{-1}}$

(см. термодинамическое описание константы равновесия), что возможно только если

${displaystyle K_{mathrm {eq} }={frac {k_{1}}{k_{-1}}}}$

Это важное соотношение даёт одну из «точек соприкосновения» химической кинетики и химической термодинамики^[4]^[6].

Множественные равновесия[править | править код]

В случае, когда в системе устанавливается сразу несколько равновесий (то есть одновременного или последовательного протекает нескольких процессов), каждый из них может быть охарактеризован своей константой равновесия, из которых можно выразить общую константу равновесия для всей совокупности процессов. Можно рассмотреть такую ситуацию на примере ступенчатой диссоциации двухосновной кислоты ${displaystyle mathrm {H} _{2}mathrm {A} }$ . Водный раствор её будет содержать частицы (сольватированные) ${displaystyle mathrm {H} ^{+}}$ , ${displaystyle mathrm {H} _{2}mathrm {A} }$ , ${displaystyle mathrm {HA} ^{-}}$ и ${displaystyle mathrm {A} ^{2-}}$ . Процесс диссоциации протекает в две ступени:

${displaystyle mathrm {H} _{2}mathrm {A} rightleftharpoons mathrm {HA} ^{-}+mathrm {H} ^{+}:K_{1}={frac {[mathrm {HA} ^{-}][mathrm {H} ^{+}]}{[mathrm {H} _{2}mathrm {A} ]}}}$

${displaystyle mathrm {HA} ^{-}rightleftharpoons mathrm {A} ^{2-}+mathrm {H} ^{+}:K_{2}={frac {[mathrm {A} ^{2-}][mathrm {H} ^{+}]}{[mathrm {HA} ^{-}]}}}$

K_1 и $K_{2}$ — константы первой и второй ступеней диссоциации соответственно. Из них можно выразить «полную» константу равновесия, для процесса полной диссоциации^[5]:

${displaystyle mathrm {H} _{2}mathrm {A} rightleftharpoons mathrm {A} ^{2-}+2mathrm {H} ^{+}:K_{1+2}={frac {[mathrm {A} ^{2-}][mathrm {H} ^{+}]^{2}}{[mathrm {H} _{2}mathrm {A} ]}}=K_{1}K_{2}}$

Другой пример множественного равновесия — анализ системы осадок/растворимое комплексное соединение.

Допустим, имеется равновесие

${displaystyle mathrm {AgI} _{2}^{-}mathrm {(aq)} rightleftharpoons mathrm {AgI} mathrm {(solid)} +mathrm {I} ^{-}mathrm {(aq)} }$

Реакцию можно представить в виде двух последовательных равновесий — равновесия разложения комплексного иона на составляющие его ионы, которое характеризуется «константой нестойкости» (величина, обратная «константе устойчивости» beta ):

${displaystyle mathrm {AgI} _{2}^{-}mathrm {(aq)} rightleftharpoons mathrm {Ag} ^{+}mathrm {(aq)} +2mathrm {I} ^{-}mathrm {(aq)} :K_{1}={frac {alpha _{mathrm {Ag} ^{+}}alpha _{mathrm {I} ^{-}}^{2}}{alpha _{mathrm {AgI} _{2}^{-}}}}=beta ^{-1}}$

и равновесия перехода ионов из объёма растворителя в кристаллическую решётку

${displaystyle mathrm {Ag} ^{+}mathrm {(aq)} +mathrm {I} ^{-}mathrm {(aq)} rightleftharpoons mathrm {AgI} mathrm {(solid)} :K_{2}={frac {alpha _{mathrm {AgI} }}{alpha _{mathrm {Ag} ^{+}}alpha _{mathrm {I} ^{-}}}}}$

с учётом того, что для твёрдых веществ активность принимается равной 1, а в разбавленных растворах активности могут быть заменены на молярные концентрации, получаем

${displaystyle K_{2}={frac {alpha _{mathrm {AgI} }}{alpha _{mathrm {Ag} ^{+}}alpha _{mathrm {I} ^{-}}}}={frac {1}{[mathrm {Ag} ^{+}][mathrm {I} ^{-}]}}={frac {1}{K_{mathrm {sp} }}},}$

где ${displaystyle K_{mathrm {sp} }}$ — произведение растворимости

Тогда суммарное равновесие будет описываться константой

${displaystyle mathrm {AgI} _{2}^{-}mathrm {(aq)} rightleftharpoons mathrm {AgI} mathrm {(solid)} +mathrm {I} ^{-}mathrm {(aq)} :K={frac {alpha _{mathrm {AgI} }alpha _{mathrm {I} ^{-}}}{alpha _{mathrm {AgI} _{2}^{-}}}}=K_{1}cdot K_{2}={frac {1}{beta cdot K_{mathrm {sp} }}}}$

И значение этой константы будет условием преобладания в равновесной смеси комплексного соединения или твёрдой соли: как и выше, если , то в равновесной смеси большая часть ионов связана в комплексное соединение, если , то в равновесном состоянии в системе большая часть ионов связана в кристаллической фазе.^[4]

Зависимость константы равновесия от температуры[править | править код]

Зависимость константы равновесия реакции от температуры может быть описана уравнением изобары химической реакции (изобары Вант-Гоффа):

${displaystyle dln K_{p}={frac {Delta H}{RT^{2}}}dT}$

и изохоры химической реакции (изохоры Вант-Гоффа):

${displaystyle dln K_{c}={frac {Delta U}{RT^{2}}}dT}$

Здесь Delta H и Delta U — тепловой эффект реакции, протекающей, соответственно, при постоянном давлении или при постоянном объёме. Если (тепловой эффект положителен, реакция эндотермическая), то температурный коэффициент константы равновесия ${frac {dln K_{p}}{dT}}$ тоже положителен, то есть с ростом температуры константа равновесия эндотермической реакции увеличивается, равновесие сдвигается вправо (что вполне согласуется с принципом Ле Шателье).

Методы расчета константы равновесия[править | править код]

Расчётные методы определения константы равновесия реакции обычно сводятся к вычислению тем или иным способом стандартного изменения энергии Гиббса в ходе реакции ( ${displaystyle Delta G^{0}}$ ), а затем использованию формулы:

${displaystyle Delta G^{0}=-RTln K^{0}}$

, где

— универсальная газовая постоянная.

При этом следует помнить, что энергия Гиббса — функция состояния системы, то есть она не зависит от пути процесса, от механизма реакции, а определяется лишь
начальным и конечным состояниями системы. Следовательно, если непосредственное определение или расчёт ${displaystyle Delta G^{0}}$ для некоторой реакции по каким-либо причинам затруднены, можно подобрать такие промежуточные реакции, для которых ${displaystyle Delta G^{0}}$ известно или может быть легко определено, и суммирование которых даст рассматриваемую реакцию (см. Закон Гесса). В частности, в качестве таких промежуточных реакций часто используют реакции образования соединений из элементов.

Энтропийный расчёт изменения энергии Гиббса и константы равновесия реакции[править | править код]

Энтропийный метод расчёта Delta G реакции является одним из самых распространённых и удобных^[2]. Он основан на соотношении:

${displaystyle Delta G_{T}=Delta H_{T}-TDelta S_{T}}$

или, соответственно, для стандартного изменения энергии Гиббса:

${displaystyle Delta G_{T}^{0}=Delta H_{T}^{0}-TDelta S_{T}^{0}}$

Здесь $Delta H^{0}$ при постоянных давлении и температуре равно тепловому эффекту реакции, методы расчёта и экспериментального определения которого известны — см., например, уравнение Кирхгофа:

$Delta H_{T}^{0}=Delta H_{{298}}^{0}+int _{{298}}^{T}Delta C_{p}dT$

Необходимо получить изменение энтропии в ходе реакции. Эта задача может быть решена несколькими способами, например:

По термическим данным — с опорой на тепловую теорему Нернста и с использованием сведений о температурной зависимости теплоёмкости участников реакции. Например, для веществ, при нормальных условиях находящихся в твёрдом состоянии:

${displaystyle S_{298}=S_{0}+int _{0}^{T}{frac {C_{pmathrm {(sol)} }}{T}}dT,}$

где $S_{0}=0$ (постулат Планка) и тогда, соответственно,

${displaystyle S_{298}=int _{0}^{T}{frac {C_{pmathrm {(sol)} }}{T}}dT}$

(здесь индекс sol — от англ. solid, «твердый»). При некоторой заданной температуре

${displaystyle S_{T}^{0}=S_{298}^{0}+int _{298}^{T}{frac {C_{pmathrm {(sol)} }}{T}}dT}$

Для жидких или газообразных при нормальной температуре веществ, или, в более общем случае, для веществ, в интервале температур от 0 (или 298) и до

претерпевающих фазовый переход, следует учитывать изменение энтропии, связанное с этим фазовым переходом.

Для идеальных газов — методами квантовой статистики.
Различными эмпирическими и полуэмпирическими методами, для этого часто достаточно небольшого объёма исходных данных. Например, для твёрдых неорганических веществ оценить энтропию можно по формуле^[7]:

${displaystyle S_{298}^{0}=Aln M+B}$

где

— табличные константы, зависящие от типа рассматриваемого соединения,

— молекулярная масса.

Итак, если известны $Delta H_{{298}}^{0}$ , $Delta S_{{298}}^{0}$ и температурные зависимости теплоёмкости, $Delta G_{T}^{0}$ может быть рассчитано по формуле:

$Delta G_{T}^{0}=Delta H_{{298}}^{0}-TDelta S_{{298}}^{0}+int _{{298}}^{T}Delta C_{p}dT-Tint _{{298}}^{T}Delta C_{p}{frac {dT}{T}}$

Несколько упрощённый вариант этой формулы получают, считая сумму теплоёмкостей веществ не зависящей от температуры и равной сумме теплоёмкостей при 298 K:

${displaystyle Delta G_{T}^{0}=Delta H_{298}^{0}-TDelta S_{298}^{0}+Delta C_{p~298}(T-298)-TDelta C_{p~298}ln {frac {T}{298}}}$

И ещё более упрощённый расчёт проводят, приравнивая сумму теплоёмкостей к нулю:

$Delta G_{T}^{0}=Delta H_{{298}}^{0}-TDelta S_{{298}}^{0}$

Переход от $Delta G_{T}^{0}$ к константе равновесия осуществляется по приведённой выше формуле.

Расчёт константы равновесия методами статистической термодинамики[править | править код]

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

Экспериментальное определение константы равновесия[править | править код]

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

См. также[править | править код]

Константа диссоциации
Константа автопротолиза
Константа гидролиза
Константа устойчивости
Константа Михаэлиса
Энергия Гиббса

Примечания[править | править код]

↑ ¹ ² Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим.-технол. спец. вузов / Под ред. А. Г. Стромберга. — 2-е изд. — М.: Высш. шк., 1988. — 496 с.
↑ ¹ ² ³ Патров Б. В., Сладков И. Б. Физическая химия. Ч. 1 : учеб. пособие. — СПб.: Изд-во Политехн. ун-та, 2009. — 127 с. — ISBN 978-5-7422-2206-4.
↑ Эткинс П. Физическая химия в 2 т., том 1. — М.: Мир, 1980. — 580 с.
↑ ¹ ² ³ Жмурко Г. П., Казаков Е. Ф., Кузнецова В. Н., Яценко А. В. Общая химия. — М.: Академия, 2012. — ISBN 978-5-7695-9188-4. — 512 с.
↑ ¹ ² Неорганическая химия в 3 т. /Под редакцией Третьякова Ю. Д. — Том 1: Физико-химические основы неорганической химии. — М.: Академия, 2004. — 240 с.
↑ Эткинс П. Физическая химия в 2 т., том 2. — М.: Мир, 1980. — 584 с.
↑ Физическая химия. Теоретическое и практическое руководство. Учеб. пособие для вузов / Под ред. акад. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. — 880 с.

Литература[править | править код]

Киреев В. А. Методы практических расчётов в термодинамике химических реакций. — 2-е изд. — М., 1975.
Жоров Ю. М. Термодинамика химических процессов. — М., 1985.

Источник

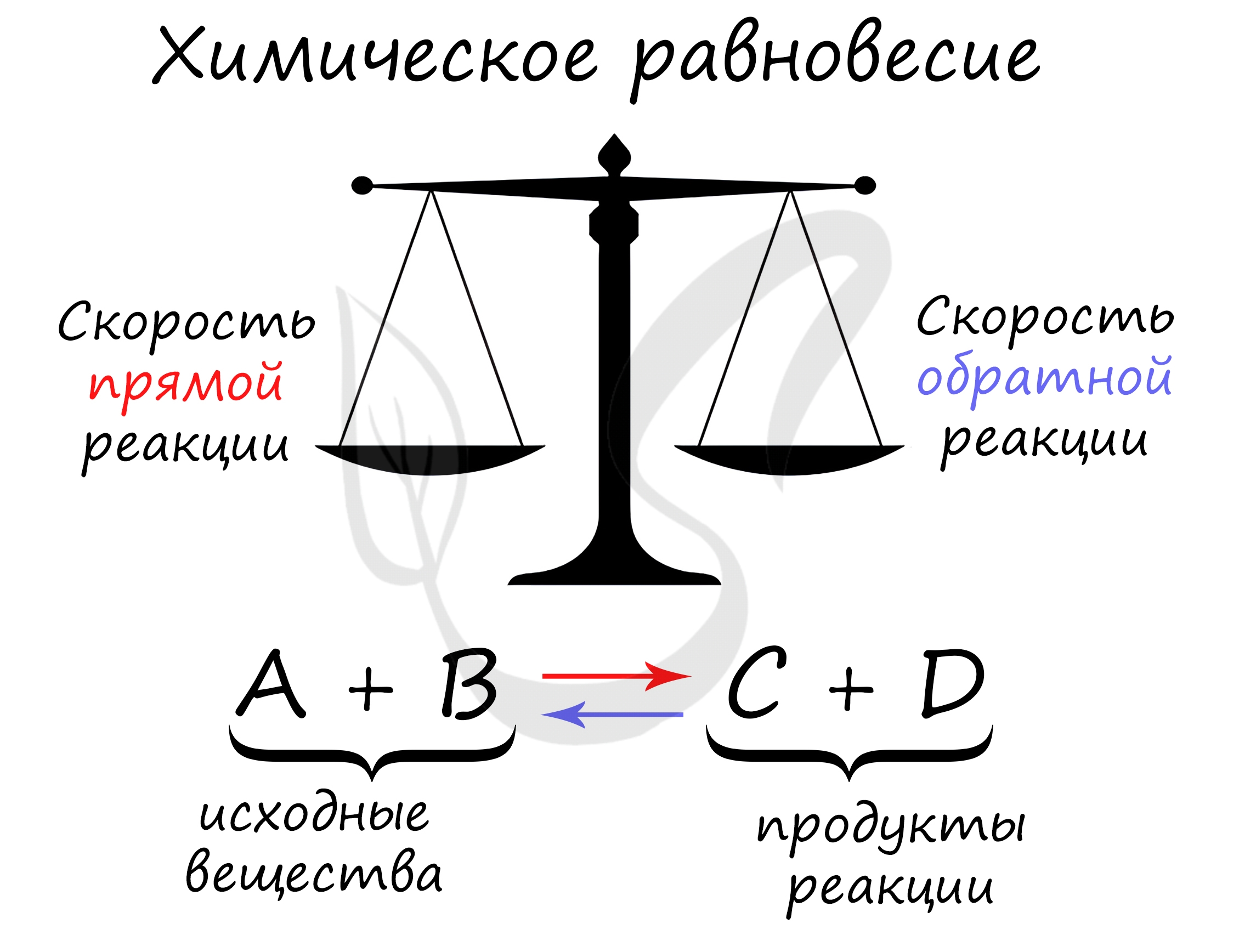
Химическое равновесие – состояние химической системы, при котором скорость прямой реакции равна скорости обратной.

В большом количестве заданий, которые мне довелось увидеть, я ни один раз видел, как коверкают это определение. Например, в заданиях верно-неверно
предлагают похожий вариант, однако говорят о “равенстве концентраций исходных веществ и продуктов” – это грубая ошибка. Химическое равновесие –
равенство скоростей.

Принцип Ле Шателье

В 1884 году французским химиком Анри Ле Шателье был предложен принцип, согласно которому, если на систему, находящуюся в состоянии
равновесия, оказать внешнее воздействие (изменить температуру, давление, концентрацию), то система будет стремиться компенсировать
внешнее воздействие.

Это принцип обоснован термодинамически и доказан. Однако в такой абстрактной формулировке его сложно применить для решения конкретных
задач по химическому равновесию. В этой статье я покажу конкретные примеры и обозначу алгоритм действия, чтобы вы могли успешно
справляться с заданиями.

Влияние изменения концентрации на химическое равновесие

При увеличении концентрации какого-либо компонента химической реакции, система будет стремиться восстановить равновесие:
равновесие будет смещаться в сторону расходования добавленного компонента.

Объясню проще: если вы увеличиваете концентрацию вещества, которое находится в левой части, равновесие сместится в правую сторону.
Если добавляете вещество из левой части (продуктов реакции) – смещается в сторону исходных веществ. Посмотрите на пример ниже.

Если мы попытаемся удалить какое-либо вещество из системы (уменьшить его концентрацию), то система будет стремиться заполнить “пустое”
место, которые мы создали. Наглядно демонстрирую на примере:

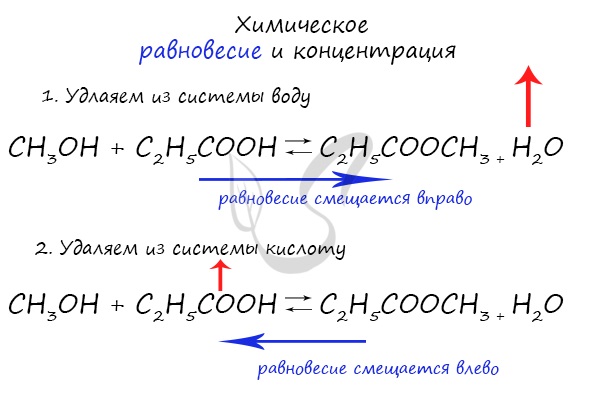
Можно подвести итог полученным знаниям таким образом: “Куда добавляем – оттуда смещается, откуда берем – туда смещается”. Воспользуйтесь
этой или придумайте свое правило для запоминания этой закономерности 😉

Изменения давления и химическое равновесие

Если речь в задании идет об изменении давления, то первое, что нужно сделать, это посчитать количество газов в уравнении слева и справа.
Твердые вещества и жидкости считать не нужно. Например:

CO_2(г) + С_(тв) ⇄ 2CO_(г) – Q

В приведенном уравнении количество молекул газа в левой части – 1, в правой – 2.

Запомните правило: “При увеличении давления равновесие смещается в сторону меньших газов, при уменьшении давления – в сторону больших газов”.
Для нашей системы правило действует таким образом:

В случае, если слева и справа количество молекул газа одинаково, например, в реакции:

H_2(г) + I_2(г) ⇄ 2HI_(г) – Q

Слева – 2 газа, и справа – 2. В такой реакции увеличение или уменьшение давления не повлияет на химическое равновесие.

Изменение температуры и химическое равновесие

Если в задании увеличивают или уменьшают температуру, то первое, что вы должны оценить: экзотермическая это реакция или
эндотермическая.

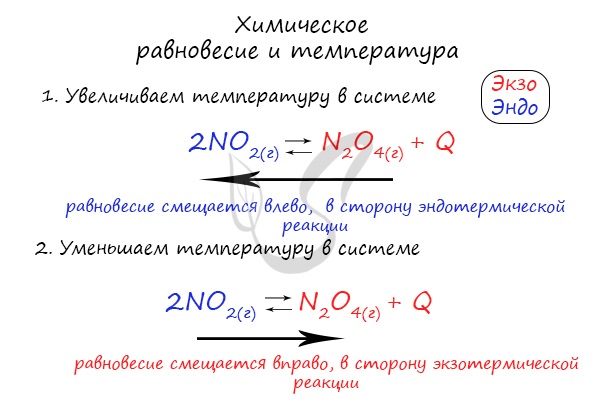
Следуйте следующему правилу: “При увеличении температуры равновесие смещается в сторону эндотермической реакции, при
уменьшении – в сторону экзотермической реакции”. У любой обратимой реакции есть экзо- и эндотермические части:

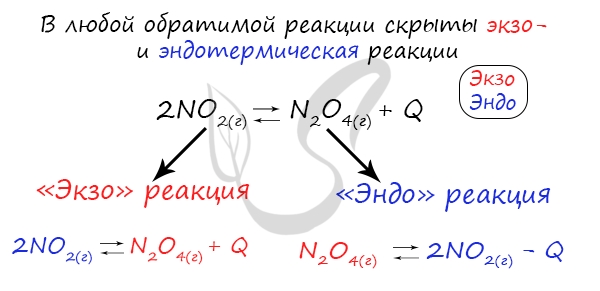
Поэтому данное правило универсально и применимо для всех реакций. Для примера разберем следующие задачи:

Чтобы не осталось белых пятен, возьмем экзотермическую реакцию и повторим с ней подобный эксперимент.

Катализатор и ингибитор

Действие катализатора и ингибитора соответственно касается только ускорения и замедления химической реакции. Они никоим образом не влияют на равновесие.

Константа равновесия

Константой равновесия называют отношения скоростей прямой и обратной реакции. Для реакции типа aA + bB = cC + dD константа
равновесия будет записана следующим образом:

Решим задачу. Дана реакция: 2NO + Cl₂ ⇄ 2NOCl . Вычислите константу равновесия, если равновесные концентрации
веществ для данной реакции: c(NO) = 1.8 моль/л , c(Cl₂) = 1.2 моль/л , c(NOCl) = 0.8 моль/л.

Константу равновесия для данной задачи можно представить в виде 1.64 * 10^-1.

Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение
(в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов
без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования,
обратитесь, пожалуйста, к Беллевичу Юрию.

Источник

ЛЕКЦИЯ
6

Химическое равновесие

План лекции:

1.
Закон действующих масс. Различные способы
выражения константы равновесия для идеальных систем.

2.
Связь константы равновесия с применением энергии
Гиббса. Уравнение изотермы химической реакции.

3.
Зависимость константы равновесия от температуры.
Уравнение изобары химической реакции.

4.
Понятия для активности и летучести (фугитивности).

Большинство химических реакций протекают одновременно в двух
направлениях: в сторону образования продуктов реакции (прямая реакция) и в
сторону разложения последних (обратная реакция). Вследствие химической обратимости
реакции не доходят до конца. Скорость прямой реакции уменьшается, а скорость
обратной, напротив, возрастает. Когда эти скорости выравниваются наступает
состояние химического равновесия.

Так как химически обратимые реакции до перехода в
равновесное состояние протекают с конечными скоростями, то с точки зрения
термодинамики они не обратимы. Однако можно мысленно представить, что эти
реакции идут бесконечно медленно через смежные равновесные состояния. Тогда к
ним можно применить общие условия термодинамического равновесия.

Для гомогенных обратимых
реакций экспериментально Гульбергом и Ваге был установлен закон действующих
масс. При постоянной температуре отношение произведения равновесных
концентраций (или парциальных давлений) продуктов реакции к произведению
равновесных концентраций (или парциальных равновесий) исходных веществ есть величина
постоянная.

Этот экспериментально установленный закон может быть получен
методом термодинамических потенциалов. Рассмотрим реакцию в газовой фазе:

аА(г) + bВ ↔
сС + dD

Когда система достигает термодинамического равновесия, то
термодинамический потенциал при фиксированных естественных переменных достигает
минимума. Равновесие, таким образом, можно охарактеризовать выражением
химических потенциалов, когда потенциалы продуктов реакции сравняются с
потенциалами исходных веществ:

с μ (с) + d μ (D) – a μ (a) – b μ (b) = 0 (6 – 1)

Если естественными переменными являются p и T, то = , а = V

Отсюда для систем,
подчиняющихся закону идеальных газов, можно получить выражения для μi

μi = μi° + RTlnCi (6 – 2)

где μi° – стандартный химический потенциал.

Подставляется
(6 – 2) в (6 – 1) и перенося постоянные величины в левую часть, получаем

сμC° + dμD° – aμA° – bμB° = –RTln (6 – 3)

Поскольку
в левой части выражение не зависит от концентраций, то выражение под логарифмом
является постоянной величиной при постоянной температуре:

Для
идеального газа парциальные давления пропорциональны концентрациям, поэтому
константа равновесия может быть всегда выражена через равновесные парциальные
давления:

Аналогично
может быть записано выражение через мольные доли:

Для
идеальных газов эти константы связаны между собой соотношением:

где

Следует
обратить внимание, что в полученных соотношениях только KN зависит от общего давления. Она позволяет нам
оценивать сдвиг равновесия в газовых реакциях при изменении общего давления. Следует
иметь в виду, что давление в этих выражениях складывается из парциальных
давлений компонентов системы и не учитывает влияние инертных газов, если они
присутствуют в реакционной смеси. Естественно инертный газ «разбавляет»
компоненты реакционной смеси и поэтому влияет на KN.

Из уравнения (6
– 3) вытекает связь константы равновесия с ∆rG°:

(6
– 4)

Это
уравнение было впервые получено Вант – Гофором методом циклов и получило
название уравнения изотермической химической реакции. Очевидно, в этом
уравнении ∆rGT° относится к этой температуре,
при которой определена Кр. Уравнение изотермической химической реакции
позволяет определить константу равновесия при заданных условиях не прибегая к
исследованию равновесия. Величина ∆rGT° может быть рассчитана на основе термических констант
для индивидуальных веществ.

Если
заданы концентрации (парциальные давления) отличные от равновесных, то можно
записать более общий вид уравнения изотермической химической реакции:

Это
выражение позволяет определить направление самопроизвольного процесса.

Уравнение
изотермы химической реакции позволяет получить выражение для температурной
зависимости константы равновесия.

Запишем
уравнение Гиббса – Гельмгольца:

Подставим
выражение для из (6 – 4)

(6 – 5)

Дифференцируем уравнение (6 – 5)

(6 –
5´)

Из
уравнения (6 – 5´) получаем уравнение изобары химической реакции:

(6 – 6)

Если
проинтегрировать уравнение (6 – 6) в
предположении, что ∆rHT° не зависит
от температуры, то получим уравнение:

где С – константа интегрирования.

Уравнение (6 – 7) хорошо выполняется в узких
интервалах температур и позволяет определить ∆rGT°.

Для широких интервалов температур ln Kр представляют в виде степенных рядов или других
аналитических формах:

Например:

Такие выражения позволяют рассчитать все
термодинамические функции для процессов, для которых данные зависимости
получены.

Выражения для термодинамических потенциалов,
полученные для идеального газа. Для реальных газов, а особенно для газовых
растворов возникают затруднения. Это связано с тем, что расчет концентраций и
давлений должен быть проведен исходя из уравнения состояния. Однако для
реальных систем единое достаточно простое уравнение состояния получить не
удалось.

В связи с этим в термодинамике реальных систем
применяется эмпирический метод, предложенный Льюисом. Льюис предложил в
уравнениях термодинамики, полученных для идеальных систем заменить давления p на величину летучести f, а концентрации С на активности a.

При такой замене выражения для констант равновесия не
меняются по форме. Но этот прием позволяет связать экспериментально найденные
свойства реального газа с термодинамическими параметрами.

Летучести и активности – это экспериментальные величины, которые
находятся из условия, что для раствора при бесконечном разбавлении или газа при
давлении стремящимся к 0 активность приближается к аналитической концентрации,
а летучесть к реальному давлению идеального газа. Исходя из этой посылки рассчитываются
активности и летучести.

Пример 6
– 1.

При 1273 К и общем равновесии 30 атм. В равновесной
системе

содержится 17% (по
общему) . Сколько процентов будет содержаться в
газе при общем давлении 20 атм.? При каком давлении в газе будет содержаться
25% ? (Газ считать идеальным).

Решение.

В соответствии с законом Авогадро, объёмный процент
равен мольному проценту. Следовательно, при 30 атм. будет равен:

Отсюда находим

В отличие от , для идеальных газов не зависит от давления. На основании
этого находим при 20 атм.

= 0,125 или 12,5%

Для 25%

Следовательно,

Пример 6
– 2.

При 2000°С и общем давлении 1 атм. 2% воды
диссоцииовано на водород и кислород. Рассчитайте константу равновесия реакции при этих условиях.

Решение.

Исходное количество	1	0	0
Равновесное количество
Равновесная мольная доля

Следовательно,

Пример 6 – 3

Константа равновесия реакции

При 500°С равна Смесь, состоящую из 1 моля СО и 5 моль нагрели до этой температуры. Рассчитайте мольную долю в равновесной смеси.

Решение.

Исходное количество	1	5	0	0
Равновесное количество	1 – х	5 – х	х	х

Поскольку
, то

, следовательно, Х = 0.96

Следовательно,

Пример 6 – 4.

Рассчитайте стандартную
энтальпию реакции, для которой константа равновесия

а) увеличивается в 2 раза,

б) уменьшается в 2 раза,

при изменении температуры от
298 К до 308 К.

Решение.

, после интегрирования получаем

или

а) Дж∙мольˉ¹

б) Дж∙мольˉ¹

Пример 6 – 5.

Оксид
ртути диссоциирует до реакции

При 420°С давление газов Па, а при 450°С Па. Рассчитайте константы равновесия при этих температурах и
энтальпию диссоциации HgO.

В соответствии с уравнением реакции.

Исходное количество
газообразных

продуктов

–

Равновесное количество
газообразных продуктов

–

Мольные доли газообразных
продуктов

–

Парциальные давления газообразных продуктов при 420°С, Па
Парциальные давления газообразных продуктов при 450°С, Па

За стандарт принят , поэтому

Рассчитываем

С
учетом того, что диссоциирует 2 моля HgO,
энтальпия диссоциации HgO составляет
154 кДж∙мольˉ¹.

Следует обратить внимание на то, что если рассчитывать исходя из ранее принятого стандартного давления
= 1атм., то их значения будут отличаться:

Пример 6 – 6:

Зависимость константы
равновесия реакции от температуры между
300К и 600К описывается уравнением:

Рассчитайте , и реакции при 400 К.

Решение:

По
уравнению изотермы химической реакции:

Отсюда находим
непосредственно температурную зависимость

Для расчета удобнее
продифференцировать по . В этом случае . Отсюда

Расчет проводим на основании
уравнения Гиббса – Гельмгольца:

Пример 6 – 7:

Рассчитайте
константу равновесия реакции , если известно, что при получении жидкого формальдегида при 198 К, а давление
пара формальдегида при этой температуре равно 1500 Торр.