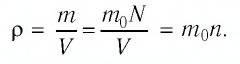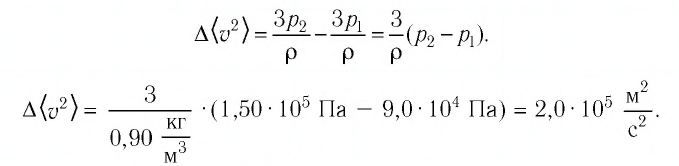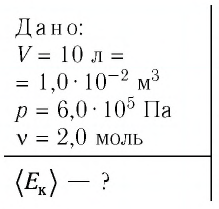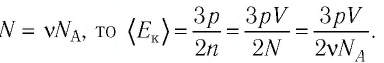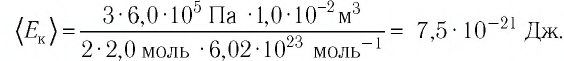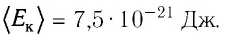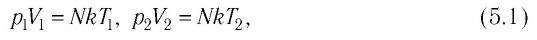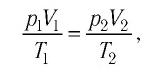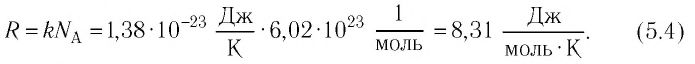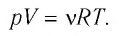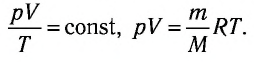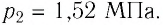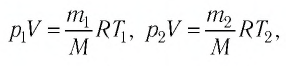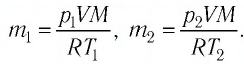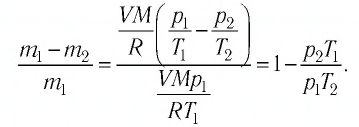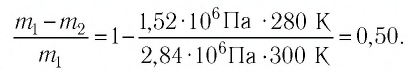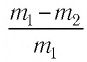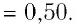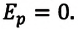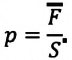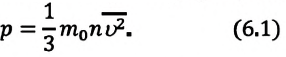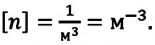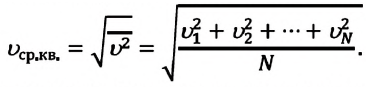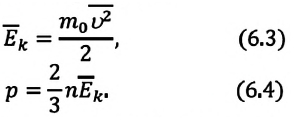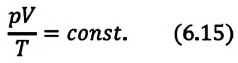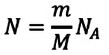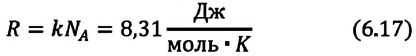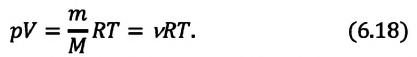Инструкция:
Найдите давление идеального газа при наличии значений средней скорости молекул, массы одной молекулы и концентрации вещества по формуле P=⅓nm0v2, где n – концентрация (в граммах или молях на литр), m0 – масса одной молекулы.
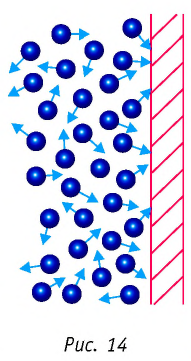
Если в условии дана плотность газа и средняя скорость его молекул, рассчитайте давление по формуле P=⅓ρv2, где ρ — плотность в кг/м3.
Вычислите давление, если вы знаете температуру газа и его концентрацию, используя формулу P=nkT, где k – постоянная Больцмана (k=1,38·10-23 моль·К-1), Т — температура по абсолютной шкале Кельвина.
Найдите давление из двух равноценных вариантов уравнения Менделеева-Клайперона в зависимости от известных значений: P=mRT/MV или P=νRT/V, где R – универсальная газовая постоянная (R=8,31 Дж/моль·К), ν — количество вещества в молях, V – объем газа в м3.
Если в условии задачи указана средняя кинетическая энергия молекул газа и его концентрация, найдите давление с помощью формулы P=⅔nEк, где Eк — кинетическая энергия в Дж.
Найдите давление из газовых законов — изохорного (V=const) и изотермического (T=const), если дано давление в одном из состояний. При изохорном процессе отношение давлений в двух состояниях равно отношению температур: P1/P2=T1/T2. Во втором случае, если температура остается постоянной величиной, произведение давления газа на его объем в первом состоянии равно тому же произведению во втором состоянии: P1·V1=P2·V2. Выразите неизвестную величину.
Рассчитайте давление из формулы внутренней энергии идеального одноатомного газа: U=3·P·V/2, где U – внутренняя энергия в Дж. Отсюда давление будет равняться: P=⅔·U/V.
При расчете парциального давления пара в воздухе, если в условии даны температура и относительная влажность воздуха, выразите давление из формулы φ/100=Р1/Р2, где φ/100 — относительная влажность, Р1 — парциальное давление водяного пара, Р2 — максимальное значение паров воды при данной температуре. В ходе расчета пользуйтесь таблицами зависимости максимальной упругости пара (максимального парциального давления) от температуры в градусах Цельсия.
Давление газа при заданной плотности газа Калькулятор
| Search | ||
| Дом | Химия ↺ | |
| Химия | Концепция родинки и стехиометрия ↺ | |
| Концепция родинки и стехиометрия | Плотность газов ↺ |
|
✖Плотность газа в г/л определяется как масса на единицу объема газа при определенных условиях температуры и давления.ⓘ Плотность газа в г/л [ρg/l] |
+10% -10% |
||
|
✖Температура газа является мерой тепла или холода газа.ⓘ Температура газа [Tg] |
+10% -10% |
||
|
✖Молярная масса – это масса данного вещества, деленная на количество вещества.ⓘ Молярная масса [Mmolar] |
+10% -10% |
|
✖Давление газа – это сила, с которой газ действует на стенки сосуда.ⓘ Давление газа при заданной плотности газа [Pgas] |
⎘ копия |
Давление газа при заданной плотности газа Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Плотность газа в г/л: 4.65 Грамм на литр –> 4.65 Килограмм на кубический метр (Проверьте преобразование здесь)
Температура газа: 45 Кельвин –> 45 Кельвин Конверсия не требуется
Молярная масса: 44.01 Грамм на моль –> 0.04401 Килограмм на моль (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
39531.954166066 паскаль –> Конверсия не требуется
17 Плотность газов Калькуляторы
Давление газа при заданной плотности газа формула
Давление газа = (Плотность газа в г/л*[R]*Температура газа)/Молярная масса
Pgas = (ρg/l*[R]*Tg)/Mmolar
Что такое уравнение идеального газа?
Идеальный газ определяется как гипотетическое газообразное вещество, поведение которого не зависит от сил притяжения и отталкивания и может быть полностью описано законом идеального газа. PV = nRT Это уравнение известно как закон идеального газа.
Содержание:
- Свойства газов
- Давление газов
- Зависимость между объёмом и давлением газа. Закон Еойля — Мариотта
- Зависимость между плотностью газа и его давлением
- Зависимость объёма газа от температуры. Закон Гей-Люссака
- Зависимость давления газа от температуры. Закон Шарля
- Абсолютная шкала температур
- Зависимость между объёмом, давлением и температурой газа
- Физическая сущность понятия абсолютного нуля
- Изменение температуры газа при быстром расширении и сжатии
- Применение сжатых газов
Газ – это одно из трёх основных агрегатных состояний вещества, характеризующееся очень слабыми связями между составляющими его частицами (молекулами, атомами или ионами), а также их большой подвижностью. Частицы газа почти свободно и хаотически движутся в промежутках между столкновениями, во время которых происходит резкое изменение характера их движения.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Свойства газов
Главные свойства газов – это подвижность и хаотичное движение частиц, направление которых меняется при столкновении. Газ – одно из 4 агрегатных состояний веществ, которые на сегодняшний день известны науке.
Давление газов
Всякий газ производит давление на оболочку, внутри которой он находится.
Давление, производимое газом на стенки сосуда, объясняется ударами движущихся молекул.
При ударе о стенку молекулы газа отдают ей определённое количество движения; стенка испытывает при этом действие некоторой силы.
Удар каждой отдельной молекулы о стенку сосуда производит очень небольшое действие. Но молекул газа очень много, удары о стенки сосуда происходят беспрерывно, поэтому в результате получается значительное давление.
Хаотичность движения молекул приводит к тому, что давление газа одинаково во всех направлениях.
При нагревании давление газа увеличивается. Так как при этом число молекул газа не изменяется, то увеличение давления можно объяснить только тем, что удары молекул о стенки заключающего газ сосуда делаются при нагревании чаще и что каждый удар становится сильнее. Удары же могут стать чаще и сильнее, если увеличивается скорость движения молекул. Это подтверждается, как мы видели (гл. V), многочисленными опытами.
Зависимость между объёмом и давлением газа. Закон Еойля — Мариотта
Состояние газа определяется его объёмом, давлением и температурой. С изменением этих величин меняется и состояние газа. Мы будем рассматривать последовательно процессы, при которых одна из величин, характеризующих состояние газа, постоянна, а две другие меняются.
Изучим сначала такой процесс, при котором давление и объём газа изменяются, а температура остаётся постоянной. Такой процесс называется изотермическим 1.
1 От греч. слов: изос — равный, термос — тёплый.
Итак, рассмотрим, как изменяется давление данной массы газа при изменении его объёма, если температура газа не меняется.
Опыты, устанавливающие эту зависимость, можно произвести на приборе, три положения которого изображены на рисунке 134.
Рис. 134. Прибор для установления зависимости между объёмом и давлением газа (в трёх положениях).
В этом приборе стеклянная трубка А соединяется резиновой трубкой с другой стеклянной трубкой В. Трубка А вверху снабжена краном 
Откроем кран 
Поднимем теперь трубку В вверх на столько, чтобы объём воздуха в трубке А уменьшился вдвое (положение II). Уровень ртути в трубке В при этом значительно поднимется над уровнем в трубке А.
Рассмотрим теперь, чему будет равно давление воздуха в трубке А. Это давление уравновешивает атмосферное давление и давление всего столба ртути в трубке В, стоящего выше уровня n1 высота этого столба n1n оказывается равной 76 см. Таким образом, давление воздуха в трубке А уравновешивает не одну, как в первом случае, а две атмосферы (р2 = 2 am).
Значит, с уменьшением объёма данной массы газа в два раза давление его увеличивается в два раза. Если уменьшить объём газа в 1,5; 2,5; 3 раза, то соответственно в 1,5; 2,5; 3 раза увеличится его давление.
Опустим теперь трубку В так, чтобы масса воздуха в трубке А заняла вдвое больший объём (положение III). Уровень ртути в трубке А при этом понизится. Атмосферное давление теперь уравновешивает давление воздуха в трубке А и давление столба ртути от уровня n в трубке А до уровня в трубке В. Измерения показывают, что высота этого столба ртути равна 38 см. Давление, производимое воздухом в трубке А, найдём, вычтя из атмосферного давления давление столба ртути: р3 = 76 см—38 см = 38 см; следовательно, р3 = 0,5 am.
Итак, при увеличении объёма газа в два раза его давление уменьшается в два раза.
Перемещая трубку В в различные положения и отсчитывая каждый раз объём и давление воздуха в трубке А, найдём, что при уменьшении объёма исследуемой массы воздуха в некоторое число раз давление его увеличивается во столько же раз. Температура воздуха при всех опытах остаётся постоянной.
Опыты, проведённые с другими газами, дали те же результаты.
Изучая на опыте зависимость давления газа от его объёма, английский учёный Бойль (1627—1691) и французский учёный Мариотт (1620—1684) независимо один от другого открыли следующий закон.
Давление данной массы газа при неизменной температуре обратно пропорционально объёму газа.
Этот закон называется законом Бойля — Мариотта.
Выразим закон Бойля — Мариотта математически. Пусть температура некоторой массы газа постоянная и пусть:
V1 — объём газа при давлении р1,
V2 » » » » р2.
Согласно закону Бойля — Мариотта можно написать:
Из этой формулы следует, что:
Полученное равенство можно рассматривать как новое выражение закона Бойля — Мариотта.
Произведение объёма данной массы газа на его давление при неизменной температуре есть величина постоянная.
Изобразим графически изотермическое изменение состояния газа. Для этого по оси абсцисс будем откладывать значения объёмов газа, а по оси ординат соответствующие им значения давлений. Выберем масштаб так, чтобы начальные значения объёма и давления были равны 1. Тогда начальное состояние газа будет изображено точкой А (рис. 135). Если давление увеличится вдвое, объём уменьшится в два раза, состояние газа изобразится на графике точкой В. При уменьшении первоначального давления вдвое объём удвоится, получим точку С. Беря далее давления в три, четыре и т. д. раза больше или меньше начального, а объёмы соответственно в три, четыре и т. д. раза меньше или больше, получим ряд точек, изображающих различные состояния одной и той же массы газа при одинаковой температуре.
Рис. 135. График изотермического процесса.
Проведя через эти точки линию, получим кривую, которая называется изотермой.
Тщательными исследованиями установлено, что для реально существующих газов закон Бойля — Мариотта имеет лишь приближённое значение. Так, например, если произведение pV при 1 am равно единице, то при 2 am оно имеет следующие значения:
для воздуха ………………………0,99977
» водорода …………………….. 1,00026
» окиси углерода………………….. 0,99974
» двуокиси углерода………………… 0,99720
При очень больших давлениях (в сотни и тысячи атмосфер) закон Бойля — Мариотта становится совершенно неприменимым; в таких случаях зависимость между объёмом и давлением газа выражается более сложными уравнениями.
Зависимость между плотностью газа и его давлением
Плотность газа численно равна массе, заключённой в единице объёма.
Масса газа не меняется при его сжатии или расширении, но объём меняется; следовательно, меняется и плотность газа.
Пусть при постоянной температуре: D1 — плотность газа при объёме V1 и давлении p1 , a D2 — плотность газа при объёме V2 и давлении p2.
Если масса газа равна m, то можно написать:
откуда:
Но 
При постоянной температуре плотность газа прямо пропорциональна его давлению.
Нетрудно понять справедливость этого вывода, исходя из молекулярно-кинетической теории. В самом деле, давление газа обусловлено ударами его молекул. Если объём газа уменьшится вдвое, то в новом объёме , плотность газа станет вдвое больше. Вдвое увеличится и число ударов молекул о стенки, т. е. давление газа возрастёт в два раза.
Зависимость объёма газа от температуры. Закон Гей-Люссака
Как и все тела, газы при нагревании расширяются, причём весьма заметно даже при незначительном нагревании. Это легко обнаружить на следующем простом опыте (рис. 136).
Рис. 136. Установка для наблюдения расширения газа при нагревании.
Колба А соединяется с расположенной горизонтально трубкой CD, которая укреплена вдоль шкалы. Внутри этой трубки находится небольшой столбик ртути. Достаточно к колбе прикоснуться рукой, как столбик ртути в трубке CD начнёт двигаться.
При охлаждении колбы столбик ртути перемещается влево, а при нагревании — вправо; следовательно, газ при охлаждении сжимается, а при нагревании расширяется. Зная объём колбы и диаметр трубки, можно измерить увеличение объёма газа.
Постепенно нагревая газ в колбе, можно установить, что при постоянном давлении изменение объёма данной массы газа пропорционально изменению температуры. Поэтому тепловое расширение газа, так же как и других тел, можно охарактеризовать при помощи коэффициента объёмного расширения.
Пусть при температуре 0°С объём газа равен V0 , а при температуре t объём Vt. Увеличение объёма, приходящееся на каждую единицу объёма, взятого при 0°С, при нагревании на один градус будет равно:
откуда: 
Величина 
Жозеф Луи Гей-Люссак (1778—1850)— один из выдающихся французских химиков и физиков. Он открыл ряд важных химических и физических законов, из которых в физике широко известен закон одинакового расширения газов и паров при одинаковом повышении температуры.
Французский учёный Гей-Люссак, исследуя на опыте тепловое расширение газов, открыл, что, коэффициент объёмного расширения у всех газов при постоянном давлении одинаков и численно равен
В этом отношении расширение газов при нагревании отличается от расширения твёрдых и жидких тел, где, как мы видели (см. § 81 и 82), коэффициент объёмного расширения зависит от химического состава тел.
Положим в формуле (1):
получим: 

Этот закон получил название закона Гей-Люссака. Процессы, подобные рассмотренному, протекающие при постоянном давлении, называются изобарными1.
1 От греч. слов: изос — равный, барос — тяжесть, вес.
Формула (1) показывает, что объём газа при температуре t° равен произведению его объёма, взятого при 0°С, на двучлен объёмного расширения
Пример. 1. Объём некоторой массы газа при 0°С равен 10 л. Найти объём его при t=273°С, если давление постоянно.
По условиям задачи нам известен объём газа при 0°С, т. е. V0 = 10 л; подставляя числовые данные задачи в формулу 
Пример 2. При температуре 273°С объём некоторой массы газа равен 10 л. Чему будет равняться объём этого газа при температуре 546°С, если давление постоянно?
Нам известен объём газа при температуре 273°С; чтобы определить объём этого газа при t2 = 546°С, надо предварительно найти его объём при 0°.
Этот объём найдётся из равенства:
откуда:
Найдём теперь объём газа при 546°:
Зависимость давления газа от температуры. Закон Шарля
Нагревая газ в закрытом цилиндре, например в папиновом котле (рис. 136а), можно по манометру заметить, что давление газа увеличивается. Следя по термометру за повышением температуры, легко установить, что при постоянном объёме давление газа возрастает пропорционально повышению температуры.
Рис. 136а. При нагревании газа в закрытом цилиндре давление его повышается.
Аналогично тому, как для характеристики теплового расширения газов мы ввели коэффициент объёмного расширения, введём величину, характеризующую изменение давления газа при изменении его температуры.
Обозначим буквой р0 давление газа при 0°С, a pt — давление при t°. Увеличение давления, приходящееся на каждую единицу начального давления при нагревании на 1°С, будет равно:

Величина 
Измерения показывают, что величина термического коэффициента давления для всех
газов одинакова и равна
Определяя из формулы (1) величину pt получим:

Положим в формуле (2) 
Отсюда следует, что давление данной массы газа при нагревании на 1° при постоянном объеме увеличивается на 
Этот закон называется законом Шарля, по имени французского учёного, открывшего его в 1787 г.
Из закона Шарля следует, что термический коэффициент давления газа 

Пусть некоторая масса газа заключена в цилиндре под поршнем (рис. 137, а) и пусть температура её в этом начальном состоянии равна 0°, объём V0 и давление р0. Закрепим поршень АВ и нагреем газ до температуры t° (рис. 137, б); тогда давление газа увеличится и станет равным рt объём же его останется прежним.
По закону Шарля:
Будем теперь газ нагревать от 0 до t° (рис. 137, в), предоставив поршню свободно перемещаться. Давление газа останется таким же, каким было в начальном его состоянии, т. е. р0 , объём же увеличится до Vt. По закону Гей-Люссака:
Рис. 137.
а) начальное состояние газа: 0°, V0, р0;
б) состояние газа, определяемое величинами:
в) состояние газа, определяемое величинами:
Итак, имеем: при температуре t° объём данной массы газа V0 и давление 

После упрощения этого выражения получаем равенство:
Выразим сначала в виде таблицы, а потом графически зависимость давления газа от температуры. Для этого воспользуемся уравнением:
Рис. 138. График изменения давления газа от температуры.
Отложим по оси абсцисс в некотором условном масштабе температуры газа, а по оси ординат соответствующие этим температурам давления, взятые из написанной выше таблицы.
Соединяя на графике отмеченные точки, получим прямую LM (рис. 138), представляющую собой график зависимости давления газа от температуры при постоянном объёме.
Процесс изменения состояния газа, происходящий при неизменном объёме газа, называется изохорным 1 процессом, а линия LM, изображающая изменение давления газа при постоянном объеме в зависимости от температуры, называется изохорой.
1 От греч. слов: изос — разный, хорема — вместимость.
Пример 1. Давление газа при 0°С равно 780 мм рт. ст. Определить давление этого газа при температуре 273°С.
По формуле 
Пример 2. Чему будет равно давление газа при температуре 546°, если давление его при температуре 273° равно 780 мм рт. cm.?
В этой задаче прежде всего надо определить давление газа при 0°С. По формуле 
Теперь можно определить давление газа при t = 546°:
Законы Гей-Люссака и Шарля так же, как и закон Бойля — Мариотта, лишь приближённо отражают свойства газов. Это можно видеть хотя бы. из того факта, что для разных газов величины 


Точные измерения показывают, что для каждого данного газа значения 

Абсолютная шкала температур
Вернёмся ещё раз к графику изменения давления газа с температурой (рис. 138).
Продолжим прямую LM на этом графике до пересечения её с горизонтальной осью, по которой откладываются температуры газа, она пересечёт эту ось в точке K. Отрезок ОК будет изображать на этом графике такую температуру газа, при которой давление его равно нулю. Чему равна эта температура?
Обратимся к уравнению 
Так как давление газа при 0°С не равно нулю 
откуда: 
Итак, давление газа равняется нулю при температуре —273°С.
Вильям Томсон (Кельвин) (1824— 1907) — выдающийся английский физик. Ему принадлежат важные открытия в области теории электричества и теплоты и изобретения, из которых наиболее значительным было усовершенствование телеграфной связи. Он ввёл в физику понятие об абсолютной температуре. Его именем названы градусы шкалы абсолютных температур — градусы Кельвина.
Английский учёный Вильям Томсон (Кельвин) предложил такую шкалу температур, при которой за нуль градусов принята температура — 273°. Эта шкала получила название абсолютной шкалы температур, или шкалы Кельвина, а нуль градусов этой шкалы, равный — 273°, называется абсолютным нулём температур.
В шкале Кельвина величина градуса та же, что и в стоградусной шкале.
Будем обозначать температуру по шкале Кельвина буквой Т.
При нормальном атмосферном давлении температура таяния льда по шкале Кельвина Т0 = 273°, температура же кипения воды T = 373°.
Всякая другая температура t° стоградусной шкалы связана с абсолютной температурой Т соотношениями:
Зависимость между объёмом, давлением и температурой газа
Объединённый закон газового состояния. Мы рассмотрели процессы, в которых одна из трёх величин, характеризующих состояние газа (объём, давление и температура), не меняется.
Вы видели, что если не меняется температура, то давление и объём газа связаны друг с другом законом Бойля —- Мариотта. При постоянном давлении объём газа изменяется с изменением температуры по закону Гей-Люссака, и, наконец, при постоянном объёме давление газа меняется с изменением температуры по закону Шарля.
Однако в природе часто имеют место процессы, когда одновременно меняются все три величины, характеризующие состояние газа. Установим теперь, какая связь существует между объёмом, давлением и температурой.
Пусть для двух каких-либо произвольных состояний некоторой массы газа эти величины будут:
Из этих состояний изменением величин р, V или t газ можно перевести в любые другие состояния. Будем, например, сохраняя постоянным давление, переводить газ из состояний 1) и 2) в состояния, при которых температура газа будет равна 0°С.
По закону Гей-Люссака объём газа V1 после уменьшения температуры от до 0° будет равен 
Новые состояния газа выразятся так:
В обоих этих состояниях температура газа одинакова, поэтому на основании закона Бойля — Мариотта можно написать:

Так как величины р, V, t, характеризующие состояние рассматриваемого газа и обозначенные индексами 1 и 2, выбраны были нами произвольно, то равенство (1) справедливо для любых состояний этого газа. Поэтому можно утверждать, что:

Для данной массы газа произведение давления газа на его объём, делённое на двучлен объёмного расширения, есть величина постоянная.
Выведенная нами зависимость между объёмом, давлением и температурой газа называется объединённым законом газового состояния, а равенство (1) или (2) — уравнением состояния газа.
Уравнение состояния газа можно упростить, введя в него вместо температуры t по стоградусной шкале температуру Т по абсолютной шкале температур. Для этого преобразуем уравнение:
Введя в него значение 
что после сокращения на 273 даст:
Но 

Это означает, что для данной массы газа произведение давления на объём, делённое на абсолютную температуру, постоянно при всех температурах:
В частности, если при температуре Т = 273° объём газа равен V0 и давление его р0 , то можно написать:
Физическая сущность понятия абсолютного нуля
Мы уже отмечали, что реальные газы лишь приближённо следуют законам Гей-Люссака, Шарля и Бойля — Мариотта. Однако можно представить себе газ, для которого эти законы выполнялись бы в точности. Молекулы такого газа можно представить себе в виде упругих шариков исчезающе малого объёма, взаимодействие между которыми осуществляется только через их столкновения друг с другом. В физике такой газ принято называть идеальным газом.
Из уравнения 
Опыт показывает, что при малых давлениях свойства реальных газов очень близки к свойствам идеального газа. Следовательно, при приближении к температуре абсолютного нуля должно прекратиться тепловое движение молекул и реального газа. Этот вывод относится не только к газам, но и к твёрдым и жидким телам.
Физикой установлено, что такое состояние вещества недостижимо, но к нему можно подойти очень близко. В настоящее время достигнута температура, которая выше абсолютного нуля всего на несколько стотысячных долей градуса.
Изменение температуры газа при быстром расширении и сжатии
Опыты показывают, что при быстром сжатии температура газа повышается, а при быстром расширении понижается.
Увеличение температуры газа при сжатии можно показать на следующем простом опыте. Возьмём толстостенный цилиндрический стеклянный сосуд, внутри которого может двигаться поршень (рис. 139). При быстром сжатии воздух в сосуде сильно нагревается, и легко воспламеняющееся вещество (например, ватка, смоченная эфиром), положенное на дно сосуда, вспыхивает. Такого рода явление используется, например, в двигателях внутреннего сгорания —дизелях: при сжатии воздуха в цилиндре двигателя горючая смесь, введённая в цилиндр, нагревается до температуры воспламенения (работа двигателя описана в § 131).
Рис. 139. При быстром сжатии воздух в цилиндре сильно нагревается и легко воспламеняющееся вещество вспыхивает.
При быстром же расширении газа температура его понижается. Это можно наблюдать на следующем опыте. Будем накачивать воздух в прочную закрытую пробкой стеклянную банку, содержащую пары воды. При достижении определённого давления пробка выскочит; при этом воздух, расширяясь, совершит работу и охладится, вследствие чего водяной пар превратится в туман (рис. 140).
Рис. 140. Сжатый в сосуде воздух, выбрасывая пробку, расширяется. Совершая при этом работу, он охлаждается, вследствие чего водяной пар в сосуде превращается в туман.
Понижение температуры при быстром расширении газа используется для получения сжиженных газов; об этом будет рассказано в § 122.
Изменение температуры тела, как было установлено в § 71, связано с изменением внутренней энергии тела. Так как при быстром сжатии температура газа повышается, то внутренняя энергия его при этом увеличивается. Увеличение внутренней энергии газа происходит в результате работы, совершённой при его сжатии. Расширяясь же, газ совершает работу; при этом внутренняя энергия его уменьшается, и если расширение происходит быстро, то температура газа, как мы видели в наших опытах, понижается.
Процесс, происходящий в теле без теплообмена с окружающими его другими телами, называется адиабатным процессом.
Все быстро протекающие процессы практически могут считаться адиабатными.
Применение сжатых газов
Многие сжатые газы в настоящее время находят широкое применение в технике.
Сжатый воздух, например, применяется в работе различных пневматических инструментов: отбойных молотков, заклёпочных молотков, в разбрызгивателях краски и др.
На рисунке 141 показана схема устройства отбойного молотка. Сжатый воздух подаётся в молоток по шлангу М. Золотники Z, аналогичные применяемым в паровых машинах, направляют его поочерёдно то в заднюю, то в переднюю часть цилиндра. Поэтому воздух давит на поршень Р то с одной, то с другой стороны, что вызывает быстрое возвратно-поступательное движение поршня и пики молотка В. Последняя наносит быстро следующие друг за другом удары, внедряется в уголь и откалывает куски его от массива.
Рис. 141. Схема устройства отбойного молотка.
Существуют также пескоструйные аппараты, которые дают сильную струю воздуха, смешанную с песком. Эти аппараты применяются, например, для очистки стен. Сейчас нередко можно видеть работу специальных аппаратов, применяемых для окраски стен, где краска распыляется сжатым воздухом. Сжатым воздухом открываются двери вагонов метро и троллейбусов. Сжатый воздух используется в работе тормозов на транспорте. Схематическое устройство одного из видов пневматического тормоза железнодорожного вагона изображено на рисунке 142.
Компрессор подаёт воздух по магистрали в стальной резервуар А. Поршень В тормозного цилиндра оказывается под одинаковым давлением справа и слева; поэтому соединённая с ним тормозная колодка D отжата от колеса. Если открыть тормозной кран М, то находящийся в магистрали под давлением воздух устремится в атмосферу; клапан К захлопнется, и, таким образом, стальной резервуар изолируется от магистрали. Теперь давление на поршень В справа станет больше, чем давление слева, вследствие чего тормозная колодка прижмётся к ободу колеса. Если теперь кран М закрыть и снова подать в магистраль сжатый воздух, то восстановится первоначальное положение.
Рис. 142. Схема устройства железнодорожного пневматического тормоза.
В технике применяется не только сжатый воздух, но и некоторые другие газы, так, например, водород, ацетилен и кислород применяются при газовой сварке; аммиак используется в холодильном деле. Чтобы газы было удобно перевозить, их помещают в прочные стальные баллоны, накачивая до давления 60—200 am.
Рис. 142а. Внешний вид мощного компрессора.
Сжатие газов осуществляется с помощью мощных нагнетательных насосов — компрессоров.
На рисунке 143, а, б дана схема работы компрессора.
Компрессор состоит из цилиндра с поршнем и двумя клапанами; один из них входной, другой выходной. При движении поршня вниз (рис. 143, б) открывается входной клапан и в цилиндр поступает воздух из помещения; при движении поршня вверх (рис. 143, а) входной клапан закрывается, вошедший воздух сжимается поршнем и через выходной клапан поступает в стальной баллон для хранения сжатого газа.
Существуют так называемые многоступенчатые компрессоры, в которых газ последовательно
сжимается в трёх или четырёх цилиндрах. Такие компрессоры позволяют получить газ, сжатый до давления в тысячи атмосфер. На рисунке 142а изображён внешний вид одного из типов многоступенчатых компрессоров.
Рис. 143, а, б. Схема работы компрессора.
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно – кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
Содержание:
Идеальный газ:
Наиболее простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ начинают с газов. Газ (греч. chaos — хаос) — такое агрегатное состояние вещества, когда составляющие его частицы почти свободно и хаотически движутся между соударениями, во время которых происходит резкое изменение их скорости. Термин «газ» предложил в начале XVII в. нидерландский химик Ян Батист ван Гельмонт (1579— 1644).
Макро- и микропараметры:
При изучении механики в 9-м классе вы познакомились с понятием «состояние механической системы тел». Параметрами этого состояния являются координаты, скорости или импульсы тел. В тепловых процессах основными физическими величинами, характеризующими состояние макроскопических тел без учёта их молекулярного строения, являются давление
Одна из важнейших задач молекулярно-кпнетической теории состоит в установлении связи между макроскопическими и микроскопическими параметрами.
Идеальный газ
Для теоретического объяснения свойств газов используют их упрощённую модель — идеальный газ.
Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия их взаимодействия равна нулю); силы действуют только во время столкновений молекул, причём это силы отталкивания.
Поведение молекул идеального газа можно описать, используя законы Ньютона и учитывая, что между соударениями молекулы движутся практически равномерно и прямолинейно.
Модель идеального газа можно использовать в ограниченном диапазоне температур и при достаточно малых давлениях. Так, например, свойства водорода и гелия при нормальном атмосферном давлении и комнатной температуре близки к свойствам идеального газа.
Изучая физику в 7-м классе, вы узнали, что давление газа на стенки сосуда, в котором он находится, как и на любое тело, помещённое внутрь сосуда, создаётся в результате ударов частиц, образующих газ (рис. 14). Вследствие хаотичности их движения усреднённое по времени давление газа в любой части сосуда одинаково, и его можно определить по формуле
Выражение (3.1) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр давление р идеального газа через массу 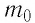
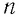
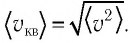
Зависимость давления газа от среднего значения квадрата скорости 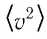
Обозначим через 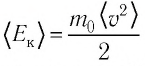
Из выражения (3.2) следует, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации.
Пример №1
Баллон электрической лампы наполнен газом, плотность которого 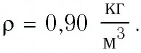
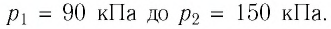
Решение. Покажем, что между плотностью р газа и концентрацией 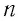
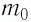
Тогда основное уравнение молекулярно-кинетической теории можно записать в виде: 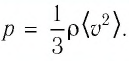
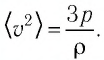
Ответ:
Пример №2
В сосуде вместимостью 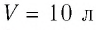
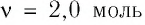
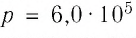
Решение. Из основного уравнения молекулярно-кинетической теории, записанного в виде 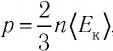
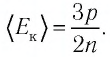
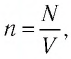
Ответ:
Уравнение состояния идеального газа
Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.
Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление р, масса 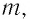
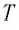
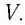
Если при переходе идеального газа из одного состояния в другое число его т
молекул 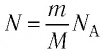
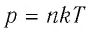
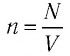
где 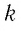
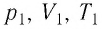
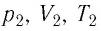
или
При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.
Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.
Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799—1864), поэтому его называют уравнением Клапейрона.
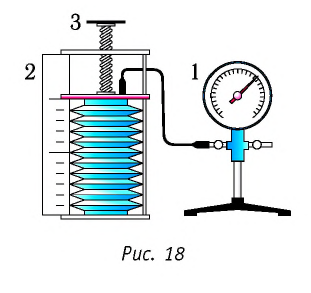
В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.
Измерив параметры газа 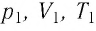
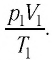
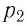
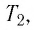
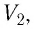
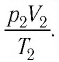
Уравнение состояния (5.2) можно применять для газов при следующих условиях:
- не очень большие давления (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с предоставленным ему объёмом);
- не слишком низкие или же высокие температуры (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).
Поскольку число частиц 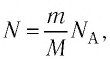
Величину, равную произведению постоянной Больцмана 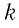
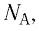
С учётом выражения (5.4) уравнение (5.3) примет вид:
Поскольку количество вещества 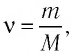
Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834—1907) в 1874 г., поэтому его называют уравнением Клапейрона—Менделеева.
Отметим, что уравнение Клапейрона—Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона-Менделеева, можно описать различные процессы, происходящие в идеальном газе.
Давление смеси газов
В повседневной жизни часто приходится иметь дело не с газом, состоящим из одинаковых молекул, а со смесью нескольких разнородных газов, не вступающих в химические реакции при рассматриваемых условиях. Например, воздух в комнате является смесью азота, кислорода, инертных газов и водорода, а также некоторых других газов.
Вследствие теплового движения частиц каждого газа, входящего в состав газовой смеси, они равномерно распределяются по всему предоставленному смеси объёму. Столкновения частиц обеспечивают в смеси тепловое равновесие.
Каждый газ вносит свой вклад в суммарное давление, производимое газовой смесью, создавая давление, называемое парциальным.
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Смесь идеальных газов принимают за идеальный газ.
Из истории физики:
Фундаментальные исследования газовых смесей провёл английский учёный Джон Дальтон (1766-1844). Им сформулирован закон независимости парциальных давлений компонентов смеси (1801-1802). В 1802 г. на несколько месяцев раньше французского учёного Жозефа Гей-Люссака (1778-1850) Дальтон установил закон теплового расширения газов, а также ввёл понятие атомного веса.
При постоянных массе и молярной массе отношение произведения давления идеального газа и его объёма к абсолютной температуре является величиной постоянной (уравнение состояния идеального газа):
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Пример №3
Баллон с газом, давление которого 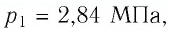
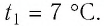
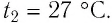
Решение. Если пренебречь тепловым расширением баллона, то его вместимость не изменяется. Запишем уравнение Клапейрона—Менделеева для начального и конечного состоянии газа, считая его идеальным:
откуда
Тогда
Ответ:
Основное уравнение молекулярно-кинетической теории идеального газа
В молекулярной физике изучаются свойства вещества во всех агрегатных состояниях, в том числе и газообразном. В природе почти нет отдельно взятого газа, реальный газ атмосферы представляют собой сложную систему разных газов.
Основная задача молекулярно-кинетической теории – установление связи между макроскопическими и микроскопическими параметрами, характеризующими свойства этой сложной системы. С этой целью реальный газ сложного состава заменяется упрощенной, идеализированной моделью.
Идеальный газ:
Первый шаг в создании любой физической теории состоит в построении идеализированной модели реального объекта. Такая модель всегда имеет упрощенный вид действительности, и с ее помощью изучаются количественные и качественные закономерности и свойства реального объекта с учетом определенных ограничений.
Для изучения свойств газов в молекулярно-кинетической теории применяется идеализированная модель – “идеальный газ”.
Идеальный газ – это газ, удовлетворяющий следующим условиям:
- — линейные размеры молекул во много раз меньше расстояний между ними и не принимаются во внимание. Поэтому можно сказать, что молекулы идеального газа не взаимодействуют друг с другом, то есть потенциальная энергия взаимодействия молекул идеального газа равна нулю:
Поэтому идеальный газ можно сколько угодно сжимать; —только при соударении молекул друг с другом или со стенками сосуда между ними возникают силы отталкивания;
- — соударения молекул абсолютно упругие;
- — скорость молекул может иметь произвольные значения, движение каждой молекулы подчиняется законам классической механики.
Свойства идеального газа характеризуются микроскопическими и макроскопическими параметрами и связями между ними.
Микроскопические параметры газа – это параметры, характеризующие движение молекул газа. К ним относятся масса молекулы, его скорость, импульс и кинетическая энергия поступательного движения молекулы.
Макроскопическими являются такие параметры газа, как ее давление, объем и температура, определяющие свойства газа в целом.
Основной задачей молекулярно-кинетической теории является установление взаимной связи между микроскопическими параметрами, характеризующими молекулы газа, и макроскопическими (измеряемыми) величинами, характеризующими газ.
Основное уравнение молекулярно-кинетической теории идеального газа:
Известно, что давление газа возникает в результате многочисленных непрерывных и беспорядочных соударений молекул газа о стенки сосуда, в котором он находится. Это давление равно среднему значению модуля равнодействующей силы, приходящейся на единицу площади:
В 1857 г. немецкий физик Рудольф Клаузиус (1822-1888), используя модель идеального газа, определил уравнение для давления газа, называемое основным уравнением молекулярно-кинетической теории идеального газа.
Основное уравнение молекулярно-кинетической теории идеального газа — это уравнение, связывающее макроскопический параметр газа – его давление, с микроскопическими параметрами, характеризующими молекулы газа:
Где 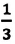
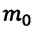
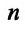
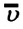
Концентрация молекул — это число молекул в единице объема:
Единица концентрации в СИ:
Средняя квадратичная скорость молекул равна корню квадратному из средней арифметической величины квадратов скоростей отдельных молекул:
Так как среднее значение квадрата скорости молекул связано со средним значением кинетической энергии их поступательного движения, то, следовательно, и давление идеального газа зависит от среднего значения кинетической энергии молекул:
Давление идеального газа прямо пропорционально концентрации молекул и среднему значению кинетической энергии молекул.
Если принять во внимание, что плотность газа 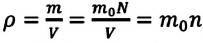
Вы исследовали идеальный газ с позиций MKT и определили связь между его макроскопическими и микроскопическими параметрами.
Уравнение Клапейрона
Связь между тремя макроскопическими параметрами (давление, объем и температура), характеризующими состояние идеального газа, определяет уравнение состояние идеального газа.
Уравнение состояния идеального газа – это уравнение, описывающее состояние газа и устанавливающее связь между параметрами его начального и конечного состояний.
Если число молекул идеального газа остается постоянным, то есть масса и молярная масса не меняются, то при переходе идеального газа из одного состояния в другое, из формул (6.2) и (6.9) имеем для этих состояний:
Где 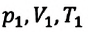
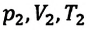
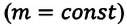
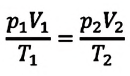
Это уравнение (6.15), характеризующее состояние идеального газа, впервые в 1834 году получил французский физик Бенуа Клапейрон (1799-1864), поэтому его назвали уравнением Клапейрона.
Отношение произведения давления идеального газа данной массы на его объем к абсолютной температуре является постоянной величиной.
Уравнение Менделеева-Клапейрона:
Приняв во внимание формулу, связывающую число частичек вещества, общую массу вещества, молярную массу и число Авогадро,
в формуле (6.14), получим:
Произведение постоянной Больцмана на постоянную Авогадро также является постоянной величиной. Оно называется универсальной газовой постоянной, обозначается буквой 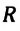
Приняв во внимание выражение (6.17) в (6.16), получаем выражение, характеризующее состояние идеального газа и называемое уравнением Менделеева-Клапейрона.
Физический смысл универсальной газовой постоянной определяется из последнего выражения.
Универсальная газовая постоянная равна отношению произведения давления и объема к абсолютной температуре одного моля любого газа.
Уравнение Менделеева-Клапейрона можно записать и в таком виде:
Где 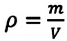
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа
- Температура в физике
- Парообразование и конденсация
- Зависимость веса тела от вида движения
- Движение тел под воздействием нескольких сил
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
Формулы для определения давления газа применимы только для так называемого идеального газа. Это такой газ, когда пренебрегается взаимодействием между молекулами. Для этого газ должен быть достаточно разряженным. Газ с хорошей точностью можно считать идеальным вплоть до давлений 20 – 30 атмосфер. Так что атмосферу Земли можно считать идеальной даже у самой поверхности Земли. Давление газа на какую-либо поверхность определяется ударами молекул об эту поверхность. Естественно, что тогда давление газа должно зависеть от скоростей движения молекул. Вот формула для определения давления газа р
p = (Nmv^2)/3V (1)
Естественно, что давление зависит от числа молекул N, от массы молекулы m, от средней скорости движения молекул v и от объема сосуда V, где находятся молекулы. Средняя кинетическая энергия молекулы равна Е = mv^2/2. Тогда получим следующую формулу для расчета давления газа через среднюю энергию молекул
р = 2NЕ/3V (2)
Больцман рассчитал, что средняя кинетическая энергия молекул пропорциональна абсолютной температуре Т. Е = (3/2)kT, где k – постоянная Больцмана и T – абсолютная температура. Тогда получим для давления идеального газа формулу р = (NkT)/V. Перепишем эту формулу в следующем виде
рV = NkT (3)
Концентрация молекул в газе равна n = N/V. Тогда формула (3) примет такой вид
pV = NkT (4)
Концентрацию молекул можно выразить через произведение числа молей ν на число частиц в моле N = νNa. Произведение Na*k = R. Где R – газовая постоянная. Тогда (4) запишется в виде
pV = νRT (5)
Число молей газа ν = M/μ, где М – масса газа и μ – масса одного моля (молярная масса). Тогда уравнение (5) примет вид
pV = (M/μ)RT (6)
Уравнение состояния идеального газа в таком виде называют уравнением Клапейрона – Менделеева. При постоянных температуре и массе из (6) следует, что
pV = const (7)
То есть давление будет обратно пропорционально объему газа. Такой закон получил название закона Бойля – Мариотта. Если же постоянным является давление, то
V = (MR/Vμ)T (8)
Давление пропорционально абсолютной температуре. Этот закон получил название закон Шарля.
Вот и используйте любую из этих формул для расчета давления газа.