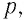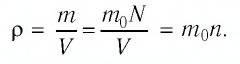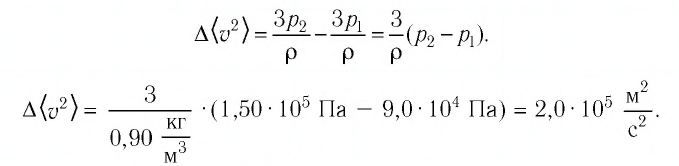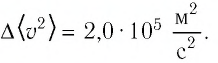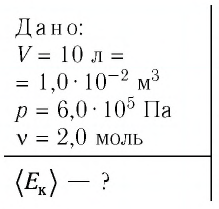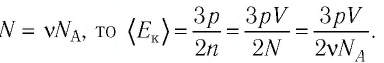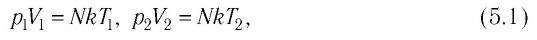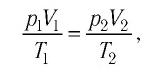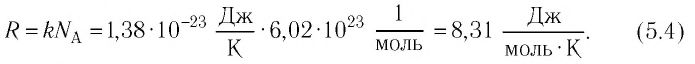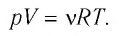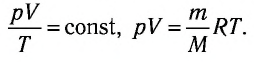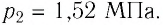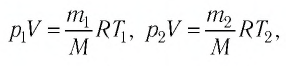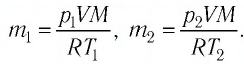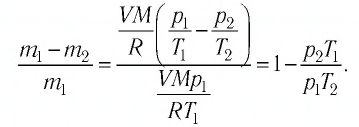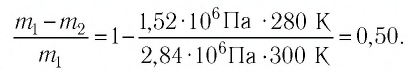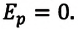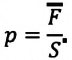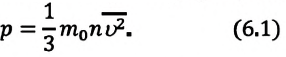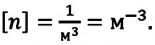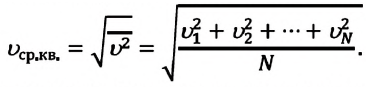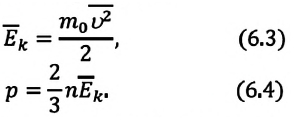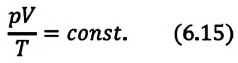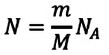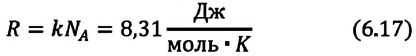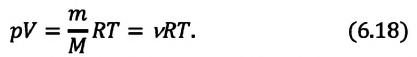При
выводе уравнения состояния идеального
газа будем считать молекулы маленькими
твердыми шарами, заключенными в ящик
объемом V.
Предположение о твердых шарах означает,
что между молекулами происходят упругие
соударения. Рассмотрим сначала одну
такую молекулу, отражающуюся от левой
стенки ящика. Средняя сила, действующая
на стенку на протяжении времени
,
равна
|
l |
В
(8.10)
Поскольку |
то на стенку со
стороны одной молекулы действует средняя
сила

Полная
сила, с которой все N
молекул в ящике действуют на стенку,
дается выражением
, (8.13)
где
–
усредненный по всем частицам квадрат
скорости.
Эта
величина называется среднеквадратичной
скоростью в направлении оси
x.
Разделив обе части этого соотношения
на площадь стенки S,
получим давление
. (8.14)
Заменим
S
l
на объем
V;
тогда
, (8.15)
откуда
. (8.16)
Уже
отсюда видно, что для данного количества
газа произведение pV
остается
постоянным при условии, что кинетическая
энергия частиц сохраняется без изменения.
Правую часть формулы (8.16) можно записать
через
.
Действительно,
.
Поскольку
молекулы совершенно одинаково отражаются
от всех шести граней, то
.
Тогда
,
или.
Подставим
теперь в (8.16) вместо
величину
:
. (8.17)
Мы
будем определять абсолютную температуру
как величину, прямо пропорциональную
средней кинетической энергии молекул
в сосуде:
(8.18)
(определение
температуры),
где
–
средняя кинетическая энергия, приходящаяся
на одну частицу.
Коэффициент
пропорциональности (2/3k)
представляет
собой константу. Значение постоянной
k
(постоянной
Больцмана)
зависит от выбора шкалы температуры.
Один из способов выбора шкалы основан
на том, что интервал температур между
точками кипения и замерзания воды при
нормальном давлении полагается равным
100 градусам (=100 К).
Таким образом, величина k
определяется путем измерения свойств
воды. Экспериментально найдено, что
(8.18)
(постоянная
Больцмана)
Если
с помощью (8.18) исключить величину
из
(8.17), то получим
. (8.19)
(уравнение
состояния идеального газа)
Таким
образом, применив уравнения ньютоновской
механики к отдельным молекулам, т.е.
использовав их на микроскопическом
уровне, мы ввели важное соотношение
между макроскопическими величинами p,
V и
T
(ср.
(8.19) с (8.7)).
Учитывая
равенство (8.19), уравнение состояния
идеального газа можно переписать в виде
, (8.20)
где
n
есть концентрация молекул.
Так
как для одноатомного газа средняя
кинетическая энергия совпадает со
средней энергией поступательного
движения
,
уравнение (8.20) представим как
. (8.21)
Произведение
дает суммарную энергию поступательного
движенияn
молекул. Таким образом, давление
равно двум третям энергии поступательного
движения молекул, содержащихся в единице
объема газа.
Соседние файлы в папке архив лекций(1 семестр)
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Давление газа
Содержание:
- Давление газа — что это за параметр
- Причина возникновения давления в газах
- Формула давления идеального газа из молекулярно-кинетической теории
- Второй способ записи основного уравнения МКТ
Давление газа — что это за параметр
Определение
Давление в физике представляет собой один из трех ключевых термодинамических макроскопических характеристик для измерения любой газовой системы.
Определение
Газ — это одно из четырех, включая плазму, агрегатных состояний материи, характеризующееся очень слабыми связями между составляющими его частицами, а также их большой подвижностью.
В газообразной среде частицы в определенной концентрации расположены не упорядоченно и перемещаются в хаотичном порядке в разных направлениях с одинаковой вероятностью. Подобное строение не позволяет газам сохранять стабильность объема и формы даже при малом внешнем силовом воздействии. Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Кроме того, расстояние, на которое удалены частицы, значительно превышает их собственные размеры. В том случае, когда молекулярными взаимодействиями и габаритами частиц допускается пренебрегать, газ считают идеальным. Для такой формы материи характерен только один тип внутреннего взаимодействия в виде упругих столкновений. Так как размер частиц пренебрежимо мал по сравнению с расстоянием, на которое они удалены, вероятность столкновений частиц между собой будет низкой.
Примечание
По этой причине в идеальной газовой среде можно наблюдать лишь столкновения частиц со стенками сосуда. Какой-либо реальный газ с хорошей точностью можно отнести к идеальному, когда их температура выше, чем комнатная, а давление несущественно больше, чем атмосферное.
Причина возникновения давления в газах
Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.
Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.
Примечание
Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична.
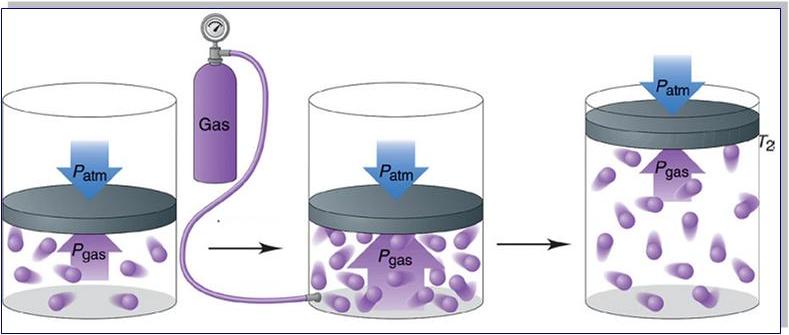
Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.
Свойства давления газа:
- Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
- Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
- В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.
Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:
(P=frac{F}{S})
Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия — это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:
(F*Δt = Δp)
Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.
Формула давления идеального газа из молекулярно-кинетической теории
Объяснение концепции идеального газа построено на основных положениях молекулярно-кинетической теории, которая вытекает из принципов статистической механики. Наука получила активное развитие во второй половине XIX, благодаря таким ученым, как Джеймс Максвелл и Людвиг Больцман. Основы дисциплины были заложены еще Бернулли в первой половине XVIII века.
Исходя из статистики Максвелла-Больцмана, все частицы в системе обладают разными скоростями движения. При этом можно наблюдать небольшой процент частиц со скоростями, приближенными к нулю, и малую долю частиц, обладающих огромной скоростью. Средняя квадратичная скорость в этом случае будет соответствовать некоторой величине, не изменяющейся с течением времени.
Средняя квадратичная скорость частиц однозначно характеризует температуру газа. Используя приближения молекулярно-кинетической теории в виде невзаимодействующих безразмерных и хаотично движущихся частиц, получают формулу для расчета давления газа в сосуде:
(P=frac{N*m*v^{2}}{3*V})
где N является количеством частиц в системе; V обозначает объем; v представляет собой среднюю квадратичную скорость; m является массой одной частицы.
При наличии указанных в формуле параметров, выраженных в единицах СИ, можно вычислить давление газа в сосуде.
Второй способ записи основного уравнения МКТ
Определение
В середине 30-х годов XIX столетия французскому инженеру Эмилю Клапейрону удалось обобщить накопленный до этого времени экспериментальный опыт изучения поведения газов во время разнообразных изопроцессов и получить формулу, которую в будущем назвали универсальным уравнением состояния идеального газа:
(P*V = n*R*T )
n является количеством вещества в молях; T представляет собой температуру по абсолютной шкале и обозначается в кельвинах.
Величина R является универсальной газовой постоянной. Этот термин был введен в уравнение русским химиком Д.И. Менделеевым. Исходя из этого, запись уравнения называют законом Клапейрона-Менделеева.
Определение
С помощью данного выражения можно определить формулу для расчета давления газа:
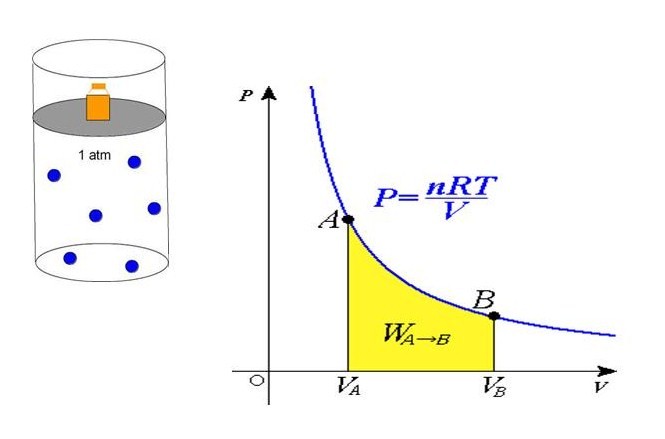
(P=frac{n*R*T}{V})
Полученное уравнение объясняет линейный рост давления при увеличении температуры в условиях стабильности объема. Если объем уменьшается с сохранением температуры, то давление увеличивается по гиперболе. Данные закономерности явления отражены в законах Гей-Люссака и Бойля-Мариотта.
Сравнивая представленное выражение с записью формулы, которая вытекает из положений молекулярно-кинетической теории, можно установить связь кинетической энергии одной частицы, либо системы в общем, и абсолютной температуры.
Важно отметить, что при расчетах с использованием формулы для Р, вытекающей из уравнения Клапейрона, связь с химическим составом газа отсутствует. Если давление определяют с помощью выражения, согласно понятию молекулярно-кинетической теории, то данную связь следует учитывать в виде параметра m. В том случае, когда определяют давление смеси идеальных газов, применяют один из следующих методов:
- Расчет средней массы частиц m, либо среднего значения молярной массы М с учетом атомных процентов каждого газа в смеси.
- Применение закона Дальтона, согласно которому давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример
Предположим, что молекулы кислорода движутся со средней скоростью в 500 м/с. Требуется рассчитать, каково давление в сосуде, объем которого равен 10 литров, содержащий 2 моль молекул.
Для того чтобы найти ответ, следует применить формулу для Р из молекулярно-кинетической теории:
(P=frac{N*m*v^{2}}{3*V})
Из-за неизвестных параметров m и N требуется выполнить некоторые преобразования формулы:
(m=frac{M}{NA})
(n=frac{N}{NA})
(m*N= M*n)
(P=frac{M*n*v^{2}}{3*V})
Таким образом, удельный объем сосуда в кубических метрах равен 0,01. Молярная масса молекулы кислорода М составляет 0,032 кг/моль. Данные параметры можно подставить в уравнение вместе со скоростью и количеством вещества. Тогда Р = 533333 Па, что представляет собой давление в 5,3 атмосферы.
Содержание:
- § 1 Особенности давления в жидкости и газе
- § 2 Формула для вычисления давления в жидкостях и газах
- § 3 Решение задачи по теме урока
- § 4 Краткие итоги по теме урока
§ 1 Особенности давления в жидкости и газе
Известно, что давление, производимое на жидкости и газы, передается в каждую точку без изменения по всем направлениям. Это утверждение называется законом Паскаля.
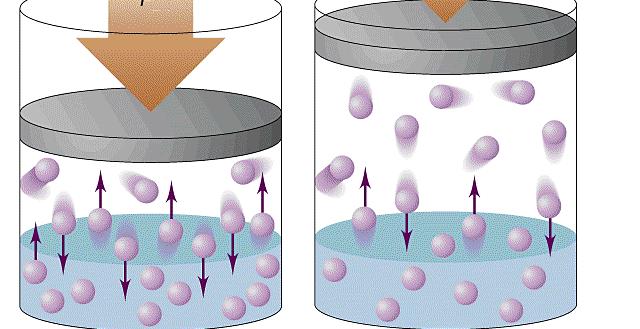
На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому верхние слои жидкости давят на нижележащие слои, это давление по закону Паскаля передается по всем направлениям. Значит, внутри жидкости существует давление. Чтобы убедиться в этом, поставим опыт.
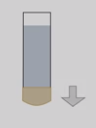
Возьмем стеклянную трубочку, затянутую снизу резиновой пленкой. Если в трубочку нальем воду, то увидим, что резиновая пленка прогибается. На резиновую пленку действуют две силы: вес воды, направленный вниз, из-за чего пленка изменяет свою форму, и возникающая при деформации сила упругости, которая стремится восстановить первоначальную форму и направленная вверх. Если две эти силы равны, то пленка будет находиться в покое.
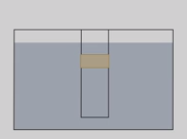
Опустим трубку с водой в другой, более широкий, сосуд с водой. Возникает третья сила, действующая на резиновую пленку, – сила давления воды снизу, она направлена вверх и заставляет пленку выпрямляться. Если уровни воды в трубке и в сосуде совпадут, то силы давления, действующие сверху и снизу на пленку, окажутся равными.
Такой же опыт проведем с трубкой, в которой есть боковое отверстие, затянутое резиновой пленкой. Если в трубку налить воду, то пленка выгибается наружу, так как вода давит не только на дно трубки, но и на стенки. Опустим трубку в воду и заметим, что пленка выпрямляется, то есть силы, действующие на пленку изнутри и снаружи, оказались равными.
Итак, опыты показывают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям.
Такое же утверждение справедливо и для газов.
§ 2 Формула для вычисления давления в жидкостях и газах
От чего зависит давление в жидкостях и газах?
Вспомним определение давления.
Давление – скалярная физическая величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: p = F/S.
Сила давления Fравна весу P: P = mg.
Мы знаем, что массу тела можно найти по плотности вещества: m = ρV, где ρ – плотность, V – объем.
Объем жидкости, находящейся в сосуде в форме прямоугольного параллелепипеда или в форме цилиндра, можно найти, умножив площадь дна на высоту сосуда: V = Sh. Подставим формулы веса, массы, объема в формулу давления и, сократив площадь, получим:
Мы вывели формулу для вычисления давления в жидкостях и газах:
p = gρh.
Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.
По формуле p = gρhможно рассчитывать:
1)давление жидкости на дно в сосуде любой формы, то есть давление жидкости не зависит от формы сосуда;
2)давление жидкости на стенки сосуда, так как давление на одной и той же глубине одинаково по всем направлениям: вверх, вниз, вправо, влево, вперед, назад;
3)давление в газах.
Проверим единицу измерения давления по формуле p = gρh.
g – коэффициент тяжести, измеряется в Н/кг,
ρ – плотность, в международной системе единиц измеряется в кг/м3,
h – высота столба жидкости (глубина) – в м.
§ 3 Решение задачи по теме урока
Рассмотрим решение задачи:
Задача:Определить давление воды на дно морской впадины, глубина которой 10900 м. Плотность морской воды – 1030 кг/м3.
Решение: Запишем условие задачи: нам известны глубина h = 10900 м, плотность ρ = 1030 кг/м3. Необходимо найти: давление p. Для решения: запишем формулу расчета давления в жидкостях и газах p = gρh и подставим числовые значения:
p = 10 Н/кг · 1030 кг/м3· 10 900 м = 112 270 000 Па = 112, 27 МПа.
Ответ: 112, 27 МПа
§ 4 Краткие итоги по теме урока
ВАЖНО ЗАПОМНИТЬ:
На жидкости и газы действует сила тяжести, поэтому они обладают весом. Вышележащие слои жидкости и газа своим весом давят на нижележащие слои, то есть оказывают давление. Давление внутри жидкости и газа на одном и том же уровнеодинаково по всем направлениям.
Давление в жидкостях и газах рассчитывается по формуле p = gρh, где g – коэффициент тяжести, ρ – плотность, h – высота столба жидкости или газа.
Давление в жидкостях и газах зависит только от плотности и высоты столба жидкости или газа и не зависит от формы и площади поперечного сечения сосуда, в котором находится жидкость или газ.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября”, 2002. – 272 с.
Содержание:
Идеальный газ:
Наиболее простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ начинают с газов. Газ (греч. chaos — хаос) — такое агрегатное состояние вещества, когда составляющие его частицы почти свободно и хаотически движутся между соударениями, во время которых происходит резкое изменение их скорости. Термин «газ» предложил в начале XVII в. нидерландский химик Ян Батист ван Гельмонт (1579— 1644).
Макро- и микропараметры:
При изучении механики в 9-м классе вы познакомились с понятием «состояние механической системы тел». Параметрами этого состояния являются координаты, скорости или импульсы тел. В тепловых процессах основными физическими величинами, характеризующими состояние макроскопических тел без учёта их молекулярного строения, являются давление
Одна из важнейших задач молекулярно-кпнетической теории состоит в установлении связи между макроскопическими и микроскопическими параметрами.
Идеальный газ
Для теоретического объяснения свойств газов используют их упрощённую модель — идеальный газ.
Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия их взаимодействия равна нулю); силы действуют только во время столкновений молекул, причём это силы отталкивания.
Поведение молекул идеального газа можно описать, используя законы Ньютона и учитывая, что между соударениями молекулы движутся практически равномерно и прямолинейно.
Модель идеального газа можно использовать в ограниченном диапазоне температур и при достаточно малых давлениях. Так, например, свойства водорода и гелия при нормальном атмосферном давлении и комнатной температуре близки к свойствам идеального газа.
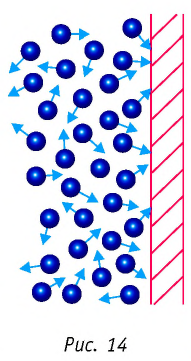
Изучая физику в 7-м классе, вы узнали, что давление газа на стенки сосуда, в котором он находится, как и на любое тело, помещённое внутрь сосуда, создаётся в результате ударов частиц, образующих газ (рис. 14). Вследствие хаотичности их движения усреднённое по времени давление газа в любой части сосуда одинаково, и его можно определить по формуле
Выражение (3.1) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр давление р идеального газа через массу 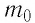
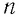
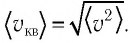
Зависимость давления газа от среднего значения квадрата скорости 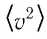
Обозначим через 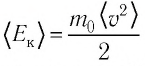
Из выражения (3.2) следует, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации.
Пример №1
Баллон электрической лампы наполнен газом, плотность которого 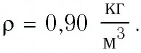
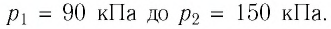
Решение. Покажем, что между плотностью р газа и концентрацией 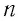
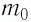
Тогда основное уравнение молекулярно-кинетической теории можно записать в виде: 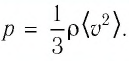
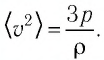
Ответ:
Пример №2
В сосуде вместимостью 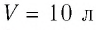
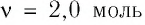
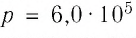
Решение. Из основного уравнения молекулярно-кинетической теории, записанного в виде 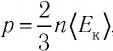
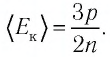
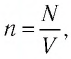
Ответ:
Уравнение состояния идеального газа
Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.
Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление р, масса 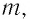
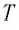
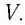
Если при переходе идеального газа из одного состояния в другое число его т
молекул 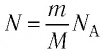
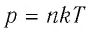
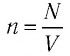
где 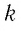
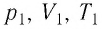
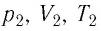
или
При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.
Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.
Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799—1864), поэтому его называют уравнением Клапейрона.
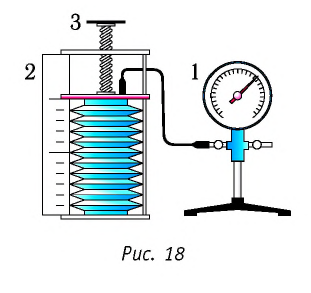
В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.
Измерив параметры газа 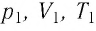
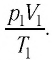
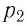
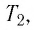
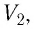
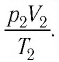
Уравнение состояния (5.2) можно применять для газов при следующих условиях:
- не очень большие давления (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с предоставленным ему объёмом);
- не слишком низкие или же высокие температуры (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).
Поскольку число частиц 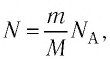
Величину, равную произведению постоянной Больцмана 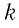
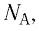
С учётом выражения (5.4) уравнение (5.3) примет вид:
Поскольку количество вещества 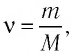
Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834—1907) в 1874 г., поэтому его называют уравнением Клапейрона—Менделеева.
Отметим, что уравнение Клапейрона—Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона-Менделеева, можно описать различные процессы, происходящие в идеальном газе.
Давление смеси газов
В повседневной жизни часто приходится иметь дело не с газом, состоящим из одинаковых молекул, а со смесью нескольких разнородных газов, не вступающих в химические реакции при рассматриваемых условиях. Например, воздух в комнате является смесью азота, кислорода, инертных газов и водорода, а также некоторых других газов.
Вследствие теплового движения частиц каждого газа, входящего в состав газовой смеси, они равномерно распределяются по всему предоставленному смеси объёму. Столкновения частиц обеспечивают в смеси тепловое равновесие.
Каждый газ вносит свой вклад в суммарное давление, производимое газовой смесью, создавая давление, называемое парциальным.
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Смесь идеальных газов принимают за идеальный газ.
Из истории физики:
Фундаментальные исследования газовых смесей провёл английский учёный Джон Дальтон (1766-1844). Им сформулирован закон независимости парциальных давлений компонентов смеси (1801-1802). В 1802 г. на несколько месяцев раньше французского учёного Жозефа Гей-Люссака (1778-1850) Дальтон установил закон теплового расширения газов, а также ввёл понятие атомного веса.
При постоянных массе и молярной массе отношение произведения давления идеального газа и его объёма к абсолютной температуре является величиной постоянной (уравнение состояния идеального газа):
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Пример №3
Баллон с газом, давление которого 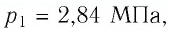
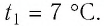
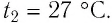
Решение. Если пренебречь тепловым расширением баллона, то его вместимость не изменяется. Запишем уравнение Клапейрона—Менделеева для начального и конечного состоянии газа, считая его идеальным:
откуда
Тогда
Ответ:
Основное уравнение молекулярно-кинетической теории идеального газа
В молекулярной физике изучаются свойства вещества во всех агрегатных состояниях, в том числе и газообразном. В природе почти нет отдельно взятого газа, реальный газ атмосферы представляют собой сложную систему разных газов.
Основная задача молекулярно-кинетической теории – установление связи между макроскопическими и микроскопическими параметрами, характеризующими свойства этой сложной системы. С этой целью реальный газ сложного состава заменяется упрощенной, идеализированной моделью.
Идеальный газ:
Первый шаг в создании любой физической теории состоит в построении идеализированной модели реального объекта. Такая модель всегда имеет упрощенный вид действительности, и с ее помощью изучаются количественные и качественные закономерности и свойства реального объекта с учетом определенных ограничений.
Для изучения свойств газов в молекулярно-кинетической теории применяется идеализированная модель – “идеальный газ”.
Идеальный газ – это газ, удовлетворяющий следующим условиям:
- — линейные размеры молекул во много раз меньше расстояний между ними и не принимаются во внимание. Поэтому можно сказать, что молекулы идеального газа не взаимодействуют друг с другом, то есть потенциальная энергия взаимодействия молекул идеального газа равна нулю:
Поэтому идеальный газ можно сколько угодно сжимать; —только при соударении молекул друг с другом или со стенками сосуда между ними возникают силы отталкивания;
- — соударения молекул абсолютно упругие;
- — скорость молекул может иметь произвольные значения, движение каждой молекулы подчиняется законам классической механики.
Свойства идеального газа характеризуются микроскопическими и макроскопическими параметрами и связями между ними.
Микроскопические параметры газа – это параметры, характеризующие движение молекул газа. К ним относятся масса молекулы, его скорость, импульс и кинетическая энергия поступательного движения молекулы.
Макроскопическими являются такие параметры газа, как ее давление, объем и температура, определяющие свойства газа в целом.
Основной задачей молекулярно-кинетической теории является установление взаимной связи между микроскопическими параметрами, характеризующими молекулы газа, и макроскопическими (измеряемыми) величинами, характеризующими газ.
Основное уравнение молекулярно-кинетической теории идеального газа:
Известно, что давление газа возникает в результате многочисленных непрерывных и беспорядочных соударений молекул газа о стенки сосуда, в котором он находится. Это давление равно среднему значению модуля равнодействующей силы, приходящейся на единицу площади:
В 1857 г. немецкий физик Рудольф Клаузиус (1822-1888), используя модель идеального газа, определил уравнение для давления газа, называемое основным уравнением молекулярно-кинетической теории идеального газа.
Основное уравнение молекулярно-кинетической теории идеального газа — это уравнение, связывающее макроскопический параметр газа – его давление, с микроскопическими параметрами, характеризующими молекулы газа:
Где 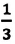
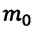
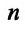
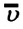
Концентрация молекул — это число молекул в единице объема:
Единица концентрации в СИ:
Средняя квадратичная скорость молекул равна корню квадратному из средней арифметической величины квадратов скоростей отдельных молекул:
Так как среднее значение квадрата скорости молекул связано со средним значением кинетической энергии их поступательного движения, то, следовательно, и давление идеального газа зависит от среднего значения кинетической энергии молекул:
Давление идеального газа прямо пропорционально концентрации молекул и среднему значению кинетической энергии молекул.
Если принять во внимание, что плотность газа 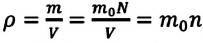
Вы исследовали идеальный газ с позиций MKT и определили связь между его макроскопическими и микроскопическими параметрами.
Уравнение Клапейрона
Связь между тремя макроскопическими параметрами (давление, объем и температура), характеризующими состояние идеального газа, определяет уравнение состояние идеального газа.
Уравнение состояния идеального газа – это уравнение, описывающее состояние газа и устанавливающее связь между параметрами его начального и конечного состояний.
Если число молекул идеального газа остается постоянным, то есть масса и молярная масса не меняются, то при переходе идеального газа из одного состояния в другое, из формул (6.2) и (6.9) имеем для этих состояний:
Где 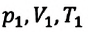
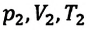
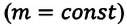
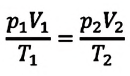
Это уравнение (6.15), характеризующее состояние идеального газа, впервые в 1834 году получил французский физик Бенуа Клапейрон (1799-1864), поэтому его назвали уравнением Клапейрона.
Отношение произведения давления идеального газа данной массы на его объем к абсолютной температуре является постоянной величиной.
Уравнение Менделеева-Клапейрона:
Приняв во внимание формулу, связывающую число частичек вещества, общую массу вещества, молярную массу и число Авогадро,
в формуле (6.14), получим:
Произведение постоянной Больцмана на постоянную Авогадро также является постоянной величиной. Оно называется универсальной газовой постоянной, обозначается буквой 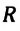
Приняв во внимание выражение (6.17) в (6.16), получаем выражение, характеризующее состояние идеального газа и называемое уравнением Менделеева-Клапейрона.
Физический смысл универсальной газовой постоянной определяется из последнего выражения.
Универсальная газовая постоянная равна отношению произведения давления и объема к абсолютной температуре одного моля любого газа.
Уравнение Менделеева-Клапейрона можно записать и в таком виде:
Где 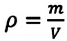
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа
- Температура в физике
- Парообразование и конденсация
- Зависимость веса тела от вида движения
- Движение тел под воздействием нескольких сил
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния
В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.