Формулы для определения давления газа применимы только для так называемого идеального газа. Это такой газ, когда пренебрегается взаимодействием между молекулами. Для этого газ должен быть достаточно разряженным. Газ с хорошей точностью можно считать идеальным вплоть до давлений 20 – 30 атмосфер. Так что атмосферу Земли можно считать идеальной даже у самой поверхности Земли. Давление газа на какую-либо поверхность определяется ударами молекул об эту поверхность. Естественно, что тогда давление газа должно зависеть от скоростей движения молекул. Вот формула для определения давления газа р
p = (Nmv^2)/3V (1)
Естественно, что давление зависит от числа молекул N, от массы молекулы m, от средней скорости движения молекул v и от объема сосуда V, где находятся молекулы. Средняя кинетическая энергия молекулы равна Е = mv^2/2. Тогда получим следующую формулу для расчета давления газа через среднюю энергию молекул
р = 2NЕ/3V (2)
Больцман рассчитал, что средняя кинетическая энергия молекул пропорциональна абсолютной температуре Т. Е = (3/2)kT, где k – постоянная Больцмана и T – абсолютная температура. Тогда получим для давления идеального газа формулу р = (NkT)/V. Перепишем эту формулу в следующем виде
рV = NkT (3)
Концентрация молекул в газе равна n = N/V. Тогда формула (3) примет такой вид
pV = NkT (4)
Концентрацию молекул можно выразить через произведение числа молей ν на число частиц в моле N = νNa. Произведение Na*k = R. Где R – газовая постоянная. Тогда (4) запишется в виде
pV = νRT (5)
Число молей газа ν = M/μ, где М – масса газа и μ – масса одного моля (молярная масса). Тогда уравнение (5) примет вид
pV = (M/μ)RT (6)
Уравнение состояния идеального газа в таком виде называют уравнением Клапейрона – Менделеева. При постоянных температуре и массе из (6) следует, что
pV = const (7)
То есть давление будет обратно пропорционально объему газа. Такой закон получил название закона Бойля – Мариотта. Если же постоянным является давление, то
V = (MR/Vμ)T (8)
Давление пропорционально абсолютной температуре. Этот закон получил название закон Шарля.
Вот и используйте любую из этих формул для расчета давления газа.
Уравне́ние состоя́ния идеа́льного га́за (иногда уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
,
где
Уравнение состояния идеального газа можно записать в виде:
,
где 


или в виде
,
где 


Эта форма записи носит имя уравнения (закона) Клапейрона — Менделеева.
Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную 
Менделеев обнаружил, что 


Связь с другими законами состояния идеального газа[править | править код]
В случае постоянной массы газа уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
— закон Бойля — Мариотта — Изотермический процесс.
— Закон Гей-Люссака — Изобарный процесс.
— закон Шарля (второй закон Гей-Люссака, 1808 г.) — Изохорный процесс
В форме пропорции 
С точки зрения химика этот закон может звучать несколько иначе: объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
.
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
.
- Закон Бойля — Мариотта
Закон Бойля — Мариотта
назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
где 

Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. Это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение 

См. также[править | править код]
- Совершенный газ
- Реальный газ
- Уравнение состояния реального газа
Примечания[править | править код]
Литература[править | править код]
- Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высшая школа, 2009. — 527 с. — ISBN 978-5-06-006161-1.
Содержание:
- § 1 Особенности давления в жидкости и газе
- § 2 Формула для вычисления давления в жидкостях и газах
- § 3 Решение задачи по теме урока
- § 4 Краткие итоги по теме урока
§ 1 Особенности давления в жидкости и газе
Известно, что давление, производимое на жидкости и газы, передается в каждую точку без изменения по всем направлениям. Это утверждение называется законом Паскаля.
На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому верхние слои жидкости давят на нижележащие слои, это давление по закону Паскаля передается по всем направлениям. Значит, внутри жидкости существует давление. Чтобы убедиться в этом, поставим опыт.
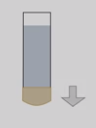
Возьмем стеклянную трубочку, затянутую снизу резиновой пленкой. Если в трубочку нальем воду, то увидим, что резиновая пленка прогибается. На резиновую пленку действуют две силы: вес воды, направленный вниз, из-за чего пленка изменяет свою форму, и возникающая при деформации сила упругости, которая стремится восстановить первоначальную форму и направленная вверх. Если две эти силы равны, то пленка будет находиться в покое.
Опустим трубку с водой в другой, более широкий, сосуд с водой. Возникает третья сила, действующая на резиновую пленку, – сила давления воды снизу, она направлена вверх и заставляет пленку выпрямляться. Если уровни воды в трубке и в сосуде совпадут, то силы давления, действующие сверху и снизу на пленку, окажутся равными.
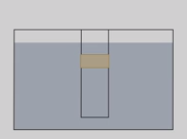
Такой же опыт проведем с трубкой, в которой есть боковое отверстие, затянутое резиновой пленкой. Если в трубку налить воду, то пленка выгибается наружу, так как вода давит не только на дно трубки, но и на стенки. Опустим трубку в воду и заметим, что пленка выпрямляется, то есть силы, действующие на пленку изнутри и снаружи, оказались равными.
Итак, опыты показывают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям.
Такое же утверждение справедливо и для газов.
§ 2 Формула для вычисления давления в жидкостях и газах
От чего зависит давление в жидкостях и газах?
Вспомним определение давления.
Давление – скалярная физическая величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: p = F/S.
Сила давления Fравна весу P: P = mg.
Мы знаем, что массу тела можно найти по плотности вещества: m = ρV, где ρ – плотность, V – объем.
Объем жидкости, находящейся в сосуде в форме прямоугольного параллелепипеда или в форме цилиндра, можно найти, умножив площадь дна на высоту сосуда: V = Sh. Подставим формулы веса, массы, объема в формулу давления и, сократив площадь, получим:
![]()
Мы вывели формулу для вычисления давления в жидкостях и газах:
p = gρh.
Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.
По формуле p = gρhможно рассчитывать:
1)давление жидкости на дно в сосуде любой формы, то есть давление жидкости не зависит от формы сосуда;
2)давление жидкости на стенки сосуда, так как давление на одной и той же глубине одинаково по всем направлениям: вверх, вниз, вправо, влево, вперед, назад;
3)давление в газах.
Проверим единицу измерения давления по формуле p = gρh.
g – коэффициент тяжести, измеряется в Н/кг,
ρ – плотность, в международной системе единиц измеряется в кг/м3,
h – высота столба жидкости (глубина) – в м.
![]()
§ 3 Решение задачи по теме урока
Рассмотрим решение задачи:
Задача:Определить давление воды на дно морской впадины, глубина которой 10900 м. Плотность морской воды – 1030 кг/м3.
Решение: Запишем условие задачи: нам известны глубина h = 10900 м, плотность ρ = 1030 кг/м3. Необходимо найти: давление p. Для решения: запишем формулу расчета давления в жидкостях и газах p = gρh и подставим числовые значения:
p = 10 Н/кг · 1030 кг/м3· 10 900 м = 112 270 000 Па = 112, 27 МПа.

Ответ: 112, 27 МПа
§ 4 Краткие итоги по теме урока
ВАЖНО ЗАПОМНИТЬ:
На жидкости и газы действует сила тяжести, поэтому они обладают весом. Вышележащие слои жидкости и газа своим весом давят на нижележащие слои, то есть оказывают давление. Давление внутри жидкости и газа на одном и том же уровнеодинаково по всем направлениям.
Давление в жидкостях и газах рассчитывается по формуле p = gρh, где g – коэффициент тяжести, ρ – плотность, h – высота столба жидкости или газа.
Давление в жидкостях и газах зависит только от плотности и высоты столба жидкости или газа и не зависит от формы и площади поперечного сечения сосуда, в котором находится жидкость или газ.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября”, 2002. – 272 с.
Давление газа
Содержание:
- Давление газа — что это за параметр
- Причина возникновения давления в газах
- Формула давления идеального газа из молекулярно-кинетической теории
- Второй способ записи основного уравнения МКТ
Давление газа — что это за параметр
Определение
Давление в физике представляет собой один из трех ключевых термодинамических макроскопических характеристик для измерения любой газовой системы.
Определение
Газ — это одно из четырех, включая плазму, агрегатных состояний материи, характеризующееся очень слабыми связями между составляющими его частицами, а также их большой подвижностью.
В газообразной среде частицы в определенной концентрации расположены не упорядоченно и перемещаются в хаотичном порядке в разных направлениях с одинаковой вероятностью. Подобное строение не позволяет газам сохранять стабильность объема и формы даже при малом внешнем силовом воздействии. Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Кроме того, расстояние, на которое удалены частицы, значительно превышает их собственные размеры. В том случае, когда молекулярными взаимодействиями и габаритами частиц допускается пренебрегать, газ считают идеальным. Для такой формы материи характерен только один тип внутреннего взаимодействия в виде упругих столкновений. Так как размер частиц пренебрежимо мал по сравнению с расстоянием, на которое они удалены, вероятность столкновений частиц между собой будет низкой.
Примечание
По этой причине в идеальной газовой среде можно наблюдать лишь столкновения частиц со стенками сосуда. Какой-либо реальный газ с хорошей точностью можно отнести к идеальному, когда их температура выше, чем комнатная, а давление несущественно больше, чем атмосферное.
Причина возникновения давления в газах
Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.
Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.
Примечание
Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична.
Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.
Свойства давления газа:
- Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
- Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
- В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.
Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:
(P=frac{F}{S})
Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия — это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:
(F*Δt = Δp)
Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.
Формула давления идеального газа из молекулярно-кинетической теории
Объяснение концепции идеального газа построено на основных положениях молекулярно-кинетической теории, которая вытекает из принципов статистической механики. Наука получила активное развитие во второй половине XIX, благодаря таким ученым, как Джеймс Максвелл и Людвиг Больцман. Основы дисциплины были заложены еще Бернулли в первой половине XVIII века.
Исходя из статистики Максвелла-Больцмана, все частицы в системе обладают разными скоростями движения. При этом можно наблюдать небольшой процент частиц со скоростями, приближенными к нулю, и малую долю частиц, обладающих огромной скоростью. Средняя квадратичная скорость в этом случае будет соответствовать некоторой величине, не изменяющейся с течением времени.
Средняя квадратичная скорость частиц однозначно характеризует температуру газа. Используя приближения молекулярно-кинетической теории в виде невзаимодействующих безразмерных и хаотично движущихся частиц, получают формулу для расчета давления газа в сосуде:
(P=frac{N*m*v^{2}}{3*V})
где N является количеством частиц в системе; V обозначает объем; v представляет собой среднюю квадратичную скорость; m является массой одной частицы.
При наличии указанных в формуле параметров, выраженных в единицах СИ, можно вычислить давление газа в сосуде.
Второй способ записи основного уравнения МКТ
Определение
В середине 30-х годов XIX столетия французскому инженеру Эмилю Клапейрону удалось обобщить накопленный до этого времени экспериментальный опыт изучения поведения газов во время разнообразных изопроцессов и получить формулу, которую в будущем назвали универсальным уравнением состояния идеального газа:
(P*V = n*R*T )
n является количеством вещества в молях; T представляет собой температуру по абсолютной шкале и обозначается в кельвинах.
Величина R является универсальной газовой постоянной. Этот термин был введен в уравнение русским химиком Д.И. Менделеевым. Исходя из этого, запись уравнения называют законом Клапейрона-Менделеева.
Определение
С помощью данного выражения можно определить формулу для расчета давления газа:
(P=frac{n*R*T}{V})
Полученное уравнение объясняет линейный рост давления при увеличении температуры в условиях стабильности объема. Если объем уменьшается с сохранением температуры, то давление увеличивается по гиперболе. Данные закономерности явления отражены в законах Гей-Люссака и Бойля-Мариотта.
Сравнивая представленное выражение с записью формулы, которая вытекает из положений молекулярно-кинетической теории, можно установить связь кинетической энергии одной частицы, либо системы в общем, и абсолютной температуры.
Важно отметить, что при расчетах с использованием формулы для Р, вытекающей из уравнения Клапейрона, связь с химическим составом газа отсутствует. Если давление определяют с помощью выражения, согласно понятию молекулярно-кинетической теории, то данную связь следует учитывать в виде параметра m. В том случае, когда определяют давление смеси идеальных газов, применяют один из следующих методов:
- Расчет средней массы частиц m, либо среднего значения молярной массы М с учетом атомных процентов каждого газа в смеси.
- Применение закона Дальтона, согласно которому давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример
Предположим, что молекулы кислорода движутся со средней скоростью в 500 м/с. Требуется рассчитать, каково давление в сосуде, объем которого равен 10 литров, содержащий 2 моль молекул.
Для того чтобы найти ответ, следует применить формулу для Р из молекулярно-кинетической теории:
(P=frac{N*m*v^{2}}{3*V})
Из-за неизвестных параметров m и N требуется выполнить некоторые преобразования формулы:
(m=frac{M}{NA})
(n=frac{N}{NA})
(m*N= M*n)
(P=frac{M*n*v^{2}}{3*V})
Таким образом, удельный объем сосуда в кубических метрах равен 0,01. Молярная масса молекулы кислорода М составляет 0,032 кг/моль. Данные параметры можно подставить в уравнение вместе со скоростью и количеством вещества. Тогда Р = 533333 Па, что представляет собой давление в 5,3 атмосферы.
- Идеальный газ:
- — теоретическая модель, широко применяемая для описания свойств и поведения реальных газов при умеренных давлениях и температурах;
- — газ, взаимодействие между молекулами которого пренебрежимо мало;
- — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией.
Общие сведения
В модели идеального газа:
-
- предполагается, что составляющие газ частицы не взаимодействуют друг с другом, то есть их размеры пренебрежимо малы, поэтому в объёме, занятом идеальным газом, нет взаимных столкновений частиц. Частицы идеального газа претерпевают столкновения только со стенками сосуда;
- между частицами газа нет дальнодействующего взаимодействия, например, электростатического или гравитационного;
- упругих столкновений между молекулами и стенками сосуда в рамках молекулярно-кинетической теории приводит к термодинамике идеального газа.
Модель идеального газа имеет широкое применения в ряде задач, например в инженерных расчетах (аэродинамический, гидравлический, теплотехнический и т.д.), связанные с воздухом и другими газами, при давлении и температуре близких к нормальным (стандартным) условиям.
При условиях сильно отличных от нормальных (стандартных) условий модель идеального газа дает результаты с погрешностью так, как модель не учитывает:
-
- притяжение между молекулами;
- конечные размеры молекул.
При высоких давления газа следует использовать различные варианты уравнений реальных газов, разработанных на базе модели идеального газа. Наиболее из известных уравнений реального газа — полуэмпирическое уравнение Ван-дер-Ваальса.
Основные уравнения состояние идеального газа
Уравнения состояния идеального газа служат для получения неизвестных параметров идеального газа или газов схожих по свойствам с моделью идеального газа.
В данном разделе будут рассмотрены варианты уравнение состояния идеального газа на основе уравнения Менделеева — Клапейрона (или уравнение Клапейрона).
P⋅VM=R⋅T или P⋅V=(m/M)⋅R⋅T
Эти уравнение имеет наибольшее практическое значение при инженерных расчетах. Но так же существуют другие варианты записи уравнения состояния идеального газа.
Основными параметрами идеального газа служат:
-
- давление идеального газа (Р), Па;
- температура идеального газа (T), °К;
- объем идеального газа (V), м3;
- молярная масса идеального газа (M), кг/моль;
- количества идеального газа (n), моль;
- масса идеального газа (m), кг;
- молярный объем (VM), м3/моль;
Другие физические величины используемые в уравнении состояния идеального газа:
-
- плотность идеального газа (ρ), кг/м3.
Калькуляторы параметров идеального газа
Калькулятор молярного объема идеального газа
Согласно закону Авогадро, одинаковые количества газов при одинаковых условиях занимают одинаковый объём. Молярный объём идеального газа рассчитается по формуле:
VM=(R⋅T)/P
Введите универсальную газовую постоянную (Run0)
Введите температуру газа (T0)
Введите давление газа (абсолютного) (PA0)
Результат расчета молярного объема газа (Vm0)
Формула расчета молярного объема газа:
Скачать результат расчета молярного объема газа:

Поделится ссылкой на расчет молярного объема:
Если по калькулятору, приведенному выше, посчитать молярный объем газа при нормальных условиях:
-
- давление Р=101325 Па;
- температура Т=273,15 ºК.
В результате получится молярный объем идеального газа при нормальных условиях равный 22,413971 литр/моль (частный случай закона Авогадро).
Молярные объёмы реальных газов и идеального газа для практических вычислений имеют не значительные отклонения и принимаются равными .
Калькулятор давления идеального газа
При решении инженерных задач часто необходимо определять давление газа в технических устройствах, для решения задачи по организации технологии, для выполнения расчета на прочность технических устройств или просто для выполнения гидравлических (аэродинамических расчетов).
Расчет давления газа, если известны:
-
- масса газа;
- объем занимаемый газом (внутри сосуда, трубопровода или другого устройства);
- молярная масса газа;
- температура газа,
выполняется по формуле:
P=(m⋅R⋅T)/(M⋅V)
Введите универсальную газовую постоянную (Run2)
Введите температуру газа (T2)
Введите молярную массу газа (Mg2)
Результат расчета давления газа (абсолютного) (PA2)
Формула расчета давления газа (абсолютного):
Скачать результат расчета давления газа (абсолютного):

Поделится ссылкой на расчет давления:
Калькулятор температуры идеального газа
Температуру газа необходимо обычно рассчитывать для:
-
- возможности принятия технологических решения;
- возможности проведения расчета на прочность технологического оборудования;
- расчета теплоизоляции оборудования и защиты персонала от повышенной или пониженной температуры.
Расчет температуры газа, если известны:
-
- масса газа;
- объем занимаемый газом (внутри сосуда, трубопровода или другого устройства);
- молярная масса газа;
- абсолютное давление газа.
выполняется по формуле:
T=(P⋅M⋅V)/(m⋅R)
Введите давление газа (абсолютное) (PA3)
Введите молярную массу газа (Mg3)
Введите универсальную газовую постоянную (Run3)
Результат расчета температуры газа (T3)
Формула расчета температуры газа:
Скачать результат расчета температуры газа:

Поделится ссылкой на расчет температуры:
Калькулятор объема идеального газа
Расчет объем занимаемый газом (внутри сосуда, трубопровода или другого устройства), если известны:
-
- масса газа;
- давление газа;
- молярная масса газа;
- температура газа,
выполняется по формуле:
V=(m⋅R⋅T)/(M⋅P)
На основе этого уравнения, так же находят объемный расход газа при различных условиях.
Введите универсальную газовую постоянную (Run4)
Введите температуру газа (T4)
Введите молярную массу газа (Mg4)
Введите давление газа (абсолютного) (PA4)
Результат расчета объема газа (V4)
Формула расчета объема газа:
Скачать результат расчета объема газа:

Поделится ссылкой на расчет объема:
Калькулятор массы идеального газа
Масса газа рассчитывают для:
-
- решения технологических задач;
- возможности проведения расчета на прочность технологического оборудования и трубопроводов (сбор нагрузок);
- на опасных производственных объектах с опасными веществами для расчета массы опасных веществ для возможности идентификации производственного объекта, как ОПО.
Расчет массы газа, если известны:
-
- абсолютное давление газа;
- молярная масса газа;
- объем занимаемый газом (внутри сосуда, трубопровода или другого устройства);
- температура газа,
выполняется по формуле:
m=(P⋅M⋅V)/(T⋅R)
Введите давление газа (абсолютное) (PA5)
Введите молярную массу газа (Mg5)
Введите температуру газа (T5)
Введите универсальную газовую постоянную (Run5)
Результат расчета массы газа (m5)
Формула расчета массы газа:
Скачать результат расчета массы газа:

Поделится ссылкой на расчет массы:
Калькулятор плотности идеального газа
Расчет плотности газа, если известны:
-
- абсолютное давление газа;
- молярная масса газа;
- температура газа,
выполняется по формуле:
ρ=(P⋅M)/(T⋅R)
Введите давление газа (абсолютное) (PA6)
Введите молярную массу газа (Mg6)
Введите температуру газа (T6)
Введите универсальную газовую постоянную (Run6)
Результат расчета плотности газа (pl6)
Формула расчета плотности газа:
Скачать результат расчета плотности газа:

Поделится ссылкой на расчет плотности :
Калькулятор параметров идеального газа системы исходя из разных состояний системы
Выполняется по формуле:
P1⋅V1/T1=P2⋅V2/T2=P3⋅V3/T3=…=const
Рассмотрим изменение параметров системы по двумя состояниям:
P1⋅V1/T1=P2⋅V2/T2
Калькулятор давления идеального газа
P1=(P2⋅V2⋅T1)/(T2⋅V1)
Введите давление газа (абсолютное) (Pg2)
Введите температуру газа (Tg1)
Введите температуру газа (Tg2)
Результат расчета давления газа (абсолютного) (Pg1)
Формула расчета давления газа (абсолютного):
Скачать результат расчета давления газа (абсолютного):

Поделится ссылкой на расчет давления:
Калькулятор температуры идеального газа
T3=(P3⋅V3⋅T4)/(P4⋅V4)
Введите давление газа (абсолютное) (Pg3)
Введите температуру газа (Tg4)
Введите температуру газа (абсолютное) (Pg4)
Результат расчета температуры газа (Tg3)
Формула расчета температуры газа:
Скачать результат расчета температуры газа:

Поделится ссылкой на расчет температуры:
Калькулятор объема идеального газа
V5=(P6⋅V6⋅T5)/(P5⋅T6)
Введите давление газа (абсолютное) (Pg6)
Введите температуру газа (Tg5)
Введите давление газа (абсолютное) (Pg5)
Введите температуру газа (Tg6)
Результат расчета объема газа (Vg5)
Формула расчета объема газа:
Скачать результат расчета объема газа:

Поделится ссылкой на расчет объема:




