Как найти давление газа по уравнению менделеева

Уравне́ние состоя́ния идеа́льного га́за (иногда уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

,

где

Уравнение состояния идеального газа можно записать в виде:

,

где  — масса,  — молярная масса, (так как количество вещества ):

или в виде

,

где  — концентрация частиц (атомов или молекул) – количество частиц,  — постоянная Больцмана.

Эта форма записи носит имя уравнения (закона) Клапейрона — Менделеева.

Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную значение которой необходимо было измерять для каждого газа:

Менделеев обнаружил, что прямо пропорциональна , коэффициент пропорциональности он назвал универсальной газовой постоянной.^{[источник не указан 1459 дней]}

Связь с другими законами состояния идеального газа[править | править код]

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта — Изотермический процесс.

 — Закон Гей-Люссака — Изобарный процесс.

 — закон Шарля (второй закон Гей-Люссака, 1808 г.) — Изохорный процесс

В форме пропорции этот закон удобен для расчёта перевода газа из одного состояния в другое.

С точки зрения химика этот закон может звучать несколько иначе: объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:

.

1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:

.

Закон Бойля — Мариотта

Закон Бойля — Мариотта

назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.

В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме

где  — показатель адиабаты,  — внутренняя энергия единицы массы вещества.

Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. Это обстоятельство может быть прояснено на основании молекулярных представлений.

С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.

С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение увеличивается.

См. также[править | править код]

• Совершенный газ
• Реальный газ
• Уравнение состояния реального газа

Примечания[править | править код]

Литература[править | править код]

• Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высшая школа, 2009. — 527 с. — ISBN 978-5-06-006161-1.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:

Примеры задач на уравнение Менделеева-Клапейрона

В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?

Некоторое количество гелия при 78 градусах Цельсия и давлении 45,6 атмосфер занимает объем 16,5 литров.
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)

В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Теперь немного формул.

где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль

Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также

где n — число молей газа

И как нетрудно заметить, соотношение

есть величина постоянная для одного и того же количества моль газа.

И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.

Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.

Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры

Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры

Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.

Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.

Уравнение Клапейрона-Менделеева

Что такое уравнение Клапейрона-Менделеева

Идеальный газ — это газ, в котором пренебрегают взаимодействием молекул газа между собой.

Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.

Идеальный газ — это упрощенная математическая модель, которая широко применяется для описания свойств и поведения реальных газов при атмосферном давлении и комнатной температуре.

Давление, объем и температура — это основные параметры состояния системы, и они связаны друг с другом. Соотношение, при котором определяется данная связь, называется уравнением состояния данного газа.

Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака, то есть:

p V = c o n s t * T

В представленном выше уравнении состоянии газа под const подразумевается количество молей.

Свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона, ниже представлена формула Менделеева-Клапейрона.

p V = m M R T = n R T , где m — масса газа, M — молярная масса газа, R = 8 , 314 Д ж / ( м о л ь * К ) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.

Таким образом давление и объем прямо пропорциональны количеству молей и температуре.

Также уравнение Клапейрона-Менделеева можно записать в ином виде:

p V = N k T , где N — это количество молекул газа массой m , k = 1 , 38 * 10 – 23 Д ж / К — постоянная Больцмана, которая определяет «долю» газовой постоянной, приходящуюся на одну молекулу и определяется по формуле:

N = m N A M , где

N A = 6 . 02 * 10 23 м о л ь – 1 ; — это постоянная Авогадро.

Какое значение имеет универсальная газовая постоянная

Универсальная газовая постоянная (R) — это величина, которая является константой, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 K.

Значение данной константы находится как произведение постоянной Больцмана ( k = 1 , 38 * 10 – 23 Д ж / К ) на число Авогадро ( N A = 6 . 02 * 10 23 м о л ь – 1 ) . Таким образом универсальная газовая постоянная принимает следующее значение: R = 8 , 314 Д ж / ( м о л ь * К ) .

Постоянную Больцмана используют в формулах, описывающих изучаемое явление или поведение рассматриваемого объекта с микроскопической точки зрения, тогда как универсальная газовая постоянная более удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.

Связь с другими законами состояния идеального газа

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех макропараметров (давление, температура или объем) — остаются неизменными.

Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами, которые связывают эти параметры.

Изопроцессы — это термодинамические процессы, во время протекания которых количество вещества и один из макропараметров состояния: давление, объем, температура или энтропия — остается неизменным.

В зависимости от того, какой параметр остается неизменным различают разные процессы, которые выражаются законами, являющимися следствием уравнения состояния газа:

• изотермический процесс (T=const);
• изохорный процесс (V=const);
• изобарный процесс (p=const).

Изотермический процесс (T=const)

Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.

Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.

Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:

Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется закон Бойля-Мариотта.

Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).

Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.

Рис.1. Изотерма в pV — координатах.

Изохорный процесс (V=const)

Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.

Из уравнения состояния следует, что отношение давлений газа данной массы при постоянно объеме равно отношению его абсолютных температур:

p 1 p 2 = T 1 T 2

Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.

Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда

p = p 0 T T 0 = p 0 γ T

Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов.

Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (Рис.2).

Рис.2 Изображение изохоры в pT-координатах.

Изобарный процесс (p=const)

Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.

Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.

V 1 V 2 = T 1 T 2

Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:

V = V 0 T T 0 = V 0 α T

Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.

Закон Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.

Коэффициент α называют температурным коэффициентом объемного расширения газов.

Зависимость объема газа от температуры при постоянном давлении изображается графической прямой, которая называется изобарой (Рис.3).

Рис. 3. Изобара в VT-координатах.

Использование универсального уравнения для решения задачи

В реальности проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа и законы, связанные с ним находят применение для решения физических и химических задач.

Определить давление кислорода в баллоне объемом 1 м 3 при температуре t = 27 C o . Масса кислорода 1 кг.

Так как в уравнении даны объем и температура — два из трех макроскопических параметров, а третий (давление) нужно определить, то мы можем использовать уравнение Клапейрона-Менделеева:

p V = n R T = m M R T

Не забываем перевести температуру в Кельвины:

T = t + 273 = 27 + 273 = 300 K

Молярная масса кислорода известна из таблицы Менделеева:

M ( O 2 ) = 2 * 16 = 32 г / м о л ь = 32 * 10 – 3 к г / м о л ь

Выразим из уравнения состояния давления и поставим все имеющиеся данные:

p = n R T V = m R T M V = 1 * 8 . 31 * 300 32 * 10 – 3 * 1 = 77 . 906 П а = 78 к П а

Ответ: p = 78 кПа.

Каким может быть наименьший объем баллона, содержащего кислород массой 6,4 кг, если его стенки при t = 20 C o выдерживают p = 1568 Н / с м 2 ?

Используем уравнение Менделеева-Клапейрона, из которого выражаем объем кислорода, который нужно найти:

p = n R T V = m R T M V

Молярная масса кислорода предполагается равной:

M ( O 2 ) = 2 * 16 = 32 г / м 3

Не забываем перевести температуру в Кельвины:

T = t + 273 = 20 + 273 = 293 K

Переводим давление: p = 15680000 Па

Выражаем из уравнения Клапейрона-Менделеева объем и подставляем значения, данные в условиях задачи:

V = n R T p = m R T M p = 6 . 4 * 8 . 31 * 293 15680000 * 32 * 10 – 3 = 3 . 1 * 10 – 2 м 3 = 31 л .

Используя уравнение состояния идеального газа, доказать, что плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Согласно уравнению Менделеева-Клапейрона:

p = n R T V = m R T M V

Плотность — это величина, характеризующая массу некоторого объема и находится по формуле:

ρ = m V и л и V = m ρ

Тогда p m ρ = n R T = m R T M

Откуда выражаем плотность газа:

Для водорода эта формула запишется следующим образом:

ρ H 2 = p M H 2 R T

По условию задачи водород и любой другой газ находятся при одинаковых условиях, откуда следует, что:

ρ H 2 M H 2 = p R T

Поставим последнее выражение в выражение для плотности любого газа:

ρ = M * ρ H 2 M H 2

Молярная масса водорода, исходя из таблицы Менделеева равна 2 г/моль и тогда. Молекулярная масса численно равная молярной и представляет собой массу молекулы в атомных единицах, поэтому в дальнейшем мы совершили переход к молекулярной массе.

ρ = M r * ρ H 2 2

Вывод: плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Рассмотрим несколько задач на законы, связанные с уравнение Клапейрона-Менделеева, то есть на изотермические, изохорные, изобарные процессы.

При уменьшении давления газа в 2,5 раза его объем увеличился на 12 л. Какой объем занимал газ в начальном состоянии, если температура на протяжении всего процесса оставалась постоянной?

По условию задачи температура в ходе всего процесса оставалась постоянной, откуда следует, что у нас изотермический процесс, и мы можем воспользоваться для решения законом Бойля-Мариотта.

p 1 V 1 = p 2 V 2 , г д е p 1 – давление газа в начальном состоянии (до расширения), V 1 — объем газа в начальном состоянии, p 2 = p 1 2 . 5 — давление газа в конечном состоянии (после расширения), V 2 = V 1 + ∆ V — объем газа в конечном состоянии.

Откуда можем найти начальный объем:

p 1 V 1 = p 1 2 . 5 ( V 1 + ∆ V ) = p 1 2 . 5 V 1 + p 1 2 . 5 ∆ V

V 1 ( p 1 – p 1 2 . 5 ) = p 1 2 . 5 ∆ V

p 1 2 . 5 V 1 ( 2 . 5 – 1 ) = p 1 2 . 5 ∆ V

V 1 = ∆ V 1 , 5 = 8 л

Ответ: первоначальный объем газа был равен 8 л.

Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?

Так как нагревание газа по условиям данной задачи происходит при постоянном объеме, значит перед нами изохорный процесс.

При изохорном процессе:

p 1 T 1 = p 2 T 2

T 2 = p 2 T 1 p 1

p 2 p 1 = 1 . 5 T 2 = 1 . 5 * T 1 = 1 . 5 * 400 = 600 K

При 27°C объем газа равен 600 мл. Какой объем займет газ при 57°C, если давление будет оставаться постоянным?

Так как давление по условию остается постоянным, то можем использовать закон Гей-Люссака.

V 1 V 2 = T 1 T 2

V_2 – искомый объем

Для правильного расчета необходимо перевести температуры из Цельсий в Кельвины:

T 1 = 273 + 27 = 300 K

T 2 = 273 + 57 = 330 K

T 2 V 1 T 1 = V 2

V 2 = ( 600 * 330 ) / 300 = 660 м л

Газ в трубе плавильной печи охлаждается от температуры t 1 = 1150 ° С д о t 2 = 200 ° С . Во сколько раз увеличивается плотность газа при этом? Давление газа не меняется.

Так как по условию задания давления газа не изменяется, значит перед нами изобарный процесс. Для решения воспользуемся законом Гей-Люссака:

V 1 V 2 = T 1 T 2

Перейдем к абсолютной температуре:

T 1 = 1150 + 273 = 1423 K

T 2 = 200 + 273 = 473 K

Масса газа: m = ρ 1 V 1 = ρ 2 V 2

Использование этих формул приводит к следующему:

Уравнение состояния идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:

Уравнение состояния идеального газа

Внимание! При решении задач важно все единицы измерения переводить в СИ.

Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.

Из основного уравнения состояния идеального газа выразим массу:

Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.

Подсказки к задачам

Важна только та масса, что осталась в сосуде. Поэтому:

Давление возросло на 15%	p2 = 1,15p1
Объем увеличился на 2%	V2 = 1,02V1
Масса увеличилась в 3 раза	m2 = 3m1
Газ нагрелся до 25 о С	T2 = 25 + 273 = 298 (К)
Температура уменьшилась на 15 К (15 о С)	T2 = T1 – 15
Температура уменьшилась в 2 раза
Масса уменьшилась на 20%	m2 = 0,8m1
Выпущено 0,7 начальной массы
Какую массу следует удалить из баллона?	Нужно найти разность начальной и конечной массы:
Газ потерял половину молекул
Молекулы двухатомного газа (например, водорода), диссоциируют на атомы
Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ)	M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль
Открытый сосуд	Объем V и атмосферное давление pатм остаются постоянными
Закрытый сосуд	Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины
Нормальные условия	Температура T0 = 273 К Давление p0 = 10 5 Па
Единицы измерения давления	1 атм = 10 5 Па

Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.

2,8 МПа = 2,8∙10 6 Па

1,5 МПа = 1,5∙10 6 Па

Так как половина молекул была выпущена, m₂ = 0,5m₁. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:

Преобразим уравнения и получим:

Приравняем правые части и выразим искомую величину:

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.

[spoiler title=”источники:”]

http://wika.tutoronline.ru/fizika/class/10/uravnenie-klapejronamendeleeva

[/spoiler]

Вы хотите познавать химию с удовольствием? Тогда вам сюда! Репетитор-профессионал, автор методики системно-аналитического изучения химии и биологии, кандидат биологических наук Богунова В.Г. делится секретами мастерства, раскрывает тайны решения задач, помогает подготовиться к ОГЭ, ЕГЭ, ДВИ и олимпиадам.

Ну как? Выдержите еще немного газовой атаки, или уже сил нет? Совсем чуть-чуть. Самую капельку. Только легенькое уравнение Менделеева-Клапейрона. И все! Что? Неинтересно?! Давайте внесем струю драйва в нашу тяжелую долю и позовем кого-нибудь в гости! Не знаю, как вы, а я уже звоню Алисе, в Страну Чудес.

Алиса удивилась, как это она не удивилась, но ведь удивительный день еще только начался и нет ничего удивительного в том, что она еще не начала удивляться.

— Если бы у меня был свой собственный мир, в нем все было бы чепухой. Ничего не было бы тем, что есть на самом деле, потому что все было бы тем, чем оно не является, и наоборот, оно не было бы тем, чем есть, а чем бы оно не было, оно было.

Что-то мне перехотелось приглашать Алису в гости. Лучше уж уравнение Менделеева-Клапейрона в классических задачах с любыми условиями протекания реакций. Давайте подумаем, в какие задачи ЕГЭ может легко вписаться и Менделеев, и Клапейрон, и ненормальные условия? Я вижу две позиции – задание 29 (количество вещества и объем газа для любых условий) и задание 35 (определение реальной молярной массы газообразного вещества в любых условиях). Пока авторы заданий ЕГЭ ограничиваются нормальными условиями (0 С, 1 атм). Но это пока…

Чтобы не было так грустно думать о приближающемся конце света ЕГЭ-шного происхождения, в конце статьи я немного повеселю вас еще одним разговором с Сири. На этот раз моя интеллектуальная помощница расскажет о своих чувствах к виртуальному объекту Облака. Не верите? Дочитайте статью до конца, решите задачи, и вы тоже услышите чувственные тайны робота. А пока – ненормальные условия газов в расчетных химических задачах.

Уравнение Менделеева-Клапейрона

Газы часто бывают реагентами и продуктами в химических реакциях, поэтому возникла необходимость определять число молей газов в любых условиях. Для этого используют уравнение Менделеева-Клапейрона – формулу, устанавливающую зависимость между давлением, молярным объёмом и абсолютной температурой газа.

Молярный объём – объём одного моля газа (или смеси газов) при данной температуре и давлении.

Абсолютная температура – температура, отсчитываемая от абсолютного нуля. Понятие абсолютной температуры было введено У. Томсоном (Кельвином) , в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры – кельвин (К) .

Абсолютный ноль – это температура -273,15 градусов Цельсия, минимальный предел температуры, которую может иметь физическое тело во Вселенной, когда тепловое движение останавливается.

Решим несколько задач, условия в которых отличаются от нормальных и подразумевают использование уравнения Менделеева-Клапейрона для расчетов количества вещества или объема газа. В процессе решения проводим анализ протекающих процессов и особенностей алгоритмических приемов. Читайте внимательно и записывайте, затем попробуйте решить задачи самостоятельно. Итак, поехали!

Задача 1

При растворении в серной кислоте 10 г сплава цинка с магнием выделилось 5,2 л водорода, измеренного при 26С и давлении 920 мм рт.ст. Определить массовые доли металлов в смеси.

Вначале, как всегда, химический экскурс. Как реагируют металлы с кислотами? Металлы, стоящие в ряду активности левее (Н), реагируют с кислотами-неокислителями с выделением водорода. Металлы, правее (Н), с кислотами-неокислителями не реагируют.

Li Rb K Ba Sr Ca Na Mg Al Mn Zn Cr Fe Cd Co Ni Sn Pb (H) Sb Bi Cu Hg Ag Pt Au

И цинк, и магний реагируют с серной кислотой (очевидно, разбавленной) с выделением водорода. Это – классическая задача на смеси, решается по Четырем Заповедям. Определим последовательность действий по Третьей Заповеди (предварительные расчеты):

1) По уравнению Менделеева-Клапейрона определяем количество вещества водорода.

2) Принимаем количества вещества цинка и магния за неизвестные – X и Y соответственно, записываем досье для каждого участника (количество вещества, молярная масса, масса)

3) Делаем расчеты по уравнениям реакций.

4) Составляем систему уравнений. Одно уравнение – закрываем на количестве вещества водорода, второе – на общей массе сплава. Решаем уравнения, находим неизвестные, записываем их значения в досье.

5) Определяем массовые доли по стандартной формуле.

Задача 2

Смесь цинка и меди массой 1 г поместили в пробирку с избытком соляной кислоты. Выделилось 200 мл водорода, измеренного при температуре 27С и давлении 740 мм рт.ст. Рассчитайте массовую долю меди в исходной смеси металлов.

Напомню еще раз: металлы, стоящие в ряду активности левее (Н), реагируют с кислотами-неокислителями с выделением водорода. Металлы, правее (Н), с кислотами-неокислителями не реагируют.

Li Rb K Ba Sr Ca Na Mg Al Mn Zn Cr Fe Cd Co Ni Sn Pb (H) Sb Bi Cu Hg Ag Pt Au

Цинк реагирует с соляной кислотой (он стоит левее водорода), медь – правее водорода, с соляной кислотой не реагирует. Задача решается по Четырем Заповедям. Определим последовательность действий по Третьей Заповеди (предварительные расчеты):

1) По уравнению Менделеева-Клапейрона определяем количество вещества водорода.

2) Делаем расчеты по уравнению реакции (по водороду определяем количество вещества цинка).

3) Определяем массовую долю цинка по стандартной формуле, а массовую долю меди – как оставшуюся разницу (обе массовые доли в сумме составляют 1 или 100%)

Задача 3

Какой объем водорода, измеренный при температуре 21С и давлении 765 мм рт.ст. необходимо использовать для восстановления оксида меди (II) массой 16 г?

Экскурс в теоретическую химию. Водородом можно восстановить железо и остальные металлы правее него в ряду активности.

Li Rb K Ba Sr Ca Na Mg Al Mn Zn Cr Fe Cd Co Ni Sn Pb (H) Sb Bi Cu Hg Ag Pt Au

В литературе имеется информация о восстановлении водородом металлов от магния до железа, но при очень высоких температурах. Основной недостаток восстановления водородом – низкий коэффициент использования водорода (на практике водорода нужно в 2 раза больше, чем рассчитано по уравнению реакции).

Задача решается по Четырем Заповедям. Последовательность действий по Третьей Заповеди (предварительные расчеты):

1) Составляем досье на оксид меди (масса, молярная масса, количество вещества)

2) Делаем расчеты по уравнению реакции (по оксиду меди определяем количество вещества водорода)

3) По уравнению Менделеева-Клапейрона определяем объем водорода

Задача 4

При действии на 10 г смеси меди и алюминия избытком соляной кислоты выделился газ объемом 5,44 л при 20С и 168 кПа. Вычислите массовую долю меди в исходной смеси.

Напомню еще раз: металлы, стоящие в ряду активности левее (Н), реагируют с кислотами-неокислителями с выделением водорода. Металлы, правее (Н), с кислотами-неокислителями не реагируют.

Li Rb K Ba Sr Ca Na Mg Al Mn Zn Cr Fe Cd Co Ni Sn Pb (H) Sb Bi Cu Hg Ag Pt Au

Алюминий реагирует с соляной кислотой (он стоит левее водорода), медь – правее водорода, с соляной кислотой не реагирует. Задача решается по Четырем Заповедям. Определим последовательность действий по Третьей Заповеди (предварительные расчеты):

1) По уравнению Менделеева-Клапейрона определяем количество вещества водорода.

2) Делаем расчеты по уравнению реакции (по водороду определяем количество вещества алюминия).

3) Определяем массовую долю алюминия по стандартной формуле, а массовую долю меди – как оставшуюся разницу (обе массовые доли в сумме составляют 1 или 100%)

Ну как? Получили удовольствие от решения задач? Это был риторический вопрос. По этому поводу у меня есть забавная история из моей практики.

Более десяти лет назад я работала с учеником Сашей (фамилия слишком известная, поэтому ее не назову, даже если пытать будете). Саша пришел ко мне с очень слабыми знаниями. За год работы у мальчика прорезался интерес к решению задач по химии, и мы подружились. Нам приходилось работать 5 дней в неделю, по 4 часа в день (это было требование отца Саши, очень влиятельного чиновника). К концу года мы оба (я и Саша) изрядно устали от такой напряженной работы. На последнее занятие мальчик пришел с огромным букетом орхидей, который едва протиснулся в дверной проем. Мне никогда еще не дарили такой шикарный и, видимо, очень дорогой букет. Я поблагодарила Сашу примерно такими словами: “Сашуля, большое спасибо! Такой роскошный букет – это подарок за большую, сложную и результативную работу, которую мы с тобой проделали!” Сашин ответ сразил меня наповал: “Валентина Георгиевна! За этот год вы стали для меня второй мамой. Я вас очень люблю. Но букет этот я дарю вам за то, что, слава Богу, сегодня последнее занятие по химии!” Мы оба смеялись до слез 😂😂😂😂😂

На закуску – тайные признания виртуального робота Сири. Смотрите, слушайте, можете попробовать сами поиграть со своими гаджетами. Только запаситесь терпением – перлы начинают появляться только после долгого доставания программы.

Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Звоните мне +7(903) 186-74-55. Приходите ко мне на курс, на Мастер-классы “Решение задач по химии” – и вы сдадите ЕГЭ с высочайшими баллами, и станете студентом престижного ВУЗа!

PS! Если вы не можете со мной связаться из-за большого количества звонков от моих читателей, пишите мне в личку ВКонтакте или на Facebook. Я обязательно отвечу вам.

Репетитор по химии и биологии кбн В.Богунова

Давление газа возникает в результате столкновений молекул со стенками сосуда ( и на помещенное в газ тело ), в котором находится беспорядочно движущиеся молекулы  газа. Чем чаше удары, тем они сильнее – тем выше давление. Если масса и объем газа неизменны, то его давление в закрытом сосуде всецело зависит от температуры. Давление зависит и от скорости поступательно движущихся газовых молекул. Единица измерения давления — паскаль p(Па). Измеряют давление газа манометром (жидкостным, металлическим и электрическим).

Идеальный газ – это модель реального газа. За идеальный газ принимают газ в сосуде, когда молекула, пролетая от стенки до стенки сосуда не испытывает столкновения с другими молекулами. Точнее, Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало ⇒ E_к >> E_р .

Основное уравнение МКТ связывает макроскопические параметры (давление p, объём V, температура T, масса m) газовой системы с микроскопическими параметрами (масса молекулы , средняя скорость их движения):       

, где n— концентрация, 1/м³; m — масса молекулы, кг;  — средняя квадратичная скорость молекул, м/с.

Уравнение состояния идеального газа  — формула, устанавливающая зависимость между давлением, объёмом и абсолютной температурой идеального газа, характеризующее состояние данной системы газа. 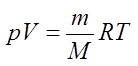— уравнение Менделеева — Клапейрона (для произвольной массы газа).             R = 8,31 Дж/моль·К  — универсальная газовая постоянная.           pV = RT – (для 1 моля).

Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества ν=const. Тогда:

Для постоянной массы идеального газа отношение произве­дения давления на объем к абсолютной  температуре в данном состоянии есть величина постоянная: 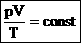  — уравнение Клапейрона. 

Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры. Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака. Эти законы называют законами для изопроцессов:

Изопроцессы – это процессы, которые совершаются при одинаковом параметре или Т-температуре, или V-объеме, или р-давлении.

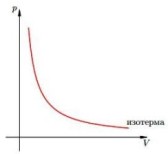
Изотермический процесс — — закон Бойля — Мариотта  (при постоянной температуре и данной массы газа произведение давления на объем есть величина постоянная)

Изобарный процесс —  — закон Гей-Люссака (при постоянном давлении для данной массы газа отношение объема к температуре есть величина постоянная)

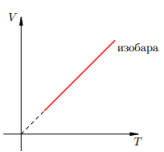
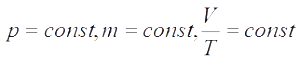
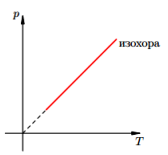
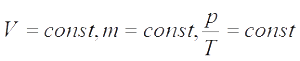
Изохорный процесс — — закон Шарля (при постоянном объеме для данной массы газа отношение давления к температуре есть величина постоянная.

Вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.