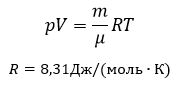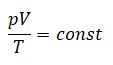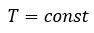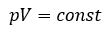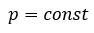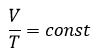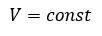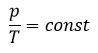Преподаватель который помогает студентам и школьникам в учёбе.
Газовые законы в физике – формулы и определения с примерами
Содержание:
Газовые законы:
С помощью уравнения состояния идеального газа можно исследовать процессы, при которых сохраняются постоянными масса газа и один из его макроскопических параметров.
Газовыми законами называются законы, определяющие количественную зависимость между двумя макроскопическими параметрами газа данной массы 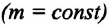
Изопроцессами (греч.: izos – “равный “) называются процессы, протекающие в газах данной массы 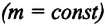
Закон Бойля-Мариотта
Этот закон был определен в 1662 году английским физиком Робертом Бойлем (1627-1691) и в 1676 году французским физиком Эдом Мариоттом (1620-1684).
Для данной массы газа при неизменной температуре произведение давления газа на его объем постоянно 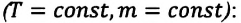

Для данной массы газа при неизменной температуре произведение давления начального состояния 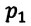 на его первоначальный объем
на его первоначальный объем 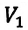 равно произведению значений этих параметров
равно произведению значений этих параметров 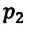 и
и 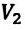 произвольного состояния:
произвольного состояния:
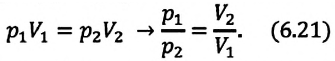
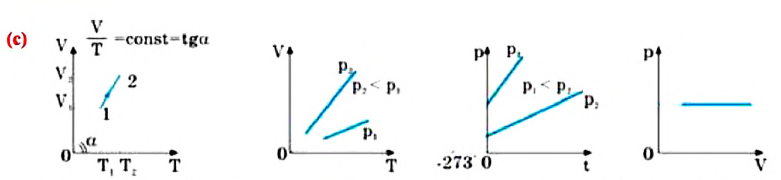
Изотермическим называется процесс изменения состояния данной массы идеального газа при постоянной температуре 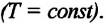 В изотермическом процессе давление газа и его объем обратно пропорциональны друг другу (b).
В изотермическом процессе давление газа и его объем обратно пропорциональны друг другу (b).
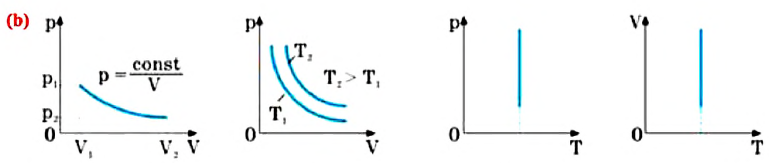
Закон Гей-Люссака
Этот закон был экспериментально установлен в 1802 году французским физиком Джозефом Луи Гей-Люссаком (1778-1850).
Для данной массы газа при неизменном давлении отношение объема газа к его абсолютной температуре постоянно 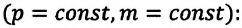
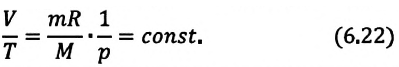
При неизменном давлении отношение первоначального объема газа 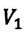 к его первоначальной температуре
к его первоначальной температуре 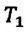 равно отношению параметров
равно отношению параметров 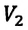 к
к 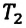 в произвольном состоянии:
в произвольном состоянии:

Закон Гей-Люссака можно выразить и так:
Для данной массы идеального газа при неизменном давлении относительное
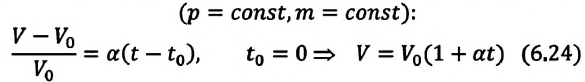
Где 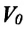 -объем идеального газа при постоянном давлении при температуре 0°С,
-объем идеального газа при постоянном давлении при температуре 0°С, 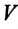 -объем конечного состояния,
-объем конечного состояния, 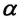 — коэффициент объемного расширения. Опыты показывают, что при нагревании любого разряженного газа на
— коэффициент объемного расширения. Опыты показывают, что при нагревании любого разряженного газа на 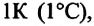 при постоянном давлении, его объем увеличивается приблизительно на
при постоянном давлении, его объем увеличивается приблизительно на 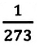 часть объема первоначального состояния:
часть объема первоначального состояния:
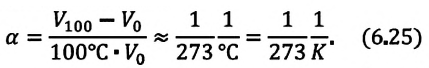
Изобарным называют процесс изменения состояния данной массы идеального газа при постоянном давлении 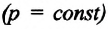 (с). При изобарном процессе объем данной массы газа прямо пропорционален его температуре.
(с). При изобарном процессе объем данной массы газа прямо пропорционален его температуре.
- Заказать решение задач по физике
Закон Шарля
Этот закон экспериментально определил в 1787 году французский физик Шарль Жак Александр Сезар (1746-1823):
Для данной массы газа при постоянном объеме отношение давления газа к его абсолютной температуре остается неизменным 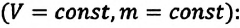
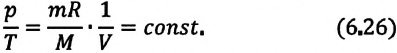
Отношение первоначального давления 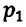 газа к его температуре
газа к его температуре 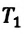 равно отношению параметров
равно отношению параметров 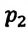 к
к 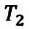 в произвольном состоянии:
в произвольном состоянии:

Закон Шарля можно выразить и так:
Для данной массы идеального газа при неизменном объеме относительное изменение давления прямо пропорционально изменению температуры 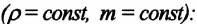
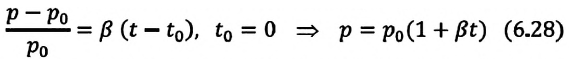
Где 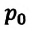 – давление начального состояния идеального газа (при температуре
– давление начального состояния идеального газа (при температуре 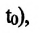
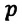 — давление конечного состояния (при температуре
— давление конечного состояния (при температуре 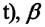 – коэффициент изменения давления. Из опытов было определено, что при нагревании любого разряженного газа на
– коэффициент изменения давления. Из опытов было определено, что при нагревании любого разряженного газа на 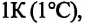 при постоянном объеме, его давление увеличивается приблизительно на
при постоянном объеме, его давление увеличивается приблизительно на 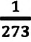 часть давления первоначального состояния:
часть давления первоначального состояния:
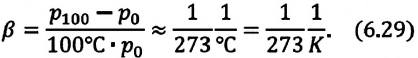
Изохорным называется процесс изменения состояния данной массы идеального газа при постоянном объеме 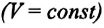 (d). При изохорном процессе давление данной массы газа прямо пропорционально его температуре.
(d). При изохорном процессе давление данной массы газа прямо пропорционально его температуре.
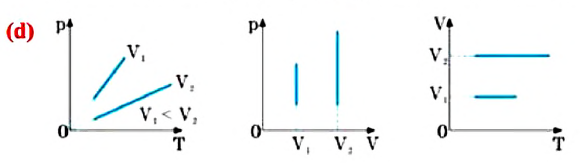
Закон Дальтона
Этот закон в 1801 году установил английский исследователь Джон Дальтон (1766-1844):
Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений этих газов:
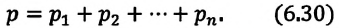
Парциальное давление — это давление отдельно взятого газа из газовой смеси.
Закон Авогадро
Этот закон, как предположение, был выдвинут в 1811 году итальянским физиком Амедео Авогадро (1776-1856). В последующем это предположение было подтверждено многочислеными опытами.
В равных объемах различных газов, взятых при одинаковых температурах и давлении, содержится одинаковое число молекул. Например, число молекул в 1 моле произвольного газа равно: 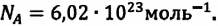 При нормальных условиях объём 1 моля газа равен 22,4 л (л/моль). Этот объём называют молярным объёмом идеального газа.
При нормальных условиях объём 1 моля газа равен 22,4 л (л/моль). Этот объём называют молярным объёмом идеального газа.
- Взаимодействие молекул
- Агрегатное состояние вещества
- Зависимость размеров тел от температуры
- Световые явления
- Физическое тело и вещество в физике
- Плотность и единицы плотности в физике
- Движение молекул в физике в газах, жидкостях и твёрдых телах
- Скорость движения молекул газа
Молекулы всех газов при одной и той же
температуре обладают одинаковой средней
кинетической энергией. Причем давление
газа при данной температуре зависит
только от числа молекул в единице объема
газа. В основе объяснений физических
свойств газов и законов газового
состояния лежит кинетическая теория.
Большинство законов газового состояния
было выведено для идеального газа.
Идеальным называют газ, в котором
молекулы рассматриваются как материальные
точки, обладающие массой, но не имеющие
при этом объёма, между которыми отсутствуют
силы взаимодействия.
При
больших объёмах и малых давлениях, когда
расстояние между молекулами во много
раз больше собственных размеров молекул,
а также при высоких температурах, когда
интенсивность хаотического движения
молекул велика и поэтому молекулы слабо
взаимодействуют между собой, складываются
условия, при которых реальный газ можно
с некоторым приближением считать
идеальным.
Закон Бойля — Мариотта.
Английский ученый
Бойль и независимо от него несколько
позднее французский физик Мариотт на
основании экспериментов пришли к выводу
о том, что объем данной
массы газа и его давление находятся в
обратно пропорциональной зависимости.
Эта зависимость между давлением и
объемом газа при постоянной температуре
выражается формулой:
![]()
, (1)
где V1
и Р1
– объем и абсолютное давление газа до
их изменения; V2
и Р2 –
то же, после изменения.
Из данной формулы можно получить
следующие математические выражения:
![]()
, (2)
или
![]()
при
![]()
. (3)
Из последней формулы следует,
что произведение
давления данной массы газа на его объем
постоянно, если температура газа не
меняется.
Закон
имеет практическое применение в газовом
хозяйстве. Он позволяет определять
объем газа при изменении его давленная
и давление газа при изменении его объема
при условии, что температура газа
остаётся постоянной.
Чем больше при постоянной
температуре увеличивается объем газа,
тем меньше становится его плотность.
Зависимость между
объёмом газа и его плотностью при
постоянной температуре выражается
формулой
![]()
, (4)
где V1
и V2
– объемы, занимаемые газом; ρ1
и ρ2
– плотности газа, соответствующие этим
объемам.
Если в формуле (1) заменим отношение
объемов газа отношением их плотностей,
то на основании формулы (4) можно получить.
![]()
или
![]()
(5)
Из формулы (5) можно сделать
вывод, что при одной
и той же температуре плотности газов
прямо пропорциональны давлениям, под
которым находятся эти газы, т.е. плотность
газа (при постоянной температуре) будет
тем больше, чем больше будет его давление.
Пример.
Объем газа при давлении 760 мм.рт.ст. и
при температуре 0°С составляет 300 м3.
Какой объем займет этот газ при абсолютном
давлении, равном 1520 мм.рт.ст. и при той
же температуре?
760 мм.рт.ст. = 101 320 Па = 101,3 кПа;
1520 мм.рт.ст. = 202 630 Па = 202,6 кПа.
Подставляем заданные
значения V1,
Р1,
и Р2
в формулу (2):
Р1 =
101,3 кПа; V1
= 300 м3;
Р2 =
202,6 кПа;
101,3 х 300 = 202,6 V2,
откуда V2
= (101,3
х 300)/202,6 = 150 м3.
Закон Гей-Люссака.
Французский химик Гей-Люссак впервые
установил зависимость объема газа от
температуры при постоянном давлении.
Сущность этой зависимости заключается
в том, что при постоянном
давлении относительное изменение объема
данной массы газа прямо пропорционально
изменению температуры.
Математически эта зависимость между
объемом и температурой газа при постоянном
давлении записывается следующим образом:
![]()
, (6)
где V
– объем газа, м3;
Т – абсолютная
температура, К.
Из формулы (6) следует, что
если определенный
объем газа нагревать при постоянном
давлении, то его объем изменится во
столько раз, во сколько раз изменится
его абсолютная температура.
Многочисленные опыты
показывают, что при нагревании газов
на 1 градус при постоянном давлении их
объем увеличивается на постоянную
величину, равную 1/273,2 первоначального
их объема. Эта величина называется
термическим
коэффициентом объемного расширения
и обозначается α
= 1/273,2 град-1.
С учетом этого закон
Гей-Люссака можно сформулировать так:
объем данной массы
газа при постоянном давлении увеличивается
линейно при повышении температуры
![]()
; (7)
![]()
; (8)
![]()
, (9)
где Vt
и V0
– объемы газа при
конечной и начальной температурах, м3;
t
и Т – начальная и конечная температуры,
оС,
К; α – термический коэффициент объёмного
расширения.
Из формулы (9) следует, что
объем газа при постоянном
давлении прямо пропорционален его
абсолютной температуре.
Закон Шарля.
Согласно закону Шарля,
давление данной массы
газа при постоянном объеме прямо
пропорционально абсолютной температуре.
Из этого закона следует, что отношение
давлений массы газа при постоянном
объеме равно отношению его абсолютных
температур. Закон
выражается следующей формулой:
![]()
или
![]()
, (10)
где Р1
и Р2
– абсолютные давления; Т1
и
Т2
– абсолютные температуры
газа, К.
Из формулы (10) можно сделать вывод, что
при постоянном объеме давление газа
при нагревании увеличивается во столько
раз, во сколько раз увеличивается его
абсолютная температура.
Пример 1.
При температуре газа 27°С его давление
равно 4 МПа (40 кгс/см2).
Каково будет избыточное давление этого
газа при температуре 47°С?
Начальная абсолютная
температура газа равна:
![]()
,
конечная абсолютная
температура газа равна:
![]()
.
Атмосферное давление примем
равным 0,1 МПа (1 кгс/см2),
тогда абсолютное давление газа до
нагревания будет:
![]()
.
Искомое абсолютное давление
газа Р2
по формуле (10) равное:
![]()
.
Следовательно, избыточное давление
газа после нагревания его до 47°С равно:
![]()
.
Пример 2.
Сжатый газ в баллоне при температуре
7°С имел избыточное давление 0,9МПа. После
нагревания давление в баллоне повысилось
до 1,1 МПа. До какой температуры был нагрет
газ?
Начальная абсолютная
температура газа:
![]()
.
Начальное абсолютное
давление газа:
![]()
.
Конечное абсолютное давление
газа:
![]()
.
Из формулы (10) после
преобразования ее относительно
неизвестной Т2
получаем:
![]()
.
Следовательно, газ в баллоне был нагрет
до температуры 63°С.
Закон
Авогадро. Итальянский
ученый Амадео Авогадро выразил
предположение, что различные
газы, занимающие одинаковые объёмы при
равных условиях (одинаковые давление
и температура), содержат одинаковое
число молекул.
Это число для одной
грамм-молекулы (1 моль) любого газа
составляет около N
= 6,064 х
1023
и называется числом Авогадро. В дальнейшем
было экспериментально установлено, что
1 грамм-молекула любого газа при нормальных
условиях занимает объем 22,4л.
В Международной системе
единиц производной является величина,
в 1000 раз большая моля, она называется
киломоль и
обозначается кмоль.
1 кмоль любого газа
при нормальных условиях (0°С и 101,3 кПа)
занимает объем 22,4 м3.
Зная эту величину, можно определить
плотность любого газа по формуле
![]()
, (11)
где М —
масса 1 кмоля газа, кг.
Пример 1.
Определить плотность метана при
нормальных условиях (ОоС
и 101,3 кПа):
![]()
.
Пример 2. В баллоне находится 100 кг
жидкого этана. Определить объем паров
этана, полученных при его полном испарении
в нормальных условиях.
Решение. Сначала определяют число
киломолей этана:
п = 100 : 30,07 = 3,33 (здесь 30,07 –
молекулярная масса этана).
Зная, что 1 киломоль этана при испарении,
т.е. в газообразном состоянии, занимает
объем 22,4 м3, находят объем паров
этана от испарения всего его количества:
V = 22,4 х
3,33 = 74,63 м3.
Уравнение Клапейрона —
Менделеева.
При одновременном изменении объема,
давления и температуры газа справедливы
законы и Бойля — Мариотта и Гей-Люссака.
Французский ученый Клапейрон пришел к
выводу о существовании для газов
некоторой универсальной функции. Русский
ученый Д.И. Менделеев вывел в более общем
виде уравнение состояния идеальных
газов, объединив уравнения законов
Бойля — Мариотта и Гей-Люссака в одно
общее математическое уравнение идеального
газа, которое называется уравнением
Клайперона—Менделеева:
![]()
. (12)
Величина
![]()
обозначается буквой “R”
называется газовой постоянной. Подставляя
обозначение газовой постоянной в формулу
(12), получаем выражение:
![]()
или
![]()
. (13)
Это
уравнение закона газового состояния
связывает все три основных параметра
данного количества газа: объем, абсолютное
давление и абсолютную температуру, и
оно относится к 1 молю газа.
Из уравнения следует, что
для определенного
количества газа произведение его объема
на абсолютное давление равно произведению
газовой постоянной на абсолютную
температуру газа. Числовое
значение газовой постоянной зависит
от величин параметров, входящих в
уравнение (13).
В Международной системе универсальная
газовая постоянная для 1 кмоля равна:
![]()
,
где 101325 – нормальное давление, Па.
Уравнением Клапейрона —
Менделеева часто пользуются при пересчете
характеристик газа. Формулы (14) и (15),
предназначенные для пересчета параметров,
характеризующих состояние газа в
нормальных и стандартных условиях,
получены путем соответствующих,
преобразований выражения
.
![]()
, (14)
![]()
, (15)
где VН Vст
– объём газа при нормальных и стандартных
условиях, м3; Vt
– объём газа при реальных условиях, м3;
Pt –
давление газа при реальных условиях,
Па; Р – давление газа при нормальных и
стандартных условиях (101325 Па).
Закон Дальтона.
Смеси газов (паров),
близких по своим свойствам к идеальным,
характеризуются аддитивностью парциальных
давлений. Аддитивность
(от лат. additivus
– прибавляемый), свойство объекта, по
которому величина всего объекта равна
сумме величин частей объекта при любом
разбиении. Так, масса тела равна сумме
масс его частей.
Парциальным давлением
компонента ρi
газовой смеси называется то давление,
которое этот компонент оказывал бы,
если бы из смеси удалить все другие
компоненты при сохранении первоначальных
объема и температуры системы. Закон
аддитивности записывается следующим
образом:
![]()
(16)
где π — общее давление смеси
газов (паров). Из уравнения
![]()
следует, что
![]()
(17)
Подставив это выражение в уравнение
(17), получим
![]()
(18)
Следовательно
![]()
(19)
или
![]()
(20)
т.е. парциальное
давление компонента равно давлению
системы, умноженному на мольную долю
этого компонента в газовой фазе.
Пример. Известен молярный состав
смеси газов, %: метан – 90, этан – 5, пропан
– 2, азот – 2, бутаны – 1. Смесь находится
под давлением 12 МПа. Требуется определить
парциальное давление компонентов смеси.
Решение. Пользуясь уравнением, вычисляют
парциальное давление компонентов:
pC1
= 0,9*12 = 10,8 МПа;
pC2
= 0,05*12 = 0,6 МПа;
pC3
= 0,02*12 = 0,24 МПа;
pC4
= 0,02*12 = 0,24 МПа;
pC5
= 0,01*12 = 0,12 МПа.
Законы реальных газов.
При повышении давления
объем реального газа становится меньше,
чем идеального. Это
обстоятельство учитывают введением
соответствующих поправок в законы
идеальных газов.
Так,
уравнение состояния реального газа
можно записать в виде:
![]()
(21)
где z
— коэффициент сжимаемости, являющийся
функцией приведенного давления Рпр
= P/Pкр
и приведенной
температуры Tпр
= T/Ткр;
Ркр
и Ткр
— критические давление и температура
(табличные значения).
Давление насыщенных
паров. Пары жидкости
могут быть насыщенными и ненасыщенными.
Насыщенным называется
пар, находящийся в равновесии с жидкостью.
Чем выше температура, тем выше давление,
при котором находится данная равновесная
система. Для насыщенных паров существует
однозначная зависимость между давлением
паров и температурой Р
= f(T).
Ненасыщенными (перегретыми)
парами называют пары, которые при данных
температуре и давлении образуют
однофазную систему.
Жидкая фаза отсутствует.
Известно, что жидкость
начинает кипеть при такой температуре,
при которой давление её насыщенных
паров Р
становится равным внешнему давлению
π. Давление насыщенных паров определяют
по табличным данным или эмпирическим
уравнениям (ур-е Антуана, Киреева).
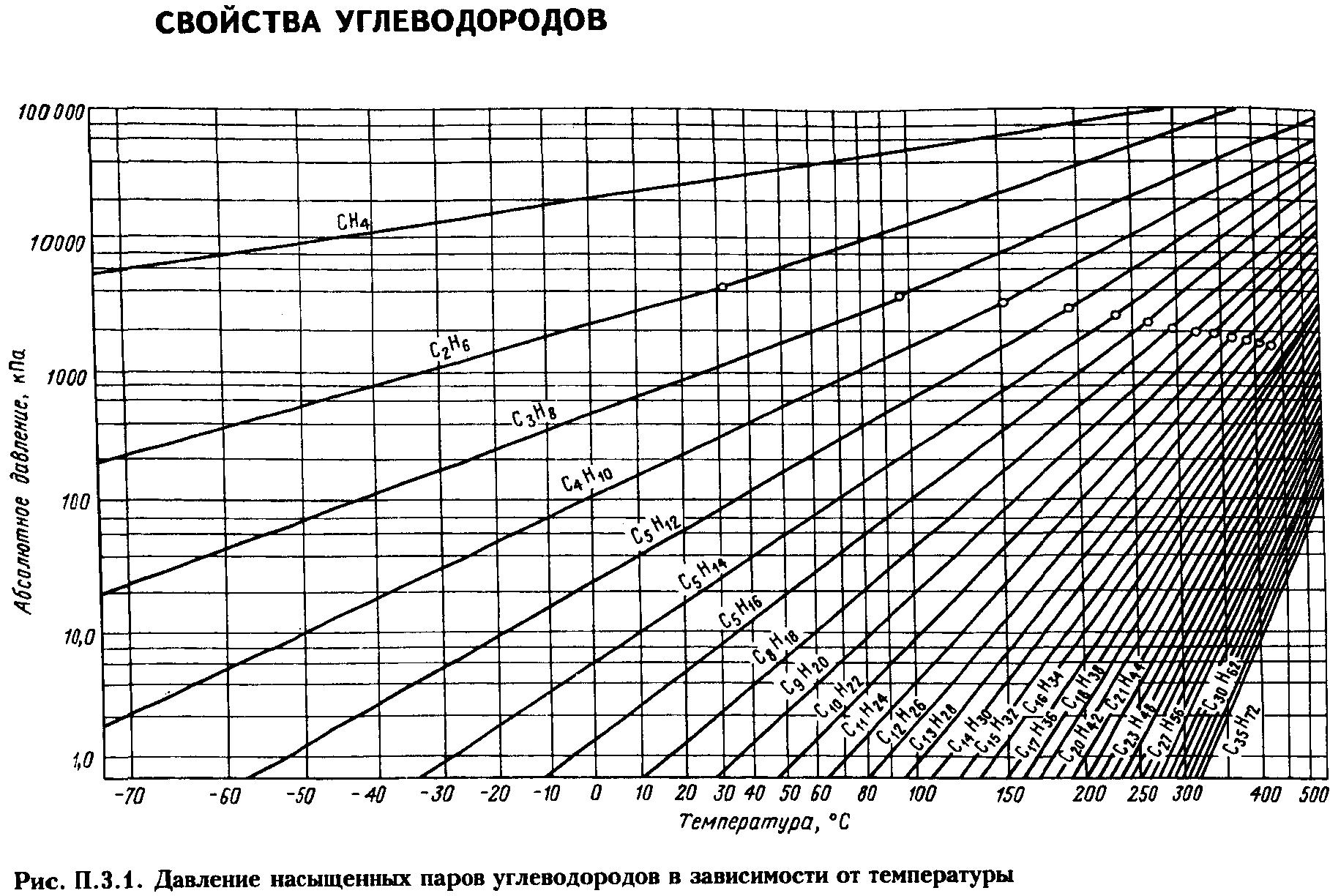
Для определения ДНП
нефтепродуктов, представляющих собой
сложные смеси углеводородов различных
классов, предложены графики и формулы
(Кокса, Ашворта, Вильсона, BWR
и др.)
Закон Рауля. Этот закон
устанавливает зависимость между
парциальным давлением компонента,
входящего в состав раствора, его молярной
концентрацией в жидкой смеси Х
и упругостью пара того же чистого
компонента при заданной температуре
Q.
Парциальное давление компонента в
жидкой смеси равно его молярной
концентрации, умноженной на упругость
его паров в чистом виде при данной
температуре:
![]()
(22)
где р – парциальное давление
компонента в растворе.
По закону Рауля, сумма парциальных
давлений всех компонентов равна общему
давлению над смесью или общей упругости
паров смеси:
![]()
![]()
где
ХnQn
– молярная концентрация и упругость
паров компонента соответственно.
Пример. Жидкая смесь состоит из
этана –60%, пропана –25 % и изобутана
–15 % (молярные доли). Требуется определить
общее давление системы при температуре
100С.
Решение. Сначала из рис. 2.1 (график Кокса)
находим давление насыщенных паров
компонентов в чистом виде при 10°С:
QC2
= 0,326 МПа; QC3
= 0,63 МПа; QC4
= 0,16 МПа
Затем по уравнению определим общее
давление системы:
![]()
Данные этого примера показывают, что
если бы указанная смесь транспортировалась
в жидком виде при 10°С, то трубопровод
работал под давлением 2,14 МПа.
Важным выводом, вытекающим из закона
Рауля, является то, что высококипящие
компоненты имеют низкую упругость,
содержатся в паровой фазе в малых
количествах; следовательно, их
основная доля находится в жидкой фазе.
Что касается низкокипящих компонентов,
обладающих высокой упругостью, то они
легко переходят в газовую фазу. На этом
положении основана работа многих
установок по частичной стабилизации
газового конденсата при выветривании
– ступенчатом снижении давления смеси
с одновременным ее расширением.

23
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение состояния идеального газа определяет связь температуры, объема и давления тел.
- Позволяет определить одну извеличин, характеризующих состояние газа, по двум другим (используется в термометрах);
- Определить, как протекают процессы при определенных внешних условиях;
- Определить, как меняется состояние системы, если она совершает работу или получает тепло от внешних тел.
Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)
– универсальная газовая постоянная, R = kNA
Уравнение Клапейрона (объединенный газовый закон)
Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный.
Количественные зависимости между двумя параметрами газа одной и той же массы при неизменном значении третьего параметра называют газовыми законами.
Газовые законы
Закон Бойля – Мариотта
Первый газовый закон был открыт английским ученым Р. Бойлем (1627—1691) в 1660 г. Работа Бойля называлась «Новые эксперименты, касающиеся воздушной пружины». И действительно, газ ведет себя подобно сжатой пружине, в этом можно убедиться, сжимая воздух в обычном велосипедном насосе.
Бойль изучал изменение давления газа в зависимости от объема при постоянной температуре. Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим (от греческих слов isos — равный, therme — тепло).
Независимо от Бойля несколько позднее французский ученый Э. Мариотт (1620—1684) пришел к тем же выводам. Поэтому найденный закон получил название закона Бойля—Мариотта.
Произведение давления газа данной массы на его объем постоянно, если температура не меняется
pV = const
Закон Гей-Люссака
Сообщение об открытии еще одного газового закона было опубликовано лишь в 1802 г., спустя почти 150 лет после открытия закона Бойля—Мариотта. Закон, определяющий зависимость объема газа от температуры при постоянном давлении (и неизменной массе), был установлен французским ученым Гей-Люссаком (1778— 1850).
Относительное изменение объема газа данной массы при постоянном давлении прямо пропорционально изменению температуры
V = V0 αT
Закон Шарля
Зависимость давления газа от температуры при постоянном объеме экспериментально установил французский физик Ж. Шарль (1746—1823) в 1787 г.
Ж. Шарль в 1787 г., т. е. раньше, чем Гей-Люссак, установил и зависимость объема от температуры при постоянном давлении, но он своевременно не опубликовал своих работ.
Давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.
p = p0 γT
| Название | Формулировка | Графики |
|
Закон Бойля-Мариотта– изотермический процесс |
Для данной массы газа произведение давления на объем постоянно, если температура не меняется |
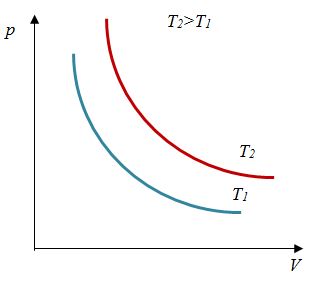   |
|
Закон Гей-Люссака– изобарный процесс |
Для данной массы газа отношение объема к температуре постоянно, если давление не меняется |
   |
|
Закон Шарля– |
Для данной массы газа отношение давления к температуре постоянно, если объем не меняется |
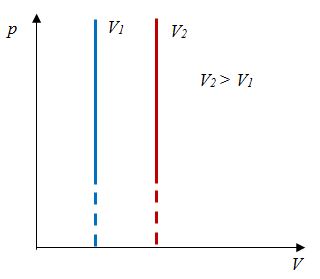 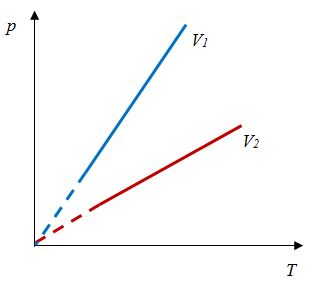 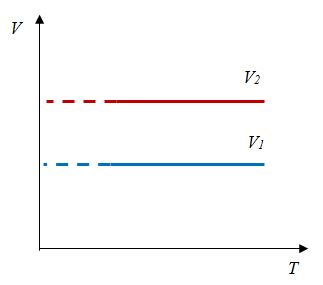 |
Графические задачи


Газовые законы


4.5
Средняя оценка: 4.5
Всего получено оценок: 380.
4.5
Средняя оценка: 4.5
Всего получено оценок: 380.
Опыты показывают, что основные макроскопичекие параметры газа (объем, температура, давление) тесно взаимосвязаны. При исследовании этой связи были открыты закономерности, названные газовыми законами. Рассмотрим кратко данную тему.
Закон Бойля-Мариотта
Исторически первым открытым газовым законом стал закон Бойля-Мариотта. В 1660 г Р. Бойль (и несколько позже Э. Мариотт) установил, что газ ведет себя подобно сжатой пружине, и увеличивает давление пропорционально уменьшению объема. Таким образом, для фиксированного количества газа при фиксированной температуре произведение давления и объема остается постоянным:
$$pV=const$$
Выполнение этого закона совершается не мгновенно. При быстром увеличении давления объем уменьшается менее, чем пропорционально давлению, но через некоторое время происходит дополнительное уменьшение объема. Позже было установлено, что происходит это потому, что при быстром сжатии газа повышается температура. Если же газ сжимать медленно, чтобы температура оставалась постоянной, то отклонений от закона не наблюдается.
Таким образом, закон Бойля-Мариотта выражает зависимость давления от объема газа при фиксированной температуре. График этой зависимости называется изотермой и в координатах $V–p$ представляет собой гиперболу, располагающуюся тем выше, чем выше температура. В других координатах изотерма является горизонтальной или вертикальной прямой.
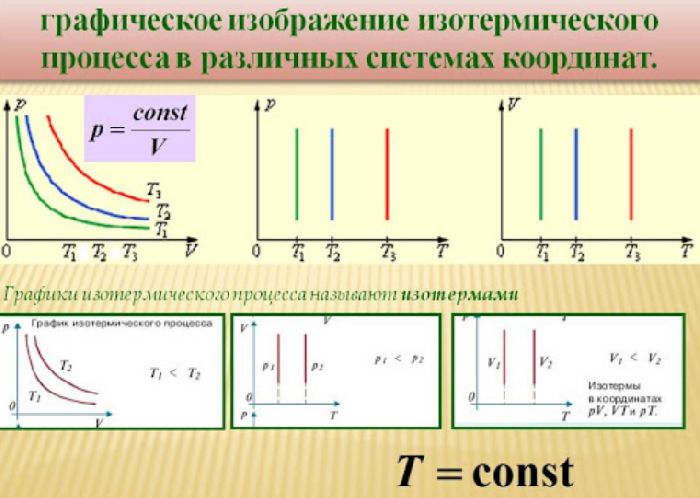
Закон Шарля
Хронологически вторым открытым газовым законом является закон, открытый Ж. Шарлем в 1787 г.
Было установлено, что давление фиксированного количества газа при фиксированном объеме изменяется прямо пропорционально его температуре. Отношение этих величин постоянно:
$${pover T}=const$$
Данный процесс называется изохорным, и его график в координатах $Т-p$ является наклонной прямой, направленной из начала координат. Прямая поднимается тем круче, чем меньше объем газа. В других координатах график изохоры является горизонтальной или вертикальной прямой.
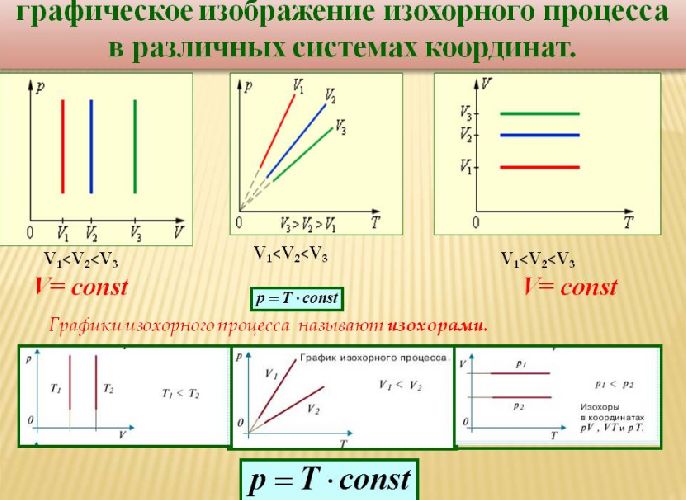
Закон Гей-Люссака
В 1802 г Ж. Гей-Люссаком был опубликован третий газовый закон, описывающий изменение состояния фиксированного количества газа при постоянном давлении. Он гласит, что объем фиксированного количества газа при постоянном давлении пропорционален температуре. Отношение этих величин постоянно:
$${Vover T}=const$$
Такой процесс был назван изобарным, и его график в координатах $Т-V$ является наклонной прямой, направленной из начала координат. Прямая поднимается тем круче, чем меньше давление газа. В других координатах график изобары является горизонтальной или вертикальной прямой.
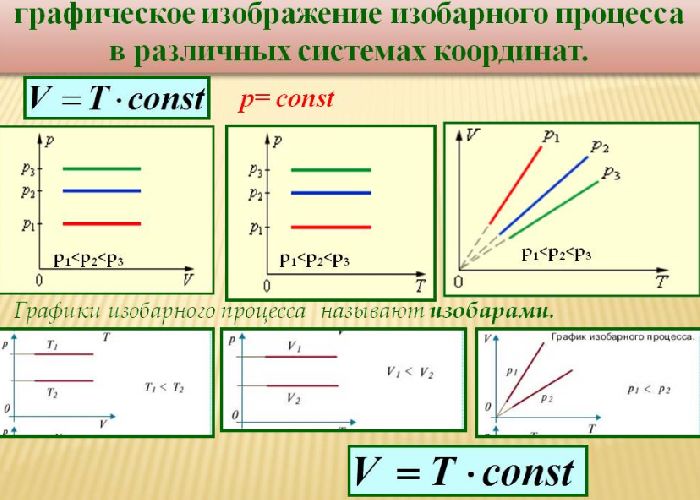
Уравнение Менделеева-Клапейрона
В 1834 г Э. Клапейрон, исследуя три перечисленных закона, и обобщая их, получил уравнение, названное его именем, и связывающее все три макроскопических параметра газа:
$${pVover T} = const$$
Это уравнение хорошо подходило для описания изменений для фиксированного количества определенного газа. Однако, константа, входящая в него, оказывалась для каждого газа разной, зависящей от исследуемого количества. Необходимо было получить более универсальную формулу.
Основой такой универсальной формулы явился закон, открытый в 1811 г. А.Авогадро. Он гласит, что равные объемы газов при равных давлениях и температурах содержат одинаковое число молекул.
В 1874 г Д. Менделеев установил, что постоянная, присутствующая в уравнении Клапейрона, прямо пропорциональна этому числу. А значит, можно ввести универсальный коэффициент пропорциональности R, физический смысл которого состоит в том, что это количества тепла, которое надо передать одному молю газа для того, чтобы нагреть его на 1К. С использованием этой универсальной газовой постоянной, уравнение приняло вид:
$$pV ={mover M}RT,$$
где:
- $p,V,T$ – макроскопические газовые параметры;
- $m$ – масса газа;
- $М$ – молярная масса газа (масса моля газа, содержащего $N_A=6×10^{23}$ молекул);
- $R$ – универсальная газовая постоянная, равная $R=8.31 {Дж over моль × К }$.
Уравнение состояния газа в таком виде связывает макроскопические термодинамические параметры идеального газа (объем, температуру, давление) с его физическими параметрами (массой и молярной массой), и называется уравнением Менделеева-Клапейрона. Основные газовые законы являются его следствием.

Что мы узнали?
Газовые законы связывают два макроскопических термодинамических параметра газа. Третий параметр, а также вид газа и его количество предполагается фиксированным. Обобщением газовых законов является уравнение Менделеева-Клапейрона, в котором термодинамические параметры связываются с физическими параметрами газа.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.5
Средняя оценка: 4.5
Всего получено оценок: 380.
А какая ваша оценка?
Уравне́ние состоя́ния идеа́льного га́за (иногда уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
,
где
Уравнение состояния идеального газа можно записать в виде:
,
где 


или в виде
,
где 


Эта форма записи носит имя уравнения (закона) Клапейрона — Менделеева.
Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную 
Менделеев обнаружил, что 


Связь с другими законами состояния идеального газа[править | править код]
В случае постоянной массы газа уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
— закон Бойля — Мариотта — Изотермический процесс.
— Закон Гей-Люссака — Изобарный процесс.
— закон Шарля (второй закон Гей-Люссака, 1808 г.) — Изохорный процесс
В форме пропорции 
С точки зрения химика этот закон может звучать несколько иначе: объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
.
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
.
- Закон Бойля — Мариотта
Закон Бойля — Мариотта
назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
где 

Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. Это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение 

См. также[править | править код]
- Совершенный газ
- Реальный газ
- Уравнение состояния реального газа
Примечания[править | править код]
Литература[править | править код]
- Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высшая школа, 2009. — 527 с. — ISBN 978-5-06-006161-1.