Содержание
- Как найти давление масла на поршни
- 2.2 Определение силы давления на поршень. Индикаторную диаграмму строим по заданной таблице значений давления в цилиндре двигателя. Таблица 4.
- 2.3. Построение графиков приведённых моментов.
- Гидравлический пресс
- Гидравлическая машина
- Определение
- Устройство
- Принцип работы
- Гидравлический пресс
- Определение
- Устройство и принцип работы
- Гидравлический тормоз
- Гидравлический домкрат
- Упражнения
- Упражнение №1
- Упражнение №2
- Упражнение №3
Как найти давление масла на поршни
Учебник Физика 7 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 страниц вышел из печати в июле 2015 г. в пятом издании. Учебник физики 7 класса рассчитан на 2 урока в неделю и содержит 6 тем курса физики, которые перечислены ниже.
 Физика 7 класс, тема 01. Физические величины (7+2 ч)
Физика 7 класс, тема 01. Физические величины (7+2 ч)
Физика. Физическая величина. Измерение физических величин.
Цена делений шкалы прибора. Погрешность прямых и косвенных измерений.
Формулы и вычисления по ним. Единицы физических величин.
Метод построения графика.  Физика 7 класс, тема 02. Масса и плотность (8+1 ч)
Физика 7 класс, тема 02. Масса и плотность (8+1 ч)
Явление тяготения и масса тела. Свойство инертности и масса тела.
Плотность вещества. Таблицы плотностей некоторых веществ.
Средняя плотность тел и их плавание.
Метод научного познания.  Физика 7 класс, тема 03. Силы вокруг нас (13+2 ч)
Физика 7 класс, тема 03. Силы вокруг нас (13+2 ч)
Сила и динамометр. Виды сил.
Уравновешенные силы и равнодействующая.
Сила тяжести и вес тела. Сила упругости и сила трения.
Закон Архимеда. Вычисление силы Архимеда.
Простые механизмы. Правило равновесия рычага.  Физика 7 класс, тема 04. Давление тел (10+0 ч)
Физика 7 класс, тема 04. Давление тел (10+0 ч)
Определение давления. Давление жидкости. Закон Паскаля. Давление газа.
Атмосферное давление. Барометр Торричелли. Барометр-анероид.
Вакуумметры. Манометры: жидкостные и деформационные.
Пневматические и гидравлические механизмы.  Физика 7 класс, тема 05. Работа и энергия (9+1 ч)
Физика 7 класс, тема 05. Работа и энергия (9+1 ч)
Механическая работа. Коэффициент полезного действия. Мощность.
Энергия. Кинетическая и потенциальная энергия.
Механическая энергия. Внутренняя энергия.
Взаимные превращения энергии.  Физика 7 класс, тема 06. Введение в термодинамику (15+2 ч)
Физика 7 класс, тема 06. Введение в термодинамику (15+2 ч)
Температура и термометры. Количество теплоты и калориметр.
Теплота плавления/кристаллизации и парообразования/конденсации.
Первый закон термодинамики. Двигатель внутреннего сгорания.
Теплота сгорания топлива и КПД тепловых двигателей.
Теплообмен. Второй закон термодинамики.

Учебник Физика 8 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 стр. вышел из печати в июле 2015 г. в четвёртом издании. Учебник физики 8 класса рассчитан на 2 урока в неделю и содержит 5 тем курса физики, которые перечислены ниже.
 Физика 8 класс, тема 07. Молекулярно-кинетическая теория (8+1 ч)
Физика 8 класс, тема 07. Молекулярно-кинетическая теория (8+1 ч)
Из истории МКТ. Частицы вещества. Движение частиц вещества.
Взаимодействие частиц вещества. Систематизирующая роль МКТ.
Кристаллические тела. Аморфные тела. Жидкие тела. Газообразные тела.
Агрегатные превращения. Насыщенный пар. Влажность воздуха.  Физика 8 класс, тема 08. Электронно-ионная теория (8+1 ч)
Физика 8 класс, тема 08. Электронно-ионная теория (8+1 ч)
Строение атомов и ионов. Электризация тел и заряд.
Объяснение электризации. Закон сохранения электрического заряда.
Электрическое поле. Электрический конденсатор. Электрический ток.
Электропроводность жидкостей, газов и полупроводников.  Физика 8 класс, тема 09. Постоянный электрический ток (13+2 ч)
Физика 8 класс, тема 09. Постоянный электрический ток (13+2 ч)
Электрическая цепь. Сила тока. Электрическое напряжение. Работа тока.
Закон Ома для участка цепи. Сопротивление соединений проводников.
Закон Джоуля-Ленца. Электронагревательные приборы.
Полупроводниковые приборы. Переменный ток.  Физика 8 класс, тема 10. Электромагнитные явления (8+1 ч)
Физика 8 класс, тема 10. Электромагнитные явления (8+1 ч)
Магнитное поле. Соленоид и электромагнит. Постоянные магниты.
Действие магнитного поля на ток. Электродвигатель на постоянном токе.
Электромагнитная индукция. Электротрансформатор. Передача электроэнергии.
Электродвигатель на переменном токе.  Физика 8 класс, тема 11. Колебательные и волновые явления (9+2 ч)
Физика 8 класс, тема 11. Колебательные и волновые явления (9+2 ч)
Период, частота и амплитуда колебаний. Нитяной и пружинный маятники.
Механические волны. Свойства механических волн. Звук.
Электромагнитные колебания. Излучение и прием электромагнитных волн.
Свойства электромагнитных волн. Принципы радиосвязи и телевидения.

Учебник Физика 9 класс Кривченко И.В., размещённый в этой рубрике, включён в федеральный перечень учебников в соответствии с ФГОС. Учебник в цветном полиграфическом исполнении с твёрдым переплетом объёмом 150 стр. вышел из печати в июле 2015 г. в третьем издании. Учебник физики 9 класса рассчитан на 2 урока в неделю и содержит 4 темы курса физики, которые перечислены ниже.
 Физика 9 класс, тема 12. Введение в кинематику (16+2 ч)
Физика 9 класс, тема 12. Введение в кинематику (16+2 ч)
Что такое кинематика. Относительность движения. Путь и перемещение.
Сложение и вычитание векторов. Проекции векторов на координатные оси.
Равномерное движение. Мгновенная скорость. Равноускоренное движение.
Графическое описание движений. Равномерное движение по окружности.  Физика 9 класс, тема 13. Введение в динамику (13+2 ч)
Физика 9 класс, тема 13. Введение в динамику (13+2 ч)
Что такое динамика. Первый, второй и третий законы Ньютона.
Законы Гука и Кулона-Амонтона. Закон всемирного тяготения.
Закон сохранения импульса. Реактивное движение.
Кинетическая энергия. Потенциальная энергия.  Физика 9 класс, тема 14. Введение в оптику (11+1 ч)
Физика 9 класс, тема 14. Введение в оптику (11+1 ч)
Источники света. Прямолинейное распространение света. Отражение света.
Зеркала. Преломление света. Линзы. Оптические приборы.
Дисперсия света и цвета тел. Фотография и полиграфия.
Корпускулярно-волновой дуализм.  Физика 9 класс, тема 15. Введение в квантовую физику (7+1 ч)
Физика 9 класс, тема 15. Введение в квантовую физику (7+1 ч)
Физика XX века. Явление радиоактивности. Регистрация частиц.
Строение атома. Характеристики атомного ядра. Ядерные реакции.
Природа и свойства радиоактивных излучений. Энергия связи ядра.
Энергия ядерных реакций. Ядерная энергетика. Физика XXI века.
Для перехода к параграфам кликайте нумерацию 01 02 03 04 05 и т.д. вверху страницы. Параграфы каждой темы курса физики снабжены интерактивными вопросами и заданиями.
Физика.ru • Клуб для учителей физики, учащихся 7-9 классов и их родителей
Источник
2.2 Определение силы давления на поршень. Индикаторную диаграмму строим по заданной таблице значений давления в цилиндре двигателя. Таблица 4.
Таблица значений давления в цилиндре двигателя
Отрезок хода поршня НВ на листе делим на 10 интервалов, дополнительно для точности построения разделим первый интервал . В каждой точке деления строим ординату диаграммы в масштабе  =10 -4 мм/Па. Максимальное давление pmax=990 кПа.
=10 -4 мм/Па. Максимальное давление pmax=990 кПа.
Для определения силы давления на поршень Fд необходимо давление умножить на площадь поршня. При построении графика силы, действующей на поршень, ординаты этого графика принимаем равными ординатам индикаторной диаграммы.  =0,018 мм/Н.
=0,018 мм/Н.
Где площадь поршня Sп= ,Sп =5,02*10 -3 м 2
,Sп =5,02*10 -3 м 2
Положительные значения силы Fд соответствуют положительному знаку работы, а отрицательные-отрицательному знаку.
2.3. Построение графиков приведённых моментов.
Суммарный приведенный момент является суммой приведенного движущего момента Mд пр и приведенного момента сопротивления Mс пр . Для определения Мд пр воспользуемся формулой Мд пр =Fд |VQB|. Сила Fд определяется по формуле Fд=
Где yF -ордината с индикаторной диаграммы, мм;  -масштаб сил, мм/Н.
-масштаб сил, мм/Н.
График строится по точкам (24 положения) для 3-го цилиндра.
Для другого цилиндра график получается путем сдвига графика на 360 o .
Для построения графика Мд пр () определяем ординаты  с шагом=30 o
с шагом=30 o
Числовые данные для построения приведены в таблице 5:
Источник
Гидравлический пресс
Насос — это не единственное устройство, принцип работы которого построен на явлении давления жидкости и газов. Большое количество гидравлических машин повсеместно используется человеком.
На данном уроке вы узнаете, что представляет из себя гидравлическая машина и гидравлический пресс, узнаете об их устройстве и принципе работы.
Гидравлическая машина
Чтобы рассмотреть устройство гидравлического пресса, сначала дадим определение гидравлической машины.
Определение
Гидравлическая машина (от греческого «гидравликос» — «водяной») — это машина, действие которой основано на законах движения и равновесия жидкостей и объясняется законом Паскаля.
Устройство
Гидравлическая машина в основе представляет собой два цилиндра разного диаметра, в каждом из которых имеется поршень (рисунок 1). Цилиндры соединены между собой трубкой и заполнены жидкостью (чаще всего минеральным маслом).
Принцип работы
Цилиндры представляют собой сообщающиеся сосуды, высота столба жидкости в них будет одинакова, пока поршни находятся в состоянии покоя.
Теперь рассмотрим ситуацию, когда на поршни действуют некоторые силы $F_1$ и $F_2$. При этом $S_1$ и $S_2$ — площади поршней. По определению давления мы уже знаем, что $p = frac$.
Тогда давление, оказываемое меньшим поршнем, определяется по формуле:
$p_1 = frac$.
А давление, оказываемое большим поршнем:
$p_2 = frac$.
Эти сосуды соединены между собой. Значит, по закону Паскаля:
$p_1 = p_2$ или
$frac = frac$.
Разделим каждую часть равенства на $F_1$ и умножим на $S_2$, чтобы получить необходимую формулу.
Сила $F_2$ больше силы $F_1$ во столько раз, во сколько раз площадь большего поршня $S_2$ больше площади меньшего $S_1$:
$frac = frac$.
Например, если площадь большого поршня $300 space см^2$, а маленького $3 space см^2$ и на него действует сила $100 space Н$, то на большой поршень будет действовать сила $10 space 000 spaceН$:
$frac<10 space 000 Н><100 space Н>=frac<300 space см^2><3 space см^2>$.
Показательное отношение $frac$ называют выигрышем в силе. Другими словами, с помощью гидравлической машины можно малой силой уравновесить большую силу.
Гидравлический пресс
Определение
Гидравлический пресс — это гидравлическая машина, служащая для сдавливания (прессования).
Гидравлические прессы (рисунок 2) эффективно работают для преобразования малой силы в большую. Они используются для спрессовывания семян при изготовлении масла, для склеивания строительных материалов, для штамповки ювелирных изделий. Современные гидравлические прессы могут развивать силу в сотни миллионов ньютонов.
Устройство и принцип работы
Рассмотрим устройство гидравлического пресса (рисунок 3).
Усложняем схему устройства гидравлической машины. Теперь над большим поршнем 2 имеется платформа, куда мы помещаем прессуемое тело 1.
С помощью малого поршня 3 мы создаем большое давление на жидкость. Оно также начинает действовать на поршень 2. Происходит это потому, что давление передается без изменения в каждую точку жидкости (закон Паскаля).
Площадь поршня 2 больше площади поршня 3. Поэтому и сила, действующая на него, будет больше (давление одинаковое). Под действием этой силы поршень 2 начинает подниматься и придавливает прессуемое тело к неподвижной верхней платформе.
Здесь же установлен манометр 4 для контроля давления жидкости и предохранительный клапан 5. Клапан автоматически открывается, когда давление превышает максимально допустимое в данном устройстве значение.
При повторяющихся движениях поршня 3 жидкость снова попадает из малого цилиндра в большой. Малый поршень поднимается и открывается клапан 6. Тогда пространство под поршнем моментально заполняется жидкостью. Когда же малый поршень 3 опускается, клапан 6 закрывается под давлением жидкости, а клапан 7 открывается. Так жидкость снова оказывается в большом сосуде.
Гидравлический тормоз
Еще одной известной разновидностью гидравлических машин является гидравлический тормоз. На данный момент практически все автомобили оснащены гидравлическими тормозами.
На рисунке 4 изображена схема автомобильного гидравлического тормоза, где 1 — тормозная педаль, 2 — цилиндр с поршнем, 3 — тормозной цилиндр, 4 — тормозные колодки, 5 — пружина, 6 — тормозной барабан. Цилиндры и трубки заполнены специальной жидкостью. Рассмотрим принцип работы этого устройства.
Водитель ногой создает давление на педаль тормоза 1. Это действие передается на поршень цилиндра с тормозной жидкостью 2. По закону Паскаля это давление передается одинаково во все тормозные цилиндры колес автомобиля. Под давлением жидкости подвижные поршни, находящиеся в тормозном устройстве 3, расходятся и прижимают тормозные колодки 4 к тормозному барабану 6 — вращение колес прекращается. Пружина 5 позволяет колодкам вернуться в исходное состояние, когда водитель убирает ногу с педали тормоза.
Гидравлический домкрат
Другое распространенное устройство — гидравлический домкрат (рисунок 5). Принцип действия домкрата идентичен принципу действия гидравлического пресса, но с помощью него можно поднимать очень тяжелые предметы.
Жидкостью здесь выступает гидравлическое масло, а также имеется нагнетательный и спускной клапаны.
Упражнения
Упражнение №1
На рисунке 6 изображена упрощенная схема гидравлического подъемника (разновидности гидравлического домкрата), где 1 — поднимаемое тело, 2 — малый поршень, 3 — клапаны, 4 — клапан для опускания груза, 5 — большой поршень. Груз какой массы можно поднять такой машиной, если известно, что площадь малого поршня $1.2 space см^2$, большого — $1440 space см^2$, а сила, действующая на малый поршень, может достигать $1000 space Н$? Трение не учитывать.
Дано:
$S_1 = 1.2 space см^2$
$S_2 = 1440 space см^2$
$F_1 = 1000 space Н$
$g = 9.8 frac<Н><кг>$
Посмотреть решение и ответ
Решение:
Гидравлический подъемник является разновидностью гидравлической машины. Поэтому мы можем использовать следующее равенство, которое мы получили на данном уроке:
$frac = frac$,
где $F_2 = gm$ — сила, с которой поднимаемое тело действует на большой поршень.
Выразим массу груза и рассчитаем ее:
$frac = frac$,
$m = frac$,
$m = frac<1000 space Н cdot 1440 см^2><9.8 frac<Н> <кг>cdot 1.2 space см^2> approx 122 space 000 space кг approx 120 space т$.
Ответ: $m = approx 120 space т$.
Упражнение №2
В гидравлическом прессе площадь малого поршня $5 space см^2$, площадь большого — $500 space см^2$. Сила, действующая на малый поршень, равна $400 space Н$, на большой — $36 space кН$. Какой выигрыш в силе дает этот пресс? Почему пресс не дает максимального (наибольшего) выигрыша в силе? Какой выигрыш в силе должен был бы давать этот пресс при отсутствии силы трения между поршнем и стенками пресса?
Дано:
$S_1 = 5 space см^2$
$S_2 = 500 space см^2$
$F_1 = 400 space Н$
$F_2 = 36 space кН = 36 space 000 space Н$
Посмотреть решение и ответ
Решение:
Рассчитаем реальный выигрыш в силе, который мы получаем при использовании данного гидравлического пресса:
$frac = frac<36 space 000 Н> <400 space Н>= 90$.
Получается, что мы имеем выигрыш в силе в 90 раз.
Но в реальной жизни при движении поршней возникает сила трения. Какой выигрыш в силе мы бы получили, если бы ее не было?
Используем соотношение площадей поршней:
$frac = frac<500 space см^2> <5 space см^2>= 100$.
Это максимальный выигрыш в силе, который бы мы получили при отсутствии силы трения между поршнями и стенками пресса.
Ответ: $frac =90$, $frac = 100$.
Упражнение №3
Можно ли создать машину, подобную гидравлической, используя вместо воды воздух? Ответ обоснуйте.
Ответ:
Гидравлические машины действуют на основе закона Паскаля. А этот закон применим не только для жидкостей, но и для газов. Поэтому, да, такую машину можно создать.
Примером подобной машины может служить пневматическая подвеска автомобиля.
Источник
Adblock
detector
Содержание:
- § 1 Гидравлическая машина
- § 2 Гидравлический пресс
- § 3 Решение задач
- § 4 Важно запомнить
§ 1 Гидравлическая машина
В этом уроке мы изучим устройство и принцип действия гидравлических машин.
В жизни человеку очень часто приходится сталкиваться с такими ситуациями, где нужно поднять груз большой массы на высоту или сжать какое-либо тело. Например, автомобилисту нужно сменить проколотое колесо. Для этого нужно приподнять автомобиль. Поднять 5 кг, 10 кг взрослому человеку не так сложно. Но поднять автомобиль? Или нужно выжать масло из семян подсолнуха, спрессовать бумагу. И вот в таких случаях на помощь приходят разные механизмы, позволяющие получить большую силу, прилагая незначительные усилия.
Одним из таких механизмов является гидравлическая машина.
Гидравлическая машина (от греческого слова гидравликос – водяной) – это машина, действие которой основано на законах движения и равновесия жидкостей. Первая гидравлическая машина была создана Паскалем, который называл ее машиной для увеличения силы.
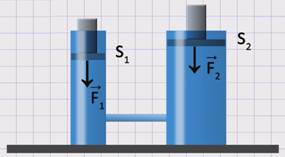
Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью (водой или маслом).
Рассмотрим принцип действия гидравлической машины. Обозначим площадь поршня в малом цилиндре S1, площадь поршня в большом цилиндре – S2, F1 и F2 – силы, действующие на поршни.
Если на поршень S1 подействовать с силой F1, то давление в малом цилиндре будет определяться по формуле:
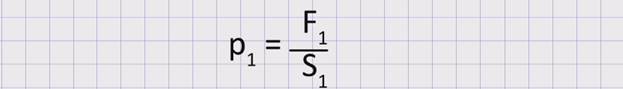
Давление в большом цилиндре:
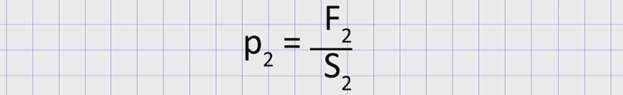
По закону Паскаля давление, производимое на жидкость или газ, передается в каждую точку по всем направлениям одинаково. Значит, давление в обоих цилиндрах будет одинаковым: p1 = p2 . Тогда можем приравнять правые части этих формул:

Читается эта формула так: сила F2, действующая на большой поршень, во столько раз больше силы F1, действующей на малый поршень, во сколько раз площадь большого поршня S2 больше площади малого поршняS1. Отношение F2 к F1показывается выигрышем в силе.
Итак, сделаем вывод. Приложив незначительное усилие F1 к малому поршню, мы можем получить во столько раз большую силу F2 на большом поршне, во сколько раз его площадь превышает площадь малого поршня.
Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.
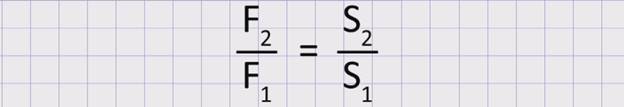
§ 2 Гидравлический пресс
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.
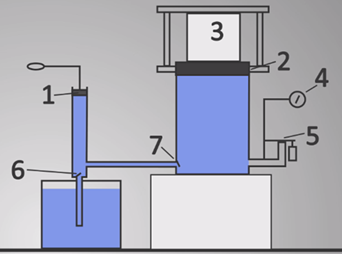
Принцип действия гидравлического пресса таков: на платформу большого поршня 2 кладется прессуемое тело 3. При помощи малого поршня 1 создается давление на жидкость, которое по закону Паскаля передается в каждую точку жидкости, заполняющей цилиндры. Так как площадь большого поршня во много раз больше площади малого, то и действующая на него сила окажется во столько же раз больше. Под действием этой силы большой поршень поднимается и сжимает тело. За значением давления, возникающего в жидкости, следят при помощи деформационного манометра 4, соединенного с предохранительным клапаном 5, который автоматически открывается при превышении допустимого значения давления. Клапаны 6 и 7 служат для перекачивания жидкости: при подъеме малого поршня 1 открывается клапан 6, и жидкость поступает в малый сосуд; при нажатии давление увеличивается, и этот клапан закрывается; открывается клапан 7, и жидкость переходит в большой сосуд.
Гидравлические прессы применяются для выжимания масла на маслобойных заводах, для прессования фанеры, картона, сена. В автомобилях используется гидравлический тормоз, в мастерских и в быту применяют гидравлический домкрат.
§ 3 Решение задач
Рассмотрим решение задачи на расчет выигрыша в силе в гидравлических машинах.

Запишем условие задачи. Нам известны масса m= 1500 кг, площадь малого поршня S1 = 10 см2 = 0, 001 м2, площадь большого поршня S2 = 0,1 м2. Найти F1.
Решение: Запишем формулу выигрыша в силе при помощи гидравлической машины:

Ответ: сила, приложенная к малому поршню,150 Н

Запишем условие задачи: F1= 200 Н, p = 400000 Па, S2 =0,04 м2. Найти показания динамометра, т.е. силу F2 = ? S1 =?

Ответ:F2 = 16 000 Н, S1 = 5 см2
§ 4 Важно запомнить
Гидравлическая машина – это машина, действие которой основано на законе Паскаля.
Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью.
Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.
Гидравлические прессы применяются для выжимания масла, для прессования фанеры, картона, сена. В автомашинах используется гидравлический тормоз, для подъема груза предназначен гидравлический домкрат.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. – М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября», 2002. – 272 с.
Использованные изображения:
Насос — это не единственное устройство, принцип работы которого построен на явлении давления жидкости и газов. Большое количество гидравлических машин повсеместно используется человеком.
На данном уроке вы узнаете, что представляет из себя гидравлическая машина и гидравлический пресс, узнаете об их устройстве и принципе работы.
Гидравлическая машина
Чтобы рассмотреть устройство гидравлического пресса, сначала дадим определение гидравлической машины.
Определение
Гидравлическая машина (от греческого «гидравликос» — «водяной») — это машина, действие которой основано на законах движения и равновесия жидкостей и объясняется законом Паскаля.
Устройство
Гидравлическая машина в основе представляет собой два цилиндра разного диаметра, в каждом из которых имеется поршень (рисунок 1). Цилиндры соединены между собой трубкой и заполнены жидкостью (чаще всего минеральным маслом).
Принцип работы
Цилиндры представляют собой сообщающиеся сосуды, высота столба жидкости в них будет одинакова, пока поршни находятся в состоянии покоя.
Теперь рассмотрим ситуацию, когда на поршни действуют некоторые силы $F_1$ и $F_2$. При этом $S_1$ и $S_2$ — площади поршней. По определению давления мы уже знаем, что $p = frac{F}{S}$.
Тогда давление, оказываемое меньшим поршнем, определяется по формуле:
$p_1 = frac{F_1}{S_1}$.
А давление, оказываемое большим поршнем:
$p_2 = frac{F_2}{S_2}$.
Эти сосуды соединены между собой. Значит, по закону Паскаля:
$p_1 = p_2$ или
$frac{F_1}{S_1} = frac{F_2}{S_2}$.
Разделим каждую часть равенства на $F_1$ и умножим на $S_2$, чтобы получить необходимую формулу.
Сила $F_2$ больше силы $F_1$ во столько раз, во сколько раз площадь большего поршня $S_2$ больше площади меньшего $S_1$:
$frac{F_2}{F_1} = frac{S_2}{S_1}$.
Например, если площадь большого поршня $300 space см^2$, а маленького $3 space см^2$ и на него действует сила $100 space Н$, то на большой поршень будет действовать сила $10 space 000 spaceН$:
$frac{10 space 000 space Н}{100 space Н}=frac{300 space см^2}{3 space см^2}$.
Показательное отношение $frac{F_2}{F_1}$ называют выигрышем в силе. Другими словами, с помощью гидравлической машины можно малой силой уравновесить большую силу.
Гидравлический пресс
Определение
Гидравлический пресс — это гидравлическая машина, служащая для сдавливания (прессования).
Гидравлические прессы (рисунок 2) эффективно работают для преобразования малой силы в большую. Они используются для спрессовывания семян при изготовлении масла, для склеивания строительных материалов, для штамповки ювелирных изделий. Современные гидравлические прессы могут развивать силу в сотни миллионов ньютонов.
Устройство и принцип работы
Рассмотрим устройство гидравлического пресса (рисунок 3).
Усложняем схему устройства гидравлической машины. Теперь над большим поршнем 2 имеется платформа, куда мы помещаем прессуемое тело 1.
С помощью малого поршня 3 мы создаем большое давление на жидкость. Оно также начинает действовать на поршень 2. Происходит это потому, что давление передается без изменения в каждую точку жидкости (закон Паскаля).
Площадь поршня 2 больше площади поршня 3. Поэтому и сила, действующая на него, будет больше (давление одинаковое). Под действием этой силы поршень 2 начинает подниматься и придавливает прессуемое тело к неподвижной верхней платформе.
Здесь же установлен манометр 4 для контроля давления жидкости и предохранительный клапан 5. Клапан автоматически открывается, когда давление превышает максимально допустимое в данном устройстве значение.
При повторяющихся движениях поршня 3 жидкость снова попадает из малого цилиндра в большой. Малый поршень поднимается и открывается клапан 6. Тогда пространство под поршнем моментально заполняется жидкостью. Когда же малый поршень 3 опускается, клапан 6 закрывается под давлением жидкости, а клапан 7 открывается. Так жидкость снова оказывается в большом сосуде.
Гидравлический тормоз
Еще одной известной разновидностью гидравлических машин является гидравлический тормоз. На данный момент практически все автомобили оснащены гидравлическими тормозами.
На рисунке 4 изображена схема автомобильного гидравлического тормоза, где 1 — тормозная педаль, 2 — цилиндр с поршнем, 3 — тормозной цилиндр, 4 — тормозные колодки, 5 — пружина, 6 — тормозной барабан. Цилиндры и трубки заполнены специальной жидкостью. Рассмотрим принцип работы этого устройства.
Водитель ногой создает давление на педаль тормоза 1. Это действие передается на поршень цилиндра с тормозной жидкостью 2. По закону Паскаля это давление передается одинаково во все тормозные цилиндры колес автомобиля. Под давлением жидкости подвижные поршни, находящиеся в тормозном устройстве 3, расходятся и прижимают тормозные колодки 4 к тормозному барабану 6 — вращение колес прекращается. Пружина 5 позволяет колодкам вернуться в исходное состояние, когда водитель убирает ногу с педали тормоза.
Гидравлический домкрат
Другое распространенное устройство — гидравлический домкрат (рисунок 5). Принцип действия домкрата идентичен принципу действия гидравлического пресса, но с помощью него можно поднимать очень тяжелые предметы.
Жидкостью здесь выступает гидравлическое масло, а также имеется нагнетательный и спускной клапаны.
Упражнения
Упражнение №1
На рисунке 6 изображена упрощенная схема гидравлического подъемника (разновидности гидравлического домкрата), где 1 — поднимаемое тело, 2 — малый поршень, 3 — клапаны, 4 — клапан для опускания груза, 5 — большой поршень. Груз какой массы можно поднять такой машиной, если известно, что площадь малого поршня $1.2 space см^2$, большого — $1440 space см^2$, а сила, действующая на малый поршень, может достигать $1000 space Н$? Трение не учитывать.
Дано:
$S_1 = 1.2 space см^2$
$S_2 = 1440 space см^2$
$F_1 = 1000 space Н$
$g = 9.8 frac{Н}{кг}$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Гидравлический подъемник является разновидностью гидравлической машины. Поэтому мы можем использовать следующее равенство, которое мы получили на данном уроке:
$frac{F_2}{F_1} = frac{S_2}{S_1}$,
где $F_2 = gm$ — сила, с которой поднимаемое тело действует на большой поршень.
Выразим массу груза и рассчитаем ее:
$frac{gm}{F_1} = frac{S_2}{S_1}$,
$m = frac{F_1 cdot S_2}{g cdot S_1}$,
$m = frac{1000 space Н cdot 1440 space см^2 cdot }{9.8 frac{Н}{кг} cdot 1.2 space см^2} approx 122 space 000 space кг approx 120 space т$.
Ответ: $m = approx 120 space т$.
Упражнение №2
В гидравлическом прессе площадь малого поршня $5 space см^2$, площадь большого — $500 space см^2$. Сила, действующая на малый поршень, равна $400 space Н$, на большой — $36 space кН$. Какой выигрыш в силе дает этот пресс? Почему пресс не дает максимального (наибольшего) выигрыша в силе? Какой выигрыш в силе должен был бы давать этот пресс при отсутствии силы трения между поршнем и стенками пресса?
Дано:
$S_1 = 5 space см^2$
$S_2 = 500 space см^2$
$F_1 = 400 space Н$
$F_2 = 36 space кН = 36 space 000 space Н$
$frac{F_2}{F_1} — ?$
$frac{S_2}{S_1} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Рассчитаем реальный выигрыш в силе, который мы получаем при использовании данного гидравлического пресса:
$frac{F_2}{F_1} = frac{36 space 000 space Н}{400 space Н} = 90$.
Получается, что мы имеем выигрыш в силе в 90 раз.
Но в реальной жизни при движении поршней возникает сила трения. Какой выигрыш в силе мы бы получили, если бы ее не было?
Используем соотношение площадей поршней:
$frac{S_2}{S_1} = frac{500 space см^2}{5 space см^2} = 100$.
Это максимальный выигрыш в силе, который бы мы получили при отсутствии силы трения между поршнями и стенками пресса.
Ответ: $frac{F_2}{F_1} =90$, $frac{S_2}{S_1} = 100$.
Упражнение №3
Можно ли создать машину, подобную гидравлической, используя вместо воды воздух? Ответ обоснуйте.
Посмотреть ответ
Скрыть
Ответ:
Гидравлические машины действуют на основе закона Паскаля. А этот закон применим не только для жидкостей, но и для газов. Поэтому, да, такую машину можно создать.
Примером подобной машины может служить пневматическая подвеска автомобиля.
Давление поршня, Гидравлический пресс
Если на жидкость действует внешнее давление, то вследствие
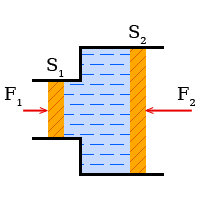
подвижности молекул это давление передается одинаково во все стороны.
В гидравлическом прессе на все поршни действует одинаковое давление. Однако, вследствие того,
что площади поршней различны, силы действующие на них, не одинаковы.
Согласно формуле:
Гидравлический пресс уравновешивает давление в ступенях.
Силы относятся друг к другу как площади поршней, т.е. как квадраты диаметров поршней:
[
p = frac{F_1}{S_1} = frac{F_2}{S_2}
]
или
[
frac{F_1}{F_2} = frac{S_1}{S_2} = frac{d_1^2}{d_2^2}
]
Это соотношение лежит в основе действия различных подъемных механизмов (домкрат, подъемник),
гидравлических тормозов, преобразователей давления и т.д.
Давление поршня, Гидравлический пресс |
стр. 500 |
|---|
|
Таблица |
||||
|
ход |
всос |
сжат |
расшир |
выпуск |
|
0 |
27193,3 |
582714 |
582714 |
27193,32 |
|
0,0014 |
0 |
446747 |
971190 |
27193,32 |
|
0,0028 |
-27193 |
388476 |
786664 |
27193,32 |
|
0,0056 |
-27193 |
291357 |
602138 |
27193,32 |
|
0,0112 |
-27193 |
174814 |
388476 |
27193,32 |
|
0,0168 |
-27193 |
106831 |
281645 |
27193,32 |
|
0,0224 |
-27193 |
66040,9 |
203950 |
27193,32 |
|
0,028 |
-27193 |
36905,2 |
145679 |
27193,32 |
|
0,0336 |
-27193 |
17481,4 |
116543 |
27193,32 |
|
0,0392 |
-27193 |
0 |
87407,1 |
27193,32 |
|
0,0448 |
-27193 |
-10683 |
62156,2 |
27193,32 |
|
0,0504 |
-27193 |
-19424 |
44674,7 |
27193,32 |
|
0,056 |
-27193 |
-27193 |
31078,1 |
27193,32 |
Отрезок
хода поршня НВ
на листе делим
на 10 интервалов, дополнительно для
точности построения разделим первый
интервал . В каждой точке деления строим
ординату диаграммы в масштабе
 =10-4
=10-4
мм/Па. Максимальное давление pmax=990
кПа.
Для определения
силы давления на поршень Fд
необходимо
давление умножить на площадь поршня.
При построении графика силы, действующей
на поршень, ординаты этого графика
принимаем равными ординатам индикаторной
диаграммы.
 =0,018
=0,018
мм/Н.
Где площадь поршня
Sп= ,Sп
,Sп
=5,02*10-3
м2
Положительные
значения силы Fд
соответствуют положительному знаку
работы, а отрицательные-отрицательному
знаку.
2.3. Построение графиков приведённых моментов.
Суммарный приведенный
момент является суммой приведенного
движущего момента Mдпр
и приведенного
момента сопротивления Mспр.
Для определения Мдпрвоспользуемся
формулой Мдпр=Fд
|VQB|.
Сила Fд
определяется по формуле Fд=
Где yF
-ордината с индикаторной диаграммы, мм;
 -масштаб
-масштаб
сил, мм/Н.
График строится
по точкам (24 положения) для 3-го цилиндра.
Для другого
цилиндра график получается путем сдвига
графика на 360o.
Для построения
графика Мдпр()
определяем ординаты
 с шагом=30o
с шагом=30o
Числовые данные
для построения приведены в таблице 5:
|
град |
Мд |
Мд правый |
|
0 |
0 |
0 |
|
30 |
68,921777 |
-2,38248116 |
|
60 |
54,185288 |
-3,79297016 |
|
90 |
22,848839 |
-3,82727898 |
|
120 |
9,1157584 |
-2,83601372 |
|
150 |
2,2623467 |
-1,44479781 |
|
180 |
0 |
0 |
|
210 |
1,4447978 |
1,238368373 |
|
240 |
2,8360137 |
1,13291121 |
|
270 |
3,827279 |
-2,46033452 |
|
300 |
3,7929702 |
-14,9009542 |
|
330 |
2,3824812 |
-36,5880423 |
|
360 |
0 |
0 |
|
390 |
-2,382481 |
68,92177653 |
|
420 |
-3,79297 |
54,18528794 |
|
450 |
-3,827279 |
22,84883856 |
|
480 |
-2,836014 |
9,115758395 |
|
510 |
-1,444798 |
2,262346746 |
|
540 |
0 |
0 |
|
570 |
1,2383684 |
1,444797814 |
|
600 |
1,1329112 |
2,836013723 |
|
630 |
-2,460335 |
3,827278978 |
|
660 |
-14,90095 |
3,792970156 |
|
690 |
-36,58804 |
2,382481164 |
|
720 |
0 |
0 |
Масштаб приведённых
моментов принимаем
 =0,79
=0,79
мм/Нм, масштаб угла поворота =24.63
=24.63
мм/рад.
Приведённый момент
сил сопротивления Мспр
= const
определяем из условия, что при
установившемся движении Aд=Ас
за цикл; Ад
пропорциональна алгебраической сумме
площадей
 (в квадратных миллиметрах) под кривой
(в квадратных миллиметрах) под кривой
Мдпр().
Тогда Мспр= ,
,
Мспр=7,1
Нм
Строим график
Мспр().
Приведённым моментом от сил тяжести
пренебрегаем, так как он мал по сравнению
с Мдпр.
Гпафик суммарного
приведённого момента М пр
пр
()
строим складывая с учётом знака ординаты
графиков Мспр()
и Мдпр().
Соседние файлы в папке 21Б
- #
04.03.201414.05 Кб47Лист2.frw
- #
04.03.2014118.53 Кб53Лист3fine.dwg
- #
04.03.20149.39 Кб49Лист3fine.frw
- #
04.03.2014163.42 Кб56Лист4fine.dwg
- #
04.03.201414.03 Кб49Лист4fine.frw
- #
